摘要:利用电磁场与分子体系的相互作用可以研究分子的物理性质及其动力学问题. 不断发展的太赫兹技术提供了能够产生亚皮秒定向强电场的太赫兹源, 其产生的强场太赫兹波拥有与分子局部电场环境相当的电场强度, 且定向电场的亚皮秒时间尺度也能覆盖众多超快物理化学反应过程. 目前太赫兹波与分子的相互作用还主要局限于共振相互作用, 即电磁波通过偶极相互作用, 使分子在不同的振转能级发生跃迁. 本文基于密度泛函理论计算和薛定谔方程的时域有限差分求解方法, 研究了强太赫兹波电场对氢分子的强场非共振作用. 结果显示, 在强场太赫兹波亚皮秒定向强电场的作用下, 氢分子将产生诱导偶极矩, 此偶极矩与外加太赫兹场作用, 引起质子概率密度分布的波动及振动能级布居数的变化. 本文基于非极性双原子分子氢气与强场太赫兹波的非共振作用, 展示了一种独特的电磁波与分子相互作用的途径, 对研究生物体非极性分子及极性较弱的分子在强太赫兹场下的动力学研究提供了方法.
关键词: 氢分子/
太赫兹波/
非共振作用/
诱导偶极矩

English Abstract

全文HTML

--> --> -->

强激光场被广泛应用于原子分子物理领域的科学研究中, 如利用强激光脉冲与分子偶极矩的各向异性极化相互作用来控制分子特别是非极性分子的排列^[1,2], 激光场中离子如Ar⁺的动力学问题^[3], 利用强场进行电离分子操作^[4]. 2000年, Trump等^[5]研究了脉宽及氢同位素效应对飞秒强场脉冲解离$ {\mathrm{H}}_{2}^{+} $, $ {\mathrm{D}}_{2}^{+} $的影响. 2002年, Rottke等^[6]基于冷靶反冲离子动量谱, 研究了氢分子在波长为795 nm, 脉宽为25 fs, 功率密度为$4\times {10}^{14}\;\mathrm{W}/{\mathrm{c}\mathrm{m}}^{2}$条件下被裂解后的相关电子和核的运动. 2007年, Kling等^[7]研究了分子解离过程中电子局域化的强场控制, 利用场的波形通过对分子引导和定位来控制分子的解离, 并推广到了复杂分子中的电子转移现象. 2014年, F?rster等^[8]研究了强激光场中氢分子的振动和排列对其电离所产生的影响.
但随着近年来太赫兹技术的发展, 人们可获得具有方向性好、时间尺度小以及幅值大等优点的亚皮秒量级的太赫兹强场^[9,10], 许多分子和物质在太赫兹频段具有独特的性质, 能够在实验中被广泛研究. 强太赫兹场已经成为未来物理化学领域研究的“智能试剂”^[11]. 目前利用导线末端的尖端以及波荡器, 人们可获得幅值达90 GV/m的单周期强太赫兹场^[12], 这样的太赫兹场, 既与分子间普遍的电场环境接近, 也能覆盖分子作用的时间尺度. 强场太赫兹波对分子的强场非共振作用的研究在多个领域开展, 如弱束缚态的解离、跨越带隙激发以及绝缘体-金属相变过程等领域^[13]. 因许多生物分子的骨架振动的本征振动频率大多位于太赫兹频段, 因此选择这样的太赫兹场更容易使得分子与太赫兹波发生互作用.
利用太赫兹场的特性来研究广泛潜在的科学现象, 如共振与非共振的现象, 为物质的非共振操控开辟了新的途径^[9,10,13]. 利用太赫兹波研究分子在太赫兹频段的一系列独有性质的研究逐渐热门. 若特定分子的振转频率处于外加场的频谱范围内, 满足相应的选择定则时, 会发生光子的吸收发射现象, 引起振动能级的跃迁. 这时分子就与太赫兹波发生共振相互作用, 从而可以利用得到的太赫兹、红外等波段的光谱来分析分子的诸多特性. 而在产生诱导偶极矩, 与太赫兹场充分地互作用, 改变分子体系的振动状态这一领域并未有研究工作涉及.
氢气是最简单的研究体系, 研究方法主要是基于量子电动力学理论测定氢分子的转动量子态^[14], 研究氢气分子的基本振动行为^[15], 测定氢气中电离能^[16]. 2000年, Saenz^[17]基于三维电场的非微扰的从头算方法, 研究发现在特定的核间距下, 氢分子的电离速率会明显增强. 2017年, Puchalski^[18]对氢分子的基态电子能量进行了相对论校正, 获得了极精确的体系能量.
氢分子是非极性分子. 一般来讲, 非极性双原子分子的振动不会改变其电偶极矩, 因此不会发生光子的吸收和发射. 所以电磁波通常不会通过偶极相互作用直接改变非极性双原子分子的振动状态. 电磁波影响非极性分子的核振动态的效果通常由产生电子激发态来间接实现, 即电磁波引起电子的能级跃迁, 使分子处于激发态, 原子核处于激发态势能面上, 核的波包在新的势能面上进行振动. ?mydke等^[19]研究了超紫外线(XUV)对氮气分子作用的短时核振动过程, 给出了激发态N₂分子的核运动的概率密度随时间的演化. Calvert等^[20]详细介绍了氢分子的核量子振动特性, 给出了氢同位素分子$ {\mathrm{D}}_{2}^{+} $波函数和对称电子态1sσ_g及反对称电子态2pσ_u的关联能量随核间距的变化, 同时, 给出了强场飞秒激光脉冲中H₂和$ {\mathrm{H}}_{2}^{+} $及其同位素变体(D₂, $ {\mathrm{D}}_{2}^{+} $, HD和HD⁺)的强场电离解离过程. 这些都是通过激发电子态的途径来实现的.
因太赫兹波的光量子能量远不能够激发分子中的电子, 故不能够与非极性的双原子分子的振动状态产生直接(偶极相互作用)或间接(电子激发态、激发态势能面)的影响. 因此本文将探讨强场太赫兹波通过诱导非极性双原子分子的电偶极矩, 直接对分子的振动状态产生影响的可能性.
本文利用量子化学计算软件ORCA^[21]的密度泛函理论计算方法, 研究强场太赫兹波对氢分子核振动态的作用. 依据氢分子在不同电场强度下的势能面以及时变场的量子力学理论, 对含时薛定谔方程进行时域有限差分法(finite-difference time-domain, FDTD)求解, 得到氢气分子的质子概率密度及各振动模式布居数的动力学演化过程. 可以探究强场太赫兹波能够在分子中产生诱导偶极矩, 从而与非极性分子发生作用的途径, 有望启发生物体非极性分子及极性较弱的分子在太赫兹场下的动力学研究方法.

2

-->

2.1.分子计算模型及氢分子的势能面扫描

首先建立如图1的分子计算模型. 1个氢分子包含2个质子和2个电子, 采用玻恩-奥本海默绝热近似, 将原子核的运动与电子的运动进行分离, 引入相对坐标及折合质量, 氢分子的振动可以简化为一维振动问题, 描述原子核振动的定态薛定谔方程为
图 1 氢分子的计算模型(球体表示氢原子), 两个氢核的连线平行于z轴
Figure1. Calculation model of hydrogen molecules (spheres represent hydrogen atoms), two hydrogen nuclei are parallel to the z axis.

$ \left[ { - \frac{{{\hbar ^2}}}{{2M}}\frac{{{{\text{d}}^2}}}{{{\text{d}}{r^2}}} + V({\boldsymbol{r}})} \right]\varphi ({\boldsymbol{r}}) = E\varphi ({\boldsymbol{r}}){, } $

其中$M = \dfrac{{{M_1}{M_2}}}{{{M_1} + {M_2}}} = \dfrac{m}{2}$, $ {\boldsymbol{r}} = {{\boldsymbol{r}}_1} - {{\boldsymbol{r}}_2} $, M为折合质量, E为能量本征值, V为势能函数, 此势函数能够由势能面扫描得到. 特定势能面决定了质子的本征波函数和本征能量. 利用时域有限差分方法, 将(1)式以一维的情况写成差分形式^[22].

$\begin{split} &- \frac{{{\hbar ^2}}}{{2m}}\frac{\psi (z + \Delta z) - 2\psi (z) + \psi (z - \Delta z)}{{\Delta {z^2}}} + V(z)\psi (z) \\&= E\psi (z),\\[-10pt] \end{split}$

求解此方程可以得到本征值能量E与本征波函数$\psi $^[23], 由此获得质子振动基态以及更高能态下的粒子的空间概率密度分布.
本文有关氢气分子结构优化, 势能面的扫描等所有关于密度泛函的计算都是基于软件ORCA完成的, 版本是4.2.0^[24]. 首先对氢分子结构进行优化, 使用的泛函为B3LYP^[25], 基组为def2-QZVPP^[26], 得到体系最稳定的结构, 键长为0.75 ?. 扫描2个质子之间的距离得到氢分子的势能面, 并利用立方样条插值法对获得的势能曲线进行平滑处理. 氢分子势能面扫描所使用的基组仍是def2-QZVPP, 泛函则使用双杂化泛函PWPB95^[27], 结合D4色散校正^[28,29]. 使用经过色散校正的双杂化泛函可以更精确地计算出两个氢原子之间的弱相互作用.
2 -->

2.2.时域有限差分法求解含时薛定谔方程

含时薛定谔方程的表达式为

$ {\text{i}}\hbar \frac{\partial }{{\partial t}}\psi ({\boldsymbol{r}},t) = H\psi ({\boldsymbol{r}},t), $

其中$\hbar$是约化普朗克常数, $\psi ({\boldsymbol{r}}, t)$是质子的波函数.
如果氢分子体系处于小振动状态, 那么振动与转动自由度的耦合部分可以不予考虑^[30]. 对体系施加随时间变化的电场, 质子的波函数将随时间发生变化. 这时, 系统总的哈密顿量可分为时变和非时变两部分^[31]:

$ H(t) = V(t) + {H_0}, $

其中时变部分$V(t)$代表与外场进行相互作用的部分, 非时变部分${H_0}$代表系统自身固有哈密顿量, 包括原子核以及电子的势能和动能^[31].
当施加的外场为时变场时, 哈密顿量中时变部分可写为$V(t) = - \mu E(t)$^[31], 其中$\mu $是系统中的电偶极矩, $E(t)$为外加电场. 外加电场的变化引起体系的哈密顿量的变化, 本文将基于密度泛函理论直接求解外电场作用下氢分子体系的能量.
本文利用太赫兹高斯脉冲电场研究对氢分子的作用, 高斯脉冲的表达式为

$ E(t) = {E_0}\exp \Big[ { - 2\ln 2{{\left( {\frac{t}{\sigma }} \right)}^2}} \Big], $

其中${E_0}$是太赫兹高斯脉冲电场的幅值, $\sigma $是脉冲的强度半高宽值. 氢分子的氢核的间距在埃量级, 而强场太赫兹波的波包尺度远大于这个尺度, 固可认为在相互作用过程中分子处于强度变化的均匀电场中.
由密度泛函理论计算得到的势能面与电场的时域波形共同决定了时变的势能函数与哈密顿量, 将此哈密顿量代入含时薛定谔方程, 利用时域有限差分法, 可以获得氢分子体系在外加强场太赫兹波作用下的时间演化过程.
利用速度Verlet迭代算法求解波函数随时间的演化^[32]:

$ \psi (z,t + \Delta t) = \psi (z,t) + v(t)\Delta t + \frac{{{{(\Delta t)}^2}}}{2}\alpha (t), $

$ v(t + \Delta t) = v(t) + \frac{{\Delta t}}{2}[\alpha (t) + \alpha (t + \Delta t)], $

其中$v(t)$和$\alpha (t)$分别为波函数对时间的一阶、二阶偏导数. 选取合适的空间步长$\Delta z = $0.005 ?以及空间步长$ \Delta t = 1\;{\text{as}} $, 使得迭代求解的结果收敛.

2

-->

3.1.静电场下氢分子的势能面

无外加电场的情形时. 经势能面扫描得到的氢分子的势能面曲线、质子振动基态及更高振动能级下的概率密度分布如图2所示. 黑色曲线代表氢分子的势能面曲线, 红色曲线表示的零点振动能为534.2 meV, 与实验值接近, 故本文对氢分子振动问题的一维近似的方法是合理的. 不同颜色的曲线表示基态及更高振动能级的氢核概率密度分布. 随着能级的增加, 概率密度分布曲线的峰数目不断增加, 同时z轴方向概率的分布区间增大, 这反映了质子位置的不确定性范围增加.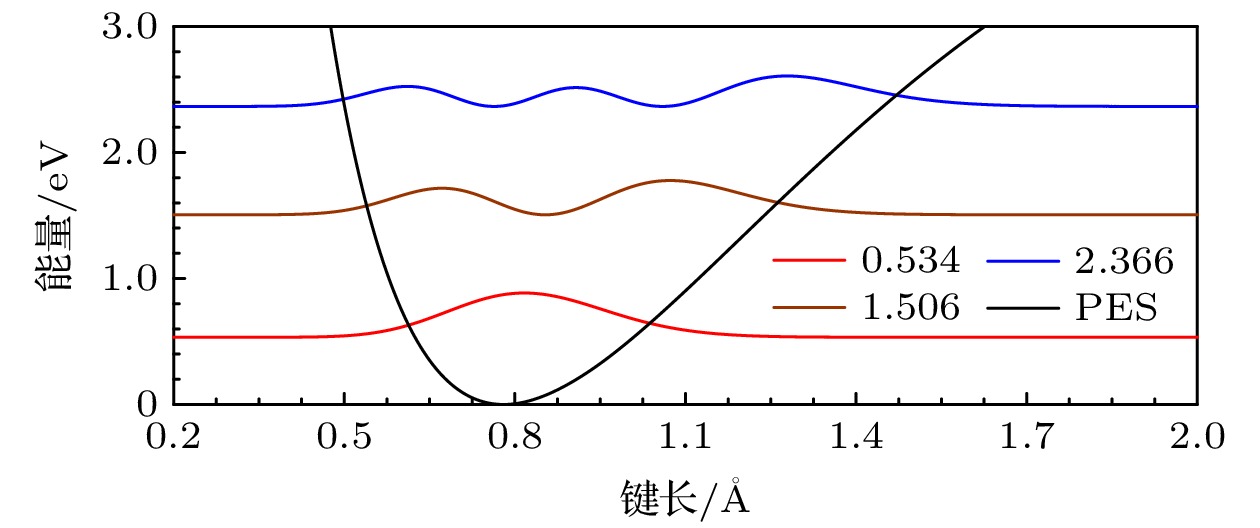
图 2 无外加电场时氢分子势能面(黑色曲线)及各能级概率密度分布曲线(彩色曲线), 氢分子的前3个本征振动模式由3条彩色曲线表示, 图例的数字代表氢分子每个本征模的能量E, 这里将势能面最低点设置为0
Figure2. Without external electric field, the potential energy surface of hydrogen molecule (black curve) and the probability density distribution curve of each energy level (color curves). The first three eigen vibration modes of hydrogen molecule are represented by three color curves, the number in the legend represents the energy of each eigenmode of the hydrogen molecule, and the lowest point of potential energy surface is set to 0.

对氢分子体系施加不同场强的z向静电场, 并进行势能面扫描, 得到如图3所示的氢分子势能面. 随着外加电场的场强从0逐渐增大, 势阱逐渐变宽. 当外加电场的强度增大至45 GV/m附近时, 最小势能点的位置会逐渐发生偏转, 新的最小势能点位置出现在2.8 ?附近.
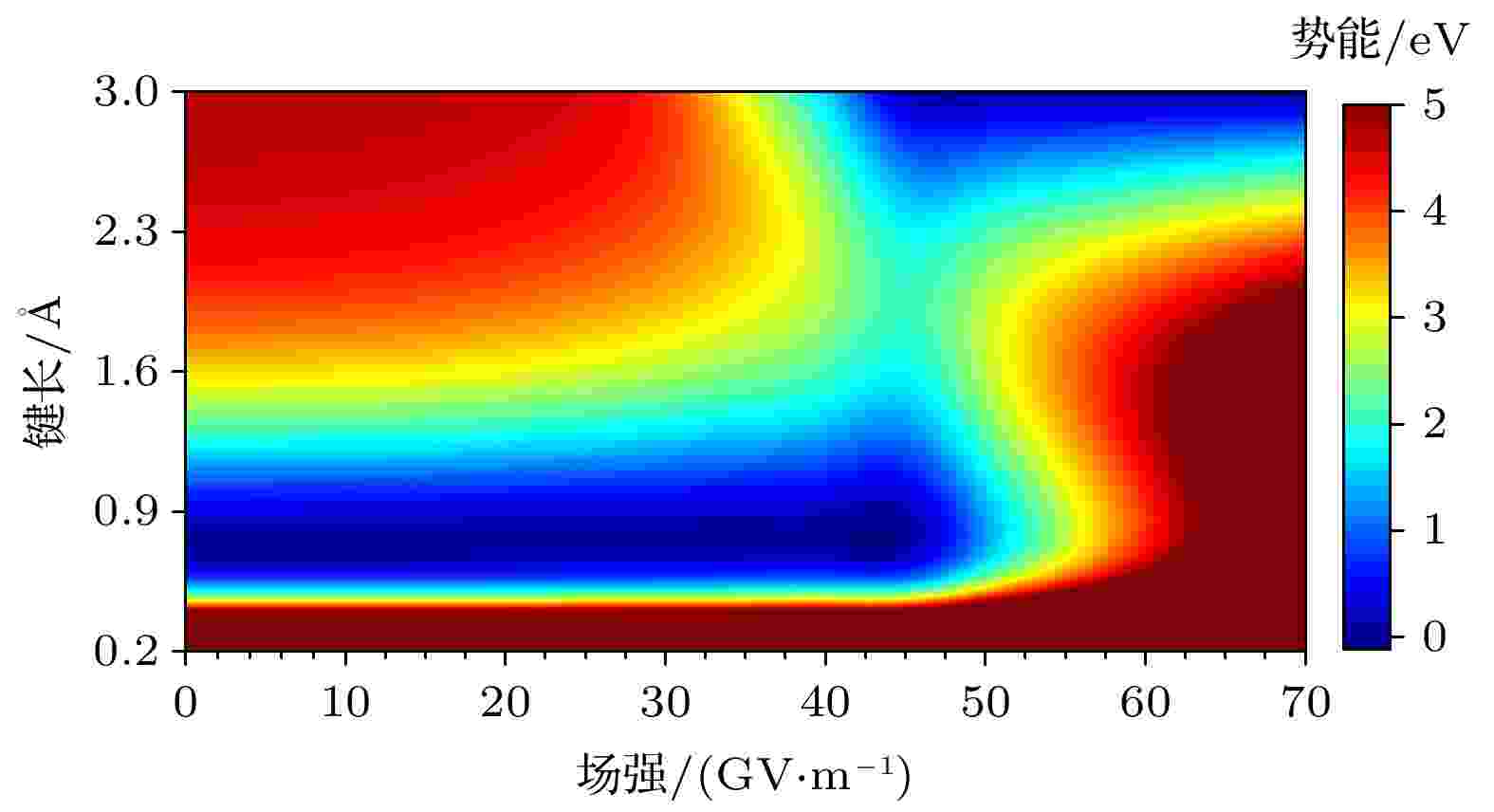图 3 氢分子的势能面随外加电场强度与键长的变化图. 这幅图是用三次样条插值方法绘制, 颜色块代表能量, 单位是eV. 在电场强度增加至45 GV/m附近时, 最小势能点发生移动, 新的最小势能点出现在2.8 ?附近. 为了更清楚地展示势能面, 大于5 eV的体系势能用深红色表示
Figure3. Variation of potential energy surface of hydrogen molecule with applied electric field intensity and bond length. This map is drawn by cubic spline interpolation method. The color block represents energy in eV. When the electric field intensity increases to 45 GV/m, the minimum potential energy point moves, and the new minimum energy point appears near 2.8 ?. In order to show the potential energy surface more clearly, the potential energy of the system greater than 5 eV is expressed in dark red.

2 -->

3.2.强场太赫兹波对氢分子振动态的作用

为模拟施加在氢分子体系中的太赫兹场波形, 考虑表达式(5)的太赫兹高斯脉冲场, 计算所用的4个太赫兹频段的脉冲场如图4所示, 脉冲中心设置在0.4 ps, 幅值有60及35 GV/m两种, 脉宽有20及90 fs两种. 幅值相同的两种脉宽的脉冲场经傅里叶变换的频谱图如图5所示. 功率分别集中在0—15 THz以及0—3 THz频谱范围内. 以下将利用这些太赫兹脉冲场作用氢分子体系来探索产生诱导偶极矩, 发生非共振作用从而引起振动能级改变的可能性.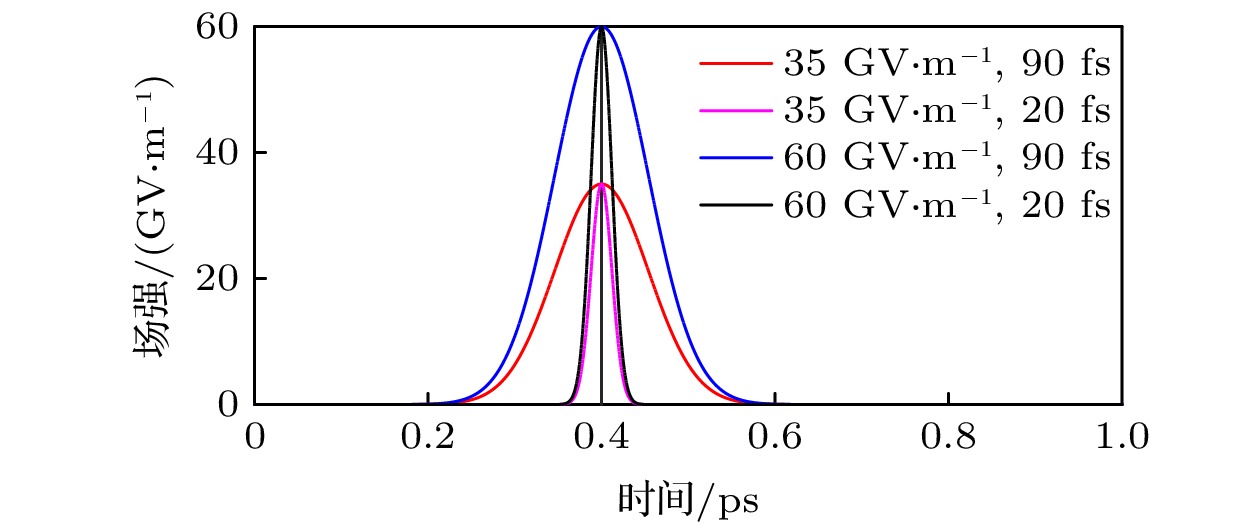
图 4 本文计算所使用的4个太赫兹高斯脉冲场的波形图, 幅值分别为35 GV/m (红色、紫色线)和60 GV/m (蓝色、黑色线), 脉宽分别为90 fs (红色、蓝色线)和20 fs (紫色、黑色线)
Figure4. Waveforms of four THz pulse fields are calculated, the amplitudes are 35 GV/m (red, purple lines), 60 GV/m (blue, black lines), pulse width are 90 fs (red, blue lines), 20 fs (purple, black lines).

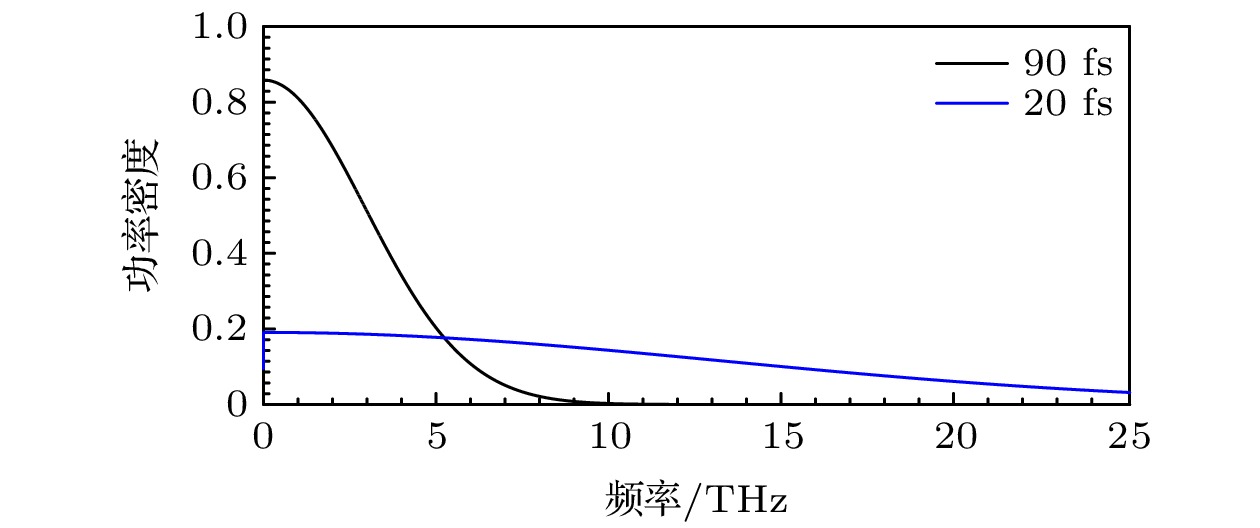图 5 脉宽为90与20 fs的太赫兹脉冲波经傅里叶变换后的频谱图, 纵轴代表归一化的功率密度
Figure5. Spectrum of THz pulse waves with 90 fs and 20 fs pulse width after fast Fourier transform. The longitudinal axis represents normalized power density.

考虑幅值为35 GV/m的太赫兹强场对氢分子振动的影响, 利用时域有限差分法, 得到随时间演化的氢分子的质子概率密度分布图(图6)及各振动能级的布居数图(图7). 由质子的概率密度分布图可看出, 两者在场作用稳定时后续均无明显的振动, 振动能级布居数几乎不变, 图中各能态布居数总和表示所有能态的占比和, 其值为1表示薛定谔方程的FDTD计算结果是收敛的.
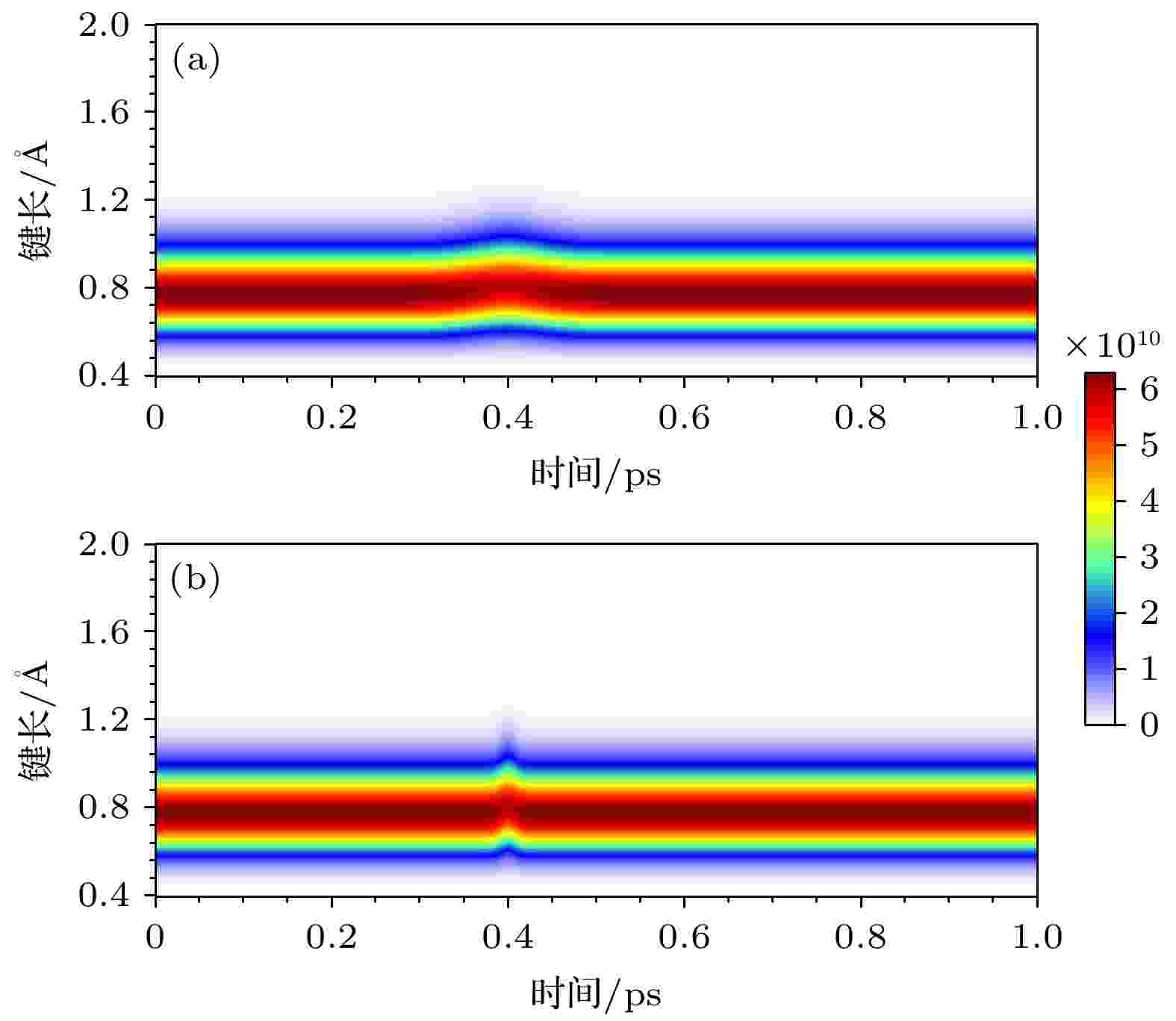图 6 氢分子在幅值为35 GV/m的z方向高斯定向强场作用下质子概率密度分布的演化图, 施加的高斯脉冲电场的脉宽分别为(a) 90 fs与(b) 20 fs, 高斯脉冲中心设置在0.4 ps, 颜色条代表质子概率密度
Figure6. Evolution diagram of proton probability density distribution of hydrogen molecule under the action of Gaussian directional intense field in z direction with amplitude of 35 GV/m. The pulse widths of applied Gaussian pulse electric field are (a) 90 fs and (b) 20 fs, respectively. The Gaussian pulse center is set at 0.4 ps, and the color strip represents the proton probability density.

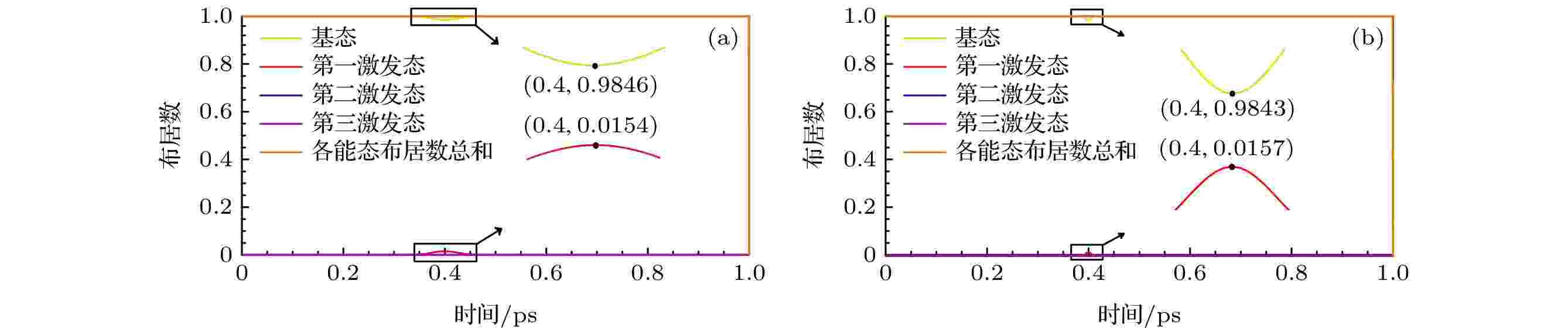图 7 氢分子在幅值为35 GV/m的z方向高斯定向强场作用下能级布居数分布的演化图, 施加的高斯脉冲电场的脉宽分别为(a) 90 fs与(b) 20 fs, 高斯脉冲中心设置在0.4 ps, 不同颜色的曲线代表不同能级的布居数
Figure7. Evolution diagram of the energy level population distribution of hydrogen molecule under the action of the Gaussian directional intense field in the z direction with the amplitude of 35 GV/m. The pulse widths of the applied Gaussian pulse electric field are (a) 90 fs and (b) 20 fs, respectively. The Gaussian pulse center is set at 0.4 ps. Curves of different colors represent populations of different energy levels.

增大太赫兹场幅值至60 GV/m, 且保持两种频率不变, 可得另外两组随时间演化的氢分子的质子概率密度图(图8)及各振动能级的布居数图(图9), 由质子的概率密度分布图可以看出, 脉宽为90 fs的太赫兹场作用稳定时, 后续无明显的振动. 而脉宽为20 fs时, 后续出现了较为稳定的波动, 在振动能级布居数图中, 稳定时基态的占比不再是1, 高能级出现且各占比稳定. 而氢分子的基态振动频率的实验值为132 THz^[33], 此频率远在90及20 fs的太赫兹高斯脉冲频谱图覆盖范围外, 但振动能级发生更明显的改变. 说明此时在太赫兹场作用下, 体系中出现诱导偶极矩, 诱导偶极矩与太赫兹场发生了非共振作用, 使原有的振动能级改变.
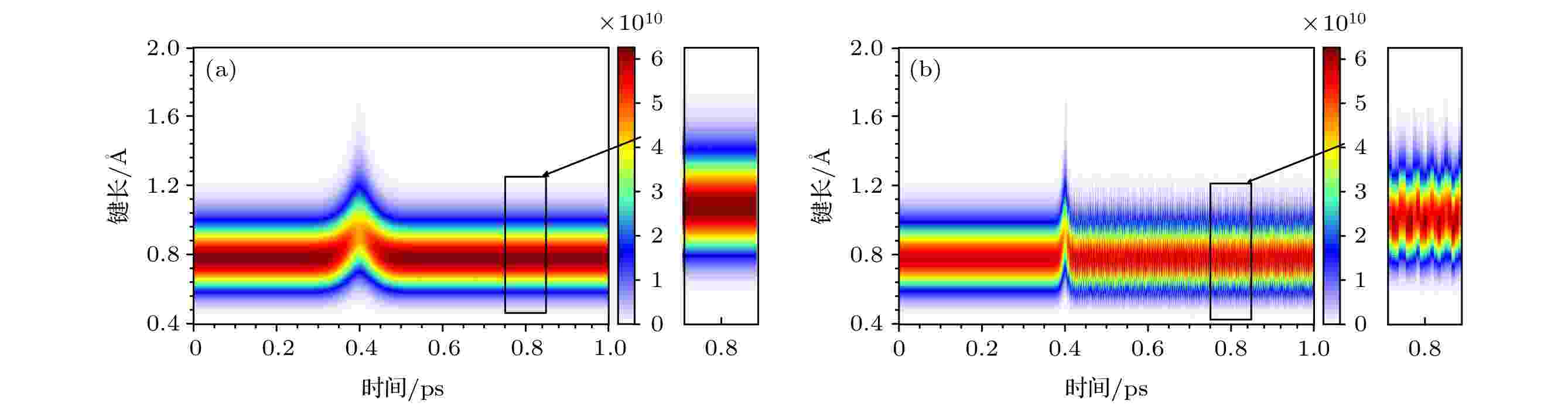图 8 氢分子在幅值为60 GV/m的z方向高斯定向强场作用下质子概率密度分布的演化图, 施加的高斯脉冲电场的脉宽分别为(a) 90 fs与(b) 20 fs, 高斯脉冲中心设置在0.4 ps, 颜色条代表质子概率密度
Figure8. Evolution diagram of proton probability density distribution of hydrogen molecule under the action of Gaussian directional intense field in z direction with amplitude of 60 GV/m. The pulse widths of applied Gaussian pulse electric field are (a) 90 fs and (b) 20 fs, respectively. The Gaussian pulse center is set at 0.4 ps, and the color strip represents the proton probability density.

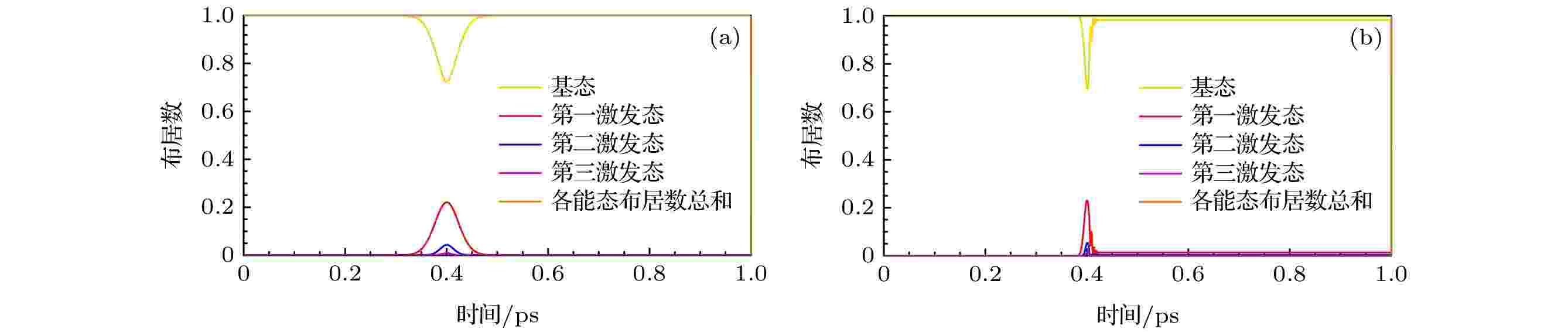图 9 氢分子在幅值为60 GV/m的z方向高斯定向强场作用下能级布居数分布的演化图, 施加的高斯脉冲电场的脉宽分别为(a) 90 fs与(b) 20 fs, 高斯脉冲中心设置在0.4 ps, 不同颜色的曲线代表不同能级的布居数
Figure9. Evolution diagram of the energy level population distribution of hydrogen molecule under the action of the Gaussian directional strong field in the z direction with the amplitude of 60 GV/m. The pulse widths of the applied Gaussian pulse electric field are (a) 90 fs and (b) 20 fs, respectively. The Gaussian pulse center is set at 0.4 ps. Curves of different colors represent populations of different energy levels

本文基于密度泛函理论以及含时薛定谔方程的求解, 研究了强太赫兹场作用下氢分子的核振动动力学. 对比无外场以及施加静电场和强太赫兹高斯脉冲场情形, 结果显示当太赫兹波电场足够强时, 太赫兹波电场会促进氢分子体系诱导偶极矩的产生, 此偶极矩能够与太赫兹波发生作用, 改变分子振动能级的布居数, 质子概率密度出现波动. 随着外加电场的逐渐增大, 体系的势能面逐渐转变, 因此太赫兹脉冲场存在一个约45 GV/m的电场阈值. 当施加太赫兹场的电场幅值接近这个阈值, 且具有较窄的脉宽时, 非共振作用的现象将会明显地显现出来. 强场太赫兹波与分子的非共振作用提供了一种独特的电磁波与分子作用的途径, 对非极性分子, 强场太赫兹波能够促进分子中诱导偶极矩的产生, 从而与太赫兹波发生非共振作用, 引起振动能级的变化.
氢气分子体系是最简单的非极性双原子分子体系, 但目前来看, 其本征振动频率为132 THz, 偏离太赫兹频段, 这也是太赫兹场与氢分子作用较微弱的原因. 可以预见, 在具有更重的原子核的分子体系, 如氩原子分子等, 强场太赫兹波将在更小的场强下, 对分子的振动产生显著作用. 本文展示的这种强场非共振作用的过程, 有望启发相关非极性分子及极性较弱的分子在太赫兹场下的动力学研究.
在后续的研究中, 会探讨太赫兹场足够大时, 体系发生电离现象的可能性及所需场的大小. 考虑氢分子体系发生强场电离现象, 则需要在时域有限差分算法中设置开放边界条件, 计算氢核的电离概率.