摘要: 量子纠缠是量子信息处理和量子计算的基本资源, 简单而高效地制备纠缠态始终是****们研究的热点问题之一. 作为量子信息编码理想载体之一的中性里德伯原子, 以其独特的优势在纠缠态制备领域占有一席之地. 本文将四能级倒“Y”型结构的里德伯原子系综放置于里德伯阻塞球内部使之形成超级原子, 在弱腔场近似下将量子信息编码在超级原子的有效能级上, 结合量子Zeno 动力学和绝热捷径的方法, 简单有效地制备了三粒子单重态. 此外, 本方案考虑了退相干因素(包括腔的衰减和超级原子的自发辐射)对单重态保真度的影响. 数值模拟结果表明, 本方案不需要对系统演化时间进行精确的控制就可以得到很高的保真度, 并且单重态的保真度对退相干因素是比较鲁棒的.
关键词: 超级原子 /
单重态 /
绝热捷径 English Abstract Fast generation of three-atom singlet state with Rydberg superatom Ji Yan-Qiang 1 ,Wang Jie 1 ,Liu Ying-Li 2 ,Zhang Da-Wei 3 ,Xiao Rui-Jie 1 ,Dong Li 1 ,Xiu Xiao-Ming 1 1.College of Physical Science and Technology, Bohai University, Jinzhou 121013, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11947078, 11674037, 11704042), the Scientific Research Starting Foundation for Doctors of Liaoning Province, China (Grant No. 2020-BS-234), and the Revitalization Talents Program of Liaoning Province, China (Grant No. XLYC1807206)Received Date: 04 November 2020Accepted Date: 04 February 2021Available Online: 07 June 2021Published Online: 20 June 2021Abstract: Quantum entanglement is a basic resource of quantum information processing and quantum computation. The simple and efficient generation of entangled states is always one of the hot research topics. As one of the ideal carriers of quantum information encoding, neutral Rydberg atom occupies a place in the field of generation of entangled state with its unique advantages. For example, Rydberg atom has a large volume and is easily ionized by an external electric field, so it is very sensitive to the change in the external electric field. Therefore, the interaction strength between Rydberg atoms can be changed by altering the external electric field. Rydberg state is a highly excited state, but its radiation attenuation is very small: the radiation lifetime can reach a millisecond level or even longer. The distance between the atomic kernel and the outermost electron is relatively long, and the electric dipole moment is very large. In this paper, the four-level inverted “Y”-type Rydberg atomic system is introduced into the Rydberg blocking ball to form a superatom, and the quantum information is encoded on the effective energy level of the superatom under the condition of weak cavity field. We construct shortcuts to adiabatic passage in a three-superatom system. Combined with quantum Zeno dynamics and shortcuts to adiabatic passage, the three-particle singlet state is simply and effectively generated. In addition, the influence of decoherence factors (including cavity decay and spontaneous emission of superatoms) on the fidelity is considered in this scheme. Numerical simulation results show that the proposed scheme can obtain high fidelity without precisely controlling the evolution time, and the fidelity of singlet state is robust to decoherence factors, since no cavity-photon population is involved in the whole process because of the quantum Zeno dynamics.Keywords: superatom /singlet state /shortcuts to adiabatic passage 全文HTML --> --> --> 1.引 言 量子纠缠体现了多个系统之间的非定域非经典的关联特性, 这种特性使量子纠缠成为了量子信息科学中的基本资源. 因此, 量子纠缠被广泛地应用在了量子信息处理任务中. 最常见的量子纠缠态有Bell态、GHZ态以及W态等. 不同的纠缠态有着各自的优点, 例如, GHZ态是最大纠缠态并且能够最大程度地违背Bell不等式; 对于一个N 粒子W态, 其任意一个粒子被测量之后, 剩下的粒子会以$ (N-1)/N $ 的概率仍然保持纠缠的特性, 也就是说W态的纠缠特性对于量子比特的丢失具有很好的鲁棒性. 在2002年, Cabello[1 ] 提出了一种新型纠缠态—N 粒子N 能级单重态. 这种纠缠态可以表示为$ \epsilon_{n_{1},\; \cdots, \;n_{N}} $ 表示列维-奇维塔符号, $ \{n_{l}\} $ 表示排列, $ |q_{n_{l}}\rangle $ 表示一个量子比特的基矢. 这类纠缠态不仅违反了Bell不等式[2 ] , 而且还可以构建无消相干子空间, 用于抵抗集体的退相干[3 ] , 因此, 单重态成为了量子秘密共享、测谎技术等的关键资源[1 ,4 ] . 近年来, ****们已经提出了一些理论方案用于制备单重态[5 -10 ] . 例如, Jin等[6 ] 在腔量子电动力学系统中基于原子-腔共振相互作用制备了单重态, 但是该方案中需要三个原子依次通过三个不同的腔, 因此, 单重态的保真度对腔的衰减比较敏感; Lin等[7 ] 的方案中由于没有涉及到腔中光子的布居, 因此对腔的衰减并不敏感, 但是当考虑到原子的自发辐射和腔的衰减时, 方案的成功概率将变成概率性的; Shao等[8 ] 利用量子Zeno动力学将两原子单重态转化成三原子单重态并将方案进行了拓展, 但是在转化过程中需要精确地控制系统的演化时间. 此外, 在大部分的方案中, ****们都利用了原子的激发态进行量子信息的编码, 而激发态的衰减往往会对方案的实现造成一定的影响.[11 -13 ] . 2009年的两组实验分别证实了相距4 μm[14 ] 和10 μm[15 ] 的两个独立里德伯原子之间存在偶极阻塞效应. 然而, 利用同时驱动的失谐补偿法[16 ,17 ] 、分步驱动的失谐补偿法[18 ] 以及同时驱动的幅值调制法[19 -21 ] , 可以实现两个基态和两个里德伯态之间的同时跃迁, 即里德伯反阻塞效应. 如今, 里德伯原子已广泛地应用在了量子信息处理任务中[16 -29 ] .n 个里德伯原子的系综研究仍然是个挑战, 这是因为随着系综中原子数的增加, 系综的维度将会指数式地增加. 幸运的是, 当里德伯原子系综位于阻塞球范围内的时候, 系综表现出的行为就像是一个多能级的系统, 即超级原子. 此时, 超级原子的基态和激发态之间的跃迁与场的耦合强度将会增加$ \sqrt{n} $ 倍[30 ,31 ] . 这些特色使超级原子成为了量子模拟的基本模块[32 -39 ] . 例如, Lukin等[32 ] 提出了一种方案用于操作存储于系综集体态上面的量子信息并制备了可扩展的量子逻辑门. Beterov等[38 ] 基于里德伯超级原子数值模拟了单量子比特和双量子比特量子态的量子层析. Paris-Mandoki等[39 ] 实现了自由空间中的单个里德伯超级原子和传播光场的相干耦合.$ \sqrt{n} $ 倍, 在一定程度上可以降低实验的要求; 3)在里德伯原子中, 一般只能利用里德伯反阻塞效应才能使每个里德伯原子都处于里德伯态, 但是实现里德伯反阻塞效应的要求比较高, 然而在里德伯超级原子中却没有这种限制; 4)利用量子Zeno动力学[40 -44 ] 将系统的演化限制在量子Zeno子空间中, 有效降低了腔衰减对方案保真度的影响; 5) 利用绝热捷径的方法有效降低了系统的演化时间.一 节为引言; 第二 节利用里德伯超级原子制备了三粒子单重态, 介绍了该系统的理论模型以及制备过程; 第三 节进行了数值分析模拟, 对绝热捷径方法和绝热近似方法所需要的时间进行了对比, 讨论了腔的衰减和超级原子的自发辐射对单重态保真度的影响; 第四 节为结论.2.利用里德伯超级原子快速制备三粒子单重态 22.1.理论模型 2.1.理论模型 考虑一个四能级的$ ^{87}{\rm{Rb}} $ 原子, 如图1(a) 所示, 四个态$ |g\rangle $ , $ |m\rangle $ , $ |e\rangle $ 和$ |r\rangle $ 分别对应于能级$|5{\rm{S}}_{1/2}, $ $ F \!= \!2, m_{\rm{F}} = 2\rangle$ , $ |5{\rm{S}}_{1/2}, F = 1, m_{\rm{F}} = 1\rangle $ , $|5{\rm{P}}_{3/2}, F = 2, $ $ m_{\rm{F}} = 3\rangle$ 和$ |60{\rm{S}}_{1/2}, F = 2\rangle $ . 其中$ |g\rangle $ ($ |m\rangle $ )态与$ |e\rangle $ 态之间的跃迁和量子化腔场的左(右)圆极化模式耦合, 耦合强度为$ g_{a} $ ($ g_{b} $ ). $ |e\rangle $ 态与$ |r\rangle $ 态之间的跃迁和经典激光场耦合, 拉比频率为Ω . $ v_{\rm{vdW}} $ 表示处于里德伯态的两个原子之间的范德瓦耳斯相互作用, 其中$ v_{\rm{vdW}} = \hbar C_{6}/R^{6} $ , $ C_{6} $ 表示范德瓦耳斯相互作用系数, R 表示相互作用距离. Δ 表示相应的单光子失谐参数. 在旋波近似下, 可以用下面的哈密顿量来描述多个里德伯原子和量子化腔场以及经典激光场之间的相互作用:图 1 (a)里德伯原子的能级结构; (b)里德伯超级原子的能级结构; (c)弱腔场极限下的里德伯超级原子能级结构Figure1. (a) Energy levels configuration for Rydberg atom; (b) energy levels configuration for Rydberg superatom; (c) effective energy levels configuration for the superatom in the weak cavity field limit.$ a^{\dagger} $ 和$ b^{\dagger} $ 分别表示a 模腔场和b 模腔场的产生算符.$ |r\rangle $ . 因此, 使用超级原子来表示处于阻塞区域中的里德伯原子系综. 原子系综的$ (n+1)^{2} $ 个集体态可以表示为$ |R^{(j)}\rangle $ , 由于里德伯阻塞效应, 在超级原子中最多只有一个里德伯原子能够被激发到里德伯态, 因此j 只能取1. 每个超级原子之间的偶极-偶极相互作用非常小, 可以忽略. 假设在超级原子中最多只有一个原子可以被激发到$ |e\rangle $ 态, 这种假设在弱腔场极限下是合理的, 此时, 这些集体态只有$ |G\rangle $ , $|M^{(1)}\rangle \! =\! \displaystyle\sum\nolimits_{j = 1}^{n}|g_{1}, \;g_{2}, \; \cdots, \; m_{j}, \; \cdots, \; g_{n}\rangle/\sqrt{n}$ , $|E^{(1)}\rangle = \displaystyle\sum\nolimits_{j = 1}^{n}|g_{1}, g_{2}, \cdot\cdot\cdot, e_{j}, \cdots, g_{n}\rangle/\sqrt{n}$ , $|R^{(1)}\rangle = $ $ \displaystyle\sum\nolimits_{j = 1}^{n} |g_{1}, g_{2}, \cdot\cdot\cdot, r_{j}, \cdots, g_{n}\rangle/\sqrt{n}$ , ${\cdots}$ (如图1(b) ). 所以可以使用四能级的倒“Y”结构来描述这个超级原子, 这四个能级分别对应集体态$ |G\rangle $ , $ |M^{(1)}\rangle $ , $ |E^{(1)}\rangle $ 和$ |R^{(1)}\rangle $ (如图1(c) ).图2 所示, 相互作用哈密顿量可以表示为图 2 腔与三个超级原子相互作用示意图Figure2. Schematic illustration of the interaction between the a cavity and three superatoms.$ n_{i} $ 表示第i 个超级原子中的里德伯原子个数, $ \sqrt{n}g_{ai} $ ($ g_{bi} $ )表示第i 个超级原子与a (b )模腔场的耦合强度. 本文中已假设$ n_{i} = n $ , $\sqrt{n}g_{ai} = g_{bi} = g_{0}$ 和$ \varDelta_{i} = \varDelta $ . 在这些假设中, 要求系综中原子个数相等, 这是为了方便理论计算. 实际上, 在系综中的原子个数相差不是很大的情况下, 只要能够使$ \sqrt{n}g_{ai}\approx g_{bi} $ , 本方案仍然有效. 此外, 方案中采用的是非简并的双模腔场, 实验上可以通过控制a (b )模腔场的本征频率以及原子到a (b )模边界的距离来控制$ g_{a} $ 和$ g_{b} $ 的大小, 因此这些假设是合理的.2.2.制备三粒子单重态 -->2.2.制备三粒子单重态 利用量子绝热捷径技术可以通过一个非绝热过程来加快绝热演化的速度, 为了设计这样的哈密顿量来快速制备纠缠态, 首先考虑$ \varDelta = 0 $ 的情况:$ (|R^{(1)}M^{(1)}G\rangle|0_{a}0_{b}\rangle-|R^{(1)}GM^{(1)}\rangle|0_{a}0_{b}\rangle)/\sqrt{2} $ (该初态实际上是一个原子的状态直积另外两个原子的纠缠态, 在本文模型的基础上稍微修改, 即忽略能级$ |e\rangle $ , 使能级$ |g\rangle $ 和$ |m\rangle $ 可以直接跃迁到$ |r\rangle $ , 就可以获得这个两原子纠缠态), 其中$ |0_{a}\rangle $ ($ |0_{b}\rangle $ )表示腔模a (b )处于真空态. 此时, 该系统将会在一个单激发子空间中演化, 这个单激发子空间的基矢为6 )式的基矢, 可以将哈密顿量重新改写为$ g_{0}\gg\varOmega_{i}' $ 的条件下, 这个单激发子空间将分裂成七个不变Zeno子空间, $Z_{1} = \{|\varphi_{1}\rangle, |\varphi_{2}\rangle, |\varphi_{3}\rangle, |\varphi_{4}\rangle, $ $ |\varphi_{5}\rangle, |\varphi_{6}\rangle, |\phi_{1}\rangle, |\phi_{2}\rangle\}$ , $ Z_{2} = \left\{|\phi_{3}\rangle, |\phi_{4}\rangle\right\} $ , $Z_{3} = \{|\phi_{5}\rangle, $ $ |\phi_{6}\rangle\}$ , $ Z_{4} = \left\{|\phi_{7}\rangle, |\phi_{8}\rangle\right\} $ , $ Z_{5} = \left\{|\phi_{9}\rangle, |\phi_{10}\rangle\right\} $ , $Z_{6} = $ $ \left\{|\phi_{11}\rangle\right\}$ , $ Z_{7} = \left\{|\phi_{12}\rangle\right\} $ . 相应的投影算符为$P_{j}^{k} = $ $ |k\rangle\langle k|$ ($ |k\rangle\in Z_{j} $ ), 与之对应的本征值为$ \lambda_{1} = 0 $ , $\lambda_{2} = $ $ g_{0}$ , $ \lambda_{3} = -g_{0} $ , $ \lambda_{4} = \sqrt{3}g_{0} $ , $ \lambda_{5} = -\sqrt{3}g_{0} $ , $ \lambda_{6} = 2 g_{0} $ 以及$ \lambda_{7} = -2 g_{0} $ . 在Zeno子空间中使用的态$ |\phi_{i}\rangle $ ($i = 1, 2, \cdots, 12$ )是哈密顿量$ H_{\rm ac}' $ 的本征态, 具体形式为$H_{\rm s}$ 重新改写为$ H_{\rm{rac}} $ 表示超级原子与腔场的相互作用项, 其表达形式是利用$ H_{\rm{ac}}' $ 的本征态对$ H_{\rm{ac}}' $ 进行对角化; $ H_{\rm{ral}} $ 表示超级原子与经典场的相互作用项, 其表达形式是利用$ H_{\rm{ac}}' $ 的本征态对$ H_{\rm{al}}' $ 进行对角化. 对(9 )式执行一个幺正变换$ U = \exp(-{\rm{i}}H_{\rm{rac}}t) $ , 忽略高频振荡项则可以获得一个有效的哈密顿量$ \varOmega_{2}' = \varOmega_{3}' $ , $|D\rangle = (|\varphi_{4}\rangle- $ $ |\varphi_{3}\rangle)/\sqrt{2}$ 和$ |T\rangle = (|\varphi_{2}\rangle+|\varphi_{5}\rangle-|\varphi_{1}\rangle-|\varphi_{6}\rangle)/2 $ . 该有效哈密顿量描述的系统可以被认为是一个具有激发态$ |\phi_{1}\rangle $ 和基态$ |D\rangle $ , $ |T\rangle $ 的三能级系统. 对于这个简单的三能级系统, 其本征态为$ \eta_{0} = 0 $ , $\eta_{1} = -\dfrac{\varOmega'}{\sqrt{3}}$ 和$\eta_{2} = \dfrac{ \varOmega'}{\sqrt{3}}$ , 其中$ \varOmega' = \sqrt{\varOmega_{1}'^{2}+2\varOmega_{3}'^{2}} $ , $\alpha = \arctan\left[\dfrac{\varOmega_{1}'}{ \sqrt{2}\varOmega_{3}' }\right]$ . 如果满足绝热条件$ |\langle m_{0}|\partial_{t}m_{1(2)}\rangle|\ll|\eta_{1(2)}| $ , 初态$ |D\rangle $ 将会沿着本征态$ |m_{0}\rangle $ 缓慢地演化. 当缓慢增加$ \varOmega_{3}' $ 并同时减小$ \varOmega_{1}' $ , 一直到时间$ t_{\rm{c}} $ 时, $ \tan\alpha = \sqrt{2} $ , 系统的状态就会演化成三粒子的单重态:$ \varOmega_{1}' $ 和$ \varOmega_{3}' $ 选为$ \varOmega_{0} $ 表示脉冲振幅, $ \{t_{0} , T \}$ 是相关的参数, $ \tan\beta = 2 $ , $ t_{\rm{c}} $ 是操作时间. 当选择合理的激光脉冲参数时, 即$ t_{0} = 0.14 t_{\rm{c}} $ 以及$ T = 0.19 t_{\rm{c}} $ , $ \varOmega_{1}' $ 和$ \varOmega_{3}' $ 如图3 所示.图 3 在$t_{0}=0.14 t_{\rm{c}}$ 和$T=0.19 t_{\rm{c}}$ 时的激光脉冲$\varOmega_{1}'$ 和$\varOmega_{3}'$ Figure3. Laser pulse $\varOmega_{1}'$ and $\varOmega_{3}'$ when $t_{0}=0.14 t_{\rm{c}}$ and $T= $ $ 0.19 t_{\rm{c}}$ .$ H_{\rm{eff}} $ 的瞬时本征态$ |m_{k}\rangle $ ($ k = 0, $ $ 1, 2 $ )并不满足Schr?dinger方程${\rm i}\partial_{t}|m_{k}\rangle = H_{\rm{eff}}|m_{k}\rangle$ . 根据Berry[45 ] 的无跃迁跟踪算法可获得能够精确驱动本征态演化的哈密顿量$ H(t) $ , 从文献[46 -49 ]可知, 最简单的哈密顿量$ H(t) $ 的形式为$\dot{\theta}(t) = \big[\sqrt{2}\big(\dot{\varOmega}_{1}(t)\varOmega_{3}(t)- \dot{\varOmega}_{3}(t)\varOmega_{1}(t)\big)\big]/\varOmega^{2}$ . 对于这样的哈密顿量, 在实际的实验中是很难实现甚至是不可能实现的, 所以应该找一个效应等同于$ H(t) $ 且技术上可行的哈密顿量. 因此, 将前面讨论的共振相互作用($ \varDelta = 0 $ ) 更改为非共振相互作用, 失谐$ \varDelta\neq0 $ . 这个非共振相互作用的哈密顿量可以表示为(4 )式. 使用类似于(4 )式到(10 )式的处理方法, 可以获得该非共振系统的有效哈密顿量为$ \varDelta\gg\varOmega_{1}, \varOmega_{3} $ ), 绝热消除$ |\phi_{1}\rangle $ 态, 并选择$ \varOmega_{1} = \varOmega_{x} $ 以及$ \varOmega_{3} = {\rm{i}}\varOmega_{x}/\sqrt{2} $ , 则可以获得最终的有效哈密顿量为$ \varOmega_{x}^{2}/(3\varDelta) = \dot{\theta}(t) $ , 哈密顿量$ \widetilde{H}_{\rm{fe}} $ 就可以将系统暗态的绝热演化进行加速, 使其能够快速地演化到目标态. 因此, $\varOmega_{x}$ 表示为3.数值模拟分析 为了说明利用绝热捷径方法制备三粒子单重态所需的时间远远小于利用绝热近似方法所需要的时间, 图4 分别给出了两种方案的保真度随$ g_{0}t $ 的变化关系.图 4 利用绝热近似方法和绝热捷径方法制备三粒子单重态所需时间对比Figure4. Comparison of the interaction time required between shortcuts to the adiabaticity method and the adiabatic approximation method.$ F = \left|\langle\varPhi_{t_{\rm{c}}}|\rho(t)|\varPhi_{t_{\rm{c}}}\rangle\right| $ , $ \rho(t) $ 是相应的含时密度算符, $ |\varPhi_{t_{\rm{c}}}\rangle $ 表示目标态. 数值模拟采用的参数为: $ t_{0} = 0.14 t_{\rm{c}} $ , $ T = 0.19 t_{\rm{c}} $ , $ g_{0} = 10\varOmega_{0} $ . 在图4 中, 红色虚线表示利用绝热近似方法制备的三粒子单重态的保真度随时间的变化关系, 选择$ t_{\rm{c}} = 500/g_{0} $ , 当$ g_{0}t_{\rm{c}} = 500 $ 时, 该方法的保真度近似等于1; 蓝色点线也表示绝热近似方法下的保真度, 选择$ t_{\rm{c}} = 100/g_{0} $ , 当$ g_{0}t_{\rm{c}} = 100 $ 时, 保真度约为0.6, 这是因为操作时间很短, 并不能满足绝热近似条件, 所以得不到很好的保真度; 绿色点虚线表示利用绝热捷径方法制备的单重态的保真度, 可以看出, 与绝热近似方法相比, 在得到相同保真度的情况下, 利用绝热捷径方式仅需要很短的时间. 也就是说, 操作时间$ t_{\rm c} $ 越长, 越能够满足绝热演化条件, 此时, 利用绝热演化方法制备的三粒子单重态的保真度越高, 但是这个过程需要非常长的时间. 相反, 利用绝热捷径的方法只需要很短的时间就可以达到一个高的保真度.19 )式中的$\hat{{\cal{L}}_{x}} = $ $ \sqrt{\gamma_{e1}/2}|G\rangle_{x}\langle E^{(1)}|$ , $\hat{{\cal{L}}_{y}} \! = \! \sqrt{\gamma_{e2}/2}|M^{(1)}\rangle_{y}\langle E^{(1)}|$ 和$\hat{{\cal{L}}_{z}} \!= $ $ \sqrt{\gamma_{r}/2}|E^{(1)}\rangle_{z}\langle R^{(1)}|$ 是描述耗散过程的Lindblad算符. $ \kappa_{a} $ 和$ \kappa_{b} $ 分别表示腔中a 模和b 模的衰减率. $ \gamma_{e1} $ 和$ \gamma_{e2} $ 分别表示能级$ |e\rangle $ 向能级$ |g\rangle $ 和$ |m\rangle $ 的自发辐射率, $ \gamma_{r} $ 表示里德伯态的自发辐射率. 在实际情况中, 里德伯态的自发辐射要远远小于其他态的自发辐射率, 因此在数值模拟中假定$ \gamma_{e1} = \gamma_{e2} = \gamma $ , $ \gamma_{r} = 0.01\gamma $ 和$ \kappa_{a} = \kappa_{b} = \kappa $ . 其他参数选择为$t_{0} = $ $ 0.14 t_{\rm{c}}$ , $ T = 0.19 t_{\rm{c}} $ , $ g_{0} = 10\varOmega_{0} $ 和$ \varDelta = 2 g_{0} $ .图5(a) 中给出了三粒子单重态的保真度随演化时间和退相干因素(包括超级原子的自发辐射和腔内光子的衰减)的变化图像, 其中已经假定了$ \kappa = \gamma $ . 在图5(b) 中给出了保真度随$ \gamma/g_{0} $ 和$ \kappa/g_{0} $ 的变化图像. 从图5 可以看出, 本方案能够在很短的时间内就达到一个理想的保真度, 同时三粒子单重态的保真度随着腔衰减率和原子自发辐射率的增加而缓慢减小, 当$ \kappa = \gamma = 0.05 g_{0} $ 时, 单重态的保真度仍然可以达到92%.图 5 (a) 三粒子单重态的保真度随相互作用时间$g_{0}t_{\rm c}$ 和原子自发辐射$\gamma/g_{0}$ 的变化; (b) 三粒子单重态的保真度随腔衰减$\kappa/g_{0}$ 和原子自发辐射$\gamma/g_{0}$ 的变化Figure5. (a) Fidelity of the singlet state versus the interaction time $g_{0}t_{\rm c}$ and the atomic spontaneous emission $\gamma/g_{0}$ ; (b) fidelity of the singlet state versus the cavity decay $\kappa/g_{0}$ and the atomic spontaneous emission $\gamma/g_{0}$ $ ^{87}{\rm{Rb}} $ 原子放在超高真空环境下的磁光阱中, 通过多次冷却, 原子云可包含25000个原子, 最终温度可以达到6 μK[39 ] . 考虑到实验中的参数[50 -53 ] : 磁光阱中的原子数为10000, $ |e\rangle $ 态的自发辐射率为$ \gamma_{e1} = \gamma_{e2}\sim2\pi\times2.62 $ MHz, 里德伯态$ |r\rangle $ 的自发辐射率为$ \gamma_{r}\sim2\pi\times1 $ kHz, 腔模的衰减率为$ \kappa\sim2\pi\times3.5 $ MHz, 耦合强度$g_{0}\sim $ $ 2\pi\times750$ MHz. 在数值模拟中代入上述参数, 最终获得三粒子单重态的保真度仍然可以达到99%.4.结 论 本文利用量子Zeno动力学和绝热捷径的方法制备了三个里德伯超级原子之间的单重态. 与单原子情况相比, 利用超级原子进行量子信息处理对实验的要求比较低且操作简单; 与量子Zeno动力学方法相比, 本方案不需要精确控制演化时间; 与绝热近似方法相比, 本方案大大缩短了演化时间. 结合量子Zeno动力学和绝热捷径的方法, 本方案不仅能够简单快速地制备三粒子单重态, 而且该理论方案也可用于制备其他纠缠态以及多体纠缠态. 希望在今后的实验上实现量子信息处理中, 该方案能够起到一定的作用. 






































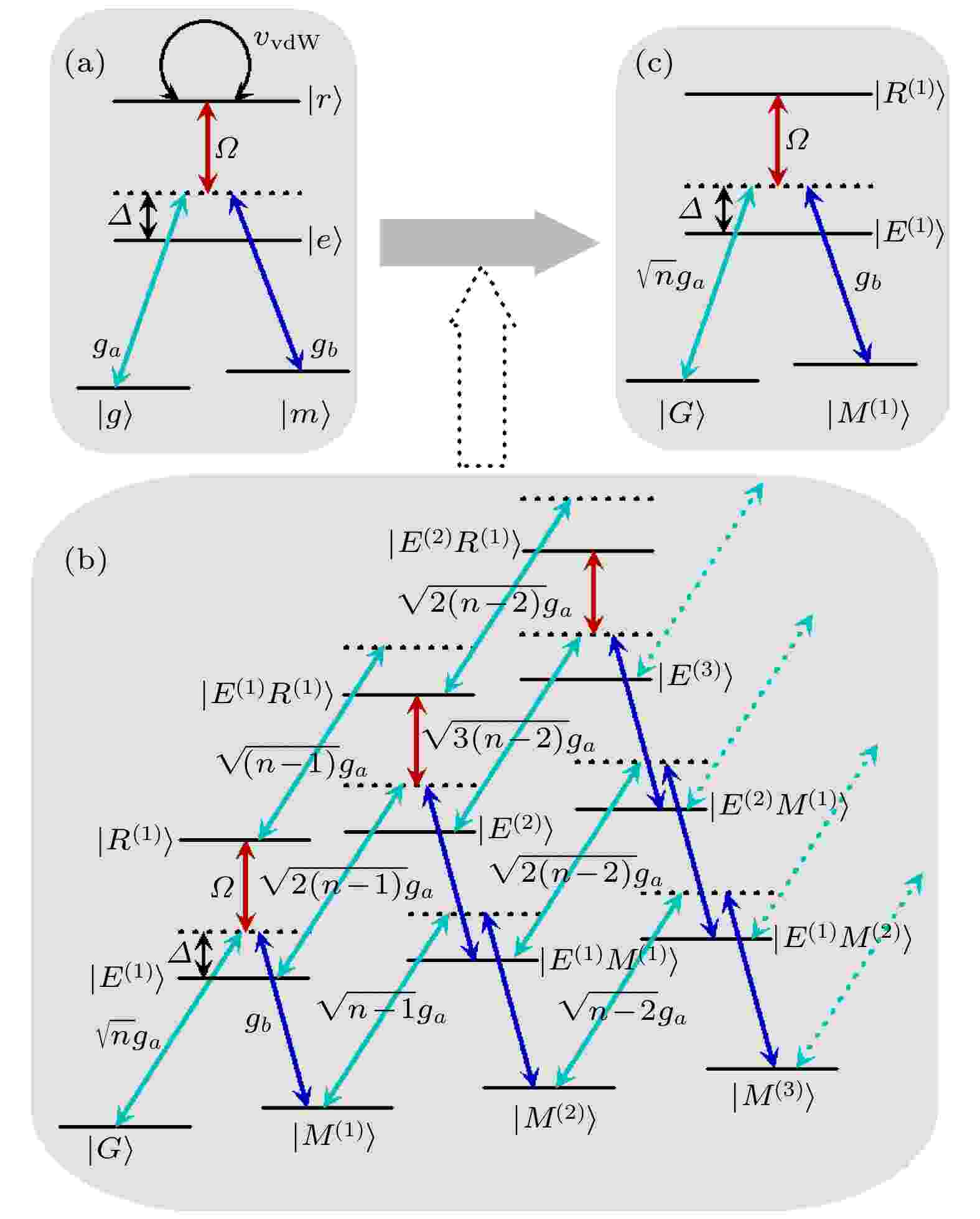 图 1 (a)里德伯原子的能级结构; (b)里德伯超级原子的能级结构; (c)弱腔场极限下的里德伯超级原子能级结构
图 1 (a)里德伯原子的能级结构; (b)里德伯超级原子的能级结构; (c)弱腔场极限下的里德伯超级原子能级结构

















 图 2 腔与三个超级原子相互作用示意图
图 2 腔与三个超级原子相互作用示意图




















































































 图 3 在
图 3 在





























 图 4 利用绝热近似方法和绝热捷径方法制备三粒子单重态所需时间对比
图 4 利用绝热近似方法和绝热捷径方法制备三粒子单重态所需时间对比



































 图 5 (a) 三粒子单重态的保真度随相互作用时间
图 5 (a) 三粒子单重态的保真度随相互作用时间



















