摘要: 托卡马克聚变堆中高能量alpha粒子的良好约束是获得稳态燃烧等离子体的前提, 除了磁场波纹损失, 不稳定性也会引起额外的损失. 本文基于中国聚变工程试验堆(CFETR)参数, alpha粒子初始分布和新经典撕裂模(NTM)扰动分布, 利用粒子导心跟踪方法分别对磁场波纹和NTM两种扰动及叠加下的粒子损失进行了详细的数值模拟. 结果显示粒子损失份额不随NTM扰动幅度增大而增大, 两种扰动的叠加效应不明显. 通过扫描装置波纹度大小以及分析相空间粒子密度和波纹损失区分布, 确认原因是CFETR波纹损失区较小, 没有覆盖高能量粒子(EP)密度和NTM扰动主要分布区. 此外, NTM没有引起直接粒子损失和俘获粒子剖面坍塌. 显著的俘获粒子密度剖面展平, 并扩展到波纹损失区是两种扰动叠加效应显著的前提. 无碰撞波纹随机扩散是CFETR初始分布alpha粒子的主要损失通道, 通行粒子约束不受磁场波纹影响. 本文研究结果对CFETR概念设计中alpha粒子物理和低频不稳定性下的EP行为具有重要意义.
关键词: 托卡马克 /
alpha粒子 /
磁场波纹 /
新经典撕裂模 English Abstract Numerical simulation of synergistic effect of neoclassical tearing mode and toroidal field ripple on alpha particle loss in China Fusion Engineering Testing Reactor Hao Bao-Long 1 ,Chen Wei 2 ,Li Guo-Qiang 3 ,Wang Xiao-Jing 3 ,Wang Zhao-Liang 3 ,Wu Bin 3 ,Zang Qing 1 ,Jie Yin-Xian 1 ,Lin Xiao-Dong 1 ,Gao Xiang 1 ,CFETR TEAM 1.Advanced Energy Research Center, Shenzhen University, Shenzhen 518060, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11905142, 11875290)Received Date: 23 November 2020Accepted Date: 16 January 2021Available Online: 28 May 2021Published Online: 05 June 2021Abstract: Confinement of fusion born alpha particles in tokamak is the key issue to burning plasma. Apart from toroidal field ripple, instabilities can induce energetic particles to lose and be redistributed. Based on the parameters of China Fusion Engineering Testing Reactor (CFETT) hybrid scenario, alpha particle distribution and neoclassical tearing mode structure, the alpha particle loss induced under perturbation of ripple and neoclassical tearing mode (NTM) is calculated with the guiding center code ORBIT. The inputs have the initial distribution of alpha particles which is obtained with the TRANSP/NUBEAM code, the static NTM perturbation with different amplitudes which is obtained from TM1 code, and the ripple field from engineering design. The results show that the heat load on last closed flux surface is about 0.1 MW/m2 , with ripple and collision included. The collisionless stochastic ripple diffusion is the main loss channel of initial alpha particle distribution in the CFETR, and the ripple perturbation has no influence on passing particles. The loss fraction does not increase with the NTM perturbation amplitude increasing, the synergistic effect is negligible. The scanning of ripple amplitude shows that the synergistic effect is slight. The monoenergetic initial distribution of alpha particles can give different types of orbits in the plane of ($ {P_\zeta },\mu $ ), such as the domains of trapped particle and passing particle, lost particle and confined particle. The trapped fraction of initial alpha particles is about 27%, ripple loss region in phase space is narrow and away from the main trapped particle distribution. The increasing of ripple perturbation in simulation does enlarge the ripple loss domain in the phase space ($ {P_\zeta },\mu $ ), which is corresponding to a lager ripple loss fraction and has more trapped-passing boundaries. The NTM perturbation does enlarge the orbit excursions of trapped particles, and thus increasing the trapped passing transition near the boundary. The slight synergistic effect in calculation with larger ripple amplitude is explained by ripple loss region having more trapped-passing boundaries, not by the profile flattening of trapped particles. The NTM perturbation and finite collision can transit the passing particle to trapped particle near the boundary. With the help of kinetic Poincare plot, neither direct particle loss nor profile flattening of trapped particles is observed. The loss fraction enhancement can happen only when the profile flattening of trapped particles takes place within the ripple loss region, which is not the case in CFETR. The conclusion of this work contributes a lot to the design of CFETR and the study of alpha particle physics.Keywords: tokamak /alpha particle /magnetic ripple /neoclassical tearing mode 全文HTML --> --> --> 1.引 言 磁约束核聚变研究在约70年的发展后到了建设聚变实验堆阶段, 国际热核聚变实验堆(ITER)的工程建设持续推进, 预期2025年开始放电. 我国在ITER物理设计和工程技术基础上发展的中国聚变工程试验堆(CFETR)作为ITER和聚变电站商用示范堆(DEMO)的过渡装置完成了初步的物理和工程设计[1 -3 ] . 氘氚聚变产物alpha粒子的良好约束是获得高能量增益的前提, CFETR作为托卡马克类型的装置, 分立存在的纵场线圈引起的磁场波纹会引起一定份额的EP损失, 此外, 各种磁流体力学不稳定性不但引起直接的粒子损失, 还会改变EP分布函数, 聚变堆面向等离子体部件的热负荷限制和物理目标的实现只能允许小尺度的alpha粒子损失和再分布[4 ,5 ] .[6 ] .[7 -9 ] . 在DIII-D, TFTR和ASDEX-U等装置上都观察到NTM引起了显著EP损失, 确认了粒子损失机制是相空间形成共振岛并被第一壁截断, 或共振岛相互重叠形成宽域的混沌区域[10 -15 ] . 这些研究表明NTM对EP约束有显著影响, 包括粒子损失和分布剖面坍塌. 作者已发表工作也表明alpha粒子分布剖面外延、展平会引起波纹损失的显著增加[16 ] , 原因是磁场波纹扰动幅度从等离子体芯部到边界呈自然指数增大, alpha粒子剖面坍塌会使更多的粒子进入波纹损失区. 显著的粒子损失不但会损伤第一壁, 且会降低聚变功率和辅助加热效率. 基于此, 本文利用CFETR混杂运行模式参数和NTM扰动数值结果, 研究NTM和磁场波纹扰动下的粒子损失叠加效应和损失机制. 本项研究对CFETR物理设计集成模拟流程中alpha粒子物理部分提供重要参考, 并有助于理解燃烧等离子体.[17 ] , 在半个慢化时间内跟踪样本粒子分布, 初始alpha粒子分布来自输运程序TRANSP/NUBEAM[18 ] , 平衡位形来自CFETR物理设计, 磁场波纹扰动来自工程设计, NTM扰动是基于初始值程序TM1物理分析结果的数值重建. ORBIT程序在直线磁面坐标系中求解哈密顿导心运动方程, 粒子的空间坐标为(${\psi _{\rm{p}}}, \theta, \zeta $ ), 分别是极向磁通, 极向角和广义环向角. 粒子的速度由能量E , 磁矩μ 和螺距角正负号决定. 粒子导心的哈密顿量为$H = \rho _{/\!/}^2 {B^2}/2 + \mu B + \varPhi$ , ${\rho _{/\!/} } = {{{v_{/\!/} }} / B}$ 是归一化的平行速度, B 是总磁场强度, $ \mu ={v}_{\perp }{}^{2}/(2 B)$ 是粒子磁矩, Φ 是本文未引入的电势. 哈密顿运动方程为$\dot \theta = {{\partial H} / {\partial {P_{\theta} }}}$ , ${\dot P_{\theta} } = - {{\partial H} / {\partial \theta }}$ , $\dot \zeta = {{\partial H} / {\partial {P_{\zeta} }}}$ , ${\dot P_{\zeta} } = - {{\partial H} / {\partial \zeta }}$ , ${P_{\zeta} }$ 和${P_{\theta} }$ 是环向和极向正则角动量[17 ] . 由于托卡马克平衡位形的轴对称假设和粒子运动周期性质, 三个物理量$({P_{\zeta} }, E, \mu )$ 即可决定EP轨道.2 节描述了CFETR混杂运行模式等离子体参数分布、alpha粒子初始分布、磁场波纹和NTM扰动的数值重建. 第3 节是详细的粒子跟踪计算结果, 包括磁场波纹损失、NTM扰动叠加以及人为增大装置波纹度下的损失模拟. 第4 节是结果讨论, 即粒子损失扰动叠加效应不显著的原因分析. 第5 节是结论.2.CFETR装置参数和全尺度粒子跟踪模拟输入 22.1.CFETR等离子体参数和初始alpha粒子分布 2.1.CFETR等离子体参数和初始alpha粒子分布 经过物理和工程设计迭代, 目前CFETR主机参数如表1 所列. 作为实现稳态氚自持的托卡马克装置, CFETR物理实验分两个阶段实现200—1500 MW的聚变功率, 等离子体放电占空比约为0.3—0.5, 能量增益因子Q 约为5—30[19 ] . 基于集成模拟流程提出了CFETR稳态运行模式和混杂运行模式两种, 本文基于混杂运行模式(v201806)参数, 利用输运程序TRANSP/NUBEAM计算得到了alpha粒子初始分布下的蒙特卡罗罗样本粒子. NUBEAM模块是分析托卡马克实验中中性束注入和聚变产物的含时集成工具. 混杂运行模式(v201806)的背景等离子体剖面见图1 , 聚变功率约为${P_{{\rm{fus}}}} = 1\;{\rm{ GW}}$ , 台基顶部的等离子体密度为格林极限的90%. 初始alpha粒子密度分布见图2 , 初始alpha粒子产自氘氚聚变反应, 能量单值分布为3.52 MeV, 速度基本各向同性. 在没有不稳定性引起的显著输运和再分布时, alpha粒子经与背景等离子体库伦碰撞慢化并形成氦灰, 符合就地慢化模型. 平衡位形为下单零偏滤器位形, 纵场和等离子体电流方向都是俯视逆时针, 安全因子剖面见图4(a) .图 1 CFETR混杂运行模式(v201806)中背景电子密度、温度和离子温度分布Figure1. Distributions of bulk electron density, electron temperature, and bulk ion temperature in CFETR hybrid scenario (v201806).参数 CFETR ITER EAST 磁轴场强${B_{{\rm{T}}0}}$/T 6.5 5.3 2 等体大半径${R_0}$/m 7.2 6.2 1.9 等体小半径a /m 2.2 2.0 0.5 等体电流${I_{\rm{p}}}$/MA 14 15 1 纵场磁体柄数N 16 18 16
表1 CFETR与其他托卡马克装置主机参数对比Table1. Main parameters comparison of CFETR and other tokomak facilities.图 2 CFETR初始alpha粒子密度分布Figure2. Density profile of alpha particle initial distribution in CFETR.2.2.纵场波纹度分布和数值重建 -->2.2.纵场波纹度分布和数值重建 CFETR的环向磁场由16柄D形线圈实现, 对比其他托卡马克装置, 柄数较少, 较大磁场波纹度对EP约束影响值得关注. 定义在极向截面的波纹度为$\delta (r, \theta ) = {{({B_{\max }} - {B_{\min }})} / {({B_{\max }} + {B_{\min }})}}$ , ${B_{\max }}$ 和${B_{\min }}$ 分别是极向位置固定但在不同环向角处的磁场最大值和最小值. 工程设计中没考虑包层铁素体钢材料, 仅有纵场线圈时的波纹度分布见图3(b) , 波纹度在等离子体外中平面附近最大, 约0.35%, 波纹扰动幅度从芯部到边界呈自然指数增大. 虽然CFETR满足托卡马克纵场磁体设计的一般要求, 即波纹度最大值小于0.5%, 但整体的波纹度较大, 芯部波纹度比ITER大一个量级. 在ORBIT中引入波纹扰动时, 磁面坐标系中叠加纵场波纹后的总磁场可表达为$B({\psi _{\rm{p}}}, \theta, \phi ) = {B_0}({\psi _{\rm{p}}}, \theta )[1 + $ $ \delta \cos (N\phi )]$ , 采用针对D形线圈波纹度几何分布的解析公式$\delta (R, Z) = {\delta _0}\exp \{ [{(R - {R_{{\rm{rip}}}})^2} + {b_{{\rm{rip}}}}{Z^2}]^{0.5}/ $ $ {w_{{\rm{rip}}}}\}$ 来拟合工程设计值. 拟合系数为${\delta _0} = 1.57 \times $ $ {10^{ - 5}}$ , ${R_{{\rm{rip}}}} = 6 - 0.0062{Z^2}\;{\rm{ m}}$ , ${b_{{\rm{rip}}}} = 0.021$ 和${w_{{\rm{rip}}}} = $ $ 0.63\;{\rm{ m}}$ . 波纹扰动的解析函数实现结果和工程设计值对比见图3 , 可知在等离子体约束区数值重建精确[16 ] .图 3 CFETR纵场波纹度分布 (a) 解析函数实现值; (b) 工程设计值Figure3. Distributions of toroidal field ripple perturbation amplitude in CFETR: (a) Ripple data by analytical equation; (b) engineering data in design.2.3.NTM扰动函数分布 -->2.3.NTM扰动函数分布 为了得到NTM扰动函数的模结构分布, 利用初始值程序TM1在柱坐标系中求解简化磁流体力学方程[20 ] , 该坐标系中磁场表达为${{B}} = {B_{0 {\rm{t}}}}\widehat {{e_{\rm{t}}}} - $ $ ({{nr} / {mR}}){B_{0 {\rm{t}}}}\widehat {{e_{\rm{p}}}} + \nabla {\psi _{\rm{h}}} \times \widehat {{e_{\rm{t}}}}$ , 即平衡磁场的环向和极向分量,再叠加螺旋磁通表达的扰动场. NTM的螺旋扰动场为$\delta {{B}} = \nabla {\psi _{\rm{h}}} \times \widehat {{{\rm{e}}_{\rm{t}}}}$ , ${\psi _{\rm{h}}}$ 是螺旋磁通, 傅里叶展开为${\psi _{\rm{h}}} = $ $ \displaystyle \sum\nolimits_i {{\psi _i}} (r)\exp [{\rm{i}}({m_i}\theta - {n_i}\phi )]$ . 针对CFETR混杂运行模式, TM1程序计算了不同电子回旋电流驱动方案下NTM的饱和幅度, 得到主要的模数是2/1和3/2 NTM, 扰动函数剖面在不同饱和幅度下保持不变, 因此基于TM1程序数值结果通过高斯拟合在ORBIT中引入NTM模结构并扫描幅度. 图4 给出的是2/1和3/2 NTM的平衡分量和一阶分量的高斯拟合结果, 平衡分量的极值点精确对应各自的有理面径向位置[21 ] .图 4 CFETR混杂运行模式 (a) 2/1和3/2 NTM的平衡分量和安全因子分布; (b), (c)一阶分量和高斯拟合曲线Figure4. (a) Safety factor profile and equilibrium helical flux of 2/1 and 3/2 NTM in CFETR hybrid scenario; (b), (c) the first order harmonics and Gaussian fitting results.$\delta {{B}} = \nabla \times \alpha {{{B}}_0}$ , $\alpha = {\alpha _{mn}}({\psi _{\rm{p}}})\sin (n\zeta - m\theta - {\omega _n}t)$ 是时间和位置的标量函数. 柱坐标系中忽略高阶分量后的扰动磁场为$\delta {{B}} = - \nabla \times {\psi _1}\widehat{\phi }$ , 平衡场的共变基表达为${{B}} = \nabla \phi + \dfrac{{{r^2}}}{{q(r)}}\nabla \theta$ , 考虑到极向磁场远比环向场小, 磁面坐标系中的扰动函数可近似为$ - {\psi _1} = \alpha $ . 因此TM1程序中NTM计算结果的一阶分量用于表达ORBIT程序中扰动函数α [22 ] . 在给定平衡位形下, 2/1和3/2 NTM扰动幅度的比例固定, 本文算例为${{{\alpha _{2/1}}} / {{\alpha _{3/2}}}} = 4.38$ . 扰动函数α 的量纲是长度, 在ORBIT程序中归一化单位为磁轴大半径${R_0}$ . 对于远比EP运动频率小的NTM, 假设为零频率磁扰动是合理且便于理论探讨的, 因此本文引入NTM为静止磁扰动. 为保持理论推导完整性, 下文保留扰动频率符号. 不同NTM扰动幅度引起的局域磁场拓扑变化见图5 的庞加莱图, 磁岛的径向宽度正比于扰动幅度平方根, 较高的扰动幅度下可观察到磁岛相互重叠后的磁场无规化.图 5 固定2/1和3/2模扰动幅度比例下扫描NTM扰动幅度下的庞加莱图 (a) ${\alpha _{2/1}} = 1.64 \times {10^{ - 4}}{R_0}$ ; (b) ${\alpha _{2/1}} = l $ $ 6.00 \times {10^{ - 4}}{R_0}$ Figure5. Poincare plot under different NTM perturbation amplitude with the ratio fixed ${{{\alpha _{2/1}}} / {{\alpha _{3/2}}}} = 4.38$ : (a)${\alpha _{2/1}} = $ $ 1.64 \times {10^{ - 4}}{R_0}$ ; (b)${\alpha _{2/1}} = 6.00 \times {10^{ - 4}}{R_0}$ .3.初始分布alpha粒子导心轨道跟踪模拟 23.1.alpha粒子磁场波纹损失 3.1.alpha粒子磁场波纹损失 理论上任何破坏托卡马克环向轴对称性质的扰动都会降低EP约束, 如有限数目纵场线圈引起的磁场波纹. 纵场波纹扰动导致EP运动的正则环向角动量不守恒, 因此粒子轨道不闭合, 有额外的漂移, 通行粒子因磁力线回旋变换会平均掉该扰动, 俘获粒子受此扰动影响, 香蕉轨道转折点有一定扰动位移. 在磁场波纹扰动下, EP有两个损失通道, 局域波纹磁阱俘获和随机波纹扩散. 局域波纹磁阱是在波纹度较大时, 如外中平面附近, 形成二级磁阱, 平行速度较小的俘获粒子经过该区域时就俘获在该环向局域磁阱内, 只剩径向漂移快速损失掉或经碰撞和漂移逃出该损失区. 波纹磁阱俘获损失依赖于粒子速度、平衡位形、磁阱分布和碰撞率, 波纹磁阱俘获损失的时间尺度在几个极向回弹周期内. 当波纹度较小不足以形成局域磁阱时, 有限的波纹扰动也会使俘获粒子连续香蕉轨道之间解耦, 形成随机波纹扩散, 碰撞效应可降低该损失机制的随机阈值[23 ] .${\nu _{\varepsilon 0}} = 1.8\;{{\rm{s}}^{ - 1}}$ , 螺距角散射率为${\nu _{{\rm{pa0}}}} = 0.16\;{{\rm{s}}^{ - 1}}$ . 试探粒子程序时采用的碰撞修正模型涉及多个前提, 等离子体中EP产生以后, 分布函数在其损失或消失前经历复杂过程. EP分布函数改变的时间尺度远比其运动特征时间尺度长, EP密度远比背景等离子体密度低, 忽略频率较小的EP之间的碰撞, 仅考虑EP与背景的碰撞. EP与背景粒子之间小角度二体碰撞累计效应在托卡马克实验参数范围附近是主要的碰撞项, 考虑到等离子体德拜屏蔽, 忽略了频率远小于此的大角度碰撞, 虽然这种近距离碰撞可以引发核聚变反应. 基于此, ORBIT程序在跟踪粒子过程中对粒子即时能量${E_i}$ 和螺距角${\lambda _i} = {{{v_{/\!/} }} / v}$ 在一个计算步长$\Delta t$ 后分别修正为${E_n} = {E_i} - (2{\nu _\varepsilon }\Delta t)\left[ {{E_i} - \left( {\dfrac{3}{2} + \dfrac{E}{{{\nu _\varepsilon }}}\dfrac{{{\rm{d}}{\nu _\varepsilon }}}{{{\rm{d}}E}}} \right)T} \right] \pm 2{[T{E_{_i}}({\nu _\varepsilon }\Delta t)]^{0.5}}$ 和${\lambda _n} = {\lambda _i}(1 - {\nu _{{\rm{pa}}}}\Delta t) \pm {[(1 - {\lambda _i}^2){\nu _{{\rm{pa}}}}\Delta t]^{0.5}}$ , $T({\rm{eV}})$ 是等离子体温度[24 ] . 高能alpha粒子的慢化主要来自与背景电子的碰撞, 电子慢化时间与EP能量无关, 因此对于短时间行为的EP能量慢化率可近似认为与能量无关${\nu _\varepsilon } \approx {\nu _{\varepsilon 0}}$ , 螺距角散射率随能量慢化降低而增大${\nu _{{\rm{pa}}}} = {\nu _{{\rm{pa}}0}}{({{{E_0}} / E})^{1.5}}$ .图6 所示. 波纹损失粒子信息如图7 , 经历和波纹扰动无关的初始轨道损失之后, 随着波纹扰动和碰撞效应的时间累计, 粒子损失份额在半个慢化时间后达到1.4%, 损失粒子能量有慢化成分, 损失粒子主要为俘获粒子. ORBIT程序在最后一个闭合磁面(LCFS)内跟踪粒子, 外出LCFS即定义为损失, 由于LCFS和装置第一壁接近, 因此可以根据该处的粒子沉积位置、数量和能量信息评估局域热负荷. 图8 是CFETR混杂运行模式下初始分布alpha粒子在一个慢化时间内损失粒子在LCFS上形成的局域热斑, 峰值约0.1 WM/M2 , 虽然在装置第一壁热负荷安全阈值范围内, 但是给其他损失通道预留安全空间较小, 考虑到各种损失通道的粒子并不沉积在同一位置, 相关设计还需要更进一步的优化和分析[25 ] .图 6 在半个EP慢化时间内不同物理效应下计算得到的粒子损失份额Figure6. The particle loss fraction after following half a slowing down time under different perturbation and collision.图 7 纵场波纹扰动下损失alpha粒子信息 (a) 损失份额随时演化; (b) 损失粒子能量分布; (c) 损失粒子螺距角分布Figure7. Information of lost alpha particles under collision and toroidal field ripple: (a) Evolution of loss fraction; (b) energy distribution of lost particles; (c) pitch angle distribution of lost particles.图 8 一个慢化时间后初始分布alpha粒子波纹损失局域沉积在LCFS处得到的热负荷Figure8. The heat load at the last closed flux surface due to ripple loss of initial alpha particle distribution after a slowing down time.3.2.波纹叠加NTM扰动后的粒子损失 -->3.2.波纹叠加NTM扰动后的粒子损失 仅考虑NTM扰动下的初始分布alpha粒子的损失全部发生在几个极向回弹周期内, 即使粒子跟踪时间为半个慢化时间, 如图6 所示. 经分析损失粒子能量、螺距角和损失时间分布后确认是初始轨道损失, 即由于产生在靠近边界的粒子有限轨道宽度引起, 扫描NTM扰动幅度不影响该损失份额. NTM扰动叠加碰撞后的粒子损失份额仅比初始轨道损失稍大, 是由于新经典效应引起. 考虑磁场波纹、NTM扰动以及碰撞效应下的粒子损失份额在1.4%附近, 扫描不同NTM扰动幅度, 损失份额基本不变. 俘获粒子轨道跨越宽度与扰动幅度成正比, 由图6 计算结果可知, NTM扰动和EP的主要分布没有覆盖波纹损失区, 粒子进入损失区数目不受NTM扰动影响.[26 ] . NTM扰动下俘获粒子的共振损失是极向回弹频率和环向进动频率接近, 从而和较低的扰动频率达到共振条件, 形成磁场漂移. 扰动频率为零时形成的共振称为几何共振, 扰动和EP没有交换能量. CFETR初始alpha粒子分布的俘获轨道运动频率并不满足与NTM的共振条件, 见图14 . 展示这些物理图像的有力工具是动理学庞加莱图.图 14 初始分布alpha粒子香蕉轨道漂移频率分布 (a) 极向回弹频率; (b) 环向进动频率Figure14. The drift frequency distributions of banana orbit of initial alpha particles: (a) Poloidal bounce frequency; (b) toroidal precession frequency.$n\zeta - $ $ \omega t = 2\pi k$ 时的平面坐标, k 是整数, 平面坐标可为(${\psi _{\rm{p}}}, \theta $ ), (${P_{\zeta} }, \theta $ )或($E, \theta $ ). 跟踪的粒子分布需要满足磁矩μ 和$\omega {P_{\zeta} } - nE$ 为固定值, 且螺距角相同符号[17 ] . 通过不稳定性扰动下的EP动理学庞加莱图可以观察到KAM面的破缺与否、共振岛位置和混沌区域宽度等信息. 图9 展示的是通行粒子和俘获粒子在扰动幅度较大时的共振岛分布, 通行粒子区域的${3 / 2}$ 和${2 / 1}$ 主共振岛和其间的高阶共振岛相互重叠形成宽域的混沌区域, EP因朗道相混而分布展平, 但是芯部和边界仍然存在完整的KAM面, 阻止了粒子直接损失. 俘获粒子区没观察到KAM面破缺, 即使增大动理学庞加莱图的记录分辨率仍如此. 值得指出的是香蕉轨道内外部分的漂移方向不同, 在记录轨迹点的庞加莱图(${P_{\zeta} }, \theta $ )平面中相互重叠, 不容易分辨, 分析时需要记录香蕉轨道转折点, 以此观察进动岛结构. NTM扰动幅度较小时, 上述相空间的岛状结构相互分立, 仅有局域的KAM面破缺. 通过动理学庞加莱图分析可推知, 无论NTM扰动幅度大小都不会引起alpha粒子的显著损失, 仅有局域的通行粒子剖面展平.图 9 同向alpha粒子动理学庞加莱图 (a) 通行粒子; (b) 俘获粒子Figure9. The kinetic Poincare plot of co-current alpha particles: (a) Passing particle; (b) trapped particle.3.3.不同磁场波纹幅度下的粒子损失 -->3.3.不同磁场波纹幅度下的粒子损失 为了验证图6 中增大NTM扰动幅度而粒子损失份额不变的原因, 增大装置整体波纹度, 进行图6 中磁场波纹叠加NTM扰动并考虑碰撞下的粒子损失计算, 结果如图10 所示. 在CFETR装置实际波纹度分布下, alpha粒子的损失份额并不随NTM扰动幅度增大而增大, 但增大波纹度从工程设计值到其9倍时, 粒子损失份额随波纹度增大而显著增大. 在波纹度较大时, 可观察到一定程度的损失份额随NTM扰动幅度增大而增大. 波纹度分布整体增大引起波纹损失区扩大, 使波纹损失区朝芯部扩展并覆盖更多的粒子. 以波纹磁阱区域为例, 不同波纹度分布对应的磁阱区域如图11 所示, 随着波纹损失区扩展, 逐渐靠近NTM扰动和EP主分布区, NTM扰动幅度增大开始影响进入损失区的粒子数.图 10 半个慢化时间内不同磁场波纹度和NTM扰动幅度下的初始分布alpha粒子损失份额Figure10. The loss fraction of initial alpha particles under different toroidal ripple and NTM perturbation amplitude.图 11 CFETR平衡位形中不同波纹度形成的波纹磁阱 (a) 工程设计值; (b) 5倍波纹度分布; (c) 9倍波纹度分布Figure11. The ripple well domain in CFETR equilibrium with different ripple amplitude: (a) Distribution with engineering design; (b) 5 times of ripple; (c) 9 times of ripple.4.讨 论 为了系统地讨论CFETR上alpha粒子经NTM和波纹扰动的损失图像, 本节采用EP相空间损失区域和粒子分布密度来评估. 初始分布的alpha粒子能量单值分布, 即决定粒子轨道的三个物理量中固定E , 可以得到一个二维平面(${P_{\zeta} }, {{\mu {B_0}} / E}$ ), ${B_0}$ 是磁轴处磁场强度, 为ORBIT中磁场强度单位. 在轴对称位形和能量守恒关系下可以在(${P_{\zeta} }, {{\mu {B_0}} / E}$ )平面内得到一系列曲线分割的不同轨道类型区域, 如图12(a) 所示, 其中T-C指约束俘获粒子轨道, T-L指损失俘获粒子轨道, ${{P_ \pm } - L}_{{{\rm{P}}_ \pm } - {\rm{L}}}$ 指损失通行粒子轨道, p± -C指约束通行粒子轨道, 下标的正负号指螺距角符号[17 ] . 该平面中还有一些特殊的轨道, 如土豆轨道和极向静止轨道, 因在本文分析对象中占比过小, 及不可见没有标记出. 在不同平衡位形和EP能量时的该平面轨道类型区域占比不同, 但拓扑结构基本不变. 图12(b) 和图12(c) 是初始alpha粒子分布中不同螺距角正负号的样本粒子在(${P_{\zeta} }, {{\mu {B_0}} / E}$ )平面的分布. CFETR混杂运行模式的初始分布alpha粒子中有28%份额的俘获粒子, 值得注意的是, 俘获粒子区域在不同螺距角正负号下的粒子轨道仅仅是香蕉轨道的内外分支, 是同一轨道.图 12 (a) (${P_{\zeta} }, {{\mu {B_0}} / E}$ )平面初始alpha粒子轨道类型分布; (b) 正值螺距角粒子分布; (c) 负值螺距角粒子分布Figure12. (a) Orbit classification in the plane of $({P_{\zeta} }, {{\mu {B_0}} / E})$ with initial alpha particles; (b) particles with positive pitch angle; (c) particles with negative pitch angle.图13 是(${P_{\zeta} }, {{\mu {B_0}} / E}$ )平面内不同波纹扰动幅度下的波纹损失区域, 其中波纹磁阱俘获区由磁阱形成条件$\varepsilon \left| {\sin \theta } \right| < qN\delta $ 确定, 无碰撞波纹随机扩散区的确定依据是简化判据GWB(Goldston, White and Boozer)${\delta _{\rm{s}}} = {{{{[{\varepsilon / {N{\text{π}}q}}]}^{1.5}}} / {({\rho _{\rm{L}}}q')}}$ , ε 是当地的纵横比倒数, $q' = {{{\rm{d}}q} / {{\rm{d}}r}}$ 是安全因子径向导数. 图13中的波纹磁阱俘获损失区主要分布在粒子轨道的俘获-通行转换边界和外边界处,同图11所示一致. 图13 展示了增大整体波纹扰动幅度时, 波纹损失区逐渐扩大, 占据大部分俘获粒子分布, 同图10 纵轴方向的计算结果一致. 当波纹度增大倍数较大时, 在俘获-通行边界附近的粒子才可能进入损失区. NTM扰动和碰撞效应可以使粒子在俘获和通行状态间转换, NTM扰动幅度越大, 越多的粒子受其扰动进入俘获粒子区域, 从而经历波纹损失, 即图10 观察到的波纹度较大时粒子损失份额随NTM扰动幅度增大而增大.图 13 不同倍数波纹度分布时的波纹磁阱和随机波纹扩散区域 (a), (b) 工程设计值; (c), (d) 5倍波纹度分布; (e), (f) 9倍波纹度分布Figure13. The ripple well trapping and stochastic ripple diffusion domain with different times of ripple distribution: (a), (b) Ripple in engineering design; (c), (d) 5 times of ripple; (e), (f) 9 times of ripple.${{{\nu ^*}} / {{{(Nq)}^2}}} - {{{\nu ^*}} / {{{(Nq)}^{0.5}}}}$ , 其中${\nu ^*} = {{\varepsilon {\omega _{\rm{b}}}} / {(2\pi )}}$ . 螺距角散射引起香蕉粒子转折点相位随机, 对应径向位移随机震荡, 需要俘获粒子一次极向周期内经历足够多的碰撞次数, 经历一次碰撞期间经历了数个波纹扰动起伏, 连续轨道之间完全解耦[23 ] . 初始alpha粒子的香蕉轨道周期运动频率图如图14 所示, 取极向回弹频率在${\omega _b}\sim 20$ —$ 40\;{\rm{ kHz}} $ , 判别频率${{{\nu ^*}} / {{{(Nq)}^2}}} \sim 0.5$ —$ 4.0\;{{\rm{s}}^{ - 1}} $ , 远高于初始分布alpha粒子的螺距角散射率, 因此无碰撞波纹随机扩散是CFETR初始分布alpha粒子的主要损失通道. 随着alpha粒子能量慢化, 粒子碰撞率增大, 碰撞效应在波纹损失过程中有更大贡献.5.结 论 本文对CFETR上磁场波纹和NTM扰动叠加下的初始分布alpha粒子损失进行了详细的数值模拟, 结果显示粒子损失份额并不随NTM扰动幅度增大而增大, 与其他装置的结论不同. 原因是CFETR运行模式下的波纹损失区域较小, 没有覆盖EP和NTM扰动主要分布区. 人为增大装置波纹度才会观察到粒子损失份额随NTM扰动增大而增大, 原因是波纹损失区扩大靠近俘获-通行边界时, NTM扰动和有限碰撞引起边界附近粒子的轨道状态转换, 使粒子不断地从通行粒子区域进入俘获粒子区域. CFETR工程实际的波纹度较小, 波纹损失区离俘获-通行边界较远, 不足以发生粒子持续的跨过转换边界进入损失区. 











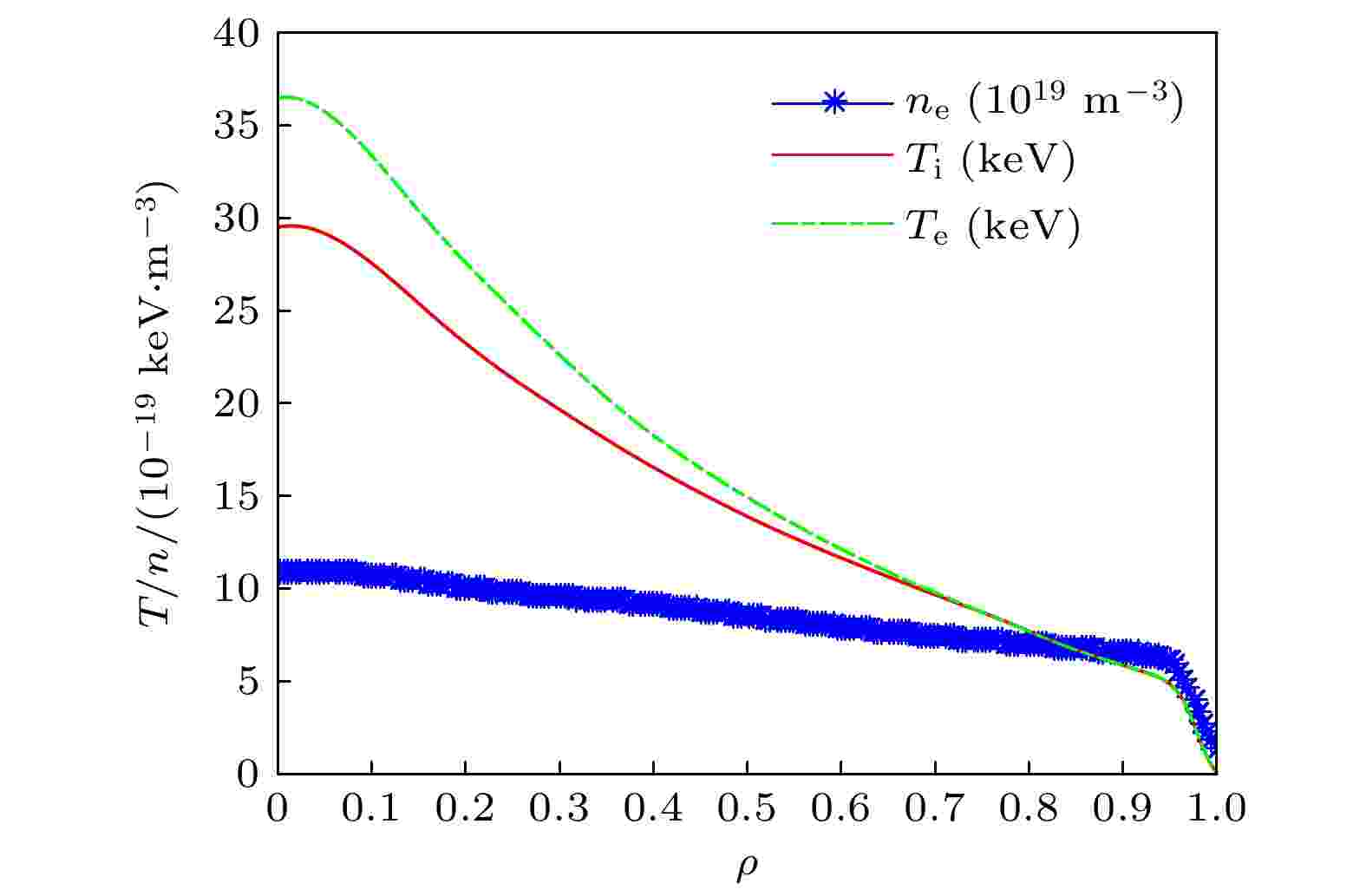 图 1 CFETR混杂运行模式(v201806)中背景电子密度、温度和离子温度分布
图 1 CFETR混杂运行模式(v201806)中背景电子密度、温度和离子温度分布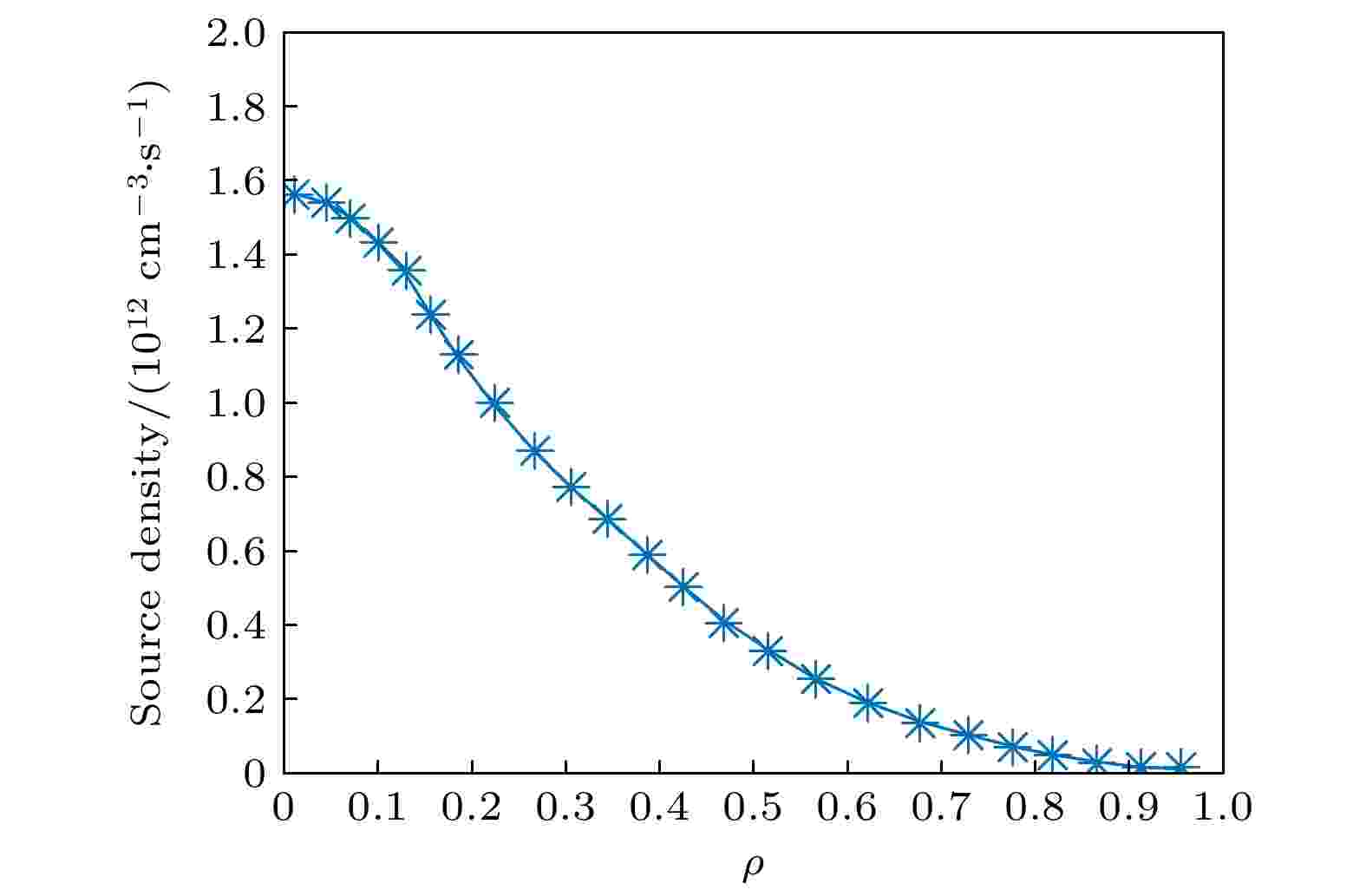 图 2 CFETR初始alpha粒子密度分布
图 2 CFETR初始alpha粒子密度分布












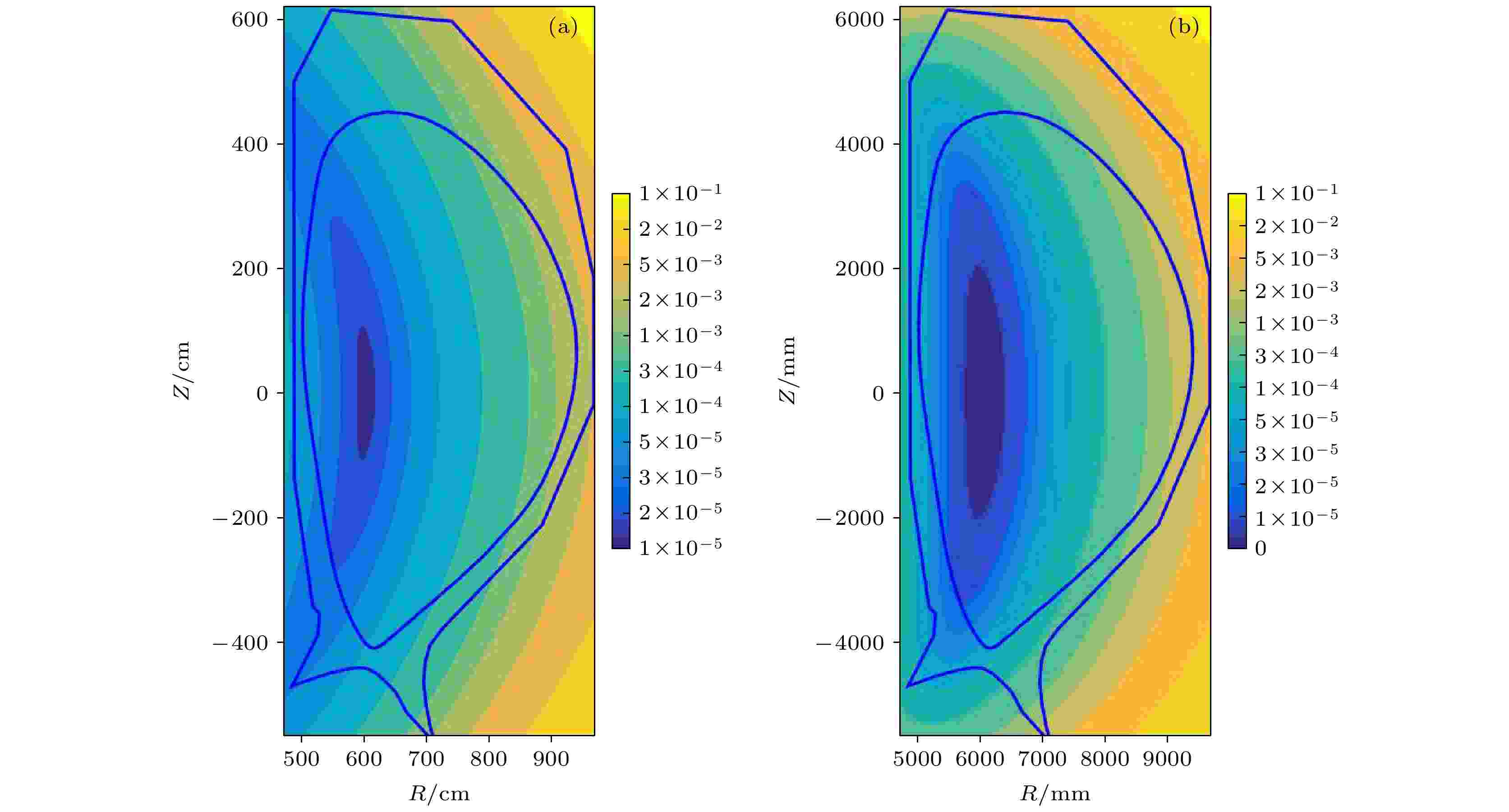 图 3 CFETR纵场波纹度分布 (a) 解析函数实现值; (b) 工程设计值
图 3 CFETR纵场波纹度分布 (a) 解析函数实现值; (b) 工程设计值





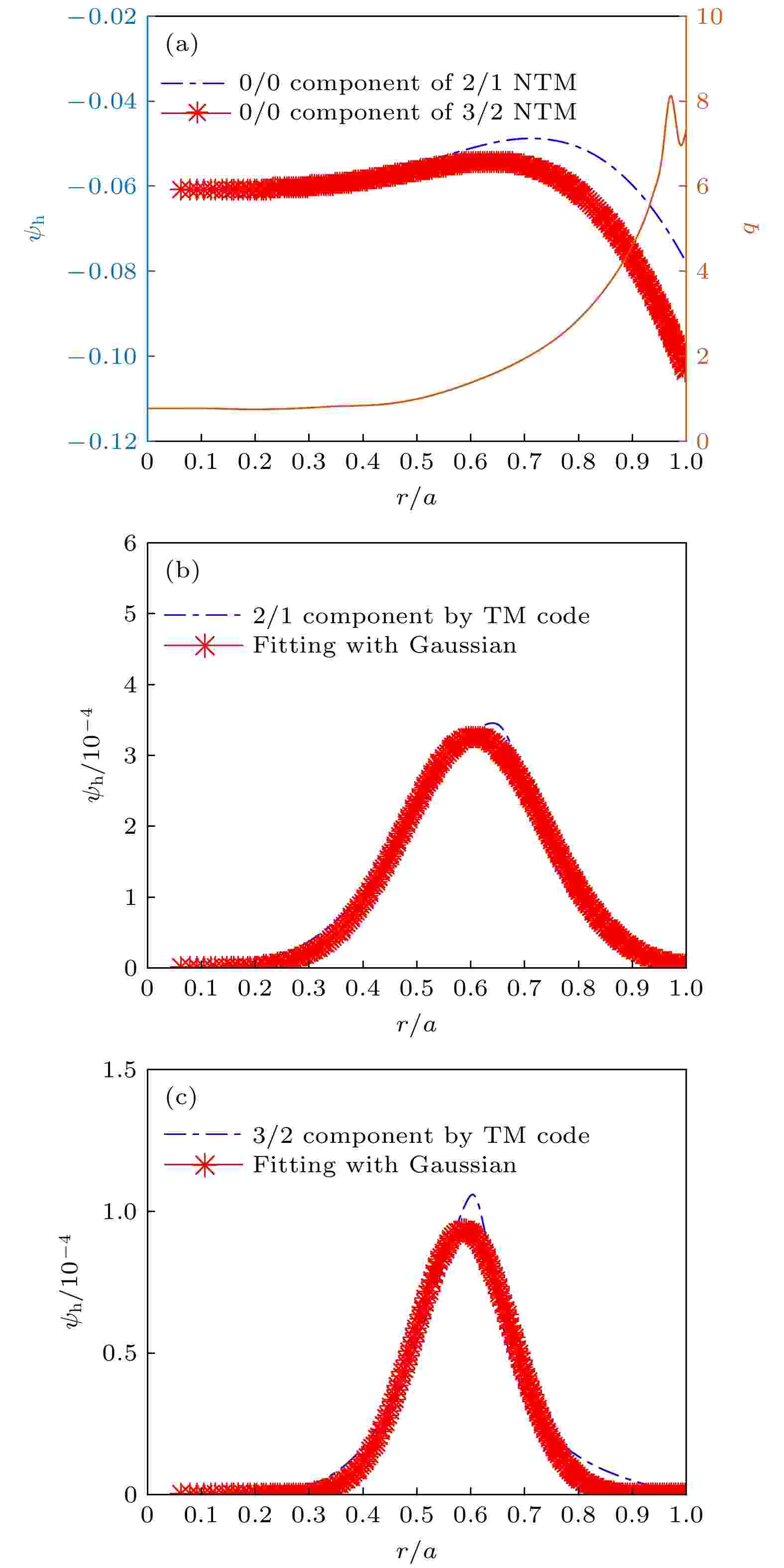 图 4 CFETR混杂运行模式 (a) 2/1和3/2 NTM的平衡分量和安全因子分布; (b), (c)一阶分量和高斯拟合曲线
图 4 CFETR混杂运行模式 (a) 2/1和3/2 NTM的平衡分量和安全因子分布; (b), (c)一阶分量和高斯拟合曲线






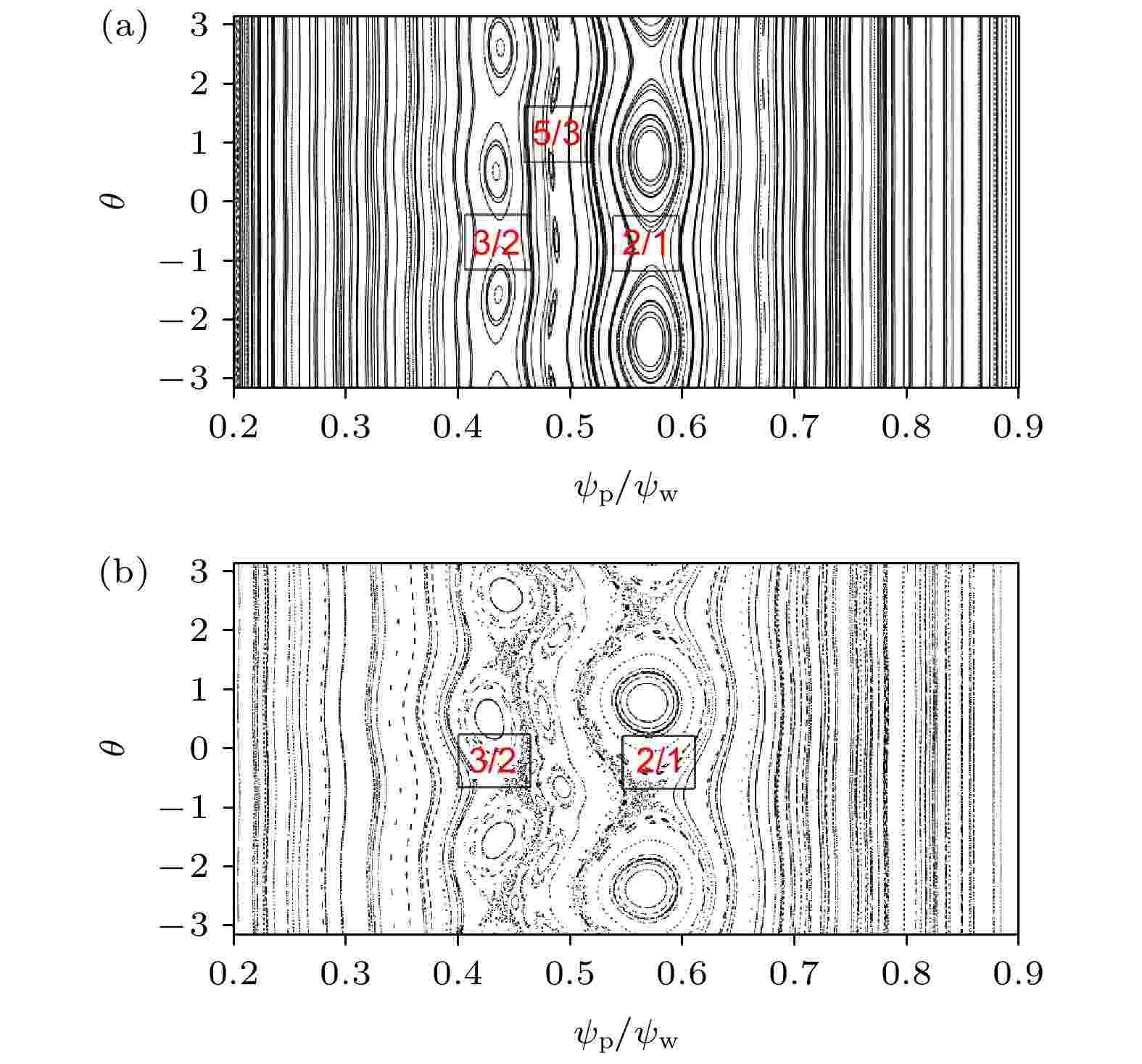 图 5 固定2/1和3/2模扰动幅度比例下扫描NTM扰动幅度下的庞加莱图 (a)
图 5 固定2/1和3/2模扰动幅度比例下扫描NTM扰动幅度下的庞加莱图 (a) 
















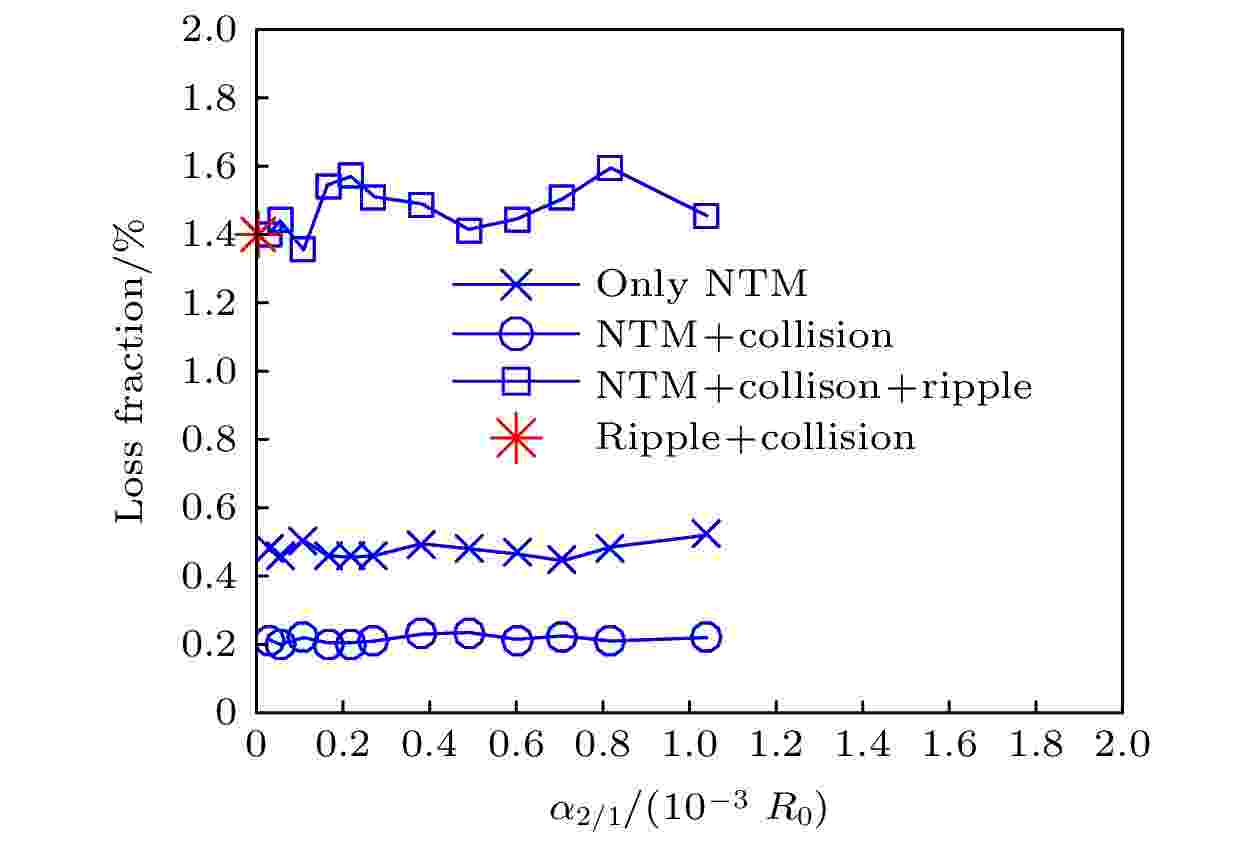 图 6 在半个EP慢化时间内不同物理效应下计算得到的粒子损失份额
图 6 在半个EP慢化时间内不同物理效应下计算得到的粒子损失份额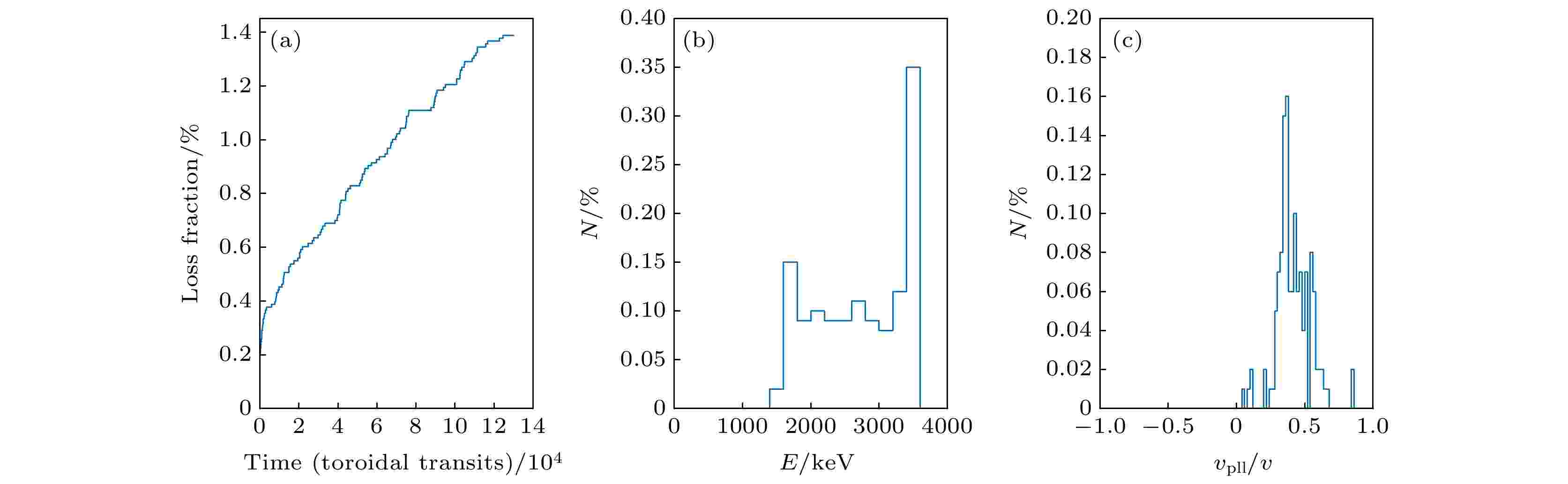 图 7 纵场波纹扰动下损失alpha粒子信息 (a) 损失份额随时演化; (b) 损失粒子能量分布; (c) 损失粒子螺距角分布
图 7 纵场波纹扰动下损失alpha粒子信息 (a) 损失份额随时演化; (b) 损失粒子能量分布; (c) 损失粒子螺距角分布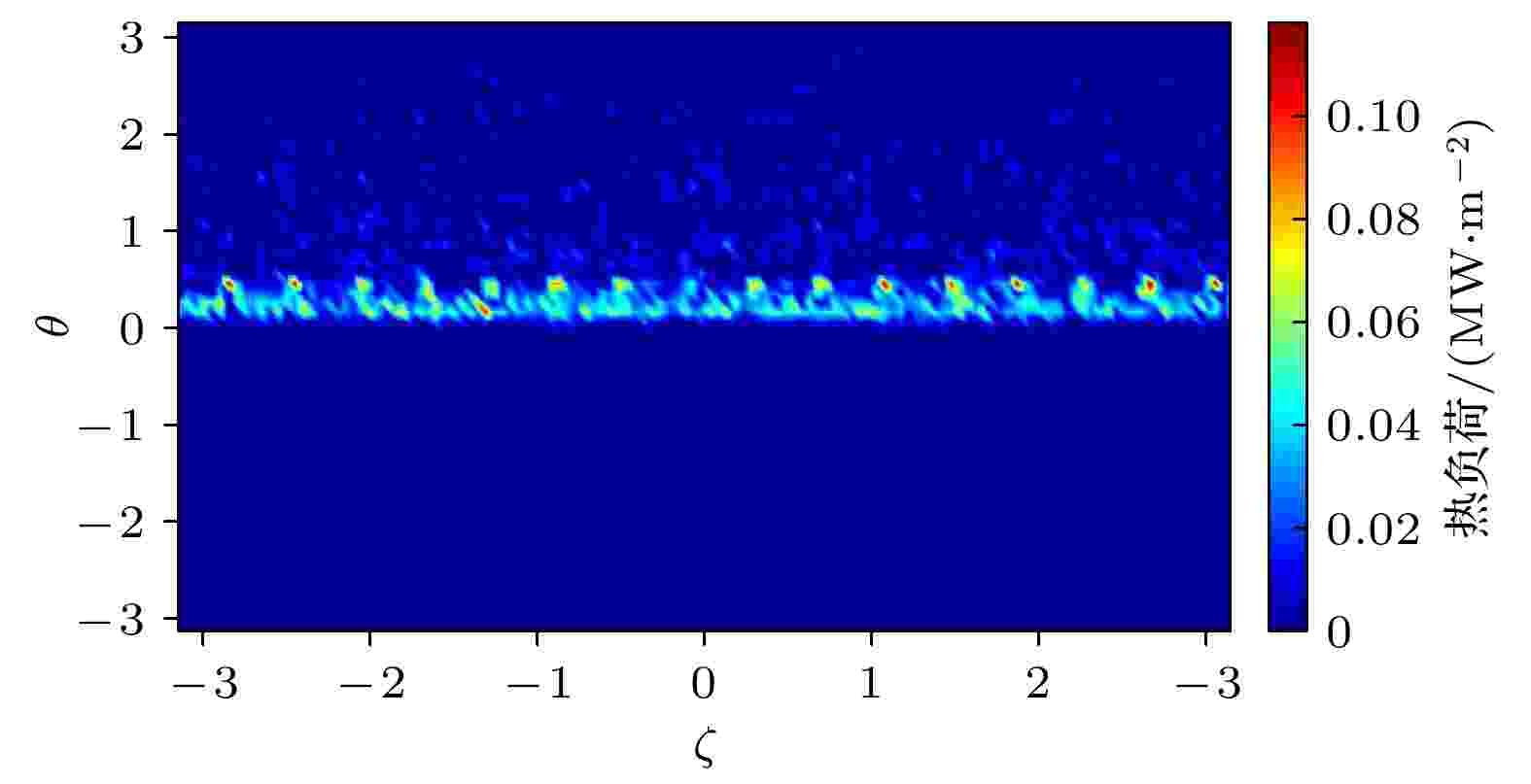 图 8 一个慢化时间后初始分布alpha粒子波纹损失局域沉积在LCFS处得到的热负荷
图 8 一个慢化时间后初始分布alpha粒子波纹损失局域沉积在LCFS处得到的热负荷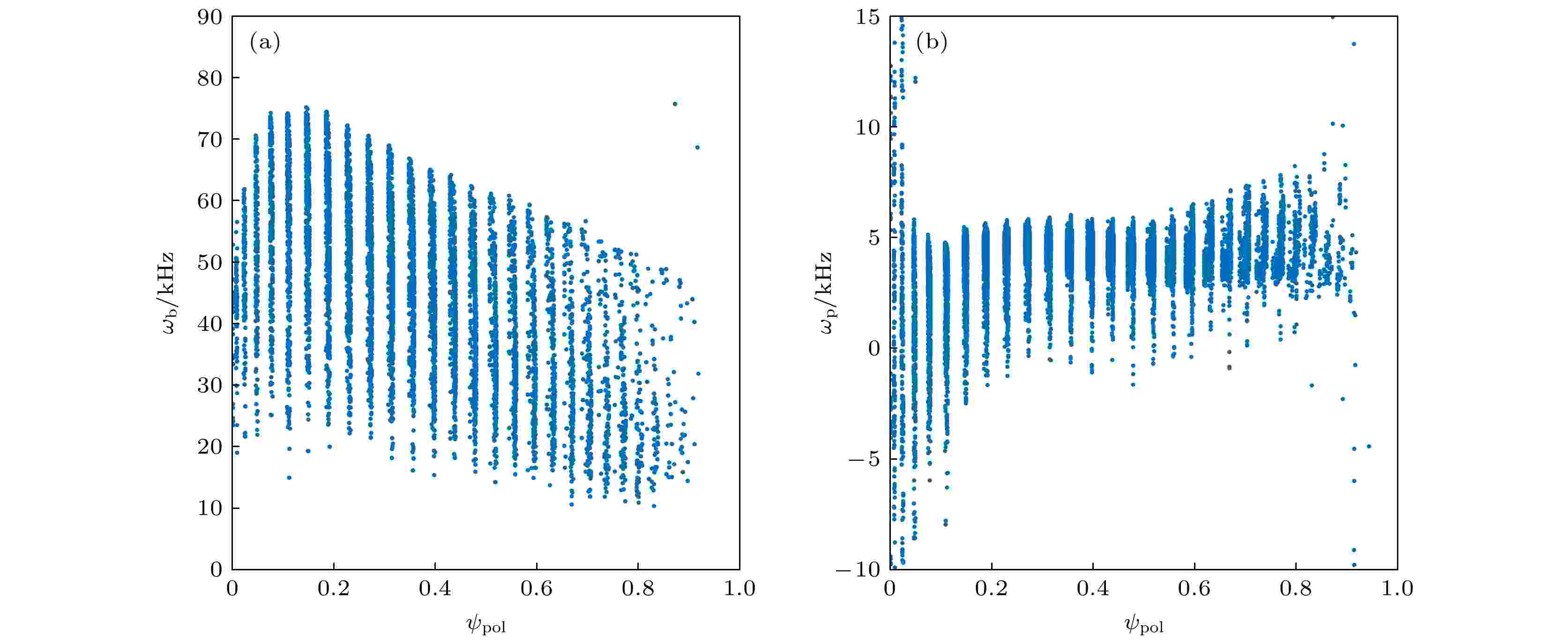 图 14 初始分布alpha粒子香蕉轨道漂移频率分布 (a) 极向回弹频率; (b) 环向进动频率
图 14 初始分布alpha粒子香蕉轨道漂移频率分布 (a) 极向回弹频率; (b) 环向进动频率










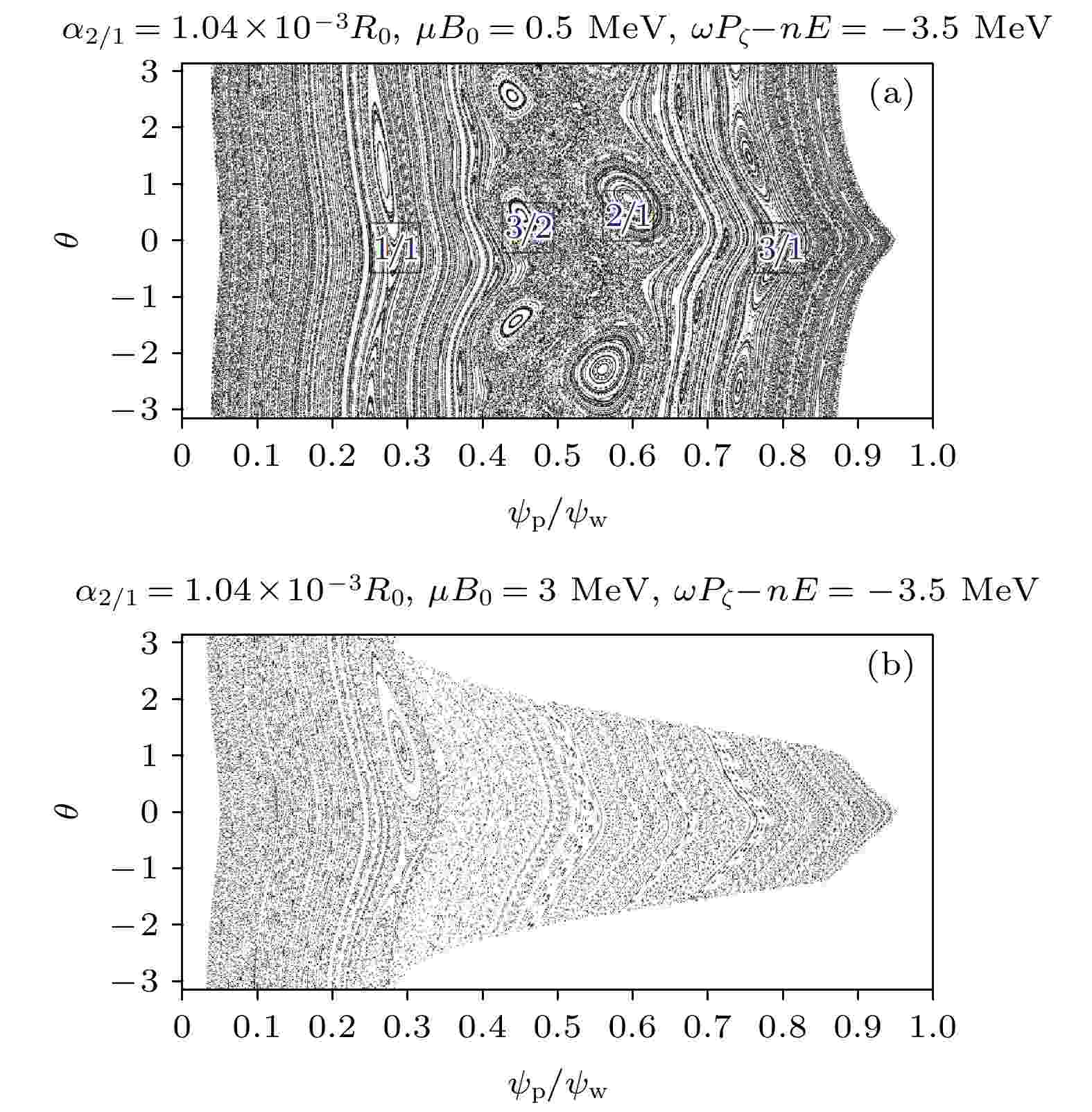 图 9 同向alpha粒子动理学庞加莱图 (a) 通行粒子; (b) 俘获粒子
图 9 同向alpha粒子动理学庞加莱图 (a) 通行粒子; (b) 俘获粒子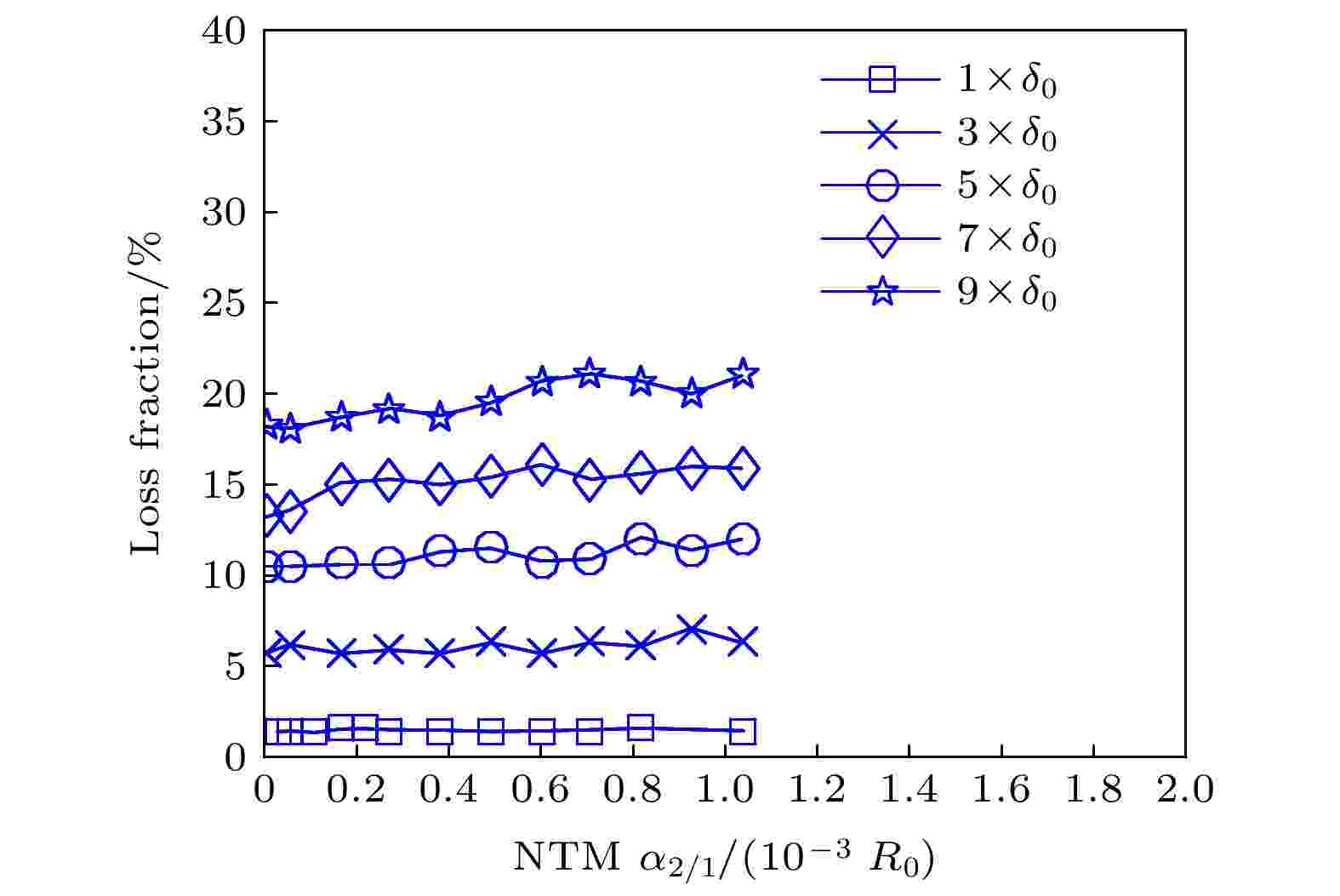 图 10 半个慢化时间内不同磁场波纹度和NTM扰动幅度下的初始分布alpha粒子损失份额
图 10 半个慢化时间内不同磁场波纹度和NTM扰动幅度下的初始分布alpha粒子损失份额 图 11 CFETR平衡位形中不同波纹度形成的波纹磁阱 (a) 工程设计值; (b) 5倍波纹度分布; (c) 9倍波纹度分布
图 11 CFETR平衡位形中不同波纹度形成的波纹磁阱 (a) 工程设计值; (b) 5倍波纹度分布; (c) 9倍波纹度分布










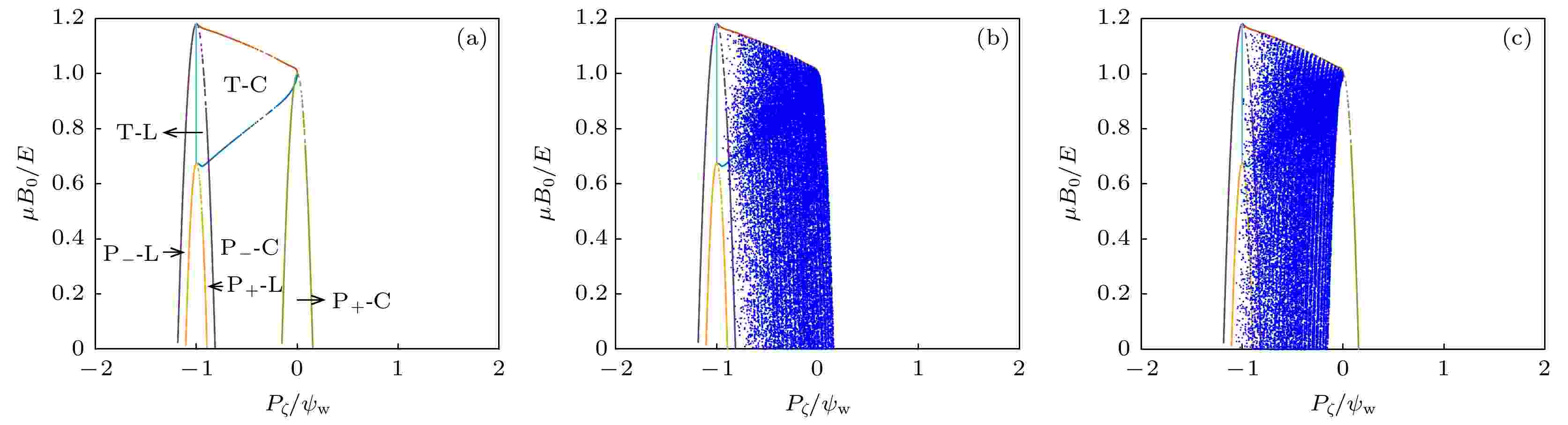 图 12 (a) (
图 12 (a) (





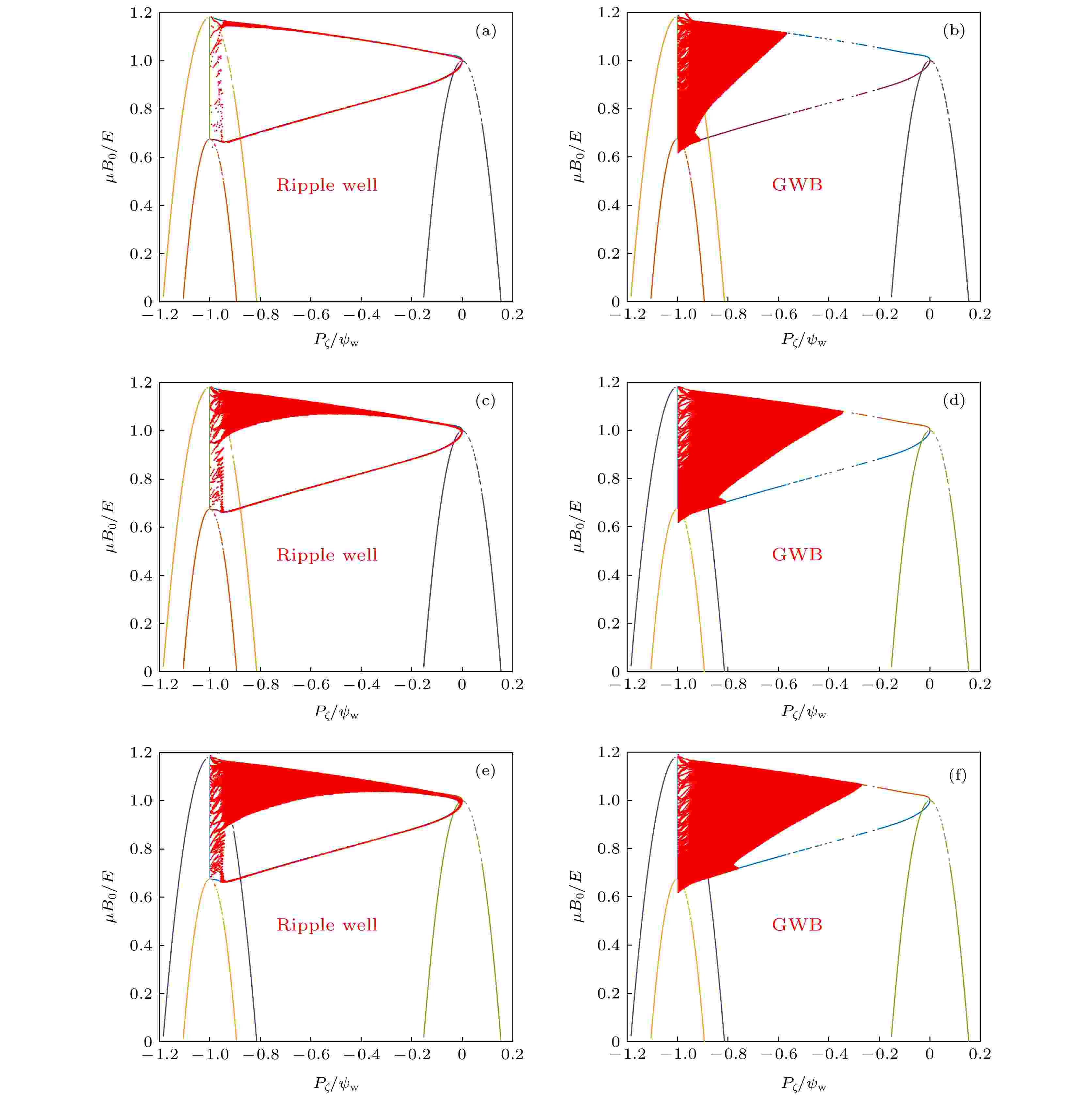 图 13 不同倍数波纹度分布时的波纹磁阱和随机波纹扩散区域 (a), (b) 工程设计值; (c), (d) 5倍波纹度分布; (e), (f) 9倍波纹度分布
图 13 不同倍数波纹度分布时的波纹磁阱和随机波纹扩散区域 (a), (b) 工程设计值; (c), (d) 5倍波纹度分布; (e), (f) 9倍波纹度分布






