摘要: 受海面强风和海-气相互作用影响, 表面声道普遍存在于冬季海洋环境中, 是一种天然有利于声传播的波导. 但是海面波浪使得海表形成粗糙界面, 会严重破坏这种优良性能. 本文利用南海北部海区的一次冬季声传播实验数据, 研究表面声道声传播特性. 研究表明, 海底底质对表面声道内声传播的影响较弱, 当海面风较小时, 涌浪造成的影响为主要原因. 实验数据显示, 考虑涌浪后的粗糙海面给
$70\;{\rm{km}}$ 远处带来了
$10\; {\rm{dB}}$ 的传播损失增长. 因此在考察南海北部海区冬季声场特性时, 不仅要考虑海面风浪的影响, 更需要考虑周围海域传来的涌浪的影响. 研究涌浪存在时的声传播特性对提升声纳设备在海况较差时的使用性能具有重要意义.
关键词: 涌浪 /
粗糙海面 /
表面声道 /
声传播 English Abstract Effects of swells on sound propagation in surface duct environment in shallow water Liu Jin 1,2 ,Peng Zhao-Hui 1 ,Zhang Ling-Shan 1 ,Liu Ruo-Yun 1,2 ,Li Zheng-Lin 1 1.State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11674349, 11974017, 11874061)Received Date: 17 September 2020Accepted Date: 24 October 2020Available Online: 25 February 2021Published Online: 05 March 2021Abstract: Surface duct is a common duct due to strong sea winds and sea-atmosphere interactions in winter and it is an excellent waveguide in which energy may propagate a long distance. However, the rough interface formed by sea surface waves will seriously damage this excellent performance. In this study, the experimental data of sound propagation over the continental slope in the South China Sea are used to analyze the characteristics of sound propagation in a surface duct. Modeling analyses based on the parabolic equation model RAM and ray trace theory BELLHOP are used to examine these characteristics. The parameters of sea bottom, source depth, wind-driven sea surface, and swell-containing sea surface are taken into consideration in the model. The results show that when the source is located in the surface duct, the parameters of the sea bottom have little influence on sound propagation, while the change of source depth exerts some effects on the sound propagation. By combining the Pierson Moscowitz (PM) spectrum with Monte Carlo method, the rough sea surface is investigated. Since the PM spectrum is related only to wind speed, the wind-driven sea surface is generated by using the actual wind speed measured by the shipborne anemometer. The swell-containing sea surface is defined as a superposition of a sinusoidal pressure-release surface and the wind-driven sea surface. By comparing the effects of two sea surfaces on sound propagation, it is found that when the wind speed is small, swells play an important role in the surface-duct propagation. Experimental data show that for the acoustic signal with a center frequency of $1000\;{\rm{Hz}}$ , the swell-containing sea surface brings around $10 \;{\rm{dB}}$ loss to a distance of $70 \;{\rm{km}}$ . For the two kinds of rough sea surfaces, rays at launch angles of $\pm 1^{\circ}, 0^{\circ}$ are plotted to examine their effects on sound propagation. The results indicate that the swell-containing sea surface which has greater roughness makes rays go toward the sea bottom, thus resulting in larger loss. Therefore, in order to investigate the characteristics of the sound field in the northern South China Sea in winter, especially with high frequency sound signals, the influences of not only winds and waves, but also the swells from the surrounding sea should be taken into consideration. It is important to study the characteristics of sound propagation with swells for improving the performance of sonar equipment in poor sea conditions.Keywords: swell /rough sea surface /surface duct /sound propagation 全文HTML --> --> --> 1.引 言 在海洋中, 由于湍流和风浪的搅拌作用, 使得近海面的水体混合均匀形成等温层, 一般为几十米到上百米. 此时海水声速受到静压力的作用呈现正梯度分布, 从而形成表面声道. 当声源位于表面声道内时, 由于没有海底损耗, 声波可以在由海面以及表面声道底部形成的波导内实现远距离传输. 但另一方面, 当声波不停地与海面碰撞时, 粗糙界面则会给声场带来很大影响.[1 ] , 还会影响声场的干涉结构, 对声场预报、水声通信[2 ] 、水下定位[3 ] 、海底参数反演[4 ] 等工作均会产生影响. 而声场特性研究是以上研究的基础, 因此开展粗糙海面下声场特性研究具有重要意义.[5 ,6 ] 以及基于抛物方程的RAM[7 ,8 ] 声场计算模型. 在这些计算模型的基础上, ****们开展了大量粗糙海面下声场特性的研究, 主要包括对声衰减、时空相关性以及信号时间到达的影响的研究. Liu和Li[9 ] 通过仿真实验指出, 在浅海环境中, 粗糙海面下声传播损失的概率分布和声场的散射衰减与风速、距离、频率等因素有关; Zou和Badiey[10 ] 通过对比宽带声源在不同风速条件下形成的声压场, 指出海面粗糙度是造成声信号衰减的主要因素, 而气泡散射和多普勒频移是次要因素; Weston和Ching[11 ] 基于一次浅海实验数据总结出声衰减系数与频率和风速的关系式; 王先华[12 ] 和姚美娟等[13 ] 分别基于不同的海浪谱模型构造粗糙海面, 通过实验验证了粗糙海面带来了传播损失上的衰减; Karjdi等[14 ] , Tindle和Deane[15 ] , Siderius和Porter[16 ] 等均使用浅海实验数据验证了粗糙表面建模对于仿真时间到达结构的重要性; Badiey等[17 ] 及Dahl[18 ] 基于浅海实验数据分别指出粗糙海面会使得信号的时间、空间相关性下降.2.声传播理论 考虑到水平变化环境和海面粗糙条件, 本文选取RAM声场计算模型, 将粗糙海面考虑进海面边界条件进行仿真和实验验证, 该方法已被实验证实具有有效性[13 ] . 考虑柱系下, 假设各个变量与方向无关, 密度$ \rho $ 随距离变化十分缓慢, 声源位于$ r = 0 $ , $ z = z_0 $ 时, 声压P 所满足的频域声压方程为$ \rho $ 为密度($ {\rm{g}}/{\rm{cm}}^3 $ ); $K = k+{\rm i}\eta\beta|k|$ , 其中$k = w/c$ , $\eta = (40\pi {\rm {log}}_{10}{\rm e})^{-1}$ , w 为角频率, c 为声速(m/s), $ \beta $ 为海底吸收系数($ {\rm{dB}}/{{\lambda}} $ ).$ Q = \sqrt r P $ , 假设$kr \gg 1$ , 只考虑外行波, 将方程(1 )进行简化近似得到方程(2 ),3 )式中根号下部分进行帕德展开近似, 并令$ Q = U{\rm e}^{{\rm i}k_0 r} $ , (3 )式可化为(5 )式的形式:$a_{j, n} = [2/(2 n\,+\,1)]\,{\rm{sin}}^2$ $[\,j\pi/(2 n+1)]$ , $b_{j, n} = {\rm{cos}}^2$ $ [j\pi/(2 n+1)] $ , 由(5 )式可解得Q 和P 依次代入(6 )式中, 并假设在远场$\Delta r \ll r$ , 由此可得到声压的递推表达式为$ P(z = 0) = 0 $ , 而在粗糙海面条件下, 假设海面起伏高度为$ h(r) $ , 这时声压所满足的上边界条件为$ P(z = h(r)) = 0 $ .3.实 验 2017年12月, 中国科学院声学研究所声场声信息国家重点实验室在南海北部陆坡海区进行了一次声传播实验. 实验采用如图1 所示的单船结合潜标的作业方式. 图中左侧为采用垂直线列阵形式的潜标接收系统, 由自容式水听器和温深传感器组成, 其中有效水听器为17个, 在深度25—330 m之间非均匀布放, 信号采样率为$16\; {\rm{kHz}}$ . 作业期间, 实验1号科考船沿着声传播路径投掷$1\; {\rm{kg}}$ TNT当量的爆炸声源, 爆炸声源标称深度为$50\; {\rm{m}}$ . 图2 给出了沿途利用万米测深仪测得的海深情况, 在接收阵附近存在一个缓坡, $20\; {\rm{km}}$ 之后海深较为平坦. 图3 给出了实验过程中的声速剖面, 通过每隔约$10\; {\rm{km}}$ 投放一枚投弃式温深仪(XBT), 获取海水温度随深度的变化, 通过接收站位投放的声速仪测得的盐度数据, 根据经验公式[19 ] 计算沿途的声速剖面. 从图3 可以发现, 实验过程中一直存在表面声道, 红色方框圈出了表面声道底部的位置, 可以看出表面声道的厚度在发生变化, 最浅为$74\; {\rm{m}}$ , 最深为$107\; {\rm{m}}$ , 在距接收阵25—44 km内表面声道深度变化较小.图 1 实验设备布放示意图Figure1. The configuration of the experiment.图 2 实测海底地形Figure2. The measured bathymetry.图 3 测线上声速剖面Figure3. Measured sound speed profiles along the track.图4 给出了第1个和第11个水听器的深度变化, 横轴表示每个爆炸声源爆炸的位置距接收阵的距离. 上层的第1个水听器深度在42—61 m, 平均深度为$51\; {\rm{m}}$ , 波动范围达到$19\; {\rm{m}}$ , 下层的第11个水听器平均深度为$206\; {\rm{m}}$ , 波动深度为$14\; {\rm{m}}$ . 尽管第1个水听器深度一直在波动, 但是始终处于表面声道内. 根据互易原理[20 ] , 在声场仿真中, 水听器所处深度为声源深度, 爆炸声源深度为接收深度, 计算结果应该不变. 此时, 相当于声源深度在表面声道内浮动. 声源深度对表面声道内声传播有重要影响[21 ] , 因此, 在后面的声场仿真中, 将采用随距离分段变化的声源深度. 在本文的实验环境中声源深度对声场的影响将在第4 节进行讨论.图 4 实测的第1个和第11个水听器的深度变化 (a) 第1个水听器; (b) 第11个水听器Figure4. Depths of the first and eleventh hydrophone measured in the experiment: (a) The first hydrophone; (b) the eleventh hydrophone.4.声场仿真与实验结果分析 24.1.底质参数对表面声道声传播的影响 4.1.底质参数对表面声道声传播的影响 本文重点研究冬季表面声道的声传播特性. 根据表面声道的特点, 当声源频率大于表面声道的截止频率时, 声能量将大部分被限制在表面声道中, 与海底作用的能量较少, 因此海底底质参数对表面声道的影响可以忽略. 下面通过传播损失和声线的仿真分析, 以及实验数据验证上述结论.$ 51\; {\rm{m}} $ , 该位置处表面声道厚度为$74\; {\rm{m}}$ . 根据文献中的表面声道截止频率公式[21 ] 可求得, 当声源深度在18.5—74.0 m之间时, 表面声道的截止频率约为$234\; {\rm{Hz}}$ . 因此, 理论上当声源频率大于$234\; {\rm{Hz}}$ 时, 声能量将大部分被限制在表面声道内, 海底底质对表面声道内的声传播影响很弱. 这里选择声源中心频率为$1000\; {\rm{Hz}}$ 进行探讨.图5 给出了中心频率为$1000\; {\rm{Hz}}$ , 带宽为1/3倍频程条件下, 声源深度为$51\; {\rm{m}}$ , 接收深度为$50\; {\rm{m}}$ 时的仿真和实验传播损失结果. 声速剖面和海底地形采用实测结果, 海面为平整的压力释放表面, 并且考虑了海水衰减[20 ] . 这里取两组海底参数, 一组偏“硬”, 一组偏“软”. 硬海底参数为文献[22 ]中反演结果, $c_{\rm s} = 1536\; {\rm{m}}/{\rm{s}},\; \rho_{\rm s} = 1. 47\; {\rm{g}}/{\rm{cm}}^3, \;\alpha_{\rm s} = 0.45\; {\rm{dB}}/\lambda$ . 对于所研究频段, 单层海底模型已经足够, 所以这里只取反演结果中的沉积层声速和密度. 另一组软海底参数为, $c_{\rm s} = 1500\; {\rm{m}}/{\rm{s}},\; \rho_{\rm s} = 1. 0\; {\rm{g}}/{\rm{cm}}^3, \;\alpha_{\rm s} = 1. 0\; {\rm{dB}}/\lambda$ . 对比红线和蓝色两个仿真结果可以发现, 海底底质对传播损失在数值上影响不大, 对干涉结构会产生一些影响, 尤其在近距离差异比较大. 主要体现在, 软海底时曲线变得光滑, 这是因为声场的模态数目减少, 干涉结构变得更加简单. 从声线角度也可以解释, 给出声源深度在$51\; {\rm{m}}$ , 声源频率为$1000\; {\rm{Hz}}$ 时, 软海底和硬海底条件下的声线图, 掠射角选择$ \pm12^{\circ} $ , $ \pm6^{\circ} $ , $ 0^{\circ} $ , 结果如图6 . 可以明显看出, 表面声道内的声场主要由只与海面触碰的反转声线和与海底海面均碰撞反射声线组成. 硬海底下, 与海底海面均触碰的声线衰减相对较慢, 与反转声线叠加, 由此造成硬海底下传播损失干涉结构相对复杂. 将图5 中仿真结果与实验结果进行对比, 可以看出仿真结果从近距离就已经开始偏低. 并且当距离超过$40\; {\rm{km}}$ 时, 仿真传播损失增大得十分缓慢, 说明能量可以在表面声道内进行高效传输, 而实测结果则不然, 传播损失随距离增加增长很明显.图 5 两种海底条件下第1个水听器的传播损失Figure5. The transmission loss of the first hydrophone under two kinds of seabed.图 6 两种海底条件下的声线 (a)硬海底; (b)软海底Figure6. Ray traces under two kinds of seabed: (a) Hard bottom; (b) soft bottom.4.2.声源深度对声场的影响分析 -->4.2.声源深度对声场的影响分析 实验期间声源深度变化较大, 考虑到表面声道中声源深度的变化可能对表面声道内声传播损失产生较大的影响, 接下来分析在本文的实验环境中, 声源深度对声场的影响. 图7 为平整海面, 海底参数与4.1 节硬海底所用参数一致时, $1000\; {\rm{Hz}}$ 中心频率, 1/3倍频程条件下, 将上下两个水听器波动到最深和最浅位置的深度作为声源深度, $50\; {\rm{m}}$ 接收深度处的传播损失的仿真结果, 并将实验结果作为参照. 对比图7(a) 和图7(b) 可以明显看出, 声源在上层时, 传播损失整体偏小. 同时上层水听器的波动对声场的影响比较大, 体现在干涉结构和能量上均有较大的差异, 波动到较深的位置时, 仿真的传播损失会较大. 而下层水听器的波动对声场的影响不大. 两个水听器的仿真结果均与实验结果相差较大.图 7 声源深度d s 为两个水听器在深度波动的两个端点时的仿真传播损失与实验结果的比对 (a) 第1个水听器; (b) 第11个水听器Figure7. Comparisons of modeled and measured transmission loss of two hydrophones at their respective depth endpoints: (a) The first hydrophone; (b) the eleventh hydrophone.4.3.粗糙海面对表面声道声传播的影响 -->4.3.粗糙海面对表面声道声传播的影响 34.3.1.风浪下粗糙海面建模 -->4.3.1.风浪下粗糙海面建模 当声波在表面声道内频繁地与海面接触时, 粗糙海面会对声场产生重要影响. 在研究粗糙海面下的声场特性之前, 首先要进行海面建模. 目前已有的海面建模研究方法主要包含两大类[23 ] . 一类是基于物理模型的线性和非线性波浪理论, 这种方法是用物理方程将波浪的运动过程描述出来, 该方法的优点是建模结果比较符合实际情况, 缺点是模型复杂, 计算量大, 实时性较差[24 ] ; 另一类是基于随机理论和统计分析的随机海浪理论法, 对不同条件下的波浪运动进行统计分析得到波浪运动的统计特性, 在这种方法的研究过程中, 发展出了海谱建模方法.[25 ] , 它给出了海面各谐波分量相对于波数的关系. 海谱相对容易通过实验观测得到. 根据海谱, 可以通过Monte Carlo方法, 又称线性过滤的方法反演海面. 其基本思路是首先对白噪声进行傅里叶变换, 然后用海谱对其进行频域滤波, 即频域相乘, 最后进行逆傅里叶变换便可以得到随机起伏的海面. 这种还原海面方法的优势在于, 一是基于实测的海浪数据的统计特性, 真实性较好; 二是利用傅里叶变换计算, 大大降低计算量, 具有较好的实时性. 因此也成为目前常用的海面建模的方法之一. 科学家们在海谱的研究上也做了许多工作, 针对本文声传播特性的研究, 这里选择在实际工程问题中应用较多的PM谱进行海面高度反演. 与此同时, 目前在水声领域里, 还有一种常用的谱, 是高斯功率谱, 下面将它与PM谱简单进行对比, 两种谱的表达式分别如(8 )式和(9 )式所示:$ k_j $ 表示离散空间波数, (8 )式为高斯功率谱, 其中$ \sigma $ 和l 分别表示均方根高度和相关长度, (9 )式为PM谱, $ \alpha = 8. 1\times 10^{-3} $ , $ \beta = 0. 74 $ , g 为重力加速度, 取$9. 8\; {\rm{m}}/{\rm{s}}^2$ , $ U_{19. 5} $ 为$19. 5\; {\rm{m}}$ 高处的风速, 与$10\; {\rm{m}}$ 高处的风速$ U_{10} $ 的对应关系为$U_{10}/U_{19. 5}\approx 0. 94$ . 两种功率谱对比下来, 高斯谱的形式较为简单, 但是需要已知均方根高度和相关长度, 且这两个参数不易测量. 而PM谱虽然形式稍微复杂一些, 但是它只与容易获得的风速有关, 并且PM谱是经过大量的观测数据统计分析得到的, 目前在海洋学应用也较为广泛, 因此本文采取PM谱进行海浪建模.[1 ] :$ f(x_n) $ 表示海面起伏高度, $ F(k_j) $ 为$ f(x_n) $ 的傅里叶变换形式, 当$ j > 0 $ 时, 使$ F(k_j) = F(k_{-j})^*, $ $ {\rm{N}}(0, 1) $ 表示期望为0, 方差为1的高斯分布, $ x_n $ 为海面的第n 个离散采样点, $ k_j $ 为第j 个离散波数, L 为海面长度, N 为总的离散点数, 在PM谱的建模中, N 的选择与风速有关, 在海面总长一定的条件下, 风速越小, 离散的点数需要取得越多. 在本文的研究中, 根据下文的风速设定, 海面长度为$70\, {\rm{km}}$ , 离散点数为$ 2^{15} $ .4.3.2.风浪下声场分析 -->4.3.2.风浪下声场分析 利用上面4.3.1 节的方法结合实际测量风速生成风浪海面, 用于仿真声传播损失并与实验数据进行对比. 首先给出船载风速仪的风速测量值, 如图8 所示. 接收阵在$0\; {\rm{km}}$ 处. 横轴表示实验船在航行过程中, 每个测量时刻船距接收阵的距离. 在船航行至距离接收阵$ 1\, {\rm{km}} $ 以内的这段时间内, 风速较大, 平均风速为$ 8. 1\, {\rm{m}}/{\rm{s}} $ , 最高达到$ 10. 5\, {\rm{m}}/{\rm{s}} $ , 航行在$1\; {\rm{km}}$ 以外时, 风速相对较小, 平均值为$3. 6\; {\rm{m}}/{\rm{s}}$ . 实际上的海面建模并不是一个简单的一维问题, 而是与距离方向时间均有关. 在这里为了简化模型, 假定风向与传播方向一致, 海面不随时间变化. 按照距接收阵$1\; {\rm{km}}$ 以内时, 风速恒为$8. 1\; {\rm{m}}/{\rm{s}}$ , $1\; {\rm{km}}$ 以外时, 风速恒为$3. 6\; {\rm{m}}/{\rm{s}}$ , 海面建模结果如图9(a) 所示. 将这种单纯基于风速值生成的粗糙海面记为风浪海面, 仿真声源中心频率为$1000\; {\rm{Hz}}$ , 带宽为1/3倍频程条件下的声传播损失, 声速剖面选择如图3 所示的实测声速剖面结果, 海底参数$c_{\rm s} = 1540\; {\rm{m}}/{\rm{s}}, \;\rho_{\rm s} = 1. 47\; {\rm{g}}/{\rm{cm}}^3, \; \alpha_{\rm s} = 0. 45\; {\rm{dB}}/\lambda$ , 声源深度采用随距离分段变化的深度, 对比光滑海面和风浪海面两种条件下的第一个水听器的传播损失, 并给出实验结果作为参考. 如图10 所示, 红色实线和绿色实线分别代表光滑海面和风浪海面下的传播损失, 可以看出, 风浪海面对声场的影响在能量上作用不大. 与实验传播损失相比, 仿真结果偏低, 在$70\; {\rm{km}}$ 处二者相差约$10\; {\rm{dB}}$ , 不能解释实验结果中出现的较高的传播损失以及较快的衰减趋势. 主要原因在于$1\; {\rm{km}}$ 后实测的海面风速较小, 因此产生的风浪的浪高较低, 对声场影响较小. 而单纯的风浪不足以完全描述当时海面的状态.图 8 船载风速仪实测的风速Figure8. Wind speeds measured by shipboard anemometer.图 9 两种粗糙海面 (a) 风浪海面; (b) 涌浪海面Figure9. Two rough sea surfaces: (a) wind-driven sea surface; (b) swell sea surface.图 10 三种海面条件下的传播损失的仿真结果与实验结果比对Figure10. Modal/data comparisons of transmission loss under three sea surfaces.4.3.3.基于涌浪的海面建模 -->4.3.3.基于涌浪的海面建模 由4.3.2 节知道, 基于PM谱的海面建模是根据风速生成的, 因此只能表征本地风浪, 无法体现周围海域传播过来的涌浪信息. 本文实验过程中没有获得实时的浪高, 但是诸多方面表明实验海域存在较大涌浪. 首先, 日本气象厅发布的实验所在时间段内附近两个时刻的观测资料表明, 研究海域内海浪的有效波高约在2—3 m, 存在3 m高涌浪[26 ,27 ] . 其次, 表面声道是由海面强风持续十几个小时, 使得上层水体混合均匀, 形成混合层而产生[28 ] , 说明该海域存在海面强风. 有文献指出, 在南海北部陆坡海区, 连续的$ 10\; {\rm{m}} $ 高度处的风速测量结果显示, 离岸距离超过$ 100\; {\rm{km}} $ 时, 海面风速在冬季的最大概率值为$ 15\; {\rm{m}}/{\rm{s}} $ 左右[29 ] . 同时注意到图8 中实测风速结果显示在接收阵附近的风速较大. 以上三点间接指出实验海域存在海面强风. 当风速较大时, PM谱的谱峰频率会向低频方向移动, 导致涌浪的成分偏多. 最后, 在文献[30 ]中也指出, 南海冬季以涌浪为主, 占比约$ 70\% $ . 因此, 可以合理推断测线位置处测量的风速并不是海面粗糙的全部依据, 涌浪具有较强的传播能力, 可能会从周围海域不断传播过来.x 方向传播的波剖面方程为[31 ] H 为波高, k 为波数, 满足$ k = 2\pi/\lambda $ , $ \lambda $ 为波长, $ \omega $ 为角频率, 满足$ \omega = 2\pi/T $ , T 为周期, 当水深为h 时, 波数和频率满足如下关系:$ h > \lambda/2 $ )时, $ {\rm{tanh}}(kh)\approx1 $ , 此时, (12 )式可近似表示为$ \omega^2 = gk $ , 由此可得到波长和周期的关系为13 )式可计算出波长在56—155 m之间, 这里假设$\lambda = 80\; {\rm{m}}$ , $ H = 2.5\; {\rm{m}} $ , 由于声速远大于波速, 可近似认为海面不随时间变化[32 ] . 取$ t = 0\; {\rm{s}} $ , 根据(11 )式得到涌浪海面, 根据线性波叠加理论, 将两种海面叠加便可以得到风浪和涌浪混合的海面(图中均简称涌浪海面), 如图9(b) 所示.4.3.4.涌浪下声场分析 -->4.3.4.涌浪下声场分析 在4.3.3 节的含涌浪的海面条件下, 再次计算声传播损失, 其他参数与风浪海面仿真时相同, 仿真结果如图10 蓝线所示. 可以发现仿真结果整体上与实验结果符合较好, 与光滑海面和风浪海面下的传播损失结果相比, 可以看出考虑了涌浪后, 海面给$ 70\; {\rm{km}} $ 远处带来了$ 10\; {\rm{dB}} $ 的传播损失增长. 为了进一步检验涌浪海面建模的有效性, 将其用于$ 400\; {\rm{Hz}} $ 中心频率以及第11个水听器的传播损失实验验证, 结果如图11 , 蓝线为仿真结果, 可以发现涌浪海面配合变化声源深度建模可以对实验数据进行较好的解释. 这也从侧面证实了该区域涌浪的存在.图 11 涌浪海面应用于不同频率和不同水听器的传播损失检验 (a) $400\; {\rm{Hz}}$ , 第1个水听器; (b) $400\; {\rm{Hz}}$ , 第11个水听器; (c) $1000\; {\rm{Hz}}$ , 第11个水听器Figure11. Examinations of transmission loss of two hydrophones with the swell surface under different frequencies: (a) $400\; {\rm{Hz}}$ , the first hydrophone; (b) $400\; {\rm{Hz}}$ , the eleventh hydrophone; (c) $1000\; {\rm{Hz}}$ , the eleventh hydrophone.4.3.5.粗糙海面对声场影响的机理解释 -->4.3.5.粗糙海面对声场影响的机理解释 下面利用上述两种粗糙海面, 从声线角度来解释粗糙海面对表面声道声传播的影响. 首先, 从前面的分析可知, 表面声道内的能量主要靠反转声线提供. 根据表面声道声传播特点可知, 在平整海面下, 小掠射角声线会陷在表面声道内不断反转进行传输. 假设声线出射角为$ \theta_{\rm i} $ , 声源位置处的声速为$ c_{\rm i} $ , 声线在表面声道下边界发生反转处的角度为$ \theta_{\rm t} = 0^{\circ} $ , 表面声道下边界声速为$ c_{\rm t} $ . 由Snell折射定律$ {\rm{cos}} \theta_{\rm i}/c_{\rm i} = {\rm{cos}} \theta_{\rm t}/c_{\rm t} $ 可得, $ {\rm{cos}}\theta_{\rm i} = c_{\rm i}{\rm{cos}}\theta_{\rm t}/c_{\rm t} $ , 进而得到声线发生反转时的临界角$ \theta_{{\rm {ic}}} = {\rm{arccos}}(c_{\rm i}/c_{\rm t}) $ . 因此出射角度在$ \pm|{\rm{arccos}}(c_{\rm i}/c_{\rm t})| $ 之间的声线, 均只和海面作用, 在表面声道内传播. 而当掠射角逐渐增大时, 声线不再向上反转, 而是向下反转, 变成不再与海面触碰的声线, 当掠射角继续增大时, 声线触碰海底后会继续与海面作用.$ \pm 1.1^{\circ} $ . 设定声线掠射角为$\pm 1^{\circ},\; 0^{\circ}$ , 分别考察平整海面、风浪海面和涌浪海面三种情形下的声线分布情况, 其他参数与4.3.2 节一致. 结果如图12 所示, 蓝、红、绿三种颜色的曲线分别代表$ -1^{\circ} $ , $ 0^{\circ} $ , $ 1^{\circ} $ 的声线. 平整海面下, 三条声线均在表面声道内反转, 不与海底接触, 损耗较小. 对比粗糙度较小的风浪海面和粗糙度较大的涌浪海面条件下的声线情况, 可以发现二者的共同点是均使得表面声道内反转的声线在与海面触碰后改变原来的掠射角, 穿透表面声道向下传播, 与海底作用. 对于粗糙度较大的涌浪海面, 经过海面作用后, 掠射角改变更大. 观察掠射角为$ -1^{\circ} $ 的声线在第一次与两种粗糙海面触碰后的角度变化情况, 如图12(b) 和图12(c) 中的小图所示, 可以明显看出反射声线的掠射角与波面倾斜度密切相关, 波面倾斜度越大, 掠射角改变量越大, 使得声线以更加垂直的角度入射到海底. 声能量会较快地衰减, 导致远处传播损失加大. 由于波高和波的分布具有随机性, 因此当声线与波面作用后, 传播方向的变化也具有随机性. 但从统计意义上, 涌浪海面具有较高的均方根波高, 即较大的粗糙度. 声线在传播过程中会以较大概率触碰到大倾斜度的波面, 致使声能量向下层水体耦合, 表面声道内的传播损失增大.图 12 不同海面条件下的声线分布情况 (a) 平整海面; (b) 风浪海面; (c) 涌浪海面Figure12. Ray traces under different sea surfaces: (a) Flat sea surface; (b) wind-driven sea surface; (c) swell sea surface.5.结 论 本文利用PM海浪谱结合Monte Carlo方法, 根据实测海面风速和涌浪高度分别进行风浪海面和涌浪海面建模. 针对南海北部陆坡海区, 仿真分析了海底底质、声源深度、风浪海面以及涌浪海面对表面声道声传播的影响. 并用实验数据进行了验证.$ 70\;{\rm{km}} $ 远处增大了$ 10\;{\rm{dB}} $ . 



























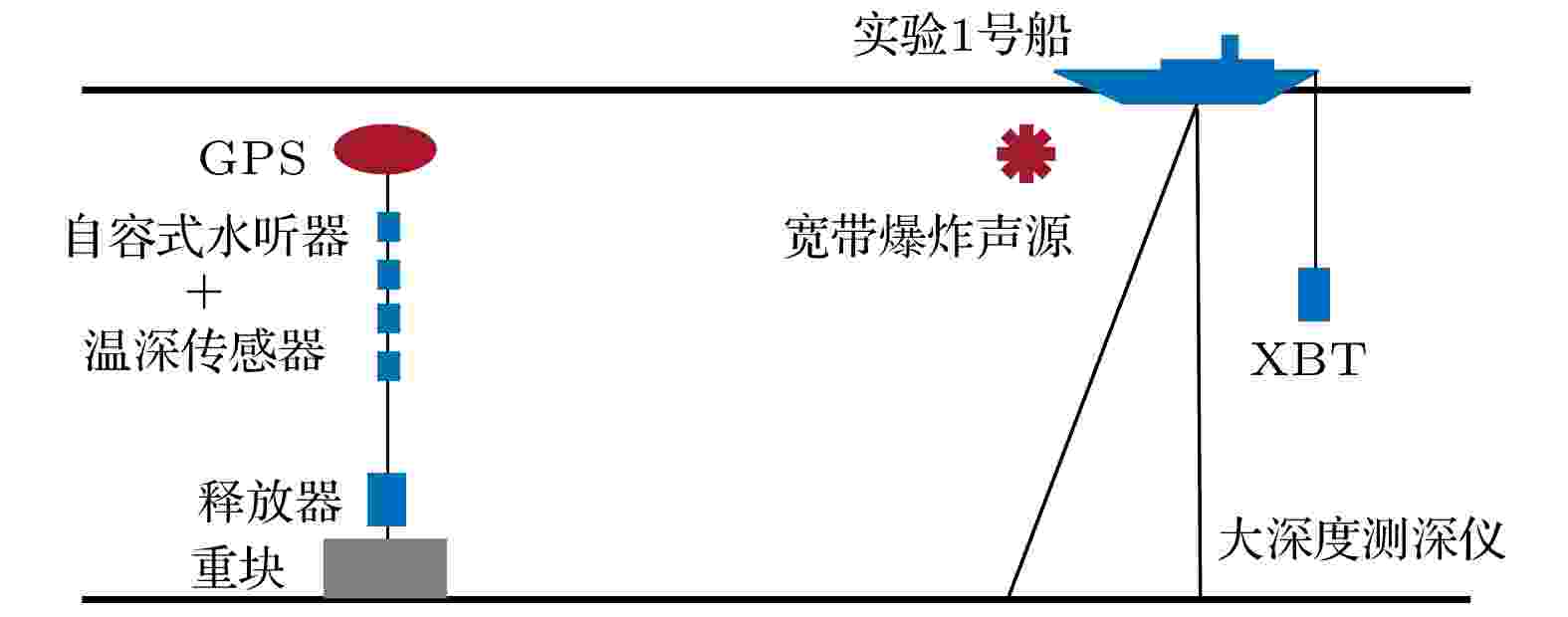 图 1 实验设备布放示意图
图 1 实验设备布放示意图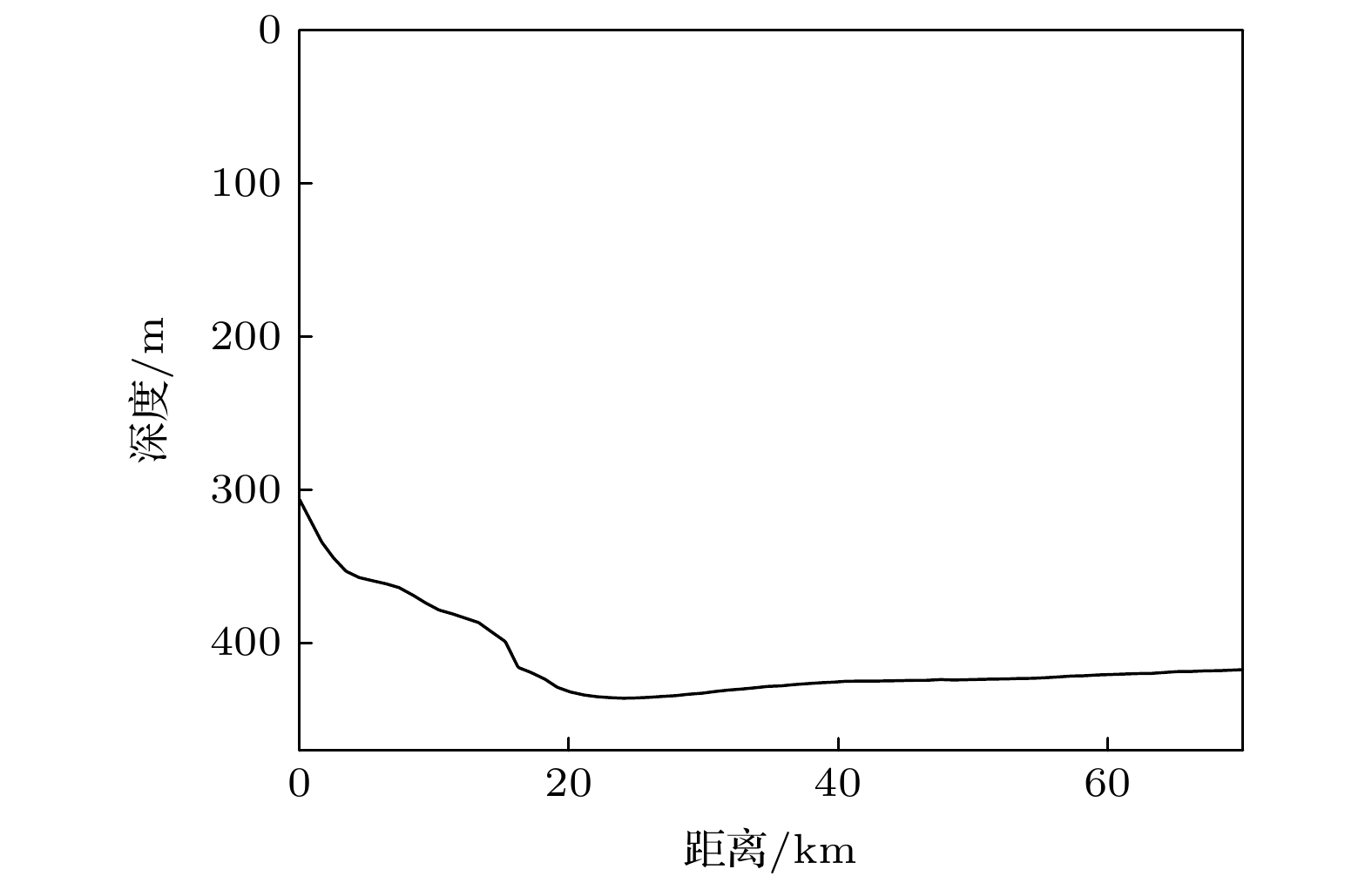 图 2 实测海底地形
图 2 实测海底地形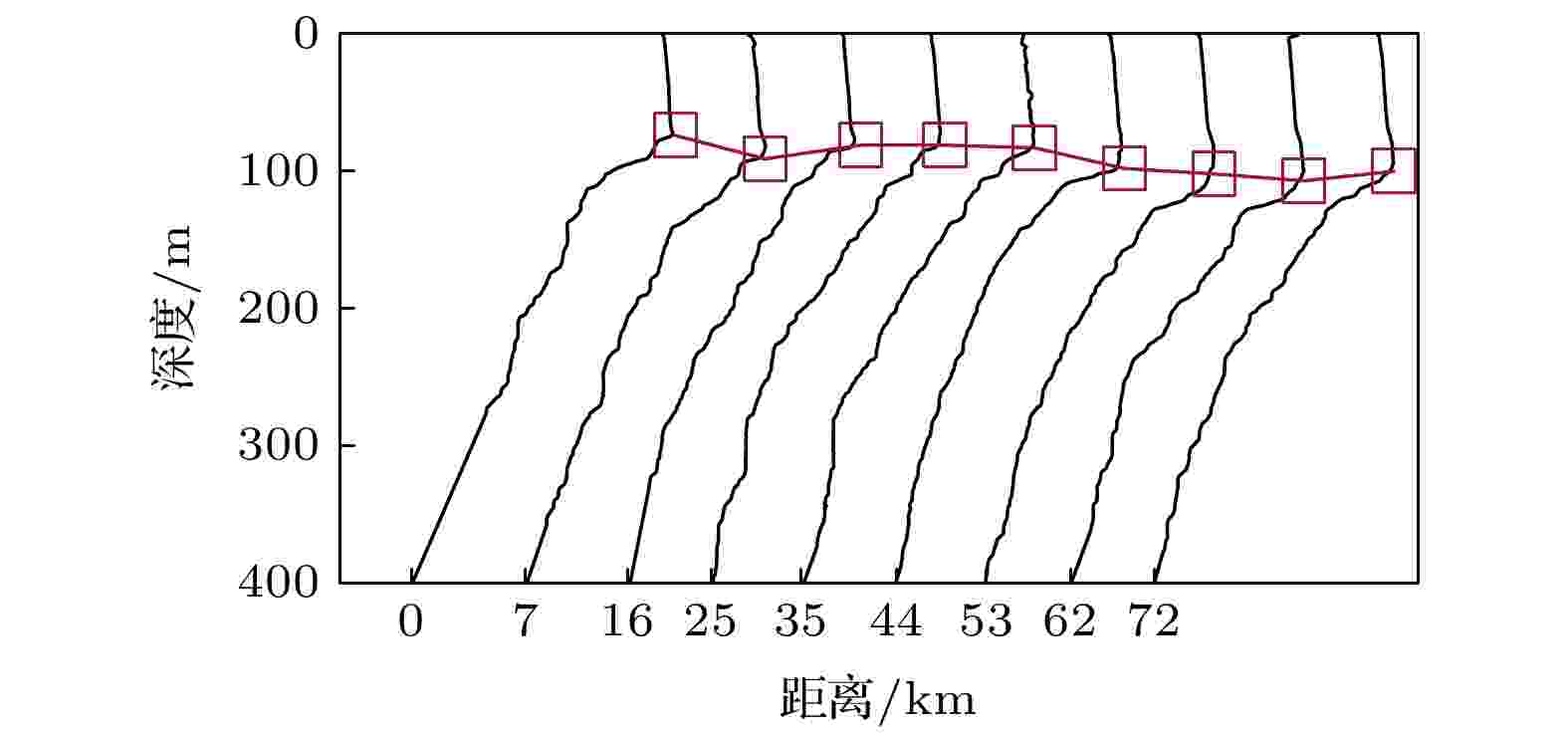 图 3 测线上声速剖面
图 3 测线上声速剖面



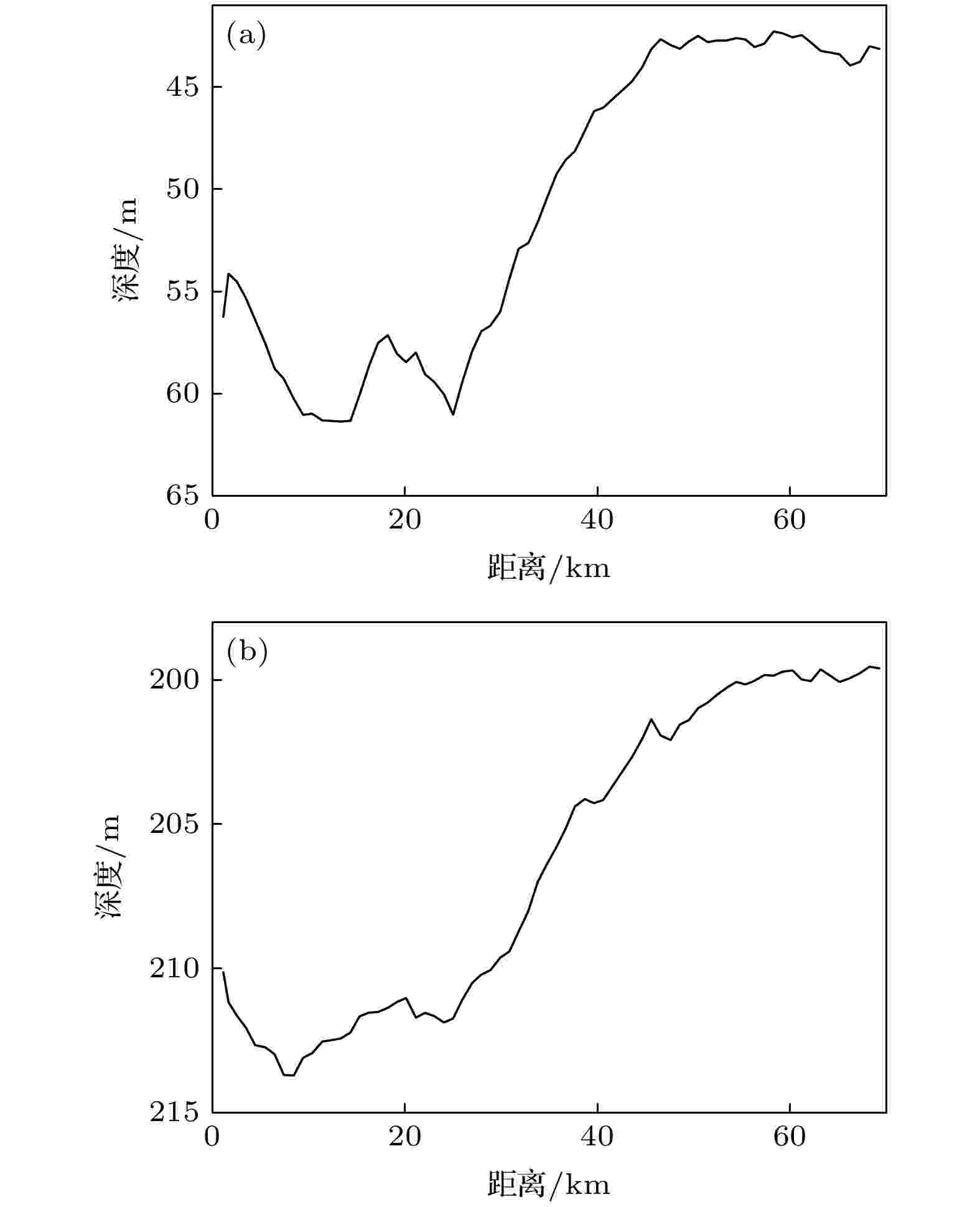 图 4 实测的第1个和第11个水听器的深度变化 (a) 第1个水听器; (b) 第11个水听器
图 4 实测的第1个和第11个水听器的深度变化 (a) 第1个水听器; (b) 第11个水听器





















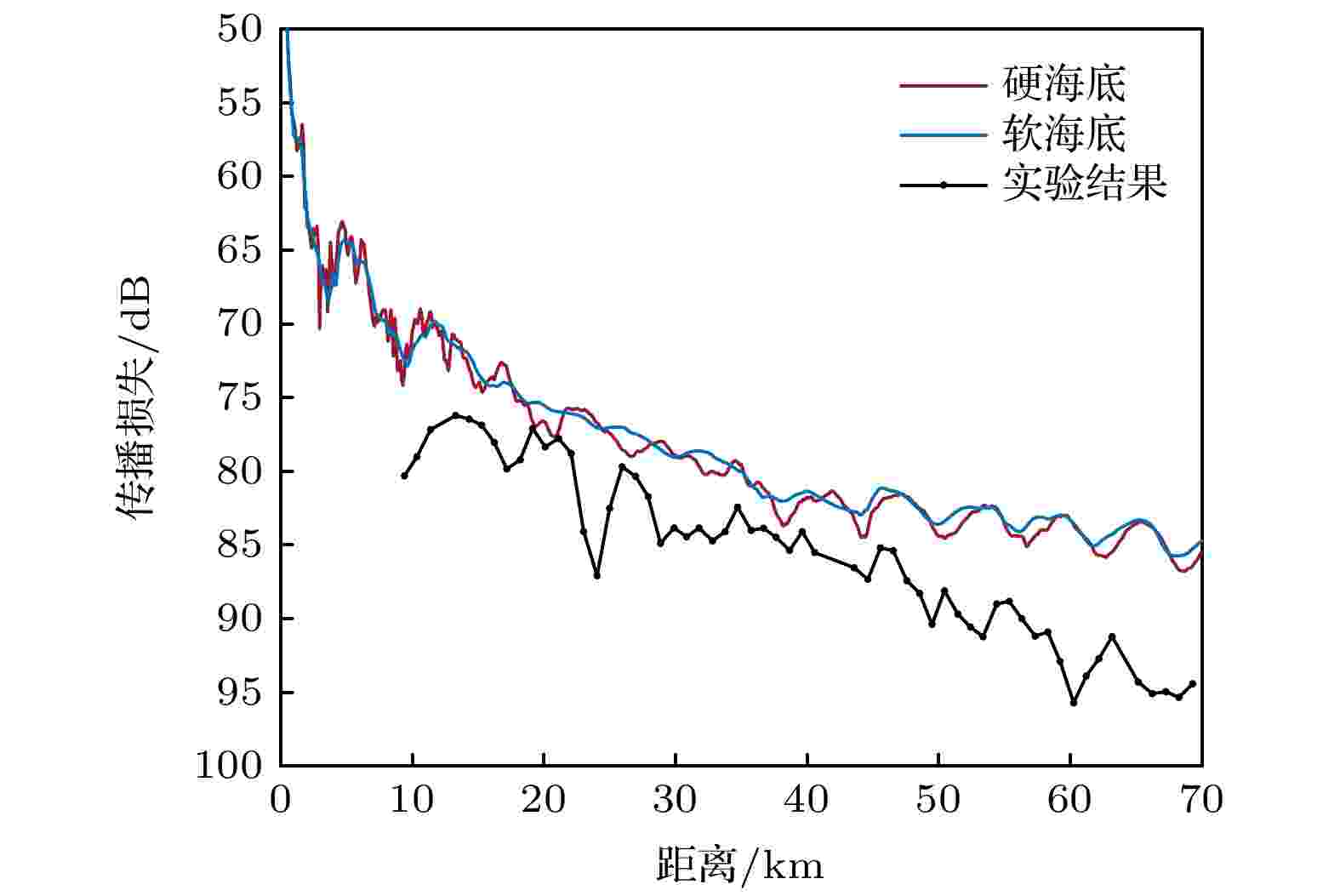 图 5 两种海底条件下第1个水听器的传播损失
图 5 两种海底条件下第1个水听器的传播损失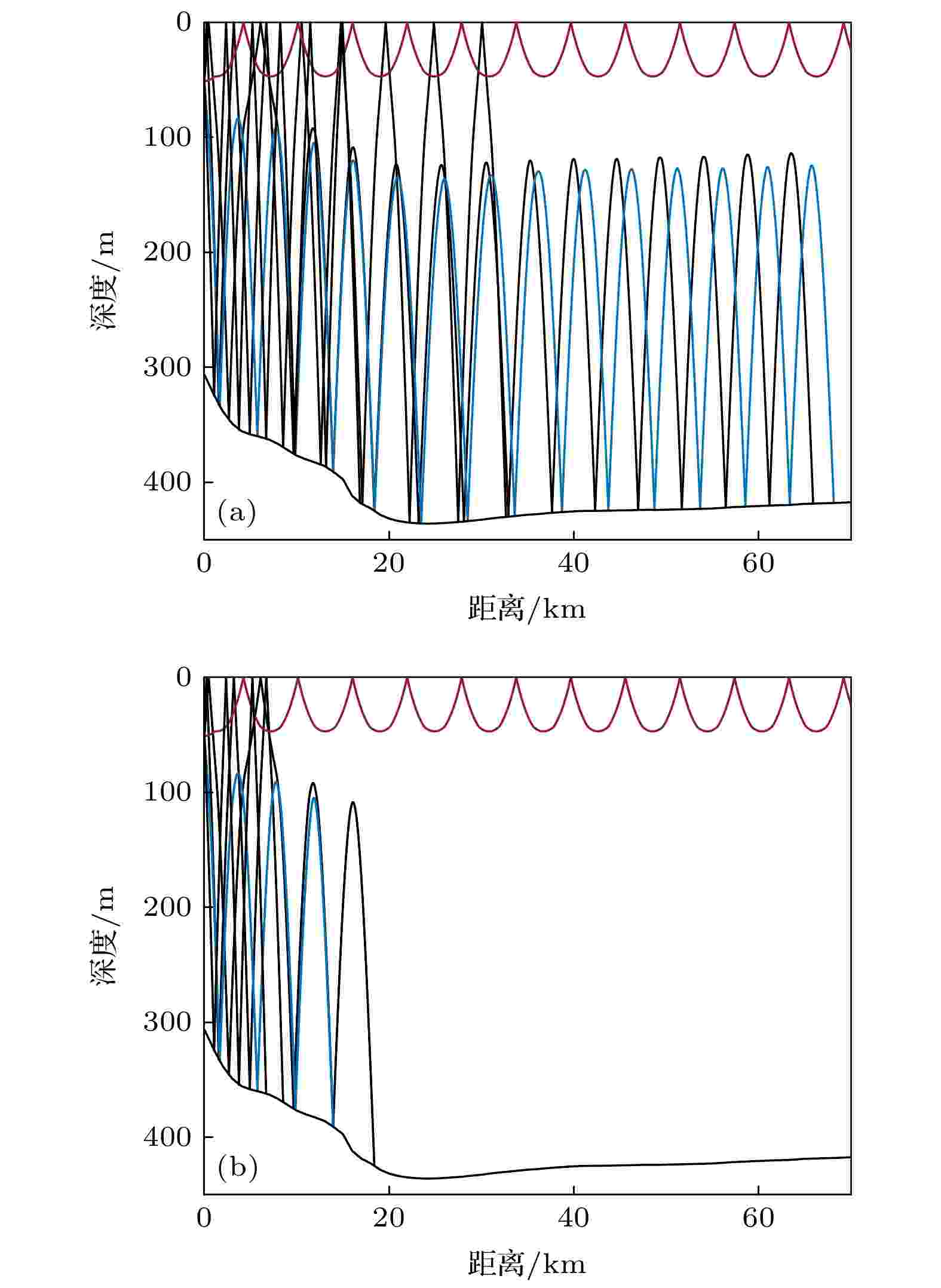 图 6 两种海底条件下的声线 (a)硬海底; (b)软海底
图 6 两种海底条件下的声线 (a)硬海底; (b)软海底

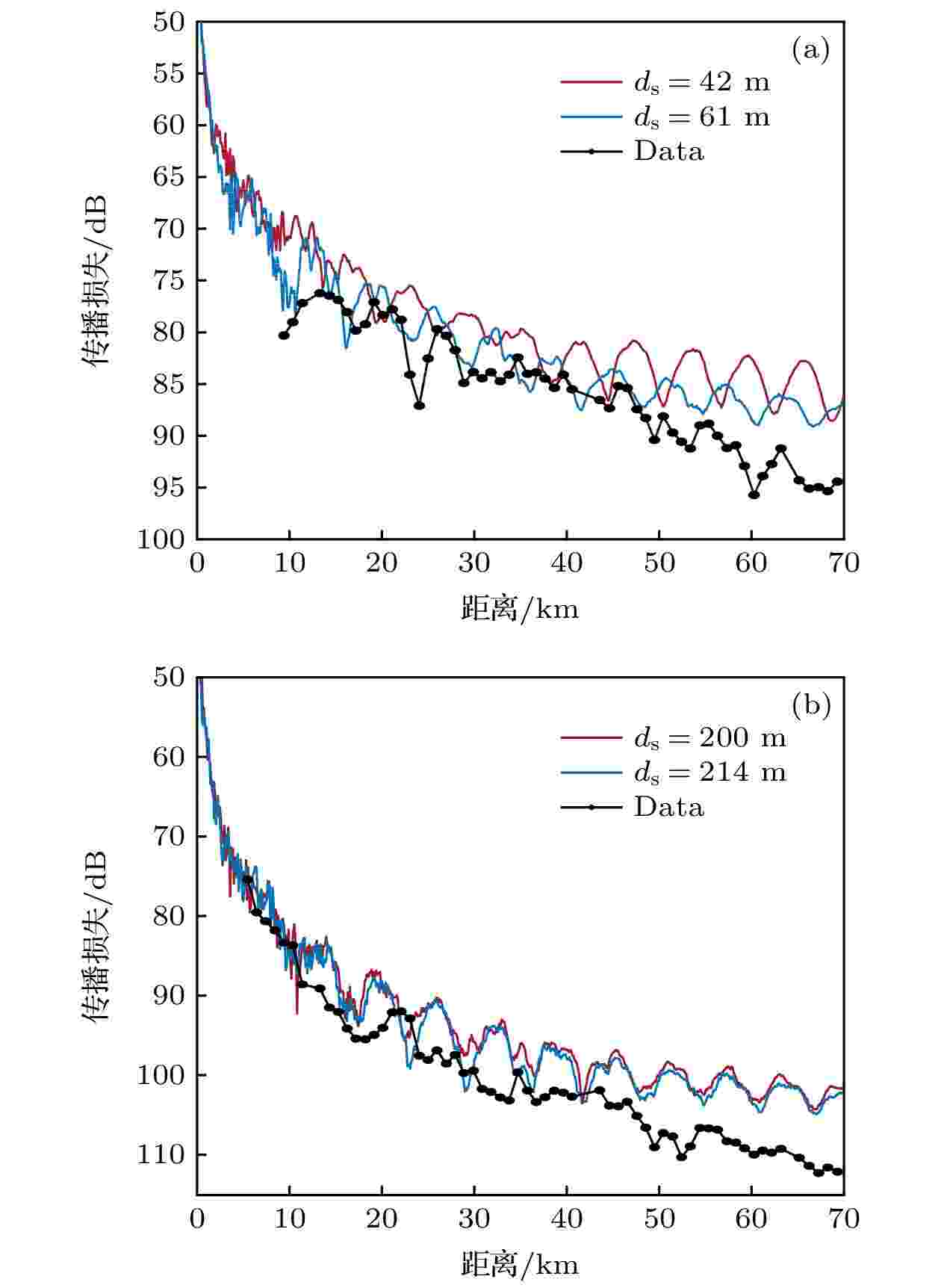 图 7 声源深度ds为两个水听器在深度波动的两个端点时的仿真传播损失与实验结果的比对 (a) 第1个水听器; (b) 第11个水听器
图 7 声源深度ds为两个水听器在深度波动的两个端点时的仿真传播损失与实验结果的比对 (a) 第1个水听器; (b) 第11个水听器


















































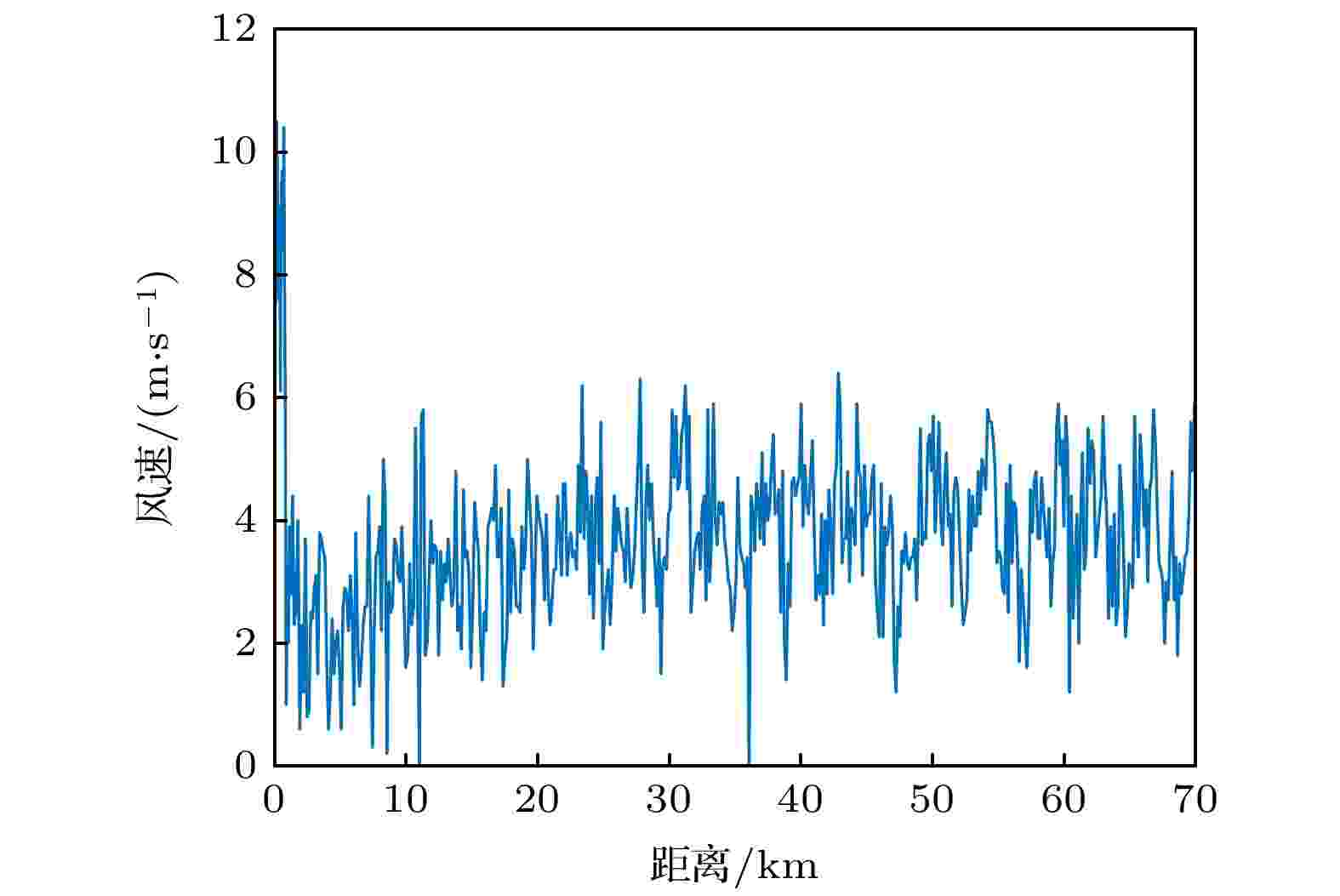 图 8 船载风速仪实测的风速
图 8 船载风速仪实测的风速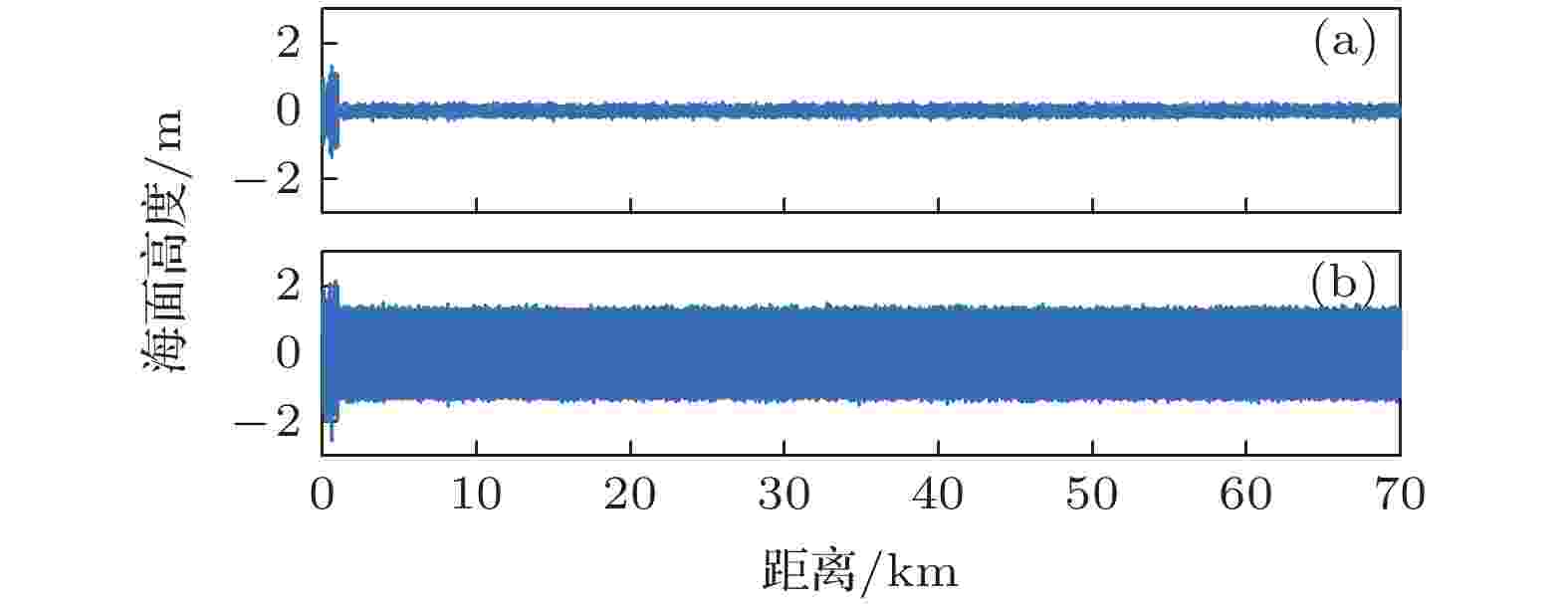 图 9 两种粗糙海面 (a) 风浪海面; (b) 涌浪海面
图 9 两种粗糙海面 (a) 风浪海面; (b) 涌浪海面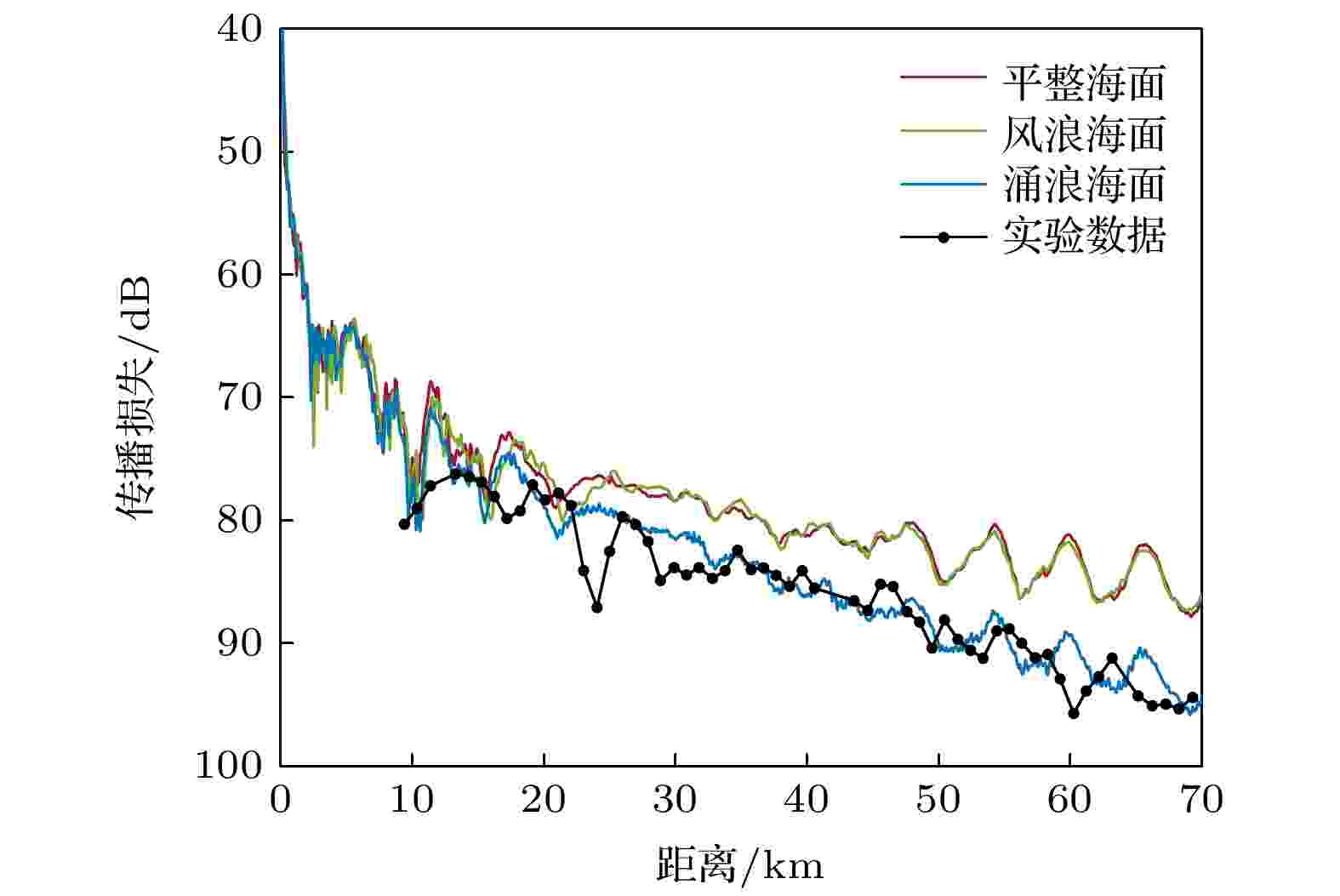 图 10 三种海面条件下的传播损失的仿真结果与实验结果比对
图 10 三种海面条件下的传播损失的仿真结果与实验结果比对
















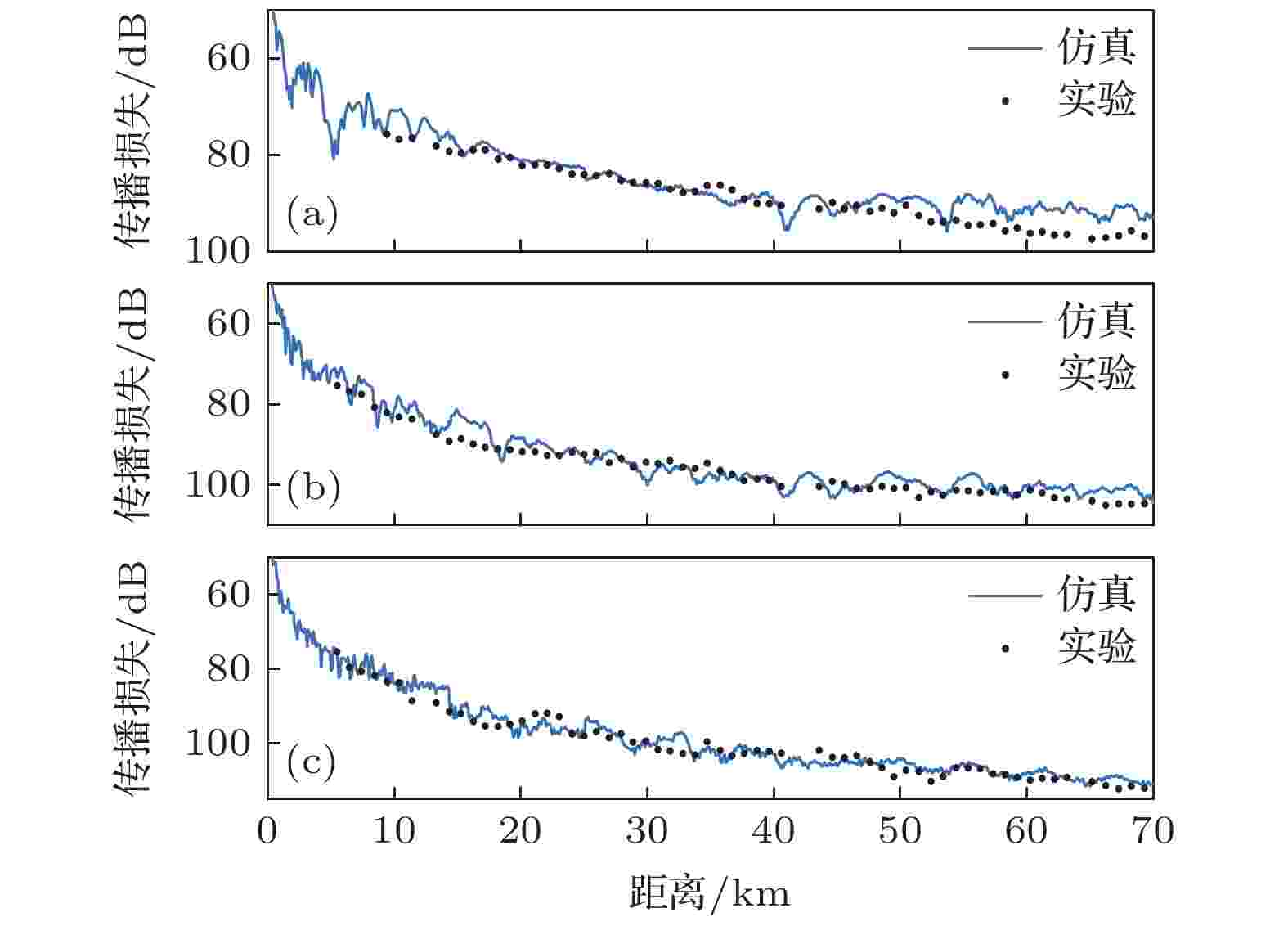 图 11 涌浪海面应用于不同频率和不同水听器的传播损失检验 (a)
图 11 涌浪海面应用于不同频率和不同水听器的传播损失检验 (a) 

























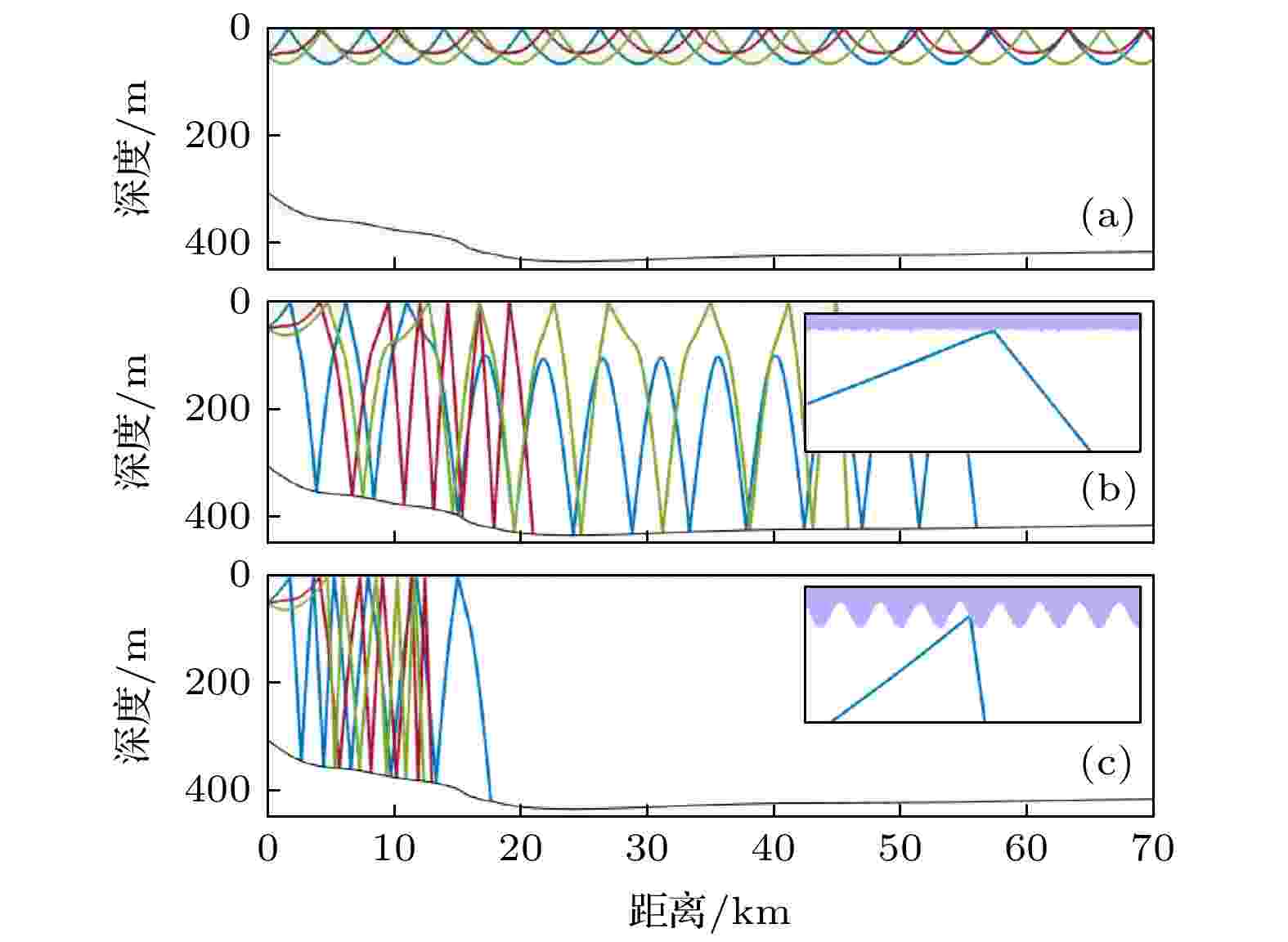 图 12 不同海面条件下的声线分布情况 (a) 平整海面; (b) 风浪海面; (c) 涌浪海面
图 12 不同海面条件下的声线分布情况 (a) 平整海面; (b) 风浪海面; (c) 涌浪海面







