全文HTML
--> --> -->国内外****对激波与液体的相互作用过程已有一定的研究, 取得了一些有价值的研究成果. Pilch和Erdman[5]对大量实验过程中液滴的破碎形态进行了归纳总结, 通过Weber数的大小对液滴不同状态下的破碎机理进行了划分. Hsiang和Faeth[6-8]基于阴影摄像实验针对液滴变形以及二次破碎现象进行了大量研究, 指出在二次破碎过程中由于液滴变形会增大阻力系数进而导致液滴的速度明显降低. Orme[9]通过实验手段研究了燃料液滴与水滴的膨胀过程, 给出了Weber数与碰撞结果的关系. 黄勇等[10]对激波抛撒柴油油膜过程进行了实验研究, 结果表明油膜黏度对抛撒后的雾化效果有重要影响, 黏度较小的油膜在激波冲击作用下雾化更均匀. 黄熙龙等[11]通过高速摄影测试技术对液滴的振荡变形、剥离破碎和爆炸破碎过程进行了研究, 指出在液滴形态发展过程中剥离破碎与爆炸破碎存在一定相似性, 气流的剪切和夹带对液滴的破碎起主导作用. 陆守香和秦友花[12]建立了液滴变形与破碎的模型, 研究指出激波与液滴碰撞后, 液滴变形、表面剥离直至完全破碎是一个渐进过程; 对该过程进行了分析, 得到了液滴变形率和完全破碎时间. 沙莎等[13,14]采用湍流的大涡模拟手段对Si等[15]的实验过程进行了数值模拟研究, 获得了激波作用下气泡内形成的高压区对射流的影响. 丁钰和刘家骢[16]研究了爆炸驱动下液体燃料破碎形成云团的过程, 结果表明云团体积增大到一定程度后开始逐渐稳定, 云团中心位置几乎没有液体燃料存在. 梁煜等[17]通过有限体积法求解多组分可压缩欧拉方程对激波汇聚下球形气泡演化规律进行了数值模拟研究, 指出汇聚激波可以有效促进气体混合以及涡量产生, 与平面激波相比, 汇聚激波作用时气泡界面形成的涡结构会更为尖锐.
前人的研究对象主要是围绕液滴破碎展开, 然而在实际的应用过程中, 通常涉及的是液膜破碎, 它们存在一定区别. 液膜不同于常见的球状液滴, 其形状为非球形, 是具有一定厚度的膜状液体, 因此无法完全参照先前的液滴研究理论[18,19]. 激波与液膜的相互作用过程时间很短, 同时液膜破碎后形成雾化云团的内部结构及详细物理量参数很难通过光学设备捕捉. 因此, 本文在验证数值模型正确性的基础上, 通过计算流体力学技术对激波与液膜的作用过程进行数值模拟研究, 获得液膜破碎雾化演变过程的详细三维流场参数分布, 研究有助于对激波冲击作用下液膜的破碎机理与雾化形态进行深入理解.
2.1.几何与网格
依据激波与液膜作用测试系统建立相应的几何模型, 结构如图1所示. 三维计算域的空间网格划分见图2.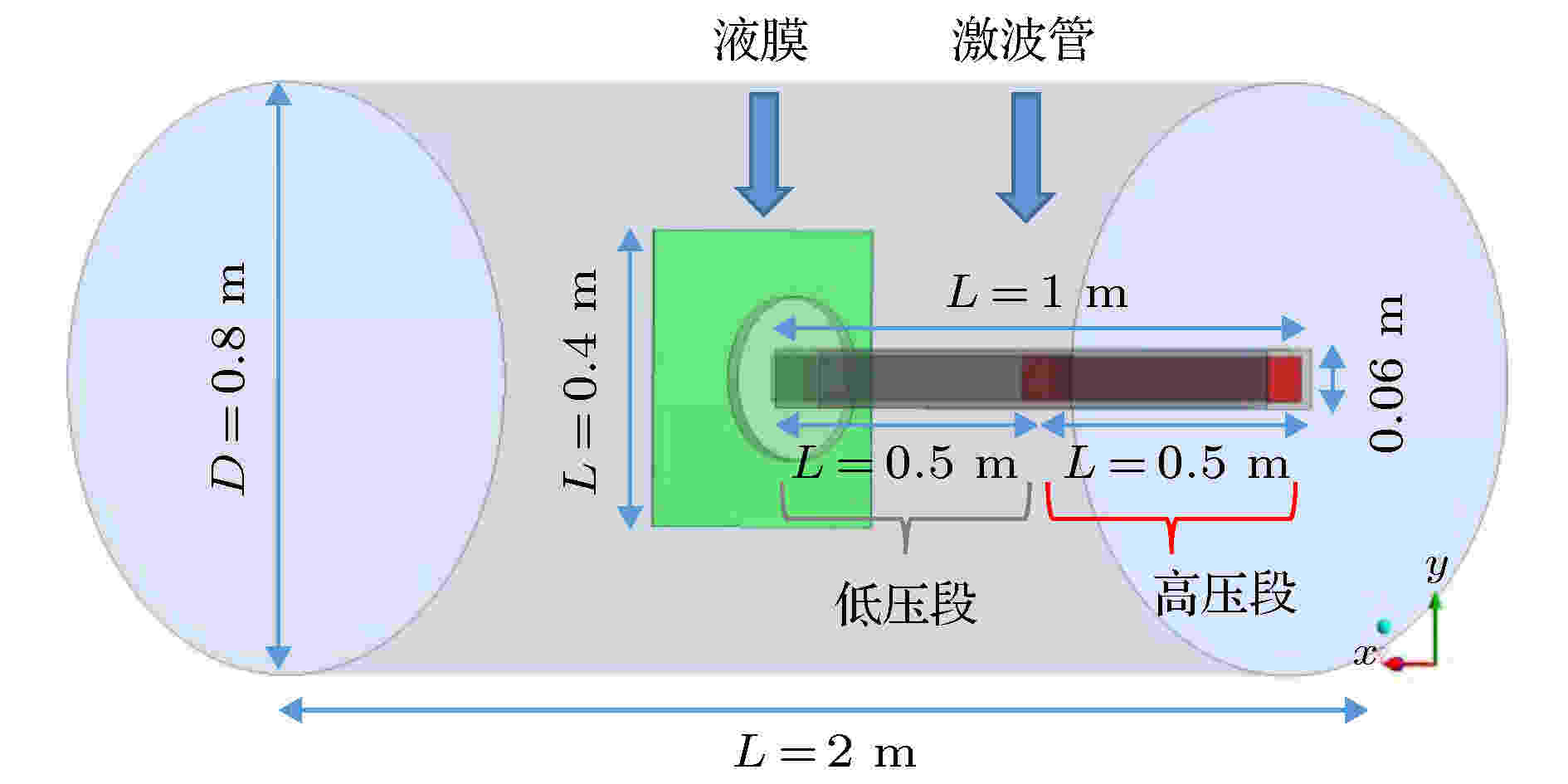
图 1 激波与液膜作用系统几何结构图Figure1. Geometry of the interaction system between shock wave and liquid film.
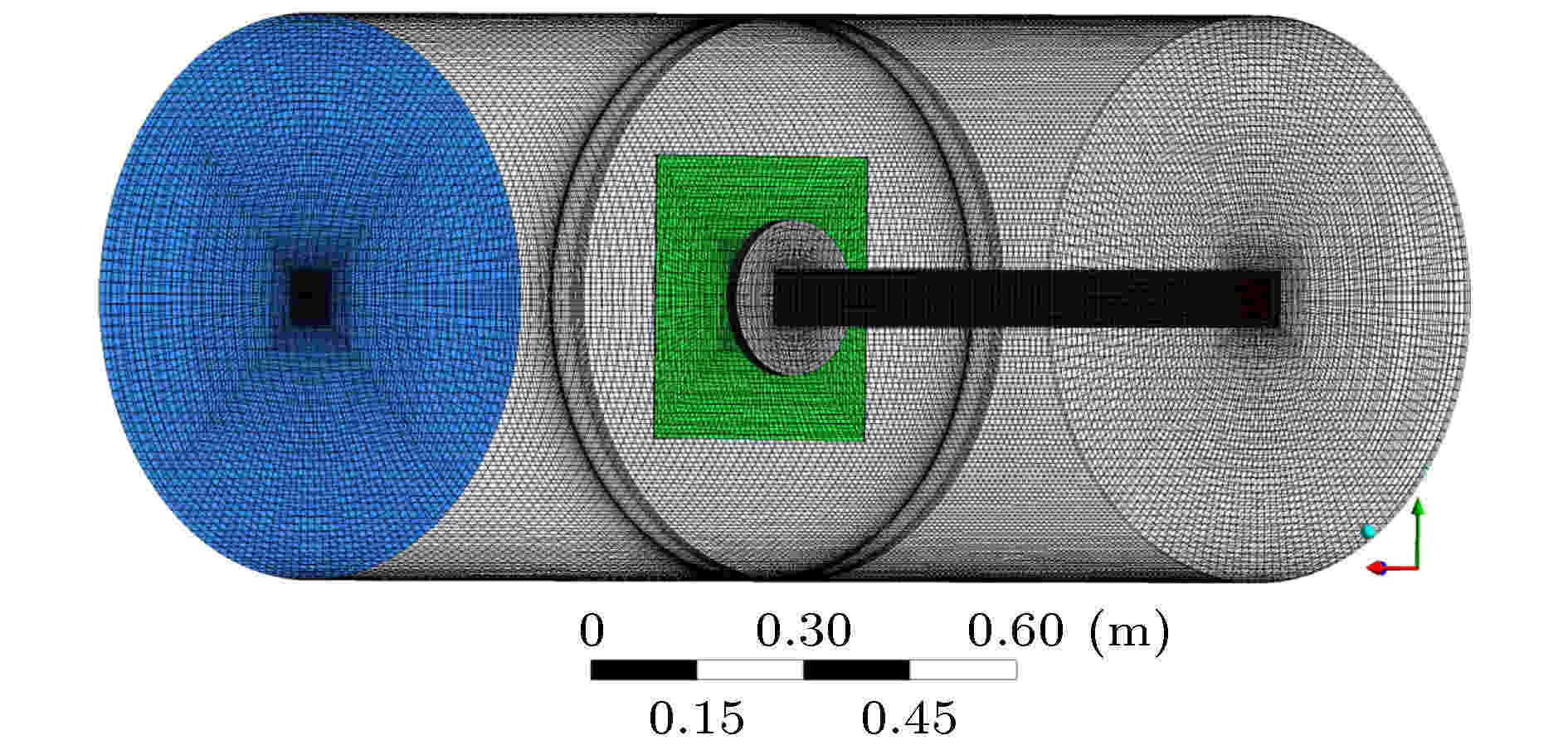图 2 计算域网格划分Figure2. Mesh generation of the calculation domain.
图1展示了计算域的几何模型, 整体为圆柱形, 包含激波管、液膜以及管外作用空间. 计算域总长度为2 m, 直径为0.8 m, 边界为压力出口. 激波管由驱动段与被驱动段组成, 全长为1 m, 膜片位于激波管中间位置. 横截面为方形, 内径60 mm× 60 mm. 液膜为400 mm (长) × 400 mm (宽) × 2 mm (厚)方形区域, 填充材料为水.
图2展示了计算域的网格分布情况. 常见的网格划分方式有六面体划分以及四面体划分, 其中六面体网格在多相流计算应用中具有较明显的计算精度以及收敛性优势, 因此采用拓扑切分方式对计算域进行高质量全六面体网格划分. 全局网格总数为168万, 对于激波管以及液膜区域进行网格加密处理, 网格最小尺寸为0.2 mm, 出现在液膜厚度方向.
2
2.2.数学模型
以质量守恒、动量守恒、能量守恒为基础, 建立描述气液两相流过程的三维可压缩纳维-斯托克斯方程组, 并引入湍流模型使方程组封闭可解. 气液两相流计算选用流体体积函数模型(volume of fluid, VOF), 气体与液相均作为连续相考虑, 采用欧拉坐标描述. 对于计算过程的湍流现象, 采用k-ε双方程湍流模型进行计算. 守恒方程组的基本形式如下[20].质量守恒方程为
采用VOF模型计算气液两相作用过程时可以考虑液相的表面张力, 对于表面张力的计算是基于连续表面力模型, 跨过表面的压力衰减与表面张力系数
k-ε双方程湍流模型是从实验总结中提出的半经验公式, 其中k是湍流脉动动能, 单位为J; ε是湍流动能耗散率, 单位为m2/s3. 它们是湍流脉动的2个关键参数. k-ε双方程湍流模型是目前应用范围最广的湍流模型之一, 同时兼具计算效率与计算精度的优点.
2
2.3.计算模型验证
为了验证数学模型在计算激波与液膜作用问题上的有效性和精度, 选取装置前期实验结果[21]与计算结果进行对照. 数值计算采用的激波强度以及液膜厚度条件与实验相一致, 激波马赫数为1.5, 液膜厚度为2 mm; 驱动段(高压段)初始表压为600 kPa, 被驱动段(低压段)与外界大气连通, 初始表压为0 kPa. 不同时刻液膜变形破碎形态的实验结果见图3, 仿真结果见图4, 液膜破碎雾化距离的对比见图5.
图 3 液膜破碎形态演变实验结果[21] (a) t = 0 ms; (b) t =1.5 ms; (c) t = 3 ms; (d) t = 3.5 msFigure3. Experiment results of liquid film breaking evolution: (a) t = 0 ms; (b) t = 1.5 ms; (c) t = 3 ms; (d) t = 3.5 ms.
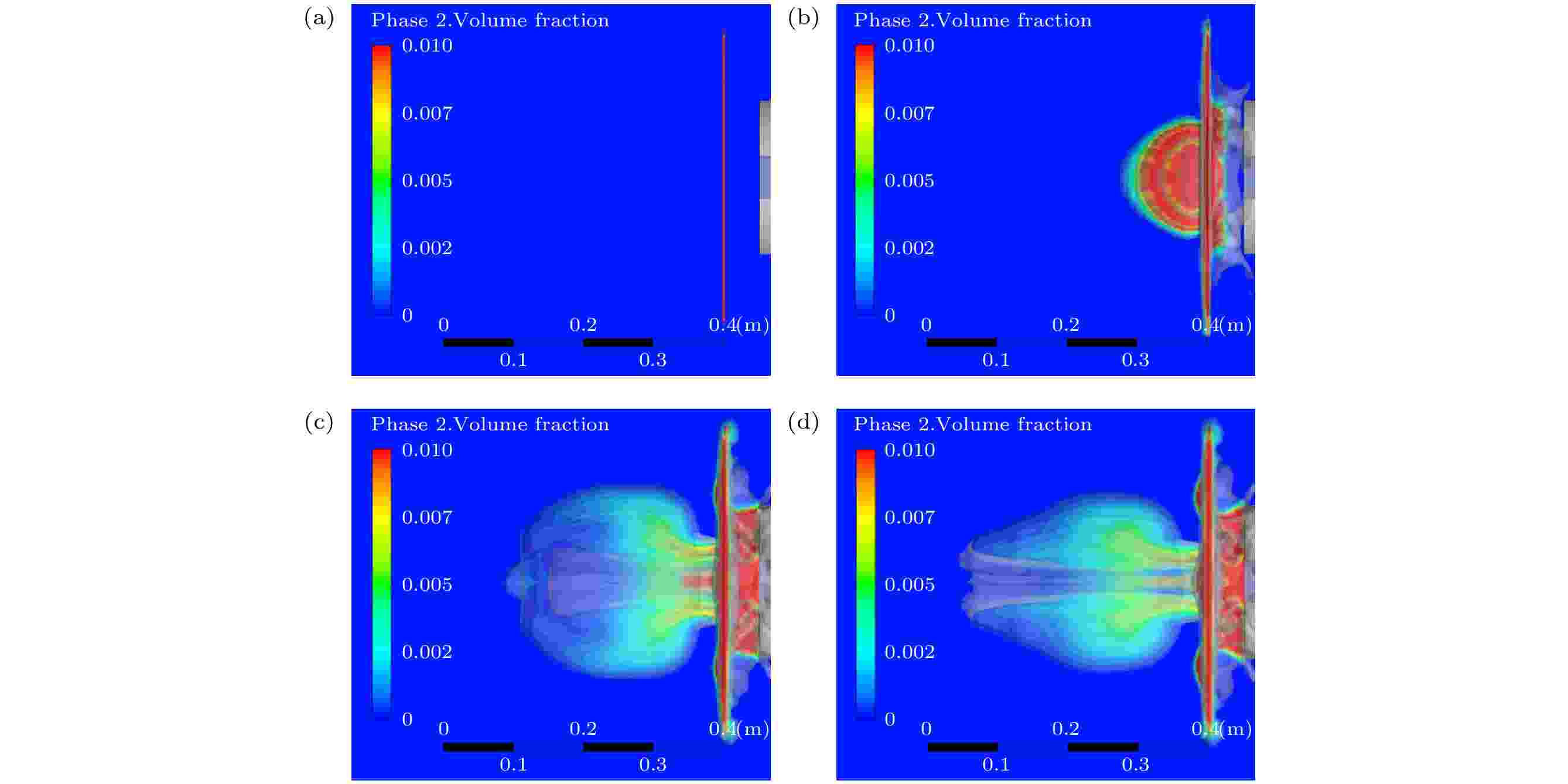图 4 液膜破碎形态演变仿真结果 (a) t = 0 ms; (b) t = 1.5 ms; (c) t = 3 ms; (d) t = 3.5 msFigure4. Simulation results of liquid film breaking evolution: (a) t = 0 ms; (b) t = 1.5 ms; (c) t = 3 ms; (d) t = 3.5 ms.
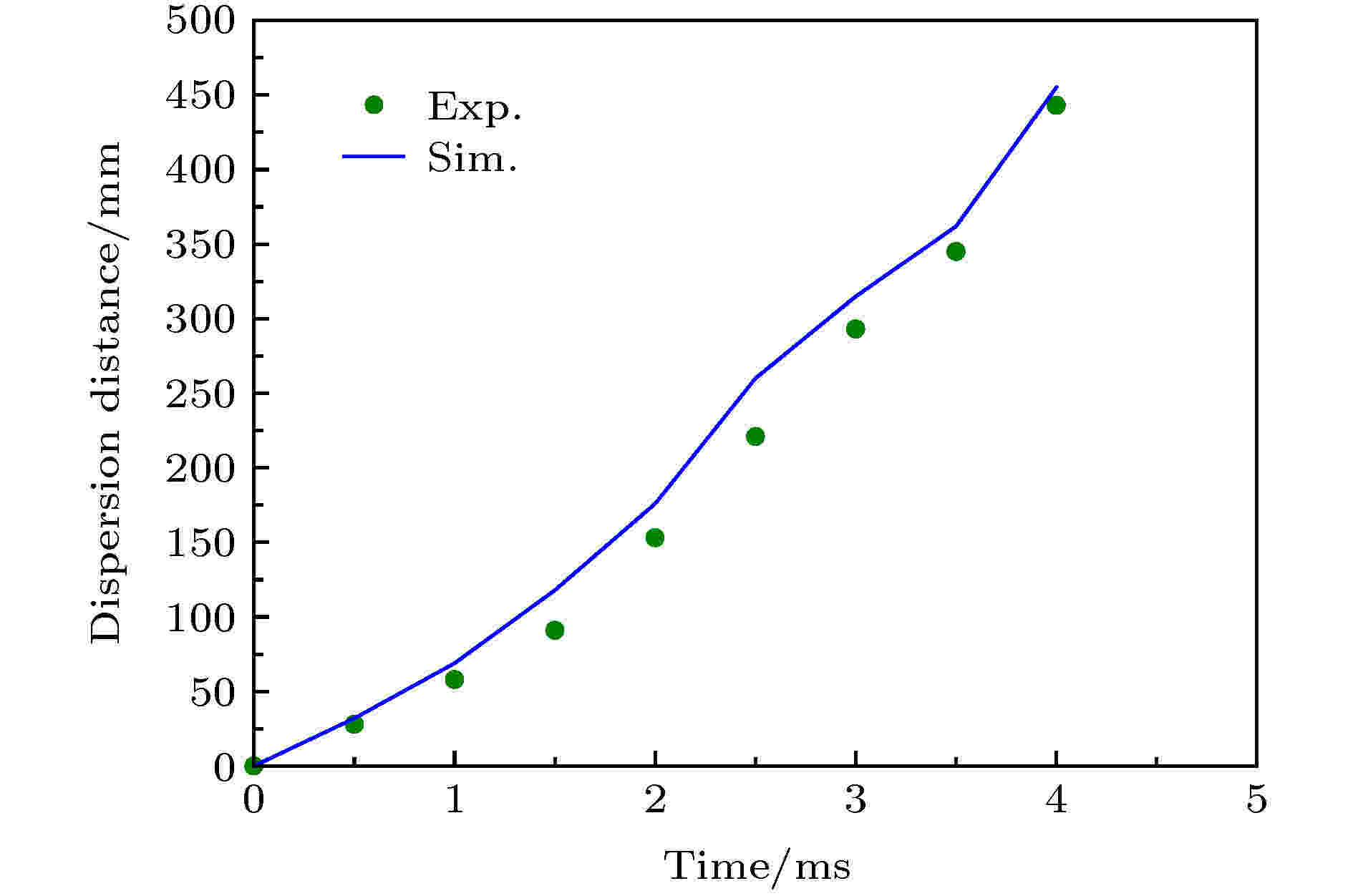图 5 液膜抛撒距离的仿真与实验对比Figure5. Comparison of simulation and experiment on the dispersal distance of liquid film.
对比图3—5可知, 仿真得到的液膜破碎形态以及抛撒距离均与实验结果基本一致, 较好地验证了所建立数学模型在计算上的有效性与正确性.
3.1.液膜破碎形态分析
液膜在激波的冲击作用下呈现剥离破碎过程, 为了对该过程进行观察, 创建液相等值面对该过程进行表征. 图6与图7为不同时刻侧向视角与正向视角下等值面的演变过程.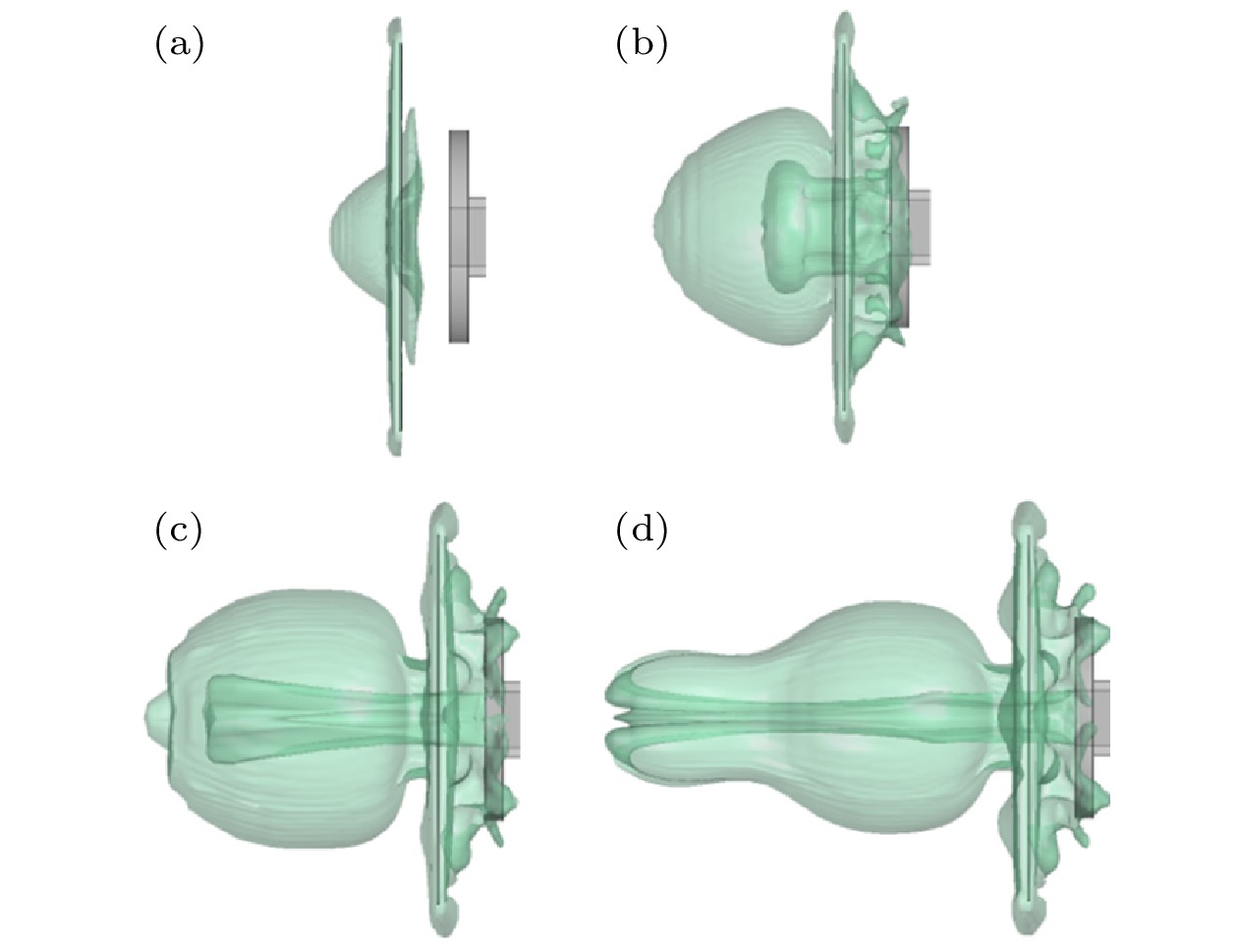
图 6 侧向视角下液膜破碎过程 (a) t = 1 ms; (b) t = 2 ms; (c) t = 3 ms; (d) t = 4 msFigure6. Process of liquid film breaking in side view: (a) t = 1 ms; (b) t = 2 ms; (c) t = 3 ms; (d) t = 4 ms.
图 7 正向视角下液膜破碎过程 (a) t = 1 ms; (b) t = 2 ms; (c) t = 3 ms; (d) t = 4 msFigure7. Process of liquid film breaking in front view: (a) t = 1 ms; (b) t = 2 ms; (c) t = 3 ms; (d) t = 4 ms.
激波作用于液膜后, 会产生向左传播的透射激波与向右传播的反射激波, 其中透射激波影响液膜左侧破碎形态, 反射激波影响液膜右侧破碎形态. 由图6可知, 1 ms时刻液膜左侧在透射激波作用下形成向外凸起的圆锥形雾化云团区域, 液膜右侧在反射激波作用下形成较薄的圆饼状雾化区域. 2 ms时刻雾化区域体积迅速扩大, 同时内部出现空腔结构, 该空腔结构内部主要为气相, 破碎后的液滴主要存在于云团外轮廓与空腔之间的区域. 3 ms时刻云团持续向外扩张, 内部空腔区域演变为狭长形态, 轴向长度迅速增长. 4 ms时刻云团在轴向长度上继续增长, 径向尺度基本保持不变; 空腔结构在长度上增长至云团顶端位置, 并与云团逐渐融合. 由图7可知在方形激波管作用下, 液膜正面破碎形态为圆形向十字形过渡, 裂口面积在作用的前2 ms时间内不断增大, 2 ms后裂口面积基本维持不变; 内部空腔结构在4 ms时刻贯穿云团区域.
云团体积随时间变化规律如图8所示.
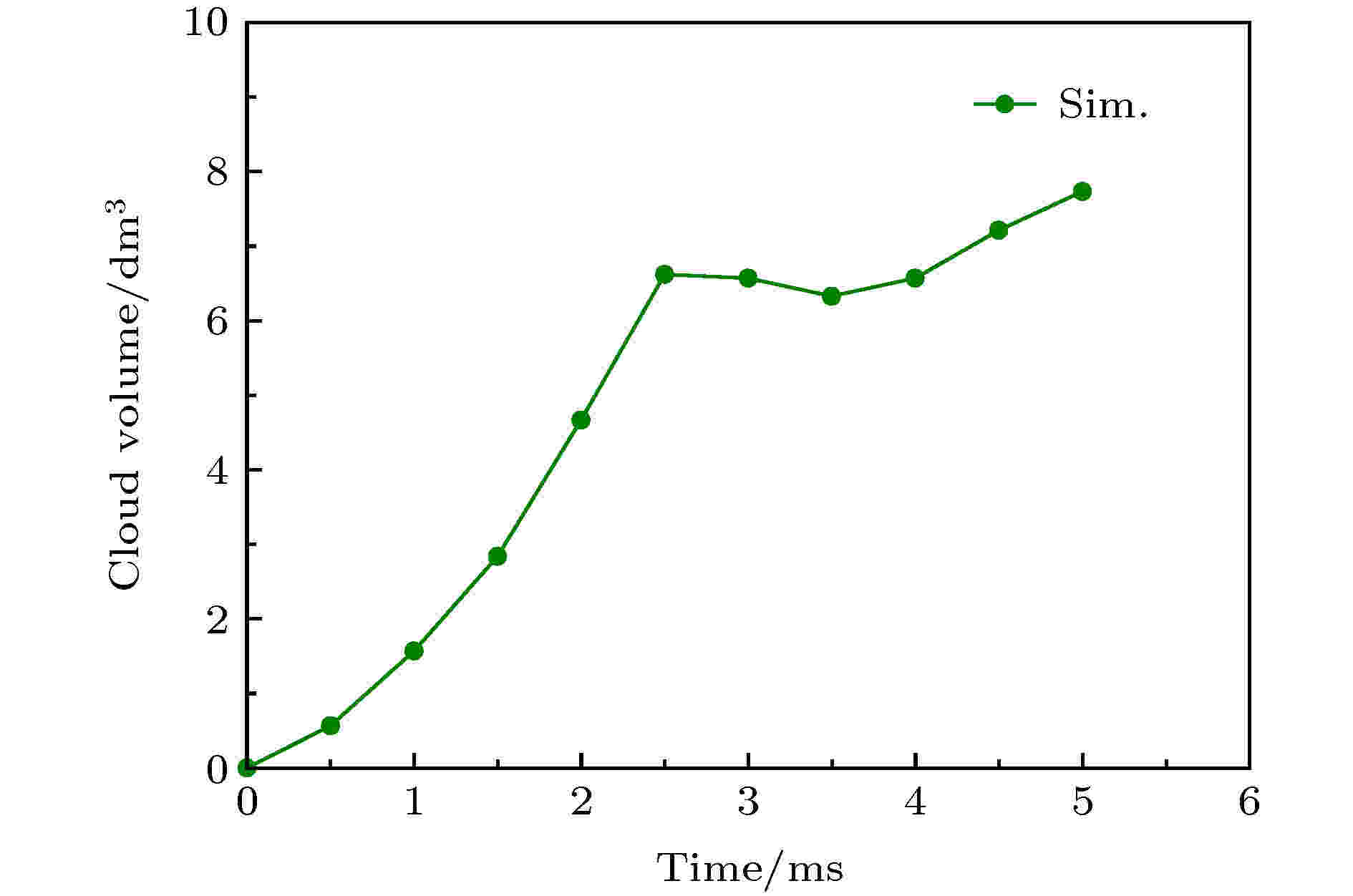图 8 液膜破碎形成的云团体积变化过程Figure8. Process of cloud volume change caused by liquid film breaking.
激波作用后液膜破碎形成由无数小液滴组成的气溶胶云团, 云团体积是重要的特征参数之一. 从图8可知, 在激波作用后的2.5 ms时间内云团体积增长迅速, 并且在2.5 ms时刻达到第一个体积峰值6.7 dm3. 2.5—3.5 ms时刻之间云团有效体积略有减小, 主要原因是内部空腔体积增长所致. 3.5 ms之后云团体积再次呈现增长趋势, 但增长速度缓慢.
2
3.2.压力变化过程分析
激波与液膜作用过程中存在复杂的波系结构, 创建通过中轴线的YZ平面对作用过程中压力场演变过程进行分析. 不同时刻压力分布见图9.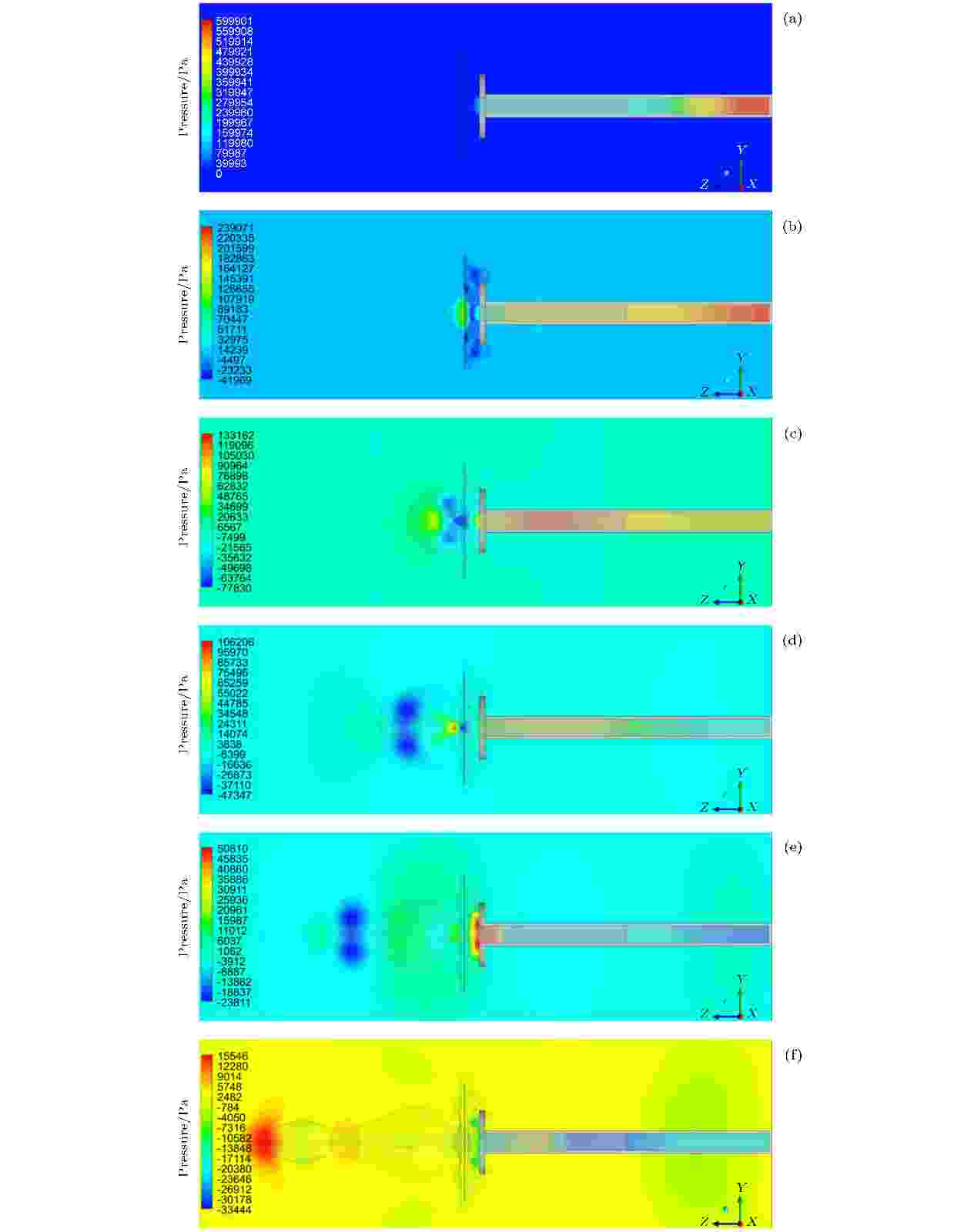
图 9 激波与液膜作用过程压力变化 (a) t = 0 ms; (b) t = 1 ms; (c) t = 2 ms; (d) t = 3 ms; (e) t = 4 ms; (f) t = 4 msFigure9. Pressure change during the interaction between shock wave and liquid film: (a) t = 0 ms; (b) t = 1 ms; (c) t = 2 ms; (d) t = 3 ms; (e) t = 4 ms; (f) t = 4 ms.
从图9可以看出, 0 ms时刻激波运动至管口位置, 此时激波管驱动段最右侧仍位于600 kPa超压区域; 管口激波与液膜开始接触, 激波阵面压力为155 kPa. 1 ms时刻液膜左右两侧均发生了破碎雾化现象, 然而左右两侧雾化云团的形状存在很大区别: 液膜左侧在透射激波作用下拉升形成圆弧状凸起, 此时表面张力会促使液膜整体向作用中心收拢, 当透射激波作用力超过表面张力后, 液膜左侧逐渐破碎雾化并与液膜主体剥离; 同时由于液膜的阻挡效应, 入射激波与反射激波在液膜右侧位置相遇叠加并发生干涉现象, 使得液膜右侧产生振动直至破碎雾化, 雾化形状呈现较薄的圆饼状. 2 ms时刻液膜左侧的雾化云团增长迅速, 云团内部空腔初步形成. 空腔的头部位置产生了圆环状湍流旋涡, 旋涡内部为负压区, 且越靠近旋涡核心位置, 压力值越低, 最大负压值达到–78 kPa. 湍流旋涡对左侧雾化云团的形状存在影响. 随着时间的推进, 3—4 ms时间段激波管内高压气体完全排出, 并且由于惯性效应, 激波管右侧会形成一定负压, 激波管外部气体开始向管内倒灌. 环状旋涡持续向左运动, 但由于周围气流的摩擦阻力效应, 旋涡强度有所减弱, 表现为旋涡核心区负压值由–47 kPa变为–24 kPa. 5 ms时刻旋涡在空间中逐渐耗散, 激波管内气体处于反复振荡状态, 并且随着时间的推移, 振荡逐渐减弱.
为了更直观地了解压力演变过程, 以激波管最右侧驱动段为坐标原点, 横轴为距离, 纵轴为压力, 绘制不同时刻激波管中轴线上压力随距离变化的分布图, 具体见图10.
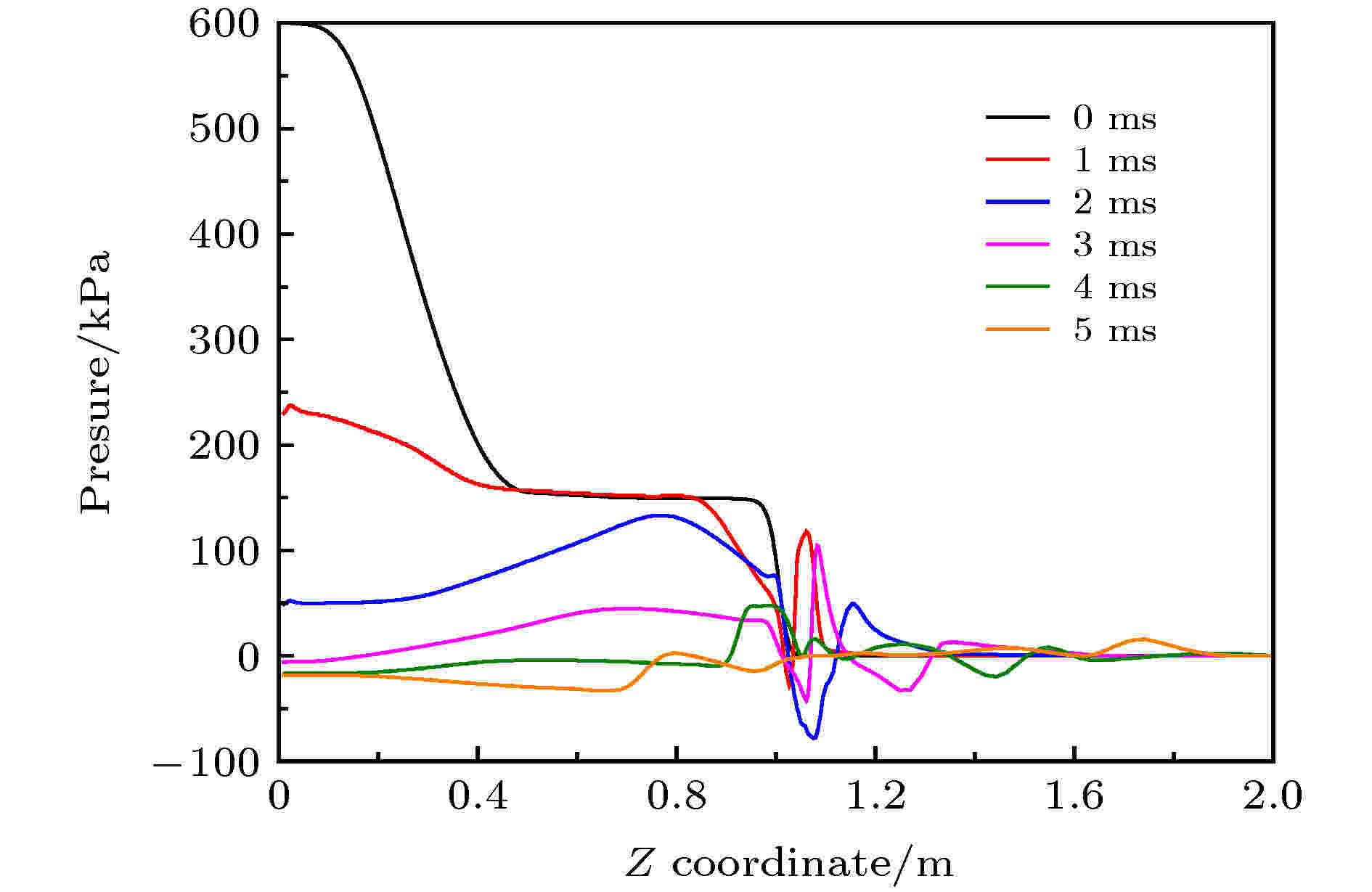图 10 不同时刻激波管中轴线上压力分布Figure10. Pressure distribution on the central axis of shock tube at different times.
从图10可以看出, 0 ms时刻激波管驱动段内存在较大压力梯度, 被驱动段压力维持在155 kPa, 激波管外维持在环境压力. 1 ms时刻驱动段内压力大幅下降, 被驱动段在靠近膜片附近区域压力仍然维持在155 kPa, 激波管外液膜位置形成了明显的压力突跃. 随着时间的推移, 驱动段压力不断下降, 2 ms时刻驱动段压力开始低于被驱动段压力, 3 ms时刻驱动段出现负压. 激波管外部压力分布较为复杂, 存在两个负压区域, 第一个负压区域为液膜初始位置附近, 第二个负压区域为旋涡的圆心位置附近. 作用过程中, 负压区域不断前移, 压力波动逐渐减小, 直至与环境压力达到平衡.
2
3.3.速度变化过程分析
激波与液膜作用过程中流场速度的演变是重要的参数之一, 不同时刻通过中轴线的YZ平面速度分布见图11.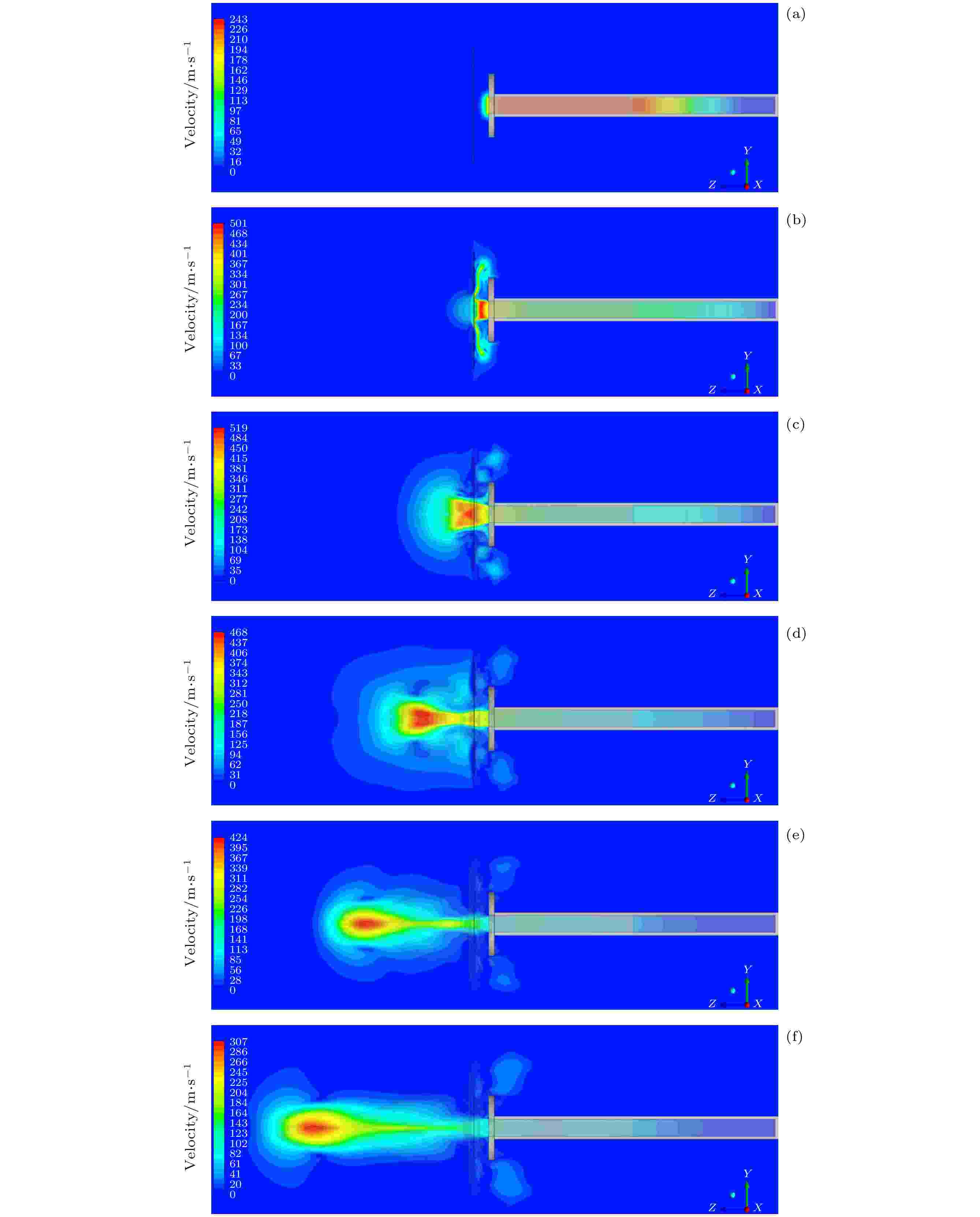
图 11 激波与液膜作用过程速度变化 (a) t = 0 ms; (b) t = 1 ms; (c) t = 2 ms; (d) t = 3 ms; (e) t = 4 ms; (f) t = 5 msFigure11. Velocity change during the interaction between shock wave and liquid film: (a) t = 0 ms; (b) t = 1 ms; (c) t = 2 ms; (d) t = 3 ms; (e) t = 4 ms; (f) t = 5 ms.
激波从管口出来后形成典型的射流现象, 其特点是射流进入静止环境中时, 会与周围静止流体之间存在速度不等的间断面, 间断面会受到不可避免的干扰, 进而发生失稳并产生涡旋, 卷吸周围流体进入射流中. 射流发展过程中会由于不断移动、变形、分裂而产生湍动, 并逐渐向内外两侧发展形成自由湍动的混合层. 由于动量的横向传递, 卷入的流体获得动量而随原射流向前运动, 原来的流体动量减小而逐渐失速, 产生一定的速度梯度. 卷吸和掺混的结果使得射流断面不断扩大, 而流速则不断降低, 流量沿程增加.
从图11可以看出, 0 ms时刻激波运动至管口位置, 被驱动段质点速度为243 m/s, 激波传播过程中相对波前气体为超音速, 相对波后气体为亚音速. 激波管被驱动段气流质点速度比较均衡, 驱动段存在明显的速度梯度. 1 ms时刻透射激波穿过液膜, 而反射激波与后续的入射激波在液膜右侧发生碰撞, 因此液膜左右两侧气流速度方向存在明显差异. 液膜左侧气流主要为沿激波管轴线水平向左, 液膜右侧气流则为沿径向四散传播. 3 ms时刻气流高速区开始穿越液膜区域, 并将周围流体卷吸进入射流中, 最高气流质点速度达到519 m/s. 之后由于激波管内高压气体已完全排出, 不能为射流提供后续能量供应, 在后续卷入气流以及周围环境的阻力下射流速度不断下降, 4 ms时刻射流核心区最大质点速度下降至424 m/s, 5 ms时刻进一步下降至307 m/s.
对比图11与图6可以发现, 不同时刻的射流高速区均位于云团内部空腔结构中, 并且从激波管内喷出的气流本身不含液相成分, 可以推断云团内部空腔结构正是由于激波后的射流对液膜前期破碎所形成的云团冲击而产生的.
激波与液膜作用过程中, 不同时刻激波管中轴线上速度分布见图12. 激波管最右侧驱动段为坐标原点, 横轴表示距离, 单位m; 纵轴表示速度, 单位m/s.
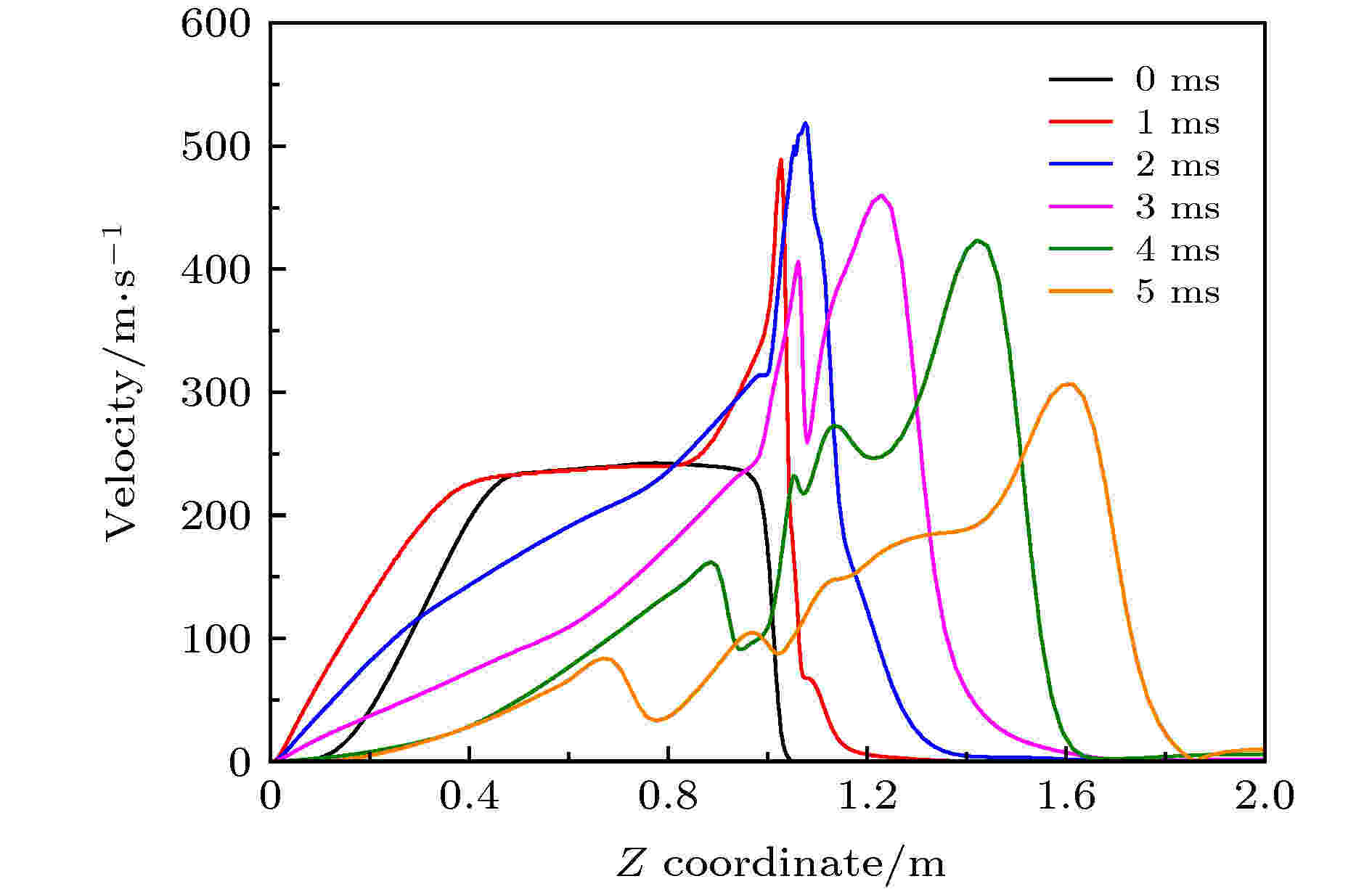图 12 不同时刻激波管中轴线上速度分布Figure12. Velocity distribution on the central axis of shock tube at different times.
从图12可以看出, 0 ms时刻被驱动段速度稳定在243 m/s左右, 激波到达管口区域, 激波阵面存在非常明显的速度梯度, 激波管外部未受扰动区域保持静止状态. 随着时间的推进, 激波管外部出现明显的速度峰值区域, 2 ms时刻达到最大速度峰值519 m/s, 之后速度峰值区域不断前移, 并且数值有所下降. 从图12与图10的对比中可以看出, 速度峰值区域与压力最低区域出现位置一致, 表明射流核心区处于高速低压状态.
1)激波与液膜作用过程中存在入射、反射与透射现象, 透射激波影响液膜左侧破碎云团形状, 入射激波和反射激波影响液膜右侧破碎云团形状.
2)液膜破碎形成的云团内部存在空腔结构, 该空腔结构形状会不断变化, 直至穿透云团区域; 云团体积在前2.5 ms时间内增长迅速, 达到6.7 dm3, 后续云团体积基本稳定.
3)云团内部的空腔结构中存在三维环状旋涡, 旋涡核心区压力为负值, 最大负压值可达–78 kPa. 在三维环状旋涡往前运动的过程中会不断将周围流体卷入, 旋涡强度下降并逐渐在空间中耗散.
4)激波从管口出来后形成狭长射流, 最大气流速度出现在射流内部位置, 2 ms时刻达到的最大气流速度为519 m/s, 之后不断衰减. 射流导致了云团内部空腔结构的产生.
