<script type="text/javascript" src="https://cdn.bootcss.com/mathjax/2.7.2-beta.0/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script>
<script type='text/x-mathjax-config'>MathJax.Hub.Config({tex2jax: {inlineMath: [['$','$'], ['\\(','\\)']]},"HTML-CSS": {linebreaks: { automatic: true},scale: 100}});</script>
摘要: 量子力学领域中对强激光场与原子分子相互作用的理论研究非常依赖于数值求解含时薛定谔方程. 本文在强场电离的背景下并行求解氢原子的三维含时薛定谔方程. 基于球极坐标系, 采用分裂算符-傅里叶变换方法将含时薛定谔方程进行了离散化. 由此可得到长度规范下的光电子连续态波函数. 图形处理器(GPU)可以依托多线程结构充分发挥细粒度并行的优势, 实现整体算法的并行加速. 计算表明, 相对于中央处理器(CPU), GPU并行计算有着最高约60倍的加速比. 由此可见, 基于GPU加速数值求解三维含时薛定谔方程能够显著缩短计算耗费的时间. 这一工作对利用GPU快速求解三维含时薛定谔方程有着重要的指导意义.
关键词: 三维含时薛定谔方程 /
强场电离 /
并行计算 English Abstract Numerical solution of three-dimensional time-dependent Schr?dinger equation based on graphic processing unit acceleration Tang Fu-Ming Liu Kai Yang Yi Tu Qian Wang Feng Wang Zhe Liao Qing Hubei Key Laboratory of Optical Information and Pattern Recognition, Wuhan Institute of Technology, Wuhan 430205, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11674257, 11604248, 11874019, 11947096) and the Program for Distinguished Middle-aged and Young Innovative Research Team in Higher Education of Hubei Province, China (Grant No. T201806)Received Date: 11 May 2020Accepted Date: 10 July 2020Available Online: 26 November 2020Published Online: 05 December 2020Abstract: In the field of quantum mechanics, the theoretical study of the interaction between intense laser field and atoms and molecules depends very much on the numerical solution of the time-dependent Schr?dinger equation. However, solving the three-dimensional time-dependent Schr?dinger equation is not a simple task, and the analytical solution cannot be obtained, so it can only be solved numerically with the help of computer. In order to shorten the computing time and obtain the results quickly, it is necessary to use parallel methods to speed up computing. In this paper, under the background of strong field ionization, the three-dimensional time-dependent Schr?dinger equation of hydrogen atom is solved in parallel, and the suprathreshold ionization of hydrogen atom under the action of linearly polarized infrared laser electric field is taken for example. Based on the spherical polar coordinate system, the time-dependent Schr?dinger equation is discretized by the splitting operator-Fourier transform method, and the photoelectron continuous state wave function under the length gauge can be obtained. In Graphics processing unit (GPU) accelerated applications, the sequential portion of the workload runs on central processing unit (CPU) (which is optimized for single-threaded performance), while the compute-intensive part of the application runs in parallel on thousands of GPU cores. The GPU can make full use of the advantage of fine-grained parallelism based on multi-thread structure to realize parallel acceleration of the whole algorithm. Two accelerated computing modes of CPU parallel and GPU parallel are adopted, and their parallel acceleration performance is discussed. Compared with the results from the existing physical laws, the calculation error is also within an acceptable range, and the result is also consistent with the result from the existing physical laws of suprathreshold ionization, which also verifies the correctness of the program. In order to obtain a relatively accurate acceleration ratio, many different experiments are carried out. Computational experiments show that under the condition of ensuring accuracy, the GPU parallel computing speeds by up to about 60 times maximally based on the computational performance of CPU. It can be seen that the accelerated numerical solution of three-dimensional time-dependent Schr?dinger equation based on GPU can significantly shorten the computational time. This work has important guiding significance for rapidly solving the three-dimensional time-dependent Schr?dinger equation by using GPU.Keywords: three-dimensional time-dependent Schr?dinger equation /strong-field ionization /parallel computing 全文HTML --> --> --> 1.引 言 强场激光物理是过去二十多年随着超短强激光技术的发展而快速发展起来的前沿学科, 主要研究超强超短激光与电子的相互作用. 早在1917年, 爱因斯坦的辐射理论就提出了受激辐射的基本概念, 预测到光可以产生受激辐射. 直至1960年, 世界上第一台激光器诞生, 此后的几十年间激光技术飞速发展, 从自由输出到调Q 技术(Q -switch)、锁模技术(mode locking), 再到啁啾脉冲放大技术, 激光的脉冲宽度越来越短, 功率越来越大. 利用先进激光技术获得的超快强激光脉冲与物质相互作用, 成为了研究物质基本性质的一种重要手段. 其中, 强场中一些非线性现象, 如高次谐波的产生(HHG)[1 -5 ] 、次序和非次序双电离[6 -8 ] 等, 受到了广泛的关注.[9 -11 ] 、强场近似(SFA)[12 -14 ] 和半经典模型[15 -17 ] . 求解三维含时薛定谔方程得到的结果可以认为相当于发生在数值上的实验. 但是求解三维含时薛定方程并非一项简单的任务, 无法获得解析解, 只能借助计算机数值求解. 在直角坐标系下哈密顿算符的表示很直观, 但由于正交网格在三个维度上均较为致密, 因此对存储空间和计算量的需求十分巨大. 而在球极坐标系中只有径向网格较为致密, 另外两个维度相对稀疏. 尽管如此, 求解三维含时薛定谔方程的计算量也是十分巨大. 为了缩短计算的时间, 更快地得到计算结果, 就有必要使用并行方法去加速计算.[18 ] . 另一方面, 采用不同的并行平台, 比如: 使用CUDA (compute unified device architecture)平台编写TDSE程序[19 ] , 使用OpenCL(open computing language)语言编写TDSE程序[20 -22 ] . 但在CUDA架构或OpenCL架构下对算法并行计算进行加速, 使用起来难度较高.2.理论方法 22.1.三维含时薛定谔方程求解方案 2.1.三维含时薛定谔方程求解方案 物理系统的时间演化由波函数$\varPsi (t)$ 来描述, 满足含时薛定谔方程$H\left( t \right)$ 指作用在约化波函数$\varPhi \left( t \right) = r\varPsi \left( t \right)$ 上的算符, 其中${L^2}$ 为系统的总角动量算符, $E(t)$ 为线偏振入射激光电场.$\varPsi (r, t)$ 在球谐函数${{\rm{Y}}_{lm}}(\theta, \varphi )$ 下展开,m 是一个好量子数, 通过对方位角$\varphi $ 进行积分并把角动量算符数值求解.含时薛定谔方程的一般步骤是先给定一个初始波函数$\varPhi (t = 0)$ , 然后将时间演化算符作用在该初始波函数上, 反复迭代直至得到任意时刻的末态波函数. 假设将波函数向前推进$\Delta t$ 时间增量, 那么t 时刻和$t + \Delta t$ 时刻的波函数关系为[23 ] 将(2 )式代入(4 )式, 可以得到$\Delta t$ 的三阶误差项. 由于m 是一个好量子数, 通过对方位角$\varphi $ 进行积分并把角动量算符${L_z}$ 替换为它的本征值m , 可以使问题大为简化. 为了方便起见, 下文只讨论$m = 0$ 的情况. 假设波函数可以在有限勒让德多项式下展开:${P_l}$ 为球谐函数${{\rm{Y}}_{l0}}$ , ${f_l}({r_i}, t)$ 可以由高斯-勒让德求积法数值计算得出,${x_j}$ 为勒让德多项式${P_{L + 1}}({x_j})$ 的$L + 1$ 个零点, ${w_j}$ 为与之对应的求积权重. 对于l 的不同取值, 一维径向波函数${f_l}({r_i}, t)$ 均定义在R 点等距径向网格上, 它的网格表示为4 )式中时间演化算符的作用可以分为三步.$T = ( - {1 / {2)}}{{{\partial ^2}} / {\partial {r^2}}}$ 独立作用在每个一维径向波函数${f_l}({r_i}, t)$ 上, 利用带边界条件的傅里叶谱方法[24 ] , 得到$O(R{\log _2}(R)L)$ .V 分为离心势能项${{{L^2}} /{(2{r^2})}}$ 和库仑势能项${{ - 1} / r}$ , 其中总角动量算符${L^2}$ 在球谐函数表象下是对角化的, 对角元为它的本征值$l(l + 1)$ , 因此可以得到$W(r, \theta, t)$ 在坐标表象$\{ r, \theta \} $ 下是对角化的, 利用 (5 )式重构波函数$\varPhi (r, x, t)$ , 得到表1 所列.算法 $\varPhi (t + \Delta t) = {{\rm{e}}^{ - {\rm{i}}H(t)\Delta t}}\varPhi (t)$ Input: ${f_l}({r_i}, t)$ Output: ${f_l}({r_i}, t)$ 1. for n do 2. for l do 3. ${f_l}({r_i}, t) = {\rm{ifft} }\left( { {\rm{diag} }\Big( { { {\rm{e} }^{ - {\rm{i} }\tfrac{ {\Delta t} }{2}\tfrac{ { {k^2} } }{2} } } } \Big) \cdot {\rm{fft} }\left( { {f_l}({r_i}, t)} \right)} \right)$ 4. end for 5. for i and l do 6. ${f_l}({r_i}, t) = { {\rm{e} }^{ - {\rm{i} }\tfrac{ {\Delta t} }{2}\left[ {\tfrac{ {l(l + 1)} }{ {2 r_i^2} }\, - \, \frac{1}{ { {r_i} } } } \right]} } \cdot {f_l}({r_i}, t)$ 7. end for 8. for i and j do 9. $\varPhi ({r_i}, {x_j}, t) = \sum\limits_{l = 0}^L {{f_l}({r_i}, t){P_l}({x_j})} $ 10. end for 11. for i and j do 12. $\left| {\varPhi ({r_i}, {x_j}, t)} \right\rangle = { {\rm{e} }^{ {\rm{i} }\Delta tE(n){r_i}{x_j} } } \cdot \left| {\varPhi ({r_i}, {x_j}, t)} \right\rangle$ 13. end for 14. for i and j do 15. ${f_l}({r_i}, t) = \sum\limits_{j = 1}^{L + 1} {{w_j}{P_l}({x_j})} \varPhi ({r_i}, {x_j}, t)$ 16. end for 17. for i and l do 18. ${f_l}({r_i}, t) = { {\rm{e} }^{ - {\rm{i} }\tfrac{ {\Delta t} }{2}\left[ {\tfrac{ {l(l + 1)} }{ {2 r_i^2} }\, - \, \frac{1}{ { {r_i} } } } \right]} } \cdot {f_l}({r_i}, t)$ 19. end for 20. for l do 21. ${f_l}({r_i}, t) = {\rm{ifft} }\left( { {\rm{diag} }\Big( { { {\rm{e} }^{ - {\rm{i} }\tfrac{ {\Delta t} }{2}\tfrac{ { {k^2} } }{2} } } } \Big) \cdot {\rm{fft} }\left( { {f_l}({r_i}, t)} \right)} \right)$ 22. end for 23. end for
表1 TDSE算法步骤Table1. TDSE algorithm steps.6 )式再次展开成径向波函数${f_l}({r_i}, t)$ , 接下来只需要依次执行步骤2)和步骤1), 就完成了波函数向前推进$\Delta t$ 的一次迭代. 在含时演化中, 重复执行上述步骤, 能够得到任意时刻的末态波函数. 步骤1)中的快速傅里叶变换操作以及(5 )式和(6 )式中的变换操作都可以通过向量化提高计算效率.${\sigma _l} = \arg \varGamma \left( {1 + l - {\rm{i}}Z/k} \right)$ 是库仑散射相移, ${\delta _l}$ 是除去长程库仑势的短程势产生的相移.2.2.并行计算方案 -->2.2.并行计算方案 本文在Matlab环境下调用设备端(GPU)来实现并行计算, 离散化的初始波函数以及传播算符均保存在主机端(CPU), 如图1 所示. GPU上数组的创建和传输通过Matlab并行计算工具箱的相关函数完成, 使用gpuArray()函数从主机端向设备端发送Matlab数组, 即将Matlab工作区内的数组传输到设备端内存. 在GPU中进行数值计算完毕以后, 再通过gather()函数从设备端向主机端发送Matlab数组, 即将设备端内的Matlab数组传输到主机端内存.图 1 数据传输流程图Figure1. The flowchart of data transmission.3.结果与讨论 23.1.测试环境与测试算例 3.1.测试环境与测试算例 本文所有计算使用的并行环境包含1个CPU (Intel Xeon E7-8880 v4, 22核, 主频2.2 GHz)和NVIDIA Tesla P100卡中的1个GPU (3584核心, 主频1.3 GHz). 程序的实现基于Matlab环境, GPU中的矩阵向量操作调用了重载的Matlab函数. 本次测试算例以线偏振红外激光电场作用下氢原子的阈上电离为背景. 红外激光电场强度$I = 9 \times {10^{13}}\;{\rm{ W}}/{\rm{c}}{{\rm{m}}^2}$ , 波长$\lambda = 800\;{\rm{ nm}}$ , 具有正弦平方脉冲包络, 共8个光学周期. 其中计算采用的空间范围${r_{\max }} = 1000\;{\rm{ a}}.{\rm{u}}.$ , 时间步长$\Delta t = 0.0037\;{\rm{ a}}.{\rm{u}}.$ .3.2.实验结果 -->3.2.实验结果 为获取GPU并行的优化表现, 需要给出CPU上的并行性能作为基准. 通过改变角量子数L 和径向网格点R 计算演化时间结束后的末态波函数, 比较不同参数下GPU相对于CPU的加速比(单个CPU计算时间与单个GPU计算时间的比值):R = 1024 × 32不变, 选取不同的角量子数L , 计算结果如表2 和图2 所示.角量子数L 计算时间/s CPU GPU 4 2164.309 159.368 9 4120.602 164.418 19 7922.537 205.440 39 17682.308 378.104 79 36774.347 757.198
表2 不同角量子数下CPU与GPU的计算时间比较Table2. Computation time of CPU and GPU under different angular quantum numbers.图 2 加速比随着角量子数的变化Figure2. Speedup ratio as a function of angular quantum number.L = 19保持不变, 改变径向网格点R 的大小, 然后将CPU与GPU的计算时间对比, 如表3 和图3 所示.径向网格点数R 计算时间/s CPU GPU 212 1118.348 148.302 213 1871.128 154.614 214 3846.120 160.763 215 7922.537 205.440 216 16862.467 354.554
表3 不同径向网格点下CPU与GPU的计算时间比较Table3. Computation time of CPU and GPU under different radial grid points.图 3 加速比随着径向网格点的变化Figure3. Speedup ratio as a function of radial grid point.fl (ri , t )}的矩阵大小, 比较CPU和GPU的计算时间, 结果如表4 和图4 所示.矩阵大小 计算时间/s CPU GPU 5 × 212 199.158 149.895 10 × 213 965.276 166.039 20 × 214 3846.120 160.763 40 × 215 17682.308 378.104 80 × 216 74761.695 1524.669
表4 不同矩阵大小下CPU与GPU的计算时间 比较Table4. Computation time of CPU and GPU under different matrix sizes.图 4 加速比随着矩阵大小的变化Figure4. Speedup ratio as a function of the size of matrix.$I = {\rm{1}} \times {10^{13}}\;{\rm{ W}}/{\rm{c}}{{\rm{m}}^2}$ , 波长$\lambda = 1600\;{\rm{ nm}}$ , 具有正弦平方脉冲包络, 共8个光学周期. 其中计算采用的空间范围${r_{\max }} = 1000\;{\rm{ a}}.{\rm{u}}.$ , 时间步长$\Delta t = 0.0037\;{\rm{ a}}.{\rm{u}}.$ . 此时与第三组实验相同, 同时改变径向网格点和角量子数的大小, 也就是改变径向波函数集{fl (ri , t )}的矩阵大小, 比较CPU和GPU的计算时间, 结果如表5 和图5 所示.矩阵大小 计算时间/s CPU GPU 5 × 212 437.584 315.448 10 × 213 2075.667 463.183 20 × 214 9252.539 629.088 40 × 215 40617.723 814.985 80 × 216 182135.643 3024.669
表5 不同矩阵大小下CPU与GPU的计算时间比较Table5. Computation time of CPU and GPU under different matrix sizes.图 5 加速比随着矩阵大小的变化Figure5. Speedup ratio as a function of the size of matrix.图6 所示, 电子末态动量分布保持一致.图 6 氢原子的光电子末态动量分布 (a) CPU计算结果; (b) GPU计算结果Figure6. Photoelectron final-state momentum distributions of hydrogen atom: (a) Calculation results of CPU; (b) calculation results of GPU.$5 \times {10^{ - 21}}$ , 动量分布误差为$2 \times {10^{ - 18}}$ . 其中波函数误差计算公式为3.3.实验结果讨论 -->3.3.实验结果讨论 通过上述的计算可以得出: 1)相同计算量下CPU与GPU的计算时间有很大的差距, 当计算量较小时加速比急剧升高, 随着计算量的增大加速比趋于一个稳定值, 最高达到了约60倍的加速提升, 加速效果十分明显; 2)从不同的计算量对比也可以看出, 当计算量越大时, 加速的效果也就越好. 并不是所有的计算都要选取GPU来计算, CPU将数据传输到GPU需要一定的时间, 当数据比较大时, 采用GPU来并行计算, 能够获得更大的加速比; 3)如果只是改变一个维度的大小, 所得到的实际加速效果有时候并不理想, 这和CPU以及GPU存储数据、读取数据的方式有关. 所以在计算的时候为了获得最好的加速比, 需要同时在至少两个维度上调整矩阵的大小; 4)无论采用CPU计算还是GPU计算, 都能得到相同的计算结果, 计算误差也在可接受的范围内, 并且该结果也符合现有的阈上电离物理规律.4.结 论 本文详细分析了在强场电离的背景下数值求解氢原子三维含时薛定谔方程基于不同硬件的并行速度. 借助于分裂算符-傅里叶变换方法, 在球极坐标下得到了三维含时薛定谔方程的末态解. 同时, 依托于GPU的多线程结构, 使得GPU发挥细粒度方面的并行优势, 实现整体算法的并行加速. 采用了CPU并行和GPU并行两种加速计算模式, 探讨了两者并行加速的性能. 通过与现有的物理规律相对比, 验证了程序的正确性. 计算结果表明, 当计算量较小时GPU相对于CPU的加速效果不突出, 随着计算量的增大加速比迅速增加, 然后趋于一个稳定值. GPU并行对于数值求解三维含时薛定谔方程有着相对于CPU最高约60倍的加速. 可见, 计算量越大, 采用GPU并行获得的加速比越大. 这一工作对利用GPU高效数值求解含时薛定谔方程有着重要的指导意义. 




































 图 1 数据传输流程图
图 1 数据传输流程图



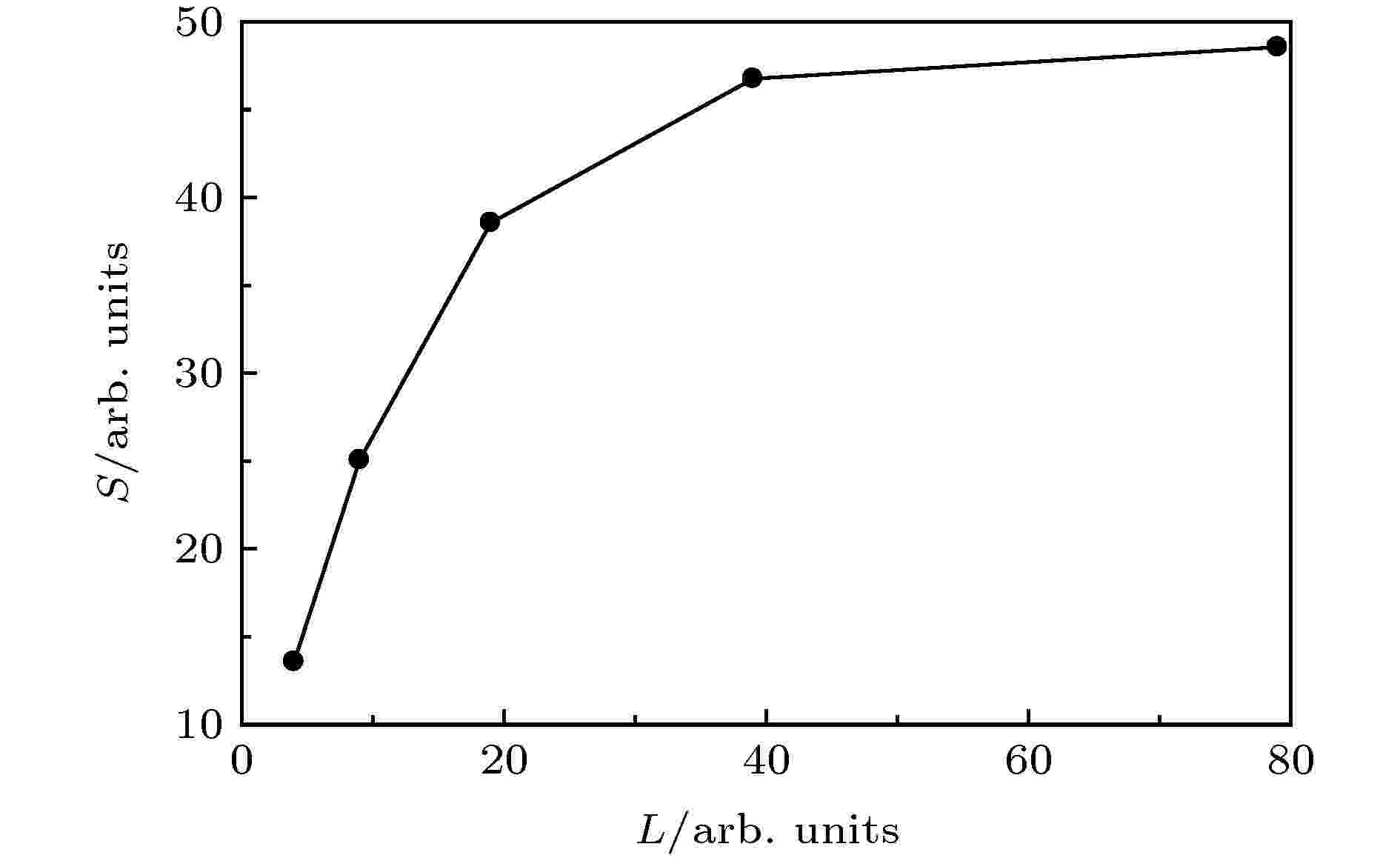 图 2 加速比随着角量子数的变化
图 2 加速比随着角量子数的变化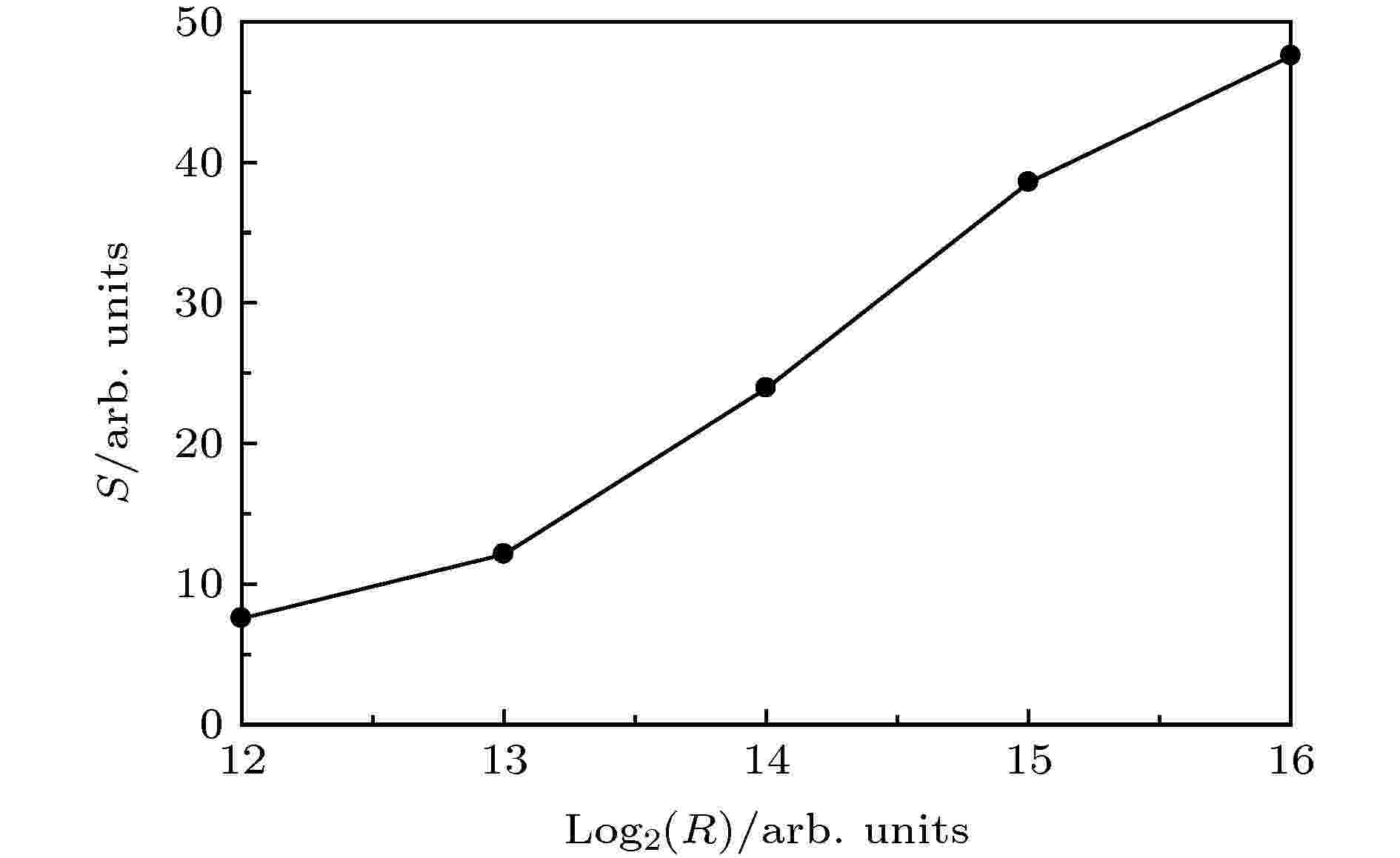 图 3 加速比随着径向网格点的变化
图 3 加速比随着径向网格点的变化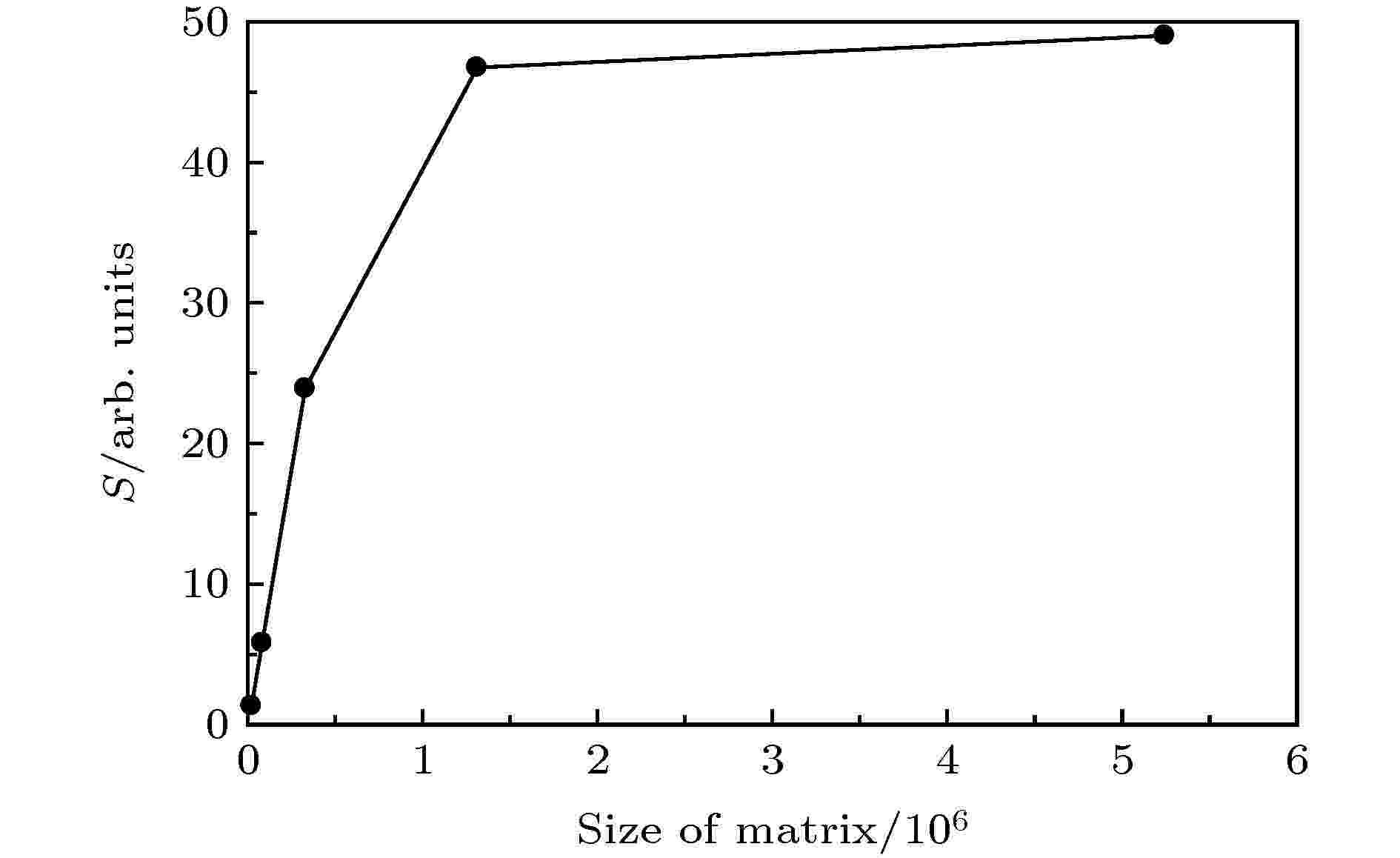 图 4 加速比随着矩阵大小的变化
图 4 加速比随着矩阵大小的变化



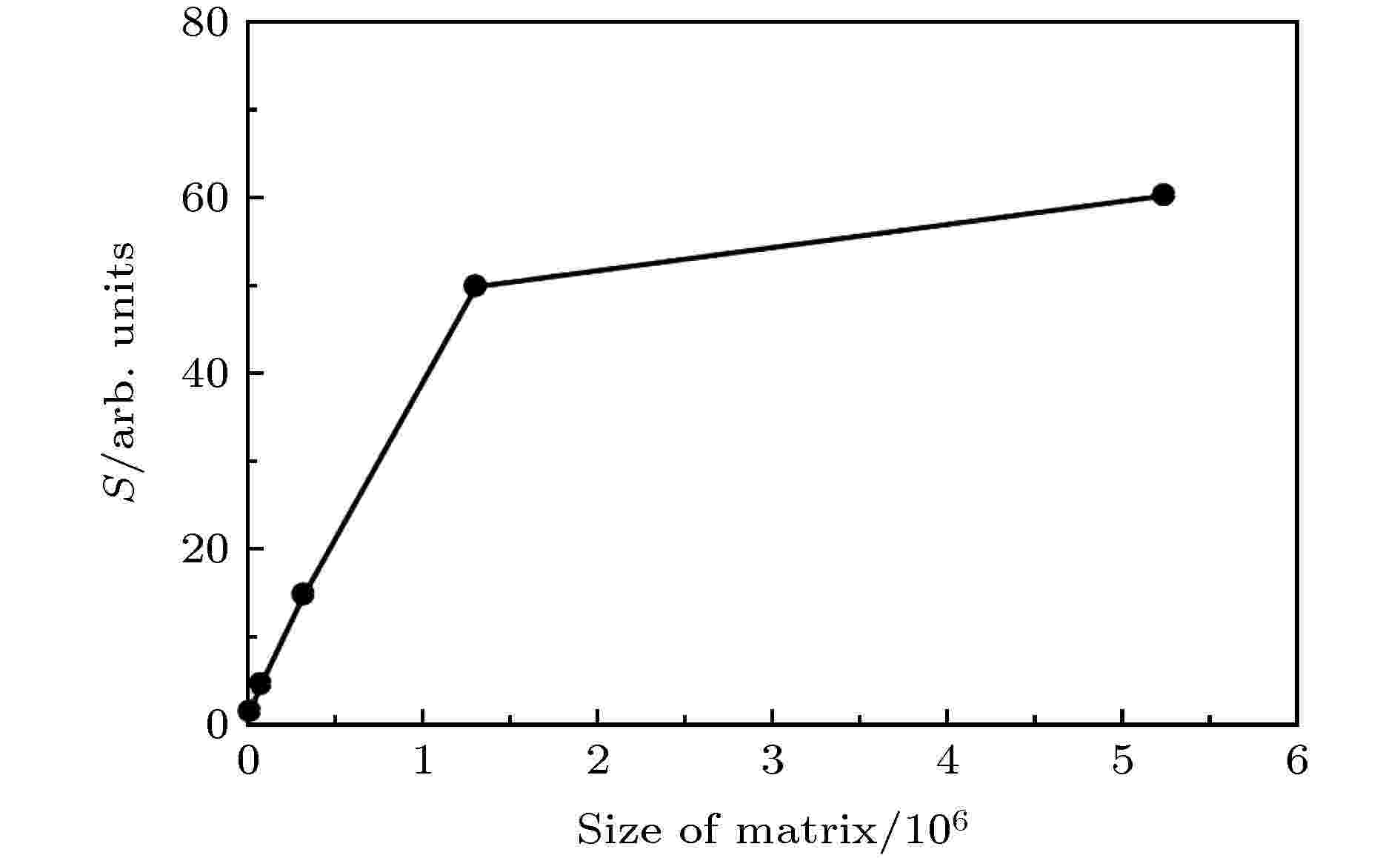 图 5 加速比随着矩阵大小的变化
图 5 加速比随着矩阵大小的变化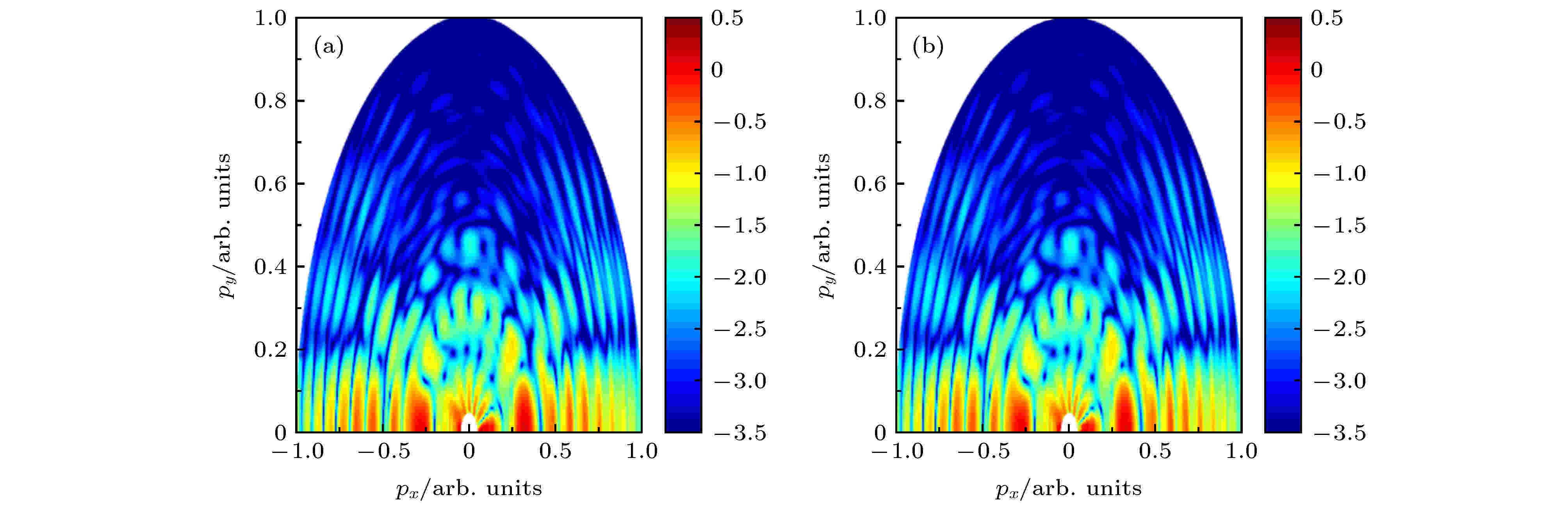 图 6 氢原子的光电子末态动量分布 (a) CPU计算结果; (b) GPU计算结果
图 6 氢原子的光电子末态动量分布 (a) CPU计算结果; (b) GPU计算结果

