摘要:基于理想磁流体动力学方程组, 采用CTU (corner transport upwind) + CT (constrained transport)算法, 数值研究了磁场控制下R22气柱界面Richtmyer-Meshkov不稳定性的演化过程. 结果描述了平面激波冲击气柱界面过程中激波结构和界面不稳定性的发展; 无磁场时, 流场结构与Haas和Sturtevant (Hass J F, Sturtevant B 1987 J. Fluid Mech. 181 41)的实验结果相符; 施加纵向磁场后, 激波结构的演化基本无影响, 但明显抑制了气柱界面的不稳定性. 进一步研究表明, 激波与界面的作用, 使磁感线在界面上发生折射, 改变流场的磁场梯度, 在内外涡量层上形成磁张力. 磁张力的形成, 对界面流体产生一个与速度剪切相反的力矩, 抑制了界面的失稳及主涡的卷起. 另外, 磁张力沿界面分布的不均匀, 改变磁感线在界面上的聚集程度, 放大磁能量, 最终增强磁场对气柱界面不稳定性的抑制作用.
关键词: Richtmyer-Meshkov不稳定性/
磁流体/
激波/
圆形气柱

English Abstract

全文HTML

--> --> -->

激波冲击密度界面过程中, 诱导界面失稳并最终向湍流转捩的现象, 称为Richmyer- Meshkov(RM)不稳定性^[1,2]. RM不稳定性广泛存在于超燃冲压发动机、惯性约束核聚变、天体物理、航空航天、兵器发射及化工等领域, 因其蕴含了流动稳定性、激波、旋涡、激波与涡作用及湍流转捩等复杂的流体物理现象, 无论在工程还是学术领域均具有重要的研究价值.
在诸多工程应用中, 如惯性约束核聚变, RM不稳定性引起的湍流混合, 导致靶心和其他燃料混合, 降低靶的产额^[3,4], 因此需对惯性约束核聚变中RM不稳定性进行控制, 提高聚变产额; 对于超燃冲压发动机, RM不稳定性可加速燃料与来流空气的混合, 提高能源的利用率^[5,6]. 基于此, 如能实现对RM不稳定性发展的控制, 将会给工程应用带来巨大的益处. 在核聚变和超燃冲压发动机等高能物理领域中, 流动物质多呈等离子状态, 易受磁场的影响, 利用磁场控制RM不稳定性的研究, 成为近年来的研究热点和难点.
由于实验研究耗资大且危险, 目前为止, 国内外仍缺乏关于磁流体动力学(magneto-hydro-dynamic, MHD)中RM不稳定性的实验研究; 对于MHD RM不稳定性的理论研究和解析解方面, 因MHD方程组耦合了常规流体方程组和Maxwell方程组, 解析解十分复杂, 目前鲜有关于MHD RM不稳定性解析解的研究. 较常规流体方程组, 数值模拟求解MHD方程组更加复杂, 但相对实验和获得解析解, 更加可行且安全, 可为未来实验研究提供理论指导, 因此数值模拟在磁控流体界面RM不稳定性的研究中占十分重要的地位.
2003年, Samtaney^[7]首次利用MHD方程, 数值研究了磁场对RM不稳定性的影响, 发现磁场抑制了界面不稳定性的发展. Hawley和Zabusky^[8]对界面卷起与促进不稳定性增长的研究指出, 斜压涡量是驱使密度界面不稳定增长的原因. 基于此, Wheatley等^[9]对磁场抑制RM不稳定性机理的研究指出, 在磁场作用下, 斜压涡量不再沉积于界面上, 而分布在Alfvén波上, 最终因界面上缺少涡量沉积而变得稳定. Wheatley等^[9,10]还提出磁场的作用是防止界面上涡量的沉积, 磁场的主要致稳机理是洛伦兹力, 它起到恢复力的作用, 将扰动拉回到平衡位置. 随后, 他们还指出^[11], 激波与界面相互作用后, 形成平行和反平行于磁场的两Alfvén波, 界面上的涡量随Afvén波被分解, 不再沉积在密度界面上.
Cao等^[12]提出在剪切流中, 密度界面扰动呈指数增加, 磁场能够有效抑制激波冲击波浪状界面的扰动. Sano等^[13]研究发现, 与RM不稳定性相关联的流体运动会拉伸磁场, 使磁场强度可放大到两个数量级以上. Mac Low等^[14]研究提出, 平行磁场能够抑制RM不稳定性和Kelvin-Helmholtz(KH)不稳定性, 有效减弱界面内外层气体混合等的重要结论. Fragile等^[15]在模拟辐射状态下激波与二维气体云的相互作用中发现, 气体云外部磁场会加强激波对气体云的压缩, 加快磁场的辐射, 增强磁场强度; 气体云内部磁场则起到相反的作用, 当磁场强度较弱时, 内部磁场可完全抑制低温气体的辐射冷却.
国内, 鲜有关于MHD RM不稳定性的研究. 李源和罗喜胜^[16]数值模拟磁流体中激波与矩形密度界面的相互作用, 描述了不同磁场中矩形密度界面的演变过程, 发现磁场能够减少界面上涡量的生成, 抑制界面的不稳定性; 另外, 磁场影响界面的加速过程及内外气体的混合率, 而界面的存在会增强波后部分区域的磁场强度. 最近, 本课题组^[17,18]对磁控条件下封闭气柱界面的RM不稳定性研究发现, 磁场抑制界面不稳定性的机理在于洛伦兹力将不稳定性产生的涡输运到界面两侧, 界面因缺少涡量堆积而不再失稳.
先前关于MHD RM不稳定性的研究, 主要集中在磁场抑制不稳定性的机理, 并一致认为磁场抑制RM不稳定性与斜压涡量不再沉积在密度界面上有关^[7-11], 磁场的致稳机理在于洛伦兹力, 它起到恢复力的作用, 将扰动拉回到平衡位置^[9,10]. 然而, 上述研究并未清晰说明洛伦兹力对界面的作用过程, 且他们的工作主要采用间断界面, 适用于理论分析, 但未考虑到气柱生成过程, 界面组分存在的扩散. 本课题组先前的研究^[19,20], 考虑了激波冲击界面组分呈高斯分布的圆形气柱, 得到射流形成机理及界面演化过程, 但未考虑磁场的影响.
基于此, 本文采用CTU + CT (corner transport upwind + constrained transport)算法求解MHD方程组, 数值研究了有、无磁场情况下, 平面激波冲击界面组分呈高斯分布的R22圆形气柱过程, 分析纵向磁场对界面演化的影响, 从物理的角度探究磁场对界面的致稳效应. 最后, 定量分析了磁感线弯曲汇聚而诱导的磁能放大现象.

2

-->

2.1.数值方法

本文采用理想MHD方程组^[21,22], 对平面激波冲击圆形气柱过程的界面不稳定性进行数值研究, 其守恒形式为

$\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left[ {\rho {{v}}} \right] = 0,$

$\frac{{\partial \left( {\rho {{v}}} \right)}}{{\partial t}} + \nabla \cdot \left[ {\rho {{vv}} - \frac{{{{BB}}}}{\mu } + {P^*}} \right] = 0,$

$\frac{{\partial E}}{{\partial t}} + \nabla \cdot \left[ {\left( {E + {P^*}} \right){{v}} - \frac{{{{B}}\left( {{{B}} \cdot {{v}}} \right)}}{\mu }} \right] = 0,$

$\frac{{\partial {{B}}}}{{\partial t}} - \nabla \times \left( {{{v}} \times {{B}}} \right) = 0,$

式中, ρ为流体密度, B为磁感应强度, v为流体速度矢量, μ为磁导率, 方程中取μ = 1. 流场总压力$ P^* $和总能E为

${P^*} = p + \frac{{{B^2}}}{{2\mu }},$

$E = p/\left( {\gamma - 1} \right) + \frac{{\rho \left( {{{v}} \cdot {{v}}} \right)}}{2} + \frac{{{{B}} \cdot {{B}}}}{{2\mu }},$

式中, p为流体压力, γ为比热比. 因此, 流场总压P ^*由流体压力与磁压力组成, 总能E则由压力能、动能和磁能量组成.
本文采用非分裂的CTU + CT^[23,24]算法对理想MHD方程组进行求解. 其中, CTU (corner transport upwind)算法是基于PPM (piecewise parabolic method)对守恒量进行三阶空间重构. 为了保证磁场散度为零, 在计算Godunov通量时, 结合用于计算电场的CT (constrained transport)算法进行通量重构. 为了能准确捕捉激波间断, 对流项离散采用Roe-HLL格式.
2 -->

2.2.计算模型

图1为平面激波与圆形气柱相互作用的计算模型. 计算域的长L × 宽H为0.25 m × 0.089 m, 气柱直径为0.05 m, 气柱中心与左边界的距离为0.05 m, 与右边界的距离D = 0.2 m. 初始时, 气柱内外压力与温度均为p₀ = 1 atm (1 atm = 1.01325 × 10⁵ Pa)与T = 300 K, 气柱外部介质为空气, 气柱内部介质为R22气体, 气柱界面组分采用高斯分布, 如图1(b)所示, 具体分布规律为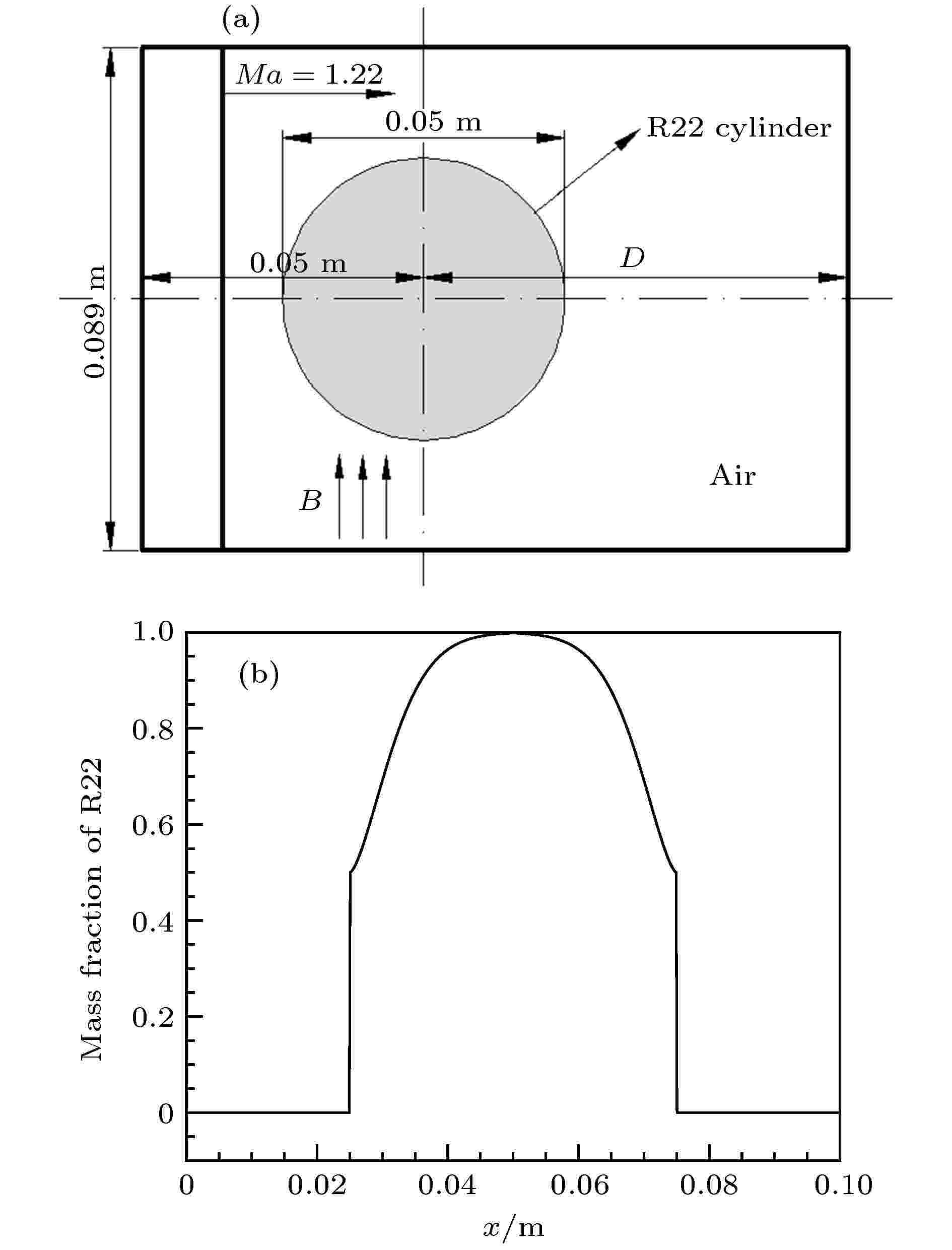
图 1 (a)计算模型; (b)界面组分沿对称轴的分布
Figure1. (a) Schematic of the computational model; (b) the distribution of R22 mole fraction along the symmetry axis of column.

$\begin{split}&Y_{\rm R22} (r) = \\& \begin{cases} 0.5 + \left[ 1.0 - \exp \left( - 5.78\Big| \dfrac{|r|}{R_0} - 1 \Big|^{1.54} \right) \right], \\ \qquad \qquad\qquad\qquad\qquad\qquad\quad | r | \leqslant R_0, \\ 0.0, \qquad\qquad\qquad\qquad\qquad \quad\; |r| > R_0,\end{cases} \end{split}$

式中, R₀为气柱半径, r为与气柱中心的径向距离, Y_R22为R22气体的质量分数.
入射激波从左向右传播, 来流马赫数Ma = 1.22. 上下边界设为固体反射边界, 右边界为出口条件. 计算域网格采用均匀分布的笛卡尔网格, 经网格收敛性测试后, 计算域网格总数为2500 × 890. 本文研究纵向磁场对气柱不稳定发展的影响, 选取磁场强度B = 10. 为了使气体受磁场影响, 假设气体已经完全电离.

图2为无磁场(B = 0)时, 平面激波(I)与圆形R22气柱(A)作用过程计算阴影图(上)与实验阴影图^[25](下)的对比, 两者具有相同的初始条件. 可见, 数值结果中激波的反射、绕射及气柱界面的演变过程均与实验结果^[25]相符.
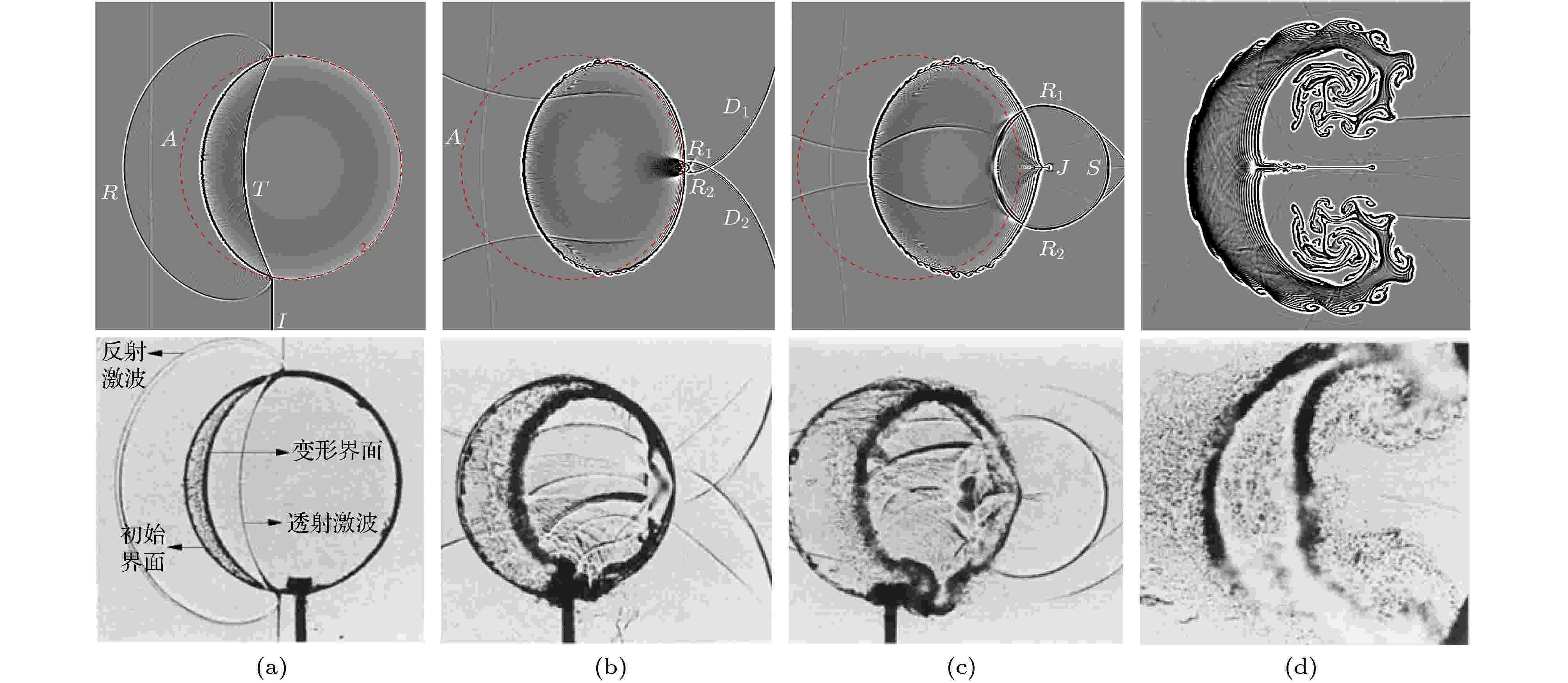图 2 激波与气柱作用过程的计算阴影结果(上)与实验结果(下)^[25]的对比　(a) t = 0.09 ms; (b) t = 0.215 ms; (c) t = 0.25 ms; (d) t = 1.20 ms
Figure2. Comparison of our numerical (up) and experimental^[25] (down) shadowgraph images of the interactions between shock wave and gas column: (a) t = 0.09 ms; (b) t = 0.215 ms; (c) t = 0.25 ms; (d) t = 1.20 ms.

激波与气柱作用过程(图2(a)), 入射激波在气柱内透射, 形成透射激波T. 因R22气体的声阻抗大于空气, T的传播速度低于入射激波. 激波经过后, 当地流场的流向速度起主导作用. 因气柱外部流场速度远高于内部流场速度, 在KH不稳定性作用下, 界面失稳并卷起形成珠状的KH小涡, 如图2(a)和图2(b)所示.
当激波经过气柱上下顶点(t = 0.105 ms)时, 其向气柱右侧绕射, 并形成绕射激波D₁与D₂ (图2(a)). 透射激波T与绕射激波D向气柱下游界面中心汇聚的过程, 提高了汇聚区域的压力, 形成局部高压区, 并在t = 0.215 ms时, 在对称轴上发生碰撞, 汇聚点压力达到峰值. 之后, 形成以汇聚点为中心, 向气柱左侧传播的稀疏波、向右侧传播的弧形二次激波S、及向上下两侧传播的反射激波R₁与R₂, 同时汇聚点的局部高压区剧烈冲击当地气体, 迅速提升了汇聚点的流场速度, 形成一道向右传播的R22射流J.
因反射激波R₁和R₂的传播方向与气柱界面的旋向相反(图2(c)), 反射激波与气柱的反向作用, 降低了气柱右侧的法向速度v. 在t = 0.3 ms时, 反射激波离开气柱表面, 继续向上、下两侧传播至激波管的壁面并反射, 形成反射激波. 在斜压效应作用下, 气柱上、下侧界面逐渐向右侧卷起, 最终形成旋向相反的主涡对, 如图2(d)所示. 同时, 反射激波与主涡层的来回作用, 加剧了涡层的失稳, 在主涡层上形成复杂的小涡串结构.
图3为施加纵向磁场后, 激波与气柱作用过程的计算阴影图. 与无磁场情况相比, 纵向磁场对流场激波结构的形成与演变基本无影响, 但明显抑制了界面的不稳定性, 界面上的小涡串结构完全消失. 在激波作用下, 气柱上、下侧界面仍会向右拉伸, 但并未形成螺旋状主涡结构, 界面始终保持光滑紧凑. 另外, 汇聚激波冲击气柱下游界面形成的射流结构J, 在后续发展过程中, 头部向上游凹陷, 剪切层被向上、下两侧拉伸, 最终嵌入到气柱下游界面中心, 形成随时间向上游阵面凹陷的结构, 如图3(e)—(h)所示.
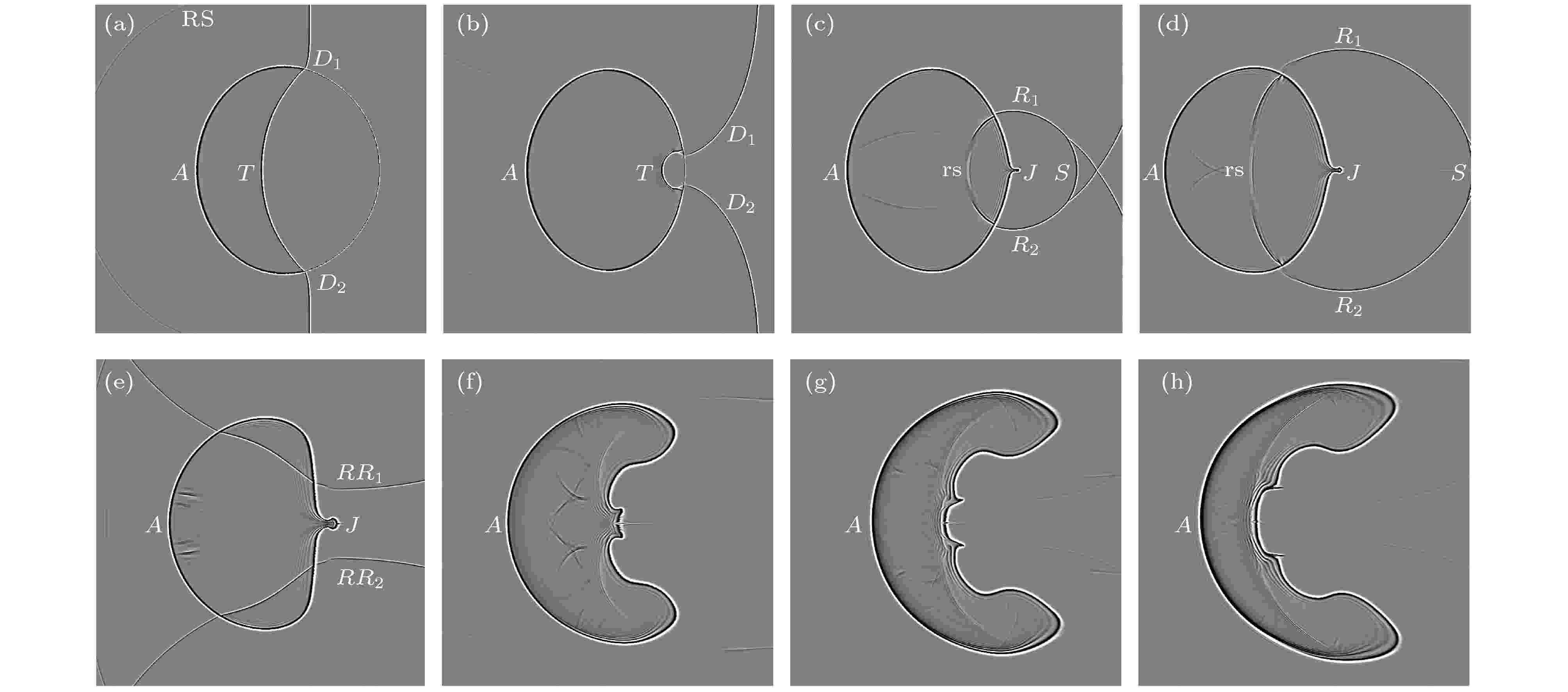图 3 施加磁场后流场的计算阴影图　(a) t = 0.12 ms; (b) t = 0.2 ms; (c) t = 0.25 ms; (d) t = 0.29 ms; (e) t = 0.425 ms; (f) t = 0.85 ms; (g) t = 1.20 ms; (h) t = 1.55 ms
Figure3. Numerical shadowgraph images of the case in the presence of a magnetic field: (a) t = 0.12 ms; (b) t = 0.2 ms; (c) t = 0.25 ms; (d) t = 0.29 ms; (e) t = 0.425 ms; (f) t = 0.85 ms; (g) t = 1.20 ms; (h) t = 1.55 ms.

平面激波与气柱界面相互作用过程中, 压力梯度方向与密度梯度方向的不一致, 导致斜压源项($\nabla \rho \times \nabla p$)的出现. 在激波与气柱界面作用问题中, 黏性效应可忽略, 涡量方程可表达为

$\frac{{D\omega }}{{Dt}} = \frac{1}{{{\rho ^2}}}\left( {\nabla \rho \times \nabla p} \right).$

(8)式表明在激波与气柱界面作用问题中, 斜压效应是涡生成的唯一原因, 涡量值是和密度梯度与压力梯度间的夹角大小成正比.
图4为无磁场时, 流场涡量分布. 在斜压效应作用下, 气柱上侧界面附近流体的顺时针旋转形成负涡量, 下侧界面流体的逆时针旋转生成正涡量. 在KH不稳定性作用下, 涡量层失稳, 卷起形成KH小涡. 随着主涡的卷起, 小涡沿涡层向涡核卷入. 在卷入过程中, 受主涡切向拉伸作用, 小涡出现切向变形. 因切向拉伸力对离涡核越近的涡层的作用越强, 所以离涡核越近的涡层上的小涡结构显得越扁长, 如图4(b)所示.
图 4 无磁场时流场涡量分布　(a) t = 0.3 ms; (b) t = 1.2 ms
Figure4. Vorticity distribution in the absence of a magnetic field: (a) t = 0.3 ms; (b) t = 1.2 ms.

图5为施加纵向磁场后, 流场涡量分布. 可见, 涡量的旋向与无磁场情况相同, 但涡量不再沉积于界面上, 向界面内外两侧传输, 呈现出涡量分层的现象(图5(a)). 由于涡量不再沉积于界面上, 当反射激波R₁和R₂反向作用于下游界面时, 界面上会形成旋向与初始涡量层相反的新涡量层(图5(c)). 因反射激波与界面的作用强度较绕射激波弱, 新涡量层相对于前涡量层的涡量值要弱. 如此, 后续反射激波(如, RR₁和RR₂等)与界面的来回作用, 最终形成多层的涡量层. 随着流场的发展, 涡量层相互分离并弯曲变形, 最终在气柱下游流场形成作用区域更广的复杂多涡量层结构, 且各涡量层始终保持光滑, 如图5(d)—(f)所示. 另外, 射流上、下剪切层被向两侧拉伸, 射流头部涡量逐渐消失, 在t = 0.425 ms时, 头部涡量被拉断. 随着剪切层继续向两侧移动, 剪切层涡量耗散并最终消失, 如图5(f)所示.
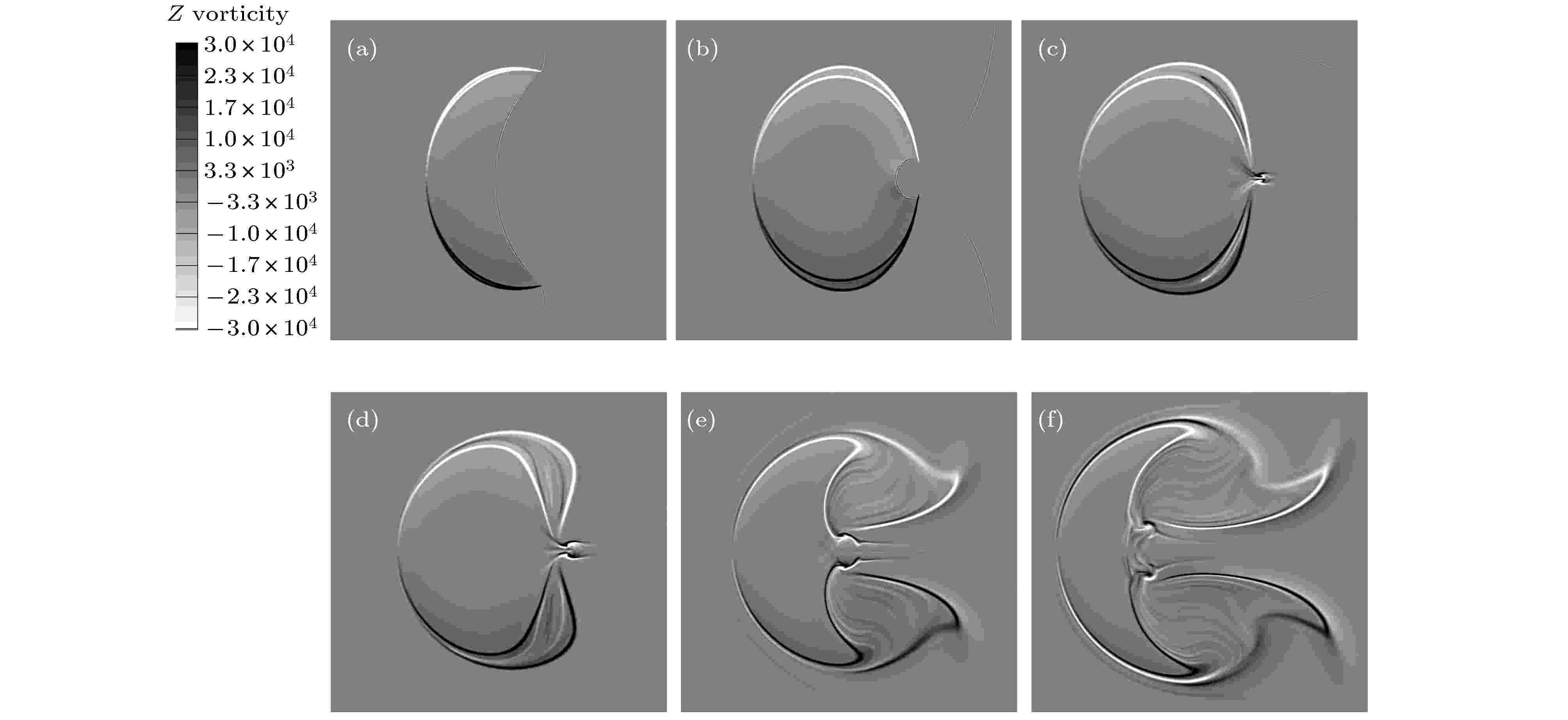图 5 施加磁场后流场涡量分布　(a) t = 0.12 ms; (b) t = 0.2 ms; (c) t = 0.29 ms; (d) t = 0.425 ms; (e) t = 0.85 ms; (f) t = 1.2 ms
Figure5. Vorticity distribution in the presence of a magnetic field: (a) t = 0.12 ms; (b) t = 0.2 ms; (c) t = 0.29 ms; (d) t = 0.425 ms; (e) t = 0.85 ms; (f) t = 1.2 ms.

现有研究一致认为, 涡量分层是磁场抑制界面不稳定性的主要原因^[7-11], 但至今仍未完全研究清楚涡量分层的致稳效应. 磁场是通过洛伦兹力对带电粒子产生作用, 其致稳效应必源于洛伦兹力. 为了说明磁场对流场结构的作用, 下面从物理的角度进行探究. 由安培环路定律和磁场无散度约束得

${{j}} \times {{B}} = {{B}} \cdot \nabla {{B}} - \nabla \left( {{{{B^2}}}/{2}} \right).$

(9)式右侧第1项为磁张力(也称为洛伦兹力)${f_B} = {{B}} \cdot \nabla {{B}}$, 第2项为磁压力(${P_B} = {{{B^2}} / 2}$)梯度.
图6为t = 0.2 ms时, 流场中横向磁场强度B_x、纵向磁场强度B_y、磁能量E_B、横向磁张力$ f_{B_x} $、纵向磁张力$ f_{B_y} $与涡量ω的分布图, 图中矢量线为磁感线, 其在计算域下边界是等间距分布. 图7为各物理量沿图6中红色虚线的分布. 图8则为磁张力矢量与涡量的叠加图, 箭头为磁张力矢量, 颜色按磁张力大小分布.
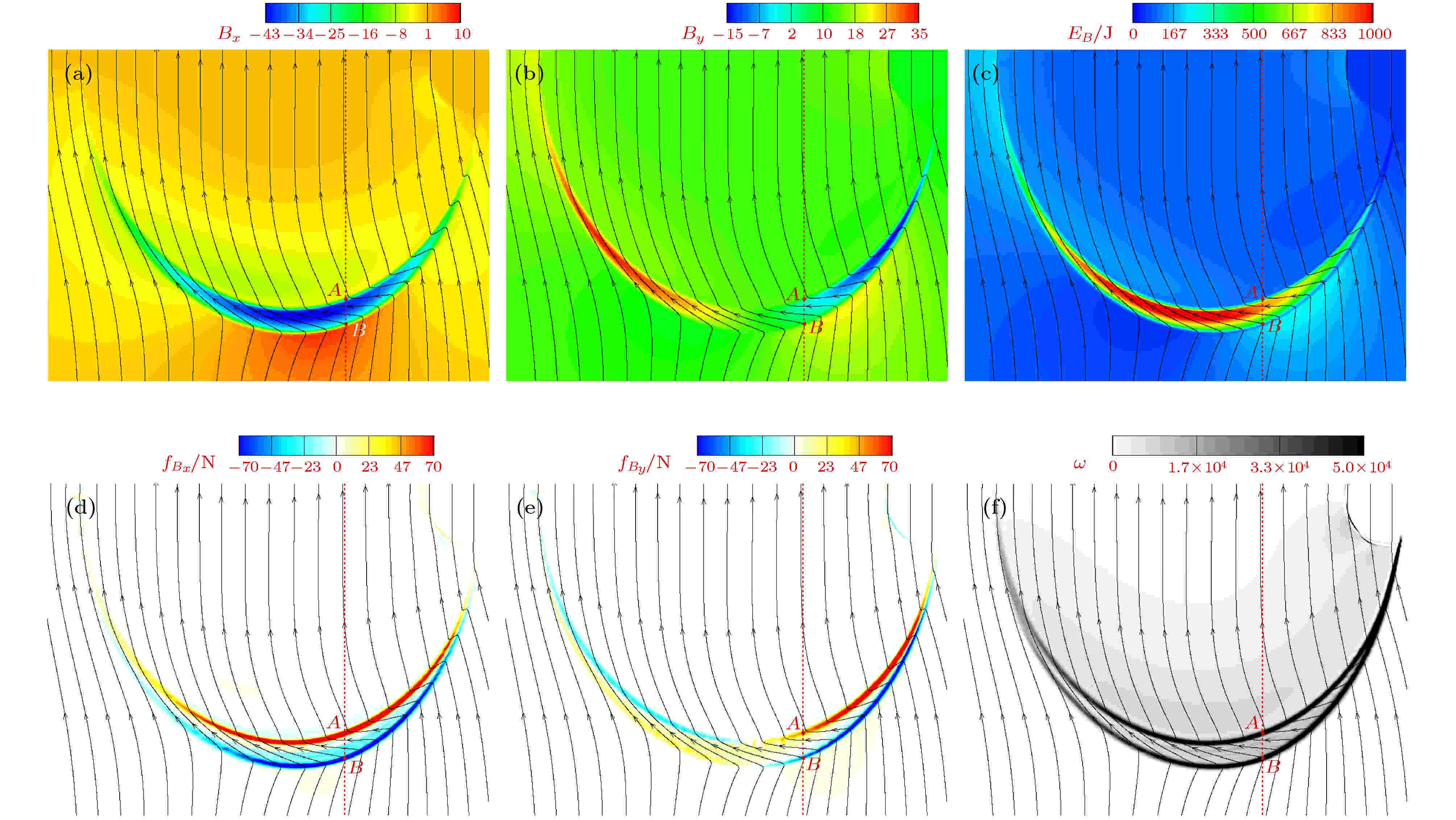图 6 t = 0.2 ms时, 流场中各物理量的分布　(a)横向磁场强度; (b)纵向磁场强度; (c)磁能量; (d)横向磁张力; (e)纵向磁张力; (f)涡量
Figure6. Spatial distribution of various physical quantities at t = 0.2 ms: (a) Transverse magnetic field; (b) longitudinal magnetic field; (c) magnetic energy; (d) transverse magnetic tension; (e) longitudinal magnetic tension; (f) vorticity.

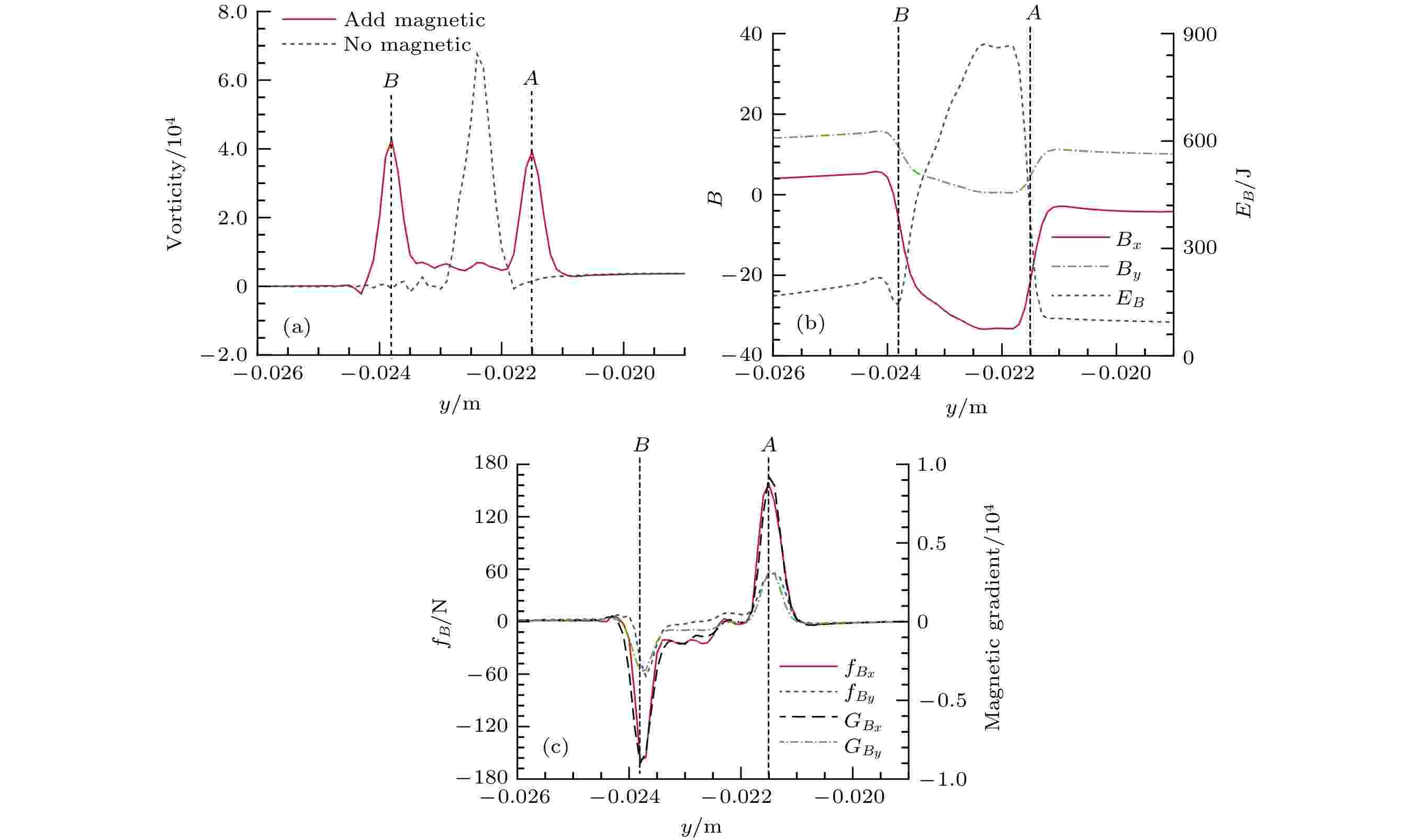图 7 各物理量沿图6中虚线的分布　(a) 涡量; (b)磁场强度与磁能量; (c)磁场梯度与磁张力
Figure7. Distribution of various physical quantities along the red dotted line of Fig. 6: (a) Vorticity; (b) magnetic field and magnetic energy; (c) magnetic field gradient and magnetic tension.

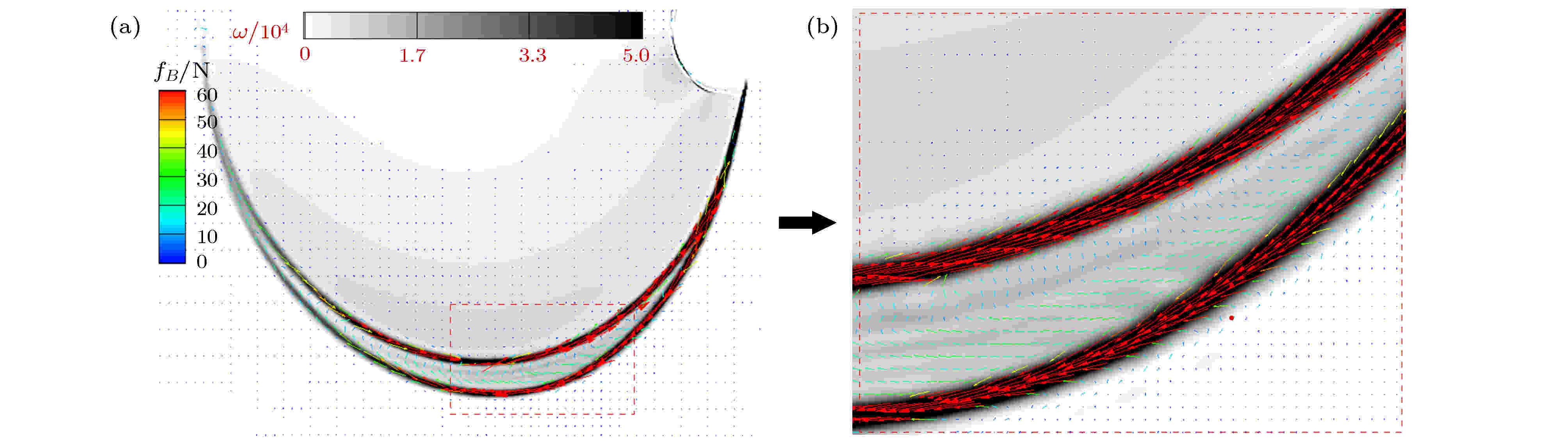图 8 t = 0.2 ms时, 涡量层上磁张力矢量分布　(a)下半流场; (b)局部放大图
Figure8. Distribution of magnetic tension vector on the vorticity layer at t = 0.2 ms: (a) Lower half flow field; (b) local enlarged drawing.

由图6可知, 激波与下半侧界面作用瞬间, 磁感线在界面上发生顺时针折射, 形成负的横向磁场B_x (图6(a)与图7(b)); 同时, 激波与左半界面的作用, 增大了左半界面的纵向磁场强度, 而与右半界面的作用则降低了纵向磁场强度, 如图6(b)所示. 界面上磁场强度的改变, 使磁场梯度不再一致(图7(c)). 由(9)式得, 磁张力与磁场梯度呈正相关, 横向$ f_{B_x} $与纵向磁张力$ f_{B_y} $的变化趋势分别跟横向$ G_{B_x} $与纵向磁场梯度$ G_{B_y} $一致, 如图7(c)所示, 因此在内外涡量层上产生比周围强的磁张力(图6(d)、图6(e)、图7(c)). 其中, 内层横向磁张力为正值, 外层为负值(图6(d), $ f_{B_x} $); 对于纵向磁张力(图6(e), $ f_{B_y} $), 左半界面的内层与右半界面的外层为负值, 左半界面的外层与右半界面的外层为正值. 由图8可知, 内层磁张力与速度剪切应力同向, 外层磁张力则与速度剪切应力反向, 根据右手螺旋定则, 内外层上的磁张力对界面流体产生一个顺时针力矩, 抵消界面因速度剪切所引起的逆时针卷起. 由图3可见, 当B = 10时, 磁场能完全抑制界面上KH涡的卷起.
由图7(a)可见, 相对于无磁场时的涡量峰值ω_max = 6.8 × 10⁴, 涡量分层后, 内外涡量层上的涡量峰值均下降, 分别为ω_B = 4.2 × 10⁴与ω_A = 3.9 × 10⁴. 另外, 在外涡量层横向磁张力的作用(图6), 使磁感线穿过外层时发生大角度的顺时针弯曲; 内涡量层横向磁张力的作用, 则对磁感线产生一个逆时针的恢复力, 使磁感线穿过内层后逐渐恢复到垂直方向. 因$ f_{B_x} $与$ f_{B_y} $沿外涡量层分布不均匀(图6(d)和图6(e)), 下游磁感线的顺时针弯曲程度大于上游, 因此上游界面上磁感线的聚集程度大于下游. 由此可知, 横向磁张力对界面附近磁感线的弯曲变形起控制作用, 横向与纵向磁张力沿外涡量层分布的不均匀, 改变了界面上磁感线的聚集程度.
磁感线的聚集, 使磁场堆积在界面上, 放大了该处的磁能量, 因此磁感线密集度越大区域所对应的磁能量越高(图6(c)). 由图7(b)可见, 横向与纵向磁场强度在外层(B点)呈现负向的快速下降, 在到达A点前, 纵向磁场强度达到最小值(${B_y}_{, \min }\! = 0.06{B_0}$), 横向磁场强度值达到最大 (${\left| {{B_x}} \right|_{\max }} = 4.17{B_0}$). 对应地, B-A点间的磁能量呈线性增大, 在横向磁场强度达到最大值时, 磁能量也到达最大值(${E_{B, \max }} = 17.4{E_{{B_0}}}$).
由(9)式可知, 磁张力跟磁场强度和磁场梯度呈正相关, 磁张力的增加又会加剧磁感线的弯曲与聚集程度, 进一步放大界面上的磁能量. 图9为气柱发展过程中, 流场磁能量及磁感线的分布. 图10为图9相应的横向磁张力、纵向磁张力及磁张力矢量分布. 由图9可见, 随着时间的推移, 界面上的磁能量不断增大, 同时加剧磁感线的弯曲程度. 在t = 0.85 ms时(图9(c)), 磁感线在进入下侧涡量层后, 大部分磁感线会沿着气柱弧形界面向上输送, 同时界面上的磁感线聚集度最密, 因此左侧弧形界面的磁能量值最高.
图 9 气柱发展过程中流场磁能量和磁感线分布　(a) t = 0.2 ms; (b) t = 0.425 ms; (c) t = 0.85 ms
Figure9. Distribution of the magnetic energy and the magnetic field lines during the evolution of gas column: (a) t = 0.2 ms; (b) t = 0.425 ms; (c) t = 0.85 ms.

图 10 磁张力对界面不稳定性的作用　(a)横向磁张力; (b)纵向磁张力; (c)磁张力矢量.
Figure10. Effect of magnetic tension on interface instability: (a) Transverse magnetic tension; (b) longitudinal magnetic tension; (c) magnetic tension vector.

由图10(a)和图10(b)可见, 上游弧形界面上磁能量的增加, 增大了界面上的横向和纵向磁张力. 磁张力增大的同时, 增强了对气柱界面的致稳作用, 因此界面始终保持光滑. 对于下游界面, 内外涡量层上的磁张力, 同样产生一个与主涡卷起方向相反的力矩(图10(c), t = 0.425 ms), 抑制了螺旋状主涡的卷起, 同时使涡量层发生弯曲变形, 最终在气柱下游形成复杂的涡量层结构(图5(e)和图5(f)). 对于射流, 射流头部较大的负向横向磁张力(图10(a)), 将射流头部阵面推向气柱上游界面; 同时, 剪切层上的纵向磁张力, 将上、下剪切层往两侧拉伸(图10(b)), 最终气柱下游界面中心形成凹型结构, 如图3(h)所示.
图11为流场中最大磁场强度与平均磁能密度随时间的变化. 由图11(a)可知, 当激波与左半气柱界面作用瞬间(t = 0.04 ms), 磁感线在气柱界面上的顺时针折射, 诱导出横向磁场(图6和图7), 并增大了界面上的纵向磁场强度(图6(b)), 使最大的横向(${\left| {{B_x}} \right|_{\max }}$)与纵向(${\left| {{B_y}} \right|_{\max }}$)磁场强度开始随时间呈线性增加, 且${\left| {{B_x}} \right|_{\max }}$的增速大于${\left| {{B_y}} \right|_{\max }}$. 此时, 流场中的最大磁场强度${\left| B \right|_{\max }}$曲线与${\left| {{B_y}} \right|_{\max }}$曲线重合; 在激波与右半气柱界面作用过程(t > 0.12 ms), 右边界面的纵向磁场强度降低(图6(b)), 因此在0.12 ms < t < 0.35 ms时间段内, 流场的最大纵向磁场强度保持不变(${\left| {{B_y}} \right|_{\max }} = 2.5{B_0}$). 此时, ${\left| {{B_x}} \right|_{\max }}$超过${\left| {{B_y}} \right|_{\max }}$, 并逐渐与${\left| B \right|_{\max }}$曲线重合. 在t > 0.35 ms时, ${\left| {{B_y}} \right|_{\max }}$呈快速的线性增加, 而${\left| {{B_x}} \right|_{\max }}$与${\left| B \right|_{\max }}$曲线则完全重合. 随后, 由于${\left| {{B_y}} \right|_{\max }}$的增速大于${\left| {{B_x}} \right|_{\max }}$, 并且在t = 0.95 ms时超过${\left| {{B_x}} \right|_{\max }}$, 最终再次与${\left| B \right|_{\max }}$曲线重合. 这表明, 横向磁场对初始流场结构的控制占主导作用, 随着流场发展过程, 纵向磁场对流场结构的控制作用则不断加强, 在后期(t > 0.95 ms)占主导作用.
图 11 流场最大磁强度　(a)与平均磁能密度(b)随时间的变化(红色虚线为基准线)
Figure11. Time evolution of the maximum (a) and average (b) magnetic field strength (the red dotted line is the reference line).

由图11(b)可知, 平面激波在流场传播过程中, 平均纵向磁能密度呈线性增加, 直到激波传出流场后(t ≥ 0.6 ms)达到饱和, 饱和值为初始磁能的1.32倍; 对于平均横向磁能密度, 其初期随时间呈线性增长, 增速与平均纵向磁能密度一致. 在t > 0.6 ms时, 平均横向磁能密度的增速逐渐减弱. 在横向与纵向磁场耦合作用下, 平均磁能密度初始时呈线性上升, 上升到初始磁能的1.44倍后, 增速开始下降. 这充分说明, 激波与气柱的作用, 放大了流场的磁场强度, 强化了磁场抑制气柱界面不稳定性的作用.
图12为环量随时间的变化曲线, 计算域中环量Г(即总涡量的大小)为
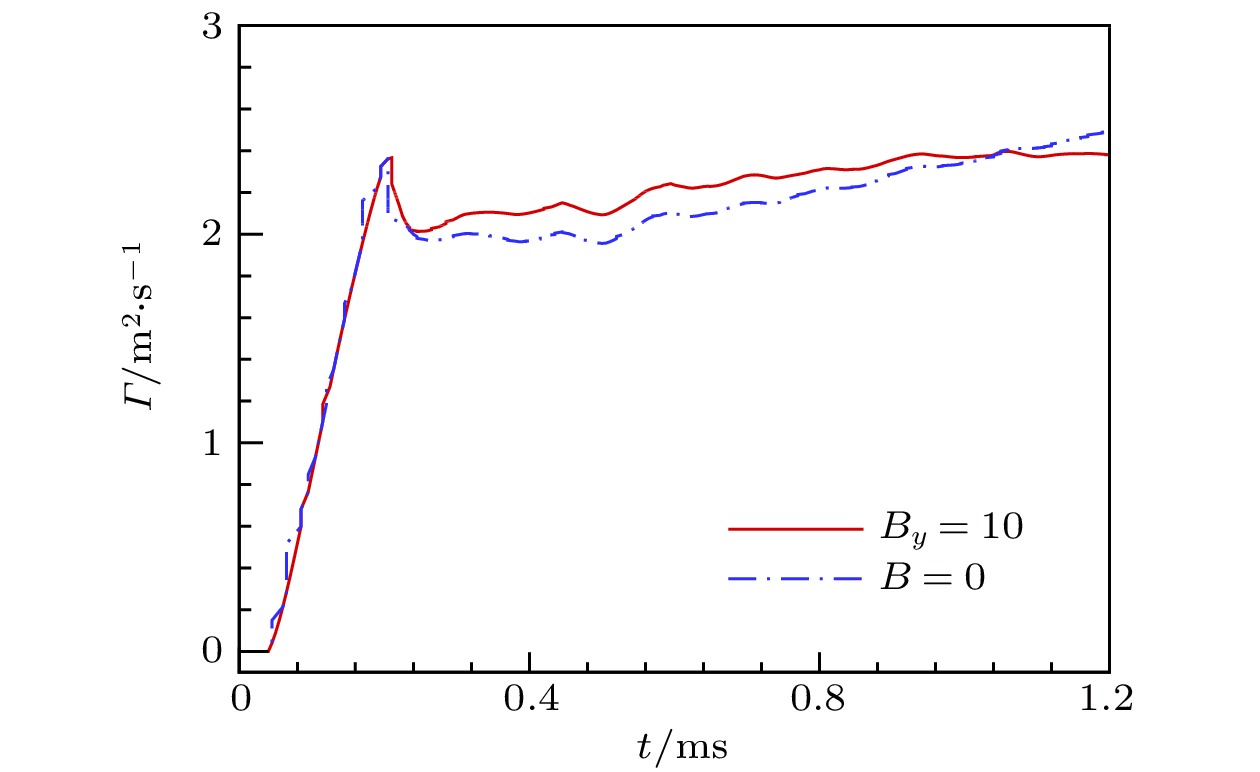图 12 流场环量随时间的变化曲线
Figure12. Time evolution of the circulation.

$\varGamma = \iint_A {\omega {\rm{d}}x{\rm{d}}y}.$

根据对称性, 式中A只取下半计算域, A = [–H/2, 0] × L.
由图12可见, 激波与下半侧界面作用前, 流场涡量为零. 当激波冲击界面瞬间(t = 0.04 ms), 环量呈线性快速上升. 反射激波(R₁与R₂)在下游界面的反向作用(t > 0.21 ms), 抑制了环量的形成, 使环量出现短暂的下降, 并在主涡环卷起过程中基本不变(t = 0.24—0.5 ms). 当气柱右侧主涡形成后(t > 0.5 ms), 环量增速增加, 且随时间基本呈线性增长.
施加磁场后, 虽内外涡量层的涡量峰值略低于无磁场情况(图7(a)), 但界面上涡量场分布区变大, 因此t < 0.205 ms时, 环量曲线与无磁场情况基本重合. 另外, 因涡量不在沉积在界面上, 后续反射激波与界面的作用, 形成新的涡量层, 使环量随时间的增长率略高于无磁场情况(t = 0.23—0.74 ms). 然而, 因磁场抑制了主涡及界面上小涡序列的卷起, 环量的增速减慢, 并在t = 0.95 ms后基本保持不变. 由此可知, 磁场的存在是使RM不稳定形成的涡量分散到气柱界面的内外两侧.

基于理想磁流体动力学方程组, 采用CTU+ CT算法, 数值研究了磁场控制下激波与R22圆形气柱界面的相互作用过程. 对于无磁场情况, 激波与界面作用过程的激波及界面不稳定性均与实验结果相吻. 施加纵向磁场后, 有效抑制了界面的不稳定性, 界面上无小涡形成. 另外, 从物理角度探讨磁场强度、磁能量、磁张力与涡量的关系, 揭示了磁场抑制界面不稳定性与磁能放大机理, 得到以下结论:
1) 激波与气柱界面的作用, 使磁感线在界面上发生顺时针折射, 形成横向磁场, 并改变了界面上纵向磁场强度. 界面上磁场梯度的不一致, 导致内外涡量层上形成强的磁张力.
2) 内外层上磁张力的形成, 对界面流体产生一个与速度剪切相反的力矩, 抵消了界面因速度剪切所引起的不稳定性, 最终抑制了界面上KH涡和主涡的卷起.
3) 内外涡层上, 横向磁张力控制着界面附近磁感线的弯曲变形, 而横向与纵向磁张力沿外涡量层分布的不均匀, 改变了界面上磁感线的聚集程度. 磁感线的聚集会放大磁能量, 磁张力则会随磁能量的增加而增大, 随着时间的推移, 界面上磁能量与磁感线的扭曲程度不断增大, 增强了磁场对气柱界面的致稳作用.
4) 磁感线在界面的折射现象, 形成横向磁场. 初始时, 横向磁场随时间呈线性增加, 其增长率大于纵向磁场. 因此, 横向磁场对初始流场结构的控制占主导作用, 随着流场发展, 纵向磁场对流场结构的控制作用不断加强, 在后期占主导作用.