摘要:针对基于声学理论的管道气泡检测技术面临的声波作用下的气泡相互作用机理问题, 本文基于自由气泡Rayleigh-Plesset模型, 通过引入次Bjerknes辐射力, 构建能够考虑管道轴向气泡分布的可压缩性双气泡动力学模型. 利用四阶龙格库塔方法开展数值计算, 对比分析了不同激励声波频率与幅度作用下自由气泡与双气泡模型引起的气泡动力学特征的区别. 同时对比了液体可压缩与不可压缩假设引起的气泡动力幅频响应的区别, 表明可压缩假设下的次Bjerknes辐射力引起气泡发生受迫振动, 不改变气泡的线性共振特征; 而不可压缩假设引起气泡间发生强耦合, 从而改变气泡系统的线性共振特征. 气泡距离直接影响次Bjerknes辐射力大小, 导致气泡动力学趋向于非线性振动, 与线性振动的频谱特征差别明显. 气泡轴向位置的变化引起外界激励声波的变化, 从而改变气泡的初始振动特征. 初始特征的差异与次Bjerknes辐射力发生耦合作用, 影响气泡动力学特征, 甚至发生非线性振动. 研究表明, 小气泡在共振的情况下, 与次Bjerknes辐射力发生耦合作用, 使得双气泡系统更容易趋向于非线性特征; 而大气泡则能够较好地保持线性共振状态.
关键词: 气泡动力学/
次Bjerknes力/
可压缩流体/
气泡检测

English Abstract

全文HTML

--> --> -->

气泡检测是航天推进管路系统在轨状态监控的一项重要指标, 气泡的存在不仅影响诸如压力泵的正常工作, 而且影响燃烧室气液混合, 引起不稳定燃烧, 导致推进系统工作不稳定, 甚至发生灾难性结果^[1]. 另外, 气泡检测可以用于评价贮箱表面张力等推进剂管理装置性能, 也可用于监控在轨流体传输中气泡吹除过程^[2]. 基于声学理论的气泡检测技术由于具备响应速度快、非接触安装等特征, 得到了广泛的重视, 并发展了“被动”以及“主动”两大类检测方法^[3,4]. 具体而言, 被动方法通过检测气泡共振信号获得气泡尺寸信息. 主动方法基于气泡与声学耦合动力学机理, 根据声波在两相流中传播特征从而实现气泡检测. 两者的理论核心是管道流动中气泡在声场作用下的动力学特征.
对于声波作用下的自由单气泡动力学特征的研究, 已有大量的****从建模^[5]、数值计算^[6,7]以及试验^[8,9]的角度开展了丰富的工作, 分别研究了气泡的线性以及非线性^[10,11]特征, 形成了较为完善的理论基础^[12]. Rayleigh^[13]首先对气泡与声学耦合机理开展理论建模工作, 基于气泡球形假设, 研究了单个气泡的溃灭过程, 推导了著名气泡径向壁面运动学方程—Rayleigh方程. 由于Rayleigh方程不计液体黏性、表面张力和液体可压缩性等, 后续研究者陆续对Rayleigh方程进行了研究并修正. Hsieh 和 Plesset^[5]考虑液体的黏性、液体表面张力的影响, 基于球形气泡的假设, 形成了较为完善的气泡壁面径向振动Rayleigh-Plesset方程.
由于实际气泡检测应用中存在大量气泡, 气泡相互作用使得单气泡模型无法准确地描述多气泡动力学特征, 研究表明, 气泡间次级辐射形成的次Bjerknes力^[14,15]显著影响气泡振动特征及气泡分布^[16]. 对多气泡动力学特征的研究主要通过两种途径展开, 分别为通过将气泡与液体构成的连续介质看作整体从而分析气泡群的整体变化以及分析气泡群内每个气泡的运动变化. 前者通常分析线性或弱非线性环境下气泡群的动力学行为. Omta^[17]发现了气泡群的共振频率远小于单气泡的共振频率. Hamilton 等^[18]描述了液体可压缩性对气泡间相互作用的影响并对气泡群生长、合并和崩溃进行模拟. 后者重点考虑泡群内气泡间的相互作用. Mettin 等^[14]研究了强声场中不同尺寸球形气泡之间的次Bjerknes力特征及其对气泡平移变化规律的影响. Pelekasis 等^[15]在确保驱动频率的二次谐波处于双气泡系统中不同半径气泡对应的共振频率之间的前提下, 研究了不同声场振幅下双气泡之间的次Bjerknes力对气泡平移变化规律的影响. Doinikov^[19]对多个任意空间排列的多气泡结构中的每个气泡的动力学特征进行了求解, 并且对不同分布下气泡的平移与径向运动特征进行了分析. Maiga等^[20]理论分析了双气泡作用下的空化现象. Yoshida等^[21]与Jiao等^[22]通过试验验证了次Bjerknes力对双气泡动力学特征的影响, Zilonova 等^[23]分析了双气泡之间的黏弹性力问题.
上述研究主要集中于气泡在同一横截面内的情况, 使得所有气泡都处于同一外界声波激励. 另一方面, 大量工作研究了相同尺寸大小气泡形成的气泡群的动力学特征. 本文拟针对基于声学理论的管道气泡检测问题, 研究管道内任意分布(轴向或者径向)的不同尺寸的双气泡(如图1所示)在外界声场激励下的线性与非线性动力学行为. 分析气泡距离与气泡轴向位置等对气泡动力学特征的影响, 对比分析不同激励声波频率与幅度等因素对气泡动力学特征的影响, 同时研究多因素耦合作用引起气泡动力学的变化.
图 1 管道内双气泡位置示意图(二维)
Figure1. Schematic diagram of two-bubble positions in the pipeline (two-dimensional).

2

-->

2.1.双气泡动力学模型

图1为二维管道内气泡分布示意图. 在分析过程中, 采用柱坐标系进行标记, 即$x$表示轴向坐标, $r$表示径向坐标. 本文只考虑激励声波对气泡半径的影响, 忽略气泡在周向的变化, 气泡动力学满足轴对称特性. 假设管道流体中两气泡大小与位置随机分布, 半径为${R_1}$的气泡1的球心位置为$\left( {{r_1}, \;{x_1}} \right)$, 半径为${R_2}$的气泡2的球心位置为$\left( {{r_2}, \;{x_2}} \right)$. 气泡2对气泡1的次Bjerknes作用力为${p_{21}}$, 气泡1对气泡2的次Bjerknes作用力为${p_{12}}$. 气泡球心之间的距离为$h$, 且球心连线与$x$轴的角度为$\theta $, 激励气泡的外界声波表示为$p'$.
由于双气泡动力学模型系统中气泡的运动受到气泡间次Bjerknes辐射力的影响, 与单自由气泡动力学特征不一致, 需要针对管路内气泡特征进行理论建模. 在建模过程中考虑液体的黏性、表面张力等影响, 并假设泡内气体是理想气体且压强分布均匀, 气泡与液体不存在滑移现象. 为简化建模, 忽略气泡内动力学特征, 包括水汽、气液界面间的热传导, 气泡的形成、破裂与合并. 当激励声波频率足够大时, 激励声波在管道中形成不同的模态, 导致声波在径向存在复杂的分布, 从而带来复杂的气泡动力学特征. 针对检测技术而言, 重点研究平面波激励下的气泡动力学特征. 此外, 忽略扰动在管道壁上反射引起的气泡额外辐射力. 需要指出的是, 当气泡在管壁附近时, 管壁的影响不可忽略^[24].
在上述假设情况下, 气泡1与气泡2的动力学模型可以表示为^[25]

$\begin{split}{R_1}{\ddot R_1} + \frac{3}{2}\dot R_1^2 =\; & \frac{1}{{{\rho _{\rm{L}}}}}\bigg( {p_{1\_\operatorname{in} }} - {p_\infty } - \frac{{2\sigma }}{{{R_1}}}\\&-\frac{{4\eta {{\dot R}_1}}}{{{R_1}}} - p'\left( {{x_1}} \right) - {p_{21}} \bigg),\end{split}$

$\begin{split}{R_2}{\ddot R_2} + \frac{3}{2}\dot R_2^2 = \;& \frac{1}{{{\rho _{\rm{L}}}}}\bigg( {p_{2\_\operatorname{in} }} - {p_\infty } - \frac{{2\sigma }}{{{R_2}}} \\&-\frac{{4\eta {{\dot R}_2}}}{{{R_2}}} - p'\left( {{x_2}} \right) - {p_{{\rm{12}}}} \bigg),\end{split}$

其中, $\sigma $与$\eta $分别表示液体的表面张力系数以及剪切黏性系数; ${\rho _{\rm{L}}}$表示液体密度; ${p_\infty }$为外界环境气压; $p'\left( {{x_1}} \right)$和$p'\left( {{x_2}} \right)$为声波激励信号. 通过气泡质量守恒($P{V^\gamma } = {\rm{constant}}$, $\gamma $为气体比热比, $V$为气泡体积)可以得到气泡内压强为^[26]

${p_{1\_\operatorname{in} }} = \left( {{p_\infty } + \frac{{2\sigma }}{{{R_{10}}}}} \right){\left( {\frac{{{R_{10}}}}{{{R_1}}}} \right)^{3\gamma }},$

$p_{2_{-} \mathrm{in}}=\left(p_{\infty}+\frac{2 \sigma}{R_{20}}\right)\left(\frac{R_{20}}{R_{2}}\right)^{3 \gamma},$

其中, ${R_{10}}$与${R_{20}}$分别表示气泡1与气泡2的平衡半径. 此外, 气泡辐射力可近似地表示为

${P_{12}} = {\rho _{\rm{L}}}{\left. {\left( {\frac{{2{R_1}\dot R_1^2 + R_1^2{{\ddot R}_1}}}{{h - {R_1} - {R_2}}}} \right)} \right|_{t - {{\left( {h - {R_1} - {R_2}} \right)} / {{c_{\rm{L}}}}}}},$

$P_{21}=\left.\rho_{\mathrm{L}}\left(\frac{2 R_{2} \dot{R}_{2}^{2}+R_{2}^{2} \ddot{R}_{2}}{h-R_{1}-R_{2}}\right)\right|_{t-\left(h-R_{1}-R_{2}\right) / c_{\mathrm{L}}},$

式中考虑液体的可压缩特征. 将(3)—(6)式分别代入(1)式和(2)式可以得到气泡1与气泡2在外界声场作用下的动力学模型:

$\begin{split}{R_1}{\ddot R_1} + \frac{3}{2}\dot R_1^2 =\; &\frac{1}{{{\rho _{\rm{L}}}}}\left( {{p_\infty } + \frac{{2\sigma }}{{{R_{10}}}}} \right){\left( {\frac{{{R_{10}}}}{{{R_1}}}} \right)^{3\gamma }} \\&- \frac{1}{{{\rho _{\rm{L}}}}}\left( {{p_\infty } + \frac{{2\sigma }}{{{R_1}}}} \right) - \frac{{4\eta {{\dot R}_1}}}{{{\rho _{\rm{L}}}{R_1}}}\\&- \frac{{p'\left( {{x_1}} \right)}}{{{\rho _{\rm{L}}}}} - \frac{{{P_{21}}}}{{{\rho _{\rm{L}}}}},\end{split}$

$\begin{split}{R_2}{\ddot R_2} + \frac{3}{2}\dot R_2^2 =\;& \frac{1}{{{\rho _{\rm{L}}}}}\left( {{p_\infty } + \frac{{2\sigma }}{{{R_{20}}}}} \right){\left( {\frac{{{R_{20}}}}{{{R_2}}}} \right)^{3\gamma }} \\&- \frac{1}{{{\rho _{\rm{L}}}}}\left( {{p_\infty } + \frac{{2\sigma }}{{{R_2}}}} \right) - \frac{{4\eta {{\dot R}_2}}}{{{\rho _{\rm{L}}}{R_2}}}\\&- \frac{{p'\left( {{x_2}} \right)}}{{{\rho _{\rm{L}}}}} - \frac{{{P_{12}}}}{{{\rho _{\rm{L}}}}}.\\[-10pt]\end{split}$

2 -->

2.2.线性化分析

利用平衡半径$R_1 \!=\! R_{10}(1 \!+\! \varepsilon _1), {R_2} \!=\! R_{20} (1 \!+\! \varepsilon _2)$, 其中${\varepsilon _1}$与${\varepsilon _2}$分别表示气泡振动引起的无量纲化半径变化小量, (7)式和(8)式可以简化为

$\begin{split}\left( {1 + {\varepsilon _1}} \right){{\ddot \varepsilon }_1} + \dfrac{3}{2}\dot \varepsilon _1^2 =\; & \dfrac{1}{{{\rho _{\rm{L}}}R_{10}^2}}\left( {{p_\infty } + \dfrac{{2\sigma }}{{{R_{10}}}}} \right)\dfrac{1}{{{{\left( {1 + {\varepsilon _1}} \right)}^{3\gamma }}}} - \dfrac{1}{{{\rho _{\rm{L}}}R_{10}^2}}\bigg[ {p_\infty } +\dfrac{{2\sigma }}{{{R_{10}}\left( {1 + {\varepsilon _1}} \right)}} \bigg] -\dfrac{{4\eta {{\dot \varepsilon }_1}}}{{{\rho _{\rm{L}}}R_{10}^2\left( {1 + {\varepsilon _1}} \right)}} \\ &- \dfrac{{p'\left( {{x_1}} \right)}}{{R_{10}^2{\rho _{\rm{L}}}}} -\left. \dfrac{{R_{20}^3}}{{R_{10}^2}} \left[ {\dfrac{{2\left( {1 + {\varepsilon _2}} \right)\dot \varepsilon _2^2 + {{\left( {1 + {\varepsilon _2}} \right)}^2}{{\ddot \varepsilon }_2}}}{{h - {R_{10}}\left( {1 + {\varepsilon _1}} \right) - {R_{20}}\left( {1 + {\varepsilon _2}} \right)}}} \right] \right|_{t - {{\left( {h - {R_1} - {R_2}} \right)} / {{c_{\rm{L}}}}}} ,\end{split} $

$\begin{split} \left( {1 + {\varepsilon _2}} \right){{\ddot \varepsilon }_2} + \frac{3}{2}\dot \varepsilon _2^2 =\;& \frac{1}{{{\rho _{\rm{L}}}R_{20}^2}}\left( {{p_\infty } + \frac{{2\sigma }}{{{R_{20}}}}} \right)\frac{1}{{{{\left( {1 + {\varepsilon _2}} \right)}^{3\gamma }}}} -\frac{1}{{{\rho _{\rm{L}}}R_{20}^2}}\left[ {{p_\infty } + \frac{{2\sigma }}{{{R_{20}}\left( {1 + {\varepsilon _2}} \right)}}} \right] - \frac{{4\eta {{\dot \varepsilon }_2}}}{{{\rho _{\rm{L}}}R_{20}^2\left( {1 + {\varepsilon _2}} \right)}} \\ & - \frac{{p'\left( {{x_2}} \right)}}{{R_{20}^2{\rho _{\rm{L}}}}} -{\left. {\frac{{R_{10}^3}}{{R_{20}^2}} \left[ {\frac{{2\left( {1 + {\varepsilon _1}} \right)\dot \varepsilon _1^2 + {{\left( {1 + {\varepsilon _1}} \right)}^2}{{\ddot \varepsilon }_1}}}{{h - {R_{10}}\left( {1 + {\varepsilon _1}} \right) - {R_{20}}\left( {1 + {\varepsilon _2}} \right)}}} \right]} \right|_{t - {{\left( {h - {R_1} - {R_2}} \right)} / {{c_{\rm{L}}}}}}} .\end{split} $

忽略高阶项并保留线性项可以得到:

$\begin{split} &{{\ddot \varepsilon }_1} + \dfrac{{4\eta {{\dot \varepsilon }_1}}}{{{\rho _{\rm{L}}}R_{10}^2}} + \frac{1}{{{\rho _{\rm{L}}}R_{10}^2}}\left[ {3\gamma {p_\infty } + \dfrac{{2\sigma }}{{{R_{10}}}}\left( {3\gamma - 1} \right)} \right]{\varepsilon _1} = - \dfrac{{p'\left( {{x_1}} \right)}}{{R_{10}^2{\rho _{\rm{L}}}}} \!-\! {\left. {\dfrac{{R_{20}^3}}{{R_{10}^2}}\dfrac{{{{\ddot \varepsilon }_2}}}{{\left( {h \!-\! {R_{10}} \!-\! {R_{20}}} \right)}}} \right|_{t \!-\! {{\left( {h \!-\! {R_{10}} \!-\! {R_{20}}} \right)}/ {{c_{\rm{L}}}}}}}, \\ \end{split} $

$\begin{split}& {{\ddot \varepsilon }_2} + \dfrac{{4\eta {{\dot \varepsilon }_2}}}{{{\rho _{\rm{L}}}R_{20}^2}} + \dfrac{1}{{{\rho _{\rm{L}}}R_{20}^2}}\left[ {3\gamma {p_\infty } + \dfrac{{2\sigma }}{{{R_{20}}}}\left( {3\gamma - 1} \right)} \right]{\varepsilon _2} = - \dfrac{{p'\left( {{x_2}} \right)}}{{R_{20}^2{\rho _{\rm{L}}}}} \!-\! {\left. {\frac{{R_{10}^3}}{{R_{20}^2}}\dfrac{{{{\ddot \varepsilon }_1}}}{{\left( {h \!-\! {R_{10}} \!-\! {R_{20}}} \right)}}} \right|_{t \!-\! {{\left( {h \!-\! {R_{10}} \!-\! {R_{20}}} \right)} / {{c_{\rm{L}}}}}}}. \\ \end{split} $

当不考虑气泡间相互作用时, 自由气泡的动力学特征可以表征为

$\begin{split}&{\ddot \varepsilon _1} + \frac{{4\eta {{\dot \varepsilon }_1}}}{{{\rho _{\rm{L}}}R_{10}^2}} + \frac{1}{{{\rho _{\rm{L}}}R_{10}^2}}\left[ {3\gamma {p_\infty } + \frac{{2\sigma }}{{{R_{10}}}}\left( {3\gamma - 1} \right)} \right]{\varepsilon _1} = - \frac{{p'\left( {{x_1}} \right)}}{{R_{10}^2{\rho _{\rm{L}}}}},\\[-10pt]\end{split}$

$\begin{split}&{\ddot \varepsilon _2} + \frac{{4\eta {{\dot \varepsilon }_2}}}{{{\rho _{\rm{L}}}R_{20}^2}} + \frac{1}{{{\rho _{\rm{L}}}R_{20}^2}}\left[ {3\gamma {p_\infty } + \frac{{2\sigma }}{{{R_{20}}}}\left( {3\gamma - 1} \right)} \right]{\varepsilon _2} = - \frac{{p'\left( {{x_2}} \right)}}{{R_{20}^2{\rho _{\rm{L}}}}}.\\[-10pt]\end{split}$

不难得到, 气泡1在自由振动下的阻尼系数与共振频率为

$\begin{split}&\delta_{1}=\frac{2 \eta}{\rho_{\mathrm{L}} R_{10}^{2}},\\& f_{\mathrm{res}_{-} 1}=\frac{1}{2 \pi} \sqrt{\frac{1}{\rho_{\mathrm{L}} R_{10}^{2}}\left[3 \gamma p_{\infty}+\frac{2 \sigma}{R_{10}}(3 \gamma-1)\right]}.\end{split}$

同理, 气泡2在自由振动下的阻尼系数以及共振频率分别为

$\begin{split}&\delta_{2}=\frac{2 \eta}{\rho_{\mathrm{L}} R_{20}^{2}},\\&f_{\mathrm{res}_{-} 2}=\frac{1}{2 \pi} \sqrt{\frac{1}{\rho_{\mathrm{L}} R_{20}^{2}}\left[3 \gamma p_{\infty}+\frac{2 \sigma}{R_{20}}(3 \gamma-1)\right]}.\end{split}$

当不考虑液体可压缩特性时, 声波扰动在液体中传播速度为无穷大, 即${c_{\rm{L}}} \to \infty $, 则(11)式和(12)式可以简化为

$\begin{split} &{{\ddot \varepsilon }_1} + 2{\delta _1}{{\dot \varepsilon }_1} + {\left( {2{\rm{\pi }}{f_{{\rm{res\_1}}}}} \right)^2}{\varepsilon _1} + \dfrac{{R_{20}^3}}{{R_{10}^2}}\frac{{{{\ddot \varepsilon }_2}}}{{\left( {h - {R_{10}} - {R_{20}}} \right)}}\\ =& - \dfrac{{p'\left( {{x_1}} \right)}}{{R_{10}^2{\rho _{\rm{L}}}}}, \\ &{{\ddot \varepsilon }_2} + 2{\delta _2}{{\dot \varepsilon }_2} + {\left( {2{\rm{\pi }}{f_{{\rm{res\_2}}}}} \right)^2}{\varepsilon _2} + \dfrac{{R_{10}^3}}{{R_{20}^2}}\dfrac{{{{\ddot \varepsilon }_1}}}{{\left( {h - {R_{10}} - {R_{20}}} \right)}}\\ =& - \dfrac{{p'\left( {{x_2}} \right)}}{{R_{20}^2{\rho _{\rm{L}}}}}. \\[-15pt] \end{split} $

(17)式描述了不可压缩液体中双气泡在外界声波扰动作用下的线性动力学特征. 其线性共振频率${f_{_{{\rm{res\_twobub}}}}}$满足:

$\left| {\begin{array}{*{20}{c}} {\left[ { - {{\left( {2{\rm{\pi }}{f_{_{{\rm{res\_twobub}}}}}} \right)}^2} + {\rm{i}}4{\rm{\pi }}{\delta _1}{f_{_{{\rm{res\_twobub}}}}} + {{\left( {2{\rm{\pi }}{f_{_{{\rm{res\_1}}}}}} \right)}^2}} \right]}&{ - \dfrac{{{{\left( {2{\rm{\pi }}{f_{_{{\rm{res\_twobub}}}}}} \right)}^2}R_{20}^3}}{{\left( {h - {R_{10}} - {R_{20}}} \right)R_{10}^2}}} \\ { - \dfrac{{{{\left( {2{\rm{\pi }}{f_{_{{\rm{res\_twobub}}}}}} \right)}^2}R_{10}^3}}{{\left( {h - {R_{10}} - {R_{20}}} \right)R_{20}^2}}}&{\left[ { - {{\left( {2{\rm{\pi }}{f_{_{{\rm{res\_twobub}}}}}} \right)}^2} + {\rm{i}}4{\rm{\pi }}{\delta _2}{f_{_{{\rm{res\_twobub}}}}} + {{\left( {2{\rm{\pi }}{f_{_{{\rm{res\_2}}}}}} \right)}^2}} \right]} \end{array}} \right| = 0.$

可以通过牛顿迭代法等求解方程(18)的根, 获得对应的双气泡共振频率. 当忽略系统振动阻尼的影响(${\delta _1} = 0$以及${\delta _2} = 0$)时, (18)式可以简化为

$\begin{split}&\left[ {1 - \frac{{{R_{10}}{R_{20}}}}{{{{\left( {h - {R_{10}} - {R_{20}}} \right)}^2}}}} \right]f_{{\rm{res\_twobub}}}^4 \\&-\left( {f_{{\rm{res\_1}}}^2 + f_{{\rm{res\_2}}}^2} \right)f_{{\rm{res\_twobub}}}^2 + {\left( {{f_{_{{\rm{res\_1}}}}}{f_{_{{\rm{res\_2}}}}}} \right)^2} = 0.\end{split}$

方程(9)的解析解即为不可压缩流动中双气泡共振频率.

本节通过数值计算研究不同尺寸大小的气泡在不同声波激励下的非线性动力学特征, 深入分析外界声波扰动、气泡间距离以及气泡轴向位置等对气泡演化的影响. 在数值计算的过程中, 外界环境气压$P_\infty = 101$ kPa, 液体密度${\rho _{\rm{L}}} = 998$ kg/m³, 表面张力系数$\sigma = 0.0725$ N/m, 黏性系数$\eta = 1\; \times {10^{ - 3}}$ kg/(m·s), 静止液体中声波的传播速度${c_{\rm{L}}} = 1480$ m/s, 气体比热比$\gamma = 1.4$. 在数值计算过程中, 声波激励信号$p'\left( x \right) = {A_0}\cos \left( {2{\text{π}}ft - {{2{\text{π}}fx} / {{c_{\rm{L}}}}}} \right)$, 其中${A_0}$为激励声波幅值, $f$为声波激励频率, 不考虑激励声波在传播过程中的损失. 假设两气泡的平衡半径分别为${R_{10}} = 0.2$ mm以及${R_{20}} = 0.8$ mm, 则根据(15)式与(16)式可以得到两气泡的共振频率分别为${f_{{\rm{res\_1}}}} \approx $ 16.45 kHz以及${f_{{\rm{res\_2}}}} \approx $ 4.10 kHz. 数值计算过程中, 结合两气泡的共振频率, 激励声波频率分别为2, 15以及50 kHz; 同时, 选择两种激励声波幅度进行对比分析, 分别为1 Pa与1 kPa. 针对气动非线性动力学系统((7)式和(8)式), 采用四阶龙格-库塔方法进行计算.
2

-->

3.1.单气泡与双气泡动力学对比分析

本小节分析不同声波频率与幅度激励下的气泡动力学特征, 并对比双气泡与自由气泡的扰动动力学特征. 为降低气泡二次辐射力的影响, 在双气泡动力学计算过程中, 两气泡之间的距离设置为$h = 8$ mm, 对应气泡间二次辐射力延时时间约为$4.73 \times {10^{ - 6}}$ s. 数值计算中时间迭代步长为10^–7 s, 气泡的初始状态设置为${R_{1, 2}} = {R_{10, 20}}$以及${\dot R_{1, 2}} = 0$. 为保证激励信号对双气泡的影响一致, 气泡球心连接线与轴向坐标$x$轴的夹角设置为${{\text{π}} / 2}$. 图2给出了相应的气泡半径的演化过程.
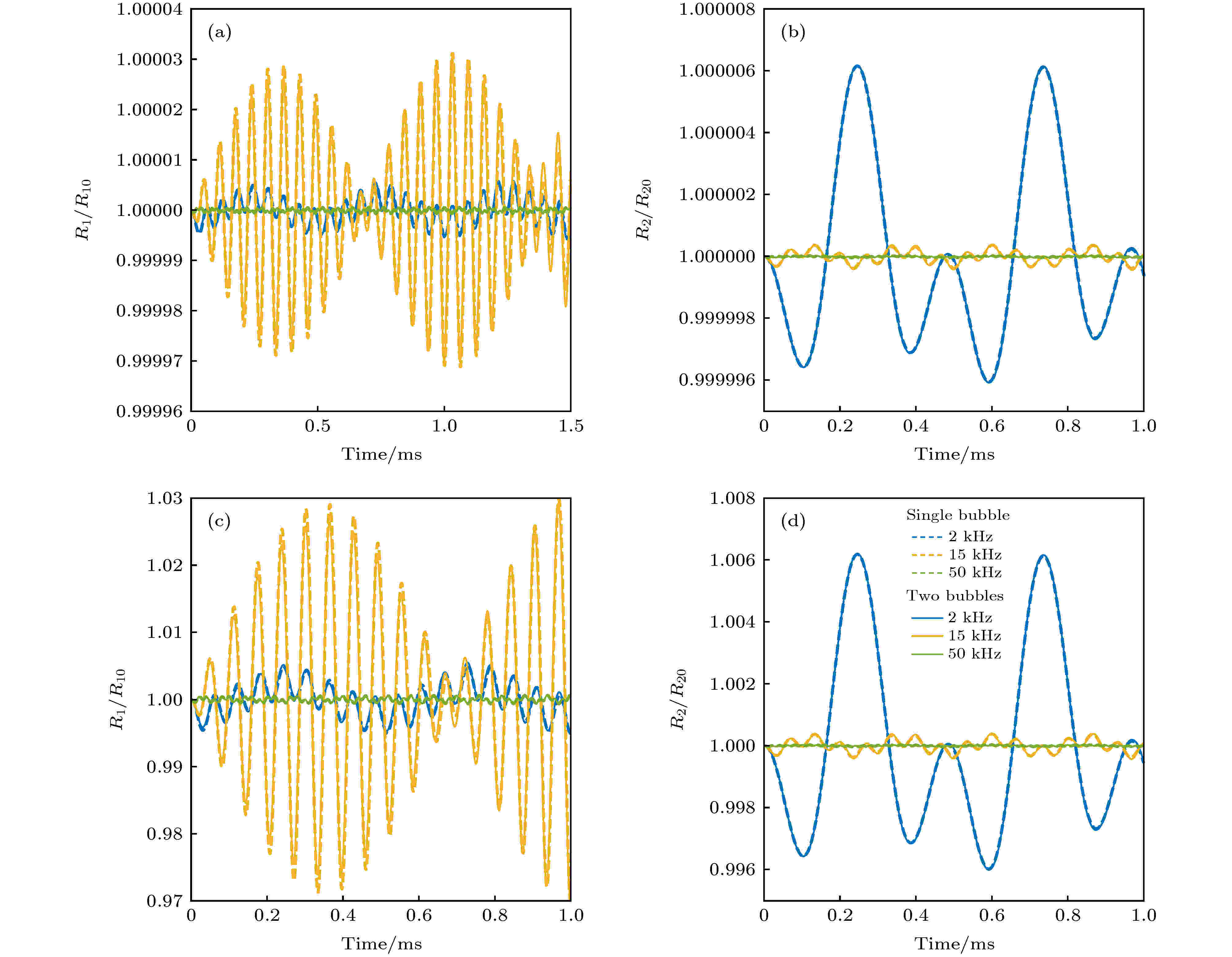图 2 三种不同频率(2, 15和50 kHz)与两类幅度(1 Pa与1 kPa)声波激励下的自由气泡与双气泡设置下半径振动特征　(a) 1 Pa声波激励下气泡1在三种激励频率工况下自由气泡与双气泡约束对应的气泡半径振动特征; (b) 1 Pa声波激励下气泡2在三种激励频率工况下自由气泡与双气泡约束对应的气泡半径振动特征; (c) 1 kPa声波激励下气泡1在三种激励频率工况下自由气泡与双气泡约束对应的气泡半径振动特征; (d) 1 kPa声波激励下气泡2在三种激励频率工况下自由气泡与双气泡约束对应的气泡半径振动特征; 图例在图(d)中给出
Figure2. Effects of acoustic excitations with different frequencies (2, 15 and 50 kHz) and amplitudes (1 Pa and 1 kPa) on the bubble dynamics under single free and regulated two-bubble vibrations: (a) Relative radius of bubble 1 between two configurations (single free and regulated two-bubble vibrations) with the amplitude of acoustic excitation being 1 Pa; (b) relative radius of bubble 2 between two configurations (single free and regulated two-bubble vibrations) with the amplitude of acoustic excitation being 1 Pa; (c) relative radius of bubble 1 between two configurations (single free and regulated two-bubble vibrations) with the amplitude of acoustic excitation being 1 kPa; (d) relative radius of bubble 2 between two configurations (single free and regulated two-bubble vibrations) with the amplitude of acoustic excitation being 1 kPa. The figure legend is given in panel (d).

具体而言, 图2(a)表示1 Pa幅度的激励声波引起的气泡1相对半径(${{{R_1}} / {{R_{10}}}}$)的演化过程, 图2(b)表示1 Pa幅度的激励声波引起的气泡2相对半径(${{{R_2}} / {{R_{20}}}}$)的变化过程, 图2(c)与图2(d)分别表示1 kPa幅度的激励声波引起的气泡1与气泡2的相对半径的演化过程. 不难看出, 在激励幅度不变的情况下, 激励声波频率越接近气泡共振频率, 引起的气泡相对半径变化幅度就越大. 具体而言, 在图2(a)与图2(c)中, 15 kHz的激励频率与气泡1的自由共振频率${f_{{\rm{res\_1}}}} \approx $ 16.45 kHz接近, 引起的半径相对变化${{{R_1}} / {{R_{10}}}}$较其他两种工况要大. 当激励频率远离共振频率时, 气泡的响应变弱, 表现为气泡1在激励频率为2 kHz工况下的相对半径变化大于50 kHz激励下相对半径变化. 同理, 在图2(b)与图2(c)中, 2 kHz的激励频率与气泡2的自由共振频率${f_{{\rm{res\_2}}}} \approx $ 4.10 kHz接近, 引起的半径相对变化${{{R_2}} / {{R_{20}}}}$较其他两种工况明显.
通过对比图2(a)与图2(c)及图2(b)与图2(d)可以得到, 在激励频率相同的情况下, 激励幅度越大, 引起的气泡半径变化越大. 需要指出的是, 当气泡间距离为$h\!=\! 8\;{\rm{mm}}$时, 气泡1和气泡2在自由振动与气泡间辐射力影响下的振动状态差别不明显.
2 -->

3.2.气泡距离对双气泡动力学影响

本小节分析气泡距离对双气泡动力学的影响. 具体而言, 设置两个工况, 即气泡间距离$h$分别为2与8 mm, 对应平衡状态下时间延时分别为$6.76 \;\times {10^{ - 7}}$与$4.73 \times {10^{ - 6}}$ s. 数值计算中时间迭代步长为10^–7 s, 气泡的初始状态设置为${R_{1, 2}} = {R_{10, 20}}$以及${\dot R_{1, 2}} = 0$. 外界声波的激励频率和幅度与3.1小节保持一致. 图3给出两个气泡的相对半径动力学特征, 图4给出了两个气泡受到的相应次Bjerknes辐射力.
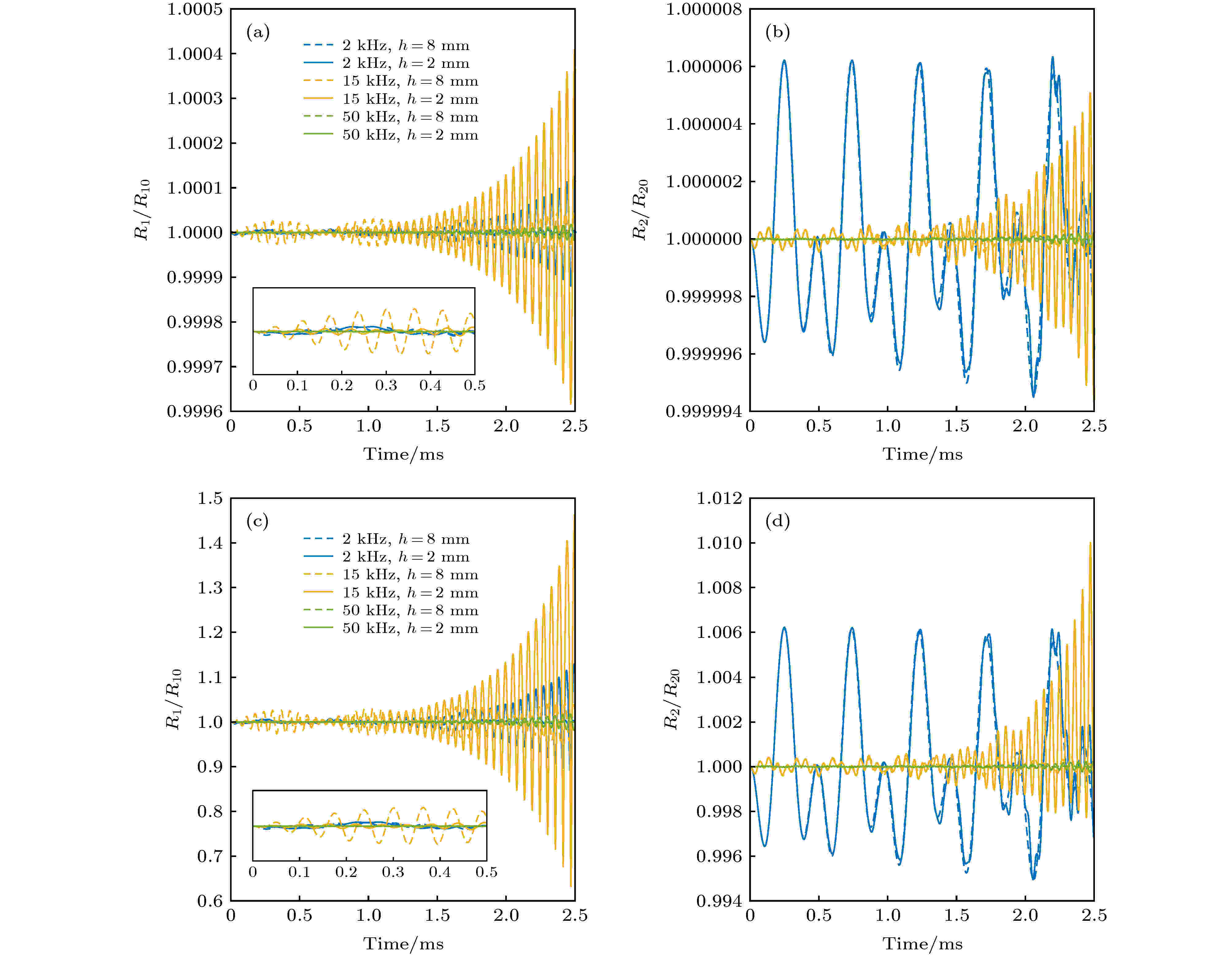图 3 三种不同频率(2, 15和50 kHz)与两类幅度(1 Pa与1 kPa)声波激励下的不同气泡距离(2与8 mm)对气泡振动动力学特征影响　(a) 1 Pa声波激励下气泡1在三种激励频率工况下不同气泡距离对应的气泡半径振动特征; (b) 1 Pa声波激励下气泡2在三种激励频率工况下不同气泡距离对应的气泡半径振动特征; (c) 1 kPa声波激励下气泡1在三种激励频率工况下不同气泡距离对应的气泡半径振动特征; (d) 1 kPa声波激励下气泡2在三种激励频率工况下不同气泡距离对应的气泡半径振动特征; 图例在图(a)和(c)中给出
Figure3. Effects of acoustic excitations with different frequencies (2, 15 and 50 kHz) and amplitudes (1 Pa and 1 kPa) on the bubble dynamics under different distances, with 2 mm and 8 mm, between the two bubbles: (a) Relative radius of bubble 1 under two different bubble’s distance with the amplitude of acoustic excitation being 1 Pa; (b) relative radius of bubble 2 under two different bubble’s distance with the amplitude of acoustic excitation being 1 Pa; (c) relative radius of bubble 1 under two different bubble’s distance with the amplitude of acoustic excitation being 1 kPa; (d) relative radius of bubble 2 under two different bubble’s distance with the amplitude of acoustic excitation being 1 kPa. The figure legend is given in panel (a) and (c).

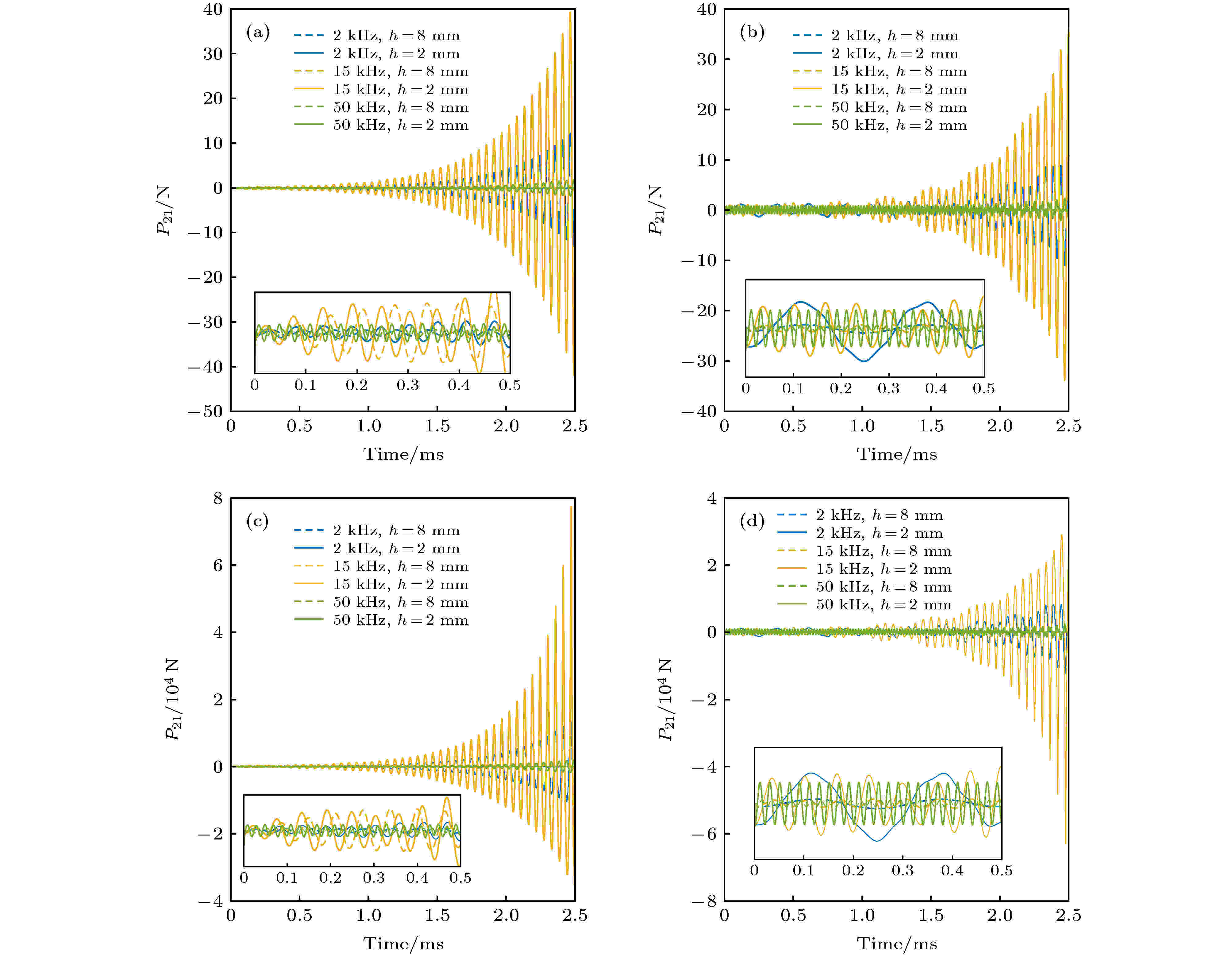图 4 三种不同频率(2, 15和50 kHz)与两类幅度(1 Pa与1 kPa)声波激励下的不同气泡距离(2与8 mm)形成的次Bjerknes辐射力　(a) 1 Pa声波激励下气泡1在三种激励频率工况下不同气泡距离对应的次Bjerknes辐射力; (b) 1 Pa声波激励下气泡2在三种激励频率工况下不同气泡距离对应的次Bjerknes辐射力; (c) 1 kPa声波激励下气泡1在三种激励频率工况下不同气泡距离对应的次Bjerknes辐射力; (d) 1 kPa声波激励下气泡2在三种激励频率工况下不同气泡距离对应的次Bjerknes辐射力
Figure4. Effects of acoustic excitations with different frequencies (2, 15 and 50 kHz) and amplitudes (1 Pa and 1 kPa) on the second Bjerknes force under different distances, with 2 mm and 8 mm, between the two bubbles: (a) Relative radius of bubble 1 under two different bubble’s distance with the amplitude of acoustic excitation being 1 Pa; (b) relative radius of bubble 2 under two different bubble’s distance with the amplitude of acoustic excitation being 1 Pa; (c) relative radius of bubble 1 under two different bubble’s distance with the amplitude of acoustic excitation being 1 kPa; (d) relative radius of bubble 2 under two different bubble’s distance with the amplitude of acoustic excitation being 1 kPa.

图3(a)表示1 Pa幅度的激励声波引起的气泡1相对半径(${{{R_1}} / {{R_{10}}}}$)的演化过程, 图4(a)表示气泡2对气泡1形成的次Bjerknes辐射力. 图3(b)表示1 Pa幅度的激励声波引起的气泡2相对半径(${{{R_2}} / {{R_{20}}}}$)的变化过程, 图4(b)表示气泡1对气泡2形成的次Bjerknes辐射力. 图3(c)与图3(d)分别表示1 kPa幅度的激励声波引起的气泡1与气泡2的相对半径的演化过程. 图4(c)与图4(d)则表征了气泡间相应的次Bjerknes辐射力. 与图2对比可以得到, 当次Bjerknes辐射力不明显时, 在激励声波频率越接近气泡共振频率时, 气泡半径变化越明显; 激励声波幅度越大, 气泡半径动态变化的幅度也相应增大.
图3(b)与图3(d)中, 2 kHz的激励声波频率由于接近气泡2的共振频率, 激发的气泡半径变化与其他两种激励频率相比更加显著. 随着时间的增加, 15 kHz的激励频率在气泡间距离为2 mm时增加了气泡1的半径变化(图3(a)与图3(c)), 进而导致气泡1对气泡2的次Bjerknes辐射力增加(图4(b)与图4(d)), 使得气泡2在15 kHz的激励声波的作用下其半径变化显著. 另一方面, 2 kHz的激励频率在气泡间距离为2 mm时对气泡2的影响与气泡间距离为8 mm时对气泡2的影响区别不显著(图4(a)与图4(c)), 使得气泡1的动力学特征变化并不明显(图3(a)与图3(c)). 而对于50 kHz的激励声波, 其频率与两个气泡的共振频率差别较大, 气泡间距离对气泡动力学较小.
从图4(a)与图4(c)可以看到, 在气泡初始振动阶段, 8 mm的气泡间距离引起的次Bjerknes辐射力存在大于2 mm气泡间距离的工况. 随着时间的推移, 2 mm气泡间距离下的次Bjerknes辐射力急剧增大, 使得气泡动力学进入非线性状态. 当激励频率接近于任意气泡共振频率时, 气泡间的次Bjerknes辐射力得到了显著加强, 使得双气泡的半径变化特征显著. 由图3可以得到, 当气泡半径比较小时, 共振频率高, 相应的次Bjerknes辐射力的影响显著提前(对应15 kHz激励声波工况). 当次Bjerknes辐射力远离气泡共振频率(50 kHz)时, 其对初始气泡动力学特征的影响较小.
2 -->

3.3.气泡轴向位置的影响

本小节对气泡轴向位置的影响进行分析, 通过改变两气泡球心连线与轴向坐标$x$轴夹角$\theta $的大小实现轴向位置的改变. 在数值计算过程中, $\theta $分别取值0, ${{\text{π}} / 2}$, ${\text{π}}$, 对应三种不同位置. 此外, 气泡球心距离设置为2 mm, 激励声波幅度为1 kPa. 数值计算中时间迭代步长为10^–7 s, 气泡的初始状态设置为${R_{1, 2}} = {R_{10, 20}}$以及${\dot R_{1, 2}} = 0$. 图5—图7给出了气泡半径的动态演化过程图.
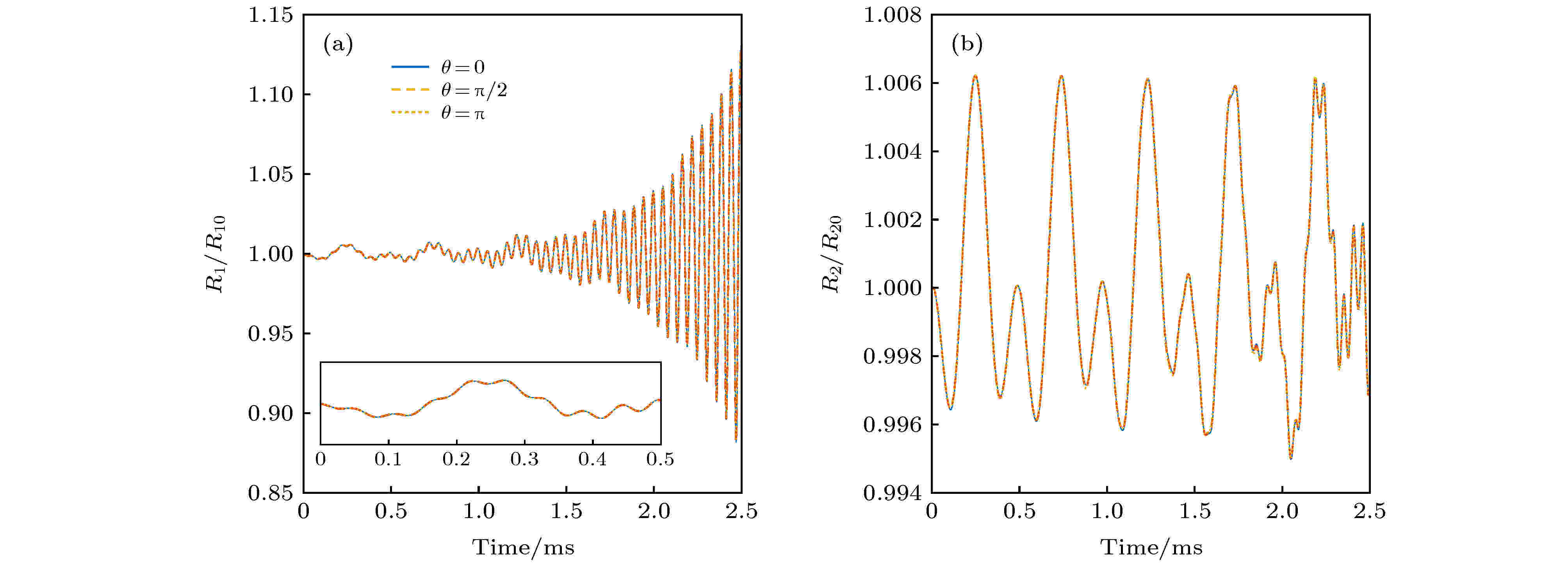图 5 2 kHz声波激励下不同气泡位置对气泡振动过程的影响　(a)三种不同相对位置工况下气泡1相对半径动态变化图; (b)三种不同相对位置工况下气泡2相对半径动态变化图
Figure5. Effects of different bubble locations on the bubble’s dynamics with the frequency of acoustic excitation being 2 kHz: (a) The radius dynamics of bubble 1 under three different locations; (b) the radius dynamics of bubble 2 under three different locations

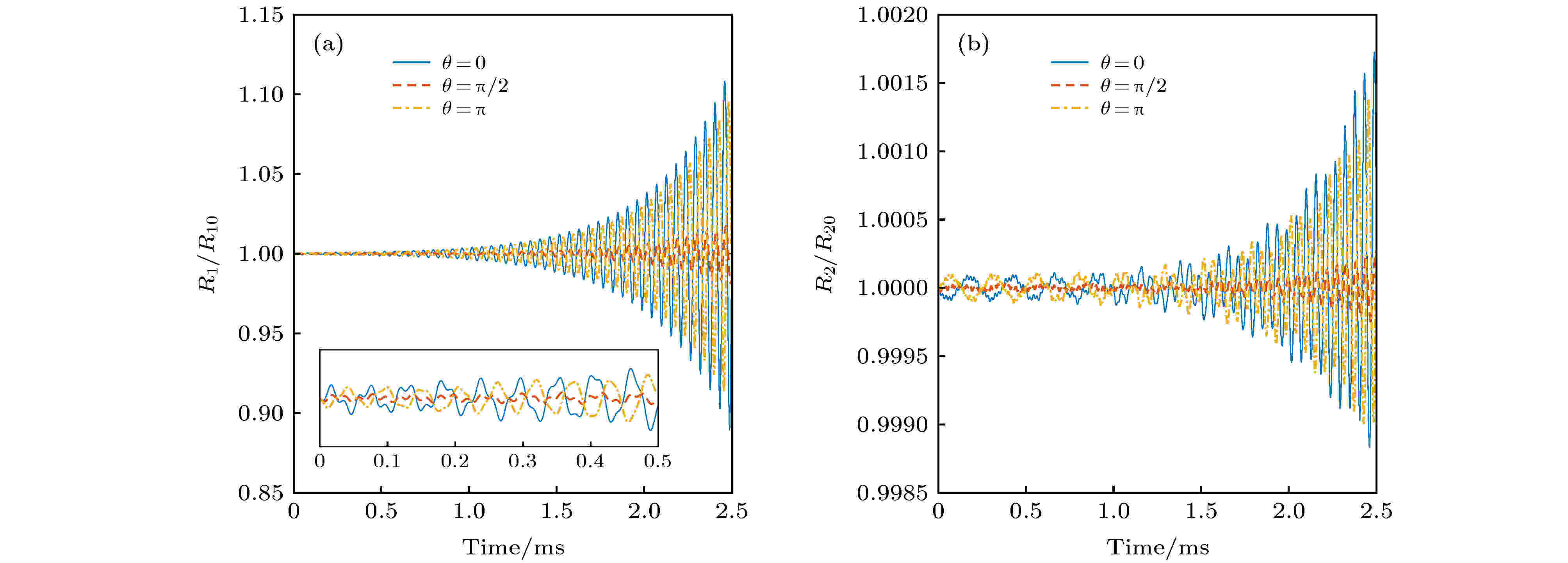图 7 50 kHz声波激励下不同气泡位置对气泡振动过程的影响　(a)三种不同相对位置工况下气泡1相对半径动态变化图; (b)三种不同相对位置工况下气泡2相对半径动态变化图
Figure7. Effects of different bubble locations on the bubble’s dynamics with the frequency of acoustic excitation being 50 kHz: (a) The radius dynamics of bubble 1 under three different locations; (b) the radius dynamics of bubble 2 under three different locations.

物理上而言, 当$\theta = {{\text{π}} / 2}$时, 两个气泡的轴向位置一致, 激励信号对两个气泡的相位和幅度保持一致. 当$\theta = 0$时, 两个气泡的轴向位置不同, 且满足${x_2} - {x_1} = 2 $ mm. 当$\theta = {\text{π}}$时, 两气泡的轴向位置满足${x_2} - {x_1} = - 2$ mm. 针对$\theta = 0$以及$\theta = {\text{π}}$的工况, 外界激励声波对两气泡存在相位的差别.
当声波激励频率为2 kHz时, 三种位置工况($\theta = 0$, $\theta = {{\text{π}} / 2}$与$\theta = {\text{π}}$)对应的相位延时分别为$0.017{\text{π}}$, 0以及$ - 0.017{\text{π}}$. 由图5可以看出, 在上述延迟工况下, 气泡1与气泡2的相对半径变化趋势在三种工况下基本保持一致. 当声波激励频率为15 kHz时, 三种位置工况对应的相位延时分别为$0.1274{\text{π}}$, 0以及$ - 0.1274{\text{π}}$.
由图6可得, 气泡1与气泡2的相对半径趋势在初始状态存在微小区别. 随着时间的增加, 由于次Bjerknes辐射力的影响, 气泡1与气泡2的相对半径变化在三种工况下的演化趋势差别明显. 相位的不一致带来次Bjerknes辐射力的变化, 次Bjerknes辐射力的改变不仅影响相位的变化, 而且明显改变气泡半径的变化幅度. 当声波激励频率为50 kHz时, 三种位置工况对应的相位延时分别为$0.4245{\text{π}}$, 0以及$ - 0.4245{\text{π}}$.
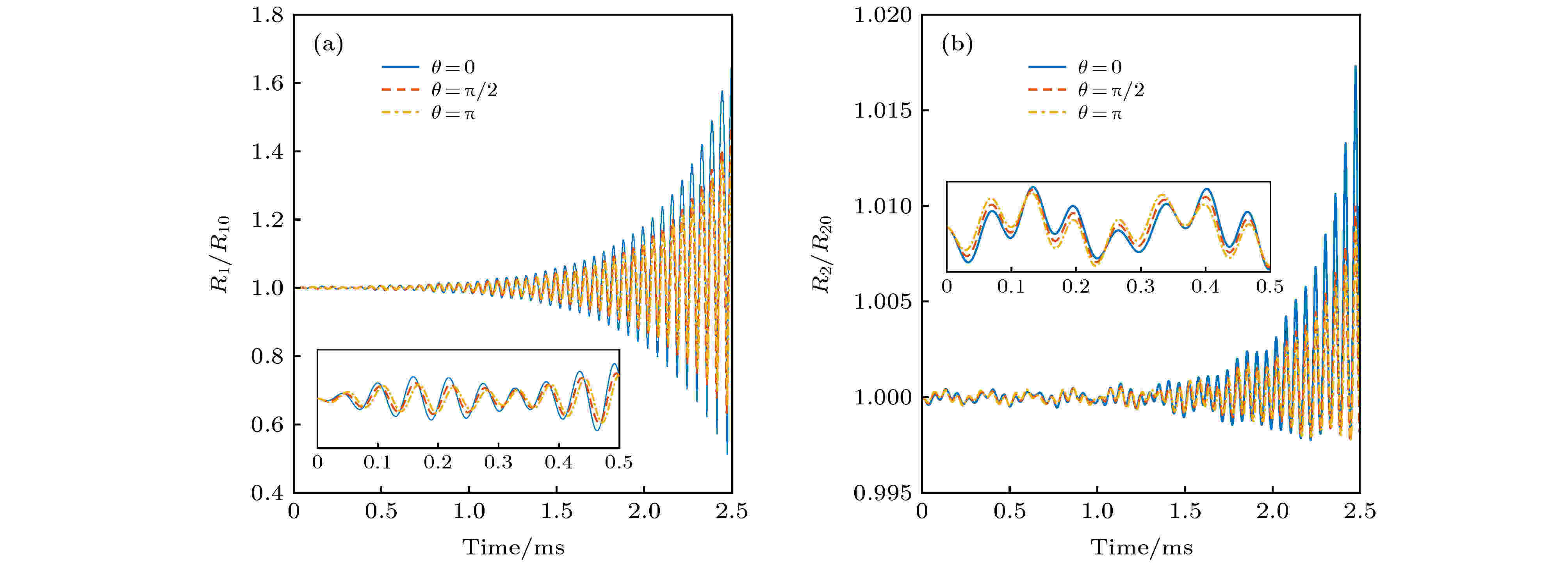图 6 15 kHz声波激励下不同气泡位置对气泡振动过程的影响　(a)三种不同相对位置工况下气泡1相对半径动态变化图; (b)三种不同相对位置工况下气泡2相对半径动态变化图
Figure6. Effects of different bubble locations on the bubble’s dynamics with the frequency of acoustic excitation being 15 kHz: (a) The radius dynamics of bubble 1 under three different locations; (b) the radius dynamics of bubble 2 under three different locations.

由图7可得, 气泡1与气泡2的相对半径趋势在初始状态下存在较大区别. 随着时间的推移, 三种工况对应的气泡1与气泡2的相对半径的演化存在明显区别, 表明相位的改变与次Bjerknes辐射力形成了如图6所示的非线性耦合. 由于激励声波的频率为50 kHz, 与气泡的共振频率差别比较大, 使得非线性耦合较15 kHz时的工况弱, 表现为图7所示的气泡相对半径比图6中气泡相对半径变化弱.
2 -->

3.4.气泡脉冲响应

本小节分析双气泡对应的脉冲响应频谱图. 为避免气泡轴向位置对气泡半径振动的影响, 气泡球心连线与轴向坐标轴角度设置为$\theta = {{\text{π}} / 2}$. 在数值计算过程中, 采用窄脉冲信号, 脉冲宽度为$3 \; \times {10^{ - 7}}$ s, 脉冲幅度为1 kPa. 在分析次Bjerknes辐射力影响时, 气泡球心距离设置为8 mm. 图8给出了自由单气泡与次Bjerknes辐射力影响下的气泡脉冲响应幅频曲线.
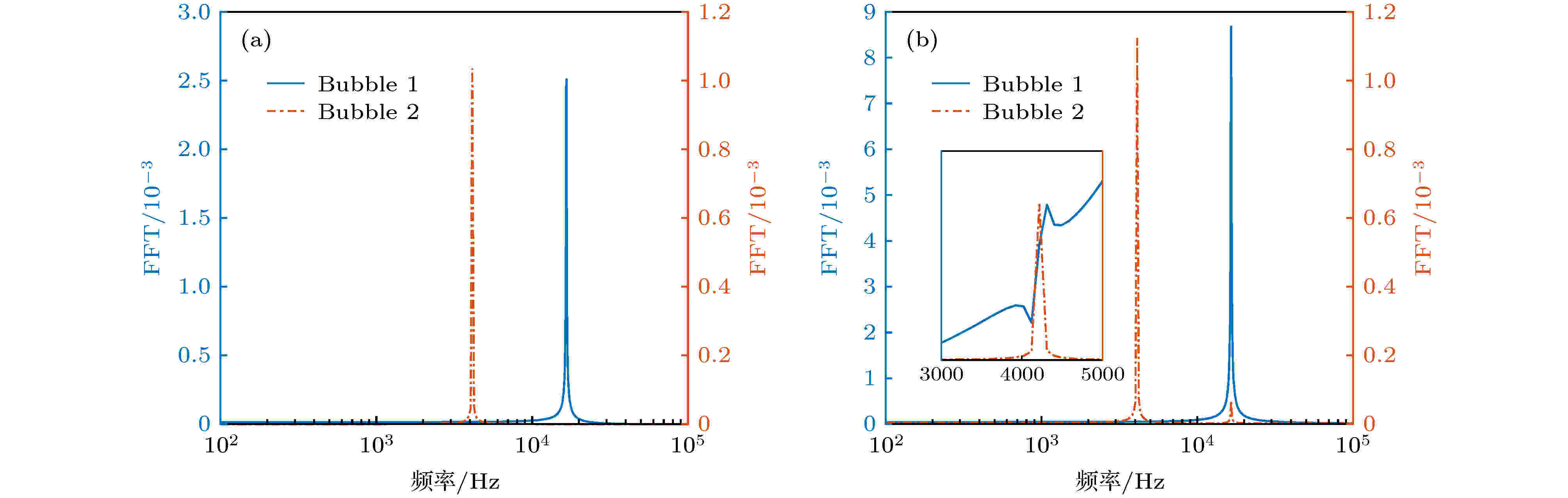图 8 脉冲激励下气泡幅频响应曲线　(a)自由单气泡对应的幅频响应图; (b)气泡间距离为8 mm下双气泡对应的幅频响应图
Figure8. Amplitude-frequency response chart of bubble dynamics under pulse excitation: (a) Amplitude-frequency response chart of free single bubble system; (b) amplitude-frequency response chart of two-bubble coupled system with bubble distance being 8 mm.

图8(a)给出了自由单气泡在脉冲激励下的气泡动力学幅频响应图. 不难看出, 气泡1对应的共振频率为16.5 kHz, 与(15)式得到的理论共振频率16.45 kHz基本一致. 气泡2对应的共振频率为4.1 kHz, 与(16)式得到的理论共振频率4.1 kHz保持一致. 当考虑两气泡之间的次Bjerknes辐射力时, 图8(b)为气泡1与气泡2的幅频响应图. 不难看出, 气泡1与气泡2包含了4.1与16.5 kHz的信号特征. 由于次Bjerknes辐射力的影响, 气泡1与气泡2的线性动力学过程((11)式和(12)式)可以理解为次Bjerknes辐射力作用下的受迫振动, 使得气泡的频谱响应既包含自身共振频率, 也包含次Bjerkness辐射力的频谱特征.
图9给出了气泡间距为2 mm时气泡1与气泡2的幅频响应. 由3.2节可以得到, 当气泡间距为2 mm时, 气泡在次Bjerknes辐射力的作用下表现为非线性振动, 可以在图9中观察到若干谐波频谱特征. 由于两气泡表现为次Bjerknes辐射力作用下的非线性受迫振动, 两气泡的频谱特征显著区别于图8所示工况的频率特征. 气泡1与气泡2的频谱不一致反映了非线性次Bjerknes辐射力的不一致, 符合图4(c)与图4(d)表现的结论. 从图9可以看到, 非线性特征的谐波基频约为17.60 kHz, 与线性工况(图8(b))下16.45 kHz略有区别.
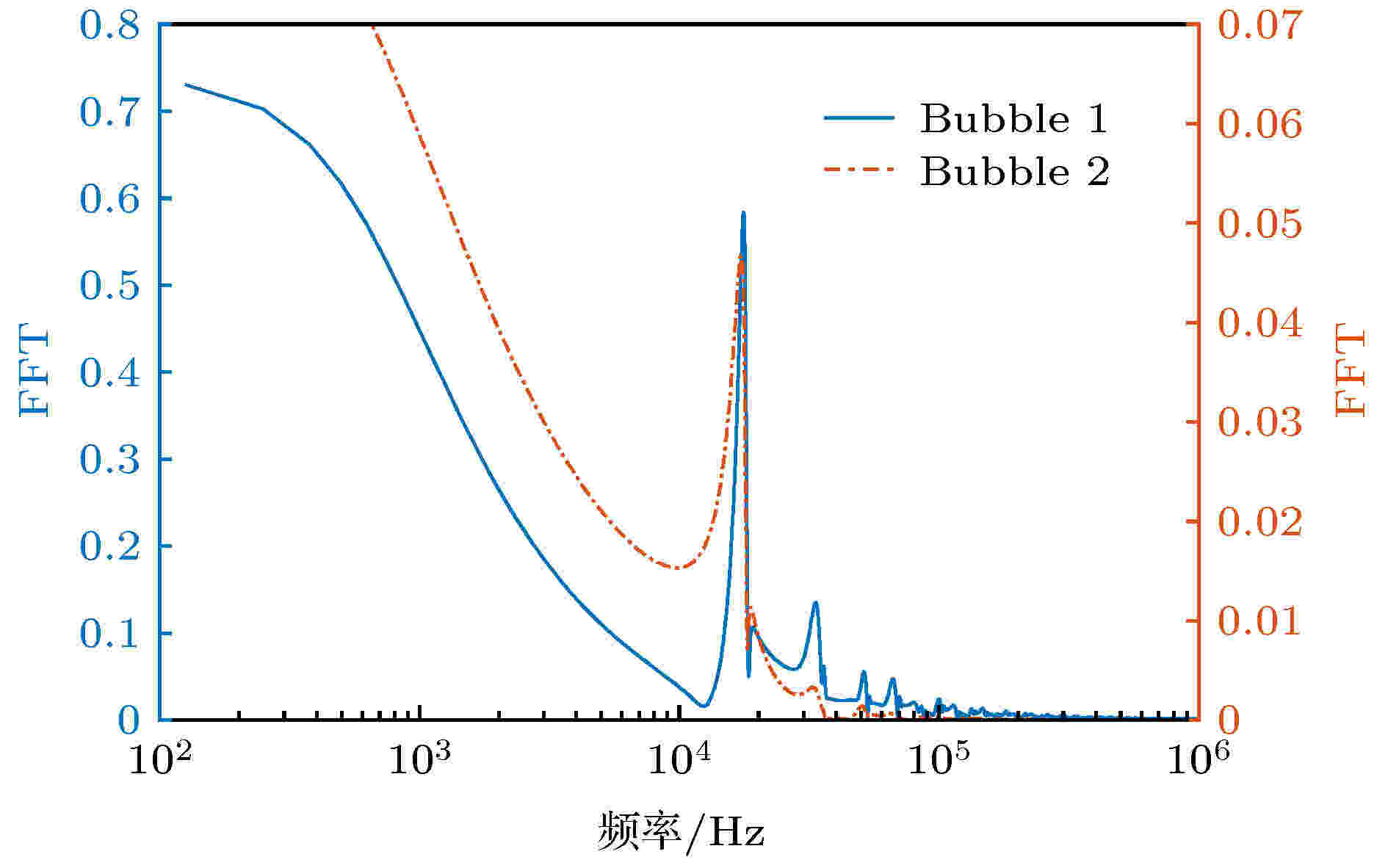图 9 双气泡非线性振动对应的频谱响应曲线
Figure9. Amplitude-frequency response chart of nonlinear two-bubble dynamics under pulse excitation.

需要指出的是, 考虑液体可压缩性特征获得的频谱特征与不可压缩假设下频谱特征((18)式和(19)式)明显不一致. 在当前参数设置下, (19)式的不可压缩双气泡线性系统的共振频率约为124 Hz, 与数值计算结果(图8与图9)不一致.

针对基于声学理论的管道气泡检测技术问题, 本文开展了声波作用下的管道内双气泡动力学建模工作. 在传统自由气泡Rayleigh-Plesset模型的基础上, 引入可压缩流体次Bjerknes辐射力, 获得了双气泡耦合动力学模型. 基于该模型, 详细分析了存在次Bjerkness辐射力时双气泡的线性/非线性动力学特征, 并与自由气泡的动力学特征进行对比分析. 研究结果表明, 次Bjerknes辐射力使得气泡处于受迫振动, 在线性变化范围内, 任意气泡的动力学幅频数据包含了双气泡所有的频谱信息. 在非线性范围内, 两气泡的频谱特征不一致, 表明次Bjerknes辐射力在非线性阶段的复杂性. 此外, 相较于线性特性, 非线性气泡振动的基频与自由气泡共振频率不一致, 发生了偏移.
本文通过分析气泡球心距离以及气泡轴向位置作用下双气泡系统动力学特征, 表明气泡球心距离对次Bjerknes辐射力影响明显, 从而显著改变双气泡振动动力学特征. 气泡球心距离越小, 双气泡越趋向于非线性振动. 气泡轴向位置显著影响气泡振动的初始状态. 当外界激励频率与气泡共振频率一致时, 初始状态的不同与次Bjerknes辐射力形成正反馈过程, 加强了气泡趋向于非线性振动.
针对基于声学理论的气泡检测而言, 由于外界声波激励产生的次Bjerknes辐射力对气泡动力学特征会产生明显的影响, 气泡检测中需要降低次Bjerknes辐射力的影响. 针对小气泡检测而言, 激励声波的频率要远离待检测气泡的共振频率范围, 同时, 激励声波的幅度要相对较小. 除此之外, 激励声波的持续时间也不宜过长, 防止气泡在次Bjerknes辐射力作用下形成非线性振动, 带来气泡的破裂等. 针对大气泡检测而言, 当考虑利用共振特征进行气泡检测时, 需要防止气泡进入非线性振动导致共振频率的偏移. 针对含有不同半径的气泡检测而言, 激励声波的幅度要相对较小, 同时激励声波应略小于大气泡共振频率, 进而利用共振特征对大气泡进行检测, 同时可以较长时间维持小气泡线性小幅振动.