摘要: 单个中性原子的超精细微波跃迁能级的相干性是基于中性原子量子计算、量子信息处理和量子模拟的基础. 我们在实验上利用微波双光子拉曼过程实现了蓝移阱中铯原子基态超精细态
$\left| {{\rm{6}}{{\rm{S}}_{1/2}},F = 3,{m_F} = - 1} \right\rangle $ 和
$\left| {{\rm{6}}{{\rm{S}}_{1/2}},F = 4,{m_F} = 1} \right\rangle $ 间的相干操控, 并研究了其相对能级频移随磁场的变化, 获得了“魔术”磁场的大小为1.4(2) Gauss (1 Gauss = 10
-4 T). 结果表明, 利用魔术磁场可大幅改善超精细态
$\left| {\rm{6}}{{\rm{S}}_{1/2}}\right.$ ,
$F = 3 $ ,
$\left. {m_F} = - 1 \right\rangle $ 和
$\left| {{\rm{6}}{{\rm{S}}_{1/2}},F = 4,{m_F} = 1} \right\rangle $ 之间的相干性, 测量到的相干时间可达1.0(1) s.
关键词: 蓝移阱 /
魔术磁场 /
磁不敏感态 /
相干时间 English Abstract Measurement of magnetically insensitive state coherent time in blue dipole trap Li Xiang-Yan Wang Zhi-Hui Li Shao-Kang Tian Ya-Li Li Gang Zhang Peng-Fei Zhang Tian-Cai Collaborative Innovation Center of Extreme Optics, State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Opto-Electronics, Shanxi University, Taiyuan 030006, China Received Date: 31 December 2019Accepted Date: 01 February 2020Published Online: 20 April 2020Abstract: Qubit encoded in single neutral atoms is a basic experimental platform for studying the quantum computation, quantum information processing and quantum simulation. The extension of the coherence time has been an important task in recent years. On the basis of the single cesium neutral atom trapped in blued-detuned dipole trap, we study the coherence time of a qubit, which is encoded in a pair of magnetically insensitive ground states of cesium atom ($\left| {\rm{0}} \right\rangle = \left| {{\rm{6}}{{\rm{S}}_{1/2}},F = 3,{m_F} = - 1} \right\rangle $ and $\left| 1 \right\rangle = \left| {{\rm{6}}{{\rm{S}}_{1/2}},F = 4,{m_F} = + 1} \right\rangle $ ), in the “magic” magnetic field condition. By adopting a two-photon process, in which a microwave photon and an RF photon are used, we obtain the coherence manipulation of the qubit. The dependence of differential energy shift on magnetic field is experimentally studied, and the “magic” magnetic field is determined. In this magic condition, the first derivative of differential energy shift between $\left| {\rm{0}} \right\rangle = \left| {{\rm{6}}{{\rm{S}}_{1/2}},F = 3,{m_F} = - 1} \right\rangle $ and $\left| 1 \right\rangle = \left| {{\rm{6}}{{\rm{S}}_{1/2}},F = 4,{m_F} = + 1} \right\rangle $ in quantized magnet field is zero, which means that the qubit is immune to the fluctuation of magnetic field and the coherence time can be substantially prolonged. The experimentally obtained magic magnetic field is B = 1.4(2) Gauss, which is in good agreement with the theoretical calculation value B = 1.393 Gauss. Finally, we measure the qubit coherence time by setting the quantized magnetic field to be at magic point B = 1.396 Gauss. The qubit coherence time is measured to be 11(1) ms by Ramsey interferometer, where the main decoherence factor is the inhomogeneous dephasing due to the atomic motion in the dipole trap. This incoherence factor can be dramatically suppressed by a spin-echo process where an additional π-pulse is inserted in between the two π/2 pulses. At the magic magnetic point the qubit coherence time can be extended to 1 s by the spin-echo method.Keywords: blue dipole trap /magic magnetic field /magnetically insensitive state /coherence time 全文HTML --> --> --> 1.引 言 量子计算是量子物理研究领域的重要课题之一, 量子比特高效的态制备以及长的退相干时间是实现量子计算的基本物理条件[1 ] . 离子阱[2 ] 、量子点[3 ] 、NV色心[4 ] 、中性原子[5 ] 等都是研究量子计算的物理实验平台. 相比其他物理系统, 光学偶极俘获的单个中性原子系统具有良好的可扩展性[6 -8 ] , 能够实现大规模的量子计算节点. 近年来, 多种可扩展的光学俘获的单原子阵列已有演示[9 -11 ] , 同时高保真的单比特[12 -14 ] 和双比特量子逻辑门[15 ,16 ] 的实现使得基于中性原子的量子计算研究更加可靠. 然而与其他系统相比, 比如离子系统的相干时间已达10 min量级[17 ] , 单原子系统的相干时间有待进一步提高.[18 -20 ] 、“魔术光强”[21 ] 、“魔术偏振”(magic polarization)[22 ] 、“魔术磁场”(magic magnetic field)等. 而“双魔术条件”(doubly magic conditions, 即微波跃迁对俘获光场的起伏和磁场的起伏同时不敏感)的探索则是获得超长相干时间的重要方法, 近年来也有多种方案被提出[21 ,23 ,24 ] .[25 ,26 ] . 而蓝移阱相比于红移阱在俘获单个中性原子方面有一定的优势, 例如蓝移阱中单个原子被俘获在光强最弱的区域, 原子受到俘获光场噪声起伏的影响要小, 原子的寿命、温度及相干时间等参数要比相同条件下的红移阱都要好[27 ] . 本文研究了780 nm蓝移阱中被俘获的单个铯原子的相干性, 通过双光子微波过程实现了铯原子超精细态$\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F\! =\! 3, {m_F}\! =\! - 1} \right\rangle $ , $\left| {\rm{6}}{{\rm{S}}_{1/2}}, F\!=\!4, {m_F}\!=\!1\right\rangle$ 之间的拉比振荡, 通过拉曼谱测量从实验找到了跃迁的磁不敏感点, 即“魔术磁场”, 为1.4(2) Gauss (1 Gauss = 10–4 T). 通过将磁场设置在魔术磁场附近可以将相应能级间的相干时间提高到1.0(1) s. 利用此方法, 并配合与磁场无关的光场“魔术”条件[24 ] 可望进一步提高单个原子的相干时间.2.蓝移阱中“魔术”磁场理论分析 在中等磁场中, 原子能级$\left. {\left| {J = \dfrac{1}{2}, {m_J}, {m_I}} \right.} \right\rangle $ 与磁场相互作用引起的Zeeman能级移动可用Breit-Rabi公式表示为[28 ] $\Delta {E_{{\rm{hfs}}}} = {A_{{\rm{hfs}}}}\left( {I + 1/2} \right)$ 为超精细分裂, $m = $ ${m_I} \pm {m_J} = {m_I} \pm 1/2$ , $x = \dfrac{{\left( {{g_J} - {g_I}} \right){\mu _{\rm{B}}}B}}{{\Delta {E_{{\rm{hfs}}}}}}$ .图1 为(1 )式给出的铯原子超精细Zeeman态$\left| {6{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle $ 和$\left| {6{{\rm{S}}_{1/2}}, F = 4, {m_F} = + 1} \right\rangle $ 之间的差分能级频移随磁场大小的变化曲线. 可以看出, 当磁场为B = 1.393 Gauss时, 相对能级频移随磁场的一阶导数为零. 当原子所处的环境磁场大小被设置为此值时, 由磁场波动引起的退相干效应被有效抑制. 此处能级相对频移只受到磁场起伏的二阶影响, 理论得到的残余的二阶系数为${\kappa _\upsilon } = {{{\partial ^{\rm{2}}}{\varDelta _{{\rm{DLS}}}}}/{{\partial ^{\rm{2}}}B\left| {_{{B_0}} = } \right.}}{\rm{0}}{\rm{.801}} \times {10^3}\;{\rm{Hz}}/{\rm{Gaus}}{{\rm{s}}^2}$ .图 1 铯原子超精细态$\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle $ 和$\left|{\rm{6}}{{\rm{S}}_{1/2}}\right.$ , F = 4, $\left.{m_F} = 1 \right\rangle $ 的相对差分频移随磁场变化, 其中蓝色点表示魔术磁场Figure1. The relative DES (differential energy shift) between cesium hyperfine states $\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle $ and $\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 4, {m_F} = 1} \right\rangle $ functional relationship with the magnetic field. The blue star indicates the magic magnetic field.3.实验装置以及实验方案设计 实验装置如图2 所示, 偶极阱光由自制的外腔反馈半导体激光器产生, 波长为780 nm, 失谐于铯原子D1 线49.5 THz, 失谐于D2 线32.9 THz. 激光器输出22 mW的种子光注入锥形放大器(TA)放大到2 W, 之后通过单模保偏光纤过滤空间模式为190 mW、腰斑1.83 mm的高斯光束. 该光束通过拓扑荷为m = 1的螺旋相位片(VL-209-M-Y-A, HOLO OR公司)后变换为LG01 模的类似于“甜甜圈”的空心光束. 方解石分束棱镜将空心光束分为两束光强相同、偏振相互垂直、间距为4 mm的平行光束. 利用高数值孔径透镜组(NA = 0.4, f = 22.9 mm)将两束平行光强汇聚则可在焦点处形成中心光强弱、四周光强较强、形状类似封闭的瓶子的蓝失谐偶极阱, 阱深为k B × 0.63 mK (k B 为玻尔兹曼常数)[29 ] . 同时, 俘获的原子散射852 nm的荧光通过同一个NA = 0.4透镜组收集, 经780 nm光透射852 nm反射的双色片反射后, 耦合进光纤由单光子探测器探测并采集分析.图 2 蓝移阱中单个铯原子俘获装置示意图Figure2. The experimental setup for the trapping of a single cesium atom in the blue detuned dipole trap.图3(a) 所示, 先利用894 nm的${\text{π}}$ 偏振光和磁光阱的再抽运光(repumping)同时作用, 将原子制备在暗态$\left| {F = 4, {m_F} = 0} \right\rangle $ . 然后利用双光子拉曼过程将原子转移到$\left| {\rm{0}} \right\rangle = \left| {F = 3, {m_F} = - 1} \right\rangle $ 态, 实现单原子量子比特的初始化. 在此过程中选择偏振为${\text{π}}$ 和${\sigma ^ + }$ 的光分别耦合跃迁$\left| {6{{\rm{S}}_{{1/2}}}, F = 4, {m_F} = 0} \right\rangle \leftrightarrow \left|6{{\rm{S}}_{{1/2}}}\right.$ , F = $\left. 3, {m_F} = 0 \right\rangle $ 和$\left| {6{{\rm{S}}_{{1/2}}}, F = 3, {m_F} = - 1} \right\rangle \leftrightarrow \left|6{{\rm{S}}_{{1/2}}}\right.$ , F = $\left. 3, {m_F} = 0 \right\rangle $ , 当单光子失谐为$\varDelta = - 35\;{\rm{GHz}}$ , 两束光腰斑分别为600 μm和50 μm, 功率分别为12.7 mW和380 μW, 可以获得$\left|6{{\rm{S}}_{1/2}}, F = 3\right., \left. {m_F} = - 1\right\rangle $ $ \leftrightarrow \left| {6{{\rm{S}}_{1/2}}, F = 4, {m_F} = 0} \right\rangle $ 的相干转移拉比频率为104.1 kHz, 如图3(c) 所示. 采用脉冲长度为4.8 μs的${\text{π}}$ 脉冲可以实现原子$\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle $ 态的高效制备. 受到$\left| {F = 4, {m_F} = 0} \right\rangle $ 制备效率的限制, $\left|{\rm{6}}{{\rm{S}}_{1/2}}\right. $ , $\left. F = 3, {m_F} = - 1\right\rangle $ 态的制备效率为0.8.图 3 光学抽运实现态初始化$\left| {F = 4, {m_F} = 0} \right\rangle $ 制备以及量子比特$\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 4, {m_F} = {\rm{0}}} \right\rangle $ 和$\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle $ 之间的相干转移 (a)初始化$\left| {F = 4, {m_F} = 0} \right\rangle $ 原理图; (b)双光子拉曼过程中量子比特$\left| {\rm{0}} \right\rangle = \left| {F = 3, {m_F} = - 1} \right\rangle $ 的制备以及利用双光子共振过程实现量子比特$\left| {6{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle \leftrightarrow \left| {6{{\rm{S}}_{1/2}}, F = 4, {m_F} = + 1} \right\rangle $ 的相干转移; (c)$\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 4, {m_F} = {\rm{0}}} \right\rangle $ 和$\left|{\rm{6}}{{\rm{S}}_{1/2}}\right.$ , F = 3, $\left.{m_F} = - 1 \right\rangle $ 的拉比振荡; (d)$\left| {6{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle \leftrightarrow \left| {6{{\rm{S}}_{1/2}}, F = 4, {m_F} = + 1} \right\rangle $ 的拉比振荡Figure3. (a) Energy scheme for initialization of Zeeman state $\left| {F = 4, {m_F} = 0} \right\rangle $ by optical pumping; (b) the preparation of qubit $\left| {\rm{0}} \right\rangle = \left| {F = 3, {m_F} = - 1} \right\rangle $ through two-photon Raman transition. $\varDelta $ is the intermediate state detuning from the excited state $6{P_{1/2}}$ ; (c) two-photon Raman Rabi oscillations on the $\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 4, {m_F} = {\rm{0}}} \right\rangle \leftrightarrow \left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle $ transition. The red solid line is fits to a Rabi sinc function; (d) two-photon Raman Rabi oscillations on the $\left| {6{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle \leftrightarrow \left|6{{\rm{S}}_{1/2}}\right.$ , F = 4, $\left. {m_F} = + 1 \right\rangle $ transition. The oscillation is a fit according to cosine function. Each point is the statistics over 100 shoots.$\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle $ 态的有效制备后, 利用微波双光子过程实现$\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle $ 和$\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 4, {m_F} = 1} \right\rangle $ 之间的相干转移, 如图3(b) 所示. 频率为9.192631267 GHz的微波场${\varOmega _{{{\text{μ}}\rm{w}}}}$ 和频率为502.25 kHz的射频场${\varOmega _{{\rm{rf}}}}$ 分别耦合原子跃迁$\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F\! =\! 3, {m_F}\! = \! - 1} \right\rangle \leftrightarrow \left|{\rm{6}}{{\rm{S}}_{1/2}}, F\!=\!4, {m_F}\!=\!0\right\rangle$ , 和$\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F\! =\! 4, {m_F}\! =\! 0} \right\rangle \leftrightarrow \left|{\rm{6}}{{\rm{S}}_{1/2}}, F\!=\!4, {m_F}\!=\!+1\right\rangle $ . 微波场的功率为10 W时对应单光子耦合的拉比频率为${\varOmega _{\text{μ}}{{\rm{w}}}} = 16.7\;{\rm{kHz}}$ , 射频场功率5 W对应的单光子耦合拉比频率为${\varOmega _{{\rm{rf}}}} = $ 45 kHz. 单光子失谐为$\varDelta = 170\;{\rm{kHz}}$ 时, 可以获得双光子跃迁的拉比频率为$\varOmega = {{{\varOmega _{{\rm{\mu w}}}}{\varOmega _{{\rm{rf}}}}}/{(2\varDelta )}} = $ 2.19 kHz. 实验测量得到的双光子拉曼转移如图3(d) 所示, 其拉比频率为2.19(4) kHz, 与理论值相符.4.相干时间测量及其结果分析 固定微波和射频脉冲作用时间为0.666 ms可以获得相应的${\text{π}}$ 脉冲, 通过扫描双光子失谐可以获得蓝移阱中原子$\left| {6{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle \leftrightarrow \left|6{{\rm{S}}_{1/2}}\right.$ ,$ F = 4, \left.{m_F} = + 1\right\rangle $ 跃迁的拉曼谱, 如图4 插图所示. 拉曼谱的中心频率反映了$\left| {6{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle $ 和$\left| {6{{\rm{S}}_{1/2}}, F = 4, {m_F} = + 1} \right\rangle $ 之间的能级间距. 固定阱深测量不同磁场下的能级间距可以获得能级间距随磁场的变化, 如图4 所示. 拟合得到魔术磁场为1.4(2) Gauss, 此处能级间距对磁场的一阶依赖消除. 拟合得到的残余二阶系数为${\kappa _\nu } = {{\partial ^2}{\varDelta _{{\rm{DLS}}}}}/$ ${{\partial ^2}B} = 0.8(2) \times {10^3}\;{\rm{Hz}}/{\rm{Gaus}}{{\rm{s}}^2} $ . 此处能级间距对磁场的一阶依赖消除.图 4 $\left| {6{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle $ 与$\left| {6{{\rm{S}}_{1/2}}, F = 4, {m_F} = + 1} \right\rangle $ 的能级间隔随磁场变化, 实线为公式拟合. 插图为对应磁场为1.233 Gauss时的拉曼谱, 纵坐标频率相对频移为$\Delta {\upsilon _{{\rm{DLS}}}} = $ –1.957(4) kHzFigure4. The relative DES between states $\left|6{{\rm{S}}_{1/2}}\right., F = 3, $ $\left. {m_F} = - 1 \right\rangle $ and $\left| {6{{\rm{S}}_{1/2}}, F = 4, {m_F} = + 1} \right\rangle $ , solid line is the functional fitting. Inset is the Raman spectrum measured at B = 1.233 Gauss, the relative offset of spectrum is $\Delta {\upsilon _{{\rm{DLS}}}} =$ –1.957(4) kHz.$\left| {6{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle $ 的原子通过${{\text{π}}/2}$ 脉冲制备到$\left| {6{{\rm{S}}_{1/2}}, F = 3, {m_F} = - 1} \right\rangle $ 和$\left|6{{\rm{S}}_{1/2}}\right. $ , F = 4, mF = $\left. + 1 \right\rangle $ 的相干叠加态, 然后自由演化一段时间t 后施加第二个${{\text{π}}/2}$ 脉冲并测量原子在$\left| 6{{\rm{S}}_{1/2}}\right.$ , F = 3, mF = $\left. - 1 \right\rangle $ 态的布居数. 通过扫描自由演化时间得到的$\left|6{{\rm{S}}_{1/2}}\right.$ , F = 3, mF = $\left. - 1 \right\rangle $ 态布居数的变化为Ramsey干涉的干涉图样, 如图5(a) 所示. 拟合得出其相干时间为11(1) ms. 采用自旋回波技术, 即在Ramsey干涉仪的两个${{\text{π}}/2}$ 脉冲中间加一个${\text{π}}$ 脉冲, 可以有效消除原子运动引起的非均匀退相干机制的影响. 实验上我们测量了不同自旋回波时间附近的干涉. 图5(b) 给出了干涉图样的振幅随自旋回波时间的变化, 拟合得出$T_2^* = 1.0(1)\;{\rm{s}}$ . 这和我们以前测量的相同蓝移阱中$\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 3, {m_F} = {\rm{0}}} \right\rangle \leftrightarrow $ $\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = {\rm{4}}, {m_F} = {\rm{0}}} \right\rangle $ 跃迁的自旋回波相干时间相比[27 ] 提高了91倍.图 5 相干时间测量结果 (a) Ramsey干涉测量量子比特的退相干时间为11(1) ms; (b)干涉图样的振幅随自旋回波时间的变化, 退相干时间延长为1.0(1) s, 利用衰减的e指数对归一化实验数据进行拟合, 插图为自由演化时间为400 ms时对应的自旋回波干涉图样, 幅值为0.41(6)Figure5. Experimental results for the coherence time measurements: (a) The Ramsey spectrum. The fitting by $P = \dfrac{{{P_0}}}{2}{{\rm{e}}^{ - \frac{t}{{{T_2}}}}}\cos \left( {2{\text{π}}\varOmega t + \phi } \right)$ gives the coherence time $\left( {{T_2}} \right)$ of 11(1) ms; (b) the decay of the amplitude of spin echo signal. The exponential fitting (solid line) gives a coherence time of $T_2^* = 1.0(1)\;{\rm{s}}$ . Insert is the spin echo signal at evolution time of ${\tau _{\rm{p}}} = {\rm{4}}00\;{\rm{ms}}$ .5.结 论 实验实现了780 nm蓝移阱中俘获的单个铯原子基态跃迁$\left| {6{{\rm{S}} _{1/2}}, F = 3, {m_F} = - 1} \right\rangle \leftrightarrow \left|6{{\rm{S}}_{1/2}}\right.$ , F = 4, mF = $\left. + 1 \right\rangle $ 的相干操控, 并通过Ramsey干涉和自旋回波技术测量了其相干时间. 通过微波双光子过程可以获得2.19(4) kHz的拉比跃迁频率, 通过拉曼谱测量了其“魔术磁场”为1.4(2) Gauss, 最终通过将磁场设置在“魔术磁场”测量了相干时间. 只用Ramsey干涉测量得到的相干时间与相同蓝移阱中$\left| {{\rm{6}}{{\rm{S}}_{1/2}}, F = 3, {m_F} = {\rm{0}}} \right\rangle \leftrightarrow \left|{\rm{6}}{{\rm{S}}_{1/2}}\right.$ , F = 4, mF = $\left. 0 \right\rangle $ 跃迁相同, 都为11(1) ms. 但是自旋回波消除原子在阱中运动引起的非均匀退相干机制的影响后相干时间提高了91倍, 为1.0(1) s. 残余的退相干机制主要为光场起伏导致的均匀退相干机制, 如能够同时实现光场的“魔术条件”其相干时间可望进一步拓展. 
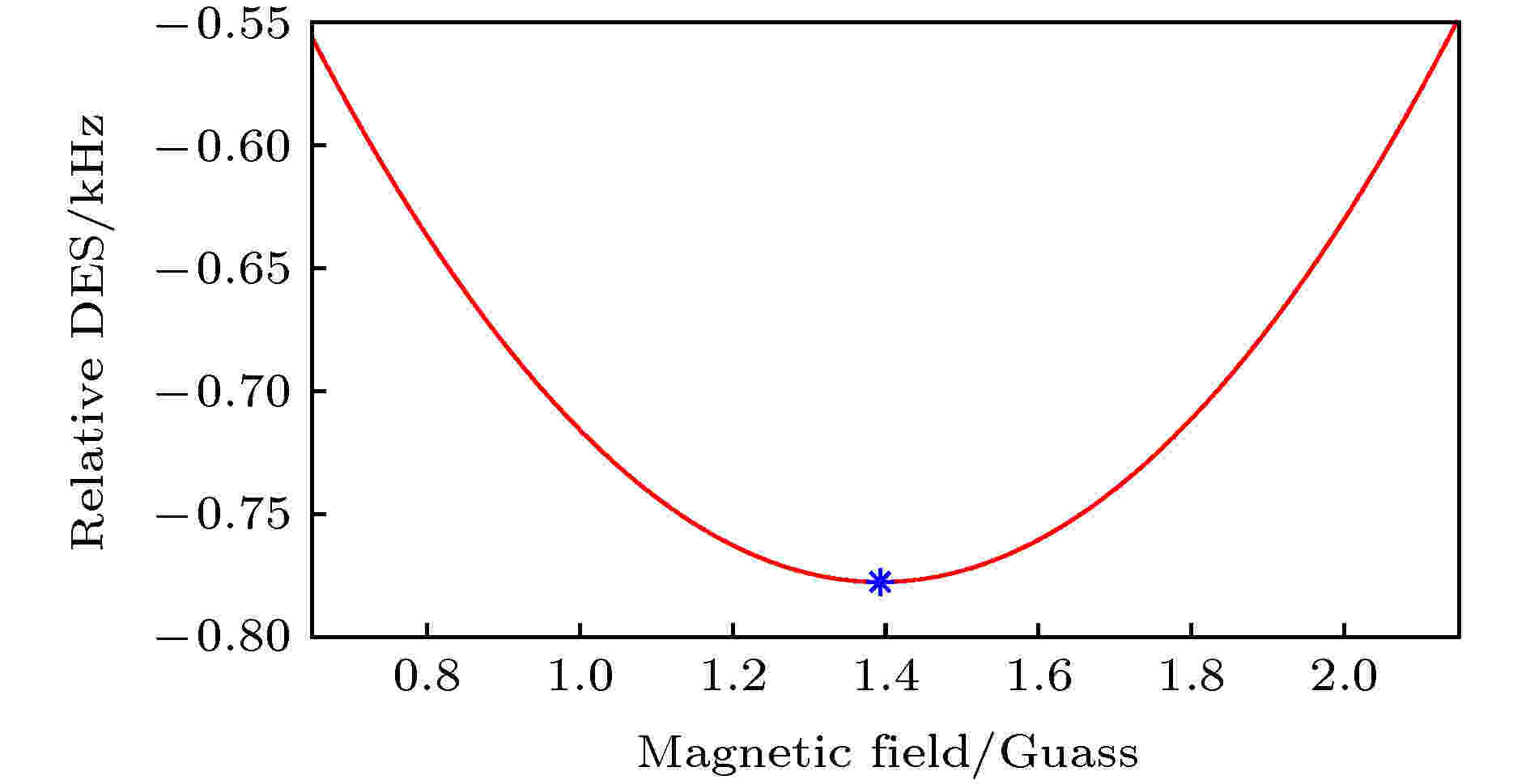图 1 铯原子超精细态
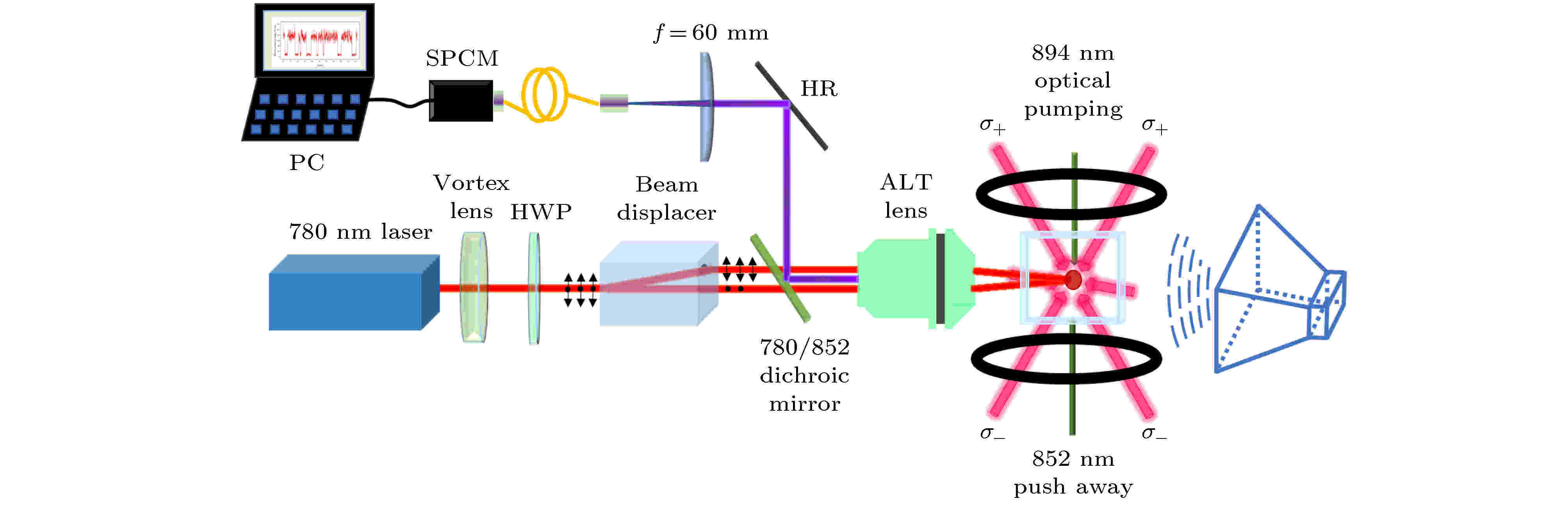图 2 蓝移阱中单个铯原子俘获装置示意图
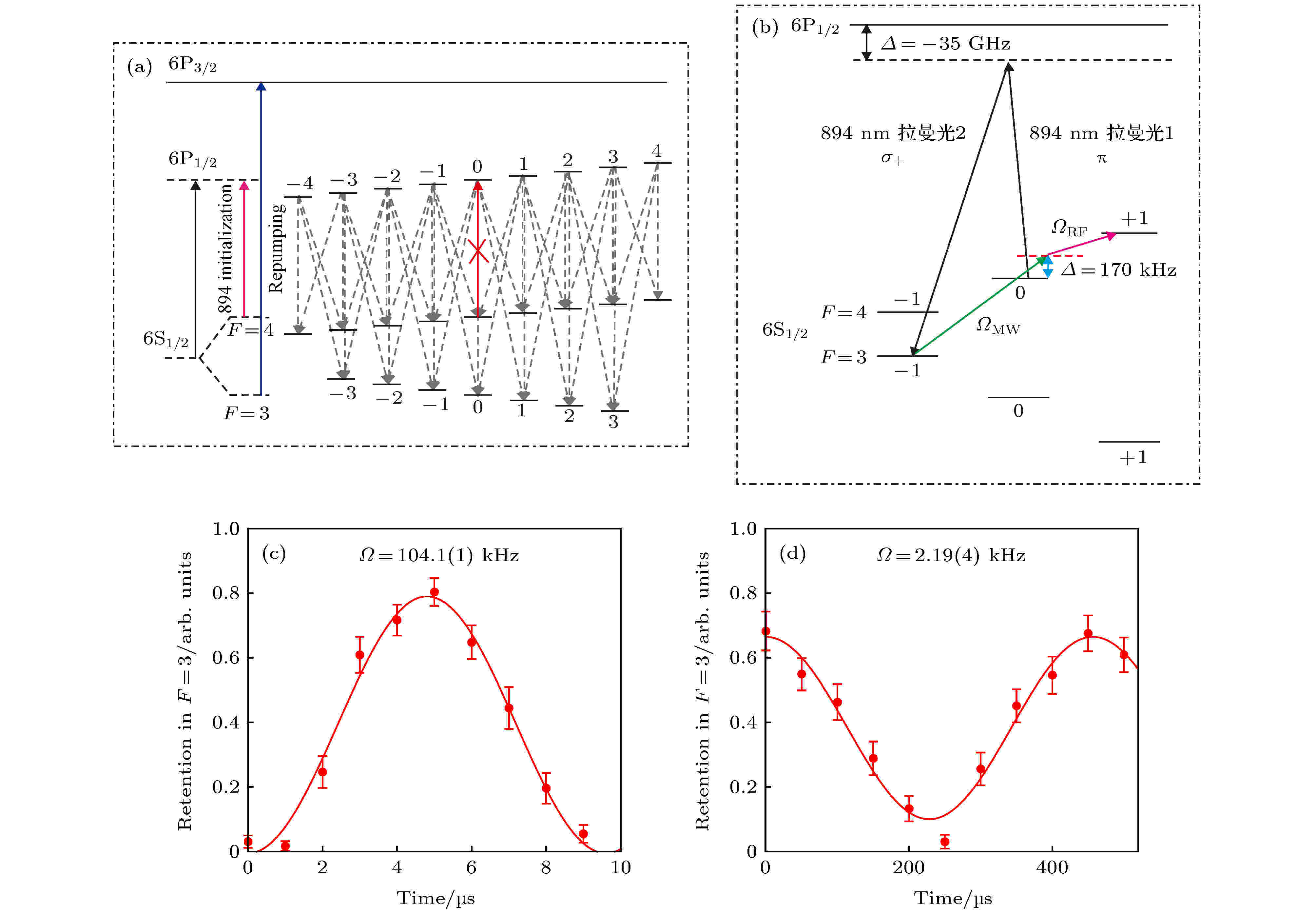图 3 光学抽运实现态初始化
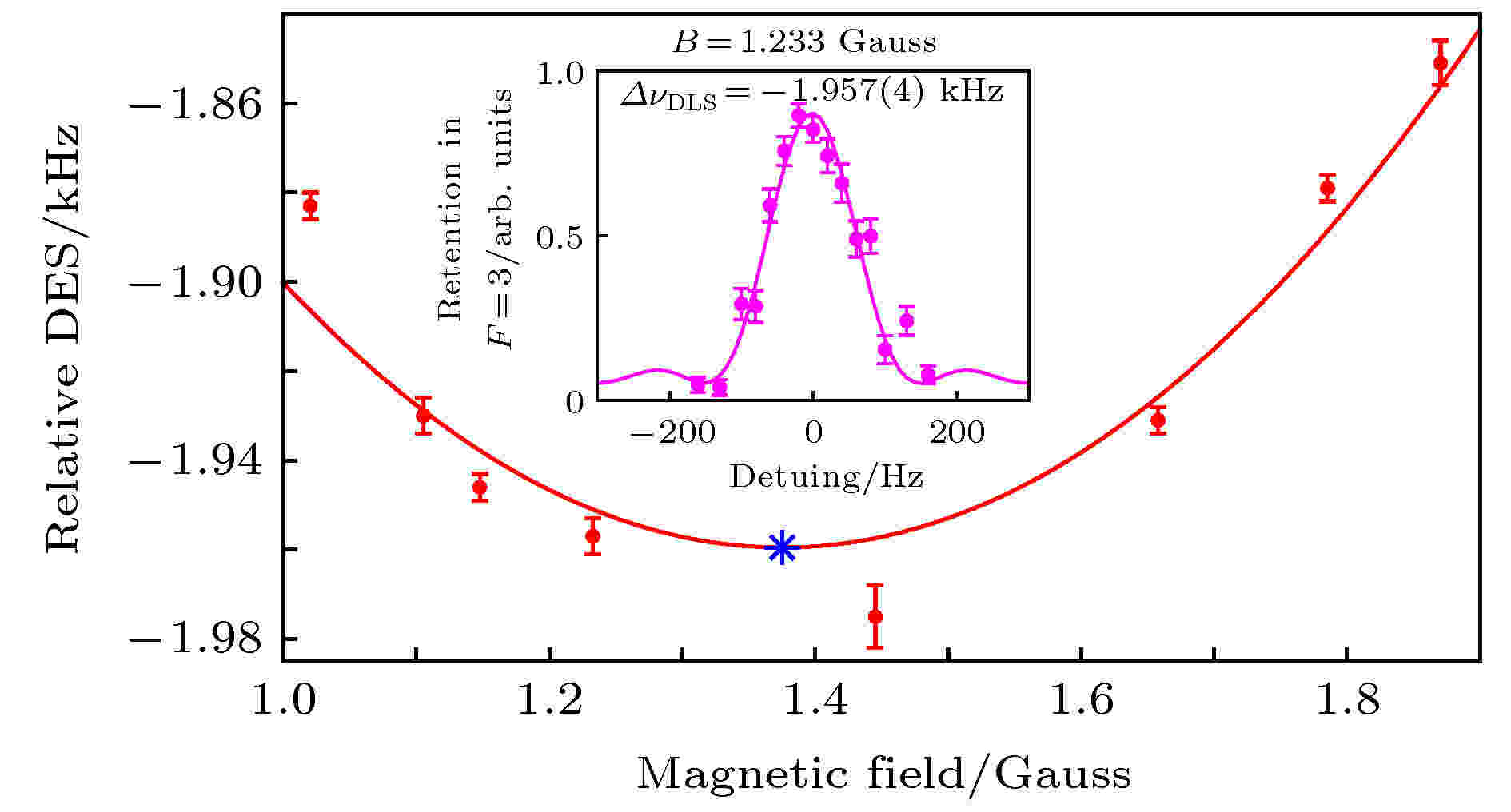图 4 
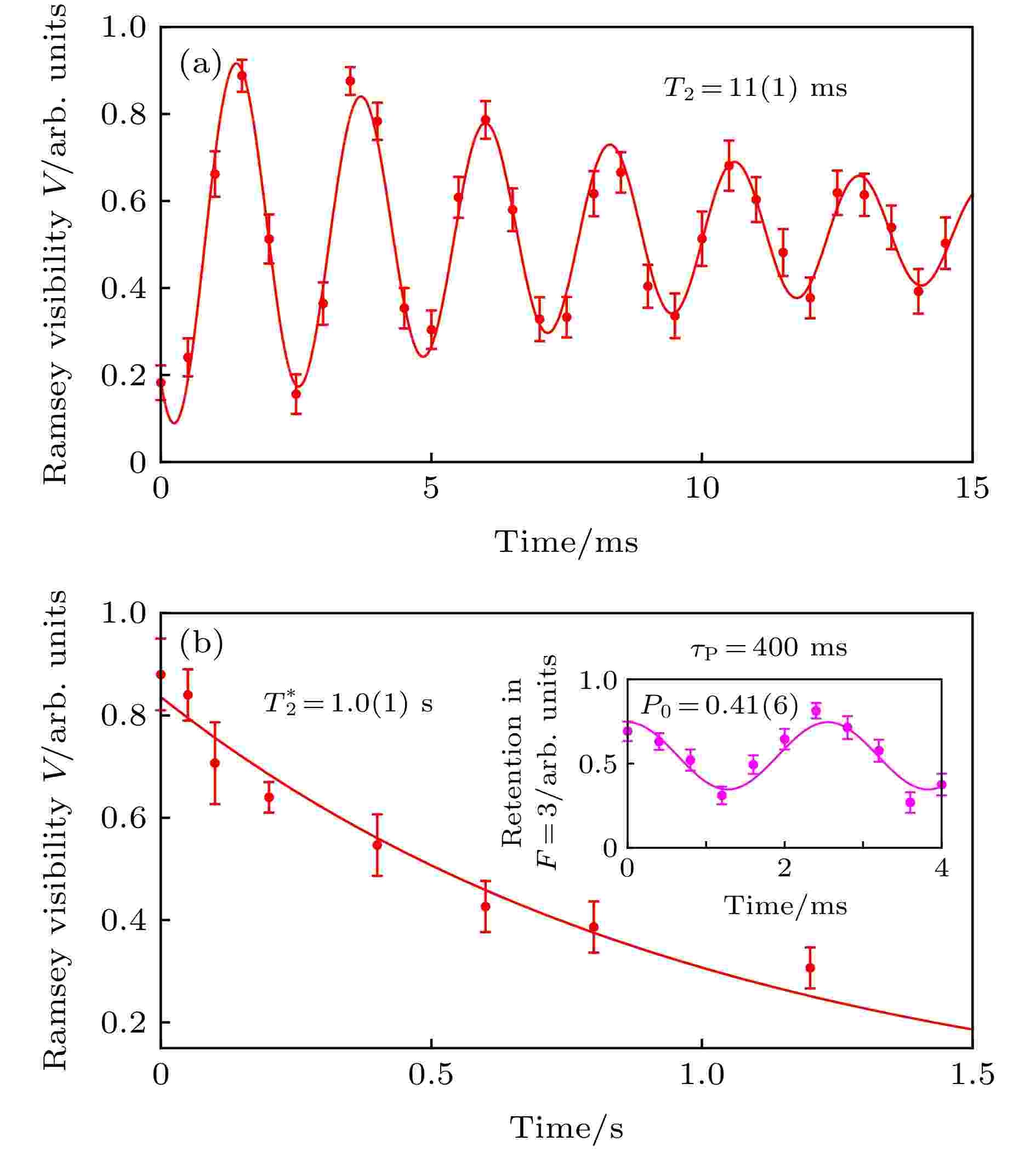图 5 相干时间测量结果 (a) Ramsey干涉测量量子比特的退相干时间为11(1) ms; (b)干涉图样的振幅随自旋回波时间的变化, 退相干时间延长为1.0(1) s, 利用衰减的e指数对归一化实验数据进行拟合, 插图为自由演化时间为400 ms时对应的自旋回波干涉图样, 幅值为0.41(6)
