删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

蚁群元胞优化算法在人群疏散路径规划中的应用

本站小编 Free考研考试/2021-12-29
摘要:针对疏散路径规划问题, 以栅格化地图为背景的基础上, 提出了蚁群元胞优化算法. 首先为统一仿真时间步长, 建立以六边形元胞为基础的栅格地图; 然后利用静态势场对启发函数进行优化, 利用分段更新规则优化信息素更新方式; 最后, 将模型参数作为粒子群优化算法的粒子位置信息进行优化, 求解参数的最优组合值. 仿真结果表明: 采用蚁群元胞优化模型进行疏散路径规划时, 不仅加快了搜索速度, 而且增大了解空间, 提高了搜索能力, 可以有效避免陷入局部最优解.
关键词: 路径规划/
人群疏散/
蚁群元胞优化算法/
粒子群优化

English Abstract


全文HTML

--> --> -->
1.引　言
随着现代工业和科技的发展, 大型建筑物结构变得越来越复杂, 突发事件的发生, 使得疏散人群的难度越来越高, 易造成重大的人员伤亡和经济损失. 如何快速及时的预警、应对突发事件已经成为世界范围内亟待解决的问题. 疏散路径规划是提升疏散成功率的有效方式之一, 大量****正进行坚持不懈的研究, 以期最大限度地降低发生突发事件所带来的危害, 因此疏散路径规划已成为当前学科研究的重点和热点.
目前, 在应急疏散路径规划中应用较为广泛的算法有Dijkstra算法、Floyd算法、A*算法、蚁群算法(ant colony clgorithm, ACO)等. 相比于时间损耗较大的Dijkstra算法、时间复杂度较高而不适应大量数据仿真的Floyd算法、以及易陷入局部最优解的A*算法, Dorigo和Gambardella [1]提出的带有正反馈、启发式的ACO算法, 具有较强的鲁棒性及全局搜索能力, 在解决路径规划问题时效果良好. Babinec等[2]提出了跳点搜索策略, 减少了遍历节点的数目, 提高了算法运算速度, 但是在所规划的路径中仍存在转折点. Cui等[3]通过改进启发式因子对蚁群算法进行优化, 提升了寻径效果. Imen等[4]提出了改进的禁忌搜索模型, 用于求解网格地图中的路径规划问题. Dorigo和Gambardella[5]通过研究提出了蚂蚁系统模型(ant colony system, ACS), 该算法能够在保持蚂蚁算法模型的基础上, 精简了算法结构. Stützle和Hoos[6,7]提出了最大-最小蚂蚁系统(max-min ant system, MMAS), 该算法通过设置信息素的阈值提高了其全局搜索能力, 避免出现停滞现象. 张玮等[8]将蚁群算法与烟花算法相结合, 通过对信息素的初始值进行优化提升算法性能. 胡启国等[9]通过优化信息素更新和状态转移规则, 解决了算法容易陷入局部最优解的问题. Hsu等[10]通过改进信息素的更新规则对蚁群算法进行优化, 缓解了原算法易陷入局部最优解的问题. 李东妮等[11]将蚁群算与遗传算法相结合, 加入交叉和变异算子, 增加了获得全局最优解的概率. 王晓燕等[12]结合人工势场法, 通过优化信息素初始值以及挥发系数, 提升了算法搜索能力. 总之, 现有研究主要依据传统四边形栅格为背景的ACO算法, 并进行优化来进行路径规划[13,14], 未能解决仿真时步长不统一问题, 同时对算法参数的优化也未能提出系统性方法[15-17].
鉴于上述问题, 本文提出蚁群元胞优化模型(ant colony cellular optimization, ACCO), 以六边形栅格为仿真地图划分依据, 重新设计并优化启发函数和信息素更新方式, 以期提升ACCO算法的搜索能力、收敛速度等. 同时系统性地提出利用粒子群优化(partical swarm optimization, PSO)算法对ACCO算法参数进行优化的方法[18]. 最后通过仿真对比分析, 验证ACCO算法的可行性和有效性.
2.蚁群元胞优化模型构建
2
2.1.栅格地图建立
-->

2.1.栅格地图建立

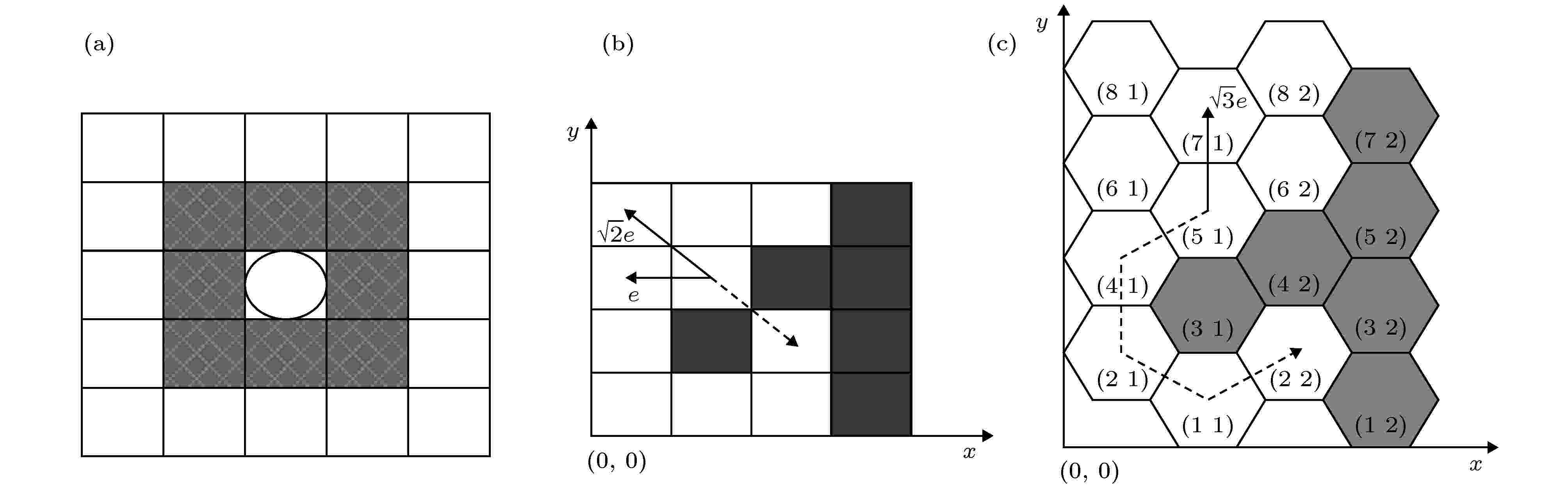在进行传统的路径规划仿真求解时, 均使用的四边形栅格地图[19,20], 且一般采用moore型邻域, 即$N = \left\{ {{s_1}, {s_2}, \cdots {s_i}} \right\}, i \in \left[ {1, 8} \right], {s_i} \in \left[ {0, 1} \right]$, i和si均取整数, i表示邻域元胞编号, si表示元胞是否被选中, 取1时表示被选中, 灰色为中心元胞即蚂蚁当前所在元胞, 黑色元胞表示障碍物或者边界, (2 1)分别表示栅格的行列号(行号以中心点所在位置为基准, 列号同理), 如图1(a)所示.
图 1 栅格示意图　(a) Moore型邻域; (b) 传统四边形栅格; (c) 改进六边形栅格
Figure1. Grid schematic: (a) Mooretype neighborhood; (b) traditional quadrilateral grid; (c) improved hexagon grid.

使用上述四边形栅格在进行系统仿真时, 假定栅格的边长为e, 则选择下一步的目标元胞时, 极轴和斜向方向的移动距离分别为e和$\sqrt 2 e$, 如图1(b)所示, 因此当元胞的移动速度v不变时, 元胞的移动时间为${e}/{v}$或者$\sqrt{2}{e}/{v}$, 产生时间步长不统一问题, 影响模型的真实性. 为有效避免“斜向穿墙”现象, 提出使用六边形栅格, 当栅格边长仍为e时, 元胞每次仿真移动的距离为$\sqrt 3 e$, 移动时间为$\sqrt{3}{e}/{v}\;$, 如图1(c).
因此, 建立六边形栅格地图, 并以地图左下角为原点建立笛卡尔坐标系, 水平方向为X轴. 设每个六边形的内切圆圆心为其中心坐标点, 则坐标值(x, y)为
$\begin{array}{*{20}{c}}{x = \left\{ {\begin{aligned}&{\frac{{5e}}{2} + \left( {j - 1} \right) \times {\rm{d}}x,} \quad{{\rm{mod}}\left( {i,2} \right) = 1,}\\&{e + \left( {j - 1} \right) \times {\rm{d}}x,}\quad{{\rm{mod}}\left( {i,2} \right) = 0,}\end{aligned}} \right.}\\{y = {\rm{d}}y \times i,}\end{array}$
其中i为当前栅格行号, $i \in \left[ {1, 2, \cdots, {N_i}} \right]$; j为当前栅格列号, $j \in [1, 2, \cdots, {N_j}]$; Ni和Nj分别为栅格的行列总数; ${\rm{d}}x = \sqrt 3 e$和${\rm{d}}y = {\sqrt{3} e}/{2}\;$分别为x, y方向上的单位增量.
2
2.2.基本模型描述
-->

2.2.基本模型描述

使用ACCO算法对疏散路径进行规划时, 采用六边形栅格将仿真环境划分为均匀的离散网格图, 然后计算出从起始节点到目的节点的可行网格链集合, 最后在集合中选择最优解[21].
蚁群元胞优化算法可表示为:
${\rm{ACCO}} = \left( {{G_{m \times n}},{P_{m \times n}},{C_{\rm{S}}},{C_{\rm{w}}},{C_{\rm{N}}},{C_{\rm{R}}},O} \right),$
其中${G_{m \times n}}$为网格地图的信息矩阵; ${P_{m \times n}}$为信息素矩阵; m和n表示矩阵的行列数, m一般与单次迭代蚂蚁数量相同; CS为元胞状态, 取值为${\rm{\{ 0, 1\} }}$, 表征此元胞是否被占用, 1表示被占用; Cw为元胞空间, w表示空间维数, 从G中获取, 这里w取2维; CN为元胞邻域, 使用2.1节中所述Moore型; CR为元胞规则, 是蚁群移动的基本约束, 主要取决于三点, 即1)所选元胞为非障碍物或边界; 2)所选元胞更加有利于到达目的元胞; 3)概率转移公式决定邻域元胞被选中的概率, 如
${p_{ij}} = \left\{ {\begin{aligned}& {\frac{{{{\left( {{\tau _{ij}}} \right)}^\alpha } \times {{\left( {{\eta _{ij}}} \right)}^\beta }}}{{\displaystyle\sum \nolimits_{{{s}} \in {\rm{tabu}}} {{\left( {{\tau _{ij}}} \right)}^\alpha } \times {{\left( {{\eta _{ij}}} \right)}^\beta }}},\;{\rm{if}}\;j \notin {\rm{tabu}},}\\& {0,~~~~~~\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{others}},}\end{aligned}} \right.$
其中pij为由元胞i转移到元胞j的概率值, τij为元胞i与j之间的信息素浓度, ηij为元胞i与j之间的启发函数, α与β为信息素启发因子和期望启发因子, tabu为当前蚂蚁的禁忌表; O为优化策略, 主要针对传统模型存在的问题进行优化, 详见第3节.
3.优化策略描述
ACCO算法的优化策略主要是对启发函数、信息素更新方式以及参数组合设定等方面优化, 以解决传统蚁群算法在进行路径规划问题时存在的收敛速度慢、搜索空间小、易陷入局部最优解等问题.
2
3.1.启发函数的设计优化
-->

3.1.启发函数的设计优化

启发函数表征各邻域元胞被选择的期望程度, 传统四边形栅格地图常选用两元胞之间的距离值为参考标准, 而六边形栅格地图两元胞之间的距离值为常数, 导致启发函数为常数而失去价值. 将静态势场引入启发函数的设计优化中. 静态势场值反映邻域元胞与目的元胞之间的距离程度, 距离越近, 静态势场值越大, 因此符合模型对启发函数的要求. 同时静态场值的引入在提高模型收敛速度的基础上, 降低了迂回现象的发生概率.
优化后的启发函数为
${\eta _{ij}} = \frac{1}{{\left| {X - {X_i}} \right| + \left| {Y - {Y_i}} \right| + C}},$
其中$\left( {X, Y} \right)$和$({X_i}, {Y_i})$分别为目的元胞和邻域元胞在元胞空间的横纵坐标, C为常数, 一般取0.001, 目的是为防止目的元胞自身的启发函数无意义.
同时, 为增加解空间的范围, 提升最优解的效果, 当ACCO算法迭代到一定次数后, 对最优路径中的节点与目的节点之间的启发函数使用(3)式进行更新:
$\begin{split}& {{\eta _{id}} = \frac{1}{{{D_{id}}}},}\\& {{D_{id}} = S - {D_{\left( {i - 1} \right)d}},}\end{split}$
其中Did为节点i与目的节点d之间的距离值, S为最优路径长度, $ i-1 $为最优路径中节点i的前一节点.
2
3.2.信息素更新规则优化
-->

3.2.信息素更新规则优化

当前常用的信息素更新方式主要分为三类: 蚁密模型, 蚁量模型, 以及蚁周模型. 以蚁周模型为基础, 将全局信息素浓度的值限定在阈值[τmin, τmax]范围内, 设计分段更新规则进行信息素的更新, 公式如下:
${\tau _{ij}} =\begin{cases}{{\tau _{{\rm{max}}}},}&{{\tau _{ij}} \geqslant {\tau _{{\rm{max}}}},}\\{{\tau _{{\rm{min}}}},}&{{\tau _{ij}} \leqslant {\tau _{{\rm{min}}}},}\\{\left( {1 - \rho } \right){\tau _{ij}}\left( t \right) + \displaystyle\sum\limits_{k = 1}^m \Delta \tau _{ij}^k\left( t \right),}&{{\text{其他}},}\end{cases}$
$ \Delta \tau _{ij}^k = \begin{cases}{\dfrac{Q}{{{L_{\rm{b}}}}},}&{\text{路径}}\left( {i,j} \right){\text{在本次迭代结果的}}\\ &{\text{最优路径中}},\\{\dfrac{Q}{{{L_k}}},}&{\text{路径}}\left( {i,j} \right){\text{在本次迭代结果的非}}\\&{\text{最优路径中}},\\0,&{\text{其他}},\end{cases}$
其中k为当前蚂蚁; 信息素浓度τmin, τmax分别为${1}/{{{L_{\rm{b}}}}}$, ${\tau}_{\text{max}}/{20}$; $\rho \in \left[ {0, 1} \right]$为信息素挥发系数; Q为信息素浓度总量; Lb为本次迭代的最优路径长度值; Lk为蚂蚁k完成本次搜索所经过的路径长度.
2
3.3.参数优化
-->

3.3.参数优化

在ACCO算法中, 参数α, β, ρ对算法的收敛速度以及解空间的大小等性能影响显著: 参数α值越小, 算法搜索的随机性增强, 但算法的收敛速度变慢; 参数β值越小, 算法越易陷入局部最优解; 参数ρ直接影响模型的全局搜索能力和收敛速度. 因此, 为提升模型性能, 将利用粒子群优化算法对参数进行优化求解.
粒子群优化算法是由Eberhart与Kennedy[22]在20世纪90年代提出的一种基于种群的全局随机优化算法. 该算法中的每个粒子根据自身及其他粒子的位置信息不断调整移动速度, 同时调整移动的方向和距离, 从而实现粒子在解空间内的全局寻优. 在算法求解的迭代过程中, 粒子通过个体极值和全局极值调整自身的速度与位置, 其公式如下:
$\begin{split}& {V_{ig}^t = \omega V_{ig}^t + {c_1}{r_1}\left( {P_{ig}^t - X_{ig}^t} \right) + {c_2}{r_2}{r_1}\left( {P_{gg}^t - X_{ig}^t} \right),}\\& {X_{ig}^k = X_{ig}^k + V_{ig}^k,}\end{split}$
其中V表示粒子速度; ${{X}} = \left( {{X_1}, \;{X_2}, \;{X_3}, \; \cdots \;{X_n}} \right)$为G维空间n个粒子组成的种群, 分别代表粒子当前位置; ω为惯性权重; $g = 1, 2,\cdots , G$; $i = 1, 2, \cdots , n$表示粒子编号; t为当前迭代次数; Pig为个体极值; Pgg为全局极值; c1和c2为非负常数, 称为加速度因子; r1和r2为介于$\left[ {0, 1} \right]$之间的随机数.
使用粒子群优化算法进行参数优化的思路是: 将ACCO算法的参数α, β, ρ作为粒子群优化算法的粒子位置信息进行求解, 通过适应度评价函数不断调整粒子位置, 从而求得参数的最优值和组合值. 因此针对解路径规划问题, 综合考虑寻优能力、运行时间、收敛速度和稳定性等影响因素, 设计出如下适应度评价函数:
$\begin{split}& { {{F}_{i}}\left( x \right)={{\lambda }_{1}}{{L}_{i}}\left( x \right)+{{\lambda }_{2}}{{S}_{i}}\left( x \right)+{{\lambda }_{3}}{{Q}_{i}}\left( x \right)-{{\lambda }_{4}}{{T}_{i}}\left( x \right),}\\& {{{L}_{i}}\left( x \right)= {1}/{\left( {{L}_{\rm{best}}}+1 \right)}\;,}\\& {{{S}_{i}}\left( x \right)={{\rm{e}}^{{}{-{{N}_{\rm{best}}}}/{{{N}_{\rm{max}}}}\;}},}\\& {{{Q}_{i}}\left( x \right)= {1}/{}{{{L}_{\rm{std}}}}\;,}\\& {{{T}_{i}}\left( x \right)=~{{\rm{e}}^{1-{}{1}/{}{\rm{Dis}}\;}},}\end{split}$
其中${F_i}\left( x \right)$为第i个粒子代表的参数所对应的适应度函数值; λ1, λ2, λ3, λ4为权重系数, 且满足λ1 + λ2 + λ3 + λ4 = 1; ${L_i}\left( x \right)$是使用粒子i运算所得的参数, 表示ACCO算法搜索最优路径的能力; Lbest表示每次PSO迭代所得到的最优路径的元胞数量; ${S_i}\left( x \right)$是使用粒子i运算所得的参数, 表征ACCO算法的收敛速度; Nbest为ACCO算法搜索到当前最优路径时自身的迭代次数; Nmax为元胞蚂蚁的最大迭代次数; ${Q_i}\left( x \right)$是使用粒子i运算所得的参数, 表示ACCO算法的稳定性; Lstd为每次PSO迭代过程中, 表征ACCO算法搜索到的路径的方差; ${T_i}\left( x \right)$表示使用粒子i运算所得的参数, 表征ACCO算法的运行时间; Dis表示元每次PSO迭代过程中ACCO算法搜索路径总和.
2
3.4.路径规划流程
-->

3.4.路径规划流程

使用ACCO算法进行路径规划的流程如图2所示.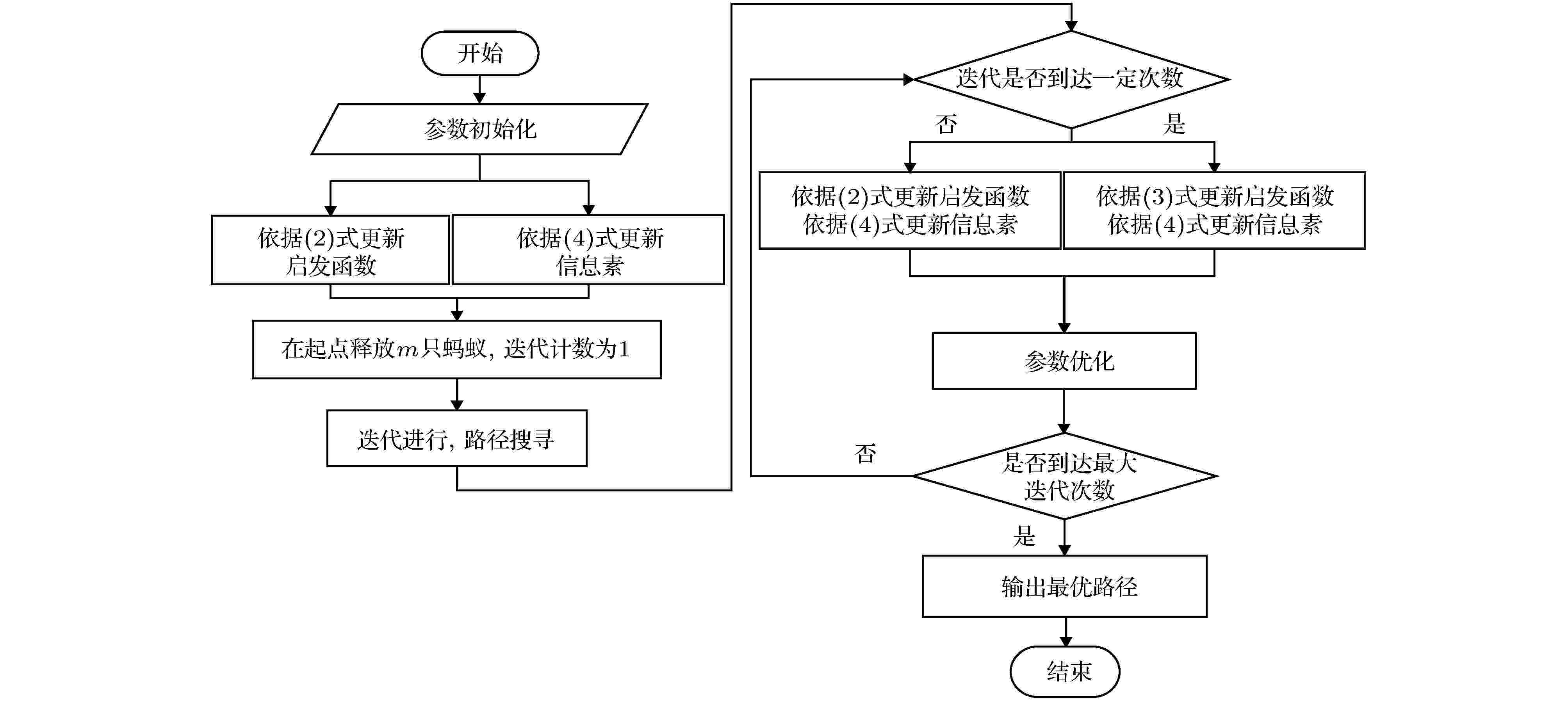
图 2 算法流程图
Figure2. Simulation flow chart.

4.仿真分析
2
4.1.仿真环境设定
-->

4.1.仿真环境设定

为验证所构建模型的性能, 以某大型邮轮的B甲板上的展厅为工程背景进行仿真, 模型的信息素浓度取14, 蚂蚁数量为30, 计算对比ACCO算法与传统算法的优劣, 邮轮B甲板构造详情如图3所示.
图 3 某邮轮B甲板构造图
Figure3. B-deck structure diagram of a cruise ship.

甲板中间位置展厅面积为20 m × 20 m的封闭空间, 其构造详情见图4(a), 仿真环境为20 × 20的栅格地图, 如图4(b)所示.
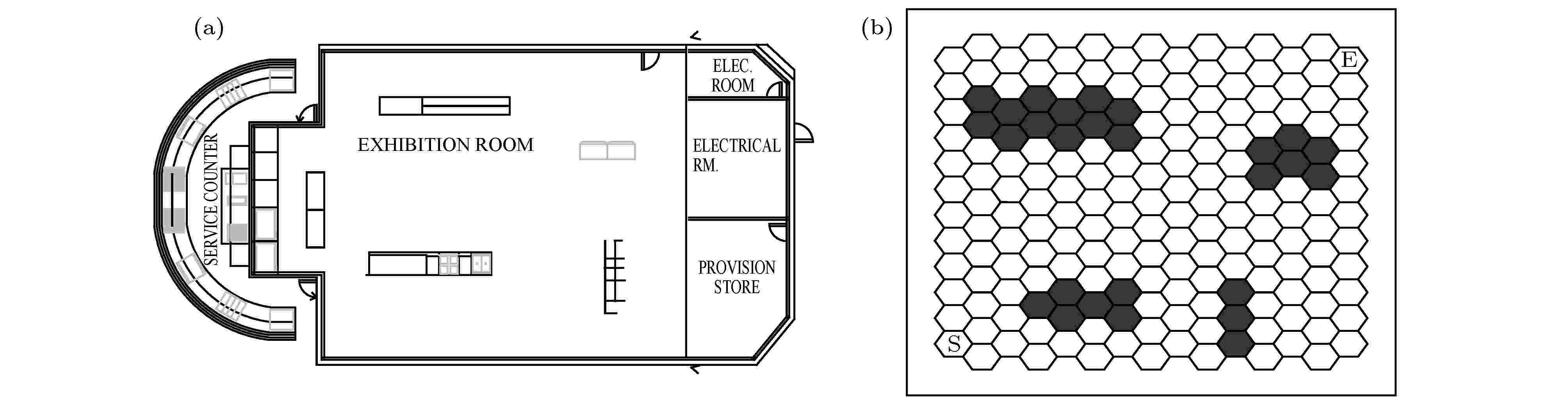图 4 展厅构造与仿真图　(a) 展厅构造图; (b) 仿真环境图
Figure4. Exhibition hall construction and simulation: (a) Exhibition hall structure; (b) simulation environment diagram.

2
4.2.仿真结果分析
-->

4.2.仿真结果分析

3
4.2.1.参数优化结果
-->
4.2.1.参数优化结果
根据专家经验法[23], 对PSO算法的其他参数值分别按照表1进行赋值.
参数名称参数取值备注
c1, c21.49445
Tmax50最大迭代次数
ω$ 0.5 \times (T_{\max} - t)/ T_{\max} + 0.2 $t 为当前迭代次数
λ10.7
λ20.1
λ30.1
λ40.1


表1PSO算法参数取值
Table1.The parameters of PSO algorithm.

根据仿真要求进行两组运算, 其求解结果如表2所列.
参数名称αβρ
参数组13.508.050.68
参数组21.358.500.36


表2　参数求解结果
Table2.Parameter solution results.

同时为观察适应度评价函数性能, 对比分析两组参数的适应度值曲线, 如图5所示.
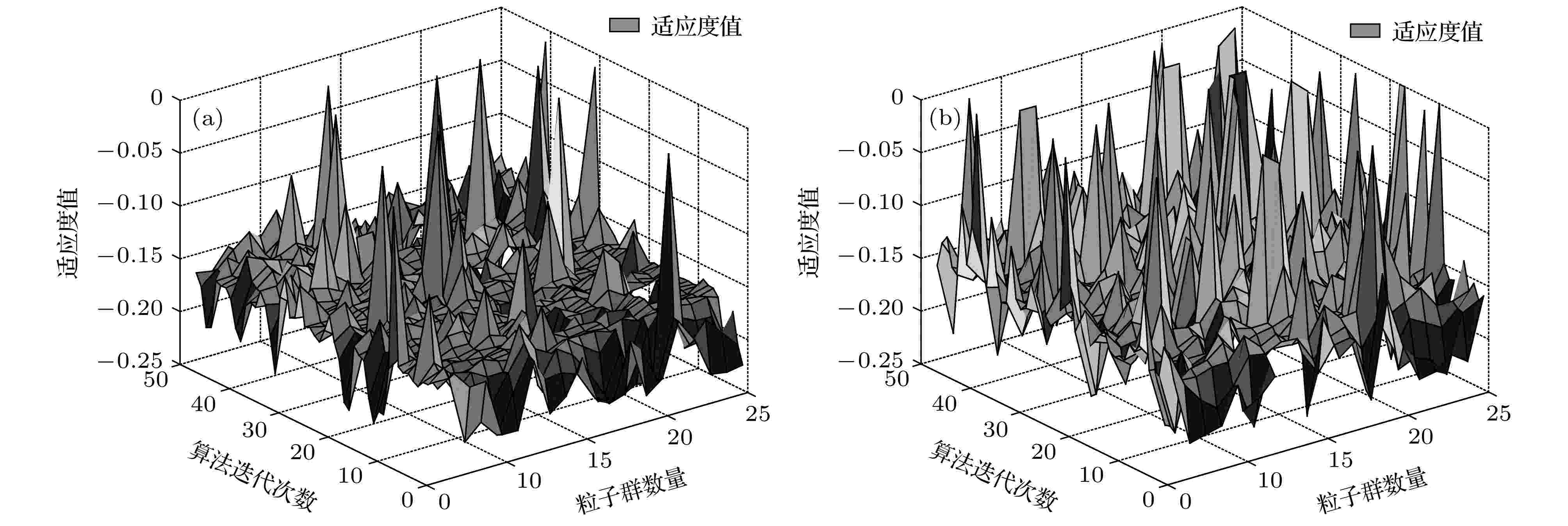图 5 粒子适应度值曲线　(a) 参数组1; (b) 参数组2
Figure5. The fitness value curves: (a) Parameter group 1; (b) parameter group 2.

3
4.2.2.路径规划结果
-->
4.2.2.路径规划结果
根据上述模型构建描述及参数设定, 分别使用传统算法与ACCO算法进行仿真, 其最终路径效果如图6所示.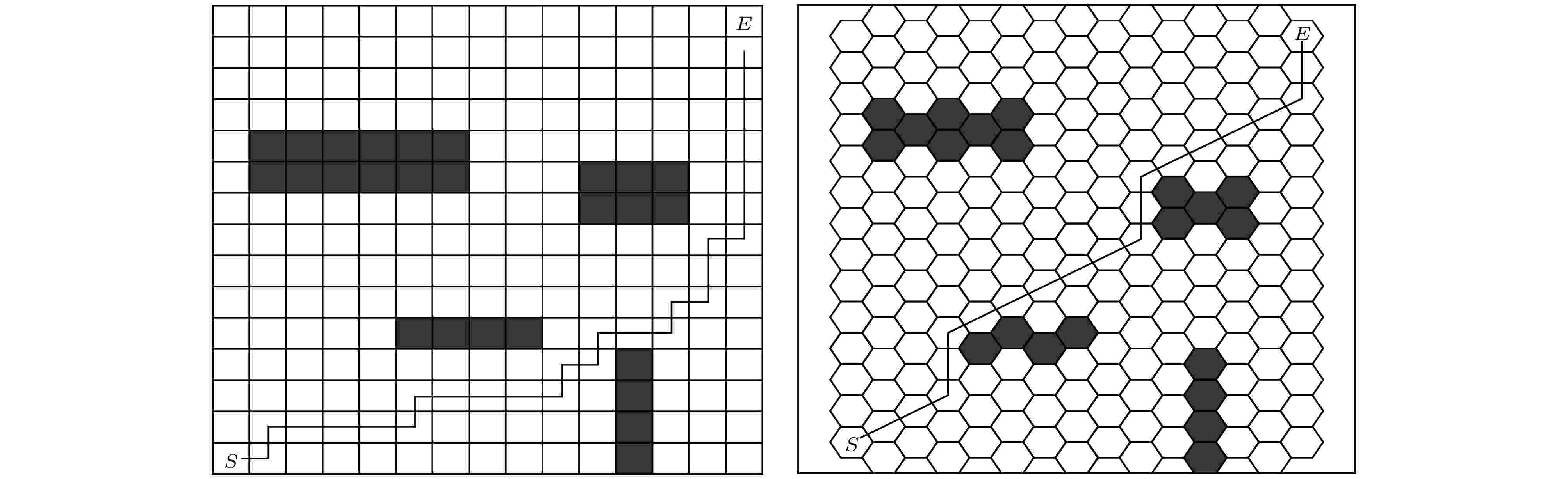
图 6 仿真效果图
Figure6. Simulation effect chart.

图6中S表示起始节点, E表示目的节点. 从图6可知, 传统模型与ACCO算法均可进行有效路径规划.
3
4.2.3.路径长度及分析
-->
4.2.3.路径长度及分析
当最大迭代次数一定时, 由于传统算法与ACCO算法在路径选择概率上的差异, 导致每次迭代所有蚂蚁搜寻的总路径长度和搜索速度也不同, 其结果如图7所示.
图 7 路径长度对比　(a) 传统算法路径统计; (b) 基于经验参数的ACCO算法路径统计; (c) 启发函数优化后的路径统计; (d) 信息素更新优化的路径统计; (e) 基于参数组1的路径统计; (f) 基于参数组2的路径统计
Figure7. Path length comparison: (a) The path statistics for traditional algorithm; (b) the path statistics for ACCO algorithm with experience; (c) the path statistics for only optimizing heuristic function; (d) the path statistics for only optimizing pheromone update methods; (e) the path statistics for parameter group 1; (f) the path statistics for parameter group 2.

由图7分析可知, 两类算法在搜索路径时, 所经过的元胞总数随着迭代次数的增加而逐渐减少; 在算法迭代次数相同的情况下, ACCO算法经过的元胞总数明显小于传统算法, 表明ACCO算法的搜索速度较快; 随着迭代的不断进行, 传统算法的搜索已基本停滞, 而ACCO算法仍在进行; 横向对比图7(a), (b), (c), (d)可知, 当只是优化启发函数或者信息素更新方式时, 优化算法所经过的元胞总数高于ACCO算法, 并且在收敛性方面也相对较弱, 但是优化算法的规划效果明显高于传统算法; 同时从图7(b)中曲线走势可明显看出, 优化后的启发函数对算法搜索能力和收敛速度的提升; 对比分析图7(b), (e), (f)可知, 基于经验值的ACCO算法的收敛速度和搜索速度明显弱于参数组1, 参数组2, 但是收敛性比参数组1强, 而参数组2在收敛速度、搜索能力以及收敛性方面均表现出明显优势. 此外, 由于存在部分断头路径问题, 传统算法在前期的搜索中波动性比较明显. 因此在算法搜索能力上, ACCO算法表现出更佳的性能.
3
4.2.4.迭代对比分析
-->
4.2.4.迭代对比分析
由于ACCO算法对部分参数进行优化, 导致其与传统算法在搜索能力上存在差距, 因此当增加迭代次数时, 解空间也表现出差异, 如图8所示.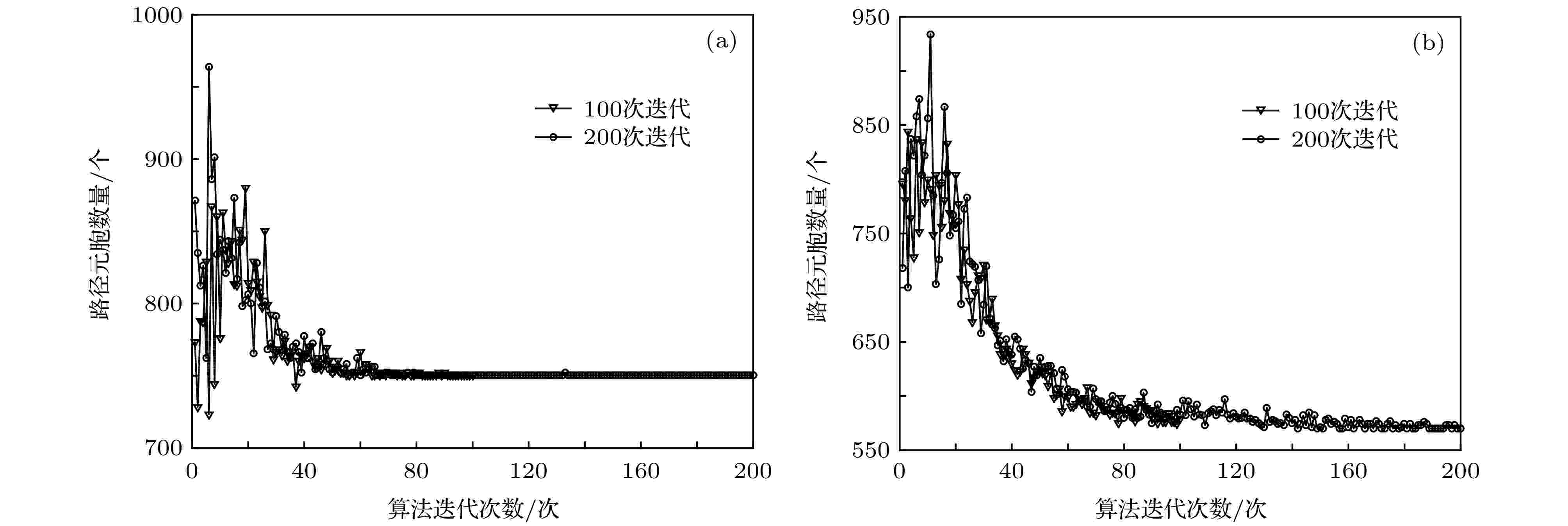
图 8 路径长度迭代对比　(a) 传统算法; (b) ACCO算法
Figure8. Iteration comparison of path length: (a) Traditional algorithm; (b) ACCO algorithm.

分析图8可知, 当迭代进行到第70次时, 传统算法的搜索路径已基本停滞, 从而解空间已经固定, 陷入局部最优解的可能性增大; 而ACCO算法在迭代进行到近200次时, 搜索路径的元胞总数依旧在减小, 解空间在不断增加, 表明仍然在搜寻全局最优解. 因此传统算法相比ACCO算法而言, 更易陷入局部最优解.
3
4.2.5.其他性能对比分析
-->
4.2.5.其他性能对比分析
在对算法的搜索能力以及收敛性等性能进行了上述分析后, 为了进一步凸显本文所提算法的优势, 现对算法其他方面性能进行分析, 主要包括:
运行时间是指在相同的运行环境中, 算法运行所消耗的平均时间;
可重复性是指对真实环境进行仿真时, 对于相同输入数据, 经过多次重复实验, 实验过程中出现完全相同的局部最优路径的概率;
收敛速率是指算法运行过程中, 相邻迭代过程中最优路径的元胞数之差的平均值; 最优性是指经过相同的迭代次数, 算法搜索到的最优路径的元胞数量, 以第100次迭代为例. 详见表3.
时间复杂度运行时间/s收敛
速率		最优性/个可重
复性
传统
算法		O(Nmaxn2m)94.157737–0.937625%
本文
算法		O(Nmaxn2m)111.091862–1.2257130%


表3算法性能对比表
Table3.Performances comparison of algorithms.

通过分析可知, ACCO算法与基本蚁群算法时间复杂度的区别主要在启发函数和信息素的更新方式上, 但是改进算法只增加了时间复杂度的常数项和低幂次项, 可以忽略, 因此时间复杂度并未改变, 但由于增加了邻域元胞的选择性从而导致运行时间有所加长. 同时改进算法在收敛速率、最优性和可重复性方面均展现出明显优势.
5.结　论
在进行路径规划算法时, 传统算法使用四边形栅格地图进行求解, 容易导致时间步长不一致、搜索速度慢、易陷入局部最优解等问题.
针对以上问题, 提出以六边形栅格替代传统四边形栅格作为背景地图栅格化方法, 从而解决四边形栅格地图的时间步长不统一的问题, 为对比算法性能奠定基础. 同时, 分别对启发函数以及信息素更新方式进行了优化设计. 最后将ACCO算法的参数作为PSO算法的位置信息进行迭代求解, 利用适应度函数值对求解性能做出评价, 从而得到ACCO的最优参数组合. 仿真实验结果表明, 提出的ACCO算法相比于传统算法, 在算法收敛速度、算法搜索速度、最优解的搜寻能力等各方面上均有明显优势, 因此可以为智能疏散系统的开发设计提供有益参考.
相关话题/优化 信息 规划 地图 空间
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 相干与路径信息
    摘要:近年来,随着对相干性量化的发展,相干与路径信息间的互补关系渐渐引起人们注意.这样的互补关系不仅在基础量子力学方面有重要的理论意义,同时也在量子信息技术中有实际应用.本文从Bures距离和明确量子态区分出发,系统地研究了二路径干涉仪中的相干与路径信息,并建立了一个全新的互补关系.与已知的类似工作 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种新型的液闪阵列成像屏空间分辨特性
    摘要:针对低强度射线成像,自主研制了一种像元为0.1mm高探测效率的液闪阵列屏.为此,基于倾斜刀口边缘响应的测量原理,建立了理论模拟方法和实验研究方法,对该液闪阵列屏开展了空间分辨性能研究.通过理论模拟,给出了液闪阵列屏在14MeV中子和1.25MeV伽马射线激发下的调制传递函数,并与像元为0.1, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 热光伏能量转换器件的热力学极限与优化性能预测
    摘要:受不可逆损失的影响,热光伏能量转换器件在高品位热能回收与利用方面受到限制.本文揭示不可逆损失来源,提供热光伏能量转换器件性能提升方案.利用半导体物理和普朗克热辐射理论,确定热光伏能量转换器件在理想条件下的最大效率.进而考虑Auger与Shockley-Reed-Hall非辐射复合和不可逆传热损 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 肖特基钙钛矿太阳电池结构设计与优化
    摘要:有机-无机杂化钙钛矿材料有高吸收系数、低廉的制作成本以及较为简单的制备工艺,在近年来表现出良好的发展前景.本文采用wx-AMPS模拟软件对平面结构钙钛矿太阳电池和肖特基钙钛矿太阳电池进行建模仿真对比,从理论上分析无载流子传输层的肖特基钙钛矿太阳电池的优势.结果显示,器件两侧电极功函数和吸收层的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 自由空间中时空复变量自减速艾里拉盖尔高斯光束的相互作用
    摘要:根据自由空间光束传输遵循的(3+1)维薛定谔方程,得到了两束时空自减速艾里复变量拉盖尔高斯(Airyelegent-Laguerre-Gaussian,AELG)光束共线传输时的解析解,并分析其共线传输时的传输特性.分析结果表明,双光束各自的模式指数、组合光束强度的权重因子、初始相位差对光束的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 光纤激光器中包层功率剥离器散热性能的优化
    摘要:光纤激光器系统中的包层功率剥离器在去除残余抽运光和高阶激光时,由于光热转换会产生大量的热能,所以将热能高效的耗散成为当前的研究热点.本文对国内外现有的五种剥离器进行了仿真研究与对比,发现用高折胶法制作剥离器时,改变填胶孔的形状,可以有效地增大热源与传热介质间的表面积-体积比,从而降低剥离器工作 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于1.06 μm波长的空间合作目标及碎片高精度激光测距试验
    摘要:常规卫星激光测距大多数采用532nm波长激光,但受激光能量和大气透过率低等瓶颈制约,在微弱目标探测如碎片激光测距、月球激光测距中使用难度较大.本文介绍了基于1.06μm波长的激光测距技术,分析了1.06μm测距技术在激光能量、大气传输、背景噪声、单光子探测等方面相对于532nm激光测距的优势, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于空间角度复用和双随机相位的多图像光学加密方法
    摘要:提出了基于空间角度复用和双随机相位的多图像光学加密新方法.加密过程中,首先将原始图像进行随机相位调制和不同距离的菲涅耳衍射;其次,将携带调制后图像的参考光与携带随机相位且具有不同立体角的参考光相干叠加,产生干涉条纹;最后,将不同方向的干涉条纹叠加形成复合加密图像.解密为加密的逆过程,将复合加密 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 优化递归变分模态分解及其在非线性信号处理中的应用
    摘要:经验模态分解一类的递归算法所产生的模态混淆和端点效应将导致所获物理信息失真,变分模态分解可改善这些问题.但因其需预设参数,对信号分解精度影响显著,为此,提出采用目标信号功率谱峰值所对应的频率以初始化变分模态分解所需中心频率,借鉴经验模态分解递归模型,基于能量截止法将变分模态分解改进为递归模式算 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 空间电子辐射环境中绝缘介质电荷沉积特性及陷阱参数研究综述
    摘要:空间电子辐射环境中绝缘介质充放电特性与介质表面电荷交换过程或内部电荷迁移过程密切相关.介质表面/内部电荷运动很大程度上取决于材料的微观特性,空间电荷与陷阱是反映绝缘介质微观特性的重要参数.本文综述了电子辐射环境中绝缘介质内部空间电荷和陷阱的形成、作用机理、测量方法、存在的问题及国内外研究现状. ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.