摘要:搭建了一种基于电动可调焦透镜(electrically tunable lens)的大范围快速光片荧光显微成像系统. 通过引入电动可调焦透镜与一维振镜以实现成像物平面和光片位置的快速移动, 再结合高速sCMOS完成快速光片荧光显微成像. 另外实验中通过改善光路与提升动态成像质量, 实现了大范围扫描并减少了伪像. 最终对成像性能进行测试, 本系统的纵向分辨率和横向分辨率分别达到约5.5 μm和约0.7 μm, 单幅图像稳定成像的速度约为275 frames/s, 成像深度可超过138 μm, 能满足对具有一定尺寸的生物样本进行实时清晰成像的需求.
关键词: 光片荧光显微成像/
电动可调焦透镜/
快速成像

English Abstract

全文HTML

--> --> -->

荧光显微成像技术通过利用荧光分子对活体生物进行标记实现特异性成像, 由于斯托克斯平移的特性, 有着较高的信噪比, 在医学生物研究等领域得到了广泛的应用^[1-3].
自1903年, Siedentopf和 Zsigmondy提出光片照明技术之后, 到2004年, Huisken等^[4]才将光片荧光显微成像技术(light-sheet fluorescence microscopy, LSFM)应用到生物细胞探测中, 然而由于传统的光片荧光显微成像技术是长时间对生物体的同一个平面成像, 不仅有相对较高的光漂白和光毒性, 而且无法捕捉到生物体的三维信息. 2009年, Huisken和Stainier^[5]首次提出了三维扫描的想法, 采用平移样品的方式实现了三维扫描. 但是, 在实验中无论是平移或者旋转样品^[6], 不仅会影响样品其本身的稳定性, 同时也会限制成像速度. 为了避免样本的振动, 近年有报道提出利用移动探测物镜的方式实现三维扫描成像^[7-9]. 这种方式虽然保证了样品的稳定性, 但是由于探测物镜的质量, 其惯性限制了这种方法的速度, 并且随着相机速度越快, 这种限制的影响将越凸显.
为了避免振动和提高成像速度, 有一种策略是通过分幅高速摄影的方式^[10]实现快速成像, 与这种方式类似的还有裁剪像素的方案^[11], 它们节省了不必要的信息获取和读取时间, 且针对于观测某一视场范围内的样本, 能够有效地提高成像速度和信噪比. 但整个系统成像速度的限制因素不仅仅源自相机. 光路的控制速度也十分重要, 为了突破移动探测物镜或移动样本等方案的速度极限, 本文研究引入电动可变焦距透镜(electrically tunable lens, ETL)置于探测物镜后方, 通过改变焦距以实现控制成像物平面的快速移动; 再采用高速科学相机sCMOS进行探测; 加以配合LABVIEW编程完成自动化控制, 使振镜、ETL和相机达到实时同步且相互协调, 有效减少了快速成像中产生的伪像. 另外, 为了突破更大的成像深度, 还引入新的透镜改善光路, 并最终实现了大扫描范围的稳定快速光片显微成像.

2

-->

2.1.光片产生的理论计算

光片的产生, 是由于通过柱透镜的光束, 随着光束的传播, 其光束一个维度维持不变, 但在另一个与之垂直的维度上会逐渐被聚焦压缩, 从而能够形成非常薄的片状光束. 具体如图1所示
图 1 柱透镜产生光片示意图
Figure1. Schematic diagram of the cylindrical lens.

光片实际上是在传播光路上形成一薄的片状光束, 且其光束强度符合高斯分布, 在横向电场分布上也满足高斯函数分布, 其电场复振幅为

$\begin{split}E(r,x) =\;& {E_0}\frac{{{\omega _o}}}{{\omega (x)}}\exp \left[ {\frac{{ - {r^2}}}{{{\omega ^2}(x)}}} \right]\\ & \times\exp \left[ { - {\rm{i}}kx - {\rm{i}}k\frac{{{r^2}}}{{2R(x)}} + {\rm{i}}\varsigma (x)} \right],\end{split}$

其中r为场内任一点距离光轴中心的径向距离, x为光轴上的位置坐标, ${\omega _o}$为x = 0时的光斑半径, i为虚数单位, k为波数, R(x)是在x点处波阵面的曲率半径, $\varsigma \left( x \right)$是与x有关的相位因子. $\omega (x)$为在x点处的光斑半径. 因此在x处的光束半径为^[12]

$\omega (x) = {\omega _o}\sqrt {1 + {{\left( {\frac{{\lambda x}}{{{\text{π}}{\omega _o}}}} \right)}^2}} , $

其中$\lambda $为激发光的波长, 此时可以认为是光片最薄位置处的厚度, 即高斯光束的束腰半径, 当高斯光束的光斑半径为束腰处半径的$\sqrt 2 $倍时, 该两处之间的距离为瑞利长度${x_{\rm{R}}}$^[13]

${x_{\rm{R}}} = \frac{{{\text{π}}\omega _o^2}}{\lambda },$

其中${\omega _o}$为束腰半径, ${x_{\rm{R}}}$的大小决定了成像视场的大小. 因此在实验中可根据实际需求在光片厚度和瑞利长度之间做出折中选择.
2 -->

2.2.整体成像光路分析

图2为本实验设计的快速光片显微成像系统光路原理图. 其整体上可分为照明和探测两个部分. 其中照明部分的光束传播过程与功能可以描述为由激光器发出的高斯光束经扩束后再通过柱透镜聚焦产生片状光, 在柱透镜的焦点处放置一维扫描透镜, 控制片状光出射的不同角度, 同时在后方放置透镜3和透镜4组成4f系统, 将片状光中继至激发物镜, 再由物镜压缩成光片照明到样品上, 进而实现对样品不同位置照明的控制.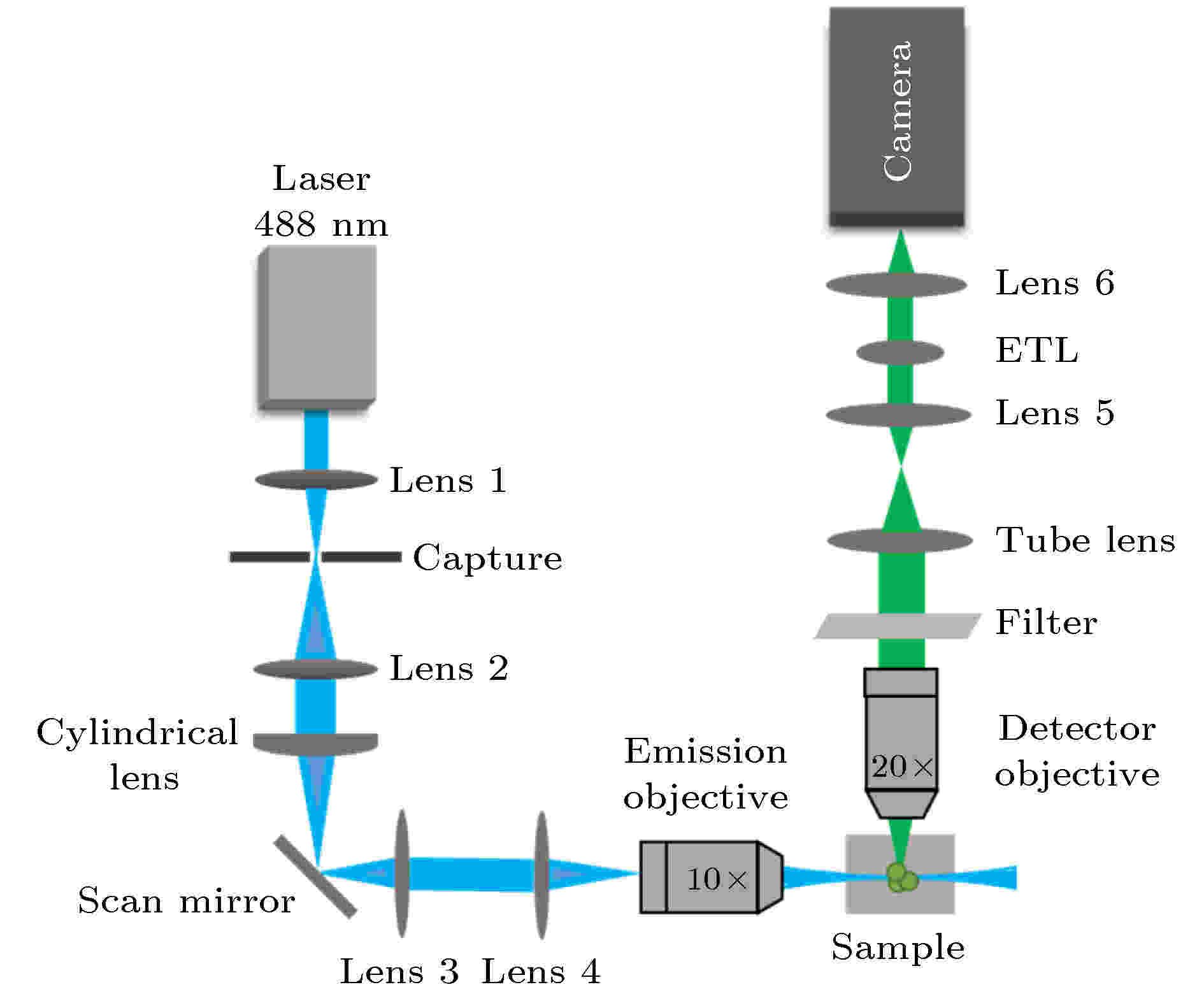
图 2 快速光片显微成像系统光路图
Figure2. Schematic diagram of rapid light-sheet fluorescence microscopy imaging system.

激发样品产生的荧光由与激发光路垂直的探测部分接收, 激发的荧光经窄带滤波片滤除非荧光波段后, 通过控制ETL的焦距, 再与镜筒透镜、透镜5和透镜6共同作用, 将荧光光束聚焦至sCMOS的阵列面, 从而实现完整的成像过程.
2 -->

2.3.电动可调焦透镜分析

本文选用的是Optotune公司型号为EL-10-30-Ci的液态透镜, 其最大的特点是避免了成像过程中机械的振动, 也因此能够获得更高的响应速度, 图3由Optotune公司提供, 是关于该ETL在全量程内变化的响应时间曲线.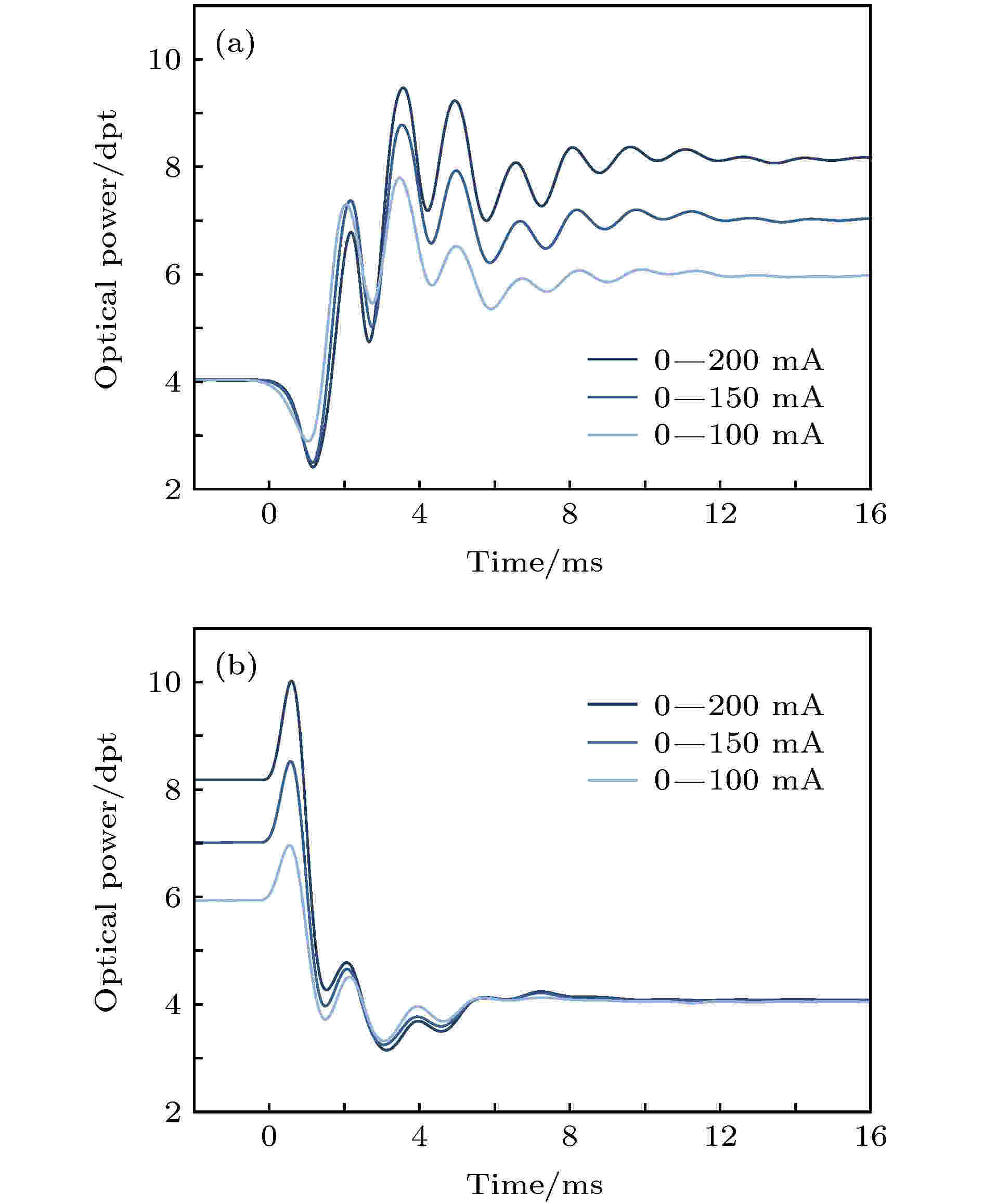
图 3 EL-10-30-C对电流阶跃的典型光学响应
Figure3. Typical optical response of the EL-10-30-Ci to a current step.

对于大阶跃信号的响应, 透镜变化焦距并达到稳定时需要约4—8 ms的响应时间, 在快速成像过程中这段时间是不可忽略的, 处理不当会导致伪像. 而实验中我们研究测试, 当以小阶跃信号驱动时其响应时间仅约2 ms, 这一发现有助于提高系统整体的成像速度. 再借助LABVIEW并行运算的优势, 保证稳定成像的前提下, 能够将ETL与扫描振镜的总响应时间压缩在约500 Hz的速度.
2 -->

2.4.大扫描范围成像分析

实验中在对一些一定尺寸的活体生物, 如幼年斑马鱼心脏(100—150 μm)等, 进行三维成像时^[14,15], 往往需要较大的纵向成像深度, 同时要求满足快速的实时成像, 因此选取了型号为EL-10-30-Ci的电动可调焦透镜^[16]. 在屈光度较小时, 其能够保持较好的波前质量. 为了减少像差的产生, ETL自身可调节的屈光度不宜过大, 但这又将限制三维成像的纵向深度, 难以满足较大体积生物的成像.
通过实验研究发现, 当ETL自身的屈光范围不变时, 光束进入ETL的孔径角越小, 其在光轴上可调焦的范围l越大, 反之, 则越小. 这为扩大扫描范围提供了思路. 原理如图4所示
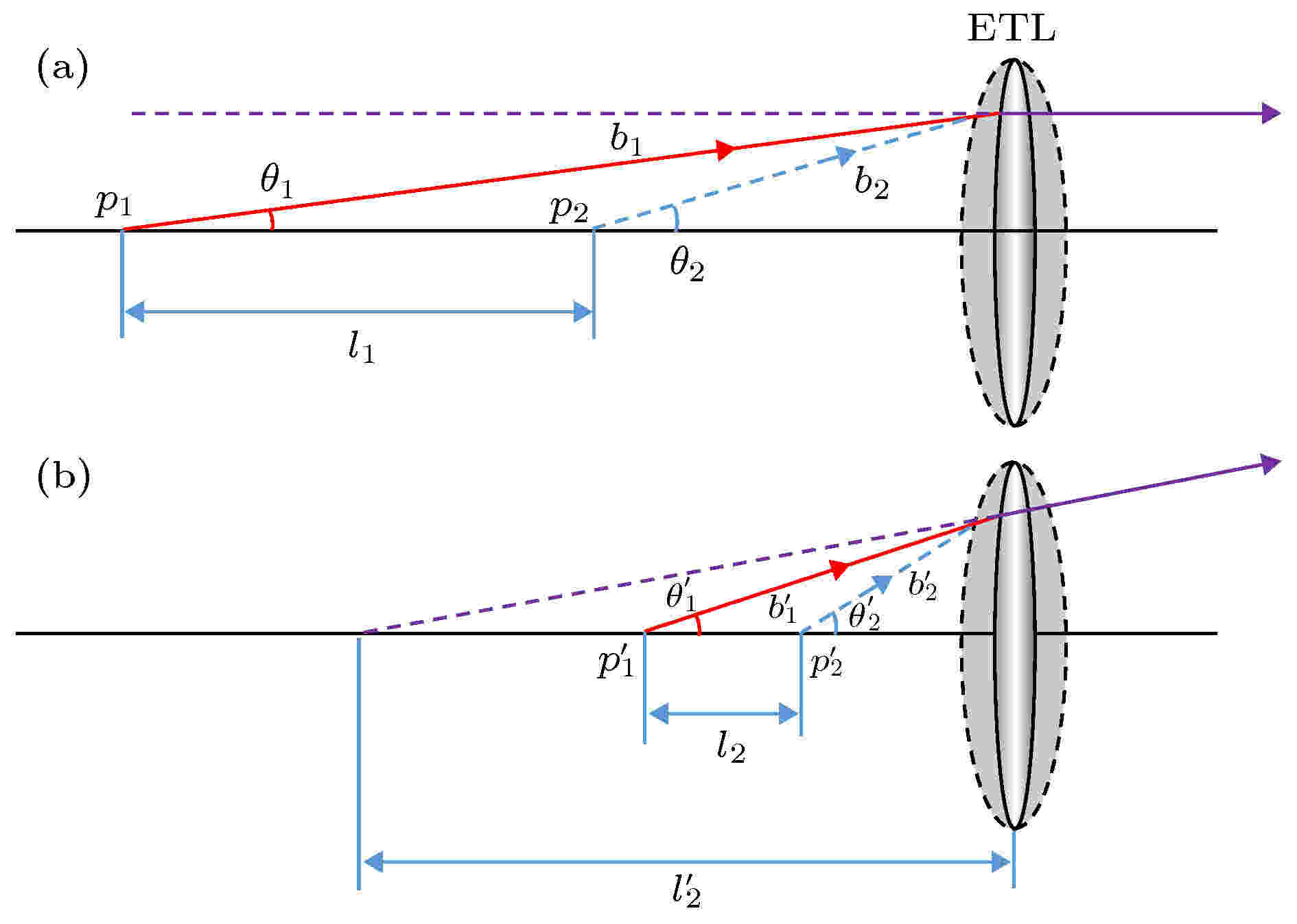图 4 光束以不同孔径角透过ETL　(a) 以小孔径角入射ETL; (b) 以大孔径角入射ETL
Figure4. The beam passing through the ETL at different aperture angles: (a) The beam passing through the ETL at small aperture angles; (b) the beam passing through the ETL at big aperture angles.

图4中红色实线光束代表当ETL处于最大焦距f₁时的光束传播路径, 蓝色虚线光束代表ETL处于最小焦距f₂时的光束传播路径, 此时光束入射的孔径角θ、出射光束的像点 l' 有如下关系:

$ \left\{ \begin{aligned} & {\theta _1} < \theta _1',\quad {\theta _2} < \theta _2', ~~~ {f_1} = f_1' , \quad {{f_2} = f_2',}\\ & l_1' = - \infty < l_2',~~~ {f_1} > {f_2}. \end{aligned} \right. $

利用高斯公式追迹不同光束与光轴相交的位置即物点$ l_{\rm p} $, 可得

$\left\{ \begin{aligned}& {l_1} = {l_{{\rm{p}}2}} - {l_{{\rm{p}}1}},~~ {l_2} = {l_{\rm p_2'}} - {l_{\rm p_1'}},\\& \frac{1}{{l'}} - \frac{1}{{{l_{\rm{p}}}}} = \frac{1}{{f'}},~~ {l_{\rm{p}}} = \frac{{f' \times l'}}{{f' - l'}},\end{aligned} \right. \Rightarrow {l_1} > {l_2},$

联立(4)式和(5)式, 能够得出${l_2} < {l_1}$, 即入射光束孔径角越小则可调焦范围越大. 同时根据光线追迹进一步的数值分析发现, 扫描范围与探测光路上距离物方的第奇数个透镜焦距的平方成正比, 与距离物方的第偶数个透镜的焦距平方成反比.
在本实验光路中, 为了实现更小的入射孔径角, 一种比较直接的方案是可以改变镜筒透镜的焦距, 但除了扫描范围, 同时还需要考虑ETL口径对光束的遮拦现象. 参考图5(a).
图 5 光束穿过ETL孔径　(a) ETL孔径阻挡光束; (b) ETL孔径未阻挡光束
Figure5. The beam passing through the ETL: (a) The beam is blocked by the aperture of ETL; (b) the beam is unblocked by the aperture of ETL.

通过实验研究分析, 为了避免图5(a)中的孔径遮拦, 实现图5(b)的结果, 我们选择引入透镜Lens 5压缩光束, 将其置于ETL与镜筒透镜之间并与镜筒透镜共轭(图2), 该透镜的焦距${f_{{\rm{L1}}}}$应满足如下关系式^[17]:

${f_{\rm{r}}} \leqslant {f_{{\rm{TL}}}} \cdot \frac{{{d_{{\rm{ETL}}}}}}{{{d_{{\rm{BFP}}}}}},$

其中f_r为透镜Lens 5的焦距, d_ETL为ETL的孔径大小, d_BFP为显微物镜后焦平面的孔径大小, 一般约等于后孔径尺寸. 在满足(6)式的情况下, 实验中若透镜焦距越小, 则可实现越大的扫描范围. 但为了保证较好的波前质量, f_r依然不能过小. 实验中根据扫描振镜的转动角度$\Delta \theta $, 结合激发光路中Lens 4的焦距${f_{{\rm{L4}}}}$及激发物镜的放大倍率${M_{{\rm{eo}}}}$, 能够找出振镜的转动角度与受振镜控制的光片位移量之间存在的关系, 进而推算出光片在样品池中的位移量$\Delta \delta $, 由图2有

$\Delta \delta = \tan \left( {\frac{{\Delta \theta }}{2}} \right) \times \frac{{{f_{{\rm{L4}}}}}}{{{M_{{\rm{eo}}}}}}.$

以(7)式为基础, 根据Thorlabs公司提供的手册可得振镜驱动电压与转角的关系, 再结合测出的振镜驱动电压即能得到转角$\Delta \theta $, 进而获得光片位移量$\Delta \delta $, 即纵向成像深度. 经测量结果显示, 当Lens 5焦距为75 mm时实验测量出清晰成像的纵向深度可达约138 μm, 这超过了最近报道^[15]在采取了ETL的光片显微成像中实现的20 μm成像深度. 综上, 设法缩小ETL的入射光束孔径角能够有效地扩大纵向成像深度, 本文基于这一思路提出的方案推动了光片显微成像在较大尺寸样本中探测的研究进展.

2

-->

3.1.系统的成像分辨率

3 -->

3.1.1.系统横向分辨率测量

系统的横向分辨率包括由瑞利判据定义的光学分辨率与探测器像素尺寸等因素决定的仪器分辨率. 在本实验中, 光学分辨率起到了主要的限制作用. 通过瑞利准则公式$\sigma = \dfrac{{0.61{\lambda _{\rm{f}}}}}{{NA}}$, 其中NA为探测物镜数值孔径, ${\lambda _{\rm{f}}}$为样品产生的荧光波长. 可得系统理论上能分辨的最小横向尺寸约为652 nm.
再由瑞利判据定义, 在成像光学系统中, 分辨本领是衡量分开相邻两个“物点”的像的能力. 为了减小物体尺寸对实验结果的影响, 我们选取尺寸小于系统理论横向分辨率, 直径约为100 nm的荧光微球作为“物点”. 通过测量其像斑的能量分辨率进而获得系统实际的横向分辨率.
由于荧光强度与激发光强成正比, 再根据光片强度又近似为高斯分布的特性, 可知当荧光微球的光强值最大时, 荧光微球最接近光片的中心. 基于此原理, 首先对图像做去卷积处理以减少背景噪声, 再采用灰度特征搜索算法找出图像中灰度值最大, 即最靠近光片中心的5个荧光微球, 在图6左侧图像中框选并分离出来, 分别如图6(b)—图6(f)所示. 图6(g)—图6(k)显示的分别为经过图6(b)—图6(f)中不同荧光微球中心的水平线的灰度剖面线, 横坐标为宽度/μm, 纵坐标为灰度值强度. 为了减少偶然误差, 将图6(b)—图6(f)的5个灰度剖面线的数据进行归一化后再做平均化处理, 从而得到图6(l)显示的曲线分布. 根据光束的高斯分布特性, 再对图6(l)的数据求高斯拟合曲线, 结果如图7所示
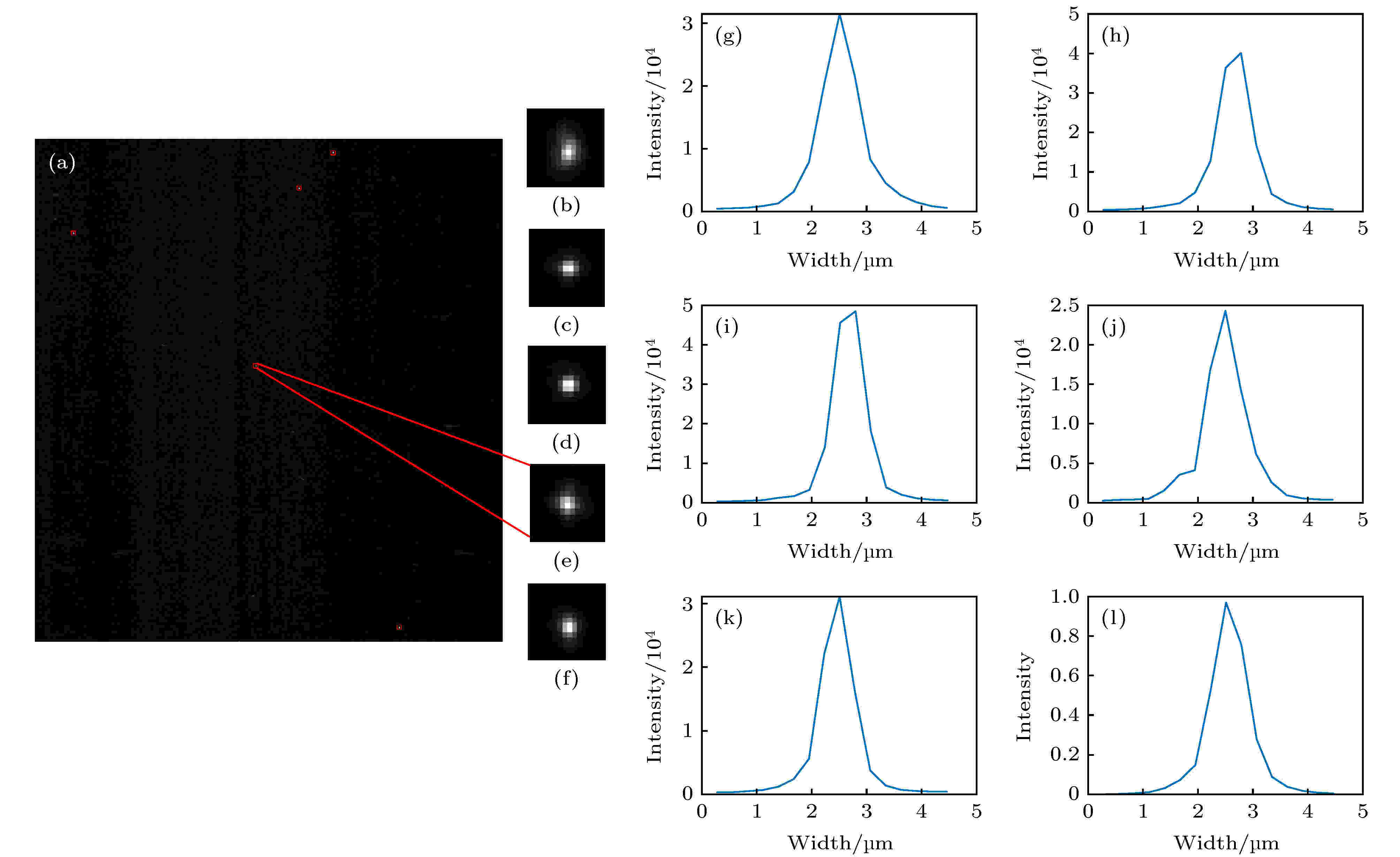图 6 100 nm荧光微球的分析　(a) 100 nm荧光微球的拍摄图像; (b)?(f) 5个光强最大的荧光小球; (g)?(k) 分别是(b)?(f)中荧光小球的灰度剖面线; (l) (g)?(k)的归一化并平均化之后的曲线
Figure6. Analysis of 100 nm fluorescent spheres: (a) Image of 100 nm fluorescent spheres; (b)?(f) five fluorescent spheres with the largest intensity; (g)?(k) intensity profile of a horizontal line passing through the center of fluorescent sphere in (b)?(f); (l) the normalized and averaged curves of (g)?(k).

图 7 高斯拟合曲线
Figure7. Gaussian fitting curve.

此时图7中拟合曲线的半高全宽值 (full width at half maximum, FWHM)即为上述提及的能量分辨率, 而系统在图像中能分辨的最小尺寸可由能量分辨率近似表征^[17-20]. 因此, 可得系统的横向分辨率${R_{{\rm{lateral}}}}$约为0.73 μm. 导致其与理论计算结果不同的因素有多方面, 主要由实验中视0.1 μm荧光微球为“物点”引入的误差与探测器像元尺寸影响的测量精度共同决定.
3 -->

3.1.2.系统纵向分辨率测量

系统的纵向分辨率主要由光片厚度和振镜控制光片在纵向的最小位移量决定. 在本实验中, 振镜的性能与光路的设计保证了光片的最小位移量小于光片厚度. 因此可将光片的厚度视为限制系统的纵向分辨率的主要因素.
实验中选取反射镜替代样品置于样品池中(图8(a)), 并使镜面与激发光路的光轴和探测光路的光轴均成45°, 实现光片轮廓在CMOS成像面上的垂直投影, 光路示意如图8(b)所示. 接着再利用与3.1.1节中类似的方法, 首先画出均匀分布的5条经过图8(b)中竖直光片的水平线的灰度剖面线, 然后将这些数据进行归一化和平均化处理以减少偶然误差, 结果如图8(c)所示, 最终通过计算平均后的曲线的FWHM值, 完成光片实际厚度的近似测量^[21].
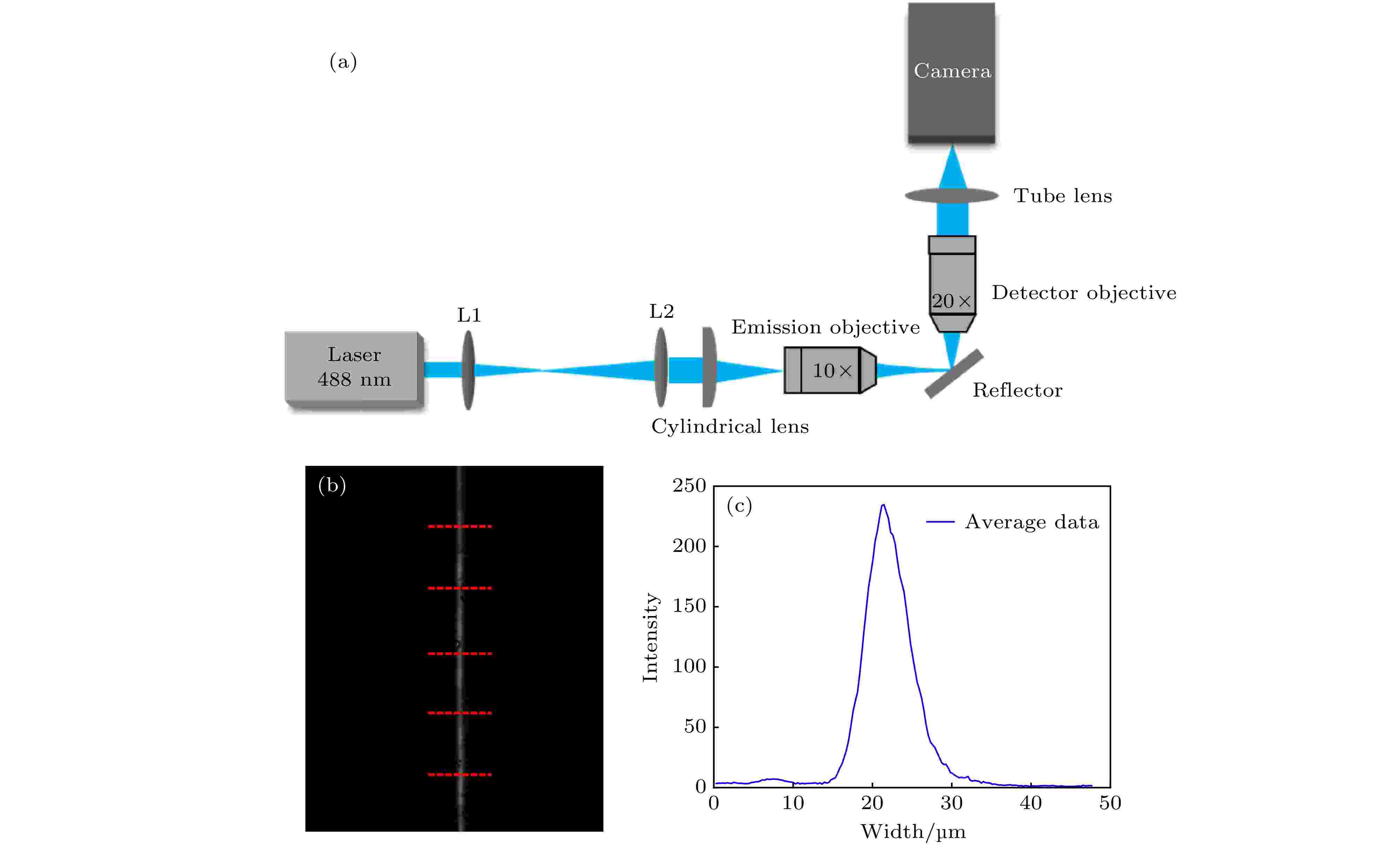图 8 光片不同横截面的荧光光强分布　(a) 记录光片轮廓的光路; (b) 光片轮廓图; (c) 灰度剖面线平均化后的曲线
Figure8. Fluorescence intensity distribution at different profile of the light sheet: (a) Optical path for recording light sheet; (b) profile of light sheet; (c) average curves of intensity profile of light sheet.

图8(c)中的纵坐标为灰度值强度, 横坐标表示宽度, 单位为μm. 根据实验结果描绘的曲线, 可计算出曲线的FWHM值约为5.5 μm, 这表示光片的厚度约为5.5 μm, 即纵向分辨率约为5.5 μm.
2 -->

3.2.动态成像特性分析与优化

动态成像特性主要包括成像过程中离焦、图像的偏移和放大率的变化等现象.
3 -->

3.2.1.图像离焦的校准

为了确保清晰成像, 在动态成像过程中, 需使光片与成像物平面保持实时重合, 否则会因离焦导致图像模糊. 为了提高信号光强度且有利于测量, 选取光强最强的光片中心作为理想的成像物平面, 当成像物平面与光片中心重合时视为成像物平面与光片达到了最佳重合度. 基于此, 采取固定物平面, 以最小步进移动光片, 同时将静止的荧光微球作为探测目标的方式, 寻找最佳重合面. 根据荧光强度与激发光强成正比的特性, 将当荧光微球的光强最强且光斑尺寸最小时的图像作为离焦程度最小、最接近光片中心的最佳重合度图像. 如图9所示.
图 9 同一个荧光小球在光片不同位置时的图像
Figure9. Image of the same fluorescent sphere at different positions of the light sheet.

对图9中5幅图像的荧光小球进行灰度测量, 结果显示图9(c)中荧光小球的灰度值最大, 表征此时成像物平面与光片重合度最佳, 即此时的图像清晰度最高.
3 -->

3.2.2.图像偏移及放大率变化的校准

在调校ETL以保证其在变焦过程中图像的稳定^[22]之前, 须检测出ETL在不同驱动电流值下的图像偏移及放大率的变化量, 并将其作为光路调校的反馈信息. 在ETL电流区间的最小值、半峰值以及峰值处分别对周期为200 μm的光栅网格进行成像, 结果如图10所示.
图 10 在ETL的范围内对200 μm网格成像　(a) I_ETL = 0 mA时的图像; (b) I_ETL = 146 mA时的图像; (c) I_ETL = 292 mA时的图像
Figure10. Images of a 200 μm grid over the ETL scan range: (a) Image when I_ETL = 0 mA; (b) image when I_ETL = 146 mA; (c) image when I_ETL = 292 mA.

实验中ETL设定的安全驱动电流区间为0—292 mA, 当驱动电流分别为0, 146和292 mA时, 此时对应的相对纵向深度分别为0, 69 和138 μm. 在不同位置处的周期性光栅图像之间可能会存在偏移或放大率的变化. 为了定量检验图像偏移及放大率的变化量. 采用霍夫变换直线检测算法找出200 μm光栅的黑色边沿并量化检测点的具体坐标, 在图中以红色点标记. 然后通过计算不同图像的检测点之间的距离变化量作为图像放大率的变化量$\Delta M$, 具体为

$\left\{ \begin{aligned}& \Delta {M_{\rm{h}}}=\sqrt {{{\left( {{x_{i1}} - {x_{i2}}} \right)}^2}} - \sqrt {{{\left( {{x_{j1}} - {x_{j2}}} \right)}^2}} ,\\& \Delta {M_{\rm{v}}}=\sqrt {{{\left( {{y_{i1}} - {y_{i2}}} \right)}^2}} - \sqrt {{{\left( {{y_{j1}} - {y_{j2}}} \right)}^2}} ,\\& \Delta M = \frac{{\sqrt {\Delta M_{\rm{v}}^2 + \Delta M_{\rm{h}}^{\rm{2}}} }}{{\min ({S_i},{S_j})}},\end{aligned} \right.$

式中$({x_{in}}, {y_{jm}})$为第i张图像中选取的第n个检测点的横坐标和第j张图像中选取的第m个检测点的纵坐标, 而$\Delta {M_{\rm{h}}}$与$\Delta {M_{\rm{v}}}$分别表示沿水平方向和垂直方向的放大率变化量, ${S_i}$则表示第i张图像中所选两个检测点之间的直线距离.
对于图像偏移量$\Delta D$的具体值, 通过测量不同图像中选定检测点坐标的自身位移量获得, 并将其位移量作为反馈信息, 微调光路最终达到校准的效果. 具体计算为

$\Delta D = \frac{{\sqrt {{{\left( {{x_{i1}} - {x_{j1}}} \right)}^2} + {{\left( {{y_{i1}} - {y_{j1}}} \right)}^2}} + \sqrt {{{\left( {{x_{i2}} - {x_{j2}}} \right)}^2} + {{\left( {{y_{i2}} - {y_{j2}}} \right)}^2}} }}{{2 \times \min ({S_i},{S_j})}}.$

根据(8)式和(9)式, 计算得出系统在整个扫描范围内的放大率变化量约为3.69%, 图像偏移量约为4.1%. 基本实现在ETL的全范围扫描过程中, 保证了较小的图像放大率变化和图像偏移.
3 -->

3.2.3.图像伪影分析与校准

在已有的一些报道实验结果中尚存在伪影图像^[17], 主要体现在荧光小球像斑的拉长. 我们对此进行研究, 建立了伪像评价方案, 首先, 通过提取动态扫描成像过程中连续时间拍摄的图像, 再采取3.1.1节类似方法, 显示出扫描过程中同一个荧光小球的灰度剖面线变化情况, 进而求取其半高全宽值并将数据进行对比. 相较于伪影较少的图, 发现伪影明显的图中其灰度剖面线的半高全宽值明显更大, 且光强不符合高斯分布. 在扫描成像过程中^[11,15,17], 若忽略了ETL和扫描振镜到达稳态所需要的时间, ETL与振镜在相机曝光期间进行的动态变化可能会导致伪像的产生. 因此为了避免伪像, 须保证系统在每次成像时均处于稳定状态, 这需要在编程中考虑到ETL、振镜的响应时间、相机的曝光时间以及它们时序的控制. 为了验证本成像系统在消除伪像方面的性能, 在实验中选取三幅连续时间的同一荧光小球图像, 并求取其半高全宽值, 结果如图11所示.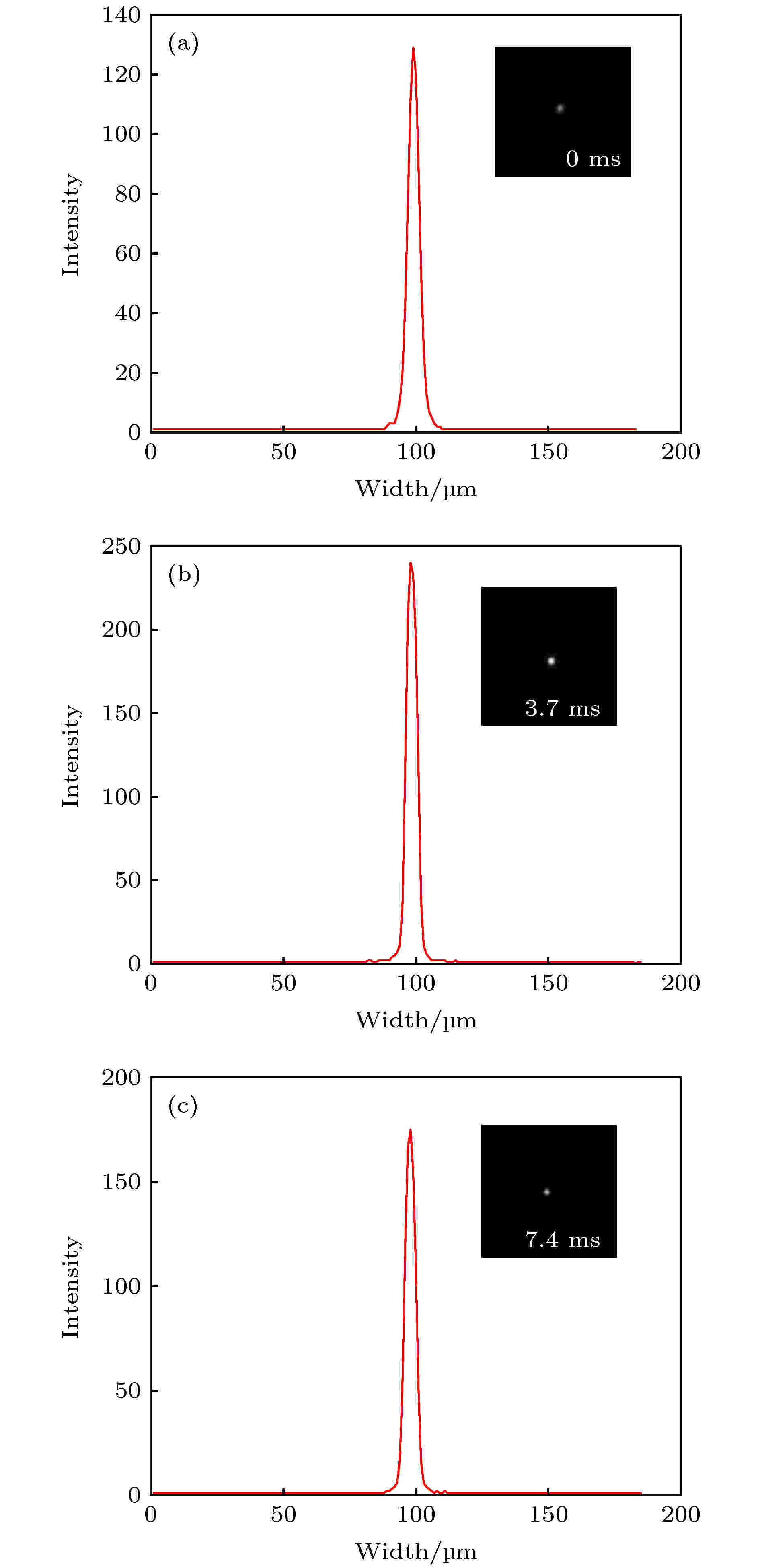
图 11 本实验结果的伪像分析　(a) 0 ms时经过荧光小球中心的灰度剖面线; (b) 3.7 ms时经过荧光小球中心的灰度剖面线; (c) 7.4 ms时经过荧光小球中心的灰度剖面线
Figure11. The artifacts analysis of the experimental results: (a) Intensity profile of a line passing through the center of fluorescent sphere captured at 0 ms; (b) intensity profile of a line passing through the center of fluorescent sphere captured at 3.7 ms; (c) intensity profile of a line passing through the center of fluorescent sphere captured at 7.4 ms.

图11(a)—图11(c)分别为同一荧光小球在三维扫描过程中, 连续时间的三幅成像结果, 画出其经过荧光小球中心的灰度剖面图, 通过计算其半高全宽值并相互对比, 可以发现虽然曲线的强度峰值变化, 但其半高全宽值变化率约为8%, 有效地控制了伪像的产生. 由此可以看出, 在动态成像中保证曝光期间系统的稳定, 能够有效减少在快速光片显微成像中产生的伪像, 实现清晰的动态成像.
2 -->

3.3.系统的成像速度

影响系统成像速度主要因素包括: ETL响应时间、振镜响应时间、相机曝光时间、相机的图像读出时间、图像存储时间、程序本身的运行时间. 实验中将对各个因素进行分析与优化, 以实现更快的成像速度.
首先采用滨松公司型号为C11440的高速sCMOS, 通过缩短相机曝光时间, 选择感兴趣的区域缩小成像范围, 达到减少图像读出时间与存储时间的目的, 实现以超过500帧/s速度拍摄512 × 512像素的图像. 其次结合Labview的并行运算优势, 在系统稳定成像的前提下, 将ETL与振镜的小阶跃信号总响应时间压缩至约500 Hz. 最终实现系统中各个器件之间的相互协调, 完成稳定的快速清晰成像(补充材料video 1). 对于成像速度的检测, 采取在程序循环周期初始位置植入计时功能的方式, 记录系统在ETL、振镜与相机共同协调工作以及程序运行一个周期耗费的总时长, 从而得到整个系统在稳定成像时的成像速度约为275帧/s.

搭建了一套基于电动可调焦透镜的大范围快速光片显微成像系统, 通过引入电动可调焦透镜、一维电控反射振镜系统, 结合Labview与高速sCMOS实现快速光片显微成像. 另外通过实验分析与研究, 有效减少了快速成像中产生的伪像. 同时引入新的透镜改善光路, 实现了大范围的扫描成像. 最终达到了单幅图像稳定成像的速度约275帧/s, 纵向分辨率和横向分辨率分别为5.5和0.73 μm, 扫描范围约达138 μm的成像性能, 这对于推动较大尺寸活体生物的实时清晰探测具有重要意义.