摘要: 尽管耦合模理论在过去几十年内已经被广泛研究, 但它的理论来源还是困扰着广大研究者. 在这里, 基于久期微扰理论, 将经典弹簧振子模型退化为耦合模理论, 并将该理论用于解释音叉耦合的实验现象. 研究表明这种方法将耦合模理论中每一项的系数都与经典力学中的相关物理量建立关联, 且理论和实验结果符合得很好. 该研究为耦合模理论中每一项的来源提供了一种较严谨的推导方法, 在线性耦合体系的理论研究方面有一定的指导意义.
关键词: 线性耦合体系 /
弹簧振子模型 /
耦合模理论 /
久期微扰理论 English Abstract The spring oscillator model degenerated into the coupled-mode theory by using secular perturbation theory Zhu Cun-Yuan 1 ,Li Chao-Gang 1 ,Fang Quan 1 ,Wang Mao-Sheng 1 ,Peng Xue-Cheng 1 ,Huang Wan-Xia 1,2 1.School of Physics and Electronic Information, Anhui Normal University, Wuhu 241002, China Received Date: 05 October 2019Accepted Date: 14 January 2020Published Online: 05 April 2020Abstract: In the past few decades, although coupled-mode theory (CMT) has been extensively studied in quantum system, atomic system, plasmon system, circuit system, and so on, the theoretical origin is still plaguing many researchers. In the book of waves and fields in optoelectronics, the second-order differential equations of the simplest LC simple harmonic vibration circuit was turned into the first-order differential equation using the method of variable substitution by Haus. However, there is not loss in the simplest LC simple harmonic vibration circuit, loss term is introduced by qualitative analysis. Although this method of dealing with problems has no problems from a physical point of view, it is not rigorous enough from a mathematical point of view. In this paper, based on the secular perturbation theory, the well-known spring oscillator model is degenerated into two-mode CMT. Starting from the second-order differential equations of the spring oscillator model, the secular perturbation theory is used to obtain first order differential equations of two-mode CMT. The results show the relationships between each term’s coefficients in two-mode CMT and the physical quantities in Classical Mechanics are established by using the secular perturbation theory. Through solving two-mode coupled-mode equations, the energy transfer efficiency has been obtained. To verify the correctness of two-mode CMT, we design a coupled tuning fork mechanical vibration system, which consists of two experimental instruments to provide driving force and receive signals, two tuning forks and springs. The amplitude spectra are measured by an experimental instrument of forced vibration and resonance (HZDH4615), which provides a periodic driving signal for the tuning fork. To clarify the mechanism of the spectra, the numerical fitting has been performed by mathematica software based on the energy transfer efficiency. Theoretically, the obtained fitting parameters can also evaluate some important attributes of the system. The theoretical results are in close correspondence with the experiment. That is to say, two-mode CMT is suitable for classical vibration system.This study provides a more rigorous derivation for each term’s origin in two-mode CMT, and has guiding significance in the theoretical research of linear coupled vibration system.Keywords: linear coupled system /spring oscillator model /coupled-mode theory /secular perturbation theory 全文HTML --> --> --> 1.引 言 振动是物质最基本的运动形式, 包括声波、机械波、电磁波等. 最初从乐器、时钟单摆等研究振动的基本规律, 工业革命时蒸汽机、内燃机的研究进一步推动了振动的发展, 到如今应用到信号中的时频傅里叶变换, 研究原子、分子团振动拉曼散射光谱等等, 使对振动的研究达到了前所未有的高度. 不过对线性振动和非线性振动的研究直到19世纪后期才引起重视. 其中被用来分析简谐振动的弹簧振子模型是物理学中的经典模型[1 ] . 因为拥有广泛的适用性, 被应用在各个领域, 特别是振子耦合[2 ,3 ] 在微纳光子学领域中产生了各种各样的奇异现象, 例如振动模式的耦合产生的透明现象[4 ] 、Fano共振[5 ] 和Rabi振荡[6 ] 等, 这些现象都可以用弹簧振子模型来解释.[7 ,8 ] 来解释两个或多个模式之间相互作用. 从19世纪50年代被人提出, 最初该理论仅用来解释微波间的相互作用, 之后在众多****的研究下, 该理论被扩展到了许多领域, 尤其在光学和电学中大放异彩. 早在19世纪70年代, Marcuse[9 ] 和Snyder[10 ] 就把耦合模理论扩展到了光学波导领域, 并在理论上和模拟上都比先前的耦合公式具有更高的精确度[11 ] . 该理论已经成功地应用到光波导和光纤器件的模型和理论分析中, 如原子阵列中的光纤耦合[12 ] 、锁相激光阵列[13 ] 、实现单向无反射光学超材料[14 ] 、耦合腔阵列中的高阶EP点[15 ] 、Fano共振在光子学中的应用[16 ] 、绝热控制拓扑能量转移[17 ] 、纳米尺度的光机械晶体中的可调光学延迟[18 ] 等. 该理论还被用来分析非线性介质中的耦合现象, 例如调制不稳定性[19 ] 、波导器件中产生的谐波[20 ] 等.[21 ] , 等离激元诱导透明[22 ] 和光机械诱导透明[18 ] , 其本质都是源于耦合出现的相干相消. 2007年Kurs等[23 ] 在充分研究EIT的基础上, 认为电路中也存在类似的透明现象, 以耦合模理论为基础, 建立了电路学的耦合理论模型, 并搭建了一个通过线圈耦合共振的能量无线传输系统, 结果表明, 理论模型与实验数据的误差在5%以内, 得到了能在2 m内达到40%能量传输效率的无线传输系统. 说明耦合模理论能够精确地描述电路中的耦合现象, 将耦合模理论拓展到了电学领域中, 此后得到了迅速发展, 包括无线传输中产生的继电效应[24 ] 、无辐射传输[25 ] 、超材料耦合共振[26 ] 等.[27 ] 在《Waves and fields in optoelectronics》一书中, 用最简单的LC简谐振动回路, 通过变量代换将二阶微分方程转化为一阶微分方程, 但由于是最简单的LC耦合回路, 不包含损耗项和输入项, 这些项他是通过定性分析加入的. 从物理角度没有任何问题, 可是从数学角度还是不够严谨的. 在本文中, 先建立耦合体系的弹簧振子模型的动力学方程, 再利用久期微扰理论, 将二阶的弹簧振子模型简化为一阶的CMT的动力学方程, 并且损耗项和输入项自然包含在方程中, 物理意义更清楚. 最后用音叉耦合实验来验证CMT理论, 结果表明理论和实验符合得很好. 该方法为振动耦合体系的理论研究提供了一定的指导意义.2.从弹簧振子模型到CMT 不失普遍性, 在此从两个音叉耦合体系入手建立弹簧振子模型. 两个音叉用劲度系数为k 的弹簧连接, 设${m_1}$ 和${m_2}$ 分别为两个音叉的等效质量, ${\tilde x_1}$ 和${\tilde x_2}$ 分别为两音叉的横向位移, ${\gamma _1}$ 和${\gamma _2}$ 为音叉的阻尼系数, ${\omega _1}$ , ${\omega _2}$ 分别是两个音叉的固有频率, $\tilde G\cos \left( {\tilde \omega \tilde t} \right)$ 表示为外来的周期性驱动力, $\tilde \omega $ 为源频率. 其原理图如图1(a) 所示. 该耦合体系的动力学方程为[1 ] 图 1 双模耦合体系的相关参数示意图 (a) 弹簧振子模型; (b) CMT模型Figure1. Parameters’ sketch of two-mode coupled system: (a) Spring oscillator model; (b) CMT model.1 )式和(2 )式组成一个二阶微分方程组, 忽略阻尼项(即损耗项), 可以得到其解析的近似解[28 ] , 但是阻尼项包含很多重要的信息和功能. Haus[27 ] 在Waves and Fields in Optoelectronics 一书中, 将最简单的简谐振动的二阶微分方程拆成两个一阶微分方程, 然后通过线性组合的方法将两个一阶微分方程合成一个一阶微分方程, 其他的损耗项和输入项都是通过定性分析引入的. 在此, 我们基于非线性方程中的久期微扰理论[29 ] , 从弹簧振子模型的二阶微分方程出发, 严格求出CMT. 为了求解的方便, 令${m_1} = {m_2} = m$ , 选${\omega _0}$ 为频率参考点, 则$m{\omega _1^2} = m{\omega _0^2} + $ $m{\varDelta _1^2} $ , $m{\omega _2^2} \!= \!m{\omega _0^2} + m{\varDelta _2^2} $ , 因此一般为了讨论方便, 取${\omega _0} \!\leqslant \!\min \left( {{\omega _1}, {\omega _2}} \right)$ , ${\varDelta _1^2}\! = \!\left( {{\omega _1}\! + \!{\omega _0}} \right)\left( {{\omega _1}\! -\!{\omega _0}} \right)$ 和${\varDelta _2^2} = \left( {{\omega _2} + {\omega _0}} \right)\left( {{\omega _2} - {\omega _0}} \right)$ 分别是每个音叉的固有频率和频率参考点的平方差, 描述的是参考点频率与音叉固有频率的频率失谐相关量. 为了使方程组具有普适性和简化计算, 进一步进行无量纲化, 令$t = {\omega _0}\tilde t$ , ${\tilde x_1} = \sqrt {m{\omega _0}^2} x$ , $\omega = {{\tilde \omega } / {{\omega _0}}}$ . 方程(1 )和(2 )可以改写为:$G = \dfrac{{\tilde G}}{{{\omega _0}^3\sqrt {{m^3}} }},~ {Q_1}^{ - 1} = \dfrac{{{\gamma _1}}}{{m{\omega _0}}}$ 与${Q_2}^{ - 1} = \dfrac{{{\gamma _2}}}{{m{\omega _0}}}$ 分别表示音叉1, 2的归一化损耗, 它们的倒数${Q_1}$ , ${Q_2}$ 为品质因子, 由于该系统为线性损耗体系, 在近共振条件下, 可设体系总损耗$Q_1^{ - 1} \equiv \varepsilon \;{\varGamma _1} \ll 1$ , $Q_2^{ - 1} \equiv \varepsilon \;{\varGamma _2} \ll 1$ , 其中$\varepsilon $ 表示小量. 由于参考点频率一般选取在接近两个音叉固有频率中较小一个, 甚至可以直接选取两个音叉固有频率中较小的一个, 而两个音叉的固有频率很接近, 所以${\alpha _1} = \dfrac{{{\varDelta _1}^2}}{{{\omega _0}^2}}, {\alpha _2} = \dfrac{{{\varDelta _2}^2}}{{{\omega _0}^2}}$ 也是小量. $\eta = - \dfrac{k}{{m{\omega _0}^2}}$ 是与两个音叉之间的交叉耦合系数相关的量, 与弹簧的劲度系数成正比. 一般即使对于强耦合体系, ${\alpha _j}, \eta, Q_j^{ - 1}~(j = 1, 2)$ 也几乎是同一个数量级, 故$\eta $ 是小量. 所以在此令$\eta = \varepsilon \mu $ , ${\alpha _1} = \varepsilon {\beta _1}$ , ${\alpha _2} = \varepsilon {\beta _2}$ . 为了确保外界驱动力有正确的强度来诱导这样的振动, 设驱动力与方程中阻尼项有相同的数量级, 故有$G = {\varepsilon ^{\textstyle\frac{3}{2}}}g$ [29 ] . 最后由于损耗很小, 期望看到接近共振频率的响应, 故对驱动力的频率做归一化处理, $\omega = 1 + \varepsilon \varOmega $ . 把上述各项代入(3 )式和(4 )式中, 可得${x_1}$ , ${x_2}$ 对小量$\varepsilon $ 做展开, 设试探解为[29 ] $j = 1, 2$ , ${i^2} = - 1$ , ${\rm{c}}{\rm{.c}}{\rm{.}}$ 表示对前一项取共轭复数, $T = \varepsilon t$ 是时间慢变量, 分离出随时间周期变化的项之后, 余下的项为随时间缓慢变化的复振幅$A(T)$ 和更高阶小量. 将(7 )式对时间求导可得$j = 1, 2$ . 将(7 )和(8 )式代入(5 )式可得9 )式, ${\varepsilon ^{\textstyle\frac{1}{2}}}$ 的系数方程是恒等于零的结果. 而${\varepsilon ^{\textstyle\frac{3}{2}}}$ 的系数方程整理给出的结果为10 )式和(11 )式右手边正比于${{\rm{e}}^{{\rm{i}}t}}$ 的项称为久期项, 作用相当于力, 在驱动左边简单线性谐振子在它共振频率处共振, 所有久期项必须消失, 以便微扰纠正$x_1^{(1)}(t)$ 不会发散[29 ] . 因为久期项如果不为0, 振子将做受迫振动, 振幅会逐渐增大, 这与$x_1^{(1)}(t)$ 是高阶小量的题设相矛盾. 当久期项为0后, 得到慢变振幅的方程, 即7 )式可知${A_1} \sim {x_1}{{\rm{e}}^{ - {\rm{i}}t}}/\left( {\sqrt \varepsilon /2} \right)$ , ${A_2} \sim {x_2}{{\rm{e}}^{ - {\rm{i}}t}}/$ $\left( {\sqrt \varepsilon /2} \right) $ , 代入(12 )式可得$\omega = 1 + \varOmega \varepsilon $ , $\varepsilon {\beta _1} = {\alpha _1}$ , $\varepsilon {\varGamma _1} = Q_1^{ - 1}$ , $\varepsilon \mu = \eta $ , $\sqrt[3]{\varepsilon }g = G$ , 则(13 )式简化为$m \omega _1^2 = m \omega _0^2 + m \varDelta _1^2$ 和${\alpha _1} = {{{\varDelta _1^2}}}/{{{\omega _0^2}}}$ , 考虑到近共振近似时, 有15 )式代入(14 )式, 得到$t = {\omega _0}\tilde t$ , $x = {{{{\tilde x}_1}} / {\sqrt {m{\omega _0}^2} }}$ , $\omega = {{\tilde \omega } / {{\omega _0}}}$ , $G = {{\tilde G} / {{\omega _0}^3\sqrt {{m^3}} }}$ , (16 )式和(17 )式进一步改写为:18 )是描述模式耦合的一阶常微分方程组. 其中方程(18 )的右边表示外界驱动信号源的贡献, 类比于Haus[27 ] 在Waves and Fields in Optoelectronics 中的表示方法, 外界输入信号改写为$ - {\rm{i}}\dfrac{{\tilde G}}{{4 m{\omega _0}}}{{\rm{e}}^{{\rm{i}}\tilde \omega \tilde t}} \equiv \sqrt {2{\gamma _{{\rm{e}}1}}} S_{\rm I}^ + $ , 其中$S_{\rm I}^ + $ 表示输入端口I, 在此表示驱动信号源的输入端, ${\gamma _{{\rm{e}}j}}$ ($j = 1, 2$ )表示为第I个输入端口与第j 个振子的耦合系数, 它为第j 个振子除内部吸收损耗之外, 由于其他方式耗散功的外部损耗率, 例如电路中由导线传输到输出端口的损耗率. 一般来说第j 个振子与输入端口的耦合系数和第j 个振子与输出端口的耦合系数相等[8 ,9 ,27 ] , 此处不做区分, 统一写成${\gamma _{{\rm{e}}j}}$ . $\dfrac{{{\gamma _j}}}{{2 m}}$ 为振子的总损耗, 取$ {{{\gamma _j}}}/({{2 m}}) \equiv {\gamma _{{\rm{e}}j}} + {\gamma _{{\rm{o}}j}},~ (j = 1, 2)$ , 其中${\gamma _{{\rm{o}}j}}$ 表示为第j 个振子的吸收损耗率, 例如电路中的欧姆损耗率以及微纳光子学中金属的内部吸收损耗率等. 另外, 设$\kappa = {k}/({{2 m{\omega _0}}})$ 为耦合体系的交叉耦合系数. 去掉方程组(18 )中变量的“~”, 因此, 方程组(18 )改写为19 )是标准的CMT的两个动力学方程[29 ] , 输出端口方程为$S_{\rm I}^ - $ 表示振子通过传输线, 将振动信号传输给测量仪器. 至此, 通过久期微扰理论很方便地将二阶微分方程转化为为CMT一阶微分方程, 使得CMT中的每一项的物理意义更加清晰明了. 如果振子体系的参数都有理论计算公式的话, 那么(19 )式和(20 )式就可以理论预言耦合体系的谱线特征, 而不再仅仅是拟合公式.${x_1}(t) = {x_{10}}{{\rm{e}}^{{\rm{i}}\omega t}}, {x_2}(t) = {x_{20}}{{\rm{e}}^{{\rm{i}}\omega t}}$ , 代入方程(19 )可得22 )式代入(20 )式可得$\zeta $ 为音叉耦合体系的传输效率24 )式描述了双模耦合体系的强度谱, 即为双模CMT的传输公式. 当两个音叉没有耦合时, 即$\kappa = 0$ , (24 )式变为如下25 )式描述了单模体系的强度谱, 即为单模CMT的传输公式.3.实验验证 为了验证推导的CMT公式(24 )式和(25 )式的正确性, 搭建了两音叉耦合实验装置, 装置图如图2(a) 所示. 两个用来输入、输出信号的HZDH4615受迫振动与共振实验仪(用R1, R2表示)和两个带有音叉的FD-VR-A受迫振动与共振实验仪(用F1, F2表示)用三根传输线连接, 两个音叉间用两根弹簧连接, 并用小磁铁将弹簧的连接端固定在音叉臂, 为了匹配音叉两臂上的质量, 在二音叉的外侧音叉臂于相同的位置放置了同一规格的两块小磁铁. 实验装置原理图如图2(b) 所示, 单个振动的音叉可视为受迫振动的谐振子, 通过弹簧连接的两个音叉可视为耦合的谐振子. R1产生驱动信号并把信号输入给F1的输入端, F1输入端接有一线圈, 线圈会随着驱动信号的交变电流产生变化的磁场, 驱动音叉F1的一个臂振动, 由于音叉一个臂振动, 另一个与弹簧相连的臂就同步反方向振动, 并通过弹簧把机械振动传送给F2, F2在振动后又会通过弹簧反过来作用于F1, 音叉F1受到两个方面的作用, 一个是驱动信号, 另一个是音叉F2, 当这两个作用正好反相位时, 出现干涉相消, 从而使R1测量的振幅谱中出现一个谷, 即一个振幅峰因耦合劈裂成两个振幅峰.图 2 (a)两音叉耦合实验装置图; (b) 实验系统工作原理的示意图; (c)音叉单独振动时的实验谱和拟合谱; (d) 双音叉耦合下的实验谱和拟合谱Figure2. (a) Experimental device diagram of our two tuning forks’ coupled system; (b) schematic diagram of the experiment system; (c) measured and fitted spectra of two tuning forks without coupling; (d) measured and fitted spectra of two tuning forks with coupling.图2(c) 所示, 其中紫色圆圈表示音叉F1的实验测量谱, 红色五角星表示音叉F2的实验测量谱. 从图中可以看出, F1的共振频率${f_1}$ = 243.5 Hz, F2的共振频率${f_2}$ = 243.8 Hz. 音叉的品质因子一般定义为$j = 1, 2$ , 其中$\Delta f$ 为强度谱的半高宽, 基于(26 )式, 计算出音叉F1和F2的振幅谱的品质因子分别为304.3和325.1. 根据(25 )式对两个实验谱进行拟合, 在图2(c) 中深紫色实线为F1的拟合谱, 红色虚线为F2的拟合谱. 其中拟合参数分别为γ e1 = 0.198 × 2π Hz, γ o1 = 0.2 × 2π Hz, ω 1 = 243.5×2π Hz, γ e2 = 0.182 × 2π Hz, γ o2 = 0.18 × 2π Hz, ω 2 =243.85 × 2π Hz. 因此无耦合理论中的圆频率与音叉共振圆频率相对应. 从图2(c) 中可以看出实验和理论符合得很好. 误差来源于两个方面, 一方面, 实验中无法避免的误差, 如接触损耗、传输损耗、数值波动和实验环境影响. 另一方面, 是因为CMT描述的是局域效应, 在远离共振位置时误差增大.图2(a) 所示的实验装置图, 测量耦合体系的实验振幅谱, 结果如图2(d) 所示. 对于这样的耦合体系具有非线性现象[30 ] , 即升频和降频谱线不一致的现象, 为此分别按照频率由小到大和由大到小的测量方法, 记录升频(用F表示)和降频(用R表示)两组数据, 其中绿色实心菱形为降频时测得的实验谱, 橘色实心三角形为升频时测得的实验谱. 从图2(d) 的实验谱中可以看出, 相比于无耦合情况下单音叉振动的单个峰, 在耦合情况下, 由一个峰劈裂成两个峰, 频率较低的峰值较高, 在232.4 Hz达到0.45, 频率较高的峰值略低, 在241.9 Hz达到0.3. 在两峰中间出现一个谷, 即在236.3 Hz时振幅几乎为零, 此时F1不再振动, F2的反作用力和驱动源相位差180°, 两者作用在F1上的力大小相同方向相反. 从图2(d) 中也可以看出, 升频谱和降频谱几乎完全重合, 说明该体系在该条件下给出的只有线性效应(关于非线性的效应我们后续会有相关文章专门研究). 根据理论推导出的耦合下的效率公式(24 )式, 对实验谱进行拟合, 并绘出拟合谱, 如图2(d) 中紫色实线所示, 相关的拟合参数分别为: ${\gamma _{{\rm{e1}}}} = 0.1 \times $ 2π Hz, ${\gamma _{{\rm{o1}}}} = 0.57 \times$ 2π Hz, ${\omega _1} = 238.5 \times$ 2π Hz, ${\gamma _{{\rm{e2}}}} = 0.245 \times $ 2π Hz, ${\gamma _{{\rm{o2}}}} \!=\! 0.4 \times 2{\text{π}}\;{\rm{Hz}}$ , ${\omega _2} \!=\! 236.4\; \times$ 2π Hz, $\kappa \!=\! 4.8\times $ 2π Hz. 理论和实验符合得很好, 其中误差主要来源于实验误差和CMT是一个局域效应. 相比于无耦合情况下的单音叉在243.8和243.5 Hz的振动峰, 耦合下的峰值都明显降低, 频率也明显向低频移动; 同时两个模式的内部吸收损耗明显变大, 为无耦合时内部吸收损耗的两倍以上. 对于音叉受迫振动的体系, 其周期的平方与音叉质量成正比. 相对于无耦合体系, 耦合体系增加了固定弹簧的四片小磁铁和两根弹簧, 它们都是有一定质量的, 导致耦合体系的两个音叉的固有频率减小, 同时阻尼损耗等内部吸收损耗也相应增大.4.总 结 在本文中, 首先利用久期微扰理论, 对弹簧振子模型的二阶微分方程进行了理论研究, 研究结果表明, 二阶微分方程自动退化为包含损耗项和输入项的一阶微分方程, 即CMT, 并且这种方法使得CMT中每一项系数的物理意义更清晰明了. 随后为了验证理论的正确性, 实验上和理论上研究了弹簧连接的音叉耦合受迫振动系统, 研究结果表明理论和实验符合得很好. 该研究为CMT推广到机械振动体系提供了一种方案, 在设计机械振动耦合体系方面具有一定的指导意义. 









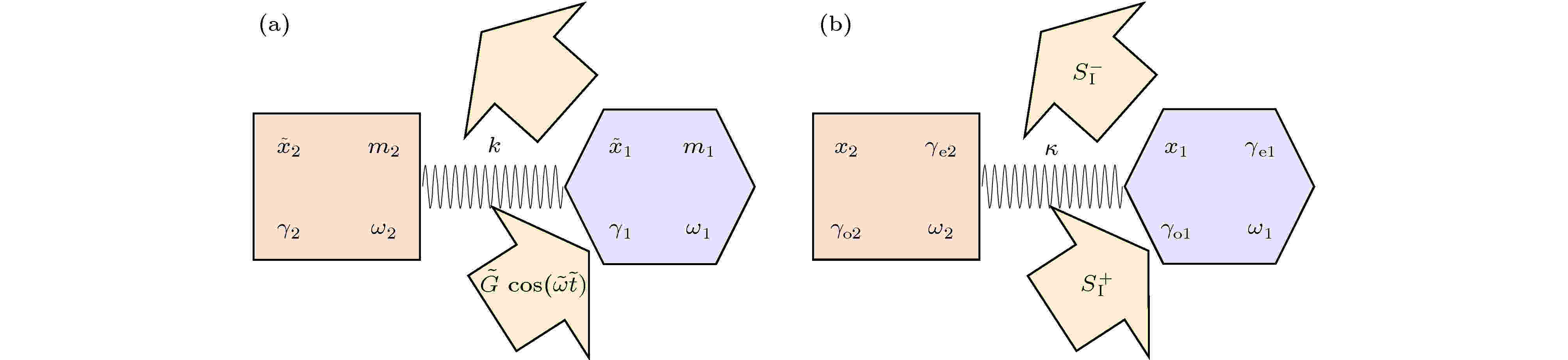 图 1 双模耦合体系的相关参数示意图 (a) 弹簧振子模型; (b) CMT模型
图 1 双模耦合体系的相关参数示意图 (a) 弹簧振子模型; (b) CMT模型







































































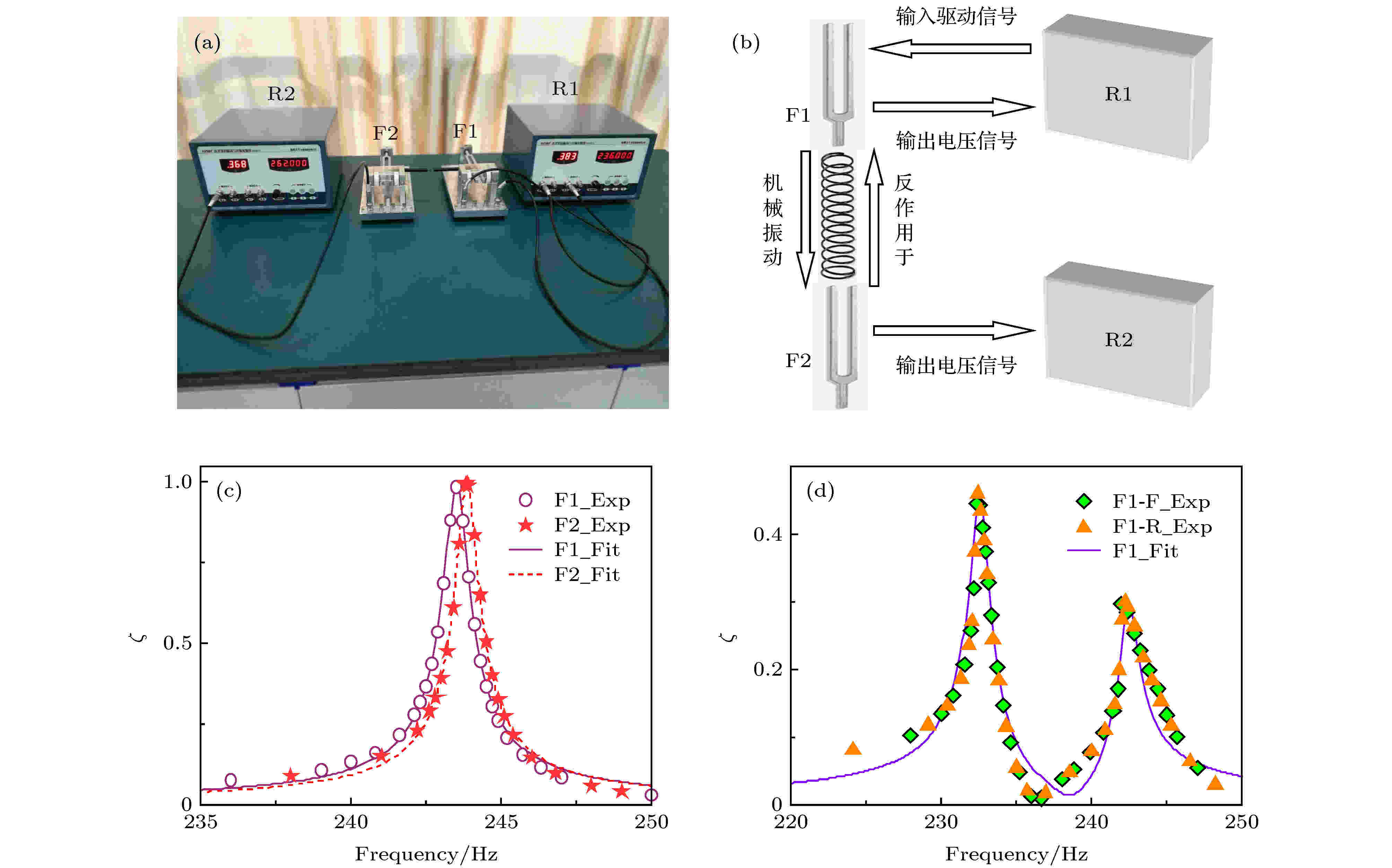 图 2 (a)两音叉耦合实验装置图; (b) 实验系统工作原理的示意图; (c)音叉单独振动时的实验谱和拟合谱; (d) 双音叉耦合下的实验谱和拟合谱
图 2 (a)两音叉耦合实验装置图; (b) 实验系统工作原理的示意图; (c)音叉单独振动时的实验谱和拟合谱; (d) 双音叉耦合下的实验谱和拟合谱










