摘要: 机械振子的基态冷却是腔量子光力学中的基本问题之一. 所谓的基态冷却就是让机械振子的稳态声子数小于1. 本文通过光压涨落谱和稳态声子数研究双光腔光力系统(标准单光腔光力系统中引入第二个光腔, 并与第一个光腔直接耦合)的基态冷却. 首先得到系统的有效哈密顿量, 然后给出朗之万方程和速率方程, 最后分别给出空腔和原子腔的光压涨落谱、冷却率和稳态声子数. 通过光压涨落谱、冷却率和稳态声子数表达式, 重点讨论空腔时机械振子的基态冷却, 发现当满足最佳参数条件(机械振子的冷却跃迁速率对应光压涨落谱的最大值, 而加热跃迁速率对应光压涨落谱的最小值)时, 机械振子可以被冷却到稳态声子数足够少. 此外分析: 当辅助腔内注入原子系综时, 若参数选择恰当可能更利于基态冷却.
关键词: 双光腔 /
基态冷却 /
朗之万方程 /
速率方程 English Abstract Ground-state cooling of mechanical resonator in double optical cavity Liu Ni Wang Jian-Fen Liang Jiu-Qing State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Theoretical Physics, Shanxi University, Taiyuan 030006, China Received Date: 09 October 2019Accepted Date: 05 January 2020Published Online: 20 March 2020Abstract: The ground-state cooling of mechanical resonator is one of the fundamental problems in cavity quantum photomechanics. The so-called ground-state cooling is to make the number of steady-state phonons of the mechanical resonator less than one. In this paper, we first propose an electromagnetically-induced-transparency-like cooling mechanism in a double-cavity optomechanical system to cool a mechanical resonator. In the double-optical cavity optomechanical system, the right additional cavity, which is directly coupled to a standard optomechanical system, contains an ultra-cold two-level atomic ensemble. By selecting the optimal parameters to meet the cooling process of the mechanical resonator corresponding to the maximum value of the optical fluctuation spectrum and the heating process of the mechanical resonator corresponding to the minimum value of the optical fluctuation spectrum, the mechanical resonator can be cooled by monitoring the phonon number. We also exert the effects of the atomic additional cavity on the quantum Langevin equations and optical fluctuation spectrum. We find that the atomic double-cavity system may have a better ground-state cooling than the double-cavity in certain parameters. To date, the researchers have proposed a number of theoretical cooling schemes in order to achieve the ground-state cooling of mechanical resonator. As far as we know, the sideband cooling for just a standard optomechanical system is a most famous scheme and the mechanical resonator is coupled to the optical field via radiation pressure force. By the quantum theory of mechanical resonator’s sideband cooling, the optical fluctuation spectrum determines the transition rate of both cooling and heating process of the mechanical resonator. That’s to say, the optical fluctuation spectrum at a mechanical resonator frequency ω m is corresponding to the cooling transition, whereas the optical fluctuation spectrum at –ω m is corresponding to the heating transition. They respectively correspond to anti-Stokes and Stokes effect in physics. Under resolvable sideband conditions, the optical field’s decay rate (the half-width of the single Lorentzian peak of optical fluctuation spectrum) is less than the frequency of the mechanical resonator. So, the ground-state cooling of the mechanical resonator can be obtained by making the maximum and minimum value of the optical fluctuation spectrum respectively correspond to the cooling anti-Stokes process and heating Stokes process. In this paper, we mainly observe the electromagnetically-induced-transparency-like ground-state cooling in a double-cavity optomechanical system with an ensemble of two-level atoms. By adjusting the maximum and minimum value of the optical fluctuation spectrum at the position of ω = ω m and ω = –ω m , the mechanical resonator could be cooled down approximately to the ground state. Even when there exists an ensemble of two-level atoms in the right additional cavity, the mechanical resonator can be better cooled than just a cavity. These results may be conducive to the ground-state cooling of the mechanical resonator in the future experiment. Keywords: double-optical cavity /ground state cooling /Langevin equation /rate equation 全文HTML --> --> --> 1.引 言 光力系统中许多奇特的量子现象已被观察, 机械运动的量子控制和光的机械控制方法已被广泛应用于高精度测量、量子信息处理和量子基本原理验证等多个领域. 目前, 机械振子的冷却是腔量子光力系统中的一个热门课题[1 ,2 ] , 且实验上[3 ,4 ] 已证明光力系统中机械振子的显著冷却. 最近, 通过机械振子与被驱动的辅助系统耦合, 使辅助系统从机械振子吸收能量从而实现机械振子的基态冷却(自冷却)[5 ,6 ] .[7 -10 ] , 最著名的方案是标准光力系统的边带冷却[11 ,12 ] , 将机械振子通过辐射压力与腔光场耦合. 根据机械振子边带冷却量子理论, 耦合到机械振子的光压涨落谱决定了机械振子冷却和加热过程的跃迁速率, 也就是说: 机械振子频率${\omega _{\rm{m}}}$ 时的频谱引起冷却跃迁, 而频率$ - {\omega _{\rm{m}}}$ 时的频谱引起加热跃迁, 且分别对应反斯托克斯和斯托克斯过程. 在可分辨边带条件下, 腔场的耗散系数远小于机械振子的频率, 也就是说, 光压涨落谱的单个洛伦兹峰的半高宽小于机械振子频率; 通过冷却反斯托克斯过程到涨落谱的最大值和加热斯托克斯过程到涨落谱的最小值, 可以获得机械振子的基态冷却.[13 -15 ] 的冷却装置很难满足边带条件, 于是人们提出很多超出边带冷却的新的基态冷却装置[16 ] . Xia 和 Evers[17 ] 将受限粒子运动的电磁感应透明(EIT)装置耦合到三能级超导通量比特来实现机械振子冷却[18 ] . 该EIT冷却装置可以在未满足边带区工作, 但依据三能级系统中EIT现象发现: 该装置压制了载体的热过程[19 ,20 ] . 同时相似的类EIT冷却装置被耦合到氮-空缺杂质的单电子自旋比特来实现机械振子冷却. 最近Genes等[21 ] 也提出了机械振子的EIT基态冷却装置, 他们是通过混合光力系统中三能级原子媒质的EIT来实现.[22 ] 中机械振子的类EIT的基态冷却装置. 事实上我们提出的是机械振子自冷却, 通过让机械振子与被驱动的辅助系统耦合, 使辅助系统从机械振子吸收能量进而实现冷却. 本文给出的双光腔光力系统具体是: 引入第二个量子光腔与标准光力系统中的第一个光腔直接耦合, 由此可以调控第一个光腔的性质. 一方面, 在边带不可分辨的条件下(即第一个光腔的耗散系数远大于机械振子频率), 利用双光腔系统的类EIT效应, 可以调整第一个光腔施加在机械振子上的光压力的涨落谱, 使得原本很宽的单峰洛伦兹谱变成具有两个较窄的峰和一个较低的谷的类EIT谱. 在新的谱中, 较窄的峰可以用来加强冷却跃迁, 而较低的谷可以用来有效抑制加热跃迁. 利用率方程方法可以求出稳态声子数解析式, 结果表明, 即便在边带不可分辨条件下, 仍可以利用双光腔系统的类EIT来实现机械振子的基态冷却. 该双光腔光力系统的类EIT的机制与三能级系统类似. 总之, 机械振子通过辐射压力耦合到双耦合单模腔(也称为光学分子[23 ] )中的第一个. 作用于机械振子的光压涨落谱是由两个耦合光腔确定, 并从标准光力系统的单个洛伦兹(Lorentzian)峰值分裂成两个相对较窄的峰, 且两峰之间出现谷. 当第二个光腔的耗散系数足够小时, 谷的最小值将近似接近于零, 对应的光谱具有类EIT形式, 类似于典型的Λ型三能级系统中的EIT现象. 将对应光压涨落谱的机械振子冷却过程(反斯托克斯)达到最大值和加热(斯托克斯)过程达到最小值, 我们发现: 此时机械振子比没有辅助腔时冷却得更好, 甚至可以冷却到基态[10 ] . 目前, 实验上已经实现两个耦合光腔或耦合谐振腔(玻色腔模或机械振荡器)[24 ] 中的类 EIT 现象. 包含两个腔模和一个机械振子的光力系统中的基态冷却方案也已提出[25 ] , 与我们提出方案的主要区别是: 1)文献[25 ]中两腔模通过混合腔系统内的1/4波片有效地间接互相耦合, 其中两腔模正交偏振, 被同频率的激光场驱动, 1/4波片提供两腔模间的线性混合相互作用; 我们提出两个单模腔以更简单的方法直接耦合, 例如光分子系统中的瞬逝耦合; 2)文献[25 ]通过复杂的方案让两腔模都耦合到机械振子; 我们的模型只需要单模腔直接耦合到机械振子, 更容易在实验中实现. 最近文献[26 ]提出一种类似于我们的冷却方案[26 ] : 引入另外的辅助机械振子代替我们模型中的一个腔来获得机械振子的基态冷却.2.系统哈密顿量和朗之万方程 22.1.系统哈密顿量 2.1.系统哈密顿量 如图1 所示, 我们考虑两个耦合的单模光腔和一个机械振子组成的光力系统. 机械振子(共振频率为${\omega _{\rm{m}}}$ , 有效质量为m , 耗散系数为${\gamma _{\rm{m}}}$ )耦合到被强抽运激光器(频率为${\omega _{\rm{L}}}$ )驱动的左光腔, 形成标准的光力腔子系统. 右光腔内包含二能级冷原子系综, 并通过耦合强度J 与左光腔进行耦合. 整个系统哈密顿量为图 1 可实现的双光腔光力系统的示意图Figure1. Schematic diagram of an achievable double-cavity optomechanical system.${\omega _1}$ 和${\omega _2}$ , ${a_1}$ 和${a_2}$ 是两个腔模的湮灭算符; 第三和第四项是机械振子的能量, m 和${\omega _{\rm{m}}}$ 为机械振子的质量和频率, 耗散系数为${\gamma _{\rm{m}}}, b$ 是机械振子的湮灭算符; 第五项表示右腔内囚禁的二能级原子系综的能量; 第六项描述右光腔内原子系综与光场的相互作用, $\sigma _z^{\left( j \right)} \!=\! {\left| 2 \right\rangle _{jj}}\left\langle 2 \right| - {\left| 1 \right\rangle _{jj}}\left\langle 1 \right|$ , $\sigma _ + ^{\left( j \right)} \!=\!{\left| 2 \right\rangle _{jj}}\left\langle 1 \right|$ , $\sigma _ - ^{\left( j \right)} = {\left| 1 \right\rangle _{jj}}\left\langle 2 \right|$ 是第j 个原子的泡利算符, 其中${\left| 1 \right\rangle _j}$ , ${\left| 2 \right\rangle _j}$ 是第j 个原子的基态和激发态, ${g_{\rm{a}}}$ 为原子-场耦合系数; 第七项是光力耦合项, ${G_0}$ 为单光子光力耦合系数, 满足${G_0} = {{{\omega _1}}}/{L}$ ; 第八项表示光腔耦合项, 其中J 是双光腔间的耦合系数; 最后一项表示外部的驱动抽运激光对光力腔的影响, ${\omega _{\rm{L}}}$ 为驱动抽运激光的频率, $\varepsilon = \sqrt {\dfrac{{2{\kappa _1}{P_{{\rm{in}}, {\rm{A}}}}}}{{\hbar {\omega _{\rm{L}}}}}} $ 则描述其强度, 其中${P_{{\rm{in}}, {\rm{A}}}}$ 是其功率.1 )式, 定义原子系综的集体算符N 是原子数目. 在大N 极限和低激发条件下, 集体自旋算符近似满足玻色对易关系$\left[ {A, {A^\dagger }} \right] \approx 1$ 以及$\displaystyle\sum\nolimits_j {\sigma _z^{\left( j \right)}} = 2{A^\dagger }A - N$ . 用集体自旋算符代替哈密顿量(1 )式中的泡利算符, 则(1 )式可以简写为3 )式进行含时规范变换${H^\prime } = UH{U^\dagger } - $ ${\rm{i}}U\dfrac{{\partial {U^\dagger }}}{{\partial t}} $ , 令幺正算符$U\left( t \right) = {{\rm{e}}^{{\rm{i}}{\omega _{\rm{L}}}t\left( {a_1^\dagger {a_1} + a_2^\dagger {a_2} + {A^\dagger }A} \right)}}$ ,${\varDelta '_1} = {\omega _1} - {\omega _{\rm{L}}}$ , ${\varDelta _2} = {\omega _2} - {\omega _{\rm{L}}}$ 分别是光腔对抽运驱动场的频率失谐量; ${\varDelta _{\rm a}} = {\omega _{\rm{a}}} - {\omega _{\rm{L}}}$ 是二能级原子频率对抽运驱动频率的失谐量.2.2.朗之万方程 -->2.2.朗之万方程 为了研究左腔的有效反馈, 首先需要分析右腔的腔场动力学. 通过非线性海森伯-朗之万方程分别得到如下系统算符的时间演化.$\dot a = \dfrac{1}{{{\rm{i}}\hbar }}\left[ {a, H} \right] + $ $\sqrt {2\kappa } {a_{{\rm{in}}}} - \kappa a $ , 得到$\dot A = \dfrac{1}{{{\rm{i}}\hbar }}\left[ {A, H} \right] +$ $ \sqrt {2{\gamma _{\rm{a}}}} {A_{{\rm{in}}}} - {\gamma _{\rm{a}}}A $ , 得到${G_0}q = {g_0}\left( {b + {b^\dagger }} \right)$ , 其中${g_0} = $ $ {G_0}\sqrt {\dfrac{\hbar }{{2 m{\omega _{\rm{m}}}}}} $ , 得到平均值的演化方程${\varDelta _1} = {\varDelta '_1} - {g_0}\left\langle {b + {b^\dagger }} \right\rangle $ 是第一个光腔频率对驱动光场频率的有效失谐量. ${\kappa _1}$ 和${\kappa _2}$ 是光腔的衰减率, 而${\gamma _{\rm{a}}}$ 是原子的相干衰减率, $\xi $ 是机械振子的噪声算符. ${a_{1, {\rm{in}}}}$ , ${a_{2, {\rm{in}}}}$ 和${A_{{\rm{in}}}}$ 是非零相关函数的噪声算符, 且满足如下关系:[27 ] $\sigma _ + ^{\left( j \right)}\sigma _ - ^{\left( j \right)} = 0$ 和$\sigma _ - ^{\left( j \right)}\sigma _ + ^{\left( j \right)} = N$ , 则稳态算符由下式给出:22 )式可以发现: 机械振子位移的稳态平均值$\left\langle q \right\rangle $ 是非零的, 是光压作用下机械振子围绕新的平衡位置$\left\langle q \right\rangle $ 振动的体现, 所以涨落量${\rm{\delta }}q = q - \left\langle q \right\rangle $ 才是真正的位移算符, 即冷却理论所要处理的关键对象.${\text{δ}}{a_1} ={a_1} - \left\langle {{a_1}} \right\rangle $ , ${\text{δ}}{a_2} = {a_2} - \left\langle {{a_2}} \right\rangle$ , ${\text{δ}}b = b - \left\langle b \right\rangle $ , ${\text{δ}}A = A - \left\langle A \right\rangle $ . 遵循通常的线性化方法[11 ] , 在$\left| {\left\langle {{a_1}} \right\rangle } \right| \gg 1$ 情形下, 得到涨落谱的有效线性哈密顿量(为简化将涨落算符摘掉$\text{δ}$ , 如仍写为${\text{δ}}{a_1} \to {a_1}$ )${\varDelta _1} = {\varDelta '_1} - {g_0}\left( {{{\left\langle b \right\rangle }^ * } + \left\langle b \right\rangle } \right)$ , g = ${g_0}\left\langle {{a_1}} \right\rangle $ 是有效光力耦合系数, 对应的稳态值$\left\langle {{a_1}} \right\rangle $ , $\left\langle {{a_2}} \right\rangle $ , $\left\langle b \right\rangle $ 和$\left\langle A \right\rangle $ 同(18 )—(22 )式, 相应的朗之万方程表示为24 )和(28 )中涨落算符的二次项, 并省略所有${\text{δ}}$ 记号, 则涨落算符的动力学朗之万方程(24 )—(28 )与系统算符的朗之万方程(5 )—(9 )具有相同形式, 即3.机械振子速率方程和光压涨落谱 23.1.机械振子速率方程 3.1.机械振子速率方程 为了方便讨论, 先假设右腔为空腔, 即未注入原子系综, 并设b 是机械振子的湮灭算符, 与坐标和动量的关系是$b = \sqrt {\dfrac{{m{\omega _{\rm{m}}}}}{{2\hbar }}} \left( {q + {\rm{i}}\dfrac{p}{{m{\omega _{\rm{m}}}}}} \right)$ , ${b^\dagger } = \sqrt {\dfrac{{m{\omega _{\rm{m}}}}}{{2\hbar }}} \left( {q - {\rm{i}}\dfrac{p}{{m{\omega _{\rm{m}}}}}} \right)$ 满足玻色对易关系. 则有效哈密顿量(23 )式整理为34 )式和文献[28 ]提供的方法, 写出机械振子的速率方程[28 ] ${p_n}$ 是机械振子处在声子数本征态$\left| n \right\rangle $ 上的概率. ${\varGamma _{n' \leftarrow n}}$ 表示机械振子从态$\left| n \right\rangle $ 跃迁到态$\left| {n'} \right\rangle $ 的跃迁速率, 由有效机械振子耦合诱导. 借助维纳-辛钦定理可得$S\left( \omega \right) = \displaystyle\int {{\rm{d}}t{{\rm{e}}^{{\rm{i}}\omega t}}} \left\langle {F\left( t \right)F\left( 0 \right)} \right\rangle $ 是光腔作用在机械振子上的力$F = a_1^\dagger + {a_1}$ 的涨落谱. 方程(35 )的后四项描述的是热库环境对机械振子的作用, 其中${\gamma _{\rm{m}}}$ 是机械振子的耗散系数, 而${n_{\rm{m}}} = {\left( {{{\rm{e}}^{{{\hbar {\omega _{\rm{m}}}} / {{\kappa _{\rm{B}}}T}}}} - 1} \right)^{ - 1}}$ 是环境温度为T 时的热态声子数.35 )可以解出机械振子稳态平均声子数:${n_{\rm{p}}}$ 时的速率.38 )式可知: 当机械振子耗散系数${\gamma _{\rm{m}}} \to 0$ 时, ${\gamma _{\rm{p}}} \to {\gamma _{\rm{c}}}$ , 则代入(37 )式可得${n_{\rm{p}}} \to {n_{\rm{c}}}$ , 而${n_{\rm{c}}}$ 定义为冷却的量子极限, ${\gamma _{\rm{c}}}$ 是冷却率. 可见, 稳态声子数${n_{\rm{p}}}$ 主要取决于力的涨落谱的正频和负频部分, 即$S\left( { \pm {\omega _{\rm{m}}}} \right)$ , 且需要注意: 与跃迁速率${\varGamma _{n \leftarrow n + 1}}$ 相关的正频部分$S\left( { + {\omega _{\rm{m}}}} \right)$ 决定冷却过程, 而与跃迁速率${\varGamma _{n + 1 \leftarrow n}}$ 相关的负频部分$S\left( { - {\omega _{\rm{m}}}} \right)$ 决定加热过程. 基态冷却时, 通常要求冷却率要远远大于机械振子的热耗散系数, 即${\gamma _c} \gg {\gamma _{\rm{m}}}$ , 则(38 )式近似为${\gamma _{\rm{p}}} \approx {\gamma _{\rm{c}}}$ ; 依据稳态声子数(37 )式可得${n_{\rm{p}}} \approx \dfrac{{{\gamma _{\rm{m}}}{n_{\rm{m}}} + {\gamma _{\rm{c}}}{n_{\rm{c}}}}}{{{\gamma _{\rm{c}}}}} = $ $\dfrac{{{\gamma _{\rm{m}}}{n_{\rm{m}}}}}{{{\gamma _{\rm{c}}}}} + {n_{\rm{c}}} $ , 可见, 要得到较小的${n_{\rm{p}}}$ 而达到基态冷却, 同时要求大的冷却率${\gamma _{\rm{c}}}$ 和小的冷却极限${n_{\rm{c}}}$ 是必要的. 也就是说, 要冷却机械振子接近基态, 需要控制光压涨落谱$S\left( \omega \right)$ , 即加强正频部分$S\left( { + {\omega _{\rm{m}}}} \right)$ , 并抑制负频部分$S\left( { - {\omega _{\rm{m}}}} \right)$ , 也就是加强冷却跃迁, 抑制加热跃迁.3.2.光压涨落谱 -->3.2.光压涨落谱 33.2.1.空腔光压涨落谱 -->3.2.1.空腔光压涨落谱 在弱耦合$ \left( {g \ll {\omega _{\rm{m}}}} \right) $ 区, 机械振子对光学模的反作用可忽略不计. 因此, 光力$F = a_1^\dagger + {a_{\rm{1}}}$ 的涨落谱$S\left( \omega \right)$ 最终只由有效哈密顿量(34 )式中的光学部分决定, 即$S\left( \omega \right)$ 可以从如下对应的朗之万方程得到44a )—(44c )式将光学部分的朗之万方程(42 )和(43 )变到频域上, 并得到代数方程45 )和(46 )式可解得15 )和光力$F =a_1^\dagger + {a_{\rm{1}}}$ 变换到频域, 得47 )—(51 )式可以得到52 )式和傅里叶逆变换可以求得涨落谱$A\left( \omega \right)$ 在(48a )式中已给出.3.2.2.原子腔光压涨落谱 -->3.2.2.原子腔光压涨落谱 如上利用傅里叶变换(44a )—(44c )式将系统朗之万方程(29 )—(31 )式变到频域上, 得到代数方程55 )—(57 )式可以求得4.参数影响的涨落谱 24.1.参数影响的空腔涨落谱 4.1.参数影响的空腔涨落谱 如上所述, 机械振子的冷却主要由涨落谱的正频和负频部分决定, 即$S\left( { \pm {\omega _{\rm{m}}}} \right)$ , 为实现基态冷却要求$S\left( {{\omega _{\rm{m}}}} \right)$ 尽可能大, 而$S\left( { - {\omega _{\rm{m}}}} \right)$ 尽可能小. 图2 刻画了光压涨落谱$S\left( \omega \right)$ 随参数(双光腔间的耦合系数J , 有效腔失谐${\varDelta _1}$ 和${\varDelta _2}$ , 耗散率${\kappa _1}$ 和${\kappa _2}$ )的变化. 根据边带冷却机制, 获得机械振子可分辨边带冷却基态的必要条件是${\kappa _1} < {\omega _{\rm{m}}}$ . 在不可分辨边带条件下, 决定冷却和加热过程的涨落谱$S\left( { + {\omega _{\rm{m}}}} \right)$ 和$S\left( { - {\omega _{\rm{m}}}} \right)$ 达不到机械振子的最佳冷却(如图2 , $ {\kappa _1} = $ $5{\omega _{\rm{m}}}$ ). 这里, 我们主要研究不可分辨边带条件下(第一个光腔的衰减率大于机械振子的频率, 即${\kappa _1} > {\omega _{\rm{m}}}$ )双光腔光力系统的基态冷却.图 2 双腔间耦合系数J 影响下涨落谱$S\left( \omega \right)$ 随频率$\omega $ 的变化(左腔和右腔的有效失谐和对应的耗散率分别为${\varDelta _1} = {\omega _{\rm{m}}}, {\kappa _1} = 5{\omega _{\rm{m}}}$ ; ${\varDelta _2} = - {\omega _{\rm{m}}}, {\kappa _2} = 0.05{\omega _{\rm{m}}}$ )Figure2. Fluctuation spectrum $S\left( \omega \right)$ as a function of the frequency $\omega $ with different double-cavity coupling coefficient J . The effective detunings of the left cavity mode and right cavity mode and the corresponding decay rates are respectively are ${\varDelta _1} = {\omega _{\rm{m}}}, {\kappa _1} = 5{\omega _{\rm{m}}}$ ; ${\varDelta _2} = - {\omega _{\rm{m}}}, {\kappa _2} = 0.05{\omega _{\rm{m}}}$ .$J = 0$ , 此时回退为标准的光力系统. 从(54 )式涨落谱$S\left( \omega \right)$ 和(48a )式可以发现, 此时涨落谱$S\left( \omega \right)$ 仅由${\kappa _1}$ 和${\varDelta _1}$ 决定, 为洛伦兹谱; 在$\omega = {\varDelta _1}$ 处是单一峰值点, 在$\omega = {\kappa _1}$ 处是峰的半高宽, 如图黑线所示. 为了让冷却过程达到最大跃迁, 涨落谱$S\left( \omega \right)$ 只有在${\varDelta _1} = {\omega _{\rm{m}}}$ 处.$J \ne 0$ , 涨落谱$S\left( \omega \right)$ 则从单峰的洛伦兹谱劈裂成相对窄的两个峰和一个谷的类EIT谱, 如图2 彩色线所示. 物理上, 双峰之间的谷的起源类似于三能级原子中的EIT[29 ] 的双光子共振, 涨落谱的最小点在位置$\omega = {\varDelta _2}$ , 对应于EIT或类EIT现象中的双光子共振条件. 因此, 为了尽可能压制热过程, 需要涨落谱在$\omega = - {\omega _{\rm{m}}}$ 时具有最小值, 推导得到的最佳条件是${\varDelta _2} = - {\omega _{\rm{m}}}$ (如图2 彩色线所示). 涨落谱的两个峰的位置强烈依赖于双光腔间的耦合系数J . 同时, 为了达到冷却过程的最大跃迁率, 涨落谱$S\left( {\omega = + {\omega _{\rm{m}}}} \right)$ 应该尽量大, 也就是说, 应该确定右峰的中心在$\omega = + {\omega _{\rm{m}}}$ 附近.41 )式为${H_{{\rm{op}}}} = \hbar {{\varDelta }'_1}{a}_1^{\prime\dagger} {{a}'_1} +$ $ \hbar {{\varDelta }'_2}{a}_2^{\prime \dagger} {{a}'_2} $ 来看出该过程.${\varDelta '_1}$ , ${\varDelta '_2}$ 是对角化简正模的本征频率, 新的简正模的湮灭算符满足如下关系:62 )式代入(61 )式, 可得${\varDelta '_1}$ 和${\varDelta '_2}$ 分别对应于涨落谱$S\left( \omega \right)$ 的右侧和左侧峰值的位置, ${\varDelta _2}$ 对应涨落谱谷的位置, 故64 )式代入(63b )式, 得到最优双光腔间的耦合系数满足${\omega _{\rm{m}} } - {\varDelta _1} < 0$ 时, 右边的峰值总是位于$\omega = + {\omega _{\rm{m}}}$ 点的右侧, $S\left( { + {\omega _{\rm{m}}}} \right) < S\left( {{{\varDelta '}_1}} \right)$ , 虽然此情况也可以冷却机械振子, 但我们主要关注${\omega _{\rm{m}}} - $ ${\varDelta _1} > 0$ 的情形. 我们让右峰点加强冷却跃迁, 而让谷点(双光子共振点)抑制加热跃迁, 并结合(64 )和(65 )式, 可以得到双光腔系统的类EIT谱给出的最优冷却条件图3 给出涨落谱$S\left( \omega \right)$ 在最佳条件${\varDelta _2} = - {\omega _{\rm{m}}}$ 下随四种不同的耗散系数${\kappa _2}$ 变化的示意图, 左腔的有效失谐量${\varDelta _1} = - {\omega _{\rm{m}}}$ , 依据(65 )式, 此时对应的最佳双腔间耦合系数$J = 2{\omega _{\rm{m}}}$ . 值得注意的是, 即使满足两个最优条件: ${\varDelta _2} = - {\omega _{\rm{m}}}$ (对应最小加热效应)和${\varDelta '_1} = + {\omega _{\rm{m}}}$ (对应最大冷却效应), 为了获得良好的冷却, 如基态冷却, 也应该要求相关谱的最小点的值接近于零, 常通过适当选择右腔耗散系数${\kappa _2}$ (${\kappa _2}$ 决定涨落谱的深度). 事实上, 当${\kappa _2}$ 非常小时, 如${\kappa _2} \ll J$ , 最小点的值接近于零, 如图3 所示. 从图3 还可以看出, 随着耗散系数${\kappa _2}$ 的减小, 峰高逐渐增大, 同时最小点趋于零. 可见, 耗散系数${\kappa _2}$ 越小越利于双光腔光力系统中机械振子的冷却. 而从${\kappa _2} > 2{\omega _{\rm{m}}}$ 开始, 尤其${\kappa _2} = 5{\omega _{\rm{m}}}$ (绿线)时, 涨落谱已不再出现明显的峰和谷, 再次验证耗散系数${\kappa _2}$ 越小越利于系统的基态冷却.图 3 不同衰减率${\kappa _2}$ 影响下的涨落谱(给定的参数分别为${\varDelta _1} = - {\omega _{\rm{m}}}, {\kappa _1} = 5{\omega _{\rm{m}}}$ ; ${\varDelta _2} = - {\omega _{\rm{m}}}, J = 2{\omega _{\rm{m}}}$ )Figure3. Optical fluctuation spectrum with different decay rates ${\kappa _2}$ . The given parameters are ${\varDelta _1} = - {\omega _{\rm{m}}}, {\kappa _1} = 5{\omega _{\rm{m}}}$ ; ${\varDelta _2} = - {\omega _{\rm{m}}}, J = 2{\omega _{\rm{m}}}$ .4.2.参数影响的原子腔涨落谱 -->4.2.参数影响的原子腔涨落谱 图4 中蓝线对应图2 空腔涨落谱中$J{\rm{ = 2}}{\omega _{\rm{m}}}$ 时的蓝线. 在相同参数下, 引入原子系综后, 发现某些参数下, 原子腔涨落谱的峰值$S\left( { + {\omega _{\rm{m}}}} \right)$ 接近于空腔时, 而谷值$S\left( { - {\omega _{\rm{m}}}} \right)$ 低于空腔时, 可见原子腔更加抑制加热跃迁, 有利于机械振子冷却. 实际作图时发现, 原子有效失谐${\varDelta _{\rm{a}}}$ 、相干衰减率${\gamma _a}$ 、原子-场耦合系数${g_{\rm{a}}}$ 、原子数N 都会影响涨落谱, 从(59a )和(60 )式也能明显看到. 而且原子有效失谐${\varDelta _{\rm{a}}}$ 影响不明显, 而原子-场耦合系数${g_{\rm{a}}}$ 增大数量级时会从类EIT谱变成单一的洛伦兹谱.图 4 参数影响下空腔和原子腔涨落谱$S\left( \omega \right)$ 随频率$\omega $ 的变化(左腔和右腔的有效失谐和对应的耗散率分别为${\varDelta _1} = {\omega _{\rm{m}}},\; {\kappa _1} = 5{\omega _{\rm{m}}}$ ; ${\varDelta _2} = - {\omega _{\rm{m}}}, \;{\kappa _2} = 0.05{\omega _{\rm{m}}}$ ; 原子的有效失谐和相干衰减率是${\varDelta _{\rm{a}}} = {\omega _{\rm{m}}},\; {\gamma _{\rm{a}}} = 10{\omega _{\rm{m}}}$ ; 原子-场耦合系数${g_{\rm{a}}} = 0.62 \times {10^{ - 4}}{\omega _{\rm{m}}}$ , 原子数$N = {10^8}$ )Figure4. Optical and atom-optical fluctuation spectrum $S\left( \omega \right)$ as a function of the frequency $\omega $ under the influence of parameters. The effective detunings of the left cavity mode and right cavity mode and the corresponding decay rates are respectively are ${\varDelta _1} = {\omega _{\rm{m}}},\; {\kappa _1} = 5{\omega _{\rm{m}}}$ ; ${\varDelta _2} = - {\omega _{\rm{m}}}, $ ${\kappa _2} = 0.05{\omega _{\rm{m}}} $ . The atomic effective detuning and the coherent decay rates are respectively are ${\varDelta _{\rm{a}}} = {\omega _{\rm{m}}}, {\gamma _a} = 10{\omega _{\rm{m}}}$ . The atom-field coupling strength is ${g_{\rm{a}}} = 0.62 \times {10^{ - 4}}{\omega _{\rm{m}}}$ . The atomic number is $N = {10^8}$ .图5 中黑线与图3 中黑线对应, 发现在恰当选择原子参数时, 辅助腔内注入原子系综时更有利于基态冷却, 因为此时更有利于抑制加热跃迁, 在$\omega = - {\omega _{\rm{m}}}$ 时对应的谷$S\left( { - {\omega _{\rm{m}}}} \right)$ 比空腔时更低.图 5 衰减率${\kappa _2} = 0.05{\omega _{\rm{m}}}$ 影响下空腔和原子腔涨落谱(给定的参数分别为${\varDelta _1} = - {\omega _{\rm{m}}},\; {\kappa _1} = 5{\omega _{\rm{m}}}$ ; ${\varDelta _2} = - {\omega _{\rm{m}}}, J =$ $ 2{\omega _{\rm{m}}} $ ; ${\varDelta _{\rm{a}}} = {\omega _{\rm{m}}}, {\gamma _{\rm{a}}} = 10{\omega _{\rm{m}}}$ ; ${g_{\rm{a}}} \!=\! 0.62 \!\times\! {10^{ - 4}}{\omega _{\rm{m}}},$ $N \!=\! {10^8}$ )Figure5. Fluctuation spectrum and atom-optical fluctuation spectrum with given decay rates ${\kappa _2} = 0.05{\omega _{\rm{m}}}$ . The given parameters are ${\varDelta _1} = - {\omega _{\rm{m}}}, \;{\kappa _1} = 5{\omega _{\rm{m}}}$ , ${\varDelta _2} = - {\omega _{\rm{m}}}$ , J = $ 2{\omega _{\rm{m}}} $ , ${\varDelta _{\rm{a}}} = {\omega _{\rm{m}}}$ , $ {\gamma _{\rm{a}}} = 10{\omega _{\rm{m}}} $ ; ${g_{\rm{a}}} = 0.62 \!\times\! {10^{ - 4}}{\omega _{\rm{m}}}$ , $N \!= \!{10^8}$ 5.基态冷却 25.1.空腔基态冷却 5.1.空腔基态冷却 图6 给出了冷却率${\gamma _{\rm{c}}}$ 随光腔耦合系数J 的变化, 可以看出: 光腔耦合系数J 越大, 冷却率${\gamma _{\rm{c}}}$ 越高, 与图2 的结论一致; 冷却率${\gamma _{\rm{c}}}$ 随着衰减率${\kappa _2}$ 的减小而增大, 该结论与方程(39 )一致. 物理解释是: ${\kappa _2}$ 越小, 光谱的谷点越接近零, 越能更好地抑制加热过程. 但要注意: 并不是光腔耦合系数J 大到任何值都利于冷却, 最优值在图上最高点附近. 当${\kappa _2} = 5{\omega _{\rm{m}}}$ 时, 无论光腔耦合系数J 取何值, 冷却率${\gamma _{\rm{c}}}$ 都变得很小, 而且随着J 增大, 冷却率先减小后增大, 最后趋于稳态值, 所以${\kappa _2}$ 越小越好.图 6 冷却速率${\gamma _{\rm{c}}}$ 在不同衰减率${\kappa _2}$ 影响下随光腔耦合系数J 的函数(给定的参数是$g = 0.5{\omega _{\rm{m}}}, {\varDelta _2} = - {\omega _{\rm{m}}},\; {\kappa _1} = 5{\omega _{\rm{m}}}$ , 最优失谐${\varDelta _1}$ 满足(66 )式)Figure6. Cooling rate ${\gamma _c}$ as a function of optical coupling coefficient J in the case of different decay rates ${\kappa _2}$ . The given parameters are $g = 0.5{\omega _{\rm{m}}},\; {\varDelta _2} = - {\omega _{\rm{m}}}, \;{\kappa _1} = 5{\omega _{\rm{m}}}$ , and the optimal detuning ${\varDelta _1}$ satisfied the Eq. (66 ).图7 给出参数影响下声子数${n_{\rm{p}}}$ 随光腔耦合系数J 变化的示意图. 依据(40 )式, 图7 中虚线给出了量子冷却极限${n_{\rm{c}}}$ 随参数的变化, 可以看出, 随着光腔耦合系数的增加, 冷却极限${n_{\rm{c}}}$ 单调递减, 直至接近于零; 然而在真实系统中, 当机械振子的热效应比光场引起的效应大很多时, 即$ {\gamma _{\rm{m}}}{n_{\rm{m}}} \ll {\gamma _{\rm{c}}}{n_{\rm{c}}} $ 时, 最终的平均声子数${n_{\rm{p}}}$ 接近冷却极限${n_{\rm{c}}}$ , 而在光腔耦合系数J 较大导致冷却极限接近零时, 平均声子数${n_{\rm{p}}}$ 与${n_{\rm{c}}}$ 偏差大. 依据图6 和图7 具体分析为: J 较小时, 随着J 的增大, 冷却率${\gamma _{\rm{c}}}$ 增大, 而${n_{\rm{c}}}$ 减小, ${n_{\rm{p}}}$ 也减小; J 较大时, 随着J 的增大, 冷却率${\gamma _{\rm{c}}}$ 逐渐趋于零, 而${n_{\rm{p}}}$ 又逐渐增大, 直至增至热态声子数${n_{\rm{m}}}$ 为止.图 7 参数影响下平均声子数${n_{\rm{p}}}$ 随最佳光腔耦合系数J 的变化(给定的参数是${\omega _{\rm{m}}} \!= \!1.55{\text{π}} \times 20\;{\rm{MHz}}$ , $ {Q_{\rm{m}}} \!=\! {{{\omega _{\rm{m}}}} / {{\gamma _{\rm{m}}}}} =$ $ 6.2 \times {10^4}, {n_m} = 403 $ , $g = 0.5{\omega _{\rm{m}}} $ , ${\kappa _1} = 5{\omega _{\rm{m}}}$ , ${\kappa _2} = 0.05{\omega _{\rm{m}}}$ , ${\varDelta _2} = - {\omega _{\rm{m}}} $ , 最优失谐${\varDelta _1}$ 满足(66 )式)Figure7. Mean phonon number ${n_{\rm p}}$ as a function of optical coupling coefficient J . The given parameters are ${\omega _{\rm{m}}} \!=\! 1.55{\text{π}} \times $ $20\;{\rm{MHz}},\;{Q_{\rm{m}}} = {{{\omega _{\rm{m}}}} / {{\gamma _{\rm{m}}}}} = 6.2 \times {10^4} $ , ${n_{\rm{m}}} = 403$ , $g = 0.5{\omega _{\rm{m}}} $ , ${\kappa _1} \!=\! 5{\omega _{\rm{m}}}, {\kappa _2} \!=\! 0.05{\omega _{\rm{m}}}, {\varDelta _2} \!=\! - {\omega _{\rm{m}}}$ , and the optical detuning ${\varDelta _1}$ satisfied the Eq. (66 ).[30 ] : ${\omega _{\rm{m}}} \!=\! 1.55{\text{π}} \!\times\! 20\;{\rm{MHz}}$ , ${Q_{\rm{m}}} \!=\! {{{\omega _{\rm{m}}}} / {{\gamma _{\rm{m}}}}} \!=\! $ $6.2 \times {10^4} $ , ${g_0} = 1.2 \times {10^{ - 4}}{\omega _{\rm{m}}}, \left| \varepsilon \right| = 6000{\omega _{\rm{m}}} $ (对应于驱动功率$P({\rm{mW}})$ ), 最初的热态声子数${n_{\rm{m}}} = 403$ (对应环境温度$T = 300\;{\rm{mK}}$ ). 我们选取的其他参数是: 光学失谐满足(66 )式的最佳条件, 光腔耗散系数分别为${\kappa _1} = 5{\omega _{\rm{m}}}$ 和${\kappa _2} = 0.05{\omega _{\rm{m}}}$ . 从图7 可以看到, 稳态声子数${n_{\rm{p}}}$ 可以小于1. 这意味着即使在通常的不可分辨边带情况下(即${\kappa _1} > {\omega _{\rm{m}}}$ ), 机械振子可以冷却到接近基态, 原因是第二个光腔与机械振子不发生直接耦合, 操作上容易提高第二个光腔品质因数. 另外辅助右腔与左腔的相互作用改变了所需的光谱: 从洛伦兹峰(其宽度大于机械振子的频率)(不可分辨边带)到具有双峰的谱(其右峰宽小于机械振子的频率). 这意味着有效的吸收边带条件得到满足, 因此可以实现机械振子的基态冷却.图7 , 选择最优冷却下的光腔耦合系数$J = 10{\omega _{\rm{m}}}$ , 图8 为平均声子数${n_{\rm{p}}}$ 随有效初始温度T 的变化. 有效初始温度越低, 对应的稳态声子数${n_{\rm{p}}}$ 越小, 即冷却越好. 当温度取T = 300 mK时, 稳态声子数约是0.0844, 这与图7 给的初始温度参数是符合的, 也是实验可行的.图 8 平均声子数${n_{\rm{p}}}$ 随有效初始温度T 的变化(给定的参数是${\omega _{\rm{m}}} = 1.55{\text{π}} \times 20\;{\rm{MHz}}$ , ${Q_{\rm{m}}} = {{{\omega _{\rm{m}}}} / {{\gamma _{\rm{m}}}}} = 6.2 \times {10^4} $ , $J = 10{\omega _{\rm{m}}} $ , $ g = 0.5{\omega _{\rm{m}}} $ , ${\kappa _1} = 5{\omega _{\rm{m}}}$ , ${\kappa _2} = 0.05{\omega _{\rm{m}}} $ , ${\varDelta _2} =$ $ - {\omega _{\rm{m}}} $ , 最优失谐${\varDelta _1}$ 满足(66 )式)Figure8. Mean phonon number ${n_{\rm{p}}}$ as a function of effective initial temperature T . The given parameters are ${\omega _{\rm{m}}} =$ $ 1.55{\text{π}} \times 20\;{\rm{MHz}} $ , $ {Q_{\rm{m}}} = {{{\omega _{\rm{m}}}} / {{\gamma _{\rm{m}}}}} = 6.2 \times {10^4} $ , $ J = 10{\omega _{\rm{m}}} $ , $ g = 0.5{\omega _{\rm{m}}} $ , ${\kappa _1} = 5{\omega _{\rm{m}}}, {\kappa _2} = 0.05{\omega _{\rm{m}}}, {\varDelta _2} = - {\omega _{\rm{m}}}$ and the optical detuning ${\varDelta _1}$ satisfied the Eq. (66 ).5.2.原子腔基态冷却 -->5.2.原子腔基态冷却 图9 和图10 分别刻画了冷却率${\gamma _{\rm{c}}}$ 和平均声子数${n_{\rm{p}}}$ 随最佳光腔耦合系数J 的变化, 通过辅助腔(右腔)内注入原子系综, 可以看出, 当参数选择恰当时, 原子系综影响下系统的加热跃迁涨落谱$S\left( { - {\omega _{\rm{m}}}} \right)$ 更低, 更抑制了加热跃迁, 并达到更高的基态冷却率${\gamma _{\rm{c}}}$ 和更少的平均声子数${n_{\rm{p}}}$ .图 9 冷却速率${\gamma _{\rm{c}}}$ 随最佳光腔耦合系数J 的变化(给定的参数是${\omega _{\rm{m}}} = 1.55{\text{π}} \times 20\;{\rm{MHz}}$ , ${Q_{\rm{m}}} = {{{\omega _{\rm{m}}}} / {{\gamma _{\rm{m}}}}} = 6.2 \times {10^4}$ , ${n_{\rm{m}}} \!=\! 403$ , $g \!=\! 0.5{\omega _{\rm{m}}} $ , ${\kappa _1} \!=\! 5{\omega _{\rm{m}}}$ , ${\kappa _2} \!=\! 0.05{\omega _{\rm{m}}} $ , ${\varDelta _1} \!=\! {\varDelta _2} \!=\!$ $ - {\omega _{\rm{m}}} $ , ${\varDelta _{\rm{a}}} = {\omega _{\rm{m}}}$ , $ {\gamma _{\rm{a}}} = 10{\omega _{\rm{m}}} $ , $ {g_{\rm{a}}} = 0.62 \times {10^{ - 4}}{\omega _{\rm{m}}} $ , $N = {10^8} $ )Figure9. Cooling rate ${\gamma _{\rm{c}}}$ as a function of optical coupling coefficient J . The given parameters are ${\omega _{\rm{m}}}\! =\! 1.55{\text{π}} \!\times \!20\;{\rm{MHz}}$ , $ {Q_{\rm{m}}} = {{{\omega _{\rm{m}}}} / {{\gamma _{\rm{m}}}}} = 6.2\! \times \!{10^4} $ , ${n_{\rm{m}}} = 403$ , $g \!=\! 0.5{\omega _{\rm{m}}}$ , ${\kappa _1} \!=\! 5{\omega _{\rm{m}}}$ , ${\kappa _2} = 0.05{\omega _{\rm{m}}}$ , $ {\varDelta _1} = {\varDelta _2} = - {\omega _{\rm{m}}}$ , ${\varDelta _{\rm{a}}} = {\omega _{\rm{m}}} $ , ${\gamma _{\rm{a}}} = 10{\omega _{\rm{m}}}$ , $ {g_{\rm{a}}} = 0.62 \times {10^{ - 4}}{\omega _{\rm{m}}}$ , $ N = {10^8} $ .图 10 平均声子数${n_{\rm{p}}}$ 随最佳光腔耦合系数J 的变化(给定的参数同图8 )Figure10. Mean phonon number ${n_{\rm{p}}}$ as a function of optical coupling coefficient J . The given parameters are same as the ones in Fig. 8 .6.结 论 本文研究了双光腔光力系统中机械振子的冷却. 首先得到系统的有效哈密顿量(34 )式, 然后利用微扰论和维纳-辛钦定理建立机械振子的速率方程, 从而得到光压涨落谱和稳态声子数表达式(37 )式. 机械振子的冷却结果主要由光压涨落谱的正频$S\left( { + {\omega _{\rm{m}}}} \right)$ 和负频$S\left( { - {\omega _{\rm{m}}}} \right)$ 部分决定. 需要注意的是: 率方程建立的稳态声子数公式必须满足弱耦合条件, 即$ g \ll {\omega _{\rm{m}}} $ 和${\gamma _{\rm{p}}}$ 远小于$S\left( \omega \right)$ 的谱宽度. 为了理解最优冷却, 图2 给出了光压涨落谱对系统参数的依赖. 该光压涨落谱$S\left( \omega \right)$ 具有类EIT特性, 最优冷却条件是$S\left( {{\omega _{\rm{m}}}} \right)$ 取峰点的值, $S\left( { - {\omega _{\rm{m}}}} \right)$ 取谷点(双光子共振点)的值, 最终得到最优冷却条件为${\varDelta _1} = {\omega _{\rm{m}}} - \dfrac{{{J^2}}}{{2{\omega _{\rm{m}}}}}, {\varDelta _2} = - {\omega _{\rm{m}}}$ . 此外, 为了得到较大的冷却率, 还需要满足${\kappa _2} \ll {\kappa _1}$ . 满足上述条件即可在边带不可分辨条件下实现机械振子的基态冷却. 当辅助腔内注入原子系综时, 恰当选择参数可以一定程度上达到优于双光腔光力系统时机械振子的冷却. 此外, 该模型已应用在声子的激光实验[23 ] . 这些研究结果有助于实验上实现机械振子的量子基态和量子信息过程. 




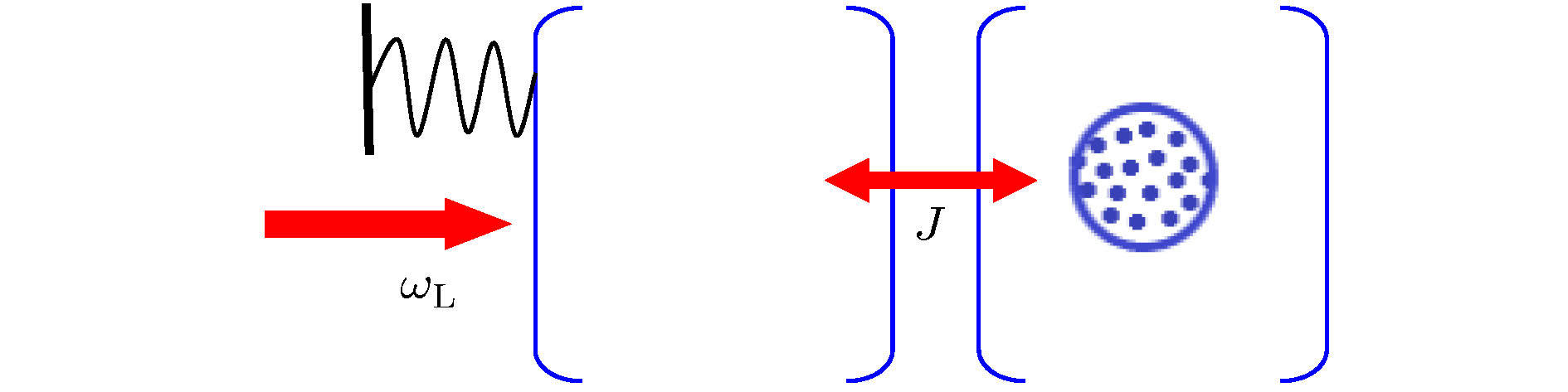 图 1 可实现的双光腔光力系统的示意图
图 1 可实现的双光腔光力系统的示意图































































































































 图 2 双腔间耦合系数J影响下涨落谱
图 2 双腔间耦合系数J影响下涨落谱






































































































 图 3 不同衰减率
图 3 不同衰减率

















 图 4 参数影响下空腔和原子腔涨落谱
图 4 参数影响下空腔和原子腔涨落谱
















 图 5 衰减率
图 5 衰减率








































 图 6 冷却速率
图 6 冷却速率































































 图 7 参数影响下平均声子数
图 7 参数影响下平均声子数































 图 8 平均声子数
图 8 平均声子数


























 图 9 冷却速率
图 9 冷却速率
























 图 10 平均声子数
图 10 平均声子数















