摘要:基于有限元法, 采用水平集方法捕捉相界面的移动, 构建了液滴撞击固体壁面的数值模型. 通过修正的幂律模型描述流体的非牛顿剪切变稀特性, 探讨了剪切变稀特性对液滴撞击固体壁面后铺展行为的影响, 分析了撞击不同浸润性壁面时剪切变稀特性对液滴撞击壁面行为的影响差异. 研究结果表明: 随着幂律指数m的减小, 液滴撞击过程中的黏性耗散减小, 液滴的形貌变化及无量纲参数变化更为显著. 接触角为55°的情况下: 当m降低至0.85时, 液滴铺展过程中开始出现显著区别于牛顿流体液滴的振荡现象; 当m降低至0.80时, 液滴在回缩过程中会出现中心液膜断裂的情况. 接触角为100°时, 剪切变稀液滴均会出现振荡行为, 振荡幅度随着m的减小而增大. 接触角为160°时, 牛顿流体液滴与剪切变稀液滴均会在回缩过程中弹起, 但剪切变稀液滴的弹起速度更快. 此外, 基于数值计算结果, 本文提出了接触角为55°情况下剪切变稀液滴撞击壁面后的最大无量纲铺展直径预测模型.
关键词: 非牛顿流体/
液滴撞击/
有限元方法/
水平集方法/
铺展动力学

English Abstract

全文HTML

--> --> -->

液滴撞击固体壁面现象广泛存在于工农业领域, 如内燃机中油滴撞击缸壁、喷雾冷却、喷涂印染、喷墨打印、农药在作物表面沉积等. 液滴撞击壁面后的行为包括沉积、边缘高速溅射、冠状溅射、回缩破碎、部分回弹及完全回弹等^[1]. 液滴的物性参数、撞击基面的理化性质以及撞击条件共同决定着液滴撞击固体壁面后的动态行为过程^[2,3].
在工业生产过程中, 流体常因添加了活性剂、高分子材料或颗粒而表现出不同的非牛顿特性, 包括黏弹性、剪切增稠、屈服应力和剪切变稀等. 牛顿流体液滴撞击固体壁面行为已被****们广泛探讨^[4,5]. 然而, 由于非牛顿流体流变学行为的复杂性, 目前有关非牛顿流体液滴撞击固体壁面行为的研究尚少. Jung等^[6]与Huh等^[7]的研究表明在流体中添加极少量的聚合物材料, 在不明显改变流体的密度, 表面张力和剪切黏度等物性的情况下, 可使流体表现出显著的黏弹性, 抑制液滴撞击固体壁面后的回弹行为. Luu等^[8]和Sa?di等^[9]通过实验发现对于表现出屈服应力特性的非牛顿流体, 液滴撞击固体壁面后的铺展和回缩行为都受到了抑制. Boyer等^[10]指出, 剪切增稠液滴撞击固体壁面后的铺展行为与牛顿流体液滴表现出极大的不同, 在撞击壁面后的初始铺展阶段液滴的变形会突然停止. 对剪切变稀流体液滴撞击固体壁面行为的研究, 主要采用的是实验方法, 关于剪切变稀特性对液滴撞击壁面行为的影响机制尚存在争议. German等^[11]研究了幂律流体液滴撞击固体壁面后的铺展直径与液膜厚度的变化, 结果表明剪切变稀特性影响着液滴撞击固体壁面后的动力学行为, 但液滴稠度系数在铺展过程中起主导作用. 然而An等^[12,13]对剪切变稀流体液滴撞击不同疏水性壁面的过程研究后指出, 在撞击过程中动态变化的剪切黏度直接影响着液滴的铺展. Andrade等^[14]的研究同样指出, 撞击到固体壁面后, 液滴内部动态变化的流场会改变剪切变稀流体液滴的剪切黏度, 直接影响着液滴的动力学行为. Laan等^[15]研究了表现出剪切变稀特性的血液液滴撞击壁面的行为, 他们指出相较于无穷剪切黏度, 剪切变稀特性对液滴行为的影响可忽略不计. 刘海龙等^[16]将纳米颗粒分散到环氧树脂中配制了表现剪切变稀特性的纳米流体, 研究了纳米颗粒的加入对液滴撞击固体壁面后铺展行为的影响, 他们指出纳米颗粒的加入显著抑制了液滴在壁面上的铺展和回缩行为, 但通过实验难以研究流变学参数对液滴撞击的独立影响.
虽然测量与分析技术的发展已经可以帮助我们通过实验从唯象的角度认知液滴撞击固体壁面这一复杂的物理现象, 但是由于实验条件的局限性, 对流场范围内的一些物理量如速度与压力仍然难以精确测定, 如相界面移动等微观物理现象也难以捕捉. 随着计算机技术和数值计算方法的不断进步, 数值模拟作为一种基本手段, 被众多****用来研究液滴撞击固体壁面行为. 由于气体和液体两相间存在的高黏度与密度比, 处理撞击液滴的相界面移动问题是采用数值模拟方法研究液滴撞击固体壁面行为的难点. 在固定网格上求解相界面移动的方法主要分为两类: 显式求解(界面追踪法)和隐式求解(界面捕捉法). 边界积分法^[17]和锋面追踪法^[18]是两种典型的界面追踪方法, 界面追踪方法提供的数值精度较高, 但它的适用范围仅限于斯托克斯流动. 与界面追踪方法不同, 界面捕捉法通过求解固定网格上独立的相函数来获得相界面的移动. 目前被****应用较多的界面捕捉方法包括相场法^[19]、流体体积法^[20]、扩散界面法^[21]、格子-玻尔兹曼方法^[22]以及水平集法^[23]等. 郑志伟等^[24]基于耦合水平集法和流体体积法的CLSVOF方法建立了中空液滴撞击固体壁面的数值模型, 研究了撞击速度和壁面浸润性对中空液滴撞击壁面动力学行为和传热特性的影响. 李玉杰等^[25]基于格子玻尔兹曼方法模拟了液滴撞击圆柱内壁面的过程, 分析了液滴的物性和圆柱内壁面浸润性等因素对撞击行为的具体影响. 高亚军等^[26]采用水平集方法模拟了双液滴同时撞击固体壁面的行为, 分析了不同撞击参数下中心射流高度和水平铺展半径随时间的演化规律. 在非牛顿流体液滴方面, 基于扩散界面方法, 韩丁丁等^[27]研究了用Oldroyd-B模型描述的黏弹性流体液滴撞击疏水壁面的动力学行为, 他们的数值模拟结果指出流体黏弹性对液滴的铺展过程没有显著影响, 界面及移动接触线处的弹性应力是液滴回弹行为受到抑制的主要原因. 通过VOF方法捕捉相界面的移动, 采用Herschel-Bulkley模型耦合流体的屈服应力-剪切变稀特性, Kim和Baek^[28]研究了屈服应力-剪切变稀液滴撞击固体壁面的行为, 他们的研究结果表明幂律指数、非牛顿雷诺数以及韦伯数决定着撞击液滴的铺展阶段, 而在液滴的回缩阶段, 非牛顿毛细数起着主要作用. 通过相场法捕捉相界面的移动, 采用Giesekus模型耦合流体的流变学特性, Wang等^[29]研究了黏弹性-剪切变稀液滴撞击固体壁面的行为, 他们指出惯性力、流体的黏性以及弹性共同影响着液滴撞击壁面后的运动状态.
上述的分析表明, 目前关于剪切变稀流体液滴撞击固体壁面行为的有限研究集中于实验工作, 尚无****对这一在相关领域中有极高应用价值的行为开展系统的数值模拟研究. 本文基于有限元耦合水平集方法捕捉相界面的移动, 通过修正的幂律模型描述流体的剪切变稀特性, 构建了剪切变稀液滴撞击固体壁面的数值模型, 深入分析了剪切变稀流体液滴撞击固体壁面过程中各参数的影响机制.

2

-->

2.1.控制方程

目前采用水平集方法求解界面演化尤其是涉及拓扑结构变化的界面演化问题已发展的较为成熟, 本研究采用水平集方法捕捉气液两相界面的移动, 用水平集方程中的$\phi $函数值来表示出具有限定厚度的液滴界面. 从相界面一侧过渡到另一侧时, $\phi $值从0到1逐渐变化, 本文中纯气相中$\phi = 0$, 液相中$\phi = 1, $相界面的位置由$\phi = 0.5$的等值线表示. 通过求解水平集方程中的$\phi $值来获取两相界面的位置. 本文求解的水平集方程为

$\frac{{\partial \phi }}{{\partial t}} + {{u}} \cdot \nabla \phi = \gamma \nabla \cdot \left[ {\varepsilon \nabla \phi - \phi (1 - \phi )\frac{{\nabla \phi }}{{\left| {\nabla \phi } \right|}}} \right],$

式中, ${{u}}$为速度; $\gamma $为水平集方程中重新初始化参数; $\varepsilon $为相界面厚度的控制参数, 通常为最小网格特征尺寸的一半; ${{n}}$为界面法向量,

${{n}} = \frac{{\nabla \phi }}{{\left| {\nabla \phi } \right|}}.$

采用界面捕捉法求解相界面移动的困难在于使高密度与黏度比的两相在界面处平滑过渡, 本文采用如下的Heaviside光滑函数对相界面进行光滑处理,

$\phi =\begin{cases} 0, &\phi \leqslant - \varepsilon , \\ \dfrac{1}{2} + \dfrac{\phi }{{2\varepsilon }} + \dfrac{1}{{2{\text{π}}}}\sin \left( {\dfrac{{{\text{π}}\phi }}{\varepsilon }} \right), &- \varepsilon < \phi < \varepsilon , \\ 1, & \phi \geqslant \varepsilon,\end{cases} $

光滑处理后, 界面处流体的密度和黏度可表示为

$\begin{split}& \rho \left( \phi \right) = {\rho _1} + \left( {{\rho _1} - {\rho _2}} \right)\phi , \\& \eta \left( \phi \right) = {\eta _1} + \left( {{\eta _1} - {\eta _2}} \right)\phi ,\end{split} $

式中, ${\rho _{\rm{1}}}$, ${\rho _{\rm{2}}}$分别为气体和液体的密度; ${\eta _{\rm{1}}}$, ${\eta _{\rm{2}}}$分别为气体和液体的黏度.
Navier-Stokes (N-S)方程可以用于描述不可压缩流体质量和动量的传输特性. 在固定的欧拉坐标系中, 连续性方程以及不可压缩, 耦合界面张力和重力作用的N-S方程如下:

$\nabla \cdot {{u}} = 0,$

$\begin{split} & \rho \left( {\frac{{\partial {{u}}}}{{\partial t}} + {{u}} \cdot \nabla {{u}}} \right) \\ =\;& \nabla \cdot \big\{ { - p{{I}} \!+\! \eta (\dot \gamma)\big[ {\nabla {{u}} \!+\! {{(\nabla {{u}})}^{\rm{T}}}} \big]} \big\} \!+\! \rho {{g}} \!+\! {{{F}}_{{\rm{st}}}},\end{split}$

式中, $\rho $为密度; $\eta \left( {\dot \gamma } \right)$为动态黏度; p为入口压力; I为单位矩阵; g为重力向量; ${{{F}}_{{\rm{st}}}}$为两相界面张力, 可以用下式求解,

${{{F}}_{{\rm{st}}}} = \nabla \cdot ((\sigma ({{I}} - {{n}}{{{n}}^{\rm{T}}}))\delta ),$

其中, $\sigma $表示气液界面张力, δ为狄克拉距离函数,

$\delta = 6\left| {\phi \left( {1 - \phi } \right)} \right|\left| {\nabla \phi } \right|.$

为了耦合剪切变稀特性对液滴撞击固体壁面后的影响, 数值模型中采用幂律模型描述液滴剪切黏度随剪切速率的动态变化,

$\eta \left( {\dot \gamma } \right) = k{\dot \gamma ^{m - 1}},$

式中, k是稠度指数, m是幂律指数. 同时为避免幂律模型在剪切速率过低时黏度失真的情况, 将幂律模型通过下式^[30]进行修正:

$\begin{split} & \dot \gamma = \max \big( {\sqrt {{{D}}:{{D}}} ,{{\dot \gamma }_{\min }}} \big), \\ & \Big\{ {{{D}} = \frac{1}{2} \big[ {\nabla {{u}} + {{\left( {\nabla {{u}}} \right)}^{\rm{T}}}} \big], \;{{\dot \gamma }_{\min }} = 0.01~{\rm s^{ - 1}}} \Big\},\end{split}$

式中D是变形张量.
通过添加壁面作用力的形式^[31]耦合了壁面浸润性对液滴铺展过程的影响, 作用于壁面处流体的力

${{{F}}_{{\rm{wall}}}} = \sigma \left( {{{{n}}_{{\rm{wall}}}} - {{n}}\cos \theta } \right)\delta - ({\eta }/{\beta }){{u}},$

式中, ${{{n}}_{\rm wall}}$为壁面处法向量; $\beta $为滑移长度, 通常为壁面处网格尺寸的大小, 设置壁面滑移边界条件可以避免移动接触线上产生应力奇点.
2 -->

2.2.数值模型验证

本文建立二维轴对称模型模拟液滴撞击壁面的动态过程. 常见的初始液滴位置设置方式有两种: 初始液滴与壁面相切或初始液滴置于壁面上方并与壁面保持一段距离, 本文采取第二种设置形式, 采用此种设置方式考虑了液滴撞击壁面过程中液滴下方气体的影响, 更为贴近真实情况. 图1为数值模型的计算域示意图, 液滴关于图左侧的对称轴对称, 在垂直壁面的初始速度${u_z}$的作用下撞击壁面并在壁面上铺展. 其中, 上边界及右边界均为法向应力等于零的开边界, 下边界为浸润壁边界条件. 对所有计算区域采用如图2所示的自由四边形网格进行剖分.
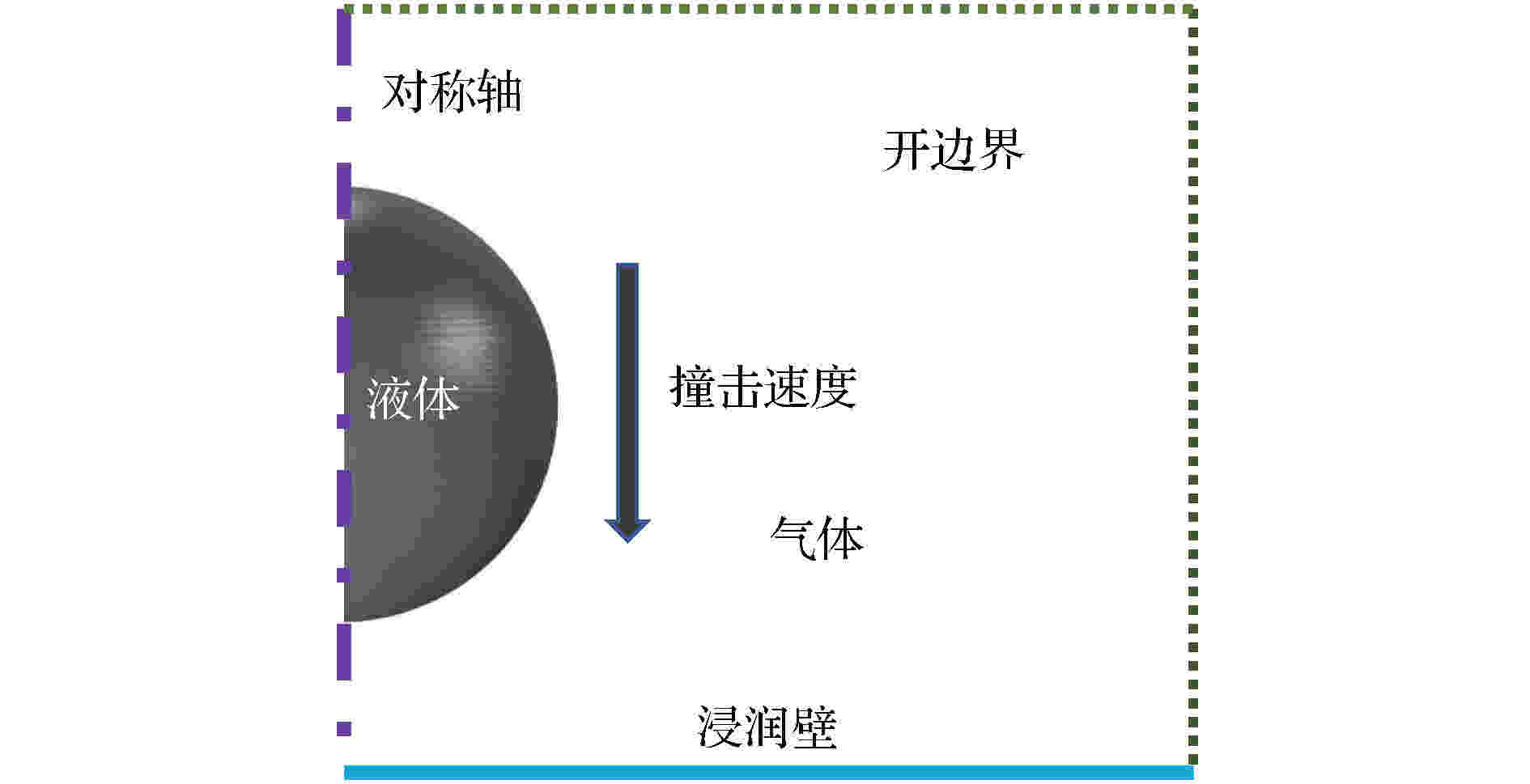图 1 数值模拟计算域设置
Figure1. Computation domain for numerical simulation.

图 2 计算域网格剖分
Figure2. Grid generation of computation domain.

为了系统地分析各因素对液滴撞击固体壁面后铺展行为的影响, 本文引入如下的无量纲参数讨论液滴的撞击铺展结果, 包括韦伯数$We = {{\rho {D_0}u_z^2}}/{\sigma }$, 非牛顿雷诺数$R{e_{\rm{n}}} = {{\rho D_0^m u_z ^{(2-m)}}}/{k}$^[28,32], 无量纲时间$\tau = ({{{u_z}}}/{{{D_0}}})t$, 无量纲直径${D^*} = {{{D_{\rm{t}}}}}/{{{D_0}}}$, 无量纲高度${H^*} = {{{H_{\rm{t}}}}}/{{{D_0}}}$, 其中, ${u_z}$为液滴在竖直方向上的速度分量, ${D_0}$为液滴初始直径, ${D_{\rm{t}}}$为液滴铺展过程中的动态直径, ${H_{\rm{t}}}$为液滴铺展过程中的动态高度, t为时间.
为了验证数值模型的准确性, 基于建立的数值模型, 首先模拟了纯水液滴撞击固体壁面的情况, 并将数值计算结果与Lim等^[33]的数值计算结果进行了对比验证. 模拟的相关参数设置见表1, 分析图3中液滴撞击固体壁面后无量纲直径随无量纲时间的变化, 可以发现本文的模拟结果与Lim等^[33]的模拟结果的误差较小(误差$ < 8\% $), 这说明了本文建立的数值模型能够较准确地模拟液滴撞击固体壁面的行为. 同时为了验证数值模型预测非牛顿流体撞击壁面行为的准确性, 基于建立的模型, 模拟了稠度系数为0.208 Pa·sⁿ, 幂律指数为0.4的剪切变稀液滴撞击疏水壁面的行为, 并将模拟结果与实验结果^[11]进行了对比. 图4为文献[11]中实验结果与本文模型模拟结果的对比, 可以看出不同时刻的数值计算结果均与实验结果高度吻合, 说明了本文建立的数值模型预测非牛顿流体液滴撞击壁面行为的准确性. 两相流模拟对网格的精度要求较高, 网格的尺寸大小直接影响着数值结果的精度, 图5为本研究的网格尺寸无关性验证, 所选择的模拟参数与表1相同. 考察3种不同的网格数量, 依次为23221, 51203, 90724. 选择直线(坐标(0, 0)至(0, 10))上无量纲速度的径向分量作为考察对象, 从图5可以看出网格数量51203和90724的数值结果基本重合, 网格收敛性较好, 因此以下研究的网格数量均为51203.

参数	符号/单位	数值
重新初始化参数	$\gamma /{\rm{m}} \cdot {{\rm{s}}^{ - 1}}$	1
界面厚度	$\varepsilon /\text{μm}$	$5 \times {10^{ - 2}}$
气体密度	${\rho _1}/{\rm{kg}} \cdot {{\rm{m}}^{ - {\rm{3}}}}$	1.2
气体黏度	${\eta _1}{\rm{/Pa}} \cdot {\rm{s}}$	$2 \times {10^{ - 5}}$
液体密度	${\rho _2}/{\rm{kg}} \cdot {{\rm{m}}^{ - {\rm{3}}}}$	1000
液体黏度	${\eta _2}{\rm{/Pa}} \cdot {\rm{s}}$	$8.9 \times {10^{ - 4}}$
温度	T/℃	25
液滴初始直径	${D_0}/{\text{μ} m }$	55
液滴撞击速度	uz$/{\rm{m}} \cdot {{\rm{s}}^{ - 1}}$	2.45
接触角	$\theta /{(^ \circ })$	55
气液界面张力	$\sigma /{\rm{mN}} \cdot {{\rm{m}}^{ - 1}}$	72.8

表1数值模拟参数设置
Table1.Symbols and constants in numerical simulation

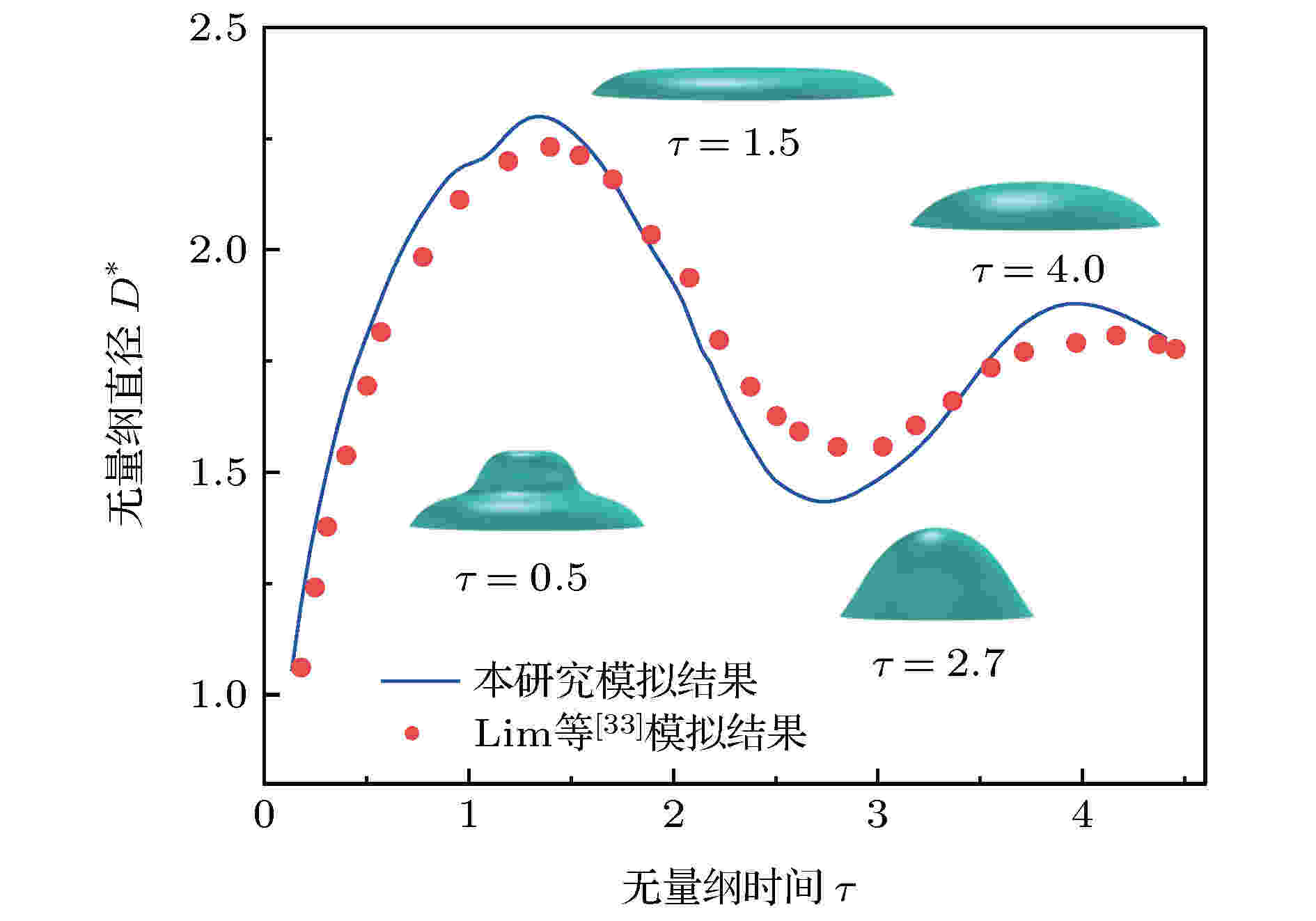图 3 本文数值模拟与Lim等^[33]相场模拟的结果比较
Figure3. Comparisons between simulation results in this work and phase-field simulation results^[33].

图 4 本文数值模拟与German等^[11]的实验结果比较(左侧为实验结果, 右侧为模拟结果)
Figure4. Comparisons between numerical simulation in this work and experiment results^[11], the left half of each image is obtained from the experiment, while the right half is the snapshots from our simulation.

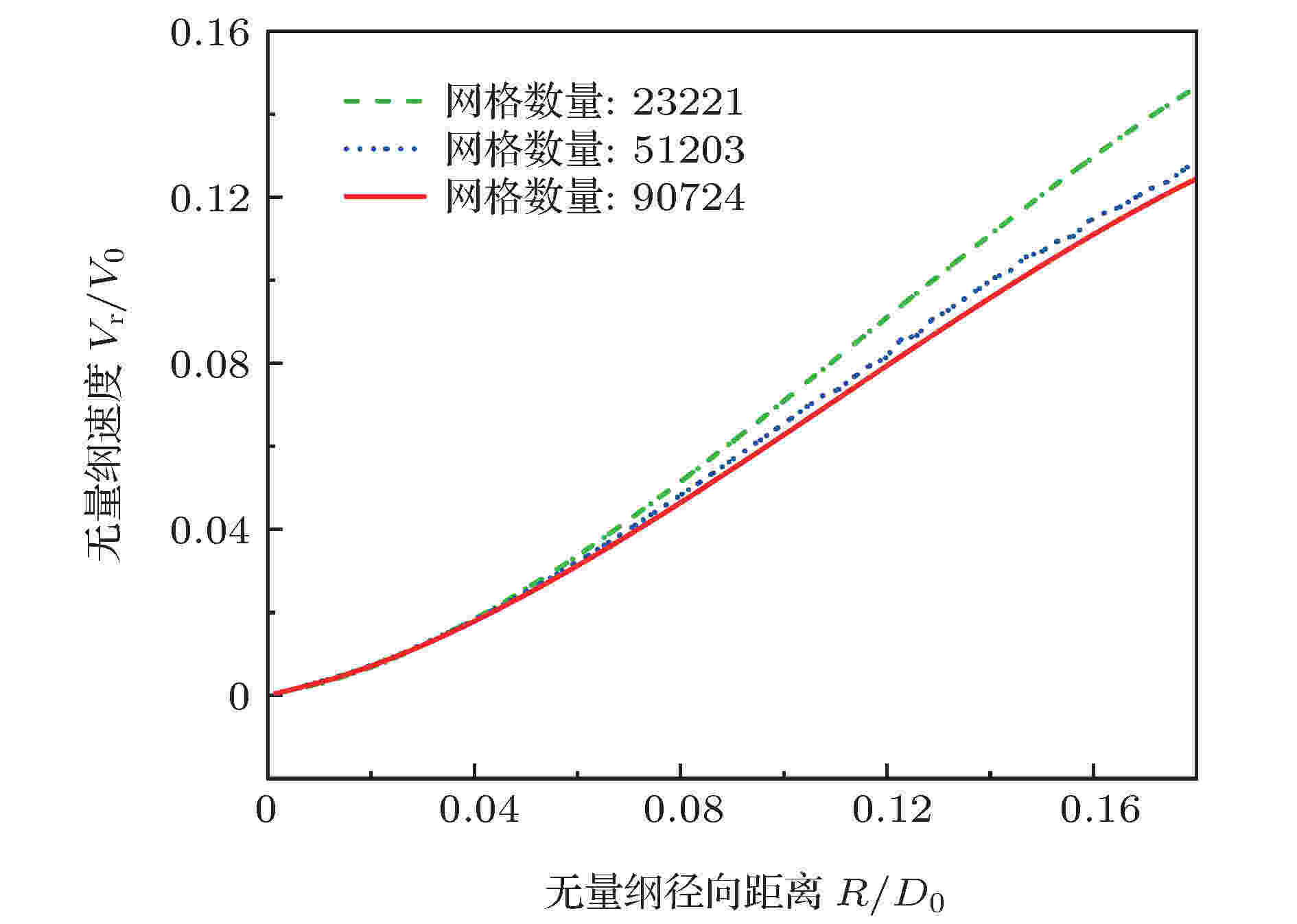图 5 液滴撞击壁面的网格收敛性验证
Figure5. Mesh convergence study of droplet impact on solid surfaces

2

-->

3.1.剪切变稀特性的影响

为了研究剪切变稀特性对液滴撞击固体壁面后铺展行为的影响, 在不改变表1中除黏度以外参数的情况下, 对比研究了牛顿流体液滴和三种表现出不同剪切变稀程度液滴的撞击壁面行为. 图6为模拟研究中不同幂律指数流体剪切黏度随剪切速率的变化, 稠度系数和幂律指数的具体数值选择参考了Lindner等^[34]对黄原胶稀溶液的流变学研究. 由幂律模型的本构关系可知在低剪切速率时, 其剪切黏度会趋近一个无穷大的值, 所以本文在剪切速率为$0.01\;{{\rm{s}}^{ - 1}}$时将曲线截断, 对黏度进行修正.
图 6 不同幂律指数流体剪切黏度随剪切速率的变化
Figure6. Variation of shear viscosity with shear rate at different power-law index.

从图7和图8可以发现, 对于表现出剪切变稀特性的液滴, 当m较小时它的铺展速度更快(更大的斜率), 但由于其在壁面上的铺展直径更大, 所以达到最大铺展的时间仍随着m减小而增大. 虽然铺展直径的增大会导致液滴与壁面间的摩擦能量耗散增加, 但从铺展直径的变化曲线可以看出, 黏性耗散在此过程中起着更大的影响. 液滴达到最大铺展直径后的回缩阶段已经不受惯性力的影响, 此时主导液滴运动的主要是表面张力和液滴黏性力, 同样由于剪切变稀特性的存在, 液滴的回缩速度更快 (更大斜率绝对值).
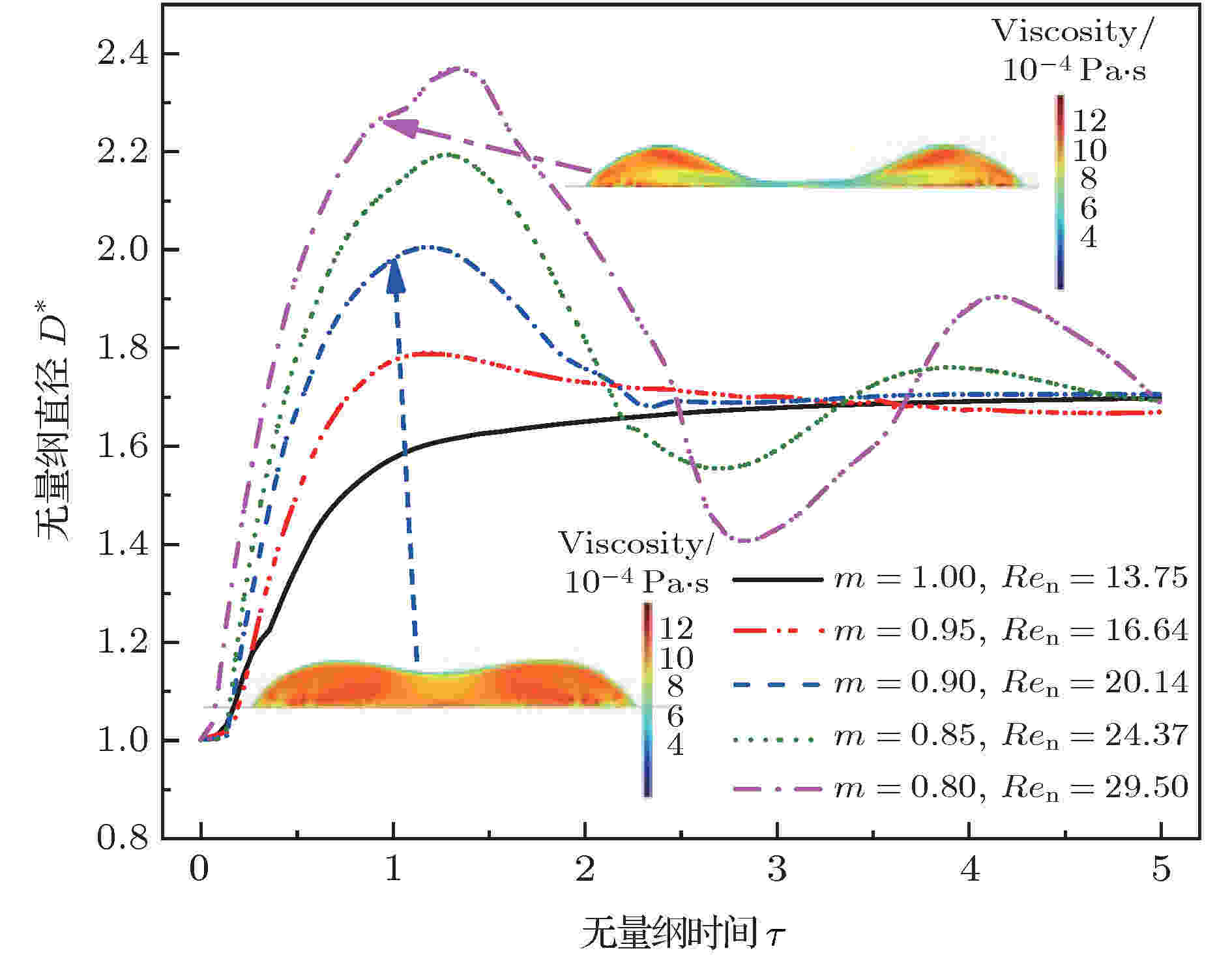图 7 不同幂律指数时无量纲直径随无量纲时间的变化(We = 4.53)
Figure7. Dimensionless diameter of droplet spread varying with dimensionless time at different power-law index (We = 4.53).

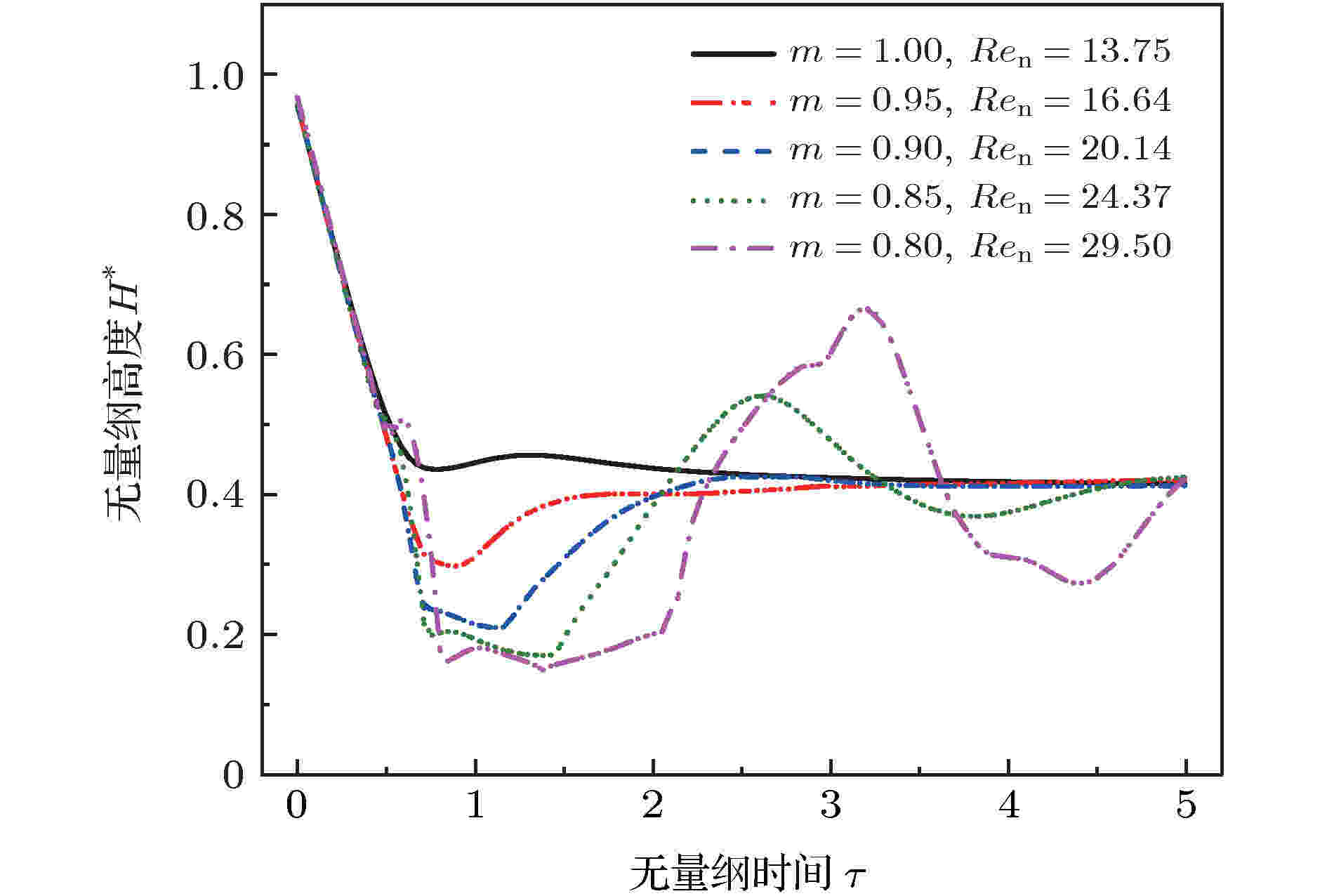图 8 不同幂律指数时无量纲高度随无量纲时间的变化(We = 4.53)
Figure8. Dimensionless height of droplet spread varying with dimensionless time at different power-law index (We = 4.53).

在$\tau $约为2.7和3.2时, m = 0.85和0.80的液滴分别达到最大的回缩高度, 但与其他3种液滴达到最大回缩后铺展直径和高度趋于恒定值不同, m = 0.85和0.80的液滴在此后无量纲直径再次增大, 无量纲高度再次减小. 这意味着液滴出现了二次铺展的情况, 也即液滴撞击固体壁面后出现振荡行为.
图9对比了m = 0.85和0.80的液滴撞击壁面(接触角为55°)时液滴形貌与速度矢量随时间的变化情况. $\tau = {\rm{1}}{\rm{.36}}$时, 可以发现m = 0.80的液滴出现内部薄液膜断裂的情况, 液滴内部液膜断裂的同时伴随着一个中心小液滴的生成. 在液滴的回缩过程中, 中心小液滴会重新合并到主液滴中. 这种液滴铺展过程中出现内部液膜断裂的行为与前人^[35,36]在数值模拟研究中发现的行为类似, 本文中出现此现象的原因是m = 0.80液滴的表观黏度最小, 液滴撞击壁面过程中的黏性耗散较小, 从图7中液滴内部黏度场分布也可以看出, 相较于幂律指数较大的液滴, 此时液滴内部液膜处的剪切较强, 剪切黏度较小, 抵抗形变的能力最弱, 最终在表面张力和惯性力的驱使下, 内部液膜断裂.
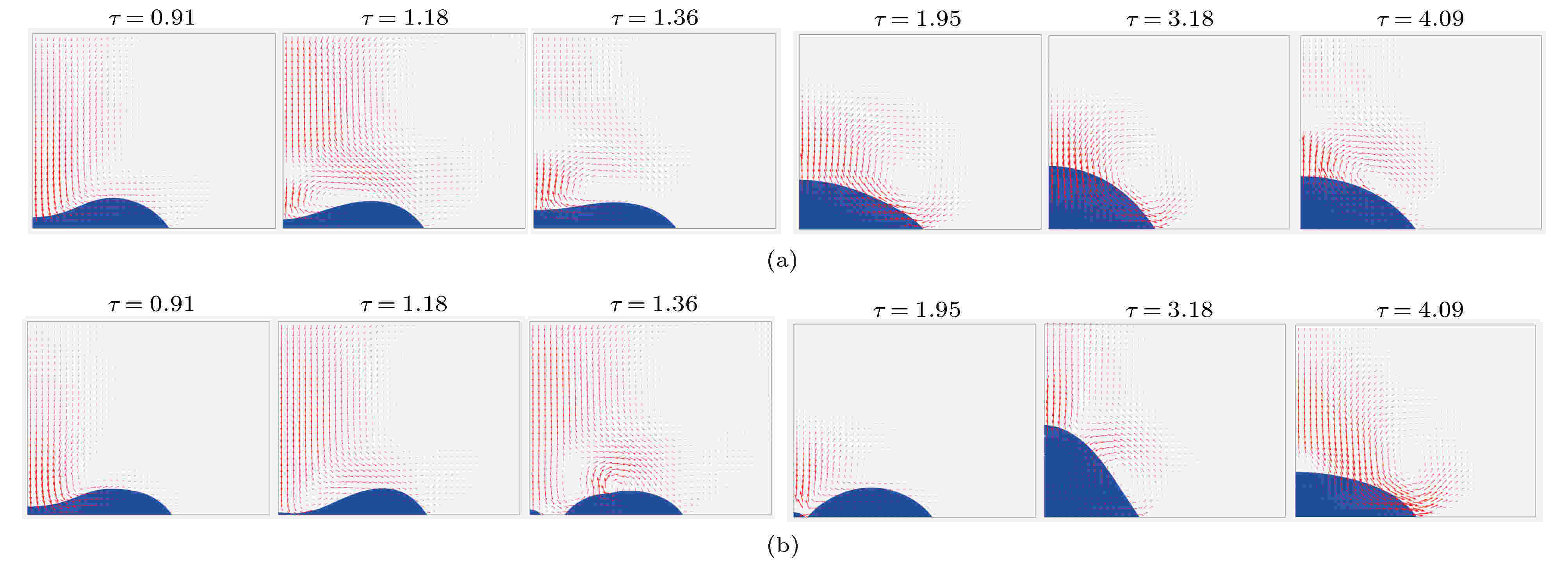图 9 不同幂律指数时液滴撞击壁面过程　(a) m = 0.85, Re_n = 24.37, We = 4.53; (b) m = 0.80, Re_n = 29.50, We = 4.53
Figure9. Process of droplet impact on surface at different power-law index: (a) m = 0.85, Re_n = 24.37, We = 4.53; (b) m = 0.80, Re_n = 29.50, We = 4.53.

2 -->

3.2.壁面浸润性的影响

液滴撞击壁面后的铺展行为被气液固三相耦合作用, 固体壁面的浸润性直接影响着壁面与液滴间力的相互作用. 通常采用接触角衡量壁面的浸润程度, 3.1节中已经研究了接触角为55°情况下液滴撞击固体壁面时的动力学行为, 为了研究壁面浸润性对液滴撞击壁面后铺展行为的影响, 继续模拟了壁面接触角分别设置为100°和160°时液滴撞击固体壁面的行为, 探讨壁面浸润性对牛顿流体液滴和剪切变稀液滴撞击壁面行为的影响差异, 图10和图11为数值计算结果的分析图.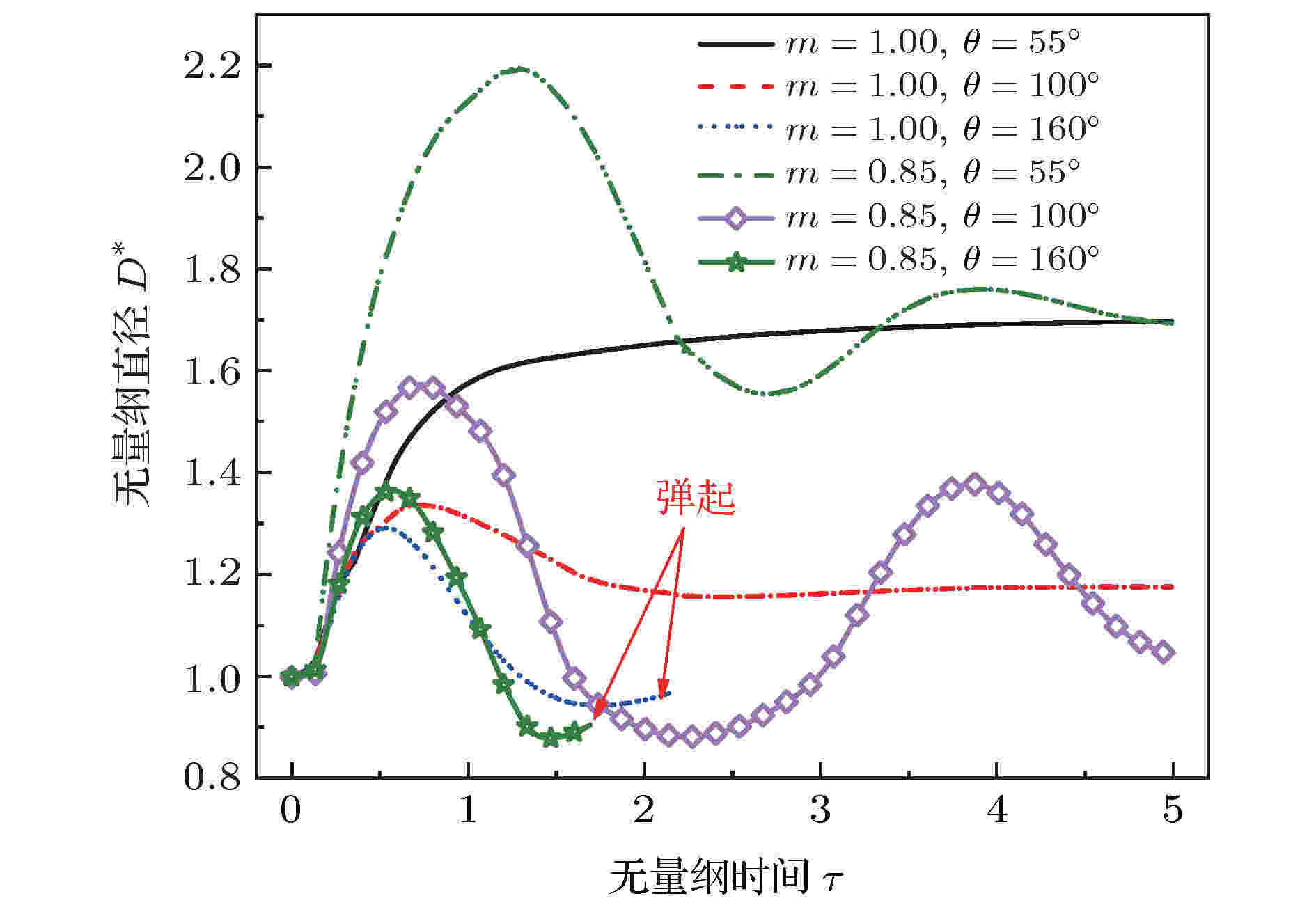
图 10 不同幂律指数时无量纲直径随无量纲时间的变化(We = 4.53, Re_n = 13.75 (m = 1.00), Re_n = 24.37 (m = 0.85))
Figure10. Dimensionless diameter of droplet spread varying with dimensionless time at different power-law index (We = 4.53, Re_n = 13.75 (m = 1.00), Re_n = 24.37 (m = 0.85))

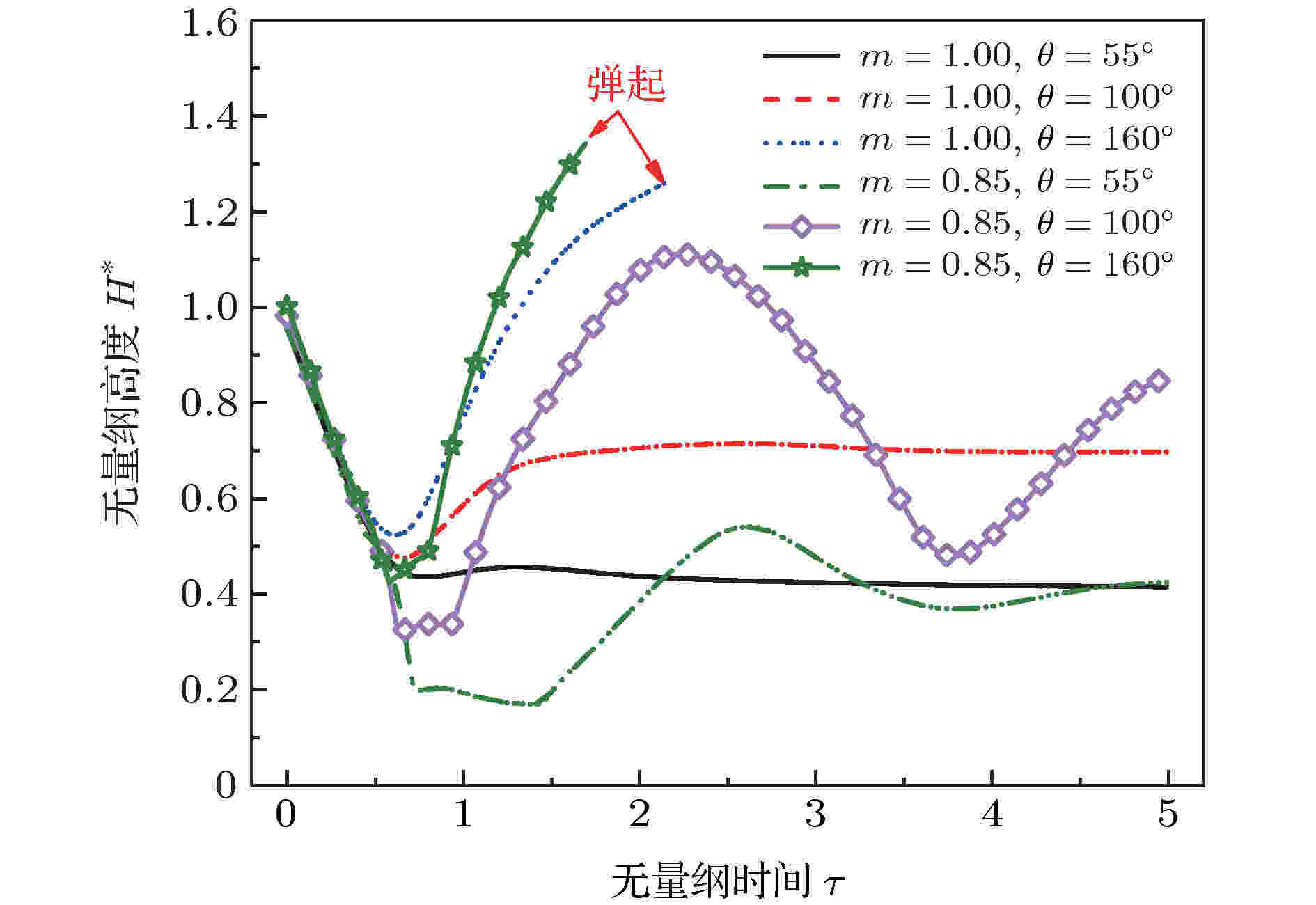图 11 不同幂律指数时无量纲高度随无量纲时间的变化(We = 4.53, Re_n = 13.75 (m = 1.00), Re_n = 24.37 (m = 0.85))
Figure11. Dimensionless height of droplet spread varying with dimensionless time at different power-law index (We = 4.53, Re_n = 13.75 (m = 1.00), Re_n = 24.37 (m = 0.85)).

从图10和图11可以看出, 随着壁面浸润性的减小 (接触角增大), 液滴撞击壁面后的最大无量纲直径增大, 但壁面浸润性对剪切变稀液滴的最大无量纲直径影响更为显著. 接触角为55°情况下, 牛顿流体液滴撞击壁面时, 液滴在达到最大铺展后基本不表现出回缩行为; 接触角为100°时液滴撞击壁面后铺展范围减小, 与壁面摩擦导致的能量耗散较小, 达到最大铺展后, 液滴的表面张力和壁面力驱使液滴回缩, 但此时并未弹起. 接触角为160°时, 液滴撞击过程中的摩擦耗散能量继续减少, 由(11)式可知壁面对液滴的作用力继续增大, 液滴最终在回缩过程中弹起.
图12(a)给出了接触角为160°时牛顿流体液滴撞击壁面过程中内部速度矢量随无量纲时间的变化. 在液滴的撞击瞬间, 液滴上部的速度几乎与撞击前一致, 此时在液滴近壁中心处的速度接近于零, 在液滴近壁边缘处则会产生较大的横向速度. 随着液滴在壁面上的铺展, 液滴边缘的横向速度逐渐减小, 液滴达到最大铺展时, 液滴边缘的横向速度减小为零. 在表面张力的作用下, 液滴开始回缩, 此时液滴近壁中心处的速度依然接近于零, 液滴上部的速度矢量方向向下, 但液滴边缘出现指向液滴中心的速度 (τ = 0.64), 这导致此时液滴内部出现了较小的速度环流. 随着液滴的回缩, 液滴横向回缩速度逐渐增大, 在液滴即将脱离壁面回弹起的时刻, 近壁中心处的横向速度达到最大值, 液滴脱离壁面后内部基本不存在径向的速度分量. 图12(b)为剪切变稀液滴撞击壁面过程中内部速度矢量分布的变化情况, 剪切变稀液滴撞击壁面后其内部的速度矢量分布变化与牛顿流体基本一致, 但由于流体的剪切变稀特性, 液滴铺展过程中的黏性耗散小于牛顿流体液滴, 黏性耗散的减少使得更多的惯性能量转化为表面能量, 在表面张力的驱使下液滴回缩的速度更快, 液滴弹起壁面的时间略早于牛顿流体液滴, 最终回弹高度也略高.
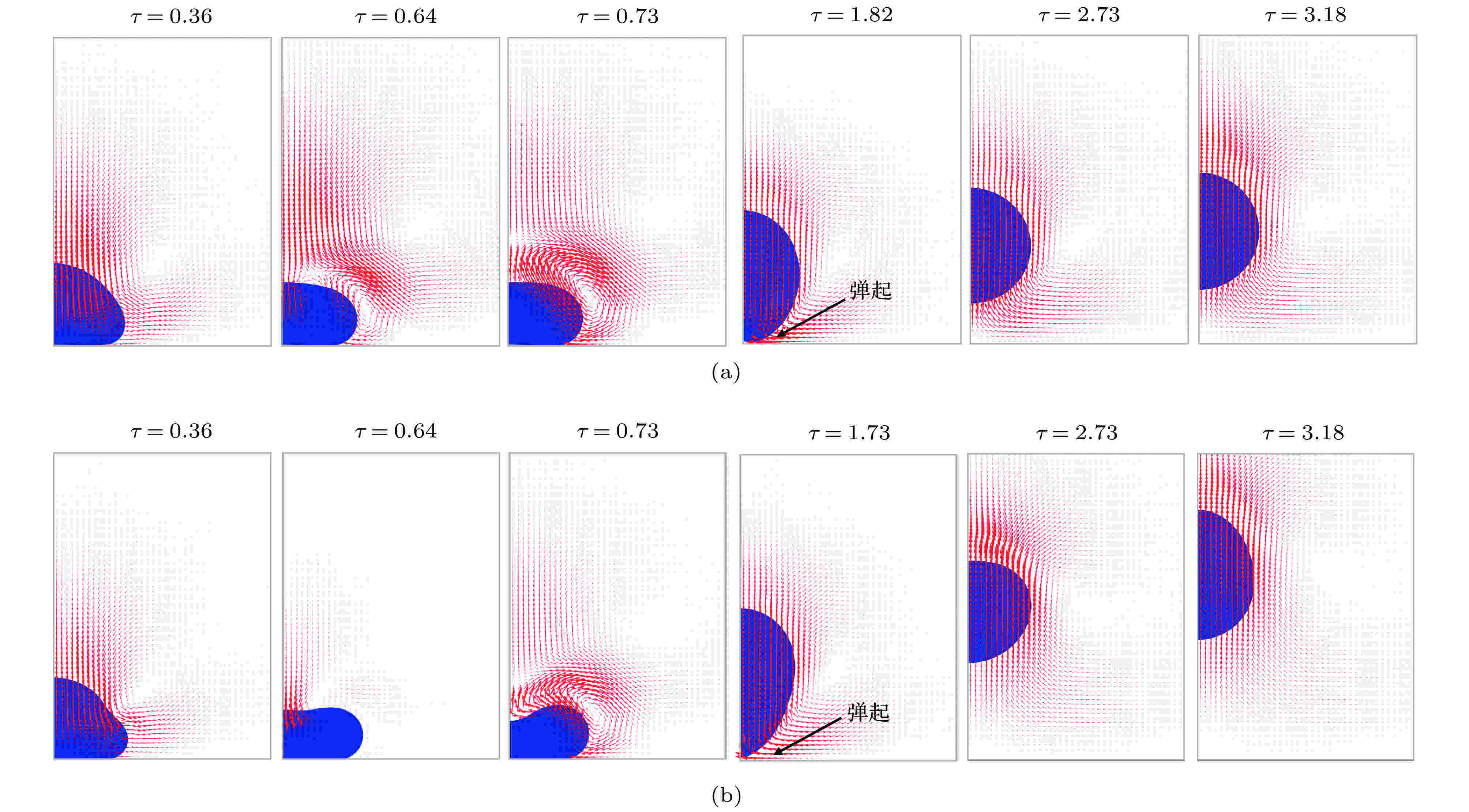图 12 不同幂律指数时液滴撞击壁面过程　(a) m = 1, Re_n = 13.75, We = 4.53; (b) m = 0.80, Re_n = 29.50, We = 4.53
Figure12. Process of droplet impact on surface at different power-law index: (a) m = 1, Re_n = 13.75, We = 4.53; (b) m = 0.80, Re_n = 29.50, We = 4.53.

2 -->

3.3.最大无量纲直径预测模型

液滴撞击壁面后无量纲直径的最大值$ D_{\max}^* $是其诸多工业应用中的一个重要参数. 例如在喷墨打印和喷雾冷却等过程中, 预测$ D_{\max}^* $对于提高不同材料和条件下的实施效果具有重要意义. ****们已经提出了大量的液滴撞击壁面后最大无量纲直径预测模型, 本文选择了如表2所列的7个典型最大无量纲直径预测模型, 列举模型中认为液滴撞击的壁面为亲水壁面或壁面浸润性对其模型预测结果影响较小, 其中包括理论模型^[37-41]和基于实验数据的拟合模型^[8,14]. 由于本文的数值模拟结果表明, 铺展阶段液滴表面张力的作用并不显著, 相比于惯性力项和黏性力项, 表面张力项对本文中液滴最大无量纲直径的影响较小, 故采用非牛顿雷诺数能够较为准确地描述剪切变稀液滴撞击壁面时的状态. 从表2中的均方根误差和图13可知, 前人所提出模型的预测结果与本文的数值计算结果存在着不可忽视的误差. 为了提高模型的预测准确度, 基于数值计算结果对经典黏性耗散模型$D_{\max }^* \text- Re_{\rm{n}}^{1/5}$修正, 提出了用于预测本文中接触角为55°时剪切变稀液滴撞击壁面后的最大无量纲铺展直径预测模型.

模型出处	方程	均方根误差
Jones[37]	$D_{\max }^* = {({\rm{4/3} }Re_{\rm{n} } ^{1/4})^{1/2} }$	0.20
Madejski[38]	$D_{\max }^* = Re_{\rm{n} } ^{1/5}$	0.31
Pasandideh-Fard等[39]	$D_{\max }^* = 0.5 Re_{\rm{n} } ^{1/4}$	0.64
Scheller和Bousfield[40]	$D_{\max }^* = 0.61{(R{e_{\rm{n}}}W{e^{1{\rm{/}}2}}{\rm{)}}^{0.166}}$	0.65
Roisman[41]	$D_{\max }^* = 0.87 Re_{\rm{n} } ^{1/5} - {\rm{0} }{\rm{.40} }Re_{\rm{n} }^{2/5}W{e^{ - 1/2} }$	0.97
Luu和Forterre[8]	$D_{\max }^* = Re_{\rm{n} } ^{1/(2 m + 3)}$	0.44
Andrade等[14]	$D_{\max }^* = 1.28 + 0.071 W{e^{1/4} }Re_{\rm{n} } ^{1/4}$	0.43
本文预测模型	$D_{\max }^* = Re_{\rm{n} } ^{0.17} = {\left[ {\rho D_0^mV_0^{2 - m}/k} \right]^{0.17} }$	0.06

表2最大无量纲直径预测模型
Table2.Prediction models of maximum dimensionless factor.

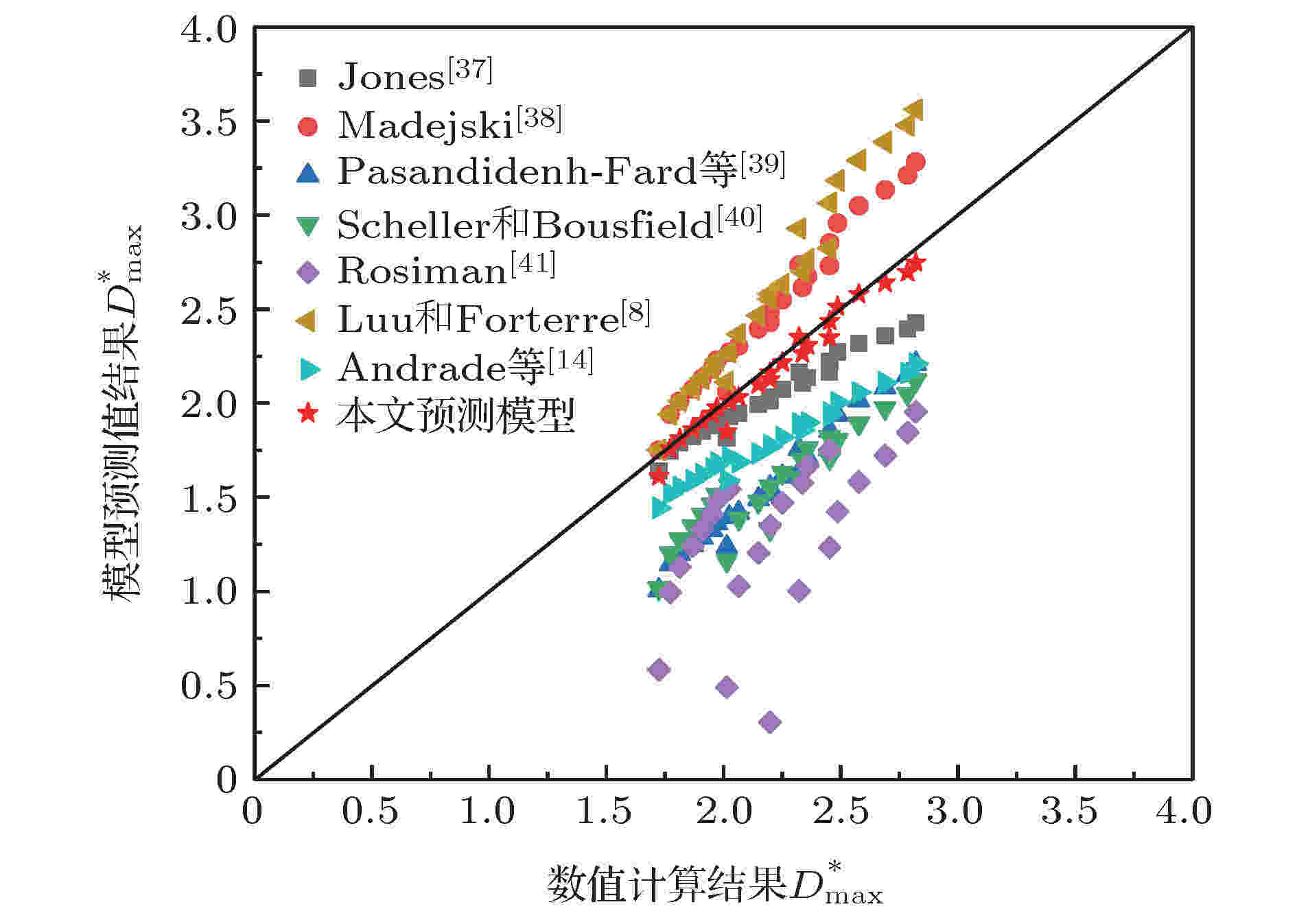图 13 最大无量纲直径模型预测值与数值计算值对比
Figure13. Comparison of $ D_{\max}^* $ between model prediction values and simulation data.

$D_{\max }^* = R{e_{\rm{n}}}^{0.17} = {\left[ {\rho {D_0}^mV_0^{(2 - m)}/k} \right]^{0.17}}.$

由图13可知(12)式的模型预测结果与本文数值计算结果具有较高的一致性.

本文基于有限元法, 通过水平集方法捕捉相界面的移动, 构建了液滴撞击固体壁面的数值模型. 采用修正的幂律模型描述流体的剪切变稀特性, 通过研究液滴形貌及无量纲参数随无量纲时间的变化规律, 分析了剪切变稀特性对液滴撞击不同浸润性壁面行为的影响机制, 得到如下结果.
1)液滴撞击壁面的过程中, 剪切变稀液滴内部剪切速率的改变使液滴的黏度动态变化. 幂律指数m较小的液滴, 液滴形貌变化更为显著. 在接触角为55°时液滴撞击壁面的情况下, 当幂律指数m小于0.85时, 液滴撞击壁面后开始表现出振荡行为, 当幂律指数m小于0.80时, 液滴撞击壁面过程中出现内部液膜断裂的情况.
2)壁面浸润性对剪切变稀液滴撞击壁面行为的影响更为显著, 在接触角为100°时液滴撞击壁面情况下, m = 0.85的剪切变稀流体表现出区别与牛顿流体的振荡行为. 当接触角为160°时, 牛顿流体液滴和剪切变稀液滴撞击壁面时均会弹起壁面, 但因黏性耗散较小, 剪切变稀液滴弹起的速度更快.
3)基于数值计算结果和前人的经典黏性耗散模型, 本文提出了接触角为55°时剪切变稀液滴撞击壁面后最大无量纲直径的预测模型, 模型预测结果与本文的数值计算结果取得了较高的一致性.