摘要: 针对用庞加莱截面分析非线性系统时较难选择合适截面的问题, 提出了一种投影时域法. 该方法可以在时域上直观地判断所选平面是否合适并实时准确地调整平面的方向与位置. 文中给出了投影时域法的完整定义并从理论上详细分析了该方法的原理; 同时研究了在时域上判断所选平面是否是合适的庞加莱截面的条件以及如何调整所选平面的方向与位置; 最后, 利用投影时域法对三种典型的三维或四维非线性系统进行了仿真实验, 实验结果证明了该方法的有效性和实用性.
关键词: 庞加莱截面 /
时域 /
非线性系统 English Abstract A new method for selecting arbitrary Poincare section Zhang Shi Wang Pan Zhang Rui-Hao Chen Hong Electronic Engineer College, Heilongjiang University, Harbin 150080, China Received Date: 17 October 2019Accepted Date: 18 November 2019Published Online: 20 February 2020Abstract: Poincare section is an important method for analyzing nonlinear systems. Choosing a suitable plane as the Poincare section is the key to using the Poincare section to analyze a nonlinear system. At present, it is still a difficult problem to select a suitable Poincare section when analyzing a nonlinear system. This is caused by two reasons. On the one hand, the classical method for selecting a partial Poincare section only applies to analyze a part of the nonlinear system orbit, whether the selected plane is a suitable Poincare section is affected by the different initial points. On the other hand, according to the actual situation, different researchers have different needs for Poincare section. In order to solve this problem, a new method named Projection Time Domain method is put forward in this paper. This method can help us not only directly reflect the intersection between the nonlinear system orbit and the selected plane, but also accurately adjust the direction and position of the selected plane in real time. It can be used to quickly find a plane which fully intersects the nonlinear system orbit or an arbitrary plane as a Poincare section. In this paper, the complete definition of Projection Time Domain method is given firstly. Then, the principle of Projection Time Domain method is theoretically analyzed in detail. At the same time, the rules for determining whether the selected plane is a suitable Poincare section in the time domain are also studied. Finally, it is introduced how to quantify the direction and position of the selected plane in the phase space. The simulation experiments are conducted with three typical three-dimensional and four-dimensional nonlinear systems by using this new method. The experimental results consistent with the theoretical analysis, which demonstrate the effectiveness and practicability of this method.Keywords: Poincare section /time domain /nonlinear system 全文HTML --> --> --> 1.引 言 在研究非线性系统的过程中, 庞加莱截面法可以有效地降低分析非线性系统的难度: 首先, 庞加莱截面将系统的连续轨线转换为离散的点, 并且保留了系统的部分拓扑结构, 成为连接离散与连续信号的重要桥梁; 其次, 庞加莱截面可以降低系统的维数; 最后, 庞加莱截面可以直观地反映系统的内部结构. 这些特征使庞加莱截面法被广泛地运用于量子力学[1 -2 ] 、语音识别[3 -4 ] 、医学研究[5 ] 和物理电子学[6 ] 等领域. 用庞加莱截面法对非线性系统进行分析时大多采用计算机数值仿真[7 -10 ] 或硬件系统实现[11 -13 ] 的形式.[14 ] . 局部庞加莱截面的选取方法仅仅适用于截取系统轨迹的一部分, 并且初始点选取的不同也会影响截面的截取效果[15 ] .[16 ] . 一些研究者将全局庞加莱截面的选择方法视为庞加莱截面参数的优化问题, 通过算法来寻找最优解: Krzysztof[17 ] 列举了可以用于优化庞加莱截面参数的几类算法, 并使用进化算法针对几个时间序列找到了合适的庞加莱截面, 以此判断该时间序列是否是随机信号; Babak和Amir[18 ] 提出了利用香农熵作为判断庞加莱截面位置是否合适的依据, 通过大量的计算针对一组离散时域信号找出了最合适的庞加莱截面. 这些基于算法的全局庞加莱截面选择方法从各自研究角度恰当地利用庞加莱截面取得了研究成果, 但是难以实时观测分析, 并且只能得到某个方向与位置固定的庞加莱截面, 不便于研究者自由地调整截面的方向与位置. 但是, 不同系统、不同研究者对于庞加莱截面的需求不同, 例如: Atefeh和Ateke[19 ] 在对PPG信号进行分析时, 通过变换角度的方式选择了多个特定角度的平面作为庞加莱截面; Carlos 和Daniel[20 ] 选取了一个平行于x 轴和z 轴的平面作为截面, 以此设计出一个基于混沌的保密通信系统; 闫登卫等[21 ] 则分别选取了平面$x = 5$ 和$y = 0$ 对一类基于忆阻器的混沌系统进行分析. 对此, 本文提出了一种在时域上选择全局庞加莱截面的方法—投影时域法(Projection Time Domain method, PTD法). 该方法既能够在时域上直观地反映系统轨道与所选平面的相交情况, 又能够实时准确地调整所选平面的方向与位置, 从而选取任意方向与位置的平面作为截面, 可以有效地降低选择全局庞加莱截面的难度.2.PTD法的定义及分析 为了方便快捷地针对不同的非线性系统选择合适的庞加莱截面, 本文提出的PTD法定义如下: 在三维空间里, 系统${\rm{d}}L/{\rm{d}}t = f(L), (L = l_1, {l_2}, {l_3})$ 的三路时域输出分别为$l_{1}(t),l_{2}(t),l_{3}(t)$ . 将系统轨道沿着$z$ 轴方向投影到任意不平行于$z$ 轴的平面$\varSigma:\alpha x + \beta y +$ $ \gamma z + \lambda = 0 (\gamma \ne 0) $ 上, 将投影线的$z$ 轴坐标随时间演化的轨迹记为$F(l_{1}(t),l_{2}(t))=Al_{1}(t)+Bl_{2}(t)+C$ . 记$l_{3}(t)$ 为参考信号, $F(l_{1}(t),l_{2}(t))$ 为平面信号, 当且仅当$F(l_{1}(t),l_{2}(t))=l_{3}(t)$ 时, 系统轨道与平面$\varSigma $ 相交, 平面$\varSigma $ 截取了系统轨道. 若存在一组参数${A_0}, {B_0}, {C_0}$ , 使得$F(l_{1}(t),l_{2}(t))$ 与$l_{3}(t)$ 交点个数较多且交点集中于$l_{3}(t)$ 的每个增幅振荡区域, 则$F(l_{1}(t),l_{2}(t)$ 所在平面${\varSigma _0}:{A_0}x + {B_0}y - z + {C_0} = 0$ 为合适的庞加莱截面.z 轴坐标方向投影到任意不平行于$z$ 轴的平面$\varSigma $ 上, 则投影线与系统轨道具有相同的$x, y$ 轴坐标, 系统轨道与平面$\varSigma $ 的相交关系可以通过比较投影线z 轴坐标与系统轨道z 轴坐标来判断(图1 ).图 1 轨道在平面上的投影Figure1. The projection of a trajectory onto a plane.图1 中, 实线为系统轨道, 虚线为被平面$\varSigma $ 遮挡的系统轨道, 点划线为系统轨道沿着z 轴方向投影到平面$\varSigma $ 上的投影线. 点${D_1}$ 是系统轨道上的任意点, 其z 轴坐标用${l_3}(t)$ 表示; 点${D_2}$ 是点${D_1}$ 在平面$\varSigma $ 上的投影点, 其z 轴坐标用$F({l_1}(t), {l_2}(t))$ 表示. 在相空间中系统轨道随着时间演化不停地远离或者靠近平面$\varSigma $ , 这种靠近或远离的趋势可以用$F({l_1}(t), {l_2}(t))$ 与${l_3}(t)$ 的差值来度量, 称$F({l_1}(t), {l_2}(t))$ 为对应平面$\varSigma $ 的平面信号, 并称${l_3}(t)$ 为参考信号. 如果平面信号与参考信号的差值为0, 则在相空间中系统轨道穿过了平面$\varSigma $ . 分别做出平面信号与参考信号的时域波形(图2 ).图 2 $F({l_1}(t), {l_2}(t))$ 与${l_3}(t)$ 的波形Figure2. Waveform of $F({l_1}(t), {l_2}(t))$ and ${l_3}(t)$ .图2 中, 实线${l_3}(t)$ 为参考信号, 表示系统轨道的z 轴坐标随时间演化的轨迹; 点划线$F({l_1}(t), {l_2}(t))$ 为平面信号, 表示投影线的z 轴坐标随时间演化的轨迹. 参考信号与平面信号的每一个交点都表示在相空间中系统轨道穿过了一次平面$\varSigma $ .z 轴的平面$\varSigma $ 的一般式方程为1 )式后, 得2 )式, 令$A = - {\alpha }/{\gamma }, B = - {\beta }/{\gamma }, C = - {\lambda }/{\gamma }$ , 则3 )式可知, 对于平面$\varSigma $ 上任意一点的$x, y$ 轴坐标值, 其z 轴坐标值为$F(x, y)$ . 将投影线的$x, y$ 轴坐标值代入(3 )式, 令$x = {l_1}(t), y = {l_2}(t)$ (投影线和系统轨道具有相同的$x, y$ 轴坐标), 则投影线的z 轴坐标为4 )式即为平面信号的函数表达式. 若改变参数$A, B, C$ , 平面信号的时域波形发生改变, 平面$\varSigma $ 在相空间中的方向与位置也会相应变化. 平面信号可以视作为非线性系统两路时域输出${l_1}(t), {l_2}(t)$ 的比例相加, 叠加的比例分别由参数$A, B$ 控制, 故改变参数$A, B$ 可以调整平面信号的形状; 参数C 作为(4 )式中的常数项, 改变参数C 可以上下平移平面信号.$\varSigma $ 是合适的庞加莱截面, 应当改变平面信号的参数$A, B, C$ , 调整平面信号的形状, 使平面信号满足某些条件. 下面分别从平面信号与参考信号交点的数量、平面信号与参考信号交点的位置两个方面分析平面信号需要满足的条件.$\varSigma $ 与系统轨道的交点个数. 在时域上参考信号与平面信号的每一个交点都对应着相空间中平面$\varSigma $ 与系统轨道的一个交点. 因此, 截取一段时间内的平面信号和参考信号, 如果该时段内参考信号与平面信号的交点个数较多, 则在相空间中系统轨道穿过平面$\varSigma $ 的次数较多; 如果该时段内参考信号与平面信号的交点较少, 则在相空间中系统轨道穿过平面$\varSigma $ 的次数较少. 平面信号与参考信号交点的数量可以直观但粗略地对平面$\varSigma $ 进行评价.$\varSigma $ 是否为合适的庞加莱截面. 在时域上, 系统轨道的涡卷与键带的波形具有明显的差异, 增幅振荡正是涡卷在时域上表现出的显著特征(图3 )[22 ] .图 3 涡卷的相轨与波形 (a)相轨; (b)波形Figure3. Phase trajectoy and waveform of vortex: (a) Phase trajectoy; (b) waveform.图3 中, 涡卷在相空间中的轨道是螺旋扩张运动, 参考信号在时域上的波形表现为振幅逐渐增大的振荡运动, 称这部分时域波形为参考信号的涡卷部分; 键带的相轨将两个涡卷连接起来, 参考信号在时域上的波形表现为单向运动, 称这部分时域波形为参考信号的键带部分. 如果在时域上平面信号与参考信号交于参考信号的涡卷部分, 则在相空间中平面$\varSigma $ 切入了系统轨迹的涡卷; 如果在时域上平面信号与参考信号交于参考信号的键带部分, 则在相空间中平面$\varSigma $ 切入了系统轨迹的键带. 参考信号与相空间中系统轨迹的联系对平面信号与参考信号交点的位置作出了明确的要求:$\varSigma $ 切入了系统轨迹的每一个涡卷.$\varSigma $ 切入了系统轨迹中这个涡卷的每一圈.$\varSigma $ 与系统轨道有足够多的交点, 2)确保了平面$\varSigma $ 切入系统轨道的每个涡卷.3.任意截平面的选取 除了选择与系统轨道充分相交的截面, 某些场合也需要选择具有特定方向与位置的平面$\varSigma $ 作为截面. 这里对平面信号的参数$A, B, C$ 的几何意义进行定量的分析, 以便对平面$\varSigma $ 的方向与位置施加准确的控制.3 )式, 平面$\Sigma $ 可以用下式描述:$\varSigma $ 的法向量为$(A, B, - 1)$ , 这说明改变参数$A, B$ 可以调整平面$\varSigma $ 的方向; 参数C 作为常量出现, 改变参数C 的值可以调整平面$\varSigma $ 在相空间中的水平高度.$\varSigma $ 与x 轴正方向的夹角${\theta _1}$ 和平面$\varSigma $ 与y 轴正方向的夹角${\theta _2}$ 描述平面$\varSigma $ 的方向. 当夹角${\theta _1}, {\theta _2}$ 的数值确定时, 平面$\varSigma $ 的方向也随之确定. 取x 轴正方向的向量为$(1, 0, 0)$ , y 轴正方向的向量为$(0, 1, 0)$ , 则${\theta _1}, {\theta _2}$ 可表示为$A, B$ 的值, 夹角${\theta _1}, {\theta _2}$ 相应地发生变化, 平面$\varSigma $ 的方向也会发生变化. 可以根据研究需要选定夹角${\theta _1}, {\theta _2}$ , 通过(6 )式求出参数$A, B$ . 下表列出了一些由(6 )式确定的常用平面所对应的参数$A, B$ .$\varSigma $ 改变前与改变后的参数值分别为${C_1}, {C_2}$ , 则$\Delta C$ 的符号为正, 说明平面$\varSigma $ 沿着z 轴正方向整体平移了$|\Delta C|$ 的距离; 若$\Delta C$ 的符号为负, 说明平面$\varSigma $ 沿着z 轴负方向整体平移了$|\Delta C|$ 的距离; 若$\Delta C$ 的值为0, 说明平面$\varSigma $ 在z 轴方向没有发生移动.6 )式与(7 )式定量地描述了参数$A, B, C$ 对平面$\varSigma $ 方向与位置的影响, 通过改变参数$A, B$ 调整平面$\varSigma $ 的方向, 改变参数C 调整平面$\varSigma $ 的水平高度, 使用者总能调整出符合要求的平面$\varSigma $ 作为庞加莱截面.4.仿真实验 本节以Lorenz系统、三涡卷Chua系统[23 ] 和超混沌Chen[24 ] 系统为例, 通过仿真实验验证PTD法的有效性与可行性. 其中Lorenz系统为有翼混沌系统的代表, 三涡卷Chua系统为多涡卷混沌系统的代表, 超混沌Chen系统为高维超混沌系统的代表. 实验中所有的系统均采用四阶龙格库塔法进行迭代仿真, 对每个系统都选取多组平面进行分析.4.1.Lorenz系统 4.1.Lorenz系统 Lorenz系统的归一化的系统方程为$a = 10, \; b = 2.667, \;c = 28$ 时, Lorenz系统处于混沌状态. Lorenz系统在相空间中的系统轨道表现为两个翅膀. 本实验将以Lorenz系统为例说明如何调整平面信号的参数以寻找到合适的庞加莱截面.x 轴正方向夹角为0度, 与y 轴正方向夹角为45o的平面作为截面. 由表1 知, 平面信号的参数$A, B$ 应当设置为$A = 0, B = 1$ , 参数C 的设置没有要求, 设置$C = 0$ , 实验结果如图4 所示.序号 ${\theta _1}$/(o) ${\theta _2}$/(o) A B 1 0 0 0 0 2 0 45 0 1 3 0 60 0 $\sqrt 3 $ 4 0 135 0 –1 5 45 0 1 0 6 60 0 $\sqrt 3 $ 0 7 135 0 –1 0
表1 常用平面的参数值Table1. Parameter values of typical planes.图 4 平面一的实验结果 (a)时域波形; (b)相图Figure4. Experimental results of the first plane: (a) Waveform; (b) phase diagram.图4(a) 中, 蓝色实线为参考信号, 红色点划线为平面信号, 参考信号与平面信号的时域波形形状不同, 并且水平高度不同, 在图4(a) 时域范围内参考信号与平面信号仅有两个交点. 相对应地, 在图4(b) 中, 截面与系统轨道并没有充分相交, 该平面仅仅切入了系统轨道的一小部分右翼. 在图4(b) 中, 截面平行于x 轴, 与y 轴正方向夹角为45o, 与本次实验想要选择的方向相符.图4(a) 中, 参考信号与平面信号不处于同一水平高度上, 不改变平面一的方向, 保持参数$A, B$ 不变, 只改变平面一的高度, 将参数C 设置为$C{{ = 25}}$ , 由此得到平面二的实验结果(图5 ).图 5 平面二的实验结果 (a)时域波形; (b)相图Figure5. Experimental results of the second plane: (a) Waveform;(b) phase diagram.图5(a) 中, 蓝色实线为参考信号, 红色点划线为平面信号, 调整位置后, 平面信号与参考信号的交点个数显著增多. 相对应地, 在图5(b) 中, 系统轨道与截面的交点个数也显著地增多.图6 为调整后的平面三的实验结果, 选取的参数为$A = 1, B = - 1, C = 25$ .图 6 平面三的实验结果 (a)时域波形; (b)相图Figure6. Experimental results of the third plane: (a) Waveform; (b) phase diagram.图6(a) 中, 蓝色实线为参考信号, 红色点划线为平面信号, 参考信号与平面信号交点较多, 且集中于参考信号的涡卷区域. 在图6(b) 中, 所选平面的方向发生了变化, 与系统轨道充分相交. 该平面截取到了系统轨道的双翼, 是合适的庞加莱截面.4.2.三涡卷Chua系统 -->4.2.三涡卷Chua系统 Chua系统因电路实现简单、动力学行为丰富而受到****的广泛研究和应用. 三涡卷Chua系统是Chua系统的一种变形, 其表达式如下:f 是多项式函数, 其表达式为$a = 12.8, b = 19.1$ 时, 系统处于三涡卷混沌状态. 本次实验中, 选取以下平面作为截面进行实验, 其中平面一是特定方向与位置的平面, 平面二是调整后合适的庞加莱截面:x 轴和y 轴的平面. 由表1 可知, 参数$A, B$ 设置为$A = 0, B = 0$ , 本次实验对参数C 设置了多组不同的数值, 实验结果如图7 所示:图 7 平面一的实验结果 (a) C = 0时的波形; (b) C = 0时的相图; (c) C = 1.5时的波形; (d) C = 1.5时的相图; (e) C = –1.5时的波形; (f) C = –1.5时的相图Figure7. Experimental results of the first plane: (a) Waveform while C = 0; (b) phase diagram while C = 0; (c) waveform while C = 1.5; (d) phase diagram while C = 1.5; (e) waveform while C = –1.5; (f) phase diagram while C = –1.5.图7 的实验结果证明: 首先, 调整参数C 可以控制平面信号的水平高度, 同时使平面在相空间中上下平移; 其次, 由于参考信号与平面信号波形不相似, 此时无论怎样调整平面信号的水平高度, 都无法得到满足选取条件的平面信号.$A = - 1, \; B = 1, \;C = 0$ , 实验结果如下:图8(a) 中, 蓝色实线为参考信号, 红色点划线为平面信号, 参考信号与平面信号交点数量较多, 在参考信号的每一处增幅振荡区域都产生足够多的交点; 在图8(b) 中, 平面二截取到了系统轨道的三个涡卷, 该平面是合适的庞加莱截面.图 8 平面二的实验结果 (a)波形; (b)相图Figure8. Experimental results of the second plane: (a) Waveform; (b) phase diagram.4.3.超混沌Chen系统 -->4.3.超混沌Chen系统 超混沌Chen系统的归一化方程为$a = 35, b = 3, c = 12, d = 7, r = 0.5$ 时, 系统处于超混沌状态. 分别令$x, y, z, w$ 中任意一个变量值为零, 得到超混沌Chen系统的某个三维相空间图, 并分别对其用PTD法选取合适的平面作为截面. 以下为实验结果.$w = 0$ , 在$XoYoZ$ 相空间中观察系统轨道, 选取的平面信号参数为: $A = 0, B = - 0.5, C{{ = 20}}$ , 实验结果如图9 所示.图 9 $w = 0$ 时的实验结果 (a)波形; (b)相图Figure9. Experimental results while $w = 0$ : (a) Waveform; (b) phase diagram.$z = 0$ , 在$XoYoW$ 相空间中观察系统轨道, 选取的平面信号参数为: $A = - 0{{.5}}, B = - 4, C = 0$ , 实验结果如图10 所示.图 10 $z = 0$ 时的实验结果 (a)波形; (b)相图Figure10. Experimental results while $z = 0$ : (a) Waveform; (b) phase diagram.$y = 0$ , 在$XoZoW$ 相空间中观察系统轨道, 选取的平面信号参数为: $A = - 1, B = - 4, C{{ = 50}}$ , 实验结果如图11 所示.图 11 $y = 0$ 时的实验结果 (a)波形; (b)相图Figure11. Experimental results while $y = 0$ : (a) Waveform; (b) phase diagram.$x = 0$ , 在$YoZoW$ 相空间中观察系统轨道, 选取的平面信号参数为: $A = - 5, B = 0, C = 0$ , 实验结果如图12 所示.图 12 $x = 0$ 时的实验结果 (a)波形; (b)相图Figure12. Experimental results while $x = 0$ : (a) Waveform; (b) phase diagram.五.结 论 本文提出的PTD法是选择全局庞加莱截面的新方法. 该方法不需要复杂的算法实现, 可以灵活地调整所选截面的方向与位置以满足不同系统、不同研究者对庞加莱截面的不同需求. PTD法将系统轨道投影到所选平面上, 利用两个时域信号的相交关系反映相空间中系统轨道与所选平面的相交关系, 可以在时域上直观地判断所选平面是否是合适的庞加莱截面. 如果在时域中平面信号与参考信号的交点个数较多且交点集中于参考信号的每个增幅振荡区域, 则所选平面为合适的庞加莱截面. 通过改变平面信号的参数可以实时准确地调整平面信号的形状和所选平面在相空间中的方向与位置, 使用者既可以快速寻找与系统轨道充分相交的平面, 又可以根据需要选择任意方向和位置的平面作为庞加莱截面. 基于双翼Lorenz, 三涡卷Chua和超混沌Chen系统的仿真实验证明了PTD法对三维、四维、多涡和超混沌非线性系统均具有有效性和可行性. 本文在分析和实验中选择了z 轴作为投影方向, 针对待测系统的实际情况, 也可以选择x 轴或者y 轴作为投影方向. 










































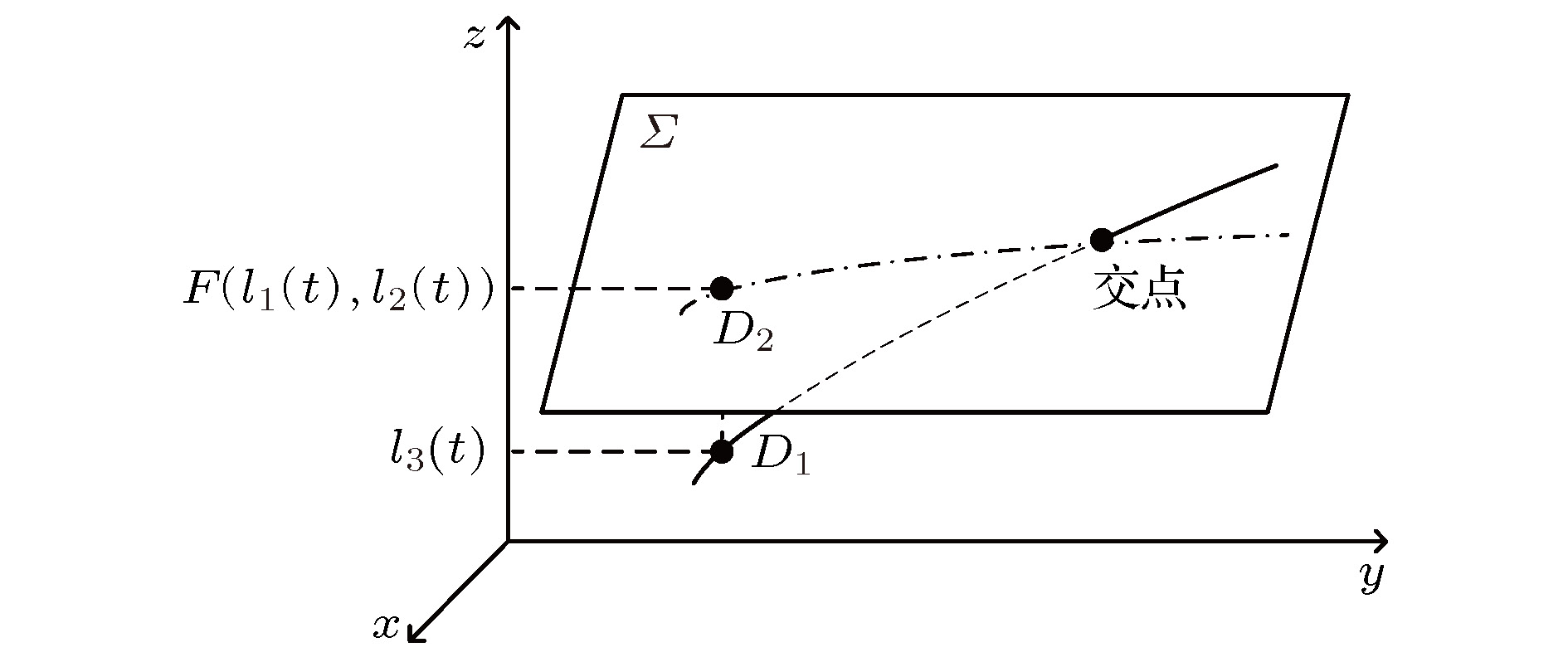 图 1 轨道在平面上的投影
图 1 轨道在平面上的投影


























































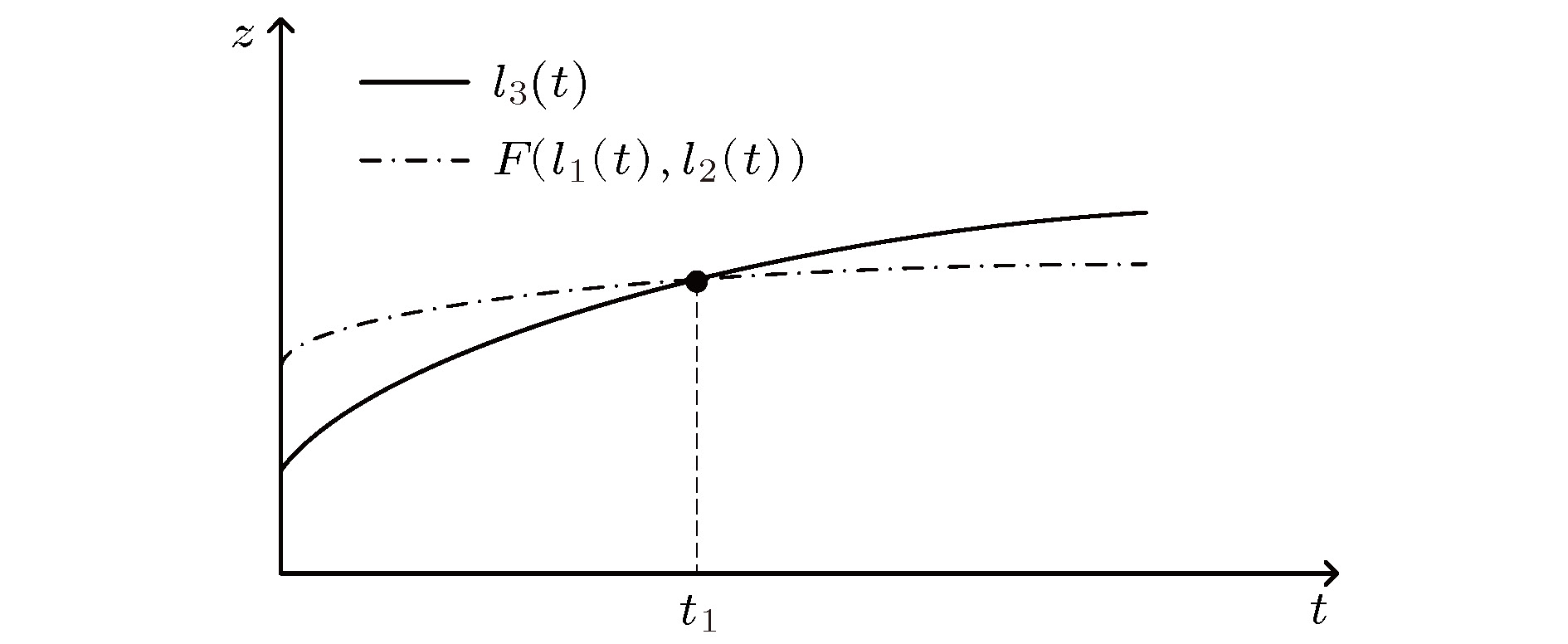 图 2
图 2 























































 图 3 涡卷的相轨与波形 (a)相轨; (b)波形
图 3 涡卷的相轨与波形 (a)相轨; (b)波形














































































































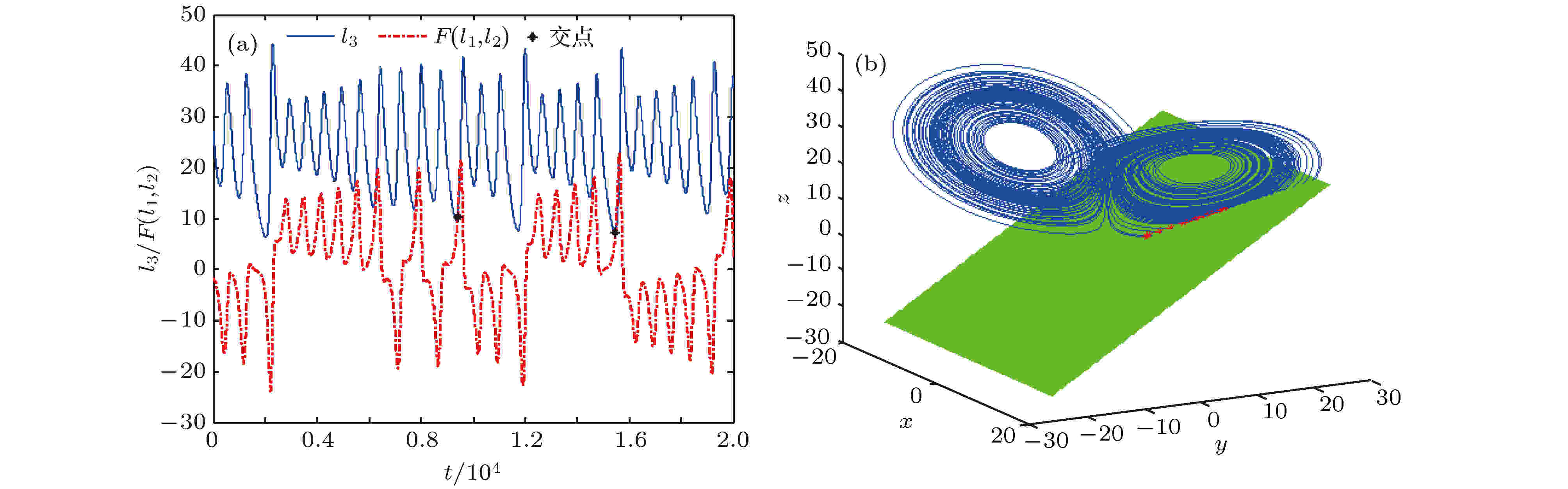 图 4 平面一的实验结果 (a)时域波形; (b)相图
图 4 平面一的实验结果 (a)时域波形; (b)相图

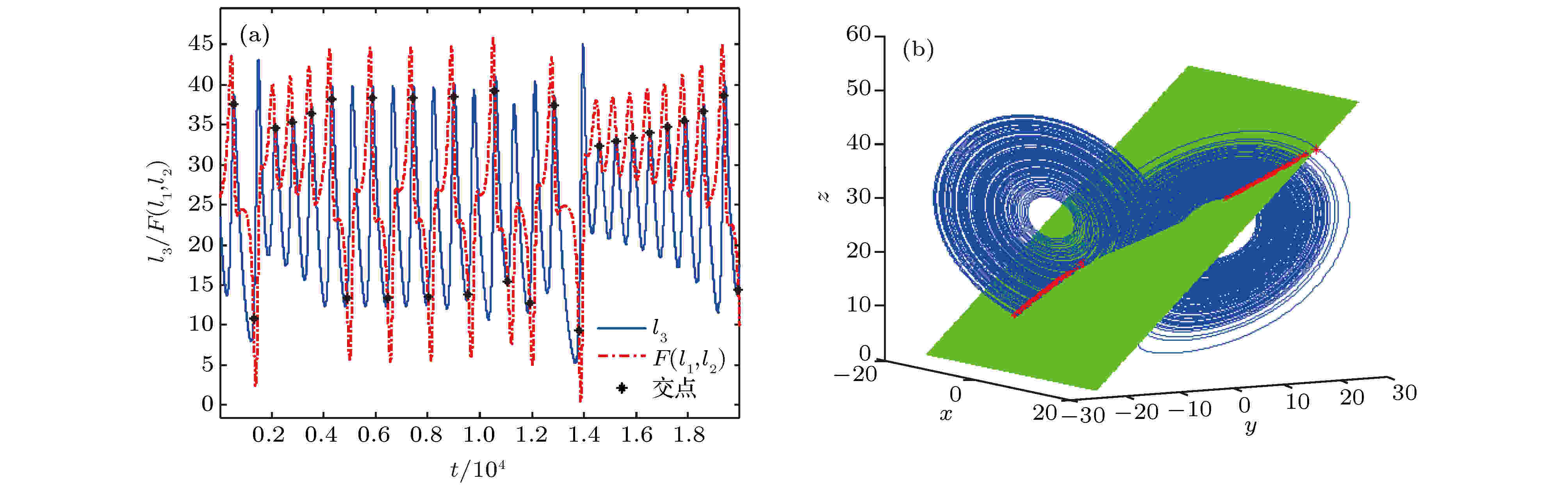 图 5 平面二的实验结果 (a)时域波形; (b)相图
图 5 平面二的实验结果 (a)时域波形; (b)相图
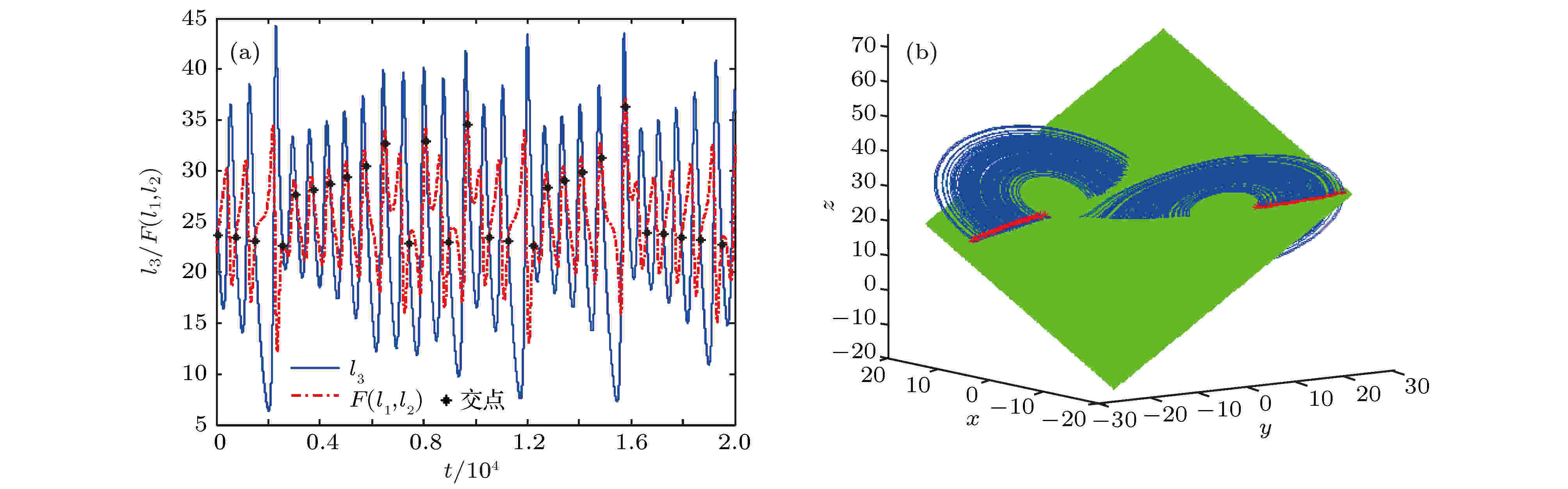 图 6 平面三的实验结果 (a)时域波形; (b)相图
图 6 平面三的实验结果 (a)时域波形; (b)相图


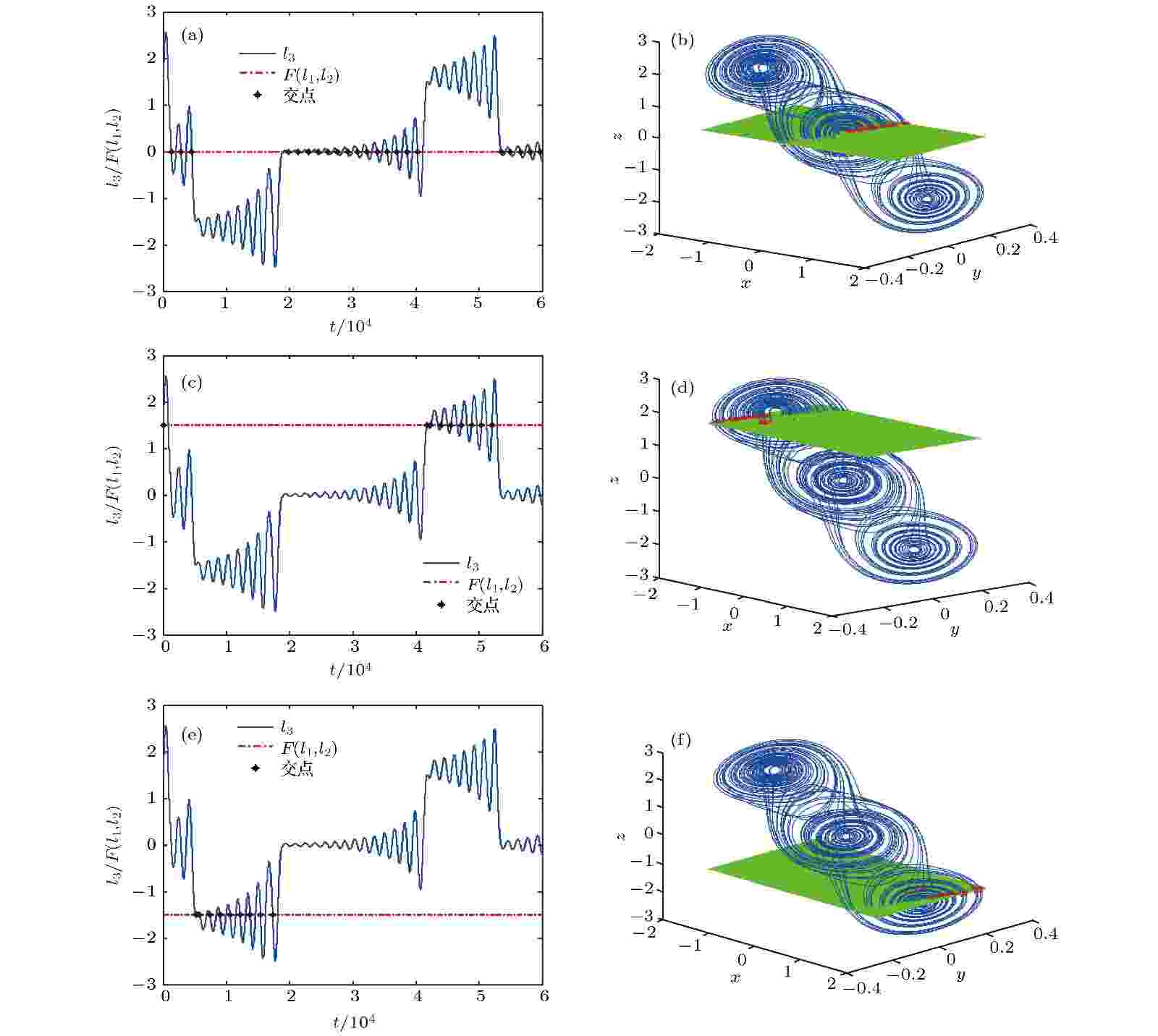 图 7 平面一的实验结果 (a) C = 0时的波形; (b) C = 0时的相图; (c) C = 1.5时的波形; (d) C = 1.5时的相图; (e) C = –1.5时的波形; (f) C = –1.5时的相图
图 7 平面一的实验结果 (a) C = 0时的波形; (b) C = 0时的相图; (c) C = 1.5时的波形; (d) C = 1.5时的相图; (e) C = –1.5时的波形; (f) C = –1.5时的相图
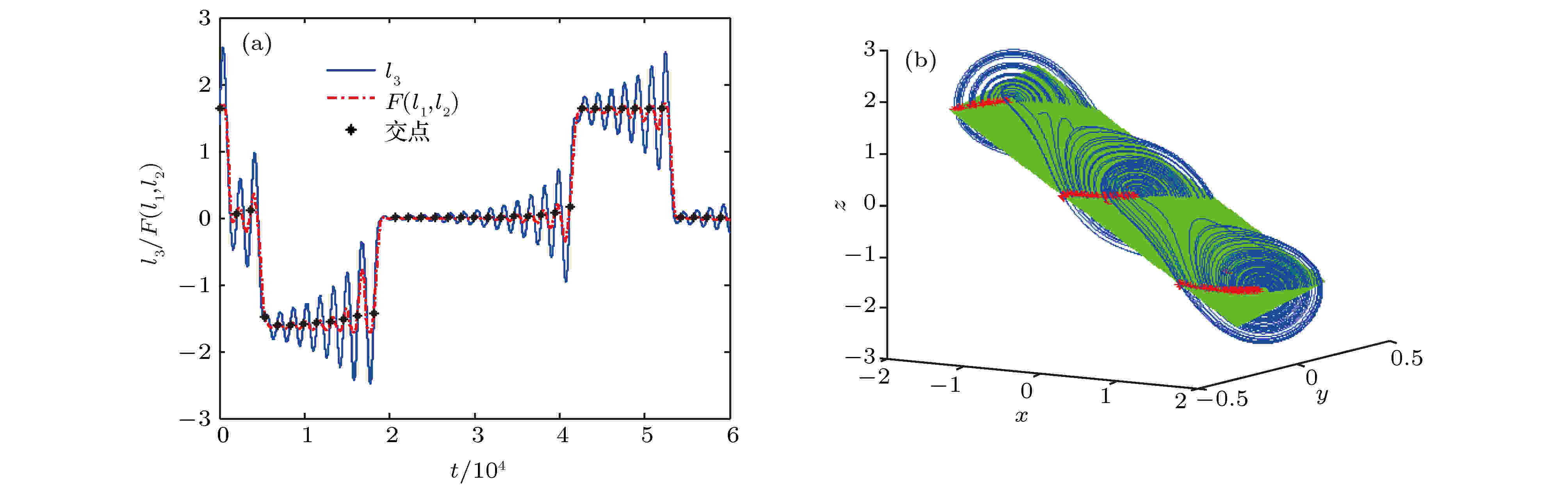 图 8 平面二的实验结果 (a)波形; (b)相图
图 8 平面二的实验结果 (a)波形; (b)相图




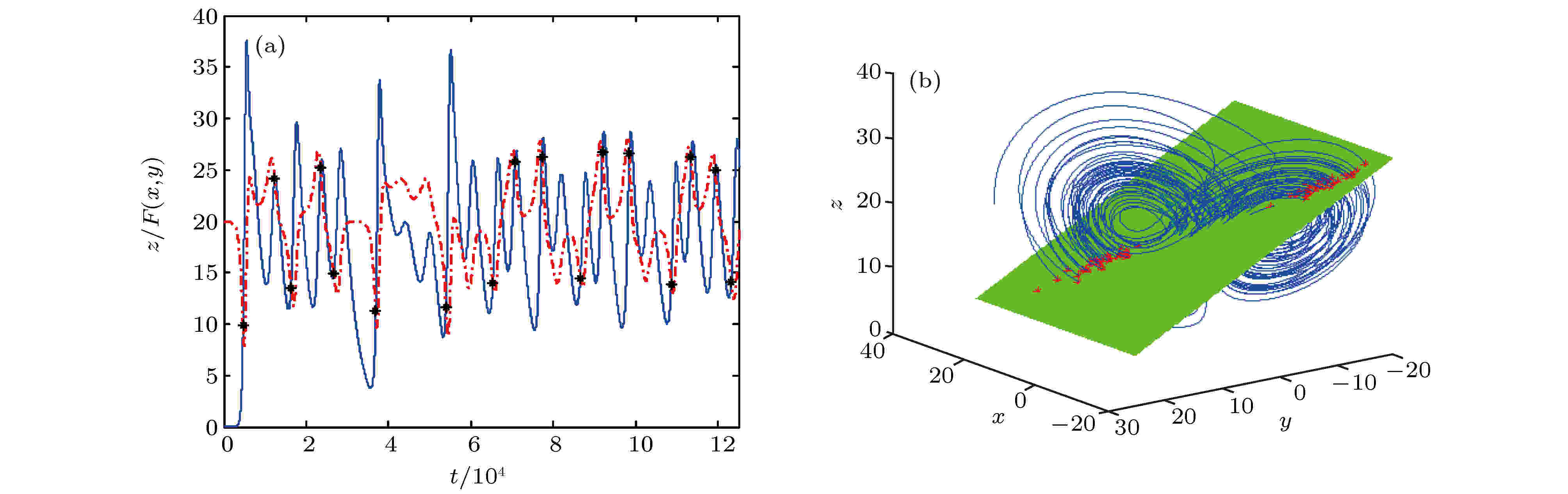 图 9
图 9 




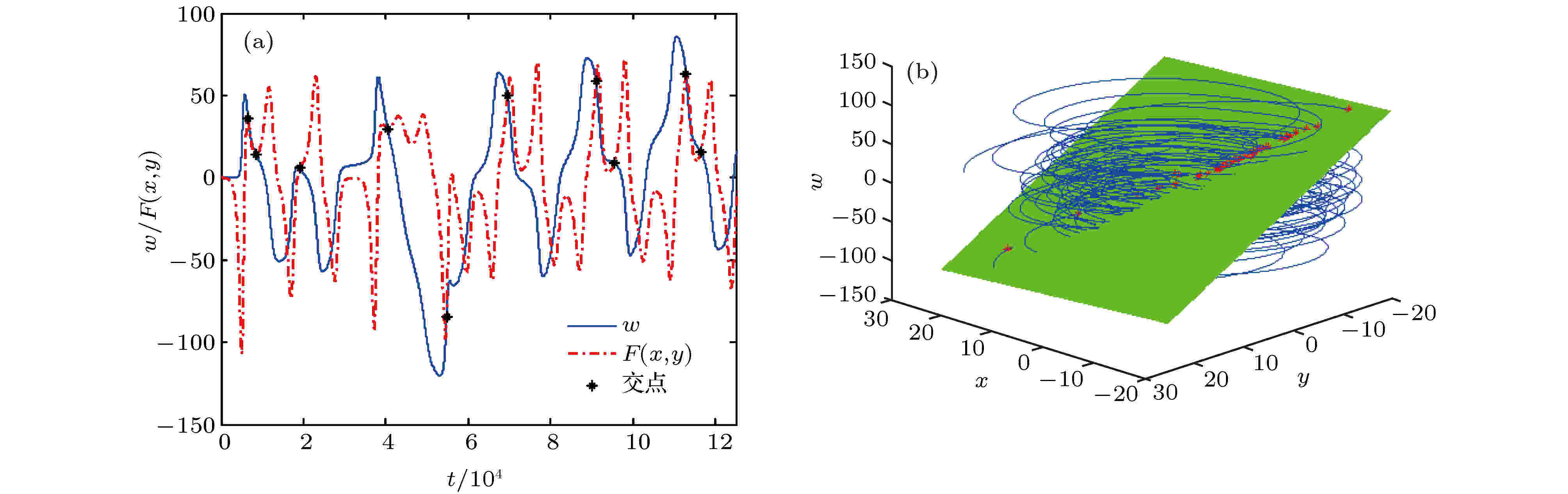 图 10
图 10 




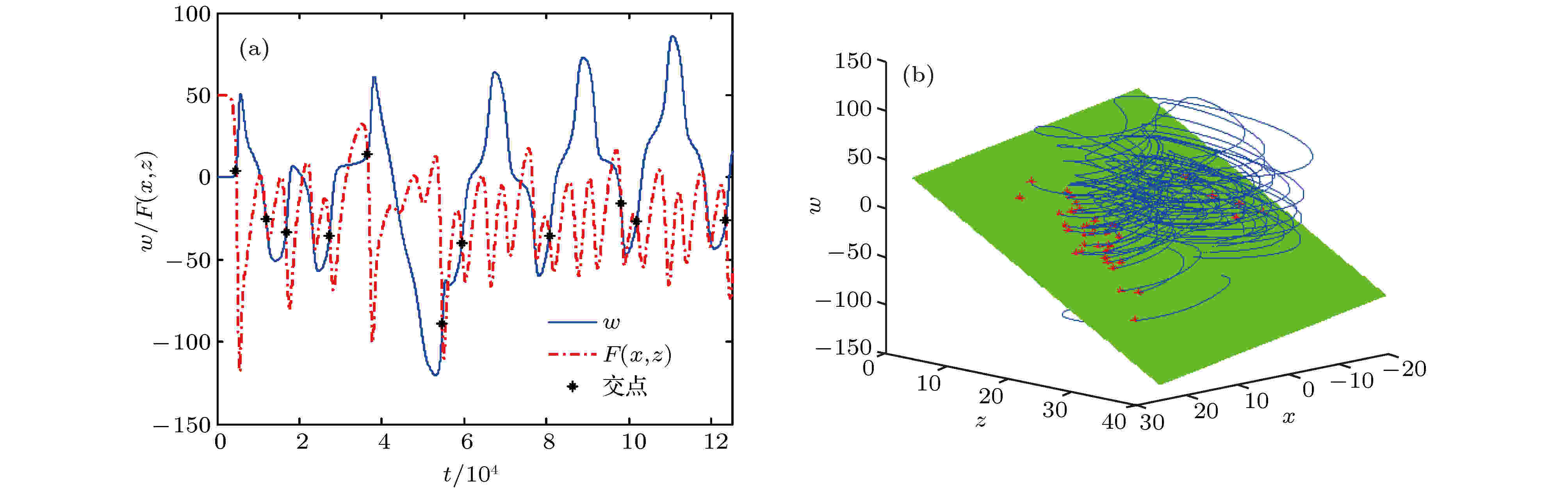 图 11
图 11 




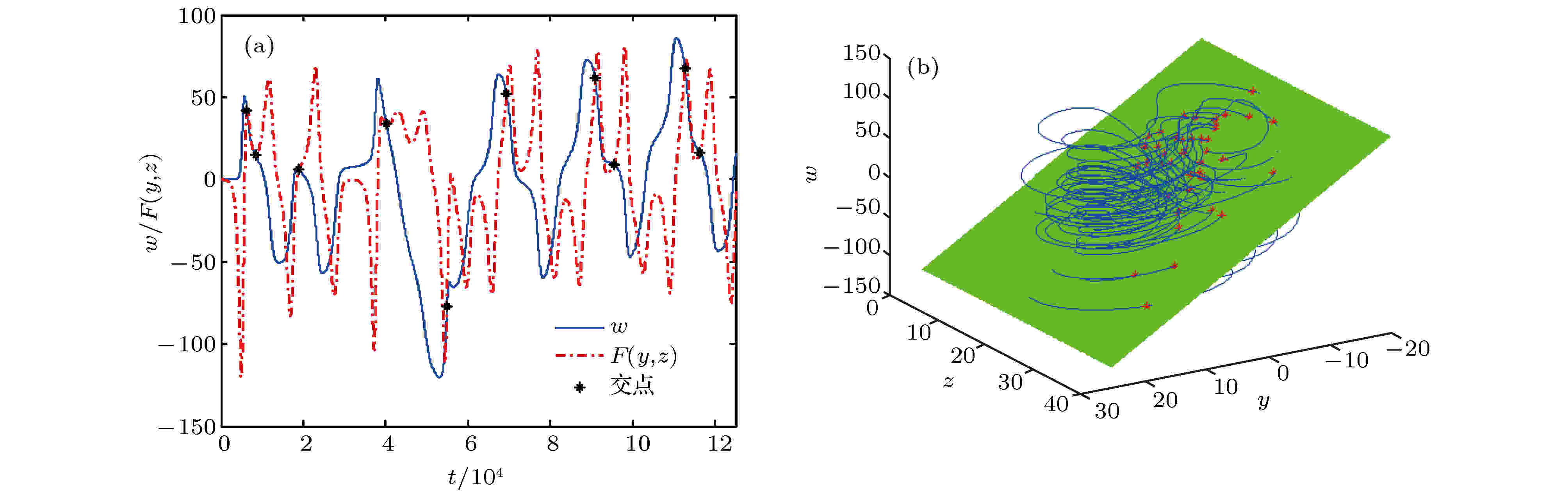 图 12
图 12 

