摘要: 磁化套筒惯性聚变(magnetized liner inertial fusion, MagLIF)结合了传统磁约束聚变和惯性约束聚变的优点, 理论上可以显著地降低聚变实现的难度, 具有极大的应用潜力. 以研究MagLIF中的关键问题为目标, 建立能够综合考虑磁化、预加热、套筒内爆、聚变反应、端面效应、磁通压缩等多种复杂机制在内的集成化物理模型, 特别是通过引入流体喷射模型, 使得可以在一维计算条件下考虑具有二维特性的端面损失情况, 并额外考虑Nernst扩散项对磁通损失的影响. 在此基础上编写实现一维集成化MagLIF数值模拟程序MIST (magnetic implosion simulation tools), 与FP-1装置(2 MA, 7.2 μs)上铝套筒内爆实验结果的对比验证了程序磁流体模块的正确性; 将聚变模块纳入后与国外同类程序LASNEX和HYDRA计算结果进行整体比较, 所得数值结果总体接近, 主要差异体现在燃料温度的计算上, 对可能影响的原因进行了简要分析. 所建立的集成化模型与程序将为未来开展MagLIF聚变实验研究提供坚实的理论基础和重要工具.
关键词: 磁化套筒惯性聚变 /
集成化数值模拟 /
端面损失 /
Nernst效应 English Abstract One-dimensional integrated simulations of magnetized liner inertial fusion Zhao Hai-Long Xiao Bo Wang Gang-Hua Wang Qiang Zhang Zheng-Wei Sun Qi-Zhi Deng Jian-Jun Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621900, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No.11205145)Received Date: 16 September 2019Accepted Date: 08 November 2019Published Online: 05 February 2020Abstract: Magnetized liner inertial fusion (MagLIF) integrates the advantages of traditional magnetic confinement fusion with those of inertial confinement fusion, and thus has promising potentials because theoretically it can dramatically lower the difficulties in realizing the controlled fusion. For the systematic simulating of MagLIF, we build up an integrated one-dimensional (1D) model to describe the complex process, which includes the terms of magnetization, laser preheating, liner implosion, fusion reaction, end loss effect, and magnetic flux compression. According to this model we develop an integrated 1D code–MIST (magnetic implosion simulation tools) , and specifically we propose a simplified model to describe the end loss effect based on the flow bursting theory, so the code is able to consider two-dimensional effects within 1D calculations. We also present a specific expression of magnetic diffusion equation where the Nernst effect term is taken into consideration, which is very important if there exists a temperature gradient perpendicular to magnetic field lines. Such conditions are fully satisfied in the MagLIF process. We use experimental data of aluminum liner implosions to verify the magneto-hydrodynamic module of our code, those shots (0607 & 0523) are performed on FP-1 facility (2 MA, 7.2 μs), and results show good agreement with the calculated velocity of inner flyer or target surface and other measurements. Comparison with code LASNEX and HYDRA (used by Sandia Laboratory) is also made to assess the fusion module, and the results show that our calculations are physically self-consistent and roughly coincide with the results from LASNEX and HYDRA, a key difference appears at fuel temperature, and the factors that might cause this difference are discussed. With this integrated model and 1D code, our work would provide a powerful tool for the future experimental research of MagLIF.Keywords: magnetized liner inertial fusion /integrated simulation /end loss /Nernst effect 全文HTML --> --> --> 1.引 言 能源是人类社会和文明发展的基础. 进入21世纪后, 核能在人类社会消耗能源中所占比例[1 ] 越来越高, 而可控核聚变被认为是解决未来能源问题的重要手段之一. 国际可控核聚变领域的研究多集中于磁约束聚变(magnetic confinement fusion, MCF)[2 -4 ] 和惯性约束聚变(inertial confinement fusion, ICF)[5 -7 ] 这两大主流方向上, 它们主要区别在于实现聚变条件的具体方式不同. 与此同时, 国内聚变研究领域也有较快的发展, 其中有代表性的如: 中国科学院等离子体物理研究所的东方超环(EAST)装置, 主要用于MCF物理过程[8 ,9 ] 研究; 中国工程物理研究院建立的神光系列装置和“聚龙一号”装置, 广泛应用于激光[10 ,11 ] 和Z 箍缩[12 ,13 ] 驱动ICF研究. 然而, 传统的聚变方式都面临着不同的工程和技术问题, 距离点火的目标仍有一定的差距, 因此有必要探索新的聚变构型, 以尽量降低实现聚变的难度.[14 ] 的磁化套筒惯性聚变(magnetized liner inertial fusion, MagLIF), 是一种在ICF中引入轴向磁场, 并结合传统MCF与ICF优势的新聚变构型, 该聚变整个过程包括3个主要阶段: 燃料磁化(magneti-zation)、激光预加热(laser pre-heating)和套筒压缩(compression), 如图1 所示. 通过简单的计算可以看出MagLIF构型对氘氚(DT)反应产生的α粒子能量利用率很高, 因此在理论上能够显著降低聚变实现的难度, 有极大的应用潜力. 初始时刻MagLIF中引入了较强(~30 T)的预置轴向磁场, 在外套筒的内爆压缩作用下, 磁场与DT燃料一起被压缩, 在压缩最紧密时刻磁场可达到数千特斯拉. 一般条件下DT反应产生的α粒子的平均自由程[6 ] 为${\lambda _{\rm{\alpha }}}\! \approx 0.5 \times {10^{12}}T_{\rm{e}}^{3/2}\!/(n\ln \varLambda )$ $ (T_{\rm e} < 5 \times $ $10^8~{\rm K})$ . 若燃料温度为7 keV, 粒子数密度1022 /cm3 , 取库仑对数lnΛ = 9时λ α 大约是5 cm, 远大于MagLIF实验负载尺寸(~1 cm). 引入轴向磁场(假设峰值为2000 T)后, 根据公式${r_{\rm{L}}} = 2.71 \times {10^5}/B$ , 可计算得到α粒子径向回旋半径为0.135 mm, 此时燃料内部的α粒子能量沉积效率显著提高.图 1 MagLIF过程示意图(包含3个主要阶段)Figure1. Schematic of MagLIF process, including three main stages.[15 -20 ] , 圣地亚实验室取得的成就引发全世界科学家对该领域的关注, 未来将朝着实现点火的目标继续发展. 在本文作者前期开展的零维聚变模型的研究中[21 ] , 氘氚燃料区被简化为质点(即密度、压强、磁场等各种物理量在燃料区都被认为是均匀分布, 燃料能量方程由解析表达式描述), 模型相对粗糙. 本文工作在前期基础上有了较大的进步, 在建模中考虑了α粒子沉积、输运以及Nernst效应等多种物理模型, 特别是引入流体喷射模型使得程序可以在一维计算中考虑二维端面损失效应, 并将燃料区和金属套筒统一纳入磁流体力学控制方程的描述中, 构建了完整的一维集成化数值模拟程序.2.物理模型 对于MagLIF而言, 发生聚变时刻状态燃料处于高温(5—10 keV)、高密度(n e > 1020 /cm3 ), 可视为全电离、理想导电流体, 驱动源来自外部电流, 同时有轴向磁场的存在, 整体上使用MHD方程组描述是合适的. 但MagLIF包含非常复杂的多个物理过程, 为便于一体化的描述, 必须适当简化:$r\text{-}\theta $ 平面二维数值模拟结果[16 ] , 在预加热后很短时间(~20 ns)内电子和离子温度快速取得平衡, Z 装置上首批氘氘(DD)实验的结果[18 ] 也证实迟滞时刻电子与离子温度差别很小, 因此程序使用单温MHD模型.2.1.MHD方程组 2.1.MHD方程组 基于上述考虑, 使用拉氏描述方式, 建立描述MagLIF过程的单温、单流体、多介质MHD方程组:ρ 为密度, u p 为压强, e 为比内能, q w 为外部能量沉积率, ${\mu _0}$ 为真空磁导率, $\eta $ 为电阻率, B $ {{J}} \equiv $ $ \dfrac{1}{{{\mu _0}}}\nabla \times {{B}}$ 为电流密度.1 )—(4 )描述, 二者的区别在于能量方程(3 )中的外部能量沉积项$\rho w$ . 对于金属套筒$\rho w = 0$ . 对于DT燃料, 由于聚变反应, 需要考虑轫致辐射和α粒子能量沉积效应, 则能量沉积项为$E_{\text{α}}$ 为单位体积的α能量; $G_{\text{α}}$ 为α能量耗散系数; ${Q_{{\rm{rad}}}}$ 为单位体积的轫致辐射损失项.2.2.α粒子能量方程 -->2.2.α粒子能量方程 α粒子能量$E_{\text{α}}$ 单独满足一个演化方程, 根据文献[22 ]该方程可写为$D_{\text{α}}$ 为方程扩散系数, $G_{\text{α}}$ 为方程耗散系数, $\dot n$ 为DT聚变反应率, ${E_{\text{α}0}}$ = 3.5 MeV为聚变反应产生的α粒子初始能量.6 )式中扩散系数${D_{\text{α}}}$ 与磁场强度相关, 具体表达式(高斯制)为$ {l_{\text{α}}} = 0.107\dfrac{{T_{{\rm{keV}}}^{3/2}}}{{\rho {L_{\text{α}}}}}\;{\rm{(cm}}),\; {\omega _{\text{α}}} = \dfrac{{{2e_{\rm{g}}}{B_{\rm{g}}}}}{{{m_{\text{α}}}{c_0}}},\;{\nu _{\text{α}}} = \dfrac{{{V_{{\text{α}}0}}}}{{{l_{\text{α}}}}} $ , 其中c 0 为真空中的光速; ${L_{\text{α}}}$ 为α粒子库仑对数, 聚变条件下一般[22 ] 取7; ${m_{\text{α}}}$ 为α粒子质量; e g 为高斯制下电子电荷; B g 为高斯制下磁场强度.2.3.DT聚变模型 -->2.3.DT聚变模型 为便于计算, 本文仅考虑DT聚变初级反应:${\left\langle {\sigma v} \right\rangle _{{\rm{DT}}}}$ 为DT聚变反应截面, 根据文献[23 ]可近似写作:$A = 1 - \dfrac{{{C_2}T + {C_4}{T^2} + {C_6}{T^3}}}{{1 + {C_3}T + {C_5}{T^2} + {C_7}{T^3}}}, B = \dfrac{{{C_0}}}{{{T^{1/3}}}}$ , T 为燃料温度, 系数C 0 到C 7 为拟合实验曲线得到的数值, 具体取值如表1 所列.C 0 /keV1/3 C 1 /cm3 ·s–1 C 2 /keV–1 C 3 /keV–1 6.661 643.41×10–16 15.136×10–3 75.189×10–3 C 4 /keV–2 C 5 /keV–2 C 6 /keV–3 C 7 /keV–3 4.6064×10–3 13.5×10–3 –0.10675×10–3 0.01366×10–3
表1 系数C 0 —C 7 的取值Table1. Values of coefficient C 0 –C 7 2.4.磁场影响下的径向热扩散 -->2.4.磁场影响下的径向热扩散 轴向强磁场的引入还会影响燃料中电子和离子沿径向的热扩散, 根据文献[22 ], 磁场影响下径向热扩散系数(高斯制)如下:c 0 为真空中的光速; m e 为电子质量; m i 为1∶1混合DT燃料等效离子质量, m i = 2.5m p ; L e 和L i 分别为电子与离子的库仑对数, 聚变条件下DT燃料密度约为1 g/cm3 , 温度约为10 keV, 此时L e 和L i 分别取值[22 ] 为7和9; e g 为高斯制下电子电荷; B g 为高斯制下磁场强度.3.流体喷射模型: 端面效应 为了实现对MagLIF中的氘氚燃料的激光预加热, 需要在聚变靶顶部开孔(用聚合物薄膜进行覆盖密封), 称为激光注入孔(laser entrance hole, LEH). 外部激光器所产生的激光束通过此孔进入燃料内部, 将燃料快速(~2 ns)加热至等离子体态, 满足预加热所需的温度要求(50—300 eV). 但是这个开孔的存在会导致在套筒压缩阶段内部的燃料向外喷射, 造成燃料质量和内能的损失, 这就是所谓的端面损失效应, 如图2 所示. 端面效应的准确模拟需要至少在二维情形下进行, 本文中为了在一维中考虑端面效应, 提出近似的简化模型并在一维方程中建立描述端面效应的质量、能量损失项. 下面予以详细讨论.图 2 端面效应简化模型示意图Figure2. Schematic of simplified model describing end loss effect.r LEH 来表示, 程序中仅当燃料网格位置r 小于r LEH 时, 才考虑端面效应, 其他情况下忽略. 对于r LEH 范围内的燃料, 忽略流体黏性后, 可采用喷射模型来描述. 查询物理手册可知, 管道内相对于外界超压为P 的流体, 其喷射速度${C_{{\rm{gs}}}}$ 为t 内, 对于r < r LEH 内任一层网格, 如果单独提取出来并考虑轴向运动情况, 如图2 中右侧柱体所示. 认为每个时间步内顶部${C_{{\rm{gs}}}} \times {\rm{d}}t$ 高度内的燃料质量dM 和内能dE 全部向外喷射丢失, 剩余的质量和内能在高度h 内重新均匀分配并计算密度. 由此可以写出单个时间步dt 内喷射质量和内能的损失为r 为网格起始沿径向所在位置, $\rho $ 为燃料密度, E 为网格内燃料的总内能, e 为网格内燃料的比内能, M 为网格内燃料的总质量, S 为网格的底面积.14 )和(15 )式推导后可得考虑端面效应后新的控制方程如下:h 为燃料高度.Φ 1 ; 若考虑流体摩擦(黏性), 应乘以速度指数Φ 2 (对于水, Φ 2 约为0.97); 若考虑喷嘴几何构型收缩, 应再乘以收缩系数Φ 3 (对于锐喷射口, Φ 3 约为0.61).4.磁扩散项: Nernst效应 为了将α粒子能量约束在氘氚燃料区的范围以内, 需要数千特斯拉的超强磁场, 在MagLIF中这是通过压缩冻结在燃料中的轴向磁场来实现的. 磁冻结效应由(4 )式等号右端的第2项和第3项描述. 轴向磁场还会发生扩散损失(如图3 所示), 这包含了两种机制, 一种是氘氚燃料和金属套筒的电阻率引起的普通磁扩散, 另一种是径向温度梯度导致的Nernst磁扩散效应. 普通磁扩散由(4 )式等号右端的第1项描述.图 3 磁通压缩与扩散过程示意图Figure3. Schematic of magnetic flux compression and diffusion process.14 ]的写法并考虑磁通量守恒的要求后, 给出的表达式为B ${\omega _{{\rm{ce}}}}{\tau _{\rm{e}}}$ 为电子霍尔参量, k B 为玻尔兹曼常数.18 )式代入MHD方程组中磁扩散方程内, 可以写出MagLIF过程中燃料内部轴向磁场扩散方程的整体表达形式:19 )式在一维柱坐标下的表达形式:5.程序对比校验 综合上述讨论, 得到了由(2 )式、(6 )式、(16 )式、(17 )式、(19 )式组成的描述MagLIF演化过程的集成化物理模型. 基于该模型, 自主编写实现一维集成化数值模拟程序MIST. 为了检验建模和程序的正确性, 本节首先对程序中的MHD模块进行了单独校验; 然后与圣地亚实验室公开发表MagLIF模拟结果进行整体比对, 以检验聚变模块的合理性.图4 所示.图 4 FP-1装置0523与0607发次实验驱动电流测量曲线Figure4. Experimental current curves of shot 0523 & 0607.图5 所示.图 5 MIST计算得到的自由面速度曲线与实验测量结果的比较 (a) 0607发次; (b) 0523发次Figure5. Comparison of inner surface velocity curves between the calculations and measurements: (a) 0607 shot; (b) 0523 shot.[24 -25 ] , 因此为表征测量结果与真实流经负载的电流差异, MHD计算中通常对实验电流进行一个系数修正, 上述计算中该修正系数分别是0.82 (0607发次)和0.76 (0523发次). 又考虑到实验中测量设备之间触发信号的抖动可能导致所测量结果的零点不一定完全对准, 因此计算结果对速度曲线从整体上在时间轴向右进行了微小的平移, 对0607发次右移0.38 μs, 占加载时间比例为1.9%, 对0523发次右移0.23 μs, 占加载时间比例为1.9%. 图5 的对比结果显示, MIST程序计算与实验测量结果吻合一致, 平均误差小于1%, 验证了MHD模块的正确性.AR = 10, 高度为5 mm, DT燃料初始密度为3 mg/cm3 , 初始轴向磁场为30 T, 预加热温度为250 eV, 加载电流为30 MA, 上升时间为120 ns, 网格数为60. 在不考虑端面效应和Nernst效应的情况下, 计算结果(如图6 所示)表明迟滞时刻燃料温度为8.4 keV, 聚变产额约为550 kJ, 能量增益为1.6, 压缩比CR约为14, 峰值压力为3.6 Gbar (1 bar = 105 Pa), 密度为0.6 g/cm3 , 压缩磁场峰值为2500 T, 峰值内爆速度为75 km/s.图 6 MIST程序计算得到的(a)监测点、(b)套筒内爆速度、(c)燃料温度, 以及(d)聚变产额等随时间的演化曲线Figure6. Calculated results of (a) grid position, (b) implosion velocity, (c) fuel temperature, and (d) fusion yield evolving with time.图7 所示. 从30 ns左右随着激光预加热的加载, 端面效应开始发挥作用, 套筒内燃料质量不断从顶部喷射损失, 到迟滞时刻125 ns左右, 仅有58.5%的初始质量残留; 此时受Nernst效应与普通磁扩散的综合影响, 套筒内相应的磁通保有量锐减至64%. 计算结果表明端面效应与Nernst效应对于MagLIF内爆结果影响很大, 即使在一维模拟中也应尽量给予考虑, 迟滞时刻套筒内燃料质量与磁通的残余量也与文献[18 ]中给出的结果相符合.图 7 端面效应与Nernst效应影响下, 套筒内(a)燃料质量与(b)磁通随时间的演化Figure7. (a) Fuel mass and (b) magnetic flux evolving with time with consideration of end loss and Nernst effect.[26 ,27 ] 中所使用的一维计算结果, 采用同样的初始参数和驱动电流开展计算, 与LASNEX和HYDRA程序的计算结果进行比对. 国外程序所使用的计算参数为: 金属铍套筒, LASNEX程序中初始半径为3.24 mm、HYDRA程序中初始半径为3.1 mm, 位型比AR = 6, 高度为5 mm, DT燃料初始密度为3 mg/cm3 , 初始轴向磁场为30 T, 预加热温度为250 eV, 加载电流为27 MA, 上升时间约120 ns.表2 所列, 可以发现MIST程序计算数值与国外程序计算结果总体接近. 计算结果的对比中, 有直接联系的燃料温度和聚变产额等都普遍大于国外程序计算结果, 而压缩比与磁场强度也一致地小于国外程序计算结果, 这说明我们程序的计算结果在物理上是自洽的. 导致计算结果差异的主要原因就在于聚变发生后燃料温度计算值偏高, 造成这种情况的原因可能有两点: 1)程序未考虑因聚变反应本身造成的质量损失, 聚变反应率的计算有所高估; 2)程序所使用的材料状态方程库在聚变温度范围内数据点比较稀疏, 调用时采用线性差值方式得到的燃料温度值可能偏高, 导致聚变反应率相应增大, 而聚变放能反过来又会继续推升温度, 使得温度计算的差异被放大.程序名称 燃料密度/g·cm–3 燃料温度/keV 磁场强度/103 T 压缩比 峰值压力/Gbar 聚变产额/kJ LASNEX 0.5 8 6—13 23 3 500 MIST 0.47 8.5 7 16 2.7 620 HYDRA 0.8—1.0 6—8 8—22 22 5 565 MIST 0.56 9.5 8 17 3.3 725
表2 MIST与LASNEX和HYDRA程序一维计算结果的对比Table2. Comparison of calculated results between MIST and LASNEX, HYDRA.6.总结与展望 MagLIF具备科学、技术和工程3个方面的应用前景, 不仅有望为未来商业能源提供低成本的聚变实现方案, 其本身也是多物理场、多学科交叉的集成化创新典范, 且能够拓展现有大型脉冲功率驱动装置应用范畴. 然而, 国内对于MagLIF领域的相关研究尚处在起步阶段, 集成化数值模拟能力亟需进一步发展和提升. 



 图 1 MagLIF过程示意图(包含3个主要阶段)
图 1 MagLIF过程示意图(包含3个主要阶段)




















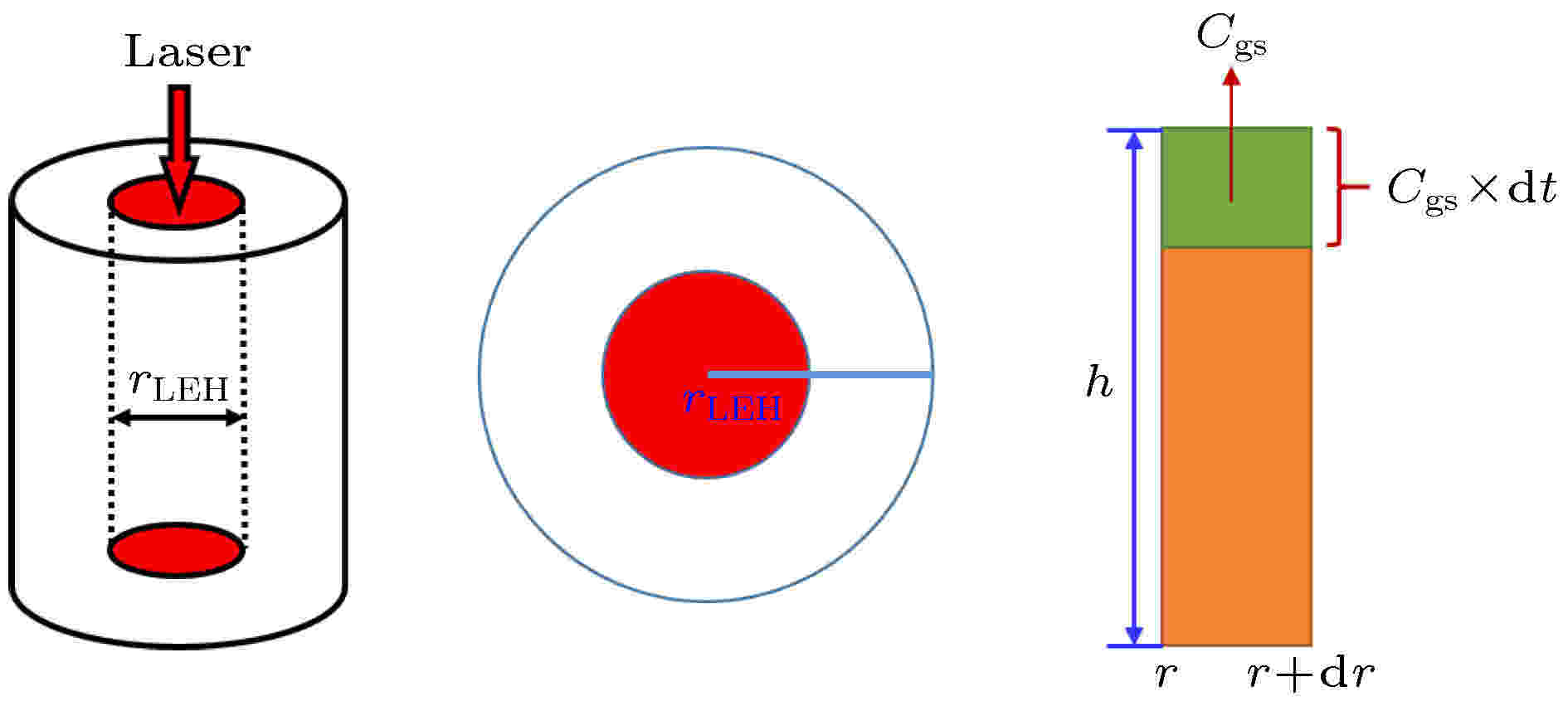 图 2 端面效应简化模型示意图
图 2 端面效应简化模型示意图


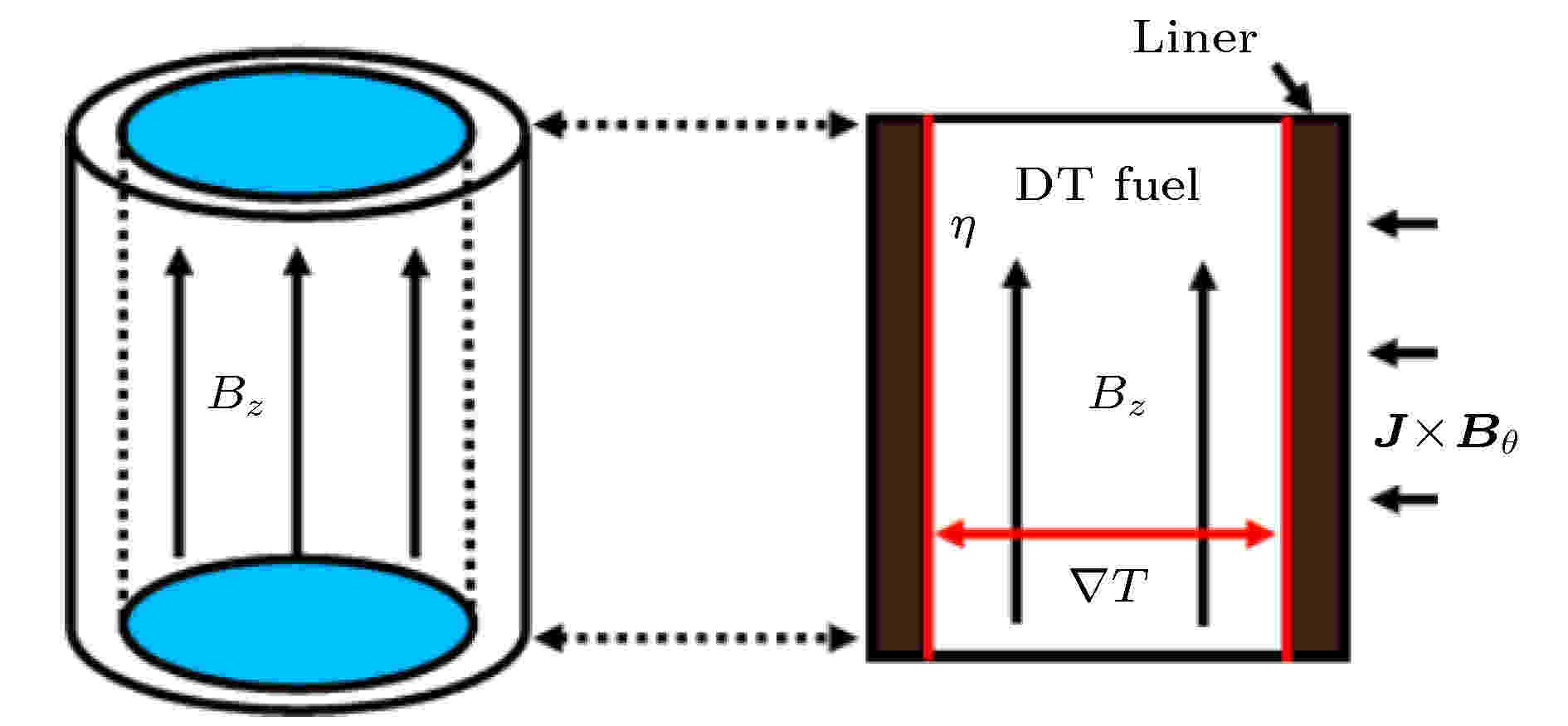 图 3 磁通压缩与扩散过程示意图
图 3 磁通压缩与扩散过程示意图
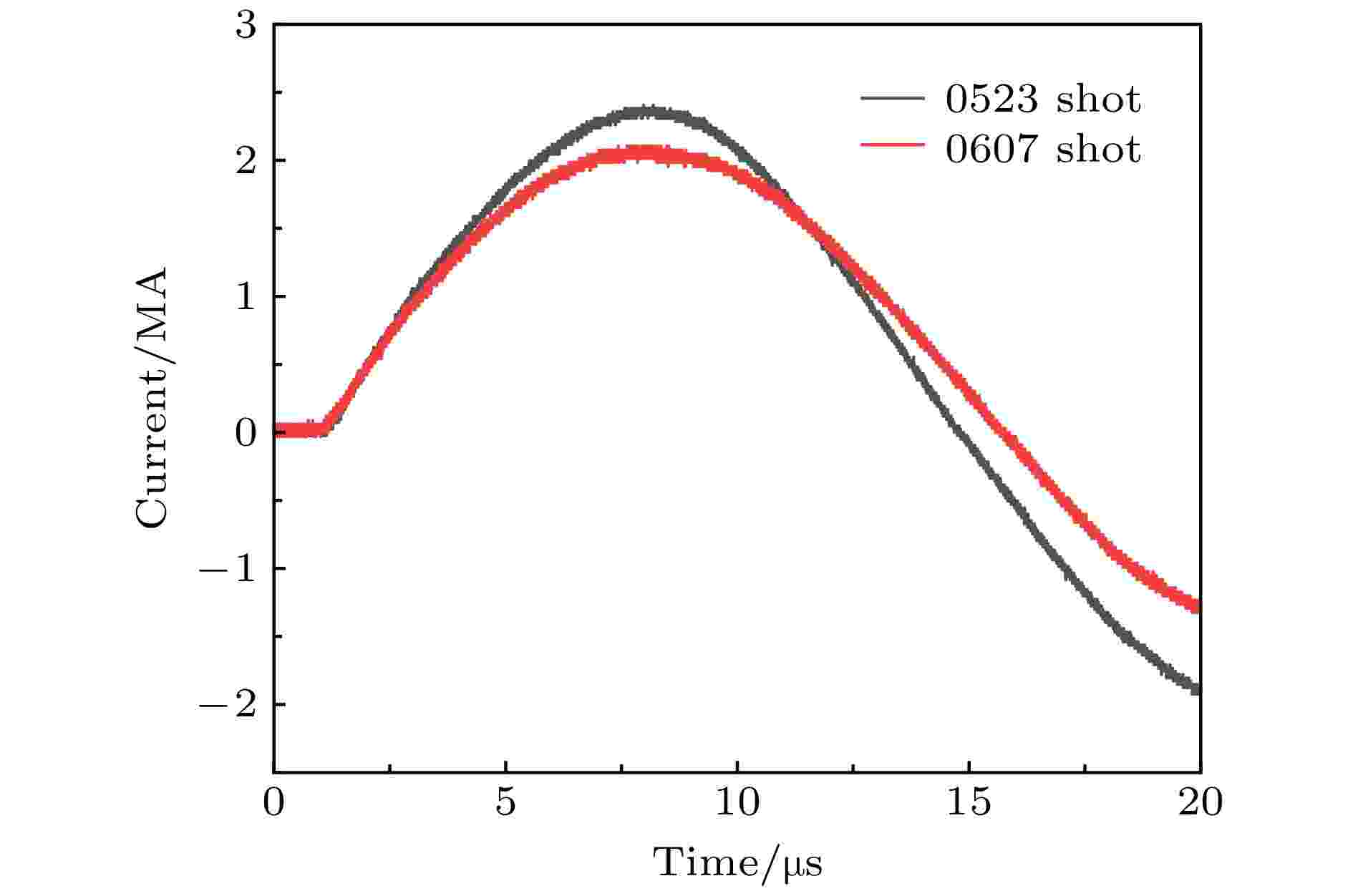 图 4 FP-1装置0523与0607发次实验驱动电流测量曲线
图 4 FP-1装置0523与0607发次实验驱动电流测量曲线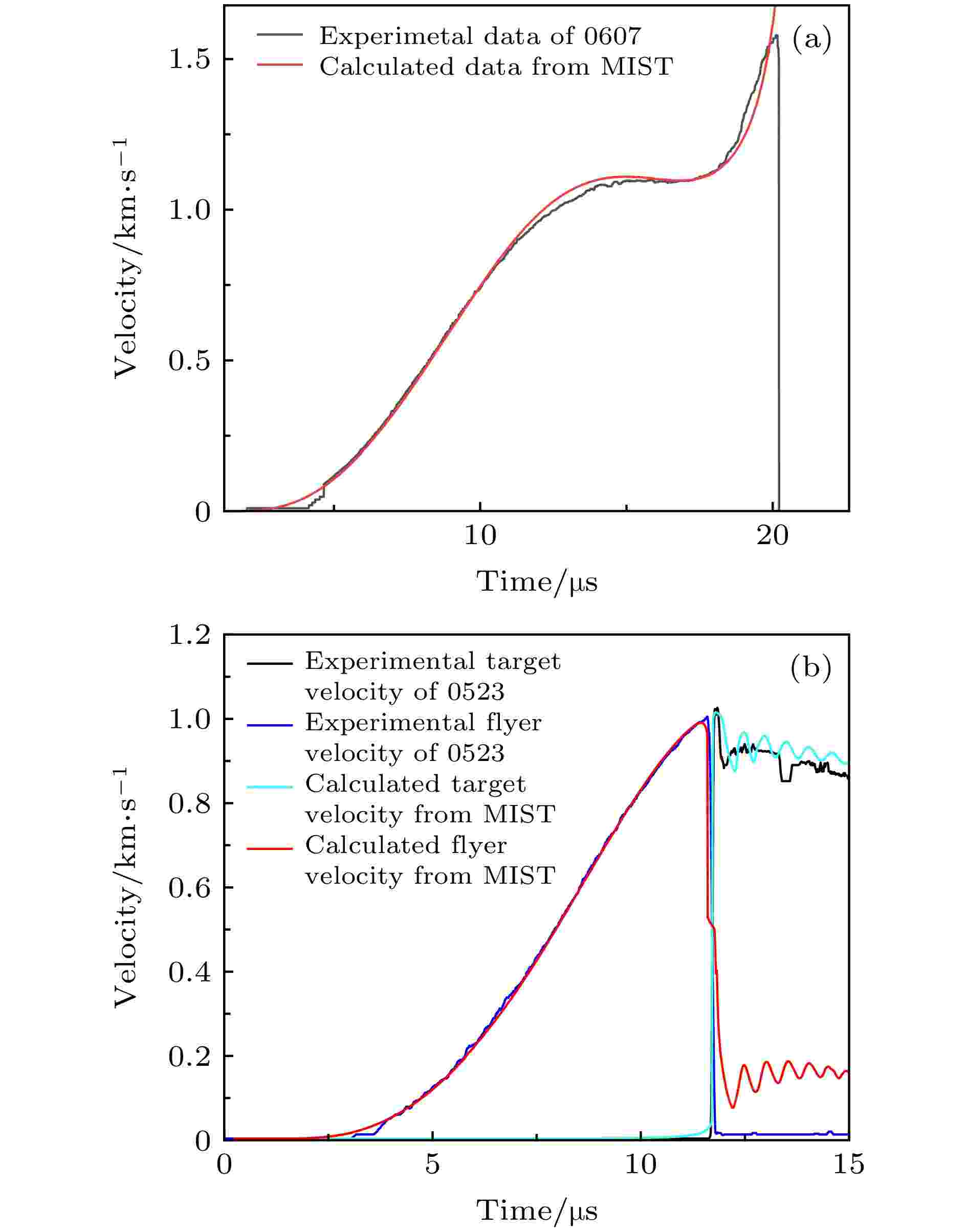 图 5 MIST计算得到的自由面速度曲线与实验测量结果的比较 (a) 0607发次; (b) 0523发次
图 5 MIST计算得到的自由面速度曲线与实验测量结果的比较 (a) 0607发次; (b) 0523发次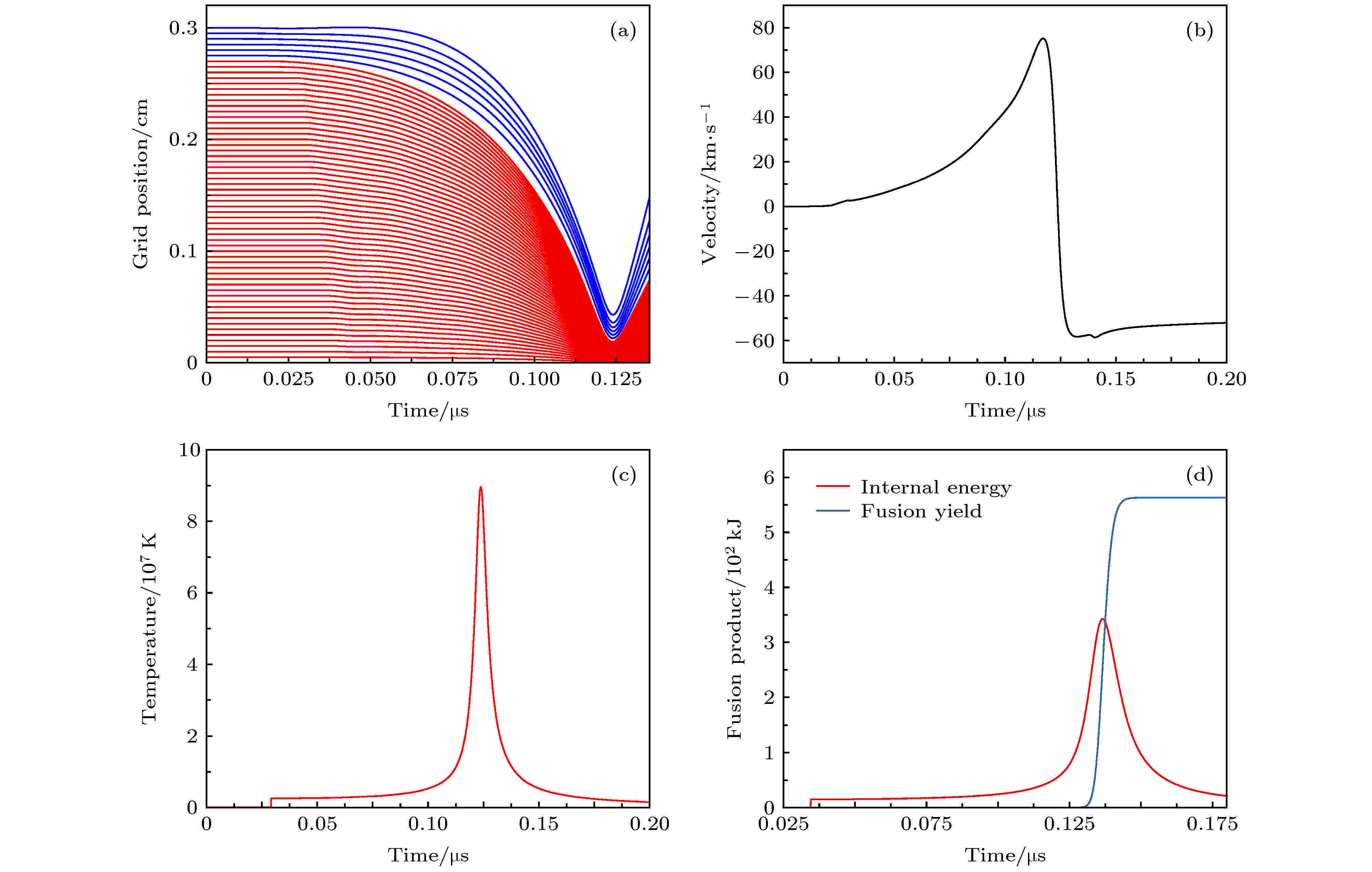 图 6 MIST程序计算得到的(a)监测点、(b)套筒内爆速度、(c)燃料温度, 以及(d)聚变产额等随时间的演化曲线
图 6 MIST程序计算得到的(a)监测点、(b)套筒内爆速度、(c)燃料温度, 以及(d)聚变产额等随时间的演化曲线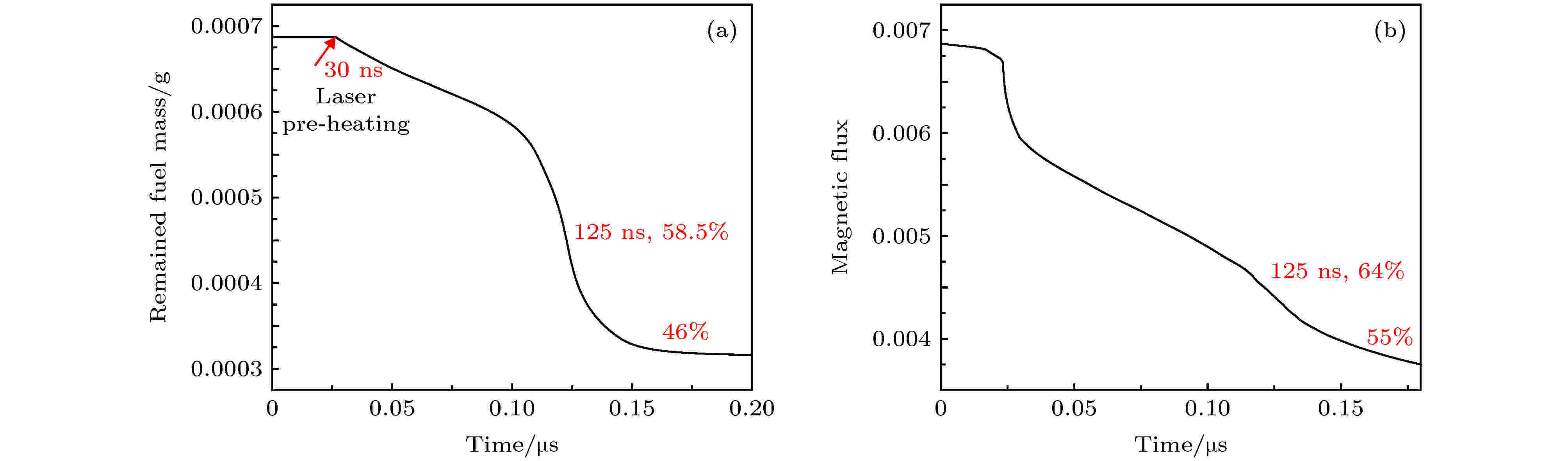 图 7 端面效应与Nernst效应影响下, 套筒内(a)燃料质量与(b)磁通随时间的演化
图 7 端面效应与Nernst效应影响下, 套筒内(a)燃料质量与(b)磁通随时间的演化