摘要:在分析星地链路几何结构及传播模型的基础上, 研究基于联合代数重建技术的星地链路反演二维垂直降雨场的方法. 利用实测降雨资料构建3类降雨场, 并搭建3条17 GHz垂直极化星地链路进行数值仿真. 实验结果表明: 单星地链路无法实现二维垂直降雨场的重构, 反演场与真实场的相关系数分别为0.556, 0.504和0.364; 基于双星地链路的反演结果和真实场的相关系数均高于0.98, 平均偏差分别为0.122, 0.159和0.537 mm/h, 欧式距离均低于0.9 mm/h, 熵的相对误差均小于1.6%, 基本实现了二维垂直降雨场的反演; 三星地链路的应用进一步提升了反演精度, 相关系数接近于1, 能够精准重构降雨场. 实验结果验证了基于星地链路的垂直降雨场反演方法的可行性、准确性和有效性. 星地链路的架设和维护简单, 探测降雨范围广, 易于在高原、山区、海岛等传统地面观测资料缺失的地区使用, 可以作为已有降水测量手段的补充.
关键词: 星地链路/
垂直降雨场/
降雨衰减/
联合代数重建技术

English Abstract

全文HTML

--> --> -->

高精度实时的区域降雨资料不仅是水资源管理和农业发展领域的重要信息, 同时也为城市内涝和自然灾害(滑坡、泥石流等)预警等提供关键指导作用. 在雨量计、天气雷达和气象卫星的基础上, 利用微波链路衰减测量降雨的新方法出现了, 因其具有精度高、成本低、易操作等特点, 吸引国内外****开展了大量的实验研究. 目前, 近地面传播的视距微波链路^[1,2]在路径平均雨强和雨滴谱的反演^[3,4]、雷达的定标^[5]、区域降雨监测^[6]以及多源资料联合重构降雨场^[7]等方面, 展现出独特的优势, 成为常规大气探测手段的辅助和补充方法. 国内方面, 国防科技大学气象海洋学院在国内首先开展了微波链路测雨技术研究, 分析了微波链路测量降雨的可行性并开展了相关的实测研究^[8,9], 分别研究了基于微波链路的区域降雨反演方法^[10]和基于支持向量机和考虑非球形雨滴的降雨反演方法^[11,12], 提高了方法的适应性和准确性.
除了近地面传播的视距微波链路以外, 地面还广泛覆盖了卫星和地面站之间传播的星地链路^[13]. 高频星地链路在大气中传播时同样会受到降水的衰减, 因此同样也可以用于降雨测量. 李黄^[14]首先提出利用Ku波段卫星通信雨衰进行降雨探测的设想, 并开展初步实验. Arslan等^[15]利用Ku波段地球同步轨道(GEO)广播卫星信号测量降雨, 其结果与雷达数据相比具有较高的一致性. Francois等^[16]搭建4条GEO卫星链路并联合四维变分同化的方法对近地面区域降雨进行反演, 证明星地链路探测区域降雨的可行性. Adirosi等^[17]使用雨量筒和激光雨滴谱仪对星地链路测雨结果进行定标, 提高了降雨探测的准确性.
现有研究大多针对GEO卫星, 卫星和地面站的位置相对固定, 仅能够探测路径平均降雨. 此外, 未来还将发射多个低轨(LEO)或中轨(MEO)的宽带通信卫星星座^[13]. 与GEO卫星不同, 在LEO和MEO卫星与地面站通信过程中, 随着卫星的移动, 星地链路像X光扫描人体一样对降雨区进行“扫描”, 并且由于星地链路倾斜穿过整层降雨区域, 其衰减中还包含各个高度上的降雨信息. 利用计算机断层成像技术等方法就可以实现对二维垂直降雨场的重建. 因此可以成为一种测量降雨垂直分布的新方法. 星地链路在搭建后可自主运行, 实测数据可通过卫星回传, 并且卫星星座覆盖全球, 因此在高原、山区、海岛等传统地面观测资料缺失的地区使用具有独特优势. 本文在建立星地链路大气衰减定量模型的基础上, 提出并研究基于联合代数重建技术的星地链路反演二维垂直降雨场方法. 利用实测降雨资料开展仿真分析, 验证星地链路反演垂直降雨场的可行性和有效性, 为发展星地链路测雨新方法奠定技术基础.

2

-->

2.1.星地链路几何结构

卫星从位置A移动到位置C时, 地球站持续接收信号过程如图1所示, 其中, O代表地心, E为卫星轨道正下方地球站位置, h和R分别表示轨道高度和地球平均半径, ${\theta _0}$表示能够接收到卫星信号时地球站最小仰角. 卫星的运行周期T为
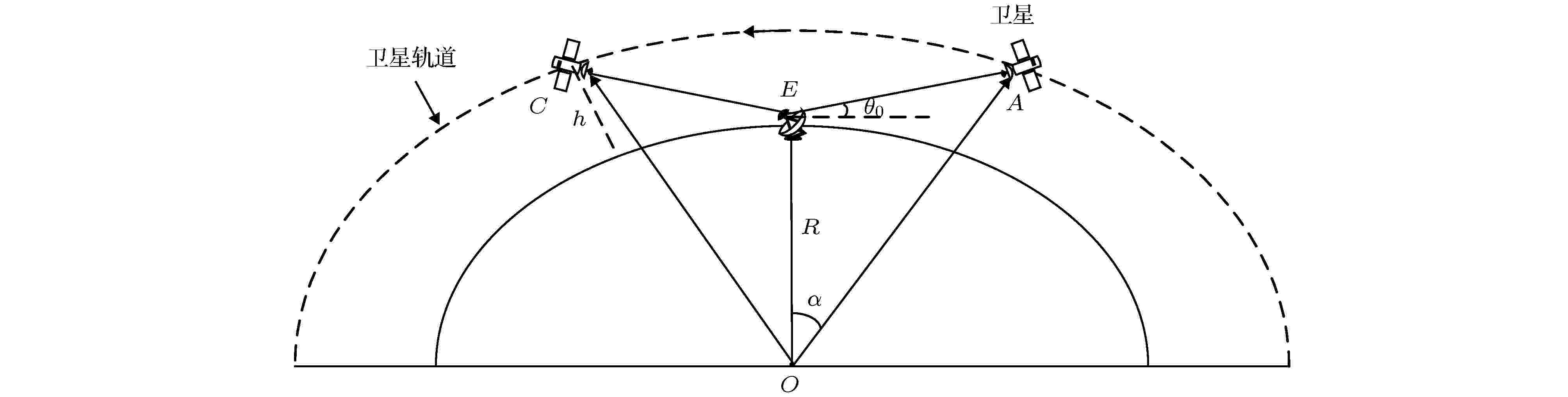图 1 星地链路几何结构
Figure1. Geometry of earth-space link.

$T = {\text{π}}\sqrt {{{{r^3}} / {(G{M_{\rm{e}}})}}} ,$

其中, $r = h + R$, M_e和G分别代表地球质量和万有引力常数. 在$\Delta EOA$中由正弦定理可得

$\alpha = \arccos \frac{{R\cos {\theta _0}}}{{R + h}} - {\theta _0}.$

由(1)式、(2)式可得地球站信号接收时间T_r为

${T_{\rm{r}}} = \frac{{\text{π}}}{{90}}\left( {\arccos \frac{{R\cos {\theta _0}}}{{R + h}} - {\theta _0}} \right)\sqrt {{{{{\left( {R + h} \right)}^3}} / {(G{M_{\rm{e}}})}}} ,$

T_r也代表星地链路对降雨区域的最大扫描时间.
假设卫星从位置A移动到位置B时地球站位于降雨区域内, 星地链路探测垂直降雨场的过程如图2所示, 图中h_rain表示雨区相对于地球站的垂直高度, L_r和L_o分别代表星地链路在雨区内和雨区外的传播距离, L_o远大于L_r, 则星地链路的水平探测尺度W为
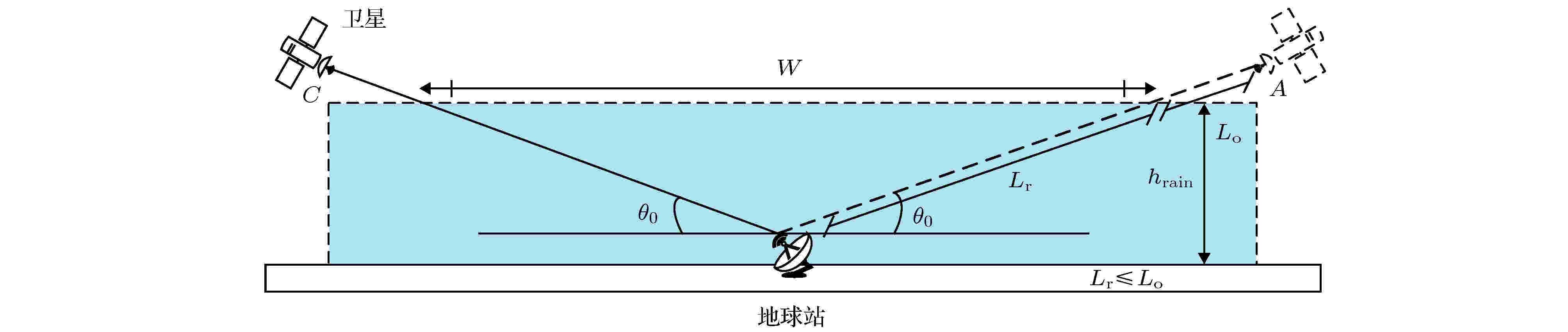图 2 星地链路探测垂直降雨场
Figure2. The detection of vertical rainfall field with earth-space link.

$W = {{2{h_{{\rm{rain}}}}}}/{{\tan {\theta _0}}}.$

当h_rain = 4.8 km, θ₀ = 5°时, W约为110 km, 可以看到单一地球站便能实现对527 km²垂直范围内的降雨场的监测.
2 -->

2.2.星地链路信号衰减

在星地通信系统中, 地球站接收功率P_r (dB)可以表示为^[18]

${P_{\rm{r}}} = {\rm{EIRP}} + {G_{\rm{r}}} - {\rm{LOSS}},$

其中EIRP为等效全辐射功率, 单位为dB; G_r为地球站接收天线增益, 单位为dB; LOSS为星地链路传输衰减, 单位为dB. 若卫星发射功率为P_tran (dB), 卫星天线增益为G_tran (dB)则

${\rm{EIRP}} = {P_{{\rm{tran}}}} + {G_{{\rm{tran}}}}.$

星地链路传输衰减LOSS主要来源于自由空间衰减A_f (dB)和对流层衰减A_trop (dB), 其中A_trop又包括闪烁衰减A_s (dB)、气体衰减A_gas (dB)、云致衰减A_cloud (dB)和降雨衰减A_rain (dB):

${\rm{LOSS}} = {A_{\rm{f}}} + {A_{{\rm{trop}}}},$

${A_{{\rm{trop}}}} = {A_{\rm{s}}} + {A_{{\rm{gas}}}} + {A_{{\rm{cloud}}}} + {A_{{\rm{rain}}}}.$

对于使用点波束天线的LEO卫星, 其等效全辐射功率EIRP恒定. 以OneWeb星座系统为例^[13], 其卫星轨道高度h = 1200 km, 最小工作仰角θ₀ = 30°, 根据(3)式可得地球站连续接收卫星信号时间T_r = 8 min, 在此时间内可认为接收天线增益G_r为常数. 因此, 地球站天线的接收功率P_r可表示为

${P_{\rm{r}}} = C - {A_{\rm{f}}} - {A_{\rm{s}}} - {A_{{\rm{gas}}}} - {A_{{\rm{cloud}}}} - {A_{{\rm{rain}}}}.$

其中, C为增益常数.
自由空间衰减、闪烁衰减、气体衰减和云致衰减的计算可参考ITU-R P.618建议书^[18], 在南京地区接收AsiaSat5卫星Ku波段信号, 电磁波为垂直极化, 卫星轨道高度为36000 km, 天线仰角为43°, 统计高层云底高为3.55 km, 云顶高为4.77 km^[19], 则在12—18 GHz范围内, 星地链路上的自由空间衰减、闪烁衰减、整层大气衰减、云致衰减以及10 mm/h和20 mm/h雨强时的降雨衰减如图3所示. 整体而言, 气体衰减最小在10^–1—1 dB范围内, 闪烁衰减和云致衰减次之在1 dB左右, 降雨引起的衰减明显, 并且随着降雨强度和频率的增加而增加, 能够达到10 dB以上, 高于气体衰减、闪烁衰减及云致衰减而不会被其淹没. 虽然自由空间衰减超过10² dB, 但由于其仅是电波频率和传播距离的函数^[18]并且当电波频率偏移200 MHz, 卫星轨道高度变化1000 km时自由空间衰减的相对变化量不足0.2%, 因此在已知卫星工作频率和轨道的条件下能够精确计算自由空间衰减, 可以将其从总衰减中剔除, 消除对降雨衰减测量的影响.
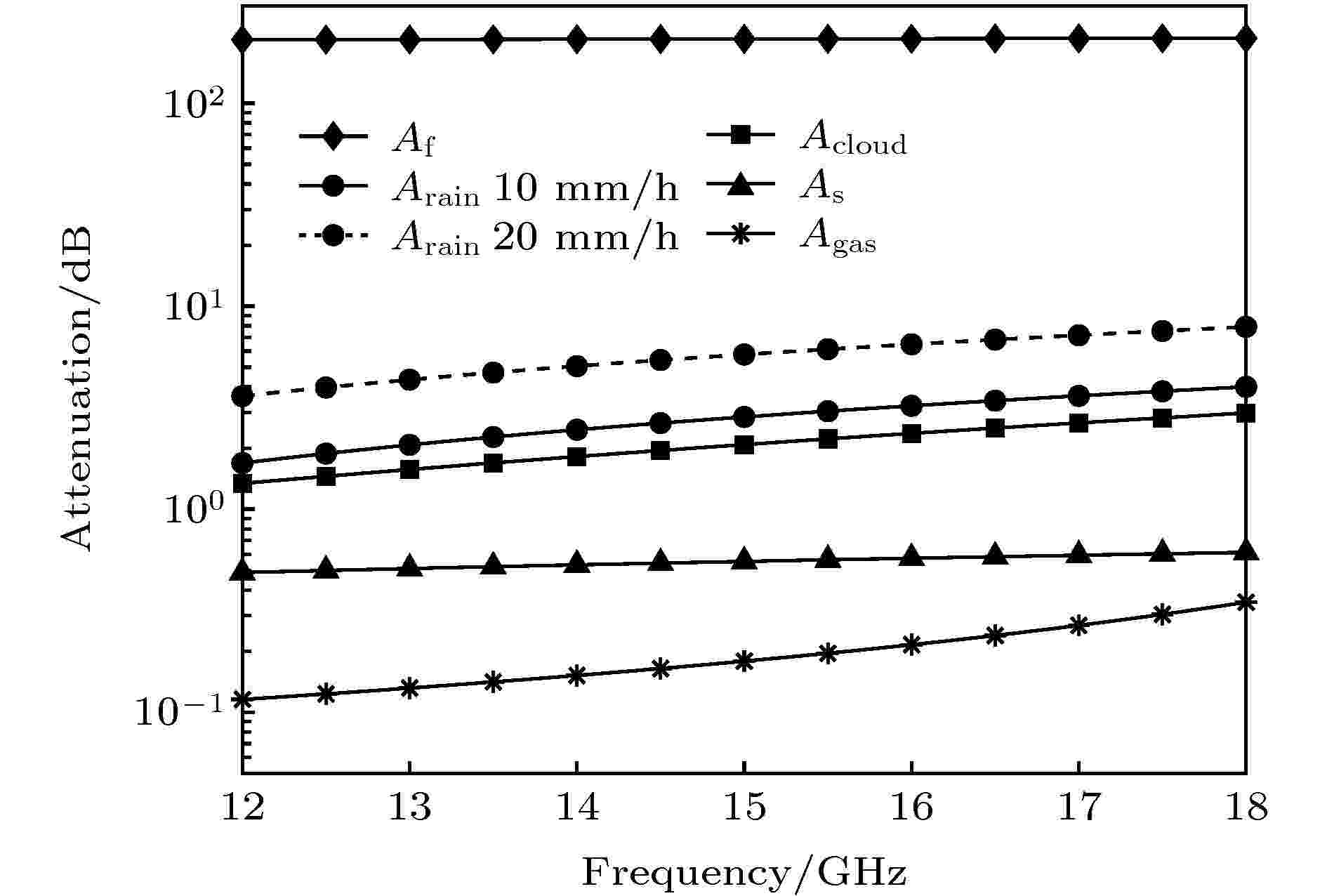图 3 星地链路闪烁衰减、云致衰减、气体衰减、雨强为10 mm/h和20 mm/h的雨致衰减
Figure3. Scintillation attenuation, cloud attenuation, gas attenuation and rain attenuation with 10 mm/h and 20 mm/h rain rate in earth space link.

2

-->

3.1.垂直降雨场反演模型

星地链路在某一条路径上的降雨总衰减为

${A_{{\rm{rain}}}} = \int_{({x_0},{h_0})}^{({x_r},{h_r})} {\gamma \left( {x,h} \right)\csc \theta {\rm{d}}h}, $

其中γ(x, h)为(x, h)处的降雨衰减系数, 单位为dB/km, 表示卫星信号在降雨区域内每经过1 km将会产生γ(x, h)的衰减; (x₀, h₀)和(x_r, h_r)分别代表地球站位置和星地链路离开雨区的位置; θ代表地球站天线仰角.
为实现垂直降雨场的反演, 首先将探测区域划分成大小相等的方形网格, 假设每个网格内衰减系数均匀, 降雨场网格化示意图如图4所示. 其中$l_i^k$表示链路在第k次探测即仰角为θ_k时在第i个网格内的长度, γ_i表示第i个网格的衰减系数, 则星地链路第k次探测时的降雨衰减可表示为
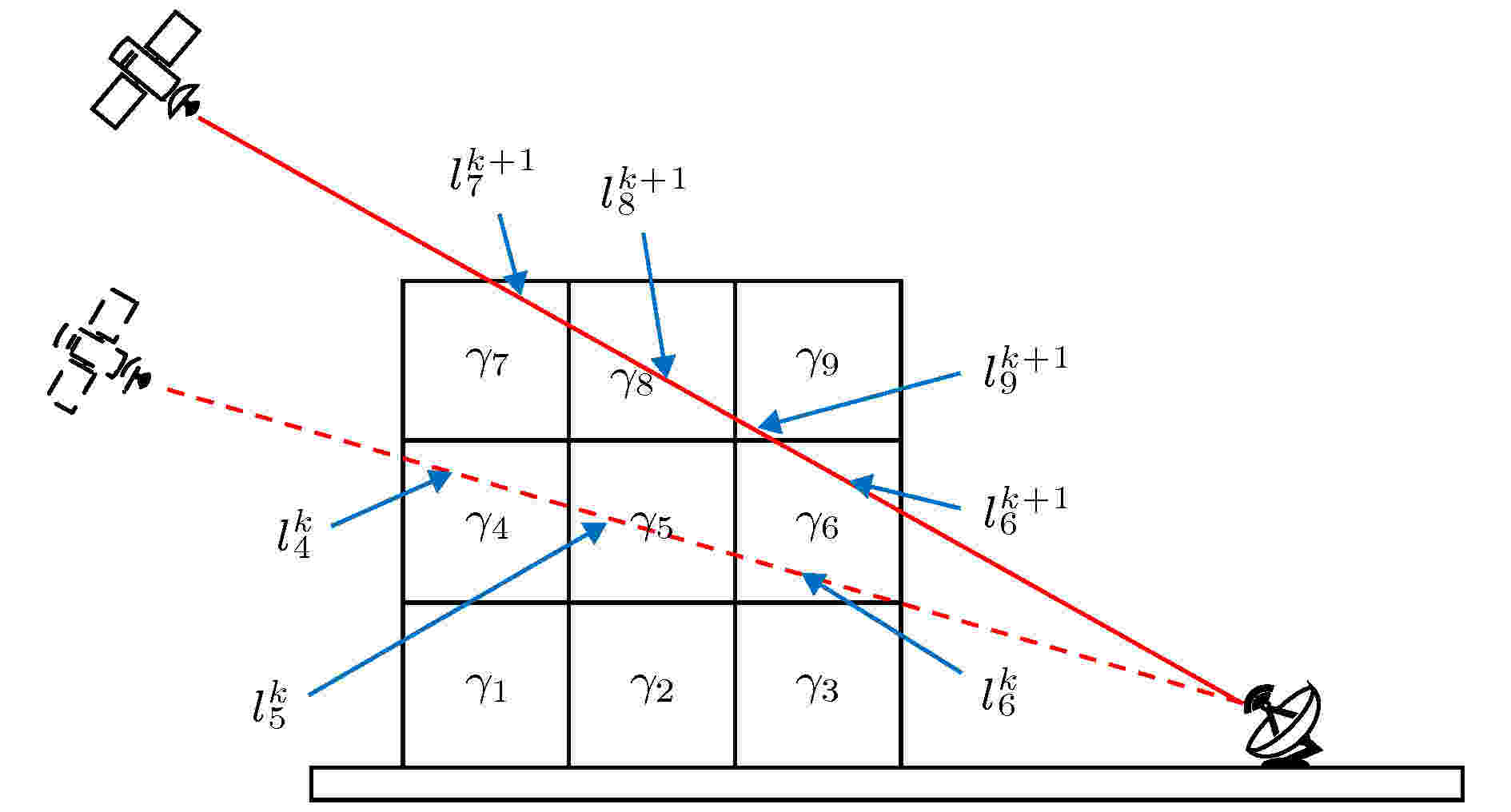图 4 计算星地链路降雨衰减简易图
Figure4. The sketch of calculation of earth-space link rain attenuation.

$A_{{\rm{rain}}}^k = {\gamma _6}l_6^k + {\gamma _7}l_7^k + {\gamma _8}l_8^k + {\gamma _9}l_9^k.$

将(11)式推广, 若降雨场被分隔成N = n × n个网格, 则第k次探测时星地链路的降雨衰减可表示为

$A_{{\rm{rain}}}^k = \sum\limits_{i = 1}^N {{\gamma _i}l_i^k} .$

假设地球站接收一次卫星信号的时间间隔为$\Delta t$, 则卫星过顶时, 星地链路每次探测的间隔角度$\Delta \theta $为

$\begin{split} \Delta \theta =& \frac{{{\text{π}}\left( {90 - {\theta _0}} \right)}}{{45\Delta t}}\left( {\arccos \frac{{R\cos {\theta _0}}}{{R + h}} - {\theta _0}} \right)\\ &\times\sqrt {{{{{\left( {R + h} \right)}^3}} / {(G{M_{\rm{e}}})}}}. \end{split}$

在星地链路探测垂直降雨场过程中, 由ITU-R P.618建议书^[18]可以得到链路第k次探测时的自由空间衰减A_f、闪烁衰减A_s、气体衰减A_gas、云致衰减A_cloud, 基于此剔除其在第k次探测时的实际接收功率$P_{\rm{r}}^k$中的影响得到P_k, 再由(9)式和(12)式可得

${P_k} = C - \sum\limits_{i = 1}^N {{\gamma _i}l_i^k} .$

在一次完整的垂直降雨场反演过程中, 假设星地链路共进行M次探测, 垂直降雨场被划分成N个网格, 令${q_k} = - {P_k}$得到

$\left[\!\! {\begin{array}{*{20}{c}}{l_1^1}&{l_2^1}& \cdots &{l_N^1}&{ - 1}\\{l_1^2}&{l_2^2}& \cdots &{l_N^2}&{ - 1}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\{l_1^M}&{l_2^M}& \cdots &{l_N^M}&{ - 1}\end{array}} \!\!\right]\left[\!\! \begin{array}{ccccccccc}{\gamma _1}\\{\gamma _2}\\ \vdots \\{\gamma _N}\\C\end{array} \!\!\right] = \left[\!\! \begin{array}{cccccccc}{q_1}\\{q_2}\\ \vdots \\{q_M}\end{array} \!\!\right],$

即

${{L\gamma }} = {{q}},$

其中, γ称为衰减系数向量.
雨衰系数γ_R与雨强R的关系满足幂律关系^[20]:

${\gamma _R} = \alpha {R^{\beta} },$

其中, 幂律系数α和β是信号频率、极化方式和链路仰角的函数, 具体计算方法可参考ITU-R P.838建议书^[20]. 因此, 可以根据衰减系数γ_R得到对应的降雨强度, 即

$R = {\left( {{{{\gamma _R}}}/{\alpha }} \right)^{\frac{1}{\beta }}},$

由此垂直降雨场反演过程变成了求解线性方程组(16)式的问题.
由ITU-R P.838-3建议书^[20]发现, 当星地链路频率为垂直极化17 GHz (Ku波段)时, 幂律系数随仰角的变化很小(图5), α和β均在0.04范围内变化, 两者的标准差(standard deviation, STD)和标准差系数(coefficient of variation, CV)分别为0.0012, 1.74%和0.0136, 1.32%, 并且β接近于1, 雨强和衰减系数近似呈线性关系. 因此, 本文在反演降雨强度时幂律系数选择为$\overline \alpha = 0.063$, $\overline \beta = 1.033$, 这样一方面简化计算过程, 另一方面又能确保反演结果的准确性.
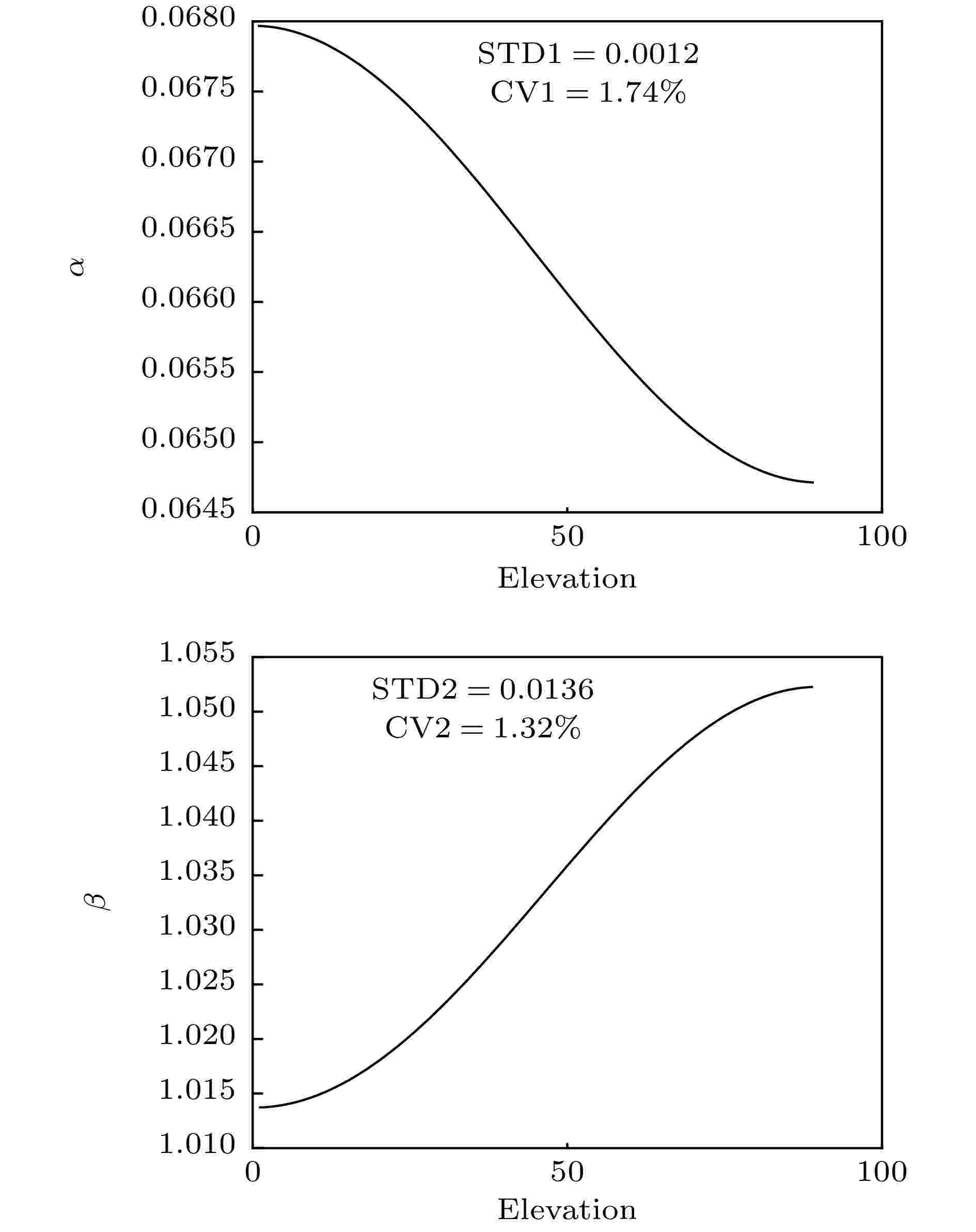图 5 幂律系数随仰角的变化
Figure5. The change of power law coefficients with elevation.

2 -->

3.2.基于联合代数重建技术(SART)的降雨场反演算法

SART作为一种CT成像技术中巨型稀疏矩阵求解的经典算法, 能够有效地解决方程组超定或欠定问题^[21], 是Kaczmarz^[22]的迭代重建技术 (algebraic reconstruction technique, ART)的进一步发展. SART算法的优势在于每次迭代过程中所有的方程都被用于像素解的更新, 实现噪声的平滑处理, 比ART算法的稳定性更高^[21]. 基于SART算法, 垂直降水场衰减系数向量γ的迭代过程为^[23]

${{{\gamma }}^{k + 1}} = {{{\gamma }}^k} + {\lambda _k}{{D}}_r^{ - 1}{{{L}}^{\rm{T}}}{{D}}_c^{ - 1}\left( {{{q}} - {{L}}{{{\gamma }}^k}} \right),$

其中, ${{{\gamma }}^k}$代表第k次迭代后的衰减系数向量解; ${\lambda _k}$为弛豫系数, 取值范围为(0, 2); ${{{D}}_{\rm{r}}}$和${{{D}}_{\rm{c}}}$分别是与矩阵L的行向量和列向量有关的对角矩阵:

${{{D}}_{\rm{r}}} = {\rm{diag}}\left( {{{\left\| {{{l}}_i^{\rm{r}}} \right\|}_1}} \right),$

${{{D}}_{\rm{c}}} = {\rm{diag}}\left( {{{\left\| {{{l}}_j^{\rm{c}}} \right\|}_1}} \right),$

其中, ${{l}}\, _i^{\rm{r}}$和${{l}}\, _j^{\rm{c}}$分别代表矩阵L的第i个行向量和第j个列向量.
由于衰减系数取值为正数, 所以需在迭代过程中要加入非负约束. 定义投影函数$\varPhi $使得所有衰减系数投影到正象限:

${\left[ {\Phi \left( \gamma \right)} \right]_i} = \left\{ {\begin{aligned}& {{\gamma _i},}\quad {{\gamma _i} \geqslant 0,}\\& {0,}\quad {{\gamma _i} < 0,}\end{aligned}} \right.$

其中, ${\gamma _i}$代表向量γ的第i个元素. 引入投影函数$\varPhi $后向量γ的迭代过程变为

${{{\gamma }}^{k + 1}} \leftarrow \varPhi \left( {{{{\gamma }}^k} + {\lambda _k}{{D}}_{\rm{r}}^{ - 1}{{{L}}^{\rm{T}}}{{D}}_{\rm{c}}^{ - 1}\left( {{{q}} - {{L}}{{{\gamma }}^k}} \right)} \right).$

为评价反演效果, 采用欧氏距离(Euclidean distance, δ)和熵(entropy, S)两个指标, 欧式距离的高低表示反演场和真实场误差的大小, 两者的熵差距越小表示降雨强度的空间分布越接近^[24]:

$\delta = {\left[ {\frac{1}{{nm}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{{\left( {{R_{ij}} - {{R'}_{ij}}} \right)}^2}} } } \right]^{{1 / 2}}}$

$S = \frac{{ - 1}}{{\ln nm}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {\left( {\frac{{{R_{ij}}}}{F}} \right)} } \ln \left( {\frac{{{R_{ij}}}}{F}} \right)$

其中, n为降雨场网格化后垂直方向网格数, m为水平方向网格数, ${R_{ij}}$和${R'_{ij}}$分别表示i行j列网格内的反演降雨强度和真实降雨强度, F为

$F = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{R_{ij}}} }. $

2 -->

3.3.反演算法流程

反演算法流程图如图6所示, 具体的反演过程为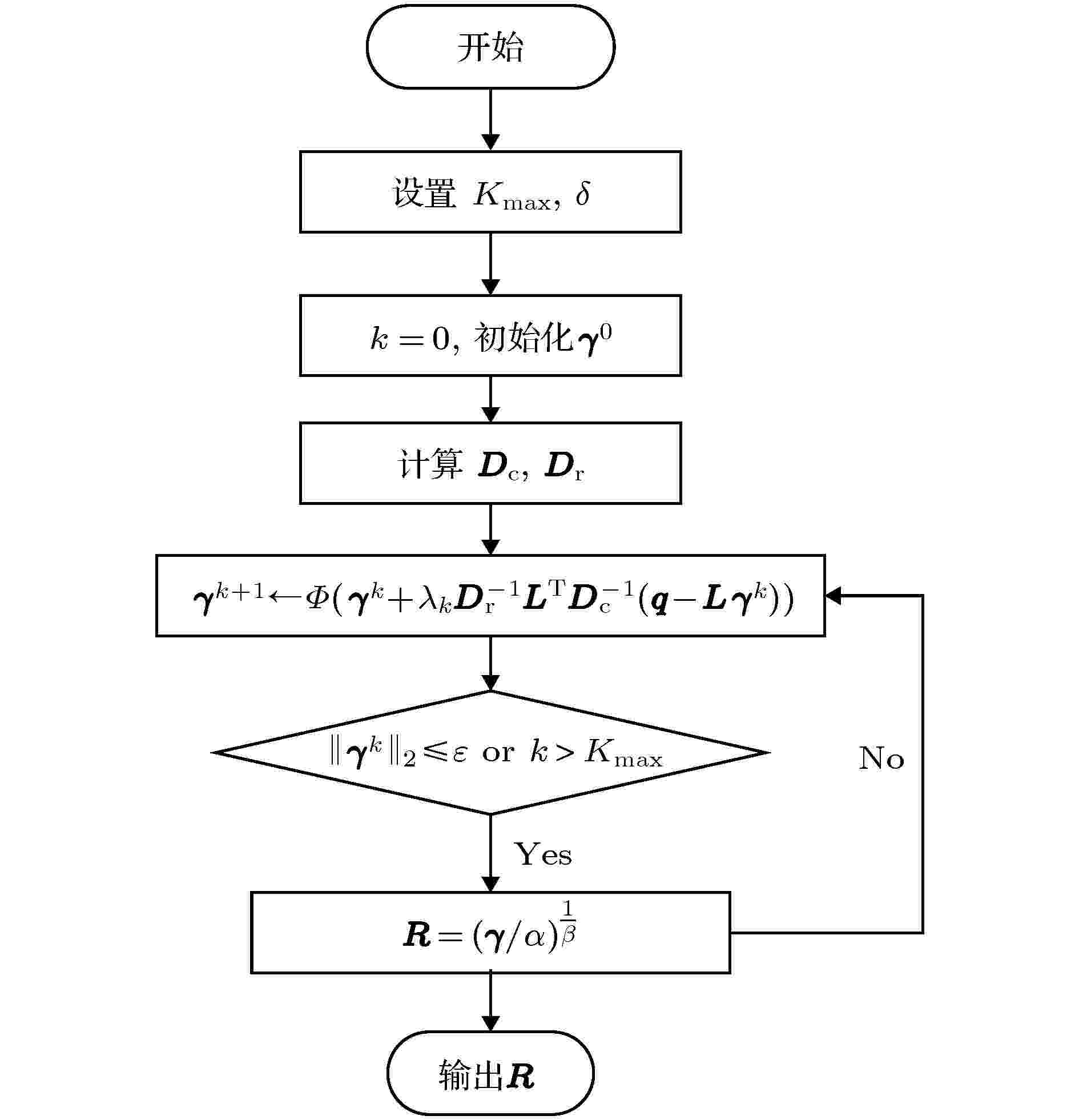
图 6 反演算法流程图
Figure6. The flow chart of vertical rainfall field inversion method.

1)设置最大迭代次数K_max和误差阈值$\varepsilon $;
2)初始化γ⁰(很小的随机向量或零向量);
3)由(22)式和(23)式计算矩阵D_c, D_r;
4)由(25)式迭代求解衰减系数;
5) k = k + 1;
6)${\left\| {{{{\gamma }}^k}} \right\|_2} \leqslant \varepsilon $或$ k > {K_{\max }}$时停止迭代, 否则返回步骤4);
7)由(18)式计算降雨强度.

2

-->

4.1.初始场参数设置

利用南京地区2014年6月30日、7月2日和10月28日的微雨雷达(micro rain radar, MRR)实测资料, 将时间尺度转为水平距离尺度, 构建3类二维垂直降雨场I, II和III, 如图7所示. 可以清楚地看到降雨垂直方向上分布的不均匀性. 其中, 降雨场I中5 km高度上出现3个强降雨中心, 并且在水平5—10 km范围上空出现连续性垂直降雨带, 最大降雨强度为8 mm/h; 在降雨场II中5 km高度上出现1个强降雨中心, 最大降雨强度为18 mm/h; 在降雨场III中3—4 km高度范围内出现连续性水平降雨区, 最大降雨强度为40 mm/h.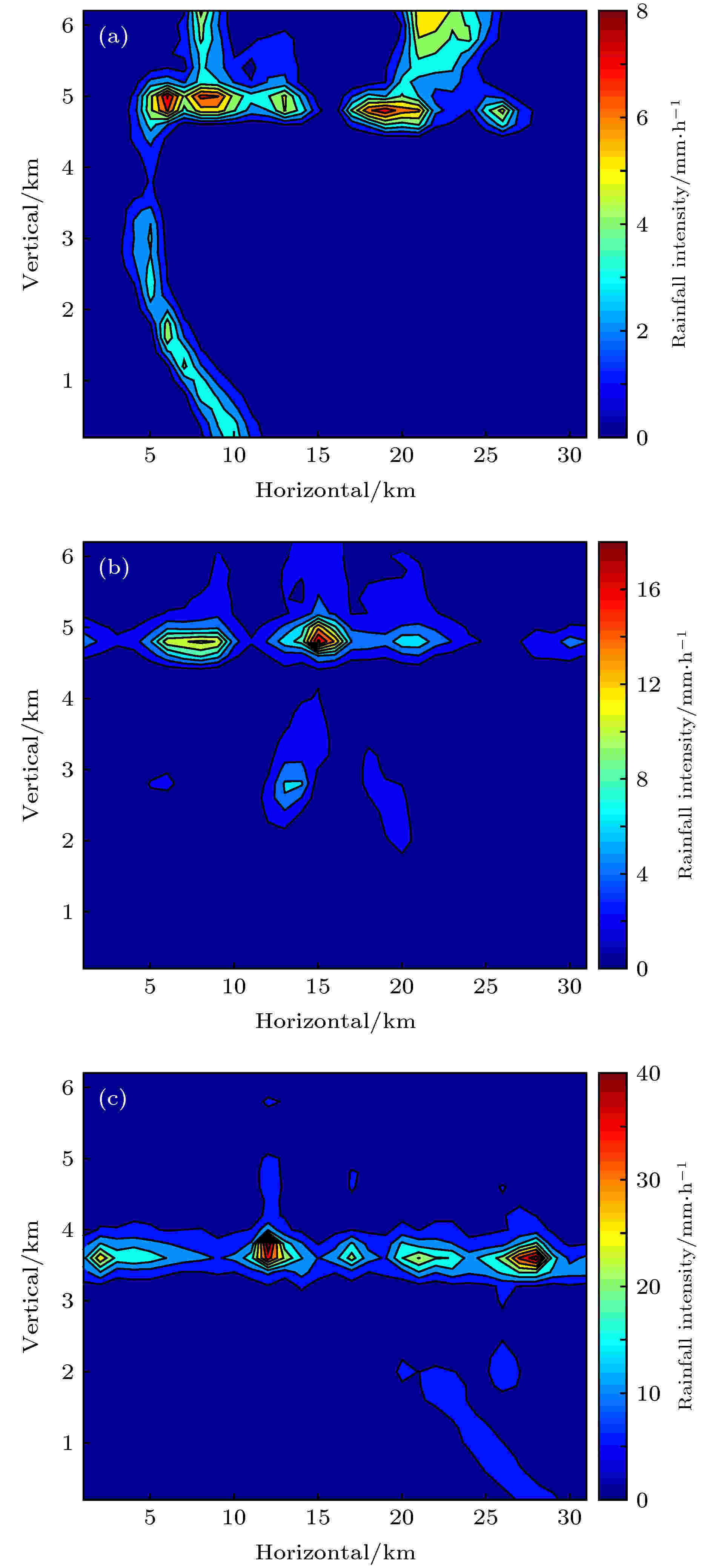
图 7 基于MRR实测资料构建的垂直降雨场　(a) 降雨场I; (b) 降雨场II; (c) 降雨场III
Figure7. Vertical rainfall field derived from the data of MRR: (a) rainfall field I; (b) rainfall field II; (c) rainfall field III.

将上述垂直降雨场划分成1个31 × 31方形组成的网格, 其垂直分辨率为200 m/格, 水平分辨率为1 km/格, 并由位于(–10 km, 0 km)的地球站1, (64 km, 0 km)的地球站2和(15 km, 0 km)的地球站3进行探测, 如图8所示, 图中θ₁, θ₂和θ₃分别表示3个地球站天线的仰角, Δθ₁, Δθ₂和Δθ₃分别表示3个天线相邻两次探测的间隔仰角. 参考Ku工作波段AsiaSat5卫星的EIRP = 56 dB, 直径为1.5 m抛物面接收天线增益G_r = 49 dB, 则增益常数C = 105 dB. 星地链路具体参数如表1所示.

地球站	频率/ GHz	极化方式	Δθ/(°)	θMin/(°)	C/dB
1	17	垂直	0.1	0.091	105
2	17	垂直	0.1	0.065	105
3	17	垂直	0.1	1.00	105

表1星地链路参数
Table1.Parameters of earth-space link.

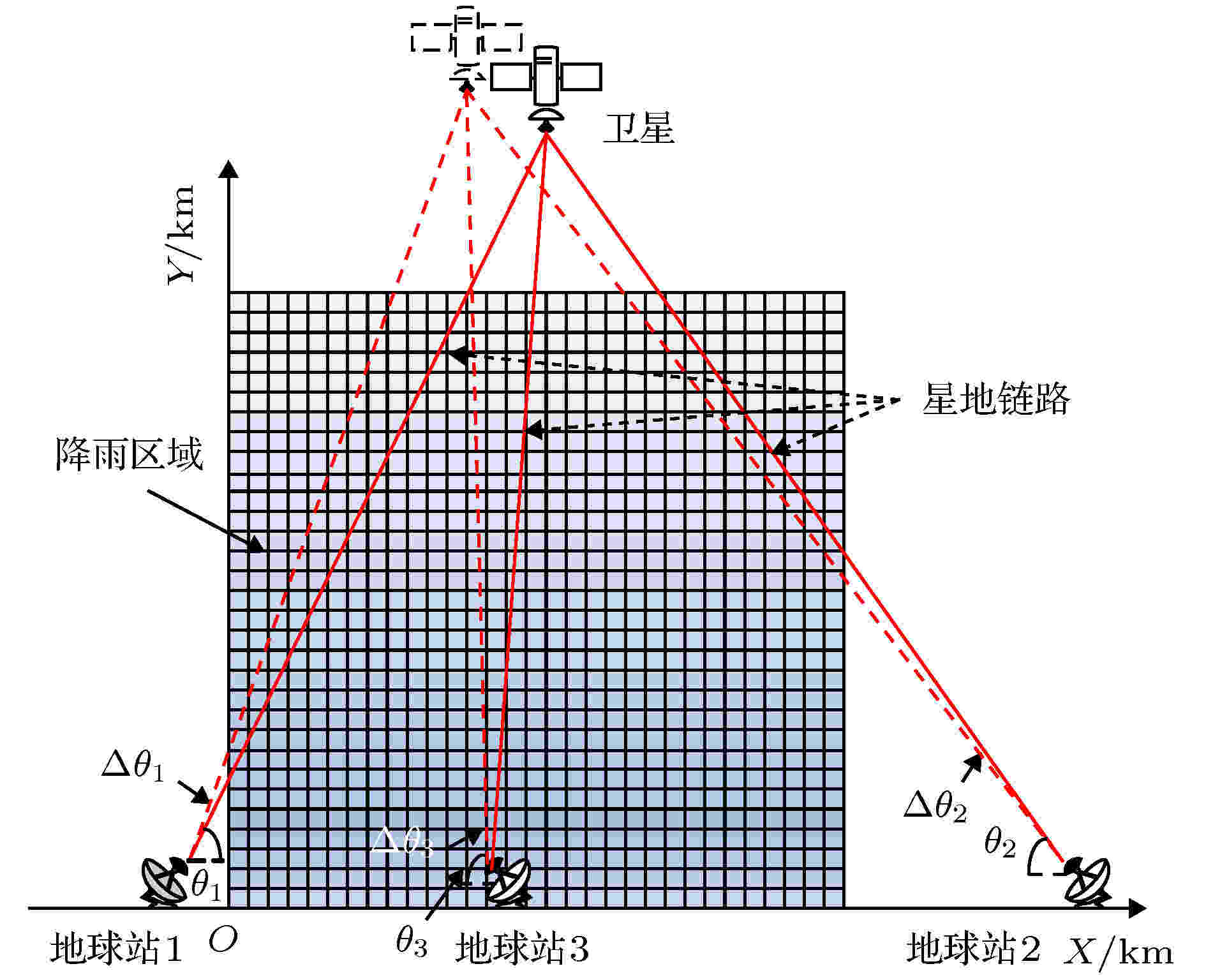图 8 降雨场网格化和星地链路探测示意图
Figure8. Sketch of grid for rainfall field and detection of earth-space links.

在MRR实测资料的基础上开展仿真实验, 由(17)式得到每个网格内的衰减系数, 根据表1中星地链路参数得到探测过程中的降雨衰减并建立线性方程组(15), 然后基于带有非负限制的SART反演算法对方程组求衰减系数解, 最后结合(18)式由衰减系数得到降雨强度, 从而重构垂直降雨场.
2 -->

4.2.反演结果分析

首先, 用地球站1的探测数据来反演垂直降雨场, 结果如图9(a)—(c)所示. 可以看到, 反演场的降雨强度及其分布与真实场相比存在明显的差异. 其中, 降雨场I, II和III与其反演场的相关系数、平均偏差分别为0.556, 0.630 mm/h; 0.504, 0.865 mm/h和0.364, 2.553 mm/h. 3个反演场欧式距离和熵随迭代次数的变化如图10(a)—(c)和图11(a)—(c)所示. 从图10(a)—(c)可以看到, 虽然整个迭代过程的反演场逐渐趋向于真实场, 但经过500次迭代后的欧式距离分别为1.046, 1.429和4.103 mm/h, 与真实场的差距较大. 图11(a)—(c)中, 黑色虚线代表实际降雨场的熵, 在整个反演过程中反演场熵的变化并不明显, 表明反演效果随迭代次数未发生显著的变化, 500次迭代后反演场熵和真实场熵的相对误差分别为11.35%, 3.65%和3.25%. 改用地球站2或地球站3的探测数据后也出现了类似的情况. 之后又尝试减小θ_min和Δθ以得到更多的探测数据, 但反演效果并没有明显的改善. 实验结果表明, 仅利用1个地球站难以实现垂直降雨场的反演. 这是因为在探测过程中出现了多条相邻星地链路经过同一组网格的现象, 导致方程组(15)的有效方程数量即矩阵L的秩减少, 即使设置Δθ = 0.05°使矩阵L的维度达到1441 × 962, 但有效方程的数量也仅为572, 同时由于降雨场网格数量庞大, 使得SART算法在迭代过程中易趋向局部最优解.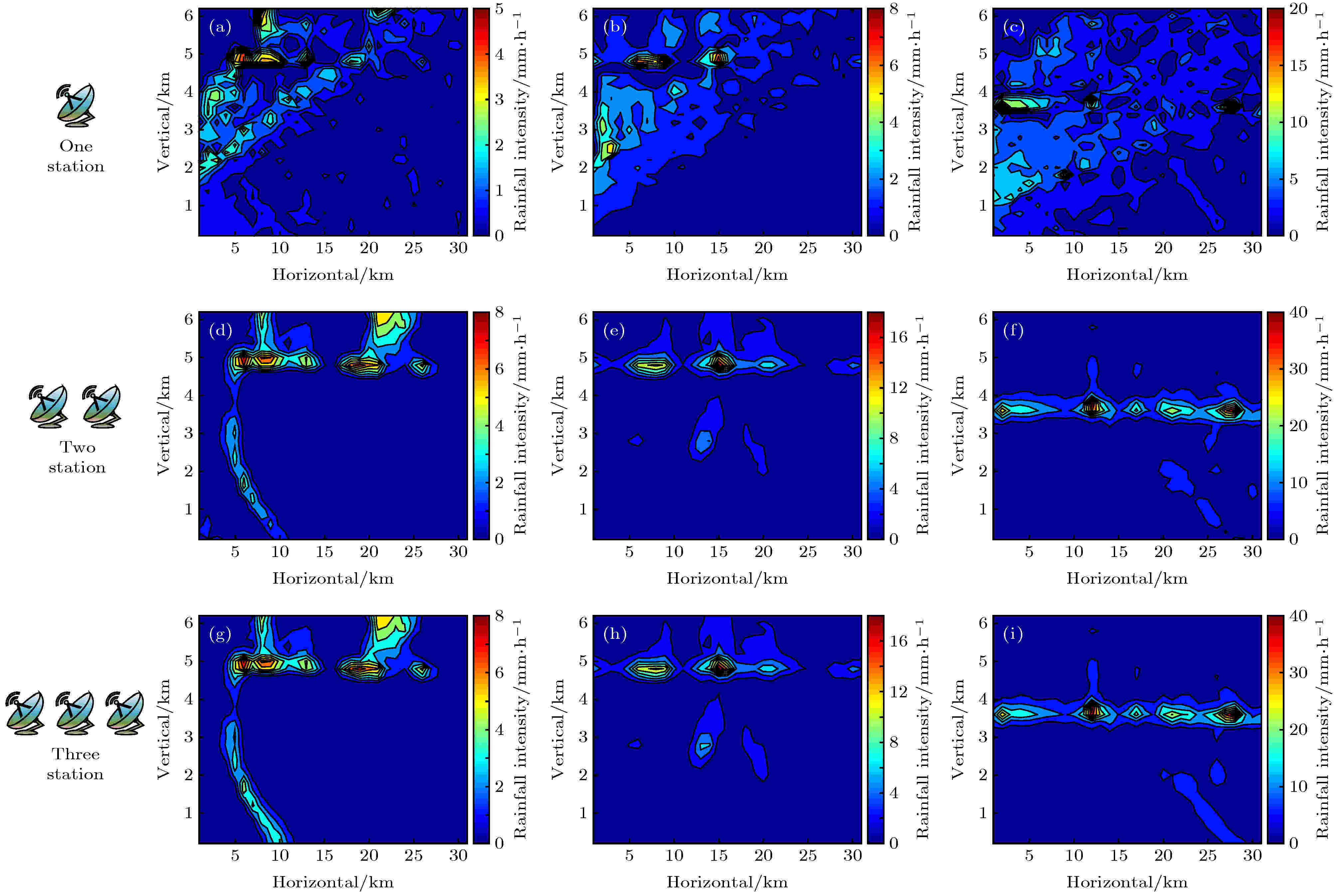
图 9 垂直降雨场反演效果图　(a) 单地球站反演降雨场I; (b) 单地球站反演降雨场II; (c) 单地球站反演降雨场III; (d) 双地球站反演降雨场I; (e) 双地球站反演降雨场II; (f) 双地球站反演降雨场III; (g) 三地球站反演降雨场I; (h) 三地球站反演降雨场II; (i) 三地球站反演降雨场III
Figure9. Inversed vertical rainfall field: (a) Inversed field I with one earth station; (b) inversed field II with one earth station; (c) inversed field III with one earth station; (d) inversed field I with two earth stations; (e) inversed field II with two earth stations; (f) inversed field III with two earth stations; (g) inversed field I with three earth stations; (h) inversed field II with three earth stations; (i) inversed field III with three earth stations.

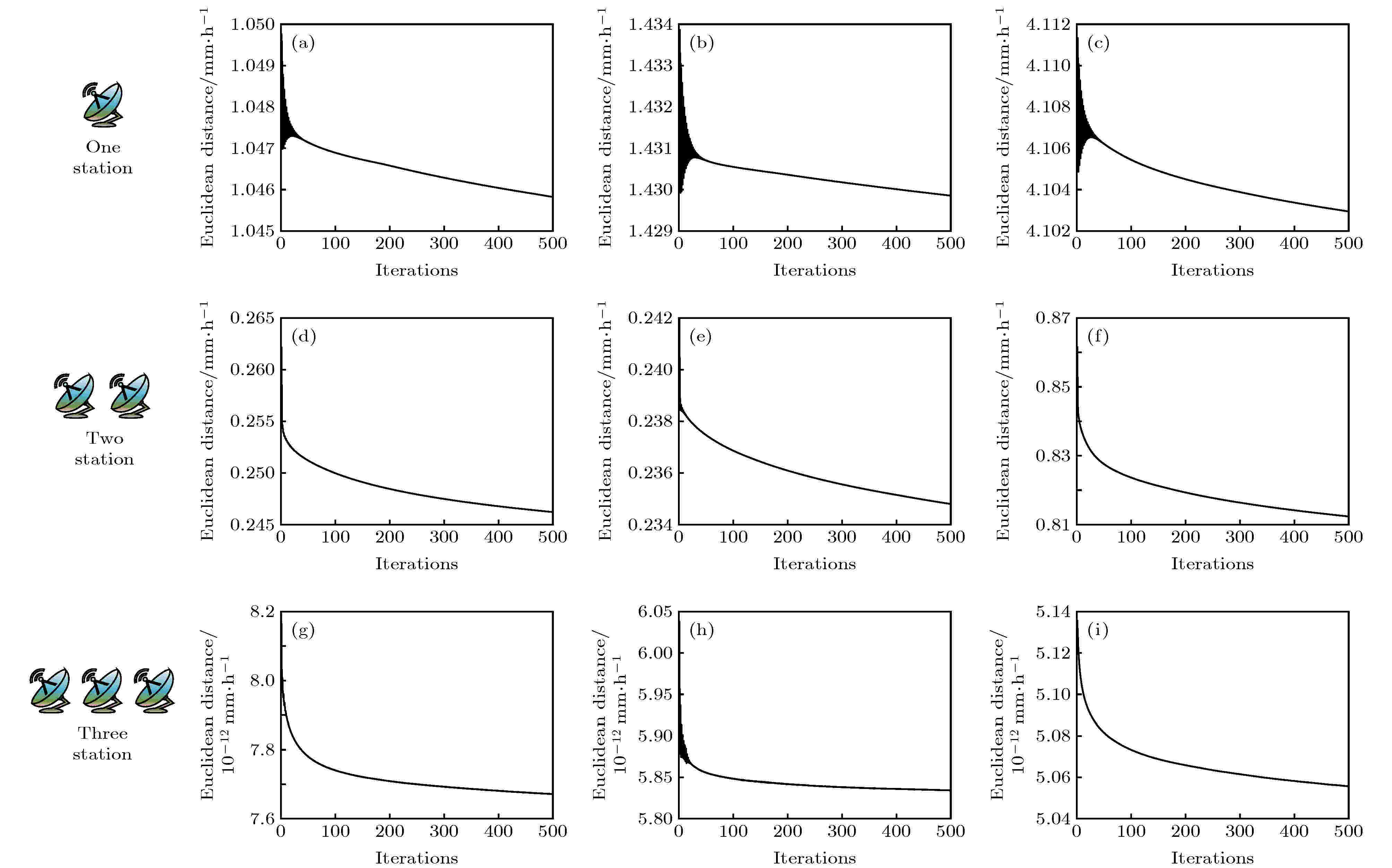图 10 欧氏距离随迭代次数的变化情况　(a) 单地球站反演降雨场I; (b) 单地球站反演降雨场II; (c) 单地球站反演降雨场III; (d) 双地球站反演降雨场I; (e) 双地球站反演降雨场II; (f) 双地球站反演降雨场III;(g) 三地球站反演降雨场I; (h) 三地球站反演降雨场II; (i) 三地球站反演降雨场III
Figure10. The change of Euclidean distance with iterations: (a) Inversed field I with one earth station; (b) inversed field II with one earth station; (c) inversed field III with one earth station;(d) inversed field I with two earth stations; (e) inversed field II with two earth stations; (f) inversed field III with two earth stations;(g) inversed field I with three earth stations; (h) inversed field II with three earth stations; (i) inversed field III with three earth stations.

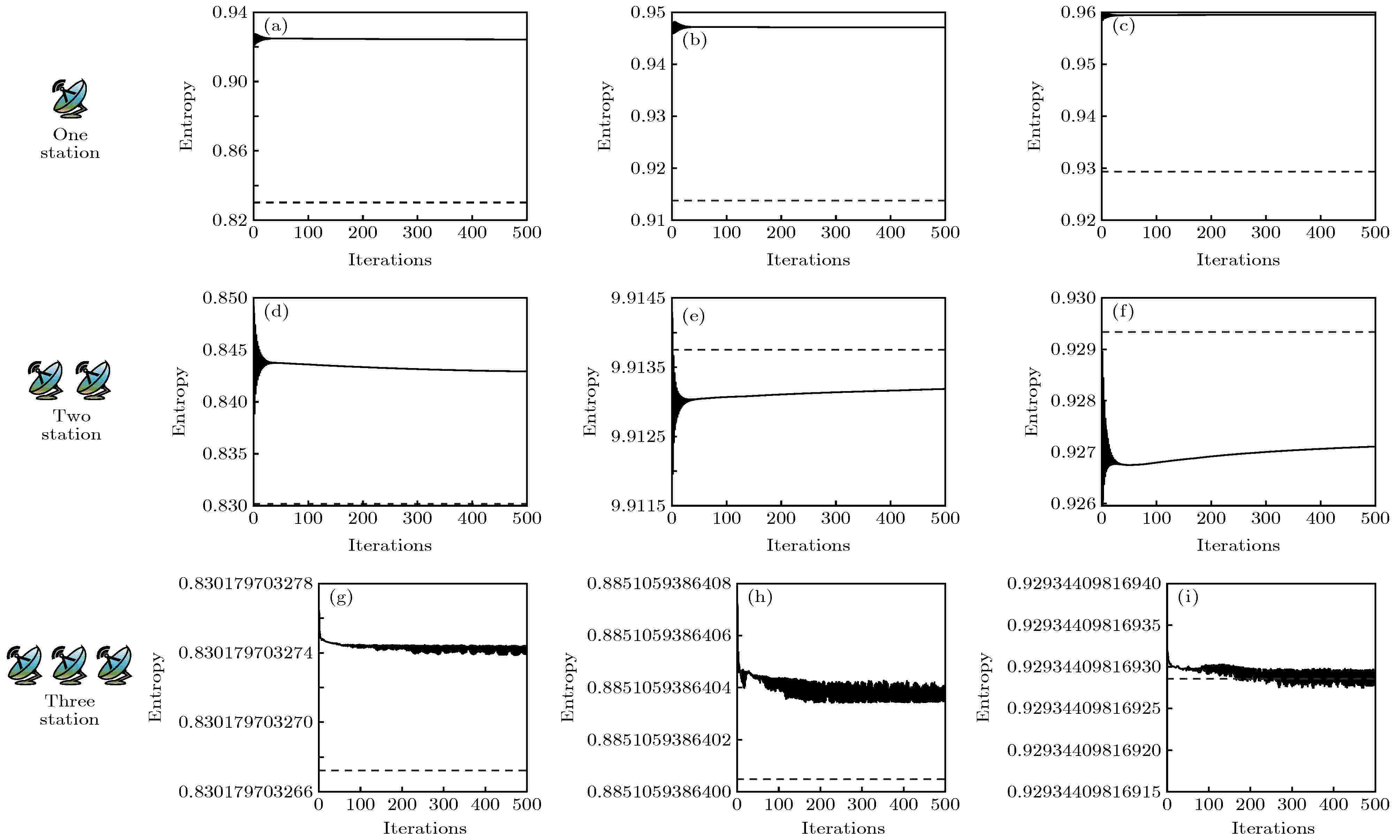图 11 欧氏距离随迭代次数的变化情况　(a) 单地球站反演降雨场I; (b) 单地球站反演降雨场II; (c) 单地球站反演降雨场III; (d) 双地球站反演降雨场I; (e) 双地球站反演降雨场II; (f) 双地球站反演降雨场III; (g) 三地球站反演降雨场I; (h) 三地球站反演降雨场II; (i) 三地球站反演降雨场III
Figure11. The change of entropy with iterations: (a) inversed field I with one earth station; (b) inversed field II with one earth station; (c) inversed field III with one earth station; (d) inversed field I with two earth stations; (e) inversed field II with two earth stations; (f) inversed field III with two earth stations; (g) inversed field I with three earth stations; (h) inversed field II with three earth stations; (i) inversed field III with three earth stations.

基于第1次的实验结果, 本文联合两个地球站1和地球站2对降雨场进行探测, 反演结果示于图9(d)—(f). 可知, 垂直降雨场的整体反演效果较好, 能够清楚地看到降雨场I中5 km高度上的3个强降雨中心和连续性垂直降雨带, 降雨场II中5 km上的1个强降雨中心和降雨场III中的连续性水平降雨区, 并且准确得到每个降雨场的最大降雨强度. 但是反演场I中连续性垂直降雨带内部的降雨分布、反演场II中3 km高度上的降雨中心以及反演场III中3 km高度以下的弱降水中心仍与真实场存在偏差. 其中降雨场I, II, III与其反演场相关系数、平均偏差分别为0.980, 0.122 mm/h; 0.989, 0.159 mm/h和0.982, 0.537 mm/h. 欧式距离和熵的变化情况如图10(d)—(f)和图11(d)—(f)所示, 经过500次迭代后3个反演场的欧式距离、熵的相对误差分别为0.246 mm/h、1.53%, 0.235 mm/h、0.061%和0.812 mm/h、0.23%. 虽然实验结果与真实场仍存在部分微小偏差, 但两个地球站已基本实现基于星地链路的垂直降雨场反演. 与单地球站相比, 在本次实验中从两个不同的位置对降雨场进行探测, 使有效方程的数量增加到944个接近与降雨场的网格数量, SART算法在迭代过程中能够更加准确地趋向全局最优解.
在前两次实验的基础上, 本文联合3个地球站对降雨场进行探测, 反演结果如图9(g)—(i)所示, 与基于双地球站的反演结果相比, 前者存在的偏差在本次实验结果中均已消失, 反演场更加接近于真实场, 其中降雨场I, II, III与其反演场的相关系数接近1, 平均偏差分别为4.22 × 10^–12, 2.65 × 10^–12和3.64 × 10^–12 mm/h. 从图10(g)—(i)可以看到欧式距离均小于0.01 mm/h, 图11(g)—(i)中反演场熵的相对误差均在0.01%以下. 实验结果表明, 基于3个地球站已实现垂直降雨场的准确反演. 同时, 在本次实验中, 有效方程的数量为961, 与降雨场网格数量相同, 在反演过程中SART算法能精准地找到全局最优解.

在建立星地链路大气衰减定量模型的基础上, 研究了基于联合代数重建技术的星地链路重构垂直降雨场方法. 利用实测降雨资料开展数值仿真, 实现二维垂直降雨场的反演. 星地链路测雨新方法的应用, 将加深了解降雨的内部结构及其发展过程, 为天气预报和自然灾害预警等提供新的技术支持. 同时, 该方法也可应用于山区、海岛等人迹罕至的地区, 作为传统地面观测手段的补充. 在未来, 随着宽带卫星星座的部署, 地球站的架设成本将持续降低, 有利于星地链路测雨方法的大范围推广. 因此该方法有着广阔的应用前景和价值.
1)对于非降雨因素引起的衰减, 气体衰减最小在10^–1—1 dB范围内, 闪烁衰减和云致衰减次之在1 dB左右, 明显小于降雨衰减而不会将其淹没. 自由空间衰减最严重为10² dB高于其他衰减的1—3个数量级, 但由于其仅是电波频率和传播距离的函数, 并且当电波频率变化为200 MHz, 卫星轨道变化为1000 km时自由空间衰减的相对变化量不足0.2%, 因此在已知卫星工作频率和轨道的条件下可以对自由空间衰减进行精确计算, 以将其从总衰减中剔除从而降低对降雨衰减测量的影响.
2)在卫星信号频率为17 GHz, 极化方式为垂直极化的条件下, 仅利用1个地球站难以实现对垂直降雨场的反演, 3个反演场与真实场之间的相关系数分别为0.556, 0.504和0.364, 平均偏差分别为0.630, 0.865和2.522 mm/h. 这是因为在探测过程中出现了多条相邻星地链路经过同一组网格的现象, 导致方程组的有效方程数量即矩阵L的秩减少, 同时由于降雨场网格数量庞大, 使得SART算法在迭代过程中易趋向局部最优解.
3)地球站数量增加到两个的情况下, 反演效果得到显著提升, 此时反演结果与真实降雨场间的相关系数分别为0.980, 0.989和0.982, 平均偏差分别为 0.122, 0.159和0.537 mm/h, 基本实现了基于星地链路的垂直降雨场反演; 当地球站数量上升到3个时, 反演结果更加精确, 此时相关系数均接近1, 真实降雨场被准确反演.
通过开展数值仿真实验证明了基于星地链路的二维垂直降雨场反演方法的可行性, 下一步在利用实际链路探测降雨时, 还需在以下方面做进一步研究: 1)考虑实际链路的信号噪声, 选用合适的信号去噪方法确保降雨衰减信息的真实有效; 2)根据实际链路的密度和结构, 选择合适的降雨场网格格距以提升反演效果.