摘要: 本文介绍了铁磁纳米线中磁化强度的一些新激发态, 包括各向同性铁磁的Akhmediev呼吸子、Kuznetsov-Ma孤子和怪波、自旋极化电流驱动下各向异性铁磁纳米线中的怪波动力学. 在各向同性情况下, 展示了形如四片花瓣的磁孤子的空间周期过程和自旋波背景的局域化过程; 在极限情况下, 得到了磁怪波解并阐明了其形成机制. 在各向异性情况下, 发现怪波的产生主要源于中心的能量积累和快速弥散; 此外, 怪波还具有不稳定性, 它和自旋波背景间的能量与磁振子的交换可以通过自旋极化电流来调控.
关键词: 呼吸子 /
磁怪波 /
自旋转移矩 /
调制不稳定性 English Abstract Rogue wave solution in ferromagnetic nanowires Li Zai-Dong 1,2 ,Guo Qi-Qi 1 1.Department of Applied Physics, Hebei University of Technology, Tianjin 300401, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 61774001) and the Natural Science Foundation of Hebei Province, China (Grant No. F2019202141)Received Date: 06 September 2019Accepted Date: 02 December 2019Available Online: 17 December 2019Published Online: 05 January 2020Abstract: In this paper, we introduce some new excited states of magnetization in ferromagnetic nanowires, including Akhmediev breathers, Kuznetsov-Ma soliton and rogue wave in isotropic ferromagnetic nanowires, and rogue wave in anisotropic ferromagnetic nanowires driven by spin-polarized current. The isotropic case demonstrates a spatial periodic process of a magnetic soliton forming the petal with four pieces and a localized process of the spin-wave background. In a limit case, we get rogue waves and clarify its formation mechanism. In the case of anisotropy, it is found that the generation of rogue waves mainly comes from the accumulation of energy and rapid dispersion in the center. In addition, rogue waves are unstable, the spin-polarized current can control the exchange rate of magnons between the envelope soliton and the background. These results can be useful for the exploration of nonlinear excitation in Bosonic and fermionic ferromagnet.Keywords: breathers /magnetic rogue wave /spin-transfer torque /modulation instability 全文HTML --> --> --> 1.引 言 在过去几十年中, 磁性纳米结构的磁化动力学研究取得了重大进展. 在这些研究中, Self-organization[1 ] 是自然界中最有趣的物理现象之一. 在磁学领域中, 这一现象已经在条状畴、磁泡、磁孤子、磁涡旋等磁畴的形成方面进行了深入细致的研究. 此外, 在二维薄膜磁性系统的研究中, 一些有趣的磁性Self-organization模式进一步被揭示, 如自旋波[2 ] 和斯格明子[3 -5 ] , 其中斯格明子可以在薄膜中作为亚稳态成核. 基于斯格明子在纳米轨道上的运动为设计磁性信息存储器提供了新的路径.[6 -11 ] . 例如, 在铁磁体中, 磁化强度形成的空间局域结构-磁畴壁, 其实可以看作是一个势垒, 将简并的两个磁状态分开[12 ,13 ] , 而这两个组态正好可以作为二进制信息存储的基本单元. 目前, 畴壁运动有多种驱动手段, 例如外磁场、自旋转移矩和磁振子等, 但畴壁的传播还受到自旋霍尔效应[14 ] 、Rashba效应[15 ] 和Dzyaloshinskii-Moriya相互作用[16 -19 ] 的影响. 近些年来, Dzyaloshinskii-Moriya相互作用引起了人们对低维磁学的极大兴趣[16 -23 ] , 这些研究不仅受到基本物理问题的启发, 还受到自旋电子存储器和逻辑纳米器件潜在应用的启发. Dzyaloshinskii-Moriya相互作用可以看作是一种各向异性超交换作用, 不仅对畴壁运动具有重要影响, 而且对孤子的激发和传播也存在重要影响. 研究表明Dzyaloshinskii-Moriya相互作用可以影响孤子能量, 从而改变了动态孤子的振幅及内部结构畸变, 形成不同结构类型的孤子[17 ] . 另外, Dzyaloshinskii-Moriya相互作用还存在于反铁磁和弱铁磁中, 同样对其孤子激发有着重要影响[24 -26 ] .[27 ,28 ] . 自旋极化电流可以在磁性多层结构中引起许多独特的现象[29 ,30 ] , 如自旋波激发[31 ,32 ] 、磁化开关[27 ] 和反转[33 -35 ] 及吉尔伯特阻尼增强[36 ,37 ] 等. 目前, 自旋极化电流通常用来创建、操纵和控制纳米尺度的磁激发, 例如畴壁[38 -41 ] 和涡旋[42 -44 ] . 众所周知, 非线性激发[12 ,13 ] 是磁性有序材料中的一般现象. 在铁磁体中, 磁振子由于相互吸引作用而趋于自局域化. 在某种意义上, 磁振子的吸引力对于一维铁磁体是至关重要的, 因为它产生准粒子(磁振子)的束缚态, 即自局域化. 自旋波可以被看作是宏观上连续的磁振子簇, 当磁化强度偏离基态时就会引起自旋波的激发, 它们的相互作用和不稳定性导致了磁畴壁和磁孤子的存在.[45 -49 ] , 从而导致呼吸子和孤子之间实现状态转换. 基于线性稳定性分析调制不稳定性, 从而分析该状态跃迁的机制已经得到大量研究[45 -47 ] , 但是当扰动增长与背景相当大时, 线性分析不再有效. 因此, 在2013年, Zakharov和Gelash[50 ,51 ] 提出了一种由小的局部扰动发展而来的超正则呼吸子解, 可以用来描述调制不稳定的非线性阶段. 并且近年来, 在一些具有高阶效应的光纤系统, 例如Hirota and Maxwell-Bloch等系统中, 这种超正则呼吸子动力学和它们的状态转换也得到了详细研究[48 ,49 ] . 众所周知, 调制不稳定性存在于光纤、玻色-爱因斯坦凝聚等众多非线性系统中, 这些结果不仅丰富了调制不稳定性的内涵, 也为其他各种系统的非线性研究提供了方法.[52 ] . 这种全磁的自旋转移力矩可以影响磁化动力学, 使磁状态发生改变. 本文研究了自旋波背景下铁磁纳米线中磁化强度的呼吸子和怪波解, 讨论了各向同性情况下由全磁的自旋转移力矩引起的亮(暗)怪波的精确解, 以及自旋极化电流驱动下的单轴各向异性的怪波动力学, 这些研究结果预期对玻色子和费米子铁磁体的非线性激发的探测具有一定的意义.2.Landau-Lifshitz-Gilbert方程 铁磁中磁化强度的动力学可以用著名的Landau-Lifshitz-Gilbert方程很好地描述. 本文采用无量纲形式[53 ] ${\rm{\alpha }}$ 为吉尔伯特阻尼系数; ${A_{\rm{J}}}$ 表示绝热自旋矩参数; ${{{h}}_{{\rm{eff}}}}$ 表示有效场, 包括交换场、各向异性场和外加磁场. 对于垂直各向异性的铁磁纳米线样品材料, 即${{{h}}_{{\rm{eff}}}} = \dfrac{{{\partial ^2}{{m}}}}{{\partial {x^2}}} + \left[ {\left( {\dfrac{{{H_k}}}{{{M_{\rm{s}}}}} - 4{\text{π}}} \right){m_z} + {h_{{\rm{ext}}}}} \right]{{{e}}_z}$ , 其中${M_{\rm{s}}}$ 为饱和磁化强度, ${H_k}$ 为各向异性常数, ${h_{{\rm{ext}}}}$ 为所施加的外磁场.3.各向同性的精确呼吸子解和怪波解 首先, 本文考虑简单的各向同性模型, 即方程(1 )可重新写为1 )是完全可积的, 可以利用达布变换构造方程(2 )的精确呼吸子解和怪波解, 这种方法的关键思想是首先从方程的一个种子解出发, 然后通过Lax方程的规范变换构造无穷多的新解析解. 本文以自旋波作为初始的“种子”解${{{m}}_0}$ , 即${{{m}}_0} \equiv \left( {{m_{01}}, {m_{02}}, {m_{03}}} \right) = \left( {{A_{\rm{s}}}{\rm{cos}}\delta, {A_{\rm{s}}}{\rm{sin}}\delta, \sqrt {1 - A_{\rm{s}}^2} } \right)$ , 其中$\delta = {k_{\rm{s}}}x - {\omega _{\rm{s}}}t$ . 将这个解带入到方程(2 ), 得到色散关系为$\omega = - k_{\rm s}^2{m_{03}}$ . 通过规范的达布变换, 可得到方程(2 )的精确解形式为[54 ] ${{\sigma}}$ 是泡利矩阵, 矩阵K 3 )表示嵌入到自旋波背景的磁孤子解. 随着$\mu $ 的增加, 自旋波背景逐渐趋于局部化, 并且由于孤子和自旋波背景之间的相互作用形成呼吸子. 仔细分析方程(3 )的解, 可以得到Akhmediev呼吸子、Kuznetsov-Ma孤子及磁怪波. 结果发现不同的磁状态取决于一个临界值$\left| \mu \right| = {A_{\rm{s}}}{k_{\rm{s}}}$ , 它也是调制不稳定过程$\left( {\left| \mu \right| < {A_{\rm{s}}}{k_{\rm{s}}}} \right)$ 和周期化过程$\left( {\left| \mu \right| > {A_{\rm{s}}}{k_{\rm{s}}}} \right)$ 及在极限$\left| \mu \right| \to {A_{\rm{s}}}{k_{\rm{s}}}$ 时的磁状态的分界线.[54 -56 ] , 其特征是小扰动和连续波背景之间的周期性能量交换. 它可以用于在非线性光纤中产生高重复率脉冲, 可以精确地描述非线性薛定谔方程的Akhmediev呼吸子. 在光纤中, Akhmediev呼吸子具有时间周期性, 在传播方向上表现出单一生长-返回循环的特性, 即著名的Fermi-Pasta-Ulam循环[57 ] . 近年来, 调制不稳定性已被发现在各种非线性物理系统中, 对高度局域化怪波的产生起着重要作用.3 )可以在$\left| \mu \right| < {A_{\rm{s}}}{k_{\rm{s}}}$ 和$\nu = {k_{\rm{s}}}{m_{03}}$ 的条件下简化, 并得到Akhmediev呼吸子解, 主要参数化简为如下形式:$\theta \!=\! \mu Nt, \phi \!=\! - N( {x \!+\! 2{k_{\rm{s}}}{m_{03}}t}), N \!=\! \!\sqrt{A_{\rm{s}}^2 k_{\rm{s}}^2 \!-\! {\mu ^2}} .$ 上述结果表明, 方程(4 )的解在空间上是以$2{\text{π}}/N$ 为周期的, 在时间上是非周期性的. 这一过程也可以看作是磁化强度动力学实现的Fermi-Pasta-Ulam循环的空间表现. 为了研究磁化调制不稳定性的渐近形式, 需考虑$t \to \pm \infty $ 的情况. 当$t \to \pm \infty $ 时, ${m_3}$ 的值近似为${m_{03}}\left( {1 - 4{\mu ^2}/k_{\rm{s}}^2} \right)$ . 当${A_{\rm{s}}} = 1$ 或$1/2 \leqslant {A_{\rm{s}}} < 1, \left| \mu \right| = {k_{\rm{s}}}/2$ 时, 磁化矢量位于${m_1}-{m_2}$ 平面中, ${m_3}$ 的值为零. 此条件下的磁振子密度分布${\left| {{m_ + }\left( {x, t} \right)} \right|^2}$ 取得最大值1, 这里${m_ + } \equiv {m_1} + {\rm{i}}{m_2}$ . (4 )式的解还可以认为是调制不稳定的过程, 这种不稳定性过程也可以通过线性化相应解的初始值来表示:${A_{\rm{s}}} = 1$ , 由于${x_0} > 0, \;\;\epsilon = \exp \left( { - {x_0}} \right)$ 是一个小量.4 )式表达的Akhmediev呼吸子解, 实际上表示自旋波背景的不稳定过程, 即在自旋波背景下的小扰动, 这些小扰动随着时间的推移可呈现指数形式放大的非线性过程. 在这个过程中, 磁孤子和自旋波背景之间发生周期性磁振子交换. 应当注意的是, 在基态背景上激发的磁孤子没有这种特性. 由此说明, 正是自旋波和磁孤子之间的相互作用导致了这一非常有趣的现象.$\left| \mu \right| > {A_{\rm{s}}}{k_{\rm{s}}}$ 和$\nu = {k_{\rm{s}}}{m_{03}}$ 的条件下, 可以得到方程(2 )另外一种形式的磁激发态, 它类似于非线性光纤中光脉冲传播的Kuznetsov-Ma孤子解, 也可以看作是怪波流体力学的原型. 经过化简后, 该解的主要特征参数如下:$\zeta \!=\! \sqrt {{\mu ^2} - A_{\rm{s}}^2 k_{\rm{s}}^2}, \theta \!=\! \zeta \left( {x + 2{m_{03}}{k_{\rm{s}}}t} \right), \phi = \mu \zeta t$ .6 )式可知, 磁性Kuznetsov-Ma孤子的主要特性表现为具有时间周期性而空间具有非周期性, 且孤子的传播速度为$ - 2{k_{\rm{s}}}{m_{03}}$ , 宽度为$1/\zeta $ . 当${A_{\rm{s}}} = 1$ 时, 参数$\theta $ 仅取决于x , 这意味着包络速度变为零, 孤子被自旋波囚禁在空间中, 这是极为有趣的现象, 等待进一步深化研究. 为了研究Kuznetsov-Ma孤子的渐近形式, 考虑极限情况$x \to \pm \infty $ . 根据方程(3 )和(6 ), ${m_3}$ 近似为${m_{03}}\left( {1 - 4 A_{\rm{s}}^2} \right)$ , 而横向分量表示为${m_ + }$ , 近似为${m_{0 + }}\left( {4 A_{\rm{s}}^2 - 3} \right)\left( {N \mp {\rm{i}}{k_{\rm{s}}}} \right)/\left( {N \pm {\rm{i}}{k_{\rm{s}}}} \right)$ , 这里${m_{0 + }} \equiv $ ${m_{01}} + {\rm{i}}{m_{02}} $ . 当自旋波通过磁孤子时, 这一结果表明自旋波相位改变了$2\arctan \left[ {2 N{k_{\rm{s}}}/\left( {{N^2} - k_{\rm{s}}^2} \right)} \right]$ . 自旋波的这种相位改变会影响磁孤子的传播速度, 表示自旋角动量从自旋波背景转移到动态孤子, 也就是前面说到的全磁自旋转移力矩效应. 另外, 要想实现${m_3}$ 的零背景情形, 可以通过两种情况来实现, 即${A_{\rm{s}}} = 1$ 或$1/2 \leqslant {A_{\rm{s}}} < 1, \left| {{\mu _1}} \right| = {k_{\rm{s}}}/2$ , 而在$x \to \pm \infty $ 时磁振子密度分布达到最大值1. 因此, ${m_3}$ 的最大和最小的演化与孤子的传播方向相同, 这一特性说明了孤子在铁磁体磁化周期解的背景下传播时的呼吸特性.3 )的磁性Kuznetsov-Ma孤子解不同于磁性Akhmediev呼吸子解, 方程(6 )的局部周期性磁振子交换表现为时间周期性演化. 因此, 高磁振子密度沿着孤子的传播方向呈时间周期性变化. 上述的讨论表明, $|\mu | = {A_{\rm{s}}}{k_{\rm{s}}}$ 是一个临界点条件, 划分了调制不稳定性过程$(|\mu | < {A_{\rm{s}}}{k_{\rm{s}}})$ 和周期化过程$(|\mu | > {A_{\rm{s}}}{k_{\rm{s}}})$ . 它会导致不同物理行为的呼吸特征, 在很大程度上取决于调制参数$\mu $ , 如图1 所示, 在$\nu = {k_{\rm{s}}}{m_{03}}$ 的条件下, 在极限$|\mu | \to {\left( {{A_{\rm{s}}}{k_{\rm{s}}}} \right)^ - }$ 和$ {\left( {{A_{\rm{s}}}{k_{\rm{s}}}} \right)^ + }$ 过程中, 绘制了两种不同的渐近行为. 前一种情况演示出了形成近乎四片瓣的空间周期过程. 随着调制参数$|\mu |$ 接近${{A_{\rm{s}}}{k_{\rm{s}}}}$ , 相邻磁性瓣的空间间隔迅速增大, 而一个谷分裂为两个, 且谷的振幅逐渐增大. 另一种情况显示了自旋波背景的局部化过程, 当调制参数$|\mu| $ 接近${\left( {{A_{\rm{s}}}{k_{\rm{s}}}} \right)^ + }$ 时, 相邻磁性花瓣的时间间隔迅速增大.图 1 方程(3 )在$\mu \to {A_{\rm{s}}}{k_{\rm{s}}}, \nu = {k_{\rm{s}}}\sqrt {1 - A_{\rm{s}}^2} $ 的极限条件下, 磁化分量${m_3}$ 的渐近过程, 参数如下: A s = 0.9, k s = 1 (a) μ = 0.82; (b) μ = 0.89; (c) μ = 0.89999; (d) μ = 1.1; (e) μ = 0.96; (f) μ = 0.9001Figure1. The asymptotic processes of the magnetic component ${m_3}$ in the limit processes $\mu \to {A_{\rm{s}}}{k_{\rm{s}}}$ and $\nu = {k_{\rm{s}}}\sqrt {1 - A_{\rm{s}}^2} $ in Eq. (3 ), where the parameters are as follows: A s = 0.9, k s = 1: (a) μ = 0.82; (b) μ = 0.89; (c) μ = 0.89999; (d) μ = 1.1; (e) μ = 0.96; (f) μ = 0.9001, respectively.$|\mu |$ 趋于$\left( {{A_{\rm{s}}}{k_{\rm{s}}}} \right)$ 的极限情况下, 可以得到方程(3 )的一种全新的磁化强度激发态, 它是一个有理解的形式, 称之为磁怪波, 其中主要参数由下式给出:$ \pm $ 表示$|\mu | \to \pm {A_{\rm{s}}}{k_{\rm{s}}}$ 的极限情况. 为了研究方程(7 )磁怪波的渐近形式, 考虑$x \to \pm \infty ~(t \to \pm \infty )$ 和$x \to 0~(t \to 0)$ 的情况. 对于+的情况, 当$x \to \pm \infty~ (t \to \pm \infty )$ 时${m_3}$ 近似为$\left( {1 - 4 A_{\rm{s}}^2} \right){m_{03}}$ , 当$x \to 0~ (t \to 0)$ 时分量${m_3}$ 近似为${m_{03}}$ ; 而对于$-$ 的情况, 当$x \to \pm \infty~(t \to \pm \infty )$ 时${m_3}$ 近似为${m_{03}}$ , 当$x \to 0 ~ (t \to 0)$ 时分量${m_3}$ 近似为$\left( {1 - 4 A_{\rm{s}}^2} \right){m_{03}}$ . 对于横向分量${m_ + }$ , 在+的情况, 当$x \to \pm \infty~ \left( {t \to \pm \infty } \right)$ 时近似为${m_{0 + }}\left( {3 - 4 A_{\rm{s}}^2} \right)$ , 当$x \to 0~ (t \to 0)$ 时分量${m_ + }$ 近似为${-m_{0 + }}$ ; 在$-$ 的情况, 当$x \to \pm \infty~ (t \to \pm \infty )$ 时分量${m_ + }$ 近似为${-m_{0 + }}$ , 当$x \to 0~ (t \to 0)$ 时近似为${m_{0 + }}\left( {3 - 4 A_{\rm{s}}^2} \right)$ . 上述分析表明情况+表示亮怪波, 而情况$-$ 对应于暗怪波. 亮和暗怪波的图形表示如图2 所示.图 2 方程(3 )和(7 )中磁化强度${{m}} = \left( {{m_1}, {m_2}, {m_3}} \right)$ 的怪波演化图, 即(a)?(c)为亮怪波, (d)?(f)为暗怪波. 参数: ${A_{\rm{s}}} = \sqrt 3 /2, {k_{\rm{s}}} = 1.5, \nu = {k_{\rm{s}}}\sqrt {1 - A_{\rm{s}}^2}, \mu = \pm 0.75 \sqrt 3 $ , ±分别表示亮怪波和暗怪波[54 ] Figure2. The graphical evolution of rogue waves for the magnetization ${{m}} = \left( {{m_1}, {m_2}, {m_3}} \right)$ in Eq. (3 ) and (7 ), i.e., bright rogue waves (a)?(c) and dark rogue waves (d)?(f). The parameters are as follows: ${A_{\rm{s}}} = \sqrt 3 /2, {k_{\rm{s}}} = 1.5, \nu = {k_{\rm{s}}}\sqrt {1 - A_{\rm{s}}^2} $ , and $\mu = \pm 0.75 \sqrt 3 $ with the sign $ \pm $ corresponding to the bright and dark rogue waves, respectively[54 ] .${A_s} = 1$ 时, 可以得到磁怪波如下:${F_1} = 1 + {t^2}k_{\rm{s}}^4 + {x^2}k_{\rm{s}}^2$ . 如图3 所示, 分量${{m_3}}$ 的特征是由两个峰一个谷分裂为两个峰和两个谷的反对称分布, 呈现出四片花瓣的结构状.图 3 方程(3 )在A s = 1, $\mu \to {A_{\rm{s}}}{k_{\rm{s}}}, \nu = {k_{\rm{s}}}\sqrt {1 - A_{\rm{s}}^2} $ 的条件下, 磁化分量${{m_3}}$ 四片花瓣结构的演化图. 参数如下: A s = 1, $ {k_{\rm{s}}} = 0.9, \mu = 0.8999$ Figure3. The formation of magnetic petal in the component ${{m_3}}$ of Eq.(3 ) under the special condition of A s = 1, $ \mu \to {A_{\rm{s}}}{k_{\rm{s}}}, \nu = {k_{\rm{s}}}\sqrt {1 - A_{\rm{s}}^2}$ . The parameters are as follows: ${A_{\rm{s}}} = 1, {k_{\rm{s}}} = 0.9, \mu = 0.8999$ .4.单轴各向异性系统中的精确怪波解 在这个部分, 本文考虑自旋极化电流驱动下各向异性铁磁纳米线中的磁怪波动力学, 这种情况下方程(1 )是不可积的, 为了达到这个目的, 需要对方程(1 )做一些近似处理和变换. 方程(1 )有两种基本激发态, 即自旋波和动力学孤子, 这两种激发态都源于磁矩对基态的微小偏移. 因此, 在各向异性情况可以引入一个合理的函数q 替换磁化强度的分量, 即$q \equiv {m_x} + {\rm{i}}{m_y}$ 和$m_z^2 = 1 - |q{|^2}$ . 在考虑无阻尼和长波近似的条件下, 方程(1 )可以转变成可积的非线性薛定谔方程的形式:${\omega _0} = 1 + {h_{{\rm{ext}}}}/\left( {{H_{\rm{k}}}/{M_{\rm{s}}} - 4\pi } \right)$ . 根据前面谈到的达布变换的思想, 方程(9 )的解析解很容易构造出来[58 -62 ] . 这里, 选择单轴各向异性情况下的自旋波解作为初始种子解$q= A_{\rm c} {\rm e}^{-{\rm i}(k_{\rm c} x - \omega_{\rm c} t)} $ , 其中${\omega _{\rm{c}}}$ 和${k_{\rm{c}}}$ 分别为无量纲的频率和波数. 经过复杂的计算, 可以得到具有呼吸特性的孤子解[53 ] .${\mu _1} = {A_{\rm{c}}}$ 且${\nu _1} = - {k_{\rm{c}}}$ 的条件下, 可得到调制不稳定过程$({\mu _1} < {A_{\rm{c}}})$ 和周期性过程$({\mu _1} > {A_{\rm{c}}})$ , 这就导致了依靠调制呼吸行为而实现不同特征. 在${\nu _1} = - {k_{\rm{c}}}$ 条件下, 取极限${\mu _1} = A_{\rm{c}}^ - $ (和$A_{\rm{c}}^ + $ )导致了两种不同的渐进行为. 当取极限条件${\mu _1} \to {A_{\rm{c}}}$ 时, 出现奇异的磁怪波, 即$\varphi = {\omega _{\rm{c}}}t - {k_{\rm{c}}}x$ , $\eta = A_{\rm{J}}^2 + A_{\rm{c}}^2 + 4 k_{\rm{c}}^2 - 4{A_{\rm{J}}}{k_{\rm{c}}}$ , $\zeta = {A_{\rm{J}}} - 2{k_{\rm{c}}}$ , $\varepsilon = 1 + {x^2}A_{\rm{c}}^2$ . 方程(10 )呈现出怪波的典型特征. 磁振子从自旋波背景向中间积聚形成临界振幅为${A_{\rm{Q}}} = 3{A_{\rm{c}}}$ . 这也表示在$x=0$ 和$t=0$ 时, 局域波完全被捕获. 如图4 所示, 表明了方程(10 )的磁怪波的实现, 当${\mu _1}$ 靠近$A_{\rm{c}}^ - $ 时, 磁振子逐渐积聚增多, 以及当${\mu _1}$ 靠近$A_{\rm{c}}^ + $ 时, 磁振子逐渐分散降低. 图4 的插图表达了在${\mu _1} \to {A_{\rm{c}}}$ 时, 临界峰将要出现, 此时磁怪波将要被激发, 它的磁振子密度峰值为$|q{|^2} = 9 A_{\rm{c}}^2$ . 为了更深入地探索铁磁纳米线中磁怪波的性质, 分析磁振子密度的分布, 以及与背景之间的交换, 这里需要引入新函数${\rho _{\rm{q}}}(x, t) =$ $ {\left| {{q_1}(x, t)} \right|^2} - {\left| {{q_1}(x = \pm \infty, t)} \right|^2} $ .图 4 不同的参数${\mu _1}$ 下的磁振子密度分布图[53 ] , 范围从0.09到0.29间隔0.05. 插图为怪波形成时的磁振子密度. 其余参数为${A_{\rm{c}}} = 0.2, {A_{\rm{J}}} = {k_c} = 0.1$ Figure4. The magnon density distribution against the background for the different parameter ${\mu _1}$ , which ranges from 0.09 to 0.29 in 0.05 steps[53 ] . The inset figure is the magnon density distribution against the background for the excited formation of magnetic rogue wave. Other parameters are ${A_{\rm{c}}} = 0.2, {A_{\rm{J}}} = {k_{\rm{c}}} = 0.1$ .10 )和$ \rho \!=\! |Q_1(x,t)|^2 \!-\! | Q_1(x = \pm \infty, $ $t)|^2, $ 可以获得磁怪波的磁振子密度分布关系:${\varGamma _1} = 1 + {t^2}A_{\rm{c}}^4, {\varGamma _2} = A_{\rm{c}}^2{\left[ {x + t\left( {{A_{\rm{J}}} - 2{k_{\rm{c}}}} \right)} \right]^2}$ , 且对于任意时间满足$\displaystyle\int_{ - \infty }^{ + \infty } \rho (x, t) = 0$ . 根据条件${\rho _{\rm{Q}}}\left( { \pm 1/{A_{\rm{c}}}, 0} \right) = 0$ , 定义怪波中波峰的空间宽度为$2/{A_{\rm{c}}}$ . 经过仔细的计算发现, 某一固定的时刻, 背景中丢失的磁振子完全转移到波峰中, 即对应面积关系${{{S}}_1} + {{{S}}_2} = {{{S}}_3}$ . 这个结果清楚地表明了带有强呼吸特点的磁怪波的产生机制, 即主要是由于能量和磁振子从背景向中间积聚, 从背景中丢失的磁振子完全转移到了磁怪波的波峰中.图5 ). 根据方程(12 ), 可知自旋极化电流能够调控磁孤子积聚和耗散率, 并且临界电流为${A_{{\rm{Jc}}}} = 2{k_{\rm{c}}}$ . 在临界电流以下, 磁振子的交换随着电流的增加而降低; 在临界电流以上, 磁振子的交换随着电流的增加而增加(图5(f) ). 从图5(a) 到图5(e) 可以看出, 自旋极化电流使怪波和背景的磁振子交换不同导致了磁怪波对于$\left( {x, t} \right)$ 空间方向的不同. 当 ${A_{{\rm{Jc}}}} = 2{k_{\rm{c}}}$ 时, 磁振子的空间积聚(或者耗散)达到最大(图5(f) ). 通过计算图 5 (a)?(e)不同电流值激发怪波在区域$\left( {x, t} \right)$ 的分布图[53 ] , 电流从0到0.8, 间隔为0.2; (f)不同电流怪波形成时的图形, 插图为磁振子积聚的最大时情况. 临界电流${A_{\rm{J}}} = 2{k_{\rm{c}}}$ , 其它参数${A_{\rm{c}}} = {k_{\rm{c}}} = 0.2$ Figure5. (a)?(e) The formation region in space $\left( {x, t} \right)$ for magnetic rogue wave with different current[53 ] . The parameter ${A_J}$ ranges form 0 to 0.8 in 0.2 steps; (f) The nonuniform exchange of magnons between rogue wave and background for the different spin current. The inset figure in (f) denotes the maximal accumulation (or dissipation) process for the critical current value${A_{\rm{J}}} = 2{k_{\rm{c}}}$ . Other parameters are ${A_{\rm{c}}} = {k_{\rm{c}}} = 0.2$ .$t < 0$ 时, 背景中的磁振子向中间积聚; 当$t = 0$ , 怪波的临界峰值出现; 同理, 当$t > 0$ , 波峰中的磁振子开始向背景转移, 波峰逐渐衰减. 最后磁怪波完全消失, 这也就证明了磁怪波仅仅是一个在时间和空间上的震荡, 充分体现了一个不稳定动力学过程的特性.[63 -65 ] , 这种情况下${m_3}$ 分量的平均值可以从直接测量自旋磁量子数为+1和–1的塞曼子能级的粒子数之差来实现. 这意味着对于磁呼吸子解, 存在时间或空间周期性的粒子数, 而对于怪波则粒子群为不均匀的. 对于费米子铁磁体, 电流通过铁磁体时, 其电阻受磁矩取向的强烈影响. 因此, 磁呼吸子解会使磁性层中的电阻发生周期性变化, 而怪波情况下, 应该会出现瞬时电阻的急剧变化.5.结 论 综上所述, 本文研究了自旋转移力矩激发下的各向同性和单轴各向异性的铁磁体的磁化动力学过程. 首先在各向同性系统中得到了Akhmediev呼吸子、Kuznetsov-Ma孤子和怪波的精确的表达式. 根据临界条件分别分析了调制不稳定过程、周期化过程和磁怪波. 这些结果对探测玻色子和费米子铁磁体的非线性激发有一定的指导意义. 然后对单轴各向异性的磁怪波进行分析发现, 能量和磁振子向中心位置的积聚对带有强呼吸子特点的怪波的产生起主要作用, 且怪波具有暂时性和局域性. 它和背景间的能量与磁振子的交换可以通过自旋极化电流调控, 并且在临界值以上和临界值以下自旋矩的作用完全不同. 这为铁磁系统中的调制不稳定性对非线性激发的可控性研究也提供了重要意义. 













































































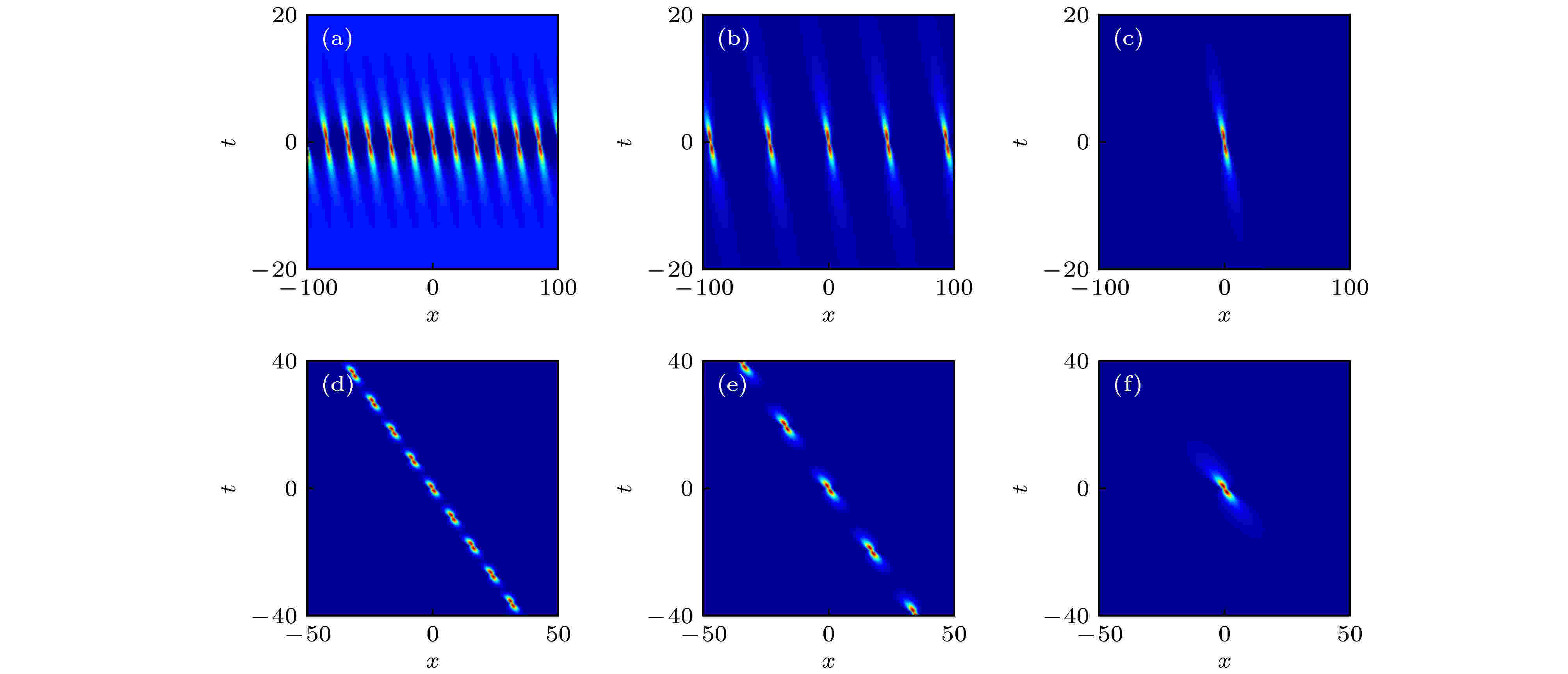 图 1 方程(3)在
图 1 方程(3)在












































































 图 2 方程(3)和(7)中磁化强度
图 2 方程(3)和(7)中磁化强度








 图 3 方程(3)在As = 1,
图 3 方程(3)在As = 1, 






































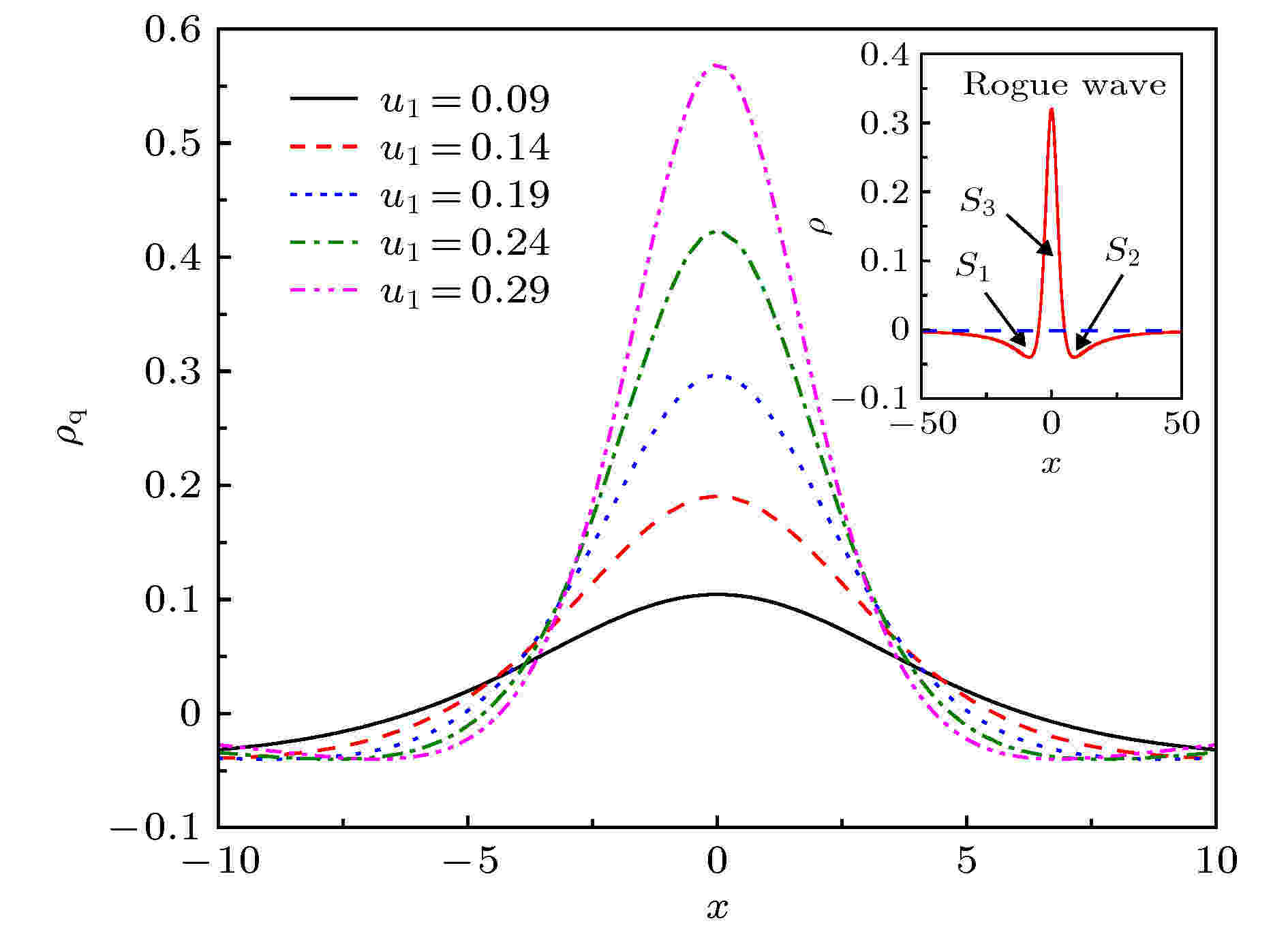 图 4 不同的参数
图 4 不同的参数















 图 5 (a)?(e)不同电流值激发怪波在区域
图 5 (a)?(e)不同电流值激发怪波在区域










