摘要:集成电磁器件尺寸的小型化一直都是该领域发展的重要方向, 具有亚波长、强束缚模式特性的表面等离激元电磁模式为集成电磁器件小型化提供了有力的解决方案. 但是, 支持表面等离激元的材料或结构不可避免地会出现杂质或者结构缺陷, 从而降低表面电磁波器件的传输性能. 为了避免表面等离激元器件性能受到杂质或缺陷的影响, 具有鲁棒传输特性的拓扑表面等离激元应运而生. 本文首先回顾了光频段表面等离激元和太赫兹/微波频段人工表面等离激元的实现方案以及电磁特性, 进而重点总结了拓扑表面等离激元的几种重要设计理论, 并展望了拓扑表面等离激元的未来发展方向.
关键词: 拓扑电磁学/
表面等离子激元/
超材料

English Abstract

全文HTML

--> --> -->

器件尺寸小型化一直以来都是集成电磁学领域发展的重要方向, 具有亚波长模场特性的表面等离激元(surface plasmon polaritons, SPPs)电磁模式为集成电磁器件小型化提供了有利的解决方案. SPPs是一种能将电磁能量束缚在金属-介质界面附近亚波长区域的表面电磁模式. 其起源可以追溯到1902年Wood在衍射光栅覆盖的镜子的反射光中发现的异常亮暗带图样^[1]. 1956年Pines从理论上描述了高速电子穿过金属所经历的特征能量损失^[2], 并将这些损失归因于金属中自由电子的集体振荡, 并将这些振荡称为“等离子体”. 此后, Ritchie^[3]研究了薄膜中的电子能量损失, 并对表面等离子体进行了第一次理论描述. 他发现等离子体模式可能存在于金属表面附近, 然后描述了在金属光栅上激发的表面等离子体共振的异常特性^[4]. 几年后, Cunningham等^[5]引入了术语表面等离子体激元(surface plasmon polaritons, SPPs). 由于SPPs来源于金属-介质界面的电子集群振荡与光子之间的相互耦合, 其常见于光频段. 但是, 金属中电子集群振荡频率远远高于太赫兹/微波频率, 因而金属在太赫兹/微波频段的电磁特性近似于完美电导体(PEC), 无法支持SPPs.
为了将SPPs电磁模式的亚波长特性拓展到太赫兹/微波频段, Pendry^[6]在2004年首次提出人工表面等离激元(Spoof SPPs, SSPPs)的概念. 人工表面等离激元是一种通过在金属表面设计超材料结构, 从而实现的表面电磁模式. 金属表面的结构起到了增强电磁场穿透的作用, 而结构的几何参数决定了等效Drude模型中有效等离子体频率, 从而决定了人工表面等离激元的色散特性^[6,7]. 由此可以通过设计不同结构、不同几何特征的褶皱状结构来调节人工表面等离激元的色散性质.
但是, 支持表面等离激元的材料或结构不可避免地会出现杂质或者结构缺陷, 从而降低表面电磁波器件的传输性能. 为解决这一挑战, 研究人员把目光投向了拓扑能带理论, 即借用拓扑学的方法对表面等离激元在倒易空间中的能带特性进行描述. 能带具有拓扑非平庸特性的表面等离激元系统, 通常被称为拓扑表面等离激元. 其表现为在无限大拓扑表面等离激元禁带对应的频率范围, 有限尺寸系统能带会出现无带隙边界态. 这种无带隙边界态在实空间体现为表面等离激元在类似杂质或者结构缺陷的微扰之下依旧可以保持优良的传输性能, 即系统具备鲁棒传输特性, 因此拓扑表面等离激元(如图1所示)近年来引起了大量关注.
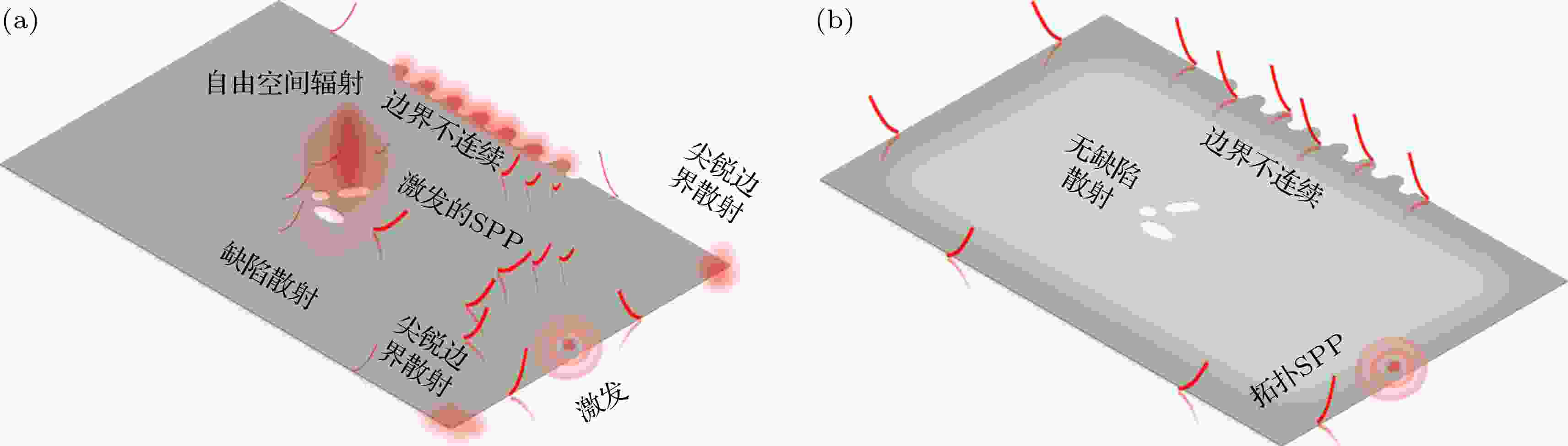图 1 (a)杂质和结构缺陷对表面等离激元传输的影响; (b)拓扑表面等离激元的鲁棒传输特性
Figure1. (a) Effect of impurity and structural defects on surface plasmon transport; (b) robust propagation characteristics of topological surface plasmons.

2

-->

2.1.拓扑电磁学简介

拓扑学是研究几何结构的一些特性在连续变化过程中保持不变的一门数学分支. 后来, 凝聚态物理学家将拓扑概念用于描述绝缘体能带在布里渊区中绝热变化过程中保持不变的特性^[8,9]. 这种不变特性可以采用陈数C_n定量表示,

${C_n} = \frac{1}{{2{\text{π}}}}\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc} {{\varOmega _n}\left( {{k}} \right){\rm{d}}{{{k}}_{{\rm{BZ}}}},} $

其中${\varOmega _n}\left( {{k}} \right) = \nabla \times {A_n}$为第n个能带在波矢k处的Berry曲率, ${A_n} = {\rm{i}}\left\langle {u_n}{\left| {{\nabla _k}} \right|{u_n}} \right\rangle $为Berry连接, $\left. {\left| {{u_n}\left( k \right)} \right.} \right\rangle $为Bloch波函数. 当C = 0时, 材料为普通绝缘体; 当C ≠ 0时, 材料为拓扑绝缘体. 当两种不同陈数材料形成交界面时, 在界面处就会出现无能隙拓扑边界态. 在微扰条件下, 这种拓扑边界态的输运将出现不会受到杂质或缺陷影响的鲁棒特性.
2008年, Haldane和Raghu^[10]将这种凝聚态中的拓扑特性引入电磁学领域, 预言了单向拓扑电磁波导的存在, 也标志着拓扑电磁学领域的开端. 一年后, Wang等^[11]从实验上验证了这种拓扑电磁波导, 他们在采用旋磁材料制成的光子晶体中实现了背向散射免疫的拓扑电磁波导模式. 此后, 针对各种光子晶体拓扑性质的研究逐渐吸引了科学家的注意, 并得到了快速发展^[12-29]. 尽管二维拓扑光子晶体易于采用传统集成工艺实现, 但是其单元结构通常是波长量级, 不利于器件小型化. 因而利用表面等离激元的亚波长特点, 进而研究实现其拓扑传输的方法, 就成为了当前研究的热点.
2 -->

2.2.表面等离激元的拓扑传输

表面等离激元是一种存在于金属(或石墨烯)与介质交界面处的亚波长电磁模式. 2017年, Jin等^[30]提出在单层石墨烯表面构造三角形排列的圆孔阵列(如图2(a)所示), 设计出特异表面等离激元能带结构, 其中在布里渊区的K点具有狄拉克简并点. 当存在垂直于石墨烯平面的磁场时, 由于时间反演对称性破缺, 原布里渊区的K处狄拉克点被打开从而形成完全的带隙, 进而在该石墨烯孔洞阵列的边缘实现了拓扑保护的单通边界态. 同时在垂直石墨烯平面上的表面等离子体模式被限制在距离石墨烯表面亚波长范围内. 与量子霍尔效应拓扑相相同, 该拓扑边界态是背散射免疫的, 如图2(c)所示.
图 2 二维拓扑表面等离激元晶体及其边界态^[30]　(a)石墨烯中圆孔三角点阵的示意图, 在外加磁场B作用下, 有限晶格支持拓扑保护的单向边缘等离子体; (b)在B ≠ 0的石墨烯中的等离激元色散能带, 当孔径d ≠ 0, 出现完全带隙; (c)不同磁感应强度下的边界态及其鲁棒性
Figure2. Two-dimensional topological surface plasmon crystals and their boundary states ^[30]: (a) Schematic diagram of triangular circular hole lattices in graphene, under the action of an applied magnetic field B, finite lattices support a unidirectional edge plasma with topological protection; (b) energy band diagram of plasmon in graphene of B ≠ 0, when d ≠ 0, the complete band gap appears; (c) edge states under different magnetic induction and their robustness

值得注意的是, 由于石墨烯具有大范围可调的费米能级, 因而其载流子浓度的动态范围较大; 同时石墨烯载流子的有效质量非常小, 在高质量的石墨烯中其载流子有长达皮秒量级的弛豫时间, 这些特点使得基于单层石墨烯的拓扑表面等离激元具有高频、短波、长传播距离及宽带隙的优势. 该理论方案在超快电子学与红外拓扑光子学领域迈出了重要一步, 为拓扑表面等离激元器件的实现指出了新方向. 同年, Abajo等^[31]提出在石墨烯上构造六边形蜂窝状超晶格, 同时施加垂直于石墨烯表面的磁场, 可以实现类似基于石墨烯的表面等离激元拓扑边界态.
除量子霍尔拓扑相外, 利用石墨烯表面等离子体也可以设计量子谷霍尔相. Shvets等^[32]提出利用化学势的周期性来调制石墨烯表面等离激元的有效折射率, 进而可以控制石墨烯能带结构, 与Jin不同的是, 这种结构不需要对单层石墨烯表面进行刻蚀, 也无需外加磁场. 如图3所示的结构, 将一个周期性三角穿孔的金属栅极放置在单层石墨烯下方, 在石墨烯与栅极间加入偏置电压, 通过其晶格与石墨烯晶格产生的夹角变换来实现谷效应. 如图3所示, 当夹角为0°时可以在布里渊区的K点观测到狄拉克简并点, 而夹角不为0°时, 原狄拉克点被打开形成完全带隙, 不同夹角对应 ± 1/2 陈数. 在两个三角形排列方向相反的阵列构成的边界可以观测到表面等离激元的拓扑谷输运特性. 特别地, 在垂直于石墨烯平面上是由石墨烯等离子体导致的表面电磁模式, 可将电磁波束缚在石墨烯表面的亚波长尺度范围内. 由于实验挑战较大, 目前对于表面等离激元拓扑传输特性的实验观测尚未实现.
图 3 (a)基于石墨烯的能谷等离子激元晶体示意图: 由偏置电压V₀与相对于石墨烯晶格存在夹角的栅结构; (b)狄拉克点处的能带; (c) yz(x = 0)平面上的电场分布; (d)两种类型的边界; (e)不同夹角对应的谷陈数值; (f)图(d)所示一维结构能带^[32]
Figure3. (a) Schematic diagram of graphene-based energy valley plasmon crystals: a gate structure with a biased voltage V₀ and an angle with respect to the graphene lattice; (b) energy band at the Dirac point; (c) electric field distribution on the yz (x = 0) plane; (d) two types of boundaries; (e) valley chern numbers corresponding to different angles; and (f) the one-dimensional structural energy band shown in Fig. (d).

2 -->

2.3.人工表面等离激元的拓扑传输

将SSPPs与拓扑能带理论相结合, 具有理论和实践的双重意义. 在理论层面上, SSPPs结构可灵活设计的优良特性为前沿拓扑理论的实验验证提供了平台, 尤其是在凝聚态系统中难以实现的物理理论^[14]. 另外, 对于经典电磁波或量子系统中微观尺度难以直接观测的模场分布或波函数信息, 可以在SSPPs平台中直接观测^[33]. 在应用层面上, 将SSPPs的拓扑保护性质引入THz芯片网络, 可以进一步减小器件尺寸, 增强器件对抗缺陷和失调的鲁棒性, 这是下一代THz器件的重要发展方向. 目前, SSPPs的拓扑传输特性主要基于以下三种类量子拓扑效应实现.
3 -->

2.3.1.SSPPs的类量子自旋霍尔效应—整数陈数

在足球比赛中, 我们常常能看到香蕉球—由于球的旋转使周围空气产生流速差, 进而产生压强差导致横向力使足球的运动轨迹弯曲, 其弯曲方向取决于球的旋转方向. 这种宏观的经典Magnus效应对于我们理解自旋霍尔效应(SH(E)很有帮助^[34]. 自旋霍尔效应本质是一种由自旋-轨道相互作用导致的自旋极化电子流在微观上的偏转现象. 20世纪70年代科研人员在石墨中便发现了自旋轨道效应^[35]. 而在石墨烯中, 由于第一布里渊区边界存在狄拉克点, Kane等人发现通过自旋轨道相互作用可以在狄拉克点周围打开带隙. 这种新的带隙相被称为量子自旋霍尔(QSH)相. 与传统的平凡绝缘体相不同的是, 该QSH相的带隙中存在两个自旋极化的拓扑边界态.
该QSH拓扑相是时间反演对称的. 传统的打破时间反演对称性得到的非平凡陈数不能用来表征这种拓扑相. 但是对于每个自旋模式, QSH模型都可以化简成两个相互独立的Haldane模型^[36], 即便不存在磁场, 也能表现出整数QHE. 对于每个自旋, 可以用整数n_↑, n_↓定义独立的自旋陈数, 其中维持时间反演对称性需要满足总的陈数${n_ \uparrow } + {n_ \downarrow } = 0$. 然而, 自旋陈数的差值$\Delta n = {n_ \uparrow } - {n_ \downarrow }$是非零整数, 并且可定义出非零Z₂数Z₂ = (Δn mod 2)^[35].
为了构建光子QSH拓扑相, 必须首先将光子“自旋”构建为与电子自旋类似的形式. 第一个实现光子QSH相的设想是利用基于电磁波的两个偏振态的同相和反相叠加得到的光子赝自旋态. 调节作为自旋-轨道相互作用的双各向异性(表征光子介质中磁场和电场之间的反常耦合的参数), 能带结构中可以产生拓扑相变^{[13,15,20,22]}. 相关性质已经在超材料结构组成的光子晶体中得到证实^[15,16].
2015年, Wu等^[27]提出了另一种构造光子赝自旋态从而实现光子QSH相的方案, 该方案基于晶体对称性而不是双各向异性. 如图4(a)所示, 他们在三角形晶格上重复阵列六边形晶胞. 这种排布使得布里渊区域产生折叠, 并且将K和K'点处的蜂窝晶格的原始狄拉克锥合并成Γ点处的双重简并狄拉克锥. 求解麦克斯韦方程组可以明确地揭示六边形簇支持的TM模式显示出了类原子轨道p波和d波的图案并扩展形成光子能带(表现出“人造原子”的特性). 通过结合线性麦克斯韦方程和C6晶体所遵循的时间反演对称性, Wu等构造的赝时间反演对称性实现了与凝聚态系统中时间反演对称性相同的作用, 在光子体系中成功模拟了Kramers简并. 两个赝自旋态分别表示为:
图 4 人工表面等离激元QSH^[27,37]　(a)基于介质圆柱的光子QSH阵列; (b)图(a)中结构的能带; (c)单元胞收缩的SSPPs结构; (d)单元胞扩张的SSPPs结构; (e)SSPPs结构的能带仿真结果; (f)通过组合(c)和(d)中的结构构建边界; (g)边界态的模场分布
Figure4. Spoof plasmonic QSH^[27,37]: (a) Photonic QSH with dielectric cylinders, the zoom in figure shows the hexagonal cluster; (b) edge states of photonic QSH; (c) spoof plasmonic structure whose unit cells of hexagonal clusters get shrunk, leading to zero spin Chern number; (d) spoof plasmonic structure whose unit cells of hexagonal clusters get expanded, which generates non vanishing spin Chern number; (e) simulated edge states at a domain wall between structures of (c) and (d); (f) constructed domain wall by combining structures in (c) and (d); (g) field patterns of edge states

$\begin{split}{{\rm{p}}_ \pm } ={}& \left( {{{\rm{p}}_x} \pm {\rm{i}}{{\rm{p}}_y}} \right)/\sqrt 2, \\ {{\rm{d}}_ \pm } ={}& \left( {{{\rm{d}}_{{x^2} - {y^2}}} \pm {\rm{i}}{{\rm{d}}_{xy}}} \right)/\sqrt 2, \end{split} $

其中p与d是人造原子的轨道.
收缩(扩张)六边形簇的晶格的自旋陈数分别为0(1). 因此, 可以通过改变六边形簇的大小来实现拓扑相变. 结合收缩/扩张结构, 可以在图4(b)所示的投影带图中观察到两个无间隙的边界态, 分别对应沿相反方向传播的两个自旋极化拓扑边界模式. 作者指出, 由于在组合结构的界面处C6对称性的破坏, 在Γ点处存在微小的带隙(在图4(b)中不明显).
之前光子QSH相的实现均基于波长尺度的光子晶体方案, 通常需要将阵列结构放置在平行平板波导中. 而人工等离激元能在亚波长尺度^[37]实现该方案, 如图4(c), 图4(d), 图4(f)所示, 这种局部共振超材料结构由平滑金属板上的四分之一波长金属棒阵列构成, 类似于原子在原子尺度排列形成晶体. 值得注意的是, 图4(e)显示, 边界态表现出类似于图4(b)的(不明显的)小带隙. 相应的拓扑边界态如图4(g)所示. 这种方法可以将光子拓扑相延伸到深亚波长尺度.
3 -->

2.3.2.SSPPs的类量子谷霍尔效应—半整 数陈数

二维过渡金属二硫化物(TMDS)具有中心反演对称破缺的六方晶格结构(如图5(a)所示). 在第一布里渊区(图5(b))的K和K' 处存在两个称为谷的导带局部极小值^[38]. 与电子的自旋自由度相似, 这两个谷通过时间反演对称相互连接, 因此称为谷赝自旋. 在物理上, 这两个谷赝自旋来自于电子波包的两种不同的回旋运动, 因此可以利用磁场测量谷赝自旋. 与自旋类似, 谷赝自旋也可以呈现谷霍尔效应(valley Hall effect, VHE类似于SH(E)和量子谷霍尔效应(quantum valley hall effect, QVH类似于QSH). 两种效应都由能谷相应的Berry曲率或半整数Chern数确定. 2014年物理学家在MoS₂中观察到VHE, 其中谷极化的布洛赫电子在输运过程中发生分离^[39]. 2015年, 人们在门控双层石墨烯上实现了QVH现象, 其晶畴边界表现出谷极化拓扑边缘态^[40].
图 5 人工表面等离激元VHE和QVH^[38,41,42]　(a)二维过渡金属二硫化物(TMDS)的示意图; (b)第一布里渊区TMDS的能带结构; (c)用于VHE的SSPPs结构; (d) SSPPs-VHE的模场扫描结果; (e)用于QVH的SSPPs结构; (f) SSPPs-QVH的模场测试结果
Figure5. Spoof plasmonic VHE and QVH^[38,41,42]: (a) Schematic of TMDS; (b) band structure of TMDS in the first Brillouin zone; (c) spoof-SPP platform for VHE; (d) experimental demonstration of spoof-SPP VHE; (e) spoof-SPP platform for QVH; (f) experimental demonstration of spoof-SPP QVH

尽管在二维材料中进行了广泛的研究, 但到目前为止, 谷自由度在光子领域的应用探索还不够全面. 文献[17,41,42]已经利用不同的光子平台实现了QVH的设计. 特别地, 谷边界态可以近乎完美地耦合到环境空间^[17], 这为宽带定向天线或拓扑激光器提供了潜在的应用前景.
人工表面等离激元可以作为一个灵活的平台来对诸如VHE, QVH和谷赝自旋等谷物理现象进行观测. 如图5(c)所示^[41], 在金属平台上构造金属柱组成的六方蜂窝状阵列, 每个晶格包含两个金属柱. 当所有金属柱高度相同时, 可以在布里渊区K(K')点出现狄拉克点. 在这里可以通过改变每个晶格中两个柱之间的高度差来打破反演对称性, 如图5(c)所示, 从而破坏布里渊区K(K')点处的狄拉克简并, 形成完全带隙. 为了实验观测VHE, 将一束窄光束经波导-同轴适配器从底部耦合入人工表面等离激元晶体, 如图5(d)所示; 基于这个平台, 成功实现了VHE并直接观察到了谷赝自旋^[41]. 由于SSPPs光子晶体中传播光束的赝自旋和传播方向锁定, 因此, 进入光子晶体的入射光会分为左右两束. 在实验中, 通过微波扫场系统在晶体最高处上方约1 mm的平面上扫描可以得到相应频率下的VHE场分布图. 从图5(d)中可以清楚地看到11.3 GHz频率下的两分离导波模式.
SSPPs的谷赝自旋可以通过分别对两路导波中的电磁场相位分布直接测量得到. 如图5(d)所示, 左移(K valley)和右移(K' valley)波束的相位分别对应逆时针和顺时针. 在这两个谷的周围, 等频线呈现为三角形, 本质上, 正是等频线这种三角形翘曲效应决定了与谷相关的波束分流. 与之前两个光子自旋(极化)被分离到两个相反的方向形成光子SHE类似^[42], 等离激元谷赝自旋的空间分离形成了等离激元VHE.
实现QVH需要构造一个边界, 这个边界两边分别为谷陈数相反的谷人工表面等离激元晶体. 界面上谷投影陈数的差是量子化的$\Delta {C_K} = | {C_K} - $${C_{K'}}| = 1 $, 这意味着沿着界面传播的每个谷都应该有一个手性边缘态.
实验结果表明拓扑谷边界态可以沿zigzag路径传播而没有能量耗散与谷间散射^[41]. 值得注意的是, 双层石墨烯的每个谷都有两个边界态, 而这里只有一个. 另一种实现SSPPs QVH的方法是利用由反演对称破缺赝LSP谐振器组成的三角形晶格, 如图5(e)所示. 相应的QVH边界态如图5(f)所示^[42].
3 -->

2.3.3.SSPPs的反常Floquet拓扑相—零陈数

除了模拟凝聚态系统中现有的拓扑相外, 人工表面等离激元系统还可以验证在凝聚态系统中尚未证实的拓扑理论. 以具有零陈数的反常Floquet拓扑相为例^[43-46], 通常根据体边对应定理, 每个带隙中拓扑边界态的数量等于该带隙下所有带的陈数之和. 然而, 这一定理并不适用于反常Floquet拓扑相, 因为Floquet能带图中的周期性角度变量代表着准能量而不是传统能量. 因此Floquet色散带没有受基态能带的限制, 换句话说, 不能在该带隙下对无穷多个能带的陈数进行求和, 也不能应用常见的基于陈数的体边对应定理^{[21,25,44-46]}.
人工表面等离激元结构的照片和示意图分别如图6(a)和图6(b)所示. 在平面金属板上周期性地排列亚波长金属棒(排列方式类似于Hafezi的设计^[19], 但在拓扑物理学中有根本区别). 被称为“晶格环”的大环被放置在正方形晶格中, 每对相邻的晶格环由一个较小的“耦合环”耦合. 可以通过晶格环中的顺时针或逆时针循环来模拟表面等离子体波的赝自旋. 如图6(b)所示, 利用放置在晶格的角上的U型输入/输出波导可以实现对指定的赝自旋模式的精准激发. 通过使用一个连接到矢量网络分析仪的单探针扫场仪获得具体的电磁场分布. 此工作与Hafezi思路^[19]的显著区别在于: Hafezi的设计中耦合环相对于晶格环具有不同的位置, 以构建有效的“磁矢量势”来模拟QHE, 而此工作中晶格的耦合环相对于晶格环具有相同的位置. 因此, 这种晶格处于零等效磁场环境下, 不能等价于量子霍尔系统. 尽管如此, 这种零场系统的能带结构依然是拓扑非平庸的^{[21,25,44-46]}.
图 6 基于SSPPs结构的反常Floquet拓扑相^[14]　(a)人工表面等离激元环的照片; (b)实验中5 × 5点阵; (c)随着环间耦合的增加产生的拓扑相变; (d)当激励源频率为11.3 GHz时在阵列内观察到的局域模场; (e)在11.3 GHz频率观察到的边界态; (f)边界态绕过缺陷晶格传播
Figure6. Spoof plasmonic demonstration of the anomalous Floquet topological phase^[14]: (a) Photo of spoof plasmonic rings; (b) a 5 by 5 lattice inexperiment; (c) topological transition as the inter-ring coupling increases; (d) observed field pattern when the excitation is inside the bulk at frequency11.3 GHz; (e) observed edge state at frequency 11.3 GHz; (f) the edge state circumvents and tunnels through a defect lattice

这种晶格可以抽象为一种网络模型^[14,21,25], 它在形式上等价于Floquet系统. 沿着一个晶格环四分之一圈的相位延迟?(如图6(a)中所示)等价于Floquet准能量^[21,25]. 当相邻晶格环之间的参数化耦合强度θ增加到超过临界值(θ = 0.25π)时, 晶格从拓扑正常相转变到具有无间隙拓扑边界态的拓扑反常相(图6(c)). 通过表征拓扑带隙内的体态(图6(d))和11.3 GHz的传播边界态(图6(e))中的场束缚程度, 可以证明这种人工表面等离激元结构的拓扑特性. 这种边界态在遇到结构转角时是无反射的.
人工表面等离激元平台不仅可以实现反常Floquet拓扑相, 还具有高度可调特性. 这使我们能够在拓扑边缘态中制造各种类型缺陷来测试其鲁棒性, 包括一些由于违反拓扑保护而在凝聚态系统中不存在的缺陷类型^[14]. 在边界上引入一个不同尺寸的晶格环, 例如将杆高度从5.0 mm减小到4.3 mm, 进一步证明了拓扑边界态的鲁棒性(图6(f)). 由于不同晶格环的色散特性差别不大, 因此该缺陷可以等效为低势垒. 低势垒允许部分模式能量直接隧穿, 而剩余能量仍然绕过势垒, 如图6(f)所示. 此外, 人工表面等离激元平台的灵活性还可以方便地测试各种缺陷, 包括电子体系中不存在的缺陷, 例如具有完美吸收和自旋翻转散射的缺陷等.

本文回顾了表面等离激元(含人工表面等离激元)的基本电磁特性, 并重点讨论了它们的拓扑传输特性. 在基础物理层面, 能够基于表面等离激元平台继续探索难以直接观察的各种基本拓扑物理现象, 如高维量子霍尔系统^[47,48]和量子化电多极绝缘体^[49]. 此外, 通过将非线性和非互易性^[50]等新元素纳入拓扑表面等离激元结构, 有望实现孤子的拓扑传输^[51], 严格的背向散射免疫边缘传输模式^[11], 和单向克莱因隧穿^[52].
在应用层面上, 通过将拓扑表面等离激元扩展到具有拓扑保护的THz信号传输可以构建稳定可调的THz电子器件. 例如, 谷光子晶体^[17]中的谷极化边界态的完美耦合或拓扑保护折射性质可用于设计高性能THz激光器^[53], 可调谐折射角可用于构造频分复用器和多路复用器^[54,55]. 稳定可调的THz电磁器件, 有望在片上宽带信号互联^[56]、信号调制^[57]等领域均具有广阔的应用前景. 随着拓扑表面等离激元相关应用潜力的逐渐显现, 我们期待着更多的工程师与科学家密切合作, 参与到拓扑表面等离子体的研究中来.