摘要:边界层感受性是层流向湍流转捩的初始阶段, 是实现边界层转捩预测和控制的关键环节. 研究结果表明, 边界层感受性问题不仅受到不同自由来流扰动条件, 壁面局部粗糙和局部吹吸的几何大小、形状和位置等参数的影响之外, 还受到一个重要参数压力梯度的作用. 因此, 本文数值研究在自由来流湍流分别与壁面局部吹入和吸出相互作用下压力梯度在激发边界层感受性过程起什么样的关键性作用, 从而揭示不同压力梯度对壁面局部吹入或吸出边界层内被激发出T-S波波包以及T-S波波包向前传播群速度的影响; 分别讨论逆压力梯度、顺压力梯度对边界层内被激发出的T-S波模态是起到加速增长的作用还是遏制增长的作用; 详细分析不同压力梯度对边界层内被激发出的T-S波的幅值、增长率、波长或波数、相速度以及特征形状函数的影响等. 这一问题的深入研究将为工程实践中各种叶片流体机械的设计和性能改善提供理论参考.
关键词: 感受性/
压力梯度/
边界层

English Abstract

全文HTML

--> --> -->

边界层感受性的物理过程是层流向湍流转捩的初始阶段, 是边界层转捩过程的预测和控制的重要环节. 1980年代初, Goldstein^[1]以及Ruban^[2]理论研究了边界层前缘感受性机制^[3,4]. 随后, Goldstein ^[5]利用三层结构理论研究了在声波扰动与二维壁面局部粗糙作用下边界层感受性的过程, 即当地感受性问题, 所取得的结果得到了Saric 等^[6]以及 Wiegel和Wlezien^[7]实验结果的验证. Dietz^[8-10]通过一系列实验证明了在自由来流涡扰动和壁面局部粗糙作用下边界层当地感受性过程是真实存在的. 随后, Wu^[11,12]利用二阶精度渐进法理论研究了自由来流涡扰动作用下边界层当地感受性问题, 所取得的计算结果与Dietz的实验结果完全一致, 并且还确定了边界层当地感受性与自由来流涡扰动的幅值, 壁面局部粗糙几何形状、位置和数量之间的内在联系. 我们也通过DNS^[13,14]充分验证了该结论. Würz 等^[15] 以及Shen和Lu^[16]实验和数值研究了在声波和涡波扰动与三维壁面局部粗糙相互作用下边界层当地感受性问题, 并在边界层内被激发出了一组呈扇形区域向下游传播的三维T-S波, 计算发现了当地感受性系数与三维T-S波展向波数和声波频率密切关联. 陆昌根和沈露予^[17]研究了在自由来流湍流和壁面局部吹吸作用下边界层感受性机制, 同样获得与Dietz实验相同的结论, 并建立了自由来流湍流度, 壁面局部吹吸强度和长度与边界层感受性问题之间的联系等.
综上所述, 现有的研究成果已经确定了边界层当地感受性机制与自由来流扰动幅值、壁面局部粗糙和吹吸的几何形状以及位置等其他因素之间的关系; 很少见到有关压力梯度对边界层感受性问题影响研究的相关报道; 直到最近, Johnson和Pinarbasi^[18]数值研究了有压力梯度边界层感受性问题, 并发现边界层内被激发出的T-S波的增长率与压力梯度紧密相关. 但是, 有关压力梯度对壁面局部吹吸边界层感受性问题影响的相关研究报道却十分少见. 因此, 本文通过直接数值模拟方法研究在自由来流湍流分别与壁面局部吹入和吸出相互作用下, 有压力梯度对壁面局部吹入和吸出边界层当地感受性问题的影响, 从而填补了压力梯度对边界层当地感受性影响研究的空缺, 并且丰富、完善了流动稳定性理论.

2

-->

2.1.基本方程

选取边界层的位移厚度δ^*、无穷远来流速度U_∞和流体密度ρ为特征物理量, 将不可压Navier-Stokes (N-S)方程无量纲化, 得无量纲N-S方程:

$\left\{ \begin{aligned}& \nabla \cdot {{V}} = 0, \\& \frac{{\partial {{V}}}}{{\partial t}} + \left( {{{V}} \cdot \nabla } \right){{V}} = - \nabla p + \frac{1}{{Re}}{\nabla ^2}{{V}} ,\end{aligned} \right.$

式中 p为压力; Re为雷诺数(Re = (U_∞δ^*)/υ), 且υ为运动黏性系数; V为速度(V = U+V′), 且V′ 为扰动速度(V′ = {u, v}^T)以及U为基本流. 以不同压力梯度系数(${\beta _H} = {{2 m}}/{{m + 1}}$, 滑移速度${U_{\rm{e}}} = {\left( {x/{x_0}} \right)^m}$)情况下Falkner-Skan边界层流的理论解为边界条件求解N-S方程, 获得基本速度场U(注: ${\beta _H} > 0$为顺压力梯度, ${\beta _H} < 0$为逆压力梯度).
2 -->

2.2.数值计算方法

数值计算方法为: 时间偏导数项用四阶修正后的Runge-Kutta格式推进; 空间偏导数项用非等间距的紧致有限差分; 例如: 对流偏导数项用五阶迎风紧致有限差分、压力梯度偏导数项用六阶紧致有限差分、黏性偏导数项用五阶紧致有限差分以及压力泊松方程用三阶非等间距有限差分格式进行迭代求解, 具体数值计算方法的离散格式详见文献[4,17].
2 -->

2.3.自由来流湍流模型

依据自由来流湍流运动的随机性和不确定性, 推导出自由来流湍流模型^[19], 其数学表达式为

$\begin{split}{{{u}}_\infty } =\, & \left( \begin{aligned} {u_\infty } \\ {v_\infty }\end{aligned} \right) = \varepsilon \sum\limits_{{{m}} = - {{M}}}^M \sum\limits_{j = - J}^J \left( \begin{aligned} {{\hat u}_\infty } \\ {{\hat v}_\infty }\end{aligned} \right)\\ & \times{\rm{exp}}\left[ {{\rm i}\left( {m{\kappa _1}x + {{j}}{\kappa _2}y - m{\kappa _1}t} \right)} \right], \end{split}$

其中:

$\left\{ \begin{aligned}& {{\hat u}_\infty } = {\rm i}\frac{{m{\kappa _1}{\rm{j}}{\kappa _2}}}{{\kappa \sqrt {{m^2}{\kappa _1}^2} }} \cdot \sqrt {\frac{{2E\left( \kappa \right){\kappa _1}{\kappa _2}}}{{4{\text{π}}{\kappa ^2}}}} \cdot {{\rm{e}}^{{\rm i}\sigma }}, \\& {{\hat v}_\infty } = - {\rm i}\frac{{\sqrt {{m^2}{\kappa _1}^2} }}{\kappa } \cdot \sqrt {\frac{{2E\left( \kappa \right){\kappa _1}{\kappa _2}}}{{4{\text{π}}{\kappa ^2}}}} \cdot {{\rm{e}}^{{\rm i}\sigma }},\end{aligned} \right.$

${\rm i} = \sqrt { - 1} $; u_∞和v_∞分别为自由来流湍流在流向和法向扰动分速度, 且${\hat u_\infty }$和${\hat v_\infty }$为扰动速度谱; ε为幅值; M和J为最大模数; ${\kappa _1}$和${\kappa _2}$分别为x和y向上的基本波数; 流向和法向波数为$\alpha = m{\kappa _1}$和$\gamma = j{\kappa _2}$, 且$\kappa = {({m^2}{\kappa _1}^2 + {j^2}{\kappa _2}^2)^{1/2}}$. ${\hat u_\infty }$和${\hat v_\infty }$与一维能量谱E($\kappa $)及相位角σ有关.
2 -->

2.4.计算区域和边界条件

图1所示为本文的数值计算区域: 流向区域x∈[0, 1000]和法向区域(大约选取五倍边界层厚度) y∈[0, 14.39]. x和y向上的网格数为512 × 200, 且x向上采用等间距网格, y向上采用非等间距网格, 这样能使网格在壁面附近流场变化剧烈的区域加密以便获得准确的流场信息. 雷诺数选取为Re = 1000.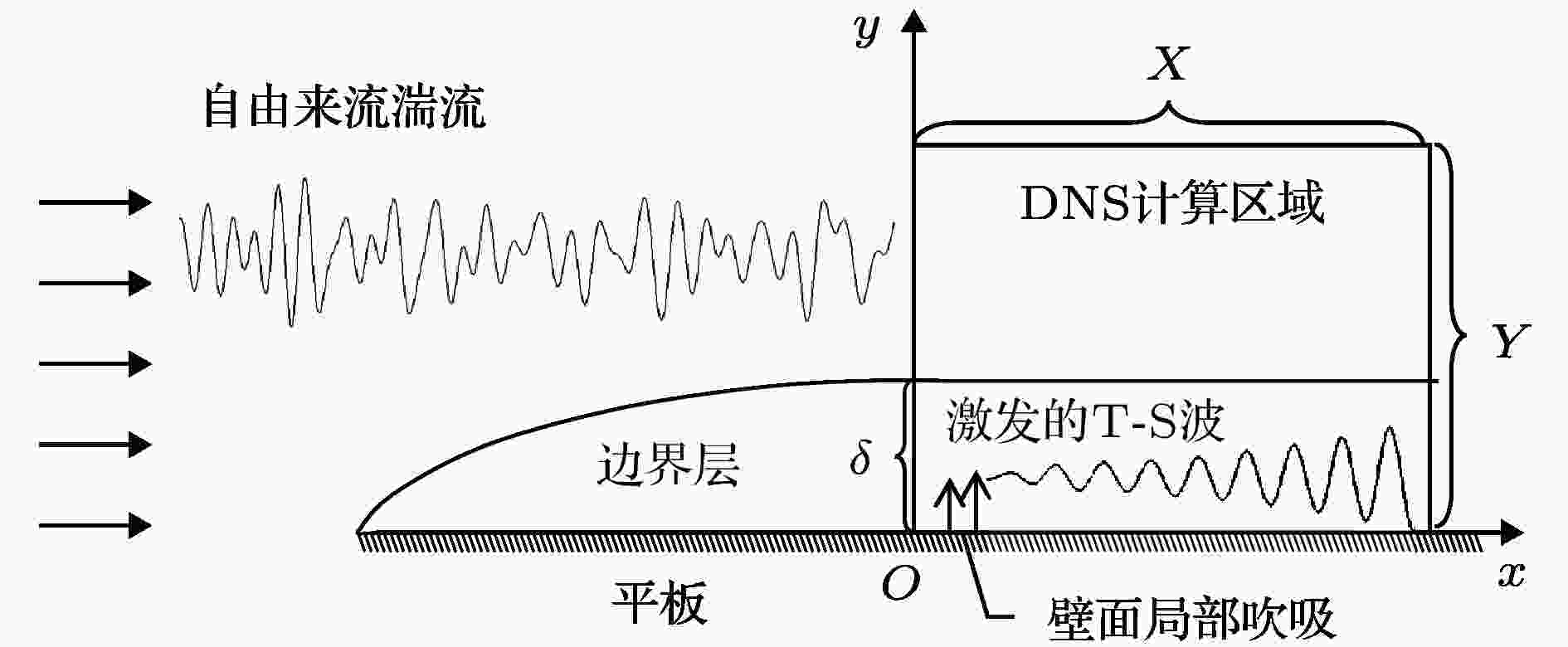
图 1 数值计算区域示意图
Figure1. The domain of numerical simulation.

上边界条件: 速度由自由来流湍流模型给出; 压力$\partial p/\partial x = 0$.
下边界条件: 无滑移条件, 即$u\left( {x, 0} \right) = 0$, $v\left( {x, 0} \right) = 0$, $\partial p/\partial y = 0$. 在平板壁面上分别设计壁面局部吹入和吸出, 数学表达式为

$v\left( {{x_w},0} \right) = q,$

其中, q为壁面局部吹入和吸出的强度, 且q > 0表示为吹入, q < 0 表示为吸出; x_w∈[x₁, x₂]为壁面局部吹吸在平板壁面上的流向长度L = x₂ – x₁.
入流条件: 速度由自由来流湍流模型给出; 压力$\partial p/\partial x = 0$.
出流条件: 速度采用无反射条件, 且数值计算将在边界层内被激发出的小扰动波未到达出流边界前结束; 压力$\partial p/\partial x = 0$.

数值研究证明在自由来流湍流分别与壁面局部吹入和吸出相互作用下激发有压力梯度边界层内的当地感受性过程是真实存在的, 具体证明过程与我们近期发表的成果^[17]验证步骤完全相同, 这里不再赘述. 本文重点关注不同压力梯度对壁面局部吹入或吸出边界层内被激发产生T-S波波包和群速度的影响, 并详细比较分析不同压力梯度对壁面局部吹入或吸出边界层内被激发产生T-S波的幅值、增长率、波长或波数、相速度以及特征函数等关键参数的作用. 无量纲频率F定义为: F = 2πfυ/U_∞² × 10⁶. 自由来流湍流的流向基本波数选取${\kappa _1}$= 0.010, 最大模数M = 8; 壁面局部吹入和吸出的强度以及流向长度分别为q = $ \pm $0.001和L = 50, 且流向长度分布在计算区域的范围为x_w∈[150, 200]; $\varepsilon = $0.001. 为方便比较分析, 将边界层外缘区域内经长时间(t > 1000)计算获得自由来流湍流的稳定值定义为自由来流湍流度A_FST, 其表达式为

${A_{{\rm{FST}}}} = \sqrt {\overline {{u_{{\rm{FST}}}}^2} + \overline {{v_{{\rm{FST}}}}^2} },$

其中$\overline {{u_{{\rm{FST}}}}^2} $和$\overline {{v_{{\rm{FST}}}}^{\rm{2}}} $分别为x和y向扰动速度平方的时均值, A_FST = 0.5%. 下面给出数值计算t = 2400时刻所获得的数值结果.
图2给出了在自由来流湍流和壁面局部吹入相互作用下具有典型压力梯度(β_H = 0.1, 0, –0.05)情况下壁面局部吹入边界层内被激发出T-S波波包沿流向的演化. 从图2可知, 在零压力梯度下壁面局部吹入边界层内被激发出T-S波波包沿流向呈现增长的演化趋势, 而顺压力梯度或逆压力梯度分别对壁面局部吹入边界层内被激发出T-S波波包沿流向的演化状态明显起着遏制或激励T-S波波包增长的作用. 同理, 研究在自由来流湍流和壁面局部吸出相互作用下不同压力梯度对壁面局部吸出边界层内被激发出T-S波波包沿流向的演化过程, 结果发现不同压力梯度对壁面局部吸出边界层内被激发出T-S波波包沿流向的演化特性影响与壁面局部吹入边界层内被激发出T-S波波包沿流向的演化过程类同, 其区别是壁面局部吸出对不同压力梯度边界层内被激发出T-S波波包都起到一定的稳定作用. 随后根据不同时刻, 跟踪记录不同压力梯度壁面局部吹入和吸出边界层内被激发出T-S波波包的最大值和最小值的流向位置和时间, 可近似计算获得T-S波波包向前传播的群速度, 结果详见表1. 从表1中可以看出, 壁面局部吹入和吸出边界层内被激发出T-S波波包向前传播的群速度随着压力梯度的不断减少而缓慢衰减; 且壁面局部吹入边界层内被激发出T-S波波包向前传播的群速度略大于壁面局部吸出边界层内被激发出T-S波波包向前传播的群速度.
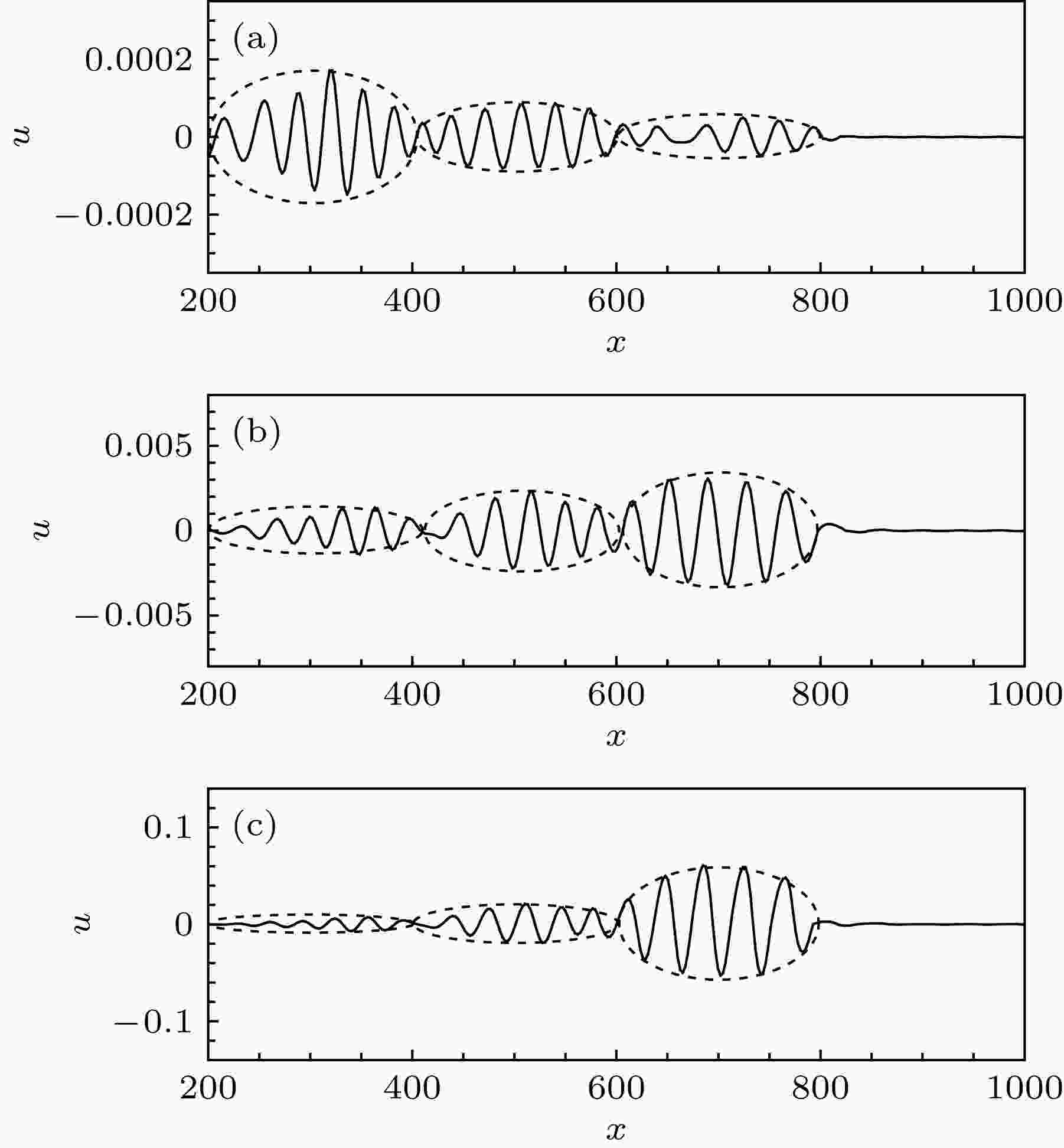图 2 在压力梯度(a) β_H = 0.1, (b) β_H = 0和(c) β_H = –0.05情况下壁面局部吹入边界层内被激发出T-S波波包沿流向呈现增长的演化趋势
Figure2. The streamwise evolutions of the excited T-S waves under the localized suction in the pressure-gradient boundary layers of (a) β_H = 0.1, (b) β_H = 0 and (c) β_H = –0.05.

βH	0.3	0.1	0.05	0	–0.05	–0.1
Cg (吹入)	0.358	0.348	0.343	0.336	0.333	0.331
Cg (吸出)	0.356	0.347	0.341	0.334	0.332	0.329

表1压力梯度对边界层内被激发出T-S波波包向前传播的群速度(C_g)的影响
Table1.The group speeds (C_g) of the excited T-S wave packets in the pressure-gradient boundary layers.

为便于分析, 在自由来流湍流分别与壁面局部吹入和吸出相互作用下将有压力梯度边界层内被激发出T-S波波包初始幅值定义为A_R, 其表达式为

${A_R} = \sqrt {\overline {{u_R}^2} + \overline {{v_R}^2} },$

其中: $\overline {{u_R}^2} $和$\overline {{v_R}^2} $代表x和y方向上在壁面局部吹入和吸出下游位置处有压力梯度边界层内被激发出T-S波波包的小扰动速度平方的时均值. 图3(a)和图3(b)分别给出了不同吹入和吸出强度情况下有压力梯度边界层内被激发出T-S波波包初始幅值随压力梯度系数${\beta _H}$的变化. 图3显示, 当压力梯度系数${\beta _H}$从顺压向逆压力梯度变化时, 壁面局部吹入边界层内激发出T-S波波包初始幅值将缓慢地线性增长; 直至压力梯度系数大约在${\beta _H} \leqslant - 0.05$之后, 初始幅值将加速增长, 几乎成几何级数增长规律发展; 逆压力梯度越大对边界层内当地感受性能力的作用就越强; 反之, 顺压力梯度越大对边界层内当地感受性能力的作用就越弱. 再根据图3(a)和图3(b)比较还可知, 壁面局部吹入强度越大, 就越容易激励有压力梯度边界层内被诱导出更强的感受性过程; 反之, 壁面局部吸出强度越大, 就越容易阻碍有压力梯度边界层内被诱导出感受性过程的发生; 壁面局部吹入作用激发有压力梯度边界层内被诱导出的T-S波波包初始幅值要远大于壁面局部吸出作用下有压力梯度边界层内被诱导出的T-S波波包初始幅值两个数量级左右. 另外, 从图3(a)和图3(b)比较还发现, 无论是壁面局部吹入还是壁面局部吸出的情况, 边界层内被激发出T-S波波包初始幅值都是随着压力梯度系数的不断减少而快速增长, 这是由于压力梯度在边界层感受性过程中起着主导的作用.
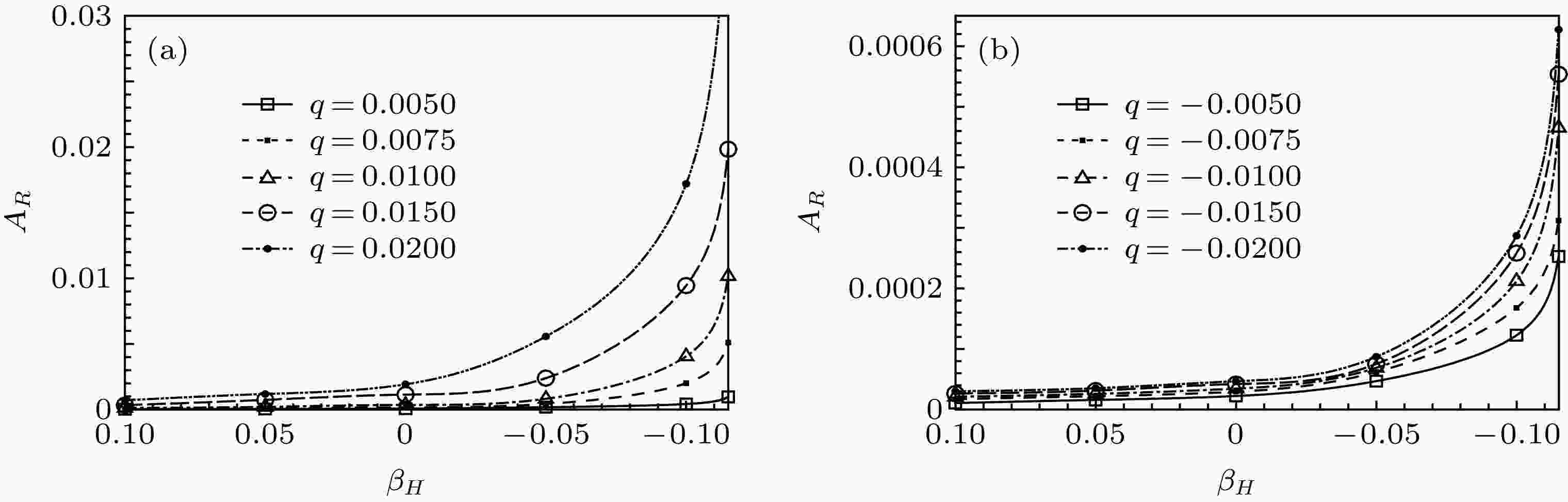图 3 局部吹入和吸出边界层内被激发出T-S波包初始幅值A_R与压力梯度的关系　(a) 吹入强度; (b) 吸出强度
Figure3. The relationships between the initial amplitudes of the excited T-S waves A_R and the pressure-gradients in the localized blowing and suction boundary layers: (a) Blowing intensity; (b) suction intensity

随后, 通过快速傅里叶变换, 从有压力梯度壁面局部吹入边界层内被激发出T-S波波包中提取获得最具有代表性频率为F = 40和F = 80的T-S波的流向扰动速度(最大值位置y = 0.66处)沿流向的演化, 如图4(a)和图4(b)所示(图4(a)左边y刻度值对应β_H = 0, –0.02被诱导出T-S波的演化, 右边y刻度值对应β_H = 0.1被诱导出T-S波的演化; 图4(b)左边y刻度值对应β_H = –0.115被诱导出T-S波的演化, 右边y刻度值对应β_H = 0, 0.05 被诱导出T-S波的演化). 图4(a)显示, 当频率F = 40时, 在零压力梯度情况下壁面局部吹入边界层内被激发出的是不稳定T-S波; 而逆压力梯度终能促使壁面局部吹入边界层内被激发出更不稳定的T-S波; 反之, 顺压力梯度终能抑制或阻碍壁面局部吹入边界层内被激发出的不稳定T-S波发展, 并可能将壁面局部吹入边界层内被激发出的不稳定T-S波转换成为稳定的T-S波; 图4(b)显示, 当频率F = 80时, 在零压力梯度情况下壁面局部吹入边界层内被激发出稳定的T-S波或衰减T-S波; 而逆压力梯度将可能使壁面局部吹入边界层内被激发出的稳定T-S波转换成不稳定的T-S波; 反之, 顺压力梯度能使壁面局部吹入边界层内被激发出的稳定T-S波趋于更加稳定的T-S波. 同样, 压力梯度对壁面局部吸出边界层内被激发出感受性现象的影响机制与壁面局部吹入边界层内被激发出感受性现象类似, 不同的是壁面局部吸出作用将在一定程度上阻碍或抑制有压力梯度边界层内的感受性过程的发生. 综上所述, 逆压梯度总能使边界层感受性能力增强; 顺压梯度总能抑制或削弱边界层感受性能力.
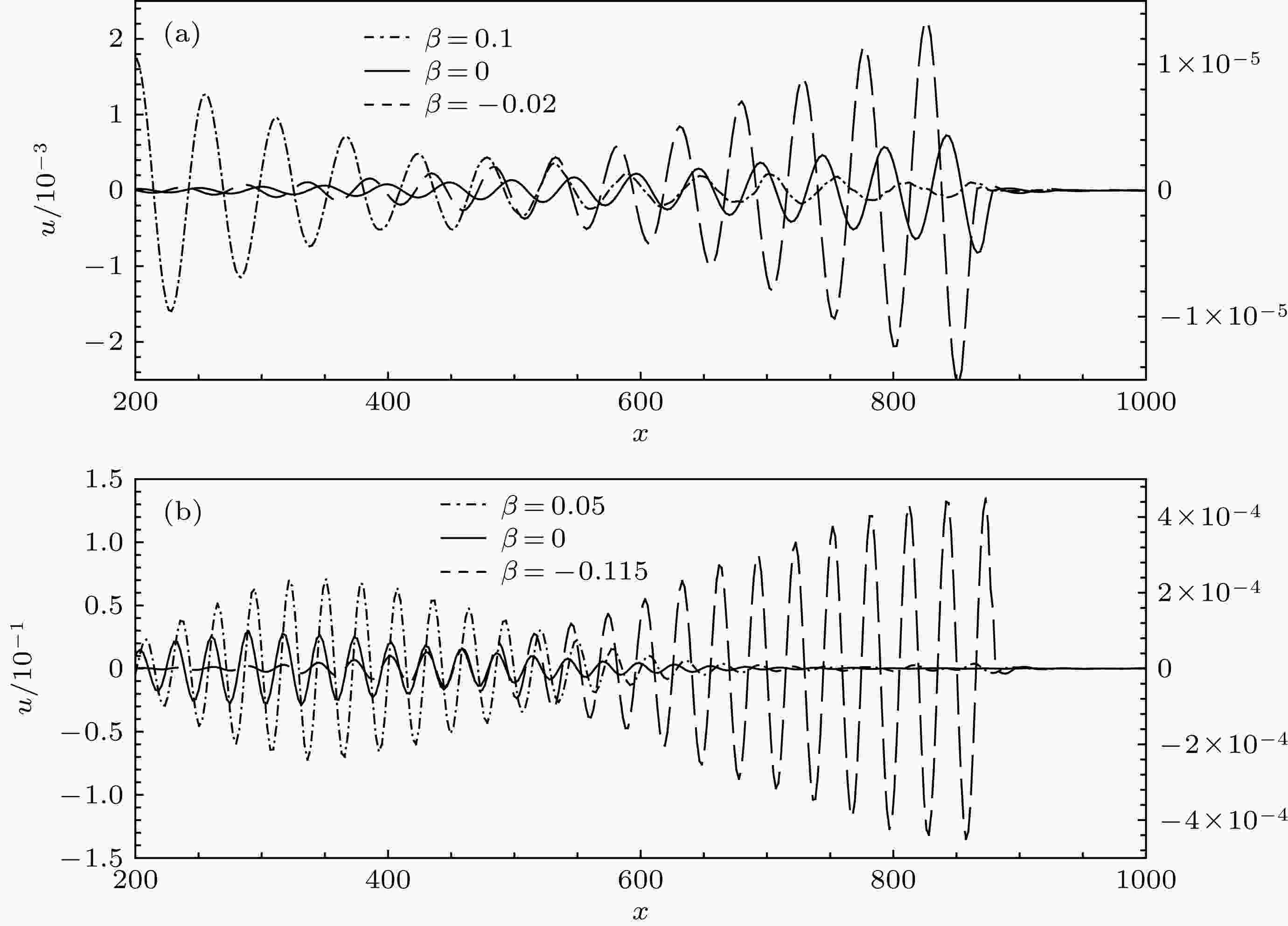图 4 不同压力梯度对壁面局部吹入边界层内被激发出的T-S波沿x向发展的影响 　(a) F = 40; (b) F = 80
Figure4. The effect of different pressure gradients on x-direction evolutions of the excited T-S waves in the localized blowing boundary layers. (a) F = 40; (b) F = 80

依据图4展示的有压力梯度边界层内被激发产生T-S波的流向扰动速度在x方向上的空间发展过程, 可近似求得T-S波的波长(或波数)和相速度; 同理可获得其他频率情况下T-S波的波长($\lambda $)和相速度, 详细结果见表2 (吹入和吸出的强度为$ \pm $0.001, ${\alpha _r} = {{2{\text{π}}}}/{\lambda }$). 从表2可知, 随着压力梯度系数${\beta _H}$的不断增大, 边界层内被激发出相同频率T-S波的波数${\alpha _r}$和相速度C分别缓慢衰减和缓慢增长的演化趋势; 另外, 在壁面局部吹入作用下有压力梯度边界层内被激发产生相同频率T-S波的波数和相速度要分别比壁面局部吸出作用下有压力梯度边界层内被激发产生相同频率T-S波的波数小和相速度大.

βH	–0.1	–0.05	0	0.05	0.1
F = 30(吹)	(0.0977, 0.3071)	(0.0960, 0.3125)	(0.0949, 0.3161)	(0.0934, 0.3212)	(0.0915, 0.3279)
F = 30(吸)	(0.0984, 0.3049)	(0.0967, 0.3102)	(0.0956, 0.3138)	(0.0943, 0.3181)	(0.0923, 0.3250)
F = 40(吹)	(0.1262, 0.3169)	(0.1251, 0.3197)	(0.1240, 0.3226)	(0.1218, 0.3284)	(0.1204, 0.3322)
F = 40(吸)	(0.1269, 0.3152)	(0.1257, 0.3182)	(0.1248, 0.3205)	(0.1226, 0.3263)	(0.1210, 0.3306)
F = 50(吹)	(0.1533, 0.3262)	(0.1522, 0.3285)	(0.1514, 0.3303)	(0.1489, 0.3357)	(0.1470, 0.3401)
F = 50(吸)	(0.1541, 0.3245)	(0.1531, 0.3266)	(0.1521, 0.3287)	(0.1497, 0.3340)	(0.1477, 0.3385)
F = 60(吹)	(0.1792, 0.3348)	(0.1784, 0.3363)	(0.1772, 0.3386)	(0.1755, 0.3419)	(0.1735, 0.3458)
F = 60(吸)	(0.1799, 0.3335)	(0.1792, 0.3348)	(0.1780, 0.3371)	(0.1763, 0.3403)	(0.1744, 0.3440)
F = 70(吹)	(0.2047, 0.3419)	(0.2036, 0.3438)	(0.2020, 0.3465)	(0.2004, 0.3493)	(0.1985, 0.3526)
F = 70(吸)	(0.2055, 0.3406)	(0.2043, 0.3426)	(0.2028, 0.3451)	(0.2012, 0.3479)	(0.1993, 0.3512)
F = 80(吹)	(0.2287, 0.3498)	(0.2279, 0.3510)	(0.2267, 0.3529)	(0.2249, 0.3557)	(0.2234, 0.3581)
F = 80(吸)	(0.2295, 0.3486)	(0.2286, 0.3500)	(0.2276, 0.3515)	(0.2261, 0.3538)	(0.2244, 0.3565)

表2压力梯度边界层被激发出的T-S波的流向波数和相速度(α_r, C)
Table2.The streamwise wave numbers and phase speeds (α_r, C) of the excited T-S wave packets in the pressure-gradient boundary layers.

进一步分析压力梯度对壁面局部吹入边界层内被激发出T-S波的幅值和增长率的影响. 将边界层内被激发出T-S波的幅值定义为A_TS, 其表达式为

${A_{{\rm{TS}}}} = \sqrt {\overline {{u_{{\rm{TS}}}}^2} + \overline {{v_{{\rm{TS}}}}^2} },$

其中: $\overline {{u_{{\rm{TS}}}}^2} $和$\overline {{v_{{\rm{TS}}}}^2} $代表x和y方向上有压力梯度边界层内被激发出T-S波的扰动速度平方的时均值.
图5(右边y刻度值对应的是零压和顺压梯度, 左边y刻度值对应逆压梯度)和图6给出了几种典型压力梯度情况下壁面局部吹入边界层内被激发出的具有代表性频率T-S波的幅值和增长率随流向的演变. 当频率F = 40时, 从图5(a)和图6(a)可见: 逆压力梯度能促使壁面局部吹入边界层内被诱导产生的不稳定T-S波模态转换成为更不稳定T-S波模态, 其幅值向下游加速增长以及在整个下游发展过程中的增长率始终大于零, 且增长速率明显大于零压和顺压梯度情况; 顺压力梯度使得壁面局部吹入边界层内被诱导产生的不稳定T-S波模态可能转换成为稳定T-S波模态, 其幅值向下游快速衰减以及在整个下游发展过程中的增长率始终小于零, 且增长速率明显小于零压和逆压梯度情况; 这一结果与e^N法和线性理论解完全吻合. 当频率F = 80时, 从图5(b)和图6(b)可见: 逆压力梯度有可能使壁面局部吹入边界层内被诱导产生的稳定T-S波模态转换成为不稳定T-S波模态, 其幅值向下游快速增长以及在整个下游演化过程中的增长率始终大于零, 且增长速率明显大于零压和顺压梯度情况; 顺压力梯度总能使得壁面局部吹入边界层内被诱导产生稳定T-S波模态转换成为更加稳定T-S波模态.
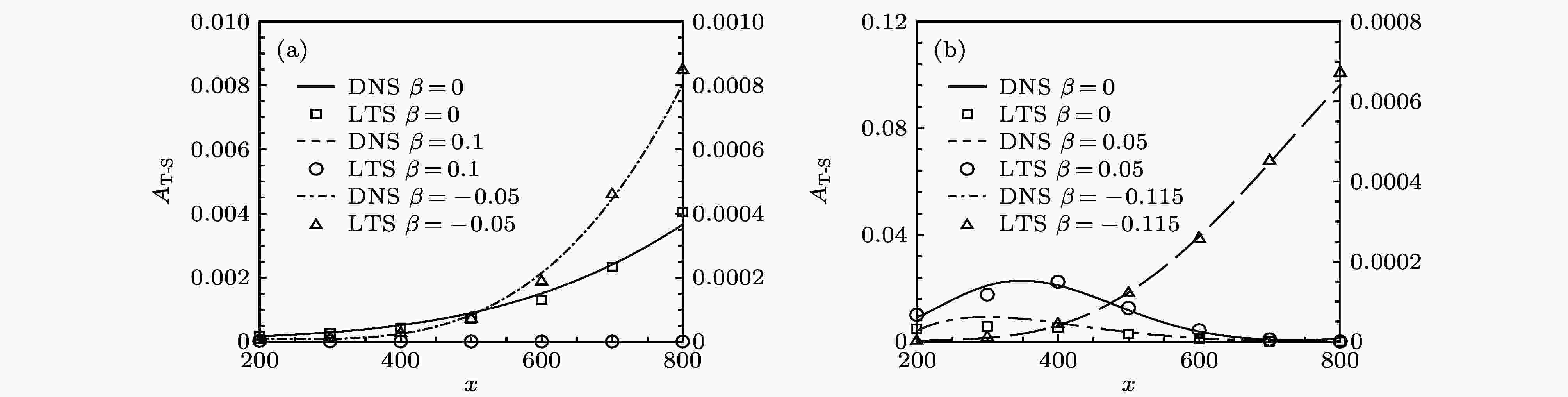图 5 壁面局部吹入边界层内被激发出T-S波的幅值A_T-S沿x向的演化(t = 2400)　(a) F = 40; (b) F = 80
Figure5. The x-direction evolutions of the amplitude of the excited T-S waves in the local blowing boundary layers (t = 2400): (a) F = 40; (b) F = 80.

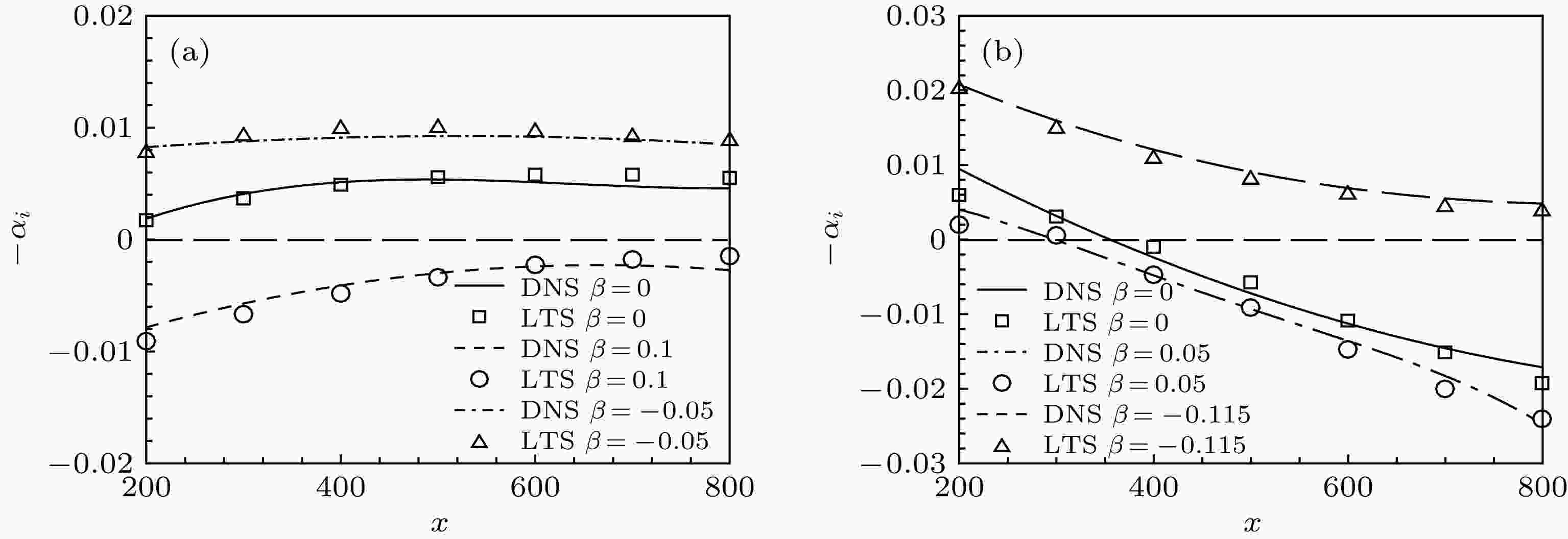图 6 壁面局部吹入边界层内被激发出T-S波的增长率(–α_i)沿x向的演化(t = 2400)　(a) F = 40; (b) F = 80
Figure6. The x-direction evolutions of the growth rate (–α_i) of the excited T-S waves in the local blowing boundary layers (t = 2400): (a) F = 40; (b) F = 80.

分别考虑在自由来流湍流分别与壁面局部吹入和吸出作用下, 讨论在不同顺压和逆压梯度情况下边界层内被激发产生T-S波波包的初始幅值分别与吹入和吸出强度之间的关系, 详见图7所示. 图7(a)和图7(b)分别表示不同顺压和逆压梯度边界层内被激发产生T-S波波包的初始幅值与吹入强度之间的关系, 其中图7(b)左边y刻度值对应压力梯度系数β_H = –0.012, –0.02和–0.05时的初始幅值, 右边y刻度值对应压力梯度系数β_H = –0.1和–0.11时的初始幅值; 图7(c)和图7(d)分别表示不同顺压和逆压梯度边界层内被激发产生T-S波波包的初始幅值与吸出强度之间的关系, 其中图7(d)左边y刻度值对应压力梯度系数β_H = –0.012, –0.02和–0.05时的初始幅值, 右边y刻度值对应压力梯度系数β_H = –0.1和–0.11时的初始幅值. 由图7(a)和图7(b)可知, 当壁面局部吹入强度不断增强时, 压力梯度系数的不断减少都将促使边界层内被激发出 T-S波波包的初始幅值快速增长; 顺压梯度情况下边界层内被激发出 T-S波波包的初始幅值始终比逆压梯度情况下边界层内被激发出 T-S波波包的初始幅值大约要小两个数量级左右. 从图7(c)可知, 当壁面局部吸出强度不断增强时, 顺压梯度系数的不断减少都将先促使边界层内被激发出 T-S波波包的初始幅值较快的增长; 直至壁面局部吸出强度等于–0.0024之后开始阻碍边界层内被激发出 T-S波波包的初始幅值发展; 其原因是壁面局部吸出和顺压梯度两者都能抑制或阻碍不稳定波增长的作用所导致波包初始幅值较快地衰减. 从图7(d)可知, 当壁面局部吸出强度不断增强时, 逆压梯度的不断增强都将先促使边界层内被激发出 T-S波波包的初始幅值较快的增长; 直至壁面局部吸出强度等于–0.002之后将抑制或阻碍边界层内被激发出 T-S波波包的初始幅值增长, 并趋于较缓慢衰减和平稳发展的状态; 其原因是壁面局部吸出始终抑制不稳定波的增长和逆压梯度始终激励不稳定波的增长两者相互作用所导致不稳波趋于缓慢衰减或平稳发展态势.
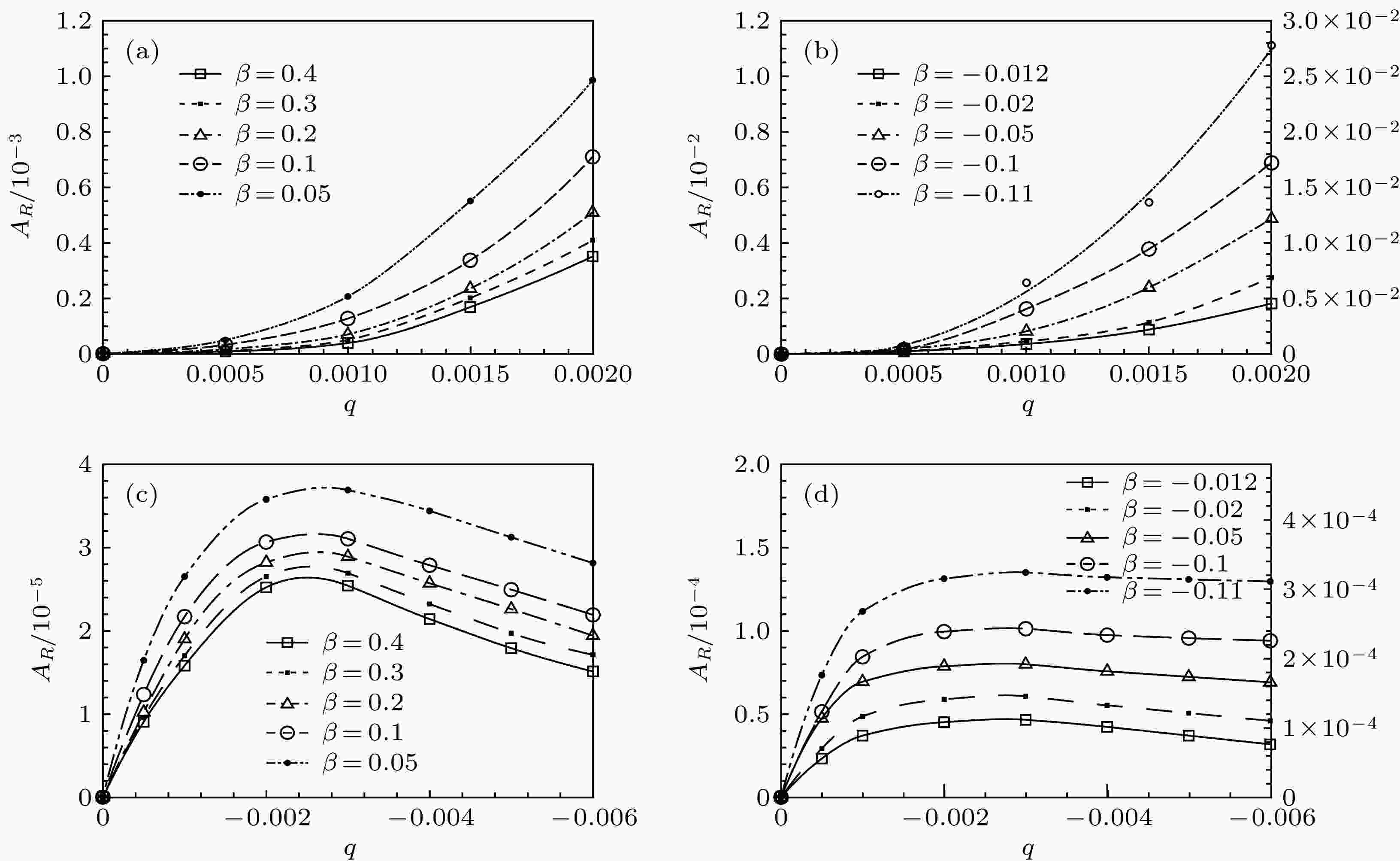图 7 在不同压力梯度情况下壁面局部吹入和吸出边界层内被激发出T-S波波包的初始幅值A_R与局部吹吸强度q之间的关系
Figure7. The relationships between the initial amplitudes of the excited T-S waves A_R and the localized blowing/suction intensity q in different pressure boundary layers

最后, 选取几种典型压力梯度的壁面局部吹入边界层内被激发出最具有代表频率(F = 40) T-S波为例, 分析其特征形状函数的幅值和相位沿法向的演变. 图8展示的结果已被零压梯度情况下壁面局部吹入边界层内被激发出T-S波的最大幅值$\left| {{u_0}} \right|$归一化. 图8显示, 几种典型压力梯度壁面局部吹入边界层内被激发出T-S波的特征形状函数的幅值沿法向变化的分布状态是相似的; 但是, 压力梯度对壁面局部吹入边界层内被激发出T-S波的特征形状函数幅值沿法向变化的影响是相当明显的, 即逆压力梯度明显大于零压和顺压力梯度的作用, 这说明逆压力梯度对边界层内被激发出的感受性能力较强; 另外, 从图9也可发现, 有压力梯度壁面局部吹入边界层内被激发出T-S波的相位沿法向变化与线性理论解也吻合一致, 且压力梯度对壁面局部吹入边界层内被激发出T-S波的相位沿法向变化的影响很小. 同理, 压力梯度对壁面局部吸出边界层内被激发出T-S波的特征形状函数的幅值和相位沿法向变化的影响相同; 其主要区别是压力梯度对壁面局部吸出边界层内被激发出T-S波的特征形状函数幅值沿法向变化的影响要明显小于壁面局部吹入的情况.
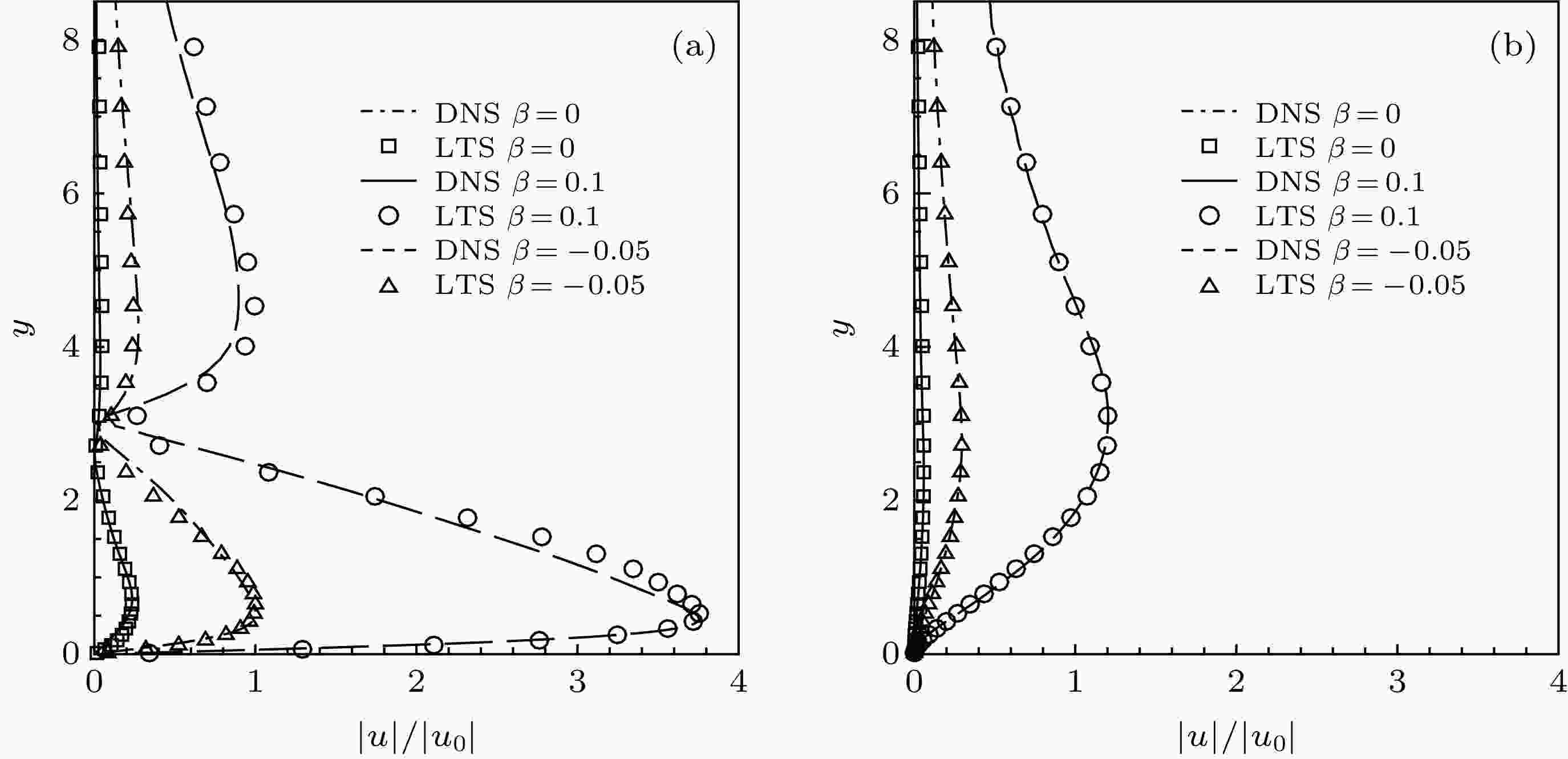图 8 压力梯度对壁面局部吹入边界层内被激发出T-S波的特征形状函数的幅值沿y向演变的影响(x = 300)
Figure8. The effects of different pressure gradients on y-direction amplitude profiles of the shape functions of the excited T-S waves in localized blowing boundary layers (x = 300).

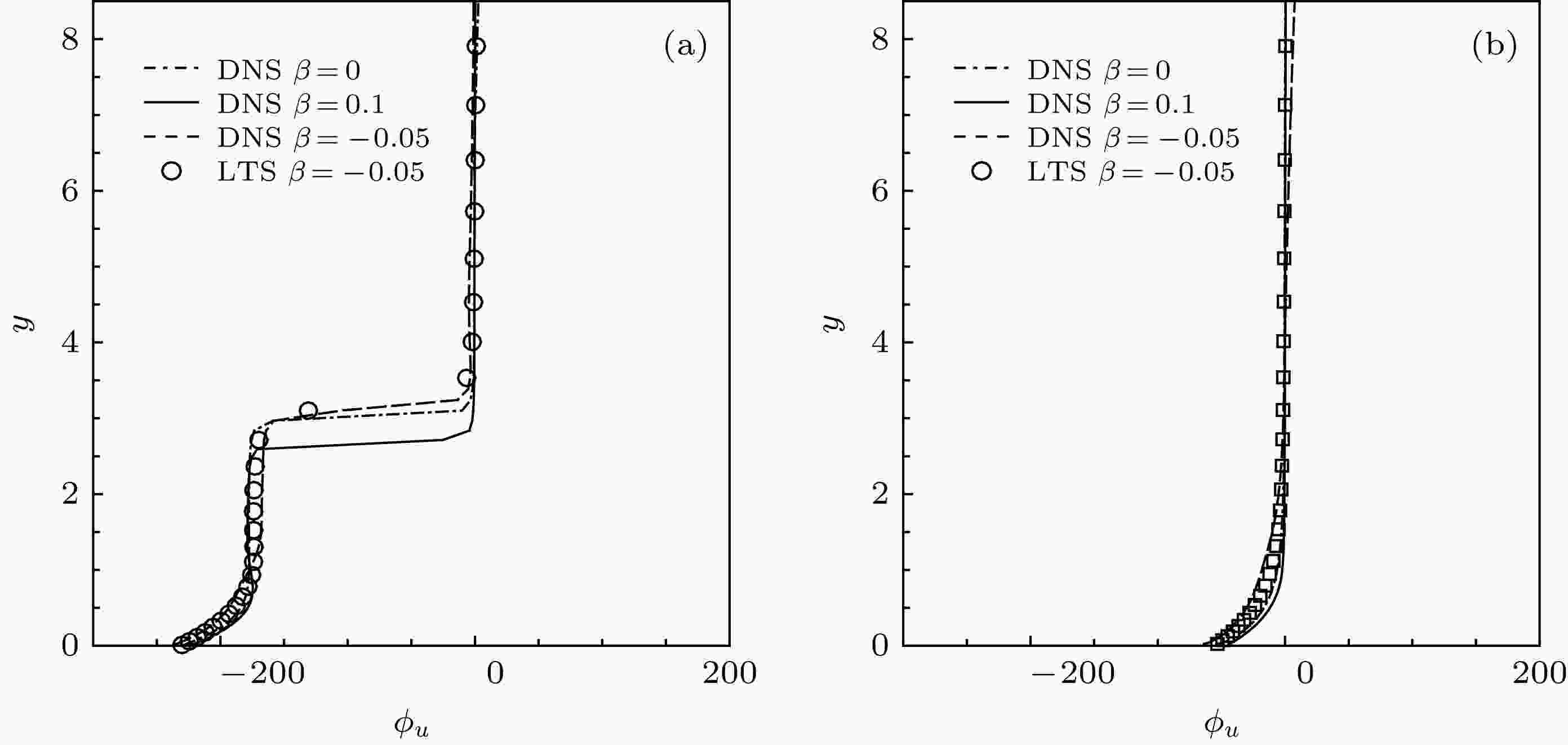图 9 压力梯度对壁面局部吹入边界层内被激发出T-S波的特征形状函数的相位沿y向演变的影响(x = 300)
Figure9. The effects of different pressure gradients on y-direction phase profiles of the shape functions of the excited T-S waves in localized blowing boundary layers (x = 300).

本文直接数值模拟研究了在自由来流湍流分别与壁面局部吹入和吸出相互作用下压力梯度对壁面局部吹入或吸出边界层感受性的影响, 获得了如下结论:
1)逆压力梯度始终对壁面局部吹入或吸出边界层内被诱导出的感受性过程起着激励或促进增长的作用, 而顺压力梯度总是对壁面局部吹入或吸出边界层内被诱导出的感受性过程起着抑制或削弱的作用; 且压力梯度对壁面局部吹入边界层内被激发出的感受性能力的影响始终远大于壁面局部吸出边界层内被激发出的感受性能力, 其量级约大两个数量级左右; 也就是说壁面局部吹入有利于激励边界层感受性过程的发生而壁面局部吸出总是阻碍边界层感受性过程的产生;
2)逆压力梯度能加速壁面局部吹入或吸出边界层内被激发出的不稳定T-S波模态转换为更不稳定的T-S波模态; 并且, 逆压力梯度也可能将壁面局部吹入或吸出边界层内被激发出的稳定T-S波模态转换为不稳定T-S波模态; 反之, 顺压力梯度将能抑制或阻碍壁面局部吹入或吸出边界层内被激发出的不稳定T-S波模态发展, 并可能将已被激发出的不稳定T-S波模态转换成为稳定的T-S波模态以及顺压力梯度总能将壁面局部吹入或吸出边界层内被激发出的稳定T-S波模态转换为更加稳定的T-S波模态, 也就是说压力梯度是边界层内被感受出不稳定T-S波模态转换机制的关键性因素;
3)压力梯度对壁面局部吹入或吸出边界层内被激发出的T-S波波包和单个T-S波的初始幅值都有明显的影响, 且逆压力梯度对壁面局部吹入或吸出边界层内被激发出的T-S波波包和单个T-S波的初始幅值比顺压力梯度情况约大两个数量级左右; 但是, 压力梯度对壁面局部吹入或吸出边界层内被激发出的T-S波波包向前传播的群速度以及在边界层内被激发出T-S波的增长率、波长或波数和相速度有一定程度的影响;
4)无论是逆压力梯度还是顺压力梯度对壁面局部吹入或吸出边界层内被激发出T-S波的特征形状函数幅值沿法向的分布是相似的; 但是, 逆压力梯度对壁面局部吹入或吸出边界层内被激发出T-S波的特征形状函数幅值要明显大于顺压力梯度情况, 其原因是逆压力梯度边界层内被感知的感受性能力较强所致; 不管何种压力梯度对壁面局部吹入或吸出边界层内被激发出T-S波的特征形状函数的相位沿法向分布的影响很小, 其分布规律类似.