摘要: 近年来, 尘埃等离子体的研究在太空、工业和实验室等领域中有着重要的作用. 该文从双温尘埃等离子体的控制方程组出发, 通过运用多尺度分析与约化摄动方法, 推导了(2+1)维的Kadomtsev-Petviashvili (KP)方程来描述双温尘埃等离子体声波的传播. 接下来, 利用半逆方法和分数变分原理, 将(2+1) 维KP方程推广到时空分数阶KP方程; 分数阶KP方程对于描述实际问题中的物理现象具有潜在的应用价值. 进一步, 基于李对称分析方法, 讨论了时间分数阶KP方程的守恒律, 得到了双温尘埃等离子体声波的守恒量. 最后, 基于双线性方法, 获得了分数阶KP方程的Lump解. 该解的存在说明双温尘埃等离子体中存在怪波, 特别地, 分析了分数阶阶数对怪波的影响.
关键词: 尘埃等离子体 /
分数阶Kadomtsev-Petviashvili方程 /
双线性方法 /
Lump解 English Abstract Fractional order model and Lump solution in dusty plasma Sun Jun-Chao 1 ,Zhang Zong-Guo 2 ,Dong Huan-He 1 ,Yang Hong-Wei 1 1.College of Mathematics and System Science, Shandong University of Science and Technology, Qingdao 266590, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11975143), the Natural Science Foundation of Shandong Province of China (Grant No. ZR2018MA017), and the Shandong University of Science and Technology Graduate Innovation Project, China (Grant No. SDKDYC190238)Received Date: 09 July 2019Accepted Date: 17 September 2019Available Online: 01 November 2019Published Online: 05 November 2019Abstract: In recent years, the dust plasma research plays an important role in the field of space, industry, and laboratory. In this paper, starting from the control equations of the double temperature dust plasma, we derive the (2+1)-dimensional Kadomtsev-Petviashvili (KP) equation to describe the double temperature dust plasma sound waves by using the multi-scale analysis, and reduce it by using the perturbation method. Then by using the semi inverse method and fractional variational principle, the (2+1)-dimensional KP equation is introduced into the time-space fractional KP equation (TFS-KP). The fractional KP equation has potential applications in describing physical phenomena in practical problems. Furthermore, based on the symmetrical analysis method, by which lie discussed the time fractional KP (TF-KP) equation of the conservation law, the dual temperature dust plasma acoustic conserves quantity. Finally, based on the bilinear method, the lump solution of fractional KP equation is obtained. The existence of this solution indicates the rogue waves existing in double temperature dusty plasma. The influence of fractional order on rogue wave is also analyzed.Keywords: dust plasma /fractional Kadomtsev-Petviashvili equation /bilinear method /Lump solutions 全文HTML --> --> --> 1.引 言 近年来, 由于等离子体物理特别是尘埃等离子体在宇宙、地球环境、半导体和电磁传播等领域的的快速发展, 尘埃等离子体的研究[1 -3 ] 引起了越来越多****的兴趣, 在等离子体科学中形成了一个崭新的分支领域. 尘埃等离子体是一种复杂的等离子体, 尘埃等离子体由一般的等离子体和十分微小的带电尘埃颗粒组成. 尘埃颗粒是尘埃等离子体的重要组成部分, 尘埃颗粒与电子离子之间的相互作用以及尘埃颗粒之间的相互作用和整个系统与外界的相互作用增加了体系的复杂性. 尘埃等离子广泛存在于地球电离层、行星环及彗星尾部、低温等离子体材料加工装置、核聚变反应器中, 这逐渐引起了国内外****的重视. 20世纪80年代初期旅行者二号宇宙飞船抵达土星时回传的土星环轮辐照片发现土星环B环中有径向辐条状的物质环绕B环外部旋转. 1989年Selwyn等[4 ] 首次报道在等离子体刻蚀导体芯片过程中的尘埃污染. 这两件大事促进尘埃等离子体的迅速发展, 使得尘埃等离子体已经发展成为了一个比较热门的研究领域, 也成为近二十年来除玻色-爱因斯坦凝聚之外发展最快的一门学科. 1995年Barkan[5 ] 在实验上证实了尘埃等离子体中的波动模式, 在随后的十年里, 人们对波与不稳定性问题的研究兴趣倍增. 尘埃等离子体中不仅可以产生非常丰富的波动模式, 而且还可以出现非线性相干结构, 当非线性效应和色散效应之间达到平衡时, 就会形成尘埃声孤波. 尘埃声孤波[6 -8 ] 是尘埃等离子体中的一种重要的非线性相干结构. 可以很好地解释实验室和空间等离子体中局域静电扰动的非线性[9 ,10 ] 特性, 是尘埃等离子体中波动研究的热点.[11 -14 ] 已广泛应用于数学、物理、生命科学、工程等各个领域. 分数微积分[15 -18 ] 也受到越来越多研究者的关注. 与整数阶模型相比, 分数阶模型能更好地描述波的传播, 有利于分析各种物理现象. 然而在尘埃等离子体的研究过程中, 往往建立的都是整数阶的物理模型. 这使得建立分数阶模型来描述和研究尘埃等离子体中波的传播是十分必要的. 随着对分数阶模型研究的不断发展, 分数阶微分方程的求解[19 ,20 ] 成为一个重要课题, 目前在整数阶方程求解方法[21 -24 ] 的基础上, 计算分数阶微分方程精确解和数值解的方法已有多种. 如$ (G'/G) $ 扩张的方法[25 ] 、$ \exp(-\varphi(\xi)) $ 方法[26 ] 、第一积分法[27 ] 、Riemann Hilbert方法[28 ] 等.[29 ,30 ] 最早是由挪威数学家Lie[31 ] 于19世纪末提出的, 之后Noether定理[32 ] 建立了对称守恒律和微分方程之间的关系, 使得守恒律的研究逐渐发展起来. 但对于守恒定律的研究往往建立在整数阶方程的基础上, 为了使守恒定律在分数阶微分方程性质的研究中得到广泛的应用, 该文利用李对称分析方法构造了分数阶微分方程的守恒定律[33 ,34 ] .[35 ,36 ] 的研究引起了许多****的兴趣. 怪波[37 -39 ] 不仅在等离子体中存在, 也存在于海洋、光学、甚至毛细管等多个领域中. 最早关于怪波的记录是1896年葡萄牙Spray号船由于怪波而倾覆. 此后在挪威北海海域、日本海域以及南非东南海域相继出现类似的海难事故. 怪波是一种单峰波, 它与孤立波有些相似, 但是怪波的波峰很尖, 波高很大, 而且怪波持续时间短, 会很快消失, 这又与孤立波有很大的区别. 对于等离子体中怪波的研究起步较晚, 2011年, Bailung等[40 ] 在实验中观测到了含有负离子的多成分等离子体中的怪波现象, 这说明等离子体中的怪波现象既存在于理论研究中又是实际存在的, 对于等离子体中怪波现象的研究具有实际的物理意义.2 节, 基于运动控制方程, 采用多尺度分析和扰动展开方法, 推导出(2+1)维整数阶Kadomtsev-Petviashvili (KP)方程; 第3 节, 利用半逆方法和分数变分原理将整数阶KP方程转化为时空分数阶 KP (TSF-KP)方程; 第4 节, 基于李对称分析方法, 得到时间分数阶 KP (TF-KP)方程的守恒向量; 第5 节, 依靠双线性的方法得到分数阶方程的精确解, 研究了尘埃等离子体声波的怪波现象以及分数阶数对尘埃等离子体中怪波的影响.2.物理模型与KP方程的推导 双温尘埃等离子体由带负电荷的尘埃颗粒、电子和双温离子(高温离子和低温离子)三部分组成. 为了更好地处理所研究的问题, 对该模型做出假定如下:x 方向传播, 但在y 方向上存在较高阶的横向扰动;$ Z_{ {\rm d}0_{j}} $ 为无扰动时尘埃颗粒的电荷数; $ n_{ {\rm il} 0} $ , $ n_{ {\rm ih} 0} $ , $ n_{ {\rm e} 0} $ , $ n_{{\rm d} 0_{j}} $ 分别为低温离子、高温离子、电子和尘埃颗粒的数密度. 控制方程组由尘埃的质量守恒、动量方程、以及泊松方程组成[41 ] :$ {{u}_{ {\rm d}_{j}}}=u_{ {\rm d}_{j}}{{i}}+v_{ {\rm d}_{j}}{{j}} $ ; $ n_{ {\rm d}_{j}} $ , $ u_{ {\rm d}_{j}} $ , $ m_{ {\rm d}_{j}} $ 分别为无量纲化的数密度、速度、尘埃颗粒质量; $ Z_{ {\rm d}_{j}} $ 为尘埃颗粒的电荷; $ \varPhi $ 为无量纲化的静电势; 无量纲化的电子数密度、低温离子、高温离子分别为$ n_{\rm e} $ , $ n_{\rm il} $ , $ n_{\rm ih} $ .1 )可以得到无量纲化形式的控制方程如下:$ n_{\rm d} $ 为尘埃颗粒数密度, $ \phi $ 为电势, $ u_{\rm d}, v_{\rm d} $ 分别为x 和y 方向上的速度. $ n_{\rm d} $ 由$ n_{ {\rm d} 0} $ 无量纲化, 空间坐标$ x, y $ 由等效德拜长度$ \lambda=\left( {\dfrac{T_ {\rm eff}}{4{\text{π}} e^{2}Z_{\rm d}n_{ {\rm d} 0}}} \right)^{\textstyle\frac{1}{2}} $ 无量纲化, 时间t 由等效尘埃等离子体频率的倒数$ \omega^{-1}= \left( {\dfrac{m_{\rm d}}{4{\text{π}} Z_{\rm d}^{2}n_{ {\rm d} 0}e^{2}}} \right)^{\textstyle\frac{1}{2}} $ 无量纲化, $ u_{\rm d} $ , $ v_{\rm d} $ 由等效声速$ C_{\rm d}= \left( {\dfrac{Z_{\rm d}T_ {\rm eff}}{m_{\rm d}}} \right)^{\textstyle\frac{1}{2}} $ 无量纲化, 电势由$ {T_ {\rm eff}}/{e} $ 无量纲化($ T_ {\rm eff} $ 为等效温度). $ C_{i} (i=1, 2, 3) $ 表示如下:$ \mu= {n_{\rm e 0}}/{n_{{\rm il} 0}} $ ; $ H_{\rm e}, H_i$ 是带电粒子的超热效应; $ C_{\rm e} $ , $ C_{{\rm i}} $ 为粒子声速的平衡值.2 ), 将复杂的非线性方程组简化为一个微分方程并且保留原方程组中最主要的非线性部分, 首先将自变量展开如下:4 )式可以得到5 )和(6 )式代入方程组(2 )中可以得到带有小参量$ \varepsilon $ 的方程组如下:7 ), 按照$ \varepsilon $ 的由低到高次幂展开得到$ \varepsilon $ 的较低次幂得到了如下关系:$ \varepsilon $ 的较高次幂得到了描述尘埃离子声波运动的(2+1)维整数阶KP方程:$ b_{1} $ , $ b_{2} $ , $ b_{3} $ 为3.TSF-KP方程的推导 在第2 节, 推导出了一个整数阶的模型. 然而, 随着科学研究的发展, 相比于分数阶模型, 整数阶模型在描述实际问题时有明显的不足. 这使得分数微积分和分形微积分成为数学、物理、工程领域的研究热点. 为了更深入地研究粉尘埃等离子体. 本节利用半逆方法和分数变分法由整数阶KP方程推导出时空分数阶KP方程.Definition 1 [42 ] 函数$ f(x, y, t) $ 的Riemann-Liouville分数阶导数算子如下:12 )可以写成如下形式:$ A(\xi, \eta, \tau)=B_{\xi}(\xi, \eta, \tau) $ , $ B(\xi, \eta, \zeta, \tau) $ 为势函数, 则(2+1)维TSF-KP方程的势方程为16 )的函数有如下表示:c i i = 1, 2, 3, 4, 5)是拉格朗日乘子.17 )使用分部积分的方法, 并且设$ B_{\xi}|_{R}\!=\!B_{\eta}|_{R}\!=\!B_{\zeta}|_{R}\!=\!B_{\tau}|_{T}\!=\!B_{\xi\xi}|_{R}\!=\!0 $ , 可以得到18 )的变分, 对每一项进行分部积分, 并应用变分最优条件, 得到16 )式等价于(19 )式. 通过比较系数, 得到拉格朗日乘子$ c_{i}\;(i=1, 2, 3, 4) $ 如下:$ D_{\xi}^{\alpha\alpha}B=D_{\xi}^{\alpha}(D_{\xi}^{\alpha}B) $ . 因此可以得到TSF-KP方程的函数如下:[18 ] , 函数式(23 )的变化可以写成:24 ), $ \delta J_{F}(B)=0 $ , 得到(2+1)维TSF-KP方程的Euler-Lagrange方程:22 )式代入(28 )式中可以得到$ D_{\xi}^{\alpha}B(\xi, \eta, \zeta, \tau)=A(\xi, \eta, \zeta, \tau) $ 并将其代入到(29 )式中, 可以得到如下方程:30 )两边求分数阶导数可以得到TSF-KP方程如下:4.TF-KP方程的守恒律 守恒律对于研究等离子体的物理现象具有重要的意义. 守恒定律是一个数学化的表述, 它表明在一个物理系统的演化过程中, 某一物理量的总量保持不变. 为了进一步研究分数阶模型的性质, 接下来对(2+1)维TF-KP方程的对称性和守恒定律进行了研究.4.1.李群分析 4.1.李群分析 (2+1)维TSF-KP方程可以写作如下形式:32 )式转化为分数阶偏微分方程形式如下:33 )式是不变的$ \varepsilon \ll1 $ 是参数; X , Y , T , $ \psi $ 是子函数; $ \psi_{\omega}^{\tau} $ , $ \psi_{\xi} $ , $ \psi_{\xi\xi\xi} $ , $ \psi_{\eta\eta} $ 为子函数的延拓, 其定义如下:$ D_{\tau}^{\omega} $ 是总分数阶导数算子. $ D_{\tau} $ , $ D_{\xi} $ , $ D_{\eta} $ 分别是$ \tau $ , $ \xi $ , $ \eta $ 的总导数算子, 其定义如下:[34 ] :$ f(t)=1 $ 时, 可以得到39 )式可写成如下形式:M 33 )的不变性导致了以下不变性条件:43 )式和(45 )式, 可以得到33 )的二次延拓, 可以得到以下不变性准则:43 )式代入(47 )式并设各单项系数为零, 可以得到如下方程组:48 )式, 可以得到32 )式 一系列点对称的李代数可以写成:4.2.守恒律 -->4.2.守恒律 4.1 节中得到了一系列点对称的李代数. 本节将基于李对称分析方法, 研究TF-KP方程的守恒律, (32 )式的守恒定律满足如下方程:$ C^{\tau} $ , $ C^{\xi} $ , $ C^{\eta} $ 是守恒向量. (32 )式的形式拉格朗日方程如下所示:$ s(\xi, \eta, \tau) $ 是一个新的因变量. 根据形式拉格朗日方程, 将作用积分定义为$ (D_{\tau}^{\omega})^{*} $ 是$ D_{\tau}^{\omega} $ 的伴随运算子, 定义如下:$ I_{p}^{n-\omega} $ 是右分数积分算子, $ _{\tau}^{C}D_{p}^{\omega} $ 是右Caputo分数微分算子. 因此, 可以得到(32 )式的伴随方程为欧拉-拉格朗日方程56 )式可以写成:W 如下所示:50 )式可得$ J(\cdot) $ 定义如下:$ C^{i}(i=1, 2, 3) $ 定义如下:$ \rho^{1}=X,\; \rho^{2}=Y $ .$ W_{5} $ 为例, 根据上述定义计算式(32 )的保守向量, 得到63 )可以表示为$ W_{5} $ 的守恒定律, 同样地方法可以计算出$ W_{1} $ , $ W_{2} $ , $ W_{3} $ , $ W_{4} $ 的守恒定律.5.TSF-KP方程的求解 本节在双线性方法的基础上得到了分数阶KP方程的Lump解, Lump解是一种特殊的有理解, 它在各个方向上都有合理的局域性, 而怪波解则是一类特别有趣的Lump解.Definition 2 [43 ] Definition 3 [43 ] 68 )式, 可以得到31 )可以写为70 )可以化为如下双线性方程:73 )可展开为$ a_{i}(i=1, 2, \cdots\!, 9) $ 是待确定的参数.75 )式代入(73 )式中, 并利用数学软件MAPLE计算可以得到$ a_{5} $ 和$ a_{5} $ 满足如下条件:71 )式, 可以得到方程(31 )的解:a 3 , a 7 , a 9 如(73 )式所示, 自变量(X , Y , T )满足如下变换:6.尘埃等离子体中的怪波 在第5 节, 通过求解得到了方程的Lump解, 接下来研究双温尘埃等离子体中的怪波问题, 利用得到的解通过调整参数画出的图像如下.图1 和图2 中的波是符合上述特点的, 这说明尘埃等离子体中是存在怪波的. 还可以发现, 怪波会在某个时间、某个空间突然出现, 波的振幅会迅速增长达到极值, 之后振幅会迅速回落并达到稳定, 所以怪波在时间和空间上会呈现出一种局部结构, 这使得怪波在短时间和一定空间内聚集巨大能量. 这种巨大能量往往会对实际问题的研究产生影响, 这不仅能够帮助我们如何避免这种高能带来的危害, 而且能够让我们了解如何获得这种高能, 因此怪波具有重要的研究价值.图 1 当a 1 = 1.8, a 2 = 2.1, a 4 = 0, a 5 = –0.3 , a 6 = 0.9, a 8 = 0时A 关于$\tau$ 和$\xi$ 的图像Figure1. When a 1 = 1.8, a 2 = 2.1, a 4 = 0, a 5 = –0.3 , a 6 = 0.9, a 8 = 0, the graph of A with respect to $\xi$ and $\eta$ .图 2 当a 1 = 1.3, a 2 = 1.1, a 4 = 0, a 5 = –0.3 , a 6 = 0.9, a 8 = 0时A 关于$\xi$ 和$\eta$ 的图像Figure2. When a 1 = 1.3, a 2 = 1.1, a 4 = 0, a 5 = –0.3 , a 6 = 0.9, a 8 = 0, the graph of A with respect to $\xi$ and $\eta$ .图3 和图4 所示.图 3 当分数阶阶数为${1}/{2}$ 时A 关于$\xi$ 的图像Figure3. Graph of A with respect to $\xi$ when the fractional order is ${1}/{2}$ .图 4 当分数阶阶数为1时A 关于$\xi$ 的图像Figure4. Graph of A with respect to $\xi$ when the fractional order is 1.图3 和图4 , 波的振幅、波峰、波谷都有明显差异, 这说明分数阶阶数对尘埃等离子体波有明显影响. 在研究某些物理问题时, 只研究整数阶的问题可能会有局限性, 因此研究分数阶的尘埃等离子体模型具有重要的意义.7.结 论 本文推导研究了双温等离子体波的分数阶模型. 通过使用约化摄动方法得到了$ (2+1) $ 维整数阶KP方程, 通过变分原理和半逆方法将整数阶KP方程转化为分数阶KP方程, 与整数阶模型相比, 分数阶模型能更好地描述波的传播并分析物理现象. 运用双线性方法得到了分数阶方程的Lump解. 通过图像发现, Lump解中存在的怪波, 怪波的特殊性及其产生的巨大能量使得其具有潜在的研究价值. 通过对比, 发现了分数阶阶数对尘埃等离子体怪波的影响. 






















































































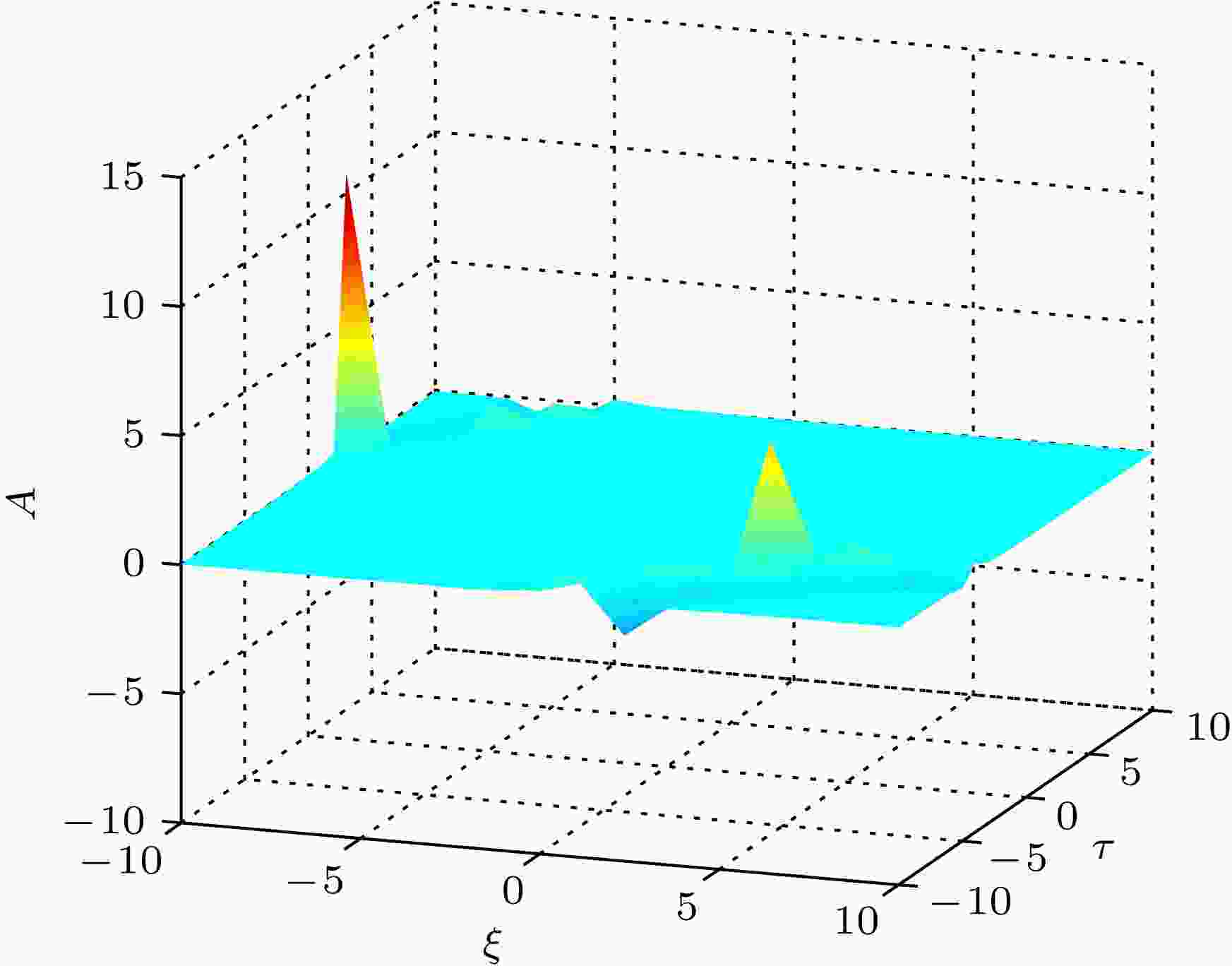 图 1 当a1 = 1.8, a2 = 2.1, a4 = 0, a5 = –0.3 , a6 = 0.9, a8 = 0时A关于
图 1 当a1 = 1.8, a2 = 2.1, a4 = 0, a5 = –0.3 , a6 = 0.9, a8 = 0时A关于



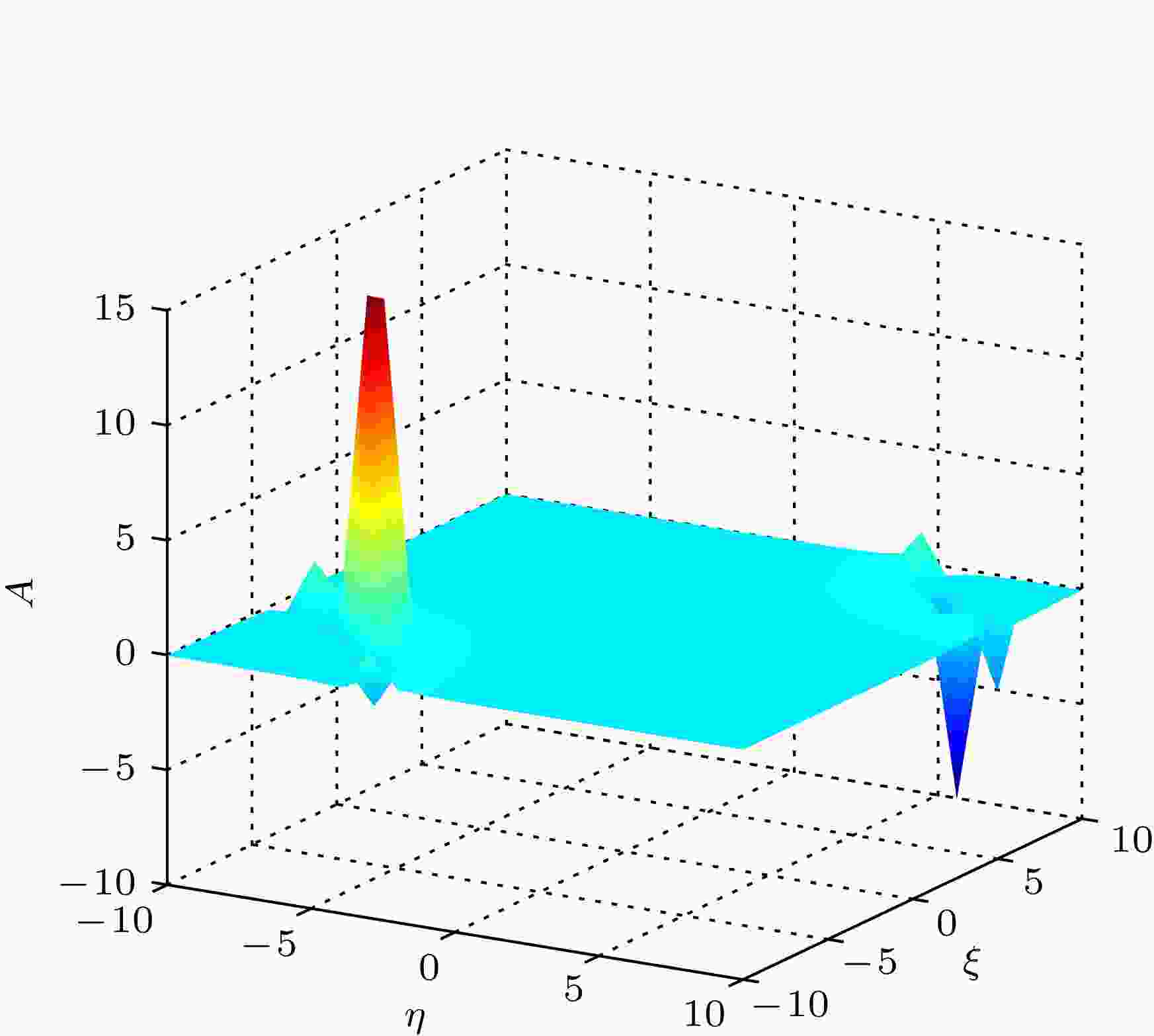 图 2 当a1 = 1.3, a2 = 1.1, a4 = 0, a5 = –0.3 , a6 = 0.9, a8 = 0时A关于
图 2 当a1 = 1.3, a2 = 1.1, a4 = 0, a5 = –0.3 , a6 = 0.9, a8 = 0时A关于



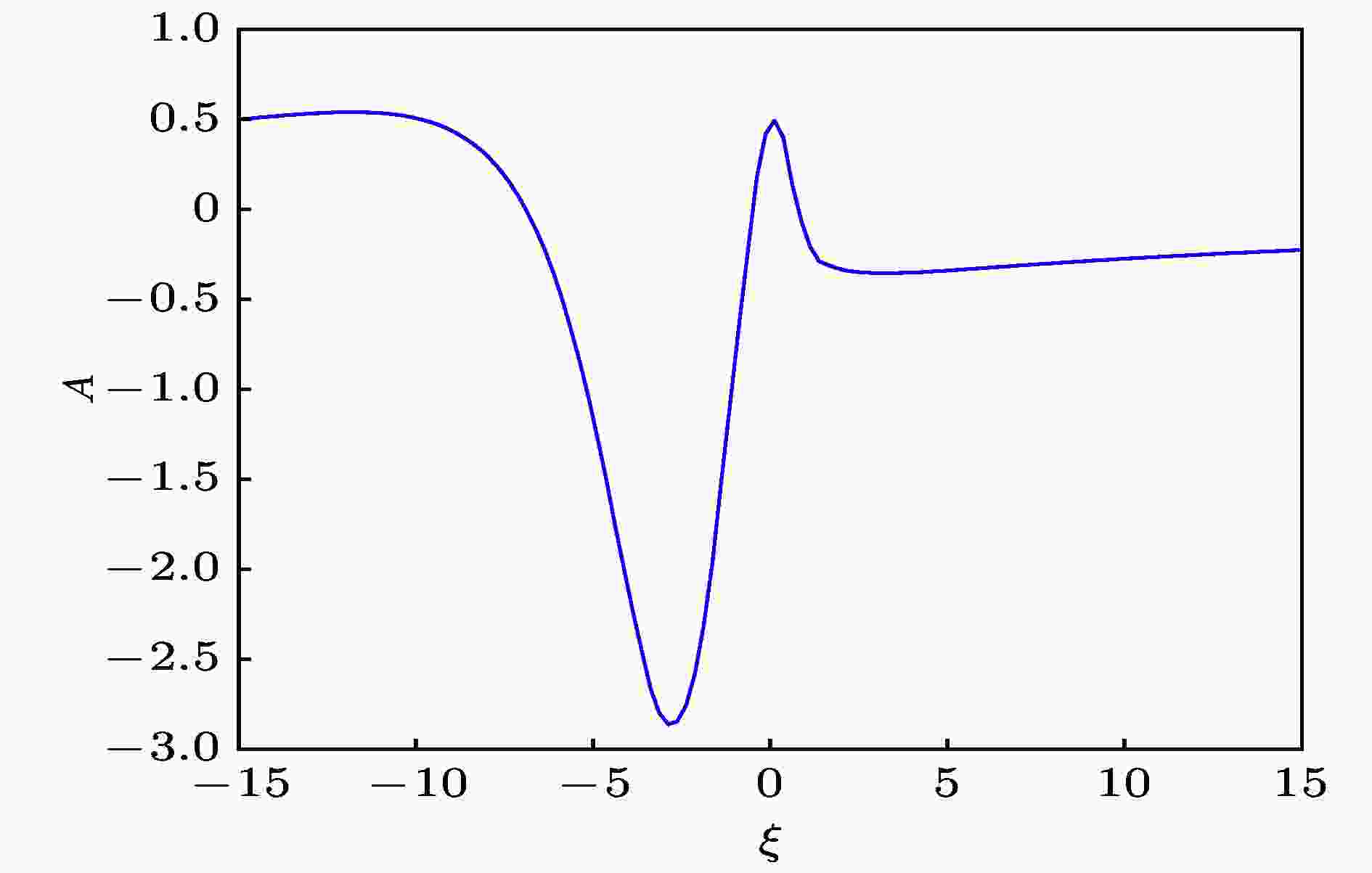 图 3 当分数阶阶数为
图 3 当分数阶阶数为



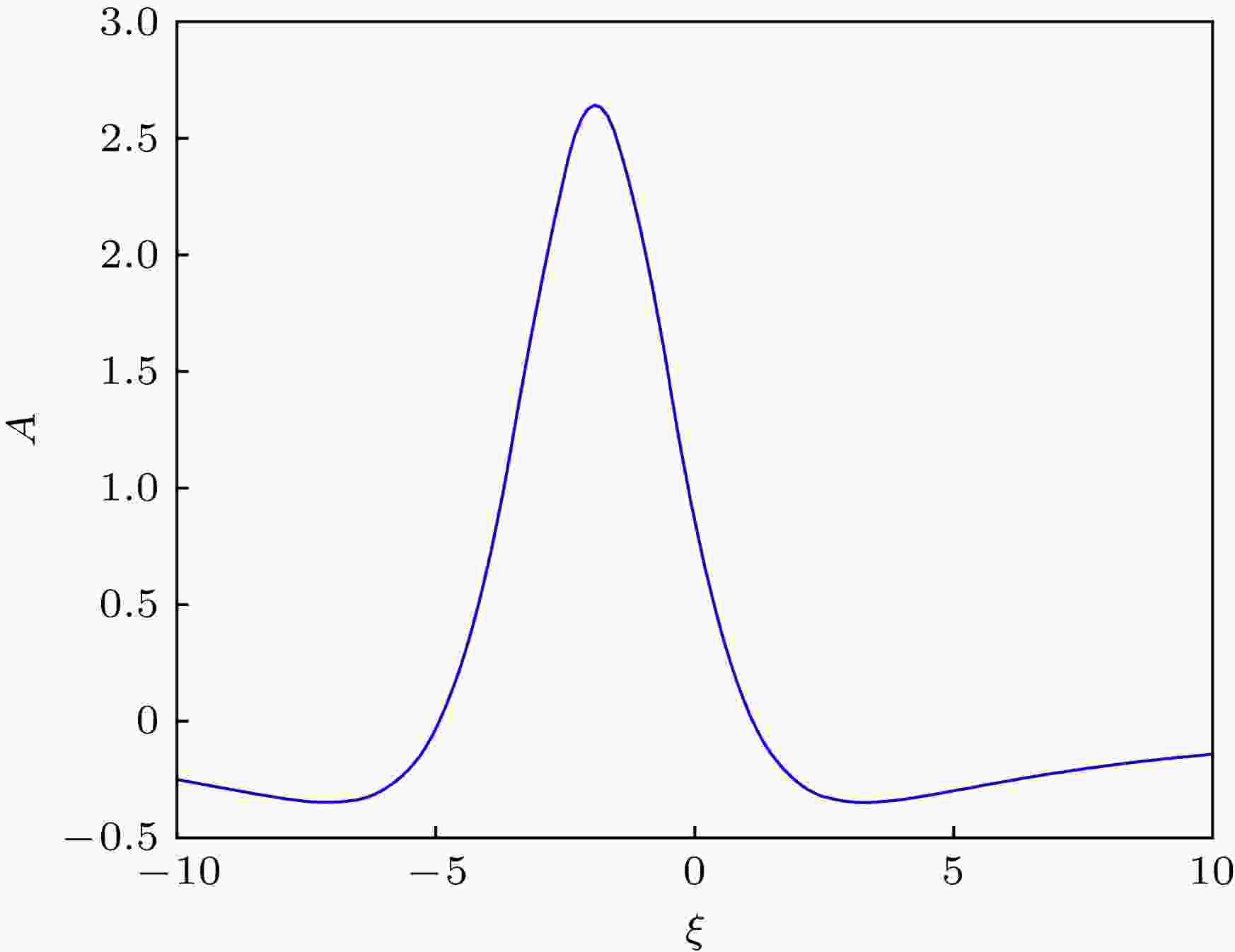 图 4 当分数阶阶数为1时A关于
图 4 当分数阶阶数为1时A关于


