摘要: 采用量子力学中的费曼路径积分方法, 推导出了更符合市场一般化情形的随机波动率股指期权定价模型. 在此基础上, 以恒指期权为例进行实证研究预测30天的期权价格, 同时将Heston模型作为对照组, 并进行稳健性检验. 研究结果表明, 本文构建的股指期权定价模型通过求解费曼定价核的数值解, 进而在线性算法上直接实现股指期权价格的预测, 相比于Heston模型利用特征函数的方法, 不论是在相同到期日不同执行价格下还是在相同执行价格不同到期日下, 定价精度显著提高. 费曼路径积分作为量子金融的主要方法, 本文的研究将为其进一步应用于金融衍生品定价提供参考.
关键词: 费曼路径积分 /
均值定价核 /
随机波动率 /
股指期权定价 English Abstract Pricing of stochastic volatility stock index option based on Feynman path integral Feng Ling Ji Wan-Ni School of Economics and Management, Fuzhou University, Fuzhou 350002, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 71573043)Received Date: 10 May 2019Accepted Date: 20 August 2019Available Online: 01 October 2019Published Online: 20 October 2019Abstract: Under the background that stock index options urgently need launching in China, the research on stock option pricing model has important theoretical and practical significance. In the traditional B-S-M model it is assumed that the volatility remains unchanged, which differs tremendously from the market’s reality. When the market fluctuates drastically, it is difficult to realize the risk management function of stock index options. Although in the Heston model, as one of the traditional stochastic volatility option pricing models, the correlation risk between the volatility and underlying price is taken into consideration, its pricing accuracy is still to be improved. From the quantum finance perspective, in this paper we use the Feynman path integral method to explore a more practical stock index option pricing model. In this paper, we construct a Feynman path integral pricing model of stock index options with stochastic volatility by taking Hang Seng index option as the research object and Heston model as the control group. It is found that the Feynman path integral pricing model is significantly superior to the Heston model either at different strike prices on the same expiration date or at different expiration dates for the same strike price. The stock index option pricing model constructed in this paper can give the numerical solution of Feynman's pricing kernel, and directly realizes the forecast of stock index option price. The pricing accuracy is significantly improved compared with the pricing accuracy given by the Heston model through using the characteristic function method. The remarkable advantages of Feynman path integral stock index option pricing model are as follows. Firstly, the path integral has advantages in solving multivariate problems: the Feynman pricing kernel represents all the information about pricing and can be easily expanded from one-dimensional to multidimensional case, so the change of closing price of stock index and volatility of underlying index can be taken into account simultaneously. Secondly, based on the relationship between the Feynman path generation principle and the law of large number, the mean values of pricing kernel obtained by MATLAB not only optimizes the calculation process, but also significantly improves the pricing accuracy. Feynman path integral is the main method in quantum finance, and the research in this paper will provide reference for its further application in the pricing of financial derivatives. Keywords: Feynman path integral /mean pricing kernel /stochastic volatility /stock index options pricing 全文HTML --> --> --> 1.引 言 2018年8月31日, 证监会对《关于上市股指期权、助力资本市场风险防范的提案》做出答复, 表示其将继续指导中金所推进股指期权的研发工作, 并于合适时机推出股指期权. 传统的期权定价模型主要有Black-Scholes (BS)期权定价模型和Heston模型. BS期权定价模型虽然形式上较为简洁, 但其仅适用于波动率为常数时的欧式期权的定价, 而对股指期权进行准确定价是发挥其风险管理功能的重要前提. Heston期权定价模型虽然考虑了波动率为随机的情形下的期权定价问题, 但其在求解过程中多次利用偏微分方程, 这些偏微分方程是在假设了特征函数解的形式的基础上, 经过推演得到相应微分方程组, 而偏微分方程的求解技术性要求较高, 且不少****在研究过程中发现该模型存在许多无法克服的不足[1 —3 ] , 本文在实验过程中就发现其在价格预测中出现缺失值. Heston模型适用于欧式期权的定价, 但其并不是为股指期权量身定制的模型. 当前, 关于随机波动率股指期权的定价研究主要有参数方法与非参数方法. 参数方法主要是围绕BS期权定价模型对股指期权定价展开研究, 侧重于股指运动变化的刻画方面, 比如在股指服从的分布中加入跳跃过程、利用广义自回归条件异方差模型(generalized autoregressive conditional heteroskedasticity model, GARCH)或时变波动率模型对BS期权定价公式进行修正[4 —7 ] . 此外, 也有****试图用一般均衡模型分析股指期权的定价问题[8 ] . 但是参数方法难以避开参数设定所带来的误差与人为影响, 随着计算机算法的飞快发展, 非参数方法可以避开求解参数受到的限制, 因此受到诸多****的青睐. 其一般都是基于计算机模拟得到数值解, 诸如神经网络模型, 遗传算法[9 —11 ] 等. 然而非参数方法不能给出具体期权定价公式, 也无法给出合理的经济解释. 因此, 更符合市场一般化情形的股指期权定价模型亟待提出. 本文基于费曼路径积分方法研究股指期权定价问题, 旨在探寻用跨学科的量子金融方法构建一个更符合市场实际情形的股指期权定价模型.[12 ] 首次提出并阐述了路径积分方法用于解决期权定价的思路. 随后其还分别对单因子期限模型和多因子期限模型给出了路径积分的分析框架. 然而, 其缺少对具体应用和数值算法的进一步研究. 1997年, Baaquie等[13 —19 ] 进一步对费曼路径积分在金融衍生品定价上的应用展开更为深入的研究, 并提供了一系列新的数值算法, 从而大大简化了数值分析的工作量. 2015年, Kakushadze[20 ] 用量子力学“半经典”近似方法给出了对债券定价的显式函数, 并且指出根据费曼图可以将微扰量子力学技术应用于“半经典”近似之外. 2017年, Issaka和Sengupta[21 ] 采用费曼路径积分方法对受列维过程驱动的金融市场的期权定价进行研究, 得到转移概率密度函数的闭式解. 2018年, Ma等[22 ] 提出了一般分数下的分数稳定过程路径积分期权定价模型. 2018年, Paolinelli和Arioli[23 ] 基于二次路径积分采用一种不同的作用量, 得到了参数较少的股票价格动态模型. 虽然上述研究已经对费曼路径积分在金融市场上的应用展开了大量的讨论, 但是该方法在股指期权价格的定价研究上并不深入. 2003年, 陈泽乾[24 ] 基于对冲的视角对量子金融的金融意义进行阐述, 解释了金融资产价格行为用量子规律刻画较经典统计规律刻画的优越性. 2007年, 陈黎明和邱菀华[25 ] 基于陈泽乾提出的二项式期权定价的量子模型, 构建了实物期权估值算法. 然而, 该算法还存在一些不足, 如阶段划分的问题以及模型参数的确定问题. 2014年, 王鹏和魏宇[26 ] 指出“金融物理学”在金融市场上众多异象(anomalies)的解释上较经典理论具有优势, 从而阐释了金融物理兴起的原因. 上述研究虽然从量子金融的理论意义与应用意义进行了解释, 但在具体的定价问题的解决上显得相对浅显.2 节对相关模型理论展开描述; 第3 节构建了随机波动率费曼路径积分股指期权定价模型; 第4 节对费曼路径积分股指期权定价模型进行算法设计, 以恒指期权的历史数据进行实证研究, 并将Heston模型作为对照组以说明随机波动率费曼路径积分股指期权定价模型的有效性、探讨本文构建的模型的适用性; 第5 节为结论.2.模型描述 22.1.Heston模型 2.1.Heston模型 诸多****针对经典BS模型下所产生的波动率微笑与波动率皱眉展开了研究, 其中较为经典的是1993年Heston[27 ] 提出的用特征函数的方法求解偏微分方程(26 ). 假定$\lambda = k\sqrt V $ , 其中k 为常数, V 为方差. 首先猜测(26 )式具有和BS公式相似的解,${P_1}$ , ${P_2}$ 又可以看成是价内期权的条件概率分布. 令$x = \ln S\left( t \right)$ , 则${P_1}$ , ${P_2}$ 必须满足偏微分方程:$j = 1,2$ , ${u_1} = \dfrac{1}{2}$ , ${u_2} = - \dfrac{1}{2}$ , $a = \alpha \theta $ , ${b_1} = \alpha + $ $\lambda - \rho \xi $ , ${b_2} = \alpha + \lambda $ , 终端条件${P_j}\left( {x,V,T;\ln K} \right) = $ ${1\;{\left( {x \geqslant \ln K} \right)}} $ .${P_1}$ , ${P_2}$ 的特征函数${f_1}\left( {x,V,T;\phi } \right)$ 和${f_2}\left( {x,V,T;\phi } \right)$ 均需满足偏微分方程(2 ), 且终端条件为${P_j}\left( {x,V,T;\ln K} \right)$ 可通过对特征函数的逆变换进行积分得到,8 )式求出概率密度${P_1}$ , ${P_2}$ , 代入(1 )式即可得欧式看涨期权的价格.2.2.费曼路径积分 -->2.2.费曼路径积分 费曼路径积分(Feynman path integral)是量子力学在薛定谔波动力学和海森伯的矩阵力学之外的第三种表示形式. 在路径积分理论中, 微观粒子处于某一时刻${t_b}$ 的运动状态$\psi \left( {{x_b},{t_b}} \right)$ , 完全由过去的某一时刻${t_a}\left( { < {t_b}} \right)$ 的所有可能的运动状态$\psi \left( {{x_a},{t_a}} \right)$ 所决定, 即$\hbar $ 为普朗克常量.$\left( {{x_a},{t_a}} \right)$ 到$\left( {{x_b},{t_b}} \right)$ 的各种路径都是可能的, 并且每条路径$\left[ {x\left( t \right)} \right]$ 均具有概率幅$ \sim {\rm{const}} \times {{\rm{e}}^{\frac{{\rm{i}}}{\hbar }S\left[ {x\left( t \right)} \right]}}$ . 传播函数$K\left( {{x_b},{t_b};{x_a},{t_a}} \right)$ 是从$x\left( {{t_a}} \right) = {x_a}$ 运动到$x\left( {{t_b}} \right) = {x_b}$ 的所有运动路径$\left[ {x\left( t \right)} \right]$ 的概率幅的叠加, 而对所有路径的求和可以表达为无穷维积分(泛函积分)的形式, 称为费曼路径积分.2.3.费曼路径积分定价理论 -->2.3.费曼路径积分定价理论 将费曼路径积分方法应用于期权定价研究时, 最为关键的是关于期权定价公式的费曼核的求解, 借鉴诸多****的研究[12 —18 ] , 本文称其为费曼定价核. 费曼定价核包含了期权定价所需的全部信息. 令$p\left( {x,y,\tau,x',y'} \right)$ 为风险中性的条件概率, 其中$\tau = T - t$ , x 和y 分别代表$\tau = T - t$ 时有价证券的价格和波动率, $x'$ 和$y'$ 分别代表$\tau = 0$ 时有价证券的价格和波动率. 在$\tau = 0$ 时, 定价核用狄拉克δ函数(Dirac delta function)表示为$t \leqslant T$ 时, 由Feynman-Kac公式得看涨期权的价格为$g\left( {x',y'} \right)$ 为贴现到时间t 的支付函数, $C\left( {\tau ;x,y} \right)$ 为看涨期权在时间t 的价格, 则终值条件为$C\left( {0,x',y'} \right) = g\left( {x',y'} \right)$ .H 的本征函数. 为此, 在对角化的哈密顿量H 中引入动量作为基矢, 这可以简单地使用狄拉克函数和傅里叶变换得到,$\left\langle {x}| {p} \right\rangle = {{\rm{e}}^{{\rm{i}}px}}$ , $\left\langle {p}| {{x'}} \right\rangle = {{\rm{e}}^{ - {\rm{i}}px'}}$ , 得$\left| p \right\rangle $ 的完备性方程为τ 拆成许多更小的时间段ε , 估计${{\rm{e}}^{ - \varepsilon H}}$ , 并把这些更小时间段内的所有估计得到的矩阵${{\rm{e}}^{ - \varepsilon H}}$ 进行连乘运算, 这在概率论上相当于把所有可能的运动路径的概率考虑进去, 因此费曼路径积分可以考虑所有可能的运动路径, 这就为将费曼路径积分应用于期权定价以得到更为精确的期权价格提供了理论支撑. 为了分析的简便, 假设将τ 拆分成N 个相同的ε , 则$\tau = N\varepsilon $ , 令$N \to \infty $ , 则$\varepsilon \to 0$ , 则$J =\displaystyle\int_{ - \infty }^{ + \infty } {{\rm{d}}x\left| x \right\rangle } \left\langle x \right|$ 对每个${{\rm{e}}^{ - \varepsilon H}}$ 矩阵进行对角化, (18 )式变为${x_N} = x$ , ${x_0} = x'$ .$L\left( {{x_i};{x_{i - 1}};\varepsilon } \right)$ 即为系统的拉格朗日量(Lagrangian), 作用量(Action)为${N_i}\left( \varepsilon \right)$ 与积分变量${x_i}$ 是独立的, 这种情形下, 归一化的常数${N_i}\left( \varepsilon \right)$ 可以忽略不计, 此时$N \to \infty $ , 并由边界条件可以得到连续时间下的费曼路径积分,22 )式即为定价核的费曼路径积分形式.3.随机波动率费曼路径积分股指期权定价模型构建 23.1.随机波动率分布形式设定 3.1.随机波动率分布形式设定 1987年, Scott[28 ] 提出波动率可能服从均值回复过程, 并用蒙特卡罗模拟算出了期权价格的数值解. 1989年, Merville和Pieptea[29 ] 使用S&P 500指数期货看涨期权进行研究, 并给出了市场波动率服从带噪声均值回复过程的证明. 1993年, Heston[27 ] 假定即期资产在时间t 服从几何布朗运动,$V\left( t \right)$ 是方差, ${\rm{d}}{W_1}\left( t \right)$ 是维纳过程, 假定波动率服从形如Stein和Stein[30 ] 提出的均值回复过程, 并借鉴Cox等[31 ] 1985年提出的平方根过程, 得到方差服从平方根过程,$V\left( t \right) = {\sigma ^2}\left( t \right)$ , θ 是方差的长期均值, α 是均值回复速度, ξ 是反映方差过程的波动率, ${\rm{d}}{W_1}$ 和${\rm{d}}{W_2}$ 为相关系数为ρ 的高斯白噪声.[27 —31 ] . 因此, 本文采用Heston的平方根过程刻画方差的运动过程.3.2.随机波动率费曼路径积分股指期权定价模型 -->3.2.随机波动率费曼路径积分股指期权定价模型 由于红利支付会使得股指的实际价值减少, 借鉴Shreve在《金融随机分析》[32 ] 关于连续支付股息的股价模型, 取股指模型为q 为股息率, 为分析的简便, 假定股息率为常数; $V\left( t \right) = {\sigma ^2}\left( t \right)$ ; μ 为股指的期望收益率, θ 是方差的长期均值, α 是均值回复速度, ξ 是反映方差过程的波动率, $\mu,\alpha,\theta,\xi $ 均为常数; ${\rm{d}}{W_1}$ 和${\rm{d}}{W_2}$ 为相关系数为ρ 的高斯白噪声. 由二次变分原理得, ${\left( {{\rm{d}}I} \right)^2} = {I^2}V{\rm{d}}t$ , ${\left( {{\rm{d}}V} \right)^2} = {\xi ^2}V{\rm{d}}t$ , ${\rm{d}}I{\rm{d}}t = {\rm{d}}V{\rm{d}}t = 0$ , ${\rm{d}}I{\rm{d}}V = \rho \xi IV{\rm{d}}t$ .λ , 根据风险中性定价原理, 股指的期望收益率μ 等于无风险利率r , 由Black和Scholes及Merton指出的任意资产价格满足的偏微分方程[27 ] , 可得$I = {{\rm{e}}^x}$ , $V = {{\rm{e}}^y}$ , 则$x = \ln I$ , $y = \ln V$ , $ - \infty < x < + \infty $ , $ - \infty < y < + \infty $ , 则${H_{{\rm{SV}}}}$ 如下:$\left\langle {x}| {p} \right\rangle = {{\rm{e}}^{{\rm{i}}px}}$ , $\left\langle {y}|{p} \right\rangle = {{\rm{e}}^{{\rm{i}}py}}$ , 可将(28 )式转化为量子场论下的哈密顿量,$\varepsilon \to 0$ 时, $\mathop {\lim }\limits_{\varepsilon \to 0} \left\langle {{x_i},{y_i}} \right|{{\rm{e}}^{ - \varepsilon {H_{{\rm{SV}}}}}}\left| {{x_{i - 1}},{y_{i - 1}}} \right\rangle = {\text{δ}}( {x_i} - $ ${x_{i - 1}}){\text{δ}}\left( {{y_i} - {y_{i - 1}}} \right) + o\left( \varepsilon \right) $ . 作用量为${L_{{\rm{SV}}}}$ 的公式可知, ${A_{{\rm{SV}}}}$ 是${x_i}$ 的二次型和${y_i}$ 的非线性函数, 因此原理上可以精确地对股指价格${x_i}$ 进行路径积分,$ Q = \displaystyle\int {DX{{\rm{e}}^{{A_x}}}},$ ${x_i} = {z_i} - \varepsilon \displaystyle\sum\nolimits_{j = 1}^i {{c_j}} $ , ${\rm{d}}{x_i} = {\rm{d}}{z_i}$ , $i = 1,$ $2, \cdots,N-1,$ 由原边界条件: ${x_0} = x'$ , ${x_N} = x$ , 得新边界条件为${z_0} = x'$ , ${z_N} = x + $ $\varepsilon \displaystyle\sum\nolimits_{j = 1}^N {{c_j}} $ ,$V\left( t \right)$ 相关, 基于风险中性的分析框架下, 投资者不要求风险补偿, 令$\lambda = 0$ . 则, 随机波动率下费曼定价核的解为${A_1}$ 是$DX$ 路径积分的结果.$x'$ 的所有可能取值范围内进行积分, 可得欧式股指看涨期权价格为38 )式. 费曼定价核包含了从时间T 到t 的股指的所有价格可能运动路径的信息, 是风险中性条件下股指期权定价的条件概率. 从费曼路径积分原理以及随机波动率费曼路径积分股指期权定价模型的推导过程可以看到, 随机波动率下的费曼定价核是股指价格以及方差从时间T 到t 的所有可能运动路径的总的几率幅. 从(38 )式可以看到, 费曼路径积分股指期权定价模型的核心在于求解随机波动率定价核${p_{{\rm{SV}}}}$ .4.基于恒指期权的实证研究 由于沪深300股指期权的仿真交易不够活跃, 数据存在诸多异常值, 不适合做实证研究. 鉴于沪港通和港股通的相继实施, 香港金融市场与上海金融市场之间的相关性越来越明显, 因此, 本文采用恒生指数期权的历史数据进行实证研究.4.1.样本数据选取及数据来源 4.1.样本数据选取及数据来源 为检验模型预测效果, 以2016年1月1日至2018年11月9日为样本内数据, 以2018年11月10日至2018年12月23日为样本外数据. 本文预测30 d的价格, 主要是考虑到有些期权即将到期, 其时间价值的衰减速度随着到期日的临近逐渐加快, 这会对定价产生非常大的影响. 为分析模型效果, 将Heston模型作为对照组, 所有参数和市场数据都一致.x 的代理变量, 并以方差的对数作为y 的代理变量. 考虑到历史波动率的不足, 本文采用指数移动加权平均模型(exponential weighted moving average, EWMA)重新计算方差. 以香港银行同业拆借利率(Hongkong inter bank offered rate, HIBOR)作为无风险利率的代理变量. 恒指日收盘价、恒指股息率、香港银行同业拆借利率HIBOR、恒指期权日收盘价数据均来自Wind金融终端.4.2.模型的参数估计 -->4.2.模型的参数估计 由于传统参数估计方法需要的前提条件较多, 且随机波动率模型中存在不可观测变量, 模型的似然函数涉及高维积分[33 ] , 马尔可夫链蒙特卡罗模拟方法(Markov chain Monte Carlo, MCMC)较传统的参数估计方法而言, 在尽量纳入市场数据的同时可以免去似然函数的推导过程. 对于某个分布${\text{π}}\left( \theta \right)$ , 一般情况下, 无论初始状态${\theta _0}$ 取何种分布, 在经过足够的迭代次数后, 马尔可夫链将逐渐忽略其初始状态, 基于细致平衡条件(detailed balance condition)[34 ] ${\theta _n}$ 将收敛到平稳分布. 因此, 本文将采用易于实现的MCMC参数估计方法, 运用Winbugs软件进行参数估计.$\sigma _n^2 = \left( {1 - w} \right)\displaystyle\sum\nolimits_{i = 1}^l {{w^{i - 1}}u_{n - i}^2 + {w^l}\sigma _{n - l}^2} $ , 其中, $\sigma $ 为波动率, u 为变化率, w 为介于0与1之间的某一常数. 当l 很大时, ${w^l}\sigma _{n - l}^2$ 项趋于零, 而对应于u 的权重以w 速度递减)对价格的连续性要求较弱. 鉴于摩根在1994年发表的RiskMetrics数据中采用$w = 0.94$ , 并且研究表明这一权重所预测得到的方差与实际方差非常接近. 因此, 本文取权重为$w = 0.94$ , 时间窗口为$l = 150$ , 计算恒指收盘价自1964年7月31日至2018年12月21日的方差, 作为恒指方差的代理变量. 以所有计算得到的方差的均值作为方差的长期均值的代理变量, 可得$\theta =0.0857$ . 虽然从方差的历史走势(见图1 )来看, 有不少方差数值较大, 但均迅速调整到较小的值.图 1 EWMA模型得到的日方差图Figure1. Daily variance diagram from EWMA modelα , ξ , ρ . 令$x\left( t \right) = $ $ \ln I\left( t \right)$ , (25 )式经伊藤引理变换, 并进行欧拉离散化后, 得${Z_1},{Z_2}$ 均服从标准正态分布. 假设$\alpha \sim $ $N\left( {5.5,0.01} \right)$ , $\rho \sim \varGamma \left( {2.5,0.1} \right)$ , $\xi \sim N\left( {1,0.0625} \right)$ . 为了获取稳定的参数估计结果, 本文通过设置两组初始值形成两个迭代链, 迭代100000次, 并舍弃前4000次迭代值, 通过观察各参数的核密度图(见图2 )均呈单峰情形, 可见参数估计结果是稳定的.图 2 核密度图Figure2. Kernel density.表1 , α , ρ , ξ 参数估计结果依次为3.393, 0.4201, 1.574.Node Mean sd MC error Quantile Start Sample 2.50% 50% 97.50% α 3.393 0.1539 0.001499 3.082 3.395 3.685 4001 192000 ρ 0.4201 0.2032 0.007068 0.09408 0.4011 0.8774 4001 192000 ξ 1.574 0.07977 8.65 × 10–4 1.416 1.574 1.73 4001 192000
表1 参数估计结果Table1. Parameter estimates.$\theta =0.0857$ , $\alpha = 3.393$ , $\rho = 0.4201$ , $\xi = 1.574$ . 接下来, 本文将基于该组参数进行价格预测.4.3.费曼路径积分股指期权定价模型的算法设计 -->4.3.费曼路径积分股指期权定价模型的算法设计 令$y = \ln V$ , 则(25 )式的方差的平方根过程由伊藤引理可得40 )式进行欧拉离散化, 可得$Z \sim N\left( {0,1} \right)$ , ${\text{δ}}{y_i} = {y_i} - {y_{i - 1}}$ , 由于$\tau =T - t$ , 而预测的是t 时刻的期权价格, 所以, 时间步长为$ - \varepsilon $ . 由此可见, ${\text{δ}}{y_i}$ 为正态随机变量, 并且其均值为$\varepsilon {{\rm{e}}^{ - {y_i}}}\left[ { - \alpha \left( {\theta - {{\rm{e}}^{{y_i}}}} \right) + \dfrac{{{\xi ^2}}}{2}} \right]$ , 方差为${\xi ^2}{{\rm{e}}^{ - {y_i}}}\varepsilon $ , 且其概率密度函数的表达式如下:Y 为由变量${y_i}$ 构成的数组, 因此Y N 维矩阵, 则其概率密度函数为44 )式可以看到, 概率密度函数$p\left( {{Y}} \right)$ 虽然看起来较为复杂, 但其实质为${y_i}$ 随机游走的概率分布.$ {p_{{\rm{SV}}}}\left( {x,y,\tau ;x'} \right) = p\left( {{Y}} \right) \cdot g\left( {{Y}} \right)$ , 则$ {\rm D}Y = {\rm{d}}{y_0} \displaystyle\prod \limits_{i = 1}^{N - 1} \dfrac{{{\rm{d}}{y_i}}}{{\xi \sqrt {2{\text{π}}\varepsilon } }}.$ 图3 所示, 将剩余到期日平均地分成N 个ε , 对应地插入$N - 1$ 个隔板, 在每个隔板上随机地取尽可能多的点(图中只呈现了8个点). 在每个隔板上随机地各取一个点相连接起来, 即可生成一条路径, 如图3 中有3条相互独立的路径. 可见, 我们无法知道具体的路径走势, 唯一可以确定的是, 根据大数定律得到的在每个隔板上所有随机点的平均值. 在费曼路径积分中, 假定每条路径都是等可能的, 那么对于模拟得到的所有的${y_i}$ 可以由大数定律得到确定的均值. 基于此, 本文在算法设计上做了简化处理: 路径的随机生成是无法预知的, 但可以确定的是在每个预测点的逼近的均值, 而这个均值是所有可能的路径共同决定的结果, 因此可以得到取均值后的费曼定价核.图 3 路径图Figure3. Path diagram.[35 ] 指出, 在路径积分期权定价中, 时间步长不宜过小. 为此, 借鉴其做法, 步数设为N = 128步, 时间步长$\varepsilon = {\tau / {128}}$ , 其中τ 为剩余交易日.${\text{δ}}{y_i}$ 的分布已知为正态分布, 因此可以用蒙特卡罗模拟在每个时间步长各模拟10000个${\rm{\delta }}y$ 的值, 并分别取均值得到$\overline {{\text{δ}}{y_1}},\overline {\;{\text{δ}}{y_2}},\;\overline {{\text{δ}}{y_3}}, \cdots,\overline {{\text{δ}}{y_N}} $ , 则$y' = {y_t} + \sum\limits_N {\overline {{\rm{\delta }}{y_i}} } $ , 其中, ${y_t}$ 为EWMA模型所得的方差的对数.$g\left( {{Y}} \right) \!=\! \dfrac{{{{\rm{e}}^{{A_1}}}}}{{\sqrt {2{\text{π}}\varepsilon ( 1 \!-\! \rho^2)\displaystyle\sum\limits_{i = 1}^N {{{\rm{e}}^{{y_i}}}} } }}, $ $p_{\rm SV}(x,y,\tau ;x')$ $= p\left( {{Y}} \right)g\left( {{Y}} \right)$ (注: $p\left( {{Y}} \right)$ 在前面的讨论中已经说明其实质为${y_i}$ 随机游走的概率分布, 本文基于此做蒙特卡罗模拟, 得到${y_i}$ 并代入$g\left( {{Y}} \right)$ 以得到$g\left( {{Y}} \right)$ 的值, 因此无需计算$p\left( {{Y}} \right)$ 的值).$\displaystyle\int_{\ln K}^{ + \infty } {{p_{{\rm{SV}}}}\left( {x,y,\tau ;x'} \right) ( {{{\rm{e}}^{x'}} - K} )} {\rm{d}}x'$ , 由于该期权价格是无穷积分形式, 不能由计算机直接求出数值解, 通过将积分方程离散化, 在$x'$ 的可能取值范围内(本文取$\left[ {1,15} \right]$ , e与${{\rm{e}}^{15}}$ 之间相差超过120万倍, 就市场数据来说该区间范围可以包含市场上所有可能极端情形), 求曲线${p_{{\rm{SV}}}}\left( {x,y,\tau ;x'} \right) \times $ $\max \big[ {( {{{\rm{e}}^{x'}} - K} ),0} \big] $ 的面积, 即可得到期权价格.4.4.基于算法设计的模型效果比较 -->4.4.基于算法设计的模型效果比较 34.4.1.相同到期日不同执行价格下的价格预测 -->4.4.1.相同到期日不同执行价格下的价格预测 在到期日均为2019年3月时, 从图4 至图6 可以看到, 不论是实值期权(K < 25800)、平值期权(K = 25800)还是虚值期权(K > 25800), 费曼路径积分股指期权定价模型与Heston模型都能较好地刻画市场价格的走势. 但是, 从定价精度来看, 费曼路径积分股指期权定价模型对于市场价格的拟合曲线都较Heston模型更为准确.图 4 实值期权(以K = 25200为例)Figure4. In-the-money option (K = 25200 as an example).图 6 虚值期权(以K = 26400为例)Figure6. Out-of-the-money option (K = 26400 as an example).4.4.2.相同执行价格不同到期日下的价格预测 -->4.4.2.相同执行价格不同到期日下的价格预测 由于平值期权的交易更为活跃, 对其进行价格预测更具有应用价值. 因此, 本文采用执行价格为25800的平值期权, 对到期日分别为2019年2月、2019年3月、2019年6月、2019年9月的恒指期权, 进行价格预测. 为了保持前后对比的一致性, 仍然以2018年11月10日至2018年12月23日为样本外数据, 预测恒指期权30天的价格. 由于到期日不同, 剩余到期日也发生了改变, 本文在实证的基础上发现步数取128步的时候模型是较为稳定的, 这与Baaquie等[35 ] 2000年的研究结果一致. 通过调整对应的时间单位长度, 发现在时间步长为0.001—0.002时, 模型的预测效果较好.图7 )、2019年3月(图5 )、2019年9月(图8 )时, 费曼路径积分股指期权定价模型的定价精度明显较Heston模型更为精确. 在到期日为2019年6月(图9 )的时候, 两种模型的定价效果基本持平.图 7 到期日为2019年2月时两模型的平值期权价格对比图Figure7. A comparison of the two models with maturity date of February 2019图 5 平值期权(K = 25800)Figure5. At-the-money option (K = 25800 as an example).图 9 到期日为2019年6月时两模型的平值期权价格对比图Figure9. A comparison of the two models with maturity date of June 2019图 8 到期日为2019年9月时两模型的平值期权价格对比图Figure8. A comparison of the two models with maturity date of September 2019.4.5.稳健性检验 -->4.5.稳健性检验 为进一步增强实证结果的说服力, 接下来对随机波动率下费曼路径积分股指期权定价模型以及Heston模型的股指期权定价效果进行稳健性检验. 本文使用均方根误差(root mean squared error, RMSE)和Theil不等系数(Theil inequality coefficient)两个评价指标对这两个模型的定价效果进行评价. 两个评价指标的计算公式分别为(47 )和(48 )式.图10 以及图11 可以直观地看到在期权到期日为2019年3月时, 不论是实值期权(K < 25800)、平值期权(K = 25800)还是虚值期权(K > 25800), 费曼路径积分股指期权定价模型的RMSE及Theil不等系数都较Heston期权定价模型来得低. 可见, 在相同到期日不同执行价格下, 费曼路径积分股指期权定价模型在价格预测上较Heston模型有了明显的改进.图 10 相同到期日不同执行价格下两种模型的RMSE对比图Figure10. RMSE for the two models on the same due date.图 11 相同到期日不同执行价格下两种模型的Theil不等系数对比图Figure11. Theil inequality coefficients for the two models on the same maturity date.表2 评价指标值可以看到, 在到期日为2019年6月时, 费曼路径积分股指期权定价模型与Heston模型的RMSE与Theil不等系数差别不大, 但在其他到期日下, 费曼路径积分股指期权定价模型的评价指标值都远小于Heston模型. 可见, 费曼路径积分股指期权定价模型显著较Heston模型准确.到期日 RMSE Theil不等系数 费曼路径积分 Heston 费曼路径积分 Heston 2019年2月 113.1631 269.8452 0.0429 0.1138 2019年3月 118.0685 282.0939 0.0401 0.1037 2019年6月 94.7388 87.9670 0.0275 0.0259 2019年9月 88.4829 230.9288 0.0230 0.0584
表2 K = 25800下两种模型不同到期日下的评价指标值Table2. K = 25800, the evaluation index values of the two models under different maturity dates.5.结 论 从以上研究可以看到, Heston模型仍然是基于传统的BS模型的思路, 结合特征函数法求解原本BS模型中的$N\left( {{d_1}} \right)$ 与$N\left( {{d_2}} \right)$ , 其所求期权价格的闭式解基于复杂的偏微分方程求解过程. 而本文所构建的随机波动率股指期权定价模型仅由费曼定价核和支付函数的无穷维积分形式构成, 费曼定价核包含了股指期权定价所需的全部信息, 通过本文的实证研究, 发现该定价核的数值解容易通过计算机运行模拟得到. 相比于Heston模型而言, 不需要其他的边界条件. 本文提出的模型, 核心在于求解费曼定价核, 本文基于费曼路径生成原理与大数定律的关系, 运用Matlab模拟得到均值定价核, 可以大大优化股指期权价格的求解过程. 基于恒指期权的实证结果表明, 在相同到期日下, 不论是实值、平值还是虚值期权, 费曼路径积分股指期权定价模型在定价精度上显著优于Heston模型. 在平值期权下, 对不同到期日的期权进行价格预测, 费曼路径积分股指期权定价模型仍然较Heston模型来得精确. 可见, 随机波动率费曼路径积分股指期权定价模型在价格预测上是稳健的, 并且可以带来较好的预测效果.$x'$ 进行离散化处理, 求均值定价核与支付函数的乘积的曲线面积以得到期权价格的数值解, 从而优化了期权价格计算过程, 并大大提高了股指期权的定价精度. 








































































































































 图 1 EWMA模型得到的日方差图
图 1 EWMA模型得到的日方差图






 图 2 核密度图
图 2 核密度图


















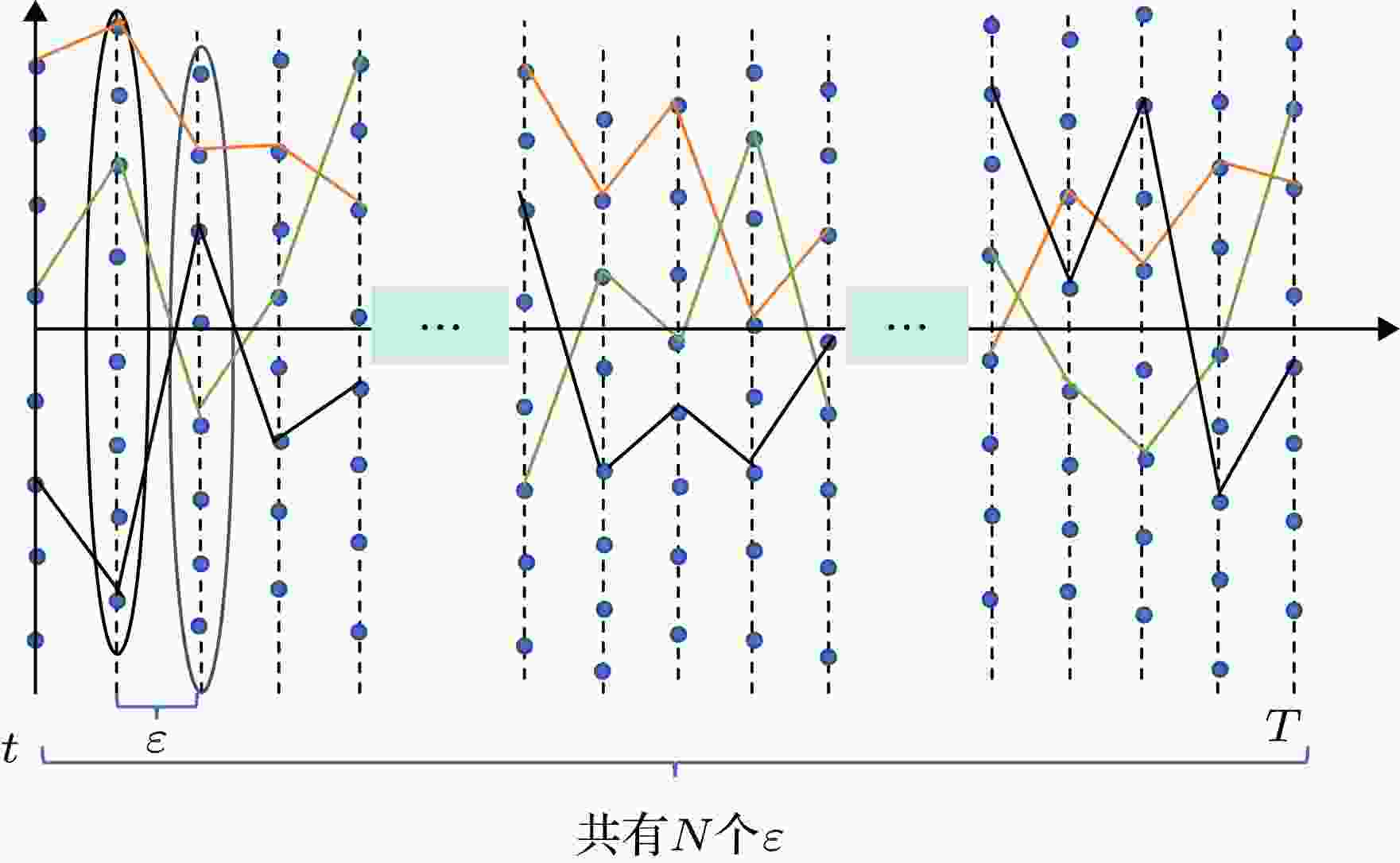 图 3 路径图
图 3 路径图


























 图 4 实值期权(以K = 25200为例)
图 4 实值期权(以K = 25200为例) 图 6 虚值期权(以K = 26400为例)
图 6 虚值期权(以K = 26400为例) 图 7 到期日为2019年2月时两模型的平值期权价格对比图
图 7 到期日为2019年2月时两模型的平值期权价格对比图 图 5 平值期权(K = 25800)
图 5 平值期权(K = 25800) 图 9 到期日为2019年6月时两模型的平值期权价格对比图
图 9 到期日为2019年6月时两模型的平值期权价格对比图 图 8 到期日为2019年9月时两模型的平值期权价格对比图
图 8 到期日为2019年9月时两模型的平值期权价格对比图 图 10 相同到期日不同执行价格下两种模型的RMSE对比图
图 10 相同到期日不同执行价格下两种模型的RMSE对比图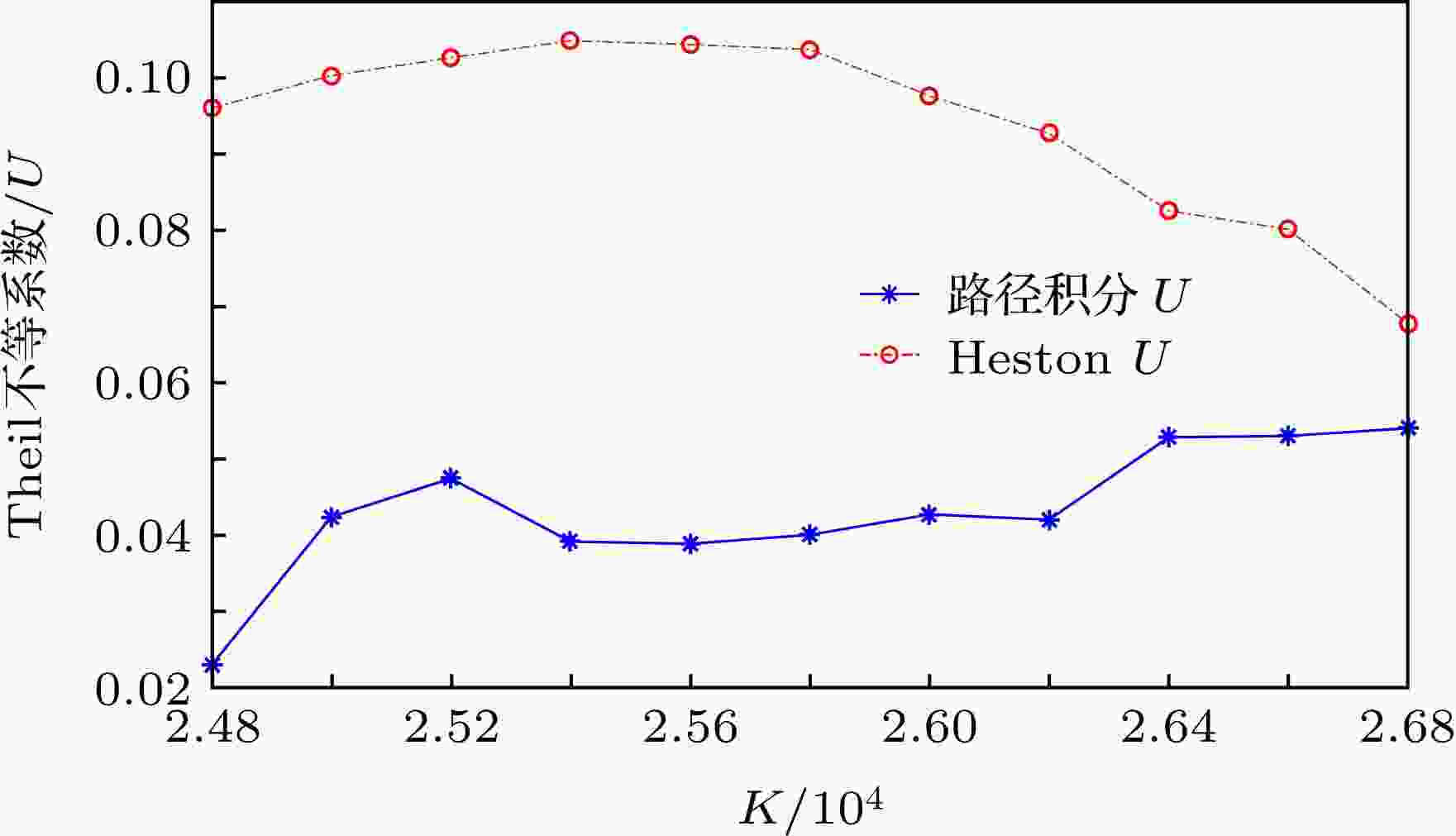 图 11 相同到期日不同执行价格下两种模型的Theil不等系数对比图
图 11 相同到期日不同执行价格下两种模型的Theil不等系数对比图


