摘要:采用密度泛函理论下的广义梯度近似方法对团簇TM@Cu₁₂N₁₂ (TM = Mn,, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt)的结构稳定性、磁性及磁各向异性能进行了系统的理论研究. 发现由于TM—Cu 和 Cu—N键的出现, 不同过渡金属原子(TM)掺杂二十面体Cu₁₃N₁₂ (ICO)团簇的中心原子可以有效提高TM@Cu₁₂N₁₂的稳定性; N原子的加入使Cu团簇的磁性显著提高, 且不同的TM掺杂有效改善了Cu团簇内部的磁性环境; 3d原子的掺杂使团簇的磁性得到进一步提升, 4d, 5d原子的掺杂虽对提高团簇轨道磁矩无明显效果, 但Rh和Pt原子的掺入使其磁各向异性能显著增大, 提高了团簇的磁稳定性. 结果表明对TM@Cu₁₂N₁₂的掺杂改性基本可以达到磁性调控目的.
关键词: 密度泛函理论/
几何结构/
磁性/
磁各向异性能

English Abstract

全文HTML

--> --> -->

稀磁半导体(dilute magnetic semiconductors, DMSs), 是一种新型的磁性半导体材料, 它同时利用了电子的电荷和自旋属性, 兼具铁磁性能和半导体性能, 在自旋电子器件领域有着重要的研究价值, 受到研究人员的广泛追捧^[1,2]. 研究人员在室温下很难获得具有半导体可调控特性的铁磁材料, 使其发展之路变得一波三折, 但研究人员对DMS的研究从未间断. 2003年, Baik等^[3]在实验上将3d过渡金属Mn原子掺入GaN半导体中发现了具有磁性的DMS, 但在实验过程中也发现在产生DMS的同时产生了Mn团簇, 此外还有一些Ga-Mn, Mn-N相的生成, 不利于DMS磁性的测定, 对DMS的磁性大小和实际应用产生影响^[4]. Cr原子掺入的结果也不尽如人意, 虽然实验过程中没有产生类似于Mn原子掺入的结果, 但掺入GaN后的Cr原子磁性远小于其孤立原子状态, 磁矩在0.2μ_B—1.8μ_B之间徘徊, 表明Cr掺入GaN后的磁矩分布并不均匀^[5,6], 进一步的理论研究证明, Cr原子掺入GaN半导体中易形成Cr-N团簇, 团簇内部原子间呈现不同程度的反铁磁性耦合, 不利于产生理想的DMS材料^[7]. 为改善上述磁性物质易聚集沉积和磁性分布不均匀问题, 研究人员考虑用本身不具有磁性的过渡金属进行半导体材料掺杂. Buchholz等^[8]用Cu原子掺入ZnO后实现了室温下的铁磁性, 而Cu原子之间相互作用产生的Cu团簇沉积也不会对DMS的磁性产生影响, Cu原子成为研发DMS过程中所需的较为满意的3d过渡金属. 随后, 文献[9,10]将Cu原子应用到GaN半导体的掺杂实验中, 也获得了较为满意的结果, Cu的掺入使其产生了高于室温的铁磁性. 最近, 为研究Cu-N结构稳定铁磁态的产生原因, Wu等^[11]应用Cu原子取代GaN中的一个Ga, 对Cu原子及其周围的N原子形成的CuN₄团簇进行理论研究, 发现Cu-N原子间的p-d轨道杂化是结构产生磁性的主要原因. N, Cu原子间轨道杂化所产生的电子转移使得原来不具有磁性的Cu原子产生了自旋极化. 反观Cu团簇, Cu由于充满的3d闭壳层电子构型(3d¹⁰4s¹), 其体材料具有非磁性特征, Cu团簇随尺寸增大总磁矩呈现奇偶振荡, 在掺入Fe, V, Pt等过渡金属原子后磁矩主要由掺杂原子提供, 团簇磁矩有所增大但增幅并不明显^[12—14]. 是否可将Cu团簇氮化使其产生巨磁效应? 基于以上实验和理论基础, Datta等^[15]对氮化Cu团簇进行理论研究, 证明了以上猜想, 并得出在Cu团簇外层的每个Cu原子上加一个N原子是氮化铜团簇最稳定的构型; 且对于实验上比较容易生成的Cu₁₃团簇而言, 氮化过程使团簇结构发生了重排, 基态具有扣状双层结构(buckled bi-planar, BBP)的Cu₁₃团簇氮化后更易形成稳定的二十面体笼(icosahedron, ICO), 且磁矩由原来的1μ_B增至29μ_B, 表现出巨磁效应.
目前对于此类团簇结构具高稳定性的原因、巨磁效应的产生原因以及团簇的磁稳定性尚不清楚. 为进一步对氮化铜团簇结构和磁性的全面理解, 我们选择TM@Cu₁₂N₁₂ (TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt)组建类二十面体团簇结构, 对其稳定性和磁性演变进行理论研究, 揭示不同掺杂原子对其磁性影响的物理机制, 促进该聚合材料在磁性存储、催化和生物医疗等领域的功能化应用; 同时, 由Cu掺杂GaN产生稀磁半导体演变而来的Cu-N团簇磁性研究可再次回归至DMS的研发中, 进一步促进该类DMS磁性起源的理解.

本节涉及的所有计算都基于密度泛函理论, 使用VASP软件包完成. 电子交换关联泛函选取广义梯度近似下的Perdew-Burke-Ernzerhof (GGA-PBE)函数, 并应用投影缀加平面波(projector-augmented wave, PAW)方法处理Kohn-Sham方程. 将Cu/TM原子的3d和4s电子以及N原子的2s, 2p电子作为价电子进行计算. 在计算过程中团簇结构将始终置于15 ? × 15 ? × 15 ?的超胞中以确保与其相邻原胞间的相互作用可忽略不计. 同时设置K点为布里渊区原点(Γ点), 平面波截断能选取600 eV. 应用共轭梯度近似(conjugate gradient)在不约束对称性的情况下对团簇的初始结构进行优化, 设置能量收敛标准10^–4 eV, 原子力的收敛标准(EDIFFG)设置为–0.005 eV/?. 计算过程中涉及自旋-轨道耦合作用(spin-orbit coupling, SOC)对结构磁性的影响, 分别进行了线性和非线性的磁性计算. 在GGA线性计算中, 充分考虑了结构所有可能的自旋多重度, 已确定最稳定结构拥有的自旋磁矩. 在此基础上, 将优化好的最稳定结构固定不动, 进行SOC计算, 结构的初始磁矩被分别指定为x, y, z, 三个不同的方向, 以确定不同结构具有的磁各向异性和磁各向异性能(magnetic anisotropy energy, MAE).
考虑到TM@Cu₁₂N₁₂ (TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt)体系中含有较强的d电子间相互关联作用的4d, 5d原子, 我们将库仑相互作用U加入其中. 本文中不同原子采用的U (U_eff)值均为LDAUU与LDAUJ的差值(U_eff = LDAUU – LDAUJ), 且均以其十三原子团簇所具有的U_eff值为标准. 结合文献, 现已得出Mn^[16], Fe^[17], Co以及Rh^[18]的十三原子团簇在保持其结构和总自旋磁矩不变的情况下, 可用的最大U值分别为0, 2.5, 1.0, 0.7 eV. 此外, 我们选择U值为0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 4.0及5.0 eV分别作用于Ni, Cu, Ru, Pd, Ir, Pt十三原子团簇的不同结构进行U_eff值测试(详见补充材料). 在此以Cu₁₃和Ru₁₃为例进行说明, 作为宿主团簇, 我们考虑了Cu₁₃团簇的BBP(在这里为Cu₁₃的基态结构, 记为GS), ICO以及双层简单立方(double simple cubic, DSC)和立方密排(cubic-closed packed, CCP)等结构的稳定性和自旋磁性变化. 如图1所示, 在U值达到2.5 eV时, 其基态BBP结构仍可保持最稳定状态, 而在不同的U值下, 基态结构始终保持Cu₁₃团簇固有的1μ_B磁矩, 所以我们最终选取U_eff = 2.5 eV作为Cu团簇的U值. 同样, 作为掺杂原子, Ru₁₃团簇中分别考虑了可能出现的DSC(GS), BBP以及ICO结构, 其中当U值达到2.5 eV时仍可保持基态结构为最稳定态, 而基态的磁矩在U_eff = 1.0 eV之后便脱离事实, 数据不可用, 因此将Ru团簇的U值定为1.0 eV. 依次类推, 我们得到了Ni, Cu, Ru, Pd, Ir, Pt十三原子团簇的U值分别为2.0, 2.5, 1.0, 2.0, 1.0, 0.5 eV. 在此基础上对团簇进行GGA + U和GGA + U + SOC计算.
图 1 利用GGA + U方法计算Cu₁₃和Ru₁₃团簇在设置不同U_eff值下拥有不同初始结构时的相对稳定性和总自旋磁矩
Figure1. Using GGA + U method to calculate the relative stability and total spin magnetic moment of Cu₁₃ and Ru₁₃ clusters with different initial structures under different U_eff values.

2

-->

3.1.TM@Cu₁₂N₁₂ (TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt)团簇的几何结构及稳定性

目前已有研究表明纯Cu₁₃团簇的稳定态呈BBP结构^[14,19,20], 若对其进行整体氮化, 最终的稳定构型将会发生明显变化^[15]. Datta等^[15]针对Cu₁₃N₁₂团簇考虑将Cu₁₃的初始结构设定为HBL, ICO以及BBP, 分别将表面用N原子均匀覆盖并进行结构优化. 结果表明, 以ICO结构的Cu₁₃团簇作为内核会使Cu₁₃N₁₂具有更强的稳定性. 在此基础上, 我们聚焦Cu₁₃N₁₂团簇的二十面体结构, 对其中心原子进行了替代掺杂, TM@Cu₁₂N₁₂ (TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt)团簇内部的金属原子总体仍保持二十面体构型, 除中心原子外, 二十面体表面的12个Cu原子被12个N原子均匀覆盖, 如图2所示. 对上述结构进行GGA + U优化后, 发现在优化过程中此类团簇保持构型不变的同时其对称性会明显降低(除Ir@Cu₁₂N₁₂外, 所有团簇均由原先设计的I_h点群降为C₁和C_s点群结构). 作为人为设计的团簇结构, 稳定性成为大家首先关注的问题. 表1中列出了包括纯Cu₁₃团簇在内的11个团簇的结合能(E_b)和杂化指数(h_kl), 其被分别定义为
图 2 Cu₁₃N₁₂和TM@Cu₁₂N₁₂(TM = Mn, Fe, Co, Ni, Ru, Rh, Pd, Ir, Pt)团簇结构图
Figure2. The geometry structures of Cu₁₃N₁₂ and TM@ Cu₁₂N₁₂ (TM = Mn, Fe, Co, Ni, Ru, Rh, Pd, Ir, Pt) clusters.

Clusters	Binding energy Eb/eV·atom–1	Hybridization index
		hsp	hsd	hpd	Htol
Cu13	1.50	0.06	0.21	0.14	0.40
Mn@Cu12N12	1.58	0.09	0.20	0.15	0.43
Fe@Cu12N12	1.58	0.12	0.21	0.17	0.50
Co@Cu12N12	1.62	0.10	0.19	0.16	0.45
Ni@Cu12N12	1.63	0.17	0.27	0.24	0.68
Cu13N12	1.56	0.12	0.20	0.19	0.51
Ru@Cu12N12	1.64	0.25	0.29	0.26	0.80
Rh@Cu12N12	1.67	0.21	0.28	0.25	0.74
Pd@Cu12N12	1.60	0.16	0.25	0.23	0.65
Ir@Cu12N12	1.70	0.22	0.30	0.23	0.75
Pt@Cu12N12	1.69	0.21	0.26	0.23	0.70

表1Cu₁₃以及TM@Cu₁₂N₁₂团簇的结合能(E_b)和杂化指数(H_kl)
Table1.The binding energies and hybridization index of Cu₁₃ and TM@Cu₁₂N₁₂ clusters.

$ \begin{split}{E_{\rm{b}}} = \; & [12E\left({{\rm{Cu}}} \right) + 12E\left({\rm{N}} \right) + E\left({{\rm{TM}}} \right)\\ & - E({\rm{TM}}@{\rm{C}}{{\rm{u}}_{12}}{{\rm{N}}_{12}})]/25,\end{split}$

${h_{kl}} = \mathop \sum \limits_{I = 1}^{25} \mathop \sum \limits_{i = 1}^{{\rm{occ}}} \omega _{i,k}^{\left({\rm{I}} \right)}\omega _{i,l}^{\left({\rm{I}} \right)}\;(k,l = {\rm{s}},{\rm{p}},{\rm{d}}),$

${H_{{\rm{tol}}}} = {h_{{\rm{sp}}}} + {h_{{\rm{sd}}}} + {h_{{\rm{pd}}}}.$

方程(1)中的E (Cu), E (N), E (TM)以及E (TM@Cu₁₂N₁₂)分别表示Cu原子, N原子, 过渡金属原子TM的能量以及TM@Cu₁₂N₁₂团簇的总能; (2)式中k, l分别表示s, p, d轨道; ${{\omega}} _{{{i}},{{k}}}^{\left({{I}} \right)}({{\omega}} _{{{i}},{{l}}}^{\left({{I}} \right)})$是指以原子I为中心, 在指定的原子球形半径内, 第i个Kohn-Sham轨道在s, p, d球形简谐波上的投影积分值^[21]. 从表1数据可知, 在众多团簇中, 作为目前公认的Cu₁₃的最稳定结构在此拥有 1.5 eV/atom的最小平均结合能, 为所有团簇中的最小值; 此外, 我们针对团簇结构中不同原子间价电子所处的s, p, d轨道的杂化情况分别进行了sp, sd以及pd轨道的杂化指数计算, 并将计算结果进行汇总, 得出不同结构总的杂化指数H_tol^[22]. 计算结果表明在Cu₁₃团簇表面覆盖N原子可效提高原子间轨道杂化程度, 并且随着中心原子的不断更替, 总的杂化指数(H_tol)持续变化, 但数值总体均高于纯Cu₁₃团簇. 结合Datta等^[15]的研究结果, 可以认为N原子的加入不仅使Cu₁₃团簇的结构改变, 而且使团簇稳定性明显提高.
而究其原因, 可归功于结构内部键种类的改变. 对纯Cu₁₃团簇而言, 原子间只成Cu—Cu键, 但在TM@Cu₁₂N₁₂ (TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt)中, 除Cu—Cu键外, 加入了大量Cu—N键, 且部分Cu—Cu键被TM—Cu键所取代. 对比结构中不同种类键长随中心原子的改变而呈现出的变化趋势可以看出Cu—N键的产生是决定结构稳定性的主要原因. 如图3(a)所示, 团簇的总杂化指数与Cu—N键长呈完美负相关, 随着Cu—N键长的缩短, 杂化指数逐渐增高, 团簇稳定性增强. 我们以Cu₂和CuN二聚体的成键情况为例来说明这个问题. 图3(b)中分别给出了Cu₂和CuN二聚体的最高已占轨道(HOMO)和最低未占轨道(LUMO)图, 不难看出, Cu₂的HOMO和LUMO是分别由两个dz²和两个s原子轨道形成的反键轨道. CuN二聚体的HOMO轨道是由N原子的p_z和Cu原子的s轨道形成的σ成键轨道, LUMO轨道为N原子的p_z和Cu原子的s轨道形成的σ反键轨道. 相比之下, 电子填入成键轨道会使结构具有更高的稳定性. 此外, 中心原子被不同的过渡金属取代, 部分Cu—Cu键被替换为TM—Cu键, 根据图4对于不同的二聚体结合能的计算结果可知, 图中列出的众多二聚体中, Cu—Cu二聚体的稳定性最差, 用更稳定的TM—Cu键替换Cu—Cu键也可使结构的稳定性有所提高. 外部以N原子覆盖对结构进行整体加固, 内部替换部分不稳定键对结构的稳定性加以辅助, 有效地说明该类二十面体结构设计的合理性.
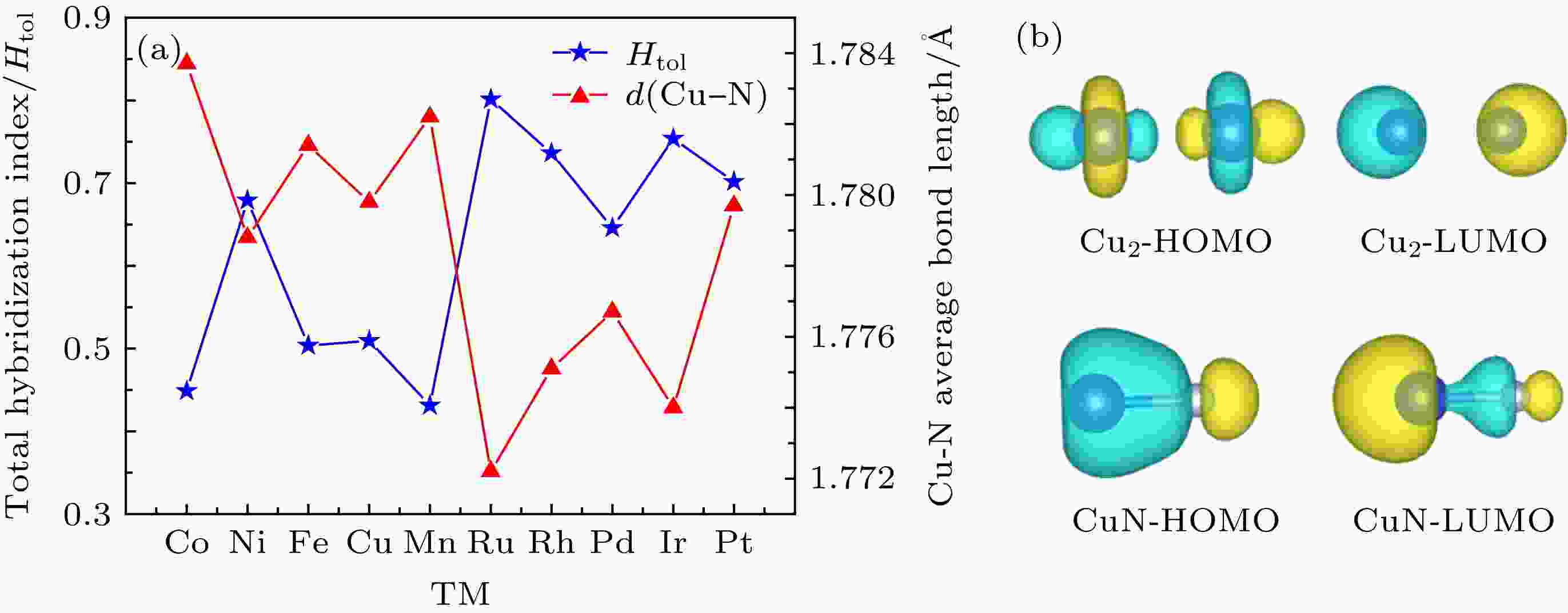图 3 (a) TM@Cu₁₂N₁₂总杂化趋势与平均Cu—N键长的关系; (b) Cu₂和CuN二聚体HOMO, LUMO图
Figure3. (a) The relationship between total hybridization index of TM@Cu₁₂N₁₂ and Cu—N average bond length in clusters; (b) the HOMO and LUMO of Cu₂ and CuN dimers.

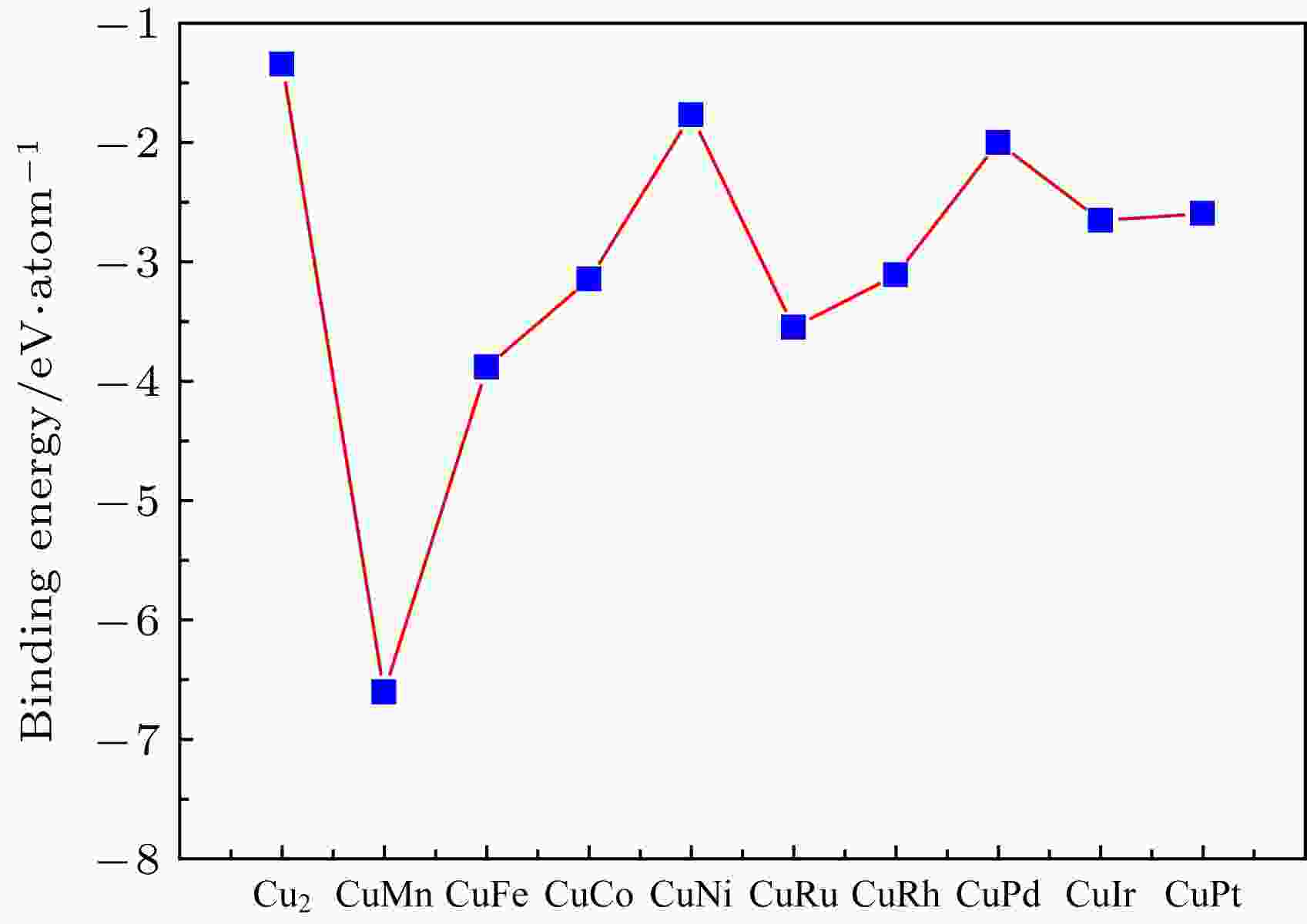图 4 Cu-TM (TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt)二聚体平均结合能
Figure4. The average binding energy of Cu-TM (TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt) dimers.

值得注意的是, 此类团簇的设计并不能为了调控其性质而随意改变内部掺杂原子的种类. 通过对团簇原子间距的进一步分析, 发现随着中心掺杂原子半径的逐渐增大, Cu原子与中心原子的距离随之增大, 中间层的Cu₁₂笼由于内部原子尺寸的增大而逐渐扩大, 导致Cu—Cu键被拉长(图5(a)); 同时, 经过测量最外层N原子与未成键Cu原子的距离(图5(b)), 可以看出Cu原子与N原子的间距要明显小于N原子与N原子的间距. 加之最外层N有较多的未配对电子, 极易与Cu原子成键, 进一步破坏人为设计的类二十面体笼状结构, 导致磁性猝灭. 这种现象在掺杂稀土原子时尤为明显, 对结构进行优化的结果显示类二十面体结构已经完全被破坏. 因此, 该类结构的设计并不适用于尺寸较大的原子掺杂.
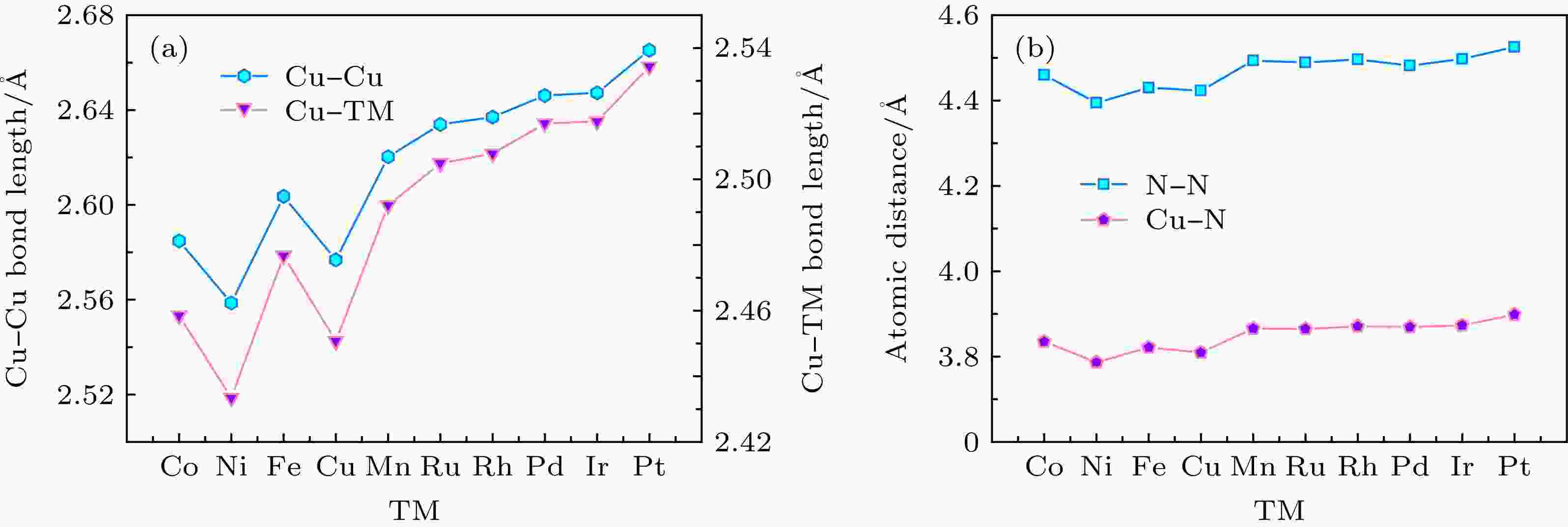图 5 (a) Cu—Cu, Cu—TM(TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt)键长; (b) 结构表面N—N, N—Cu原子间距
Figure5. (a) Bond lengths of Cu—Cu, Cu—TM (TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt); (b) atomic distance of N—N, N—Cu on cluster surface.

2 -->

3.2.TM@Cu₁₂N₁₂(TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt)团簇的自旋磁矩

通过对Cu₁₃N₁₂团簇的研究, Datta等^[15]指出, 相比于纯Cu₁₃团簇1μ_B的磁矩而言, 氮化后的Cu₁₃N₁₂磁矩可达29μ_B, 磁性显著提高. 究其原因, Cu₁₃表面的N原子(平均局域磁矩可达1.4μ_B)为团簇提供了主要磁矩; 与此同时, Cu原子的部分电子转移至表面N原子, 原本排满的d轨道产生孤电子, 进而产生0.25μ_B的平均原子磁矩; 此外, N原子与Cu原子的磁矩呈铁磁性耦合, 致使团簇磁矩显著增大, 产生巨磁效应^[15]. 而在本节中, 我们将结构中心Cu原子用TM(Mn, Fe, Co, Ni, Ru, Rh, Pd, Ir, Pt)原子替代, 对团簇磁性的调控进行进一步讨论.
图6(a)给出了TM@Cu₁₂N₁₂(TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt)团簇的总磁矩. 不难发现, 当中心原子为Mn, Fe, Co时, 团簇的磁矩明显高于Cu₁₃N₁₂的29μ_B, 分别达到35μ_B, 32μ_B和33μ_B, 而替换为Ni, Ru, Rh, Pd, Ir, Pt时磁矩明显降低, 分别为24μ_B, 11μ_B, 15μ_B, 20μ_B, 15μ_B和22μ_B, 但仍远高于Cu₁₃团簇所拥有的磁矩值1μ_B. 通过分析结构自旋密度可知, N原子间和Cu原子间的反铁磁耦合是造成部分团簇磁矩降低的最直接原因. 如图7所示, 与Cu₁₃N₁₂相同, TM@Cu₁₂N₁₂(TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt)团簇的磁矩主要还是来自于表面N原子, 对于具有较小磁矩的TM@Cu₁₂N₁₂(TM = Ni, Ru, Rh, Pd, Ir, Pt)团簇而言, 其内部部分N原子之间和与之相连的Cu原子之间存在不同程度的反铁磁耦合现象, 致使团簇磁矩降低. 而这与团簇的结构, 特别是Cu—N键的变化有密切关系. 图6(b)给出了不同团簇的平均Cu—N键长, 显然, 与团簇的磁矩变化呈现明显正相关, 且当Cu—N键长小于1.78 ?(Cu₁₃N₁₂团簇的平均Cu—N键长)时, 团簇内部出现反铁磁态, 进而影响团簇总体磁矩. 具体到一个团簇中也是如此, 反铁磁态总是出现在具有较小Cu—N键长的Cu原子和N原子上. 而对于Cu—N键长与反铁磁之间的关系, 还需进一步分析团簇内部的电子分布状态.
图 6 (a) TM@Cu₁₂N₁₂团簇总磁矩; (b)团簇内部Cu—N平均键长
Figure6. Total magnetic moments (a) and average Cu—N bond lengths (b) of TM@Cu₁₂N₁₂ clusters.

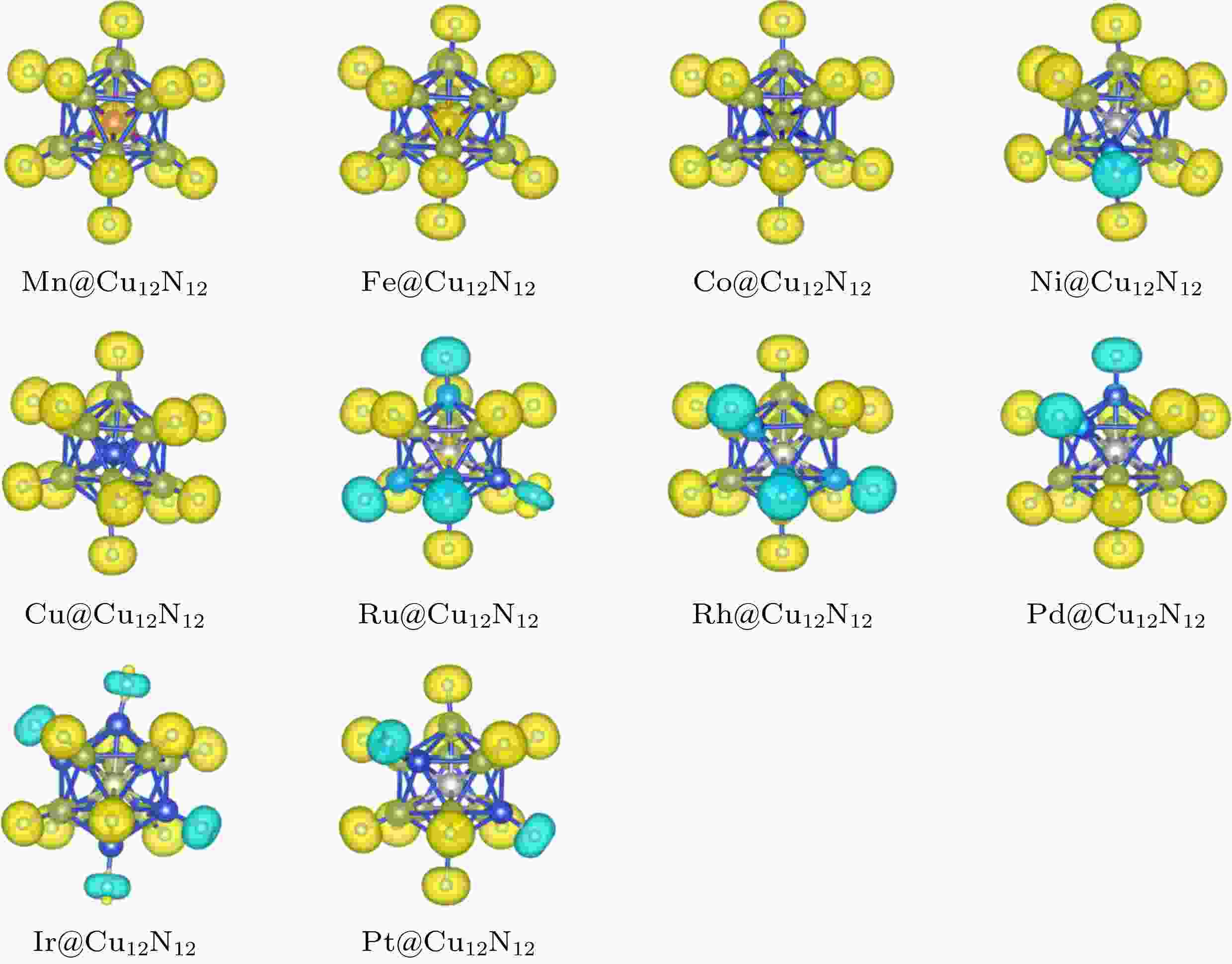图 7 TM@Cu₁₂N₁₂团簇自旋密度图(isosurfaces level = 0.024)
Figure7. The plot of spin density isosurfaces of TM@Cu₁₂N₁₂ clusters (the isosurfaces level set as 0.024).

以结构优化后呈现不同磁性状态的Ni@Cu₁₂N₁₂, Ru@Cu₁₂N₁₂和Rh@Cu₁₂N₁₂团簇(从自旋密度图中可以看出分别具有1个, 4个和3个反铁磁态的N原子)为例对键长与反铁磁之间的关系加以说明. 对于每一个团簇, 中心TM原子与中间层4个Cu原子和与Cu原子相连的4个N原子可形成一个9原子单元, 在每个团簇中可得三个不同的9原子单元, 即三个不同方位的电子局域函数(the electron localization function, ELF)切片, 结果如图8所示. 根据ELF定义可知, ELF的数值一般分布在0和1之间, 分别代表电子的完全离域(或者说此处无电子)和完全局域, 数值为0.5则表示此处形成了类似于电子气的电子对分布(the electron-gas-like pair probabilities)^[22-24]. 如图, 在较短的Cu—N键中, N原子的一侧和Cu, N原子之间的电子密度可达到1.00, 表明此处电子的高度局域, 这与其他Cu—N离子键上的电荷分布有明显差别. 另外, 由Bader电荷分析(表2)可知, 结构中Cu原子上部分电子会向N原子转移, 对于Ni@Cu₁₂N₁₂, Ru@Cu₁₂N₁₂和Rh@Cu₁₂N₁₂ 团簇而言, 部分Cu, N原子之间表现明显的电子局域行为, 且这几个Cu—N键长较其他Cu—N键偏小, N原子又具有较高的电负性, 致使电子对更倾向于靠近N原子一侧, 进而使N上本身的孤电子向Cu—N键的另一侧偏移, ELF显现的更加局域, 造成N上的电子分布明显不同于其他N原子, 导致自旋方向改变.
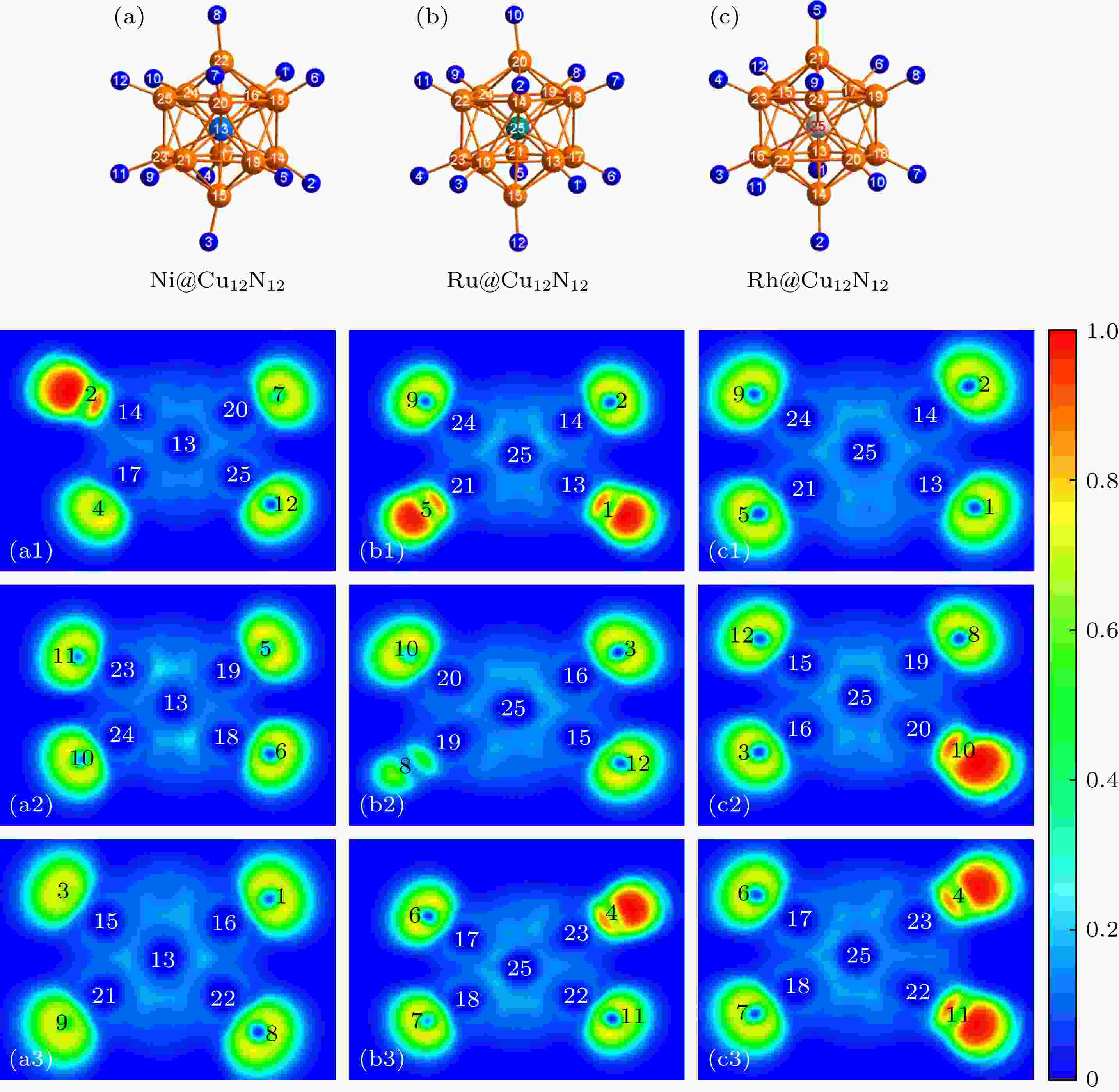图 8 Ni@Cu₁₂N₁₂(a1)—(a3), Ru@Cu₁₂N₁₂(b1)—(b3)及Rh@Cu₁₂N₁₂(c1)—(c3)团簇的结构和ELF图
Figure8. The plot of structures and ELF for Ni@Cu₁₂N₁₂ (a1)?(a3), Ru@Cu₁₂N₁₂ (b1)?(b3) and Rh@Cu₁₂N₁₂ (c1)?(c3) clusters.

Cluters	Bader charge/e				Local magnetic moments/μB
	TM	Cu	N		TM	Cu	N
Mn@Cu12N12	0.29	0.25	–0.27		3.49	0.39	1.50
Fe@Cu12N12	0.09	0.27	–0.28		2.73	0.31	1.44
Co@Cu12N12	–0.15	0.29	–0.28		1.69	0.39	1.49
Ni@Cu12N12	–0.33	0.31	–0.28		0.10	0.27	1.40
Cu13N12	–0.19	0.30	–0.28		0.05	0.29	1.43
Ru@Cu12N12	–0.59	0.35	–0.30		0.29	0.27	1.33
Rh@Cu12N12	–0.64	0.35	–0.30		0.09	0.31	1.42
Pd@Cu12N12	–0.62	0.33	–0.28		0.03	0.29	1.41
Ir@Cu12N12	–0.94	0.37	–0.29		0.14	0.30	1.34
Pt@Cu12N12	–0.92	0.36	–0.29		0.10	0.31	1.41

表2TM@Cu₁₂N₁₂团簇的原子平均Bader电荷分布和原子平均局域磁矩
Table2.The excess Bader charge and local magnetic moments of atoms in TM@Cu₁₂N₁₂ clusters.

表2列出了各团簇中的原子平均Bader电荷分布. 很明显, 随着结构中心TM原子的电负性的逐渐增强, Cu原子上电子的转出情况呈逐渐增多趋势. 一方面, 与之成键的N原子由于强电负性会吸引部分Cu原子电荷转出; 另一方面, 除中心TM原子为Mn, Fe时会提供部分电荷至Cu或N原子外, 其他TM原子的掺入都会不同程度地吸引Cu上电子转出. 对于中间层Cu原子而言, 内外双向的电荷转出可增加其d轨道上的单电子数量, 进而产生微小磁矩; N原子由于具有半满的P轨道填充(2s²2p³), 电荷的转进使得磁矩较孤立的N原子有所减小, 但并不影响其对团簇总磁矩的贡献; 最后, 对于中心TM原子, 电荷的转入对于后过渡金属而言会使其磁矩降低. 因此造成团簇内部不同原子的磁矩随着不同TM的掺杂呈逐渐降低趋势. 同时, 可以注意到, 随着TM原子电负性的增强, 中间层的Cu原子的电荷转出量虽逐渐增大, 但其磁矩却始终保持降低趋势. 对此, 我们进行了团簇的分波态密分析. 如图9所示, 根据不同团簇中Cu原子的d电子分布情况可知, 以Cu₁₃N₁₂为界, 中心原子为Ru, Rh, Pd, Ir, Pt时, 随着电荷转出量的增大, Cu原子d轨道电子密度降低, 且自旋向下d电子的离域程度明显增大, 能级劈裂减弱, 导致Cu原子磁性不增反降. 此外, TM与Cu原子之间始终存在微弱的d-d轨道杂化. 而在TM = Ru, Rh, Pd, Ir, Pt时, TM原子存在不同程度的d电子离域, 与Cu原子间的作用增强, 是导致部分TM原子几乎不提供磁矩的原因之一.
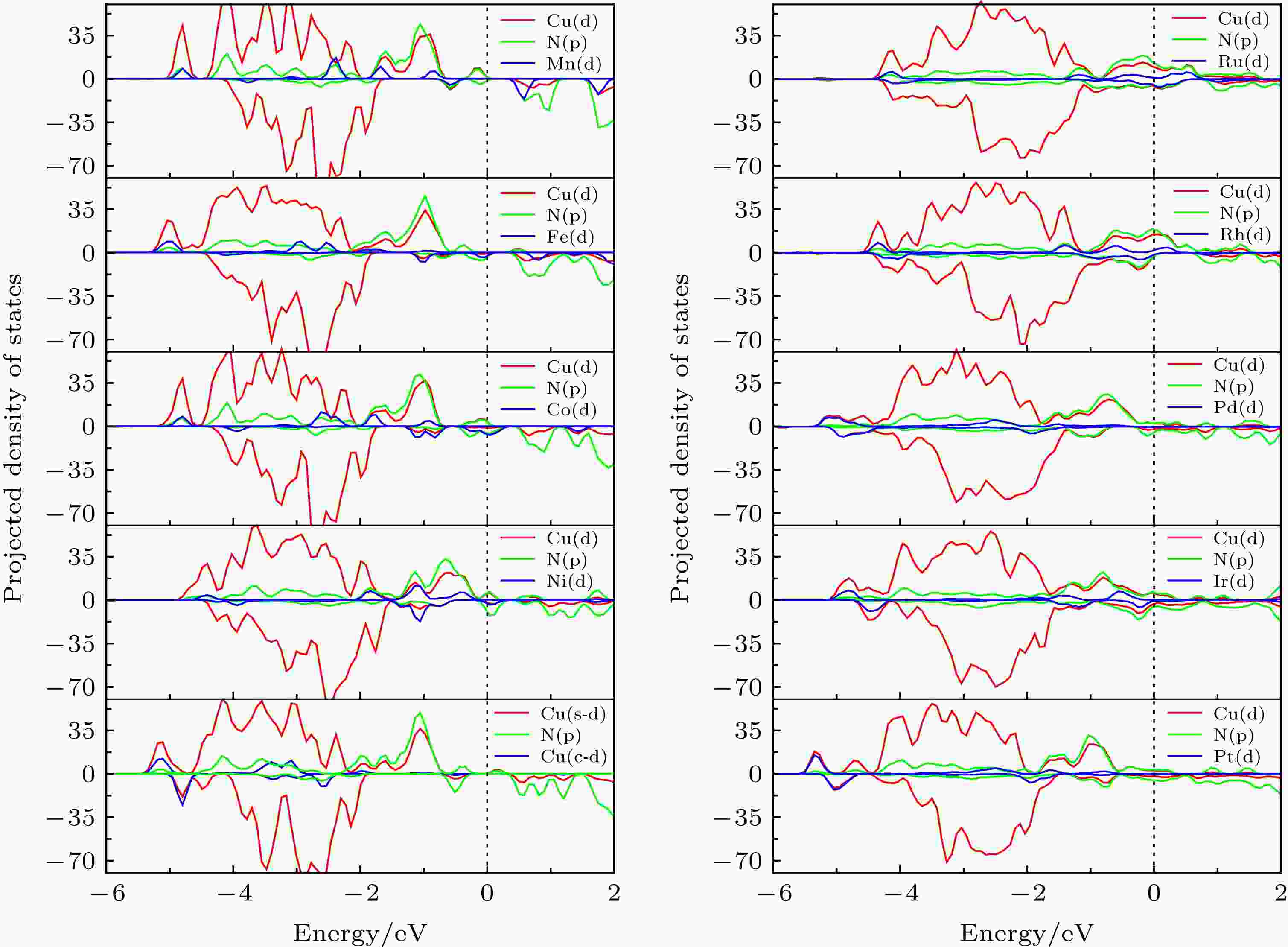图 9 TM@Cu₁₂N₁₂团簇分波态密度(PDOS)
Figure9. The PDOS of TM@Cu₁₂N₁₂ clusters.

2 -->

3.3.TM@Cu₁₂N₁₂团簇的轨道磁矩和MAE

图10(a)给出了团簇TM@Cu₁₂N₁₂随着TM原子的更替, 其轨道磁矩的变化情况. 根据洪特规则可知, 理论上当TM = Co, Ni, Ru, Rh, Ir时, 由于原子本身具有较大的轨道角动量, 可以诱导团簇产生可观的轨道磁矩. 而实际情况表明只有在TM = Co, Ru, Ir时, 团簇的轨道磁矩出现极大值. 这与原子间的电荷转移有密不可分的关系.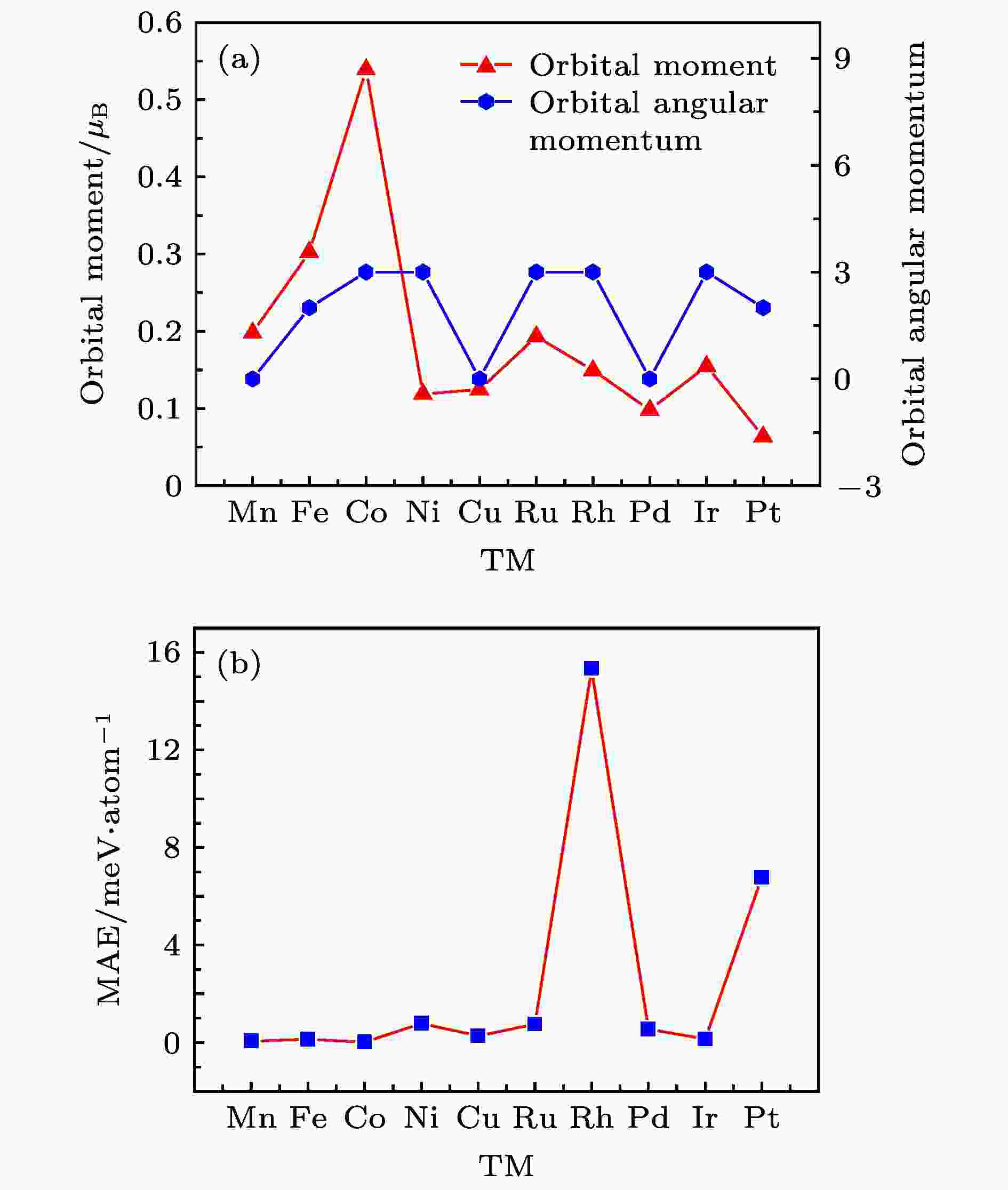
图 10 TM@Cu₁₂N₁₂团簇固有轨道角动量和轨道磁矩(a)及每个团簇的MAE(b)
Figure10. The orbital angular momentum, orbital moment (a) and MAE (b) of TM@Cu₁₂N₁₂ clusters.

根据轨道角动量的产生原理可知, d轨道的空穴可以为电子提供移动空间, 从而使电子在绕核运动中形成环电流, 产生轨道磁矩^[25]. 而通过Bader电荷分析(表2)可知, 从Co原子开始, 中心TM原子始终保持吸引中间层Cu原子电子的状态, 且随着TM原子电负性的不断增大, 吸引的电子数目呈逐渐增大的趋势, d轨道空穴逐渐减少; 相反, 由于中间层Cu原子的电荷转出, 使原先排满的d轨道出现空位, 继而产生微弱的轨道磁矩. 理论上团簇的轨道磁矩由中心TM原子和中间层Cu原子共同给出, 但TM原子作为轨道磁矩的主要提供者, 其轨道磁矩值的减小直接影响到团簇的总体轨道磁矩的降低; 同时又受到其固有轨道角动量的影响, 导致在TM = Co, Ru, Ir时出现极大值.
图10(b)给出了团簇TM@Cu₁₂N₁₂的MAE值, 通过不同原子的掺杂, 我们得到了具有较大MAE值的Rh@Cu₁₂N₁₂ (15.34 meV/atom)和Pt@Cu₁₂N₁₂(6.76 meV/atom)团簇. 因此, 部分4d, 5d元素的掺杂确实可起到提高团簇MAE值的效果, 使团簇的磁稳定性增强.
为了进一步探究MAE大小的物理起源, 在这里我们将以Rh@Cu₁₂N₁₂ (15.34 meV/atom), Pt@Cu₁₂N₁₂ (6.76 meV/atom), Ni@Cu₁₂N₁₂ (0.78 meV/atom) 三种团簇为例, 阐释其具有较大的MAE的原因. 首先基于二阶微扰理论^[26], MAE这个值是来自于体系的SOC效应在垂直和平行于体系平面方向的能量差, 可以根据角动量算符L_z和L_x近似地计算:

$ \begin{split} {\rm {MAE}} =\; & {(\xi )^2}\mathop \sum \limits_{{{u}},{{o}},{\bf{\alpha }},{\bf{\beta }}} {\left( { - 1} \right)^{1 - {{{\delta}} _{{\bf{\alpha \beta }}}}}}\\ &\times\left[ {\frac{{{{\left| {\left\langle {{{u}}{{\alpha }}\left| {{{{L}}_{{z}}}} \right|{{o\beta}} } \right\rangle } \right|}^2} - {{\left| {\left\langle {{{u\alpha }}\left| {{{{L}}_{{x}}}} \right|{{o\beta}} } \right\rangle } \right|}^2}}}{{{\varepsilon _{{{u\alpha }}}} - {\varepsilon _{{{o\beta }}}}}}} \right],\end{split} $

式中${{\varepsilon}} _{{{u}},{{a}}}\left( {{{{\varepsilon}} _{{{o}},{{\beta }}}}} \right)$是未占据的(占据的)自旋向上(自旋向下)态的能级, ξ代表SOC的强度. 磁各向异性能主要与过渡金属原子的d轨道分布有关, 费米附近的轨道分布对MAE的影响比较大. 因此为了进一步理解磁各向异性的起源, 在图11中我们分别呈现了Rh@Cu₁₂N₁₂(a), Pt@Cu₁₂N₁₂(b), Ni@Cu₁₂N₁₂(c)三个体系中的Ru, Pt, Ni不同的d轨道的分波态密度(PDOS). 如图11(a)所示, 可以看到在Rh@Cu₁₂N₁₂体系中, 在自旋向上通道中, 费米面附近d轨道的占据态主要分布在–1.5—0 eV, d轨道的未占据态主要分布在3—4.5 eV, 并且它们的峰值都很大. 在此我们主要考虑相同自旋通道中自旋向上的情况. 根据(4)式, 可以确定自旋向上通道中Rh原子的$ \big\langle {{{d}}_{{{yz}}}^{{o}}|{{{L}}_{{x}}}|{{d}}_{{{{x}}^2} - {{{y}}^2}}^{{u}}} \big\rangle$和$ \big\langle {{{d}}_{{{xz}}}^{{o}}|{{ {L}}_{{x}}}|{{d}}_{{{{x}}^2} - {{{y}}^2}}^{{u}}}\big\rangle$强的偶联作用为Rh@Cu₁₂N₁₂体系中大的MAE提供了主要贡献, 表现面内磁各向异性. 在图11(b), Pt@Cu₁₂N₁₂体系中, Pt的d电子分布情况与Rh的相似, 体系的MAE主要来自于Pt原子的$\big\langle {{{d}}_{{{yz}}}^{{o}}|{{{L}}_{{x}}}|{{d}}_{{{{x}}^2} - {{{y}}^2}}^{{u}}} \big\rangle $, $\big\langle {{{d}}_{{{xz}}}^{{o}}|{{{L}}_{{x}}}|{{d}}_{{{{x}}^2} - {{{y}}^2}}^{{u}}} \big\rangle $和$\big\langle {{{d}}_{{{{z}}^2}}^{{o}}|{{{L}}_{{x}}}|{{d}}_{{{xz}}/{{yz}}}^{{u}}} \big\rangle $强的偶联作用. 但是Pt的态密度相对Rh的有所降低了, 因此相互偶联所用也比Pt的有所减小, 产生了小于Rh的MAE值, 同样表现面内磁各向异性. 另外, 在图11(c), Ni@Cu₁₂N₁₂体系中, 费米面以上d轨道的未占据态分布很少, 仅在费米面附近存在非常少量的占据, 相对于Rh和Pt, 它的d轨道之间表现很弱的偶联作用, 最终产生了一个很小的MAE值. 类似的阐释也出现在5d过渡金属茂络合物和调控磁性二维材料的磁各向异性能工作中^[27,28].
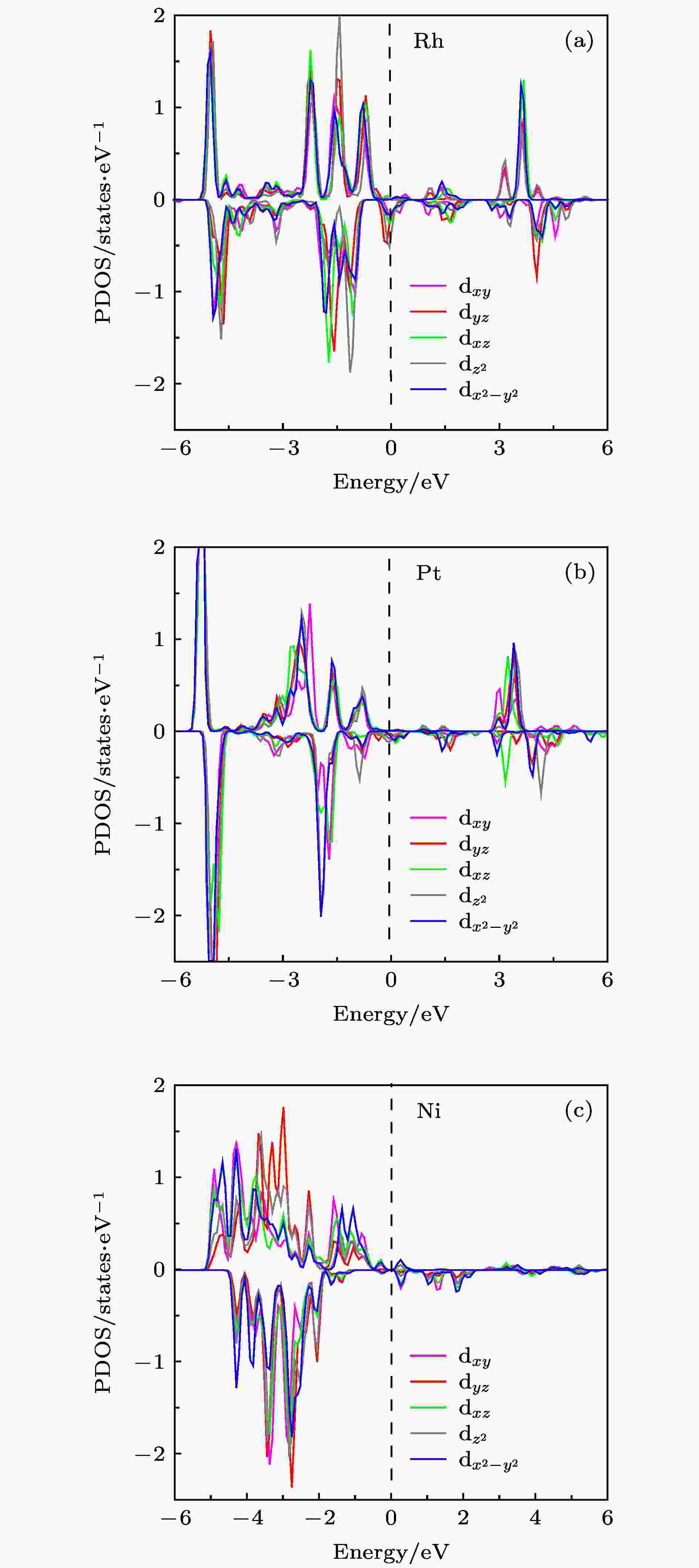图 11 TM@Cu₁₂N₁₂(TM = Rh, Pt, Ni)团簇中原子的d轨道的分波态密度(PDOS)
Figure11. PDOS of Rh (a), Pt (b), Ni (c) atoms in Rh@Cu₁₂N₁₂(a), Pt@Cu₁₂N₁₂(b), Ni@Cu₁₂N₁₂(c) clusters, respectively

基于密度泛函理论, 对TM@Cu₁₂N₁₂ (TM = Mn, Fe, Co, Ni, Cu, Ru, Rh, Pd, Ir, Pt)团簇磁性进行了系统的研究. 结果表明: 二十面体Cu₁₃N₁₂的中心原子被不同的TM 原子替代后，结构在保持二十面体的情况下，存在一定微小形变，其稳定性显著增强; 在Cu₁₃N₁₂团簇的基础上, 将中心原子替换为Mn, Fe, Co原子可有效提高其自旋磁矩, 产生巨磁效应; 同时, 4d和5d原子的掺入虽然没有达到团簇轨道磁矩增大的效果, 但在Rh@Cu₁₂N₁₂ (15.34 meV/atom)和Pt@Cu₁₂N₁₂(6.76 meV/atom)中发现的较大的磁各向异性能(MAE), 表明部分4d和5d原子的掺杂确实可提高团簇的磁稳定性.