摘要:采用数值模拟的方法, 研究了p层空穴浓度和厚度对不同铟组分InGaN p-i-n同质结太阳电池性能的影响规律及其内在机理. 模拟计算的结果显示: 随着p层空穴浓度和厚度的增加, 太阳电池的转换效率均呈先增加、后略微下降的趋势; 而且铟组分越高, p层空穴浓度和厚度的影响越大. 为更好地理解这一规律, 本文从太阳电池的收集效率、I-V特性、内建电场和载流子输运等方面分析, 阐述了其背后的物理机理; 研究结果对InGaN太阳电池的结构设计及实验制备有一定的理论指导意义.
关键词: 数值模拟/
InGaN/
同质结/
太阳电池

English Abstract

全文HTML

--> --> -->

Ⅲ族氮化物材料因其极具吸引力的固有特性在半导体行业中备受瞩目^[1—4], 其中三元合金InGaN材料以其优越的光伏特性得到众多科研工作者的青睐. 通过调节铟组分可以使InGaN材料的禁带宽度从3.4 eV(GaN)到0.65 eV(InN)连续可调^[5,6], 对应的吸收波长覆盖整个可见光太阳光谱^[7]. 此外, InGaN材料具有高吸收系数(～10⁵ cm^–1)^[8]、高载流子迁移率^[9]、高化学稳定性^[10,11]、高耐辐射性^[12]和高导热性^[7]. 因此, 其具有成为高效太阳电池和空间太阳电池^[12]的巨大潜能.
由于异质结界面势垒的存在, 在理论上, InGaN同质结相对于异质结具有更好的光伏特性^[13]. 另外, p-i-n结构中本征层(i层)可以起到拓宽入射光吸收区的作用^[14], 因此p-i-n结构比p-n结构更具优势. 很多研究团队对InGaN p-i-n同质结太阳电池进行了大量的实验研究, 但是实验室制备出的电池光电转换效率均低于5%^[14—17]. 众所周知, 太阳电池的转换效率是太阳电池光电性能的综合体现, 也是衡量电池优劣的重要参数; 它由各种影响因素—掺杂、厚度、铟组分、少数载流子寿命、缺陷密度等共同决定. 深入理解上述因素对转换效率的影响机理是改善太阳电池性能的关键. Feng等^[18]以及Wu等^[19]通过模拟研究了In_xGa_1–xN p-i-n同质结太阳电池中i层背景掺杂浓度, 铟组分, 厚度和缺陷密度对电池转换效率的影响规律, 但均未对p层参数进行研究. 虽然周梅和赵德刚^[20]研究了p-InGaN层厚度对p-i-n结构InGaN单结太阳能电池的短路电流(J_sc)、开路电压(V_oc)、转换效率等性能的影响, 但未进行深层物理机制的剖释. Benmoussa等^[21]和Mesrane等^[22]通过模拟软件分别优化了In_0.52Ga_0.48N pn结以及In_0.622Ga_0.378N pn结中p层的最佳掺杂浓度, 优化后得到的最佳掺杂浓度分别为1 ×10¹⁵ cm^–3和1.5 × 10¹⁸ cm^–3. 他们未考虑器件模型中p层掺杂剂Mg的离化问题, 且均未就p层掺杂浓度对太阳电池性能的影响规律及其内在机理进行详细分析. 综合他们的结果可得: 对于不同铟组分的InGaN太阳电池, p层的最佳掺杂浓度不同. 但是目前尚未见有文献对该现象进行解释. 随着铟组分的增加, InGaN材料的临界厚度变薄^[23]、p型掺杂困难^[21], 这使得研究p层空穴浓度及厚度的影响机理变得十分重要而迫切. 本文,通过数值模拟, 分别研究p层空穴浓度和厚度对不同铟组分In_xGa_1–xN p-i-n同质结太阳电池转换效率的影响规律, 并从物理机理上分析形成这一影响规律的内在原因. 本文的研究将有助于理解p层参数对电池转换效率的影响规律, 为实验现象的合理分析提供详细的理论支持, 对今后InGaN同质结太阳电池的设计及制备有一定的指导作用.

模拟求解的主要物理方程包括输运方程(漂移扩散输运模型和能量平衡输运模型)、泊松方程、自由空穴的连续性方程和自由电子的连续性方程等. 本文通过商业模拟软件ATLAS^[24]模块建立InGaN p-i-n同质结太阳电池数值模型, 在300 K, 一个太阳AM1.5(100 mW/cm²)的辐照环境下进行一系列的器件性能模拟.
In_xGa_1–xN p-i-n同质结太阳电池结构如图1所示. 整个器件面积为100 μm × 100 μm. 由于是同质结, 器件内部界面处由极化产生的等效界面电荷为零; 另外, 考虑到表面态的补偿作用, 整个器件上、下表面由极化产生的束缚电荷均被假设为零. GaN中Mg受主的热激活能高达140—220 meV, Mg受主的离化率为1%—5%^[25,26], 使得p型GaN空穴浓度很低. 所以在模型中p型In_xGa_1–xN材料中Mg掺杂剂的离化率设为1%^[27]; 电池表面无光反射; 电池的电极接触为欧姆接触且阳极的遮光面积为5%^[28]; 前表面和背表面复合速度为1 ×10⁴ cm/s^[28]; 复合模型为俄歇复合和Shockley-Read-Hall (SRH)复合, 电子和空穴的俄歇复合系数均为1.4 × 10^–30 cm⁶/s^[29], In_xGa_1–xN材料的SRH少子寿命设定为1 ns^[30]. 表1中的参数作为器件结构的基准参数, 通过仅改变其中的某一个参数来模拟计算该参数对太阳电池性能的影响规律.
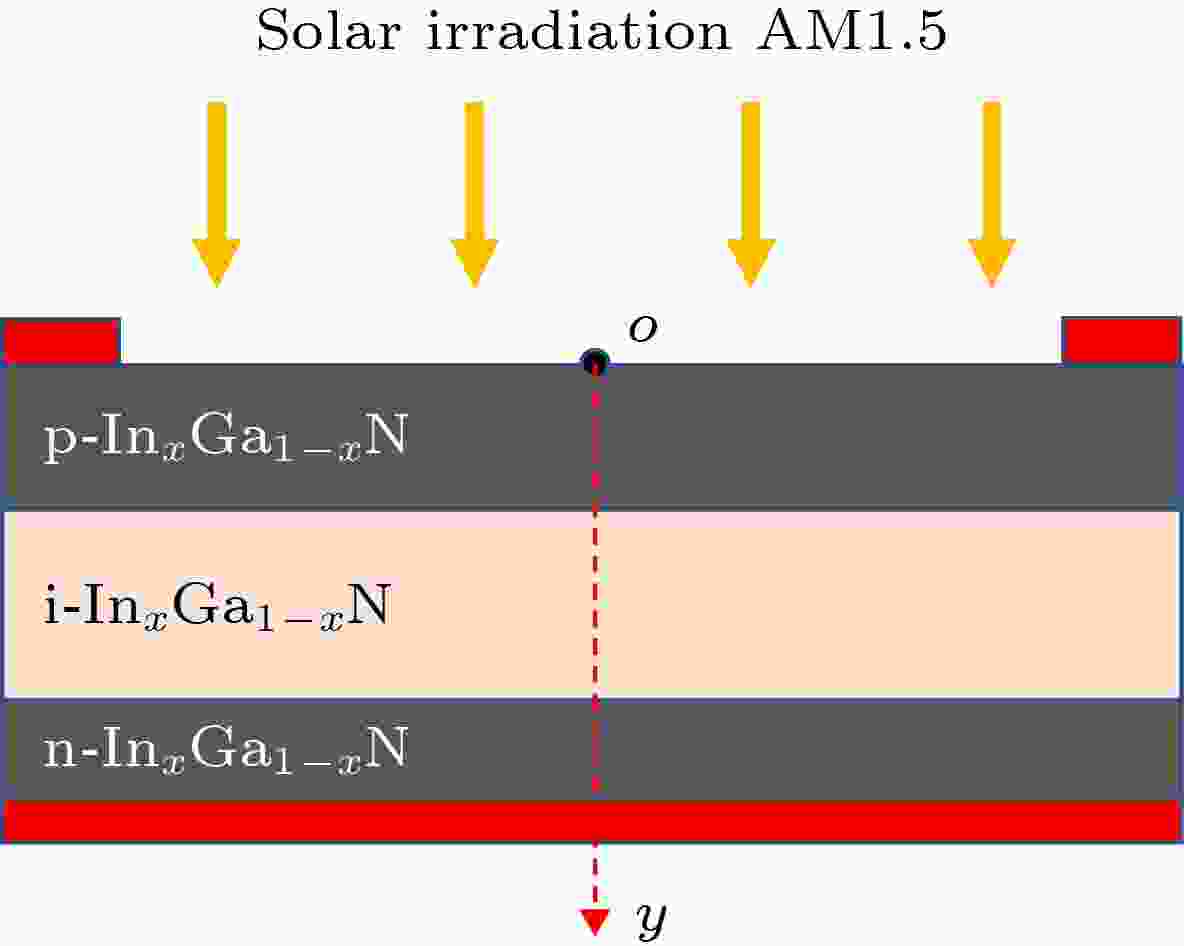图 1 In_xGa_1–xN p-i-n同质结太阳电池结构示意图y是距离p层表面的位置, y = 0代表p层表面
Figure1. Schematic of In_xGa_1–xN p-i-n homojunction solar cells. y is the position measured from the p-layer surface and y = 0 represents the p-layer surface.

参数	基准值
铟组分/%	20, 40, 60
少子寿命/ns	1
p层掺杂激活浓度/cm–3	5 × 1017
i层掺杂浓度/cm–3	1 ×1017
n层掺杂浓度/cm–3	5 × 1017
p层厚度/μm	0.2
i层厚度/μm	0.4
n层厚度μm	2
表面复合速度/cm·s–1	1 ×104

表1In_xGa_1–xN p-i-n同质结器件中的基准参数
Table1.Parameters of baseline for In_xGa_1–xN p-i-n homojunction solar cells.

In_xGa_1–xN三元合金的禁带宽度可通过(1)式^[31]计算得到:

${E_{\rm{g}}}({\rm{I}}{{\rm{n}}_x}{\rm{G}}{{\rm{a}}_{1 - x}}N) = {E_{{\rm{g}},{\rm{InN}}}}x + {E_{{\rm{g}},{\rm{GaN}}}}\left( {1 - x} \right) - bx\left( {1 - x} \right), $

式中, $ {E_{{\rm{g}},{\rm{InN}}}} = 0.65\;{\rm{eV}}$和$ {E_{{\rm{g}},{\rm{GaN}}}} = 3.42\;{\rm{eV}}$分别为InN与GaN的禁带宽度; b为In_xGa_1–xN的弯曲因子, 值为1.43 eV^[32].
In_xGa_1–xN三元合金的吸收系数可根据(2)式^[28]计算得到:

$\alpha \left( E \right) = {10^5} \times \sqrt {a\left( {E - {E_{\rm{g}}}} \right) + b{{\left( {E - {E_{\rm{g}}}} \right)}^2}} {\rm{c}}{{\rm{m}}^{ - 1}}, $

式中, E为入射的光子能量;$ {E_{\rm{g}}}$为材料的禁带宽度; a和b为拟合参数^[33], 拟合参数在模拟文献中很容易找到^[8,28,32,34].
电子亲和势($ {E_a}$)的表达式为

${E_a}({\rm{I}}{{\rm{n}}_x}{\rm{G}}{{\rm{a}}_{1 - x}}N) = {E_{a,{\rm{InN}}}}x + {E_{a,{\rm{GaN}}}}\left( {1 - x} \right) + cx\left( {1 - x} \right), $

式中, $ {E_{a,{\rm{InN}}}} = 5.6\;{\rm{eV}}$, $ {E_{a,{\rm{GaN}}}} = 4\;{\rm{eV}}$, 分别为InN与GaN的电子亲和势; c = 0.8 eV是弯曲因子^[34].
GaN及InN的电子迁移率和空穴迁移率分别通过(4)式^[35]计算得到:

${\mu _{{\rm{e}},{\rm{h}}}} = {\mu _{{\rm{min}}}} + \frac{{\left( {{\mu _{{\rm{max}}}} - {\mu _{{\rm{min}}}}} \right)}}{{\left\{ {1 + {{\left( {\dfrac{N}{{{N_{\rm{g}}}}}} \right)}^\gamma }} \right\}}}, $

式中, N为掺杂浓度; $ {\mu _{{\rm{max}}}}$, $ {\mu _{{\rm{min}}}}$和γ为指定半导体材料的参数^[28].
In_xGa_1–xN三元合金的电子迁移率($ {\mu _{{\rm{I}}{{\rm{n}}_x}{\rm{G}}{{\rm{a}}_{1 - x}}{\rm{N}},{\rm{e}}}}$)和空穴迁移率($ {\mu _{{\rm{I}}{{\rm{n}}_x}{\rm{G}}{{\rm{a}}_{1 - x}}{\rm{N}},{\rm{h}}}}$)则分别通过线性插值进行计算, 见(5)和式(6).

${\mu _{{\rm{I}}{{\rm{n}}_x}{\rm{G}}{{\rm{a}}_{1 - x}}{\rm{N}},{\rm{e}}}} = {\mu _{{\rm{InN}},{\rm{e}}}}x + {\mu _{{\rm{GaN}},{\rm{e}}}}\left( {1 - x} \right), $

${\mu _{{\rm{I}}{{\rm{n}}_x}{\rm{G}}{{\rm{a}}_{1 - x}}{\rm{N}},{\rm{h}}}} = {\mu _{{\rm{InN}},{\rm{h}}}}x + {\mu _{{\rm{GaN}},{\rm{h}}}}\left( {1 - x} \right), $

(5)和(6)式中, $ {\mu _{{\rm{InN}},{\rm{e}}}}$, $ {\mu _{{\rm{InN}},{\rm{h}}}}$分别为InN的电子迁移率和空穴迁移率; $ {\mu _{{\rm{GaN}},{\rm{e}}}}$, $ {\mu _{{\rm{GaN}},{\rm{h}}}}$分别为GaN的电子迁移率和空穴迁移率. 均可通过(4)式计算得到.
载流子产生率G(y)^[19]可表示为

$ G\left( y \right) = \int {g}\left( {\lambda ,y} \right)\frac{\lambda }{{hc}}{\rm{d}}\lambda , $

(7)式中, $ {g}\left( {\lambda ,y} \right) = - \dfrac{{{\rm{d}}I\left( {\lambda ,y} \right)}}{{{\rm{d}}y}} = {I_0}\left( \lambda \right)\alpha \left( \lambda \right){{\rm{e}}^{ - \alpha \left( \lambda \right)y}}$, λ为入射光波长, h为普朗克常数, c为光在真空中的传播速度.
在整个p-i-n太阳电池结构中, 收集效率$ {\eta _{{\rm{Collection}}}}$ (collection efficiency)定义为光生电流产生的电荷载流子数与光生电荷载流子总数之比^[18]. 表达式如下:

${\eta _{{\rm{Collection}}}} = \left( {\frac{{{J_{{\rm{sc}}}}}}{q}} \right)\bigg/ \int {G}\left( y \right){\rm{d}}y, $

式中, $ {{J_{{\rm{sc}}}}}$为太阳电池的短路电流密度, q为电子电荷量.
太阳能电池的转换效率$ {\eta _{{\rm{Conversion}}}}$由方程(9)^[22]给出:

${\eta _{{\rm{Conversion}}}}\left( \% \right) = \frac{{{I_{{\rm{sc}}}} \times {V_{{\rm{oc}}}} \times FF}}{{{P_{{\rm{in}}}}}}, $

式中, $ {{P_{{\rm{in}}}}}$为太阳光谱的入射功率, $ {{I_{{\rm{sc}}}}}$为短路电流, $ {{V_{{\rm{oc}}}}}$为开路电压, FF为太阳电池的填充因子.
In_xGa_1–xN三元合金的介电常数、电子质量、空穴质量等均通过线性插值进行计算获得. 模拟中, GaN与InN的光学和电学参数来源于参考文献[28].

2

-->

3.1.p层空穴浓度对电池转换效率的影响

图2(a)为电池转换效率随p层空穴浓度的变化图, 整体趋势为: 随着空穴浓度的增加, 转换效率先增加后略微下降. 但对于不同铟组分的同质结电池, 其达到最大转换效率的空穴浓度不同. 铟组分为20%, 40%和60%的同质结分别在1 × 10¹⁷, 2 × 10¹⁷及1 ×10¹⁸ cm^–3时获得最大转换效率, 其与3 × 10¹⁶ cm^—3所对应的最小转换效率之间的降低率分别为9.13%, 40.62%及62.27%. 降低率随着铟组分的增加而增大, 说明p层空穴浓度对高铟组分太阳电池转换效率的影响更大. 那么当p层空穴浓度改变时, 影响电池转换效率的主导因素是什么？本文通过收集效率, 内建电场及I-V曲线来分析其内在机理.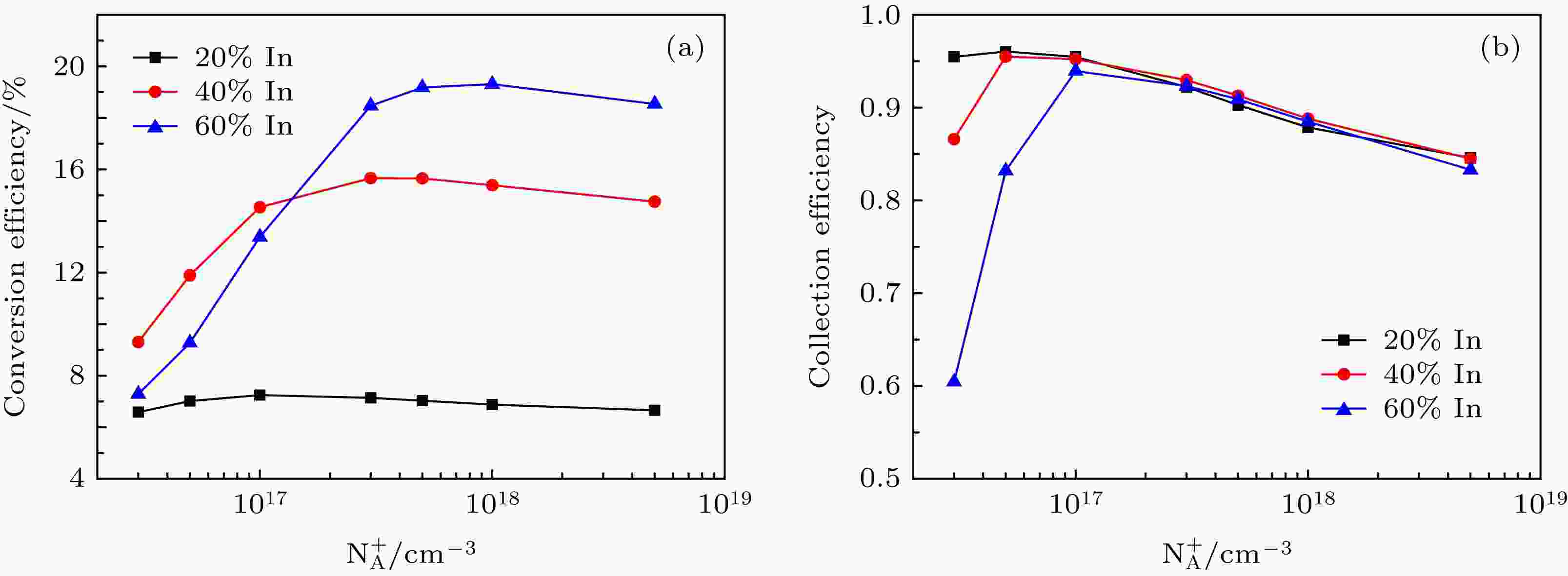
图 2 In_0.2Ga_0.8N, In_0.4Ga_0.6N和In_0.6Ga_0.4N p-i-n同质结电池中, (a)转换效率和(b)收集效率随p层空穴浓度N_A⁺的关系
Figure2. (a) Conversion efficiencies and (b) collection efficiencies with various N_A⁺ for In_0.2Ga_0.8N, In_0.4Ga_0.6N, In_0.6Ga_0.4N p-i-n homojunction solar cells, respectively.

通过分析不同铟组分太阳电池在光照下的内建电场(图3(a), (c), (e)), 发现空穴浓度降低, 主电场区的电场强度也随之降低(本文把p层与i层之间的内建电场称为主电场, n层与i层之间的电场称为副电场). 这会使得主电场对光生电子空穴对的分离能力减弱, 最终导致收集效率和转换效率的降低. 图2(b)为不同铟组分太阳电池的收集效率随空穴浓度的变化图, 图中表明, 收集效率在达到最大值前, 随着空穴浓度的降低而降低. 这与上述分析相吻合. 图2(b)中收集效率随空穴浓度改变的变化趋势与图2(a)中转换效率的变化趋势一致. 那么, 收集效率是否就是影响转换效率的主要原因呢？
图 3 (a) In_0.2Ga_0.8N, (c) In_0.4Ga_0.6N和(e) In_0.6Ga_0.4N p-i-n同质结在零偏压及光照下, 不同空穴浓度(N_A⁺)下的内建电场; (b) In_0.2Ga_0.8N, (d) In_0.4Ga_0.6N和(f) In_0.6Ga_0.4N p-i-n同质结在不同空穴浓度(N_A⁺)下的I-V曲线
Figure3. Under AM1.5 illumination and zero bias, electric-field of (a) In_0.2Ga_0.8N, (c) In_0.4Ga_0.6N and (e) In_0.6Ga_0.4N p-i-n homojunction solar cells with various hole concentration (N_A⁺); I-V curves of (b) In_0.2Ga_0.8N, (d) In_0.4Ga_0.6N and (f) In_0.6Ga_0.4N p-i-n homojunction solar cells with various hole concentration (N_A⁺), respectively.

通过进一步比较图2(a)和图2(b), 发现转换效率达到最大值所对应的空穴浓度比收集效率达到最大值所对应的空穴浓度更大. 例如In_0.6Ga_0.4N在空穴浓度为1 ×10¹⁸ cm^–3时达到最大转换效率, 而在1 ×10¹⁷ cm^–3就已经达到最大收集效率. 这说明随着p层空穴浓度的变化, 光生载流子的收集效率并不是制约电池转换效率的唯一因素. 通过比较不同空穴浓度下的I-V曲线(如图3(b), (d), (f)), 发现短路电流密度(J_sc)相差很小时(即收集效率相差不大), I-V曲线的最大功率点会随着空穴浓度的降低而塌陷. 这是因为空穴浓度越低, 串联电阻(体电阻)越大. 对于p型半导体, 其电导率$ \sigma = pq{\mu _{\rm{p}}}$(式中p为p型半导体中的空穴浓度), 假设铟组分对$ {\mu _{\rm{p}}}$的影响忽略不计, 那么不同铟组分的太阳电池因空穴浓度变化引起的串联电阻的阻值变化相同. 由于铟组分越高, 其产生的电流密度越大, 那么串联电阻带来的功率损耗就越大, 最终导致最大功率点的塌陷程度越严重. 所以当主电场强度不再成为阻碍电子空穴对分离的原因时, 串联电阻依然是影响电池转换效率的一大因素, 这也就是为什么收集效率已经达到了最大值, 而转换效率还未达到最大值的内在原因. 而图2(a)中的转换效率达到最大值后, 随着p层空穴浓度的增加, 转换效率会略微降低的原因则是因为随着p层掺杂浓度的增加, 少数载流子的迁移率会降低, 导致收集效率减小(如图2(b)所示), 进而降低了转换效率.
图2(a)中还表明高铟组分的太阳电池需在相对更高的空穴浓度下才能达到最佳转换效率. 通过分析发现这背后的原因有两个: 其一, 同一空穴浓度下, 铟组分越高, 材料带隙越窄, pn结的内建电场场强降低, 即光照下的主电场场强越弱. 如图3(a)和图3(e)所示, In_0.6Ga_0.4N需要在高于1 ×10¹⁷ cm^–3的空穴浓度下的电场强度才能与In_0.2Ga_0.8N在5 × 10¹⁶ cm^–3的空穴浓度下的内建电场强度相当. 当电场强度低于某一临界值时, 其分离能力不足以将绝大部分光生电子空穴对分离, 会对收集效率造成不利影响; 只有当电场强度达到或超过该临界值时, 其对载流子的收集才不会造成影响. 本文把该临界值所对应的电场称为“阈值电场”. 其二, 铟组分越高, 能吸收的太阳光谱波段越宽, 其光生载流子越多, 所需的阈值电场就越高. 因此, 高铟组分的电池在更高的空穴浓度下才能达到最大转换效率.
综上, 当空穴浓度很低时, 内建电场和串联电阻共同限制了电池的转换效率; 随着空穴浓度的增加, 内建电场达到阈值, 对收集效率不再产生影响; 此时, 串联电阻的影响尽管减弱, 但它仍旧会降低有效输出功率, 限制了转换效率; 当空穴浓度很大时, 迁移率成了限制转换效率的因素. 不同铟组分的In_xGa_1–xN p-i-n同质结电池所对应的最优空穴浓度不同, 铟组分越高, 空穴浓度也需更高. 在空穴浓度低于1×10¹⁷ cm^–3时, In_0.4Ga_0.6N太阳电池比In_0.6Ga_0.4N太阳电池的转换效率更高(如图2(a)所示). 在实验中, 铟组分越高, p型掺杂越困难, x > 60%的p型In_xGa_1–xN甚至还会发生表面反型^[36,37]; 因此, 当工艺上无法实现合适的p层空穴浓度时, 不应一味追求高铟组分, 否则会产生适得其反的效果.
2 -->

3.2.p层厚度对电池转换效率的影响

In_xGa_1–xN合金的带边吸收系数高达10⁵ cm^–1, 几百纳米的厚度就可以吸收绝大多数的入射光^[38]. 图4(a)为转换效率随p层厚度变化的曲线图, 由图可知, 转换效率达到最大值后会随着p层厚度的增大而降低. 这是由于p层厚度增大, 收集效率降低造成的(如图4(b)所示). 在同质结中, p层也会吸收大量的入射光, 为了让i层尽可能多地吸收入射光, p层厚度是否越薄越好呢？周梅等人通过数值模拟研究p层厚度对InGaN p-i-n太阳电池的影响发现太阳电池的转换效率会随着p层厚度的增加而单调降低, 他们认为造成这一现象的原因是由于短路电流会随着p层厚度的增加而持续降低^[20]. 但在本文中, 随着p层厚度的增加, InGaN太阳电池的转换效率先增加后降低(如图4(a)所示), 与周梅等人所报道的变化规律不同. 那么导致图4(a)所示的变化规律的因素是什么？有研究者指出: 当把表面复合纳入考虑后, 在p层厚度很薄时, 太阳电池转换效率较低是由于p层表面离耗尽区太近使收集效率降低造成的^[22]. 但是本文中太阳电池的收集效率并没有随着p层厚度的减薄而急剧下降(如图4(b)所示).
图 4 In_0.2Ga_0.8N, In_0.4Ga_0.6N和In_0.6Ga_0.4N p-i-n同质结电池中, (a)转换效率和(b)收集效率随p层厚度的变化
Figure4. (a) Conversion efficiency and (b) collection efficiency versus p-layer thickness for In_0.2Ga_0.8N, In_0.4Ga_0.6N and In_0.6Ga_0.4N p-i-n homojunction solar cells, respectively.

为澄清这一问题, 本文进一步分析了不同表面复合速度下, In_0.6Ga_0.4N p-i-n同质结太阳电池J_sc和转换效率随p层厚度变化的曲线, 如图5所示. 由图可知, 随着表面复合速度的增大, J_sc呈现下降的趋势. 这说明表面复合速度越大, 会造成短路电流的减小, 从而导致转换效率的降低. 但在同一表面复合速度下, 即使表面复合速度非常大(= 1 ×10⁶ cm/s)时, J_sc未如文献[22]那样随着p层厚度的减小而降低, 反而是单调增加的, 这是因为p层越薄, p层被主电场覆盖的区域占p层的比重就越大, 更有利于p层产生的光生载流子的分离. 且p层越薄, 主电场离阳极的距离就越短, 载流子的输运距离变短, 也有利于光生载流子的收集; 同时, 在p层厚度小于0.1 μm后, 仍旧存在转换效率随着p层厚度的减小而降低的现象; 而且, 表面复合速度越大, 最佳的p层厚度反而越薄, 如图5(b)所示. 由此可知, 尽管表面复合速度对转换效率的影响很大, 但其显然并不是“转换效率随着p层厚度减薄而下降”现象的主要原因, 即图4(a)中p层厚度较薄时, 转换效率随着p层厚度减薄而下降的现象可能并不是如文献[22]所述的由于p层表面离耗尽区太近造成, 而可能是由另一物理机理造成的.
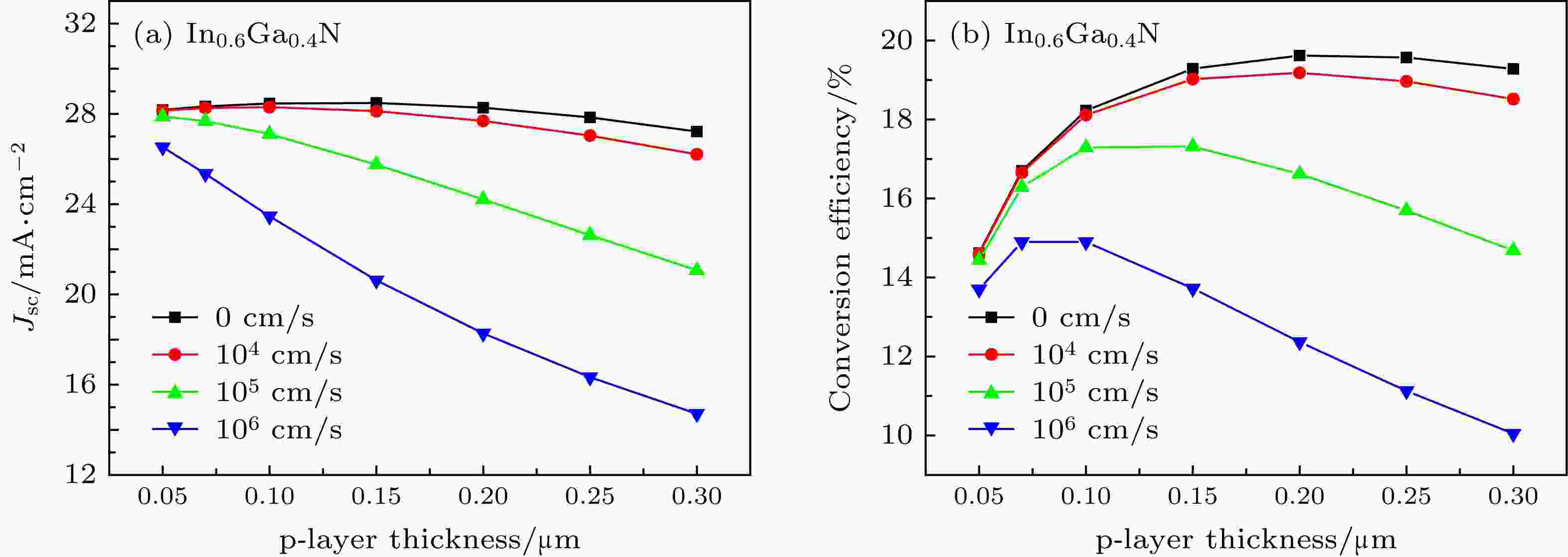图 5 不同表面复合速度下, In_0.6Ga_0.4N p-i-n同质结太阳电池在不同p层厚度下的(a)短路电流密度(J_sc)和(b)转换效率
Figure5. (a) Short current density (J_sc) and (b) conversion efficiency of In_0.6Ga_0.4N p-i-n homojunction solar cells with various p-layer thickness at different surface recombination velocities.

为了探究上述的疑惑—p层厚度较薄时, 转换效率为什么会随着p层厚度的减薄而下降？本文比较了不同铟组分太阳电池在不同p层厚度下的I-V曲线(图6(a)), 发现p层厚度越薄, 不同铟组分太阳电池的I-V曲线上的最大功率点均存在不同程度的坍塌现象, 该现象显然是由串联电阻造成的. 分析其机理: 当p层厚度越薄, 沿平行于pn结的载流子横向输运的比重逐渐增大; 同时横向输运的截面积减小, p层载流子横向输运受到的阻碍就越大; 这两者都会使得串联电阻增大, 即串联电阻会随着p层厚度的减薄而增大. 串联电阻越大, 填充因子就会越小, 电池的转换效率也会随之降低. 我们根据电阻计算公式$ R = \rho \dfrac{l}{S}$(ρ为电阻率, S为p层横向截面积, l为p层厚度)计算了整个p层的横向电阻. 图6(b)为In_0.6Ga_0.4N p-i-n太阳电池在不同p层厚度下, 整个p层的横向电阻阻值, 可知当p层厚度降低时, 其横向电阻会急剧增大. 这从侧面证明了p层厚度的减薄, 会导致载流子在p层横向输运时受到的阻碍增大. 图6(a)还表明, 铟组分越高, 最大功率点坍塌越严重. 根据ΔV = IR_s, 铟组分越高, 其光生电流密度越大, 其串联电阻(R_s)的分压ΔV则越大, 串联电阻带来的功率损耗也越大. 这解释了图4(a)中60%铟组分太阳电池转换效率的降幅大于20%和40%铟组分太阳电池的降幅的现象.
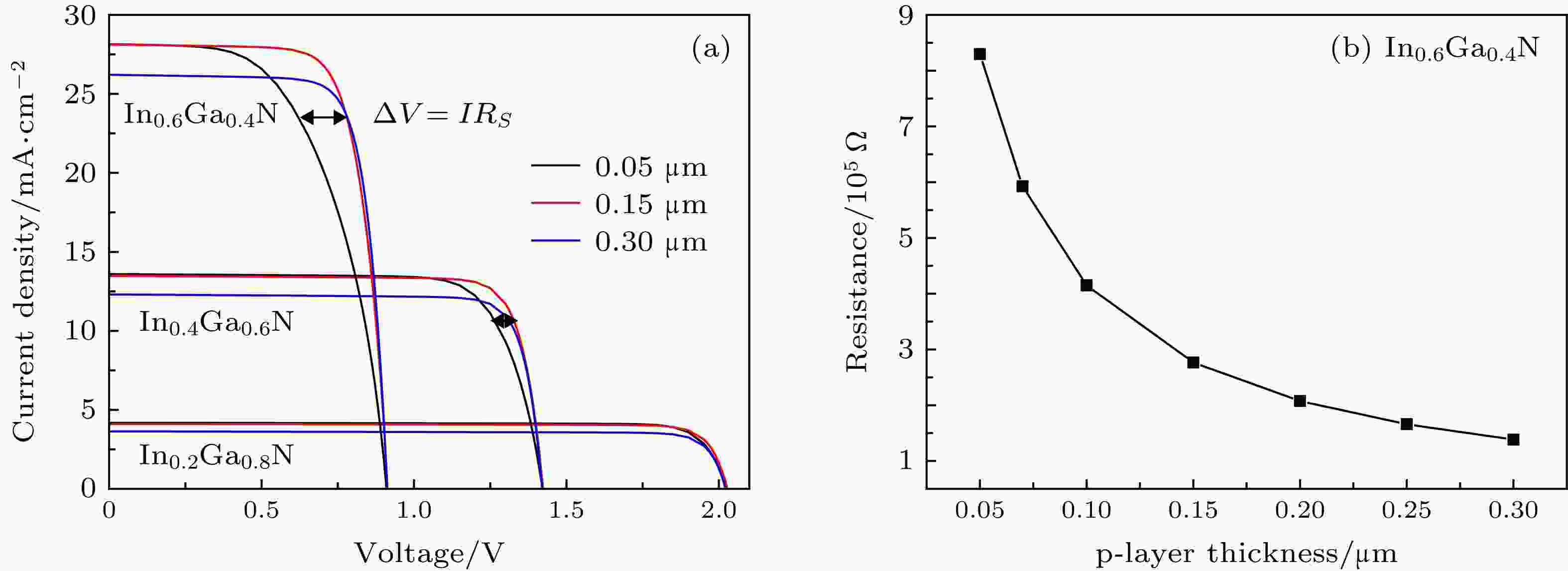图 6 (a) In_0.2Ga_0.8N, In_0.4Ga_0.6N和In_0.6Ga_0.4N p-i-n同质结电池在不同p层厚度下的I-V曲线; (b)不同p层厚度下In_0.6Ga_0.4N p-i-n同质结电池p层的横向电阻
Figure6. (a) I-V curves of In_0.2Ga_0.8N, In_0.4Ga_0.6N and In_0.6Ga_0.4N p-i-n homojunction solar cells with various p-layer thickness and (b) the lateral resistance of p-layer for In_0.6Ga_0.4N p-i-n homojunction solar cells.

综上, 通过分析p层厚度对太阳电池转换效率的影响发现, 当p层厚度降低时, 收集效率会略微降低且载流子在p层的横向扩散受阻, 串联电阻增大, 这使得太阳电池转换效率下降; 铟组分越高, 串联电阻带来的功率损耗越大, 导致高铟组分的太阳电池转换效率的降幅随p层厚度的减薄而增大; 当p层厚度超过一定值时, 随着p层厚度的增加, p层表面产生的电子空穴对由于距主电场区较远导致很多电子空穴对因复合而无法被两端的电极收集, 最终导致转换效率下降. 在实验中, In_xGa_1–xN材料的临界厚度会随着铟组分的增加而降低^[23], 这凸显了p层厚度在高铟组分太阳电池设计中的重要性. 当表面复合速度大于1 ×10⁴ cm/s时, 为了减小表面复合对p层光生电子空穴对的影响, 高铟组分的p层厚度不应超过0.1 μm.

本文模拟研究了In_xGa_1–xN p-i-n同质结太阳电池p层空穴浓度和p层厚度对太阳电池性能的影响规律, 并从物理上详细阐述了该变化规律下的内在机理. p层空穴浓度的增加会使转换效率先增加后略微下降. 当p层空穴浓度很低时, 内建电场场强较弱, 对光生电子空穴对的分离能力不足导致收集效率下降. 此外, p层空穴浓度越低, 太阳电池的串联电阻就越大, 这使得串联电阻带来的功率损耗越大. 所以收集效率降低和串联电阻增大共同导致了转换效率降低. 随着空穴浓度的增大, 内建电场达到阈值, 对收集效率不再产生影响; 此时, 串联电阻的影响尽管减弱, 但它仍旧降低了有效输出功率, 限制了转换效率; 当空穴浓度很大时, 迁移率成了限制转换效率的主要因素. 模拟结果还表明, p层厚度的增加也会使转换效率先增加后略微下降. p层厚度越薄, 沿平行于pn结的载流子横向输运的比重逐渐增大; 同时横向输运的截面积减小, p层载流子横向输运受到的阻碍就越大. 即p层越薄, 带来的串联电阻越大. 所以, 随着p层厚度的减薄, p层横向串联电阻的增大是导致转换效率降低的主要原因. 当p层厚度超过一定厚度时, 随着p层厚度的增加, p层表面产生的很多电子空穴对因为扩散到主电场距离的增大而复合了, 进而导致收集效率和转换效率的降低. 当表面复合速度大于1×10⁴ cm/s时, 为了减小表面复合对p层光生电子空穴对的影响, 高铟组分的p层厚度应不超过0.1 μm.