摘要:K-壳分解法在度量复杂网络中节点的重要性方面具有重要的理论意义和应用价值. 但K-壳方法中, 存在大量壳值相等的节点, 从而无法精确地比较这些具有相同壳值节点的相对重要性. 因此, 本文基于网络中节点自身壳值与其多阶邻居的壳值, 设计利用向量的形式来表示节点在复杂网络中的相对重要性程度, 提出了多阶邻居壳数向量中心性方法, 并设计了该中心性向量比较方法. 通过在七个真实网络中进行消息传播与静态攻击实验, 发现基于多阶邻居壳数向量的中心性方法具有计算复杂度低, 能够有效发现具有高传播能力的节点, 在传播实验中具有优越的性能. 并在静态攻击实验过程中倾向于优先破坏网络中的传播核心结构. 多阶邻居壳数向量中心性方法在保留K-壳中心性信息的前提下, 极大提高了节点重要性的区别程度, 平衡了对节点在复杂网络中联通结构的重要性的度量和对传播结构重要性的度量, 因此具有重要理论意义与应用价值.
关键词: 中心性/
多阶邻居壳数向量中心性/
易感-感染传播模型/
静态攻击

English Abstract

全文HTML

--> --> -->

复杂网络理论可以用来研究多种类型的复杂系统, 这些系统中的主要元素被抽象成节点, 主要元素间的关系抽象成节点之间的连边. 近些年来, 科学界见证了复杂网络研究领域诞生了一系列的重要成果^[1,2]. 除了针对边进行预测应用在推荐系统等问题中之外^[3,4], 复杂网络模型里中心性研究也具有较高的应用价值^[5], 中心性是网络拓扑中度量节点重要程度的一个指标^[6], 对中心性的研究工作有着非常重要的理论意义, 除了搜索引擎对网页网络的排序外, 还有对恐怖分子和毒品贩卖等网络进行蓄意攻击^[7]、防止传染病在生物群体中进行传播^[8]、阻断谣言的传播^[9]以及引导有效信息在网络中迅速传播^[10]等等应用领域^[11]. 因此, 研究网络中节点的重要性程度具有重要的理论意义和应用价值, 也是复杂网络研究中的热点问题之一^[12,13].
经典评估节点重要性的方法有度中心性(Degree)^[14]、介数中心性(BC)^[15]、接近中心性^[16]和特征向量中心性(EC)等. 度中心性仅考虑与该节点相连的邻居节点, 结果存在片面性, 而介数中心性和接近中心性都需要计算最短路径, 计算过程相对复杂. 于是在2010年Kitsak等^[17]提出了K-壳分解法(K-shell), 他们认为将网络按层把节点移除, 越靠近壳心的节点重要性越高. K-壳分解法优点在于方法简单且计算复杂度低. 研究表明^[13], K-壳分解法的排序结果过于颗粒化, 使得很多节点处在同一壳层上, 节点的重要性区分度不大. 其次, K-壳分解法在网络分解时仅考虑剩余度的影响, 这相当于认为同一层的节点在外层的邻居数目对节点重要性并不重要, 这样得到的中心性是不合理的.
国内外****提出了基于K-壳的改进方法. 罗仕龙等^[18]利用节点权重和权重分布重新定义边的扩散性, 提出适用于加权网络结构的基于冗余边过滤的K-壳分解排序算法: filter-shell. Jiang等^[19]受K-壳分解方法去除外围节点后网络聚类系数会增大的启发, 选择K-壳方法中壳值最高且相互连接的节点作为核心, 形成初始群来确定网络节点的重要性. Gong和Kang^[20]在K-壳方法的基础上提出了一种新的社区网络识别方法, 该方法能够识别加速疾病传播的有影响力的传播者. 朱晓霞等^[21]为了对节点影响力给出具体排序, 在已有的各种最具影响力节点识别方法的基础上, 提出了一种基于社团结构和K-shell节点法的节点影响力识别方法. 其基本思想是利用某个节点处于不同社团的邻居节点的ks值判断节点影响力, 以识别ks值相同的节点的不同影响力. 李慧嘉^[22,23]等利用动态迭代技术, 提出了一种新型的社团探测技术, 能够准确而快速地识别网络中的社团结构. 首先引入一种动态系统, 可以使社团归属从随机状态逐步收敛到最优划分, 进一步利用严格的数学分析给出了社团归属在离散时间内收敛到最优的条件. Zhang等^[24]根据度值和核值的差值来识别复杂网络中的重要节点. 在上述研究中讨论了对网络加权和引入社团等信息来评估节点的重要性, 但是尚未讨论目标节点的邻居节点对目标节点重要性排序的影响.
在本文的研究中, 为了提高网络中节点重要性的区分度, 同时考虑在相同条件下提高重要节点的影响力范围. 本文提出了多阶邻居壳数的向量中心性方法: multi-order K-shell vector(MKV). 通过对大量网络进行SI传播实验和静态攻击网络实验来验证MKV方法的有效性, 分别与度中性、K-壳中心性、介数中心性和特征向量中心性四种中心性方法进行比较. 实验结果表明, MKV方法的计算复杂度低, 在对网络进行静态攻击时, MKV方法能较大程度地破坏网络. 本文提出的中心性方法有效地提高了节点的重要程度的区分度, 并且通过传播实验分析发现该中心性方法具有较强的传播能力. MKV方法能够发现具有较强传播能力的节点, 同时这些节点对网络造成的破坏也远胜于K-壳方法. 通过对真实的网络进行实验, 对网络进行攻击时, MKV方法能较大程度地破坏网络; 同时在网络中进行信息传播时, MKV方法的传播能力相对较强, MKV方法可应用于实际网络中快速搜索具有传播能力强的节点.

2

-->

2.1.基于多阶邻居壳数的向量中心性方法

本文的算法是基于K-壳分解法进行的, K-壳分解法是一个递归的过程, 具体的分解过程如下: 第一步, 找到网络G中所有度值为1的节点, 将度值为1的节点及其连边一并删除, 得到一个子网络G1, 再选取子网络G1中所有度值为1的节点, 将该类节点及其连边删除, 直至子网络G2中不包含度值为1的子节点. 将这一步骤中删除节点的壳值ks定义为1; 第二步, 删除子网络G2中度值为2的节点及其连边, 重复第一步的递归过程, 将这一步骤中删除节点的壳值ks定义为2. 重复上述过程, 直到所有的点都分解到某个壳中^[12]. K-壳分解的示意图如图1所示.
图 1 K-shell分解法的示意图
Figure1. A diagram of the K-shell.

发掘二阶邻居的方法^[25]是: 1)查找目标节点vi的直接(一阶)邻居集合N_i¹; 2)查找 N_i¹中包含的所有节点的邻居节点集N_i², 且满足N_i¹ ∩ N_i² = $\emptyset$. 以此类推, 得出节点vi的多阶邻居.
设计该算法的思路是因为在K-壳分解法中节点的区分度很低, 需要设计一种新的方法提高节点壳数所度量的区分度. 本文将节点自身的壳值与其多阶邻居的壳值构造一个向量, 把多阶邻居的壳数放入权值不同向量元素中, 通过一个向量而不是一个简单的数值来度量节点的重要性程度, 该向量代表这个节点在网络中能够波及到的其各阶邻居节点的壳值的大小.
需要指出的是, 算法中多阶邻居的壳值, 指的是多阶低壳值邻居. 计算目标节点的多阶邻居过程中, 可能会出现部分壳值高于目标节点壳值的邻居, 在本文设计的算法中, 这些邻居并不统计.
对任意节点集合V中的节点v_i, 该节点的多阶邻居节点集合为N_i. 节点集合N_i中节点的数量为n_i. 设对每个节点v_i都存在一个m维(每个网络中节点最大的壳值是不同的, 此处的m是随着网络最大壳值的变化而变化的)向量x_i, 可将其表示为${{x}_{i}} = {\left( {{x_{i1}},{x_{i2}},\cdots,{x_{im}}} \right)^{\rm{T}}}$. 每一个向量x_i中的元素x_ij可以通过如下的式子来计算${C_j}\left(\! {{M_j}\left(\! {{v_k}}\! \right)} \!\right), {x_{ij}} = \mathop \sum \nolimits_{k = 1}^{{n_i}} $$j = 1,2, \cdots ,m$, 其中M_j(v_k)是一个给定的中心性指标, 在本文的情况下, 是节点v_k的K-shell中心性, v_k ∈ N_i. C_j(ξ)是一个如下给出的函数.

${C_j}\left( \xi \right) = \left\{\!\!\!{\begin{array}{*{20}{c}}{0,\quad {\rm{if}}\;\xi \ne j}\\{1,\quad {\rm{if}}\;\xi = j}\end{array}} \right..$

记${C_d}\left( {{v_i}} \right) = \mathop \sum \nolimits_{j = 0}^{{n_i}} {x_{ij}}$. 那么, x_i就是节点v_i的邻居向量. MKV算法的流程图如图2所示.
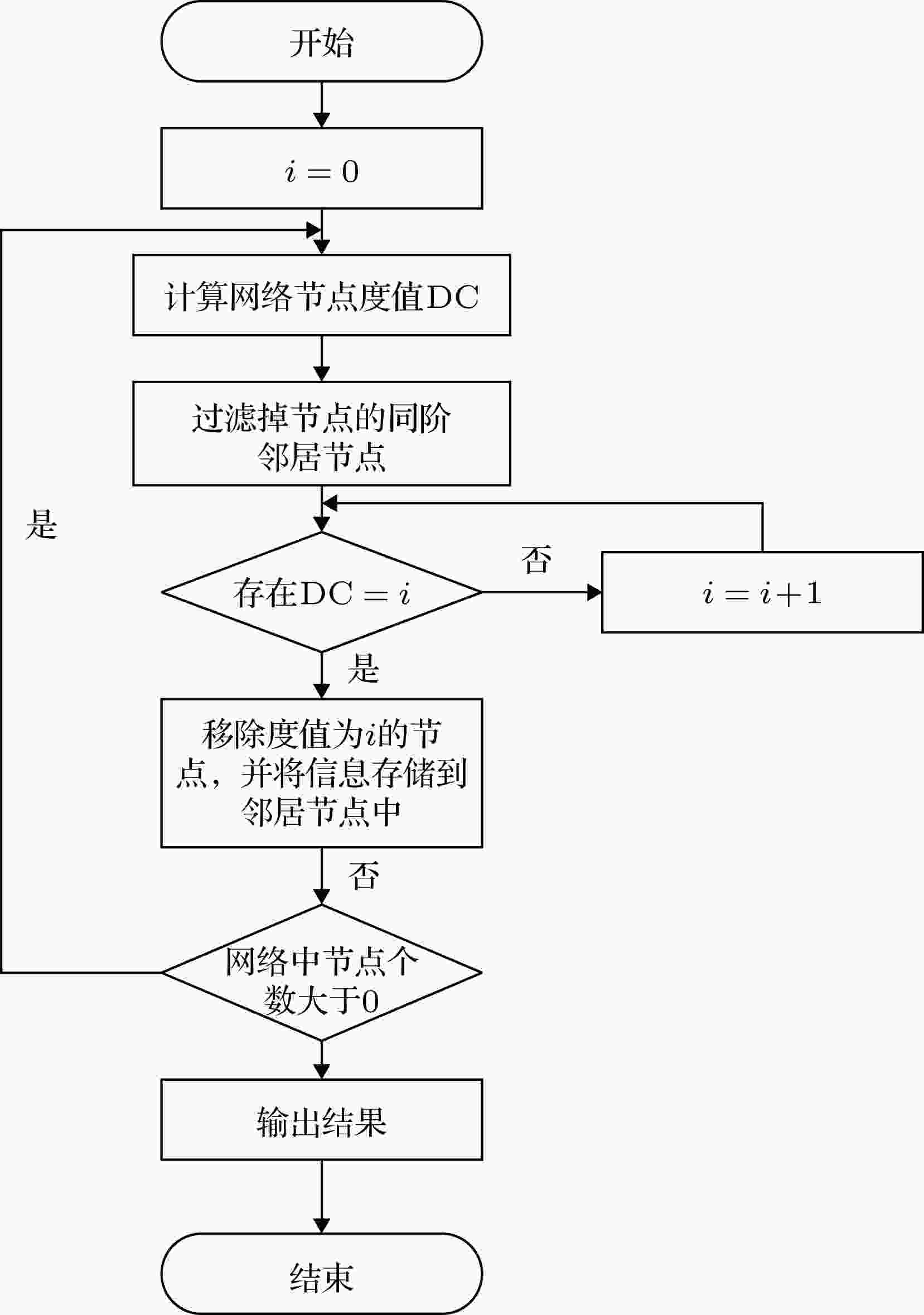图 2 MKV算法实现流程图
Figure2. MKV algorithm implementation flow chart.

通过流程图可以看出, 算法通过不断迭代, 将低壳数节点的信息记录在对应的高壳数邻居的向量中, 故此最终形成的向量, 带有该节点低壳数邻居的信息, 而阶数在同一网络中固定不变, 在不同网络中则不尽相同.
基于多阶邻居壳数的向量中心性构造的基本思想是本文希望将一个简单的壳值按照某种方式展开成一个向量. 一方面, 该方法可以使得节点的重要性更具区分度, 另一方面, 也可以通过对每个节点的自身及其多阶邻居的综合考察来考虑该节点在网络中的重要程度. 这样, 对于向量中的每个元素, 用一个数字来表示目标节点有多少个多阶邻居节点具有某一壳层的壳值. 对于节点v_i, 向量x_i中元素x_i1保存的是目标节点v_i多阶邻居中壳数为1的节点总数, x_i2保存的是目标节点v_i多阶邻居中壳数为2的节点总数, 以此类推, x_in表示节点v_i目标节点自身的壳数. 因此, 目标节点v_i的多阶邻居通过向量中的不同元素将其考虑成具有几个不同壳值等级, 这样可以直观地了解节点v_i.
以图1中的节点8和节点9为例来解释向量的含义, 节点8的展开向量为x₈ = (1,3,1)^T, 表示节点8的多阶邻居中壳值为1的节点个数有一个, 是节点4, 壳值为2的节点数有3个, 分别是节点9、节点10和节点11, 节点8自身的壳数是3; 节点9的展开向量为x₉ = (1,1,0)^T, 该向量表示节点9的多阶邻居中壳值为1的节点存在一个, 是节点4, 节点9自身的壳数为2, 不存在壳数为3的多阶邻居.
多阶邻居的壳数向量能够清楚地表明该节点在整个网络中的潜在影响力, 不仅表明了节点的层次性, 还可以表明该节点在多阶邻居中的影响力. 在K-shell方法中节点壳值相同时, 节点的影响力往往是不同的, 但是本文的方法可以度量出上述节点的重要性.
2 -->

2.2.多阶邻居壳数向量的比较方法

给定任意的两个向量x_q ∈ X与x_p ∈ X, 记${\varepsilon } = {{x}_q} - {{x}_p} = {({\varepsilon _1},{\varepsilon _2}, \cdots ,{\varepsilon _m})^{\rm{T}}}$. 使
${\varepsilon ^*} = \left\{ {\begin{array}{*{20}{c}}{{\varepsilon _m},{\varepsilon _m} \ne 0}\\{{\varepsilon _i},{\varepsilon _{i + 1}} = \cdots = {\varepsilon _m} = 0,{\varepsilon _i} \ne 0}\\{{\varepsilon _1},{\varepsilon _2} =\cdots= {\varepsilon _m} = 0}\end{array}} \right.$.
一个给定的二元关系$\prec$如下: 如果ε^* < 0, 那么x_q $ \prec $ x_p, 对应地, x_q的迭代壳数的向量中心性小于x_p. 同理, 如果ε^* > 0, 那么x_q$ \succ $x_p, 多阶邻居壳数向量x_q大于x_p. 同理, 如果ε^* = 0, 那么x_q = x_p, 也就是说多阶邻居壳数向量x_q等于x_p.
根据上述基于多阶邻居壳数向量的比较的定义, 向量比较算法流程图如图3所示.
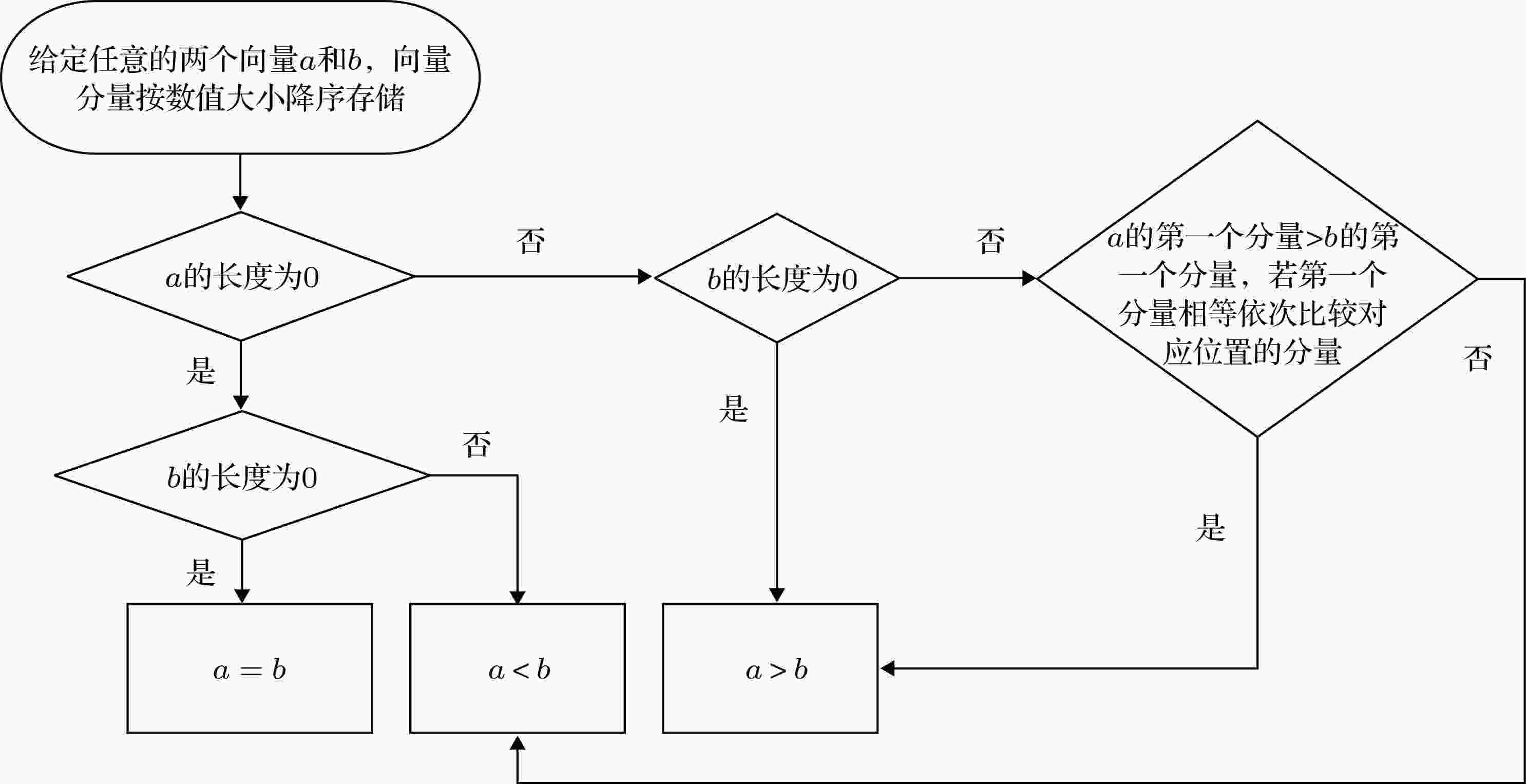图 3 向量比较大小算法流程图
Figure3. Flow chart of vector comparison size algorithm.

本文下面将进一步给出说明, 来证明本章的方法可以将目标网络中的所有节点进行有效的排序, 即, 向量集合S对于给定的二元关系$ \prec $是严格的全序集^[26].
定理: 二元关系$ \prec $使集合S是严格全序集, 等价于, 二元关系$\prec$满足如下条件:
1) $\forall$x, y ∈ S, x $\prec$ y, y $\prec$ x, x = y三个式子中, 仅有一个成立(三分性);
2) $\forall$x, y ∈ S, 如果x $\prec$ y, 那么y $\prec$ x不成立(不对称性);
3) $\forall$x, y, z ∈ S, 如果x $\prec$ y并且y $\prec$ z, 那么x $\prec$ z成立(传递性).
证明如下:
首先, 对任意的x, y ∈ S, 使得ξ = x – y. 那么一定有ξ_* < 0, ξ_* > 0或ξ_* = 0三者当中一个关系成立. 因此, 基于二元关系$\prec$的定义, 二元关系$\prec$是三分的.
其次, 如果x $\prec$ y, 那么ξ_* < 0. 所以, ξ_* > 0一定不成立, 也就等价于y $\prec$ x不成立.
最后, 对于任意给定的x, y, z ∈ S, 使得α = x – y, β = y – z, 那么ξ = α + β, 于是$x - z = $$ \left( {x - y} \right) - \left( {y - z} \right) = \alpha + \beta = \xi $. 基于二元关系$\prec$, 如果x $\prec$ y, 那么α_f < 0或者α_f = 0或者α_m < 0中的某一个成立. 类似地, y $\prec$ z意味着β_f < 0或者β_f = 0或者β_m < 0中的某一个成立. 因此, ${\xi _*} = \left\{ {{\xi _f}{\rm{|}}{\xi _f} \ne 0} \right\} \cup \left\{ {{\xi _m}{\rm{|}}{\xi _f} = 0} \right\} < 0$并且x $\prec$ z. 综上所述, 二元关系$\prec$具有传递性.
通过上面的证明, 可以看出多阶邻居向量和二元关系$\prec$的定义保证向量集合S是严格全序的. 因此, 本文给出的定义也就能够完成对所有节点重要性的排序.
2 -->

2.3.相关常用中心性方法

3 -->

2.3.1.度中心性(Degree Centrality)

度中心性是指一个节点的度越大就意味着这个节点越重要. 一个包含N个节点的网络图中, 节点度的中心性值定义为

${\rm{D}}{{\rm{C}}_i} = \frac{{{k_i}}}{{N - 1}},$

其中k_i表示节点i的度值, N – 1是指节点最大可能的度值为N – 1.
3 -->

2.3.2.介数中心性(Betweenness Centrality)

介数中心性是指经过某个节点的最短路径的数目来刻画节点重要性的指标. 将介数定义为

${\rm{B}}{{\rm{C}}_i} = \mathop \sum \limits_{s \ne i \ne t} \frac{{n_{st}^i}}{{{g_{st}}}},$

g_st是从节点s到节点t的最短路径数目, n_stⁱ是从节点s到节点t的g_st条最短路径中经过节点i的最短路径条数.
3 -->

2.3.3.特征向量中心性(Eigenvector Centrality)

一个节点的重要性既取决于其邻居节点的数量(即该节点的度), 也取决于其邻居节点的重要性, 记x_x为节点i的重要性度量值, 则:

${x_x} = c\mathop \sum \limits_{j = 1}^N {a_{ij}}{x_j},$

其中c为一个比例常数, 记${x} = {\left[ {{x_1},{x_2},{x_3}, \cdots ,{x_n}} \right]^{\rm{T}}}$, 经过多次迭代到达稳态时, 可以写成如下的矩阵形式:

${x} = cA{x}.$

2 -->

2.4.基于多阶邻居壳数的向量中心性方法时间复杂度分析

假设图G中节点个数为N, 边的数量为M, 度中心性的计算复杂度在稠密矩阵中为O(N²), 在稀疏矩阵中为O(M); 早期的介数中心性的时间复杂度为O(N³)^[27], Brandes^[28]改进的介数中心性时间复杂度为O(NM); EC算法的时间复杂度为O(N²); K-shell的时间复杂度是O(N).
本文提出的MKV方法要对网络中的每个节点的信息进行记录, 而对其中一个节点的邻居进行遍历的时候, 效率最差的情况就是B树的情形, 这种情形下时间复杂度是O(logN), 网络中节点总数是N, 所以MKV的时间复杂度是O(NlogN).
当变量N增大时, 时间复杂度的排序是$O\left( 1 \right) < O\left( {{\rm{log}}N} \right) < O\left( N \right) < O\left( {N{\rm{log}}N} \right) < O\left( {{N^2}} \right) <$$ O\left( {{N^3}} \right) < O\left( {{2^n}} \right).$ MKV比BC, EC方法的时间复杂度小, 表明MKV方法的算法效率更高; 与Degree, K-shell方法相比时间复杂度相对较低, 但是其节点包含的信息要远高于这两种方法.

2

-->

3.1.实验数据

为了证明本文设计的多阶邻居壳数的向量中心性方法的有效性和适用性, 本文选用了七个经典的复杂网络模型: 由小说《悲惨世界》中人物关系构成的悲惨世界复杂网络(简记为LesMiserables)^[29], 美国西部电力网拓扑结构构成的电力网(简记为PowerGrid)^[30], Rovira I Virgili大学(塔拉戈纳)成员之间电子邮件交换组成的网络(简记为Email)^[31], 2006年以前在网络科学领域所有科学家的论文合作网络数据集(Coauthorships in network science, 简记为Coauthor)^[32], 生活在新西兰两个街区的海豚之间的网络(Dolphin social network, 简记为Dolphin)^[33], 大肠杆菌代谢网络(简记为C. Elegans)^[34]以及著名的空手道俱乐部数据(Zachary's karate club, 简记为Club)^[35]. 上述这七个复杂网络来源于大量的复杂网络研究文献, 网络的具体信息如表1所列.

网络	节点数量	边数量	平均度值	聚集系数	平均路径长度	同配系数
LesMiserables	77	254	6.597	0.736	2.641	–0.4756
PowerGrid	4941	6594	2.669	0.107	18.989	0.4616
Email	1134	6556	11.563	0.526	1.992	–0.0436
Coauthor	1589	2742	3.451	0.878	5.823	0.0035
Dolphin	62	159	5.129	0.303	3.357	–0.1652
C.Elegans	453	4596	9.007	0.657	2.664	–0.1085
Club	34	78	2.29	0.588	2.408	–0.2145

表1本文中用到的几个网络基本信息
Table1.Several basic network information used in this paper.

2 -->

3.2.中心性的区分度实验

对于任意一种给定的中心性方法, 求得的节点中心性在数值上会存在一致的, 这就代表中心性的值是重复的. 在理论上, 具有相同中心性数值的节点的重要程度是没有办法区分的. 而在一个有N个节点的网络中, 中心性的重复度的定义为${\rm{RR}} = {r}/{N}$, 其中r表示该中心性方法中重复的中心性值的个数, 而中心性的区分度则可以定义为${\rm{DR}} = (N - r)/N$^[26]. 对本文用到的七个网络的中心性区分度分析计算得到结果如表2所列.

DR	BC	EC	Degree	K-shell	MKV
C.Elegans	66.225%	88.962%	8.830%	2.208%	40.839%
Club	61.765%	79.412%	32.353%	11.765%	47.059%
Coauthors	9.880%	29.264%	1.447%	0.692%	9.880%
Dolphin	87.097%	96.774%	19.355%	6.452%	70.968%
Email	62.346%	94.533%	4.586%	0.970%	53.263%
Power	59.279%	86.217%	0.324%	0.101%	8.561%
LesMiserables	41.558%	67.532%	23.377%	10.390%	37.662%

表2中心性的区分度在不同网络中的取值情况(越大越好)
Table2.Value of Centrality Distinction in Different Networks(the larger, the better).

根据中心性区分度的定义, 可以得出一个结论: 中心性指标的区分度DR值越大, 那么这就意味着网络中节点重要程度的区分度就越高. 通过表1得出, MKV方法的DR值要远远高于K-shell和度值中心性Degree, 虽然本文方法的中心性指标的区分度DR比BC和EC小, 但是与BC的DR值已经很是接近. 由此可以得出, MKV方法明显地提高了节点重要性的区分度.
2 -->

3.3.基于多阶邻居壳数的向量中心性的复杂网络的静态攻击

本文通过蓄意对网络进行静态攻击并观察网络的形态, 以此来验证评估节点的重要性. 具体过程如下:
1)计算每种中心性的度量值, 按照评估节点重要性算法的度量大小选取网络中重要性最高的n个节点;
2)蓄意地逐个移除网络中选中的重要节点及其连边;
3)计算并估计上述的攻击过程对网络造成的影响;
4)将删除的节点数量从0.1%增加到30%, 重复上述过程, 观察网络的状态, 并做出相关记录和分析.
在对复杂网络进行静态攻击的仿真实验中, 网络受到攻击后会破碎成零散的连接部件, 这些连接部件的数量表明了网络的破碎程度. 而网络中的最大连通子团可以表示剩余网络的网络连通性. 所以在评判网络的连通性时既要考虑子团的数量, 也需要考虑最大连通子团的节点数量. 美国电力网power在蓄意攻击后的最大连通子团以及子团数量的变化情况如图4和图5所示.
图 4 美国电力网power在静态攻击实验中最大连通子团变化情况
Figure4. Largest connected component during static attack experiment on power.

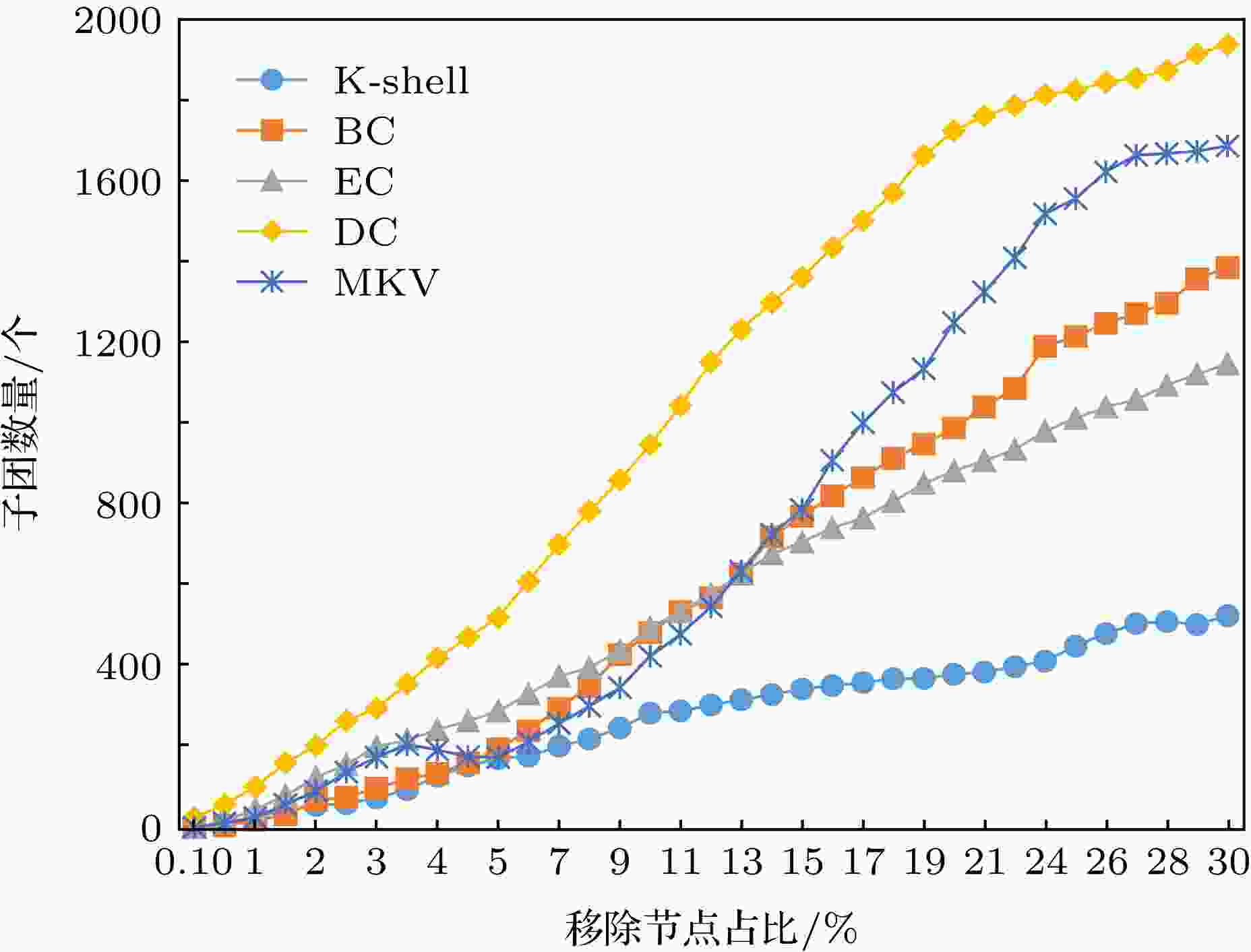图 5 美国电力网power在蓄意攻击实验中子团数量变化情况
Figure5. Total component number during static attack experiment on power.

最大连通子团的节点数量越少表明网络的连通性越差, 在网络中移除的节点越重要. 在图4中, 在删除节点数量到2%的时候MKV方法中最大连通子团的节点数量变化趋势接近于除了Degree外的几种方法, 而删除节点大于2%时本文方法的最大子团数量迅速减小, 相较于EC和K-shell两种方法是有一定优势的, 当移除节点达到15%后, MKV方法的结果要优于其他方法. 同样的在图5中, 子团数量在删除节点小于7%时, MKV方法和K-shell方法结果很相近, 而删除节点高于13%时, MKV方法效果明显优于EC, BC和K-shell方法, 与Degree方法的结果趋于一致. Degree方法在移除节点初期, 最大连通子团节点数量变化明显的原因是, 按Degree方法选择的重要节点移除时, 节点的邻居数量相对其他方法更多, 移除重要节点及其连边后最大连通子团的节点数量会锐减, 同时子团的数量会迅速上升. 在power网络的实验中, 攻击开始初期, MKV方法的效果不及EC, BC和Degree, 但是后期的效果是具有优势的, 可见, 对网络的蓄意攻击, MKV方法尽可能考虑的是长期收益, 而非短期收益.
为了量化度量攻击实验与节点重要性之关系, 本文对上述七个网络中选取移除节点的不同时间段的最大连通子团节点数量和子团数量进行了统计. 选取K-shell方法为基准方法, 根据公式${\rm{rl}} = {a}/{b}$求出七个网络在这些时间段的最大连通子团数量的平均值和最大值, 此处的b表示K-shell最大连通子团节点的数量, a分别代表其他四种中心性方法对网络蓄意攻击同时刻的最大连通子团节点的数量, 则rl表示其他方法攻击网络核心结构时最大连通子团比K-shell方法提升了多少. 同理, 子团数量根据公式${\rm{rb}} = {c}/{d}$求出其他方法在子团数量上比K-shell方法优化多少, 再统计其平均值和最小值, 此处的d代表K-shell中心性方法对网络蓄意攻击同时刻的连通子团的数量, c表示其他方法得到的连通子团的数量, 则 rb表示其他方法的子团数量对比K-shell方法的提升. 统计结果如图6和图7所示.
图 6 七个网络受到蓄意攻击中最大连通子团的统计情况(越小越好)　(a) 最大连通子团平均值情况; (b) 最大连通子团最值情况
Figure6. Largest connected component during static attack experiments on the seven networks(the smaller, the better)

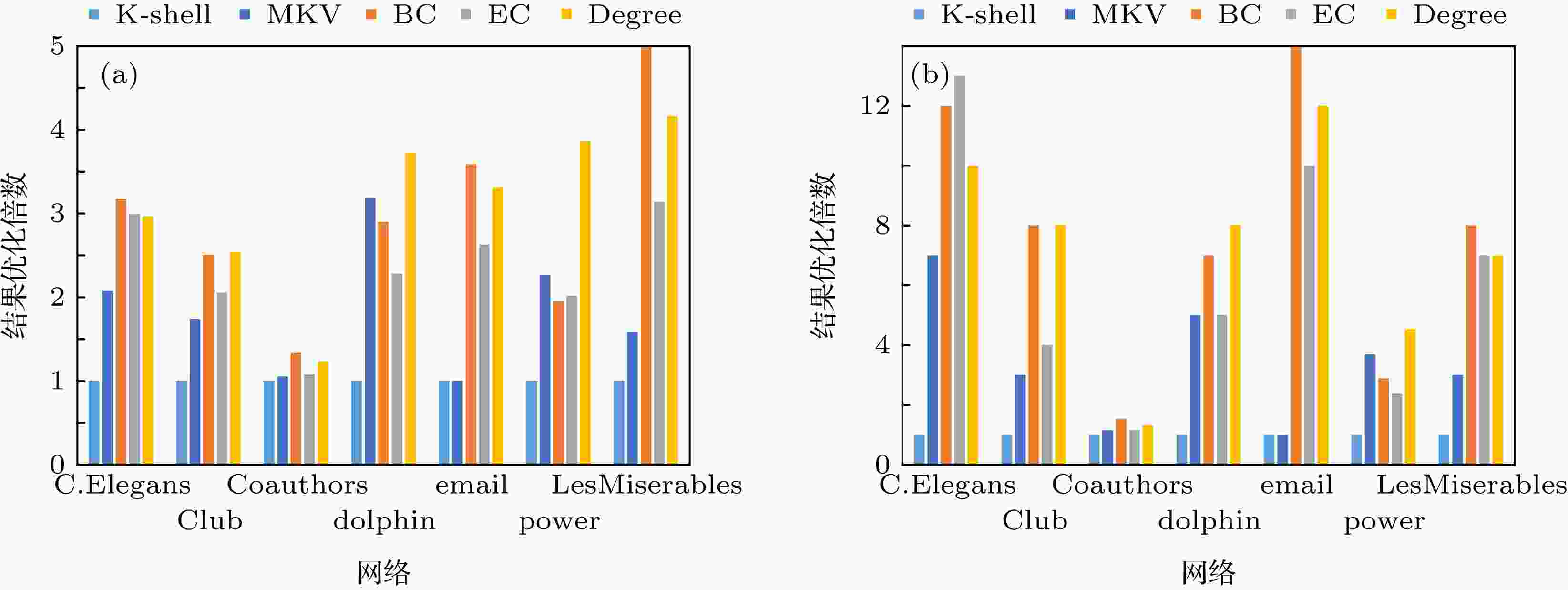图 7 七个网络静态攻击重要节点的子团数量的统计情况(越大越好)　(a) 子团数量平均值情况; (b) 子团数量最值情况
Figure7. The number of components during static attack experiments on the seven networks (the larger, the better)

在图6中, 以K-shell方法得到的结果为基准, 其他方法分别与K-shell方法比较, 图6中的值越小越好, 在不同的网络中MKV方法要优于K-shell方法, 与其他方法相比效果不明显, 但是与度值相比, MKV方法提高了节点重要性的区分度, 与BC, EC方法相比, 在时间复杂度上得到了有效的提升. power网络不是一个社交网络, 其平均路径长度较大且聚类系数较低, 在这个网络中最大连通子团的效果相对是有提升的. 因此对power这种类型的网络进行蓄意攻击时, MKV方法更具优势.
在图7中, 值越大表明网络受到蓄意攻击时得到的子团数量越多, 网络越破碎, 该度量节点重要性的方法就越具备优势. 从图7中看到五种评估节点重要性的方法得到的子团数量的最终结果, MKV方法得到的子团数量的结果要完全优于K-shell方法. MKV方法的效果虽不及其他几种方法, 但是在时间复杂度上要优于BC和EC, 在节点重要性的区分度上要优于度值中心性. 在power网络和dolphin网络中, 子团数量的效果占很大优势, 原因是这两个网络的聚集系数较低且平均路径长度较长, 在这类网络中, MKV方法得到的结果占优势. 综合上述图片的内容, 在对不同网络进行蓄意攻击时, MKV方法明显优于K-shell方法. 对于低聚类系数跟高平均路径长度的网络, MKV方法是占优势的, 且效果相对明显. MKV方法虽不是平均降低网络连通性的最佳选择, 但是MKV方法计算复杂度相对较低且倾向于优先破坏网络中的传播核心结构.
2 -->

3.4.基于多阶邻居壳数的向量中心性的复杂网络传播实验

本文采用SI(susceptible-infected)模型^[36]来仿真网络中重要节点的传播行为, SI模型将传染范围内的人群划分为两类: 1) S类: 易感人群, 这类人是指还未染病但是与感染病患者接触后以一定的概率α受到感染; 2) I类: 染病人群, 这类人是指已经患病的人群. SI传染过程如图8所示.
图 8 SI传播模型图
Figure8. SI propagation model diagram.

计算每种中心性的度量值, 将得出的度量值按数值降序排列, 选取网络中每种中心性度量值最大的节点设置为感染节点I, 该节点以感染比率α去感染易感节点, 将该传染过程迭代M次, 统计感染节点的数量. 并用所求得的感染节点数量来度量所选初始节点在网络中的传播能力.
以美国电力网power为例, 选取复杂网络中按评估节点重要方法度量值最高的节点设置为感染节点I, 感染节点以α = 0.001的概率去感染易感节点S, 将这个过程迭代1000次, 统计出迭代过程结束后的感染节点数量, 选取部分迭代次数的感染节点的数量绘制统计图. 美国电力网power的不同迭代次数感染节点统计图和大肠杆菌代谢网络C.Elegans不同迭代次数感染节点统计图如图9和图10所示.
图 9 美国电力网power在SI传播模型下感染节点的变化情况
Figure9. Change of infected nodes in Power of American Electric Power network under SI propagation model.

图 10 大肠杆菌代谢网络C. Elegans在SI传播模型下感染节点的变化情况
Figure10. Changes of infection nodes in C. Elegans network under SI propagation model.

在SI模型的实验中, 传播感染的节点数量越多, 证明该节点在网络中的重要程度越高. 如图9中结果显示的那样, 多阶邻居壳数的向量中心性MKV在美国电力power网络中传播的效果是第二优的, 通过分析得到EC算法的时间复杂度为O(N²), 而MKV方法是时间复杂度为O(NlogN), 在相同的条件下, MKV的传播效果虽然比EC的传播效果差, 但是MKV方法要比EC的计算代价低. 而在图10大肠杆菌代谢网络C.Elegans的SI传播实验中, 迭代壳数的向量中心性MKV方法要优于其他四种方法. 因为本文的目的是验证哪个中心性参数在度量节点重要程度上有最好的结果, 所以本文试图在这几种中心性传播过程中能感染最多的节点. 为了量化这一目标, 本文从上述七个网络SI传播实验中选取不同迭代次数的感染节点数对其统计. ${r_{{\rm{si}}}} = {p}/{q}$, q表示K-shell方法感染节点数量, p表示其余中心性方法感染节点数量, r_si表示其他方法感染的节点数量要比K-shell方法感染节点的数量高多少, 分别求出这些时间段的平均值和最大值. 统计结果如图11所示.
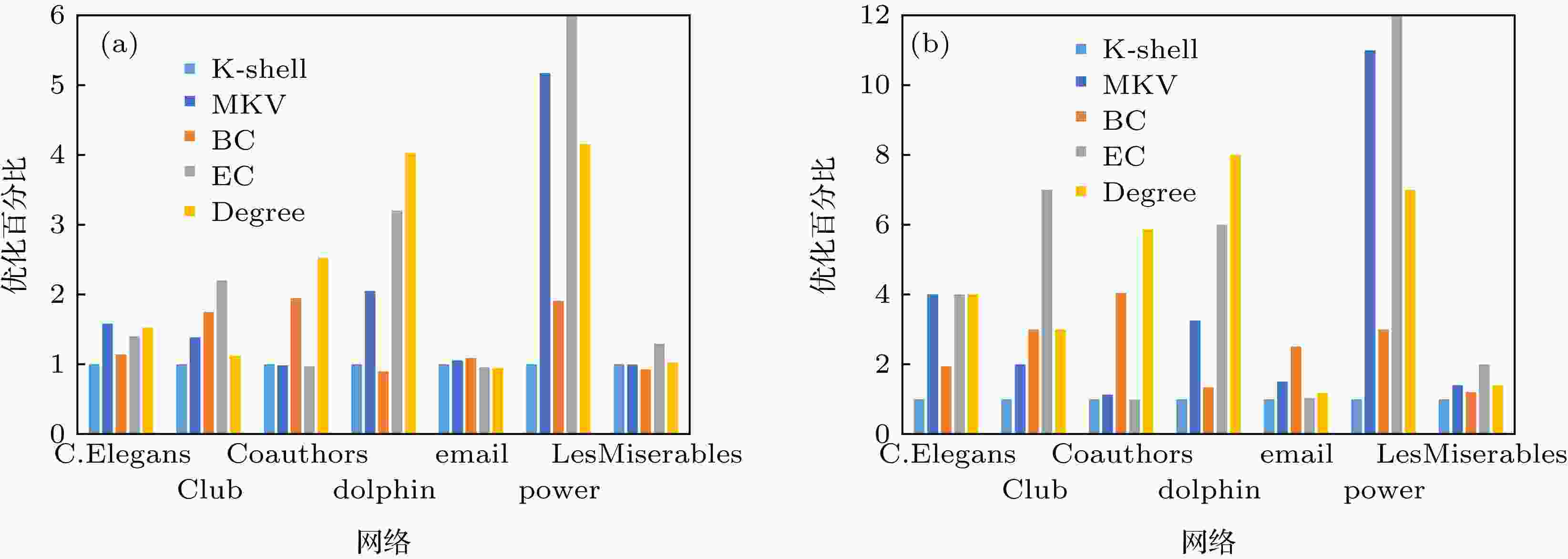图 11 七个网络传播感染节点的统计情况(越大越好)　(a) SI传播节点数量比较平均值; (b) SI传播节点数量比较最值
Figure11. The statistical result of infected nodes of seven network (the larger, the better)

对网络中进行SI传播实验时, 平均值和最大值的数值越大表明传播感染节点的效果越明显. 在图11中, 值越大表明感染的节点数量越多, 度量节点重要性的方法就越好. 在上述七个网络中, MKV方法得到的感染节点的数量与K-shell方法相比领先的比率是明显的. 在C.Elegans这个网络中, MKV方法的传播效果要完全优于其他方法, 在power网络中MKV方法的传播效果仅略低于EC方法传播的效果, 除此之外, 感染节点的数量要远高于其他方法的平均值和最大值, 在Coauthors网络和LesMiserables中MKV方法所占优势不太明显, 原因是这两个网络的平均度值相对较大且网络节点连接密集, 对该类型网络进行感染传播时, MKV方法的优势不太明显. 因此在传播感染的实验中, MKV在传播过程中在大多数网络中优于K-shell方法, 在半数网络中传播的效果要优于BC和Degree. MKV方法与度值相比, 提高了节点重要性的区分度, 而与BC, EC方法相比, 降低了时间复杂度, 所以MKV方法能够快速有效地发现具有强传播力的节点, 是网络传播信息的最佳选择. 对于少数平均度值高、网络连接密集的网络MKV方法的传播优势不太明显; 但是能够在大多数网络中发现具有强传播能力的节点, MKV方法是信息传播的最佳选择.

本文提出了多阶邻居壳数的中心性方法, MKV方法将节点自身及多阶邻居节点的重要性考虑在内, 并通过对七个不同类型真实网络进行SI传播和蓄意攻击网络两种实验, 与其他四种常用中心性方法进行了比较.
结果表明: 本文设计的MKV方法基于K壳中心性, 还保留了K壳中心性对节点在网络中层次的信息, 同时展示出节点低阶壳数邻居的分布情况. 此外, MKV方法具有高区别度、计算复杂度仅略高于度值, 但比度值提供了更多网络结构的信息; 在传播效率上, 仅次于特性向量中心性, 计算却更快捷; 在攻击实验过程中绝大多数情况下优于K壳中心性, 证明MKV方法在度量节点重要性程度上具有一定特点与部分优势.