摘要:在众多实验和理论研究中已经发现自突触通过自反馈电流调节神经元电活动和网络时空行为来实现生理功能. 本文通过理论研究, 发现在一些合适的时滞下, 抑制性自反馈电流能引起放电频率增加, 这是不同于传统结果—抑制性作用引起频率降低的新发现. 进一步, 对于没有自反馈的神经元, 发现在作用相位合适的抑制性脉冲电流的作用下, 放电的相位会提前, 导致放电频率增加, 这就表现出对应Hopf分岔的II型相位响应曲线的特征. 引起放电频率增加的抑制性脉冲刺激的相位与自反馈的时滞相对应, 这也就给出了自反馈能够引起放电频率增强的原因. 最后, 发现抑制性自反馈的时滞较长或耦合强度较大时, 噪声诱发的神经元放电峰-峰间期的变异系数较小, 也就是放电精确性提高, 与实验发现的慢抑制性自突触诱发放电精确性增加的结果相一致. 研究结果揭示了负反馈能增强系统响应这一新现象和相应的非线性动力学机制, 提供了调控神经电活动的新手段, 有助于认识现实神经系统的自突触的潜在功能.
关键词: Hopf分岔/
相位响应曲线/
抑制性自突触/
精确放电

English Abstract

全文HTML

--> --> -->

生物系统是复杂的非线性系统, 一直受到非线性科学的重点关注. 非线性动力学在识别神经系统中各种复杂的放电或振荡模式中起着重要的作用^[1-4]. 神经元的电活动包括静息和放电等. 静息对应于动力学中的稳定平衡点. 而膜电位处于大幅值振荡状态称为放电, 放电包括峰放电和簇放电等, 这与动力学中稳定的极限环相对应. 神经元从静息到放电以及从放电到静息的变化, 可以用动力学中的平衡点分岔进行描述^[1-4]. 已知的平衡点分岔包括不变圆上的鞍结分岔和Hopf分岔等. 不变圆上的鞍结分岔和Hopf分岔会导致神经元产生两类不同的兴奋性类型^[4-6], 即I型兴奋性和II型兴奋性. 随着去极化电流的增加, I型兴奋性的放电频率从零逐步增加到某个非零值, 对应于不变圆上的鞍结分岔; 而Ⅱ型兴奋性的放电频率则从某个非零值开始, 对应于Hopf分岔. I型和II型兴奋性神经元对应的外界兴奋脉冲扰动的相位响应曲线(phase response curve, PRC)^[7-10]不同. 脉冲扰动下的放电相位提前, 也就是PRC的值全正, 对应I型兴奋性; 扰动后放电的相位依赖于刺激脉冲相位, 可能提前, 也可能延迟, 也就是PRC的值部分为正、部分为负, 对应于II型兴奋性. 这分别对应I, II型PRC, 在经典的二维Morris-Lecar (ML)模型^[7,10]中得到了广泛的研究.
除了脉冲式的调控, 神经元电活动还受到噪声和突触介导的耦合电流等诸多因素的影响. 比如, 在很多类的神经元, 其放电模式的变化会受到自突触的调控^[11-15]. 自突触, 即神经元通过突触与自己建立联系, 这在大脑皮层、新皮层、视觉皮层、纹状体、海马和小脑等神经系统中都有解剖学观察^[11-15]. 通过生物学实验发现, 抑制性自突触是存在的^[15-19], 实验结合理论模型的工作确认了慢抑制性突触的存在性^[15,20], 可引起精确放电^[15]. 精确放电可用多次相同刺激试验中依次产生的动作电位的产生时间的标准差(standard deviation, STD)来度量, 或通过放电的峰峰间隔(interspike intervals, ISIs)的变异系数(coefficient of variation, CV)来刻画^[15-20]. CV值越小, 动作电位产生的时刻越准时, 放电序列越有规律, 意味着放电时刻越精确. 抑制性自突触诱发的精确放电发生在大脑皮层的新皮层, 并被认为通过影响新皮层的同步行为参与信息处理、行为整合和认知功能. 例如, Bacci等^[15,16]研究发现在新皮层上通过抑制性中间神经元的自突触传输可增加放电的精确性. 当Theta和Gamma振荡出现在海马和新皮层时, 海马中间神经元表现出精确的放电^[17,18]. Zhao等^[19]通过仿真发现超极化激活非特异性阳离子电流诱导神经元模型产生精确放电. 数值仿真还发现, 兴奋性自突触和抑制性自突触对神经元放电频率产生不同的影响^[21-27]. 因为实验发现慢抑制性自突触的存在, 即抑制性耦合电流再作用回神经元是需要时间的, 可以用时滞来模拟这一慢特征. 例如, 当引入时间延迟时, 自突触可以帮助增强神经元网络的集群活动和诱发靶波、螺旋波及同步行为^[28,29]; 带有时间延迟的抑制性自突触可以抑制神经元的混沌行为^[25]、产生相干共振^[30]等. 此外, 大量的电生理实验中采用动态钳(dynamic clamp)技术来调控突触或反馈电流的幅值或快慢来调控神经元或网络的电活动或时空行为^[31-33]. 其中, 自反馈调控也是一种潜在的调控神经元电活动的手段. 与现实神经系统的突触的快慢相对不能方便调控不同, 动态钳能够方便地调控突触的快慢. 例如, 当抑制性突触的时间常数由5 ms调整到600 ms, 交互抑制耦合的两个神经元可以从反相同步达到同相同步^[31]. 因此, 从理论上研究较长时滞的自反馈或自突触的调控作用对于认识现实的自突触的特性或者提出能用于动态钳实验的调控措施有指导意义.
一般情况下, 兴奋性作用增加放电, 抑制性作用降低放电^[34], 表现在放电频率或峰峰间隔ISIs的变化. 但是, 最近的研究发现抑制性作用可以增强放电, 如抑制性自突触可引起簇放电的增加^[27,35,36]; 而兴奋性作用也会降低放电个数^[37]. 实际上, 目前的峰放电的II型PRC曲线都是针对兴奋性脉冲的, 其特征是兴奋性脉冲在一些作用相位下可以使得放电提前, 在另外的相位可以使得放电延后. 抑制性脉冲激励下的II型相位响应会表现出什么特征, 目前并不清晰. 抑制性的脉冲激励是否能使得放电提前也就是增强放电? 假若能, 那么抑制性自反馈或自突触会不会引起峰放电的增加呢? 这都是亟待回答的非线性动力学问题. 此外, 抑制性自反馈或自突触诱发的精确放电是否能够在理论模型中获得解释, 也是对神经科学问题有重要意义的.
因此, 本文通过理论模型研究神经峰放电在抑制性作用下的PRC, 发现某些相位下放电提前; 进一步研究了峰放电频率在抑制性自反馈作用下会提高, 可以用PRC进行解释; 最后, 较长时滞的自反馈能够诱发放电精确性提高, 与实验发现的慢抑制性自突触诱发放电精确性增加相一致. 研究结果揭示了抑制性作用的新功能并给出了非线性动力学解释, 给出了调控放电频率增加的新措施, 抑制性反馈而不是兴奋性反馈; 这些结果有助于认识现实神经系统的抑制性自突触的潜在功能.

2

-->

2.1.ML模型和自反馈模型

ML模型和自反馈模型^[10,20,23]如下:

$\begin{split}C\,\frac{{{\rm{d}}{\kern 1pt} V(t)}}{{{\rm{d}}{\kern 1pt} t}} = & - {g_{{\rm{Ca}}}}{m_\infty }(V(t))(V(t) - {V_{{\rm{Ca}}}}) \\ & - {g_{\rm{K}}}w(t)(V(t) - {V_{\rm{K}}}) - {g_{\rm{L}}}(V(t) - {V_{\rm{L}}}) \\ & + I + {I_{{\rm{aut}}}}, \end{split}\tag{1a}$

$\frac{{{\rm{d}}{\kern 1pt} w(t)}}{{{\rm{d}}{\kern 1pt} t}} = \phi \,\frac{{{w_\infty }(V(t)) - w(t)}}{{{\tau _{\rm{w}}}(V(t))}},\tag{1b}$

其中C是膜电容, V(t)和w(t)分别是膜电压和延迟整流K⁺电流的激活变量. (1a)式等号右边的前三项分别表示Ca²⁺电流、电压门控延迟整流K⁺电流和漏电流. 参数g_Ca, g_K和g_L分别是钙电流、钾电流和漏电流的最大电导率. V_Ca, V_K和V_L分别是钙电流、钾电流和漏电流的反转电位. I表示外激励的(去极化)电流; I_aut为自反馈电流, 可以对应现实神经系统的自突触电流. I_aut的表达式如下:

${I_{{\rm{aut}}}} = - {g_{{\rm{aut}}}}(V\left( t \right) - {V_{{\rm{syn}}}})\varGamma (t - \tau ),\tag{1c}$

其中$\varGamma (t - \tau ) = 1/\{1 + \exp [ - (V(t - \tau ) - {\theta _{{\rm{syn}}}})/\lambda ]\}$. 这里θ_syn = –20 mV, λ = 1, τ表示时间延迟, g_aut是自反馈强度, 可以对应自突触的电导. 当V_syn = –60 mV时, I_aut是抑制性自反馈电流, 可以对应抑制性自突触电流; 当V_syn = 50 mV时, I_aut是兴奋性自反馈电流, 可以对应兴奋性自突触电流. 相关的函数的表达式如下:

$\begin{split} & {m_\infty }(V) = 0.5\left[ {1 + \tanh \left( {\frac{{V - {V_1}}}{{{V_2}}}} \right)} \right], \\ & {w_\infty }(V) = 0.5\left[ {1 + \tanh \left( {\frac{{V - {V_3}}}{{{V_4}}}} \right)} \right], \\ & {\tau _{\rm{w}}}(V) = {\left[ {\cosh \left( {\frac{{V - {V_3}}}{{2{V_4}}}} \right)} \right]^{ - 1}}. \end{split}$

ML模型产生II型兴奋的参数设置如下: C = 5 mF/cm², V_K = –80 mV, V_Ca = 120 mV, V_L = –60 mV, g_K = 8 mS/cm², g_Ca = 4 mS/cm², g_L = 2 mS/cm², V₁ = –1.2 mV, V₂ = 18 mV, V₃ = 4 mV, V₄ = 17.4 mV, ? = 0.066667.
2 -->

2.2.PRC的定义

PRC, 又称相位重置曲线^[7-10], 用于描述神经元振子做周期性放电时, 外界激励对峰放电发放时间或相位偏移的影响. 假设神经元模型存在一个周期为T₀的稳定极限环. 外界激励作用于以峰值时刻开始计时的时刻t_s, 刺激后的放电的峰值出现在时刻T₁, 如图1(a)所示, 则刺激相位φ = t_s/T₀, 放电的相位为T₁/T₀, 因此, 相位重置Δ(φ)定义为
图 1 当I = 45.5 μA·cm^–2, 方波脉冲幅值A = 1.65 μA·cm^–2, 宽度d = 4.4 ms时, ML模型的放电序列和PRC　(a) 方波脉冲刺激电流(短划线)、没有方波脉冲的放电(点线)和有方波脉冲的放电(实线); (b) PRC
Figure1. Spiketrains and PRC of the ML model when I = 45.5 μA·cm^–2, A = 1.65 μA·cm^–2, and d = 4.4 ms: (a) Square pulse disturbance current (dashed line), and spike trains without (dotted line) and with square pulse disturbance (solid line); (b) PRC.

$\Delta \left( \varphi \right) = ({T_0} - {T_1})/{T_0},$

Δ(φ)与φ的关系曲线即相位重置曲线(或PRC). 此外, 为了方便, 也可以定义

$PR\left( {{t_s}} \right) = {\rm{ }}({T_0} - {T_1})/{T_0}.$

本文使用外激励电流为幅值为A, 宽度为d的方波脉冲. 例如, 当I = 45.5 μA/cm²时, ML模型的放电周期$T_0 \approx $ 56.37 ms, 如图1(a)中的点线所示; 在t_s = 40 ms处, 受方波脉冲电流(幅值A = 1.65 μA/cm², 宽度d = 4.4 ms)激励, 如图1(a)中的实线所示, 方波脉冲扰动后的放电发生在T₁ $ \approx$ 52.3 ms. 由(3)式可计算在t_s = 40 ms处的相位重置PR $\approx$ 0.072, 对应φ $ \approx$ 0.71的Δ(φ) $\approx $ 0.072. 若计算周期内每一点的相位重置, 则可得PRC, 如图1(b)所示. 在图1(b)中, 大约在t_s < 27 ms时, PRC取值为负, 表明方波脉冲激励使峰放电延后, 而在t_s > 27 ms时, PR取值为正, 说明方波脉冲激励使峰放电提前. 这种相位有正有负的PRC即为II型PRC, 对应Hopf分岔附近的放电^[7-10].
2 -->

2.3.精确放电的度量

由于现实的神经元放电受噪声的影响, 因此噪声会影响神经元放电的精确性. 为了研究噪声对神经元放电的影响, 在模型的方程(1a)的右端加入高斯白噪声I_noise如下:

${I_{{\rm{noise}}}} = D\xi \left( t \right),$

其中, ξ(t)表示高斯白噪声, D表示噪声强度. 为了估计放电的规律性, 假设放电序列中的尖峰时刻发生在t_i (0 ≤ i ≤ N), 那么放电的峰峰间隔ISIs定义为ISIs_i = t_i+1 – t_i.
本研究采用ISIs的CV来刻画放电的精确性. 通过如下公式计算CV:

$CV = \frac{{\sqrt {Var\left( {ISIs} \right)} }}{{\left\langle {ISIs} \right\rangle }},$

其中, $\sqrt {Var\left( {ISIs} \right)} $表示ISIs的标准差, $\left\langle {ISIs} \right\rangle $表示ISIs的平均值. CV值越小, 放电序列越有规律, 即放电定时越精确. 本文主要研究了放电模式下ISIs的标准差和CV值, 并采用N = 2000个ISIs计算CV值.

2

-->

3.1.ML模型的平衡点的亚临界Hopf分岔

在没有自突触的作用下(I_aut = 0), 以I作为分岔参数, ML模型的平衡点分岔见图2(a). 随着分岔参数I的增大, ML模型在I $\approx $ 45.23 μA/cm²处发生亚临界的Hopf分岔. 通过该分岔点, 稳定焦点(粗实线)转化为不稳定的焦点(虚线), 同时产生不稳定的极限环(点线). 不稳定极限环和稳定极限环(细实线)在I $\approx $ 44.65 μA/cm²处发生极限环的鞍结分岔. 当44.65 μA/cm² < I < 45.23 μA/cm²时, 系统出现共存行为, 即稳定的极限环(放电)和稳定的焦点(静息)共存, 如图2(a)所示. 而当I > 45.23 μA/cm²时, 系统只出现稳定的极限环, 即单稳状态. 如当I = 45.5 μA/cm²时, 可得到ML模型的单稳放电序列, 放电周期T₀ $\approx $ 56.37 ms, 如图2(b)所示. 而当I < 44.65 μA/cm²时, ML模型处于静息状态, 如图2(c)(当I = 44 μA/cm²时的静息状态)所示. 在极限环稳定的范围内, 随着I的增大, 放电周期ISIs (图2(d)实线)单调减小, 频率(图2(d)虚线)单调增加, 但二者在单稳放电区域内变化不大, 如图2(d)所示. 本文研究的是靠近分岔点的放电/单稳极限环.
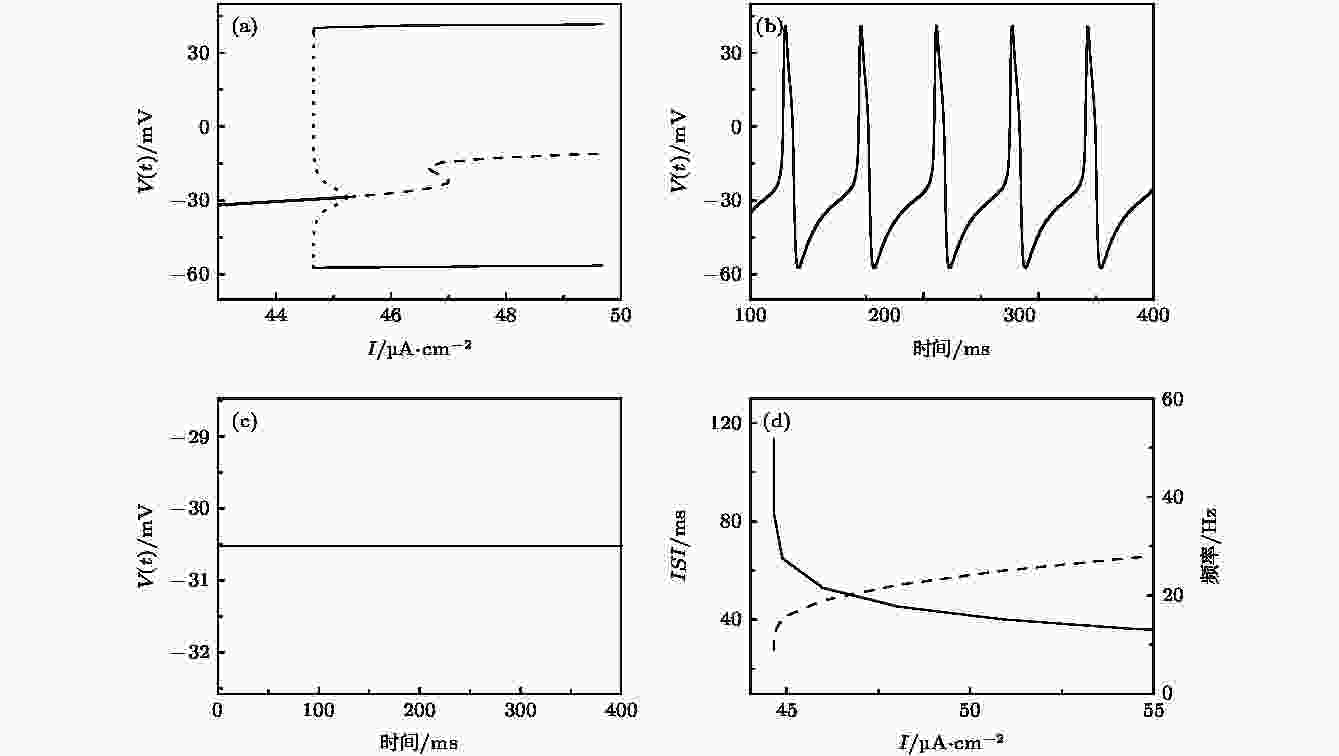图 2 (a) ML模型随I的平衡点分岔; (b) 当I = 45.5 μA·cm^–2时, ML模型的放电序列图; (c) 当I = 44 μA·cm^–2时, ML模型处于静息状态; (d) ISIs和频率随I的变化(实线表示ISIs, 虚线表示频率)
Figure2. (a) Bifurcation of ML model with respect to I; (b) spike trains of ML model when I = 45.5 μA·cm^–2; (c) resting state of ML model when I = 44 μA·cm^–2; (d) the changes of ISIs (solid line) and frequency (dashed line) with respect to I.

2 -->

3.2.抑制性脉冲作用下的II型PRC及推测

3 -->

3.2.1.抑制性脉冲作用下的II型PRC

以前的研究表明, 正向方波脉冲电流可使靠近Hopf分岔点的放电提前或延迟, 即II型PRC, 如图1所示. 本文研究负向方波脉冲电流作用于放电的不同相位的PRC, 发现该曲线与正向方波脉冲引起的PRC的形状关于横坐标(刺激时刻)轴大约是对称的, 其相位也是有正有负的. 例如, 当I = 45.5 μA/cm²时, ML模型峰放电靠近Hopf分岔, 接受负向脉冲电流的刺激, 刺激相位不同时, 可使得放电提前或延迟, 如图3所示. 图3中红色的点线表示没有方波脉冲刺激, 也就是原始的放电序列, 虚线表示负向方波脉冲电流, 实线表示负向方波脉冲扰动后的放电序列. 取负向方波脉冲的幅值A = –0.6 μA/cm², 宽度d = 4.9 ms, 作用在t_s = 22 ms处, 可得到负向方波脉冲激励后的放电序列(实线在红色的点线前)提前了, 如图3(a)所示. 同样地, 增大负向方波脉冲幅值的绝对值, 如A = –1.65 μA/cm², d = 4.8 ms, 负向方波脉冲激励后的放电序列(实线在红色的点线前)也提前了, 如图3(b)所示. 而当负向方波脉冲作用在t_s = 40 ms处, 负向脉冲作用后的峰放电(实线在红色的点线后)延迟了, 如图3(c)和图3(d)所示. 刺激强度越大, 放电的延迟越大, 如图3(d)比图3(c)的刺激强度大, 其延迟就越大.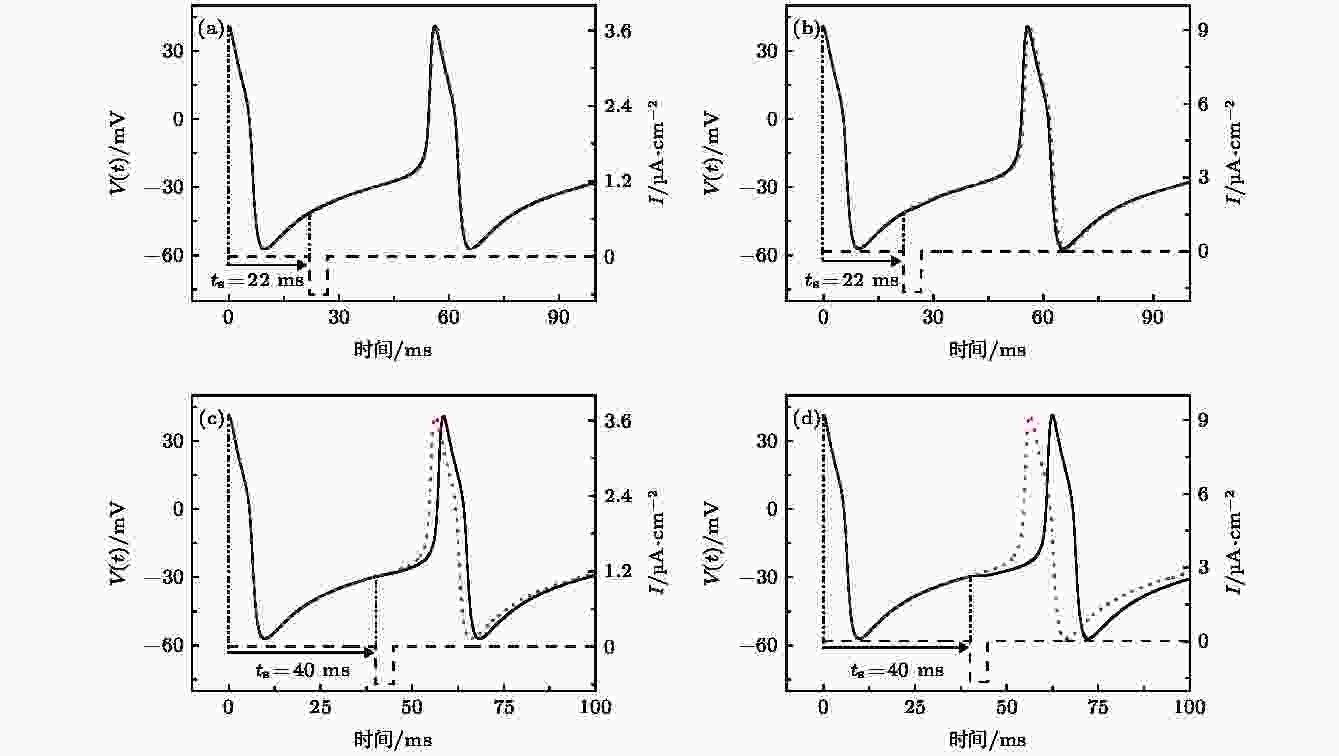
图 3 当I = 45.5 μA·cm^–2时, 负向方波脉冲电流(虚线)作用在不同相位的放电序列(实线)和无方波脉冲作用的放电序列(红色的点线)　(a) t_s = 22 ms, A = –0.6 μA·cm^–2, d = 4.9 ms; (b) t_s = 22 ms, A = –1.65 μA·cm^–2, d = 4.8 ms; (c) t_s = 40 ms, A = –0.6 μA·cm^–2, d = 4.9 ms; (d) t_s = 40 ms, A = –1.65 μA·cm^–2, d = 4.8 ms
Figure3. Spike trains induced by square pulse current applied at different phases when I = 45.5 μA·cm^–2. The spike trains (solid line) influenced by negative square pulse current (dashed line) and the trains (red dotted line) without negative square pulse current. (a) t_s = 22 ms, A = –0.6 μA·cm^–2, d = 4.9 ms; (b) t_s = 22 ms, A = –1.65 μA·cm^–2, d = 4.8 ms; (c) t_s = 40 ms, A = –0.6 μA·cm^–2, d = 4.9 ms; (d) t_s = 40 ms, A = –1.65 μA·cm^–2, d = 4.8 ms.

利用图3中负向方波脉冲的幅值和宽度可分别做出其对应的PRC曲线, 如图4所示. 图4(a)中, 当负向方波脉冲的幅值A = –0.6 μA/cm², 宽度d = 4.9 ms时, 大约在t_s < 27.2 ms时, PR取值为正, 表明负向方波脉冲激励使峰放电提前, 而在t_s > 27.2 ms时, PR取值为负, 说明负向方波脉冲激励使峰放电延迟, 这与图3(a)和图3(c)相一致. 类似地, 当负向方波脉冲的幅值A = –1.65 μA/cm², 宽度d = 4.8 ms时, 其PRC如图4(b)所示. 大约在t_s < 27.4 ms时, PR取值为正, 而在t_s > 27.4 ms时, PR取值为负, 这也较好地与图3(b)和图3(d)相吻合. 图4所示的负向脉冲PRC与图1(b)所示的正向脉冲诱发的PRC的形状关于横坐标(刺激时刻)轴大约是对称的. 刺激强度越大, 放电的延迟越大, 如图4(b)比图4(a)的刺激强度大, 其延迟就越大.
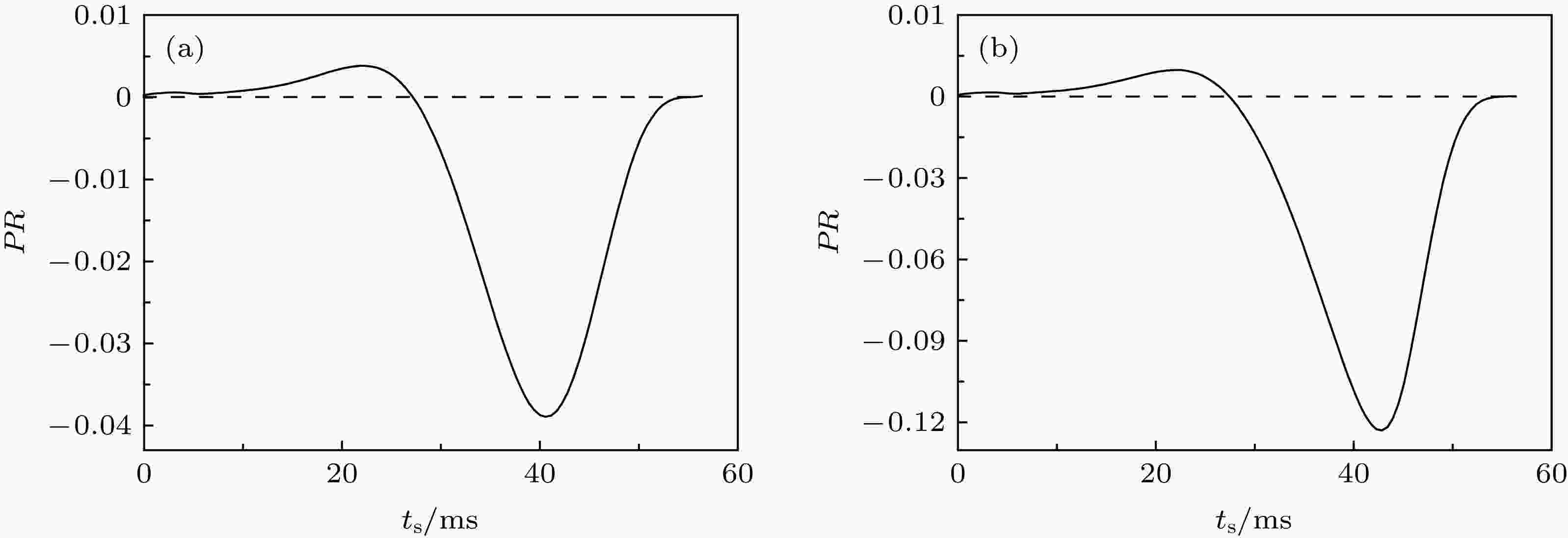图 4 当I = 45.5 μA·cm^–2时, ML模型在Hopf分岔点附近的负向脉冲刺激诱发的PRC　(a) A = –0.6 μA·cm^–2, d = 4.9 ms; (b) A = –1.65 μA·cm^–2, d = 4.8 ms
Figure4. PRC induced by negative square pulse current near the Hopf bifurcation point in the ML model when I = 45.5 μA·cm^–2: (a) A = –0.6 μA·cm^–2, d = 4.9 ms; (b) A = –1.65 μA·cm^–2, d = 4.8 ms.

3 -->

3.2.2.基于II型PRC推测抑制性自反馈电流的作用

图4所示的II型PRC有助于理解抑制性自突触作用下神经元电活动的动力学性质和频率变化. 对于具有抑制性自突触的神经元, 抑制性自突触电流的表达式为${I_{{\rm{aut}}}} = - {g_{{\rm{aut}}}}(V\left( t \right) - {V_{{\rm{syn}}}})\varGamma (t - \tau )$, 其时间历程如图5中的虚线所示, 在很大程度上与图3中的激励脉冲相似. 自突触的时滞τ可以调节抑制性自突触电流脉冲的作用相位, 对应于刺激相位t_s; 而抑制性自突触脉冲电流的幅值由自突触强度g_aut决定, 对应于刺激脉冲电流的幅值A. 因此, 自突触电流作用下的放电与PRC曲线有一定的对应关系. 合适的τ值下, 抑制性自突触电流会引起动作电位间隔变小, 也就是放电峰峰间期变小, 放电频率增加, 即放电增强; 另外的τ值下, 抑制性自突触电流会引起动作电位间隔变大, 放电频率降低, 即放电减弱. 不同的自突触电导g_aut, 对应于刺激强度A值的不同, 放电ISIs或频率的变化程度是不同的.
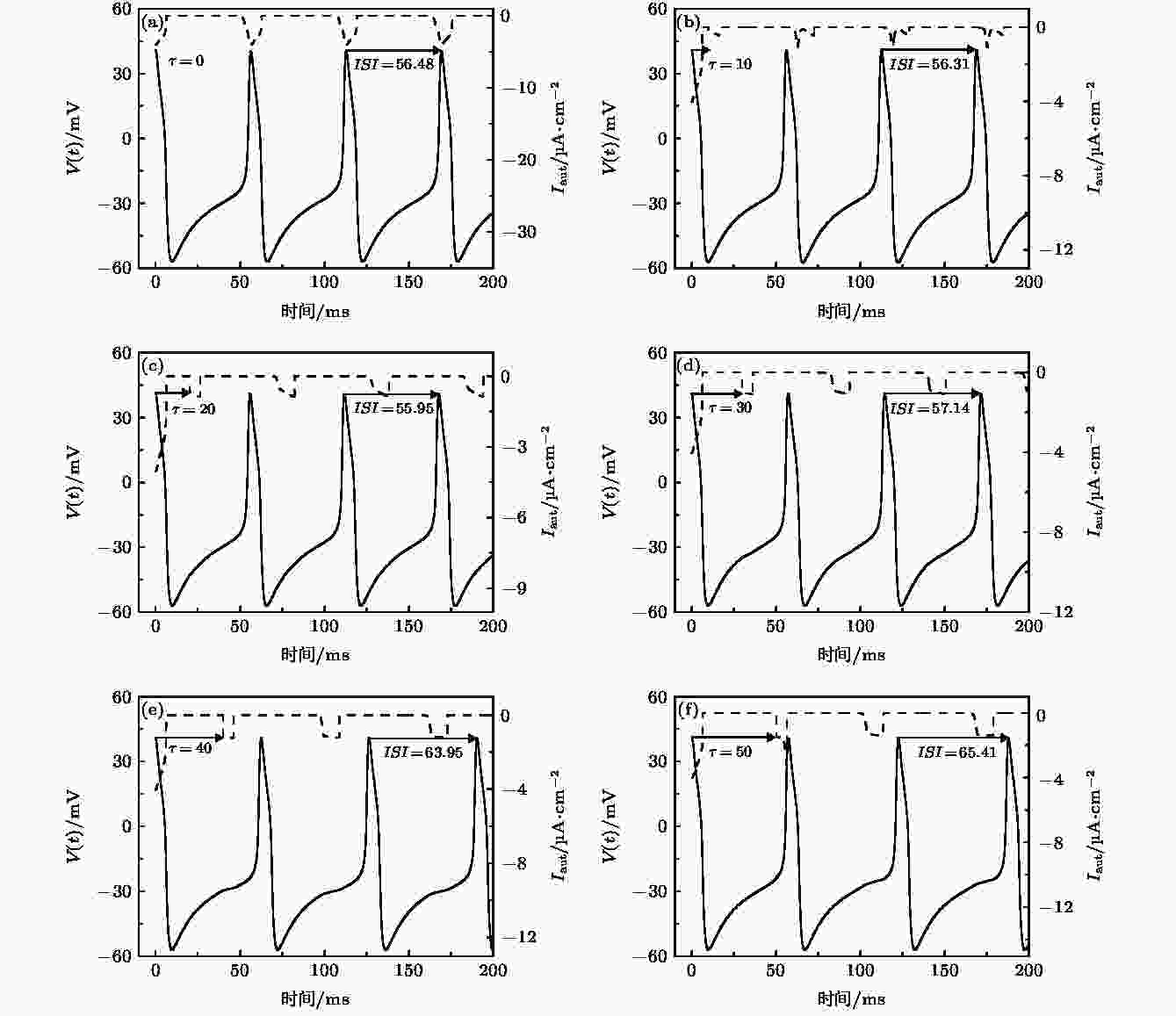图 5 当I = 45.5 μA·cm^–2, g_aut = 0.04 mS·cm^–2, 具有抑制性自突触ML模型的放电模式(实线)与抑制性自突触电流(短划线) (a) τ = 0 mS; (b) τ = 10 mS; (c) τ =20 mS; (d) τ = 30 mS; (e) τ = 40 mS; (f) τ =50 mS
Figure5. Inhibitory autapse current (dashed line) and spike trains (solid line) of the ML model with inhibitory autapse when I = 45.5 μA·cm^–2 and g_aut = 0.04 mS·cm^–2: (a) τ = 0 mS; (b) τ = 10 mS; (c) τ = 20 mS; (d) τ = 30 mS; (e) τ = 40 mS; (f) τ =50 mS.

2 -->

3.3.抑制性自反馈对神经元模型峰放电模式的影响

3 -->

3.3.1.抑制性自反馈的时滞τ对ML模型峰放电的影响

具有自反馈的ML模型的数值模拟结果验证了上述的推测结果. 下面以I = 45.5 μA/cm², g_aut = 0.04 mS/cm²为例介绍ML模型在抑制性自反馈电流作用下, 随着时滞τ 的增大放电模式的变化. 虚线表示抑制性自反馈电流, 实线表示神经元模型放电序列, 如图5所示. 图5中, 抑制性自反馈电流的幅值和宽度大约分别与图3中抑制性脉冲的幅值和宽度相对应. 当τ = 0 ms时, 放电周期为56.48 ms, 大于单神经元的放电周期; 当τ = 10和20 ms时, 放电周期分别为56.31和55.95 ms, 小于单神经元的放电周期, 即峰放电提前, 这与图4(b)中大约在t_s < 27.4 ms时, PR取值为正相吻合; 当τ = 30, 40和50 ms时, 放电周期分别为57.14, 63.95和65.41 ms, 大于单神经元的放电周期, 即峰放电延迟, 这与图4(b)中大约在t_s > 27.4 ms时, PR取值为负相一致.
3 -->

3.3.2.不同耦合强度g_aut下的归一化ISIs随时滞τ的变化

在抑制性自反馈电流作用下, 神经元模型可能不会立即引起尖峰, 但可以改变ISIs, 即放电周期. 利用时滞τ调节抑制性自反馈电流作用在神经元模型放电周期的不同相位, 可以测量ISIs随时滞τ的变化. 为了更好地揭示神经元模型放电周期如何随时滞τ变化, 将ISIs进行归一化处理, 即将ISIs除以没有自反馈电流的放电周期T $\approx$ 56.37 ms. 若ISIs/T > 1, 则放电周期延长; 若ISIs/T < 1, 则放电周期缩短. 例如, 当g_aut = 0.01 mS/cm²时, 归一化的ISIs随时滞τ的变化如图6所示. 图6(a)中, 粗实线表示归一化的ISIs随时滞τ的变化, 细实线表示其放电频率随时滞τ的变化. 图6(a)和图6(b)中ISIs/T = 1对应的τ值大约分别是27.2 ms和27.4 ms. 当时滞τ < 27.2 ms时, ISIs/T几乎都小于1, 这与图4(a)中PR值大于0相对应, 说明放电周期缩短, 其对应的放电频率增加. 抑制性自反馈可以诱发放电频率增加是一个不同于抑制性作用降低放电频率的传统观念的新观点. 而在时滞τ > 27.2 ms时, ISIs/T几乎都大于1, 这与图4(a)中PR值小于0相对应, 说明放电周期延迟, 其对应的放电频率降低. 同样地, 当g_aut = 0.04 mS/cm²时, 也可以得到类似的结论, 这与图4(b)中的PRC相对应, 如图6(b)所示. 图6(a)中频率的变化范围大约从17.06—17.78 Hz, 图6(b)中频率的变化范围大约从13.9—17.9 Hz; 刺激强度越大, 对PR的影响越大.
图 6 不同耦合强度g_aut下归一化的ISIs (粗实线)和放电频率(细实线)随时滞τ的变化　(a) g_aut = 0.01 mS·cm^–2; (b) g_aut = 0.04 mS·cm^–2
Figure6. Change of normalized ISIs (boldsolid line) and firing frequency (thin solid line) with respect to time delay τ: (a) g_aut = 0.01 mS·cm^–2; (b) g_aut = 0.04 mS·cm^–2.

3 -->

3.3.3.在噪声扰动下的ISIs变化和PRC特征

当噪声强度D = 0.5 μA/cm²时, 平均ISIs对时滞τ和耦合强度g_aut的依赖关系如图7所示. 红色区域表示平均ISIs小于56.37 ms, 即平均ISIs降低; 绿色区域表示平均ISIs大于56.37 ms, 即平均ISIs增加. 说明在τ约小于31 ms时放电是提前的, τ约大于31 ms时放电是延迟的. 与图3所示的确定性模型的结果相一致, 说明PRC曲线的特征在噪声作用下有一定的鲁棒性.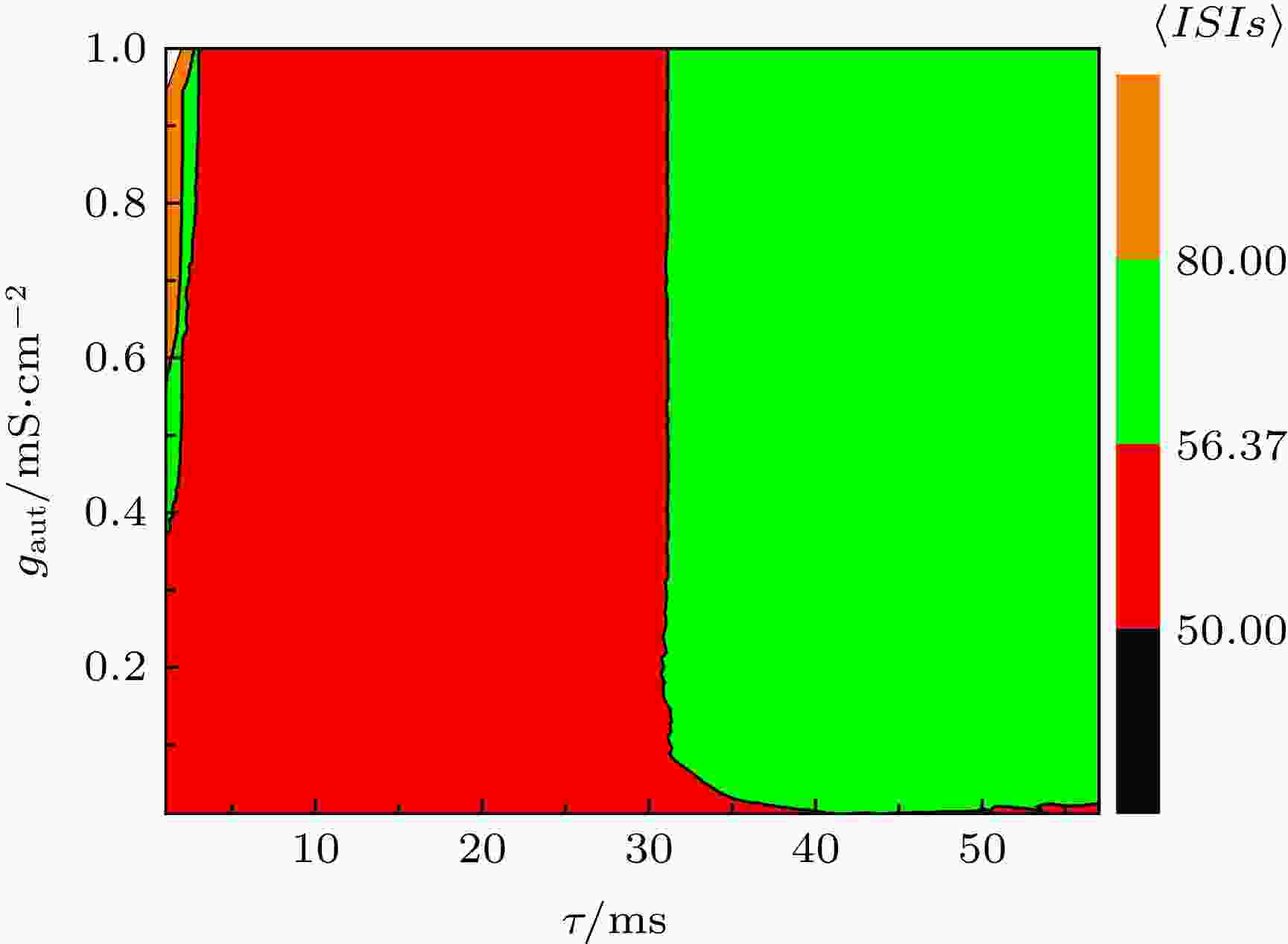
图 7 当噪声强度D = 0.5 μA·cm^–2时, 平均ISIs对时滞τ和耦合强度g_aut的依赖关系
Figure7. Dependence of average ISIs on time delay τ and coupling strength g_aut when D = 0.5 μA·cm^–2.

2 -->

3.4.抑制性自反馈引起精确放电

生物学实验中将神经元发放的精确性定义为动作电位峰值时刻的抖动(jitter), 量化为多次相同刺激实验中顺序产生的动作电位的尖峰时间的标准差STD^[15,16], 也可量化为动作电位平均ISIs的CV^[15,16]. 放电精确性衡量神经系统的电活动在存在外界扰动比如噪声的情况下的响应特性. 通过神经元模型的平均ISIs的标准差和CV来反映抑制性自反馈引起的精确放电现象.
当I = 45.5 μA/cm², 噪声强度D = 0.5 μA/cm²时, 放电的平均ISIs的标准差STD在 (τ, g_aut)平面的分布, 也就是对时滞和耦合强度的依赖关系, 如图8(a)所示. 平均ISIs的标准差有以下几个特点: 首先, STD的低值主要出现在(τ, g_aut)平面中间的区域, 即放电精确性高的产生区域; 如在g_aut = 0.25—1 mS/cm²和τ = 25—31 ms, STD的变化范围大约是3—6. 其次, 当g_aut < 0.25 mS/cm², 或τ < 25 ms, 或τ > 31 ms时, STD的值都较大(大于6). 最后, 在延迟较小时(τ = 1—2 ms), 随着耦合强度的增大(g_aut > 0.35 mS/cm²), STD出现较大的波动.
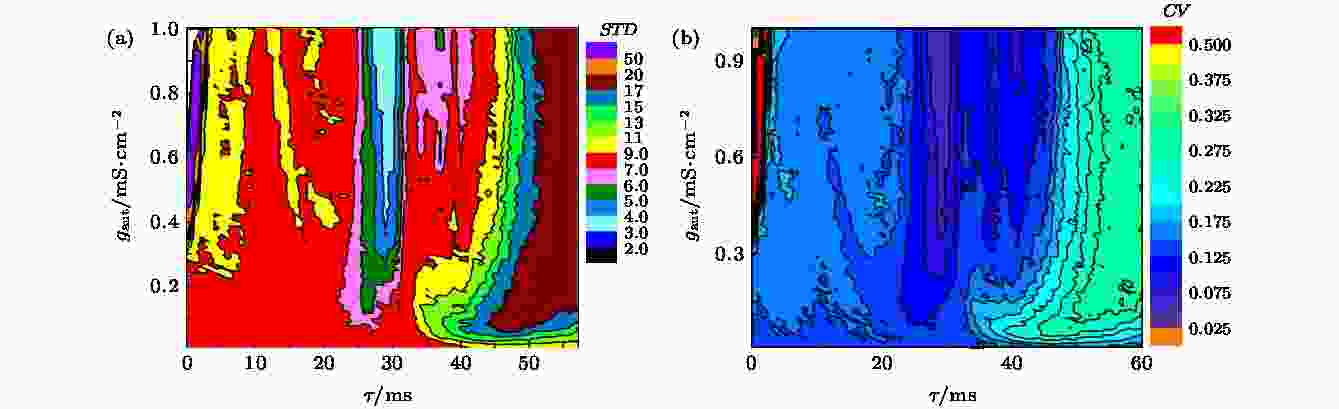图 8 当I = 45.5 μA·cm^–2, D = 0.5 μA·cm^–2时, (a) ISIs的STD对时滞τ和耦合强度g_aut的依赖关系, (b) ISIs的CV对时滞τ和耦合强度g_aut的依赖关系
Figure8. (a) Dependence of standard deviation of ISIs (STD) on time delay τ and coupling strength g_aut; (b) the dependence of coefficient of variation of ISIs (CV) on delay τ and coupling strength g_aut. The parameter values are I = 45.5 μA·cm^–2 and D = 0.5 μA·cm^–2.

当I = 45.5 μA/cm², 噪声强度D = 0.5 μA/cm²时, 放电的平均ISIs的CV在(τ, g_aut)平面的分布, 也就是对时滞和耦合强度的依赖关系, 如图8(b)所示. CV的值越小, 表明神经元模型放电具有较高的放电精确性. 从图8(b)可以看出, 时滞τ大约在25—35 ms的范围内、及在耦合强度g_aut > 0.2 mS/cm²且时滞τ大约在35—48 ms的范围内神经元模型放电具有较高的放电精确性. 上述结果说明精确放电发生在时滞相对较大的情况下, 这与实验发现抑制性自突触是慢突触有一定的对应性^[15].
在图8(b)中, 若固定时滞τ, 可得到ISIs的CV随着耦合强度g_aut的变化, 如图9所示. 当D = 0.5 μA/cm²时, 在时滞τ = 27 ms, 随着耦合强度g_aut的增大, CV的值逐渐变小, 说明放电越来越精确, 如图9(a)所示. 在时滞τ = 30, 40, 46 ms时, 耦合强度越大, 放电精确性越高, 如图9(b)—(d). 因此当固定时滞τ时, 随着耦合强度g_aut的增大, 峰放电精确性越高, 这与实验现象相一致^[15].
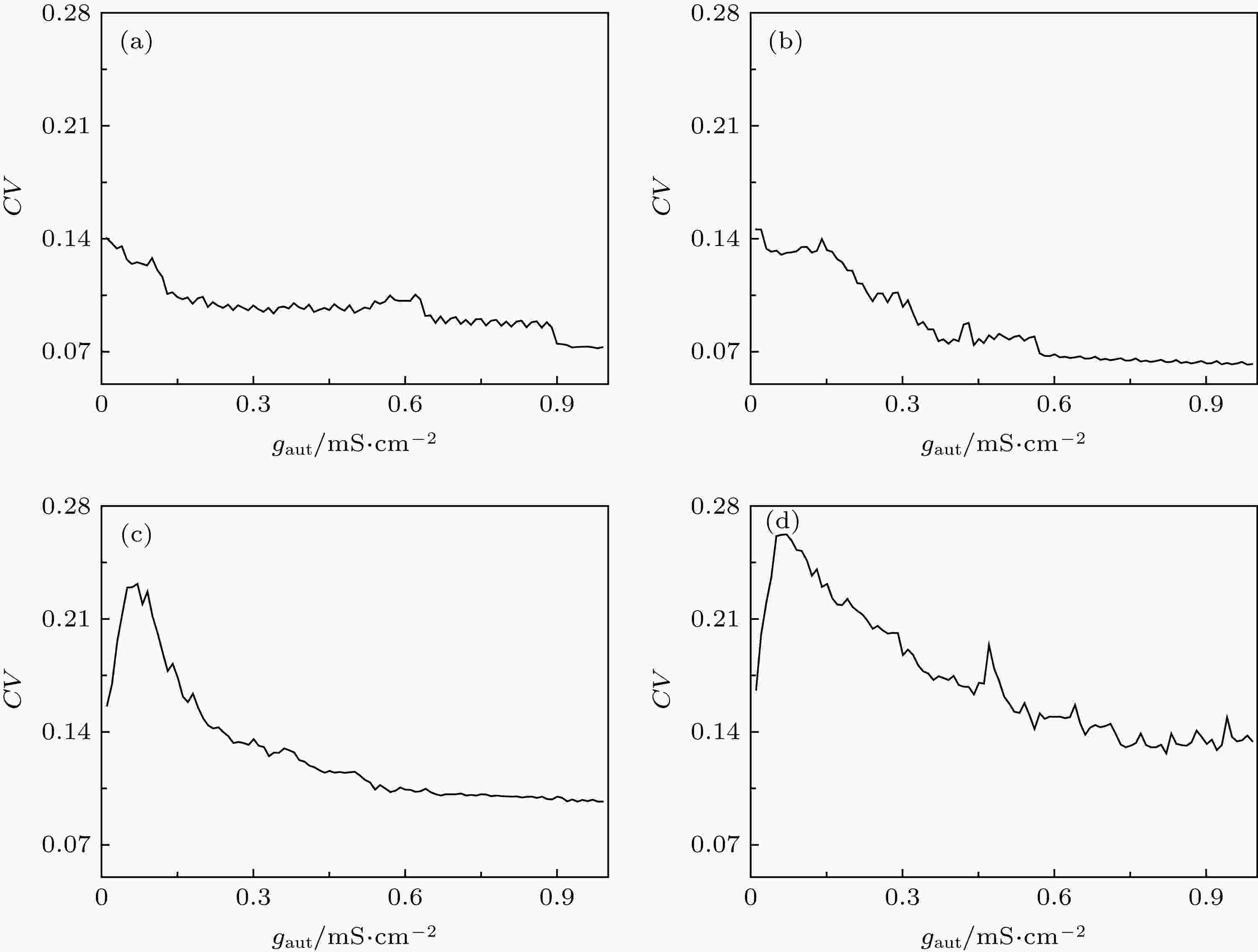图 9 固定时滞τ在不同水平下, ISIs的CV随着耦合强度g_aut的变化　(a) τ = 27 ms; (b) τ = 30 ms; (c) τ = 40 ms; (d) τ = 46 ms
Figure9. Changes of coefficient of variation (CV) of ISIs with respect to coupling strength g_aut when time delay τ is fixed at different values: (a) τ = 27 ms; (b) τ = 30 ms; (c) τ = 40 ms; (d) τ = 46 ms.

与图9类似, 若固定耦合强度g_aut, 可得到ISIs的CV随着时滞τ的变化, 如图10所示. 在图10(a)中, 随着时滞τ的增大, CV的值先变小后逐渐变大, 大约在τ = 28 ms时, CV达到最小值. 同样地, 在g_aut = 0.61 mS/cm², τ = 30 ms时(图10(b)), CV达到最小值.
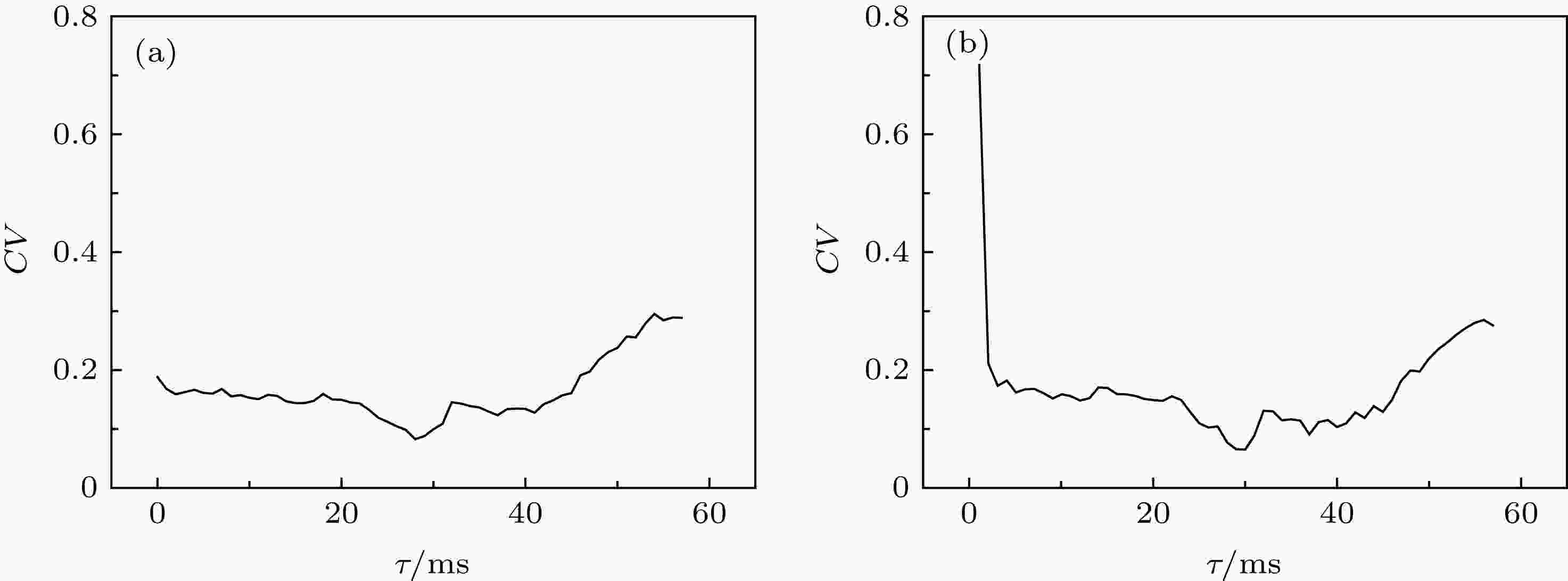图 10 固定耦合强度g_aut在不同水平下, ISIs的变异系数CV随着时滞τ的变化　(a) g_aut = 0.31 mS·cm^–2; (b) g_aut = 0.61 mS·cm^–2
Figure10. Changes of coefficient of variation (CV) of ISIs with respect to time delay τ when coupling strength g_aut is fixed at different levels: (a) g_aut = 0.31 mS·cm^–2; (b) g_aut = 0.61 mS·cm^–2.

从神经元模型的放电序列图也可以看出时滞的变化对精确放电的影响. 例如当I = 45.5 μA/cm², D = 0.5 μA/cm², g_aut = 0.61 mS/cm²时, 在图11中展示了不同时滞下精确放电的差异. 当时滞τ = 1, 10, 30, 50 ms时, 其变异系数CV的值约分别为0.72, 0.16, 0.06和0.22, 即在τ = 30 ms时, CV的值最小. 说明在τ = 30 ms时抑制性自反馈可较好地使神经元模型放电精确, 如图11(c)所示.
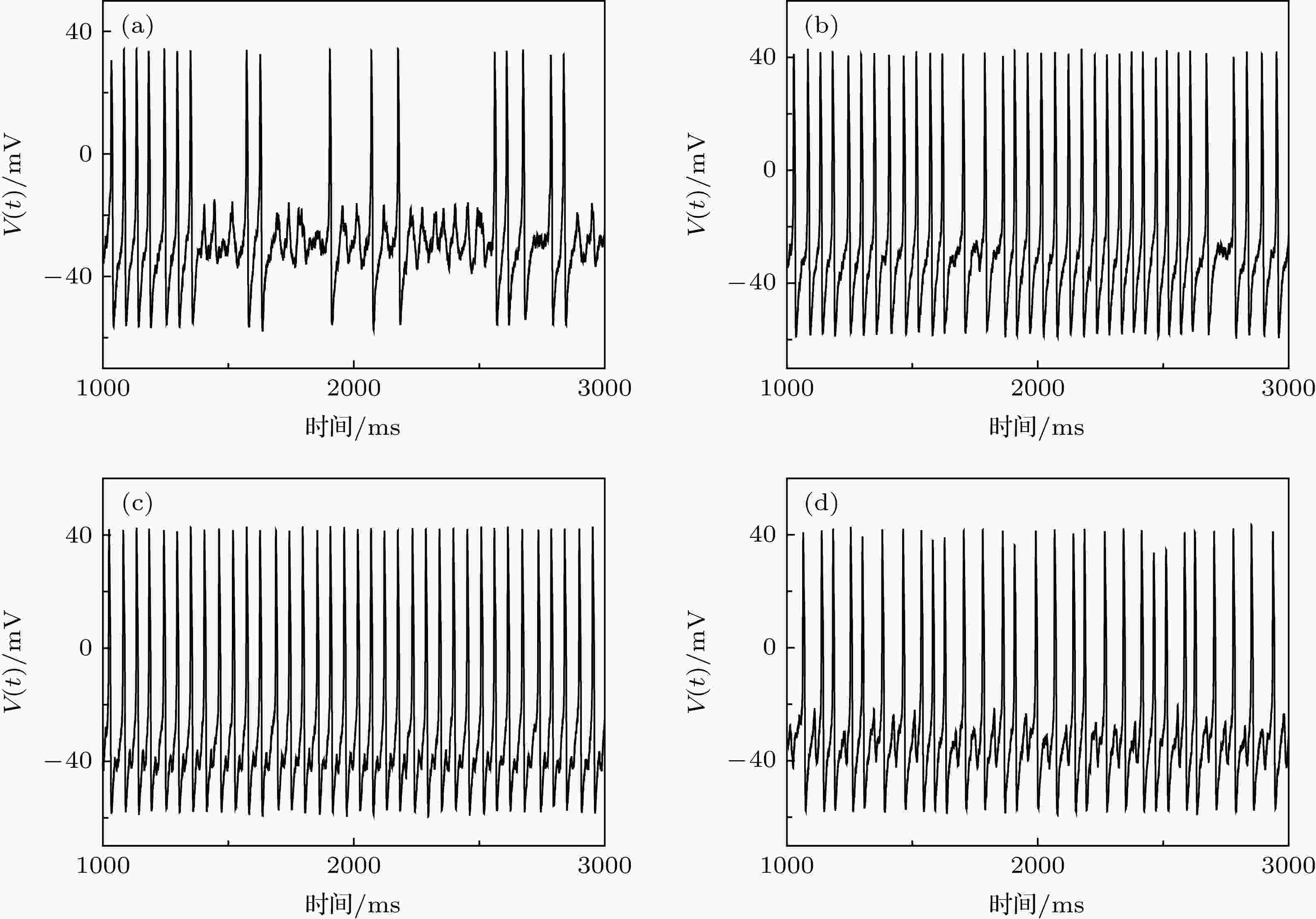图 11 当I = 45.5 μA·cm^–2, D = 0.5 μA·cm^–2, 耦合强度g_aut = 0.61 mS·cm^–2时, 时滞τ对神经元模型的精确放电的影响　(a) τ = 1 ms; (b) τ = 10 ms; (c) τ = 30 ms; (d) τ = 50 ms
Figure11. Effect of time delay τ on spike-timing precision of neuron model when I = 45.5 μA·cm^–2, D = 0.5 μA·cm^–2, and g_aut = 0.61 mS·cm^–2: (a) τ = 1 ms; (b) τ = 10 ms; (c) τ = 30 ms; (d) τ = 50 ms.

本文研究了抑制性自反馈增强放电活动这一新现象, 并可以用PRC进行解释, 提示了自突触的新的潜在功能, 主要结论如下.
1)抑制性自反馈的负反馈电流能引起峰放电频率增加, 在噪声作用下这一特性仍旧能够维持, 这是不同于传统结果—抑制性作用引起频率降低的新发现, 也是反常的神经动力学和神经电活动现象. 以前抑制性刺激引起的反常神经电活动研究包括抑制性刺激诱发静息变为放电^[26]、抑制性耦合引起簇放电频率增强^[27]和抑制性耦合增强同相同步^[35,36], 而本文则揭示了抑制性作用增强峰放电的放电频率, 是一个不同于前两个结果的抑制性刺激增强电活动的新例证, 丰富了神经动力学关于反常电活动的内涵.
2)抑制性作用增强电活动的反常现象可以用PRC进行解释, 揭示了抑制性电流脉冲激励引起峰放电增强的动力学机制. 以前的研究主要关注了正向方波脉冲电流可使靠近Hopf分岔点的放电提前或延迟, 即II型PRC, 并用PRC揭示了多类神经电活动的动力学特征如兴奋性和同步等^[7-9,38-40], 这些结果有利于认识兴奋性作用的特性和功能. 而本文研究了负向方波脉冲电流作用于放电的不同相位的PRC, 发现该曲线与正向方波脉冲引起的PRC的形状关于刺激时刻的坐标轴大约是对称的, 其相位也是有正有负的, 即放电提前或延迟, 从而揭示了抑制性电流脉冲激励引起峰放电增强的动力学机制. 因此, 该II型PRC将有助于进一步理解-抑制性作用下神经元电活动的动力学性质和功能.
3)本文还揭示了抑制性自反馈可以增强放电精确性, 这是在较长的时滞下产生的, 与实验发现的慢抑制性自突触诱发精确放电相一致^[15]; 进一步, 抑制性耦合越强, 精确放电越高, 也与实验结果相一致^[15]. 研究结果理论仿真了抑制性自突触诱发和增强放电精确性的实验结果, 这就通过理论模型揭示了抑制性自突触新的潜在功能. 而放电精确性是神经系统实现生理功能的重要保证.
因此, 本研究揭示了新的神经电活动的反常现象和相应的动力学机制, 提供了调控神经电活动和生理功能的新手段, 对于进一步认识抑制性作用的动力学机制和生理功能有重要的意义.