摘要:运用分子动力学方法探索了水-黑磷流-固界面各向异性、水流驱动力、黑磷通道宽度和黑磷层数等对黑磷通道内Poiseuille水流流动特性的影响规律. 研究结果表明: 随着驱动力的增加, 边界滑移速度随之增加; 各向异性也会对压力驱动作用下纳米通道内的水分子的流动特性产生影响, 具体表现为边界滑移速度会随着手性角度的增加而减小, 而水分子黏度系数却不受各向异性的影响. 发现黑磷表面天然的褶皱结构所产生的粗糙势能表面, 是导致流固界面各向异性特性的本质原因. 在加速度值保持不变的情况下, 研究纳米通道宽度和黑磷层数对水分子流动特性的影响, 发现随着纳米通道宽度的增加, 水分子滑移速度随之减小; 双层模型中水分子的速度分布与单层模型差异微小, 而随着层数的增加, 黑磷-水流固交互界面能随之增加, 各向异性规律依然保持不变. 研究结果将为水-黑磷流体器件设计与制备提供理论基础.
关键词: 黑磷/
各向异性/
流-固界面/
分子动力学

English Abstract

全文HTML

--> --> -->

近年来, 随着微/纳尺度技术的不断发展, 越来越多的低维材料开始走出实验室并应用于实践中, 低维材料^[1-3]在物理、化学、电学和光学等方面所表现出来的优良性能也推动着微/纳流体器件的发展, 使得微/纳流体器件的生产与应用成为可能, 例如: 微/纳机电系统^[4-6]、微/纳生物传感器^[7]和微/纳芯片^[8]等. 这些微纳流体器件^[9,10]可以进入宏观流体器件无法到达的区域, 并具有低能耗、高灵敏度和高精度等特点, 但目前关于微/纳流体器件的机理研究还处于探索阶段, 需要进行相应的研究和补充, 而微/纳流体器件中经常涉及的问题就是流体在纳米通道内的流动特性^[11,12]和流-固界面机理的研究^[13,14].
黑磷^[15-17]作为目前比较热门的低维材料, 不仅具有特殊的光学、电学特性, 还具有高载流子迁移率及天然带隙等特点^[18]. 除此之外, 由于黑磷表面特殊的褶皱结构所导致的各向异性也是一个非常值得深入研究的特性. 目前关于黑磷各向异性的研究主要集中于力学^[19]、电学^[20]和光学^[21]方面. Chen等^[19]利用原子力显微镜测量放置在凹槽上的不同手性的黑磷纳米带的力学特性, 结果发现沿锯齿型方向和扶手椅型方向上测得的理想弹性模量分别为65和27 GPa, 得到黑磷的力学性能会受到各向异性影响的结论. Liu等^[20]将黑磷应用于场效应管中, 通过将四对金属接触点按间距45°进行放置, 研究各向异性对黑磷场效应管的影响, 结果发现黑磷场效应管的漏极电流会随着角度的变化而变化. Xia等^[21]分别将厚度为2—5 μm的黑磷薄膜按30°的间距进行分块, 并进行红外偏振处理, 结果发现不同角度黑磷的波长存在很大区别, 即各向异性可以对黑磷的光学特性产生影响. 而目前关于各向异性对黑磷表面上流体流动特性影响的研究却很少, 需要进行相应的研究, 故本文利用黑磷构建纳米通道, 并研究各向异性等参数对黑磷纳米通道内水分子流动特性的影响, 为黑磷的进一步发展以及在微/纳流体器件中的应用提供了理论研究基础.

本文选用的材料为单层黑磷, 黑磷是由磷原子通过sp³杂化形成褶皱状的蜂窝结构, 其特殊的褶皱结构导致的各向异性是非常值得研究的内容, 单层黑磷模型的尺寸为6.56 nm × 4.00 nm, 磷原子数为720, 参考石墨烯和碳纳米管手性^[22,23]的概念, 将各向异性的概念应用于黑磷, 将黑磷沟槽走向与水分子流动方向之间的夹角定义为手性角θ, 考虑构建周期性模型的需要, 边界处的磷原子需要相互匹配, 目前, 本文只构造了0°, 37.4°, 66.6°和90°四种使得边界处黑磷原子能够匹配的不同手性的单层黑磷模型, 图1(a)为单层黑磷的模型图. 为了研究各向异性等参数对黑磷纳米通道内水分子流动特性的影响, 将两个平行的单层黑磷构造成黑磷纳米通道, 并在黑磷纳米通道内填充水分子组成本文使用的Poiseuille流系统模型图, 如图1(b)所示, 其中水分子的模型选用TIP4P模型, 不同于石墨烯的是, 单层黑磷的所有原子并不在同一平面上, 而是如图1(b)所示的两个平面, 这里使用蓝色和绿色两种颜色代表不同平面的黑磷原子. 模拟系统在x和y两个方向的尺寸分别为6.5和4.0 nm, 两个单层黑磷之间的垂直距离即为纳米通道的宽度, 用H进行表示, 对黑磷纳米通道内的水分子施加一个加速度g_x, 形成Poiseuille流, 研究各向异性等参数对黑磷纳米通道内水分子的Poiseuille流流动特性的影响.
图 1 (a)单层黑磷模型图, 其中手性角度θ指黑磷褶皱方向与水分子流动方向夹角; (b)黑磷纳米通道内水分子流动的Poiseuille流模型图
Figure1. (a) Monolayer black phosphorus models, chiral angle θ is the intersection angle between water flow direction adjacent the top plate and the ripple direction of BP monolayer; (b) poiseuille flow model of water molecules in black phosphorus nanochannels.

本文采用分子动力学模拟的方法研究各向异性等参数对压力驱动作用下黑磷纳米通道内水分子的Poiseuille流流动特性的影响. 整个模拟系统中, x和y方向设置为周期性边界, z方向设置为固定边界. 首先需要对模拟系统进行弛豫作用, 使得整个系统达到平稳状态, 系综为正则系综(NVT), 时间步长为1 fs, 弛豫步数为1000000, 使得模拟系统的温度稳定在300 K. 由于采用的是假设恒温条件, 所以x和y方向采用Langevin恒温器保持298 K的恒温, 并且不考虑黑磷-水界面间的热蠕变和温度跃变. 势函数选择方面, 选用Stillinger-Weber (SW)^[23]势函数描述黑磷原子之间的相互作用, 水分子模型选取改进版的四位TIP4P-Ew模型^[24], 通过particle-particle particle?mesh (PPPM)方法计算水分子之间的长程库仑势作用, 库仑相互作用的截止距离为12 ?, 为了保持水分子的O—H距离和H—O—H键角的稳定性, 这里选用SHAKE算法^[25]. 黑磷与水分子的相互作用采用Lennard-Jones (L-J)势函数进行描述, 作用参数可以通过Lorentz-Berthelot混合算法计算, 具体参数见表1^[26,27]. L-J作用的截止距离为10 ?. 整个系统的模拟过程为5 ns (5 × 10⁶步), 先用1 ns的时间进行弛豫, 使模拟系统达到平衡, 接着对黑磷纳米通道内的水分子施加一个加速度, 使得水分子形成稳定的Poiseuille流, 此过程持续时间为2 ns,最后2 ns用来输出和计算处理分子动力学模拟获得的数据, 对这些数据进行处理得到需要研究的参数.

Atoms	ε/kcal·mol–1	σ/?
P-P	0.36760	3.43800
O-O	0.16275	3.16435
P-O	0.24460	3.30120

表1L-J势能函数的参数值
Table1.Parameter values of L-J potential function

2

-->

3.1.驱动力对黑磷纳米通道内水分子的边界滑移的影响

采用如图1(b)所示的Poiseuille流系统模型, 选用手性角度为0°的单层黑磷模型, 将两个相同单层黑磷平行放置, 间隙设置为6 nm, 即纳米通道的宽度设置为6 nm, 对黑磷纳米通道内水分子沿x方向施加不同加速度(g_x = 1.0 × 10¹², 1.5 × 10¹², 2.0 × 10¹² m/s²), 探究驱动外力对黑磷纳米通道内水分子Poiseuille流流体特性的影响. 将黑磷纳米通道内的水分子进行分层统计, 沿纳米通道宽度方向按每层0.3 nm的高度对纳米通道内的水分子进行分层, 通过分子动力学方法对每层内的水分子进行平均汇总, 得到如图2所示的在不同驱动外力作用下的黑磷纳米通道内水分子的速度分布图, 从图中可以看出, 在不同驱动外力下, 黑磷纳米通道内的水分子沿纳米通道宽度方向都近似为二次曲线分布, 满足Poiseuille流的速度分布情况, 并且在边界处出现轻微的滑移现象. 已有研究表明^[28,29], 在恒外力条件下的牛顿平板Poiseuille流问题中, 可以在宏观N-S方程的基础上考虑线性边界滑移条件, 进行描述Poiseuille流中流体速度分布问题. 确有文献^[30]对壁面速度运用高阶多项式进行拟合, 但考虑到本模拟中边界处数据曲线相对于拟合曲线并未出现太大波动, 而且本文重点在于研究黑磷各向异性的影响, 故采用假定线性边界条件进行处理. 运用Origin软件对图中的曲线进行非线性拟合处理, 进而得到各曲线关于水分子流动速度与位置坐标之间拟合的二次曲线方程式, 通过将边界处水分子(最外层水分子)的位置坐标代入方程式求得边界滑移速度, 三种驱动外力对应计算得到的滑移速度V_s分别为6.933, 9.956和13.491 m/s, 显而易见, 随着驱动外力增加, 黑磷纳米通道内边界处水分子滑移速度也随之增加, 从而对黑磷纳米通道内水分子的流动特性产生影响.
图 2 模型手性角度为0°时水分子的速度分布
Figure2. The velocity distribution of water molecules when the chiral angle of the model is 0°.

数密度分布曲线可以清晰地显示出纳米通道内流体的分布情况, 对了解流体的流动特性具有很大帮助. 同速度分布曲线的获得方法相同, 数密度分布曲线同样需要对黑磷纳米通道内水分子进行分层划分, 分别对四组模型内水分子按照层高为0.01 nm进行分层, 通过分子动力学模拟对每层的水分子数目进行统计, 输出数据, 将每层获得的数据除以所属层的体积, 得到黑磷纳米通道内水分子沿纳米通道宽度方向的数密度分布图, 如图3所示, 图中y轴数密度的单位代表着每平方纳米内水分子的数目. 可以看出, 曲线大致分为两个部分, 第一部分为两边靠近边界处的曲线, 可以看出此时水分子的数目受到黑磷壁面的影响, 分布情况较为不均, 边界处水分子发生密度堆积和分层现象, 出现“类固体”效应, 数密度分布曲线的第一个峰值即为边界层, 而随着距壁面距离的增加, 水分子的分布情况逐级平稳, 最后达到稳定状态, 即图中的第二部分——平稳曲线. 从图3的密度分布图还可以看出, 壁面处的确出现了密度涨落, 从第一个峰值的放大图可以看出, 水分子的数密度分布出现了轻微的差异, 但这种差异对结果影响很小, 而且水分子的速度曲线在边界处的波动较小, 剪切应变率波动也就很小, 根据公式$\tau = \mu \dot \gamma $ (τ为剪应力, μ为剪切黏性系数, $\dot \gamma $为剪切应变率), 边界处与通道中央处水分子的黏性差异较小. 并且, 边界层占通道宽度的比例较小, 因此本文仍采用通道宽度方向上的均匀化近似, 并用线性边界滑移条件进行了处理.
图 3 黑磷纳米通道内水分子沿通道宽度方向的数密度分布图
Figure3. Number density distribution of water molecules along the channel width in the black phosphorus nanochannels.

2 -->

3.2.各向异性对压力驱动作用下黑磷纳米通道内水分子流动特性的影响

在纳米通道宽度不变的情况下, 研究各向异性对压力驱动作用下黑磷纳米通道内水分子Poiseuille流流动特性的影响, 分别使用手性角度分别为0°, 37.4°, 66.6°和90°的单层黑磷模型构造黑磷纳米通道, 在通道内填充水分子组成四个不同的黑磷-水模拟系统, 分别对四个模拟系统中的水分子施加三种不同加速度(g_x = 1.0 × 10¹², 1.5 × 10¹², 2.0 × 10¹² m/s²), 通过分子动力学方法模拟计算, 研究各向异性对压力驱动作用下黑磷纳米通道内水分子流动特性的影响.
3 -->

3.2.1.各向异性对压力驱动作用下黑磷纳米通道内水分子滑移特性的影响

如3.1节所述, 为了研究各向异性对边界滑移特性的影响, 需要获得纳米通道内水分子沿纳米通道方向的速度分布图, 针对四种不同手性的模拟系统, 分别对黑磷纳米通道内的水分子施加不同的加速度(g_x = 1.0 × 10¹², 1.5 × 10¹², 2.0 × 10¹² m/s²), 得到如图4所示的速度分布图(图4(a)—图4(c)包含三种手性角, 图2为一种), 综合比较可以看出, 从四个不同手性模拟系统中计算得到的速度分布图都近似为二次曲线分布, 符合纳米通道内Poiseuille流的速度分布图特征, 对四幅图分别进行非线性拟合后得到在施加不同加速度下对应的四组非线性曲线, 使用与3.1节相同的方法, 分别计算得到不同手性模拟系统在施加不同加速度的条件下边界处水分子的滑移速度V_S (m/s), 如表2所列. 从表中数据可以看出, 在不同手性模拟系统中, 随着加速度值的增加, 边界滑移速度都呈现增加的趋势; 当施加的加速度值相同时, 随着手性角度的增加, 黑磷纳米通道内边界处的水分子的滑移速度也呈现减小的趋势. 图4(d)给出了流-固界面相互作用势能云图, 可以看出, 黑磷表面特殊的褶皱结构, 导致了其表面规则、粗糙的势能分布, 从而影响了边界处水分子的流动特性, 这是造成黑磷表面各向异性流动的内在原因^[31].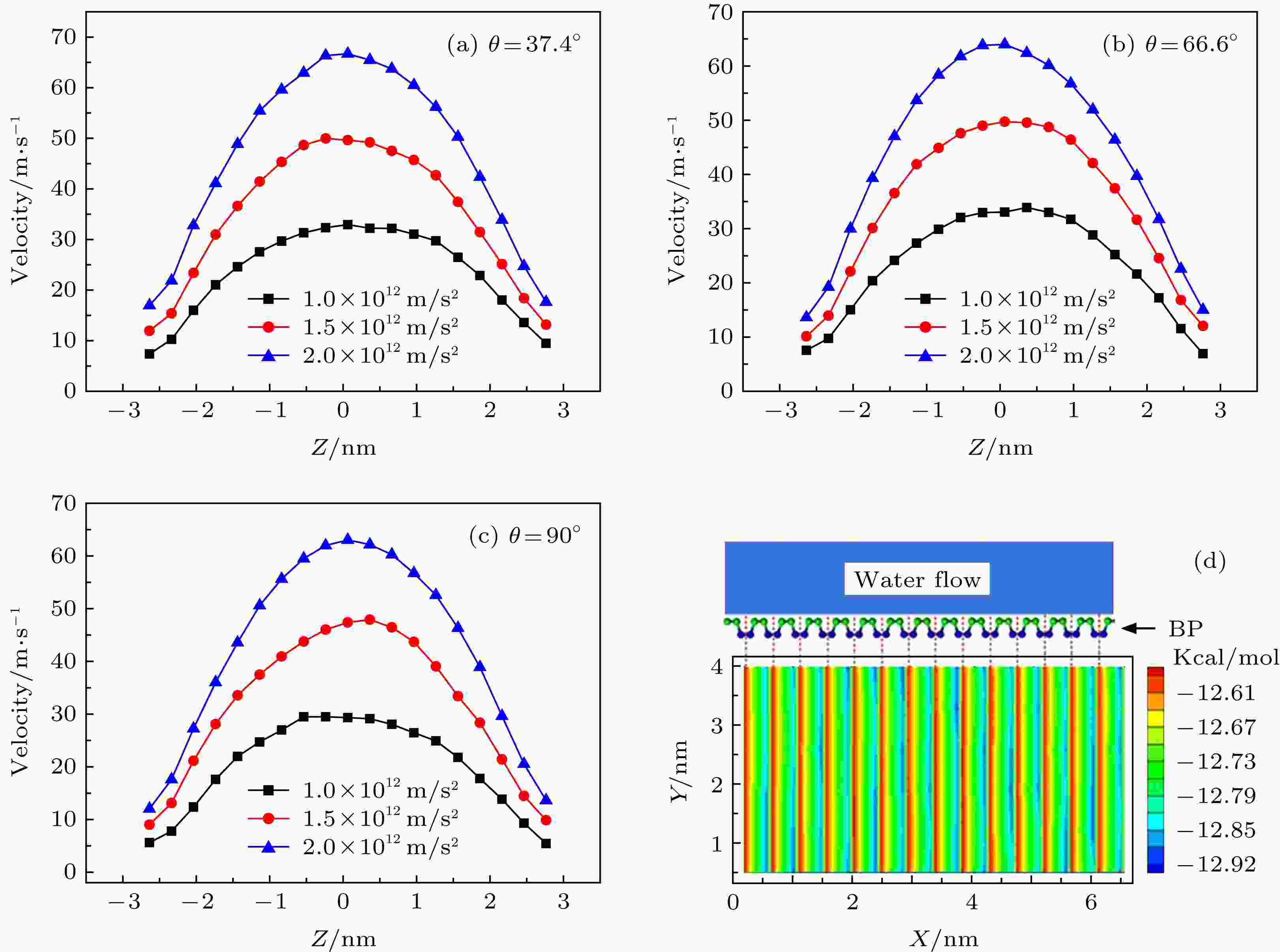
图 4 速度分布图及势能云图　(a) 模型手性角度为37.4°时水分子的速度分布; (b) 模型手性角度为66.6°时水分子的速度分布; (c) 模型手性角度为90°时水分子的速度分布; (d)模型手性角度为90°时的势能分布云图
Figure4. Velocity distribution diagram and potential energy cloud diagram: (a) The velocity distribution of water molecules when the chiral angle of the model is 37.4°; (b) the velocity distribution of water molecules when the chiral angle of the model is 66.6°; (c) the velocity distribution of water molecules when the chiral angle of the model is 90°; (d) potential energy cloud diagram when the chiral angle of the model is 90°.

gx/m·s–1	Angle/(°)
	0	37.4	66.6	90
1.0 × 1012	6.3305	5.7990	4.7818	3.5462
1.5 × 1012	8.9847	8.7979	6.8867	5.8156
2.0 × 1012	13.4912	12.9694	10.6995	7.5839

表2不同手性情况中, 不同加速度对应的水分子边界滑移速度V_S统计表
Table2.Statistical table of water molecule boundary slip velocity V_S corresponding to different accelerations in different chiral conditions.

3 -->

3.2.2.各向异性对压力驱动作用下黑磷纳米通道内水分子黏度系数的影响

纳米通道内流体的黏度系数也是反映纳米通道内Poiseuille流的一个重要参数, 尤其在许多的物理传输过程中扮演着非常重要的角色, 因此流体黏度系数的计算和研究也非常重要. 不同于纳米通道内Couette流中使用剪切应力比上剪切应变率的方法, 在纳米通道内Poiseuille流的黏度系数通常通过对速度分布曲线拟合计算得到, 从图4中可以发现黑磷纳米通道内水分子的速度分布曲线近似为二次分布, 符合Poiseuille流特征. 根据Stokes方程^[32]可以得到关于水分子流动速度u(z)和位置坐标z之间的关系式

$u\left( z \right) = \left( {z - {z_1}} \right)\left( {{z_2} - z} \right)\rho g/\left( {2\mu } \right),$

式中z₁, z₂为黑磷壁面坐标, μ为黏度系数. 由于水分子密度参数ρ可以在模拟计算中得到, 加速度g为预先设定值, 水分子沿纳米通道宽度方向速度分布关系式u(z)可以通过速度分布曲线拟合得到, 故可以利用(1)式计算出水分子的黏度系数, 通过对公式两边求二次导数并变形可以得到

$\mu = \frac{{ - \rho {g_x}}}{{{{\rm{d}}^2}{u_x}/{\rm{d}}{z^2}}}.$

对速度分布曲线拟合得到的曲线u_x (z)可以描述为

${u_x}\left( z \right) = {u_0} + a{(z - {z_0})^2},$

其中u₀和a可以在拟合中直接得到, z₀为通道中心坐标, 故d²u_x/dz² = 2a, (2)式可以最终转变为

$\mu = \frac{{ - \rho {g_x}}}{{2a}}.$

针对不同手性的模拟系统, 将不同的加速度值以及拟合速度分布曲得到的参数a代入(4)式中就可以计算得到相对应的黏度系数μ (mPa·s), 如表3所列. 从表中可以发现, 不同手性的模拟系统在不同加速度条件下, 黑磷纳米通道内水分子的黏度系数几乎保持不变. 为了更直观地表现出这一结果, 将表中数据汇总绘制出黏度系数方差图, 如图5所示, 从图中可以清晰地看出, 随着手性角度的增加, 黑磷纳米通道内水分子的黏度系数几乎为一条直线, 不同手性的模拟系统中水分子的黏度系数值差别很小, 由此可以得出水分子的黏度系数值基本不随手性角度变化而变化的结论.

gx/m·s–1	Angle/(°)
	0	37.4	66.6	90
1.0 × 1012	0.1182	0.1209	0.1116	0.1212
1.5 × 1012	0.1193	0.1173	0.1123	0.1168
2.0 × 1012	0.1171	0.1203	0.1201	0.1183

表3不同手性的模拟系统在不同加速度条件下的水分子黏度系数μ分布表
Table3.Distribution of water molecular viscosity coefficient μ of simulation systems with different chirality under different acceleration conditions.

图 5 不同手性的模拟系统在不同加速度条件下的水分子黏度系数方差分布图
Figure5. Variance distribution of water molecular viscosity coefficient of a simulation system with different chirality under different acceleration conditions.

2 -->

3.3.通道宽度对压力驱动作用下黑磷纳米通道内水分子流动特性的影响

纳米通道宽度也是影响纳米通道内Poiseuille流流动特性的重要参数, 为了研究纳米通道宽度的影响, 分别构建了通道宽度分别为H = 3, 4, 5, 6 nm的四个模拟系统, 其中单层黑磷选用手性角度为90°的黑磷模型(即黑磷褶皱方向垂直于水分子的流动方向). 四个模拟系统中的水分子被施加的加速度值g_x都为2.0 × 10¹² m/s², 通过分子动力学计算得到如图6的速度分布图. 从图中可以看出, 不同孔宽模型内水分子的流动符合Poiseuille流动特征, 并且都在边界处出现滑移现象, 通过对图中曲线分别进行非线性拟合, 结合边界处水分子坐标计算得到相应的滑移速度, 如表4所列, 从表中可以发现, 随着通道宽度的增加, 通道内水分子的边界滑移速度随之增加.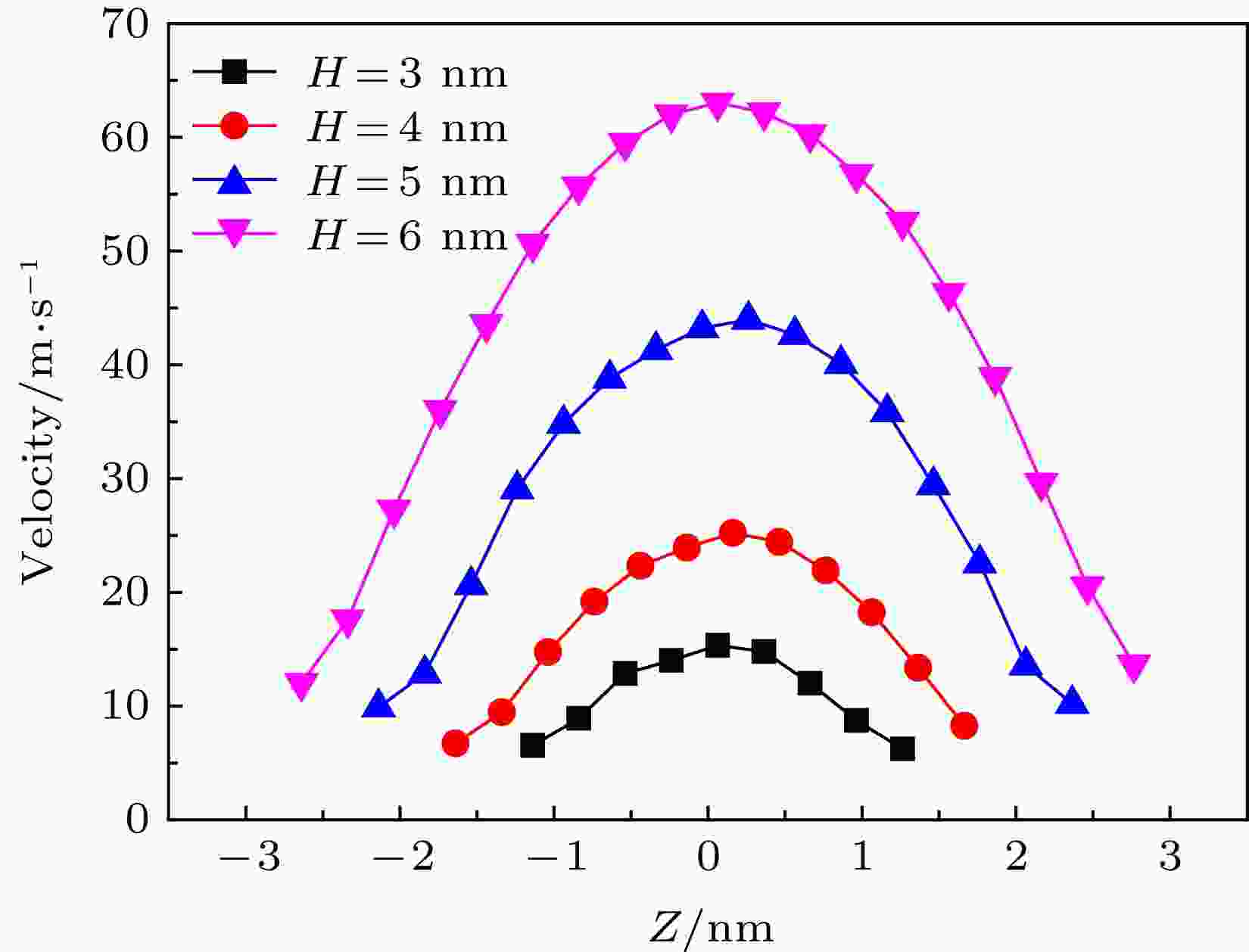
图 6 不同纳米通道宽度内水分子沿通道宽度方向速度分布图
Figure6. Velocity distribution of water molecules along the width of different nanochannel widths.

H/nm	3	4	5	6
VS/m·s–1	4.0267	4.3547	5.8005	7.5839

表4不同纳米通道宽度内水分子的边界滑移表
Table4.Boundary slip of water molecules at different nanochannels widths.

2 -->

3.4.黑磷层数对压力驱动作用下黑磷纳米通道内水分子流动特性的影响

黑磷层数也是研究黑磷纳米通道内Poiseuille流中需要考虑的一个参数, 黑磷层与层之间的间隔为0.53 nm, 本分子动力学模拟中所选用的L-J势函数的截断半径为1 nm, 故当黑磷层数超过两层时, 最外层黑磷片对纳米通道内的水分子的影响几乎可以忽略不计, 故本节在单层黑磷纳米通道的基础上构造双层黑磷片组成的纳米通道, 在其中填入水分子构成Poiseuille流模拟系统, 并考虑其对纳米通道内水分子流动特性的影响.
选取手性角度分别为0°和37.4°的黑磷片构建黑磷纳米通道, 同样对纳米通道进行分层统计, 获取水分子沿纳米通道宽度方向的速度分布曲线, 并与单层黑磷纳米通道模型系统进行对比, 得到如图7所示的速度分布图. 可以看出, 当对纳米通道内水分子施加相同加速度时, 黑磷层数对水分子的流动影响较小, 单层黑磷纳米通道和双层黑磷纳米通道内的水分子的速度分布曲线存在轻微差异, 整体趋势基本一致. 比较两种情况下纳米通道内水分子的边界滑移速度、黏度系数以及交互界面能等参数, 如表5所列, 结果表明双层模型相对于单层模型边界滑移速度出现轻微减小, 黏度系数基本保持不变, 通过比较两种模型的交互界面能, 发现双层模型与水分子的界面能较单层模型轻微增加, 因此边界滑移速度的轻微减小是由于交互界面能的增加所造成的, 通过比较不同手性模型的模拟结果, 不难发现黑磷的各向异性不受黑磷层数的影响.
图 7 不同层数模型对应的速度分布图
Figure7. Velocity distributions corresponding to different layer models.

	VS/m·s–1			μ/mPa·s			Ew-BP/kcal·mol–1·nm–2
	Monolayer	Bilayer		Monolayer	Bilayer		Monolayer	Bilayer
0°	13.4912	12.9256		0.1171	0.1216		–13.7663	–13.9138
37.4°	12.9694	12.4460		0.1203	0.1204		–13.7797	–13.9285

表5不同黑磷层数纳米通道模型中流固界面参数对比
Table5.Comparison of the interfacial parameters for the models with different BP layers.

以黑磷材料构建纳米通道, 基于Poiseuille模型研究了各向异性等参数对压力驱动作用下黑磷纳米通道内水分子的滑移及黏度特性的影响, 探究了各向异性对黑磷-水流固界面的影响作用, 揭示了驱动力、各向异性、纳米通道宽度和黑磷层数等对纳米通道内水分子Poiseuille流流动特性的影响规律. 研究结果表明: 随着驱动力的增加, 边界滑移速度随之增加; 各向异性也会对压力驱动作用下纳米通道内的水分子的流动特性产生影响, 具体表现为边界滑移速度会随着手性角度的增加而减小, 而水分子黏度系数却不受各向异性的影响; 最后, 在加速度值保持不变的情况下, 研究纳米通道宽度和黑磷层数对水分子流动特性的影响, 发现随着纳米通道宽度增加, 水分子滑移速度减小; 双层模型中水分子的速度分布和沿通道宽度方向的数密度分布情况依旧与单层模型差异很小, 双层黑磷与水分子之间交互界面能相对于单层黑磷也呈现增加的趋势, 各向异性规律依然保持不变.