摘要:1950年黄昆先生与A. Rhys(里斯, 黄昆先生夫人, 中文名李爱扶)发表了F-中心的光吸收与非辐射跃迁理论的论文, 这一论文被公认为是处理电子-声子互作用在固体缺陷光吸收的先驱开创性量子理论工作, 其中首先由黄昆先生所推导和明确的一个用于表征电子-声子耦合强度的无量纲因子, 被广泛采用和推崇为黄-里斯因子(Huang-Rhys factor), 也被简称为S因子. 本文试图总结黄-里斯因子的物理内涵, 以及它在阐释几种固体有关光学性质中的关键作用, 包括在深缺陷中心发光以及带边浅杂质束缚激子发光中的支配作用. 研究发现, 在不同性质的固体材料中, 电子(激子)-声子耦合强度可以分为极弱耦合(黄-里斯因子远远小于1)、中等耦合(黄-里斯因子在1—5之间)以及强耦合(黄-里斯因子远远大于1)等几种情况. 限于篇幅及个人理解, 本文仅讨论GaN各种带边激子、二维单原子层半导体激子、无机卤族钙钛矿纳米晶片激子以及金刚石单晶中NV复合中心等极弱及中等强度耦合等几种情况, 以纪念黄昆先生诞辰百周年.
关键词: 声子-电子互作用/
黄-里斯因子/
固体光学性质/
发光

English Abstract

全文HTML

--> --> -->

黄昆先生与A. Rhys(这里译成里斯)于1950年在英国皇家学会院刊A第204卷上发表了题目为“Theory of Light Absorption and Non-radiative Transitions in F-Centres”的论文^[1]. 论文甫一发表即受到****的重视^[2,3], 并被O’Rourke在其论文中开篇首语评价为首个关于F-中心光吸收的仔细量子力学计算^[3]. 所谓F-中心源自德文Farbe center, 德语Farbe即英文color之意. 它是一种晶体点缺陷, 如晶体中的阳离子空位, 那里被一个或多个未配对的电子所占据. F-中心之所以被称为color center, 中文即“色心”, 是因为德国****最先发现原本透明的晶体在有缺陷的情况下会呈现出一定颜色.
黄先生在与Rhys合写的这篇论文中不但导出了S因子表达式, 而且首先明确S因子是其理论处理中的最重要参数^[1]. 鉴于S因子的关键作用, 这里不妨重复一下黄先生导出的表达式:

$ S = \frac{{\hbar {\nu _{\rm{a}}}}}{{2\omega _{\rm{l}}^3}}\mathop \sum \limits_\lambda \mathop \int \nolimits {\left( {A_{y\lambda }'' - A_{y\lambda }'} \right)^2}{\rm{d}}y, $

其中ν_a是晶体原胞体积; ${\omega _{\rm{l}}} = {\left( {{\varepsilon _0}/{\varepsilon _\infty }} \right)^{\frac{1}{2}}}{\omega _0}$, ε₀是晶体的静态介电常数, ε_∞是晶体的高频介电常数, ω₀是晶体的远红外色散频率, 即声子角频率.
黄先生最终推导出了F-中心光吸收系数:

$\begin{split}\alpha \left( \nu \right) =\, & A\nu {\rm{exp}}\left[ { - S\left( {2\bar n + 1} \right)} \right]{\left( {\frac{{\bar n + 1}}{{\bar n}}} \right)^{\frac{1}{2}p}}\\ & \times{{\rm{I}}_p}\left( {2S\sqrt {\left[ {\bar n\left( {\bar n + 1} \right)} \right]} } \right),\end{split}$

其中ν为光子频率; A是一个常数; $\bar n = \left\{ {\rm exp}\left[ \hbar {\omega _{\rm{l}}}/\right.\right.$$\left.\left.{k_{\rm{B}}}T\right] - 1 \right\}^{ - 1}$是统计平均声子数, 为晶体温度的函数; I_p是贝塞尔函数.
由于多声子参与光跃迁理论的重要性和普遍性, 当然也由于问题本身因多体参与而具有的复杂性, 后来不少****已经或者现在仍然在致力于理论及处理方法的进一步发展, 如不同声子模广泛参与的多声子跃迁以及更为普遍的理论处理方法^[2—5], 但基本原理已经确立^[6—8], 尤其是其中黄-里斯因子在理论和实践中的关键重要性得以确立和广泛承认^[9—13]. 实际上, 按照黄先生的说法, 多声子跃迁理论的基本思想是十分简单的^[8]. 多声子跃迁是指在固体中电子跃迁过程中, 同时发射或吸收多个声子. 由于电子跃迁是发生在晶体晶格中, 而晶格则一直处于波动状态, 晶格整体振动波的量子化即是声子. 因此, 电子的跃迁自然会受到晶格波动的影响. 也就是说, 在考虑电子在晶格波动状态下的跃迁时, 就不得不考虑声子的作用. 但是在用量子跃迁理论来处理有电子-声子互作用下的电子跃迁时, 数学处理如此的一个多体问题还是相当复杂和困难的. 比如, 晶格振动波函数和电子波函数以及它们之间耦合之后的波函数等难以准确求解, 尤其是在存在晶格缺陷以及需要考虑激子(电子空穴耦合对)效应的情况下, 问题的处理变得更加复杂和困难^[14—16].
由于电子和构成晶格的原子核之间的质量相差悬殊, 人们可以采用绝热近似(adiabatic approximation或称为Born-Oppenheimer approximation)方法来处理电子-声子耦合系统. 在这种近似下, 总的波函数可以写成电子波函数与声子波函数的乘积形式. 对于晶格振动或声子的处理一般都采用简谐振动近似, 即晶格振动的哈密顿量写成谐振子的形式^[8]. 对于电子-声子之间的耦合, 一般也都处理成线性耦合^[1,8]. 在这样的近似下, 晶格振动哈密顿量及波函数将只是一个位移坐标Q_m的函数, 这里指标m代表不同的声子模. 相应地, 电子态的本征波函数也将只取到Q_m的线性项. 不难证明, 在这样的近似处理下, 电子态对晶格振动的影响只是使各振动膜的位移坐标零点发生一定的偏移, 导致所谓最基本形式的晶格弛豫^[8]. 黄昆先生首先考虑所有振动模都具有相同频率的简单模型, 之所以这样做, 是因为这样做不仅有利于理解问题以及简化理论处理, 而且在很多实际应用问题中正是这个最简单模型的结果是最有用的^[8].
现在考虑光跃迁发生在两个电子态i和j之间. 注意由于电子-声子之间的耦合, 光跃迁会伴随晶格弛豫的发生. 这样的晶格弛豫可以用Δ_ji来表示. 假设与电子发生互作用的振动膜数目N很大, 而且它们的频率相同(ω₀, 或许可称为单一频率近似). 最终黄-里斯因子可以表达为

$S = \frac{1}{N}\mathop \sum \limits_m \left( {\dfrac{{{\omega _0}}}{{2\hbar }}} \right)\Delta _{jim}^2.$

很明显, 黄-里斯因子与电子态光跃迁中所发生的晶格弛豫的大小密切关联.如果我们以声子特征能量$\hbar {\omega _0}$乘以黄-里斯因子, 将得到新表达式为

$S\hbar {\omega _0} = \mathop \sum \limits_m \frac{1}{2}\omega _0^2{\left( {\dfrac{{{\Delta _{jim}}}}{{\sqrt N }}} \right)^2}.$

上式中${\Delta _{jim}}/\sqrt N = \left( {{\Delta _{jm}} - {\Delta _{im}}} \right)/\sqrt N $代表电子态从j态到i态发生光跃迁所引起的晶格振动坐标原点的位移. 所以(4)式表明$S\hbar {\omega _0}$正好等于光跃迁中所伴随的晶格弛豫的弹性能变化. 实际上, (4)式或许可以更简洁地表示为$S\hbar {\omega _0} = \Delta E$^[7]. 鉴于S因子鲜明的物理意义, 以及它在理论阐释固体色心光谱、多声子非辐射复合跃迁等物理过程中的核心作用, 它通常被用来划分电子-声子耦合的几种状况, 如当$S \gg 1$, 电子-声子耦合被定性为强耦合状况, 反之当$S \ll 1$被定性为弱耦合状况. 在绝大多数处理中, S因子被当成一个经验参数, 因为包括康登近似(Condon approximation)等多重近似在黄先生的理论处理中所使用. 自黄先生的工作之后, 不少后来的国外理论****试图对黄-里斯因子进行更深入和细致的量子理论处理, 其中包括不少著名****如Toyozawa^[17], Duke和Mahan^[18]等. Ridley^[19]在不使用康登近似的情况下对固体中电子的多声子非辐射复合跃迁进行了量子力学计算, 他发现使用康登近似可能显著低估了多声子非辐射复合跃迁几率. 其实Kovarskii^[20]更早的理论工作已经发现, 不使用康登近似所获得的理论多声子非辐射复合跃迁几率显著增加. 以色列****则理论预测了几种立方晶体结构主体材料中Co²⁺离子的黄-里斯因子与主体材料德拜温度以及晶格常数的依赖关系^[21]. 而对于束缚在浅施主和受主杂质的激子, Ungier等^[22]理论推导出了它们的黄-里斯因子表达式:

$S = \frac{{{e^2}}}{{a\hbar {\omega _0}}}\left( {\frac{1}{{{\varepsilon _\infty }}} - \frac{1}{{{\varepsilon _0}}}} \right) \cdot X\left( \sigma \right),$

其中e是电子电荷; ε_∞是晶体高频介电常数, ε₀是晶体静态(低频)介电常数; $a = {\hbar ^2}{\varepsilon _0}/{e^2}{m_{{\rm{e}}\left( {\rm{h}} \right)}}$是施主(受主)的有效玻尔半径, ${m_{{\rm{e}}\left( {\rm{h}} \right)}}$是电子(空穴)的有效质量; 而$X\left( \sigma \right)$是一个随参数$\sigma = {m_{\rm{e}}}/{m_{\rm{h}}}$单调增加的函数. 很显然, 在其他参数不变的情况下, 杂质的有效玻尔半径越小, 束缚激子的S因子越大. 如此的理论预测已在极性六方氮化镓晶体中得到了实验验证^[23].
黄先生及其他理论****都已经证明, 在低温极限情况下, 例如晶格热能量远远小于纵光学(LO)声子特征能量(${k_{\rm{B}}}T \ll \hbar {\omega _0}$), 则多声子发光谱线的强度分布基本上是一个泊松分布^[8]. 当然, 对于这样一个固体物理中极其复杂的多体问题, 各种近似处理一般都在所难免. 这里我们采用Ungier等^[22]在处理束缚于晶格内浅杂质的激子复合准粒子与晶格纵光学声子互作用的发光理论公式来做进一步的分析和讨论. 根据他们的理论推导, 发射m个LO声子的浅杂质束缚激子的发光谱线强度可表达为

$\begin{split}&{I_m} = \frac{{4\sqrt {{\varepsilon _\infty }} }}{{3{c^3}}}{\left| {\vec M} \right|^2}{\left( {{\omega _{{\rm{ZPL}}}} - m{\omega _0}} \right)^4}{P_m}\left( S \right),\\ &\qquad\qquad m = 0,\;1,\;2,\;3 \cdots ,\end{split}$

${P_m}\left( S \right) \equiv \frac{{{S^m}}}{{m!}}{{\rm{e}}^{ - S}}.$

(7)式即为泊松分布, $\hbar {\omega _{{\rm{ZPL}}}}$即是所谓零声子线(ZPL)的光子能量, $\vec M$为束缚激子的电偶极子跃迁矩阵元. 注意(6)和(7)式所给出的谱线强度仅仅是高度, 因为这样的理论谱线的宽度是零. 很显然, 黄-里斯因子是决定发光谱线强度分布的最主要参数. 由于一般情况下${\omega _{{\rm{ZPL}}}} \gg {\omega _0}$, 当束缚激子的电偶极子跃迁矩阵元是个慢变函数或者常数时, 我们容易得到一个近似结果${I_m}/{I_{m - 1}} \approx S/m$, 特别是${I_1}/{I_0} \approx S$^[23]. 也就是说, 一阶声子伴线与零声子线强度(高度)比值近似等于黄-里斯因子, 这一结论为我们实验测定黄-里斯因子奠定了理论基础. 在接下来的分析和讨论环节, 我们将从实验结果来验证黄-里斯因子在决定一些固体光学性质中的关键作用.

首先从宽禁带半导体氮化镓(GaN)的带边束缚激子的发光谱线开始讨论. 作为第三代宽禁带半导体的典型代表材料, GaN在新一代高温、高速、大功率电子器件以及固态照明技术革命中的重要性不言而喻. 它的典型晶体结构是六方纤锌矿结构(hexagonal wurtzite structure), 其中氮原子作六方密堆积, 而镓原子则填充在氮原子构成的四面体空隙中. 这样的六方GaN的低温禁带宽度约为3.5 eV^[24], 自由激子结合能约为25 meV^[25]. 同时, 六方结构的GaN由于其晶体结构的非中心对称性而展现出极性和压电特性, 这也导致其中电子与LO声子的耦合最为突出.例如, GaN自由激子发光谱线中可观察到多达6阶的LO声子伴线(replicas, 或叫sidebands(侧带))^[26].
这里实验所测的GaN是一个高质量的非故意掺杂的外延片, 用金属有机物气相沉积(MOCVD)方法生长于蓝宝石衬底上. 该GaN外延层的生长厚度约为4 μm. 进行光致发光(PL)谱测量所用的激发光是氦镉(He-Cd)激光器的325 nm激光线, 样品低温的获得是在牛津仪器Spectromag变温超导磁场系统中实现的, 而荧光信号的色散与探测则是在具有焦距长度为2 m的超高分辨单色仪(McPHERSON 20621)及日本滨松R-928光电倍增管系统上实现的^[27]. 为提高荧光信号的信噪比, 我们使用了标准的锁相放大技术(Standard Research R830). 图1所示为实验测得的该GaN样品在T = 1.5 K低温时的PL谱. 注意, 图1的竖坐标采用对数坐标, 以凸显各激子发光峰的LO声子伴线. 从图1所示的光谱看, 高质量GaN外延层的主要带边发光由A带浅施主束缚激子(D⁰X_A)、表面类受主缺陷束缚激子(SX_A)及自由激子(FX_A)构成. 除此之外, B带自由激子峰(FX_B)尽管很弱, 但还是能清晰分辨. 这反映六方纤锌矿半导体的价带结构有分离的重空穴和轻空穴带(通常称为A带和B带). 至于自旋轨道耦合导致的第三个空穴C带, 由于光生载流子的快速弛豫到低能位的A带和B带, 所以一般在荧光谱中都观察不到. 对于B带自由激子发光, 我们通过采用近共振激发的方式可以大大增强其相对发光强度^[28], 从而可以对轻空穴激子进行深入研究. 除了轻空穴激子发光峰, 还有一个位于SX_A峰低能侧的弱发光峰, 它是所谓双电子卫星峰(two-electrons satellite, TES), 是由一个束缚于中性施主的激子中的电子与中性施主中的一个电子双双参与的多体发光所产生.进一步的研究表明, 所谓TES跃迁其实是一种独特的俄歇型多体辐射复合跃迁^[29]. 这里主要讨论GaN各种带边激子与LO声子的耦合现象. 经室温拉曼散射测量, 六方结构GaN的LO声子特征能量约为92 meV (737.9 cm^－1)^[30]. 由于六方GaN的非中心对称性晶体结构及电极性, 占主导地位的电子-声子耦合是电子(激子)与LO声子的耦合. 因此, 如图1所示, 可观察到各个激子峰的LO声子伴线. 图中“-1LO”和“-2LO”分别表示各激子峰的一阶和二阶LO声子伴线. LO声子的特征能量92 meV也在图中标出.
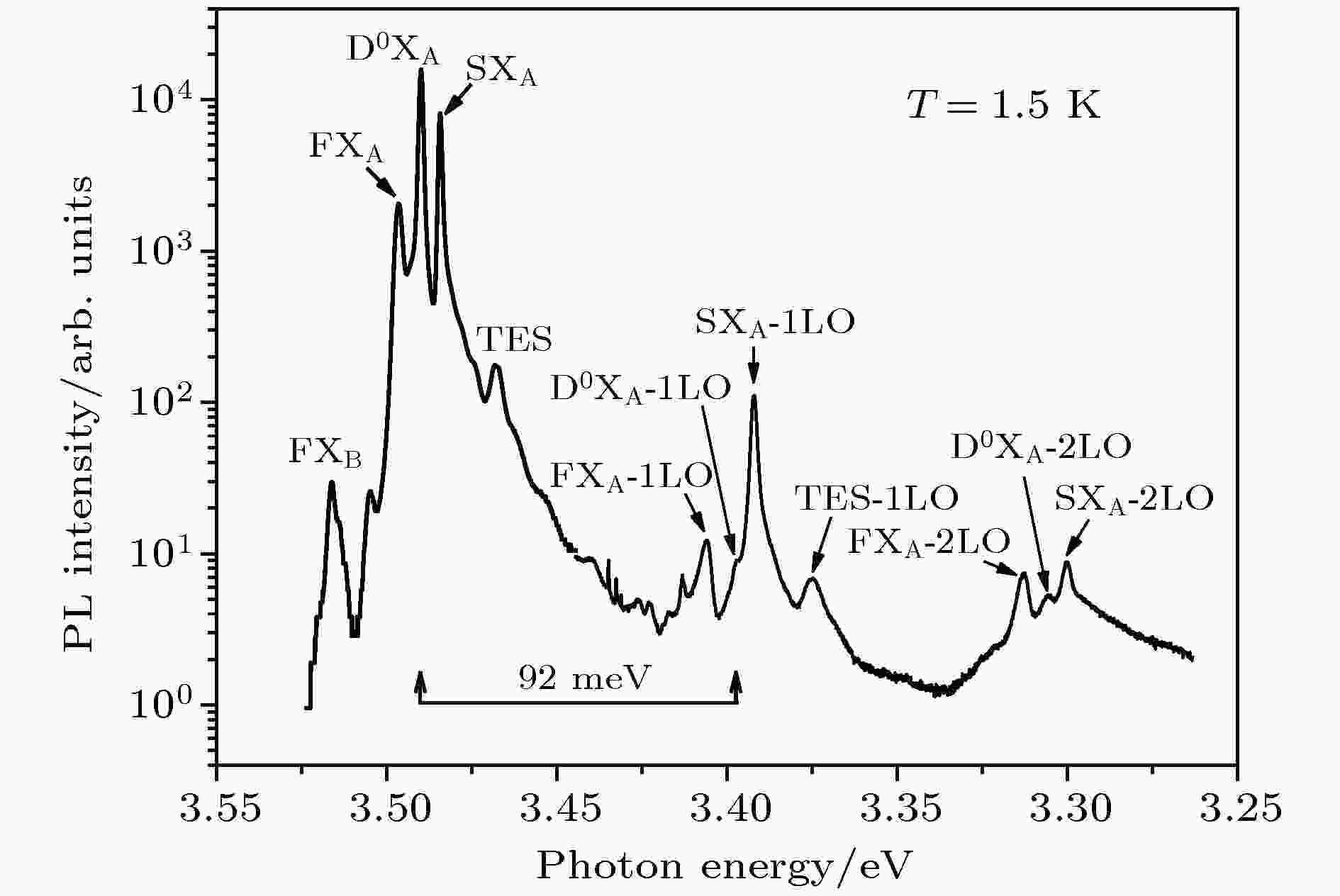图 1 GaN的1.5 K低温带边PL谱　其中中性施主束缚激子发光峰(D⁰X_A)最强, 其次是A带表面类受主缺陷束缚激子发光峰(SX_A)以及A带自由激子发光峰(FX_A); 低于这些主要发光峰分别为一个及两个LO声子能量处的发光峰分别为它们的一阶和二阶LO声子侧带; 除这些主要发光峰以及它们的声子侧带外, A带施主束缚激子的双电子跃迁卫星峰(TES)以及B带自由激子发光峰(FX_B)仍能分辨
Figure1. PL spectrum of the GaN sample at 1.5 K. Three peaks, namely D⁰X_A, SX_A, and FX_A are the main structures in the PL spectrum. Their first- and second-order LO phonon sidebands are clearly seen and located at lower energy of one and two LO phonon energy, respectively, due to the simultaneous emission of one and two LO phonons. In addition to these distinctive structures, TES and FX_B peaks can be also resolved.

根据前面所述的理论公式(6)可知, 极低温下浅杂质束缚激子的发光谱线, 包括所谓零声子线与各阶LO声子伴线之间的高度强度基本满足一个泊松分布规律. 依据这个规律, GaN浅杂质束缚激子的黄-里斯因子可以由一阶声子伴线与零声子线的高度比来确定. 图2给出了所测得的各个带边激子发光峰0阶、1阶和2阶LO声子伴线的高度. 可用实验测量的一阶声子伴线与零阶声子线的高度比值确定黄-里斯因子. 很明显, GaN各种带边激子的黄-里斯因子均远小于1, 皆属于极弱耦合的情况. 即使其中最大的表面受主所束缚的激子, 其S因子也仅约为1.37 × 10^－2. 而施主束缚激子的S因子仅为万分之五大小, 远小于表面受主型缺陷束缚激子的S因子. 根据(5)式, 这是可以合理解释的.因为受主空穴的有效质量一般远大于施主电子的有效质量, 使得受主的有效玻尔半径远小于施主的有效玻尔半径, 所以受主所束缚激子的黄-里斯因子就相对大得多. 也如理论所预测的那样, 浅杂质束缚激子的谱线强度分布基本符合泊松分布. 我们还研究了GaN杂质束缚激子谱线相对强度在低温区内随温度的变化关系, 发现一阶声子伴线与零声子线高度比的平方随温度上升呈线性变化, 与Hopfield的理论预测相一致^[5,23]. 但自由激子谱线的温度依赖则明显偏离该理论预测, 原因是自由激子的动能在声子辅助的辐射复合机制中起了重要作用, 我们不得不用更复杂的量子理论如格林函数来处理自由激子-LO声子-光子之间的互作用及光谱^[14—16].
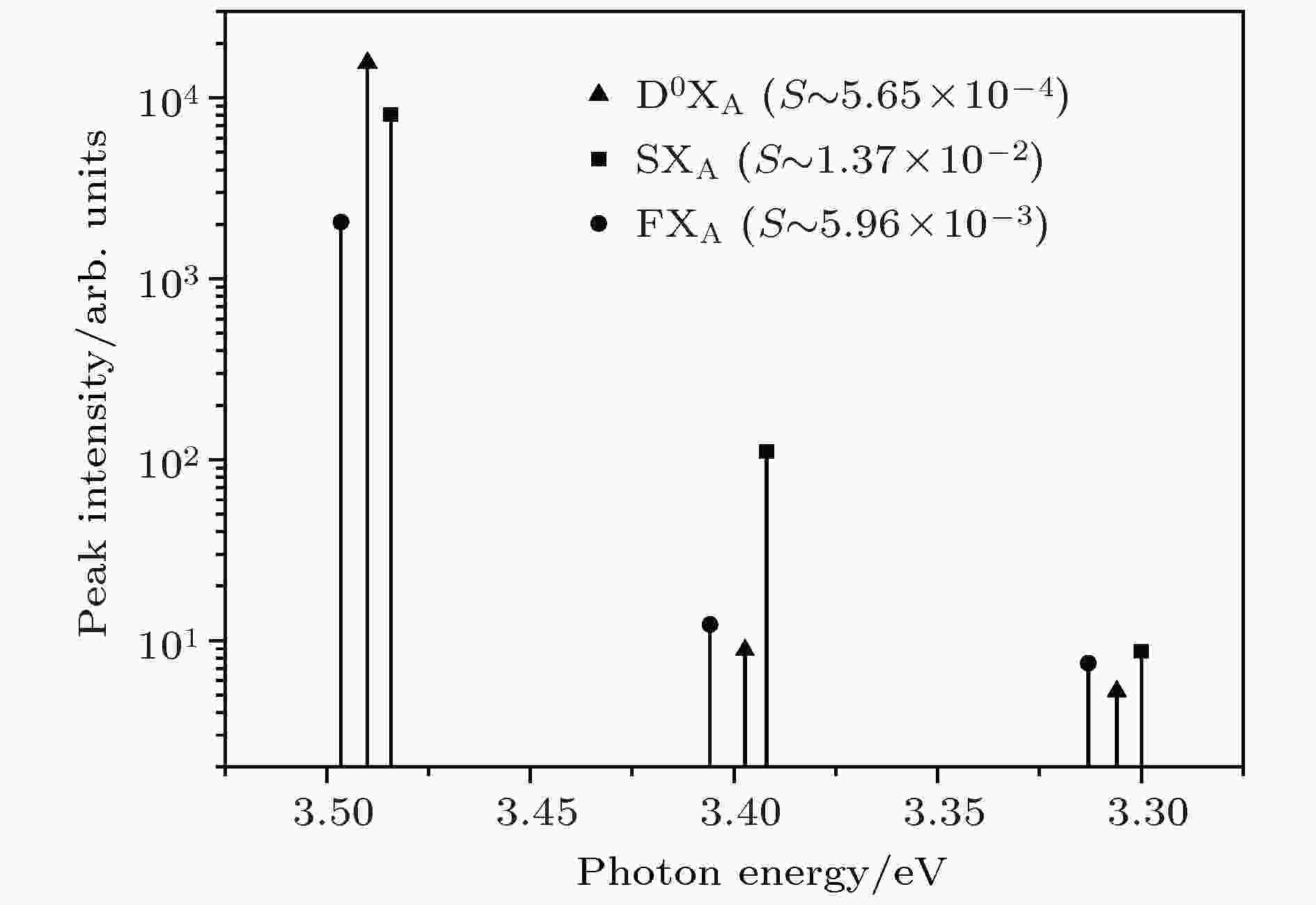图 2 GaN各个激子发光谱线及声子伴线峰值强度实验值, 它们的黄-里斯因子由一阶声子伴线与零声子线的高度比值给出很显然, 在低端低温下, GaN各种激子与LO声子的互作用十分微弱, 即使其中最强的表面缺陷束缚激子的黄-里斯因子也仅有百分之一左右; 这些结果表明, 在极端低温条件下, 伴随GaN各种激子辐射复合的晶格弛豫非常小; 但是如此的结论并不一定适用于中高温情况, 因为激子-声子互作用可能是一个温度的强函数, 尤其是对于自由激子而言
Figure2. Experimental peak-intensity values of various excitonic luminescence lines of GaN at 1.5 K. Huang-Rhys factors of various excitons are simply determined by the peak-intensity ratios of the first-order LO phonon sidebands and their respective ZPL lines. Clearly, the coupling strength of various excitons with LO phonons is very weak at 1.5 K. For example, the Huang-Rhys factor of acceptor-like surface-defect bound excitons was only ~1.37 × 10^－2, suggesting thatvery small amount of lattice relaxation occurs during the radiative recombination of various excitons of GaN at extremely low temperatures. However, it is worth pointing out that such concluding point may not be valid at medium and high temperatures because the interactions between exciton and phonon could be a strong function of temperature, especially for free excitons.

受石墨烯单原子层材料优异性质研究的启发, 近年来其他二维单原子层材料也得到了重视和重要发展. 其中WS₂单原子层二维半导体就是一个重要例子^[31,32]. 与其体单晶以及两层或两层以上的多层结构的电子结构不同, 单原子层WS₂是一种直接带隙半导体, 即使在室温下都展现出杰出的发光特性^[33]. 我们曾研究了用“top-down”和“bottom-up”两种方法所制备的WS₂单原子层的光学特性^[34], 并观察到光致掺杂效应^[35]. 在这里我们集中讨论二维WS₂单原子层半导体的带边激子与声子的互作用, 特别是探讨这种互作用在带边激子发光峰位随温度变化中的作用. 我们将采用O’Donnell 与Chen^[36]所建议的三参数理论公式, 通过拟合实验数据, 以确定自由激子与缺陷束缚激子在它们的发光峰位随温度变化所展现出的有效黄-里斯因子^[36].
这里我们实验所采用的样品是用手工剥离方法从体单晶所得到的WS₂单原子层薄片, 其光学照片及室温拉曼光谱可参考已发表文献^[37]. 样品的变温PL谱是在Renishaw inVia共焦显微拉曼光谱仪上完成的, 激发光是一个氩离子气态激光器的514.5 nm激光线, 激发光以及荧光信号都是通过一个50倍的显微镜头进行的. 为尽量减少激光可能对单原子层样品所造成的严重影响^[34,35], 我们在进行变温PL谱测量时使用的激光功率仅为30 μW. 由于共焦显微镜的高效收光效率, 即使在这样微弱功率激光激发下, WS₂单原子层的发光在室温下仍能被系统采集和探测到足够好的荧光信号, 如图3所示. 样品的变温实验是在能与显微镜集成的Linkam液氮冷却变温系统上实现的.
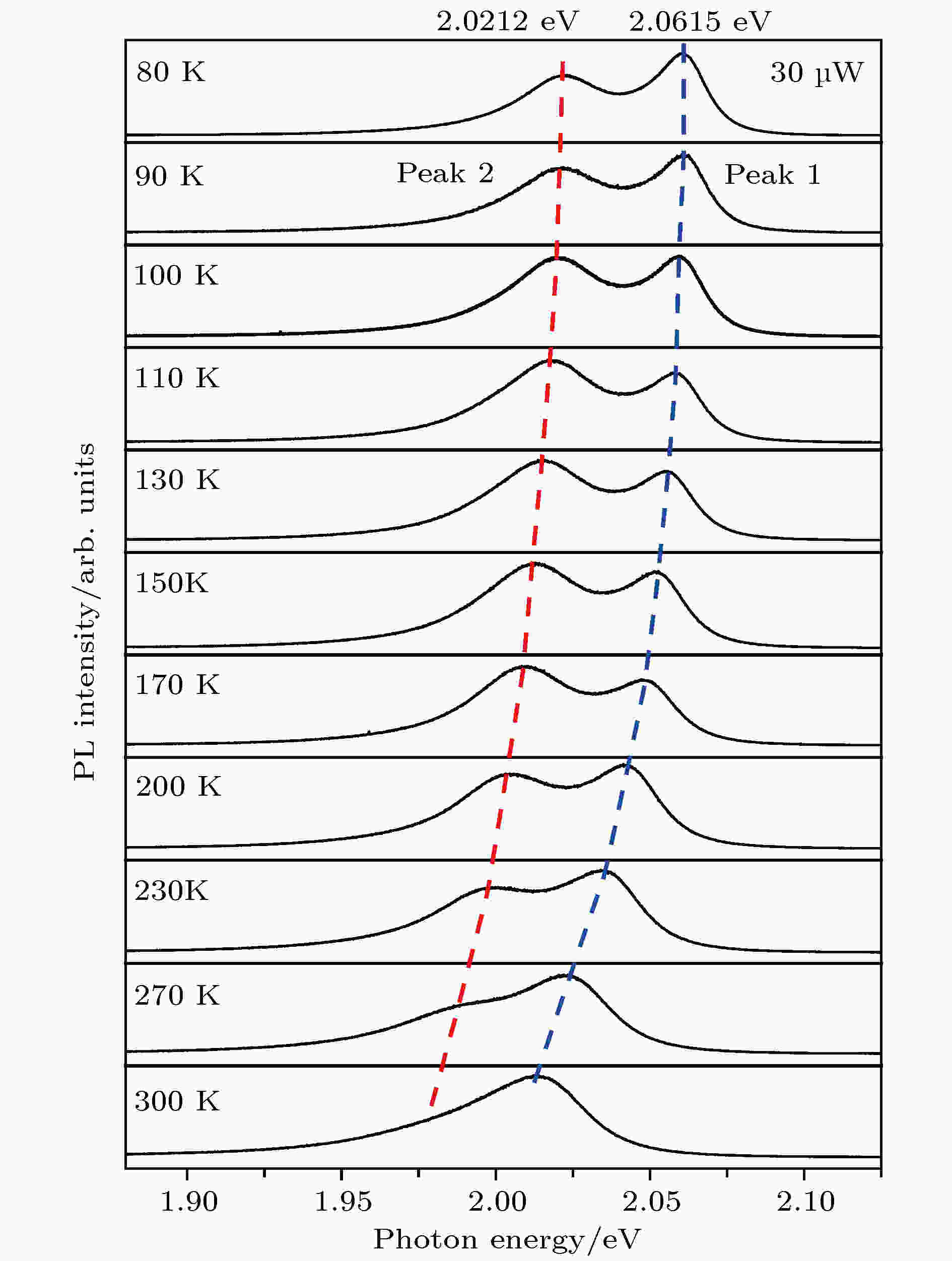图 3 WS₂单原子层二维半导体的变温PL谱　双发光峰及其峰位随温度向低能方向移动(红移)趋势清晰可辨, 而如此的带边发光峰峰位随温度红移的规律有可能是激子-声子耦合造成的
Figure3. Variable-temperature PL spectra of the WS₂ monolayer semiconductor. Double PL peaks can be well resolved. The red-shift temperature dependence of their peak positions is clearly seen. Note that the red-shift dependence of peak positions of the two emission peaks may be due to the exciton-phonon coupling.

图3所示为测得的WS₂单原子层二维半导体的变温PL谱, 变温范围是从80 K到300 K. 双发光峰结构在270 K以下温度清晰可辨. 依据两个发光峰的能位、谱型、低温激发强度依赖以及温度依赖行为等, 我们将能位高一些的发光峰判定为自由激子发光, 而能位较低的发光峰则是缺陷束缚激子发光^[35,37]. 在图3中, 由虚画线标出两个发光峰峰位随温度的变化趋势. 很显然, 随着晶格温度上升, 它们都呈现出单调红移(向低能方向移动)行为.
为了更清晰地反映两个发光峰随温度的红移行为, 图4给出了从图3中所读出的发光峰位(方块与圆点)随温度的变化趋势. 如前文所述, 我们采用O’Donnell 与Chen所建议的三参数经验公式, 对实验数据进行了拟合, 所获得的拟合曲线如图4中实线所示. 考虑电子-声子耦合是造成半导体能带随温度红移的主要机制, O’Donnell 与Chen建议了一个三参数理论公式:
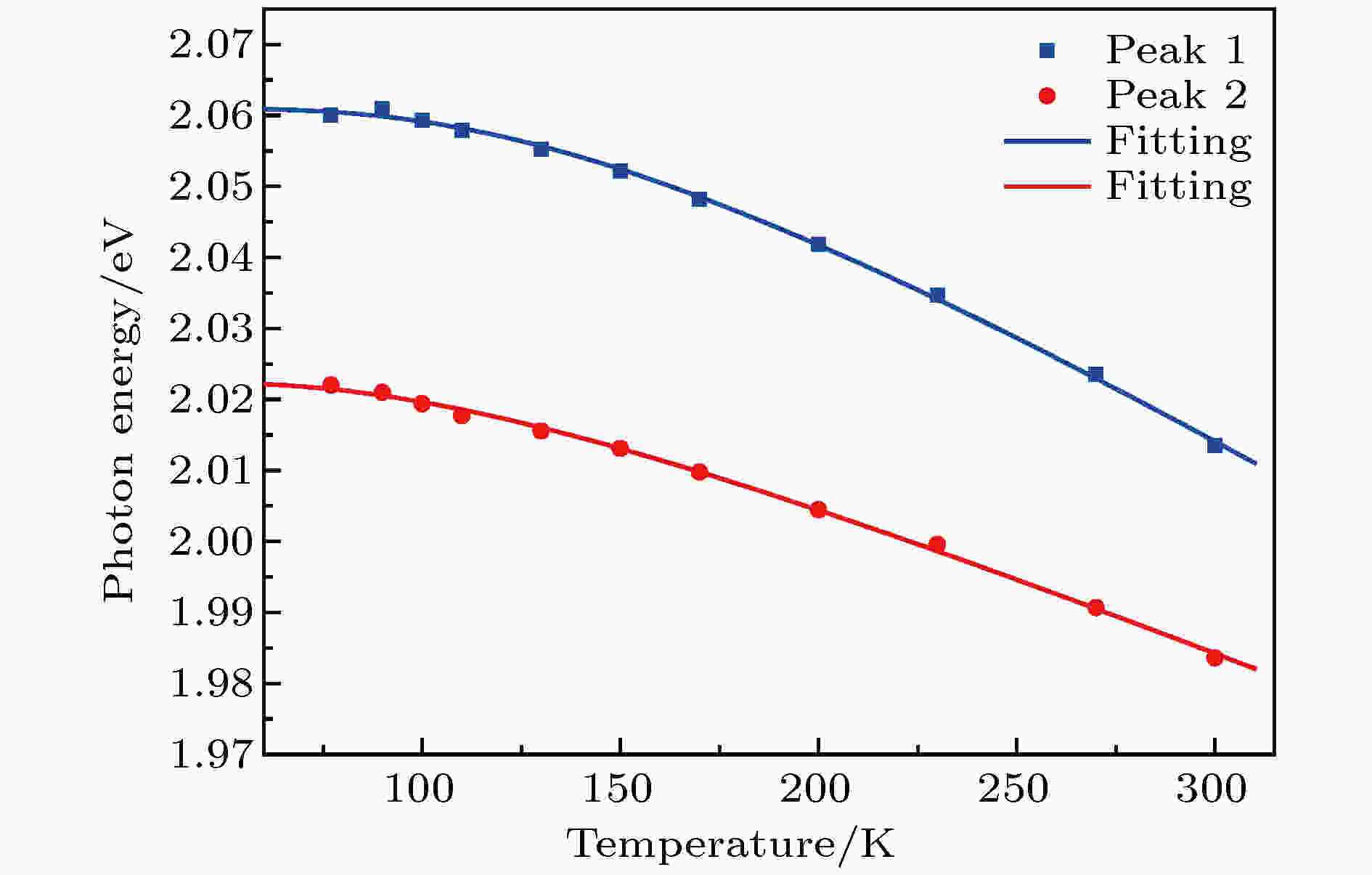图 4 WS₂单原子层二维半导体的两个发光峰位(方块和圆点)随温度的变化趋势, 实线是用O’Donnell与Chen^[36]所建议的电子-声子耦合所引起的带隙红移三参数理论公式所得到的拟合曲线
Figure4. PL Peak positions (filled squares and circles) of the WS₂ monolayer semiconductor vs. temperature. Solid lines are the fitting curves with the bandgap red-shift formula due to electron-phonon coupling suggested by O’Donnell and Chen^[36].

${E_{\rm{g}}}(T) = {E_{\rm{g}}}(0) - S \cdot \left\langle {\hbar \omega } \right\rangle \Big( {\coth \Big( {\frac{{\left\langle {\hbar \omega } \right\rangle }}{{2{k_{\rm{B}}}T}}} \Big) - 1} \Big),$

上式中${E_{\rm{g}}}(0)$即为$T = 0$时晶体的禁带宽度, $\left\langle {\hbar \omega } \right\rangle $代表平均或有效的声子能量, S参数即为黄-里斯因子.
如图4所示, 实验数据和理论拟合曲线符合得非常好. 拟合所用的三参数值在表1中列出. 可以看出, 缺陷束缚激子的有效黄-里斯因子和声子能量均小于自由激子的相应值. 两个有效声子能量虽接近但小于WS₂单原子层的平面内(in-plane)及平面外(out-of-plane)振动模的特征能量^[37]. 较小的黄-里斯因子以及较小的有效声子能量导致缺陷束缚激子的发光峰位随温度变化具有较小的红移速率, 尤其是在温度较高时, 可以比较清楚地看到如此的变化趋势. 这个实验表明, 即使在单薄如单原子层的晶体物质内, 晶格振动对于其光学性质仍然有着显著的影响, 这对于发展二维单原子层材料电子和光子器件是必须要考虑的因素.

Peak	Eg(0)/eV	S	$\left\langle {\hbar \omega } \right\rangle / \rm{meV} $
1	2.0610 ± 0.0004	2.1046 ± 0.0972	38.7739 ± 1.9522
2	2.0225 ± 0.0006	1.3664 ± 0.0691	29.0564 ± 2.4535

表1用(8)式拟合实验点所用的三参数值
Table1.Values of the three parameters adopted in the fitting to the temperature dependence of peak positions with Eq. (8).

由于具有良好的光电特性和热稳定性, 纯无机的钙钛矿结构材料是当前的一个研究热点, 尤其是其各种纳米尺度的材料, 更是吸引了人们的研究兴趣^[38,39]. 最近有关电子(激子)-声子互作用对低维钙钛矿结构材料光电性质的影响亦受到重视.例如, Gong等^[40]研究了二维钙钛矿单晶中电子-声子互作用对于其发光效率的影响; 而Iaru等^[41]的研究则揭示出在无机CsPbBr₃纳晶中存在强电子-声子互作用, 并引起带边激子发光的声子伴线; 而Saran等^[42]的研究表明, 在铯铅卤族化合物纳晶中, 激子发光峰被强Fr?hlich型激子-LO声子互作用所展宽. 这些研究均说明, 电子(激子)-声子互作用对于无论是有机-无机混合型还是纯无机型金属卤族钙钛矿材料的光学与电学性质都有着重要的影响, 必须认真而深入地研究. 基于前人研究结果以及如此的研究动机, 我们最近对于纯无机CsPbBr₃纳米晶片的发光机制进行了比较深入的研究^[43,44], 对于激子-声子互作用在CsPbBr₃纳米晶片的发光机制中的重要作用获得了一些较为深入的认知. 比如, 我们发现自由激子与LO声子耦合的黄-里斯因子在低温区随温度的上升而减小, 而与准连续声学声子的摩擦系数却在随温度持续增加^[44]. 如此的发现显然丰富了以及在一定程度上深化了我们对于固体中复杂的激子声子多体互作用机制的认知, 有利于对于固体发光乃至发热机制的更进一步理解. 下面简要讨论我们所获得的结果.
研究所用的纯无机CsPbBr₃纳米晶片是用所谓热注入(hot injection)化学方法所合成,具体的合成步骤和细节可参阅合作者文献[45]. 变温PL谱测量是在一套自我组装的高分辨荧光谱仪上完成的, 光谱仪的具体描述等请参阅我们以前发表的论文^[25].
图5所示为CsPbBr₃纳米晶片的三个不同温度下所测得的PL谱(空圆圈), 实线为用多模布朗振子(MBO)模型所计算的理论曲线. MBO模型是一个量子理论模型, 是由Mukamel及其合作者^[46]为计算一个溶解于溶液并作布朗运动的分子的非线性瞬态光学响应而发展. 2006年, 作者与合作者^[47]率先将该量子理论模型成功应用于计算和诠释晶体内缺陷中心发光谱. 我们认为，该模型之所以能成功应用于计算复杂晶体内缺陷中心的发光和吸收光谱, 是因为晶体内，尤其是极性晶体如GaN, ZnO等内的缺陷光学中心, 可以模型为一个缺陷电子与晶体LO声子(主振动模, primary oscillator)的耦合振子, 并受到其余振动模(例如准连续的声学声子)的摩擦, 这和Mukamel等^[48]所考虑的溶解分子-溶液体系高度相似.我们还将该理论模型推广到计算固体量子点体系的发光谱. 考虑到量子点尺寸分布或者缺陷中心的可能能态分布, 可用一个高斯函数来计量非均匀展宽^[48]:
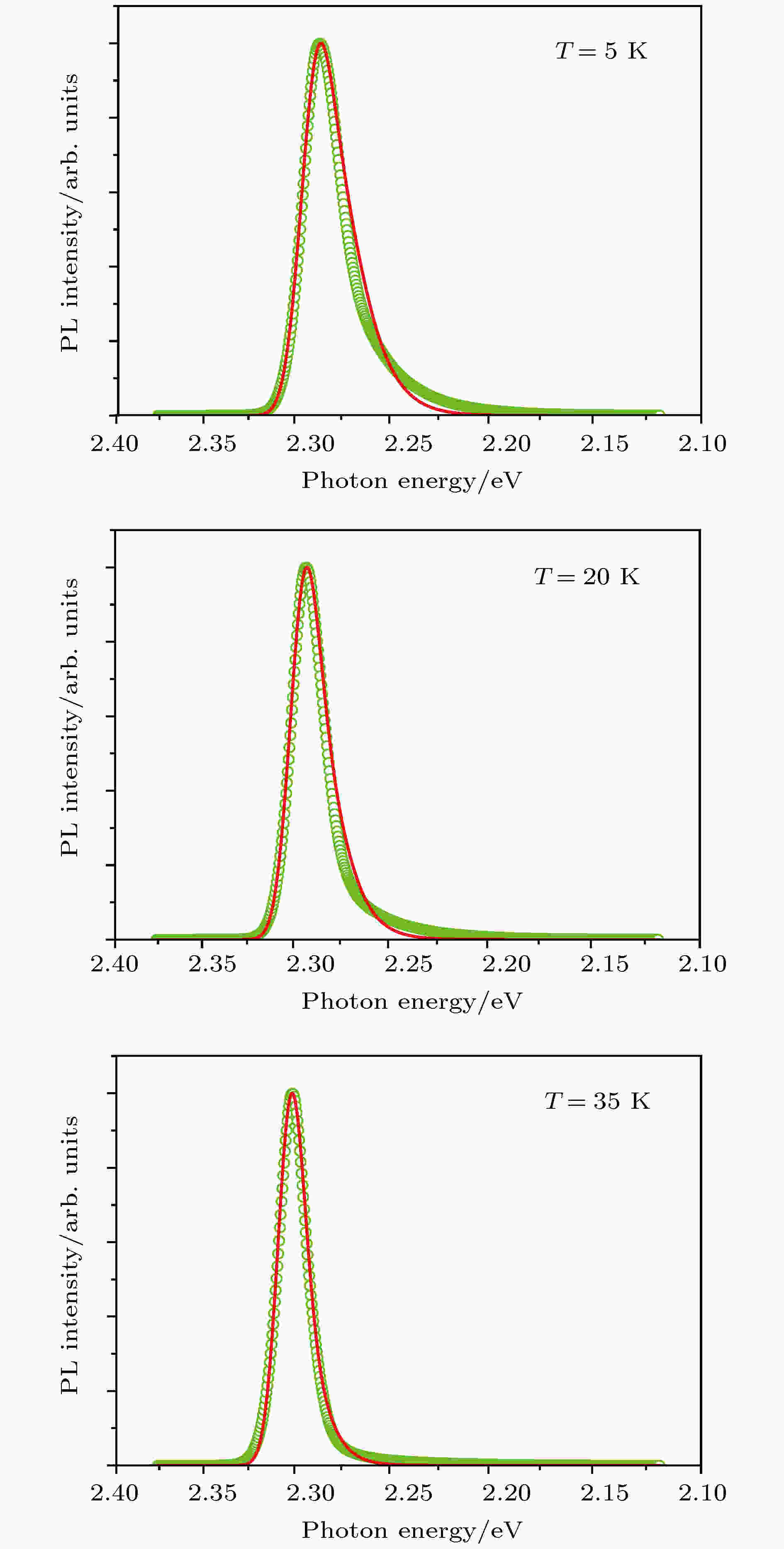图 5 CsPbBr₃纳米晶片在三个不同温度下所测得的PL谱(空圆圈), 实线则为用考虑了电子与多模声子相耦合的多模布朗振子(MBO)模型所计算的理论曲线, 考虑到固体系统中有无穷多的复杂多体互作用, 实验谱线和相对简单的多模布朗振子模型理论谱线符合程度可以说是相当令人满意的
Figure5. PL spectra (open circles) of the CsPbBr₃ nanosheets measured at three different temperatures. Solid lines are the theoretical curves with the multiple mode Brownian oscillator (MBO) model. Agreement between experiment and theory is satisfactory if considering the complexity of many-body interactions in a solid system.

$f({\omega _{{\rm{eg}}}}) = \exp [ - 2{W^{ - 2}}{({\omega _{{\rm{eg}}}} - \omega _{{\rm{eg}}}^{\rm{0}})^2}],$

这里$\hbar \omega _{{\rm{eg}}}^{\rm{0}}$是高斯分布的中心能位, 即前文所谓零声子线的能位, W是与分布宽度有关的一个参量. 在这样计量了非均匀展宽之后, 在MBO模型中, 计算固体中电子-声子耦合系统的发光谱公式或可表示为^[48]

$\begin{split} & {I_{{\rm{PL}}}}(\omega ) =\, \frac{1}{\text{π}}\int_0^\infty {f({\omega _{{\rm{eg}}}})} {\rm{d}}{\omega _{{\rm{eg}}}} \\ & \times \operatorname{Re} \int_0^\infty {\exp [{\rm{i}}(\omega \!-\! {\omega _{{\rm{eg}}}} \!+\! S\hbar {\omega _{{\rm{LO}}}})t \!-\! {g^*}(t)]{\rm{d}}t} ,\end{split}$

上式中$\operatorname{Re} $表示为所求复数积分的实部, g*(t)是谱响应函数g(t)的共轭复数, 它的表达式为^[46]

$\begin{split}g(t) =\, & - \frac{1}{{2\text{π}}}\int_{ - \infty }^\infty {{\rm{d}}\omega } \frac{{2S\hbar \omega _{{\rm{LO}}}^3\gamma }}{{{\omega ^3}{\gamma ^2} + \omega {{(\omega _{{\rm{LO}}}^2 - {\omega ^2})}^2}}} \\ &\times [1 + \coth (\beta \hbar \omega /2)]({{\rm{e}}^{ - {\rm{i}}\omega t}} + {\rm{i}}\omega t - 1),\end{split}$

其中S即为黄-里斯因子, $\gamma $是电子与LO声子的耦合振子与准连续声学声子的耦合系数, $\beta \equiv {{\rm{1}} / {{k_{\rm{B}}}T}}$.
从上述表达式可以看出, 即使是在考虑有准连续声学声子摩擦之后的MBO理论模型里, 黄-里斯因子仍然是一个最重要的参数. 应用(9)—(11)式, 我们计算了CsPbBr₃的带边激子发光谱, 其中LO声子的能量固定为18 meV, 仅改变$\hbar \omega _{{\rm{eg}}}^{\rm{0}}$, S以及$\gamma $等3个参数. 所获得理论拟合光谱以实线形式在图5中给出. 应该说, 对于如此复杂的固体系统而言, 理论和实验谱线的符合程度是相当好的. 最有趣的一个结果是, 表征CsPbBr₃纳米晶片的激子与LO声子之间耦合强度的黄-里斯因子在5—40 K的低温范围内, 随着温度的上升而减小. 图6给出了用MBO量子理论模型所拟合出的S因子(实三角)与温度的关系, 其中实线是一个用最小二乘法所拟合得到的直线, 这表明CsPbBr₃纳米晶片的激子的黄-里斯因子在感兴趣的低温范围内, 是随温度上升而线性减小的.这里需要提到的是, 我们所获得的S因子值与Iaru等^[41]用荧光一阶声子伴线与零声子线高度比值所得到的S因子值相符. 至于在低温范围内, CsPbBr₃钙钛矿纳米晶片的黄-里斯因子, 也就是说激子与LO声子的耦合强度随温度上升而减小的物理机制, 我们是用该种金属卤化物钙钛矿材料的静态介电常数随温度的上升而增大来解释的^[44]. 这是因为根据(5)式, 极性材料中激子的S因子与材料的静态介电常数密切关联.
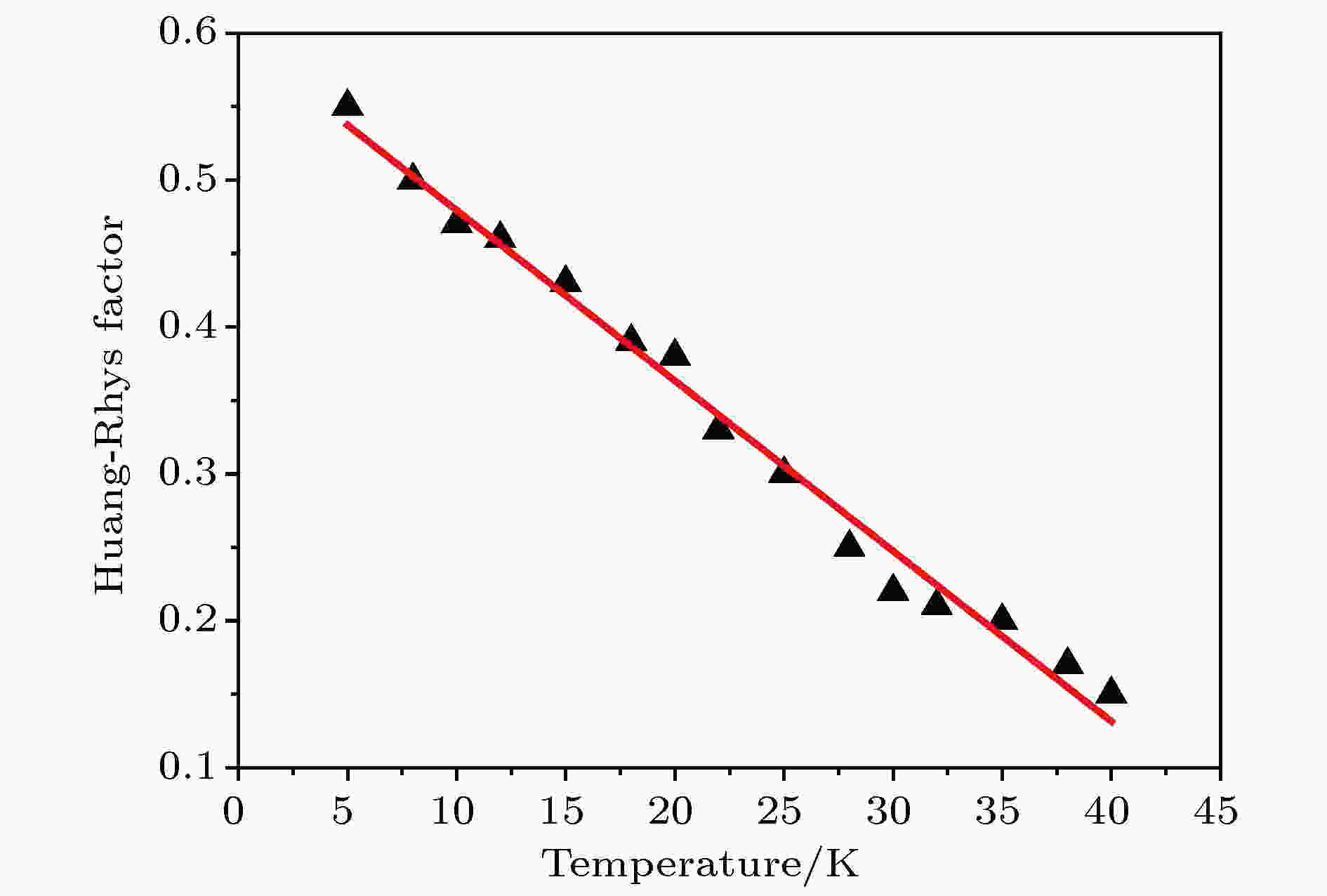图 6 用MBO理论模型所拟合出的CsPbBr₃纳米晶片在5—40 K低温范围内的黄-里斯因子(实三角), 实线则为线性拟合线　注意, 在5—40 K温度范围内, 黄-里斯因子随温度上升而减小, 表明激子-声子耦合强度是随温度上升而下降的
Figure6. Huang-Rhys factors (solid triangles) of the CsPbBr₃ nanosheets in the low temperature of 5－40 K with MBO model. Solid line is a linear fitting curve. Note that the Huang-Rhys factor of excitons in the CsPbBr₃ nanosheets interestingly decreases with increasing the temperature.

黄昆先生在其论文中指出, 晶体中的杂质和缺陷有时可以引起只限于邻居少数原子的局域振动模, 形成区别于完整晶格振动谱的振动频率. 而这类局域振动模可以和杂质中心的电子态有较强的耦合^[8]. 金刚石晶体中的NV中心, 也就是一个替位C原子的N原子和一个最邻近C原子空位(vacancy)所组成的复合缺陷中心^[49], 或许可理解为黄先生所讨论的这样一种晶体缺陷中心. 本节简要讨论金刚石NV复合缺陷中心电子态与准局域化振动模的耦合以及黄-里斯因子, 详细结果可参阅文献[50].
我们所研究的高质量金刚石样片是由西安电子科技大学课题组利用微波等离子体气相沉积技术所同质外延生长的, 其具体的生长环节和细节可参阅该课题组的论文^[51]. 金刚石样片的变温PL谱也是在Renishaw inVia共焦显微拉曼光谱仪上完成的, 激发光也是氩离子气态激光器的514.5 nm激光线. 图7所示为测得的金刚石样片的77 K低温PL谱. 可以清楚地看到两条非常窄的NV缺陷中心的发光谱线, 它们已被鉴定为NV复合缺陷中心的零电荷以及带一个负电荷两种电荷态的所谓零声子谱线^[48]. 能位高一些的谱线是零净电荷态的, 被标为NV⁰, 而能位低于2.0 eV的窄谱线则是带一个负电荷态的, 被标为NV^–. 除了这两条窄发光谱线外, 展宽的周期结构分别出现在两条窄谱线的低能侧, 如图7中向下的短箭头所示. 而且, 两个周期结构的能量周期并不相同. NV⁰的约45 meV, 而NV^–的约63 meV. 这两个周期结构的谱结构就是不同荷电状态的NV缺陷中心与周围准局域化的振动模相耦合的结果^[50]. 为了能对展宽的光谱进行理论拟合以得到较为深刻的理解, 须引入声子模的态密度$\rho ({\omega _{\rm{s}}})$来计算准局域化振动模对光谱的贡献^[8]. 而且, 在有限温度情形下, 黄-里斯因子将是晶格温度以及声子态密度的函数^[8].
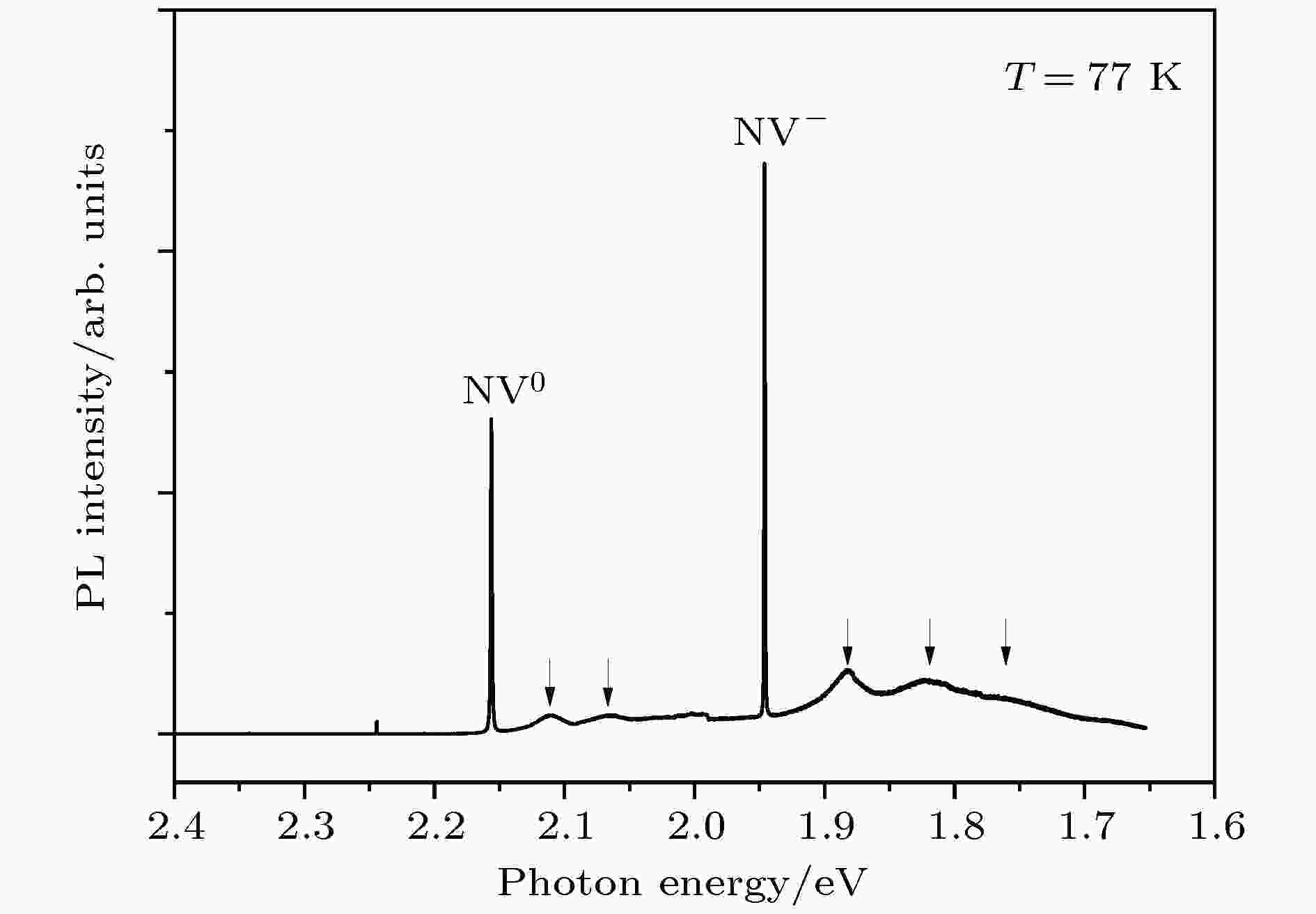图 7 同质外延生长的金刚石晶片的低温PL谱　NV缺陷中心两种荷电状态的零声子发光谱线以及它们的准局域振动模的周期谱结构清晰可见, 图中若干朝下的箭头标出了这种由于电子与准局域振动模耦合造成的周期性结构; 注意, NV缺陷中心的两种电荷状态所展现出的周期性发光结构具有不同的能量周期, 表明它们各自感受到不同的局域振动模
Figure7. 77 K PL spectrum of the diamond flake grown on diamond substrate. It is clearly seen that two sharp lines of NV⁰ and NV^－ as well as their respective phonon sidebands for the two quasi-localized vibrational resonances. Downward arrows indicate such phonon sidebands.

我们采用Maradudin等^[52]所导出的理论公式来计算金刚石NV中心的PL谱. Maradudin等是采用$m > 1$个声子跃迁几率可以用$m - 1$个声子的跃迁几率与1个声子的跃迁几率的卷积来计算^[52,53]:

${I_m}(\omega ) = {N_m}\int_0^{{\omega _{\rm{c}}}} {{I_{m - 1}}(\omega - x){I_1}(x){\rm{d}}x} ,$

上式中${I_1}(x)$可表达为

${I_1}(\omega ) = a{{\rm{e}}^{ - S}}[\bar n(\omega ) + 1]\rho (\omega )/{\omega ^2},$

这里a是一个常数.(12)式中的${\omega _{\rm{c}}}$是晶体声子的截止频率, 而${N_m}$的选择是使${I_m}(\omega )$的如下积分满足泊松分布

$\int {{I_m}(\omega ){\rm{d}}\omega } = \frac{{{{\rm{e}}^{ - S}}{S^m}}}{{m!}}.$

最终电子声子耦合系统的PL谱可由下式计算^[52,53]:

${I_{{\rm{PL}}}}(\nu ) \propto {\nu ^3}\sum\limits_1^\infty {{I_m}({\nu _{{\rm{ZPL}}}} - \nu )}. $

如图8中左侧图所示, 计算出的金刚石NV缺陷中心的PL谱与实验谱相符合.同时, 我们首次获得了声子态密度分布, 如图8中右侧图所示. 我们所获得的NV⁰与NV^－的黄-里斯因子分别为1.9与2.6. 显然, 金刚石NV缺陷中心在带一个净负电的情形下与周围准局域化振动模的耦合要强一些. 总之, 上述结果再次印证了黄-里斯因子在决定固体一些光学性质上的关键作用.
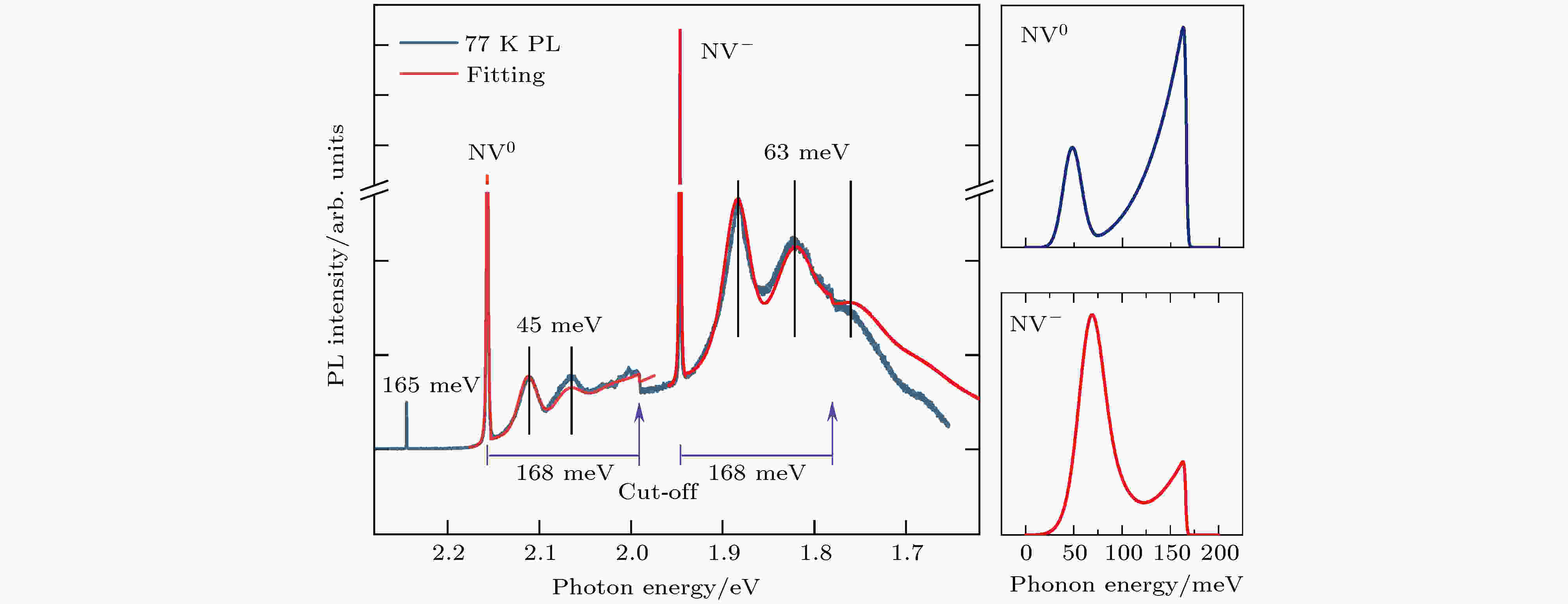图 8 左侧为金刚石晶片的低温PL谱(灰线)以及理论拟合谱线(红线), 金刚石声子的截止能量为168 meV, 与图中的拉曼峰能量(165 meV)很接近; 右侧为对实验谱线进行理论拟合所获得与NV缺陷中心两种荷电态相耦合的准局域振动模的声子态密度
Figure8. Left panel: measured 77 K PL spectrum (gray line) of the diamond flake and theoretical spectrum (red line). The cut off energy of phonons of diamond is also given. Right panel: densities of phone states obtained via theoretical fitting to the experimental PL spectrum.

从以上所讨论的若干不同材料体系的有关光学性质来看, 黄-里斯因子可以从万分之几变化到大于1, 显示出不同材料体系的声子-电子耦合强度是千差万别的. 大量实验工作已经证实了这一点, 这里不再一一罗列和赘述. 实际上, 在黄先生及后续他人的理论研究中, 也都已经讨论了极弱耦合、中强耦合以及强耦合的情况, 有兴趣的读者可以参阅已有的文献. 对于不同材料体系, 黄-里斯因子有差别是自然可以理解的, 因为材料不同, 它们的物理、化学性质, 包括光学性质不同是自然的事. 既然光学性质不同, 在相关光学跃迁中所伴随的晶格弛豫不同是可以理解的. 有趣的是, 即使在同一种材料中如GaN以及金刚石中, 激子或缺陷中心的性质不同, 它们的黄-里斯因子也不同, 是因为不同的激子或具有不同的电荷状态的同种缺陷中心, 可以具有相当不同的量子态波函数及本征能量, 它们和晶格振动的耦合强度也就可以是不同的, 如按照黄-里斯因子的物理定义, 其因子的大小一定是不一样的, 这也体现出黄-里斯因子在表征不同激子及缺陷态有关光学性质上的关键性甚至指纹性.

本文试图总结和论证黄-里斯因子的深刻物理内涵以及在决定固体一些光学性质上的关键作用.从黄先生所推导出的S因子的理论表达式出发, 我们首先讨论了其与电子跃迁过程中所引起的晶格弛豫的密切关联等物理内涵, 然后对黄-里斯因子在决定数种重点和热点固体材料, 包括六方GaN、二维WS₂单原子层半导体、无机钙钛矿结构纳米晶片以及金刚石的一些光学性质, 主要是发光性质中的关键作用进行了论证. 从中得到的一个主要结论是, 黄-里斯因子得确是一个决定固体一些光学性质的关键性参数, 具有普遍性, 但其对于晶格温度、晶格结构、缺陷态局部微结构、荷电状态等的细致关联关系仍然是一个有待进一步深刻理解的课题.也由于固体内缺陷电子与晶格声子等准粒子多体作用的复杂性与丰富性, 可以预计未来黄-里斯因子仍将是固体物理研究中的一个重要课题, 笔者相信和期待会有更多更丰富的研究结果出现. 但无论如何发展, 黄昆先生有关固体中电子-声子互作用的开创性理论工作都将被进一步地证明其基础性和关键性, 也会进一步彰显黄先生在固体物理中的杰出贡献.
作者感谢王俊、郑昌成、宁吉强、王小虎、苏志成、劳祥周、包一天、王铭正、李广起、施申蕾、耶红刚、唐飞等在光谱测量以及理论模拟工作中的重要贡献. 感谢中国科学院半导体研究所赵德刚研究员提供高质量外延GaN样品, 西安交通大学杨智博士提供高质量的CsPbBr₃钙钛矿纳米晶片样品, 以及西安电子科技大学郝跃院士课题组提供高质量的外延金刚石样品.