删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

一种基于内潮动力特征的浅海声速剖面构建新方法

本站小编 Free考研考试/2021-12-29
摘要:为了降低反演参数空间的维数, 常利用正交经验函数(EOF)来构建声速剖面. 然而, EOF方法的样本依赖性使之难以用于缺乏现场实测数据的海域. 本文提出一种全新的利用历史数据而不依靠现场实时数据即可获得的声速剖面展开基函数. 基于水质子流体静力方程和物态方程, 推导了在缺乏实时测量的情况下从历史数据获得水动力模式基函数(HMB)的办法. 利用WOA13季节平均温盐数据获得代表内潮动力特征的HMB进行分析. 较之EOF, HMB及其对应的投影系数与海洋动力特征直接相关并具有明确的物理含义. 基于东中国海实验获得的CTD (conductance-temperature-depth)及宽带爆炸声源声信号数据, 利用声速剖面重构以及匹配场声层析对HMB进行了分析, 并与EOF进行对比研究. 结果表明: HMB可以以较好的精度构建浅海声速剖面. 在对现场实时测量依赖更小的情况下, 基于HMB方法的声场预报及声层析结果与EOF方法一样好. HMB的获取更简单且直接关联海水的物理特性, 该方法可在实时测量样本不足的海域有效替代EOF进行海洋动力现象的声学监测.
关键词: 声速剖面/
声层析/
水动力模式基函数/
反演

English Abstract


全文HTML

--> --> -->
1.引　言
声速剖面是海洋声场分析必要的先验信息, 海洋内波、潮汐、锋面等动力活动的声学监测往往也是通过声速剖面或者其扰动的反演来实施的[1—3]. 从理论上讲, 声速剖面可以表示为时间或空间随深度变化的矩阵形式, 矩阵越大精度越高. 然而, 参数的增加会极大地增加逆问题的求解难度, 必须通过一定的降维技术来构建声速剖面才能保证其快捷有效地获取. 因此, 声速剖面构建方法的准确性和适用性, 以及其能否有效反映海洋动力过程的物理特征, 成为了海洋动力活动声监测中的一个关键问题.
目前最广泛使用的声速剖面构建方法[4—6] 是正交经验函数(empirical orthogonal functions, EOF). 通过若干组声速剖面正交基以及对应的投影系数, 极大地减少了描述声速剖面垂直结构所需参数, 可有效地应用于海洋声层析[7—10]、声速剖面时空变化分析[11,12]、海洋活动监测[13,14]、声源定位[15—17]等领域. 大量的理论研究及实际应用证实了EOF方法的有效性和可行性, 同时也暴露了其在海洋环境声监测领域存在着以下两方面的不足: 1)方法需要一定量的样本进行特征提取, 当样本过少或者没有完整覆盖海洋活动周期时, 难以有效地对声速剖面进行构建; 2) EOF实质上是样本数据矩阵的特征, 是“数据”的展开基函数, 它并没有明确的物理意义, 从反演获得的若干个投影系数上很难直观地获得海洋动力活动的信息. 在实际海上应用中, 最亟待监测动力活动的海域往往是缺乏现场测量数据的. 缺乏样本的情况下EOF方法获取基函数较为困难, 对反演结果的进一步分析处理也会影响监测的实时性. 除了EOF方法, 声速剖面也可以通过一定的解析函数模型进行构建. 解析函数模型一般通过一系列的数学表达式及参数描述声速随深度的变化关系, 例如Munk模型[18]、连续介质力学的离散元方法模型[19]、分层声速剖面模型[20]等. 然而, 解析模型通常有一定的适用区域, 为保证精度参数往往较多, 且涉及的参数也与海洋动力特征没有直接联系, 因此很少应用于海洋动力活动的监测中.
本文提出一种全新的基于内潮动力特征的声速剖面构建方法. 根据流体动力学原理, 结合声速扰动与水质子运动的关系, 利用内潮简正模式建立声速剖面的水动力模式基函数(hydrodynamic mode bases, HMB)进行声速剖面构建. 由于潮汐运动具有较强的周期性和季节性特征, HMB可以从WOA13气候态数据[21]等历史资料中直接计算获得, 实现了不借助实时现场测量样本的声速剖面展开基获取. 同时, 这种基函数及其对应投影系数与海洋动力过程有直接的联系, 较之传统的方法具有更明确的物理意义. 结合2001年东中国海中美联合实验数据的声速剖面重构证实了方法的有效性, 对比EOF方法对HMB的准确性和物理意义进行了讨论. 最后, 将HMB应用于匹配场声层析, 初步探讨了这种声速剖面基函数应用于海洋动力活动监测的可行性. 与EOF等传统方法相比, 基于内潮动力特征的HMB可以仅依靠数据库历史数据获得, 其参数与海洋动力活动的物理特性直接相关, 这些特点在海洋动力活动的声学监测中是非常有意义的.
2.基于内潮动力特征的水动力模式基函数
按照时间尺度的不同, 海水声速剖面的变化可以分为大尺度的背景变化以及小尺度动力活动引起的变化[22]. 大尺度的变化主要影响较长时间段内声速剖面的稳态背景特性, 例如温跃层的深度与厚度等, 它带有明显的季节特性; 而小尺度的变化通常指短时间内的变化, 例如线性和非线性内波等引起的声速剖面扰动, 它对稳态背景剖面没有影响. 以EOF为代表的传统声速剖面构建方法主要采用的是数据特征提取的原理, 在构建某时刻声速剖面时必须对临近时间和空间内的声速剖面进行特征提取, 这就决定了其样本依赖性. 从海洋物理动力过程的角度出发, 季节性的海洋背景层化特征是较为稳定的, 而短时间的内波等垂向动力过程特性是受稳态的背景层化特性所控制的, 所以已知稳态背景层化特性的情况下可以对某时刻声速剖面的瞬态扰动特性进行推断. 与此同时, 随着WOA13气候态数据等数据库的建立, 全球绝大多数海域的季节性层化背景特征是已知的, 这就为无现场实时测量的情况下仅凭数据库历史数据来获得声速剖面展开基函提供了可能.
取直角坐标原点于静止海平面, 不考虑背景流场影响的水质子运动满足方程[23]:
$\begin{split}\frac{{{{\rm{d}}^2}W}}{{{\rm{d}}{z^2}}} &+ \left({N^2}/g\right)\frac{{{\rm{d}}W}}{{{\rm{d}}z}} + \left({N^2} - {\sigma ^2}\right)\\&\times \left({\chi ^2} + k\beta /\sigma \right)W/\left({\sigma ^2} - {f^2}\right) = 0, \end{split}$
其中水质子的振速包含三个分量$(x, y, z)$, $x$轴沿着纬度向东, $y$轴沿着经度向北, $z$轴垂直于海面向上; $W$是水质子垂向运动速度$w$的振幅; $\sigma $是频率; $k$和$l$对应为水平方向$(x, y)$的波数且${\chi ^2} = {k^2} + {l^2}$; $g$是重力加速度; $f$是科氏力; $N$浮力频率. 引入海洋研究中常用的刚盖近似等假定, 方程可进一步简化为
$\frac{{{{\rm{d}}^2}W}}{{{\rm{d}}{z^2}}} + {k^2}\left({N^2} - {\sigma ^2}\right)W/\left({\sigma ^2} - {f^2}\right) = 0.$
中尺度的海洋动力活动会引起声速剖面的变化, 其变化过程是满足上述流体力学控制方程的. 同时, 海水质子受到海底和海面两个边界的制约, 其垂向的运动具有简正模式, 质子的垂向运动可以表示为模式的叠加. 考虑到内潮几乎存在于所有浅海海域, 且具有稳定的半日或全日周期的内潮波往往是造成等声速线波动的主要因素[24]. 基于历史数据的季节性层化信息, 考虑内潮波的运动, 引入长波近似并忽略地转效应, 本征函数${\psi _n}$可以利用更为简单的Sturm-Li-ouville方程计算:
$\frac{{{{\rm{d}}^2}{\psi _n}}}{{{\rm{d}}{z^2}}} + \frac{{{N^2}}}{{{c_n}^2}}{\psi _n} = 0, $
其中${c_n}$是相速度. 这里本征函数随频率的变化可以被忽略, 质子的垂向运动可以表示为[25]
$w = \sum\limits_j {{W_j}{\psi _j}{{\rm{e}}^{{\rm{i}}\left( {{k_j}x + {l_j}y - \sigma t} \right)}}} , $
其中${W_j}$是第$j$号简正模式${\psi _j}$幅值.
由于温度对声速的影响远大于盐度, 且通常情况海洋的盐度变化区间相对较小, 下面的分析只考虑了温度的影响(如果要考虑盐度的影响, 分析方法类似).
海水物态满足热力学公式:
$\frac{{{\rm{d}}\left(\rho {c_{\rm{v}}}T\right)}}{{{\rm{d}}t}} = \nabla \left({k_{\rm{r}}}\nabla T\right) + {Q_{\rm{T}}}, $
其中$\rho $是相速度, $T$是温度, ${c_{\rm{v}}}$是等体积比热容, ${k_{\rm{r}}}$是热导率, ${Q_{\rm{T}}}$代表热源. 将水质子活动视作没有热源的绝热过程, ${k_{\rm{r}}}$和${Q_{\rm{T}}}$均为零, 水质子运动引起的温度随时间$t$的变化可以简化为[26]
$\frac{{\partial T}}{{\partial t}} = - w \cdot \frac{{\partial T}}{{\partial z}}.$
将(4)式代入(6)式得到:
$\frac{{\partial T}}{{\partial t}} = - \frac{{\partial T}}{{\partial z}}\sum\limits_j {{W_j}{\psi _j}{{\rm{e}}^{{\rm{i}}\left( {{k_j}x + {l_j}y - \sigma t} \right)}}} .$
与声速的变化类似, 温度可以表示为季节性的稳态背景${T_0}$以及短时间内动力活动造成的扰动${T'}$, 那么${\rm{d}}{T_0}/{\rm{d}}z > > {\rm{d}}{T'}/{\rm{d}}z$, 对(7)式两边进行积分可以得到温度剖面的表达式:
$T(z, t) = {T_0}(z) + \frac{{{\rm{d}}{T_0}}}{{{\rm{d}}z}}\sum\limits_j {\frac{{{W_j}}}{{{\rm{i}}\sigma }}{\psi _j}{{\rm{e}}^{{\rm{i}}\left( {{k_j}x + {l_j}y - \sigma t} \right)}}} .$
这里温度就被表示成与EOF方法类似的展开形式:
$T = {T_0} + \left[ {\begin{array}{*{20}{c}} {{B_1}}&{{B_2}}& \cdots &{{B_n}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\varphi _1}} \\ {{\varphi _2}} \\ \vdots \\ {{\varphi _n}} \end{array}} \right].$
展开基函数${\varphi _n}$为背景剖面梯度与对应阶数本征函数的乘积:
${\varphi _n} = \frac{{{\rm{d}}{T_0}}}{{{\rm{d}}z}}{\psi _n}, $
投影系数为
${B_n} = \frac{{{W_n}}}{{{\rm{i}}\sigma }}{{\rm{e}}^{{\rm{i}}\left( {{k_n}x + {l_n}y - \sigma t} \right)}}.$
在浅海环境中, 海水声速与温度有非常强的相关性, 温度每升高1 ℃声速也随之增加约4.0 m/s, 因此也可以近似地用${\varphi _n}$来作为声速剖面的展开基. 声速剖面$C$可以展开为如下的形式:
$C = {C_0} + \left[ {\begin{array}{*{20}{c}} {{\eta _1}}&{{\eta _2}}& \cdots &{{\eta _n}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\varphi _1}} \\ {{\varphi _2}} \\ \vdots \\ {{\varphi _n}} \end{array}} \right]. $
实际应用中${C_0}$为季节性的稳态背景声速剖面(也可以通过一个海洋动力活动的周期平均获得), ${\eta _n}$为第$n$阶投影系数. 因为是从海水动力方程中推导获得, 这里将这种声速剖面展开基称作HMB. 在文献[25]中, 基于数据库历史数据计算的水动力模式被直接用来构建声速剖面. 由于声速不是一个动力学量, 所以其有效性难以保证. 文献[26]解决了动力模式转化为声速扰动的问题, 但是由于动力方程适用性的限制, 仍然必须依靠现场实时测量的样本数据才能求得基函数. HMB方法结合了两种方法的特点, 实现了依靠数据库历史数据获得有效的声速剖面展开基函数.
较之EOF声速剖面基函数, HMB最大的特点在于它有明确的物理表达式, 而不再是单纯的样本数据特征提取. 从季节性的稳态分层特征可以计算浮力频率$N$, 这就决定了水质子运动的各阶模式$\psi $. 考虑温度为声速扰动主要因素的情况下, 结合背景温度剖面的梯度就可以计算水动力基函数$\varphi $. 季节性的稳态背景剖面可以从WOA13等数据库的多年统计平均或者同化数据中获得, 这就使不依靠现场实时的测量而获得声速剖面展开基函数成为了可能. 此外, 较之EOF方法, HMB有更明确的物理含义. 一方面, 季节性层化特性决定了水动力模式, HMB中包含了水质子运动的模态信息. 另一方面, 季节性层化特征对内波等海洋动力活动有控制作用, HMB对应的投影系数也与海洋动力活动存在着一定的内在联系. 下面将通过海上实测数据的处理, 对HMB进行分析.
3.东中国海实验数据分析
实验数据来自2001年夏季中美两国在东中国海进行的联合科学考察实验[27], 本节将利用CTD(conductance-temperature-depth)测量数据进行声速剖面重构分析, 并基于声传播实验数据进行匹配场层析.
2
3.1.水动力模式基函数分析
-->

3.1.水动力模式基函数分析

从2001年6月2日19点35至6月6日23点23分, 实验3号在抛锚点(29°40.47′N, 126°49.21′E, 海深105 m)按照约1 h的间隔(辅机停电时, 暂停测量)进行了52次CTD测量, 图1为换算所得的声速剖面数据. 可以看到声速剖面随时间的变化较大, 20—70 m的深度范围内有明显的跃层, 海深80 m到海底变化相对较小. 实验观测中发现30 m和60 m深度附近可能存在冷水团, 这可能是导致部分数据相应深度出现较低声速的原因.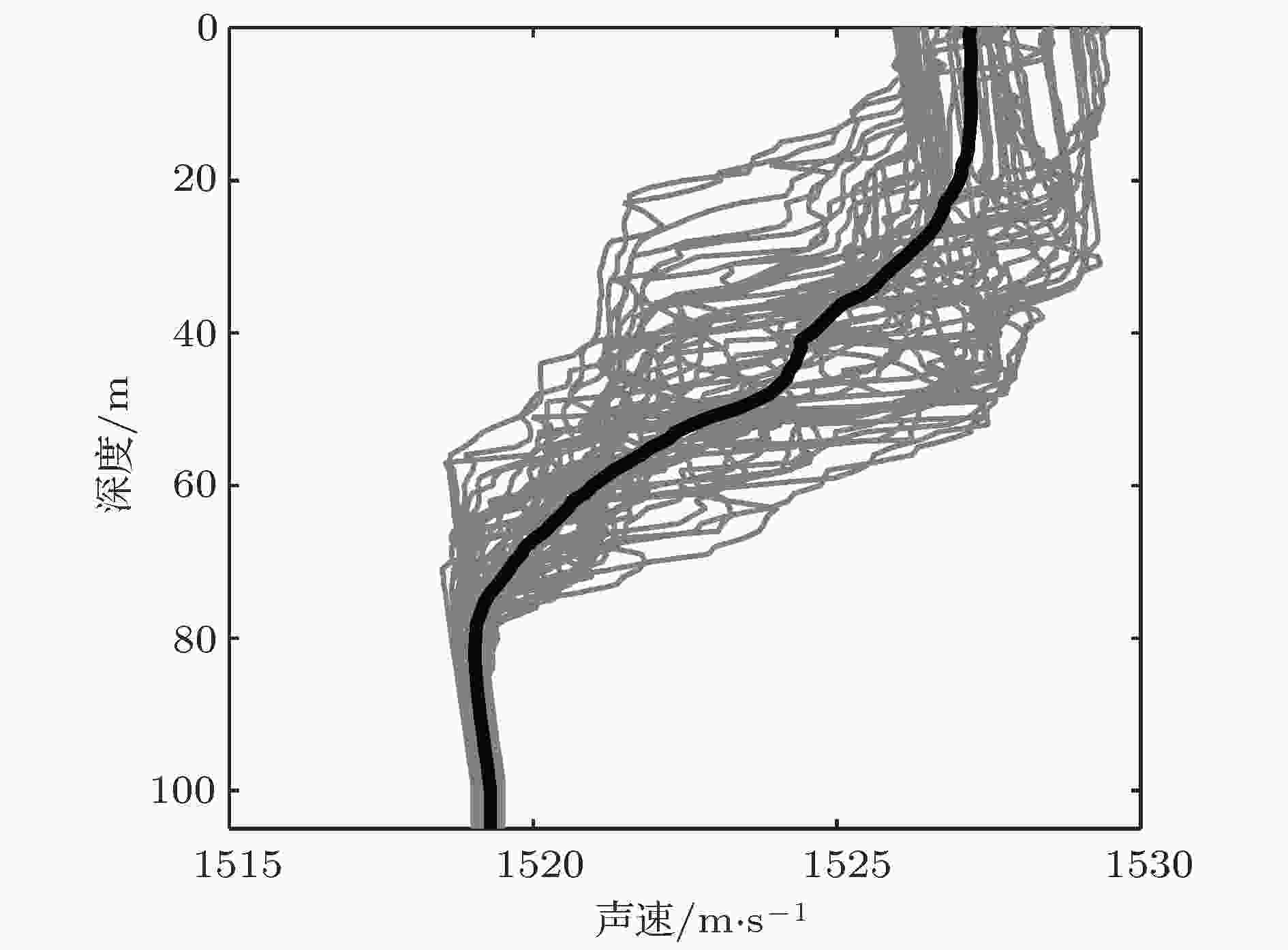
图 1 CTD测得的声速剖面(细线)和平均声速(粗线)
Figure1. Sound speed profiles (thin line) and average sound speed profile (rough line) measured by CTD.

为了分析不依靠现场实时样本情况下获得的声速剖面展开基, 这里从WOA13夏季气候态数据中提取了实验点温度和盐度剖面, 并计算了海水的浮力频率. WOA13是美国国家海洋大气局发布的海洋气候态数据集产品(https://www.nodc.noaa.gov/OC5/woa13), 包含了全球海洋温度、盐度、密度、溶氧量、磷酸盐等多种海洋要素. 它是一种整合了多种数据集和实测数据的平均格点化数据, 分为年平均数据、季节平均数据以及月平均数据, 空间分辨率有5°, 1°, 0.25°三种. 深度上, 数据集采用内插法, 其中0—100 m的分辨率为5 m[21]. 本文选用了多年(1955—2012)空间分辨率0.25°的季节平均数据, 图2为实验点夏季的平均温度、盐度以及浮力频率剖面. 从海水的层结特性来看, 浮力频率在20—70 m的深度有较大的值, 这与实测数据中温度跃层位置对应, 体现了数据的季节性稳态背景特征.
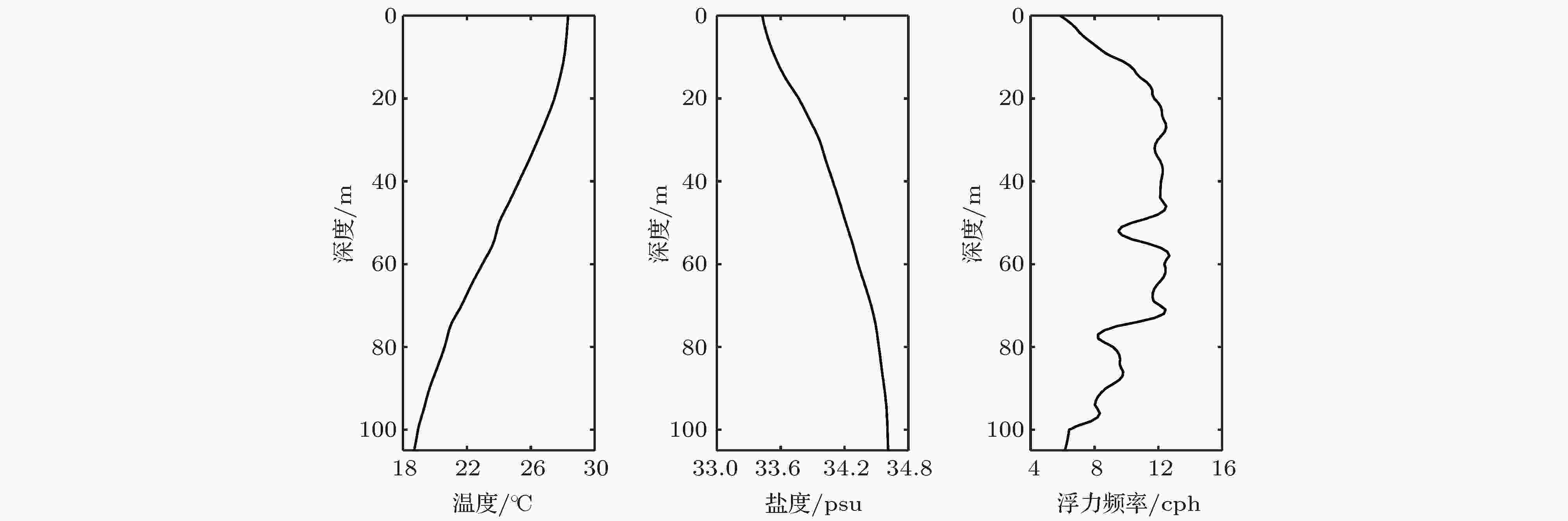图 2 温度、盐度以及浮力频率剖面
Figure2. Temperature, salinity and buoyancy frequency profile.

通过(10)式可以计算得到HMB, 这里将其与EOF方法的声速基函数进行比较, 前三阶的计算结果如图3所示. 可以看出, 由于水动力声速基源自海水层结的特征函数, 随着模态数的增加其拐点相应地递增. 其中第一阶声速展开基的极大值在58 m的深度, 这与EOF方法获得正交基有一些不同, 但两者的垂直分布上有一定的相似之处, 这表明季节性稳态背景剖面虽然能体现一定的稳态特性, 但是并不能非常精确地描述剖面在某一特定时刻的瞬态变化. 其他阶声速剖面基函数的分布也体现了相同的特点, 接下来将通过声速剖面的重构分析对这种稳态特性获得的声速剖面展开基的有效性进行分析.
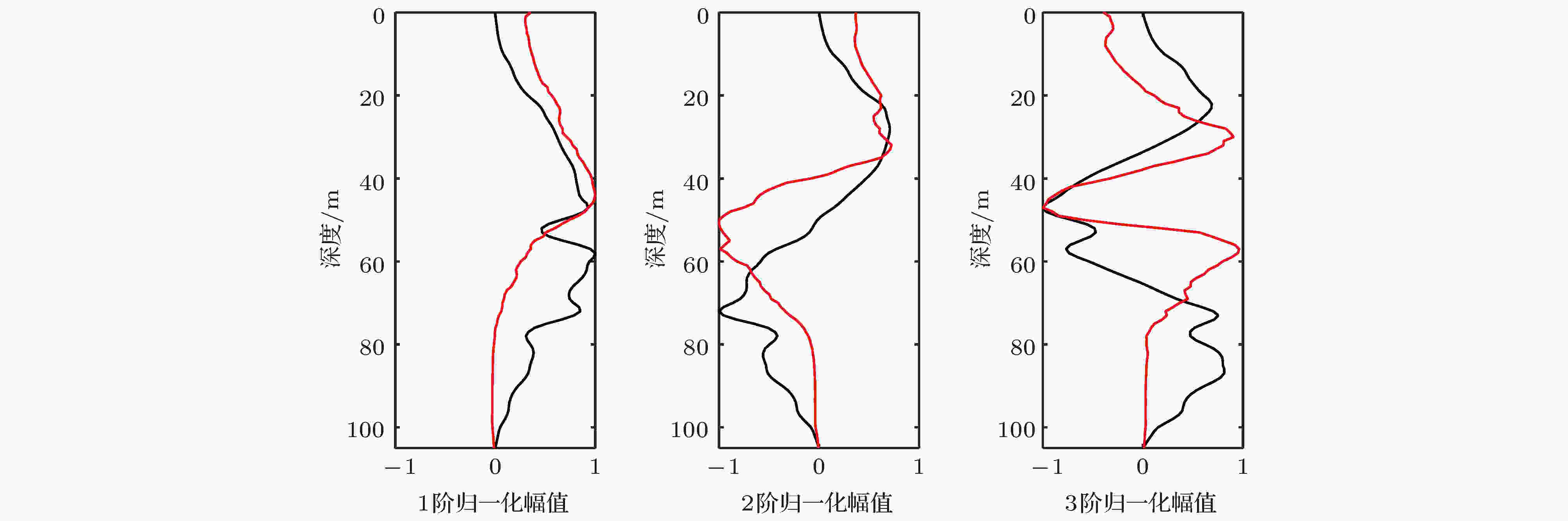图 3 不同方法获得的声速剖面展开基比较(黑线, HMB方法; 红线, EOF方法)
Figure3. Comparison of the sound speed profile bases obtained by different methods (black line, HMB; red line, EOF).

2
3.2.声速剖面重构分析
-->

3.2.声速剖面重构分析

为了检验声速剖面构建效果, 本节分别基于HMB和EOF方法对声速剖面进行重构分析. 考虑到CTD测量中不可能完全在等距离点处进行采样, 因此采用样条插值法得到了从海面到海底采样距离为1 m的106个等距离点的声速值, 并基于这些采样点与声速剖面展开基函数进行了重构. 为分析重构剖面的准确性, 定义重构的均方根误差为
$RMSE=\sqrt {\frac{1}{N}\sum\limits_{i = 1}^N \left({c_i} - c_i'\right)^2} , $
其中${c_i}$中$c_i'$分别为测量和重构剖面对应深度的声速值, $N$为深度上的采样点个数.
表1为HMB及EOF方法的重构误差分析. 可以看出除了只用一阶重构以外, 两种方法的重构误差相差不多, EOF方法效果稍好于HMB方法. 对比其他文献对同组数据的重构[28], 两种方法使用前六阶基函数均能较好地构建出声速剖面. 由于HMB方法在计算基函数时只利用了稳态的季节性分层特性, 包括年际变化、海气相互作用、水团等因素的影响势必会导致HMB方法重构效果不及现场样本的特征提取. 但是, 从重构结果来看, 从数据库历史数据获得的HMB仍然能保证较高的重构精度, 基于稳态层结信息的声速剖面构建是可行的. 表2为不同方法中各阶所占声速剖面变化比重, 可以看到两种方法中前两阶基函数所占百分比远大于其他阶. 结合表1和表2的数据, EOF方法由于提取了包含重构剖面在内的多个样本特征, 重构效果稍好于HMB方法. 但是, HMB方法基于历史数据获得的基函数是可以获得较好的重构效果的.
阶数
12345678
HMB方法
均方根误差		1.00.690.600.540.490.420.370.34
EOF方法
均方根误差		0.760.590.470.420.340.290.250.22


表1不同方法重构效果的误差分析(单位: m/s)
Table1.Error analysis of different reconstruction methods (m/s).

阶数
12345678
HMB方法
所占变化比		55.618.19.34.73.73.12.11.8
EOF方法
所占变化比		71.415.15.74.21.50.90.50.2


表2不同方法各阶所占声速剖面变化比重
Table2.Proportion of sound speed variety for each order in different methods.

参考逆问题应用中的通常做法, 这里选择了两种方法的前三阶基函数重构结果进行分析. 图4给出了均方根误差随样本的变化, 总体来看重构效果与表1结果一致, 绝大多数的重构均方误差都在0.5 m/s以下. HMB和EOF重构均出现了一些误差稍大的情况, 下面将对HMB误差最大(1.14 m/s)的第8号样本进行分析.
图 4 不同样本重构效果的误差分析
Figure4. Error analysis of different samples.

图5为第8号样本两种方法重构结果与真实声速剖面的对比. 由于湍流混合、水团等因素的作用, 声速剖面有时会在很小的深度范围内出现剧烈的拐点或者大梯度变化. 因为这种声速的变化并不受季节性层结特征控制, 用若干阶的HMB重构难以表现这种细微的突变结构; 与之对应, 由于这种声速剖面的突变具有随机性, 并非大量样本具有的共有特征, 所以若干阶的EOF重构常常也难以避免这种误差. 图5中EOF重构结果在一定程度上体现了这种声速剖面的突变, 主要是由于图1所示的样本数据中很多都在30 m和60 m附近出现了低温水团的影响, 因此这一特征被保留进了EOF基函数并反映在声速剖面的重构上. 值得一提的是, 这种声速的突变是具有随机性的, 所以图4中某些样本HMB方法的重构效果要好于EOF方法. 总体来讲, 由于EOF方法是数据特征的提取, 在突变的细结构描述上它可能是好于HMB方法的. 但是, 当突变结构并非样本普遍特征时, 包括HMB方法在内的几乎所有声速剖面重构方法都是难以描述.
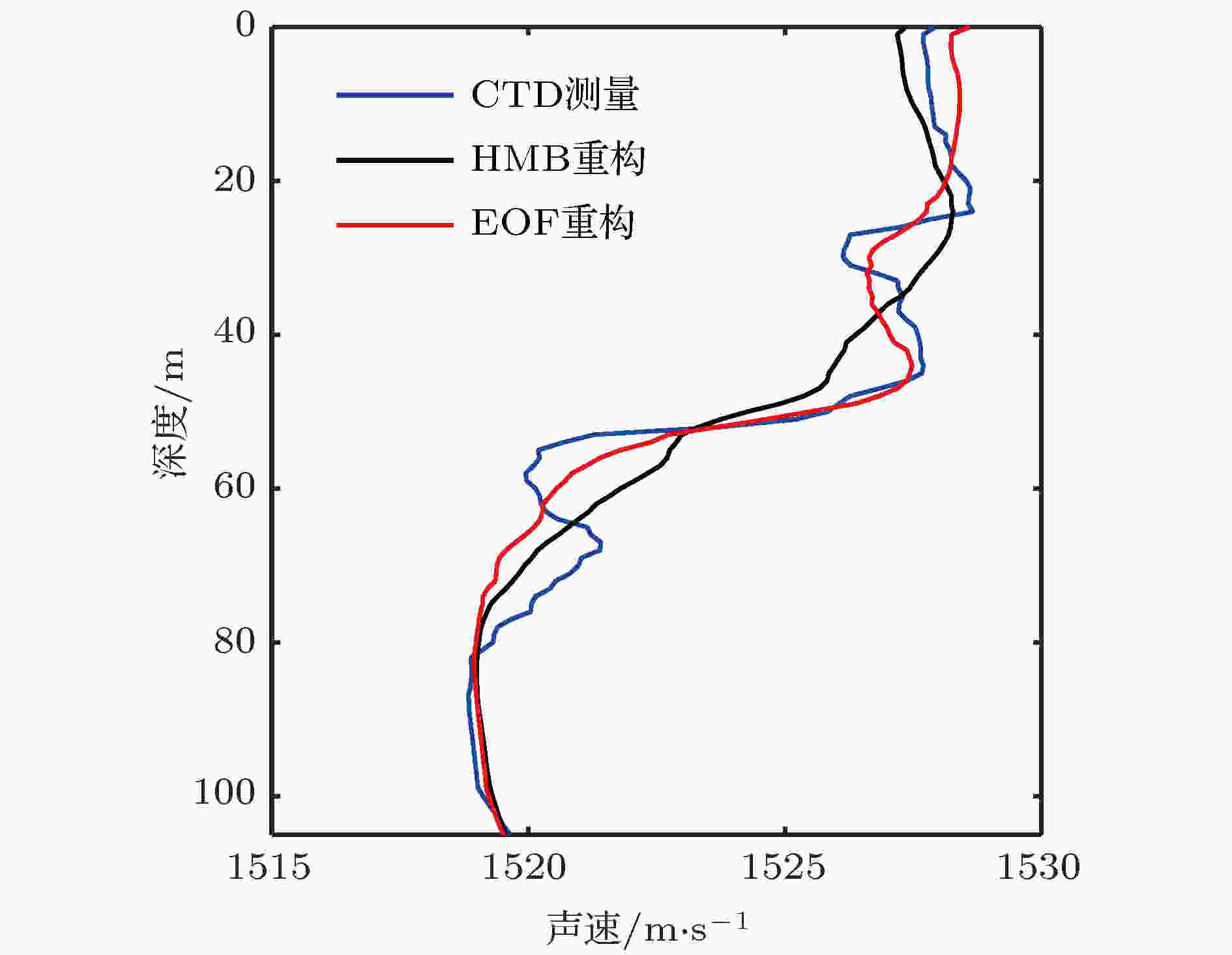图 5 第8号声速剖面重构
Figure5. The 8th sound speed profile reconstruction.

2
3.3.基于重构声速剖面的声场计算分析
-->

3.3.基于重构声速剖面的声场计算分析

从声速剖面的重构来看, HMB方法可以保证较高的精度, 但是无法避免在细结构上的一些误差. 由于声场的计算是重构声速剖面最核心的目标, 重构剖面能够准确计算声场就成为了评价方法有效性的核心问题. 本节采用重构误差最大的第8号样本的声场计算进行分析. 重构仍然采用前三阶基函数, 波导参数与实验保持一致, 声源深度为50 m, 频率200 Hz, 采用水平不变波导, 海底密度1.86 g/cm3、声速1610 m/s、衰减系数0.15 dB/λ, 海深105 m.
图6为利用所得声速剖面计算的传播损失. 可知两种方法计算的声场与它们对应的CTD数据计算声场基本一致. 在50 km的范围内, HMB方法计算非相干传播损失的误差不超过1.6 dB, EOF方法的误差不超过0.8 dB. 声场计算结果表明虽然在重构过程中一些细结构存在误差, 但仍然能保证较高的声场计算精度, 两种方法均能有效地表示声速剖面结构. 从声学应用的角度来讲, HMB方法在依靠数据库历史数据获得基函数的情况下重构的声速剖面仍然能保证较高的声场计算精度.
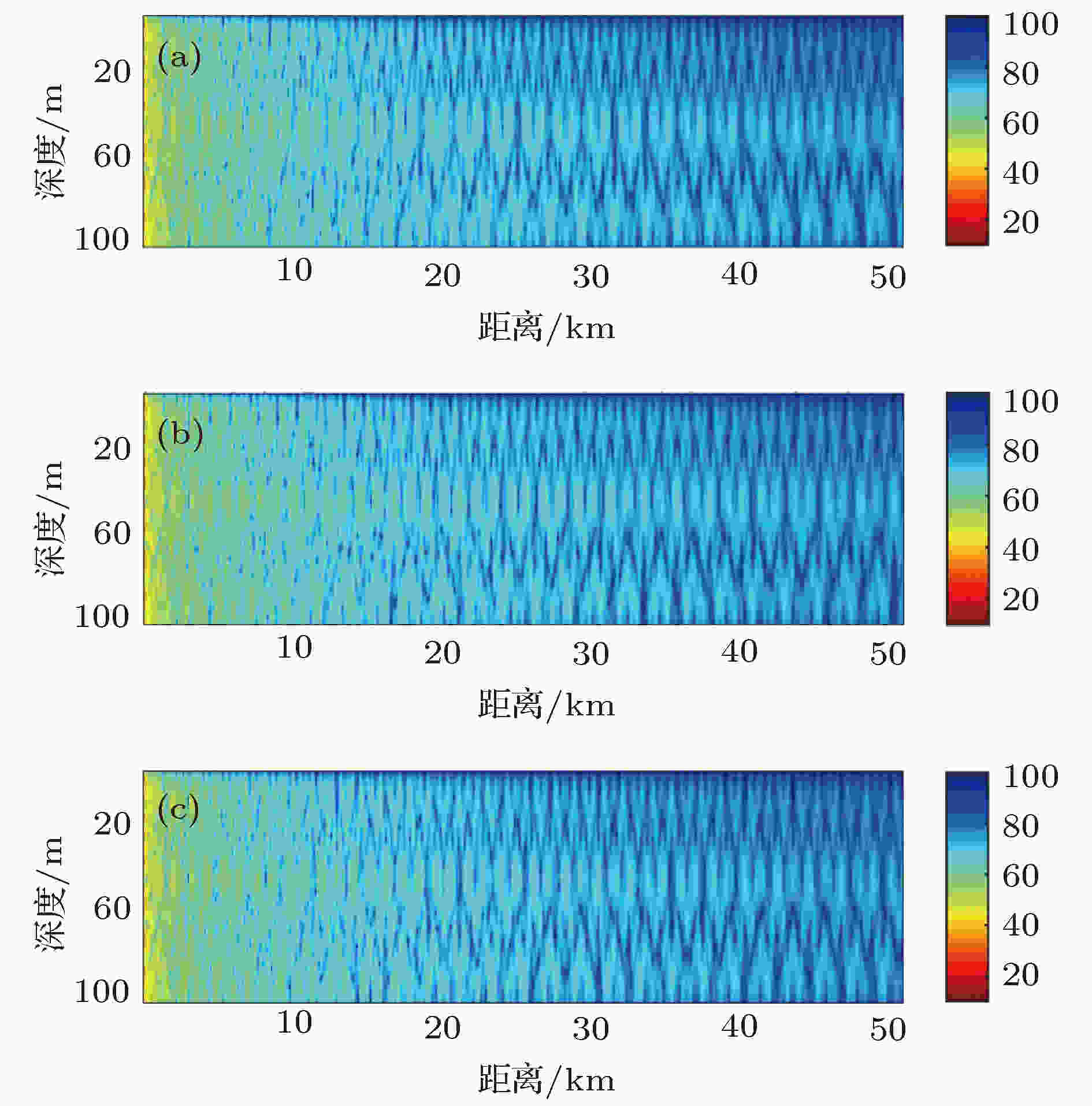图 6 声速剖面计算传播分析(单位: dB)　(a) CTD测量; (b) HMB重构; (c) EOF重构
Figure6. Analysis of transmission loss calculated by sound speed profiles (dB): (a) CTD measurement; (b) HMB reconstruction; (c) EOF reconstruction.

2
3.4.投影系数的物理意义
-->

3.4.投影系数的物理意义

根据(10)式的推导, 可以看出HMB方法的声速基函数与水质子的运动模态相关, 声速基函数包含了水质子运动各阶模态的规律. 在实际的声学逆问题应用中, 各阶投影系数通常是反演获得的直接结果, 建立它们与海洋动力活动的直接联系将极大地便利海洋动力活动的监测.
这里对前两阶垂直模态及其投影系数进行分析. 图7为前两阶模态的归一化幅值, 可以看到随着序号的增加, 幅值的拐点增加. 第一阶模态的幅值在整个水体中的符号是一致的, 它代表了不同深度水体以不同振速的同向运动. 因为模态间的正交关系, 在第一阶模态取最大值的深度第二阶模态幅值为零. 由于前两阶基函数在声速剖面构建中所占权重非常高, 如果忽略其他阶的贡献, 可以利用第一阶投影系数来近似描述特定深度等声速线的振幅. 图8为重构声速剖面中1525 m/s等声速线深度与第一阶投影系数随样本的变化. 两者的变化趋势非常相近, 两条曲线的Pearson相关系数为0.96, 说明第一阶模态的系数与等声速线的变化具有非常强的相关性. 这里1525 m/s是第一阶模态最大值50 m深度附近平均声速值, 仿真表明距离一阶幅值最大深度越近, 两者的相关性越高. 第二阶模态具有两个极值, 两个极值的符号相反且分别位于一阶极值深度的上方和下方. 它代表了等声速线在不同深度相反方向的运动, 这意味着跃层厚度的变化, 同时也代表了跃层内声速梯度的变化. 据此原理, 可以利用第二阶投影系数来描述温跃层内的声速梯度变化. 图9为跃层(30—70 m)内声速梯度与第二阶投影系数随样本的变化. 两者的变化趋势基本一致, 两条曲线的Pearson相关系数为0.99, 说明第二阶模态的系数可以用于推导温跃层内声速梯度的变化. 基于HMB方法获得的反演结果本身与海洋动力活动直接相关, 结合模态的分布可以对一些基本海洋动力参数进行求解, 这在海洋动力活动监测方面是非常实用的.
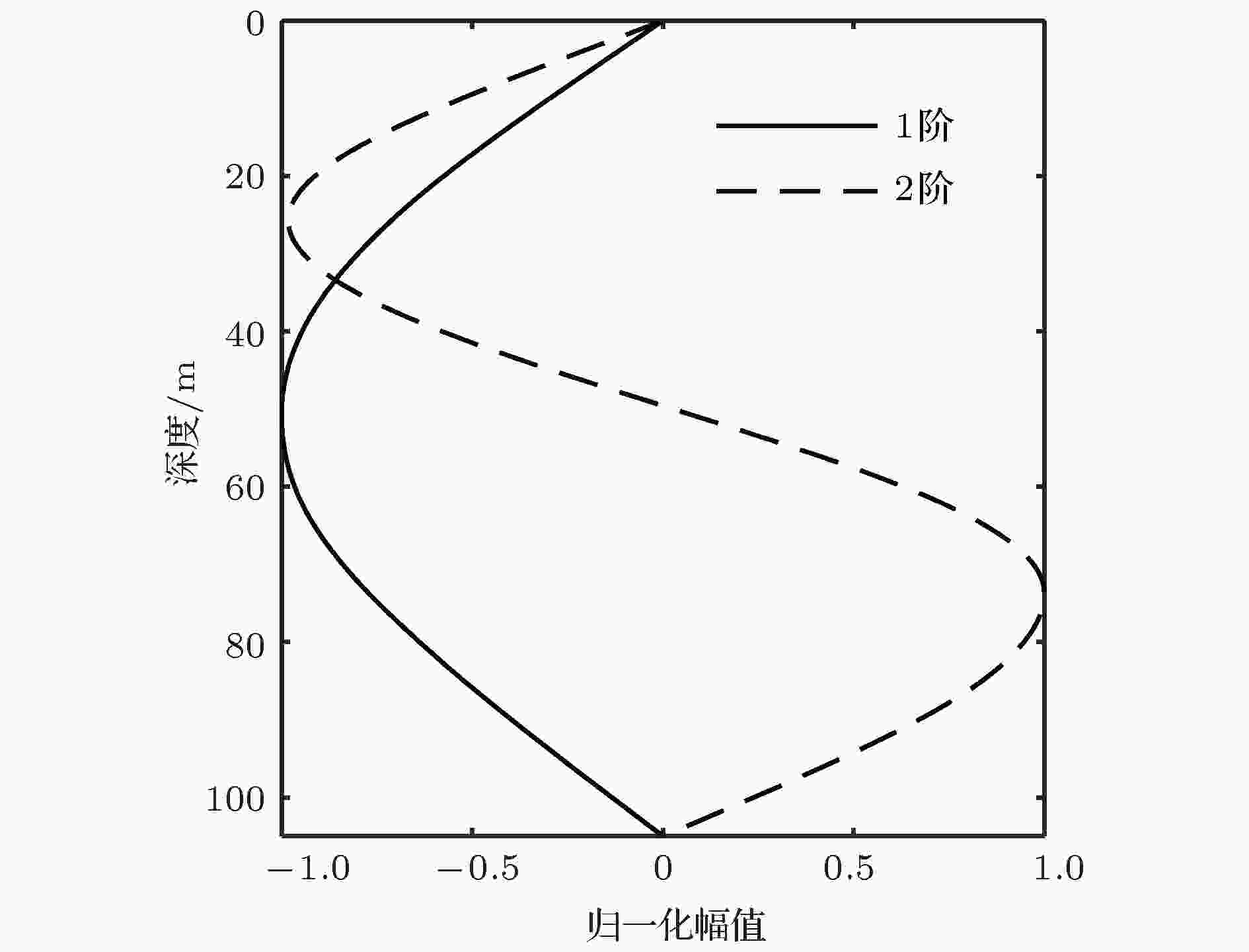图 7 前两阶模态振幅
Figure7. Amplitude of the first two modes.

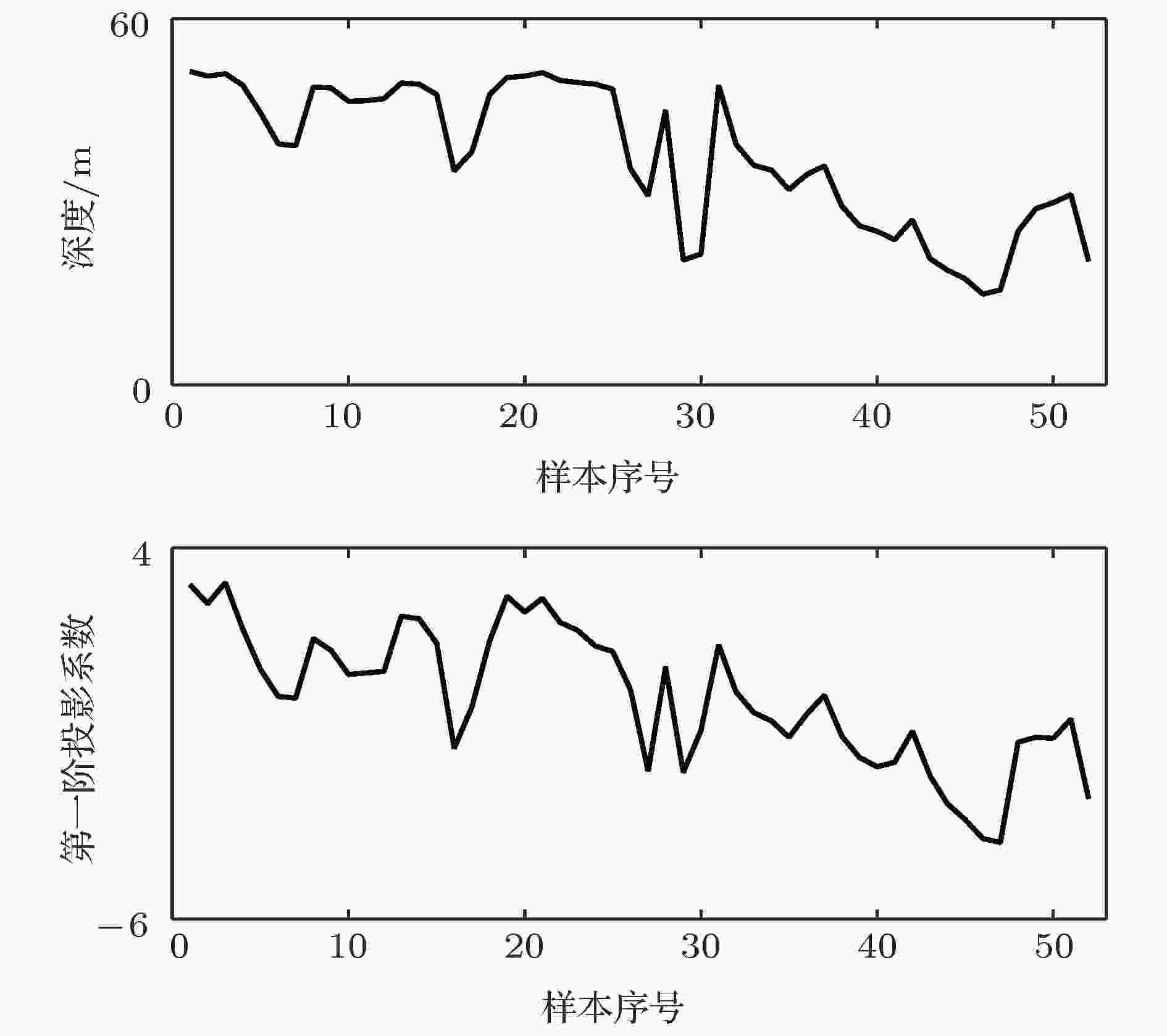图 8 1525 m/s等声速线深度和第一阶投影系数随样本的变化
Figure8. Variations of the depth at a sound speed of 1525 m/s and the first-order projection coefficient with samples.

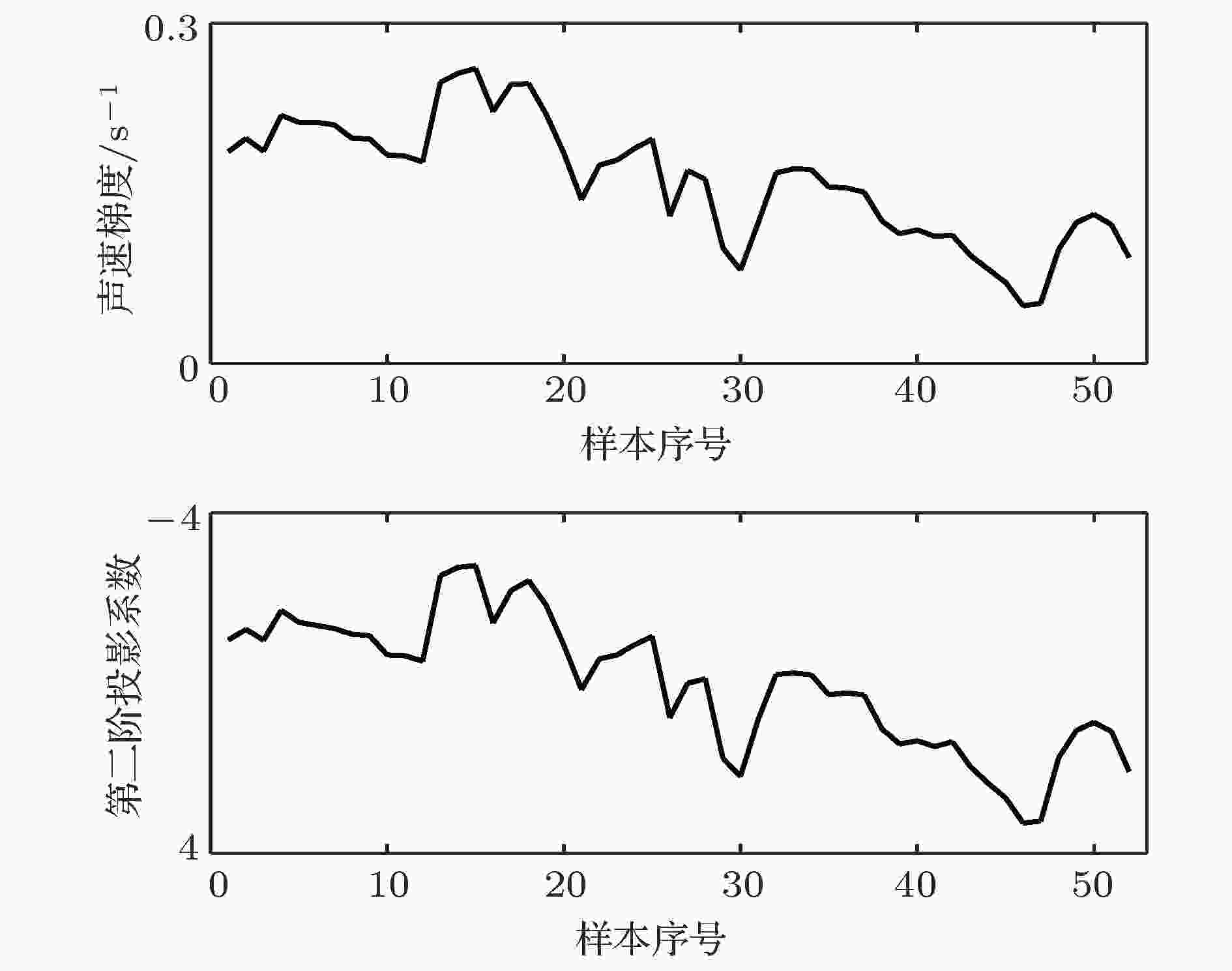图 9 声速梯度和第二阶投影系数随样本的变化
Figure9. Variations of the sound speed gradient and the second-order projection coefficient with samples.

2
3.5.匹配场声层析应用
-->

3.5.匹配场声层析应用

上面的讨论中得到HMB方法可以有效构建声速剖面的结论. 然而, 声速剖面展开基函数最重要的应用场合是在水声学逆问题的求解中. 反演过程中存在的多种复杂因素与基函数的相互作用影响着反演的效果, 因此有必要通过实际的反演对HMB方法在逆问题应用中的效果进行分析.
在前述东中国海实验中也进行了声传播实验, 声源为38 g定深50 m的爆炸声源, 接收采用32元垂直阵. 水听器覆盖的深度为4.5—90.5 m, 32.5 m以上水听器间隔约2 m, 32.5 m以下间隔约4 m, 其中36.5 m及52.25 m的两个水听器损坏, 所以反演使用了余下的30个水听器的声压数据. 传播实验过程中, 海深可近似为恒定105 m. 为检验HMB方法的普遍适用性, 采用常规的匹配场声层析方法. 反演使用宽带非相关Bartlett处理器, 匹配处理使用频段为99—201 Hz, 共35个频率点数, 整体流程如图10所示. 使用遗传算法在寻优空间中快速寻找一组参数向量$m$使得代价函数
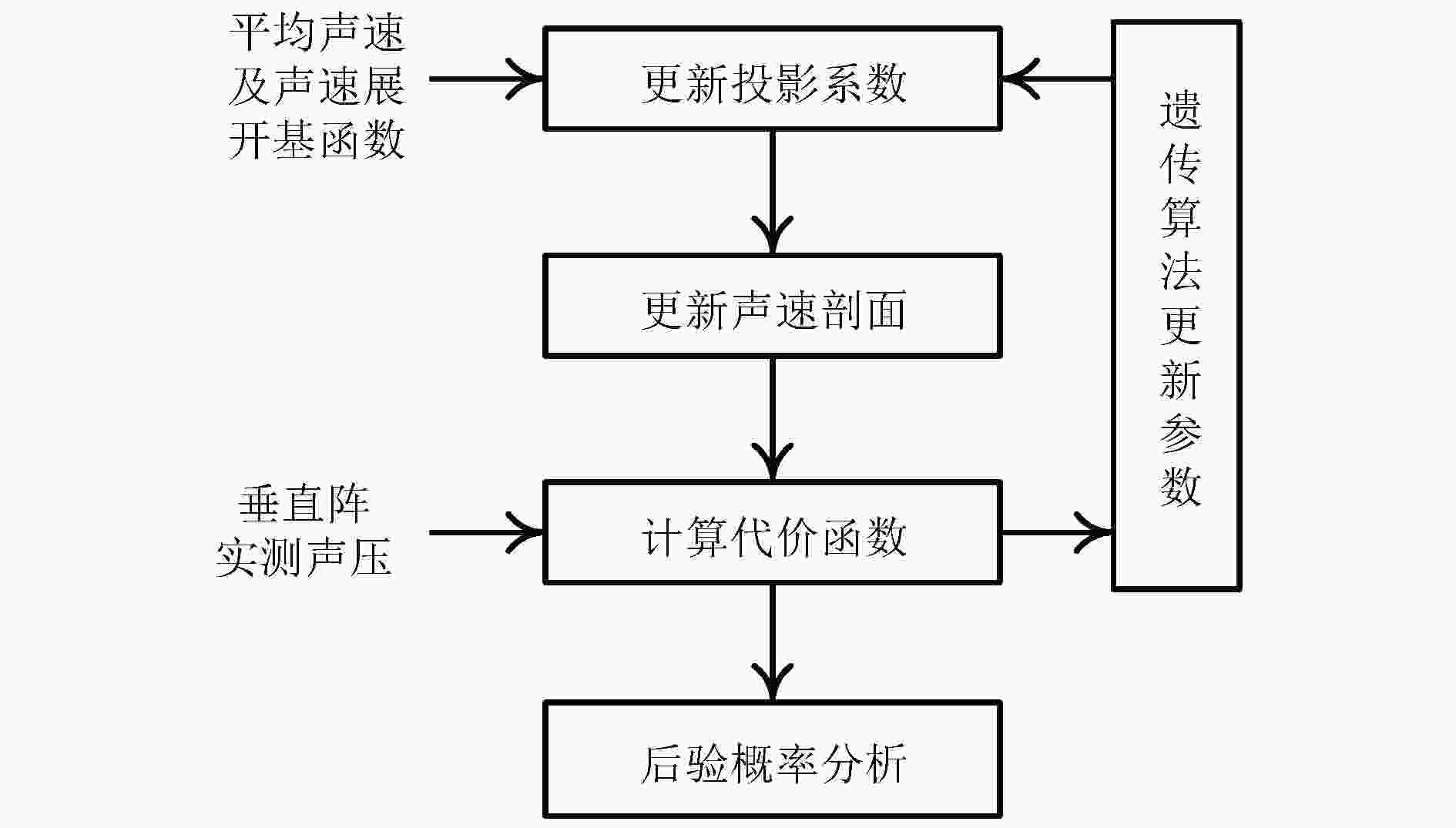图 10 反演流程
Figure10. Inversion process.

$E(m) = \frac{1}{L}\sum\limits_{l = 1}^L {\frac{{\left| {\displaystyle\sum\limits_{n = 1}^N {p_{nl}^{\rm{e}}(m)p_{nl}^{\rm{c}}{{(m)}^ * }} } \right|}}{{\left[ {\displaystyle\sum\limits_{n = 1}^N {{{\left| {p_{nl}^{\rm{e}}(m)} \right|}^2}} } \right]\left[ {\displaystyle\sum\limits_{n = 1}^N {{{\left| {p_{nl}^{\rm{c}}(m)} \right|}^2}} } \right]}}} $
达到最小值, 其中$L$为频率点数, $N$为水听器阵元数, $P_{nl}^{\rm{e}}(m)$及$P_{nl}^{\rm{c}}(m)$为取参数向量$m$时第$n$号水听器在第$l$个频率点的实测声压和拷贝场声压, *号表示共轭. 反演中采用三阶声速剖面基函数反演声速剖面, 投影系数的搜索区间均为–5—5, 海底采用前述海底参数, 选择概率为0.5, 变异概率为0.05, 交叉概率为0.8, 种群数为100, 遗传5000代, 采用多组并行计算的办法保证结果的收敛性并为后验概率分析采集样本.
图11为声源在不同距离时的反演结果, 爆炸声源分别为10.2 km (2个)及12 km处. 从图11可以看出, 两种方法反演的结果基本一致, 在不同距离HMB方法获得的声速剖面也基本一致.
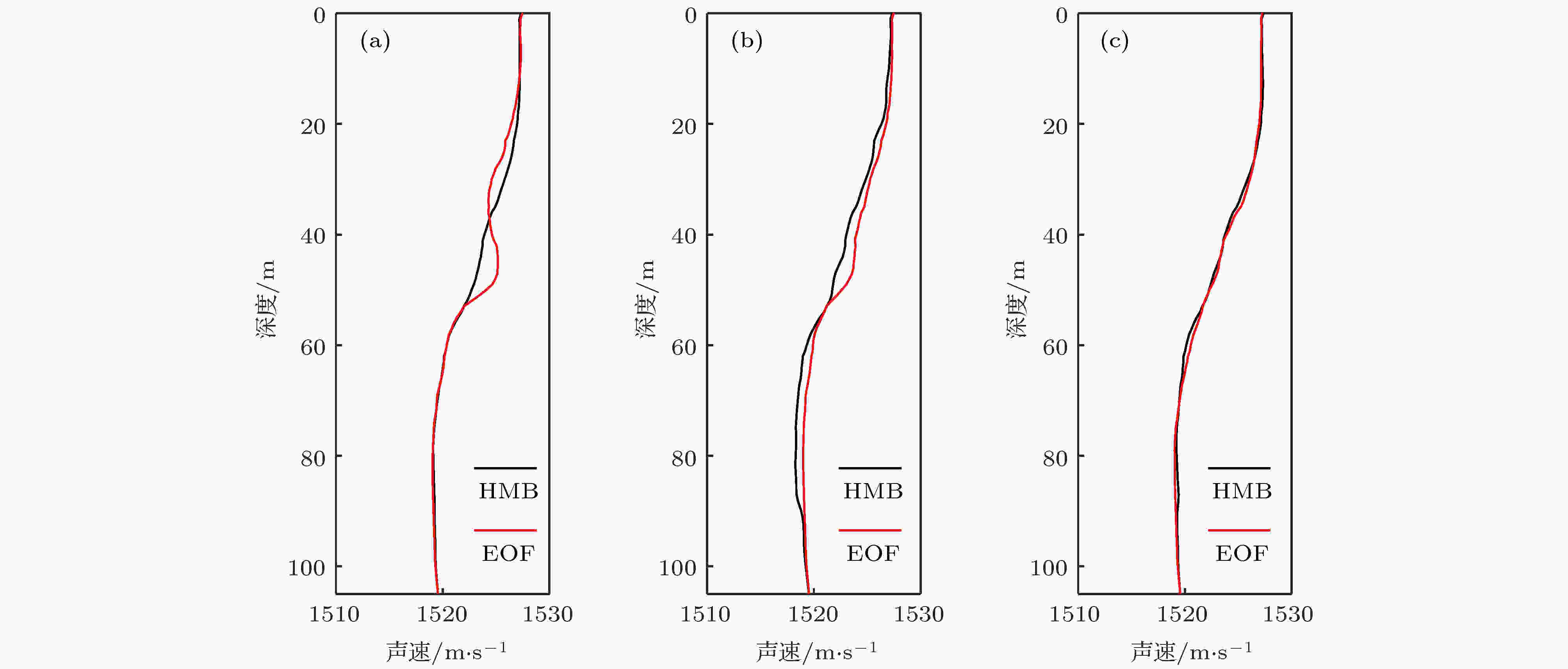图 11 不同距离的反演结果　(a) 10.2 km; (b) 10.2 km; (c) 12 km
Figure11. Inversion results at different ranges: (a) 10.2 km; (b) 10.2 km; (c)12 km.

为了考察结果的可靠性, 对反演结果的后验概率分布进行分析. 将遗传算法产生的采样值按照对应代价函数的大小进行排序, 在形成概率分布时通过Boltzmann函数进行加权, 可以得到第$k$组的参量的概率分布为[29]
$\sigma \left({m_k}\right) = \frac{{\exp \left( - \left[ {E\left({m_k}\right)} \right]/T\right)}}{{\sum\limits_{l = 1}^{{N_{{\rm{obs}}}}} {\exp \left( - \left[ {E\left({m_l}\right)} \right]/T\right)} }}, $
其中${N_{{\rm{obs}}}}$为样本数量, $T$为类似模拟退火算法中的温度控制参数, 可以取优化过程中最佳目标函数的平均值. 样本向量中第$i$个参数取值$\kappa $的边缘概率分布为
$\sigma \left({m^i} = \kappa \right) = \frac{{\displaystyle\sum\limits_l^{{N_{{\rm{obs}}}}} \!{\exp ( -\!\!\left[ {E({m_l})} \right]\!/T)\delta (m_l^i = \kappa )} }}{{\displaystyle\sum\limits_{l = 1}^{{N_{{\rm{obs}}}}} {\exp ( - \left[ {E({m_l})} \right]/T)} }}, $
其中$\delta $为狄拉克函数. 图12给出了对10.2 km处(图11(a))宽带爆炸声源信号进行匹配场声层析所得前三阶投影系数的归一化一维边缘概率密度分布. 可以看出: 1) 3个参数均以最高概率收敛于全局最优值, 反演结果可信度高; 2)随着参数远离最优结果, 概率密度迅速下降且基本无旁瓣, 说明参数敏感和结果唯一性较好. 根据反演的分析, 基于HMB方法声速逆问题求解结果有效且唯一性好, 这有利于基于反演结果和声速基函数对海洋动力参数进行直接的求解分析.
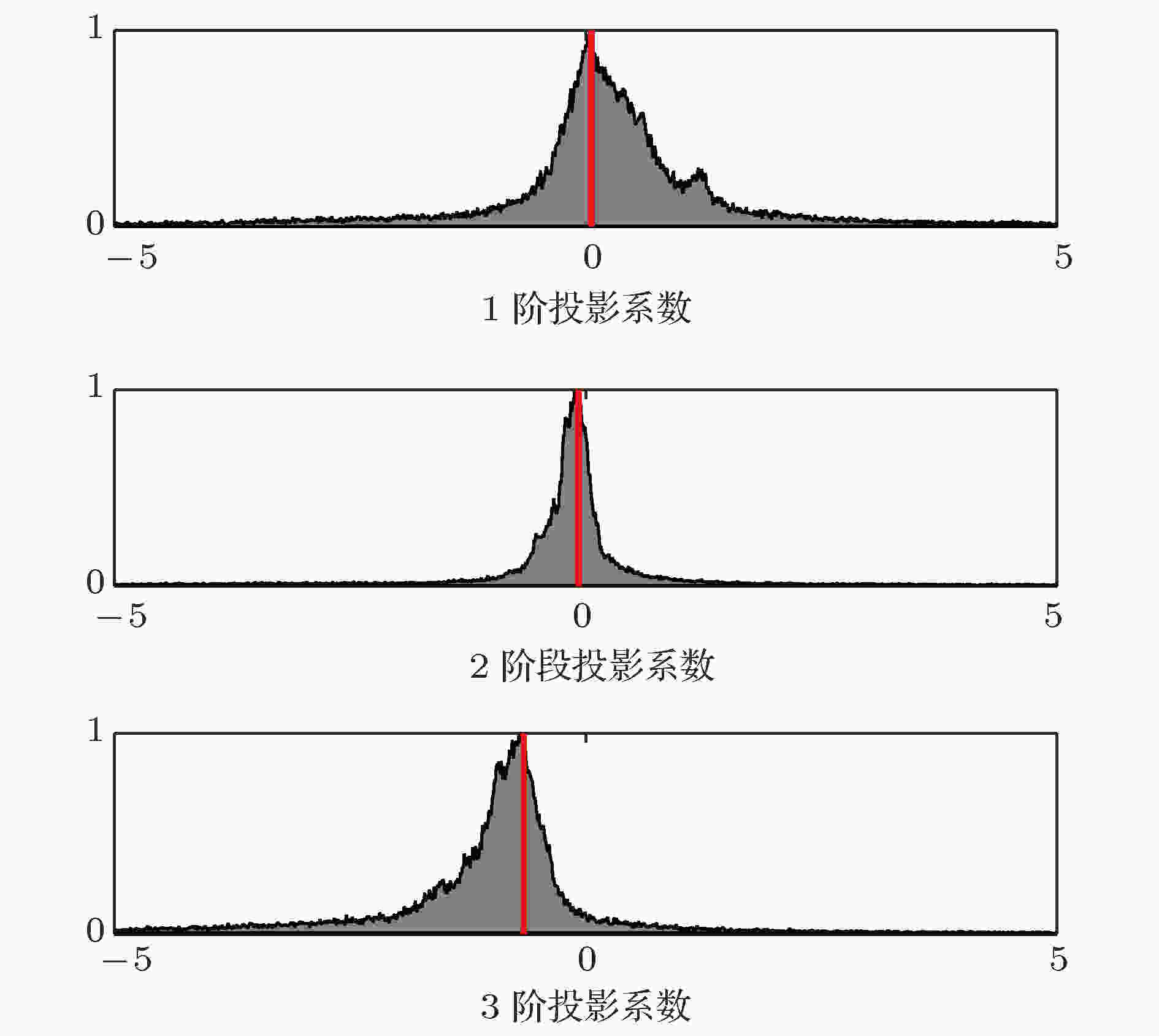图 12 3个反演参数的边缘概率密度分布 (红线为代价函数最优值对应参数)
Figure12. Probability distribution for the three inversion parameters (the red line is the optimum value for the objective function).

利用HMB方法反演所得的声速剖面对64.5 m深度的200 Hz单频信号传播损失进行了预报, 预报值与水听器真实测量值的对比如图13所示. 预报值与实测值符合得较好, 除个别异常的点, 预报曲线与实测值比较贴近. 实验中由于爆炸声源源级和爆炸深度有一定的波动, 这可能会导致预报的误差. 同时, 由于走航路线海深是缓慢增加的, 这导致了用水平不变模型计算的传播损失预报值比实测值略微偏大的情况. 但是总体来看, 预报值能较好地反映传播损失的变化趋势. 传播损失预报结果和图11中反演结果的一致性可以证实HMB方法在水声学逆问题应用中的有效性, 基于数据库历史数据获得的声速剖面展开基能有效反演出准确的声速剖面.
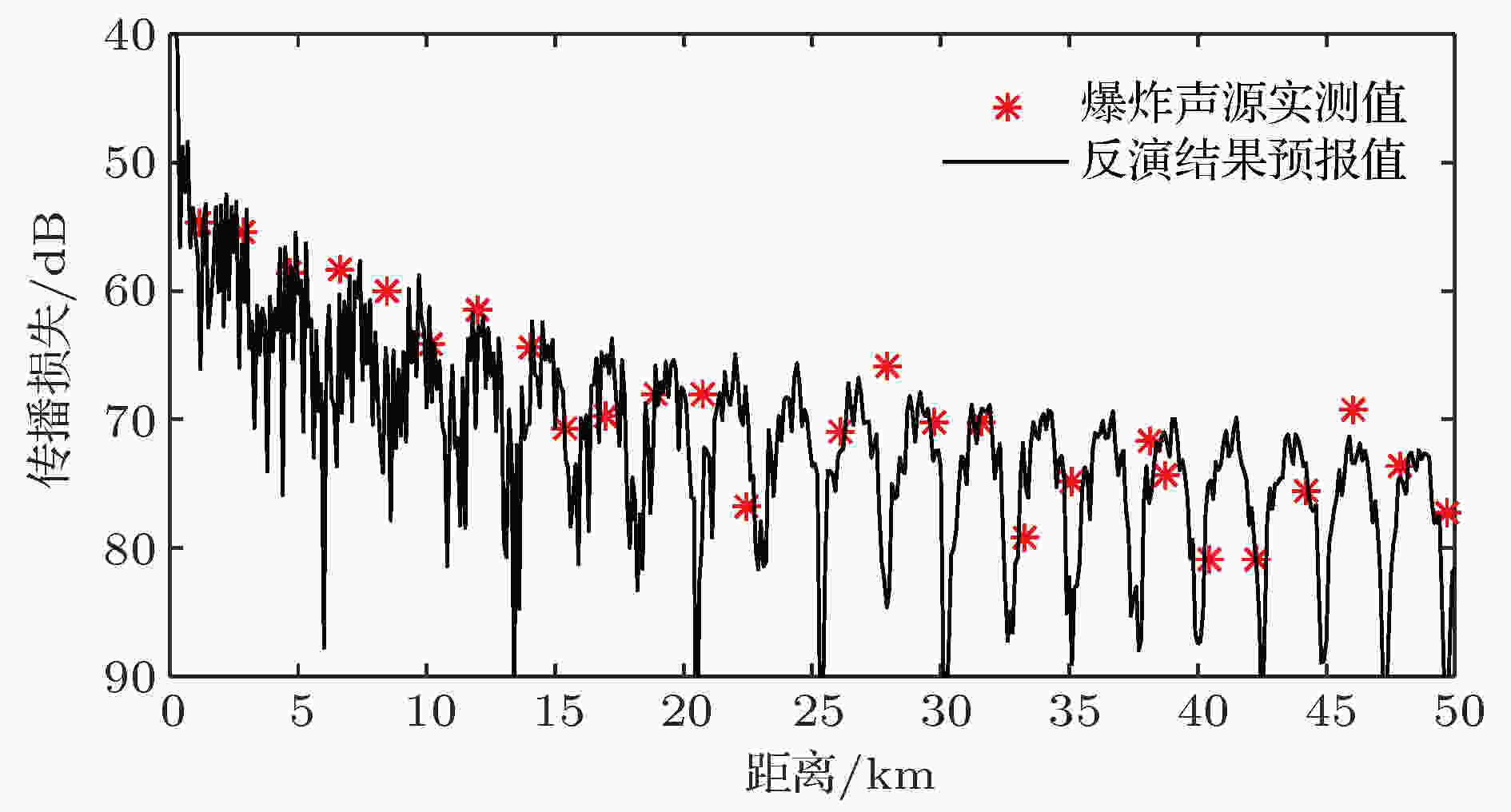图 13 传播损失预报与观测值
Figure13. Transmission loss predicted and measured.

4.结　论
针对海洋监测中对声速剖面表示的降维需求, 本文提出了一种基于水质子运动模态的声速剖面展开基函数. 该基函数仅需历史数据中的季节平均剖面即可获得. 从声速剖面的构建效果来看, HMB能够较为准确地进行声速剖面的构建. 较之经典的EOF方法, HMB方法具有更明确的物理含义: 基函数中包含了水体运动的各阶模态特征, 而前两阶投影系数可以有效描述等声速线及声速梯度的变化. 最后利用匹配场声层析实验对HMB方法在逆问题求解中的有效性进行了分析, 结果表明反演的投影系数有较好的敏感性, 结果可信度高且唯一性好.
HMB方法对现场实时测量的要求相对低, 且直接联系海洋动力活动特性, 适合用于现场实时样本不太充分海区的动力活动监测. 此外, 结合反演所获投影系数以及声速剖面基函数, 可以进一步推导海洋动力学参数用于水下动力活动监测以及其他一些用途, 相关方法是下一步研究的重点.
相关话题/动力 数据 海洋 计算 运动
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于冗余图态的多人协作量子计算
    摘要:量子计算是一种基于量子力学基本原理设计的新型计算模型,在某些特定问题上表现出了远超经典计算机的处理能力.随着量子计算任务复杂度的提高,如何分配量子计算资源,实现多方协作的量子计算,将成为量子计算领域待解决的一个重要问题.本文在一次性量子计算的基础上,提出了基于冗余图态的多人协作量子计算方案.不 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于计算全息和<i>θ</i>调制的彩色图像加密方法
    摘要:提出了一种基于计算全息和θ调制的彩色图像光学加密新方法.该方法利用彩色三基色原理和计算全息编码技术,首先将彩色图像的红、绿、蓝三基色分量进行随机相位调制和菲涅耳衍射变换,然后经过θ调制后进行图像叠加并编码为计算全息图,即加密过程是将一幅彩色图像加密为一幅实值的二元计算全息图,得到单幅密文.解密 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • <sup>7</sup>Li<sub>2</sub><sup>(0, ±1)</sup>分子体系基态振-转能级的全电子计算
    摘要:采用单参考与多参考耦合簇理论结合相关一致高斯基组计算研究了7Li2(0,±1)分子体系的电子基态的势能曲线,计算考虑了体系所有电子的关联效应与相对论效应,拟合得到了体系的光谱常数,并获得了电子基态的振动-转动能级信息.计算得到的中性与阳离子体系的光谱常数与实验值符合得很好;对于阴离子体系,平衡 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 微通道疏水表面滑移的耗散粒子动力学研究
    摘要:了解疏水表面的滑移规律对其在流动减阻方面的应用至关重要.利用耗散粒子动力学(dissipativeparticledynamics,DPD)方法研究了微通道疏水表面的滑移现象.采用固定住的粒子并配合修正的向前反弹机制,构建了DPD固体壁面边界模型,利用该边界模型模拟了平板间的Couette流动 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 三氨基三硝基苯基高聚物粘结炸药热力学性质的理论计算研究
    摘要:高聚物粘结炸药(PBX)的热力学性质是用于炸药结构响应、安全性评估、数值模拟分析等的重要参数.由于PBX结构的多尺度特性,完全采取实验方法精细表征这些参数存在巨大的挑战.本文运用第一性原理和分子动力学计算的方法,系统研究了三氨基三硝基苯(TATB)基高聚物粘结炸药的热力学参数和界面热传导性质. ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 非线性薛定谔方程的高阶分裂改进光滑粒子动力学算法
    摘要:为提高传统光滑粒子动力学(SPH)方法求解高维非线性薛定谔(nonlinearSchr?dinger/Gross-Pitaevskiiequation,NLS/GP)方程的数值精度和计算效率,本文首先基于高阶时间分裂思想将非线性薛定谔方程分解成线性导数项和非线性项,其次拓展一阶对称SPH方法对 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于数据库进行乏燃料鉴别的多元统计分析研究
    摘要:近年来,随着国际核军控形势的变化,包含防扩散、防核恐及核安保的多边国际军控合作越来越受到重视.核取证技术作为防扩散、防核恐及核安保的一项核心技术,在对涉核非法活动的威慑、阻止以及响应方面具有重要作用,值得深入研究.目前针对核取证技术的研究较多,主要集中于材料的表征和数据的解读.其中解读作为核取 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 曲波域统计量自适应阈值探地雷达数据去噪技术
    摘要:非线性、非平稳探地雷达数据常掺杂各种复杂噪声源,其对精确提取弱反射波信号、识别绕射波双曲线同相轴特征具有严重影响,忽略噪声影响给探地雷达探测数据全波形偏移成像及后续解译造成较大误差.采用传统阈值函数的曲波变换去噪需要根据数据噪声水平人为确定合理阈值控制系数.对此,本文开展自适应阈值函数的曲波变 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 钫原子磁偶极超精细结构常数及其同位素的磁偶极矩的理论计算
    摘要:应用基于B样条基组的相对论耦合簇理论方法,计算了212Fr原子的nS(n=7—12),nP(n=7—12)和nD(n=6—11)态的磁偶极超精细结构常数.与精确实验值的比较说明这套理论方法能精确计算出磁偶极超精细结构常数,其中7P态的磁偶极超精细常数的理论值与实验值之间的差异小于1%.在忽略场 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 线性塞曼劈裂对自旋-轨道耦合玻色-爱因斯坦凝聚体中亮孤子动力学的影响
    摘要:利用变分近似及基于Gross-Pitaevskii方程的直接数值模拟方法,研究了自旋-轨道耦合玻色-爱因斯坦凝聚体中线性塞曼劈裂对亮孤子动力学的影响,发现线性塞曼劈裂将导致体系具有两个携带有限动量的静态孤子,以及它们在微扰下存在一个零能的Goldstone激发模和一个频率与线性塞曼劈裂有关的谐 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.