摘要: 输运测量是了解物质性质的一个重要手段. 本文简单介绍最近在量子气体中实现的输运实验及其主要结论, 包括在类似于介观物理器件中的Landauer输运和强相互作用费米气体中的自旋输运行为. 我们着重讨论自旋动力学的特殊性以及其由于全同粒子相互作用所导致的特殊自旋扩散流的形式.
关键词: 自旋扩散 /
电导量子化 /
朗道-玻尔兹曼方程 /
全同自旋旋转效应 English Abstract Transport phenomena in dilute quantum gases Zhang Shi-Zhong Department of Physics and Centre for Theoretical and Computational Physics, The University of Hong Kong, Hong Kong, SAR, China Fund Project: Hong Kong Research Grant Council, General research fund (Grant No. 17303215), and Croucher Foundation.Received Date: 05 November 2018Accepted Date: 13 December 2018Available Online: 01 February 2019Published Online: 20 February 2019Abstract: Transport measurement is one of the most important ways to study the properties of matter. In this article, we discuss recent experiments in ultracold atomic gases where the analog of Landauer transport in mesoscopic devices is realized and spin dynamics in a strongly interacting Fermi gas is probed. In the latter case, we pay special attention to the peculiarity of spin dynamics due to identical spin rotation effect which leads to a novel form of spin diffusion current. This modifies the usual diffusion equation into a more complicated form and leads to important consequence for, in particular, transverse spin diffusion in ultracold Fermi gases.Keywords: spin diffusion /Landauer transport /Landau-Boltzmann equation /identical spin rotation effect 全文HTML --> --> --> 1.引 言 最近几年来, 输运行为成为量子气体研究中的一个主要方向. 这些研究主要集中在以下几个方面. 首先是一般集体运动中的弛豫行为, 比如说在谐振子势中呼吸模式的衰变和体积黏度的关系[1 ] . 这类实验关心的是体系的集体激发, 测量的物理量一般是在势阱中密度平均之后的结果, 因此其物理解释需要比较多的模拟. 其次是类似于传统固体物理实验中的输运, 比如说在磁势阱或者光晶格中电导以及自旋扩散的研究[2 -9 ] . 量子气体的一个突出优点是它具有比较高的可控性和可调制性. 实验中可以较容易地改变体系的相互作用, 维度等等. 尤其重要的是, 利用光学控制, 人们可以在比体系本征时间尺度更短的时间内调节体系的参数, 从而为研究骤变现象提供了一个很好的平台.2.量子气体的特殊性 相比于传统的凝聚态(包括电子气, 液氦等), 量子气体这种比较新的多体量子系统具有其特有的性质, 从而也导致了一些特有的现象和问题[10 -12 ] .$ - {{\rm{C}}_6}/{r^6}$ 和一个强烈的短程排斥势所构成, 如图1 . C6 是范德瓦耳斯常数. 对于这样的两体相互作用而言, 我们可以定义一个特征长度, 范德瓦耳斯长度r 0 , 其大小可以通过平衡两体动能和相互作用能的大小来得到[9 ,10 ] 图 1 原子之间的范德瓦耳斯吸引势和短程排斥势Figure1. van der Waals attractive potential and short-range repulsive potential between atoms.${r_0} = {\left( {m{{\rm{C}}_6}/{\hbar ^2}} \right)^{1/4}}$ . 它对应着在范德瓦尔斯吸引势中最靠近零能的两体束缚态的特征大小. 一般而言, r 0 的大小大概是50 ?. 它一方面远远大于一般分子的大小, 但同时又远远小于一般是几个微米的原子间距d . 对应于这些长度尺度, 冷原子中的能量尺度也相差很大. 对费米系统而言, 体系的费米能EF 一般是20 kHz左右, 比范德瓦尔斯吸引势中能量最小的两体束缚态的能量小很多. 这就导致我们在考虑多体问题的时候, 只关心低能两体散射, 因此只需要为数不多的几个散射参数就可以描述体系的相互作用了. 对于s-波而言[9 ,10 ] , 一般只需要一个散射长度as ; 对于p-波而言[13 -15 ] , 就需要同时考虑低能散射体积和有效长度. 另外在有限温度下, 热德布罗意波长${\lambda _T}$ 也是一个重要的长度尺度, 它决定了在考虑相互作用的时候原子的粒子性和波动性的相对重要性. 在高温下, ${\lambda _T} \ll {r_0}$ , 这时候粒子基本上可以看成经典粒子, 散射可以看成经典散射. 然而当${\lambda _T} > {r_0}$ 的时候, 两体散射不能看成是经典散射, 而必须考虑衍射的效果. 在这种情况下, 我们可以进一步依据${\lambda _T}$ 和d 的相对大小来分两类情况. ${\lambda _T} > d$ 对应于量子简并气体: 玻色子形成玻色-爱因斯坦凝聚而费米子表现出简并费米压. 在这种情况下, 原子的空间运动自由度是量子化的. ${\lambda _T}<d$ 对应于简并温度之上, 空间运动自由度是经典的, 但散射过程必须要考虑粒子的量子性质. 具体比较见表1 . 长度尺度 备注 经典气体 ${\lambda _T} < {r_0} < d$ 经典散射; 量子气体 ${r_0} < {\lambda _T} < d$ 量子散射; 量子简并气体 ${r_0} < d < {\lambda _T}$ 量子散射;
表1 冷原子物理研究中的三个不同区域Table1. Three different regimes in the study of cold atom physics.dL 提供了一个新的长度尺度[16 ] . 对于现有的实验而言, 一般$d\sim {d_L}$ . 另外, 单个光晶格可以近似为一个简谐振子势$\dfrac{1}{2}m\omega _0^2{r^2}$ , 其中$\hbar {\omega _0} = 2{E_L}{({V_0}/{E_L})^{1/2}}$ . V 0 是光场势的幅度, ${E_L} = {\hbar ^2}{k^2}/2m$ 是反冲能量. k 是光晶格相干激光的波矢. 实验上可以通过控制V 0 的大小来控制单个光晶格势束缚的强弱. 我们可以定义谐振子长度${a_0} = {(\hbar /m{\omega _0})^{1/2}}$ . 一般而言${a_0} < {d_L}$ , 其对应的能量尺度$\hbar {\omega _0}$ 给出光晶格中能带之间能隙的大小. 如果$\hbar {\omega _0} \gg {E_F}$ , 我们可以忽略激发能带的贡献.[9 ,17 ] $\psi \left( {r\sim 0} \right)$ 是指波函数在接近零点(${r_0} \ll$ $ r \ll d$ )的幅度大小. 如果还需要继续使用上面的式子描述非平衡过程, 就要求在动力学过程中, 多体波函数在以上尺度的行为必须可以绝热的跟随局域体系参量(温度、压强等)变化以保证上面简化的正确性. 在现有的实验中, 上述条件似乎都是成立的. 不过在某些特殊情况下, 比如说骤变实验, 我们还是有必要回头看看上述假设是否成立.3.量子气体中的输运实验 本文着重讨论类似于固体物理中的输运实验. 我们大概可以将这类输运实验分成两类. 一类实验关注类似于介观量子结构的特殊势场构型的输运行为. 另一类实验注重于测量束缚在谐振子势场或者盒子势中的量子气体的输运系数. 首先简单介绍前一类实验(详细介绍可参考文献[2 ]), 之后再讨论后一类实验.3.1.类似于介观物理器件的输运实验[2 ] 3.1.类似于介观物理器件的输运实验[2 ] 在这类实验中, 玻色子或费米子被束缚在一个各向异性的谐振子势中. 谐振子势的频率满足如下条件: ${\omega _z} = {\omega _y} \gg {\omega _x}$ . 沿着y 方向, 一束蓝失谐的激光将原子团沿着x 方向分成三部分: 两侧未经扰动的原子和中间的准二维区域. 一般而言, 原子团在x 方向的大小约为300微米, 而准二维区域在x 方向的大小约为50—60微米. 沿着垂直于准二维区域的z 方向上, 谐振子频率可以达到3.9 kHz. 注意到准二维束缚区域的大小比起原子气体的所有特征长度都大. 在这个范围内, 束缚势导致的空间运动量子效果可以忽略, 体系处于多通道区域. 在进行类似电导输运实验的测量中, 可以调节两侧原子的相对数目($\Delta {N} \equiv {{N}_L} - {{N}_R}$ )来产生两侧化学势差:$\kappa = {\left(\dfrac{{\partial {\mu _L}}}{{\partial {{N}_L}}} + \dfrac{{\partial {\mu _R}}}{{\partial {{N}_R}}}\right)^{ - 1}}$ 可以看作整个体系的有效压缩率. 在$\Delta {N} \ll N$ 的情况下, $\kappa $ 可以认为不随$\Delta {N}$ 变化, 其大小可以由平衡态的热力学测量得到. 实验上可以通过测量两侧原子相对数目随着时间的变化, $\Delta {N}\left( t \right)$ , 来得知粒子流的大小.$I\left( t \right) = G\Delta \mu \left( {\rm{t}} \right) = G{\kappa ^{ - 1}}\Delta {N}\left( {\rm{t}} \right)/2$ , 我们可以得到二维区域电导G 或者电阻G –1 的大小. 对于无相互作用或者弱相互作用的费米子而言, 实验上发现二维区域的粒子输运行为满足一般的欧姆定则$I\left( t \right) = G\Delta \mu \left( {\rm{t}} \right)$ , 初始的原子数差别以指数形式衰减,$\tau = \kappa /G$ . 实验中$\tau $ 一般是200毫秒左右. 由于原子自由程远大于体系的尺度, 原子在二维区域属于弹道输运, 所以以上的电阻几乎完全是由三维和二维势接触区域贡献的(接触电阻). 需要说明的是, 这里的接触区域相比于凝聚态介观体系要光滑很多. ETH实验组还测量了在二维区域加上由激光散斑产生的无序势后的输运行为. 同样的实验装置也可以用来测量自旋以及热的传导.$\Delta N\left( t \right)$ 依旧满足指数形式衰减; 当密度变大到使得体系处于超流状态时候, $\Delta N\left( t \right)$ 的长时行为不再满足指数衰减形式, 反而呈现出残余震荡的迹象. 另外$\Delta N\left( t \right)$ 的短时指数衰减行为被解释成由于涡旋的产生所导致的超流衰变, 但是这还有待于进一步的研究.x 方向; 沿着垂直方向的束缚非常强, 有效的谐振子频率最高可达${\omega _y} = 50$ KHz, 尺度大约1.5微米. 在这种情况下, 我们需要计入径向的量子化的后果. 由于$\hbar {\omega _y}\sim {E_F}$ , 输运处于单个或少数几个通道的区域. 通过改变${\omega _y}$ 的大小, 实验上可以调节有效通道的数目. 对于无相互作用或者弱相互作用费米系统, 弹道输运给出量子化的电导G = n/h, n是费米面下的通道数目, h是普朗克常数. 这在实验上被验证了.${\omega _y}$ 的改变仍然表现出量子化的结构, 但是量子化的值不再是之前的n/h的形式, 而是$\alpha /{\rm{h}}$ , $\alpha $ 是一个依赖于温度以及相互作用的常数(不一定是整数). 一类的理论解释认为这是在强相互作用下超流温度附近的涨落效应导致的[18 ,19 ] ; 另一类解释认为在量子点接触处的强束缚导致原子密度较高, 从而该处处于超流态. 因为两边的量子气体仍旧在正常态, 所以边界处的安德烈夫反射导致电导加强[20 ] .3.2.量子气体中的自旋扩散实验 -->3.2.量子气体中的自旋扩散实验 下面着重讨论第二类输运实验. 解释这类实验的一个复杂之处在于实验中的原子是被束缚在谐振子势中, 所以一般情况下输运行为和谐振子势中的动力学过程是耦合在一起的. 区分内秉的输运行为和谐振子势中的集体行为通常不是那么容易. 在下面的讨论中, 假设实验上的这些麻烦可以被适当的处理, 而只讨论由于强相互作用而导致的内秉的输运行为. 作为一个例子, 我们将讨论强相互作用的费米系统中的自旋扩散行为[7 -9 ] . 关于强相互作用费米子体系粘滞系数的行为请参见文献[21 ,22 ].M 1 和M 2 , 密度分别为${\rho _1}$ 和${\rho _2}$ , 速度分别为${{{v}}_1}$ 和${{{v}}_2}$ . 如果${{{v}}_1} \ne {{{v}}_2}$ , 扩散现象就会发生. 设想一体积元$\Delta {\rm{V}}$ , 其质心运动速度为${{v}} = ({\rho _1}{{{v}}_1} + {\rho _2}{{{v}}_2})/({\rho _1} + {\rho _2})$ . 对于单纯扩散行为, 在质心系中两种原子的流密度可以写成${{{J}}_{1,2}} = {\rho _{1,2}}\left( {{{{v}}_{1,2}} - {{v}}} \right)$ . 然而, 宏观的观察告诉我们, 扩散流密度的大小和密度的梯度成正比关系:$\rho = {\rho _1} + {\rho _2}$ 是总密度, D 是扩散系数, 它将流密度(流量)和密度梯度线性的联系起来. (原则上D 有下标D 1, 2 , 描述第一种和第二种原子的扩散系数, 但是很容易说明两者相等. 这是昂萨格倒易关系的一个特例). D 是一个唯象的参数, 它的计算涉及到具体物理体系的微观细节. 我们注意到, 因为这里扩散的物理量(密度)是一个标量, 所以只对应一个扩散系数.$\Delta {V}$ 中的自旋密度是${{s}}\left( {{r}} \right)$ . 它的梯度可以写成两项:${{s}}\left( {{r}} \right) = s\left( {{r}} \right)\hat e\left( {{r}} \right)$ , $s\left( {{r}} \right)$ 是自旋密度的大小而$\hat e\left( {{r}} \right)$ 描述自旋密度的方向. 上式第一项对应于纵向的自旋扩散, 由自旋密度大小的梯度驱动; 第二项对应于横向的自旋扩散, 由自旋密度方向的梯度驱动. 在考虑自旋扩散时, 我们一般可以比较好的分辨这两类扩散过程. 纵向的自旋扩散过程和二元流体中的扩散过程类似, 它所引起的自旋流(沿着x 方向)可以写成${\bf{\nabla}} \hat e\left( {{r}} \right)$ 或者${{s}}\left( {{r}} \right) \times {\bf{\nabla}} \hat e\left( {{r}} \right)$ . 具体计算发现[23 ] ,$\mu $ 是一个新的参数(Leggett-Rice参数). 最初上面的方程是在研究简并费米液体氦-3中推导出来的. 其后的研究发现, 这样的自旋流不仅仅描述简并费米液体里面的自旋输运, 同时也描述了非简并量子气体中的自旋扩散行为(全同自旋旋转效应[24 ] ). 在后面一种情况下, 它描述了由于全同粒子交换不变性所导致的自旋进动. 具体物理可以由图2 中描述的两体散射看出来[25 ] .图 2 全同自旋旋转效应Figure2. Identical spin rotation effect.${{{s}}_1}$ , 粒子2的自旋为${{{s}}_2}$ . 散射势是与自旋无关的, 所以总自旋${{{v}}_1}$ 和${{{v}}_2}$ , 那么自旋流的大小就是s ${{{s}}_1}$ 改变$\delta {{{s}}_1}$ , $ {{{s}}_2}$ 改变$\delta {{{s}}_2}$ . 那么$\delta {{{s}}_1} + \delta {{{s}}_2} = {\bf{0}}$ . 但自旋流因此改变了,$\delta {{{J}}_{{s}}}$ 在自旋空间是沿着$\delta {{{s}}_1}$ 的方向, 垂直于${{{s}}_{\bf{1}}}$ 和${{{s}}_{\bf{2}}}$ 所决定的平面. 也就是说即使两体散射是和自旋无关的, 自旋流也会在垂直方向产生一个分量, 绕着总自旋作进动. 通过自旋守恒的方程$\delta {{{J}}_{{s}}}$ 可以改变自旋密度的大小和方向. 具体的微观计算发现[25 ] $T\left( \theta \right)$ 是两体散射矩阵, $\theta = {\text{π}} $ 时对应交换散射的幅度. 对于两分量费米子而言, 理论计算的目标是要给出${D_ \bot }$ 以及$\mu $ 随着温度以及相互作用的变化.$ \pm \dfrac{1}{2}$ , 或者$ \uparrow $ 和$ \downarrow $ 来表示), 它的哈密顿量可以写成${\epsilon_k} = {k^2}/2m$ 是单粒子的能量. ${\mu _\sigma }$ 是自旋为$\sigma $ 的费米子的化学势. g 是两个费米子之间的相互作用强度, 它和散射长度as 的关系由众所周知的公式${g^{ - 1}} +\displaystyle\int\dfrac{m}{{{k^2}}}\dfrac{{{d^3}k}}{{{{(2{\text{π}} )}^3}}} = \dfrac{m}{{4{\text{π}} {a_s}}}$ 给出. 在真空中, 两体散射可以由自由散射T 矩阵来描述. 在质心系内, 如果两个粒子的总能量是E , 那么${\epsilon_k} = {k^2}/2m$ 的散射粒子(E =$ 2{\epsilon_k}$ ), 散射振幅可以写成,$\sigma = $ $ \dfrac{{4{\text{π}} }}{{a_s^{ - 2} + {k^2}}}$ . 这告诉我们, 在弱相互作用下(${a_s} \ll {k^{ - 1}}$ ), 散射截面正比于as 2 . 在强相互作用下, 散射截面正比于k -2 , 和散射长度无关. 相应的输运自由程$\ell = $ $ 1/\left( {n\sigma } \right)$ 在弱相互作用下正比于$\left( {1/{k_F}} \right) \times 1/{({k_F}{a_s})^2}$ , 远远大于粒子之间的距离; 而在强相互作用下$\ell \sim {k^2}/n$ , 它依赖于粒子的动量$\hbar k$ 以及体系的密度. 对于在低温下的费米子体系, $k\sim {n^{1/3}}$ , $\ell \sim $ ${n^{ - 1/3}}$ , 仅是粒子之间距离的尺度. 需要指出的是, 当自由程和粒子间距相当的时候, 自由程就失去了其物理意义, 以上的讨论只能作为一个定性的分析.v 是平均速度. 因为上面的讨论对纵向和横向自旋扩散都适用, 所以我们先不区分${D_\parallel }$ 和${D_ \bot }$ , 而统一写成D . 在实际推导中, 平均速度的定义并不是非常明确, 而且上式中的系数$\dfrac{1}{3}$ 也不是很确定的系数. 但是扩散系数的量纲以及其随温度和相互作用的变化是可以由上面的表达式确定下来[26 ] . 考虑在简并温度之上, ${T_F} < T \ll \dfrac{{{\hbar ^2}}}{{2mr_0^2}}$ , 粒子的平均速度$v \propto \sqrt T $ , 对于弱相互作用体系因为自由程不依赖于温度, 所以$D \propto \sqrt T $ ; 在强相互作用下, ${k^2} \propto T$ , 所以$D \propto {T^{3/2}}$ . 在低温下$T \ll {T_F}$ , 我们需要计入由于费米面的存在而导致的散射相空间变小, 另外我们也不能使用高温时的粒子观念, 而应该计入相互作用对粒子的重整化效果(朗道准粒子). 最终的结果是$D = C{({T_F}/T)^2}$ ; 这样的$1/{T^2}$ 温度依赖在低温朗道液体理论里是非常常见的. 常数C 在弱相互作用的时候还是和${({k_F}{a_s})^{ - 2}}$ 成正比; 在强相互作用下, ${a_s} = \infty $ , 它就是一个常数. 从上面的分析可以看出, D 随温度的变化是非线性的. 高温以及低温D 都是比较大. 在温度$T\sim {T_F}$ 的时候达到最小值. 其大小可以由量纲分析得到D 会有一个最小值: $D \propto v\ell = \dfrac{\hbar }{m}k\ell > \dfrac{\hbar }{m}$ , 因为自由程不能小于德布罗意波长. 但是这类论证依赖于扩散系数的动力学表达式, 而在自由程和德布罗意波长相当的时候, 针对粒子或者准粒子的玻尔兹曼方程不一定成立, 所以不是很有说服力. 实验上的确发现在散射共振附近, 扩散系数达到一个最小值, 见表2 . 我们注意到二维纵向自旋扩散还没有被测量, 另外实验给出的二维横向自旋扩散也存在相互矛盾, 这还有待进一步实验研究. 实验测量值 实验组 二维费米系统 横向自旋扩散 0.0067 剑桥[8 ] 1.7 多伦多[9 ] 三维费米系统 纵向自旋扩散 1.34 MIT[6 ] 三维费米系统 横向自旋扩散 1.08 多伦多[7 ]
表2 强相互作用费米系统的自旋扩散系数Table2. Spin diffusion constants for strongly interacting Fermi gases.$\mu $ 的大小, 我们需要考虑碰撞积分的详细形式. 从动力学理论我们可以得到${D_ \bot }$ 的表达式[27 ,28 ] ${f_{{{k}}\sigma }}$ 是粒子在动量空间的分布函数. ${v_{{{k}},i}}$ 是动量为k i 方向的速度. ${\tau _ \bot }$ 是横向自旋扩散弛豫时间. ${\tau _ \bot }$ 可以写成如下形式[27 ] ${\alpha _ \bot }$ 是一个参数, 其具体表达式可以见文献[27 ], $h =$ $ {\mu _ \uparrow } - {\mu _ \downarrow }$ . 上式中的下标1, 2, 3, 4分别代表以下四个动量, ${{{p}}_{1,2}} = {{q}}/2 \pm {{k}}$ 以及${{{p}}_{3,4}} = {{q}}/2 \pm {{k}}'$ . Leggett-Rice参数$\mu $ 则可以表示为[27 ,28 ] $T\left( {{{k}},{{k}}'} \right)$ , 我们可以使用不同的近似. 最粗糙的是使用两粒子在真空中的散射矩阵, 其次我们可以加入费米面对于散射的影响, 或者可以做一些更自洽的计算; 具体可以参见文献[27 ,28 ].[29 ] .4.结 论 作为总结, 我们想提一下最近在光晶格中的原子输运和自旋输运实验[3 -5 ] . 这一类实验的主要目的在于模拟Fermi-Hubbard模型在低温乃至零温下的性质. 这些冷原子模拟实验中的温度还没有达到超交换相互作用的尺度, 因此输运行为可以认为是相对高温下Fermi-Hubbard模型的行为. 一个比较值得关注的发现是在低参杂时出现类似于高温超导中电导和温度的线性关系[4 ] , 另一个是在高参杂的时候电导在强相互作用下的饱和行为[3 ] . 在冷原子体系, 这方面的探索现在才刚刚开始, 我们期待之后更多的实验和理论发现. 
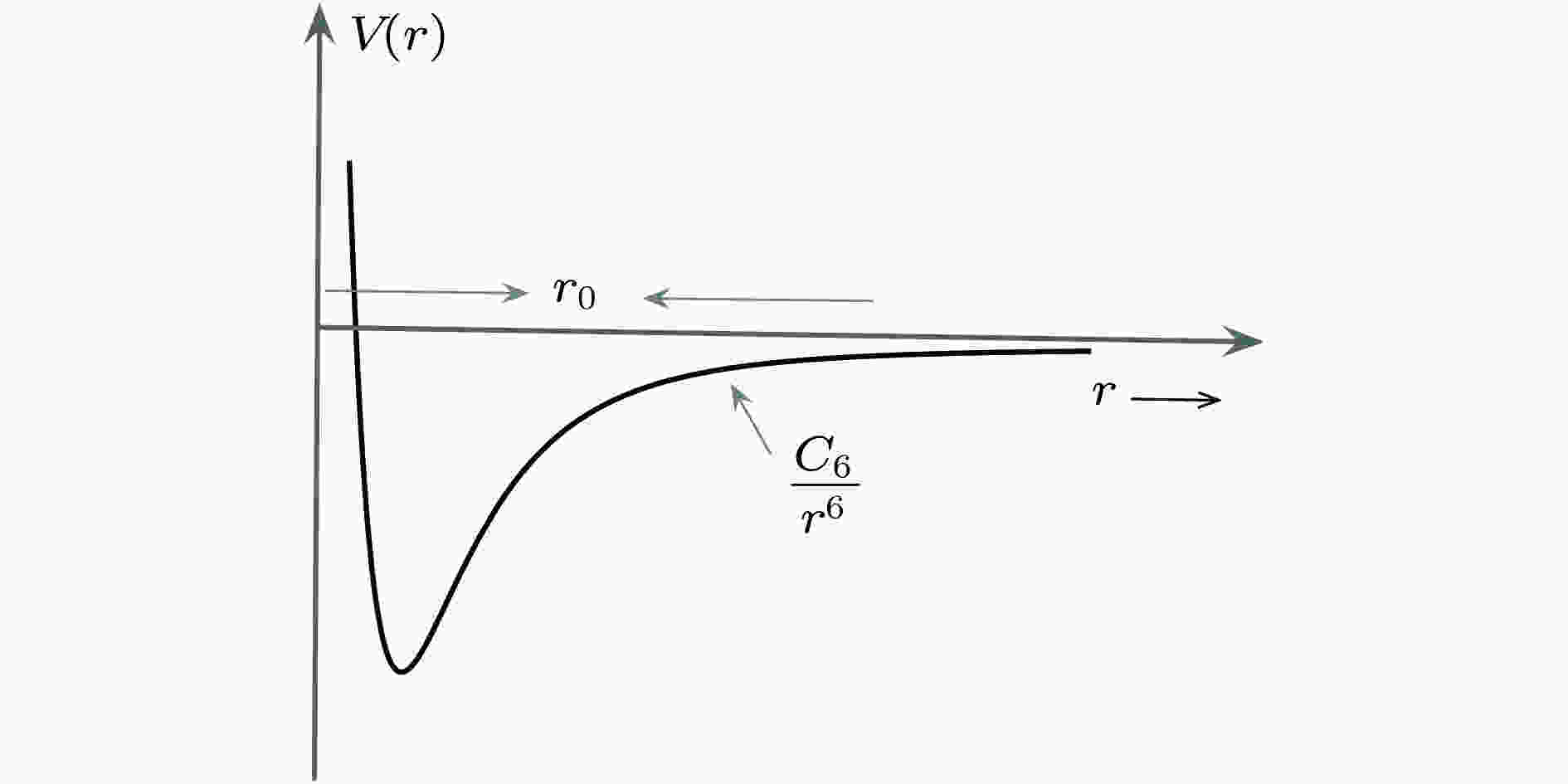 图 1 原子之间的范德瓦耳斯吸引势和短程排斥势
图 1 原子之间的范德瓦耳斯吸引势和短程排斥势






























































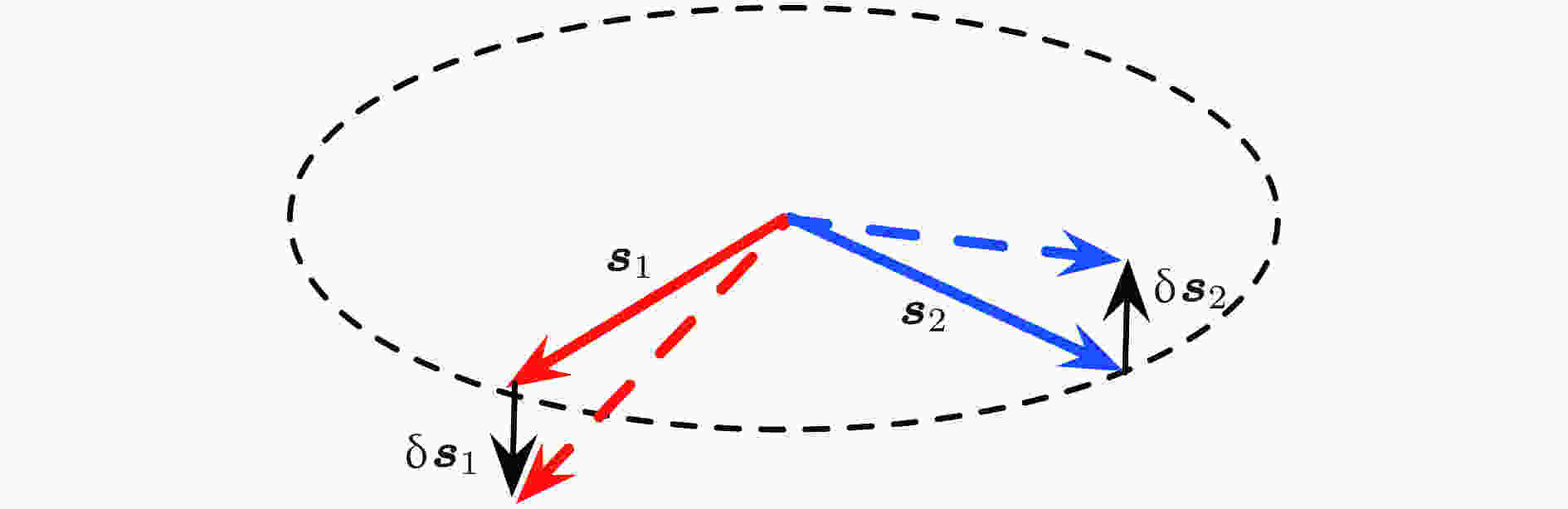 图 2 全同自旋旋转效应
图 2 全同自旋旋转效应



































































