摘要: 量子纠缠是一种重要的量子资源, 在多个空间分离的量子存储器间建立确定性的量子纠缠, 然后在用户控制的时刻将所存储的量子纠缠转移到量子信道中进行信息的分发和传送, 这对于实现量子信息网络是至关重要的. 本文介绍了用光学参量放大器制备与铷原子D1吸收线对应的非经典光场, 而且在三个空间分离的原子系综中确定性量子纠缠的产生、存储和转移. 利用电磁感应透明光和原子相互作用的原理, 将制备的多组分光场纠缠态模式映射到三个远距离的原子系综以建立原子自旋波之间的纠缠. 然后, 存储在原子系综中的纠缠态通过三个量子通道, 纠缠态的量子噪声被转移到三束空间分离的正交纠缠光场. 三束释放的光场间纠缠的存在验证了该系统具有保持多组分纠缠的能力. 这个方案实现了三个量子节点间的纠缠, 并且可以直接扩展到具有更多节点的量子网络, 为未来实现大型量子网络通信奠定了基础.
关键词: 确定性量子纠缠 /
电磁感应透明 /
多组分纠缠态 /
量子节点 English Abstract Deterministic quantum entanglement among multiple quantum nodes Liu Yan-Hong 1 ,Wu Liang 1 ,Yan Zhi-Hui 1,2 ,Jia Xiao-Jun 1,2 ,Peng Kun-Chi 1,2 1.Institute of Opto-Electronics, State Key Laboratory of Quantum Optics and Quantum Optics Devices, Shanxi University, Taiyuan 030006, China Fund Project: Project supported by the National Key R&D Program of China (Grant No. 2016YFA0301402), the National Natural Science Foundation of China (Grant Nos. 61775127, 11474190, 11654002), the Program for Sanjin Scholars of Shanxi Province, China, the Shanxi Scholarship Council of China, and the Fund for Shanxi “1331 Project” Key Subjects Construction, China.Received Date: 29 August 2018Accepted Date: 09 October 2018Available Online: 01 February 2019Published Online: 05 February 2019Abstract: Quantum entanglement is a significant quantum resource, which plays a central role in quantum communication. For realizing quantum information network, it is important to establish deterministic quantum entanglement among multiple spatial-separated quantum memories, and then the stored entanglement is transferred into the quantum channels for distributing and transmitting the quantum information at the user-control time. Firstly, we introduce the scheme of deterministic generation polarization squeezed state at 795 nm. A pair of quadrature amplitude squeezed optical fields are prepared by two degenerate optical parameter amplifiers pumped by a laser at 398 nm, and then the polarization squeezed state of light appears by combining the generated two quadrature amplitude squeezed optical beams on a polarizing beam splitter. Secondly, we present the experimental demonstration of tripartite polarization entanglement described by Stokes operators of optical field. The quadrature tripartite entangled states of light corresponding to the resonance with D1 line of rubidium atoms are transformed into the continuous-variable polarization entanglement via polarization beam splitter with three bright local optical beams. Finally, we propose the generation, storage and transfer of deterministic quantum entanglement among three spatially separated atomic ensembles. By the method of electromagnetically induced transparency light-matter interaction, the optical multiple entangled state is mapped into three distant atomic ensembles to build the entanglement among three atomic spin waves. Then, the quantum noise of entanglement stored in the atomic ensembles is transferred to the three space-seperated quadrature entangled light fields through three quantum channels. The existence of entanglement among the three released beams verifies that the system has the ability to maintain the multipartite entanglement. This protocol realizes the entanglement among three distant quantum nodes, and it can be extended to quantum network with more quantum nodes. All of these lay the foundation for realizing the large-scale quantum network communication in the future.Keywords: deterministic quantum entanglement /electromagnetically induced transparency /multipartite entanglement /quantum nodes 全文HTML --> --> --> 1.引 言 压缩和纠缠是量子力学的核心概念, 在量子信息技术的发展中起着核心作用, 它们已被深入研究[1 ,2 ] 并且广泛应用于各种量子通信和计算协议中. 纠缠是量子力学中一个特有的概念, 所谓纠缠态是指在空间上有非定域关联的量子系统. 两个或两个以上的子系统构成的量子体系的态矢量不能表示为各子系统态矢直积的形式时, 这些子系统之间不可分, 如果对其中一个子系统测量, 必然会影响其他子系统的测量结果. 根据可观测量的本征态是分离谱还是连续谱可以分为分离变量和连续变量. 分离变量用有限维度的希尔伯特空间表征, 例如光子的偏振; 连续变量例如光场的正交振幅和相位, 其本征态构成了无限维的希尔伯特空间. 分离变量的特点是对损耗不敏感, 存在一定的概率性, 效率低. 相比于分离变量, 连续变量量子信息具有确定性、产生的高效性, 但其对损耗较为敏感. 在分离变量和连续变量方面, 单光子和压缩光场是构建量子纠缠的重要资源, 已经用于各种量子信息方案, 如量子隐形传态[3 ?5 ] 、量子纠缠交换[6 ?8 ] 、量子秘密共享[9 ?11 ] 、量子计算[12 ,13 ] 等方面. 目前, 人们的兴趣主要集中在构建量子节点和量子信息传输信道组成的的量子互联网上[14 ] . 连续变量偏振纠缠光场可以被高效地操纵和测量, 并且明亮的偏振纠缠光场在测量的过程中不需要本地振荡光[15 ,16 ] . 此外, 光的偏振和原子自旋都可以由斯托克斯(Stokes)算符描述, 光的偏振分量的波动可以很容易地映射到原子系综的自旋波的集体涨落, 因此, 连续变量偏振态和原子系综的自旋态之间的量子态转移可以很容易实现.[14 ] . 由量子通道和量子节点构成的量子网络吸引了越来越多的关注. 光由于具有传播速度快并且和周围环境相互作用影响较小的特点, 是最好的量子信息载体, 在量子网络中可作为量子通道. 量子节点可以用来快速地存储和处理量子信息, 原子系综[17 ?21 ] 、单原子[22 ,23 ] 、囚禁离子[24 ,25 ] 、光力系统[26 ?29 ] 、超导[30 ] 和固体系统[31 ?33 ] 均可以作为量子节点. 光和原子相互作用强, 因此原子系综作为量子节点是用来存储和处理量子信息的最佳候选者之一.[34 ] 提出了通过Duan-Lukin-Cirac-Zoller (DLCZ)的方法实现分离变量原子系综之间的纠缠, 首先将原子制备在基态, 两个原子系综同时被抽运光作用产生Stokes光子, 两个系综分别产生的Stokes光子在50/50的分束片上干涉之后用单光子探测器探测. 在实验上, 通过利用拉曼(Raman)散射[35 ,36 ] 或者将纠缠光子对的量子态映射[37 ,38 ] 的方法可以实现分离变量原子系综的纠缠. 2010年, Kimble研究组[39 ] 在四个原子存储器中利用将原子系综间的纠缠相干转移到四个光子通道中演示了分离变量的测量诱导纠缠. 这个实验证明了原子系综的多组分W纠缠态可以通过纠缠的预告映射到光子W态模式中, 并且该实验也证明了量子网络中多组分纠缠的分布.[40 ] 和光与原子的耗散机制[41 ] , 实现了两个原子系综自旋波之间的连续变量纠缠. 除此之外, 三波或者四波混频均可以实现原子系综之间的纠缠[42 ,43 ] . 上述关于连续变量原子系综之间的纠缠的制备方案, 由于不可避免的传输损耗限制了传输距离, 因此本研究组在理论上提出了利用光和原子间的混合纠缠及纠缠交换的方法克服传输损耗实现两个原子系综间的纠缠[44 ] . 为了实现量子计算和量子通信, 需要将非经典光场存储到原子系综中并且根据需求将其释放. 压缩光和纠缠光的量子存储在理论上已经被研究[45 ,46 ] , 并且很多研究组在实验上已经实现了压缩光场的存储. 2008年, Furusawa和Lvovsky研究组均提出了通过电磁感应透明(electromagnetically induced transparency, EIT)的原理实现压缩光场的存储释放[47 ,48 ] , 随后两个原子系综间的连续变量纠缠存储在实验上已经实现[49 ] . 到目前为止, 所有关于原子系综连续变量纠缠的产生和存储的实验报道都集中在两个系综之间[40 ,41 ,49 ] . 关于纠缠的存储, 2011年, Polzik研究组[49 ] 将一束光的两个边带模式代替纠缠态作为初始量子资源实现了两个原子系综之间的纠缠.[50 ] 在实验上首次利用光场和原子系综间量子态映射的方法实现了三个原子系综间的纠缠, 并且我们建立的纠缠是确定性的, 该方案具有良好的拓展性, 可以直接扩展到更多的量子节点, 并且引入的额外噪声小, 为实现实用化量子网络提供了理论和实验参考.2.偏振压缩态光场 压缩态是一种重要的非经典光场, 也是量子力学中的一种基本资源, 利用压缩态可以实现相关物理量的精密测量[51 ?54 ] , 以及实现引力波探测[55 ] . 随着原子物理的快速发展, 光与物质的相互作用受到人们的广泛关注, 因此制备和原子吸收线对应的压缩态[56 ] 已成为一种趋势. 2002年, Korolkova等[57 ] 提出了连续变量偏振压缩态的概念. 原子的自旋分量可以用布洛赫球上的Stokes分量来描述, 同样光场的偏振分量可以在庞加莱球上用Stokes矢量来表示. 光场的偏振分量可以直接和原子的自旋波相互作用, 实现量子态信息在光与原子之间的相互传递, 而且偏振压缩态光场测量的过程中不需要本地振荡光. 光场的偏振态在长距离的量子通信和量子存储中有重要的应用前景[49 ,58 ] .2.1.偏振压缩态产生的理论分析 2.1.偏振压缩态产生的理论分析 在量子力学中, 光场的偏振分量可以用Stokes算符${\hat S_0}$ , ${\hat S_1}$ , ${\hat S_2}$ , ${\hat S_3}$ 来表示, 它们满足球面方程$\hat S_0^2 + 2{\hat S_0} = \hat S_1^2 + \hat S_2^2 + \hat S_3^2$ 并且符合庞加莱球的构造. ${\hat S_0}$ 代表光束的强度; ${\hat S_1}$ , ${\hat S_2}$ , ${\hat S_3}$ 分别表征了光束的水平、45°和右旋圆偏振特性并形成了笛卡尔坐标系, 光场的偏振分量可以很容易映射到原子的自旋波. 纯态的Stokes参量可以由水平(H)和垂直(V)偏振模对应的产生$\hat a_{{\rm{H}}({\rm{V}})}^?$ 和湮灭${\hat a_{{\rm{H}}({\rm{V}})}}$ 算符来表示:$\theta $ 是水平和竖直偏振模式的相对相位. 利用算符线性化, 任意算符均可以写成其平均值和起伏的和, 即$\hat a = \alpha + {\text{δ}}\hat a$ , 我们假设这两束偏振相互垂直的光束的强度相等, 即${\alpha _{\rm{H}}} = {\alpha _{\rm{V}}} = \alpha $ , 得到各Stokes分量的量子起伏可表示为如下形式:${\hat X_{{\rm{H}}({\rm{V}})}}$ 和${\hat Y_{{\rm{H}}({\rm{V}})}}$ 分别代表水平和竖直偏振场的振幅和相位分量.${V_j} = \left\langle {\hat S_j^2} \right\rangle - {\left\langle {{{\hat S}_j}} \right\rangle ^2}$ )满足关系:${V_1}{V_2}\geqslant$ $ {\left| {\left\langle {{{\hat S}_3}} \right\rangle } \right|^2}$ ,${V_2}{V_3}\geqslant{\left| {\left\langle {{{\hat S}_1}} \right\rangle } \right|^2}$ , ${V_3}{V_1}\geqslant {\left| {\left\langle {{{\hat S}_2}} \right\rangle } \right|^2}$ .${V_i} < \left| {\left\langle {{{\hat S}_j}} \right\rangle } \right|$ 时, 该Stokes参量被压缩.2.2.偏振压缩态的实验制备及测量 -->2.2.偏振压缩态的实验制备及测量 目前, 国际上有很多研究组已经在实验上制备了偏振压缩态光场. 为了实现长距离的量子通信, Leuchs研究组[58 ] 利用非对称光纤Sagnac干涉仪产生了光纤通信波段的偏振压缩态光场, 并且将其应用于大气通道中的偏振压缩态的分发. 量子节点需要和原子吸收线波长对应的偏振压缩态, Giacobino研究组[59 ] 制备了基于高精细光学腔中的冷铯原子云的852 nm的偏振压缩态. 除此之外, 利用工作于阈值以下的光学参量放大器和偏振分束棱镜也可以制备偏振压缩光. Lam研究组[60 ] 将两束正交压缩光在偏振分束棱镜上耦合得到了1064 nm的偏振压缩光.图1 是实验制备偏振压缩光场的原理示意图. 实验中, 钛宝石激光器产生的795 nm的红光作为基频光, 先通过外腔倍频产生398 nm的蓝紫光, 抽运两个完全相同的DOPAs, 通过自发参量下转换制备两束正交振幅压缩态光场, 然后将这两束正交压缩光以相互垂直的偏振在偏振分束棱镜上耦合得到偏振压缩光[61 ] .图 1 偏振压缩光场制备原理图Figure1. Schematic of generation system of polarization squeezing.图2(a) —(d) 所示. 在测量过程中, 偏振压缩光的水平和竖直分量被偏振分束棱镜分开, 水平和竖直分量的和(差)代表Stokes分量${\hat S_0} ({\hat S_1})$ , 因此一对光电二极管探测到的量子噪声的和(差)表示Stokes分量${\hat S_0}({\hat S_1})$ 的量子噪声的起伏. Stokes分量${\hat S_0}$ 和${\hat S_1}$ 的测量不需要任意波片, 只需要功率加法和减法器, ${\hat S_0}$ 的测量在偏振分束棱镜后用以对光电二极管探测得到的噪声经过加法器后得到Stokes分量${\hat S_0}$ 的噪声起伏, ${\hat S_1}$ 的测量仅需要一个功率减法器就测量得到Stokes分量${\hat S_1}$ 的噪声起伏. Stokes分量${\hat S_2}$ 的测量在偏振分束棱镜前加一个二分之一波片, 将偏振分束棱镜前的二分之一波片旋转22.5°后用一个减法器来测量${\hat S_2}$ 分量的量子噪声. 在偏振分束棱镜前插入四分之一波片和二分之一波片, 通过将四分之一波片和二分之一波片分别旋转0°和22.5°, 来测量${\hat S_3}$ 分量的量子噪声. 实验上, 最终三个Stokes分量${\hat S_0}$ , ${\hat S_1}$ , ${\hat S_2}$ 被压缩?4.0 dB, ${\hat S_3}$ 反压缩9.0 dB, 如图3 所示.图 2 Stokes分量(a) ${\hat S_0}$ , (b) ${\hat S_1}$ , (c)${\hat S_2}$ , (d) ${\hat S_3}$ 的量子噪声的实验测量(HWP, 二分之一波片; QWP, 四分之一波片; PBS, 偏振分束棱镜; +/?, 功率加法/减法器)Figure2. Measurement of quantum noise of Stokes component (a) ${\hat S_0}$ , (b) ${\hat S_1}$ , (c) ${\hat S_2}$ , (d) ${\hat S_3}$ . HWP, half-wave plate; QWP, quarter-wave plate; PBS, polarization beam splitter; +/?, positive/negative power combiner.图 3 偏振压缩光Stokes分量的量子噪声[61 ] (a) ${\hat S_0}$ ; (b) $\hat S{}_1$ ; (c) ${\hat S_2}$ ; (d) ${\hat S_3}$ Figure3. Quantum noises of Stokes component of polarization squeezedlight[61 ] : (a) ${\hat S_0}$ ; (b) ${\hat S_1}$ ; (c) ${\hat S_2}$ ; (d) ${\hat S_3}$ .3.偏振纠缠态 多组分偏振纠缠光场是未来量子信息网络的必要资源, 并且可以直接和原子系综的自旋态相互作用, 它能够用来在多个由原子节点组成的量子网络间传输和转换量子态. 连续变量偏振纠缠态光场能够被高效率地操控和探测, 而且明亮偏振纠缠光场的测量不需要本地振荡光. 光和原子的偏振分量均可用Stokes算符来表示, 而且偏振分量的量子噪声起伏可以在光和原子之间相互映射, 因此量子态的转移在偏振光场和原子之间很容易实现.3.1.两组分偏振纠缠 3.1.两组分偏振纠缠 2002年, Korolkova等[57 ] 引入了偏振纠缠的概念, 提出了偏振纠缠的产生方案, 并且给出了偏振纠缠实现的不同的判据. 同年, Lam研究组[60 ] 在实验上制备了1064 nm的两组分偏振纠缠态光场, 实验制备原理图如图4 所示. 首先利用两个光学参量放大器制备一对空间分离的等功率的正交振幅压缩光, 之后将两束正交振幅压缩光在50/50的分束器上耦合, 并将两束光的相对相位锁定在${\text{π}}/2$ , 输出态是一对Einstein-Podolsky-Rosen (EPR)纠缠态光场. 将产生的EPR纠缠光的两束光(${\hat a_{{\rm{H}},x}}$ , ${\hat a_{{\rm{H}},y}}$ )分别和功率是30倍纠缠光的本地光(${\hat a_{{\rm{V}},x}}$ , ${\hat a_{{\rm{V}},y}}$ )在偏振分束棱镜上耦合, 并且将水平偏振和竖直偏振的相对相位锁定在${\text{π}}/2$ , 最终输出态是偏振纠缠态光场. 最终利用两组分不可分判据来判断纠缠的建立. Leuchs研究组[58 ] 利用非对称光纤Sagnac干涉在两束光之间实现了偏振纠缠. 除此之外, 偏振纠缠态还可以通过放置于高精细度的光学腔内的冷的铯原子系综产生[62 ] .图 4 偏振纠缠制备原理图Figure4. Schematic for the generation system of polarization entanglement.${\hat S_2}$ 和${\hat S_3}$ 之间的关联噪声小于1, 即Stokes分量${\hat S_2}$ 和${\hat S_3}$ 之间存在纠缠.3.2.三组分偏振纠缠 -->3.2.三组分偏振纠缠 随着量子信息的快速发展, 构建量子网络需要制备多组分纠缠态光场[63 ] . 2012年, 本研究组[64 ] 利用两个级联的工作于阈值以上的非简并光学参量放大器(non-degenerate optical parametric oscillator, NOPO)制备三色纠缠态光场. 之后, 我们利用工作于阈值以下的四个完全相同的非简并光学参量放大器(non-degenerate optical parametric amplifier, NOPA)制备了八组分Cluster纠缠态光场[65 ] . 2015年, 我们从理论上提出了产生三色偏振纠缠光场的方案[66 ] . 先用两个级联的NOPO制备三色明亮正交纠缠态, 然后分别和强相干光在偏振分束棱镜上耦合得到三色偏振纠缠光场. 2016年, 为了实现光学存储和光与原子的相互作用, 本研究组在实验上制备了795 nm的三组分连续变量偏振纠缠态[67 ] . 根据三组分不可分判据, 我们将得到的偏振纠缠态定量表征, 同样实验制备的三组分偏振纠缠满足Teh和Reid提出的多组分纠缠判据[68 ] . 该实验系统和方案可以拓展到多组分偏振纠缠的制备.图5 所示. 正交相位压缩光${\hat a_1}$ 与两束正交振幅压缩光${\hat a_2}$ 和${\hat a_3}$ 在反射率和透射率比R ︰T = 1︰2和R ︰T = 1︰1分束片BS1和BS2上干涉, 产生三组分GHZ纠缠态光场${\hat b_1}$ , ${\hat b_2}$ 和${\hat b_3}$ , 三个弱的水平偏振子模${\hat b_1}$ , ${\hat b_2}$ 和${\hat b_3}$ 分别和强的竖直偏振的相干光${\hat c_1}$ , ${\hat c_2}$ 和${\hat c_3}$ 在偏振分束棱镜(PBS1—PBS3)上耦合得到三组分偏振纠缠光${\hat d_1}$ , ${\hat d_2}$ 和${\hat d_3}$ . 一般而言, 三束压缩光和相干光的功率分别相等$\alpha _{a1}^2 = \alpha _{a2}^2 = \alpha _{a3}^2 = \alpha _a^2$ ($\alpha _{c1}^2 = \alpha _{c2}^2 = $ $\alpha _{c3}^2 = \alpha _c^2$ ), 并且三个子模的功率是三束相干光功率的1/30. 分束片BS1, BS2和PBS1—PBS3的相对相位均锁定在0. 通过把正交分量的噪声投影到Stokes分量上, 计算可得到三组分偏振纠缠各子模的Stokes分量的量子噪声起伏${{\text{δ}}^2}{\hat S_{{0_{{d_1}({d_2},{d_3})}}}}$ , ${{\text{δ}}^2}{\hat S_{{1_{{d_1}({d_2},{d_3})}}}}$ , ${{\text{δ}}^2}{\hat S_{{2_{{d_1}({d_2},{d_3})}}}}$ 和${{\text{δ}}^2}{\hat S_{{3_{{d_1}({d_2},{d_3})}}}}$ .图 5 三组分偏振纠缠态产生方案(BS1, 光学分束器1; BS2, 光学分束器2; PBS1, 偏振分束棱镜1; PBS2, 偏振分束棱镜2; PBS3, 偏振分束棱镜3)Figure5. Schematic for the generation of tripartite polarization entangled state. BS1, beam splitter1; BS2, beam splitter2; PBS1, polarization beam splitter1; PBS2, polarization beam splitter2; PBS3, polarization beam splitter3.[69 ] 拓展到偏振纠缠不可分[70 ] , van Loock 和 Furusawa证明了多组分纠缠态的不可分判据[71 ] . 我们从理论上计算了三组分偏振纠缠不可分判据[66 ] :I 1 , I 2 和I 3 是Stokes算符间的归一化关联方差; ${g_i} (i = 1, 2, 3)$ 是最佳增益因子. 当同时违背上述三个不等式中的两个时, 三个子模满足三组分偏振纠缠.[68 ] 提出了真正的N 组分纠缠和完全的N 组分不可分之间的区别, 并提出了真正的N 组分纠缠的标准. 参考文献[68 , 72 ], 我们知道可观测量的方差的和总是大于等于任意混合态方差的加权和:P k k 上可分离的概率($\sum\nolimits_k {{P_k}} = $ 1), ${\text{δ}}_k^2({\hat S_{2(3)}})$ 表示系统在态${\rho _k}$ 时${\hat S_{2(3)}}$ 的方差[65 ] . 对于三组分, I 1 是两个方差的和, 我们得到${I_2} \geqslant {P_2} + {P_3}$ 和${I_3} \geqslant {P_3} + $ ${P_1}$ . 对于任意混合态$\sum\nolimits_k {{P_k}} = 1$ , 所以${I_1} + {I_I} + $ $ {I_3} \geqslant 2$ . 当违背上述不等式时, 我们就说三个子模满足真正的三组分偏振纠缠.图6 所示. 图6(a) —(f) 分别表示${{\text{δ}}^2}({\hat S_{{2_{{d_2}}}}} - {\hat S_{{2_{{d_3}}}}})$ , ${{\text{δ}}^2}({g_1}{\hat S_{{3_{{d_1}}}}} + {\hat S_{{3_{{d_2}}}}} + {\hat S_{{3_{d3}}}})$ , ${{\text{δ}}^2}({\hat S_{{2_{{d_1}}}}} - $ ${\hat S_{{2_{d3}}}})$ , ${{\text{δ}}^2}({\hat S_{{3_{{d_1}}}}} + {g_2}{\hat S_{{3_{{d_2}}}}} + {\hat S_{{3_{d3}}}})$ , ${{\text{δ}}^2}({\hat S_{{2_{{d_1}}}}} - {\hat S_{{2_{d2}}}})$ 和${{\text{δ}}^2}({\hat S_{{3_{{d_1}}}}} + {\hat S_{{3_{{d_2}}}}} + {g_3}{\hat S_{{3_{d3}}}})$ 的关联方差. 通道(i)表示对应的归一化量子噪声极限(SNL), 通道(ii)表示测量到的关联噪声. 在测量${{\text{δ}}^2}({g_1}{\hat S_{{3_{{d_1}}}}} + {\hat S_{{3_{{d_2}}}}} + $ $ {\hat S_{{3_{d3}}}})$ , ${{\text{δ}}^2}({\hat S_{{3_{{d_1}}}}} + {g_2}{\hat S_{{3_{{d_2}}}}} + {\hat S_{{3_{d3}}}})$ 和${{\text{δ}}^2}({\hat S_{{3_{{d_1}}}}} + {\hat S_{{3_{{d_2}}}}} + $ ${g_3}{\hat S_{{3_{d3}}}})$ 的关联噪声时, ${g_{1(2,3)}}$ 取最佳增益因子, 此时得到最大纠缠态. ${g_{1(2,3)}} = {g^{{\rm{opt}}}} = 0.845$ 时, 上述的关联方差在分析频率为1.3—6 MHz间量子噪声都在SNL以下. 5 MHz处, 观测到最大纠缠态, ${I_1} = 0.42 \pm 0.08$ , ${I_2} = 0.41 \pm 0.08$ , ${I_3} = 0.42 \pm 0.08$ , 并且${I_1} + {I_2} + {I_3} = 1.25 \pm 0.07$ , 上述证明了该态同时违背了三组分不可分判据和真正的三组分纠缠判据. 因此, 实验中我们制备的三组分偏振纠缠态是真正的三组分偏振纠缠.图 6 分析频率在1—6 MHz间测量的Stokes关联方差 (a) ${{\text{δ }}^2}({\hat S_{{2_{{d_2}}}}} - {\hat S_{{2_{{d_3}}}}})$ ; (b) ${{\text{δ }}^2}({g_1}{\hat S_{{3_{{d_1}}}}} + {\hat S_{{3_{{d_2}}}}} + {\hat S_{{3_{d3}}}})$ ; (c) ${{\text{δ }}^2}({\hat S_{{2_{{d_1}}}}} - {\hat S_{{2_{d3}}}})$ ; (d) ${{\text{δ }}^2}({\hat S_{{3_{{d_1}}}}} + {g_2}{\hat S_{{3_{{d_2}}}}} + {\hat S_{{3_{d3}}}})$ ; (e) ${{\text{δ }}^2}({\hat S_{{2_{{d_1}}}}} - {\hat S_{{2_{d2}}}})$ ; (f) ${{\text{δ }}^2}({\hat S_{{3_{{d_1}}}}} + {\hat S_{{3_{{d_2}}}}} + {g_3}{\hat S_{{3_{d3}}}})$ Figure6. Measured correlation variances of (a) ${{\text{δ }}^2}({\hat S_{{2_{{d_2}}}}} - {\hat S_{{2_{{d_3}}}}})$ , (b) ${{\text{δ }}^2}({g_1}{\hat S_{{3_{{d_1}}}}} + {\hat S_{{3_{{d_2}}}}} + {\hat S_{{3_{d3}}}})$ , (c) ${{\text{δ }}^2}({\hat S_{{2_{{d_1}}}}} - {\hat S_{{2_{d3}}}})$ , (d) ${{\text{δ }}^2}({\hat S_{{3_{{d_1}}}}} + {g_2}{\hat S_{{3_{{d_2}}}}} + {\hat S_{{3_{d3}}}})$ , (e) ${{\text{δ }}^2}({\hat S_{{2_{{d_1}}}}} - {\hat S_{{2_{d2}}}})$ , (f) ${{\text{δ }}^2}({\hat S_{{3_{{d_1}}}}} + {\hat S_{{3_{{d_2}}}}} + {g_3}{\hat S_{{3_{d3}}}})$ over the analysis frequency rangefrom 1 to 6 MHz.4.三个原子系综确定性纠缠的建立 随着量子信息技术的不断发展, 由量子通道和量子节点构成的量子信息网络由于其安全性和高效性受到人们的广泛关注. 光场具有传输速度快、不易受环境影响等特点, 是量子信息的理想载体; 光纤等可以作为量子信息的传输通道, 但不可忽视的是不论光纤还是大气等都对光场有着吸收和散射等作用. 这样在量子通信的过程中不可避免地会引入传输损耗, 限制了量子传输的距离. 为了解决这一问题, 量子中继的概念被提出, 量子节点可以作为量子中继站克服由于远距离传输引入的损耗, 而原子系综可以构成量子节点, 并且利用原子系综可以进行高效率长寿命的量子信息存储和处理. 量子中继以量子存储和纠缠交换两大内容为基础, 利用量子存储还可以建立量子节点间的纠缠, 实现量子测量、量子计算、量子网络等诸多应用.[73 ?80 ] . 量子存储的方法有: EIT[73 ,81 ?83 ] , QND[84 ] , DLCZ[34 ,36 ] , 光子回声[85 ,86 ] 等.4.1.相干态的量子存储 4.1.相干态的量子存储 关于相干态的量子存储, 2001年Lukin研究组在实验上报道了将光脉冲有效地减速并被捕获在铷原子的蒸汽中, 存储一段时间后根据需要释放[87 ] . 这种光存储技术基于光在介质中群速度减慢的现象, 该种存储技术被称为EIT. 在慢光实验中, 一束外部场作为控制场用来使不透明的介质在接近原子共振时变得透明. 另一束弱光作为信号光在特定的频率和极化下可以在没有耗散和损耗的情况下传播, 而且传播的群速度大大降低. 慢光在空间上极大程度地被压缩, 并且其信号脉冲几乎完全处于原子介质中.[87 ] :E 表示信号光场, ${\sigma _{13}}$ 表示原子的自旋相干性, g 为光与原子耦合强度, $\varOmega $ 是控制光场的拉比频率. 当控制光被关掉时, $\cos \theta (t) \to 0$ , 暗态极子最终表现为原子的量子特性; 当打开控制时, $\sin \theta (t) \to 0$ , 暗态极子表现为光场的量子特性. 通过暗态极子的理论, 可以解释量子态在光场和原子之间相互映射. 在关闭控制光时, 光场中的量子态信息被映射到原子系综中, 实现量子态的存储, 再打开控制光, 将存储在原子介质中的光场释放出来, 量子态被映射到释放的光场中. Lukin等利用EIT效应, 在实验上将相干光存储在热的铷原子系综中, 存储时间为200 $\mu {\rm s} $ .[84 ] 利用QND的机制将光存储在铯原子中. 光的存储可以分为三个步骤: 1)输入的光脉冲和自旋极化的铯原子相互作用; 2)测量透射光场; 3)将测量到的结果通过射频磁脉冲反馈到原子上. 脉冲光和自旋极化的原子相互作用后[84 ] ,$\hat X_{\rm{L}}^{{\rm{out}}}$ , 将测量到的结果$x = \hat X_{\rm{L}}^{{\rm{in}}} + \kappa \hat P_{\rm{A}}^{{\rm{in}}}$ 在反馈增益因子为$g$ 时反馈到原子变量${\hat P_{\rm{A}}}$ 上, 则有$g$ 和相互作用参量$\kappa $ 可以实现光到原子的映射. 同样, 通过测量最终读出光的$\hat X_{\rm{L}}^{{\rm{read{\text{-}}out}}} = \hat X_{\rm{L}}^{{\rm{read{\text{-}}in}}} + \kappa \hat P_{\rm{A}}^{{\rm{final}}}$ 验证相干态存储的实现. Polzik研究组最终实现了在铯原子中存储相干光4 ms.[88 ] . 为了克服这一困难, 也有实验方案提出了利用可控恢复能级非均匀展宽技术[86 ,89 ] (controlled reversible inhomogeneous boarding, CRIB)和原子频率梳技术(atomic frequency comb, AFC). CRIB是通过外加电场或磁场实现量子存储, AFC则是制备等间距的脉冲梳吸收谱来实现.4.2.非经典光的量子存储 -->4.2.非经典光的量子存储 光场量子态的存储是实现量子光学计算的一个重要组成部分, 是实现量子中继必不可少的, 也大大拓展了量子通信的范围. 量子光学存储的方法有很多, 众所周知的是EIT, 在经典光的存储中我们已经详细介绍了EIT存储机制. 要实现真正的量子通信网络, 需要将非经典光进行存储. 相比于经典光的存储, 压缩态和纠缠态存储要求更为严格. 非经典光的存储要求存储效率和存储寿命要高, 可以在多个节点之间实现存储, 除此之外引入的额外噪声要低, 否则会淹没非经典光的量子噪声, 而且实验方案要有很强的拓展性.[47 ] 和Lvovsky研究组[48 ] 都利用EIT机制实现了压缩光的存储. Furusawa研究组在冷的铷原子系综中成功实现了压缩真空光的存储和释放, 释放光的正交噪声用零拍探测器监视. 实验中利用激光冷却铷原子系综作为存储介质, 初始冷原子样品制备在$5{}^2{\rm{S}_{1/2}}$ 态, 冷原子样品的光学厚度是5. 探针光和控制光分别和原子跃迁线$F = 1 \leftrightarrow F' = 2$ 和$F = 2 \leftrightarrow F' = 2$ 对应. 钛宝石激光1和2的差拍信号经过混频器后输出, 差拍的频率被降低足够来驱动声光调制器(AOM), 钛宝石激光器1和控制光的频率差来源于AOM的衍射. 压缩真空光作为探针光, 压缩真空光通过光学参量振荡器制备, 产生的压缩真空光的正交振幅噪声用平衡零拍探测器来探测. 压缩真空光脉冲的存储和释放通过动态地改变控制光的功率来实现. 实验中, 用两套AOM来将连续的压缩真空光斩断为930 ns的脉冲, 为了避免不必要的损耗利用AOM的零级光作为探针光. 将压缩真空光脉冲注入冷原子系综, 当光脉冲由于群速度减慢被压制在原子系综中时, 关断控制光光场的量子态映射到原子中. 在存储3 $\mu {\rm s} $ 后打开控制光, 初始的光脉冲信号被释放. 最后利用两种方法来计算时域上的正交噪声: 1)傅里叶变换分析时域上的量子噪声; 2)利用相干态存储过程估算的时间模式函数. 经分析, 该实验利用EIT实现了存储效率为20%的压缩真空态的存储, 存储前压缩是?2.0 dB, 释放后压缩是?0.16 dB. 当压缩真空态被存储在原子中时原子自旋波被压缩.2 Pa)的惰性气体, 并且包裹在磁屏蔽内加热到65 ℃. 控制场和信号场偏振互相垂直, 且在原子气室内光斑600 $\mu {\rm m} $ , 存储寿命1.3 $\mu {\rm s} $ . 最终实现了输入态压缩?1.86 dB, 释放压缩?0.21 dB, 并且对比输入态和释放态保真度达到0.89.[49 ] 提出了利用QND的方法将连续变量纠缠光存储在铯原子系综中. 国内郭光灿研究组[90 ] 利用Raman机制实现了轨道角动量纠缠的量子存储. 非经典光的量子存储为实现量子网络奠定了基础, 量子存储是实现多个量子节点间纠缠的重要基础, 目前已经有很多种方案实现两个原子系综之间的纠缠. 不论在分离变量还是连续变量领域, 实现原子系综纠缠的方案有: DLCZ, 量子态映射, QND, 耗散机制和纠缠交换等.4.3.双原子系综的纠缠 -->4.3.双原子系综的纠缠 2016年, 我们在理论上提出了将光与原子混合纠缠和纠缠交换结合的方法实现两个原子系综确定性的纠缠[44 ] , 其制备原理示意图如图7 . 系统包括两个独立的原子系综A (B), 一个分束片BS和一对平衡零拍探测器(BHD1, BHD2). BHD1(BHD2)由一个分束片、一对光电探测器和一个功率减法器组成. 原子节点A放置在一个射频线圈内. 在原子系综A和B内通过自发拉曼散射过程产生的两束斯托克斯光束$\hat a_{\rm{1}}^{{\rm{out}}}$ 和$\hat a_2^{{\rm{out}}}$ 在50/50的分束偏上干涉, 干涉后的输出光束${\hat a_3}$ 和${\hat a_4}$ 的正交振幅和正交相位的起伏分别用平衡零拍探测器BHD1和BHD2测量. 由于$\hat a_{\rm{1}}^{{\rm{out}}}$ 和$\hat a_2^{{\rm{out}}}$ 分别和各自的原子系综A和B纠缠, 因此它们在分束片上干涉后原子系综之间的量子信息由A (B)到B (A). BHD1和BHD2探测到的信号通过经典通道射频线圈反馈到原子系综A, 最终通过纠缠交换建立了两个远距离原子系综之间的纠缠.图 7 原子系综纠缠示意图Figure7. Schematic of atom-atom entanglement generation system.$\eta = {\kappa _{{\rm{eg}}}}\kappa _{_{{\rm{es}}}}^{\rm{*}}\sqrt {{N_{\rm{a}}}} /\varDelta $ , ${\kappa _{{\rm{eg}}}}$ , ${\kappa _{{\rm{es}}}}$ 分别表示光和原子的耦合系数, ${N_{\rm{a}}}$ 表示原子总数, $\varDelta $ 是失谐. 强的写光已经被处理为经典光, 归一化振幅$A{}_{\rm{W}}$ 正比于写光脉冲的拉比频率${\varOmega _{\rm{W}}}$ .[69 ] 和Simon[91 ] 提出的不可分判据, 当关联方差和小于4时, 自发拉曼散射过程产生的斯托克斯光束和各自的原子系综纠缠. 两束斯托克斯光束以0相位在平衡分束片上干涉, 其输出场用BHD1和BHD2探测. 当输出光${\hat a_3}$ 和${\hat a_4}$ 分别和自己的本地光干涉时, 我们将其相对相位分别锁定在${\text{π}}$ /2和0, BHD1和BHD2分别测量${\hat a_3}$ 和${\hat a_4}$ 的正交相位和正交振幅的量子波动:${\text{δ}}{\hat Y_3}$ 和${\text{δ}}{\hat X_4}$ 通过经典的通道, 调节合适的可归一化的经典增益因子, 反馈到放置在射频线圈内原子系综A的总的原子自旋波$\hat S_{\rm{1}}^{{\rm{out}}}$ , 经过反馈后原子系综A的最终输出态:${g_1} = {g_2} = g$ , 当选取最合适的增益因子时得到原子系综的最佳关联.$g = {g^{{\rm{opt}}}}$ 时, 原子系综之间的纠缠永远存在, 并且得到最佳纠缠. 该理论方案通过利用光和原子的混合纠缠的制备和纠缠交换实现了两个远距离原子系综之间的纠缠, 建立的纠缠是无条件的确定的.4.4.多原子系综纠缠的建立 -->4.4.多原子系综纠缠的建立 为了建立实用化的量子网络, 就必须实现多个量子节点之间的纠缠. 目前, 国际上本研究组在实验上首次实现了三个原子系综间确定性的纠缠. 利用EIT相互作用的机制, 通过光场和原子间量子态相互映射的方法实现了三个原子系综间的纠缠, 并且我们建立的纠缠是确定性的, 方案具有良好的拓展性, 可以直接扩展到更多的量子节点, 并且引入的额外噪声小, 这样为构建实用化更多节点的量子网络提供了理论和实验参考.图8 所示为我们建立三个原子系综间确定性纠缠的实验装置图. 钛宝石激光器输出3 W的795 nm的红光, 作为倍频腔的抽运光和DOPA的种子光. 倍频腔和三个DOPA腔都是结构相同的四境环形腔, 且都用1 mm × 2 mm × 10 mm的周期极化的PPKTP晶体. 倍频腔产生的398 nm的倍频光和基频光$\hat a_{{\rm{S1}}}^{\rm{0}}$ , $\hat a_{{\rm{S2}}}^{\rm{0}}$ , $\hat a_{{\rm{S3}}}^{\rm{0}}$ 同时注入三个DOPAs, DOPA1工作于参量放大状态, DOPA2和DOPA3工作于参量反放大状态, 分别产生正交相位和正交振幅压缩光. 这三束压缩光在两个分束片上干涉, 正交相位压缩光${\hat a_{{\rm{S1}}}}$ 和正交振幅压缩光${\hat a_{{\rm{S2}}}}$ 在反射和透射比是1︰2的分束片BS1上干涉, BS1其中一束输出光和来源于DOPA3的正交振幅压缩光${\hat a_{{\rm{S3}}}}$ 在1︰1的分束片BS2上干涉, 两个分束片的相对相位均锁定在0. 将产生的三组分连续变量纠缠态通过三套AOM斩成三束脉冲纠缠$\hat a{(0)_{{\rm{S1}}}}$ , $\hat a{(0)_{{\rm{S2}}}}$ , $\hat a{(0)_{{\rm{S3}}}}$ . 三束光脉冲分别注入三个原子系综, 通过开关控制光和信号光的时序, 用三套平衡零拍探测器测量释放的三束光学子模之间的关联噪声来验证三个原子系综间的纠缠. 图9 所示为实验中所使用的控制光和信号光的开关时序, 控制光利用AOM的+1级衍射, 信号光用两套AOM的0级衍射. 在初始的2 ms内, 信号光和控制光均没有关断, 用来实现相位的锁定; 之后关断信号光制备真空纠缠, 并且在这段时间内打开信号光500 ns, 在500 ns内控制光和信号光同时打开, 信号光场的量子信息写入原子系综; 在光场的量子态信息转到原子系综后, 关断控制光1 $\mu {\rm s} $ 后打开控制光, 原子系综中的量子态释放.图 8 三原子系综纠缠实验装置图Figure8. Experimental device diagram of quantum entanglement among three distant atomic ensembles.$\hat J = \sum\nolimits_i {\left| g \right\rangle } \left\langle m \right|$ , 原子总角动量的y , z 分量是规范变量${\hat X_{\rm{A}}} = (\hat J + {\hat J^?})/\sqrt 2 = {\hat J_y}/\sqrt {\left\langle {{{\hat J}_x}} \right\rangle } $ , ${\hat P_{\rm{A}}} = (\hat J - {\hat J^?})/$ $\sqrt 2 {\rm{i}} = {\hat J_z}/\sqrt {\left\langle {{{\hat J}_x}} \right\rangle } $ [49 ] . 在EIT介质中, 量子态能够从输入光学子模$\hat a{(0)_{\rm{S}}}$ 映射到原子自旋波$\hat J$ , 也能从原子自旋波映射到光学模. 由于控制场的光强远远大于信号场, 因此控制场可以当作经典场处理. 在EIT过程中, 信号场$\hat a{(0)_{\rm{S}}}$ 和原子自旋波$\hat J$ 的有效相互作用哈密顿量类似于分束片相互作用模型, 可以写为图 9 信号光与控制光的时序控制图Figure9. Sequence control of signal and control light.$\hat X(\hat P){(0)_{{\rm{L}}j}}$ 映射到原子自旋波$\hat X(\hat P){(t)_{{\rm{A}}j}}$ , 在写的过程中量子态映射过程的表达式可以表示为如下形式:${\eta _{\rm{M}}} = {\eta _{\rm{T}}}{\eta _{\rm{W}}}{{\rm e}^{ - t/{\tau _{\rm{s}}}}}$ , ${\eta _{\rm{T}}}$ 是光学传输效率, ${\eta _{\rm{W}}}$ 是写效率, ${\tau _{\rm{s}}}$ 是受原子退相干影响的原子的存储寿命. 在存储过程中由于有限的存储效率会引入原子系综的额外噪声$\hat X(\hat P)_{{\rm{A}}j}^{{\rm{vac}}}$ .$[{X_{\rm{A}}},{P_A}] = {\rm{i}}$ , 因此运用同样的方法得到类似的原子自旋波三组分不可分判据:${g_{{\rm{A1}}}}$ , ${g_{{\rm{A2}}}}$ , ${g_{{\rm{A3}}}}$ 是原子系综的增益因子.$\hat a{(t)_{{\rm{S1}}}}$ , $\hat a{(t)_{{\rm{S2}}}}$ , $\hat a{(t)_{{\rm{S3}}}}$ . 释放的光学子模的正交振幅和相位分量$\hat X{(t)_{{\rm{L}}j}}$ 和$\hat P{(t)_{{\rm{L}}j}}$ 可以用原子自旋波的正交振幅和相位来描述:${\eta '_{\rm{M}}}$ 是原子系综到光场的释放效率; $\hat X(\hat P)_{{\rm{L}}j}^{{\rm{vac}}}$ 表示在读出的过程中引入的来源于光场的真空噪声.${g'_{{\rm{L}}1}}$ , ${g'_{{\rm{L}}2}}$ 和${g'_{{\rm{L3}}}}$ 是释放的光场的最佳增益因子. 最终测得的纠缠受到总映射效率$\eta (\eta = {\eta _{\rm{M}}}{\eta '_{\rm{M}}})$ 的限制, 同时也受到初始注入的三组分脉冲纠缠光纠缠度的影响. 假设实验中我们所用的三个DOPA的压缩参量r 相等, 三个原子系综总的映射效率也完全相等, 那么三个关联不等式的左边$I{(t)_{{\rm{L1}}}} = I{(t)_{{\rm{L2}}}} = I{(t)_{{\rm{L}}3}} = I{(t)_{\rm{L}}}$ , $I{(t)_{\rm{L}}}$ 的值越小, 得到的纠缠度就越大.表1 列出了存储释放后的三个光学子模式的正交分量的不同组合的归一化关联方差, 输入和释放的模式的关联方差用三个平衡零拍探测器测量. 原子系综间的归一化关联方差是通过表达式(22 )推断得到的, 其中读过程的释放效率是68%.不同组合的关联方差 输入模式/dB 原子自旋波/dB 释放模式/dB $\left\langle {{{\text{δ}}^2}({{\hat X}_2} - {{\hat X}_3})} \right\rangle $ ?3.30 ± 0.05 ?0.56 ± 0.03 ?0.37 ± 0.03 $\left\langle {{{\text{δ}}^2}({g_1}{{\hat P}_1} + {{\hat P}_2} + {{\hat P}_3})} \right\rangle $ ?2.93 ± 0.05 ?0.15 ± 0.02 ?0.10 ± 0.02 $\left\langle {{{\text{δ}}^2}({{\hat X}_1} - {{\hat X}_3})} \right\rangle $ ?3.25 ± 0.05 ?0.53 ± 0.03 ?0.35 ± 0.03 $\left\langle {{{\text{δ}}^2}({{\hat P}_1} + {g_2}{{\hat P}_2} + {{\hat P}_3})} \right\rangle $ ?2.91 ± 0.05 ?0.15 ± 0.02 ?0.10 ± 0.02 $\left\langle {{{\text{δ}}^2}({{\hat X}_1} - {{\hat X}_2})} \right\rangle $ ?3.25 ± 0.05 ?0.52 ± 0.03 ?0.34 ± 0.03 $\left\langle {{{\text{δ}}^2}({g_1}{{\hat P}_2} + {{\hat P}_2} + {{\hat P}_3})} \right\rangle $ ?2.90 ± 0.05 ?0.14 ± 0.02 ?0.09 ± 0.02
表1 释放光模正交分量不同组合的归一化关联方差Table1. Values of normalized correlation variances for different combinations.图10 是测得的归一化关联方差, 实验中三个DOPA的压缩参量r 均是0.38, 存储的总映射效率16%. 三个释放子模的正交振幅和正交相位关联方差的和$I{(t)_{\rm{L}}} = 0.96 \pm 0.01$ , 其关联方差和小于1, 因此释放的模式是三组分纠缠态光场. 原子系综间的纠缠依赖于总的量子映射效率和输入态的压缩参量, 输入态的压缩参量越大, 总的映射效率越大, 原子系综纠缠越大. 在目前实验系统中, 总映射效率主要受到光学传输损耗和读写效率的影响, 其中光学传输损耗主要来源于原子系综、滤波腔、格兰棱镜和其他光学元件, 这些因素均导致最终释放的纠缠度小于输入态的纠缠度, 然而得到的量子噪声依然在对应的真空噪声水平线下方, 验证了原子系综间存在纠缠.图 10 测量的输入模式和释放模式的关联方差Figure10. Measured normalized correlation variances of input and released optical submodes.5.总结与展望 量子网络的实现需要制备与铷原子D1吸收线对应的非经典光场[92 ] , 由于光场和原子自旋波均可以用Stokes算符来描述, 并且彼此之间可以直接相互作用, 因此本研究组在实验上分别实现了偏振压缩光、两组分偏振纠缠光[93 ] 以及三组分偏振纠缠光的制备, 为建立量子网络提供了基本资源. 不仅如此, 我们在实验上演示了三个空间分离的量子节点间确定性纠缠的产生、存储和转移. 在存储寿命期间, 多组分纠缠存储在三个空间分离的原子系综中, 然后在我们希望的时间内存储的原子纠缠可以通过控制转换到作为量子信道的三个光学子模式. 我们的工作证明, 利用EIT相互作用通过转移制备好的光学模式间的纠缠到原子系综中, 可以建立远距离的宏观物体之间的多组分连续变量纠缠. 由于多组分的光学模式间的无条件连续变量纠缠在实验上已实现[60 ,94 ,95 ] , 成熟的量子光学技术可用于实现更多量子节点间纠缠的量子网络中.[48 ] , 另一方面是在原子系综中EIT和四波混频同时发生[96 ] , 四波混频产生的闲置场也会引入额外的噪声, 这些机制都导致了在EIT相互作用过程中额外噪声总是存在. 因此, 一些方案被提出用来提高EIT过程中的经典信号的存储效率[96 ?98 ] , 例如减小控制光和信号光的失谐, 增加控制光的功率, 加大铷原子气室的温度, 这些方法不可避免地会引入过多的额外噪声, 降低了原子系综间的量子关联. 实验中, 可通过选择合适的最佳实验参数使得额外噪声最小[53 ,96 ] .[14 ] 、量子计算[99 ] 和纠缠提纯[100 ] . 目前在实验上已经证明, 通过光学谐振腔技术可以显著提高原子映射效率而不会引入过多额外噪音[101 ?103 ] , 并且如果用囚禁在三维光学阱中的冷原子代替热原子可以大大提高存储寿命. 迄今为止, 在实验上已经实现了高达15 dB的压缩[104 ] , 为建立更好的多个量子节点间纠缠提供了初始的量子资源. 高效率的量子存储以及高质量的量子资源为未来构建量子网络和实现基于光和原子存储的确定性连续变量纠缠分布式量子计算提供了新的可能. 





























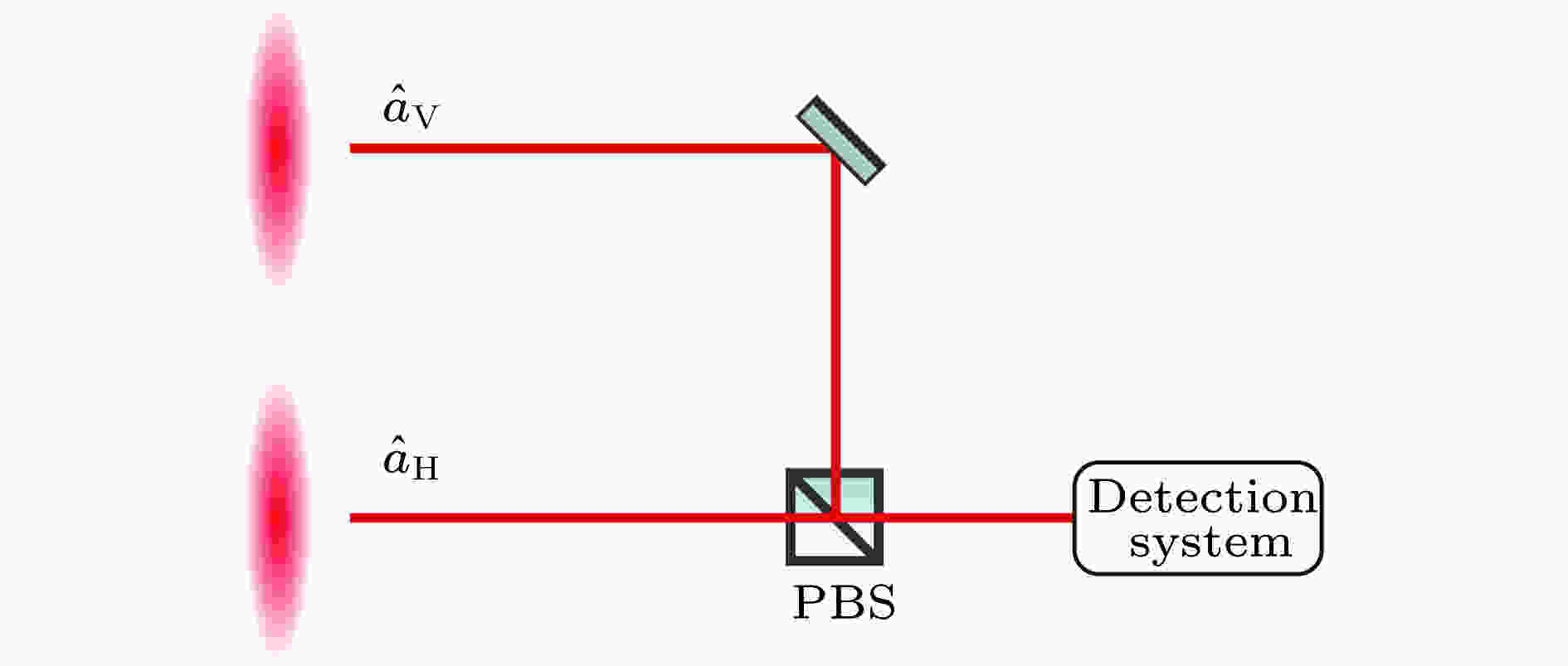 图 1 偏振压缩光场制备原理图
图 1 偏振压缩光场制备原理图














































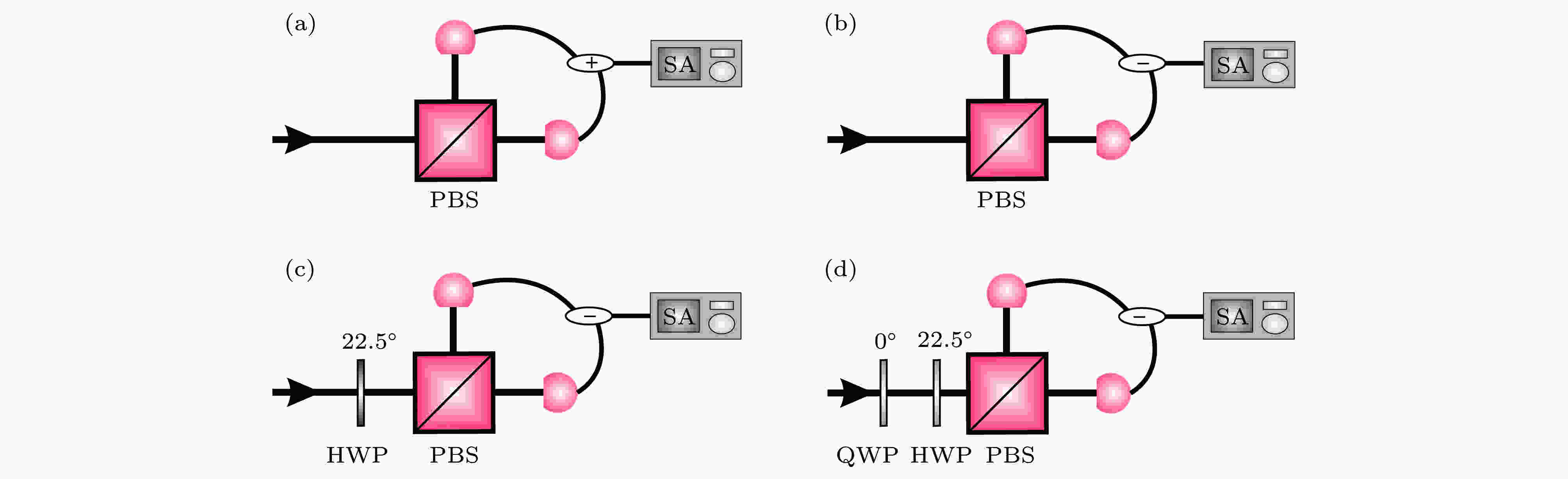 图 2 Stokes分量(a)
图 2 Stokes分量(a) 







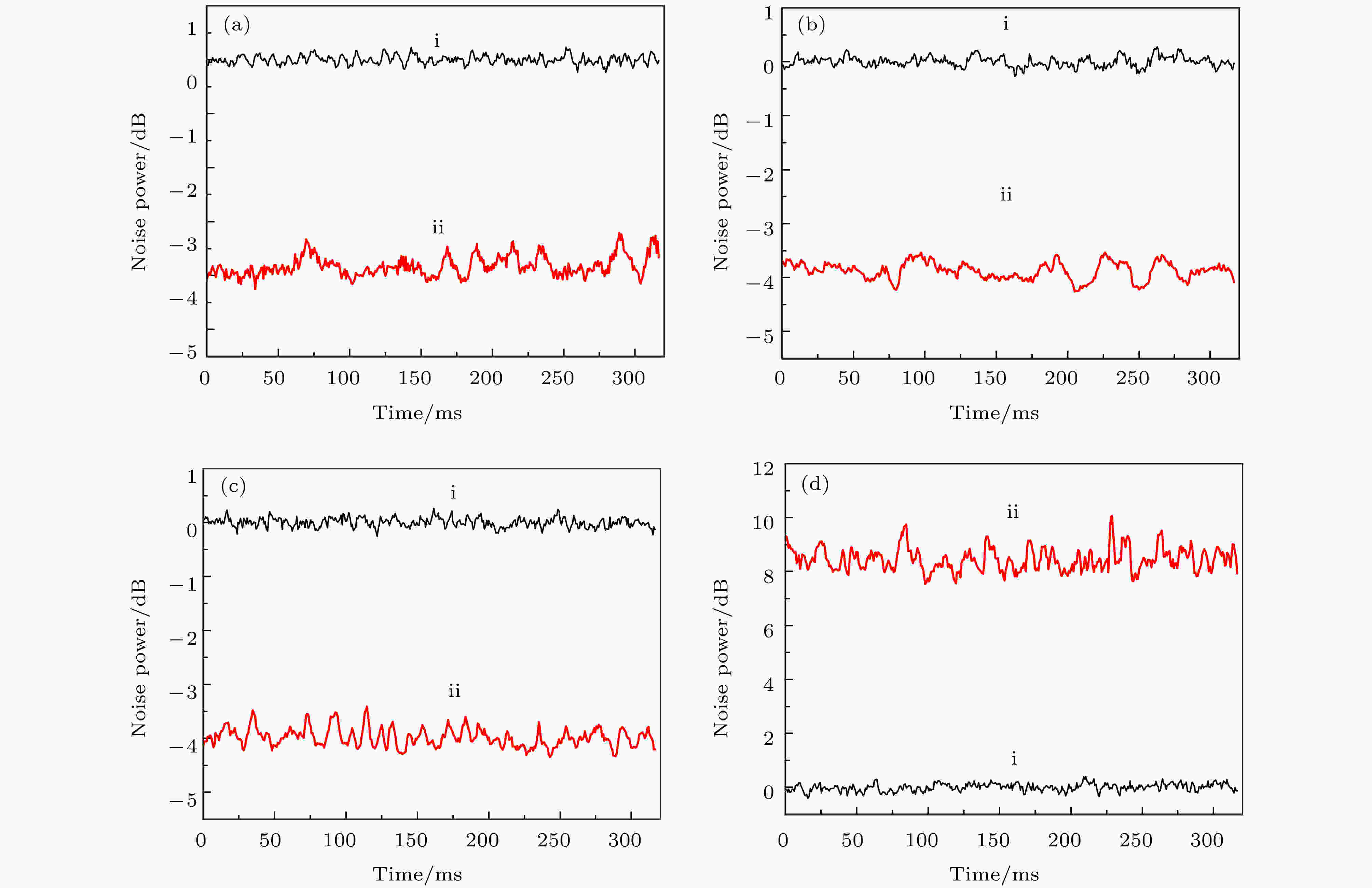 图 3 偏振压缩光Stokes分量的量子噪声[61] (a)
图 3 偏振压缩光Stokes分量的量子噪声[61] (a) 















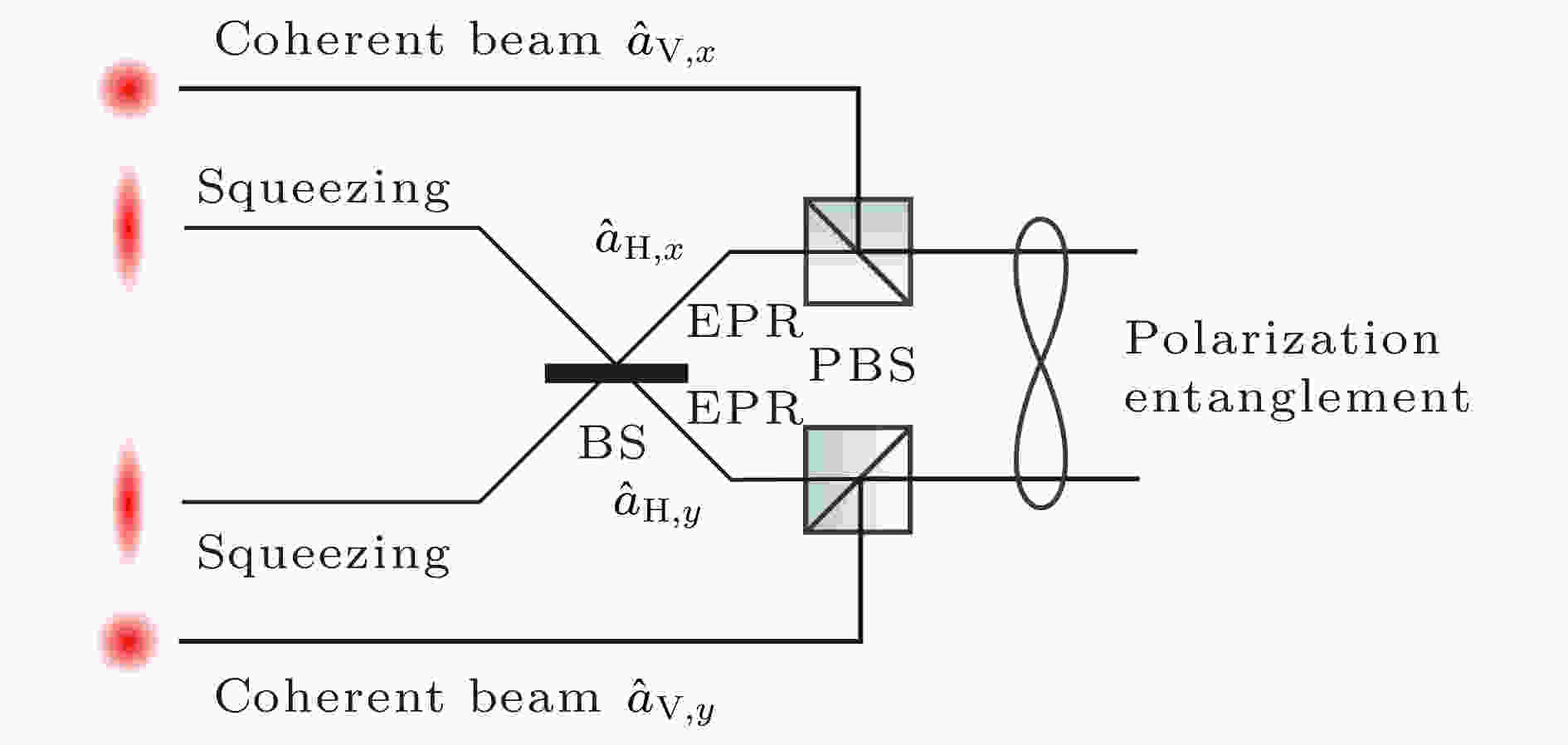 图 4 偏振纠缠制备原理图
图 4 偏振纠缠制备原理图



































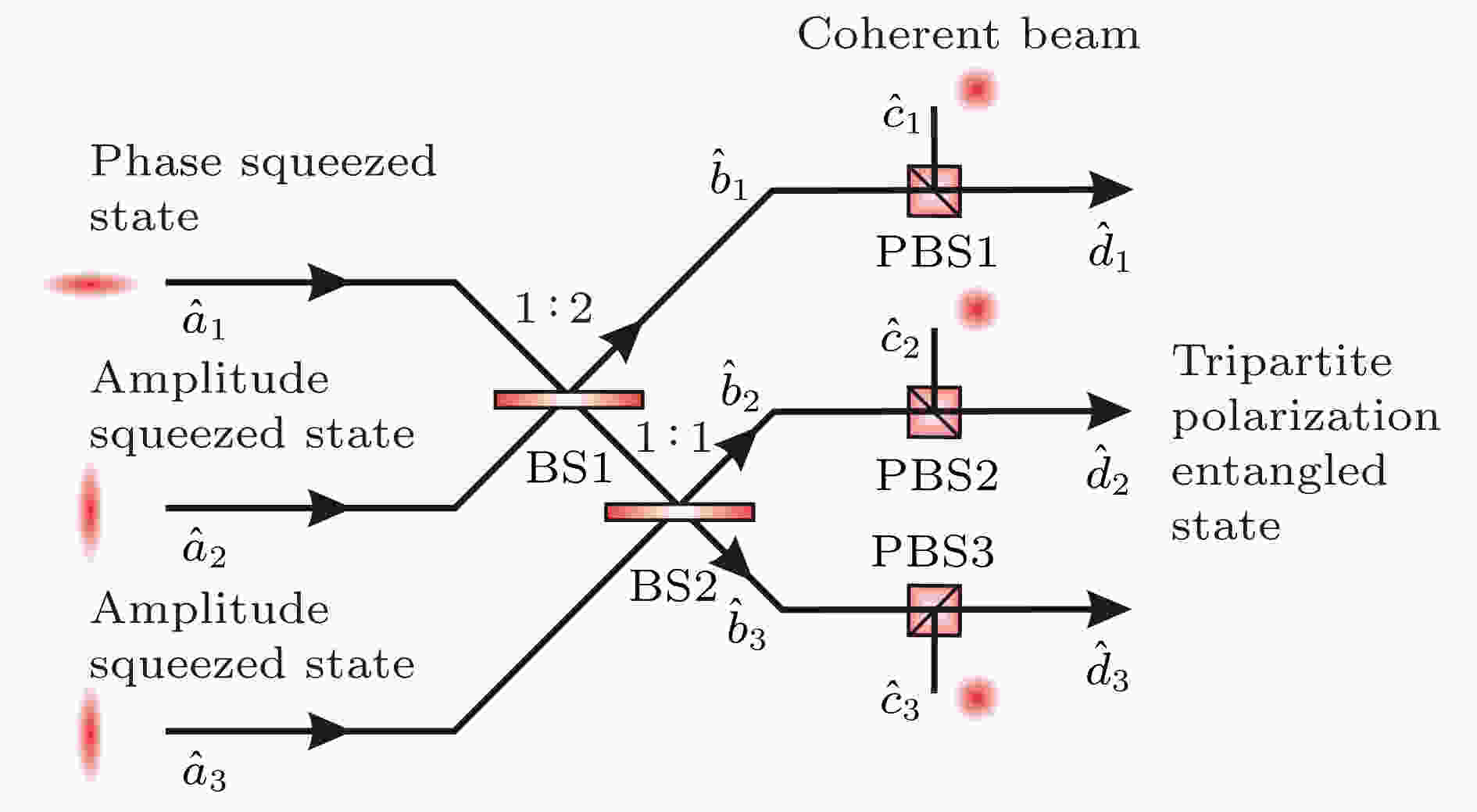 图 5 三组分偏振纠缠态产生方案(BS1, 光学分束器1; BS2, 光学分束器2; PBS1, 偏振分束棱镜1; PBS2, 偏振分束棱镜2; PBS3, 偏振分束棱镜3)
图 5 三组分偏振纠缠态产生方案(BS1, 光学分束器1; BS2, 光学分束器2; PBS1, 偏振分束棱镜1; PBS2, 偏振分束棱镜2; PBS3, 偏振分束棱镜3)






























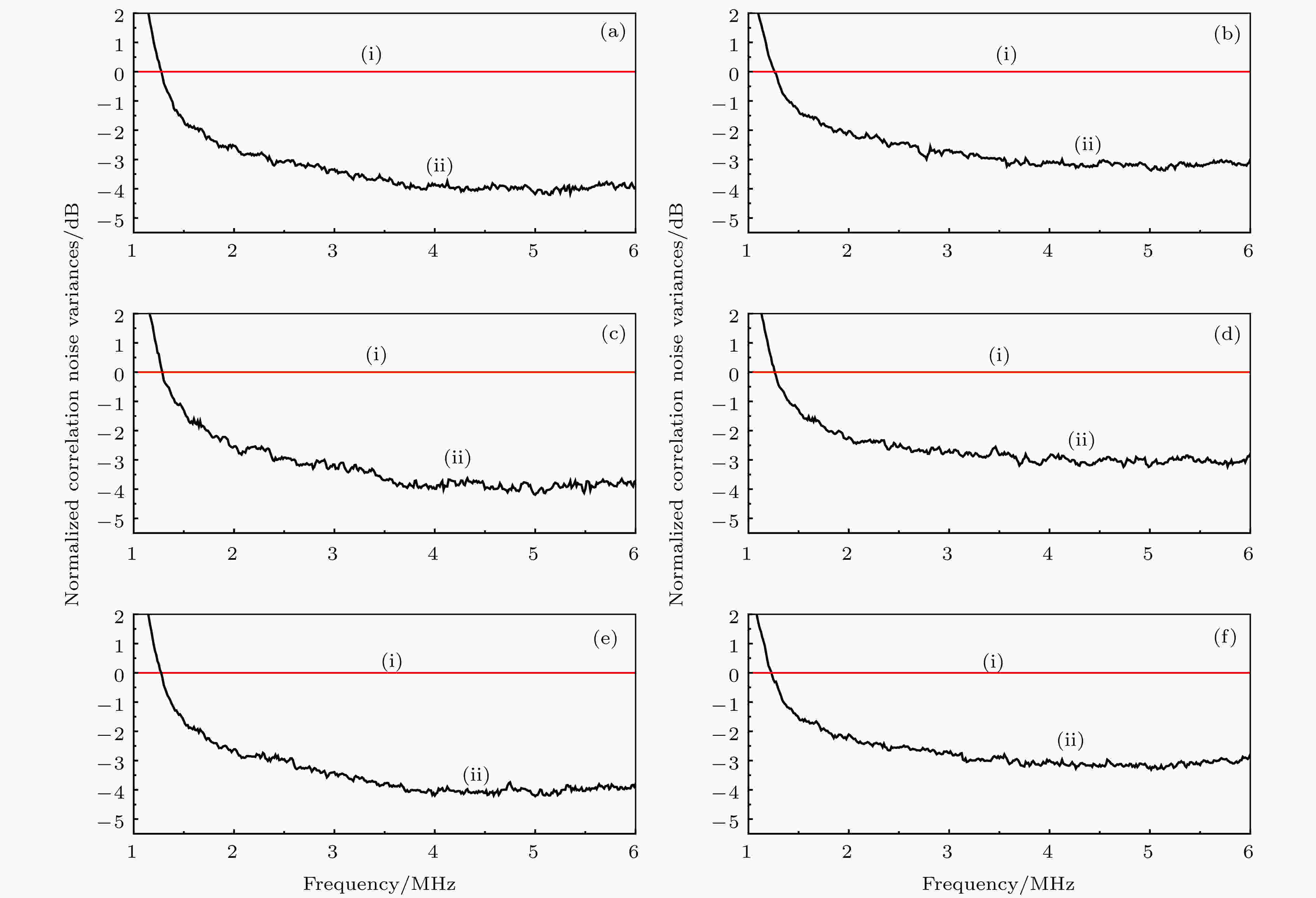 图 6 分析频率在1—6 MHz间测量的Stokes关联方差 (a)
图 6 分析频率在1—6 MHz间测量的Stokes关联方差 (a) 







































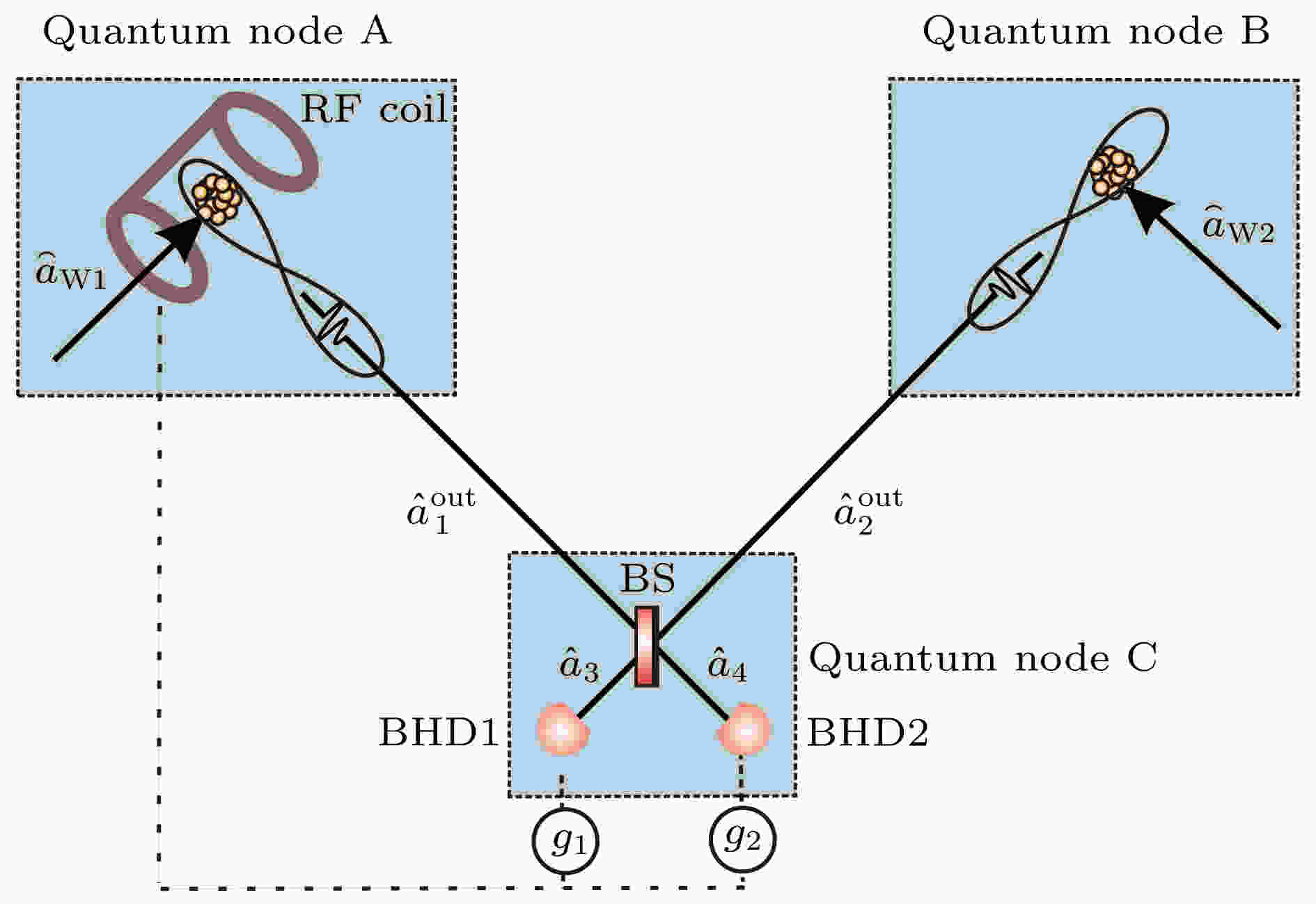 图 7 原子系综纠缠示意图
图 7 原子系综纠缠示意图






























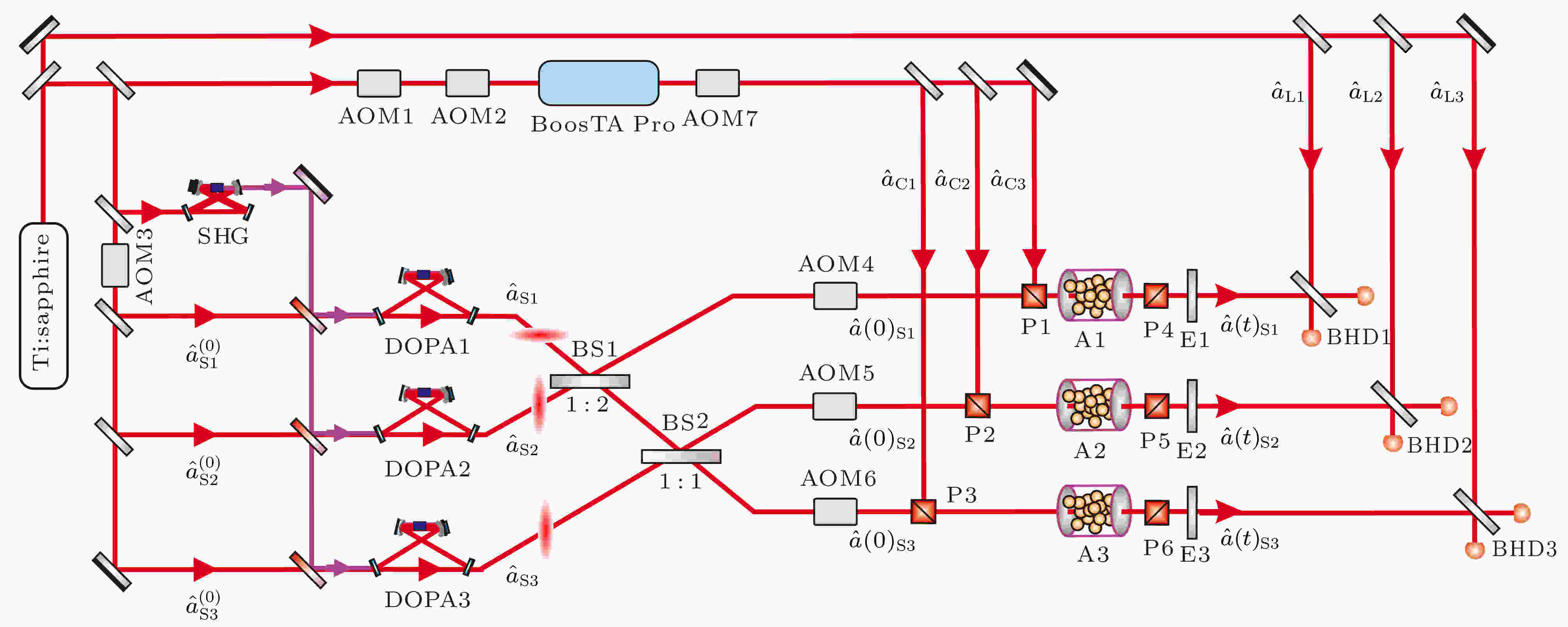 图 8 三原子系综纠缠实验装置图
图 8 三原子系综纠缠实验装置图











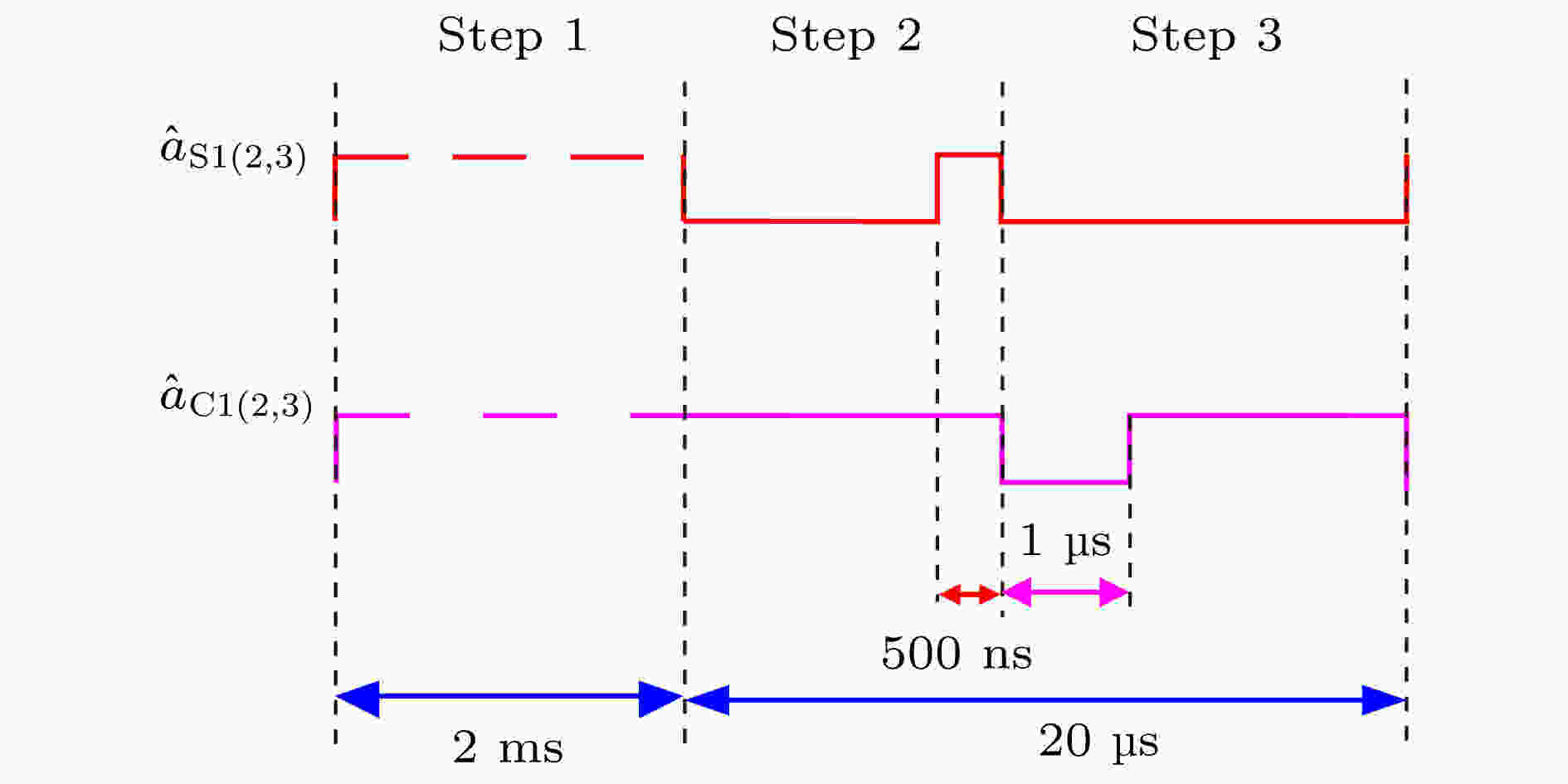 图 9 信号光与控制光的时序控制图
图 9 信号光与控制光的时序控制图
























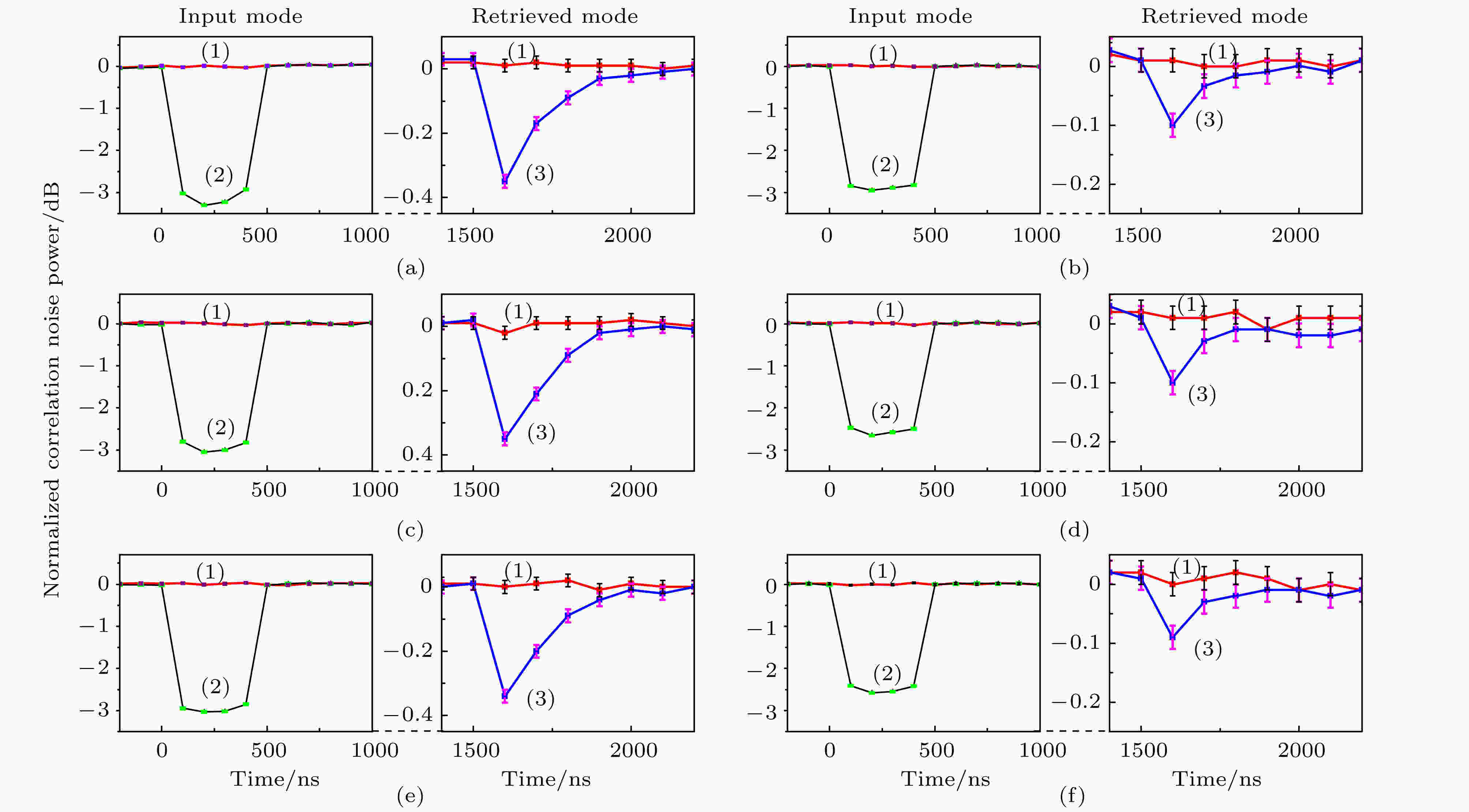 图 10 测量的输入模式和释放模式的关联方差
图 10 测量的输入模式和释放模式的关联方差