近年来在凝聚态系统中寻找高能物理对应的准粒子激发，一直是凝聚态物理的前沿热点研究之一。 其中，外尔准粒子是一种非常稳定的拓扑激发，可以广泛地存在于晶体材料的电子，声子以及磁子激发中。在电子系统（自旋 1/2）的外尔半金属中，研究人员发现多种新奇的拓扑量子现象，比如表面费米弧、手征反常、负磁阻和手征光伏效应等。目前人们逐步开始研究各种玻色系统中的外尔准粒子。 通常，寻找系统中的外尔点（零能隙且带有拓扑荷）并不是一件简单的事情，往往需要大量计算资源来对布里渊区中的k点做一个高密度的搜索。虽然外尔点不需要对称性保护，但是对称性可以把它钉扎在特定的k点。 所以，体系的对称性可以简化我们寻找外尔点的难度。我们知道，在时间反演对称的电子系统中，在手征空间群对称下，时间反演不变的k点处的任一Kramers pair都是一个外尔点。但是，对于玻色体系，有没有这种对称性保护的外尔点的存在呢？如果有，它将极大地方便人们寻找玻色系统中的二度简并准粒子。
　　最近，中国科学院物理研究所/北京凝聚态物理国家研究中心王志俊特聘研究员与华中科技大学物理学院傅华华教授合作，在对玻色系统中230个空间群做了系统的分析后，完整地给出了可以出现二度简并准粒子的空间群号和对应的高对称k点（见表一）。这些二度简并点都被相关的对称性钉扎在固定的k点 (对称性保护的外尔点)，同时，它对应的拓扑Chern数也在表一中给出。其中，既有C=±1的常规单外尔点，也有C=±2的双外尔点，同时还发现之前没有报道过的C=±4的四外尔点。这将为人们在玻色系统（或者自旋轨道耦合可以忽略的电子体系）中寻找各种外尔点提供有力的支撑和引导。
　　通过对称性操作和不可约表示的进一步分析之后，作者发现在表一中的某些k点（由*标注），只存在表中所列的二度简并表示。即这些k点的外尔点的存在是由对称性保证的（对称性保证的外尔点），与电子系统的时间反演对称保证的Kramers 外尔点形成完美对应。不同的是，后者在电子系统中通常需要比较大的自旋轨道耦合才能很好地显露出来，而这里提出的外尔点完全受晶体对称性保护，在玻色系统中可以很容易“暴露”出来，从而导致非常大和清晰的表面弧。随后作者计算了对应材料的声子谱，验证了理论分析的结论。例如，在空间群号为199的K₂Sn₂O₃材料的声子谱中，很容易地在P点发现Weyl点（见图1）。值得一提的是，在具体考虑第39和第40两个声子谱之间的拓扑简并点时，由于两个P的外尔点具有相同的Chern数 (C=-1)，这就需要有其他的拓扑简并点的存在，于是在H点发现了一个三重的自旋1的简并点(C=+2)，在其(110)表面声子谱中，表面弧被清晰地显示出来（图1）。
　　这项工作近期发表在npj Computational Materials 6: 95 (2020)上。此项工作得到国家自然科学基金委、中组部专项人才计划和中科院战略性先导科技专项(B类)支持。

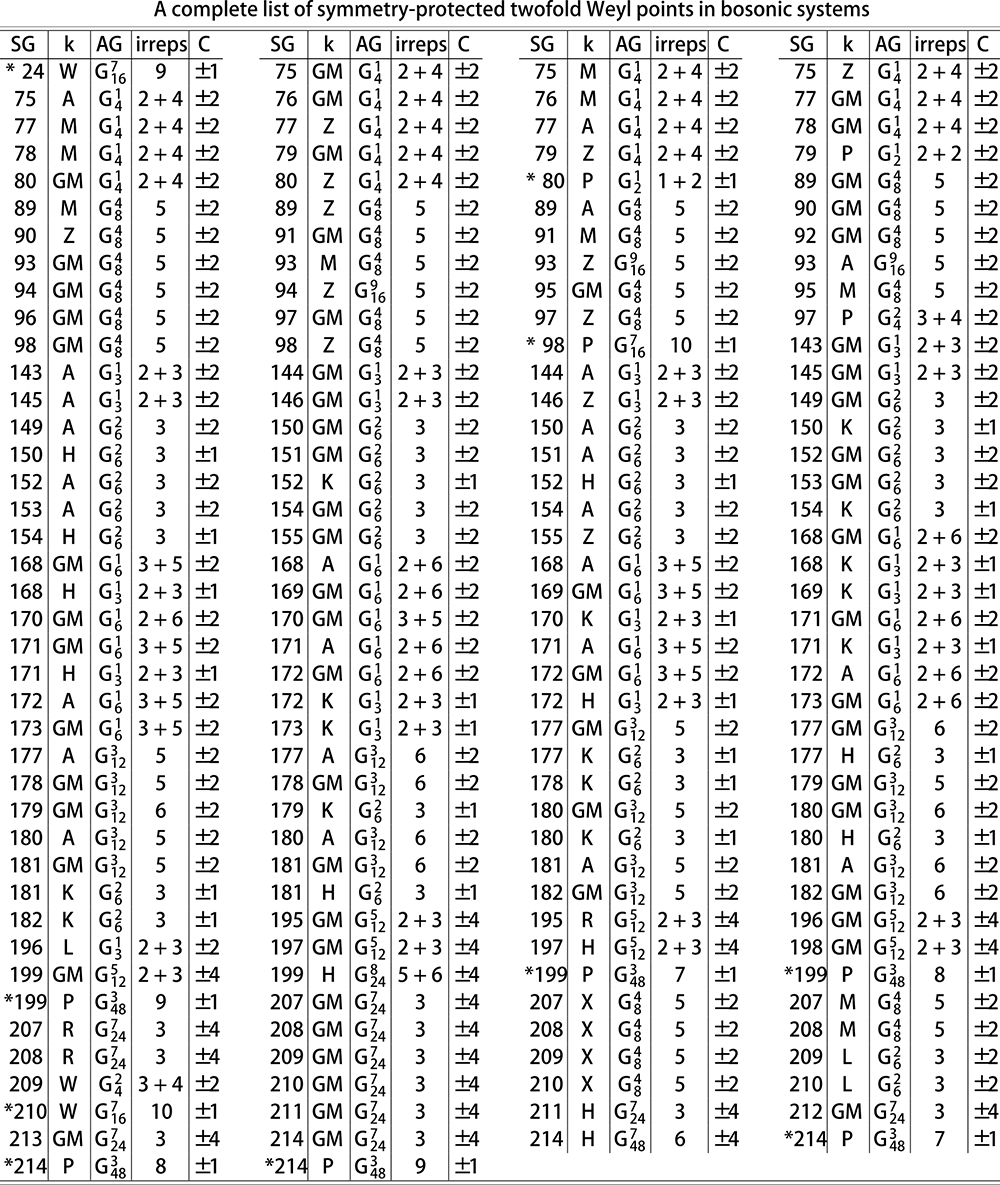
表一： 玻色体系中对称性保护的外尔点。第一列和第二列分别标记空间群号(SG)和高对称的k点，第三列和第四列标记k点的小群对应的抽象群（AG）以及对应的不可约表示（irreps），最后一列给出了对应的拓扑Chern数。星号标记对称性保证的外尔点。

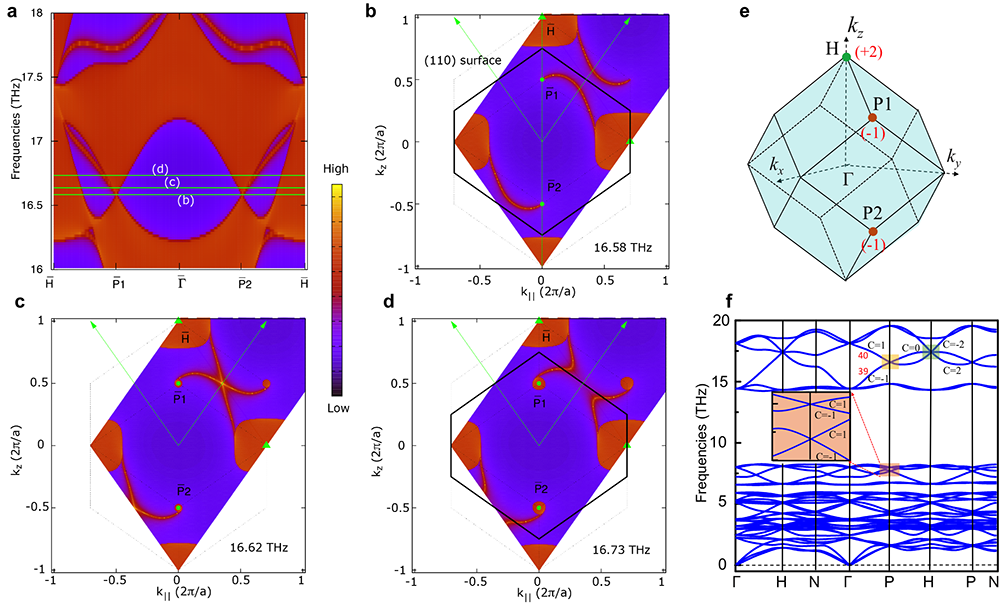
图1 : (a-d) 是K₂Sn₂O₃的表面色散谱和表面声子的等频率谱，(e)为第一布里渊区图，(f)为K₂Sn₂O₃的声子谱。

npj Computational Materials 6, 95 (2020).pdf
supplemantary information.pdf