引言

柱体绕流这一现象普遍存在于自然界, 最早注意到这一现象的是意大利著名画家达·芬奇. 法国科学家Benard于1908年进行了圆柱绕流实验, 最早在实验中发现绕流圆柱后出现的涡旋脱落现象. 1911年冯·卡门教授对圆柱绕流后的涡旋脱落现象进行了理论推导, 确定了涡旋生成的条件^[1]. 1925年, Relf等^[2]通过在均匀水流中喷射油的方法, 对Re = 1100、自转速比为0 ~ 10.4时旋转圆柱的流场进行摄影, 得到了5种转速比流场的概貌. 1959年, Taneda^[3]对圆柱绕流的尾流和涡街进行实验研究, 结果表明当Re > 45时尾流处出现卡门涡街, 且涡在下游发展处形成了二次卡门涡街. 基于实验和数值模拟的方法, Tamura等^[4-7]通过对方柱绕流研究, 发现相较于尖角方柱, 圆角r/D = 1/6方柱的平均阻力和升力有一定的减小. Kawai^[8]通过方棱柱和矩形棱柱的风洞实验, 指出圆角、切角、凹角3种处理方法中, 圆角化处理对方棱柱的气动弹性不稳定性抑制效果最好, 风致振动的幅值随着圆角参数的增大而减小. Hu等^[9]基于不同转角半径方柱的近尾迹实验研究, 指出当r/D从0增大到1/2时, 脱落涡的最大强度逐渐减弱, 与涡旋相关的环流逐渐减小50%, 斯特劳哈尔数St增大约60%, 涡旋对流速度随尾迹宽度增加约25%, 涡旋形成长度和尾迹闭合长度增加近一倍. Shadaram等^[10]通过风洞试验对矩形柱体的绕流进行研究, 结果表明尾流处的湍流强度与方柱的长宽比有关, 但在高雷诺数下斯特劳哈尔数(St)基本不变. Kumar等^[11]基于实验研究指出圆角参数对绕流体的流动特性有显著影响, 且r/D值越高, 尾迹附近的脱落越均匀, 并可以抑制圆柱体可能发生的失稳. 工程上通过对方柱角部的处理(如圆角、切角、凹角等), 达到降低流致振动, 减小流动阻力和脉动升力的效果^[12-16]. Zhao等^[17]通过数值研究指出, 在Re = 200的情况下, 当圆角参数r/D = 0.1时, 圆角完全抑制了驰振; 当圆角参数r/D = 0.01时, 对驰振的抑制作用不大; 当圆角参数r/D为0.03和0.05时, 圆角有效地抑制了驰振, 驰振幅度极小; 振动频率是位移的主频, 涡脱落频率是升力系数的主频. Rocchio等^[18]基于大涡模拟指出圆角化柱体的流动特征与尖角柱体的流动特性有明显的差异, 即使r/D的值很小, 平均回流区的长度也会显著增加. 文献[19-24]基于柱体绕流, 更好地分析高层建筑、架空线路在风中的性能, 改进结构, 提高安全系数.

受迫振动作为一种简化的运动形式相对容易实现, 并且流致振动和受迫振动的流场信息在一定程度上具有相似性, 许多****将研究重心放在受迫振动问题上. Bishop等^[25]较早进行了圆柱受迫振动的研究, 对圆柱流向以及横向的受迫振动进行了实验. Bearman等^[26-27]对低雷诺数下横流振动圆柱的流动进行研究指出最大振幅出现在锁定区域的下限附近, 而从静止状态发展起来的柱体振幅和已经振动柱体的自由流速度之间的最终响应没有明显的差别; 当振幅大于0.6D时, 观察到不对称的涡旋脱落模式. Sarpkaya^[28]曾提出, 涡激振动研究的目的是根据受迫振动的结果来预测自激振动的运动和受力情况, 或是通过自激振动的研究结果来预测受迫振动的升力、阻力系数等情况. Yokoi等^[29]对三维圆柱受迫振动进行数值模拟和实验, 发现了沿展向方向涡旋脱落的不同时性, 并指出三维效应对涡脱模态的影响. 平焕等^[30]对低雷诺数下的直圆柱和波浪型圆柱横向受迫振动进行了数值模拟研究, 通过改变圆柱振动的频率和振幅, 来分析二者所受升力、阻力及锁定区间, 并且观察到锁定区间内二者尾涡模式有所不同. Ma等^[31]基于受迫振动实验, 对方柱脉动横向力特性与气动弹性不稳定现象之间的联系进一步分析研究, 对非定常力特性与气动弹性振动幅值之间的关系提出了新的见解. 刘俊等^[32]通过实验研究分析指出涡激振动迟滞现象通常伴随振动的幅值阶跃和频率跃迁. Huang等^[33]指出无论运动方向如何, 如果流体与振动圆柱之间的相对速度的最大值和最小值保持相同, 则可以产生类似的尾迹结构, 同时指出流动与结构之间能量传递的变化征兆不一定是尾迹模式的改变, 而是涡旋脱落时间的改变. Qu等^[34]提出非线性耦合尾迹振子模型, 它是能够同时再现自由振动和强迫振动实验的模型, 但它存在一个重要挑战即对于频率有一定的限制, 这是Zhang等^[35]基于已建立的硬质涂层圆柱壳非线性强迫共振特性的非线性解析公式, 指出NiCoCrAlY + YSZ硬质涂层有利于抑制柱体的过度振动. Chen等^[36]通过受迫振动法, 指出柔性振动管上升力主要取决于管道本身在提升方向上的振幅, 而受管道振动的自由度、旋转方向和主振动方向的影响较小. Wang等^[37]通过对均匀流和线性剪切流中柔性长圆柱体的单频自由振动与规定正弦运动的刚性圆柱体强迫振动进行对比研究, 指出两种情况下的水动力系数有很强的相似性, 强迫振动与自由振动的尾迹截面非常相似. Chen等^[38]基于小间隙直径比近壁圆筒在Re = 200时的流致横向振动进行的数值模拟结果, 指出运动振幅一般随折减速度的增大而先增大后减小, 没有明显的滞回转变; 当小间隙直径比减小时, 最大振幅减小, 出现最大振幅的折合速度增大, 且从圆柱上部脱落的顺时针涡流仍然很强, 而从圆柱下部脱落的逆时针涡流逐渐减弱, 涡街向上偏转较小. 本课题组曾在超临界雷诺数条件下, 通过使用大涡模拟方法, 研究了波浪型圆柱和折线形圆柱等变截面立式圆柱的绕流问题以寻找降低涡激振动的最优解. 通过对绕流时的均方根升力系数对比, 发现折线形圆柱的减振效率大于波浪型圆柱^[39].

最近, 杜晓庆等^[40]针对不同风攻角分析了方柱圆角化处理后的流场作用机理, 结果表明, 方柱在绕流时稳定性较差, 圆角化有助于改善其稳定性. 但他们并未结合柱体的受迫振动进行研究分析, 前人对于圆角化受迫振动柱体的深入研究也未曾有过. 故本文将进一步研究圆角化对受迫振动方柱绕流特性的影响机理. 为了分析圆角化对受迫振动方柱造成影响的流场作用机理, 本文采用了Fluent软件用户自定义函数(UDF)中的DEFINE_ CG_MOTION宏进行编程, 并采用了流场计算域区域划分以及动网格技术中的动态层技术, 在Re = 200时, 考虑方柱截面不同圆角化的影响, 研究了均匀流作用下5种圆角化r/D = 1/2, 1/4, 1/5, 1/8和0受迫振动方柱的绕流特性, 以期为受迫振动方柱绕流稳定性的提高提供参考依据.

1.
数值模型

1.1
基本控制方程

对于不可压缩的黏性牛顿流体, 其控制方程为Navier?Stokes方程. 在二维直角坐标系下, 连续性方程为

$$frac{{partial u}}{{partial x}} + frac{{partial v}}{{partial y}} = 0$$

(1)

动量方程为

$$frac{{partial u}}{{partial t}} + ufrac{{partial u}}{{partial x}} + vfrac{{partial u}}{{partial y}} = - frac{1}{ ho }frac{{partial p}}{{partial x}} + upsilon left(frac{{{partial ^2}u}}{{partial {x^2}}} + frac{{{partial ^2}u}}{{partial {y^2}}} ight)$$

(2)

$$frac{{partial v}}{{partial t}} + ufrac{{partial v}}{{partial x}} + vfrac{{partial v}}{{partial y}} = - frac{1}{ ho }frac{{partial p}}{{partial x}} + upsilon left(frac{{{partial ^2}v}}{{partial {x^2}}} + frac{{{partial ^2}v}}{{partial {y^2}}} ight)$$

(3)

式中u和v分别为x和y方向的速度分量, p为压力, $;
ho $为流体的密度, t为流体运动时间, v为流体的运动黏度系数.

1.2
动网格守恒方程

对于边界移动的任意控制体积上的一般标量的守恒方程可以写为

$$begin{split} &frac{{ m{d}}}{{{ m{d}}t}}int_V { ho emptyset { m{d}}V + int_{partial V} { ho emptyset { m{(}}{boldsymbol{u}}{ m{ - }}{{boldsymbol{u}}_{ m{g}}}{ m{)}}} } cdot { m{d}}{boldsymbol{A}} = &qquadint_{partial V} {varGamma nabla emptyset cdot { m{d}}} {boldsymbol{A}} + int_V {{S_emptyset }}{ m{d}}Vend{split} $$

(4)

式中, V为大小和形状都随时间变化的控制体积, $partial V$为控制体积的运动边界, ${{boldsymbol{u}}_{
m{g}}}$为运动网格的运动速度, ${boldsymbol{u}}$为流体速度矢量, $varGamma $为耗散系数, S为源项, $emptyset$为单位质量某种物理量.

对式(4)中时间导数项用一阶向后差分公式可得

$$frac{{ m{d}}}{{{ m{d}}t}}int_V { ho emptyset { m{d}}V} = frac{{{{( ho emptyset V)}^{n + 1}} - {{( ho emptyset V)}^n}}}{{Delta t}}$$

(5)

式中, 上标n和n+1分别代表当前和下一步的时间层, 第n+1个时间步的控制体积由下式得到

$${V^{n + 1}} = {V^n} + frac{{{ m{d}}V}}{{{ m{d}}t}}Delta t$$

(6)

为了满足网格的守恒定律, 控制体积随时间的导数可由下式求得

$$frac{{{ m{d}}V}}{{{ m{d}}t}} = int_{partial V} {{{boldsymbol{u}}_{ m{g}}}} cdot { m{d}}{boldsymbol{A}} = sumlimits_j^{{n_{ m{f}}}} {{{boldsymbol{u}}_{{{{ m{g}}}}{{j}}}}} {{boldsymbol{A}}_{{j}}}$$

(7)

式中, ${n_{
m{f}}}$为控制体积上面网格的数量, ${{boldsymbol{A}}_{{j}}}$为面j的面积矢量.

$${{boldsymbol{u}}_{{{{ m{g}}j}}}}{{boldsymbol{A}}_{{j}}} = frac{{delta {{boldsymbol{V}}_{{j}}}}}{{delta t}}$$

(8)

式中, $partial {{boldsymbol{V}}_{{j}}}$是控制体上面j在时间$Delta t$内扫出来的空间体积.

1.3
无量纲参数

无量纲参数的使用是为了把不同条件下得到的结果进行类比. 受迫振动涉及到的无量纲参数有流动参数和流固耦合参数, 下面将分别对这些参数进行介绍.

1.3.1
雷诺数

雷诺数是描述流体流动最基本的参数, 雷诺数表示了流体微元惯性力与黏性力的比值

$$Re = frac{{ ho UD}}{mu } = frac{{UD}}{upsilon }$$

(9)

式中, $;
ho $和U分别为来流流体的密度与速度, D为柱体的特征长度, $mu $为流体的动力黏度系数.

雷诺数的大小不同, 所表示的物理意义也不同. 黏性力倾向于使流体中的扰动衰减, 而惯性力倾向于使流体中的扰动增加, 因此雷诺数的大小决定了流动是处于层流还是湍流, 一般当雷诺数小于2300时, 流动为稳定层流; 当雷诺数大于2300时, 流动为不稳定湍流. 在圆柱绕流问题中, 雷诺数的大小还会影响到柱体尾流涡旋的脱落形态.

1.3.2
斯特劳哈尔数

在流体流过柱体后会出现一系列交替的涡旋, 斯特劳哈尔数是用于表征其涡旋脱落特性的重要相似准则数, 也即涡旋脱落的无量纲频率, 用于表征涡旋脱落的快慢, 是描述非定常性的重要特征参数, 其表达式为

$$S!t = frac{{{f_{ m{s}}}D}}{U}$$

(10)

式中, f_s为柱体涡旋脱落频率, D为柱体的特征长度, U为来流流体的速度.

St数的大小与雷诺数、柱体形状以及表面粗糙度等因素有关, 其中最主要的影响因素为雷诺数. 在较大的雷诺数范围内斯特劳哈尔数的值没有太大的变化(在亚临界雷诺数区域内, St数稳定在0.2左右)^[41]. 本文Re数为200, St数也基本可视为0.2不变.

1.3.3
升力、阻力系数

在流体流经柱体过程中, 可以将柱体受到的总作用力分解为与来流方向垂直的升力和与来流方向平行的阻力两部分. 升力的产生原因是柱体尾流涡旋的脱落, 升力的值随时间周期性变化, 稳定工况下时均值为0. 绕流所产生的阻力包括压差阻力和摩擦阻力, 摩擦阻力的产生是由于流体的黏性. 压差阻力的产生是由于流体流经柱体产生了边界层分离, 在柱体后方涡旋脱落形成负压区, 而在柱体前方, 流体由于受到阻碍速度减小压力增加, 柱体前后压力一大一小产生压差. 虽然绕流升力与阻力产生的原因不同, 但是二者均是由摩擦力与压力构成. 柱体绕流升力、阻力积分表达式如下

$${F_{ m{D}}} = - frac{1}{2}Dint_0^{2{text{π}} } {pcos theta { m{d}}theta } - frac{1}{2}Dint_0^{2{ m{{text{π}} }}} {tau { m{sin}}theta { m{d}}theta } $$

(11)

$${F_{ m{L}}} = - frac{1}{2}Dint_0^{2{text{π}} } {psin theta { m{d}}theta } - frac{1}{2}Dint_0^{2{ m{{text{π}} }}} {tau cos theta { m{d}}theta } $$

(12)

式中, F_D和F_L分别为阻力与升力, D为特征长度, p和$tau $分别为压力和摩擦力.

对阻力、升力进行无量纲化可得阻力系数和升力系数

$${C_{ m{D}}} = frac{{{F_{ m{D}}}}}{{dfrac{1}{2} ho D{U^2}}}$$

(13)

$${C_{ m{L}}} = frac{{{F_{ m{L}}}}}{{dfrac{1}{2} ho D{U^2}}}$$

(14)

1.3.4
无量纲振幅

无量纲振幅为柱体振幅与柱体特征长度之比, 是计算受迫振动的重要无量纲参数

$${A^*} = A/D$$

(15)

式中, A为柱体振幅.

1.3.5
无量纲频率

无量纲频率为柱体受迫振动的驱动频率与静止柱体自然泻涡频率之比

$$F = {f_{ m{e}}}/{f_{ m{s}}}$$

(16)

式中, f_s为柱体涡旋脱落频率, f_e为柱体受迫振动的驱动频率.

无量纲频率在受迫振动中是十分关键的无量纲数, 它的改变会影响到锁定区间以及尾涡模态.

1.4
计算域及模型网格

本文中雷诺数为200, 计算域为40D × 20D的矩形, 方柱中心距离上游入口距离为10D, 距离下游出口为30D, 距离上下对称边界距离为10D, 其中D为方柱棱边边长. 流体从左向右流动, 左侧上游为速度入口, 右侧下游为压力出口, 上下两侧边界为对称边界, 方柱为无滑移壁面. 流场划分网格时采用结构网格, 由于方柱进行受迫振动需要采用到动网格, 为避免计算域内的所有网格都运动而影响计算效率, 在距方柱中心左右3D处各设置一个滑移面来分割静止网格与动网格, 如图1所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
计算域示意图



Figure
1.
Schematic diagram of the calculation domain



下载:
全尺寸图片
幻灯片


网格的运动通过Fluent中的UDF实现, 利用刚体的运动宏(DEFINE _CG_MOTION)把方柱的速度传递给网格, 网格进一步通过动态层法进行更新, 在上下边界处对网格进行分裂和合并. 在方柱周围的网格划分较密, 远离方柱处网格划分稀疏, 取壁面法向第一层网格高度为0.004D, 网格增长率为1.1. 在对控制方程进行离散时, 速度与压力耦合采用SIMPLEC算法, 各物理量参数残差控制在10^?5.

通过把方柱的尖角优化为圆角从而对其进行被动控制, 圆角特征参数为r/D, 其中r为圆角半径. 本文选r/D = 1/2, 1/4, 1/5, 1/8和0, 5种不同的圆角参数, 对其进行柱体绕流模拟, 并分析不同圆角参数对柱体绕流的影响. 随后对圆角方柱进行受迫振动的数值模拟, 并将模拟结果进行比较, 观察圆角化对其受迫振动的影响.

圆角化时, 计算区域与尖角方柱计算域一致. 采用相同的棱边节点数和柱体壁面法向第一层网格高度, 以保证模拟结果不受网格划分方式的影响. 同样的, 为了方便动网格的生成与计算, 将整个计算域通过“interface”边界分为3部分, 中间部分为动网格和圆角化方柱所在的区域, 此处网格尺寸较小, 柱体壁面处网格较密. 如图2所示为r/D = 1/4的网格划分情况.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
圆角方柱网格划分情况



Figure
2.
Grid division of rounded square column



下载:
全尺寸图片
幻灯片

2.
计算结果及分析

本文对方柱横向受迫振动进行研究, 方柱横向受迫振动的方程为

$$y = Asin (2{text{π}} {f_{ m{e}}}t)$$

(17)

式中y为方柱横向运动的位移, 对其求导可得到速度方程

$$u = 2{text{π}} {f_{ m{e}}}Acos (2{text{π}} {f_{ m{e}}}t)$$

(18)

2.1
网格无关性验证

分别取单条棱边上节点数为60, 90, 120, 三种网格划分方式观察对结果的影响; 另取节点数为90时, 壁面法向第一层网格高为0.002D, 0.01D进行无关性验证, 并与文献[41-45]实验和数值模拟结果做对比进行正确性验证,如表1所示.




表
1
静止方柱扰流结果比较



Table
1.
Comparison of perturbation results of stationary square column



table_type1 ">

Working condition	CD,mean	St
grid 1 has 60 nodes	1.554	0.143
grid 2 has 90 nodes	1.533	0.15
grid 3 has 120 nodes	1.537	0.148
normal first grid 0.01D	1.561	0.139
normal first grid 0.002D	1.529	0.146
Ref. [41]	1.435	0.1434
Ref. [42]	1.523	0.153
Ref. [43]	1.651	0.149
Ref. [44]	1.63	0.151

下载:
导出CSV
|显示表格



从表1中可以看出, 当单条棱边节点数为90时, 其阻力系数和St与其他实验和数值模拟结果吻合较好, 且网格高度为0.002D和0.004D模拟所得结果相近. 在确保正确性的前提下, 考虑到计算时间, 故选择棱边节点数为90, 第一层网格高度为0.004D的网格划分方式进行后续模拟计算.

2.2
模型验证

在验证网格无关性与边界条件设置正确性后, 对圆柱r/D = 1/2受迫振动进行模拟以验证模型及自编UDF的准确性. 圆柱受迫振动与自激振动均包含流向振动和横向振动, 而在实际涡激振动中流向振动振幅相对于横向振动振幅普遍较小, 鉴于大多数****将研究重点放在横向振动上, 因此本文也将进行柱体横向受迫振动的模拟研究.

对圆柱受迫振动的研究主要是在不同的振幅和振动频率下对其升力、阻力系数, 锁定区间以及尾涡脱落模式进行分析. 在流体力学问题的研究中, 为使研究的结果更加直观和准确, 通常引入无量纲参数进行分析研究, 本文引入无量纲振幅A^*与无量纲频率F, 由前述提及的St公式以及St值可知f_s = 0.386. 本文对无量纲振幅为0.2下不同无量纲频率的受迫振动进行模拟, 图3为不同频率下的升力、阻力系数历时曲线.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-3.jpg'"
class="figure_img
figure_type2 ccc " id="Figure3" />



图
3
Re = 200, A^* = 0.2时受迫振动的升力、阻力系数历时曲线



Figure
3.
Diachronic curve of lift and drag coefficient of forced vibration when Re = 200 and A^* = 0.2



下载:
全尺寸图片
幻灯片


由图3可知, 在不同的无量纲频率下升力、阻力系数历时曲线变化趋势有所不同. 在图3(a)中可以看出升力、阻力系数存在明显的“差拍振动”现象, 数值上波动较大存在周期性. 随着无量纲频率的增加振动进入锁定状态, 此时升力、阻力系数曲线变为规律的正弦周期曲线, “拍”现象消失, 升力、阻力系数的数值要小于静止绕流时的数值. 随着无量纲频率的继续增大, 受迫振动仍处于锁定区间内, 升力、阻力系数的大小随着无量纲频率的增大而增大. 当无量纲频率进一步增大超过锁定区间上限的无量纲频率时, 升力、阻力系数曲线再一次出现“拍”现象, 且由于无量纲频率的增加升力、阻力系数曲线振动更加剧烈, 升力系数幅值也明显增大. 将本文模拟得到的锁定区间范围与Bearman^[26-27]研究给出同工况下锁定区间范围相比, 可以得到基本一致的结果. F = 0.75, 1.15处于锁定区间外, F = 0.85, 1.05处于锁定区间内, 同时证明了本文自编程序和模拟的正确性. 文献[42,45-46]给出关于柱体绕流三维尾迹的Re的范围, 方柱在Re $leqslant $ 300左右, 圆柱Re $ approx $ 180, 而本文选取Re = 200, 并根据以上验证的准确性可知, 文本选取二维是可行的.

2.3
圆角化对静止方柱绕流的影响

图4为静止方柱在不同圆角参数下的阻力系数和升力系数的历时曲线. 从图4中可以看出, 由于圆角的存在, 方柱绕流时阻力系数会有明显的减小, r/D = 0, 1/8, 1/5, 1/4时随着圆角半径的增加, 减阻效果越来越好, 在选取圆角参数为r/D = 1/4时, 减阻效果最佳; r/D = 1/2时较于圆角化方柱r/D = 1/8, 1/5, 1/4, 其阻力系数增加, 减阻效果下降; 同样, 当方柱圆角化r/D = 0, 1/8, 1/5, 1/4时, 其升力系数也有明显的减小, 但随着圆角的增大其减小程度不如阻力系数明显; r/D = 1/2时较于圆角方柱, 其升力系数增加, 减阻效果较差. Tamura等^[4]曾对圆角方柱和尖角方柱的气动特性进行了绕流模拟对比, 其结果显示圆角方柱的气动阻力较尖角方柱明显减小, 与本文模拟结果相符, 从而再次验证了本文模拟结果的正确性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
不同圆角半径下的绕流参数



Figure
4.
Flow parameters under different fillet radii



下载:
全尺寸图片
幻灯片


图5为r/D = 1/4和r/D = 0时的绕流涡量图, 从图5中可以看出当方柱存在圆角时其脱落涡旋之间的间隔变小, 也即涡旋脱落的频率加快, 但其尾部涡旋脱落宽度有所变窄, 涡量在数值上也较小于尖角方柱, 因此阻力减小. 综上所述, 对方柱进行圆角化可以降低阻力而升力降低较小, 故能提高其绕流稳定性.



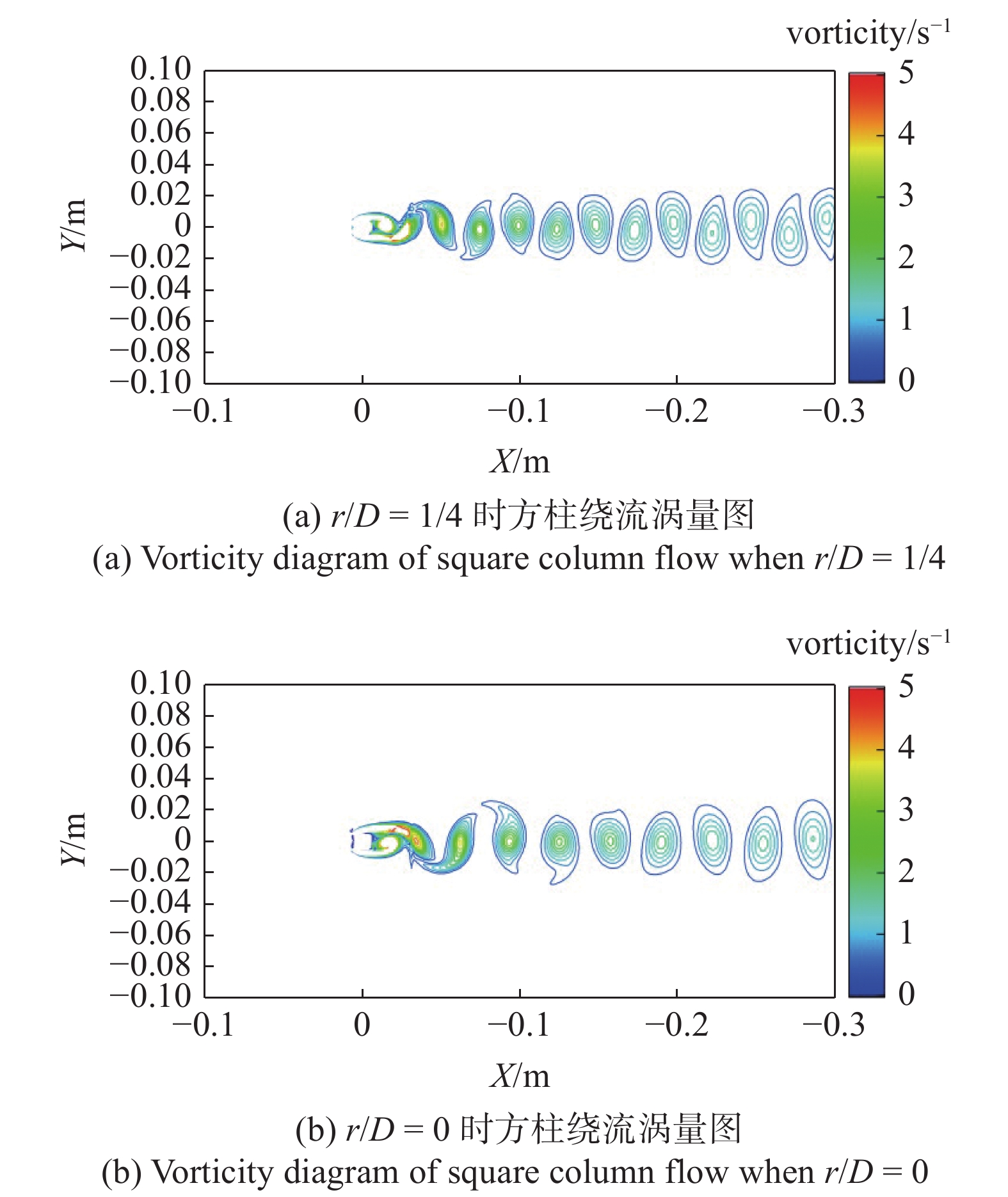onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
方柱绕流涡量图



Figure
5.
Vorticity of the flow around the square column



下载:
全尺寸图片
幻灯片

2.4
圆角化对受迫振动方柱的影响机理分析

通过前文的模拟, 圆角参数为r/D = 1/4的方柱有着较小的升力、阻力系数, 故对方柱进行圆角化可有效减阻. 本节将通过模拟不同圆角参数下的受迫振动方柱, 分析圆角化对受迫振动方柱绕流的影响机理.

2.4.1
圆角化能改变其锁定区间范围

(1)圆角参数r/D = 1/4

在无量纲振幅A^*为0.2和0.4的工况下对不同无量纲频率的受迫振动进行模拟, 观察其升力、阻力系数历时曲线及锁定区间.



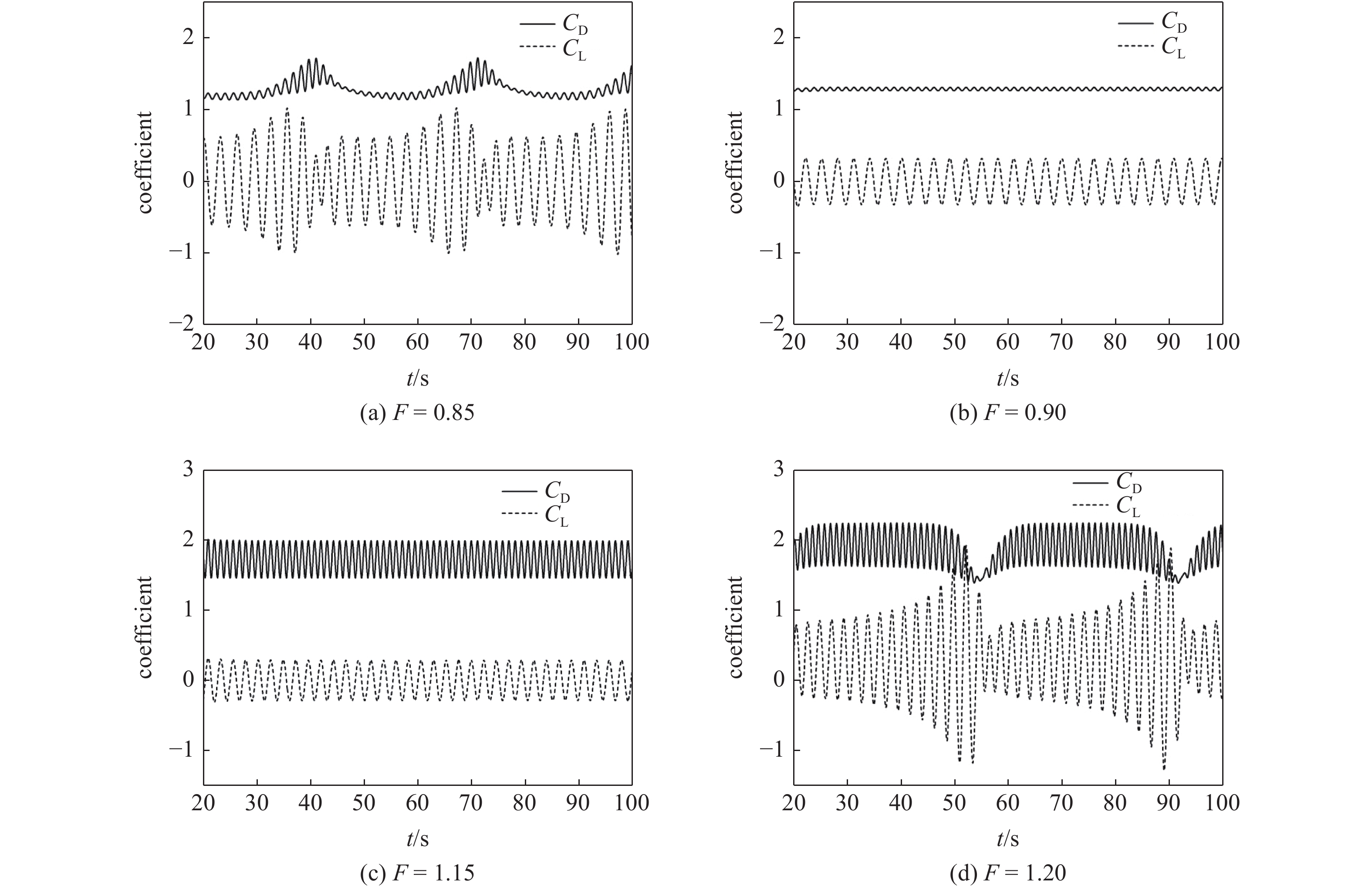onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-6.jpg'"
class="figure_img
figure_type2 ccc " id="Figure6" />



图
6
A^* = 0.2时圆角方柱不同无量纲频率下的升力、阻力系数历时曲线



Figure
6.
Duration curve of the lifting resistance coefficient under different dimensionless frequency of square columns with rounded corners when A^* = 0.2



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />



图
7
A^* = 0.4时圆角方柱不同无量纲频率下的升力、阻力系数历时曲线



Figure
7.
Duration curve of the lifting resistance coefficient under different dimensionless frequency of square columns with rounded corners when A^* = 0.4



下载:
全尺寸图片
幻灯片


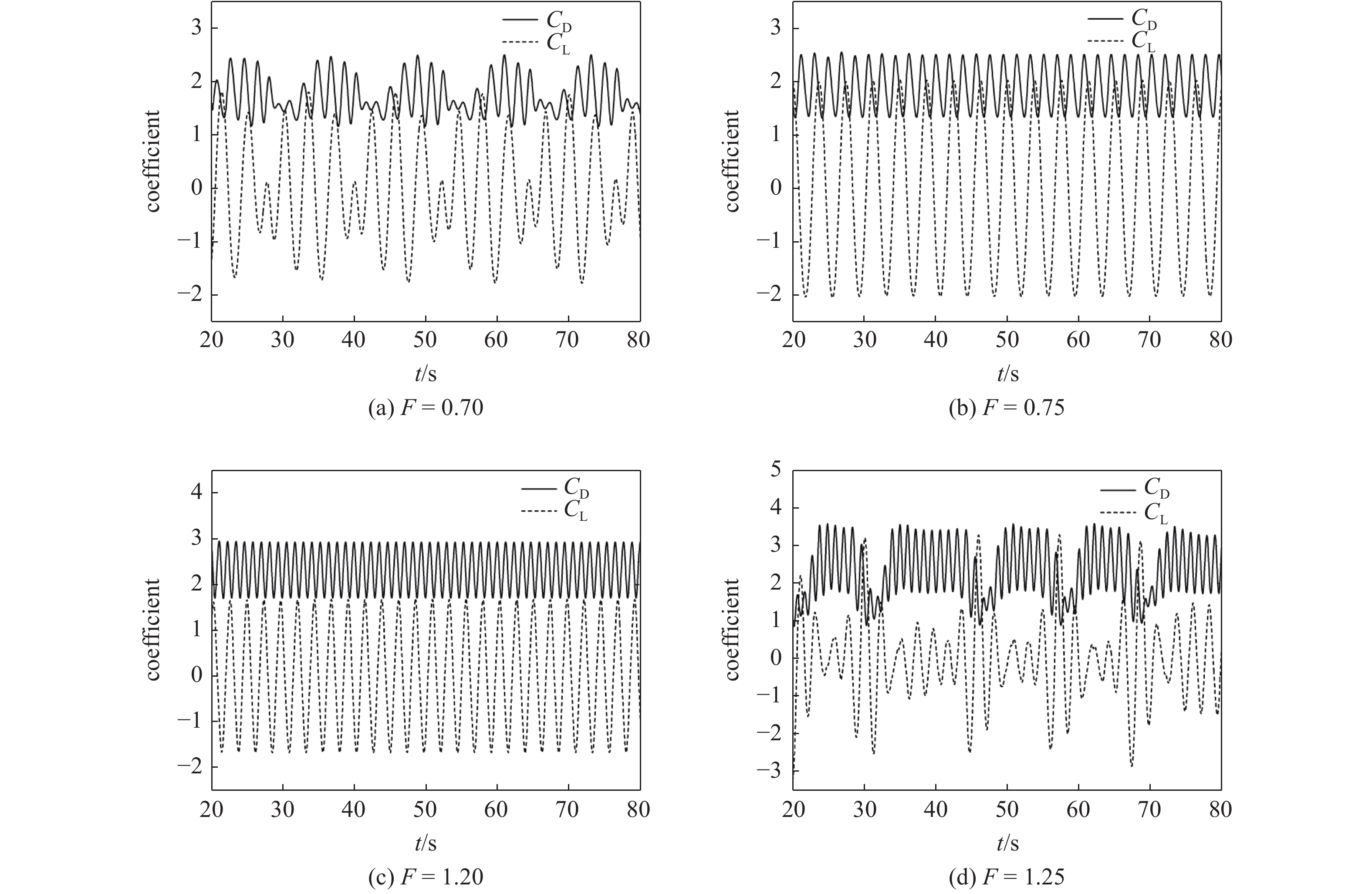
由图6和图7可知, 圆角参数为r/D = 1/4, 在A^* = 0.2工况下, 当F = 0.85时振动为差拍振动, F = 0.9时受迫振动就已经进入锁定区间; 当F = 1.15时仍处于锁定, F = 1.2时又进入了差拍振动状态. 由此可以推断出A^* = 0.2下圆角方柱的受迫振动锁定区间. 同理, 在A^* = 0.4工况下, 当F = 0.75时振动为差拍振动, F = 0.8时受迫振动就已进入锁定区间; 当F = 1.2时处于锁定, F = 1.25时又进入了差拍振动状态. 由以上模拟结果可知, 随着圆角方柱受迫振动振幅的增大, 其锁定区间范围也随之增加. 圆角化方柱同时具有方柱和圆柱的某些性质, 在绕流过程中流场的变化不及尖角圆柱剧烈, 且在振动过程中也不存在由驰振向涡激振动转变的情况, 可提高其振动稳定性^[41-44].

(2)圆角参数r/D = 1/8

同样对无量纲振幅A^*为0.2和0.4的工况下对不同无量纲频率的受迫振动进行模拟.

结合图8和图9可知, r/D = 1/8圆角方柱在A^* = 0.2工况下当F = 0.8时振动为差拍振动, F = 0.85时受迫振动就已经进入锁定区间; 当F = 1.2时处于锁定状态, F = 1.25时又已进入差拍振动状态. 在A^* = 0.4工况下当F = 0.7时振动为差拍振动, F = 0.75时受迫振动已进入锁定区间; 当F = 1.2时处于锁定状态, F = 1.25时又进入了差拍振动状态.



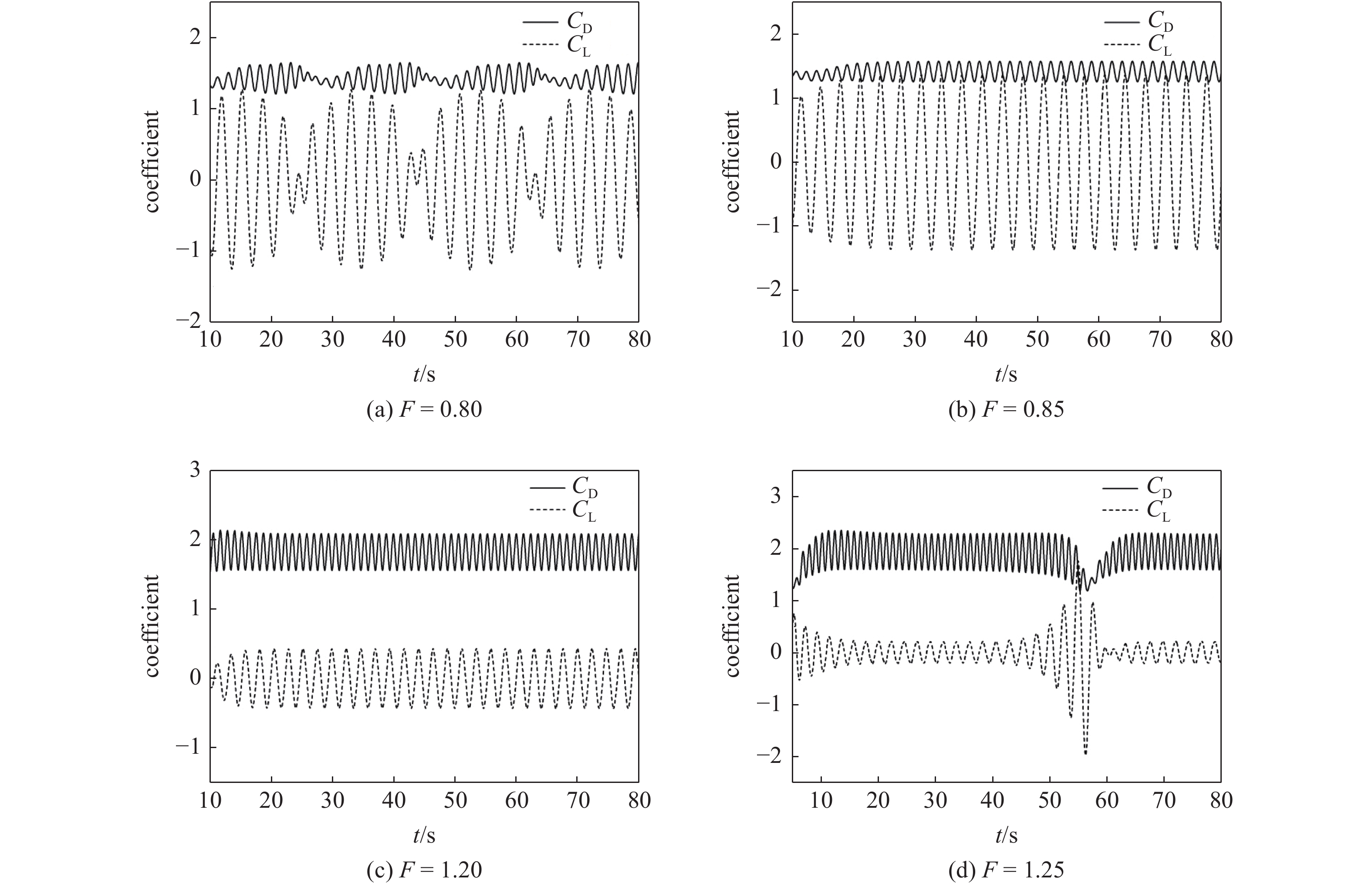onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-8.jpg'"
class="figure_img
figure_type2 ccc " id="Figure8" />



图
8
r/D = 1/8, A^* = 0.2时圆角方柱不同无量纲频率下的升力、阻力系数历时曲线



Figure
8.
Duration curve of lifting resistance coefficient under different dimensionless frequency of rounded square column with r/D = 1/8 and A^* = 0.2



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-9.jpg'"
class="figure_img
figure_type2 ccc " id="Figure9" />



图
9
r/D = 1/8, A^* = 0.4时圆角方柱不同无量纲频率下的升力、阻力系数历时曲线



Figure
9.
Duration curve of lifting resistance coefficient under different dimensionless frequency of rounded square column with r/D = 1/8 and A^* = 0.4



下载:
全尺寸图片
幻灯片


由此可知, r/D = 1/8参数下的圆角方柱其锁定区间范围同r/D = 1/4类似, 随着振幅比的增加而增宽, 一方面说明了圆角方柱流场性质相似, 另一方面相互验证了模拟结果的准确性. 圆角半径越大, 其锁定区间范围越小, 振动稳定性越好.

(3)圆角参数r/D = 0

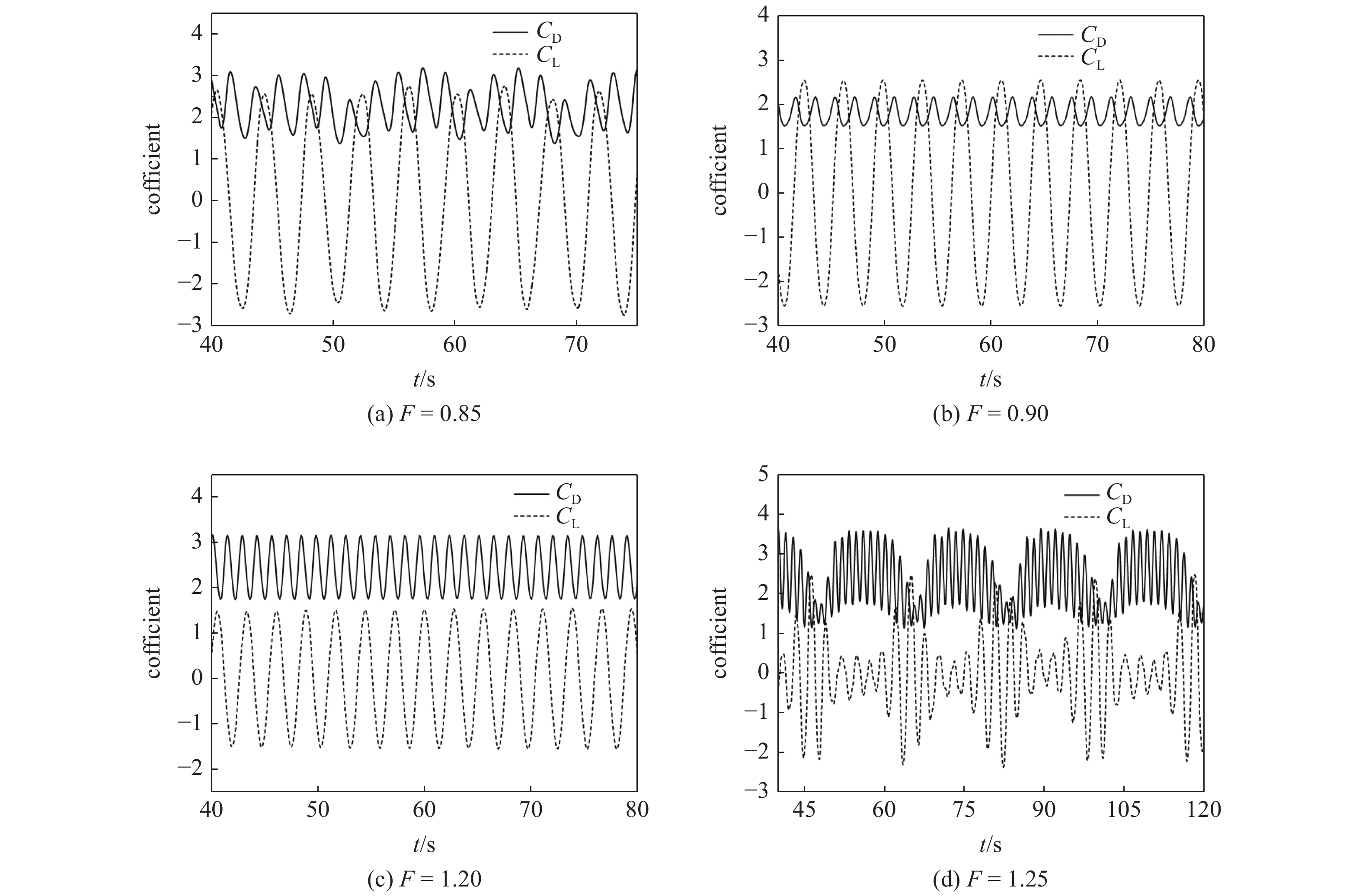
同样对r/D = 0参数下的圆角方柱, 无量纲振幅A^*为0.2和0.4的工况下对不同无量纲频率的受迫振动进行模拟. 当A^* = 0.2时, 在F = 0.8时振动表现为“差拍振动”, 当F = 0.85时就已经进入了锁定状态, 相对于 A^* = 0.4时较为提前; 在F = 1.25时, 仍处于锁定区间内, 锁定区间的下限较A^* = 0.4工况后移. 方柱在A^* = 0.2下的锁定区间长度较A^* = 0.4时宽, 且由图10和图11可知, 各个无量纲频率下的阻力系数均较A^* = 0.4时小. 在锁定区间内, 随着无量纲频率的增加阻力系数也会相应增加. 由前述运动方程可知, 当A较小时, 方柱运动速度也较小, 流场在相同的时间内变化不剧烈, 方柱在流场内受到的阻力也就随之降低. 随着无量纲频率的增加, 方柱运动速度幅值增加, 同时在流场中受到的阻力也增加.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-10.jpg'"
class="figure_img
figure_type2 ccc " id="Figure10" />



图
10
r/D = 0, A^* = 0.2时圆角方柱不同无量纲频率下的升力、阻力系数历时曲线



Figure
10.
Duration curve of lifting resistance coefficient under different dimensionless frequency of rounded square column with r/D = 0 and A^* = 0.2



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-11.jpg'"
class="figure_img
figure_type2 ccc " id="Figure11" />



图
11
r/D = 0, A^* = 0.4时圆角方柱不同无量纲频率下的升力、阻力系数历时曲线



Figure
11.
Duration curve of lifting resistance coefficient under different dimensionless frequency of rounded square column with A^* = 0.4, r/D = 0



下载:
全尺寸图片
幻灯片


当A^* = 0.4时, 在F = 0.85时升力、阻力系数均呈不规则的振动状态, 阻力系数的“差拍振动”现象较升力系数明显. 这是由于方柱振动既受到了给定驱动频率的作用, 又受到了静止方柱自然泻涡频率的影响. 当无量纲频率继续增大到0.9时, 这种现象消失, 升力、阻力系数变为较规则的等幅值振动状态, 当无量纲频率增加到1.25, 升力、阻力系数曲线再次出现拍动现象, 由此可以推断出方柱在A^* = 0.4下的锁定区间. 从图11中还可以看出, 当方柱处在非锁定区间时, 其升力、阻力系数幅值较大, 造成这一现象的原因是方柱前缘后缘都有尖锐的棱边, 其涡旋脱落点是固定的, 会使得本就处于“差拍振动”的流场变得更加复杂. 与Bearman^[26-27]研究的同雷诺数同无量纲振幅下圆柱的锁定区间相比, 方柱的整体锁定区间更偏向于无量纲频率大于1处.

2.4.2
圆角化能改变升力、阻力大小

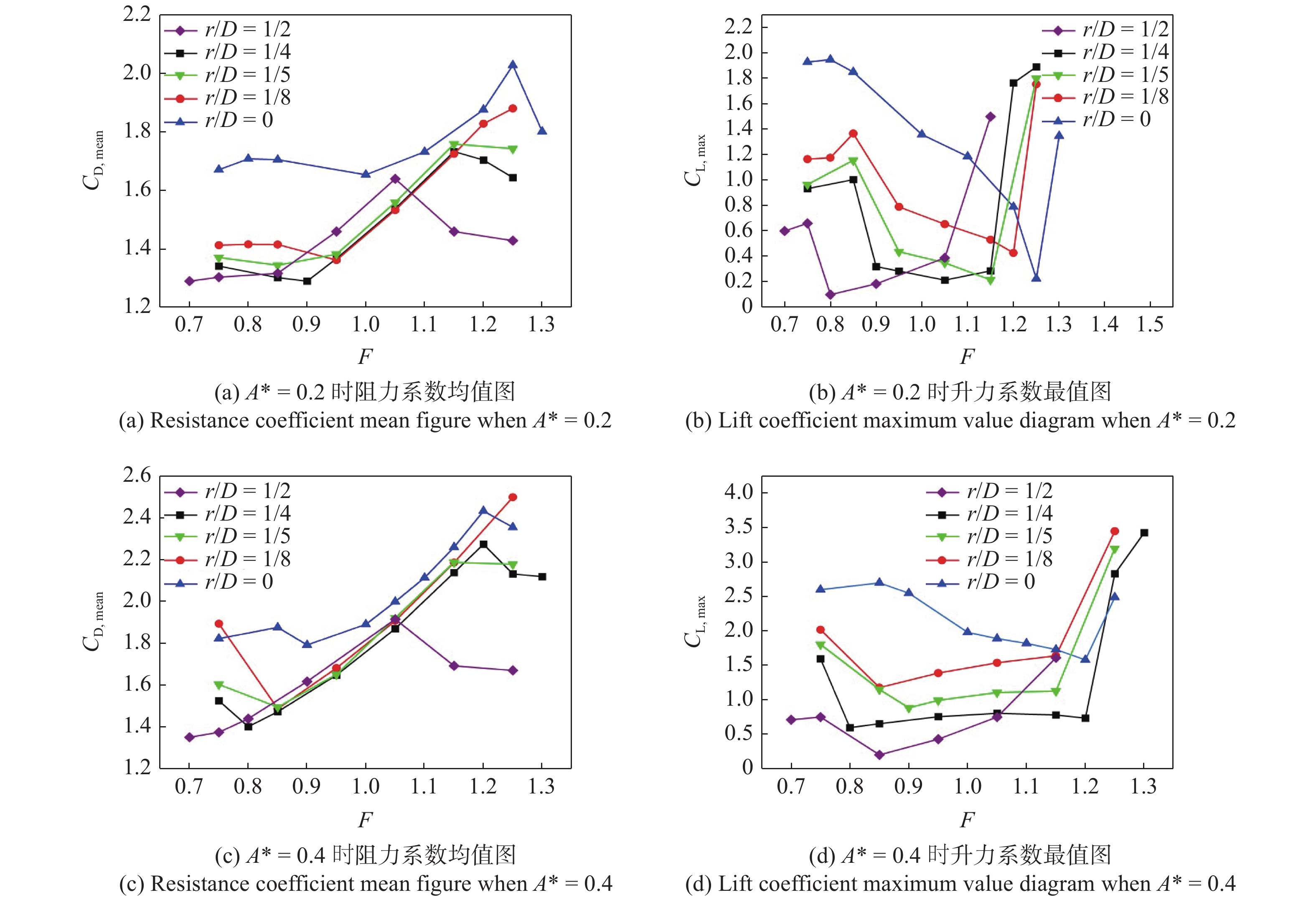
由上所述, 圆角参数为r/D = 1/5时, 其基本性质及无量纲参数变化趋势会与前两种圆角化r/D = 1/4, 1/8方柱相似, 本小节着重对比不同圆角参数下的升力、阻力系数均值及最值的大小.

由图11可知, 在各个对应工况下, 尖角方柱的升力系数和阻力系数均大于圆角方柱的升力、阻力系数. 且随着方柱圆角半径的增加, 升力、阻力系数数值也越来越小, 对方柱进行圆角化被动控制的效果也越加明显.

不同圆角参数下的阻力系数曲线趋势较为一致, 由图11可知尖角与圆角的锁定区间差别较大, 圆角方柱的锁定区间随着振幅比的增加而有所增加, 与圆柱的变化趋势较为一致. 对比图12(a)和图12(c)不同圆角参数下的阻力系数曲线可知, 在锁定区间内阻力系数的数值相差较小, 振幅比的提高使得圆角减阻作用减弱. 另可观察到, 尖角方柱的锁定区间偏向于无量纲频率大于1处, 而经过圆角化后的方柱, 其锁定区间整体左移, 且锁定区间范围有所减小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-12.jpg'"
class="figure_img
figure_type2 ccc " id="Figure12" />



图
12
不同圆角参数下的升力、阻力系数图



Figure
12.
Lifting resistance coefficients under different fillet parameters



下载:
全尺寸图片
幻灯片


在升力系数曲线图12(b)和图12(d)中, 可以明显观察到尖角方柱在锁定区间内其升力系数是逐渐减小的, 而优化过后的圆角方柱随着圆角半径的增大和振幅比的提高, 其升力系数在锁定区间内逐渐增大. 在低振幅比和低圆角半径下, 升力系数值虽呈下降趋势, 但下降斜率不及尖角方柱的大, 升力系数的数值也较小. 由于方柱自身形状的原因, 在其发生振动时会在低无量纲频率下先发生驰振, 驰振振动剧烈, 在横向振动时代表振动剧烈程度的升力系数自然也会较大, 随着无量纲频率的增大, 振动由驰振向涡激振动转变, 升力系数也随之减小. 等到振动完全转变为涡激振动时, 升力系数达到最小值, 在这之后随着无量纲频率的增加, 升力系数又随之变大. 驰振通常发生于带有尖锐棱边的柱体, 例如方柱和三角形柱等, 同样会造成结构体的安全性问题. 本文通过对方柱进行圆角化处理, 可有效减弱驰振的发生. 且通过圆角化的处理, 使方柱的振动性质更接近于圆柱和六边形柱体, 提高了振动的稳定性和安全性^[41].

2.4.3
圆角化能改变尾涡脱落范围

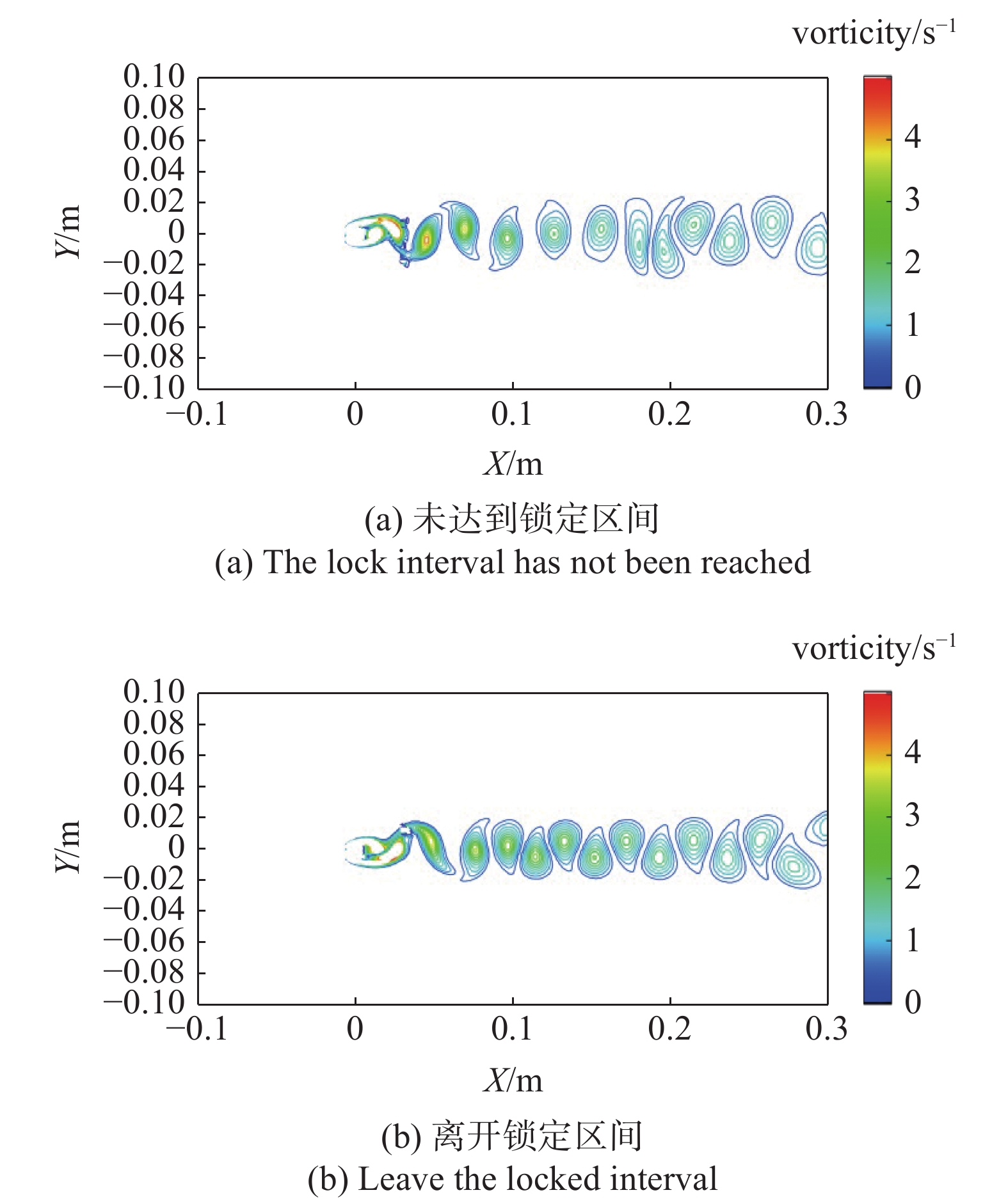
由图13所示, 当方柱静止时尾流处出现卡门涡街, 尾涡模态呈现为经典的2S模态. 当方柱处于受迫振动的锁定区间内时, 尾涡模态与静止方柱相似同为2S, 涡与涡之间的间距受自身振动频率的影响, 频率越大间距越小. 当方柱受迫振动还未进入锁定区间时, 其尾流场较为复杂, 涡旋之间的流向间距变大, 尾涡模态表现为P+S模态. 当方柱受迫振动远离锁定区间时, 随着自振频率的增大涡旋之间的流向间距进一步减小, 而横向间距逐渐拉大, 在下游较远处形成两列涡旋. 而圆柱分别在相同工况下受迫振动时, 尾涡脱落模式始终呈现为2S模态, 其脱落涡旋的间隔与自振频率有关. 由图13还可知, 圆柱的涡旋脱落点并不固定, 方柱的涡旋脱落点固定在后缘棱边处, 方柱涡旋脱落后, 会在方柱后缘处形成较大的负压区, 负压区的出现会使得速度变化剧烈, 这是导致方柱和圆柱受迫振动差别较大的主要原因之一.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-13-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
等值线涡量图



Figure
13.
Contour line vorticity diagram



下载:
全尺寸图片
幻灯片


图14为圆角化受迫振动方柱在A^* = 0.2时的涡量图. 由图14可知, 圆角方柱不论是在进入锁定区间之前还是在离开锁定区间后, 其尾涡脱落模式均为2S, 与同工况下受迫振动圆柱的尾涡脱落模式相似. 尖角方柱未进入锁定区间时, 其脱落模式为P+S且尾迹宽度较大; 在高无量纲频率下, 二者涡旋脱落模式均为2S, 但圆角方柱的尾迹宽度较尖角方柱窄且脱落涡旋之间的间隔较大, 涡旋脱落频率较慢, 负压区有所减小和后移, 流场较为稳定. 由于圆角的存在, 其涡旋脱落点下移至圆角后缘处, 进而使得分离层更易相遇, 减弱了流场的扰动, 因此圆角越大减阻效果越好. 相较之下, 方柱圆角化后尾涡流场情况更接近圆柱. 综上所述, 对方柱进行圆角化可改变方柱在振动时受到的外力, 有效减弱振动时流场的复杂程度及振动剧烈程度, 虽不及圆柱流场稳定, 但仍可大幅提高柱体振动安全性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-066-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
r/D = 1/4时受迫振动方柱尾流涡量图



Figure
14.
Vorticity diagram of forced vibration square column wake when r/D = 1/4



下载:
全尺寸图片
幻灯片

3.
结论

对Ansys Fluent进行二次开发, 并对流场计算域进行区域划分以便利用动网格技术中动态层法实现柱体受迫振动, 从而实现对受迫振动柱体绕流流场的流固耦合模拟. 在Re = 200时, 对均匀流作用下圆角化r/D = 1/2, 1/4, 1/5, 1/8和0受迫振动方柱的绕流进行数值模拟研究, 分析了圆角化受迫振动方柱的升力、阻力系数、尾流涡量和锁定区间的变化规律, 澄清了圆角化对受迫振动方柱稳定性的影响机理. 得到如下主要结论:

(1)与尖角方柱相比, 圆角化方柱的升力、阻力系数更小, 且随着圆角半径的增加, 升力、阻力系数会进一步减小, 不同圆角参数下阻力系数曲线的趋势较为一致; 圆角化方柱振动时的尾涡流场与圆柱相似, 低振幅比下圆角方柱的涡旋脱落模式均为2S模态, 尾流涡旋形状更加规则, 涡旋脱落尾迹更窄, 流场剧烈程度更小; 圆角方柱锁定区间范围有所减小, 且圆角半径越大, 锁定区间越小, 圆角化方柱锁定区间更偏向关于F = 1对称.

(2)更进一步地, 圆角化方柱随着圆角半径的增大和振幅比的提高, 其升力系数在锁定区间内逐渐增大; 圆角化方柱可有效减弱方柱振动时的驰振效应, 使方柱的振动与圆柱的振动相似, 大大提高柱体振动时的安全稳定性.

本文通过二维数值计算, 在低雷诺数Re = 200下, 对不同圆角化方柱进行研究分析, 为研究柱体二维向三维流动转变对应的临界雷诺数提供一定参考. 应用本文方法可进行多体模型以及多自由度的模拟. 对于工程实际如海底电缆等低流速下的安全稳定性具有一定参考意义. 由于实际工程中雷诺数往往较高, 故可把雷诺数增大, 采用合适的湍流模型, 对不同截面柱体的受迫振动进一步研究分析. 本文中数值计算的柱体受迫振动均是在垂直于来流的横向进行的, 而在实际工程领域, 柱体不仅在横向有运动, 同时在来流方向也会有运动, 因此进行多自由度的受迫振动研究更具有工程实际意义.