引言

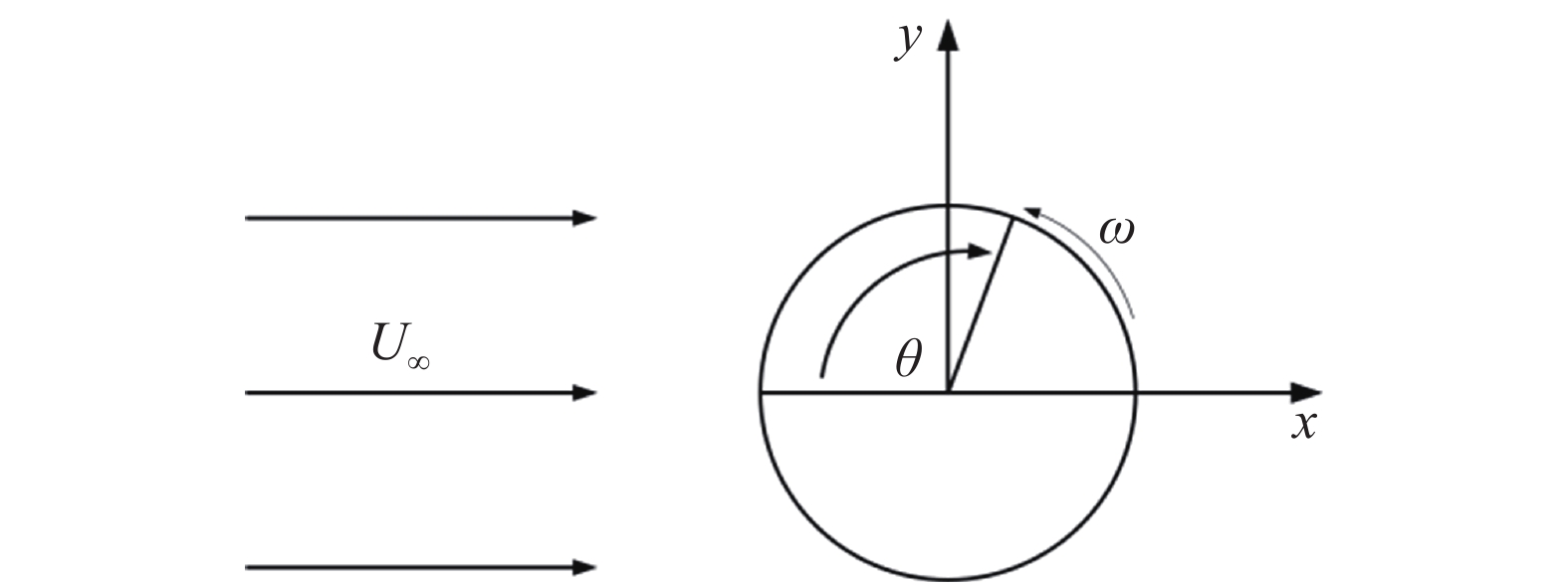
旋转导弹在飞行过程中由于攻角α的存在, 此时流经弹体的横流速度为V_∞sinα, 由于导弹的旋转从而产生了马格努斯力. 因此, 旋转导弹马格努斯力的产生从流动机理上分析是旋转圆柱绕流问题. 由于导弹飞行速度高, 致使横流速度高. 所以, 研究高雷诺数、低转速比条件下的旋转圆柱绕流问题对深入分析旋转导弹马格努斯力的机理有着重要意义.

为了系统地研究圆柱尾迹层流向湍流的转变, 人们进行了大量的实验和数值研究^[1-9]. 当圆柱体绕轴旋转时, 由于马格努斯效应, 会使圆柱后方产生非对称尾流. 雷诺数和相对转速的变化都会对旋转圆柱的尾流产生影响^[10-13]. 研究发现, 当相对转速α < 2时, 旋转圆柱尾迹的脱落涡街与卡门涡街相似^[14-15]. 当相对转速α > 2时, 旋转圆柱后方的脱落涡被抑制^[16-17]. Lam^[5]利用粒子图像测速法对雷诺数Re = 3600 ~ 5000的旋转圆柱进行了实验测量. 结果表明, 随着圆柱转速的增加, 尾迹变窄并向一侧偏转. Aljure等^[18]采用直接数值模拟的方法对雷诺数为5000时不同相对转速下的旋转圆柱绕流进行了数值模拟, 得出了涡旋停止脱落的相对转速, 分析了相对转速变化对驻点和分离点的影响. Ray和Ezadi等^[19-20]对雷诺数为5000到11800的旋转圆柱绕流进行了数值计算和实验分析, 总结出了升力系数和阻力系数的变化规律, 分析了旋转圆柱后方的流场特征. 何颖等^[21-22]采用大涡模拟方法对高雷诺数下旋转圆柱绕流问题进行了数值模拟, 分析了旋转对圆柱绕流分流流动的控制.

目前对于旋转圆柱在高雷诺数、低转速比条件下的实验研究相对较少, 此外关于旋转圆柱后方流场速度变化的研究也相对较少. 因此本文对雷诺数Re = 20000 ~ 90000、相对转速(ɑ = ωD/(2U_∞)) ɑ = 0 ~ 0.72的旋转圆柱后方流场进行了实验测量, 分析了旋转圆柱后方不同剖面处的速度分布规律和湍流度分布规律. 采用大涡模拟方法对旋转圆柱绕流问题进行数值模拟, 分析流场变化规律. 而后建立理论模型, 分析后方涡位置的改变对圆柱升力和尾流区自由剪切层的影响.

1.
实验装置与测量技术

1.1
风洞装置

实验在南京理工大学HG-1风洞中进行, 该风洞为开口环流式风洞. 风洞实验段截面积为700 mm × 700 mm、长1.1 m、速度范围为0.1 ~ 40 m/s, 湍流度0.97%.

1.2
热线风速仪

采用Dantec StreamLine Pro型热线风速仪对旋转圆柱后方流场进行测量. 热线探头由一根1.25 mm长、5 μm直径的镀金钨丝焊接于两根不锈钢针尖构成的支架上, 并接入电路中. 热线风速仪的采样频率为5 kHz, 采样时间设定为2 s, 每一组实验之前对热线风速仪进行标定.

1.3
移测坐标架控制系统

实验采用的是奈凯移测坐标架系统, 该系统由精密丝杆传动器、步进电机、步进电机驱动器、驱动控制板、计算机和控制软件组成. 奈凯移测坐标架移测距离为600 mm × 600 mm × 600 mm, 移测精度为0.02 mm, 通过软件控制该坐标架可以实现定步长运动.

1.4
圆柱旋转机构

通过电机驱动圆柱旋转, 通过遥控器控制电子调速器进而控制圆柱的旋转速度. 圆柱的直径D = 50 mm、长度L = 700 mm.

1.5
流场测量方法

如图1所示, 将热线风速仪固定在移测坐标架的支壁上, 通过软件控制移测坐标架的移动, 从而对旋转圆柱的后方流场进行准确的测量. 热线风速仪分别对旋转圆柱后方四处截面的速度进行测量, 每个截面到圆柱轴心的距离分别为1D, 1.5D, 2D和3D.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
实验装置图



Figure
1.
Experimental device



下载:
全尺寸图片
幻灯片


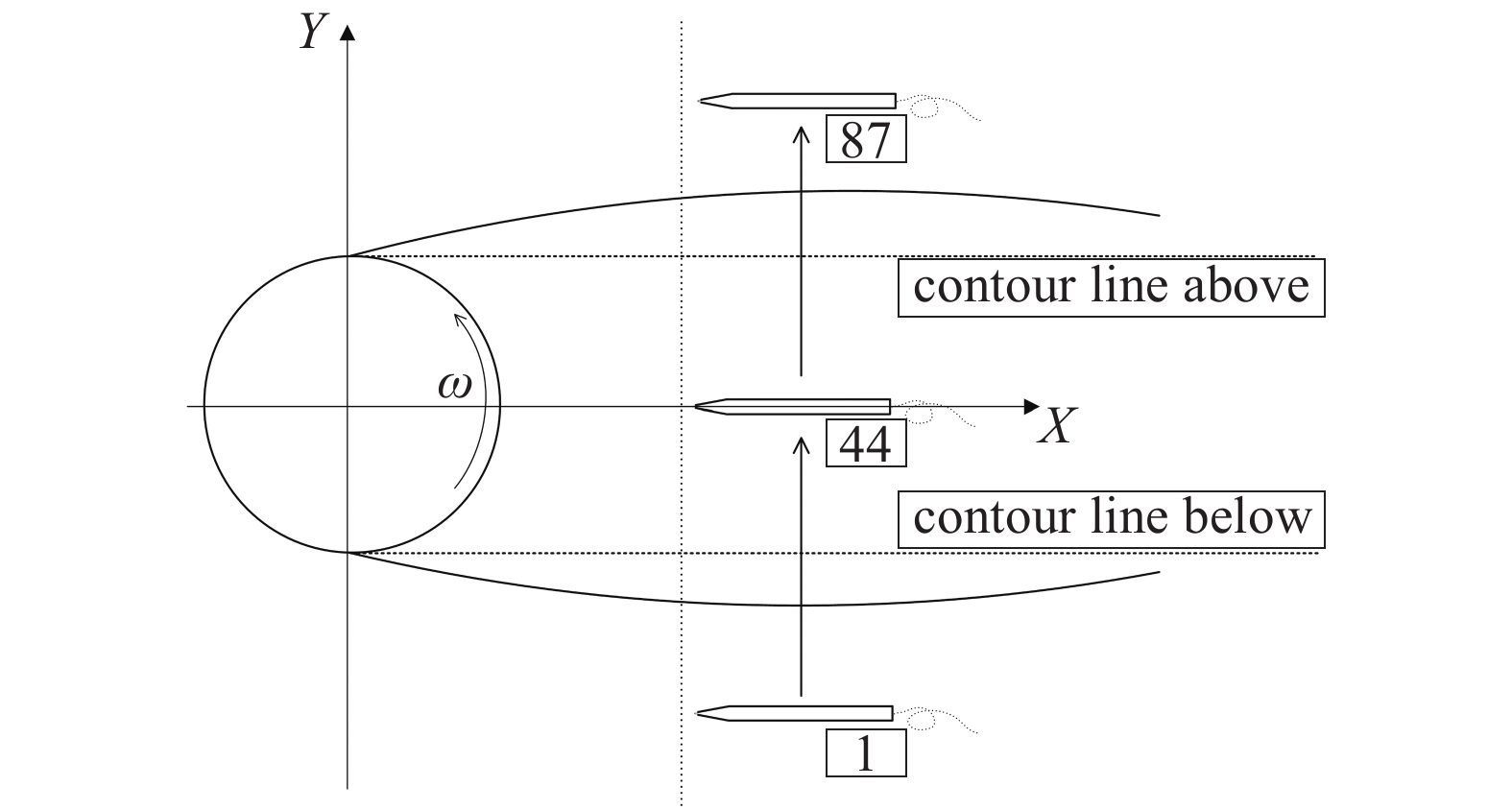
如图2所示, 以圆柱轴线为中心向上、下共选取87个测量点, 每两个测量点之间的距离为2.5 mm. 为了保证测量的准确性, 在每一组实验之前对热线风速仪进行标定, 并对表1中的工况进行了实验测量.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
旋转圆柱测量示意图



Figure
2.
Schematic diagram of measuring a rotating cylinder



下载:
全尺寸图片
幻灯片





表
1
实验工况



Table
1.
Experiment cases



table_type2 ">

α	ω/(rad·s?1)
	Re	20000	30000	40000	50000	60000	70000	80000	90000
	v/(m·s?1)	6	9	12	15	18	21	24	27
0.2		?	?	96	120	144	168	192	216
0.4		96	144	192	240	288	?	?	?
0.72		1650	?	?	?	?	?	?	?

下载:
导出CSV
|显示表格

2.
实验结果分析

2.1
时均速度

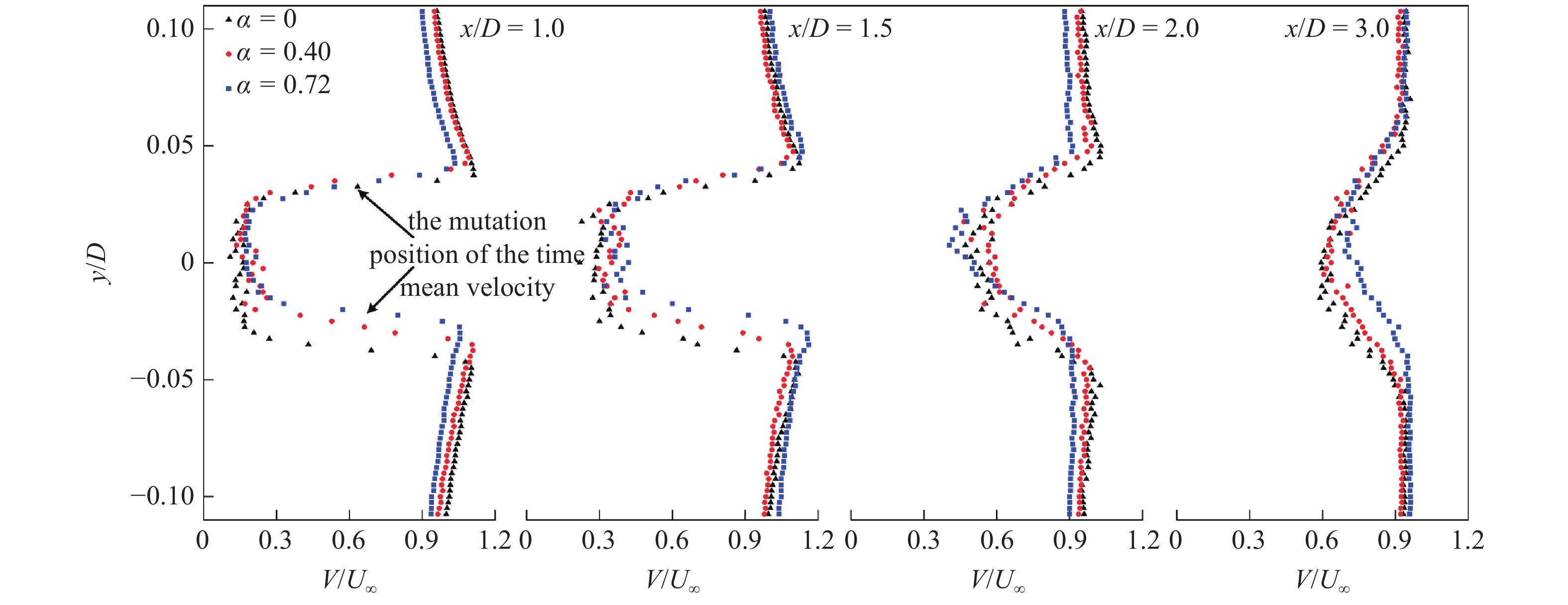
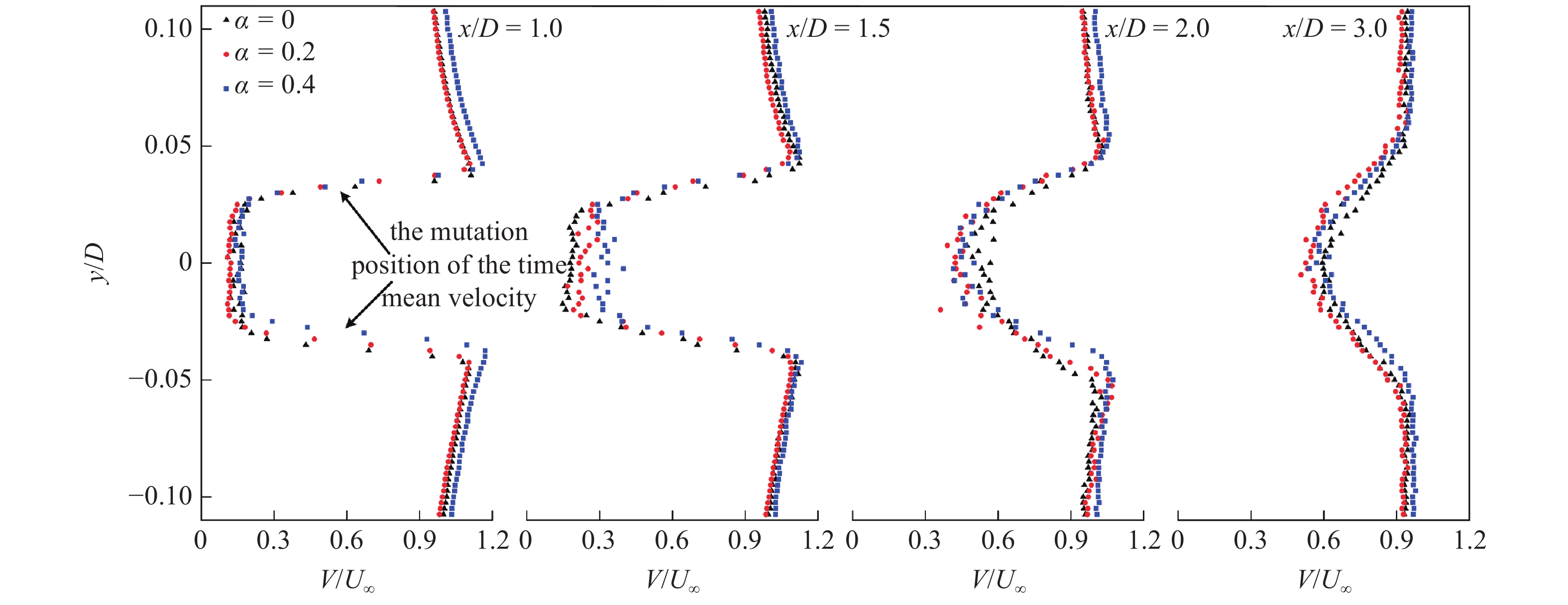
图3和图4给出了雷诺数为20000和60000时旋转圆柱后方4个剖面处无量纲时均速度分布. 当雷诺数一定时, 旋转对圆柱的尾流区产生了一定的影响, 致使尾流向一侧偏离. 旋转圆柱尾迹区域下方速度突变处的位置随着相对转速的增加而上移, 而旋转圆柱尾迹区域上方速度突变处的位置随着相对转速的增加并未发生太大变化. 例如: 当Re = 20000, x/D = 1时, 随着相对转速由0增大到0.4、再增大到0.72, 其时均速度突变位置分别上移了0.25D和0.11D. 时均速度的测量是圆柱后方多个周期涡脱落的时均结果, 速度突变位置的变化说明了后方涡时均位置的改变. 对于不旋转的圆柱, 其后方涡在Y方向上的时均位置是对称的. 旋转圆柱尾迹区域下方速度突变处位置的上移说明圆柱的旋转导致了尾迹区域下方涡的上移. 而上方速度突变处位置几乎不变说明上方涡的位置并未发生太大的变化. 图5和图6给出了ɑ = 0.2和ɑ = 0.4时旋转圆柱后方4个剖面无量纲时均速度分布, 随着雷诺数的增加, 旋转圆柱尾迹区域下方速度突变处位置有小幅度的下移(在ɑ = 0.2, x/D = 1.5处, 随着雷诺数的增加, 其时均速度突变位置分别下移0.05D和0.05D), 旋转圆柱尾迹区域上方速度突变处位置变化不明显. 雷诺数增加对尾迹区域的影响随着x/D的增加表现得越来越明显.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-3.jpg'"
class="figure_img
figure_type2 ccc " id="Figure3" />



图
3
Re = 20000时旋转圆柱后方4个剖面无量纲时均速度分布



Figure
3.
Dimensionless time averaged velocity distribution of four sections behind the rotating cylinder when Re = 20000



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-4.jpg'"
class="figure_img
figure_type2 ccc " id="Figure4" />



图
4
Re = 60000时旋转圆柱后方4个剖面无量纲时均速度分布



Figure
4.
Dimensionless time averaged velocity distribution of four sections behind the rotating cylinder when Re = 60000



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-5.jpg'"
class="figure_img
figure_type2 ccc " id="Figure5" />



图
5
ɑ = 0.2时旋转圆柱后方4个剖面无量纲时均速度分布



Figure
5.
Dimensionless time averaged velocity distribution of four sections behind the rotating cylinder when ɑ = 0.2



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-6.jpg'"
class="figure_img
figure_type2 ccc " id="Figure6" />



图
6
ɑ = 0.4时旋转圆柱后方4个剖面无量纲时均速度分布



Figure
6.
Dimensionless time averaged velocity distribution of four sections behind the rotating cylinder when ɑ = 0.4



下载:
全尺寸图片
幻灯片

2.2
湍流强度

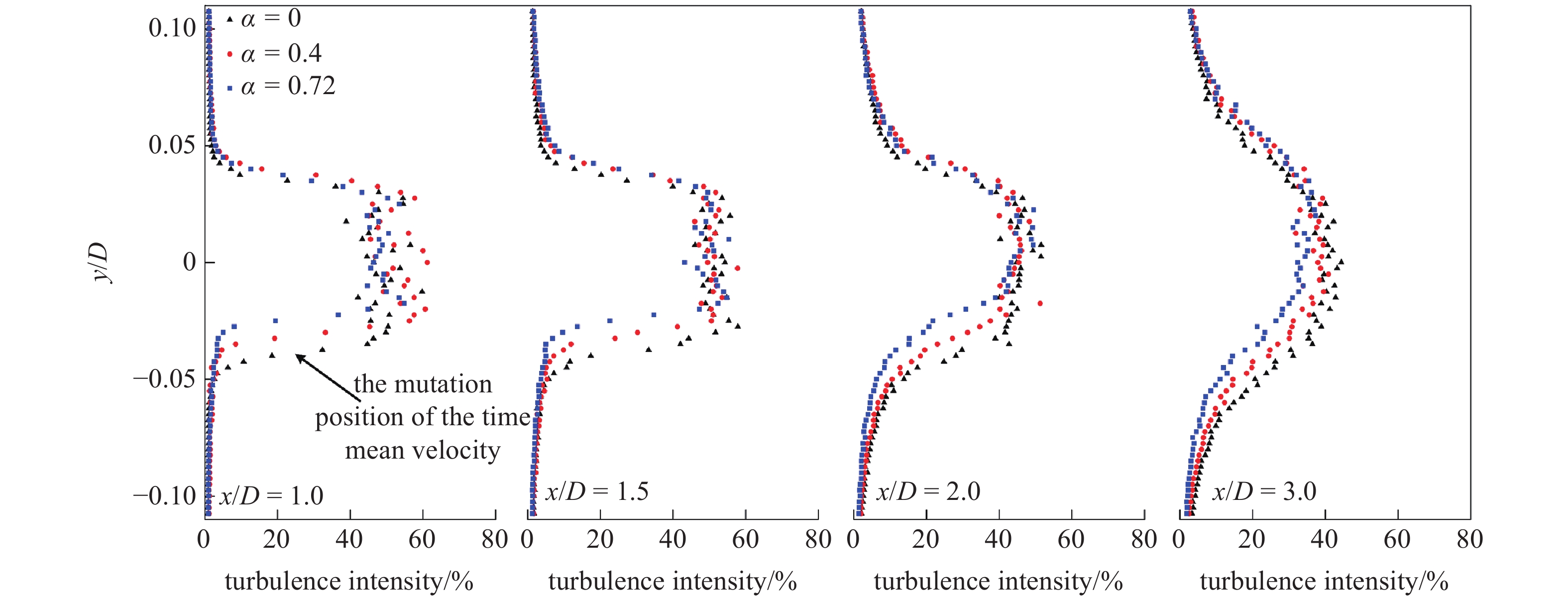
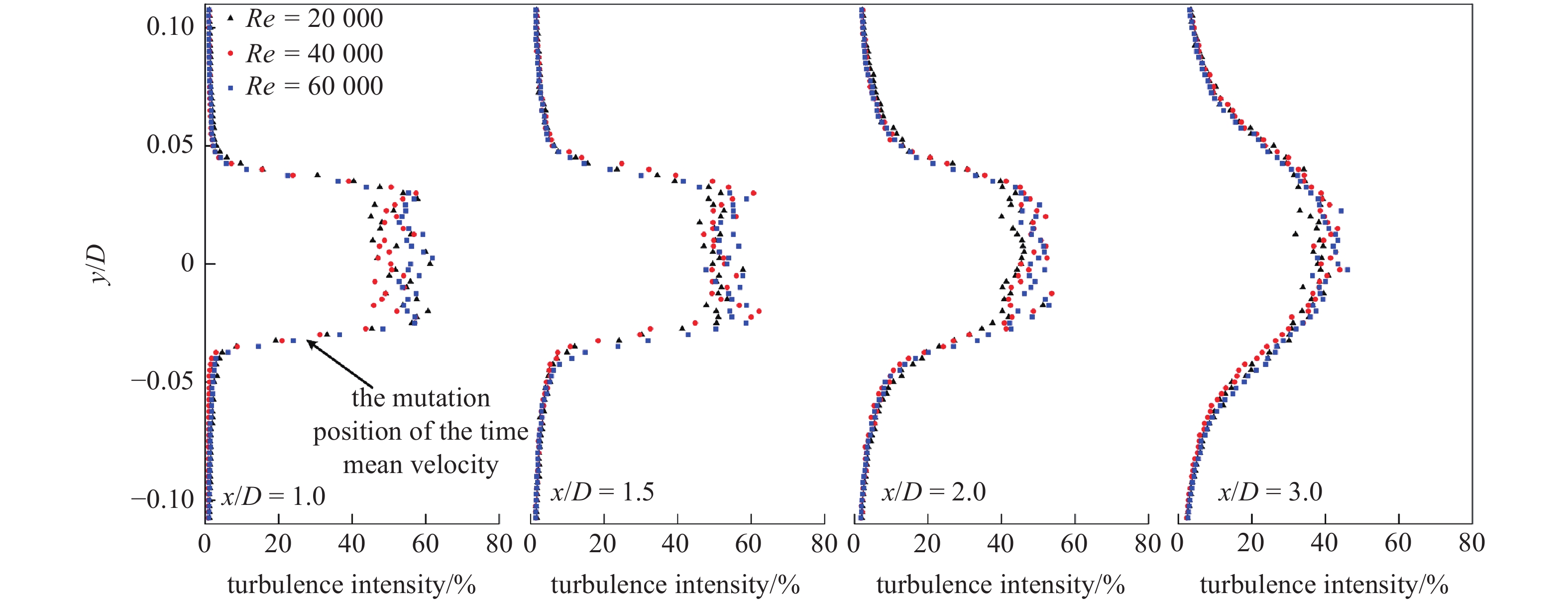
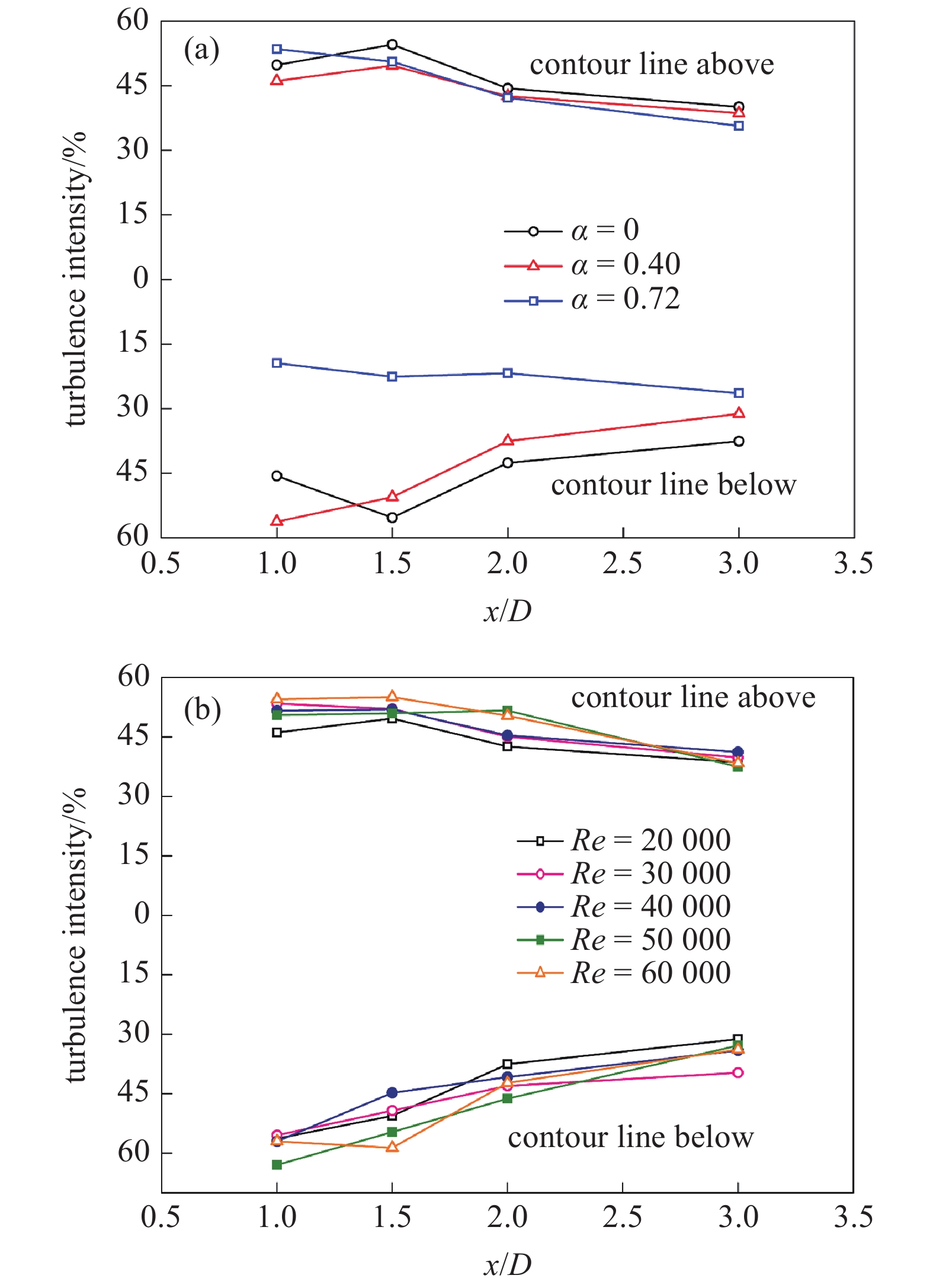
图7和图8给出了不同雷诺数、不同相对转速下圆柱后方4个剖面上湍流度的分布. 与速度分布相似, 圆柱尾流区下方湍流强度突变点随着相对转速的增加而上移, 尾流区上方湍流强度突变点随着相对转速的增加变化很小. 随着雷诺数的增加, 旋转圆柱尾迹区域下方湍流度突变处位置有小幅度的下移, 旋转圆柱尾迹区域上方湍流度突变处位置变化较小. 图9给出了不同工况下圆柱后方上、下轮廓线湍流强度分布(上、下轮廓线位置如图2所示), 相对转速的增加致使下轮廓线的湍流强度减小, 而对上轮廓线的影响不大. 从图9(b)中也可以看出, 由于圆柱的旋转, 下轮廓线湍流强度随x/D增加的减小速度要大于上轮廓线. 这说明圆柱的旋转对圆柱后方流场下侧的影响较大, 而对上侧影响相对较小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />



图
7
Re = 20000时旋转圆柱后方4个剖面湍流强度



Figure
7.
Turbulence intensity distribution of four sections behind the rotating cylinder when Re = 20000



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-8.jpg'"
class="figure_img
figure_type2 ccc " id="Figure8" />



图
8
ɑ = 0.4时旋转圆柱后方4个剖面湍流强度



Figure
8.
Turbulence intensity distribution of four sections behind the rotating cylinder when ɑ = 0.4



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
(a) Re = 20000和(b) ɑ = 0.4时旋转圆柱后方上、下轮廓线湍流强度分布



Figure
9.
Turbulence intensity distribution of upper and lower contour behind the rotating cylinder when (a) Re = 20000 and (b) ɑ = 0.4



下载:
全尺寸图片
幻灯片

3.
数值模拟

3.1
控制方程

采用大涡模拟方法求解物理空间盒式滤波形式的三维纳维?斯托克斯方程

$$frac{{partial {{bar u}_i}}}{{partial t}} + {bar u_j}frac{{partial {{bar u}_i}}}{{partial {x_j}}} = - frac{1}{ ho }frac{{partial bar p}}{{partial {x_i}}} + nu frac{{{partial ^2}{{bar u}_i}}}{{partial {x_i}partial {x_j}}} - frac{1}{ ho }frac{{partial tau _{ij}^{{ m{sgs}}}}}{{partial {x_j}}}$$

(1)

$$frac{{partial {{bar u}_i}}}{{partial {x_i}}} = 0qquadquadquadqquadqquadqquadqquadqquad$$

(2)

式中$tau _{ij}^{{
m{sgs}}}$ 为亚格子应力

$$tau _{ij}^{{ m{sgs}}} = ho {bar u_i}{bar u_j} - ho {u_i}{u_j}$$

(3)

3.2
网格划分与边界条件

选取来流方向沿x轴正向, 圆柱直径为D, 如图10所示. 计算区域的长为50D、宽为40D, 圆柱中心与上、下边界的距离为20D, 与左、右边界的距离分别为20D和30D. 圆柱长度为πD. 圆柱的旋转是通过滑移网格区域的网格运动实现的, 如图11所示. 滑移网格技术是将整个计算域分为两个或多个单元区域. 在计算过程中, 单元区域沿着网格分界面相互滑动, 而各自区域的网格不会发生变化, 区域边界之间进行数据交换. 圆柱的旋转区域采用旋转坐标系方法, 壁面第一层网格高度由y⁺ ~ 1确定, 近壁面网格增长率为1.02. 进口边界条件为速度入口, 出口边界条件为压力出口, 圆柱壁面为无滑移条件, 展向设为周期边界条件. 通过对网格进行独立性验证, 最终选择的网格数量为1340万. 计算时间步长由$C = dfrac{{{U_{max }} Delta t}}{{Delta {x_{min }}}}$确定, 最终选择时间 步长为5 × 10^?5 s, 每一次步长内迭代60次. 空间离散采用通量差分分裂格式, 时间推进方法采用双时间步隐式迭代推进方法.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
流动示意图



Figure
10.
Schematic diagram



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
网格示意图



Figure
11.
Grid diagram



下载:
全尺寸图片
幻灯片

3.3
数值计算验证

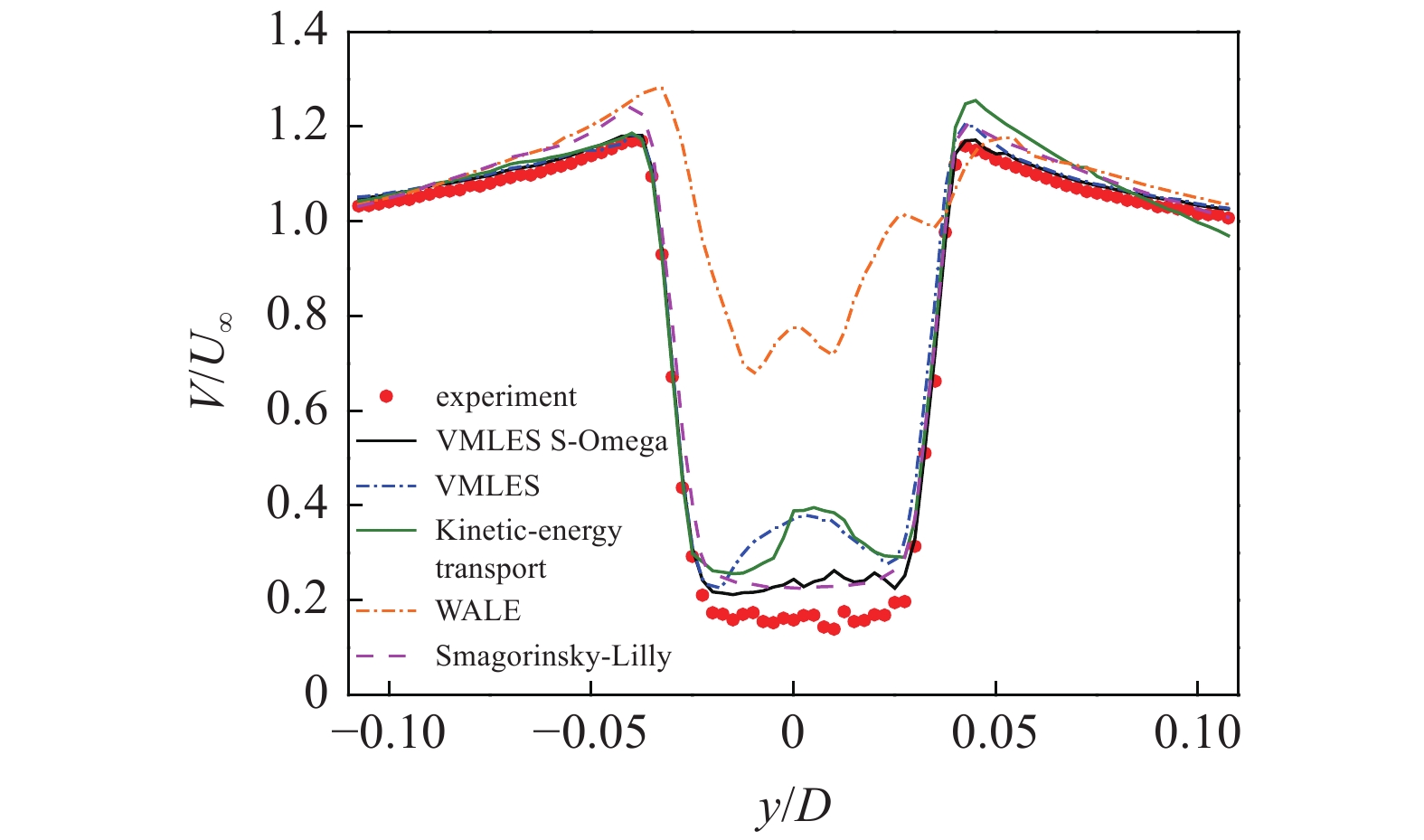
图12是雷诺数Re = 60000, x/D = 1时不同亚格子模型计算结果对比图, 通过将不同亚格子模型得到的计算结果与实验值进行对比得出, 采用VWLES S-Omega模型和Smagorinsky-Lilly模型的计算结果与实验值最为接近, 虽然在最小速度值方面数值模拟得到的结果要高于实验值, 但是其变化趋势完全吻合. 图13为雷诺数Re = 60000, x/D = 3时VWLES S-Omega和Smagorinsky-Lilly模型的计算结果, 两者与实验值均吻合较好. 相比之下, VWLES S-Omega模型的计算结果更为精确, 因此在后续的数值模拟中均采用VWLES S-Omega亚格子模型进行计算.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
Re = 60000, x/D = 1时不同亚格子模型计算结果对比图



Figure
12.
Calculation results of different subgrid model when Re = 60000 and x/D = 1



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
Re = 60000, x/D = 3时两种亚格子模型计算结果对比图



Figure
13.
Calculation results of different subgrid model when Re = 60000 and x/D = 3



下载:
全尺寸图片
幻灯片

3.4
数值计算分析

3.4.1
旋转对圆柱流场特性的影响

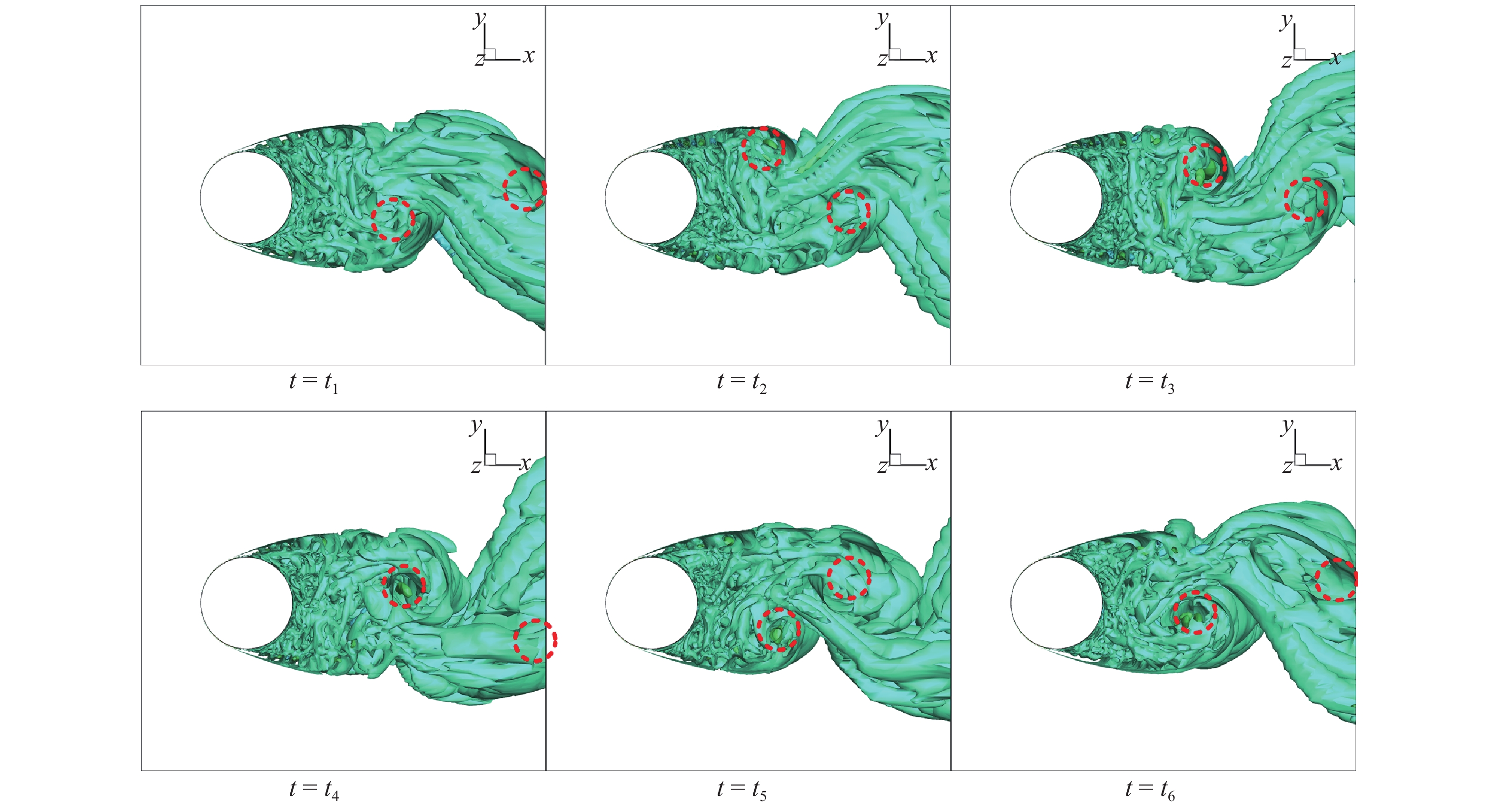
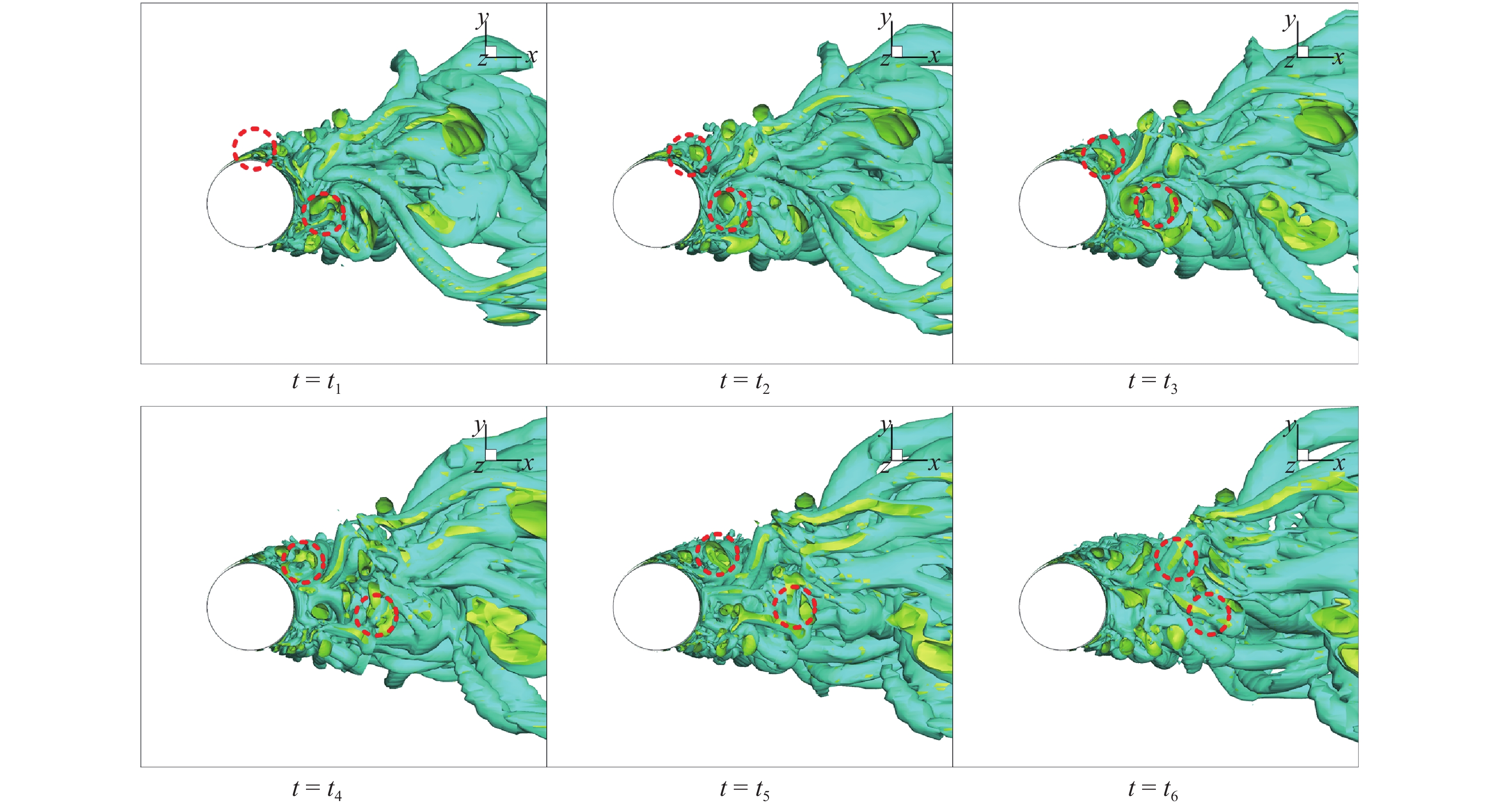
图14和图15为Re = 20000, ɑ = 0和 ɑ = 0.72时圆柱后方三维涡量图, 给出了不同转速下涡的发展和自由剪切层的差异. 当圆柱不旋转时, 圆柱后方的涡脱落位置是上、下对称的, 上下的涡交替生成. 但是当圆柱旋转之后, 圆柱后方下侧涡的位置明显上移, 且幅度较大. 在下方涡的挤压下, 上方涡的位置有小幅度的上移. 不旋转的圆柱其自由剪切层上下对称, 但当圆柱旋转后, 下方的自由剪切层有明显的上移, 上方的自由剪切层位置变化较小. 图16和图17为Re = 20000, ɑ = 0和ɑ = 0.78时圆柱后方烟流图. 与数值模拟结果相同, 旋转后的圆柱下方自由剪切层的位置明显上移. 图14 ~ 图17的结果说明, 圆柱旋转后下方自由剪切层的上移导致了圆柱后方流场下侧速度突变位置的上移. 圆柱后方流场上侧速度突变位置基本不变也是因为圆柱后侧上方自由剪切层位置变化不大.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-14.jpg'"
class="figure_img
figure_type2 ccc " id="Figure14" />



图
14
Re = 20000, ɑ = 0时圆柱后方涡量图



Figure
14.
Vorticity diagram behind cylinder at Re = 20000, ɑ = 0



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-15.jpg'"
class="figure_img
figure_type2 ccc " id="Figure15" />



图
15
Re = 20000, ɑ = 0.72时圆柱后方涡量图



Figure
15.
Vorticity diagram behind cylinder at Re = 20000, ɑ = 0.72



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-16.jpg'"
class="figure_img
figure_type2 ccc " id="Figure16" />



图
16
Re = 20000, ɑ = 0时圆柱后方烟流图



Figure
16.
Smoke plume behind cylinder at Re = 20000, ɑ = 0



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-17.jpg'"
class="figure_img
figure_type1 bbb " id="Figure17" />



图
17
Re = 20000, ɑ = 0.78时圆柱后方烟流图



Figure
17.
Smoke plume behind cylinder at Re = 20000, ɑ = 0.78



下载:
全尺寸图片
幻灯片


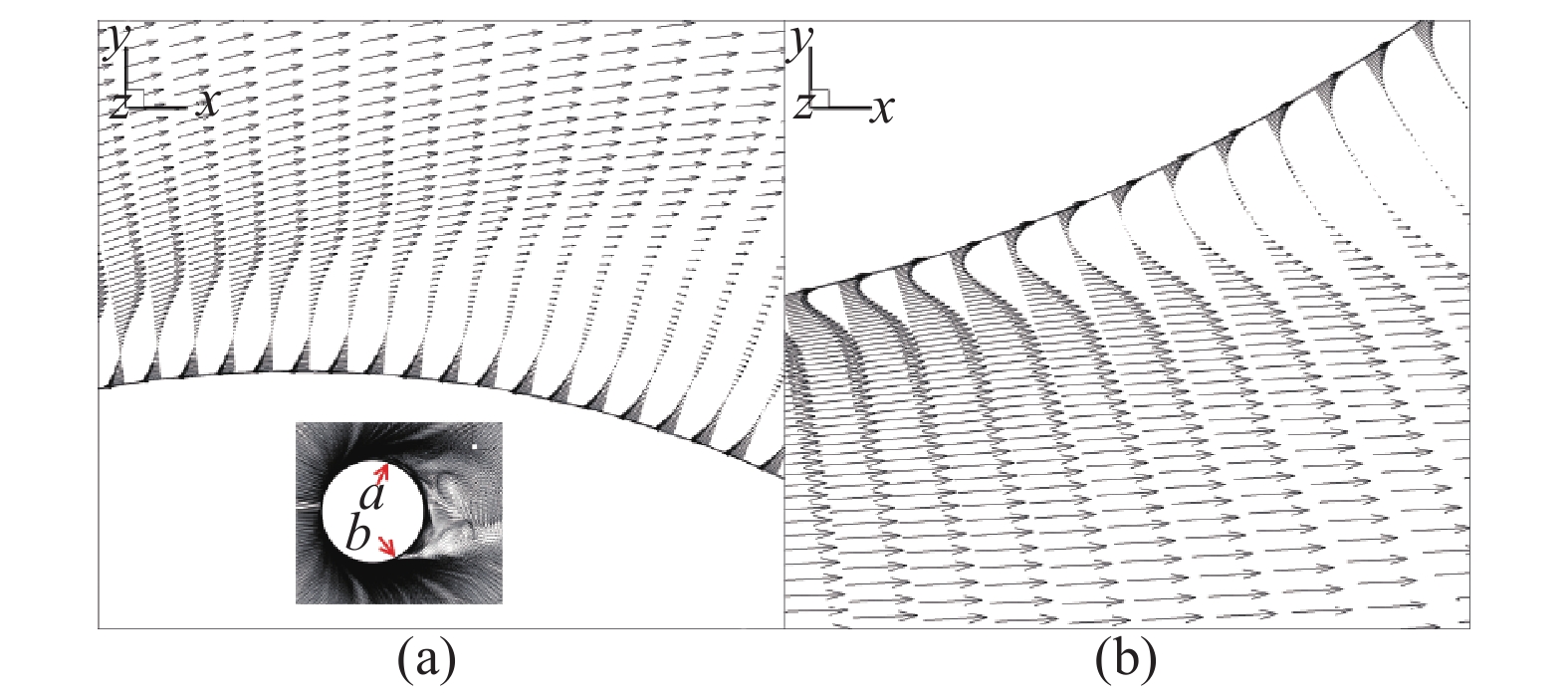
图18为Re = 20000, ɑ = 0.72时圆柱周围速度矢量图, 上、下表面附近的流场流动有所不同. 由于圆柱的旋转, 圆柱下表面的运动方向与主流方向相同, 甚至下表面的运动速度要大于主流的运动速度. 因此, 圆柱下表面会带动周围的流体向右上方移动, 这导致了圆柱后方下侧涡位置和自由剪切层的上移.

圆柱上表面的运动方向与主流方向相反, 这就使得上表面附近的流体运动方向与主流相反. 但是上表面并没有像下表面一样对尾迹区产生严重的影响. 这是因为当雷诺数较高而相对转速较低时, 上表面带动附近流体向着与主流相反方向运动的现象被较大的主流速度所覆盖. 但是下表面则不同, 它带动着流体顺着主流方向运动, 最终由于逆压梯度的作用导致流体无法继续随壁面运动而产生分离涡, 这就使得下表面的分离涡上移, 也导致了自由剪切层的上移.

3.4.2
雷诺数对圆柱流场特性的影响

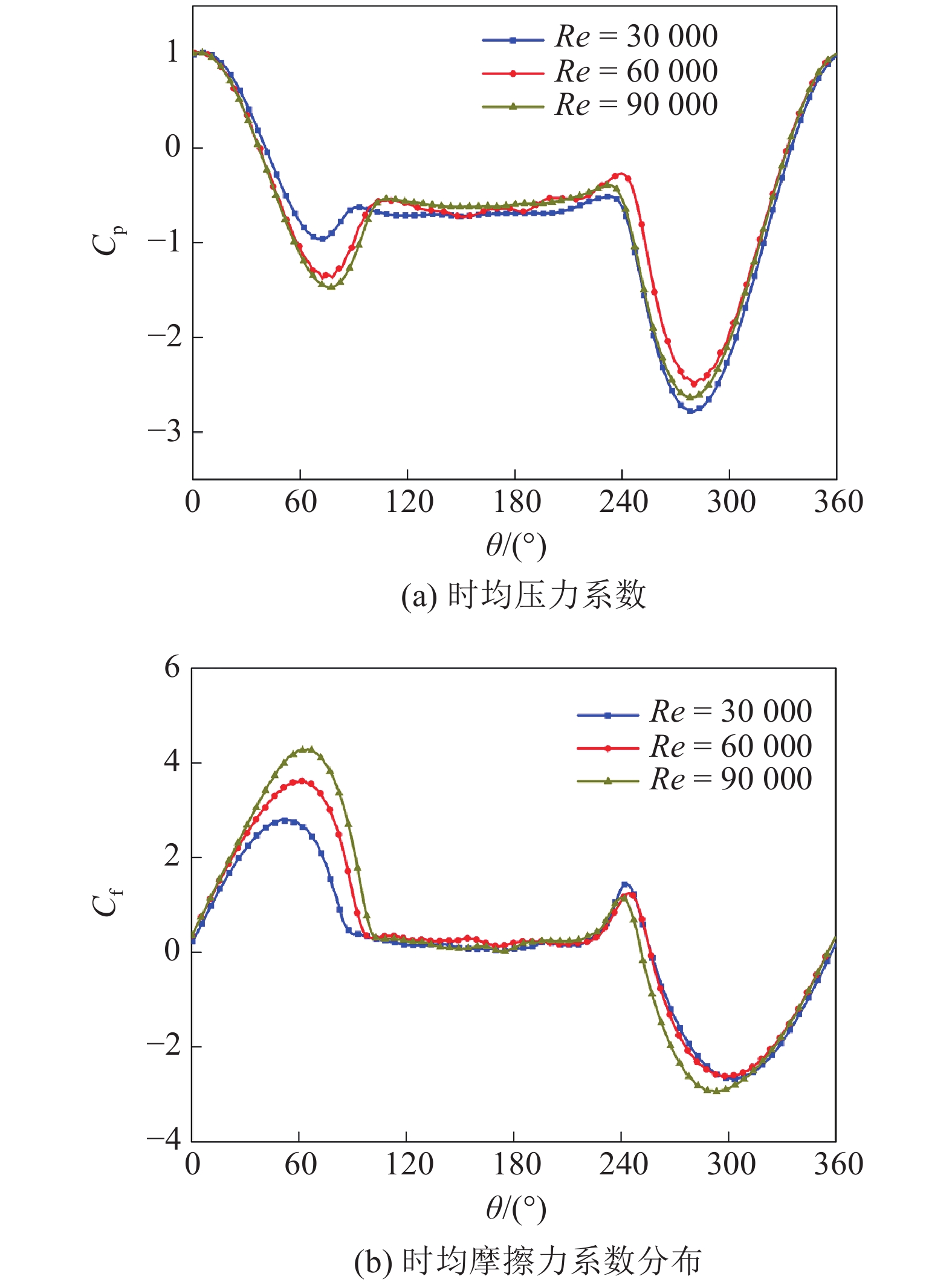
从图19中可以看出, 由于圆柱的旋转, 致使圆柱上、下表面时均压力系数(${C_{
m{p}}} = (p - {p_0})/({
ho _infty }U_infty ^2/2)$)分布不对称, 进而产生了马格努斯力. 雷诺数的变化对圆柱表面时均压力分布影响较小, 只是对上、下表面最小压力系数的极值产生了一定的影响. 从表面时均摩擦力系数(${C_{
m{f}}} = [{tau _0}/({
ho _infty }U_infty ^2)]sqrt {{mathop{ Re}nolimits} }$)分布可知, 随着雷诺数的增加, 上表面的流动分离点后移, 下表面的流动分离点也后移. 但是, 上表面的流动分离点位置的变化要比下表面明显.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-18.jpg'"
class="figure_img
figure_type1 bbb " id="Figure18" />



图
18
Re = 20000, ɑ = 0.72时速度矢量图



Figure
18.
Velocity vector diagram at Re = 20000, ɑ = 0.72



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-19.jpg'"
class="figure_img
figure_type1 bbb " id="Figure19" />



图
19
a = 0.4时不同雷诺数下圆柱表面(a)时均压力系数和(b)时均摩擦力系数分布



Figure
19.
Distribution of (a) the average pressure coefficient and (b) the average wall shear stress coefficient on the cylinder surface under different Reynolds numbers when ɑ = 0.4



下载:
全尺寸图片
幻灯片

4.
理论模型

对于绕圆柱的有环量流动, 传统上采用均匀直线流动、偶极流、点涡三者叠加后的复合流动来表示, 其速度势函数为

$$psi = {V_infty }left(r - dfrac{{{R^2}}}{r} ight)sin theta + dfrac{varGamma }{{2{text{π}} }}ln r$$

(4)

其中r² = x² + y², θ = arctan(y/x).

考虑一个有限的点涡列(图20所示), 每一个涡的强度都是K, 沿一条直线分布在点0, a, 2a,···, na处, 2n+1个涡的复势为

$$omega = { m{i}}K[lg {textit{z}} + lg ({textit{z}} pm { m{a}}) + cdots + lg (n{textit{z}} pm { m{a}})]$$

(5)

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-20.jpg'"
class="figure_img
figure_type1 bbb " id="Figure20" />



图
20
单涡列



Figure
20.
Single vortex column



下载:
全尺寸图片
幻灯片


对数项的有限和等于一个正弦项和一个对数项的积

$$omega = { m{i}}Klg left(sin frac{{{text{π}} {textit{z}}}}{a} ight)$$

(6)

因此其流函数为

$$psi = frac{K}{2}lg frac{1}{2}left(cosh frac{{2{text{π}} y}}{a} - cos frac{{2{text{π}} x}}{a} ight)$$

(7)

在流场中任一点处速度为

$$u = - dfrac{K}{{2a}}dfrac{{sinh ({{2{text{π}} y}/{a}}})}{{cosh ({{2{text{π}} y}/{a}}) - cos ({{2{text{π}} x}/{a}})}}$$

(8)

$$v = dfrac{K}{{2a}}dfrac{{sin ({{2{text{π}} x}/{a}}})}{{cosh ({{2{text{π}} y}/{a} })- cos ({{2{text{π}} x}/{a}})}}$$

(9)

假设有两个平行的点涡列, 两个点涡列之间的距离是b, 同一列中连续的两个涡之间的距离为a, 两个点涡列中涡的强度分别为+K和?K. 假设参考点涡分别位于z₁和z₂, 其复势为

$$begin{array}{l}omega = { m{i}}{K_1}lgleft[ sin dfrac{{text{π}} }{a}({textit{z}} - {{textit{z}}_1}) ight]+ { m{i}}{K_2}lg left[sin dfrac{{text{π}} }{a}({textit{z}} + {{textit{z}}_2}) ight]end{array}$$

(10)

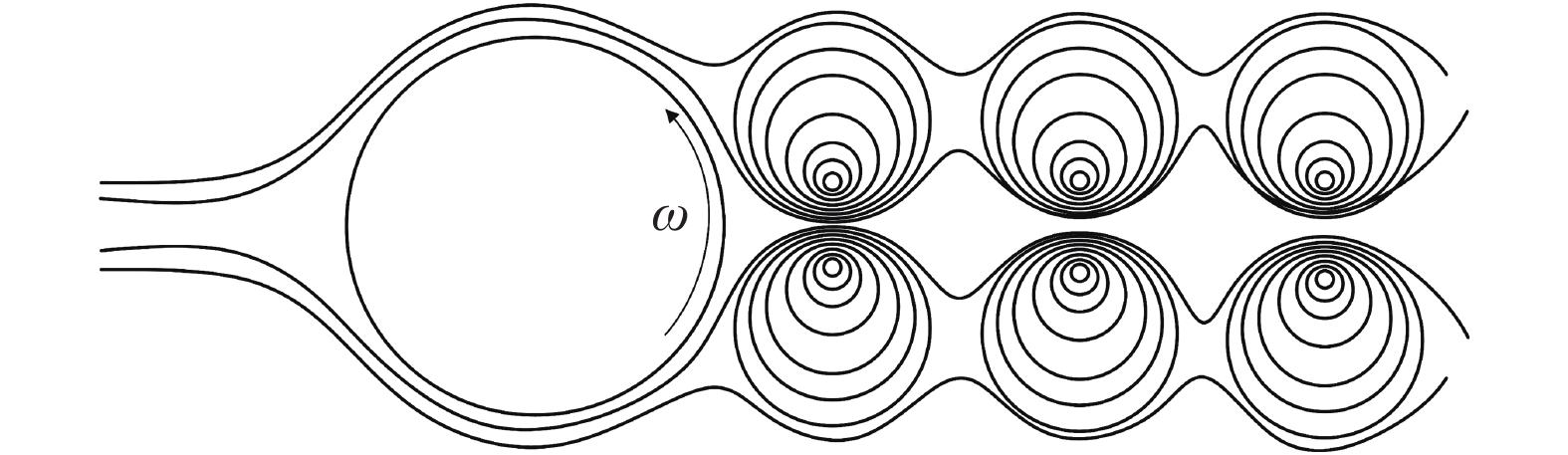
因此, 将绕圆柱的有环量流动与两个平行的点涡列进行叠加, 就得到了如图21所示的流动分布. 它可以最大程度上还原圆柱背风区域的流动特征. 圆柱后方流场中任一点处速度为

$$begin{split}u =& {V_infty }left[1 - dfrac{{{R^2}({x^2} - {y^2})}}{{{{({x^2} + {y^2})}^2}}} ight] + dfrac{varGamma }{{2{text{π}} }}dfrac{y}{{{x^2} + {y^2}}}+&{ dfrac{{{K_1}}}{{4{text{π}} a}}dfrac{{sinh dfrac{{2{text{π}} (y - {y_1})}}{a}}}{{cosh dfrac{{2{text{π}} (y - {y_1})}}{a} - cos dfrac{{2{text{π}} (x - {x_1})}}{a}}}}-&{ dfrac{{{K_2}}}{{4{text{π}} a}}dfrac{{sinh dfrac{{2{text{π}} (y + {y_2})}}{a}}}{{cosh dfrac{{2{text{π}} (y + {y_2})}}{a} - cos dfrac{{2{text{π}} (x - {x_2})}}{a}}}}end{split}$$

(11)

$$begin{split}v = & - dfrac{{2xy{R^2}}}{{{{({x^2} + {y^2})}^2}}} - dfrac{varGamma }{{2{text{π}} }}dfrac{x}{{{x^2} + {y^2}}}- &{ dfrac{{{K_1}}}{{4{text{π}} a}}dfrac{{sin dfrac{{2{text{π}} (x - {x_1})}}{a}}}{{cosh dfrac{{2{text{π}} (y - {y_1})}}{a} - cos dfrac{{2{text{π}} (x - {x_1})}}{a}}}}+&{ dfrac{{{K_2}}}{{4{text{π}} a}}dfrac{{sin dfrac{{2{text{π}} (x - {x_2})}}{a}}}{{cosh dfrac{{2{text{π}} (y + {y_2})}}{a} - cos dfrac{{2{text{π}} (x - {x_2})}}{a}}}}end{split}$$

(12)

其中, x₁, x₂, y₁, y₂的位置由Foppl等^[23-25]提出的图像法获得, $varGamma = displaystyleint_0^{2{text{π}} } {{V_theta }} R{
m{d}}theta$, 经过与实验值对比, 取K₁ = K₂ = 0.0001Re?0.5.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-21.jpg'"
class="figure_img
figure_type1 bbb " id="Figure21" />



图
21
带有两个平行点涡列的有环量圆柱绕流



Figure
21.
Circular cylinder with two parallel vortex column



下载:
全尺寸图片
幻灯片


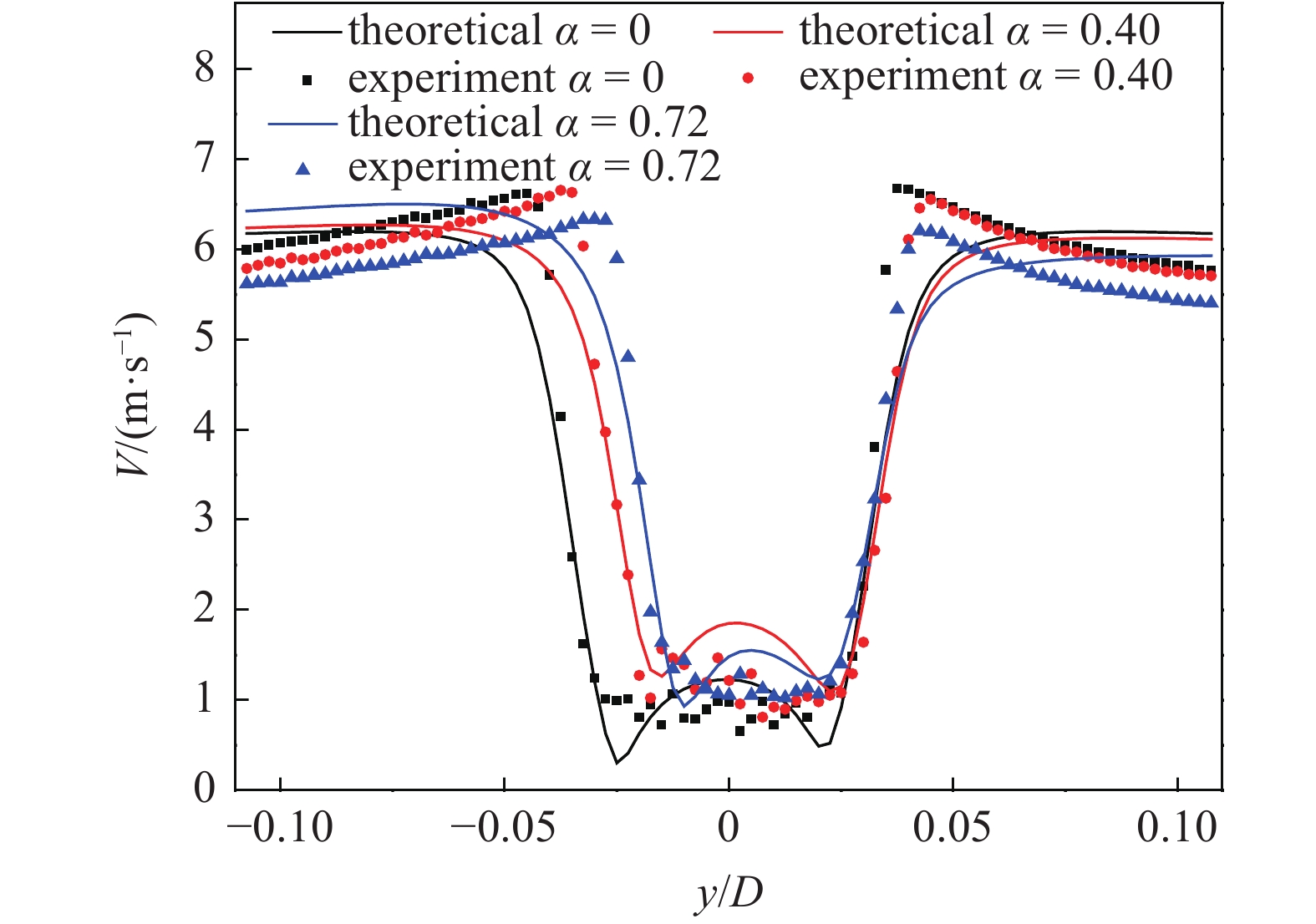
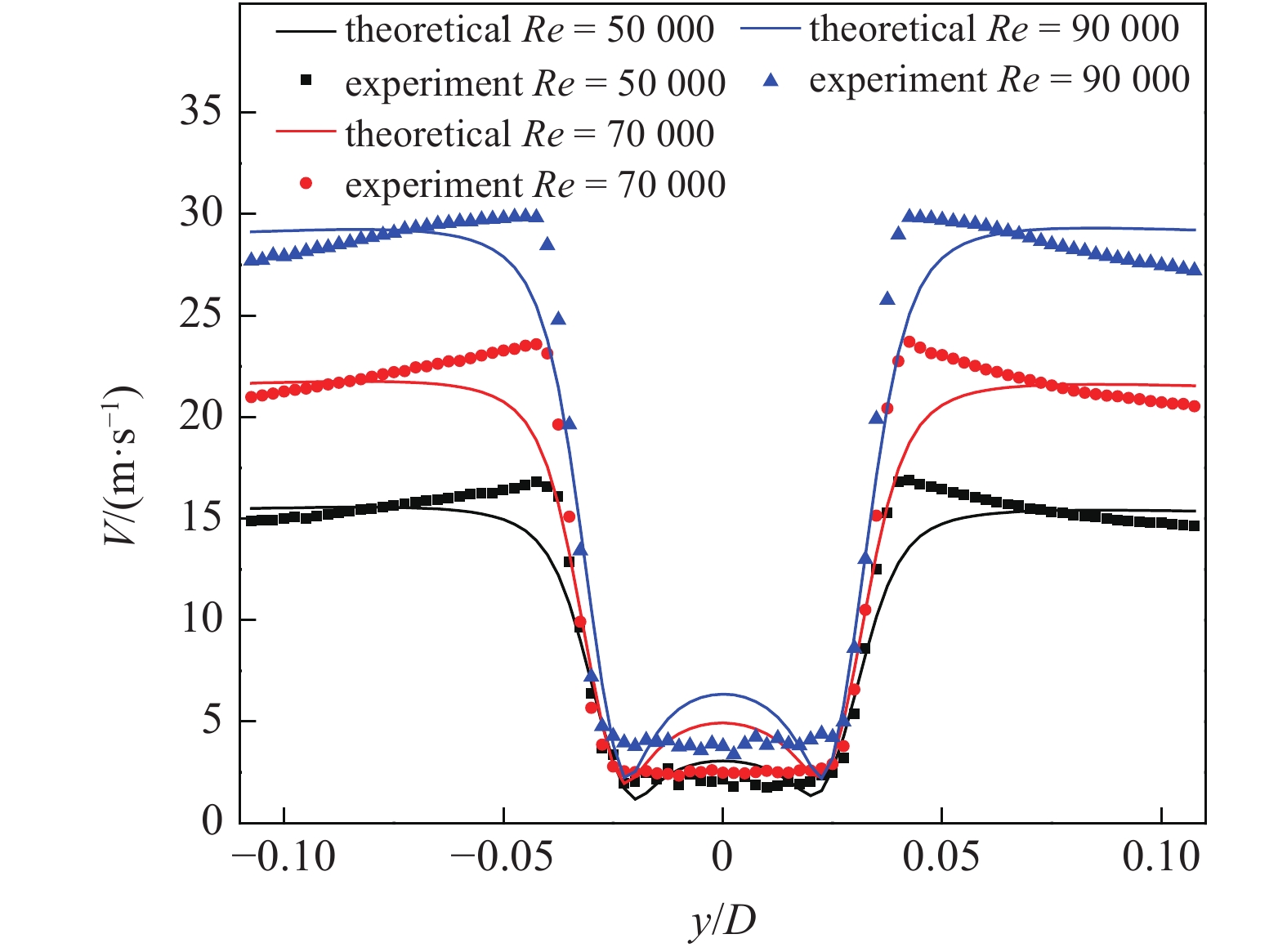
图22和图23分别为雷诺数Re = 20000时旋转圆柱后方x/D = 1处理论模型与实验结果对比结果和相对转速ɑ = 0.2时旋转圆柱后方x/D = 1处理论模型与实验结果对比结果. 从图中可以看出, 理论模型的计算结果与实验结果吻合良好, 能够较为准确地预测相对转速变化时旋转圆柱后方速度突变的位置, 证明了理论模型的正确性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-22.jpg'"
class="figure_img
figure_type1 bbb " id="Figure22" />



图
22
Re = 20000时旋转圆柱后方x/D = 1处理论模型与实验结果对比



Figure
22.
Comparison of theoretical and experimental results at x/D = 1 behind a rotating cylinder when Re = 20000



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-23.jpg'"
class="figure_img
figure_type1 bbb " id="Figure23" />



图
23
ɑ = 0.2时旋转圆柱后方x/D = 1处理论模型与实验结果对比



Figure
23.
Comparison of theoretical and experimental results at x/D = 1 behind a rotating cylinder when ɑ = 0.2



下载:
全尺寸图片
幻灯片


由伯努利方程求得圆柱表面的压强分布

$$p = {p_infty } + frac{1}{2} ho left[V_infty ^2 - ({u^2} + {v^2}) ight]$$

(13)

圆柱在Y方向上的受力为

$${F_s} = - Lsin theta mathop int nolimits_{{s}}^{} p{ m{d}}s$$

(14)

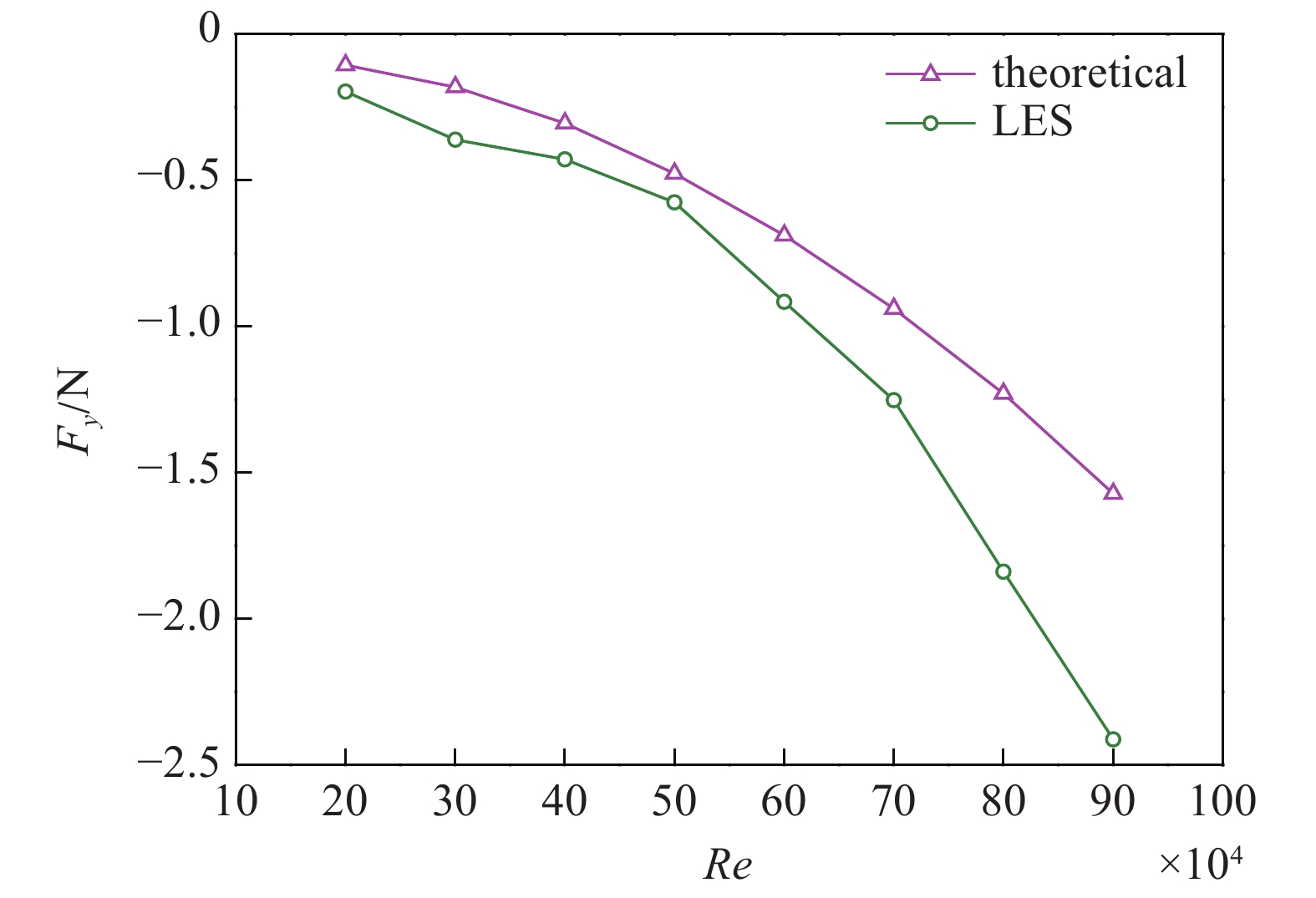
式中ds = Rdθ, 为单位长度圆柱侧表面的微面积. 图24是相对转速ɑ = 0.4时理论模型和LES升力计算结果对比. 随着雷诺数的增加旋转圆柱的升力逐渐增加. 理论模型的计算结果与LES的计算结果相对吻合, 其变化趋势相同, 但是两者之间存在一定的差别. LES计算得到的升力随雷诺数变化曲线越来越陡, 而理论模型计算得到的升力随雷诺数变化曲线要比其平缓. 通过分析涡量图可以得出如下两个原因是造成理论模型与LES存在一定差距的原因. 首先, 随着相对转速和雷诺数的增加, 圆柱后方的分离涡是向上方偏移的, 而在理论模型中圆柱后方的分离涡是对称分布的. 其次, 圆柱后方上、下两列分离涡的强度是不同的, 而在理论模型中圆柱后方的分离涡强度是相等的.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-24.jpg'"
class="figure_img
figure_type1 bbb " id="Figure24" />



图
24
ɑ = 0.4时理论模型和LES升力计算结果对比



Figure
24.
Comparison between theoretical and LES lift calculation results when ɑ = 0.4



下载:
全尺寸图片
幻灯片


为了判断旋转圆柱后方涡的位置对旋转圆柱升力的影响, 采用理论模型进行了如图25所示的灵敏度分析, 其中Δy为正表示涡向上移动. 可以看出当圆柱逆时针旋转时, 圆柱后侧下方点涡列位置的改变对升力的影响显著, 升力的变化与下方点涡列位置的改变呈负相关, 而上方点涡列位置的改变对升力的影响相对较小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-153-25.jpg'"
class="figure_img
figure_type1 bbb " id="Figure25" />



图
25
涡位置灵敏度分析



Figure
25.
Sensitivity analysis of vortex position



下载:
全尺寸图片
幻灯片


通过理论分析发现, 圆柱后侧下方涡位置的上移对圆柱升力影响十分显著, 图24所示数值模拟值要小于理论值, 而理论值恰好是随着下方涡的上移而减小. 根据数值模拟的结果可知, 圆柱后侧下方涡的位置明显向上移动. 因此, 足以说明在高雷诺数、低相对转速的条件下, 旋转圆柱后侧下方涡位置的改变对旋转圆柱的升力、尾流区自由剪切层的变化起到了重要的影响.

5.
结论

本文采用热线风速仪对雷诺数为20000 ~ 90000的旋转圆柱后方流场进行了测量, 通过大涡模拟和理论建模对旋转圆柱绕流问题进行了分析, 得出如下结论:

(1)当圆柱逆时针旋转时, 同一雷诺数下随着相对转速的增加, 旋转圆柱尾迹区域下方速度突变处的位置随着相对转速的增加而上移, 而圆柱尾迹区域上方速度突变处的位置随着相对转速的增加并未发生太大变化. 同一相对转速下雷诺数的增加使旋转圆柱尾迹区域下方速度突变处位置有小幅度的下移, 旋转圆柱尾迹区域上方速度突变处位置变化不明显.

(2)通过数值模拟发现, 圆柱旋转之后, 圆柱后方下侧涡的位置明显上移, 且幅度较大. 在下方涡的挤压下, 上方涡的位置有小幅度的上移. 不旋转的圆柱其自由剪切层上下对称, 但当圆柱旋转后, 下方的自由剪切层有明显的上移, 上方的自由剪切层位置变化较小.

(3)通过理论分析发现, 圆柱后侧下方涡位置的上移对圆柱升力影响十分显著, 在高雷诺数、低相对转速的条件下, 旋转圆柱后侧下方涡位置的改变对旋转圆柱的升力、尾流区自由剪切层的变化起到了重要的影响.