引言
高速航行体出水破冰具有重大的工程应用背景. 与常规水下发射过程相比, 航行体需要穿越水面覆盖冰层或穿越含冰块结构的冰水混合区域, 是一个涉及多相多介质动力耦合的复杂过程. 该过程中, 航行体的受载环境及弹道稳定性与在纯水介质出水过程有很大差别, 例如冰载荷的增加, 冰层受到冲击后复杂的断裂破碎行为, 都将直接导致航行体和冰面的受力分布发生剧烈变化, 增大出水冰发射的不确定性. 因此, 开展航行体出水破冰的动力学特征与载荷作用机理研究, 具有重要的应用价值和科学意义.
目前冰与结构相互作用的研究主要集中在冰的力学性能、船?冰碰撞方面, 而结构物穿冰作用的研究还较少. 在冰的力学性能方面, 温度和应变率是两个重要的影响因素[1-6], 例如, Arakawa和Maeno[1]的研究表明, 在准静态单轴压缩条件下, 0 ~ ?100 °C时, 多晶冰的抗压强度随着温度降低而升高, 但是温度在 ?100 ~ ?175 °C时, 抗压强度并没有明显变化. Wu和Prakash[7]通过分离式霍普金森压杆(split Hopkinson pressure bar, SHPB)研究了冰的动态压缩强度, 实验结果表明, 在 ?15 ~ ?125 °C范围内降低温度时, 冰的强度从32 MPa增大到112 MPa, 而在 ?125 ~ ?173 °C范围内继续降低温度时, 强度大约为110 ~ 120 MPa, 并无明显增强. 在应变率效应方面, Jones[8]对温度 ?11 °C时应变率10?1 ~ 10 s?1范围内多晶冰力学性能的研究表明, 冰的强度随应变率的增大而增大, 并建立了压缩强度与应变率的近似关系式. 季顺迎等[9]则结合Hibler黏塑性本构模型和K-V体黏弹性模型, 建立了海冰的黏弹塑性本构模型, 兼顾小应变率下的弹性以及大应变率下的塑性, 以模拟海冰的相互作用. Gao等[10]通过建立新的失效准则, 结合“Tsai-Wu”屈服模型建立了海冰的弹塑性本构模型, 以模拟船?冰山碰撞过程. 在冰的破碎失效方面, 静态和准静态压缩条件下, 冰的塑性应变可超过0.1, 翼型裂纹萌生、扩展及导致的劈裂破坏是主要的失效机制. 随着应变率的增大, 冰表现出由韧转脆的现象[11]. 在更高应变率条件下, 冰的失效模式以大块的劈裂转向了碎片和碎粒, Shazly等[12]采用SHPB对单晶和多晶冰在应变率60 ~ 1400 s?1范围内的力学性能进行了研究, 实验中单晶和多晶冰均碎裂成很多细小颗粒, 并且冰失效后具有较高的残余强度. Carney等[13]发展了高应变率下冰的失效模型. 冰载荷是船冰碰撞过程中的研究重点, 因此国内外****对冰破坏的物理过程开展了大量的试验和数值模拟研究[14-17]. 例如, Sodhi[18]对冰层进行了小尺度压痕试验, 发现低压痕速度下冰发生延性变形, 主要是蠕变, 而高速下发生连续脆性压碎, 并且断裂前的冰变形大多是弹性的. 郭春雨等[19]对冰区船舶在碎冰中的航行过程进行数值模拟, 获得的航行阻力和实验结果在定性上保持一致. 吴炜和黄焱[20]通过开展冰水池模型试验, 研究了海冰漂移和船速对冰载荷分布的影响. 程文霞[21]则通过在近场动力学模型中考虑爆炸破冰中的气泡载荷作用, 对涉及的载荷形式进行了分析.
目前关于航行体出水破冰的研究鲜有报道, 因此, 本文基于量纲分析, 系统地开展航行体出水破冰数值模拟, 研究冰?水?结构多介质耦合作用机理, 以获得航行体的运动特性及动载荷特征, 为复杂冰区环境下航行体的高速出水发射提供理论依据.
1.
量纲分析
为了系统地开展数值模拟研究, 首先对航行体出水破冰多介质耦合过程(见图1示意图)进行量纲分析. 对于航行体的速度v、过载a以及头部应力σ, 控制参数主要来自以下5个方面.
(1) 时间t;
(2) 冰的参数: 密度ρi, 厚度hi, 弹性模量Ei, 泊松比υi, 极限应变εimax, 特征尺寸li;
(3) 水的参数: 密度ρw, 声速cw;
(4) 航行体与冰的初始距离s;
(5) 航行体参数: 密度ρp, 弹性模量Ep, 泊松比υp, 长度lp, 直径dp, 初始速度v0.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-082-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
航行体出水破冰示意图
Figure
1.
Schematic diagram of ice break by vehicle launched underwater
下载: 全尺寸图片
幻灯片
1.1
航行体速度v
v应当是上述5组控制参数的函数, 即
$$v = f(t;{ ho _{ m{i}}},{h_{ m{i}}},{E_{ m{i}}},{upsilon _{ m{i}}},{varepsilon _{{ m{imax}}}},{l_{ m{i}}};{ ho _{ m{w}}},{c_{ m{w}}};s;{ ho _{ m{p}}},{E_{ m{p}}},{upsilon _{ m{p}}},{l_{ m{p}}},{d_{ m{p}}},{v_{ m{0}}})$$  | (1) |
取ρp，Ep和dp作为基本量, 式(1)可化为无量纲关系
$$begin{split} &frac{v}{{sqrt {{{{E_{ m{p}}}} / {{ ho _{ m{p}}}}}} }} = fBiggr(frac{t}{{{d_{ m{p}}}sqrt {{{{ ho _{ m{p}}}} / {{E_{ m{p}}}}}} }};frac{{{ ho _{ m{i}}}}}{{{ ho _{ m{p}}}}},frac{{{h_{ m{i}}}}}{{{d_{ m{p}}}}},frac{{{E_{ m{i}}}}}{{{E_{ m{p}}}}},{upsilon _{ m{i}}},{varepsilon _{{ m{imax}}}},frac{{{l_{ m{i}}}}}{{{d_{ m{p}}}}};&qquadqquadfrac{{{ ho _{ m{w}}}}}{{{ ho _{ m{p}}}}},frac{{{c_{ m{w}}}}}{{sqrt {{{{E_{ m{p}}}} / {{ ho _{ m{p}}}}}} }};frac{s}{{{d_{ m{p}}}}};{upsilon _{ m{p}}},frac{{{l_{ m{p}}}}}{{{d_{ m{p}}}}},frac{{{v_{ m{0}}}}}{{sqrt {{{{E_{ m{p}}}} / {{ ho _{ m{p}}}}}} }}Biggr)end{split}$$  | (2) |
若材料不变, 并且保持航行体几何形状相似, 式(2)可简化为
$$frac{v}{{sqrt {{{{E_{ m{p}}}} / {{ ho _{ m{p}}}}}} }} = fBiggr(frac{t}{{{d_{ m{p}}}sqrt {{{{ ho _{ m{p}}}} / {{E_{ m{p}}}}}} }};frac{{{h_{ m{i}}}}}{{{d_{ m{p}}}}},frac{{{l_{ m{i}}}}}{{{d_{ m{p}}}}};frac{s}{{{d_{ m{p}}}}};frac{{{v_{ m{0}}}}}{{sqrt {{{{E_{ m{p}}}} / {{ ho _{ m{p}}}}}} }}Biggr)$$  | (3) |
1.2
航行体过载${boldsymbol{a}} $
a也是上述5组控制参数的函数, 并且若保持材料不变以及航行体几何形状相似, 函数有以下形式
$$frac{a}{{{{{E_{ m{p}}}} Big/ {left( {{ ho _{ m{p}}} cdot {d_{ m{p}}}} ight)}}}} = fBiggr(frac{t}{{{d_{ m{p}}}sqrt {{{{ ho _{ m{p}}}} / {{E_{ m{p}}}}}} }};frac{{{h_{ m{i}}}}}{{{d_{ m{p}}}}},frac{{{l_{ m{i}}}}}{{{d_{ m{p}}}}};frac{s}{{{d_{ m{p}}}}};frac{{{v_{ m{0}}}}}{{sqrt {{{{E_{ m{p}}}} / {{ ho _{ m{p}}}}}} }}Biggr)$$  | (4) |
1.3
航行体头部应力σ
σ也是上述5组控制参数的函数. 同样地, 若材料不变, 并且保持航行体几何形状相似, 函数有以下形式
$$frac{sigma }{{{E_{ m{p}}}}} = fBiggr(frac{t}{{{d_{ m{p}}}sqrt {{{{ ho _{ m{p}}}} / {{E_{ m{p}}}}}} }};frac{{{h_{ m{i}}}}}{{{d_{ m{p}}}}},frac{{{l_{ m{i}}}}}{{{d_{ m{p}}}}};frac{s}{{{d_{ m{p}}}}};frac{{{v_{ m{0}}}}}{{sqrt {{{{E_{ m{p}}}} / {{ ho _{ m{p}}}}}} }}Biggr)$$  | (5) |
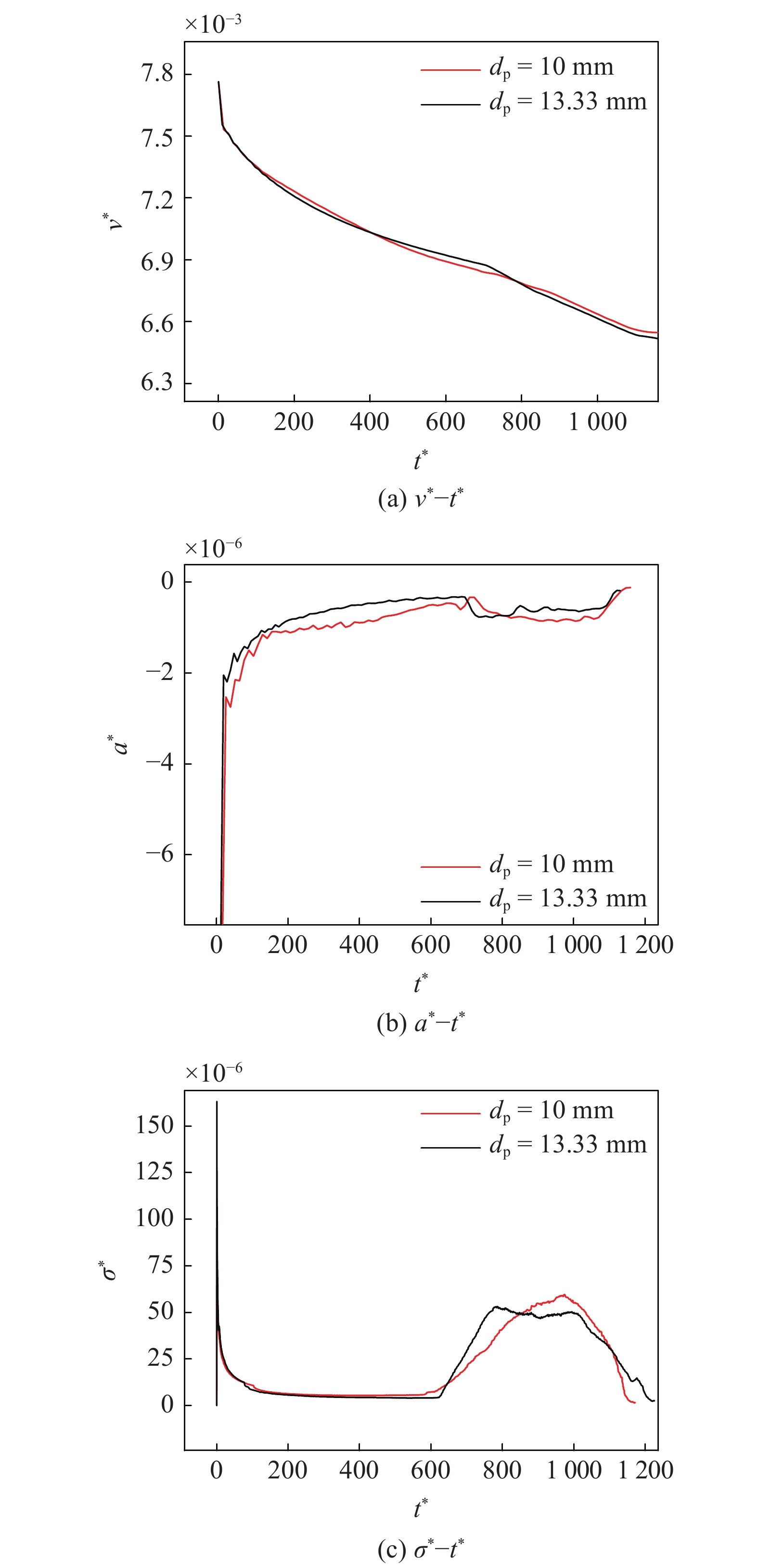
为了验证上述推导的量纲分析结果, 采用LS-DYNA对两种不同参数条件下的航行体出水破冰工况分别进行了数值计算. 两种工况中保持材料相同以及航行体长径比10∶1不变, 第一种工况航行体直径dp = 10 mm、冰层厚度hi = 3 cm、冰层为无限大冰层即li趋于无穷, 航行体与冰的初始距离s =5 cm, 初始速度v0 = 40 m/s; 第二种工况航行体的直径相对第一种增大1/3, 即dp = 13.33 mm, 其余量也相应增大或不变, 保持和第一种工况的无量纲参数相同. 采用的计算模型及方法具体在下文2.1介绍. 图2分别为计算的两种工况的无量纲航行体速度v*、过载a*以及头部应力σ*随无量纲时间t*的变化, 由图2可以看出, 两种工况的无量纲结果吻合得较好, 验证了上述推导的无量纲关系的正确性.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-082-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
两种工况数值计算结果对比(上角标*表示各参数对应的无量纲量)
Figure
2.
Comparison of the numerical results for the two cases (superscript * denotes the dimensionless quantity)
下载: 全尺寸图片
幻灯片
由量纲分析可以看出, 除了时间t外, 影响航行体速度v、过载a和头部应力σ的因素主要为无量纲的冰厚度hi*、冰特征尺寸li*、航行体与冰的初始距离s*以及航行体初速度v0*. 考虑到关于航行体水下运动的研究已经很多并且相关机制较为清楚[22], 本文不着重于航行体的水下运动过程, 在数值模拟研究中保持航行体与冰的初始距离s*不变, 重点关注其余3个因素的影响规律.
2.
流固耦合计算方法
2.1
计算模型
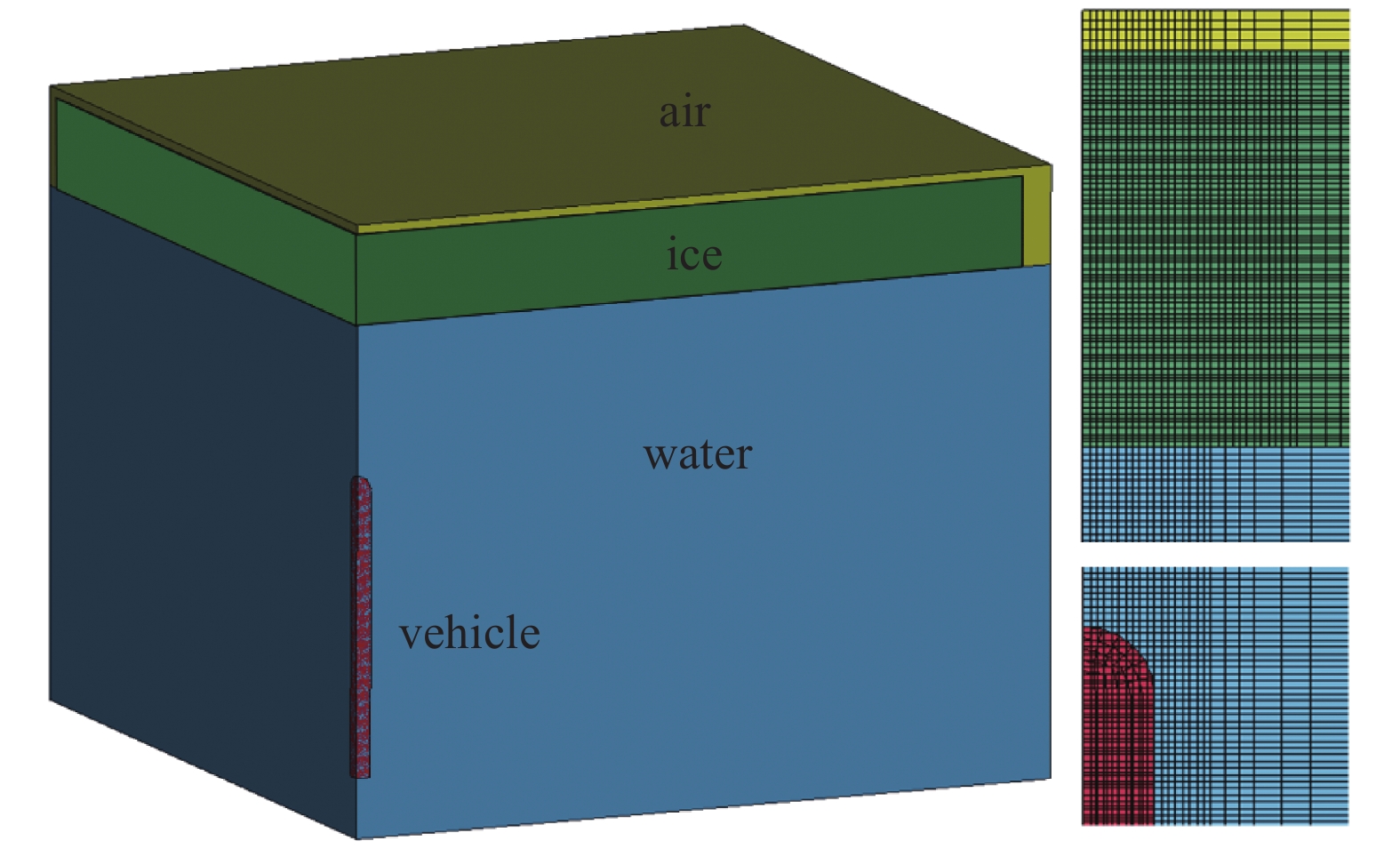
考虑到问题的轴对称特性, 建立1/4模型进行计算. 图3为计算模型以及局部的网格划分, 模型包括航行体、水域、空气域以及冰层, 均采用Truegrid进行六面体网格建模. 为了提高计算效率, 对称轴附近的水、冰、空气采用精细网格, 而外围部分采用较大的渐变网格. 在对称轴附近主要的流固耦合作用区域, 水、冰的网格为0.5 mm; 空气网格横向为0.5 mm, 轴向为0.75 mm; 航行体的网格为水、冰网格的1.6 ~ 1.7倍, 约0.83 mm. 2.2节给出了具体的网格无关性验证结果. 对称面上采用对称边界条件, 水和空气域的外围以及上下面采用无反射边界条件. 对于冰层, 无限大工况下在外围采用无反射边界条件, 而碎冰情况下采用自由边界条件. 计算单位制采用cm-g-μs.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-082-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
计算模型及局部网格划分(不同工况内冰层尺寸不同)
Figure
3.
Full view of simulation components and part of meshed model (ice sheet size is different in different cases)
下载: 全尺寸图片
幻灯片
各介质的计算域、计算模型以及参数分别列于下表1 ~ 表4中. 固体介质航行体和冰采用拉格朗日(Lagrangian)算法, 并且两者之间定义侵蚀面?面接触; 流体介质水和空气采用任意拉格朗日?欧拉(ALE)算法. 通过*CONSTRAINED_LAGRANGE_IN_SOLID定义流固耦合关系. ALE算法的控制方程为[23]
$${left( {frac{{partial ho }}{{partial t}}} ight)_kappa } = - ho frac{{partial {v_i}}}{{partial {x_i}}} - {c_i}frac{{partial ho }}{{partial {x_i}}} quadquadquad;;;$$  | (6) |
$$ ho {left( {frac{{partial {v_i}}}{{partial t}}} ight)_kappa } = frac{{partial {sigma _{ij}}}}{{partial {x_j}}} + ho {f_i} - ho {c_i}frac{{partial {v_i}}}{{partial {x_j}}} ;;;$$  | (7) |
$${left( { ho frac{{partial e}}{{partial t}}} ight)_kappa } = {sigma _{ij}}frac{{partial {v_i}}}{{partial {x_j}}} - frac{{partial {q_i}}}{{partial {x_i}}} - ho {c_i}frac{{partial e}}{{partial {x_i}}}$$  | (8) |
式中, ρ为密度, vi为拉格朗日坐标下的速度, σij为应力张量, fi为单位质量体力, ci为对流速度, qi为热通量, e为内能.
表
1
冰计算模型及参数[24]
Table
1.
Ice details[24]
table_type1 ">
| Properties | Values |
| dimensions: infinite ice sheet dimensions: broken ice | 24 cm × 24 cm × hi 6 cm × 6 cm × hi |
| density | 897 kg/m3 |
| Young’s modulus | 9.31 GPa |
| maximum pressure | 9.2 MPa |
| minimum pressure | ?0.92 MPa |
| element type | *SECTION_SOLID (brick) |
| typical element size | 0.5 mm |
| material properties | *MAT_ELASTIC, *MAT_ADD_EROSION |
| *hi is the height of the ice target, and the infinite ice sheet model uses the non-reflecting boundary. | |
下载: 导出CSV
|显示表格
表
2
航行体计算模型及参数
Table
2.
Vehicle details
table_type1 ">
| Properties | Values |
| dimensions | 1 cm diameter, 10 cm length and spherical head |
| initial vehicle-ice separation, s | 5 cm |
| density | 7800 kg/m3 |
| Young’s modulus | 207 GPa |
| yield strength | 2.1 GPa |
| element type | *SECTION_SOLID (brick) |
| typical element size | 0.83 mm |
| material properties | *MAT_PLASTIC_KINEMATIC |
下载: 导出CSV
|显示表格
表
3
水计算模型及参数[25]
Table
3.
Water box details[25]
table_type1 ">
| Properties | Values |
| dimensions | 25 cm × 25 cm × 17 cm |
| density | 1000 kg/m3 |
| element type | *SECTION_SOLID (brick) |
| typical element size | 0.5 mm |
| material properties | *MAT_NULL, *EOS_GRUNEISEN |
下载: 导出CSV
|显示表格
表
4
空气计算模型及参数[25]
Table
4.
Air box details[25]
table_type1 ">
| Properties | Values |
| dimensions | 25 cm × 25 cm × ha |
| density | 1.25 kg/m3 |
| element type | *SECTION_SOLID (brick) |
| typical element size | 0.5 mm, 0.75 mm |
| material properties | *MAT_NULL, *EOS_LINEAR_POLYNOMIAL |
| *ha is the height of the air domain, and is bigger than the height of the ice target hi. | |
下载: 导出CSV
|显示表格
由于冰体在高应变率载荷下呈现脆性, 因此参考文献[24-25], 冰采用弹脆性模型以及失效算法[24], 航行体材料采用DT300钢, 水、空气分别采用标准大气压下的参数[25].
本文中水采用Gruneisen状态方程[23], 其表达式如式(9)所示, 具体参数列于表5中. 空气采用线性多项式状态方程[23], 表达式如式(10)所示, 具体参数列于表6中.
$$ p !=!! left{ begin{array}{l} !!!!!!! dfrac{{{ ho _0}{C^2}mu left[ {1 !+! left( {1 !-! dfrac{{{gamma _0}}}{2}} ight)mu !-! dfrac{a}{2}{mu ^2}} ight]}}{{{{left[ {1 !-! left( {{S_1} !-! 1} ight)mu !-! {S_2}dfrac{{{mu ^2}}}{{mu !+! 1}} !-! {S_3}dfrac{{{mu ^3}}}{{{{left( {mu !+! 1} ight)}^2}}}} ight]}^2}}} !+! left( {{gamma _0} !+! amu } ight){ m{E}},;mu leqslant 1 { ho _0}{C^2}mu !+! left( {{gamma _0} !+! amu } ight)E, ;qquadqquad;quadqquadqquadqquadmu > 1; end{array} ight. $$  | (9) |
式中, μ = ρ/ρ0 ? 1, ρ和ρ0分别为水的密度和初始密度. C为vs(vp)曲线的截距, S1 ~ S3是vs(vp)曲线斜率的无量纲系数, γ0为常数, E为比内能.
$$p = {C_0} + {C_1}mu + {C_2}{mu ^2} + {C_3}{mu ^3} + ({C_4} + {C_5}mu + {C_6}{mu ^2})E$$  | (10) |
式中, μ = ρ/ρ0 ? 1, C0 ~ C6是与气体性质有关的常数, E为比内能, ρ和ρ0分别为空气的密度和初始密度.
表
5
水的Gruneisen状态方程参数
Table
5.
Gruneisen EOS parameters for water
table_type1 ">
| C /(m·s?1) | S1 | S2 | S3 | γ | a |
| 1520 | 1.92 | 0 | 0 | 0.28 | 0 |
下载: 导出CSV
|显示表格
表
6
空气线性多项式状态方程参数
Table
6.
Polynomial EOS parameters for air
table_type1 ">
| C0 | C1 | C2 | C3 | C4 | C5 | C6 | E/(J·m?3) |
| 0 | 0 | 0 | 0 | 0.4 | 0.4 | 0 | 2.53×105 |
下载: 导出CSV
|显示表格
2.2
网格无关性验证
为了验证计算网格的无关性, 将2.1节表格所列的网格均缩小为原来的0.75倍, 分别采用这两套网格, 对初速度40 m/s的航行体出水破冰(3 cm厚无限冰层)进行了数值计算.
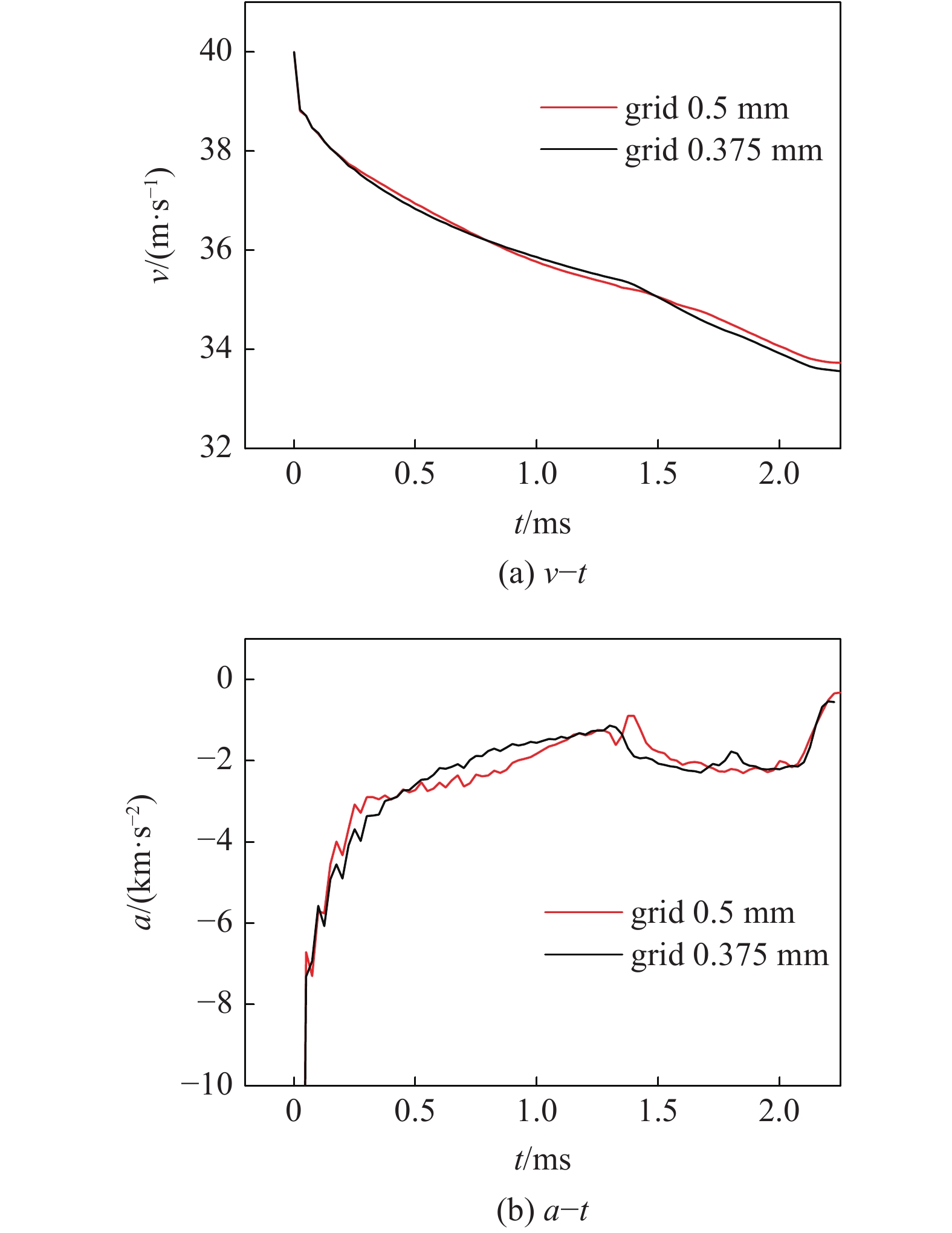
图4为计算的航行体速度以及加速度的变化历史, 由图4可以看出, 无论是水中运动还是破冰过程, 两套网格计算的结果基本一致, 表明可以采用表1～表4所列的以0.5 mm为主的一套网格进行数值计算.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-082-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
不同网格计算的航行体速度和加速度变化
Figure
4.
Simulated vehicle speed history and acceleration history by different grid sizes
下载: 全尺寸图片
幻灯片
3.
计算结果与分析
基于量纲分析, 本文针对表2所示航行体, 并且保持航行体与冰的初始距离s = 5 cm不变, 通过改变航行体初始发射速度v0、冰的厚度hi以及冰的尺寸li (具体值列于表7中), 对18种不同工况的航行体出水破冰进行了数值模拟.
表
7
不同工况计算条件
Table
7.
Calculation conditions for different cases
table_type1 ">
| Parameters | Value |
| initial velocity of vehicle, v0/(m·s?1) | 20, 30, 40 |
| ice thickness, hi/cm | 1, 3, 5 |
| ice size/(cm×cm) | infinite, 6 × 6 |
下载: 导出CSV
|显示表格
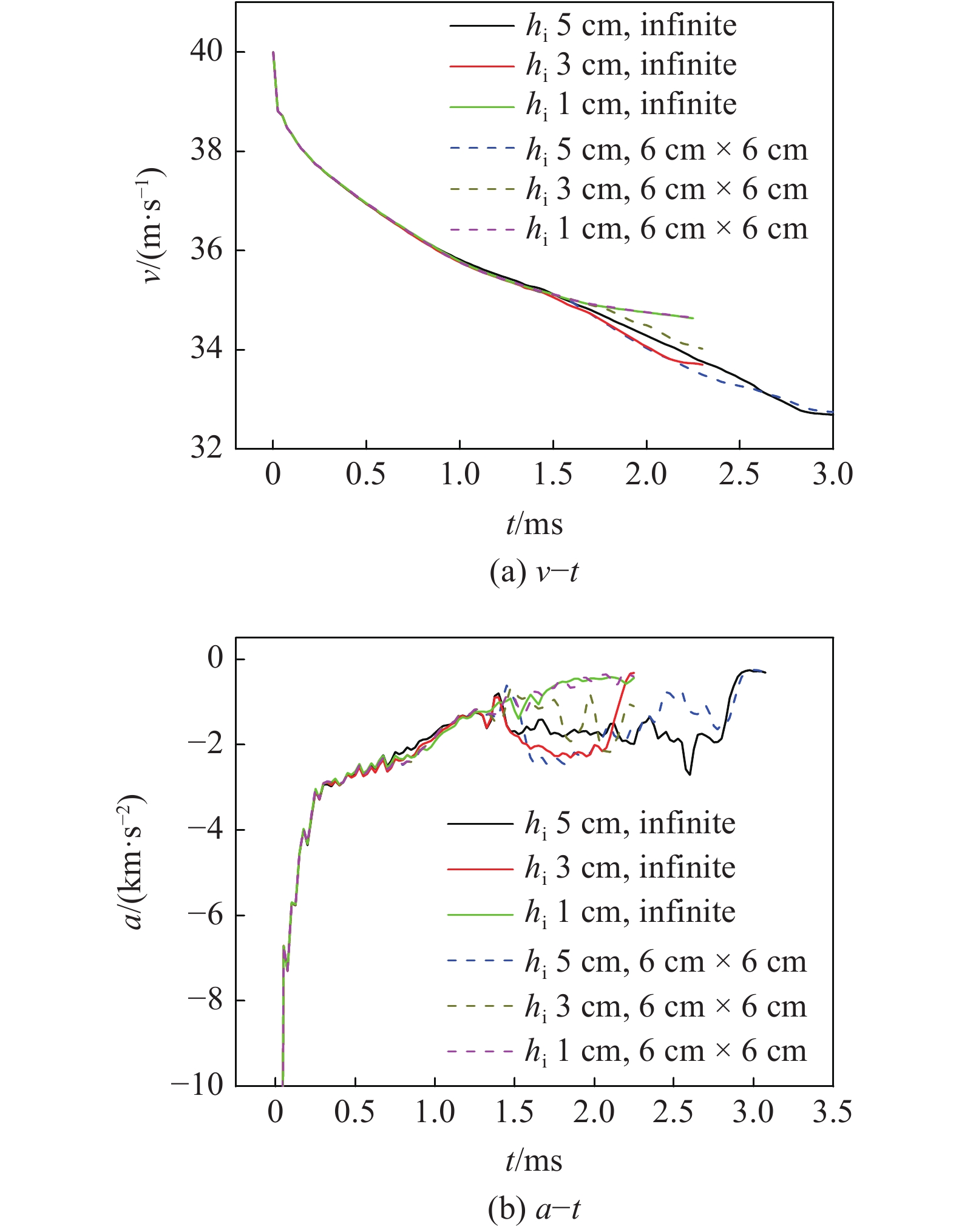
图5分别为计算的不同冰层条件下初速度40 m/s的航行体的速度变化和加速度变化历史. 由图5可以看出, 当航行体在水中的运动流场稳定后, 其加速度约200g ~ 300g. 约1.15 ms时刻, 航行体撞击冰层, 此时航行体的速度为35.6 m/s. 对于无限大的冰层, 1 cm厚的冰并没有对航行体造成较明显的载荷, 和在水中运动时的速度衰减趋势基本相同, 航行体穿冰后的剩余速度约34.8 m/s; 而对于3 cm和5 cm厚的冰层, 它们对航行体造成的平均加速度约220g, 其中的细小差距是由于冰层的破碎形态不同造成的, 航行体穿越3 cm冰层后的剩余速度约33.7 m/s, 而穿越5 cm冰层后的剩余速度约32.8 m/s.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-082-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
不同冰层时初速度40 m/s的航行体的速度和加速度变化
Figure
5.
Speed and acceleration history for 40 m/s vehicle impacting with different ice targets
下载: 全尺寸图片
幻灯片
对于尺寸为6 cm × 6 cm的碎冰, 当冰厚度为1 cm或5 cm时, 其对航行体运动的影响和无限大冰层基本相同, 只有瞬时的加速度会因为冰的破碎不同有一定差别; 而对于3 cm厚的碎冰, 其对航行体速度和加速度的影响不及无限冰层, 平均加速度约180g, 航行体剩余速度约34.3 m/s. 这是因为, 对于较厚的冰, 无论是无限大冰层还是碎冰, 在水的冲击作用下损伤较小, 因此航行体撞击前其完整性均较好, 两者对航行体运动特性的影响差别不大; 而对于较薄的冰, 无论是无限大冰层还是碎冰, 在水的冲击作用下几乎完全断裂破碎, 因此对航行体运动特性的影响都很小, 冰的尺寸效应也不明显. 只有对于3 cm厚的冰, 水对无限大冰层或碎冰的冲击破坏程度区别 较大, 导致两者后续与航行体的撞击作用出现明显 差别.
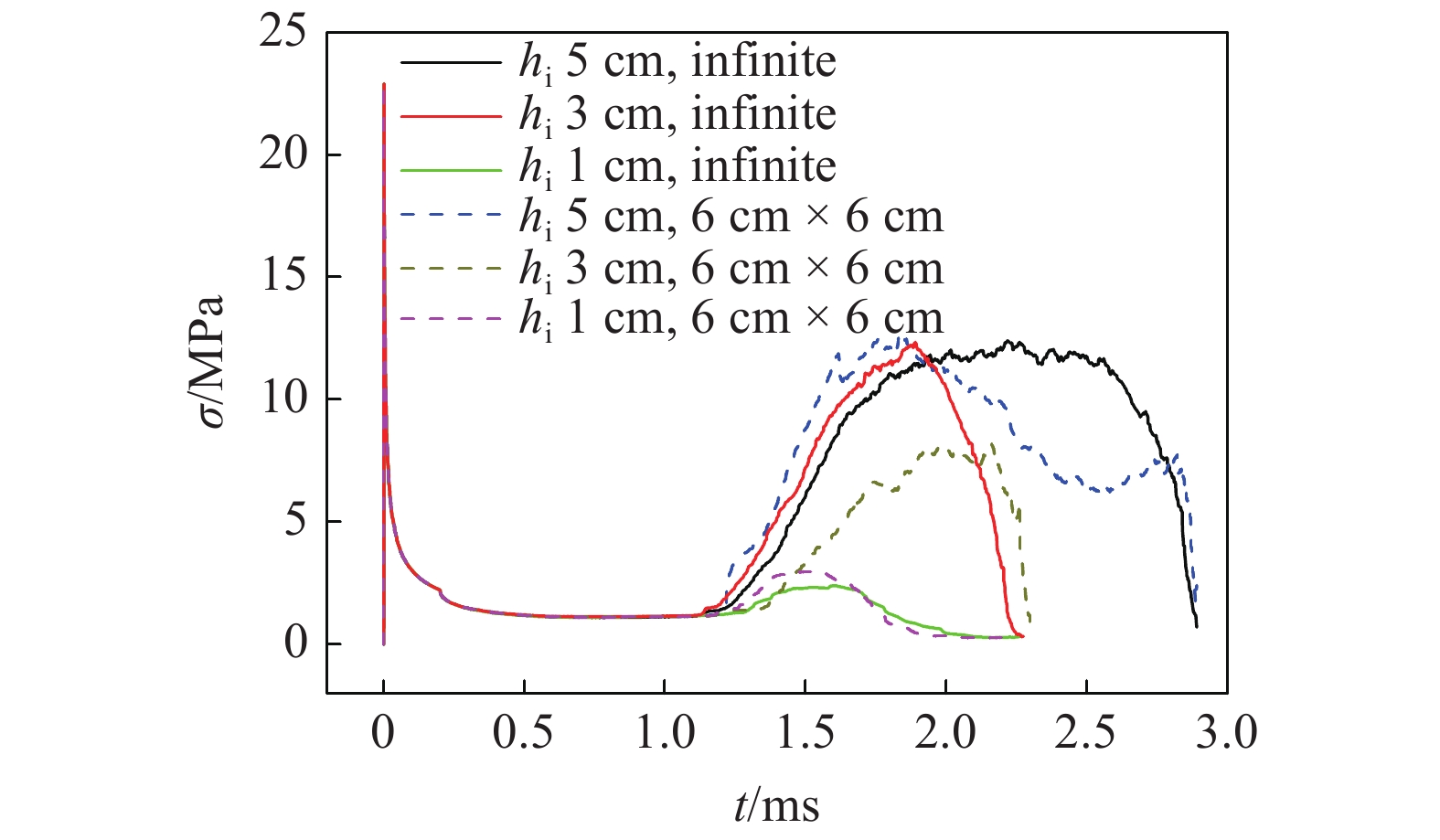
图6为计算的初速度40 m/s的航行体撞击不同冰层时头部的应力变化历史. 对于无限大冰层, 航行体撞击1 cm厚的冰产生的最大头部应力仅有2.2 MPa, 这是薄冰在撞击前损伤较大的缘故. 撞击3 cm和5 cm厚的无限大冰层时, 产生的最大头部应力基本相同, 约12.3 MPa, 且在穿越5 cm厚的冰时, 出现约1 ms的稳定侵彻阶段, 以上现象表明: 当无限大冰层超过3 cm厚时, 航行体头部应力只和其速度有关, 而和冰的厚度无关. 对于大小为6 cm × 6 cm的碎冰, 当厚度为1 cm或5 cm时, 其在航行体头部产生的最大应力和无限大冰层基本相同, 而厚度为3 cm时, 相对无限大冰层, 碎冰产生的最大头部应力较小, 仅有7.5 MPa.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-082-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
不同冰层时初速度40 m/s的航行体的头部应力历史
Figure
6.
Stress history at the 40 m/s vehicle head with different ice targets
下载: 全尺寸图片
幻灯片
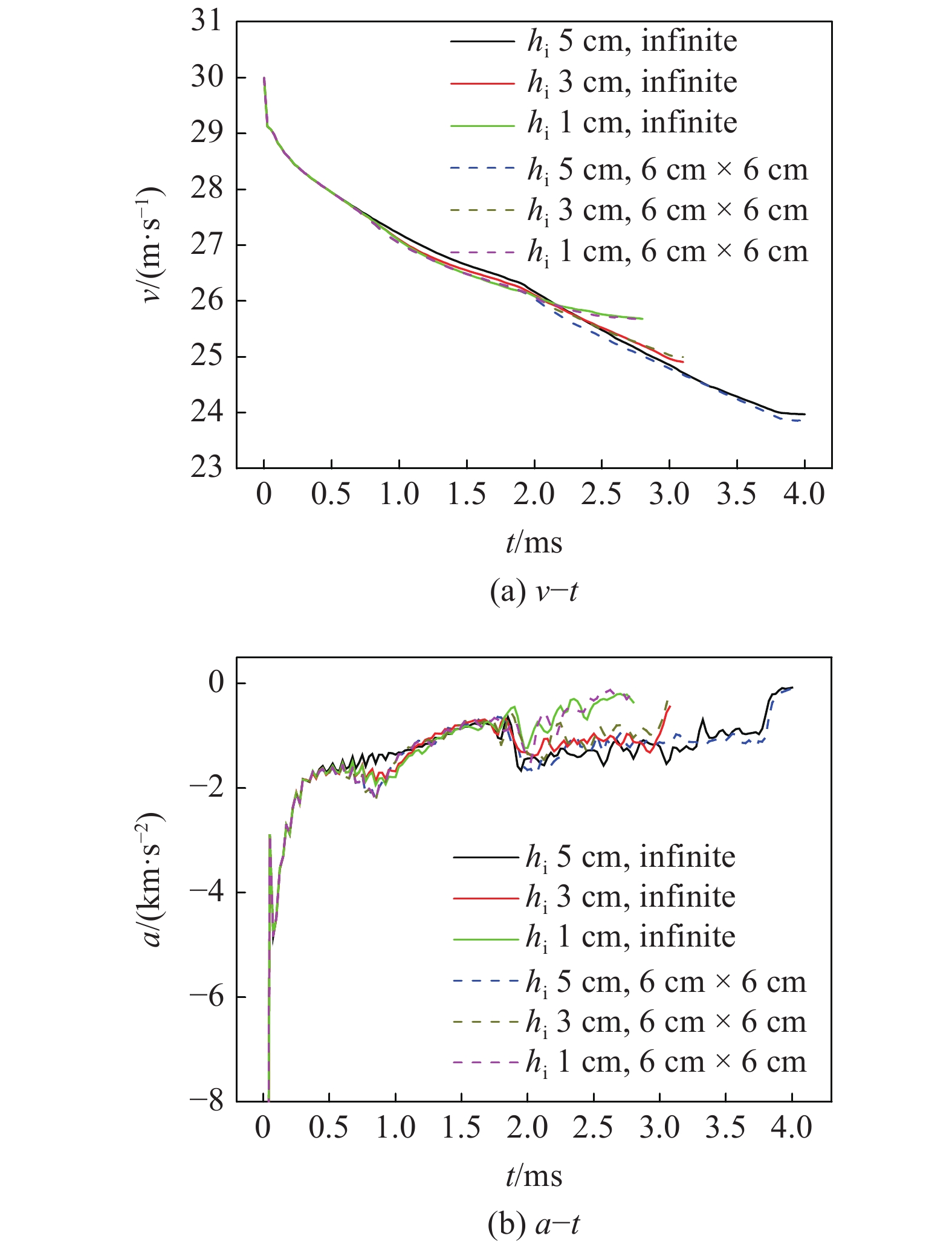
图7(a), 图7(b)分别为计算的初速度30 m/s的航行体的速度变化和加速度变化历史. 当航行体在水中的运动流场稳定后, 其加速度约90g ~ 180g. 约1.65 ms时刻, 航行体撞击冰层, 此时航行体的速度为26.6 m/s. 由图7中计算结果可以看出, 对于3 cm和5 cm厚的冰, 无论是无限冰层还是6 cm × 6 cm碎冰, 它们对航行体速度和加速度的影响基本相同, 加速度约130g, 呈现稳定侵彻现象, 航行体穿越5 cm冰层后的剩余速度约24 m/s, 穿越3 cm冰层后的剩余速度约24.9 m/s. 而1 cm厚的无限大冰层或碎冰, 对航行体运动特性的影响均较小, 加速度仅有100g, 航行体穿冰后的剩余速度约25.7 m/s.
图8为计算的不同冰层条件下初速度30 m/s的航行体的头部应力变化历史. 由计算结果可以看出, 对于5 cm厚的无限大冰层、碎冰以及3 cm厚的无限大冰层, 它们在航行体头部造成的平均应力基本相同, 约7.7 MPa, 明显低于初速度40 m/s时的最大应力12.3 MPa, 并且3 cm厚的碎冰可以造成相当的最大头部应力, 只是其应力脉冲略小; 而对于1 cm厚的无限大冰层或碎冰, 其在航行体头部产生的最大应力为3.8 MPa, 高于初速度40 m/s时的最大应力2.2 MPa, 这是因为对于1 cm厚的薄冰, 航行体速度越大, 其通过水的运动冲击越容易使冰层中间开裂上鼓, 所以造成航行体的头部应力较小.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-082-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
不同冰层时初速度30 m/s的航行体的速度和加速度变化
Figure
7.
Speed and acceleration history for 30 m/s vehicle impacting with different ice targets
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-082-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
不同冰层时初速度30 m/s的航行体的头部应力历史
Figure
8.
Stress history at the 30 m/s vehicle head with different ice targets
下载: 全尺寸图片
幻灯片
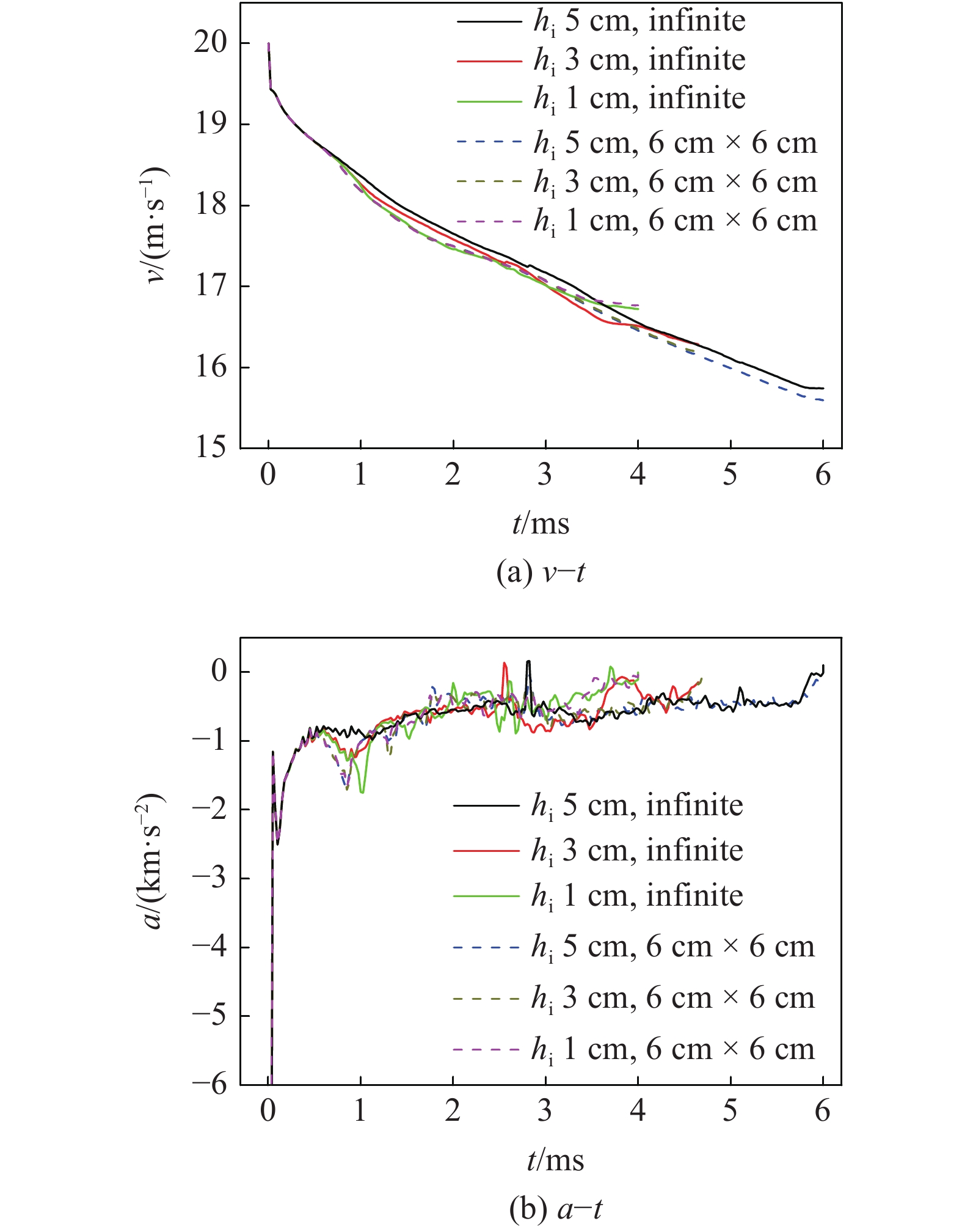
图9(a), 图9(b)分别为计算的初速度20 m/s的航行体的速度变化和加速度变化历史. 航行体在水中的运动流场稳定后, 其加速度约50g ~ 90g. 约2.45 ms时刻, 航行体撞击冰层, 此时航行体的速度为17.3 m/s. 由计算结果可以看出, 不同厚度冰层对航行体加速度的影响差别较小, 平均加速度约60g ~ 80g. 无论对于碎冰还是无限冰层, 航行体穿越1 cm，3 cm和5 cm冰层后的剩余速度分别为16.7 m/s，16.3 m/s和15.8 m/s.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-082-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
不同冰层时初速度20 m/s的航行体的速度和加速度变化
Figure
9.
Speed and acceleration history for 20 m/s vehicle impacting with different ice targets
下载: 全尺寸图片
幻灯片
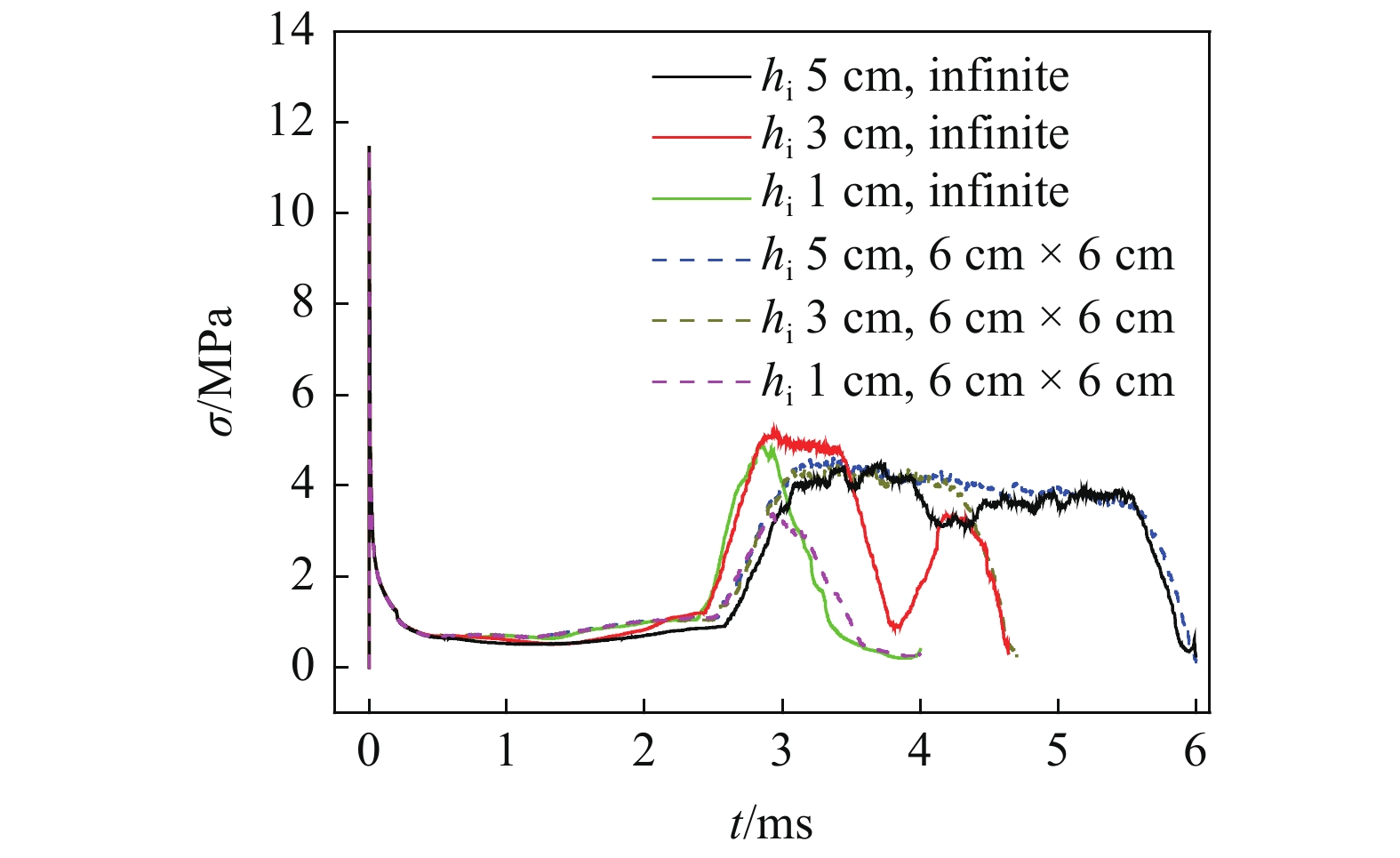
图10为计算的初速度20 m/s的航行体撞击不同冰层时头部的应力变化历史. 由计算结果可以看出, 对于低速撞击, 不同厚度冰层对航行体头部造成的最大应力基本相同, 约4.5 MPa, 仅有1 cm厚碎冰造成的头部应力较小, 只有3.1 MPa, 表明航行体在该速度下的水下运动对1 cm厚的无限冰层和碎冰造成的前期破坏不同. 值得注意的是, 1 cm厚的无限冰层造成的航行体头部最大应力高于初速度40 m/s和30 m/s时的结果, 这同样是由于对于薄冰, 航行体初速度越小, 其通过水的运动对冰层中间的前期破坏越小, 致使其头部应力较大.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-082-10.jpg'" class="figure_img
figure_type1 bbb " id="Figure10" />
图
10
不同冰层时初速度20 m/s的航行体的头部应力历史
Figure
10.
Stress history at the 20 m/s vehicle head with different ice targets
下载: 全尺寸图片
幻灯片
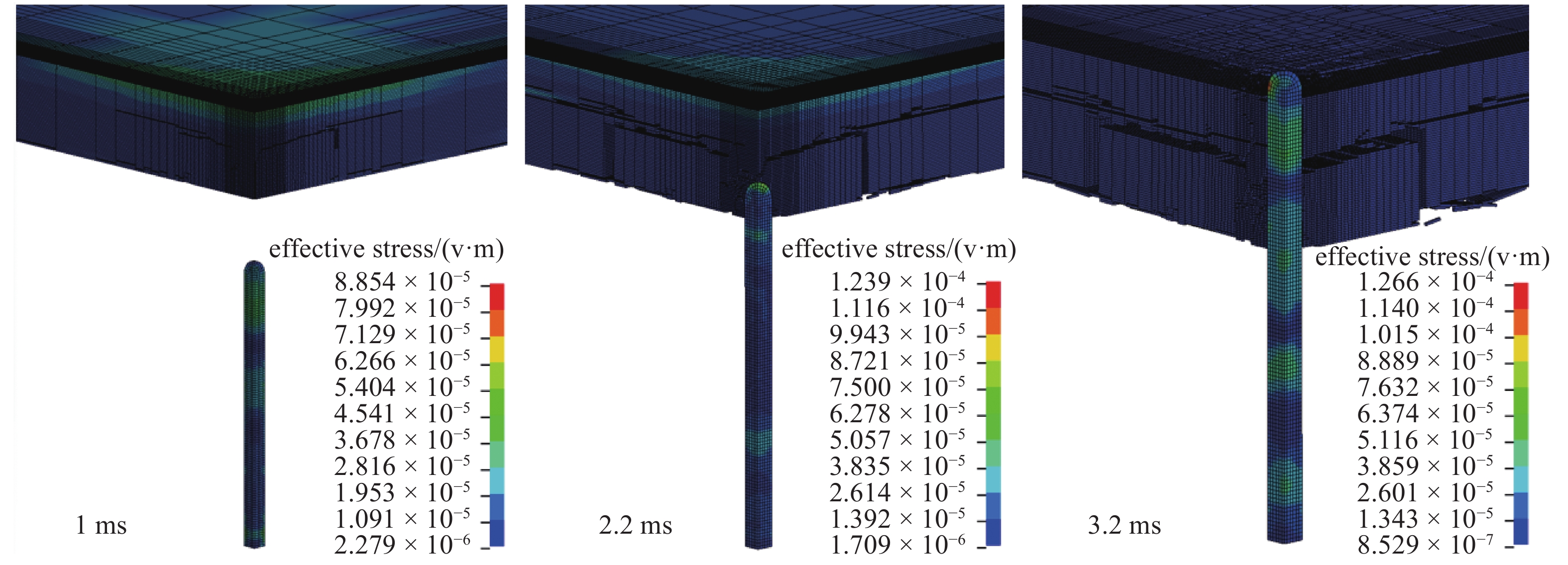
图11为初速度30 m/s的航行体出水穿越3 cm厚无限冰层时不同时刻的应力分布, 为了清晰可见, 隐去了水和空气流体介质单元, 仅显示航行体和冰层固体单元. 由图11可以看出, 1 ms时刻, 由于航行体高速运动引起周围的水介质向上运动, 导致冰内部出现应力, 并且由于局部单元失效出现裂纹; 2.2 ms时刻, 冰层断裂为碎冰块, 此刻航行体头部已进入冰层, 出现稳定的侵彻阶段; 3.2 ms时刻, 航行体头部已完全穿出冰层, 此时冰内应力已经很小, 仅有航行体内部应力波的传播和衰减.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-082-11.jpg'" class="figure_img
figure_type2 ccc " id="Figure11" />
图
11
初速度30 m/s的航行体撞击3 cm厚冰层不同时刻的应力分布
Figure
11.
Stress distribution of vehicle with initial velocity 30 m/s and 3 cm thick ice target at different time
下载: 全尺寸图片
幻灯片
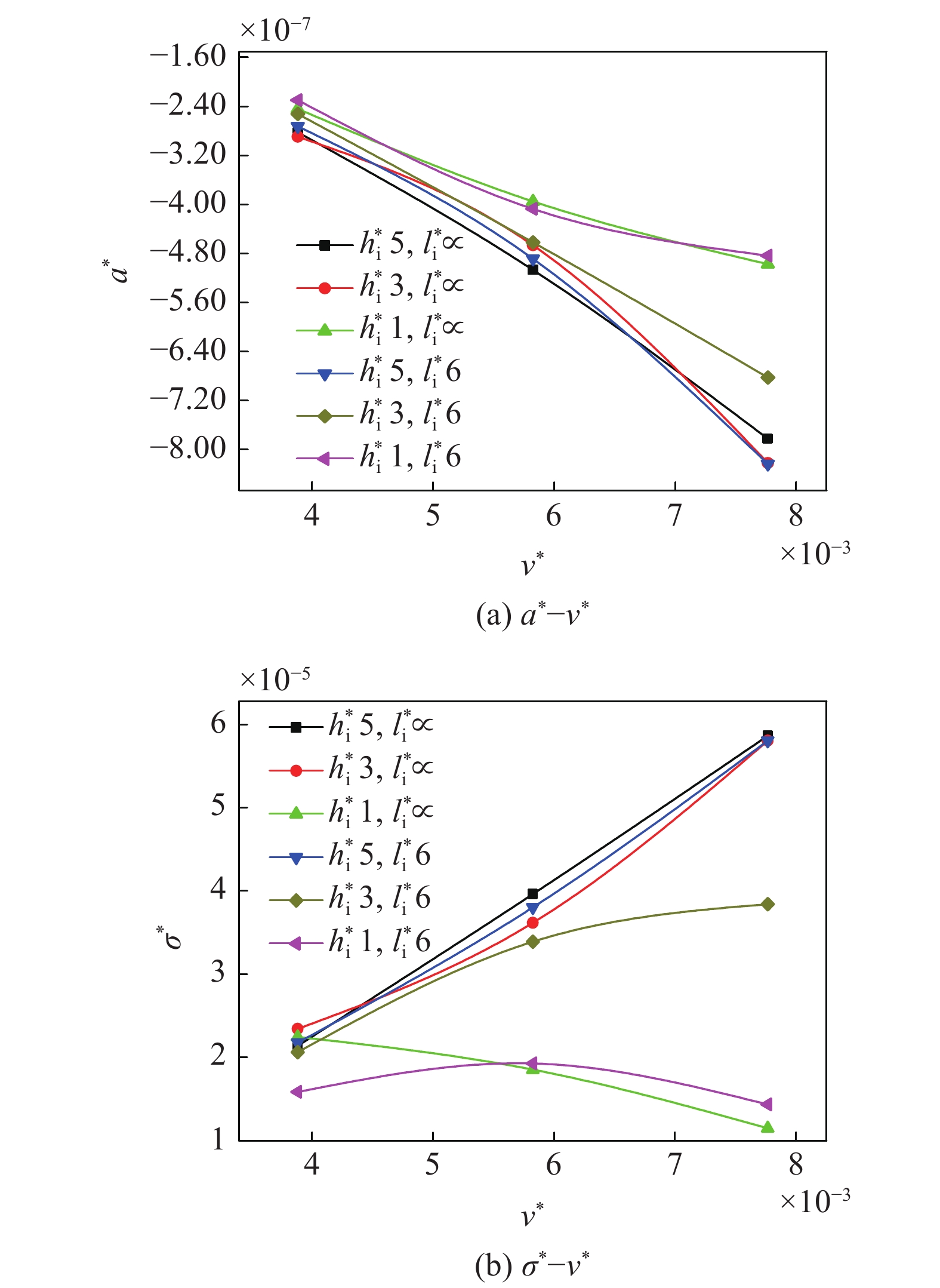
图12分别为不同工况下航行体的无量纲最大过载和最大头部应力随无量纲初始发射速度的变化情况. 由计算结果可以看出, 航行体速度越大, 不同冰层对其过载和头部应力的影响差别越大, 这主要是因为在航行体速度较大时, 不同冰层受到的前期破坏程度不同. 从碎冰和无限冰层尺寸效应来看, 无量纲厚度hi*为3的两种冰对高速航行体的过载和头部应力的影响差别较大, 而无量纲厚度hi*为1和5的碎冰与同厚度无限冰层的影响差别均较小. 当冰层较厚、较大时, 航行体速度越大, 其过载和头部应力越大; 而对于较薄的的冰层, 由于其前期破坏较严重, 所以航行体过载随速度增大而增大的趋势相对较小, 尤其对航行体头部应力的影响规律性较差.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-082-12.jpg'" class="figure_img
figure_type1 bbb " id="Figure12" />
图
12
不同冰层时航行体最大过载与最大头部应力随速度的变化
Figure
12.
Variation of maximum overload and head stress of vehicle with speed for different ice targets
下载: 全尺寸图片
幻灯片
4.
结论
本文针对航行体出水破冰的应用背景, 通过量纲分析, 获得了影响航行体动载荷及其头部应力的主控参数和相似律. 利用LS-DYNA, 对不同初速度的航行体出水穿越不同冰层进行了数值模拟研究, 获得了其动力学载荷特性及作用机理. 计算结果表明, 航行体速度越大, 通过水介质对不同冰层的前期破坏差别越大, 导致冰?水?结构耦合作用的影响效果差异明显. 对于较厚的冰层, 航行体穿冰后期呈现稳定的侵彻现象, 航行体的载荷特征仅与其速度和冰的动态力学性能相关. 对于较薄的冰层, 需要考虑其撞击前的破坏程度. 对于中等厚度的冰, 在较高冲击速度下才表现出径向尺寸效应相关的载荷作用机制, 低速条件下, 径向尺寸大于6倍航行体直径的碎冰和无限大冰层的影响效果基本相同. 本文研究 结果可为冰区环境下航行体的出水发射提供理论 参考.
