 ,2), 林鹏智
,2), 林鹏智 ,3)
,3)WAVE-INDUCED FORCE ON FLEXIBLE MARSH PLANTS1)
Zhang Xiaoxia ,2), Lin Pengzhi
,2), Lin Pengzhi ,3)
,3)通讯作者: 2)张小霞, 博士, 主要研究方向: 环境流体力学及生态减灾. E-mail:zhangxiaoxia@stu.scu.edu.cn;3)林鹏智, 教授, 主要研究方向: 计算流体动力学及其工程应用. E-mail:cvelinpz@scu.edu.cn
收稿日期:2020-12-15接受日期:2021-02-28网络出版日期:2021-04-08
| 基金资助: |
Received:2020-12-15Accepted:2021-02-28Online:2021-04-08
作者简介 About authors

摘要
草本盐沼植物广泛分布于海岸带形成滨海湿地系统, 这些滨海湿地具有生态、旅游、养殖及减灾等多方面价值. 草本植物的消浪作用在海岸稳固和沿海防灾减灾等方面发挥了重要作用. 已有植物消浪研究通常过度简化, 将植物视为刚性圆柱并依赖于调节经验拖曳力系数来提高预测准确度, 对柔性植物与波浪的相互作用机理研究还很欠缺. 草本植物通常由多片柔性叶片和一根柔性相对较小的杆茎组成. 在波浪作用下, 植物的叶片与杆茎产生不同程度的动态变形以及相互作用, 从而改变波浪与植物间的相对运动速度, 使得柔性植物受力特性十分复杂. 本文采用简单柔性结构物受力尺度定律计算单片叶片和单根杆茎受力, 并用遮蔽系数量化叶片与杆茎间相互作用引起的叶片受力降低程度, 提出了波浪作用下柔性草本植物动态受力计算公式. 与单片叶片、单根杆茎和既有叶片又有杆茎的模型植物及真实植物样本测量受力比较表明, 本文提出的植物受力模型可较好地预测植物最大受力及植物受力随波浪周期的变化情况.
关键词:
Abstract
Salt marshes are common features in coastal regions and forming eco-rich wetlands. These wetlands provide ecosystem services, tourism and fishery benefits, as well as coast protection. Salt marshes can dissipate wave energy, which enhances coastal stability and protects the shoreline from storms and small tsunami waves. Previous wave damping predicting methods are usually oversimplified by modeling plants as rigid cylinders. Further, these studies strongly depend on the adjustment of empirical drag coefficient, while a knowledge gap exists between the mechanism of flexible plant-wave interaction. A marsh plant usually consists of multiple flexible leaves and a less flexible central stem, both the geometric and flexibility of the leaves and the stem affect the drag on the full plant. Under waves, the leaves and the stem reconfigure to different degrees at different speeds. The dynamic response of plant elements reduces the relative velocity between the wave and the plant. Further, the leaves and the stem interact with one another, making the characteristics of wave-induced plant force highly complicated. Build on the force scaling law for a simple plant element, such as a flat leaf or a cylindrical stem, we proposed a simple equation to predict the drag on plants with both leaves and stem. The force on the full plant is the sum of the force on the leaves and the force on the stem. The force on a representative leaf and the stem were estimated by the force scaling law. The force due to all the leaves was estimated by the force on the representative leaf using a sheltering coefficient, which accounts for the drag reduction in the leaves due to the interaction between the leaves and the stem. The model predicted maximum drag and the drag force over the wave period agreed well with the experiment measured drag force on an individual leaf, an individual stem, and model and live plants with both leaves and stem.
Keywords:
PDF (7422KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
张小霞, 林鹏智. 波浪作用下柔性草本植物受力特性研究1). 力学学报[J], 2021, 53(4): 1018-1027 DOI:10.6052/0459-1879-20-429
Zhang Xiaoxia, Lin Pengzhi.
引言
以芦苇、碱蓬、互花米草和海三棱麃草等主要植物种类构成的滨海盐沼湿地广泛分布于河口及海岸带[1], 覆盖了全球约22 000 $\sim$ 400 000 km$^{2}$的区域[2]. 随着海岸带经济快速发展, 草本岸线遭受严重破坏[3], 研究发现在人类历史上, 全球12个大型河口湿地面积流失比例高达67${\%}$[4]. 人类在大量侵占和破坏滨海草本湿地的同时, 也逐渐认识到这些滨海湿地在维持近岸及海洋生物多样性, 净化和美化海岸环境, 促进水产和旅游资源可持续利用以及稳固海岸和防治海洋灾害等方面有着十分重要的作用[5].滨海湿地是天然的海岸屏障, 盐沼植物能够减小床面冲刷[6]和植被区泥沙再悬浮[7], 促进泥沙在植物区淤积[8], 防治海岸侵蚀[9-10], 消减波浪[11-12]并减小沿海城市洪水灾害[13-14]. 研究表明, 波浪在植物区传播时波高消减率远远高于邻近无植物光滩[13], 盐沼植物区波高消减率达每米7.4${\%}$, 而邻近相似底床条件下的无植物光滩仅为每米0.53${\%}$[15-16]. 盐沼植物结构复杂, 其杆茎和叶片具有不同的柔性和几何形态. 在波浪作用下, 柔性较大的叶片产生大幅度摆动, 叶片受力传递到杆茎上进而影响杆茎的动态响应和受力特性. 盐沼植物叶片与杆茎对波浪的阻力做功消耗波浪能量, 叶片和杆茎的柔性及几何形态均会影响盐沼植物的消浪特性[17-18]. 然而, 已有研究对波浪作用下既有叶片又有杆茎的柔性植物响应机理及受力特性研究还很欠缺[19]. 对植物变形和受力特性研究的不足进一步限制了对滨海湿地植被消浪效率的预测能力.
已有研究对简单刚性植物[20-21]及柔性海草[22-24]在波浪作用下的受力研究较深入. 首先, 矩形叶片研究人员通过试验获取了单根刚性圆柱杆茎和叶片的拖曳力系数和惯性力系数随波浪条件的变化规律[21]. 其次, 假定柔性植物的拖曳力系数和惯性力系数与对应的刚性圆柱杆茎和矩形叶片的系数相同, 但考虑植物变形引起的阻水面积及水流与植物间的相对运动速度变化, 建立了简单柔性植物的受力理论模型[22-23,25]. 这些模型预测与试验测量植物受力吻合较好, 表明合理的考虑植物柔性及水体与植物间的相对运动速度时, 刚性植物的拖曳力系数可以用于计算柔性植物受力[23]. Luhar和Nepf[26]及Lei和Nepf[24]采用单根柔性叶片受力模型预测单根海草受力, 准确预测了不同密度和波浪条件下的海草群消浪效率, 表明单根植物柔性变形可准确描述柔性植物受力特性并可用于建立植物群消浪预测模型. 在波浪作用下, 草本植物叶片和杆茎产生不同程度的动态变形, 且叶片与杆茎间产生互相影响使得波浪与盐沼植物相互作用机制十分复杂,已有研究对植物的结构特征及其动态响应考虑还很欠缺[27]. Zhang和Nepf[28]将盐沼植物受力视为叶片和杆茎受力之和, 采用遮蔽系数量化杆茎与叶片间的相互影响, 提出了计算单根盐沼植物在波浪作用下的最大受力预测模型. 本文进一步优化Zhang和Nepf[28]提出的草本植物受力模型并将其拓展到预测整个波浪周期内的植物动态受力.
1 理论模型
1.1 简单刚性植物受力
刚性植物对恒定水流产生的阻力与植物阻水面积和流速平方成正比. 波浪作用下, 水质点运动速度随时间变化引起植物受力随波浪周期性变化, 而且水体运动加速度对植物产生惯性力. 滨海地区通常为浅水波(水质点垂向运动速度明显小于水平运动速度), 植物受到的垂向作用力与水平作用力相比可以忽略. 水平方向上植物受力可采用Morison公式计算[20]式中, $F_{r} $为刚性植物受到的波浪作用力, $F_{d} $为拖曳力, $F_{i} $为惯性力, $\rho $为流体密度, $C_{D}$为波浪条件下的拖曳力系数, $A$为植物阻水面积(即植物在垂直于来波方向的平面上的投影面积). $u=u(t,z)$为波浪水质点水平运动速度, $C_{M} $为惯性力系数, $V_{p}$为植物淹没体积.
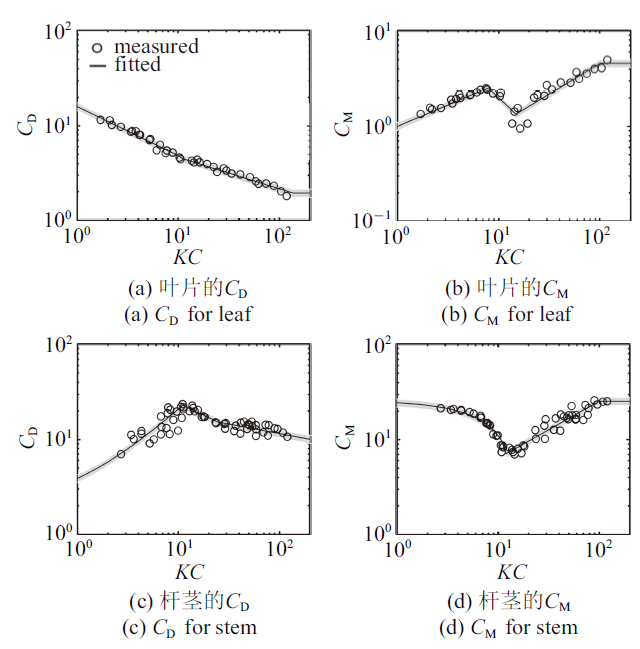
早期试验研究发现$C_{D} $与物体的几何形态相关, 而且对于同一物体$C_{D}$也会随水动力条件, 如雷诺数($Re)$以及Keulegan和Carpenter数($KC)$等的变化而变化. Keulegan和Carpenter[21]试验测量了刚性圆柱(本文用于代表植物杆茎)和刚性薄平板(代表植物叶片)在波浪作用下的受力并分析得到拖曳力系数和惯性力系数. 该研究发现$C_{D} $和$C_{M} $均可表示为$KC$数的函数, 对于叶片$KC=U_{w} T_{w} /b$, $U_{w} $为波浪作用下水质点的最大水平运动速度, $T_{w} $为波浪周期, $b$为叶片宽度, 对于圆柱杆茎$KC=U_{w} T_{w} /D$, $D$为圆柱直径. 依据Keulegan和Carpenter[21]试验数据, 按$KC$数分区拟合得到叶片和杆茎的拖曳力系数及惯性力系数表达式如式(2) $\sim\!$式(5), 拟合公式(曲线)与试验数据(圆圈)比较情况如图1所示, 试验数据基本分布在拟合结果的10${\%}$误差范围(图1灰色填充区域). 注意在$KC>100$时测量数据缺乏, 本文将这一范围内的惯性力系数设为常数, 与$KC=100$时的惯性力系数相等. 随着$KC$数增大, 水流特性将趋近于明渠流, 因此在大$KC$数时, 叶片和杆茎拖曳力系数趋于常数, 分别为1.95和1. 采用式(1)和式(2) $\sim\!$式(5)可以计算出刚性叶片和刚性杆茎在波浪作用下的受力大小随波浪相位的变化.
叶片
杆茎
图1
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图1叶片和杆茎的拖曳力系数和惯性力系数
Fig.1Drag and inertial coefficient for the leaves and the stem
1.2 简单柔性植物受力尺度定律
一些盐沼及海草植物结构较为简单, 仅由柔性杆茎或叶片组成, 如Scirpus tabernaemontani仅有单根杆茎, 多数海草的地上结构以叶片为主, 可视为单片叶片组成的植物群落. 与刚性植物相比, 简单柔性植物在水流作用下弯曲变形形成更具流线型特性的结构, 同时, 植物阻水面积也会降低, 从而减小植物受力. 在波浪作用下, 柔性植物动态变形响应, 使得植物与水流间的相对运动速度$u_{R} $不同于水质点运动速度$u$, 通常情况下$u_{R} <u$, 进一步减小植物受力. 为描述柔性植物变形以及这一过程对植物受力的影响, 研究人员针对简单柔性结构物建立了一些理论模型[22,29-30]. 在此基础上, Luhar和Nepf[23]全面考虑柔性植物的各项受力, 建立了波浪作用下海草叶片的动态平衡方程, 将叶片受力表示为3个无量纲参数的函数: 浮力系数$B$, 表示因浮力和叶片刚度产生的恢复力的比值; 波浪Cauchy数$Ca$, 表示水流拖曳力和叶片刚度引起的恢复力的比值; 长度比尺$L$, 表征叶片长度$l$与波浪水质点迁移幅值($A_{w} =U_{w} T_{w} /(2\pi ))$的比值式中$\Delta \rho $为水密度$\rho $与植物密度$\rho_{p} $之差, $g$为重力加速度. $E$为弹性模量, $I=bd^{3}/12$为二阶截面矩, $b$, $d$和$l$分别为叶片的宽度、厚度和长度. 采用对应的几何及力学参数也可定义植物杆茎的无量纲参数, 为便于区分, 分别以下标l和s表示与叶片($B_{l} $, $Ca_{l} $和$L_{l} )$和杆茎($B_{s} $, $Ca_{s} $和$L_{s} )$相关的参数.
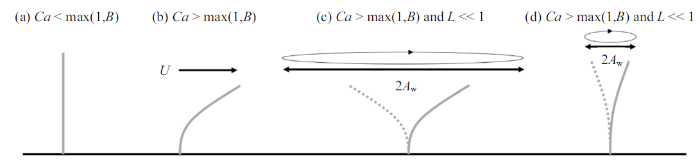
当水流拖曳力小于变形引起的恢复力($Ca<1)$或浮力引起的恢复力($Ca<B)$时, 叶片保持直立, 表现出刚性特性(图2(a)), 柔性植物有效受力$F_{e} $与刚性植物受力相近, 即$F_{e} \approx F_{r} $. 当水流拖曳力大于叶片变形产生的恢复力和浮力时, 即$Ca>\max (1,B)$, 叶片开始变形(向水流下游弯曲)(图2(b)), 使叶片更具流线型特征且阻水面积减小从而减小叶片受力. Luhar和Nepf[31]研究表明这一范围内叶片受力服从尺度规律$F_{e} /F_{r} \sim Ca^{-1/3}$.
图2
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图2叶片(或杆茎)在流体作用下的变形随无量纲参数$B$, $Ca$和$L$的变化图
Fig.2Reconfiguration of leaf (or stem) under flow with varying $B$, $Ca$, and $L$
波浪作用下, $L$也会影响叶片变形和受力, 当$L\ll 1$时, 波浪水平迁移幅值远大于植物长度, $A_{w} \gg l$, 叶片在波浪周期内的运动位移远小于水质点的运动位移, 水质点与叶片的相对速度接近水质点的运动速度, $u_{R} \approx u$ (图2(c)). 因此叶片变形和受力接近恒定流尺度规律, 即当$Ca>\max(1, B)$且$L\ll1$时, 叶片有效长度服从尺度规律$F_{e} /F_{r} \sim Ca^{-1/3}$, 不受$L$影响.
波浪作用下, $Ca>\max(1, B)$且$L>1$时, 波浪水平运动幅值$A_{w} <l$, 叶片随波浪往复运动, 叶片尖部运动幅值与波浪水平迁移幅值接近(图2(d)). Luhar和Nepf[31]提出了有效长度$l_{e} $, 其物理含义为叶片与水流有明显相对运动的长度, 超过这一长度的部分随着流体同步运动, 由此可知叶片受力仅由有效长度段提供. Luhar和Nepf[23]试验结果和理论模型预测结果表明在这一范围内, 柔性叶片受力$F_{e} $与几何结构相同的刚性叶片受力$F_{r} $服从
式中, $K$为比例系数. Lei和Nepf[24]采用柔性叶片开展的大量叶片受力测试表明$K=K_{l} =0.94\pm 0.06$, 为简便起见本文采用$K_{l} =1$. 柔性杆茎与叶片受到相同的外力作用项, 因此式(9)也可用于描述杆茎的有效受力. 但应注意Lei和Nepf[24]在定义波浪Cauchy数时没有包含拖曳力系数, 因此杆茎与叶片$Ca$相同时, 两者拖曳力系数不同使得波浪对两者的拖曳力大小不同, 需要采用对应的系数$K_{s} $和$K_{l} $加以反映. 研究表明采用$Ca'=C_{D} Ca$定义的Cauchy数[32]时, 截面形状不同的柔性杆受力规律相同, 即$F_{e} /F_{r} =K'(Ca'L)^{-1/4}$, $K'$为通用的比例系数. 分别考虑叶片和杆茎的参数可得$K_{s} =K_{l} (C_{D,s} /C_{D,l} )^{-1/4}$. 由图1知, 叶片的拖曳力系数明显大于圆柱杆茎, 在$4\leqslant KC\leqslant 100$的范围内, 两者的平均比值为$C_{D,s} /C_{D,l} =1/2.6$, 取这一比例, 有$K_{s} =(1/2.6)^{-1/4}$.
1.3 盐沼草本植物受力公式
典型的盐沼草本植物, 可视为$N_{l} $片叶片和一根杆茎组成, 通常叶片可看作柔性薄平板, 杆茎可视为柔性圆柱杆, 这些叶片沿杆茎高度及四周均匀分布. 为简化问题假定植物的几何参数(叶长$l_{l}$、叶宽$b$、叶厚$d$、杆茎高度$l_{s} $和直径$D)$, 材料密度$\rho_{p}$和弹性模量($E_{l}$和$E_{s} )$均为常数. 对于常见的盐沼植物, 材料密度分布在800 $\sim$ 1000 kg/m$^{3}$[24,33], 在较广的植物参数及海岸水动力条件下均满足$Ca>\max(1, B)$且$L>1$(图2(d))[34], 在波浪作用下, 叶片和杆茎单独作用时均服从尺度定律式(9). 多个结构物近距离分布时会影响彼此的动态响应和受力[35-36], 采用单片垂直放置叶片和单根杆茎单独作用时的受力, 并用遮蔽系数$C_{s} (0\leqslant C_{s} \leqslant 1$, 其中$C_{s} =0$表示完全遮蔽, $C_{s} =1$表示无遮蔽)表征叶片与杆茎间相互作用引起的叶片受力减小程度, 提出波浪对单根植物的总作用力表达式(10). 式(10)基于Zhang和Nepf[28]式(14), 并采用系数$K_{l} $和$K_{s}$来反映拖曳力系数差异对叶片和杆茎受力的影响, 此外, 采用$F_{r,l} $和$F_{r,s}$计算代表性刚性叶片和杆茎受力代替Zhang和Nepf[28]式(14)中的最大刚性叶片和杆茎受力以便将该公式推广到预测整个波浪周期内的植物受力情况, 即忽略植物参数的垂向变化, 考虑线性波作用下水质点水平运动速度$u(t,z)$ = $a_{w} \omega$ $(\cosh kz/\sinh kh)\times$ $\cos (\omega t)$ = $U_{w} \cos (\omega t)$, 其中$a_{w} $为波幅, $\omega =2\pi /T_{w} $为波浪角频率, $k$为波数, $t$和$z$分别表示时间和垂向坐标, 于是基于式(1)可将$F_{r,l} $和$F_{r,s} $表示为式(11)和式(12). 注意$F_{r,l}$定义为沿杆茎的积分, 并假定沿杆茎分布的多片叶片受力大小均相同. 这一叶片受力定义方式与杆茎受力形式相近, 可以简化植物整体受力计算, 得
2 模型验证与分析
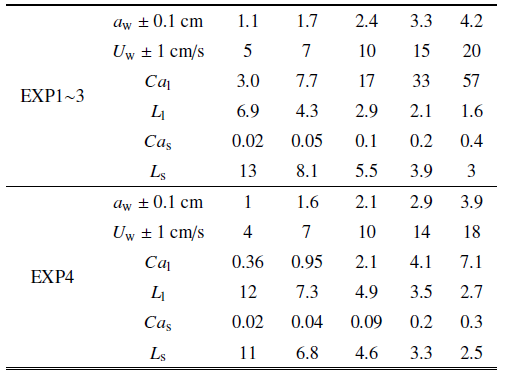
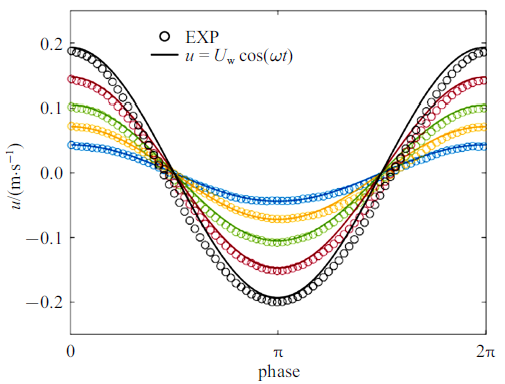
Zhang和Nepf[28]测量了单片叶片、单根杆茎、完整模型植物及真实互花米草植物样本4种植物在波浪作用下的受力, 分别为试验1 $\sim$ 4. 所用植物参数及测试工况如表1和表2所示(同Zhang和Nepf[28]研究中表1和表2), 其中试验3所用的模型植物由10片叶片(叶片参数与试验1相同)和1根杆茎(与试验2相同)组成. 试验4所用真实植物具有5片叶片, 表中$l_{l} $, $b$, $d$为这些叶片长度、宽度和厚度的平均值$\pm$标准差, 杆径$D$为沿杆长的平均直径. 所有试验水深均为32 cm, 波浪周期均为2 s. 在每组试验中, Zhang和Nepf[28]同步采集了水面波动和植物受力, 数据采集时长为3 min (包含90个完整波浪周期). 本节分别采用基于尺度定律的植物受力预测公式(9)和(10)预测四种植物的受力并与Zhang和Nepf[28] 测量的相位平均植物受力和水面波动进行比较, 分析本文公式的预测准确性. 为简化计算并保证模型准确性, 式(11)和式(12)中速度取为淹没植物高度范围的测量垂向平均速度最大值$U_{w} $ (见表2)定义的线性波速度, 即$u(t,z)=U_{w} \cos (\omega t)$, 这一速度与测量速度比较如图3所示, 两者误差为5${\%}$ $\sim$ 10${\%}$.Table 1
表1
表1试验植物材料参数表
Table 1
 |
新窗口打开|下载CSV
Table 2
表2
表2试验工况及无量纲参数
Table 2
 |
新窗口打开|下载CSV
图3
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图3试验1至3测量速度与线性波速度比较(不同颜色代表不同波幅)
Fig.3Comparison of measured and linear wave orbital velocity for EXP1 to 3. Different color corresponds to different $a_{w} $
2.1 单片叶片和单根杆茎的受力
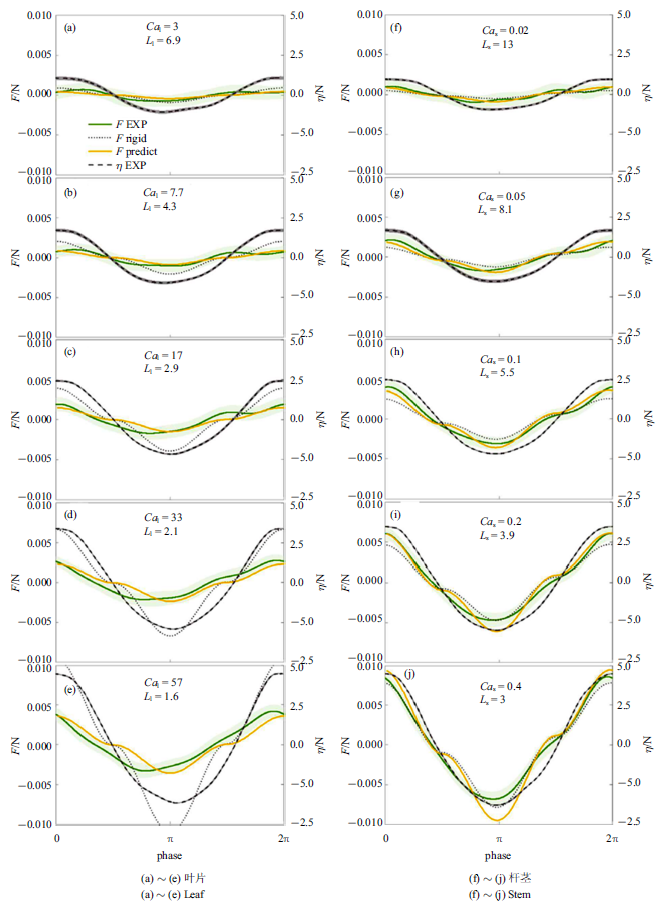
采用$K_{l} =1$和$K_{s} =(1/2.6)^{-1/4}$, 基于简单柔性植物尺度定律的植物受力预测公式(9)预测结果与Zhang和Nepf[28]测量单片叶片(图4(a) $\sim\!$图4(e))和单根杆茎(图4(f) $\sim\!$图4(j))受力总体吻合较好. 图4中左右两列图从上至下波幅依次增大, 图中绿色和灰色阴影分别为测量受力及水面波动在对应相位的标准差. 其中, 最大和最小受力值的平均相对误差分别为 19${\%}$ (叶片)和15${\%}$ (杆茎). 实测叶片受力在波谷处超前于波浪相位约$\pi /4$ (图4(a) $\sim\!$图4(e)), 但杆茎测量受力与水面波动间无明显相位差(如图4(f) $\sim\!$图4(j)). 前人试验也观察到柔性植物变形幅度与水面波动间可能存在相位差[22-23,37], 最大相位差达$\pi /2$. 但简化受力计算式(9)预测植物受力与水面波动间相位一致. 在波浪反向时(水面波动幅度$\eta=0$), 预测受力与测量结果的变化规律有所不同, 这主要是因为预测公式采用周期平均的拖曳力系数, 而式(9)中拖曳力项含$u$平方项($\sim \cos (\omega t)\left| {\cos (\omega t)} \right|)$故在$\eta =0$处出现拐点. 试验中, 植物与波浪相互作用时拖曳力系数会随$u$的变化而变化[21], 在$u$较小时, 拖曳力系数较大, 因而测量受力在波浪周期内的变化曲线更加光滑. 此外还观察到, 杆茎(图4(f) $\sim\!$图4(j))在前半个波浪周期(波浪从波峰转向波谷)的受力小于后半个波浪周期(从波谷转向波峰), 而叶片(图4(a) $\sim\!$图4(e))受力在前后半个波浪周期内大致对称相等. 这是因为惯性力在前半个波浪周期($u$减小, $\partial u/\partial t<0)$降低$F_{e} $, 而在后半个波浪周期($u$增大, $\partial u/\partial t>0)$增加$F_{e} $, 且惯性力与植物横截面积成正比, 所以横截面积更大的圆柱杆茎呈现明显的不对称性, 但横截面积较小的叶片大致对称.图4
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图4式(9)预测受力与测量相位平均受力比较
Fig.4Comparison of Eq.(9) predicted force with the measured phase-averaged force
采用式(11)预测刚性叶片(图4(a) $\sim\!$图4(e)黑色点线)受力明显高于柔性叶片测量受力, 且高估程度随波幅增加而增大, 这与尺度定律式(9)吻合. 相反的, 式(12)预测刚性杆茎受力却小于杆茎实际测量受力. 这是因为测量杆茎刚度较大($Ca_{s} <1)$, 杆茎单独作用时出现了涡激振动(vortex induced vibration)现象[38]使得测量最大受力(绿色曲线)比绝对刚性的圆柱(黑色点线)受力更大[28], 最大高出68${\%}$(图4(f)). 随着波幅增加, $Ca_{s} $增大并趋近1, 式(12)预测的刚性圆柱受力和测量结果间的误差逐渐减小.
以上分析表明, 尺度定律公式(9)可以捕捉到柔性叶片($Ca_{l} >1)$随波浪运动引起的植物受力减小程度, 在测试范围内($0.02\leqslant Ca_{s} \leqslant 0.4)$也与杆茎涡激振动引起的杆茎受力增大幅度相吻合. 但应注意, 涡激振动仅在特定波浪频率和速度下产生, 随着波幅减小($Ca$减小), 植物逐渐趋于完全刚性, 尺度定律公式(9)应退回到$F_{e} =F_{r} $.
2.2 盐沼草本植物受力特性
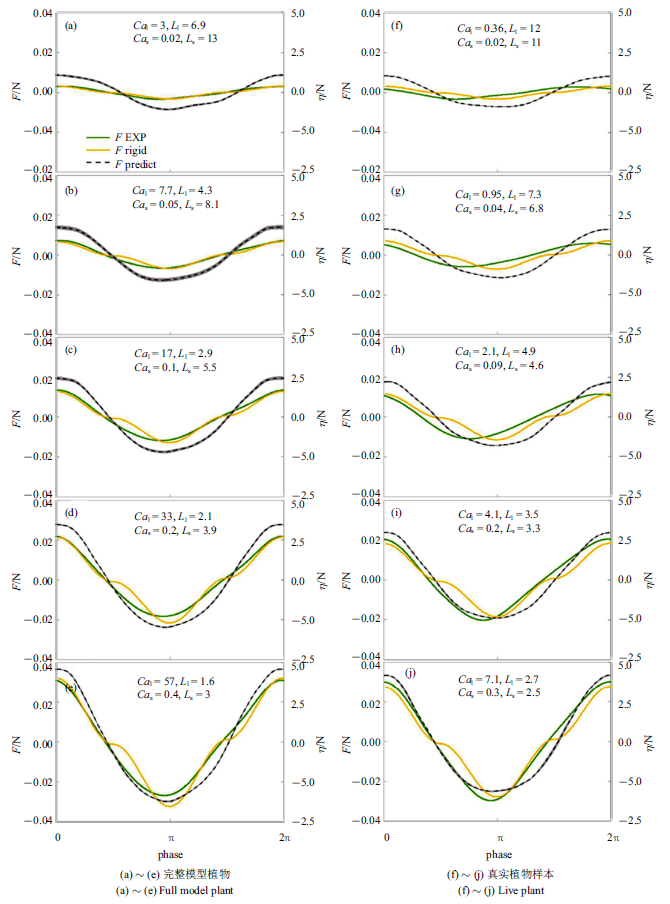
大部分盐沼植物由多片叶片和一根杆茎组成, 波浪作用下, 通常叶片产生大部分阻力[28], 杆茎可能存在的涡激振动引起的杆茎受力增大对植物整体受力预测结果影响很小, 可不考虑. 本节采用式(10)计算既有叶片又有杆茎的草本植物受力(植物参数及测试工况见表1和表2)并与Zhang和Nepf[28]试验 测量模型植物及真实植物样本受力进行比较. 预测模型植物和真实植物样本受力时同样采用$K_{l} =1$, $K_{s} =(1/2.6)^{-1/4}$, 但当$Ca_{s} <1$时, 令$F_{e,s} =F_{r,s} $. 遮蔽系数主要与植物形态和叶片分布方式有关, 定性来讲, 叶片与杆茎贴合越紧密, 单位杆茎长度叶片数量越多, 遮蔽作用越强, 即$C_{s}$越小, 本文完整模型植物和真实植物样本遮蔽系数依据Zhang和Nepf[28]试验结果分别采用$C_{s} =0.6$和$C_{s} =0.4$.预测模型植物和真实植物样本受力与试验测量的相位平均植物受力对比结果如图5所示, 图中左右两列图从上至下波幅依次增加, 绿色和灰色阴影分别为测量受力及水面波动在对应相位的标准差. 在整个波浪周期内, 式(10)预测完整模型植物(图5(a) $\sim\!$图5(e))和真实植物样本(图5(f) $\sim\!$图5(j))受力均与试验结果大体吻合, 预测与试验测量最大受力平均相对误差分别为7${\%}$ (完整模型植物)和10${\%}$ (真实植物样本). 预测植物受力与水面波动相位一致, 模型植物测量受力也大致和波浪相位同步, 真实植物样本测量受力超前波浪相位$\pi /10\sim \pi /3$, 超前幅度随波幅增大而减小. 这同单片叶片受力与波浪间的相位差接近. 预测受力在波浪反向时的规律与单片叶片单独作用时相似, 在前后半个波浪周期的受力大致对称相等, 这主要是因为叶片受力达植物总受力的72${\%}$[28]并且预测模型中叶片与杆茎的拖曳力系数均采用定值(不随波浪相位变化).
图5
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图5式(10)预测受力与测量相位平均受力比较
Fig.5Comparison of Eq.(10) predicted force with the measured phase-averaged force
3 结论
草本植物通常由多片柔性叶片和一根杆茎组成, 已有研究很少兼顾杆茎及叶片两者的作用并合理的考虑植物柔性. 本文基于Luhar和Nepf[23]提出的简单柔性植物受力尺度定律和Zhang和Nepf[28]提出的既有叶片又有杆茎的草本植物模 化方法及最大植物受力预测公式, 提出了考虑叶片和杆茎结构差异及柔性变形特性的植物受力预测公式, 所提公式可预测草本植物受力在波浪周期内的变化. 与测量受力结果比较表明, 本文计算公式可以较好地预测波浪周期内的植物最大受力及植物受力随波浪周期的变化, 当$Ca>\max (1,B)$且$L>1$时, 式(10)中的尺度系数$K_{l} =1$, $K_{s} =(1/2.6)^{-1/4}$可较好地预测复杂草本植物受力. 为简化问题, 当$Ca<\max (1,B)$时, 可将植物视为刚性, 并令式(10)中$F_{e,s} =F_{r,s} $ (即$K_{s} (Ca_{s} L_{s} )^{-1/4}=1)$.本文仅验证了模型对淹没情况下的植物受力预测准确性, 但Zhang和Nepf[28]对非淹没工况的测量及预测结果表明本文模型同样适用于非淹没情况, 只需注意预测时植物参数应对应地采用淹没部分的参数. 本文模型可以考虑水体运动速度的非规则变化, 具体来讲, 可通过修改式(11)和式(12)中的速度项来反应非规则波作用下的植物受力, 但模型的具体预测表现及非规则波作用下的模型参数(如拖曳力系数)的取值及无量纲参数(如$KC$, $Ca)$的定义还需进一步深入研究. 此外, 采用周期平均的拖曳力系数和惯性力系数不能准确反映波浪反向时的植物受力变化趋势, 本文模型也不能捕捉植物受力与波浪间的相位差, 这些仍需进一步研究.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURLPMID [本文引用: 1]

Estuarine and coastal transformation is as old as civilization yet has dramatically accelerated over the past 150 to 300 years. Reconstructed time lines, causes, and consequences of change in 12 once diverse and productive estuaries and coastal seas worldwide show similar patterns: Human impacts have depleted >90% of formerly important species, destroyed >65% of seagrass and wetland habitat, degraded water quality, and accelerated species invasions. Twentieth-century conservation efforts achieved partial recovery of upper trophic levels but have so far failed to restore former ecosystem structure and function. Our results provide detailed historical baselines and quantitative targets for ecosystem-based management and marine conservation.
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURLPMID [本文引用: 1]

Agriculture and waste are thought to account for half or more of the U.S. anthropogenic methane source. However, current bottom-up inventories contain inherent uncertainties from extrapolating limited in situ measurements to larger scales. Here, we employ new airborne methane measurements over the U.S. Corn Belt and Upper Midwest, among the most intensive agricultural regions in the world, to quantify emissions from an array of key agriculture and waste point sources. Nine of the largest concentrated animal feeding operations in the region and two sugar processing plants were measured, with multiple revisits during summer (August 2017), winter (January 2018), and spring (May-June 2018). We compare the top-down fluxes with state-of-science bottom-up estimates informed by U.S. Environmental Protection Agency methodology and site-level animal population and management practices. Top-down point source emissions are consistent with bottom-up estimates for beef concentrated animal feeding operations but moderately lower for dairies (by 37% on average) and significantly lower for sugar plants (by 80% on average). Swine facility results are more variable. The assumed bottom-up seasonality for manure methane emissions is not apparent in the aircraft measurements, which may be due to on-site management factors that are difficult to capture accurately in national-scale inventories. If not properly accounted for, such seasonal disparities could lead to source misattribution in top-down assessments of methane fluxes.
[本文引用: 1]
DOIURLPMID [本文引用: 1]

Interest in the role that ecosystems play in reducing the impacts of coastal hazards has grown dramatically. Yet the magnitude and nature of their effects are highly context dependent, making it difficult to know under what conditions coastal habitats, such as saltmarshes, reefs, and forests, are likely to be effective for saving lives and protecting property. We operationalize the concept of natural and nature-based solutions for coastal protection by adopting an ecosystem services framework that propagates the outcome of a management action through ecosystems to societal benefits. We review the literature on the basis of the steps in this framework, considering not only the supply of coastal protection provided by ecosystems but also the demand for protective services from beneficiaries. We recommend further attention to (1) biophysical processes beyond wave attenuation, (2) the combined effects of multiple habitat types (e.g., reefs, vegetation), (3) marginal values and expected damage functions, and, in particular, (4) community dependence on ecosystems for coastal protection and co-benefits. We apply our approach to two case studies to illustrate how estimates of multiple benefits and losses can inform restoration and development decisions. Finally, we discuss frontiers for linking social, ecological, and physical science to advance natural and nature-based solutions to coastal protection.
[博士论文].
[本文引用: 1]
[PhD Thesis].
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 5]
[本文引用: 4]
[本文引用: 6]
[本文引用: 5]
DOIURLPMID [本文引用: 1]

Floating plastic debris is an increasing source of pollution in the world's oceans. Numerical simulations using models of ocean currents give insight into the transport and distribution of microplastics in the oceans, but most simulations do not account for the oscillating flow caused by global barotropic tides. Here, we investigate the influence of barotropic tidal currents on the transport and accumulation of floating microplastics, by numerically simulating the advection of virtual plastic particles released all over the world's oceans and tracking these for 13 years. We use geostrophic and surface Ekman currents from GlobCurrent and the currents caused by the four main tidal constituents (M 2 , S 2 , K 1 , and O 1 ) from the FES model. We analyze the differences between the simulations with and without the barotropic tidal currents included, focusing on the open ocean. In each of the simulations, we see that microplastic accumulates in regions in the subtropical gyres, which is in agreement with observations. The formation and location of these accumulation regions remain unaffected by the barotropic tidal currents. However, there are a number of coastal regions where we see differences when the barotropic tidal currents are included. Due to uncertainties of the model in coastal regions, further investigation is required in order to draw conclusions in these areas. Our results suggest that, in the global open ocean, barotropic tidal currents have little impact on the transport and accumulation of floating microplastic and can thus be neglected in simulations aimed at studying microplastic transport in the open ocean.
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 16]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
DOIURLPMID [本文引用: 1]

A method for the computation of low Reynolds number dynamic blood cell systems is presented. The specific system of interest here is interaction between cancer cells and white blood cells in an experimental flow system. Fluid dynamics, structural mechanics, six-degree-of freedom motion control and surface biochemistry analysis components are coupled in the context of adaptive octree-based grid generation. Analytical and numerical verification of the quasi-steady assumption for the fluid mechanics is presented. The capabilities of the technique are demonstrated by presenting several three-dimensional cell system simulations, including the collision/interaction between a cancer cell and an endothelium adherent polymorphonuclear leukocyte (PMN) cell in a shear flow.
[博士论文].
[本文引用: 1]
[PhD Thesis].
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
