赵希宁, 杨晓东
, 2) , 张伟北京工业大学机械结构非线性振动与强度北京市重点实验室, 北京 100124
NONLIEAR BENDING WAVES OF A PIEZOELECTRIC LAMINATED BEAM WITH ELECTRICAL BOUNDARY1) Zhao Xining, Yang Xiaodong
, 2) , Zhang WeiBeijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures, College of Mechanical Engineering, Beijing University of Technology, Beijing 100124, China
通讯作者: 2)杨晓东, 教授, 主要研究方向: 非线性动力学. E-mail:
jxdyang@163.com 收稿日期: 2020-12-1
接受日期: 2021-01-15
网络出版日期: 2021-04-08
基金资助: 1)国家自然科学基金 .11972050 国家自然科学基金 .11672007
Received: 2020-12-1
Accepted: 2021-01-15
Online: 2021-04-08
作者简介 About authors
摘要 非线性科学己成为近代科学发展的一个重要标志, 特别是非线性动力学和非线性波的研究对于解决自然科学各领域中遇到的复杂现象和问题有着极其重要的意义. 本文研究了含电学边界条件的压电层合梁的非线性弯曲波传播特性.首先, 考虑几何非线性效应和压电耦合效应, 利用哈密顿原理建立了一维无限长矩形压电层合梁弯曲波的非线性方程.其次, 采用Jacobi椭圆函数展开法对非线性弯曲波方程进行求解, 得到了非线性弯曲波动方程在近似情况下对应的冲击波解和孤波解.最后, 利用约化摄动法得到了非线性薛定谔方程, 进一步得到了亮孤子和暗孤子解.基于两种方法具体研究了外加电压、压电层厚度等参数对冲击波和孤立波以及亮孤子和暗孤子特性的影响. 研究结果表明, 在波速较小时, 外加电压对冲击波的影响较大, 波速较大时, 外加电压对孤立波影响减弱.通过调整作用在压电层合梁上的电压发现了存在亮孤子和暗孤子, 分析结果表明随着外加电压值的增大, 亮孤子和暗孤子的振幅都增大.
关键词: 弯曲波 ;
Jacobi椭圆函数 ;
非线性薛定谔方程 ;
冲击波 ;
孤立波 Abstract Nonlinear science has been an important symbol in the development of modern science, especially the researches in nonlinear dynamics and nonlinear waves have extraordinary significance in solving the complex phenomena and problems encountered in various fields of natural science. In this paper, the nonlinear bending wave propagation of a piezoelectric laminated beam with electrical boundary conditions is studied. Firstly, considering the geometric nonlinear effect and piezoelectric coupling effect, the nonlinear equation of the one-dimensional infinite rectangular piezoelectric laminated beams is established by using Hamiltonian principle. Secondly, the Jacobi elliptic function expansion method is used to treat the nonlinear flexural wave equation, and the corresponding shock wave solution and solitary wave solution of the nonlinear flexural wave equation are obtained in the approximate case. Last, the nonlinear Schrodinger equation is obtained by using the reduced perturbation method, and the bright and dark soliton solutions are further obtained. Moreover, the effects of external voltage and the thickness of the piezoelectric layer on the characteristics of shock wave and solitary wave as well as bright and dark solitons are studied. The results show that when the wave velocity is small, the external voltage has a great influence on the shock wave, and when the wave velocity is large, the external voltage has no effect on the solitary wave. The bright solitons and the dark solitons can be obtained by adjusting the external voltage applied to the piezoelectric laminated beam. It is found that the amplitudes of bright and dark solitons increase with the increase of external voltages.
Keywords: bending wave ;
Jacobi elliptic function ;
nonlinear Schrodinger equation ;
shock wave ;
solitary wave PDF (4267KB) 元数据 多维度评价 相关文章 导出 EndNote |
Ris |
Bibtex 收藏本文 本文引用格式 赵希宁, 杨晓东, 张伟. 含电学边界的压电层合梁的非线性弯曲波
1) .
力学学报 [J], 2021, 53(4): 1124-1137 DOI:
10.6052/0459-1879-20-409 Zhao Xining, Yang Xiaodong, Zhang Wei.
NONLIEAR BENDING WAVES OF A PIEZOELECTRIC LAMINATED BEAM WITH ELECTRICAL BOUNDARY1) .
Chinese Journal of Theoretical and Applied Mechanics [J], 2021, 53(4): 1124-1137 DOI:
10.6052/0459-1879-20-409 引言 在工程实际与科学实践中都存在大量的非线性因素, 其中很多因素都可归纳为非线性波问题, 因此对非线性弹性波理论的研究有着重要的理论和实际意义
[1 -2 ] . 孤立波和冲击波现象的研究最早可以追溯到1834年, 英国科学家Russell偶然发现了一种在行进的过程中波形和速度没有明显变化的波, 并称这种波为孤立波
[3 ] . 1895年, Korteweg等
[4 ] 在研究浅水波的运动时, 得到了能产生孤立波的浅水运动的非线性方程, 并求得了孤立波解, 首次证实了孤立波的存在. 1965年, Zabusky和Kruskal
[5 ] 运用仿真手段研究了两个孤立波的碰撞特性, 发现孤立波在碰撞前后, 波形特性不发生变化, 说明了非线性理论中不存在线性叠加原理. 1970年, Taylor等
[6 ] 解释了没有色散项只有非线性项的孤立波现象, 证明了只有非线性项的孤立波波形比较尖陡, 而加入色散项后孤立波的波形变得平缓. 1980年, 国内朱位秋
[7 ] 研究了弹性杆中非线性波的传播行为
[7 ] .
21世纪以来, 科学家们推导出了固体中非线性演化方程的孤立波解和冲击波解
[8 -12 ] . Duan等
[13 ] 基于非线性弹性杆的纵波运动方程, 利用摄动理论证明了非线性弹性杆中存在孤立子. Parkes等
[14 ] 利用雅可比椭圆函数展开法构造并求解了非线性波动方程的精确周期解.研究表明, 用该方法可以得到许多新的周期解, 且在其极限条件下可以得到更多的激波解或孤立波解. Dai等
[15 -16 ] 分别研究了可压缩和不可压缩杆中的非线性波传播问题, 导出了一类新的非线性色散方程, 证明了这两类系统中存在冲击波、孤立波、周期冲击波等. Zhang和Liu
[17 -20 ] 在考虑有限变形、黏性效应和横向惯性的影响时, 得到了弹性圆柱壳和杆的非线性薛定谔方程, 证明了孤立解和激波解的存在. Xue等
[21 -22 ] 建立了磁电弹杆的非线性波动方程, 并通过雅可比椭圆函数展开法进行求解, 结果表明在磁电弹杆存在孤立波. Bulut等
[23 ] 建立了磁电弹杆的非线性纵波方程, 并运用sinh-Gordon展开法对其求解, 得到了拓扑孤子解、非拓扑孤子解和奇异孤子解. Lpbal等
[24 ] 研究了含有泊松效应的弹性杆中的非线性纵波扩散问题.
除了对弹性杆非线性纵波的研究之外, 对梁结构非线性弯曲波的研究也取得了很多进展
[25 -28 ] . Zhang等
[29 -30 ] 考虑了横向、轴向和旋转惯性效应, 导出了大挠曲梁的非线性波动方程, 得到了孤立波解和冲击波解. Wei等
[31 ] 建立了压电层合梁的弯曲波方程, 利用拓展的F-展开法和约化摄动法得到了冲击波解、孤立波解以及亮孤子和暗孤子解.然而, 到目前为止, 关于压电耦合效应以及电学边界条件下压电层合梁模型非线性弯曲波的研究还没有报道.
本文提出了含有电学边界条件的无限长压电层合梁模型, 研究了非线性弯曲波的传播问题. 首先, 考虑梁的大挠度引起的几何非线性效应、压电耦合效应和电学边界条件, 利用欧拉-拉格朗日方法建立了无限长矩形压电层合梁弯曲波的非线性模型.其次, 采用椭圆函数展开法对非线性弯曲波方程进行求解, 得到了非线性弯曲波动方程的精确周期解及在极限情况下对应的冲击波解和孤波解. 最后, 利用约化摄动法得到了非线性薛定谔方程, 进一步得到了亮孤子和暗孤子解, 且具体研究了外加电压、压电层厚度等参数对冲击波、孤立波以及孤子特性的影响.
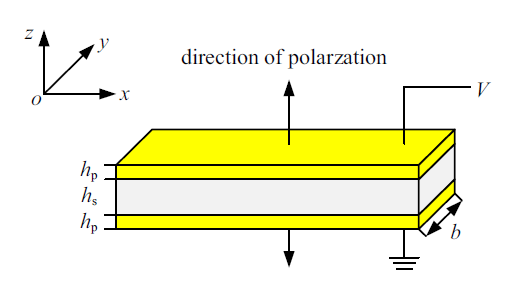
1 压电层合梁模型建立 图1 给出了矩形压电层合梁的简化几何模型, 压电层合梁由均匀压电材料和基体材料组成, 梁的横截面在变形前后均保持平面.不考虑泊松效应, 以$x$方向为轴向方向, $z$轴为弯曲变形方向, 其他两个方向梁不受任何力. 基体厚度$h_{s}$, 压电材料厚度$h_{p}$, 基体梁和压电层的宽度都是$b$. 压电层合梁上表面压电层的极化方向沿$z$轴正方向, 受到电势$V$作用, 下表面压电层的极化方向与上表面相反, 沿$z$轴负方向, 下表面压电层接地且电势为0, 压电层合梁的振动方向沿厚度方向.
图1 新窗口打开 |
下载原图ZIP |
生成PPT 图1矩形压电层合梁的示意图 Fig.1Schematic of the rectangular piezoelectric laminated beam 取梁变形前的轴为$x$轴, 梁发生横向弯曲的方向与中性面垂直, 在$x$方向没有外力作用的情况下, 可以采用下列位移表达式
(1) $\begin{eqnarray} \label{eq1} u_{x} =-z\frac{\partial W}{\partial x}, \ \ u_{z} =W\left( {x,t} \right) \end{eqnarray} $式中$W$为$z$方向的挠度, 考虑有限挠度的情况下, 梁截面上任意点处的应变可以表示为
(2) $\begin{eqnarray} \label{eq2} \varepsilon_{x} =-z\frac{\partial^{2}W}{\partial x^{2}}+\frac{1}{2}\left({\frac{\partial W}{\partial x}} \right)^{2} \end{eqnarray} $基体梁和压电层的本构方程分别为
(3) $\sigma_{x}^{s} =E\varepsilon_{x} $(4) $\sigma_{x}^{p} =c_{11} \varepsilon_{x} -e_{31} E_{z} , \ \ D_{z} =e_{31} \varepsilon_{x} +\varepsilon_{33} E_{z} $其中$\sigma_{x}^{s}$和$\sigma_{x}^{p}$为基体梁和压电层的轴向应力, $E_{z}$和$D_{z}$是分别为$z$方向上的电场和电位移, $E$是基体梁的弹性模量, $c_{11}$为压电材料的弹性模量, $e_{31}$和$\varepsilon_{33}$式中分别为压电应变系数和介电常数.假设电场$E_{z}$只存在于$z$方向, 它可以由电势$\phi $决定
(5) $\begin{eqnarray} \label{eq5} E_{z} =-\frac{\partial \phi }{\partial z} \end{eqnarray} $然后, 考虑在没有自由电荷的情况下, 满足高斯定律
(6) $\begin{eqnarray} \label{eq6} \frac{\partial D_{z} }{\partial z}=0 \end{eqnarray} $将方程(6)代入到压电本构方程(4)中, 结合电边界条件$\phi \left(-h_{s}/{2}-h_{p} \right)=0$和$\phi \left( {h_{s}/{2}+h_{p} } \right)=V$, 可以得到电势表达式
(7) $\begin{eqnarray} \label{eq7} \phi =-\frac{e_{31} }{2\varepsilon_{33} }\left[ {z^{2}-\left( {\frac{h_{s} }{2}+h_{p} } \right)^{2}} \right]\frac{\partial^{2}W}{\partial x^{2}}+z\frac{V}{h_{s} +2h_{p} }+\frac{V}{2}\quad \end{eqnarray} $结合方程(7)和(4)可以得到压电层轴向应力表达式
(8) $\begin{eqnarray} \label{eq8} \sigma_{x}^{p} =-\left( {c_{11} +\frac{e_{31}^{2} }{\varepsilon_{33} }} \right)z\frac{\partial^{2}W}{\partial x^{2}}+\frac{c_{11} }{2}\left( {\frac{\partial W}{\partial x}} \right)^{2}+\frac{e_{31} V}{h_{s} +2h_{p}} \end{eqnarray} $压电梁微元段的动能可以表示为
(9) $\begin{eqnarray} \label{eq9} &&T=\frac{1}{2}\int_{V_{s} } {\rho_{s} \left[ {\left( {-z\frac{\partial ^{2}W}{\partial x\partial t}} \right)^{2}+\left( {\frac{\partial W}{\partial t}} \right)^{2}} \right]} {d}V_{s} +\\ && \frac{1}{2}\int_{V_{p} } {\rho_{p} \left[ {\left( {-z\frac{\partial ^{2}W}{\partial x\partial t}} \right)^{2}+\left( {\frac{\partial W}{\partial t}} \right)^{2}} \right]}{d}V_{p} \end{eqnarray} $方程(9)进一步写为
(10) $\begin{eqnarray} \label{eq10} T=\frac{1}{2}\int_0^l \Bigg[{K_{1} \left( {\frac{\partial W}{\partial t}} \right)^{2}+K_{2} \left( {\frac{\partial^{2}W}{\partial x\partial t}} \right)^{2}}\Bigg]{d}x \end{eqnarray} $其中式(10)中的$K_{1}$和$K_{2}$为
(11) $K_{1} =\rho_{s} bh_{s} +2\rho_{p} bh_{p} $(12) $K_{2} =\rho_{s} \frac{bh^{3}_{s}}{12}+\frac{2}{3}\rho_{p} b\left[ {\left( {\frac{h_{s} }{2}+h_{p} } \right)^{3}-\left( {\frac{h_{s} }{2}} \right)^{3}} \right] $压电梁的势能可以表示为三部分
(13) $\begin{eqnarray} \label{eq13} U=U_{1} +U_{2} +U_{3} \end{eqnarray} $其中$U_{1}$表示基体梁的应变势能, $U_{2}$表示压电层的应变势能, $U_{3}$表示压电层的电势能, $U_{1}$, $U_{2}$和$U_{3}$可以进一步表示
(14) $U_{1} =\frac{1}{2}\int_{V_{s} } {\sigma_{x}^{s} \varepsilon_{x} } {d}V_{s} =\\ \frac{1}{2}\int_0^l {\left[ {\frac{1}{4}Ebh_{s} \left( {\frac{\partial W}{\partial x}} \right)^{4}+E\frac{bh_{s}^{3} }{12}\left( {\frac{\partial ^{2}W}{\partial x^{2}}} \right)^{2}} \right]} {d}x $(15) $\begin{eqnarray} \label{eq15} && U_{2} =\frac{1}{2}\int_{V_{p} } {\sigma_{x}^{p} \varepsilon_{x} } {d}V_{p} =\\ && \frac{1}{2}\int_{0}^l \Bigg\{ \frac{1}{2}e_{31} bV\frac{2h_{p} }{h_{s} +2h_{p} }\left( {\frac{\partial W}{\partial x}} \right)^{2}+\\ && \frac{1}{2}c_{11} bh_{p} \left( {\frac{\partial W}{\partial x}} \right)^{4} +\frac{2b}{3}\left[ {\left( {\frac{h_{s} }{2}+h_{p} } \right)^{3}-\left( {\frac{h_{s} }{2}} \right)^{3}} \right]\cdot\\ && \left( {c_{11} +\frac{e_{31}^{2} }{\varepsilon_{33} }} \right)\left( {\frac{\partial ^{2}W}{\partial x^{2}}} \right)^{2} \Bigg\}{d}x \end{eqnarray} $(16) $U_{3} =\frac{1}{2}\int_{V_{p} } {D_{z} E_{z} } {d}V_{p} =\\ \frac{1}{2}\int_0^l {\left[ {\varepsilon_{33} b\frac{V^{2}2h_{p} }{\left( {h_{s} +2h_{p} } \right)^{2}}-\frac{e_{31} bVh_{p} }{h_{s} +2h_{p} }\left( {\frac{\partial W}{\partial x}} \right)^{2}} \right]} {d}x $结合方程(14)$ \sim $(16)可以得到总的势能
(17) $\begin{eqnarray} \label{eq17} &&U=\frac{1}{2}\int_{0}^l \Bigg[ K_{3} \left( {\frac{\partial ^{2}W}{\partial x^{2}}} \right)^{2}+K_{4} \left( {\frac{\partial W}{\partial x}} \right)^{4}+ K_{5} \left( {\frac{\partial W}{\partial x}} \right)^{2}-K_{6} \Bigg]{d}x \end{eqnarray} $其中式(17)中的$K_{3}$, $K_{4}$, $K_{5}$和$K_{6}$可以表示为
(18) $K_{3} =E\frac{bh_{s}^{3} }{12}+\frac{2b}{3}\left[ {\left( {\frac{h_{s} }{2}+h_{p} } \right)^{3}-\left( {\frac{h_{s} }{2}} \right)^{3}} \right]\left( {c_{11} +\frac{e_{31}^{2} }{\varepsilon_{33} }} \right) $(19) $K_{4} =\frac{1}{2}c_{11} bh_{p} $(20) $K_{5} =e_{31} bV\frac{2h_{p} }{h_{s} +2h_{p} } $(21) $K_{6} =\varepsilon_{33} b\frac{V^{2}2h_{p} }{\left( {h_{s} +2h_{p} } \right)^{2}} $引入能量密度函数$L$, 其中
(22) $\begin{eqnarray} \label{eq22} L=T-U \end{eqnarray} $通过欧拉-拉格朗日方程
(23) $\begin{eqnarray} \label{eq23} &&\frac{\partial L}{\partial W}-\frac{\partial }{\partial x}\frac{\partial L}{\partial W_{x} }-\frac{\partial }{\partial t}\frac{\partial L}{\partial W_{t} }+\frac{\partial^{2}}{\partial x^{2}}\frac{\partial L}{\partial W_{xx} }+\\&& \frac{\partial^{2}}{\partial x\partial t}\frac{\partial L}{\partial W_{xt} }+\frac{\partial^{2}}{\partial t^{2}}\frac{\partial L}{\partial W_{t} }-\cdots =0 \end{eqnarray} $可以得到压电梁的非线性弯曲波方程
(24) $\begin{eqnarray} \label{eq24} &&K_{1} \frac{\partial^{2}W}{\partial t^{2}}-2K_{4} \frac{\partial \left( {W_{x}^{3} } \right)}{\partial x}-K_{2} \frac{\partial^{2}}{\partial x^{2}}\left( {\frac{\partial ^{2}W}{\partial t^{2}}-K_{3} \frac{\partial^{2}W}{\partial x^{2}}+K_{5} W} \right)=0 \end{eqnarray} $令
(25) $\begin{eqnarray} \label{eq25} c_{1}^{2} =\frac{2K_{4} }{K_{1} }, \ \ r_{1}^{2} =\frac{K_{2} }{K_{1} }, \ \ c_{0}^{2} =\frac{K_{3} }{K_{2} }, \ \ c_{2}^{2} =\frac{K_{5} }{K_{2} } \end{eqnarray} $$c_{1}$和$r_{1}$是常数, $c_{0}$是纵波波速, 将方程(24)对$x$求偏导
[11 ,17 ] , 并假设${\partial W}/{\partial x}=w$, 进一步得到
(26) $\begin{eqnarray} \label{eq26} &&\frac{\partial^{2}w}{\partial t^{2}}-c_{1}^{2} \frac{\partial ^{2}\left( {w^{3}} \right)}{\partial x^{2}}-r_{1}^{2} \frac{\partial^{2}}{\partial x^{2}}\left( {\frac{\partial^{2}w}{\partial t^{2}}-c_{0}^{2} \frac{\partial^{2}w}{\partial x^{2}}+c_{2}^{2} w} \right)=0 \end{eqnarray} $注意到方程(26)是含三次非线性的弯曲波方程, 因此需要考虑由梁的大挠度引起的非线性效应, 色散效应以及压电耦合效应.当非线性效应和色散效应相互作用并达到平衡时, 就会出现孤立波或者冲击波解.
2 椭圆函数展开法 Jacobi椭圆函数展开法是一种求解非线性方程孤立波解和冲击波解的有效方法
[18 ] . 下文将运用Jacobi椭圆函数展开法对该模型下的非线性波动方程进行分析求解. Jacobi椭圆函数展开形式可以是正弦函数sn$\xi $、余弦函数cn$\xi $和第三类Jacobi椭圆函数dn$\xi$.首先利用Jacobi椭圆函数正弦展开法, 将$w(\xi )$展开为sn$\xi $的级数
(27) $\begin{eqnarray} \label{eq27} w\left( \xi \right)=\sum\limits_{j=0}^n {a_{j} } {sn}^{j}\xi \end{eqnarray} $其中$n$为解展开的项数, $a_{j}$为待定系数.为了确定展开项数$n$的值, 需要满足非线性方程最高阶导数项和最高阶非线性项的次数相等, 且满足
(28) $\begin{eqnarray} \label{eq28} o\left( {w^{2}\frac{{d}^{2}w}{{d}\xi^{2}}} \right)=3n+2, \quad o\left( {\frac{{d}^{4}w}{{d}\xi^{4}}} \right)=n+4 \end{eqnarray} $方程(28)两式平衡可以得到$n = 1$, 因此对Jacobi椭圆正弦函数做一阶展开, 就能得到非线性方程的精确解, 此时解的形式具体可以表示为
(29) $\begin{eqnarray} \label{eq29} w\left( \xi \right)=a_{0} +a_{1} {sn}\xi \end{eqnarray} $设方程(26)的解为
(30) $\begin{eqnarray} \label{eq30} w=w\left( \xi \right), \ \ \xi =k\left( {x-ct} \right) \end{eqnarray} $其中$k$是波数, $c$是波速.将解的形式(30)代入到非线性方程(26), 可以得到非线性常微分波动方程
(31) $\begin{eqnarray} \label{eq31} k^{2}\frac{{d}^{4}w}{{d}\xi^{4}}+\delta_{1} \frac{{d}^{2}w}{{d}\xi^{2}}+3\delta _{3} \left[ {2w\left( {\frac{{d}w}{{d}\xi }} \right)^{2}+w^{2}\frac{{d}^{2}w}{{d}\xi ^{2}}} \right]=0 \end{eqnarray} $其中
(32) $\begin{eqnarray} \label{eq32} \delta_{1} =-\frac{c^{2}+r_{1}^{2} c_{2}^{2} }{r_{1}^{2} \left( {c^{2}-c_{0}^{2} } \right)}, \ \ \delta_{3} =\frac{c_{1}^{2} }{r_{1}^{2} \left( {c^{2}-c_{0}^{2} } \right)} \end{eqnarray} $将方程(29)代入到非线性方程(31)中, 并应用
(33) $\frac{{d}\left( {{sn}\xi } \right)}{{d}\xi }={cn}\xi {dn}\xi $(34) $\frac{{d}\left( {{cn}\xi } \right)}{{d}\xi }=-{sn}\xi {dn}\xi $(35) $\frac{{d}\left( {{dn}\xi } \right)}{{d}\xi }=-m^{2}{sn}\xi {cn}\xi $方程(35)中的$m$ ($0<m<1$)为模数, 可以得到
(36) $\begin{eqnarray} \label{eq36} &&k^{2}\Big( a_{1} {sn}\xi {dn}^{4}\xi +14a_{1} m^{2}{sn}\xi {cn}^{2}\xi {dn}^{2}\xi -\\ && 4a_{1} m^{2}{sn}^{3}\xi {dn}^{2}\xi -4a_{1} m^{4}{sn}^{3}\xi {cn}^{2}\xi + \\ && a_{1} m^{4}{sn}\xi {cn}^{4}\xi \Big)+\delta_{1} \Big( -a_{1} {sn}\xi {dn}^{2}\xi -a_{1} m^{2}{sn}\xi {cn}^{2}\xi \Big) +\\ && 3\delta_{3} \Big( 2a_{0} a_{1}^{2} {cn}^{2}\xi {dn}^{2}\xi +2a_{1}^{3} {sn}\xi {cn}^{2}\xi {dn}^{2}\xi \Big)+ \\ && 3\delta_{3} \Big( -a_{0} a_{1}^{2} {sn}\xi {dn}^{2}\xi -a_{1} a_{0}^{2} m^{2}{sn}\xi {cn}^{2}\xi -\\ && a_{1}^{3} {sn}^{3}\xi {dn}^{2}\xi -a_{1}^{3} m^{2}{sn}^{3}\xi {cn}^{2}\xi -2a_{0} a_{1}^{2} {sn}^{2}\xi {dn}^{2}\xi -\\ && 2a_{0} a_{1}^{2} m^{2}{sn}^{2}\xi {cn}^{2}\xi \Big)=0 \end{eqnarray} $为了确定待定系数$a_{0}$和$a_{1}$, 令sn$^{5}\xi $, sn$^{4}\xi$, sn$^{3}\xi $, sn$^{2}\xi $和sn$^{1}\xi $以及常数项sn$^{0}\xi $系数方程分别等于零, 结合Jacobi椭圆函数的性质, 可以确定方程(29)中的待定系数
(37) $\begin{eqnarray} \label{eq37} a_{0} =0, \ \ a_{1} =\pm \sqrt {-\frac{2}{\delta_{3} }} km, \ \ k^{2}=\frac{\delta_{1} }{1+m^{2}} \end{eqnarray} $因此, 解的形式(29)具体可以写为
(38) $\begin{eqnarray} \label{eq38} w\left( \xi \right)=\pm \sqrt {-\frac{2}{\delta_{3} }} km{sn}\xi \end{eqnarray} $应当指出, 当$\delta_{1}<0$且$\delta_{3}>0$时, 上式成立, 且当模数$m$趋于1时, 有sn$\xi $趋于tanh$\xi $, 则方程(38)可以退化为冲击解形式
(39) $\begin{eqnarray} \label{eq39} w\left( \xi \right)=\pm \sqrt {-\frac{2}{\delta_{3} }} k\tanh \xi \end{eqnarray} $进一步, 将式(32)中的$\delta_{1}$和$\delta_{3}$代入式(39), 可以得到
(40) $\begin{eqnarray} \label{eq40} a_{1} =\pm \sqrt {-\frac{4r_{1}^{2} \left( {c^{2}-c_{0}^{2} } \right)}{c_{0}^{2} }} k, \ \ k=\sqrt {-\frac{c^{2}+r_{1}^{2} c_{2}^{2} }{2r_{1}^{2} \left( {c^{2}-c_{0}^{2} } \right)}} \end{eqnarray} $冲击波解可以写为
(41) $\begin{eqnarray} \label{eq41} w\left( \xi \right)=A\tanh \left( {\frac{x-ct}{\varLambda }} \right) \end{eqnarray} $其中的系数
(42) $\begin{eqnarray} \label{eq42} A=\pm \sqrt {\frac{2\left( {c^{2}+r_{1}^{2} c_{2}^{2} } \right)}{c_{0}^{2} }}, \ \ \varLambda =\sqrt {-2\frac{r_{1}^{2} \left( {c^{2}-c_{0}^{2} } \right)}{c^{2}+r_{1}^{2} c_{2}^{2} }} \end{eqnarray} $同理, 运用Jacobi椭圆余弦函数展开法对非线性弯曲波方程进行求解, 此时解的形式可以表示为
(43) $\begin{eqnarray} \label{eq43} w\left( \xi \right)=b_{0} +b_{1} {cn}\xi \end{eqnarray} $可以得到相应的解的系数
(44) $\begin{eqnarray} \label{eq44} b_{0} =0, \ \ b_{1} =\pm \sqrt {\frac{2}{\delta_{3} }} km, \ \ k^{2}=\frac{\delta_{1} }{1-2m^{2}} \end{eqnarray} $非线性弯曲波方程解的具体形式可以写为
(45) $\begin{eqnarray} \label{eq45} w\left( \xi \right)=\pm \sqrt {\frac{2}{\delta_{3} }} mk{cn}\xi \end{eqnarray} $方程(45)是非线性弯曲波方程的另一个精确解, 显然当$\delta_{1}<0$且$\delta_{3}>0$时, 上式成立.根据椭圆函数的性质, 当模数$m$趋于1时, cn$\xi $趋于sech$\xi $, 则方程(45)可以退化为孤立波解形式
(46) $\begin{eqnarray} \label{eq46} w\left( \xi \right)=\pm \sqrt {\frac{2}{\delta_{3} }} k{sech}\xi \end{eqnarray} $或者
(47) $\begin{eqnarray} \label{eq47} w\left( \xi \right)=A{sech}\left( {\frac{x-ct}{\varLambda }} \right) \end{eqnarray} $其中
(48) $\begin{eqnarray} \label{eq48} A=\pm \sqrt {\frac{4\left( {c^{2}+r_{1}^{2} c_{2}^{2} } \right)}{c_{0}^{2} }} , \ \ \varLambda =\sqrt {\frac{r_{1}^{2} \left( {c^{2}-c_{0}^{2} } \right)}{c^{2}+r_{1}^{2} c_{2}^{2} }} \end{eqnarray} $特别地, 如果运用第三类Jacobi椭圆函数展开法, 当模数$m$趋于1时, 也可以得到孤立波解.
3 约化摄动法 在弱非线性的情况下, 将$w$展开为如下形式
(49) $\begin{eqnarray} \label{eq49} w=\varepsilon w_{1} +\varepsilon^{2}w_{2} +\varepsilon^{3}w_{3}+ \cdots \end{eqnarray} $且最低阶解的形式为
(50) $\begin{eqnarray} \label{eq50} \varepsilon w_{1} =\varepsilon A{e}^{{i}\left( {kx-\omega t} \right)}+c.c. \end{eqnarray} $其中$\varepsilon $是远远小于1的参数, $k$是波数, $\omega $是频率, $c.c$.表示复数共轭, 其中
(51) $\begin{eqnarray} \label{eq51} \xi =\varepsilon \left( {x-c_{g} t} \right), \ \ \tau =\varepsilon^{2}t \end{eqnarray} $其中$c_{g}$为群速度, 进一步得到$\left( {\varepsilon w_{1} } \right)^{3}$的表达式
(52) $\begin{eqnarray} \label{eq52} \left( {\varepsilon w_{1} } \right)^{3}=\varepsilon^{3}\left[{A^{3}{e}^{3{i}\left( {kx-\omega t} \right)}+3A^{2}\bar{{A}}{e}^{{i}\left({kx-\omega t} \right)}} \right]+c.c. \end{eqnarray} $考虑如下关系
(53) $\begin{eqnarray} \label{eq53} \left.\begin{array}{l} \dfrac{\partial }{\partial x}=\dfrac{\partial }{\partial x}+\varepsilon \dfrac{\partial }{\partial \xi } \\[3mm]\dfrac{\partial^{2}}{\partial x^{2}}=\dfrac{\partial^{2}}{\partial x^{2}}+2\varepsilon \dfrac{\partial^{2}}{\partial x\partial \xi }+\varepsilon^{2}\dfrac{\partial^{2}}{\partial \xi^{2}} \\[3mm]\dfrac{\partial }{\partial t}=\dfrac{\partial }{\partial t}-\varepsilon c_{g} \dfrac{\partial }{\partial \xi }+\varepsilon^{2}\dfrac{\partial }{\partial\tau } \\[3mm]\dfrac{\partial^{2}}{\partial t^{2}}=\dfrac{\partial^{2}}{\partial t^{2}}-2\varepsilon c_{g} \dfrac{\partial^{2}}{\partial t\partial \xi }+\varepsilon^{2}c_{g}^{2} \dfrac{\partial^{2}}{\partial \xi^{2}}+ 2\varepsilon^{2}\dfrac{\partial^{2}}{\partial \tau \partial t}-2\varepsilon ^{3}c_{g} \dfrac{\partial^{2}}{\partial \tau \partial \xi }+\varepsilon ^{4}\dfrac{\partial^{2}}{\partial \tau^{2}} \end{array}\right\} \end{eqnarray} $结合方程(53), 方程(26)可以写为如下形式
(54) $\begin{eqnarray} \label{eq54} &&\frac{\partial^{2}w}{\partial t^{2}}-2\varepsilon c_{g} \frac{\partial ^{2}w}{\partial t\partial \xi }+\varepsilon^{2}c_{g}^{2} \frac{\partial ^{2}w}{\partial \xi^{2}}+2\varepsilon^{2}\frac{\partial^{2}w}{\partial \tau \partial t}-\\ && 2\varepsilon^{3}c_{g} \frac{\partial^{2}w}{\partial \tau \partial \xi }+\varepsilon^{4}\frac{\partial^{2}w}{\partial \tau^{2}}-\\ && c_{1}^{2} \left[ {\frac{\partial^{2}\left( {w^{3}} \right)}{\partial x^{2}}+2\varepsilon \frac{\partial^{2}\left( {w^{3}} \right)}{\partial x\partial \xi }+\varepsilon^{2}\frac{\partial^{2}\left( {w^{3}} \right)}{\partial \xi^{2}}} \right]- \\ && r_{1}^{2} \left( {\frac{\partial^{2}}{\partial x^{2}}+2\varepsilon \frac{\partial^{2}}{\partial x\partial \xi }+\varepsilon^{2}\frac{\partial ^{2}}{\partial \xi^{2}}} \right)\Bigg[ \frac{\partial^{2}w}{\partial t^{2}}-2\varepsilon c_{g} \frac{\partial^{2}w}{\partial t\partial \xi }+ \\ && \varepsilon^{2}c_{g}^{2} \frac{\partial^{2}w}{\partial \xi ^{2}}+2\varepsilon^{2}\frac{\partial^{2}w}{\partial \tau \partial t}-2\varepsilon^{3}c_{g} \frac{\partial^{2}w}{\partial \tau \partial \xi }+\varepsilon^{4}\frac{\partial^{2}w}{\partial \tau^{2}}- \\ && c_{0}^{2} \left( {\frac{\partial^{2}w}{\partial x^{2}}+2\varepsilon \frac{\partial^{2}w}{\partial x\partial \xi }+\varepsilon ^{2}\frac{\partial^{2}w}{\partial \xi^{2}}} \right)+c_{2}^{2} \Bigg]=0 \end{eqnarray} $将解的形式(49)代入到方程(54)中, 首先可以得到关于$\varepsilon $一次幂的系数方程
(55) $\begin{eqnarray} \label{eq55} \varepsilon \frac{\partial^{2}w_{1} }{\partial t^{2}}-\varepsilon r_{1}^{2} \frac{\partial^{2}}{\partial x^{2}}\left( {\frac{\partial^{2}w_{1} }{\partial t^{2}}-c_{0}^{2} \frac{\partial^{2}w_{1} }{\partial x^{2}}+c_{2}^{2} w_{1} } \right)=0 \end{eqnarray} $通过观察上式, 可以发现是方程(26)去掉非线性项以后的线性方程, 将最低阶方程的解(50) 代入方程(55), 简化得到线性方程下的色散方程
(56) $\begin{eqnarray} \label{eq56} -\omega^{2}-r_{1}^{2} k^{2}\omega^{2}+r_{1}^{2} c_{0}^{2} k^{4}+r_{1}^{2} c_{2}^{2} k^{2}=0 \end{eqnarray} $化简线性色散方程, 得到
(57) $\begin{eqnarray} \label{eq57} \omega =\pm \sqrt {\frac{r_{1}^{2} k^{2}\left( {c_{0}^{2} k^{2}+c_{2}^{2} } \right)}{1+r_{1}^{2} k^{2}}} \end{eqnarray} $根据相速度的定义, 可以得到线性方程下的相速度
(58) $\begin{eqnarray} \label{eq58} c_{p} =\frac{\omega }{k}=\pm \sqrt {\frac{r_{1}^{2} \left( {c_{0}^{2} k^{2}+c_{2}^{2} } \right)}{1+r_{1}^{2} k^{2}}} \end{eqnarray} $同理, 对于$\varepsilon $的二次幂, 系数方程可以表示为
(59) $\begin{eqnarray} \label{eq59} &&\varepsilon^{2}\frac{\partial^{2}w_{2} }{\partial t^{2}}-\varepsilon ^{2}r_{1}^{2} \frac{\partial^{2}w_{2} }{\partial x^{2}\partial t^{2}}+\varepsilon^{2}r_{1}^{2} c_{0}^{2} \frac{\partial^{2}w_{2} }{\partial x^{4}}=\\ && 2\varepsilon \Bigg\{ c_{g} \frac{\partial^{2}w_{1} }{\partial t\partial \xi }+r_{1}^{2} \Bigg[ -c_{g} \frac{\partial^{4}w_{1} }{\partial x^{2}\partial t\partial \xi }-c_{0}^{2} \frac{\partial^{4}w_{1} }{\partial x\partial \xi \partial x^{2}}+\\ && 2c_{2}^{2} \frac{\partial^{2}w_{1} }{\partial x\partial \xi }+\frac{\partial^{2}}{\partial x\partial \xi }\left( {\frac{\partial ^{2}w_{1} }{\partial t^{2}}-c_{0}^{2} \frac{\partial^{2}w_{1} }{\partial x^{2}}} \right) \Bigg] \Bigg\} \end{eqnarray} $消除长期项, 令方程(59)等号右端等于零, 并将解的形式(50)代入, 简化后得到关于群速度$c_{g}$的表达式
(60) $\begin{eqnarray} \label{eq60} &&c_{g} \left( {-{i}\omega } \right)+r_{1}^{2} \Big[ -{i}\omega c_{g} k^{2}+{i}c_{0}^{2} k^{3}+\\ && 2{i}c_{2}^{2} k+{i}k\left( {c_{0}^{2} k^{2}-\omega^{2}} \right) \Big]=0 \end{eqnarray} $根据方程(60), 可以求得对应线性方程的群速度表达式
(61) $\begin{eqnarray} \label{eq61} c_{g} =\pm \frac{2r_{1}^{2} \left( {c_{0}^{2} k^{3}+c_{2}^{2} k} \right)\left( {1+r_{1}^{2} k^{2}} \right)-r_{1}^{4} k^{3}\left( {c_{0}^{2} k^{2}+c_{2}^{2} } \right)}{\sqrt {r_{1}^{2} k^{2}\left( {c_{0}^{2} k^{2}+c_{2}^{2} } \right)\left( {1+r_{1}^{2} k^{2}} \right)^{3}} }\qquad \end{eqnarray} $经计算, 群速度表达式(61)和利用$c_{g} ={{d}\omega }/{{d}k}$得到的一致.假设$w_{2}=0$, 对于$\varepsilon $的三次幂, 系数方程可以表示为
(62) $\begin{eqnarray} \label{eq62} &&\varepsilon^{3}\frac{\partial^{2}w_{3} }{\partial t^{2}}-\varepsilon ^{3}r_{1}^{2} \frac{\partial^{2}w_{3} }{\partial x^{2}\partial t^{2}}+\varepsilon^{3}r_{1}^{2} c_{0}^{2} \frac{\partial^{2}w_{3} }{\partial x^{4}}= \\ && \varepsilon^{2}\left( {c_{g}^{2} \frac{\partial^{2}w_{1} }{\partial \xi ^{2}}+2\frac{\partial^{2}w_{1} }{\partial \tau \partial t}} \right)-c_{1}^{2} \frac{\partial^{2}\left( {w_{1}^{3} } \right)}{\partial x^{2}}- \\ && r_{1}^{2} \varepsilon^{2}\Bigg\{\Bigg[ \left( {\frac{\partial^{2}}{\partial x^{2}}\left( {c_{g}^{2} \frac{\partial^{2}w_{1} }{\partial \xi ^{2}}+2\frac{\partial^{2}w_{1} }{\partial \tau \partial t}-c_{0}^{2} \frac{\partial^{2}w_{1} }{\partial \xi^{2}}} \right)} \right)\Bigg]+ \\ && 2\frac{\partial^{2}}{\partial x\partial \xi }\left( {-2c_{g} \frac{\partial ^{2}w_{1} }{\partial t\partial \xi }-c_{0}^{2} \frac{\partial^{2}w_{1} }{\partial x\partial \xi }} \right)+ \\ &&\frac{\partial^{2}}{\partial \xi^{2}}\left( {\frac{\partial ^{2}w_{1} }{\partial t^{2}}-c_{0}^{2} \frac{\partial^{2}w_{1} }{\partial x^{2}}+c_{2}^{2} w_{1} } \right) \Bigg\} \end{eqnarray} $同样消除长期项, 令方程(62)等号右端等于零, 并将解的形式(50)代入方程右端, 得到
(63) $\begin{eqnarray} \label{eq63} &&2\left( {1+r_{1}^{2} k^{2}} \right)\left( {-{i}\omega } \right)\frac{\partial A}{\partial \tau }+c_{1}^{2} 3A^{2}\bar{{A}}k^{2}+c_{g}^{2} \frac{\partial^{2}A}{\partial \xi^{2}} -\\ && r_{1}^{2} \left( {-\omega^{2}+4c_{0}^{2} k^{2}-4c_{g} k\omega -k^{2}c_{g}^{2} +c_{2}^{2} } \right)\frac{\partial^{2}A}{\partial \xi ^{2}}=0\qquad \end{eqnarray} $进而得到非线性薛定谔方程
(64) $\begin{eqnarray} \label{eq64} {i}\frac{\partial A}{\partial \tau }+\alpha \frac{\partial^{2}A}{\partial \xi ^{2}}+\beta A^{2}\bar{{A}}=0 \end{eqnarray} $在式(64)中, $\alpha $和$\beta $分别为色散系数和非线性系数
(65) $\alpha =\frac{r_{1}^{2} \left( {-\omega^{2}+4c_{0}^{2} k^{2}-4c_{g} k\omega -k^{2}c_{g}^{2} +c_{2}^{2} } \right)-c_{g}^{2} }{2\omega \left( {1+r_{1}^{2} k^{2}} \right)} $(66) $\beta =\frac{3c_{1}^{2} k^{2}}{2\omega \left( {1+r_{1}^{2} k^{2}} \right)} $根据孤子理论, 非线性薛定谔方程在某些条件下存在亮孤子解和暗孤子解.下面继续推导非线性方程的孤子解.设
(67) $\begin{eqnarray} \label{eq67} A\left( {\xi ,\tau } \right)=\phi \left( \eta \right){e}^{{i}\left( {k_{1} \xi -\varpi \tau } \right)}, \ \ \eta =\xi -2\alpha k_{1} \tau \end{eqnarray} $$k_{1}$和$\varpi $是波数和频率, 将上式解的形式代入到非线性薛定谔方程中, 可以得到常微分方程
(68) $\begin{eqnarray} \label{eq68} \alpha \frac{{d}^{2}\phi }{{d}\eta^{2}}-\left( {\alpha k_{1}^{2} -\varpi } \right)\phi +\beta \phi^{3}=0 \end{eqnarray} $进一步运用Jacobi椭圆函数展开法求解非线性薛定谔方程, 得到非线性薛定谔方程的振幅为
(69) $\begin{eqnarray} \label{eq69} \phi =\pm \sqrt {\frac{2\gamma }{\beta \left( {2-m^{2}} \right)}} {dn}\left( {\eta ,m} \right) \end{eqnarray} $考虑$\alpha >0$, $\beta>0$, 当$m$趋于1时, 可以得到亮孤子解
(70) $\begin{eqnarray} \label{eq70} A=\pm \sqrt {\frac{2\alpha }{\beta }} {sech}\left( {\xi -2\alpha k_{1} \tau } \right){e}^{{i}\left[ {k_{1} \xi -\alpha \left( {k_{1}^{2} -1} \right)\tau } \right]} \end{eqnarray} $考虑$\alpha <0$, $\beta>0$, 当$m$趋于1时, 可以得到暗孤子解
(71) $\begin{eqnarray} \label{eq71} A=\pm \sqrt {\frac{-2\alpha }{\beta }} \tanh \left( {\xi -2\alpha k_{1} \tau } \right){e}^{{i}\left[ {k_{1} \xi -\alpha \left( {k_{1}^{2} -1} \right)\tau } \right]} \end{eqnarray} $解(70)和(71)的形式与文献[
16 ]类似, 但是方程中系数的含义有很大差别, 尤其是在考虑压电效应和电学边界条件以后, 孤子解的特性也会受到这些参数的影响, 下面将着重讨论.
4 冲击波和孤立波分析 在数值计算中, 基体梁采用铝, 压电层为PZT压电陶瓷, 压电层合梁的结构参数和压电片的材料参数如下表所示.
Table 1 表1 表1 压电层合梁参数
Table 1
Parameters of the piezoelectric laminated beam 新窗口打开 |
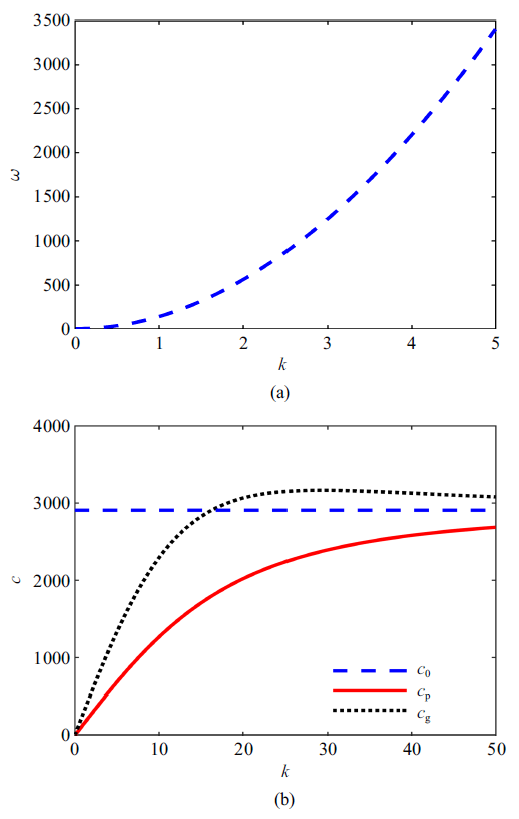
下载CSV 图2 分别给出了线性方程下的色散关系以及对应的相速度曲线和群速度曲线.通过
图2 (a)可以看出, 随着波数$k$的增大, 频率也随着增大, 并且增大的速率越来越快.
图2 (b)可以看出, 随着波数的增大, 群速度大于相速度, 也就是说, 此时弯曲波有反常的色散.
图2 新窗口打开 |
下载原图ZIP |
生成PPT 图2(a)色散曲线; (b)相速度和群速度与波数的关系 Fig.2(a) Dispersion curves; (b) relationship between phase velocity and group velocity and wave number 首先, 考虑压电层厚度和基体梁厚度均为} 0.05 m, 此时可以求得纵波波速$c_{0}= 2905.4$ m/s.
图3 分别给出了冲击波解和孤立波解随时间$t$和空间$x$的变化, 如
图3 (a)所示. 当波速$c$等于20 m/s时, 结构产生冲击波解, 当波速$c$等于4000 m/s时, 结构产生孤立波解, 且冲击波解和孤立波解是非周期的.
图3 新窗口打开 |
下载原图ZIP |
生成PPT 图3不同波速下的冲击波和孤立波 Fig.3Shock wave and solitary wave under different wave velocities 图4 给出了没有加外电压时不同波速下冲击波随空间$x$的变化曲线. 从
图4 (a)可以看出, 当波速分别为200 m/s和500 m/s时, 冲击波的振幅分别为0.1 m和0.25 m.说明随着波速的增大, 冲击波的振幅增大. 但是当波速$c= 500$ m/s时, 冲击波的波面要比波速$c = 200$ m/s时的波面要陡, 说明冲击波的波宽降低. 同样
图4 (b)给出了不同压电层厚度对冲击波的影响.可以明显看出, 当压电层厚度为0.05 m时, 冲击波的振幅大约为0.1 m, 当压电层厚度为0.01 m时, 冲击波的振幅大约为0.08 m, 说明冲击波的振幅和波宽都略有降低.
图4 新窗口打开 |
下载原图ZIP |
生成PPT 图4不同(a)波速和(b)压电层厚度下的冲击波 Fig.4Shock wave at different (a) wave velocities and (b) thicknesses of the piezoelectric layer 图5 给出了没有外加电压情况下不同波速下的孤立波解的曲线. 由
图5 (a)可知, 当波速$c =3000$ m/s时, 冲击波的振幅约为1.5 m, 当波速$c = 4000$ m/s时, 冲击波的振幅约为2 m, 说明随着波速的增大孤立波振幅增大, 同样可以看出孤立波的波宽有所增大.
图5 (b)给出了压电层厚度对孤立波的影响, 可以看出, 当压电层厚度为0.05 m时, 孤立波的振幅略大于压电层厚度为0.01 m时的孤立波振幅, 但是当压电层厚度为0.05 m时的孤立波波宽小于压电层厚度为0.01 m时的波宽.通过分析
图4 和
图5 中不同时刻下的冲击波和孤立波的行波曲线, 发现冲击波和孤立波都是右行波.
图5 新窗口打开 |
下载原图ZIP |
生成PPT 图5不同(a)波速和(b)压电层厚度下的孤立波 Fig.5Solitary waves with different (a) wave velocities and (b) thicknesses of the piezoelectric layer 图6 分别显示了波速和压电层厚度对冲击波振幅的影响. 由
图6 (a)可以看出, 随着波速的增大, 冲击波的振幅增大, 当波速较小时, 外电压也会对冲击波的振幅产生影响, 随着外电压的增大, 冲击波的振幅也随之增大.
图6 (b)给出了压电层厚度对冲击波振幅的影响, 随着压电层厚度的增大, 冲击波的振幅增大, 且波速较小时, 冲击波振幅变化不明显.
图7 给出了波速和压电层厚度对冲击波波宽的影响.由
图7 (a)不难发现, 随着波速增大, 冲击波波宽有所降低.当波速较小时, 随着外电压的增大, 冲击波的波宽增大.
图7 (b)讨论了压电层厚度对冲击波波宽的影响, 随着压电层厚度的增大, 且当波速较小时, 冲击波的波宽会先减小后增大, 对于波速较大的情况, 冲击波的波宽变化不明显.总的来说, 冲击波的波宽和振幅主要受波速的影响较大, 当波速较小时, 外电压对冲击波的振幅以及波宽影响较大.
图6 新窗口打开 |
下载原图ZIP |
生成PPT 图6(a)波速和(b)压电层厚度对冲击波振幅的影响 Fig.6Influences of (a) wave velocity $c$ and (b) piezoelectric layer thickness $h_{p}$ on the amplitude of the shock wave 图7 新窗口打开 |
下载原图ZIP |
生成PPT 图7(a)波速和(b)压电层厚度对冲击波波宽的影响 Fig.7Influences of (a) wave velocity $c$ and (b) piezoelectric layer thickness $h_{p}$ on the width of the shock wave 图8 分别给出了不同波速和压电层厚度下的孤立波振幅的变化.由于孤立波产生的条件, 所需波速必须大于纵波波速$c_{0}$, 通过
图6 和
图7 的分析可以确定: 外电压的影响在波速较小的情况下对冲击波的振幅和波宽影响较大, 当波速较大的时候, 压电的影响可以忽略.如
图8 (a)所示, 随着波速$c$的增大, 孤立波的振幅近似为线性增大, 且随着电压的增大, 孤立波的振幅基本不变.通过
图8 (b)可以看出, 随着压电层厚度的增大, 孤立波的振幅逐渐增大, 但是增大的幅度逐渐减小, 随着波速的增大, 孤立波的振幅增大.通过
图9 (a)和
图9 (b)可以看出, 随着波速和压电层厚度的增大, 孤立波的波宽也随之增大, 外加电压对孤立波波宽几乎没有影响.
图8 新窗口打开 |
下载原图ZIP |
生成PPT 图8(a)波速和(b)压电层厚度对孤立波振幅的影响 Fig.8Influences of (a) wave velocity $c$ and (b) piezoelectric layer thickness $h_{p}$ on the amplitude of the solitary wave 图9 新窗口打开 |
下载原图ZIP |
生成PPT 图9(a)波速和(b)压电层厚度对孤立波波宽的影响 Fig.9Influences of (a) wave velocity $c$ and (b) piezoelectric layer thickness $h_{p}$ on the width of the solitary wave 5 亮孤子和暗孤子分析 根据亮孤子和暗孤子存在条件, 可试图通过调节外电压或者压电层厚度来分别实现亮孤子和暗孤子的条件, 所以有必要研究色散系数$\alpha $和非线性系数$\beta $随压电层厚度$h_{p}$和外电压$V$的变化.下面着重分析外加电压和压电层厚度对色散系数的影响.
图10 (a)给出了外加电压对色散系数的影响, 可以看出, 随着外加电压$V$的增大, 色散系数呈线性增大.观察到色散系数随着外加电压的增大出现正负变化, 当色散系数$\alpha>0$时, 结构有亮孤子解; 当色散系数$\alpha <0$时, 结构有暗孤子解.另外, 当压电层厚度$h_{p} = 0.01$ m时, 色散系数与外加电压的斜率更大.
图10 (b)可以看出, 随着压电层厚度的增大, 色散系数的绝对值先增大后减小, 但是色散系数的符号不发生变化.当取不同外加电压时, 色散系数的符号才会发生变化, 且外加电压对亮孤子解和暗孤子解的影响更大, 因此可以通过调整作用在压电层合梁上的电压来实现亮孤子和暗孤子.
图10 新窗口打开 |
下载原图ZIP |
生成PPT 图10(a)外加电压和(b)压电层厚度对色散系数的影响 Fig.10Influences of (a) external voltage and (b) the thickness of the piezoelectric layer on the dispersion coefficient 接下来给出了不同参数下的亮孤子解和暗孤子解.
图11 (a)给出了波数$k = 0.02$, 外电势$V = 10$ V和压电层厚度$h_{p} = 0.05$ m时的压电层合梁中亮孤子解随慢变$\tau $和$\xi $的变化关系, 可以看到振幅较大的范围分布主要集中在中心附近的狭小区域内, 最大振幅为0.01 m, 当离开中心区域, 振幅很快下降到零, 且随着$\tau $的变化, 亮孤子解的振幅和波形均不发生变化.
图11 (b)给出了当波数$k = 0.02$, 外电势$V =-10$ V和压电层厚度$h_{p} = 0.05$ m时的压电层合梁中暗孤子解随$\tau $和$\xi $的变化关系, 可以看到在中心点附近, 振幅最小且为零, 离开中心点, 振幅很快增大并达到最大值, 此时最大振幅约为0.01 m.
图11 新窗口打开 |
下载原图ZIP |
生成PPT 图11亮孤子解和暗孤子解 Fig.11Bright soliton and dark soliton 图12 (a)给出了不同压电层厚度下亮孤子解的特性, 当$h_{p} = 0.05$ m时, 亮孤子解的振幅约为0.021 m; 当$h_{p} = 0.01$ m时, 亮孤子解的振幅大约为0.031 m. $\tau = 0$时刻, 亮孤子位于中心, $\tau = 5$ s时刻, 亮孤子发生右移, 且压电层厚度$h_{p}$为0.05 m时亮孤子移动的幅度比压电层厚度$h_{p}$等于0.01 m时要大, 且在移动后亮孤子振幅不发生变化, 波形不发生改变. 同样通过观察
图12 (b)可以发现, 当$V= 10$ V时, 亮孤子的振幅约为0.021 m; 当$V = 50$ V时, 亮孤子解的振幅大约为0.048 m.在$\tau= 0$时刻, 亮孤子位于中心, $\tau = 5$ s时刻, 亮孤子发生右移, 且外加电压$V$为50 V时亮孤子移动的幅度比外加电压$V$等于10 V时要大, 且在移动后亮孤子振幅和波形同样不发生改变.综上, 可以得出结论: 压电层厚度和外加电压对亮孤子特性有明显的影响.
图12 新窗口打开 |
下载原图ZIP |
生成PPT 图12不同(a)压电层厚度和(b)外加电压的亮孤子解 Fig.12Bright soliton at different (a) thicknesses of the piezoelectric layer (b) external voltages 图13 (a)给出了不同压电层厚度下暗孤子解的特性, 当压电层厚度$h_{p} = 0.05$ m时, 暗孤子解的振幅约为0.021 m; 当$h_{p} = 0.01$ m时, 暗孤子解的振幅大约为0.031 m. 在$\tau= 0$时刻, 暗孤子位于中心; $\tau = 5$ s时, 亮孤子发生左移, 且压电层厚度$h_{p}$为0.05 m时亮孤子移动的幅度比压电层厚度$h_{p}$等于0.01时要大, 且在移动后暗孤子振幅不发生变化, 波形不发生改变.同样由
图13 (b)可以看出, 当$V$等于$-$10 V时, 暗孤子解的振幅约为0.021 m; 当$V$等于$-$50 V时, 暗孤子解的振幅大约为0.048 m. 在$\tau= 0$时刻, 暗孤子位于中心; $\tau = 5$ s时刻, 亮孤子发生左移, 且外加电压$V$为$-$50 V时暗孤子移动的幅度比外加电压$V$等于$-$10 V时要大, 且在移动后暗孤子振幅和波形同样不发生改变, 因此, 压电层厚度和外加电压对暗孤子特性也有明显的影响.
图13 新窗口打开 |
下载原图ZIP |
生成PPT 图13不同(a)压电层厚度和(b)外加电压的暗孤子解 Fig.13Dark soliton at different (a) thicknesses of the piezoelectric layer (b) external voltages 继续研究了压电层厚度和外电压对亮孤子振幅的影响.通过
图14 (a)和
图14 (b)可知, 随着压电层厚度的增大, 亮孤子解的振幅均有所减小, 同时减小的幅度随压电层厚度的增大而减小; 而随着电压的增大, 亮孤子解的振幅增大.
图14 新窗口打开 |
下载原图ZIP |
生成PPT 图14(a)压电层厚度和(b)外加电压对亮孤子振幅的影响 Fig.14Influences of (a) the thickness of the piezoelectric layer and (b) external voltage on the amplitude of the bright soliton 6 总结 本文将矩形压电层合梁简化为一维无限长模型, 导出了含有电学边界条件下的矩形压电层合梁的非线性弯曲波动方程. 用传统的Jacobi椭圆函数展开法得到了相应的冲击波解和孤立波解. 并用多尺度摄动方法求得了相应的亮孤子解和暗孤子解.得到如下结论:
(1) 随着波数$k$增大, 频率随之增大, 且增大的速率越来越快; 随着波数$k$增大, 群速度大于相速度, 此时弯曲波有反常色散. (2) 当波速$c$和小于纵波波速$c_{0}$时, 存在冲击波解, 且随着波速$c$的增大, 冲击波的振幅增大, 波宽减小; 随着压电层厚度$h_{p}$增大, 冲击波振幅增大, 波宽先减小后增大; 外加电压对波速较小时的冲击波的振幅和波宽有一定影响, 随着电压的增大, 冲击波的振幅增大, 波宽减小. (3) 当波速$c$和大于纵波波速$c_{0}$时, 存在孤立波解, 随着波速$c$的增大, 冲击波的振幅和波宽增大; 随着压电层厚度$h_{p}$的增大, 冲击波振幅和波宽增大; 外加电压对孤立波几乎没有影响. (4) 随着外加电压$V$增大, 色散系数$\alpha $增大, 且外加电压$V$对色散系数的影响比压电层厚度$h_{p}$对色散系数的影响更大, 可以通过调整作用在压电层合梁上的电压来改变色散系数的符号, 得到亮孤子和暗孤子. (5) 随着压电层厚度$h_{p}$的增大, 亮孤子和暗孤子的振幅均有所减小, 随着外加电压$V$增大, 亮孤子和暗孤子的振幅增大.
[1] 杨洪升 , 李玉龙 , 周风华 . 孤立波与淹没平板相互作用的三维波面和水动力实验研究,力学学报 , 2019 ,51(6 ):1605 -1613 [本文引用: 1] (Yang Hongsheng Li Yulong Zhou Fenghua Chinese Journal of Theoretical and Applied Mechanics 2019 ,51(6 ):1605 -1613 (in Chinese)) [本文引用: 1] [2] 王畅畅 , 王国玉 , 黄彪 等 . 可压缩空化流动空穴演化及压力脉动特性实验研究力学学报 , 2019 ,51(5 ):1296 -1309 [本文引用: 1] (Wang Changchang Wang Guoyu Huang Biao et al . Experimental investigation of cavitation characteristics and dynamics in compressible turbulent cavitating flowsChinese Journal of Theoretical and Applied Mechanics 2019 ,51(5 ):1296 -1309 (in Chinese)) [本文引用: 1] [3] Sussell RJ Report on waves//Fourteen Meetingof the British Association for the Advancement of Science , 1844:311 -390 [本文引用: 1] [4] Kortewrg DJ Vries G Philosophical Magazine 1895 ,39(240 ):422 -443 [本文引用: 1] [5] Zabusky NJ Kruskal MD Physical Review Letters 1965 ,15(6 ):240 -243 [本文引用: 1] [6] Taylor RJ Baker DR Ikezi H Physical Review Letters 1970 ,24(5 ):206 -209 [本文引用: 1] [7] 朱位秋 . 弹性杆中的非线性波固体力学学报 , 1980 ,2:247 -253 [本文引用: 2] (Zhu Weiqiu Chinese Journal of Solid Mechanics 1980 ,2:247 -253 (in Chinese)) [本文引用: 2] [8] 庄蔚 , 杨桂通 . 孤波在非线性弹性杆中的传播应用数学和力学 , 1986 ,7(7 ):571 -581 [本文引用: 1] (Zhuang Wei Yang Guitong Applied Mathematics and Mechanics 1986 ,7(7 ):571 -581 (in Chinese)) [本文引用: 1] [9] Zhang NM Yang GT European Journal of Mechanics A——Solids 2003 ,22(6 ):917 -923 [10] Guo JG Zhou LJ Zhang SY Applied Mathematics and Mechanics-English Edition 2005 ,26(5 ):667 -674 [11] Seadawy AR Manafian J Results in Physics 2018 ,8:1158 -1167 [本文引用: 1] [12] Darvishi MT Najafi M Wazwaz AM Waves in Random and Complex Media 2020 ,30(2 ):340 -353 [本文引用: 1] [13] Duan WS Zhao JB Chaos Solitons & Fractals 2000 ,11(8 ):1265 -1267 [本文引用: 1] [14] Parkes EJ Duffy BR Abbott PC Physics Letters A 2002 ,295(5 ):280 -286 [本文引用: 1] [15] Dai HH Acta Mechanica 1998 ,127(1 ):193 -207 [本文引用: 1] [16] Dai HH Huo Y Proceedings of the Royal Society A——Mathematic Physical and Engineering Sciences 2000 ,456(1994 ):331 -363 [本文引用: 2] [17] Zhang SY Zhuang W Acta Mechanica Sinica 1987 ,3:62 -72 [本文引用: 2] [18] Zhang SY Liu ZF Applied Mathematics and Mechanics-English Edition 2008 ,29(7 ):909 -917 [本文引用: 1] [19] Liu ZF Zhang SY Acta Mechanica Solida Sinica 2006 ,19(1 ):1 -8 [20] Liu ZF Zhang SY Applied Mathematics and Mechanics-English Edition 2006 ,27(10 ):1431 -1437 [本文引用: 1] [21] Xue CX Pan E Zhang SY Smart Materials and Structures 2011 ,20(10 ):105010 [本文引用: 1] [22] Xue CX Pan E International Journal Engineering Science 2013 ,62:48 -55 [本文引用: 1] [23] Bulut H Sulaiman TA Baskonus HM Optical and Quantum Electronics 2018 ,50(2 ):87 [本文引用: 1] [24] Iqbal M Seadawy AR Lu DC Modern Physics Letters B 2019 ,33(18 ):1950210 [本文引用: 1] [25] Schiffer A Lee D Kim E International Journal of Solids and Structures 2018 ,152:39 -50 [本文引用: 1] [26] Kumar S Kumar A Wazwaz AM European Physical Journal Plus 2020 ,135(11 ):870 [27] Hacinliyan I Erbay S Chaos Solitons & Fractals 2002 ,14(8 ):1127 -1135 [28] 王千 , 刘桦 , 房詠柳 等 . 梯形应力脉冲在弹性杆中的传播过程和几何弥散力学学报 , 2019 ,51(6 ):1605 -1613 [本文引用: 1] (Wang Qian Liu Hua Fang Yongliu et al . The propagation process and the geometric dispersion of a trapezoidal stress pulse in an elastic rodChinese Journal of Theoretical and Applied Mechanics 2019 ,51(6 ):1820 -1629 (in Chinese)) [本文引用: 1] [29] Zhang SY Liu ZF Applied Mathematics and Mechanics-English Edition 2010 ,31(11 ):1347 -1358 [本文引用: 1] [30] Zhang SY Liu ZF Lu GY Acta Mechanica Solida Sinica 2009 ,22(4 ):287 -294 [本文引用: 1] [31] Wei CP Xue CX Acta Mechanica Sinica 2020 ,36(5 ):1099 -1108 [本文引用: 1] [32] 刘式适 , 傅遵涛 , 刘式达 等 . Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用物理学报 , 2001 ,50(11 ):2068 -2073 (Liu Shikuo Fu Zuntao Liu Shida et al . Expansion methodabout the Jacobi elliptic function and its applications to nonlinear wave equationsActa Physica Sinica 2001 ,50(11 ):2068 -2073 (in Chinese))  ,2), 张伟北京工业大学机械结构非线性振动与强度北京市重点实验室, 北京 100124
,2), 张伟北京工业大学机械结构非线性振动与强度北京市重点实验室, 北京 100124 ,2), Zhang WeiBeijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures, College of Mechanical Engineering, Beijing University of Technology, Beijing 100124, China
,2), Zhang WeiBeijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures, College of Mechanical Engineering, Beijing University of Technology, Beijing 100124, China
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT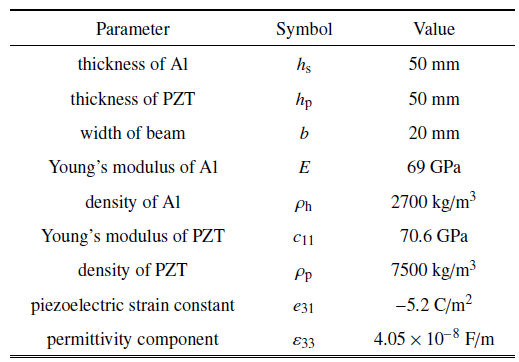
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT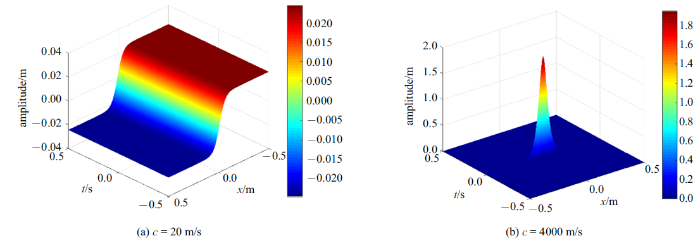 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT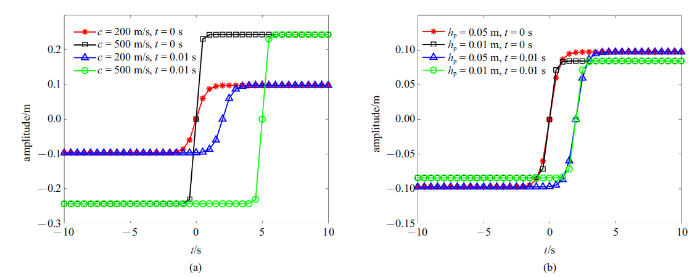 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT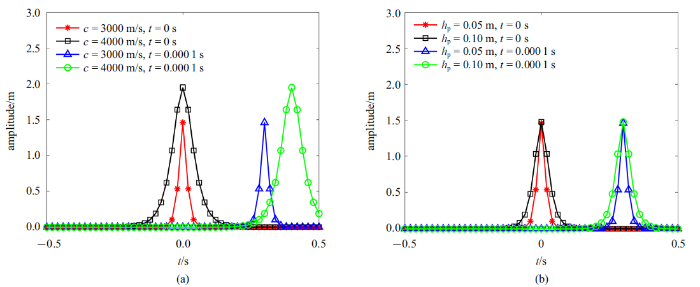 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT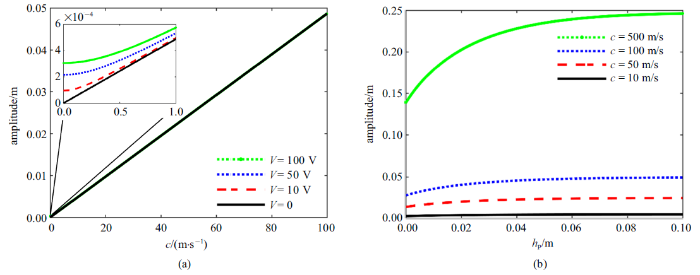 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT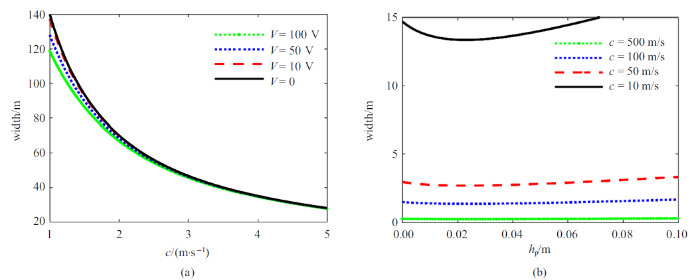 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT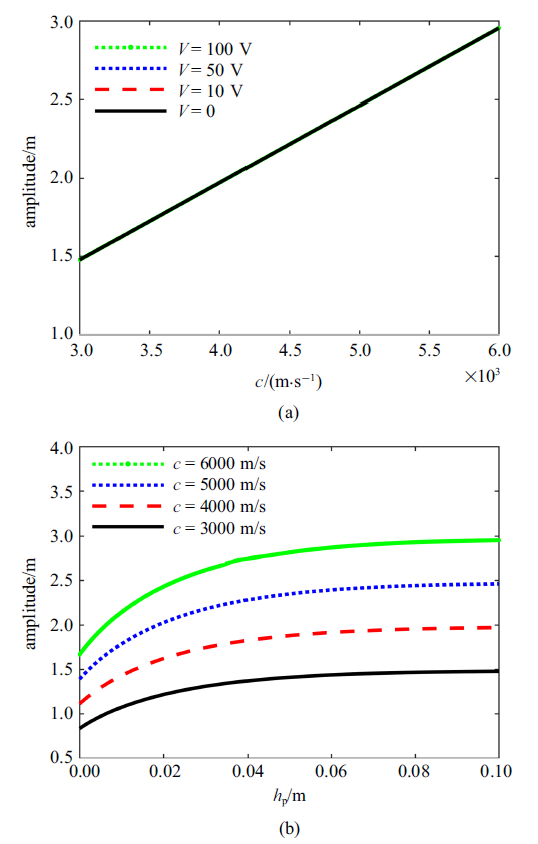 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT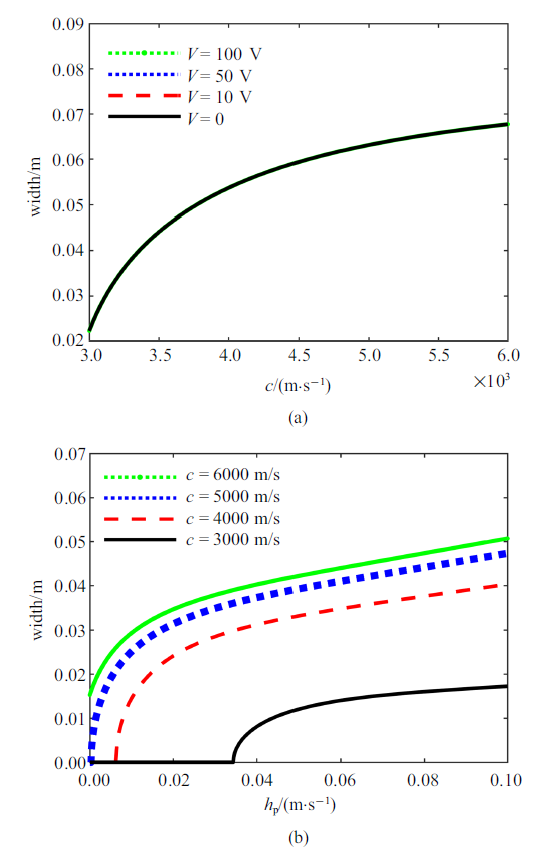 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT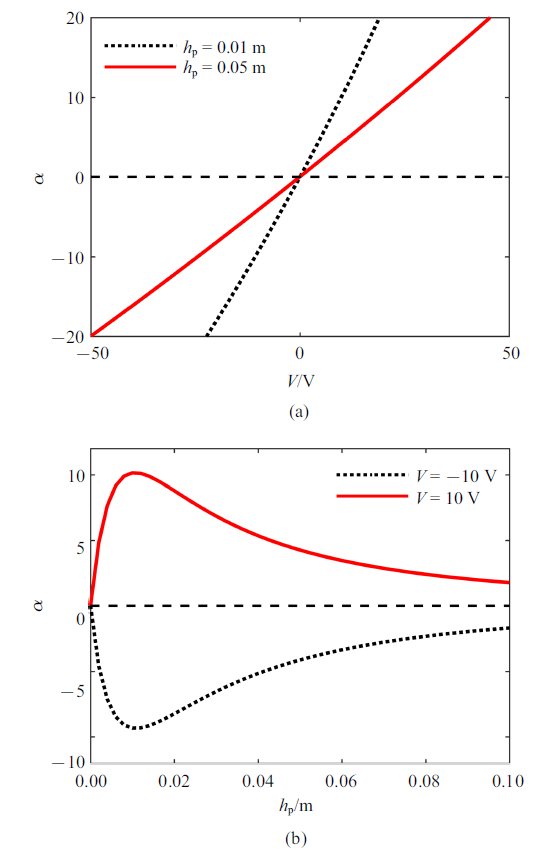 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT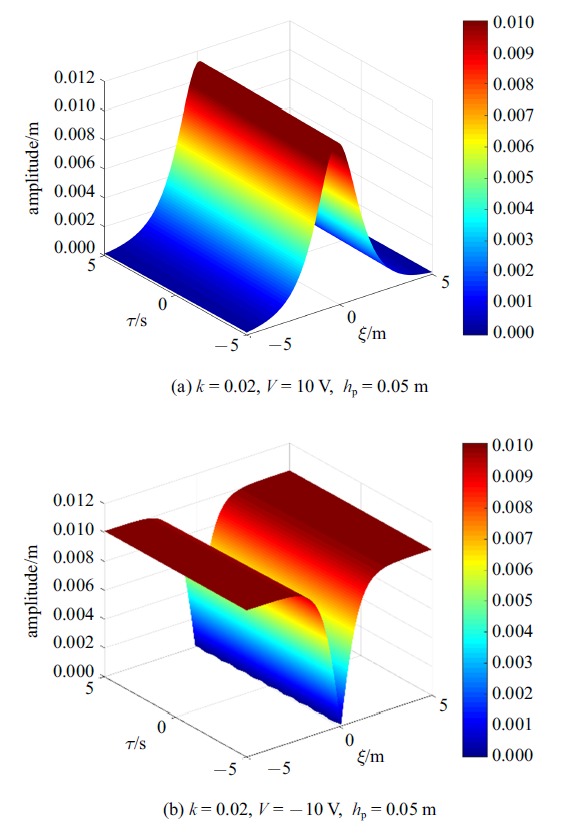 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT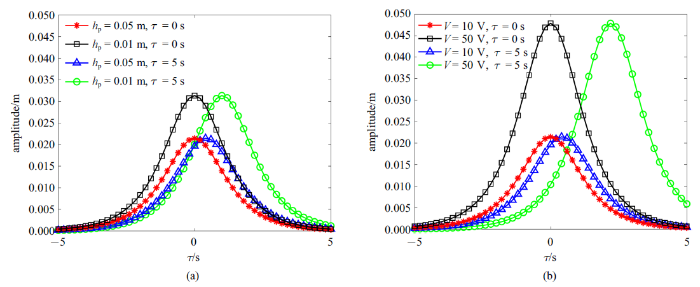 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT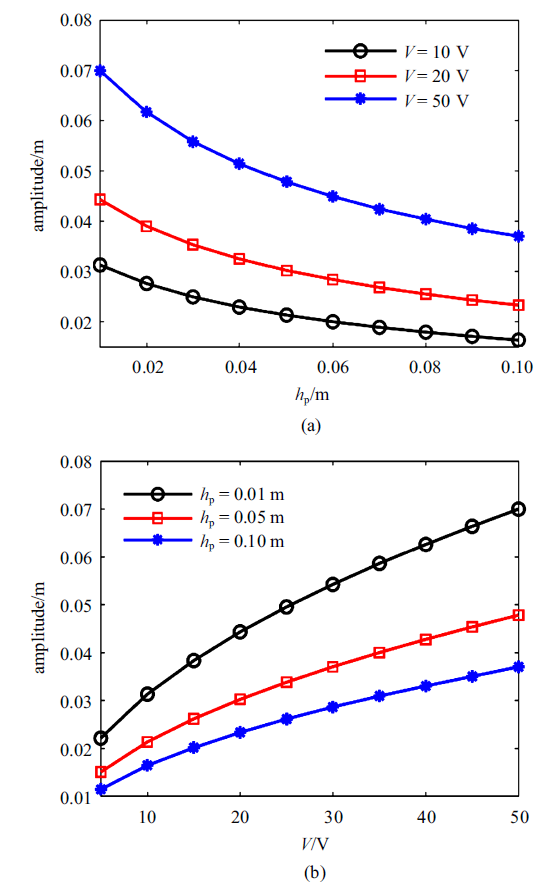 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT