刘岩^*, 王惠明^,*,?,2)*浙江大学工程力学系, 杭州 310027
^?浙江省软体机器人与智能器件研究重点实验室, 杭州 310027

HOMOGENEOUS AND INHOMOGENEOUS SWELLING AND PARAMETRIC STUDY OF HYDROGELS CONSIDERING THE MICROSTRUCTURAL DEFORMATION¹⁾

Liu Yan^*, Wang Huiming^,*,?,2)*Department of Engineering Mechanics, Zhejiang University, Hangzhou 310027, China
^?Key Laboratory of Soft Machines and Smart Devices of Zhejiang Province, Zhejiang University, Hangzhou 310027, China

通讯作者: 2) 王惠明, 教授, 主要研究方向: 多场耦合力学,智能软材料非线性力学. E-mail:wanghuiming@zju.edu.cn

收稿日期:2020-10-23接受日期:2020-12-29网络出版日期:2021-02-07

基金资助:

1) 国家自然科学基金资助项目.11772296

Received:2020-10-23Accepted:2020-12-29Online:2021-02-07
作者简介 About authors


摘要
本文给出考虑微观变形的水凝胶溶胀的分析模型,该模型假设构成聚合物网络的单链受到由于周围链的作用而产生类似圆管状的约束,并且认为每个单链变形与网络变形之间存在非仿射关系.利用该模型分析了凝胶在自由溶胀情形,预拉伸凝胶单一方向溶胀情形以及具有刚性核的球形凝胶溶胀至平衡状态情形的变形特征.研究表明, 对于自由溶胀的均匀变形情形, 水凝胶微观单链与宏观网络的变形相一致,伸长率随链段数的增加而增大, 随单链密度的增大而减小.伸长率也会随有效圆管几何参数数值的增大而增大,但是当外部溶剂压力达到一定数值以后单链的圆管约束对凝胶溶胀变形影响逐渐减小.在单一方向溶胀状态下,预拉伸凝胶会出现微观单链和宏观网络伸长率相等的溶胀平衡状态,此时约束应力等于零.具有刚性核的球形凝胶溶胀至平衡状态时产生径向和环向伸长率不相等的非均匀球对称变形.在刚性核的附近, 单链和网络的径向伸长率均大于自由溶胀状态伸长率.在远离刚性核的位置, 单链和网络的伸长率均接近自由溶胀状态的伸长率.网络渗透压随有效圆管几何参数数值的增大而降低,溶剂分子体积分数则随有效圆管几何参数数值的增大而增大.所建立的分析模型可以模拟凝胶溶胀导致的微观单链变形.
关键词： 水凝胶;均匀溶胀;非均匀溶胀;非仿射;微观变形

Abstract
An analytical model is proposed to analyze the swelling-induced deformation of the hydrogels considering the microstructural deformation of the polymer chains. It is assumed that the chain is constrained to a tube-like space due to the action of the surrounding chains, and the chains experience the non-affine deformation. Based on the presented model, we studied the free swelling deformation, the swelling along one direction with the pre-stretches in other two directions and the constraint swelling of a spherical hydrogel with a rigid core. For the free swelling case, the deformation is homogeneous and the deformation of the network is equal to that of the chains. The stretches of the network and the chains increase with the increase of the number of polymer segments and decrease with the increase of the density of the chains. The stretches also increase with the increase of the effective tube geometry parameter (ETGP). The effect of the ETGP on the swelling-induced stretch gradually disappears when the external solvent pressure exceeds a certain value. For the swelling along one direction with pre-stretches in other two directions, the equilibrium state with which the stretch of micro-chain equals to that of macro-network can be reached. At this state, the stresses in the hydrogel become zero. For the constraint swelling of a spherical hydrogel with a rigid core, the hydrogel deforms inhomogeneously and the swelling-induced radial stretch is different from the tangential stretch. At the region near the rigid core, the stretch of micro-chain and the stretch of macro-network in the radial direction are larger than that of the free swelling state. At the region far from the rigid core, the stretch of the micro-chain and the radial and tangential stretches of the macro-network approach to that of the free swelling state. The osmotic pressure decreases with the increase of the ETGP, while the volume fraction of the solvent molecules increases with the increase of the ETGP. The presented model can be used to predict the swelling-induced deformation of micro-chain.
Keywords：hydrogel;homogeneous swelling;inhomogeneous swelling;non-affine;microstructural deformation


PDF (1534KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
刘岩, 王惠明. 考虑微观变形特征的水凝胶均匀和非均匀溶胀分析及其影响参数研究¹⁾. 力学学报[J], 2021, 53(2): 437-447 DOI:10.6052/0459-1879-20-368
Liu Yan, Wang Huiming. HOMOGENEOUS AND INHOMOGENEOUS SWELLING AND PARAMETRIC STUDY OF HYDROGELS CONSIDERING THE MICROSTRUCTURAL DEFORMATION¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(2): 437-447 DOI:10.6052/0459-1879-20-368

引言

聚合物网络是由聚合物链交联构成的一种复杂三维网状结构, 在外界激励下可能产生超大变形. 由于凝胶具有良好弹性、生物相容性和生物降解性, 被广泛应用于组织工程^[1]、药物运输^[2]和细胞培养^[3]等领域. 浸没在溶剂中的聚合物吸收大量溶剂分子形成凝胶并伴随发生溶胀^[4]. 溶胀过程受化学势的影响^[5], 当凝胶内外溶剂分子化学势相等且满足力学平衡时凝胶达到平衡状态, 此时网络不再吸纳溶剂分子, 进入饱和状态. 凝胶的溶胀变形同时也受环境温度、pH值和网络交联密度等因素影响^[6-7].

关于凝胶的溶胀响应分析, 通常采用基于自由能理论的模型, 包括两部分, 一部分是聚合物网络被拉伸产生的自由能, 另一部分是溶剂分子与网络混合产生的混合能. 对于聚合物网络被拉伸产生的自由能部分, 基于宏观唯象模型的有neo-Hookean模型^[8]、Money-Rivlin模型^[9]、Gent模型^[10]和Ogden模型^[11]等. 从微观角度, 认为聚合物变形响应主要源于单链构形熵的变化, 其理论模型包括三链模型^[12](认为空间内单链主要分布在3个相互垂直的方向), 四面体模型^[13-14] (4条链交联在正四面体中心点), 八链模型^[15](单链分布在六面体对角线)以及全网络模型^[16](考虑空间中单链具有随机取向), 其中三链模型认为聚合物在变形过程中宏观网络与微观单链变形是仿射关系(即宏观网络和微观单链变形相等), 而四面体模型和八链模型认为宏观与微观变形是非仿射关系.

采用仿射变形假设的全网络模型预测能力介于三链模型和八链模型之间^[17]. 当凝胶进入大变形阶段后, 主方向上单链的伸长率逐渐接近极限值, 随着变形的进一步增大, 主方向上的单链伸长率增大量很小, 但是其他方向上的单链还没有接近极限伸长率, 因此采用仿射变形假设预测的其他方向上的单链伸长率就会低于实际伸长率^[18]. Miehe等^[19]采用非仿射变形假设的全网络模型, 同时考虑了单链的圆管约束, 很好地模拟超弹性材料的单轴拉伸、等双轴拉伸和剪切变形的实验结果, Huang等^[20]系统地总结了各种智能凝胶的本构模型. Li等^[21]基于仿射变形假设的全网络模型, 通过聚合物网络被拉伸时单链伸长率的变化预测了水凝胶的断裂行为. Lei等^[22]构建了一个介观尺度模型研究水凝胶的大变形和断裂机理.

利用超弹性材料自由能模型^[23-24] (如neo-Hookean模型和八链模型等), 可开展软材料结构的变形预测^[25], 结合Flory提出的混合能模型^[26], 可进行溶胀引起的变形分析和预测^[27-29]. 用neo-Hookean模型和Flory混合能模型可以较准确地预测凝胶中小变形情况, 当凝胶进入大变形阶段, neo-Hookean模型预测能力受到限制并且不能分析单链变形情况. 采用单链末端距服从Langevin分布的模型可以解决这一问题, Cohen等^[30]采用仿射变形假设的全网络模型, 根据Langevin函数计算单链有限伸长, 然后利用数值微球方法将单链集合成网络 ^[31], 最后获得凝胶发生溶胀变形时单链和网络的力学响应, 该方法已经被广泛应用^[32-37].

本研究利用非仿射变形的全网络模型, 假设每个单链变形受到由周围链形成的类似圆管状的约束, 开展凝胶发生溶胀变形时微观单链和宏观网络的变形分析. 为了更直观地解释单链变形, 分析凝胶在三种溶胀状态下网络和单链的变形情况, 第一种溶胀状态为自由溶胀, 凝胶没有外力和约束作用, 放入给定压力溶剂中溶胀至平衡状态; 第二种溶胀状态为单一方向溶胀, 首先将立方体凝胶进行等双轴预拉伸, 然后放入装有给定压力溶剂的容器中, 使其沿单一方向溶胀. 这两种状态下, 凝胶和单链都产生均匀变形(在各个位置的单链变形相同). 第三种溶胀状态为具有刚性核的球形凝胶溶胀, 将球形凝胶放入具有一定压力的溶剂中使其发生溶胀. 本文给出的模型可以模拟凝胶在溶胀变形情况下具有确定链段数的单链的有限伸长以及网络变形情况, 更好地理解影响溶胀变形的微观机理, 为凝胶性能的微观设计提供指导.

1 自由能函数

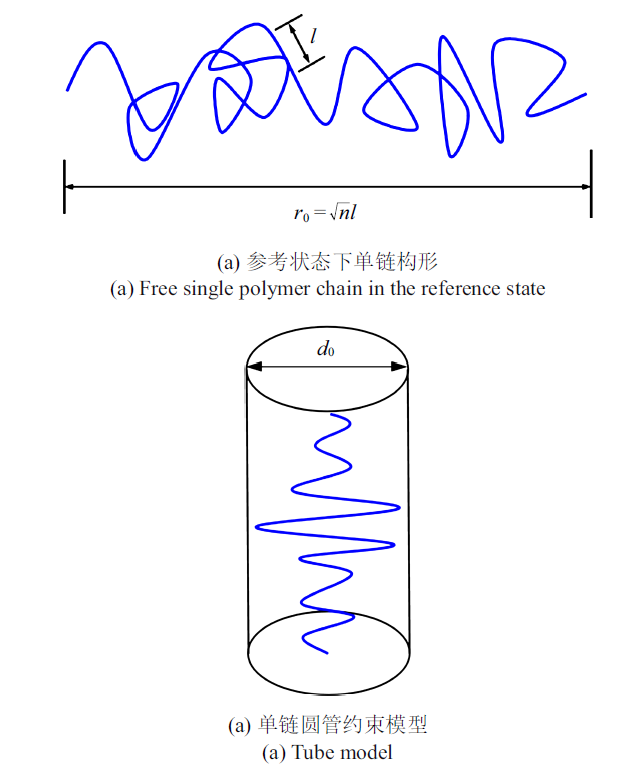
将聚合物网络中没有水分子进入的状态设置为参考状态. 考虑一个不可压缩的聚合物网络, 单位参考体积内含有$N$条具有随机取向且均匀分布的单链, 每条单链由$n$个长度为$l$的链段组成^[38]. 聚合物网络占据的体积为$V_{\rm p} =nNv_{\rm p} $, 其中$v_{\rm p} $是一个链段占据的体积. 单链构形示意图如图1(a)所示. 参考状态下, 每个单链的平均末端距$r_{0} =\sqrt n l$. 若单链完全伸展, 末端距$L=nl$. 在图1(b)中, 每个单链受到由周围单链构成的半径为$d_{0} $的类似圆管状约束.

图1

新窗口打开|下载原图ZIP|生成PPT
图1网络中单链构形以及圆管约束模型^[19]

Fig.1Geometry of a polymer chain and the tube model^[19]



将参考构型中任一物质点的位置矢量用$ X$表示, 当网络发生变形时, 物质点会移动到新的位置, 相应的位置矢量为$ x\left( { X} \right)$. 定义网络的变形梯度为$ F={\partial x\left({ X} \right)}/{\partial X}$. 将聚合物放入压力为$p$的溶剂中, 使其溶胀至平衡状态, 假设有$m$个溶剂分子进入网络, 此时凝胶的体积就等于$V_{\rm p} +mv_{\rm l} $, 其中$v_{\rm l} $是一个液体分子的体积.

假设液体分子和链段均是不可压缩的, 且在三维空间中占据$m+nN$个晶格位置, 每个晶格的体积为$v_{\rm c} $. 为了简化计算, 认为链段、液体分子和晶格体积是相等的, 记为$v_{\rm p} =v_{\rm l} =v_{\rm c}$^[30], 每个单元的体积变化率$J=\det F={1}/{c_{\rm p} }$, 其中$c_{\rm p} ={nN}/({m+nN})$是聚合物网络的体积分数, 溶剂分子的体积分数记为$c_{\rm l} =1-c_{\rm p} $.

在变形状态下, 定义每个单链的伸长率和相对伸长率分别为$\lambda ={r/{r_{0}}}$和$\lambda_{\rm rel} ={r/L}$, 其中$r$为变形状态下单链的末端距, 则有$\lambda \in [ {0,\sqrt n } )$和$\lambda_{\rm rel} \in[ {0,1})$. 每条单链受到由周围单链构成的类似圆管状约束^[39], 这样的几何形状约束了单链构形数. 将每条单链受到的约束用无量纲量$g=\left({{{d_{0} }/d}} \right)^{2}$表示, 其中$d$是当前状态下圆管的直径, $d_{0} $是参考状态下圆管的直径, 关于长度为$l$的Kuhn链段约束直径见文献[40].

当其发生溶胀变形时, 网络的构形熵会降低, 但网络和溶剂分子形成的混合物的熵增加^[41]. 根据统计力学, 每个单链的自由能由式(1)给出

(1)$\begin{eqnarray} \label{eq1} W_{\rm chain} =-TS=-TK\ln \varOmega \end{eqnarray}$
式中, $T$是绝对温度, $K$是玻尔兹曼常数, $\varOmega $是单链的构形数密度. 整个网络的自由能等于所有单链自由能的总和, 由式(2)计算

(2)$\begin{eqnarray} \label{eq2} W_{\rm s} =\sum\limits_{i=1}^N {W_{\rm chain}^{i} } \end{eqnarray}$
式中, $W_{\rm chain}^{i} $是第$i$个单链的自由能. 在单位参考体积中, 将溶胀凝胶的自由能表示为

(2)$\begin{eqnarray} \label{eq3} W=W_{\rm s} +W_{\rm m} +\varPi \left( {\frac{1}{c_{\rm p} }-J} \right)-pJ \end{eqnarray}$
式中, $W_{\rm m} $是网络与溶剂分子混合过程产生的自由能, $\varPi $是拉格朗日乘子. 第三项是拉格朗日乘子与(溶剂分子和聚合物)体积不可压缩性条件的乘积. 拉格朗日乘子解释为网络和溶剂分子混合物的总压力, 第四项是静水压力对凝胶做功.

由于neo-Hookean模型没有考虑单链的有限拉伸, 因此该模型普遍适用于中小变形的预测, 当凝胶发生大变形时, neo-Hookean模型的预测能力将会降低. 本研究采用Langevin模型分析单链有限伸长以及预测大变形情况. 假设网络中的每个单链都服从Langevin分布, 其构形数概率密度^[19]

(4)$\begin{eqnarray} \label{eq4} &&\varOmega =a_{0} \exp \left[ {-n\left( {\lambda_{\rm r} \beta +\ln \frac{\beta }{\sinh \beta }} \right)} \right]\cdot \\&&\qquad\exp \left[ {-\alpha \left( {\frac{r_{0} }{d_{0} }} \right)^{2}g} \right] \end{eqnarray}$
式中, $a_{0} $是无量纲参数, $\alpha $是与管截面形状有关的修正因子^[42], 其中$\beta =\ell^{-1}\left( {\lambda_{\rm r} } \right)$, $\ell \left( \beta \right)=\coth \beta -{1/\beta }$是Langevin函数, 逆Langevin函数可用Padé估计值^[43]

(5)$\begin{eqnarray} \label{eq5} \ell^{-1}\left( {\lambda_{\rm r} } \right)\approx \lambda_{\rm r} {{\left( {3-\lambda_{\rm r}^{2} } \right)}\Big/{\left( {1-\lambda_{\rm r}^{2} } \right)}} \end{eqnarray}$
由式(1), 每个单链自由能可表示为

(6)$\begin{eqnarray} \label{eq6} W_{\rm chain} =nKT\left[ {\left( {\lambda_{\rm r} \beta +\ln \frac{\beta }{\sinh \beta }} \right)+Ug} \right]-c \end{eqnarray}$
式中, $c=KT\ln a_{0} $是常数, $U=\alpha \left( {{l/{d_{0} }}} \right)^{2}$称为有效圆管几何参数^[19].

聚合物网络发生溶胀变形时, 其体积会逐渐增大, 因此网络变形产生的自由能需要考虑其体积变化, 将式(2)中添加体积变化引起的自由能, 得到网络自由能函数^[18]

(7)$\begin{eqnarray} \label{eq7} W_{\rm s} =\sum\limits_{i=1}^N {W_{\rm chain}^{i} } -NKT\ln J \end{eqnarray}$
网络和溶剂分子混合过程产生的混合能通过自由能函数表示^[4]

(8)$\begin{eqnarray} \label{eq8} W_{\rm m} =KT\left( {m\ln c_{\rm l} +N\ln c_{\rm p} +\chi mc_{\rm p} } \right) \end{eqnarray}$
式中, $\chi $是凝胶网络和溶剂分子相互作用参数. 凝胶中溶剂分子化学势为

(9)$\begin{eqnarray} \label{eq9} \mu_{\rm l} =\frac{\partial W}{\partial m} =KT\left[ {\ln c_{\rm l} +\left( {1-\frac{1}{n}} \right)c_{\rm p} +\chi c_{\rm p}^{2} } \right]+\varPi v_{\rm c} \end{eqnarray}$
当$n\to \infty $时的结果与Hong等^[5]结果一致. 当凝胶达到溶胀平衡时, 凝胶内外溶剂分子的化学势相等, 此时凝胶处于动态平衡状态, 即溶剂分子进出凝胶时刻保持相等.

将外部溶剂的参考状态设置为液体, 此时液体在室温下与自身气体状态达到平衡. 如果将自身气体状态下的压力设置为$p_{0} $, 该压力可视为气液相转化的临界值. 若当前状态外部溶剂压力$p$小于$p_{0} $, 溶剂分子的化学势等于$\mu_{\rm l} =KT\ln ({p/{p_{0} }})$, 若当前状态外部溶剂压力$p$大于$p_{0} $, 溶剂分子化学势$\mu_{\rm l} =(p-p_{0} )v_{\rm c}$^[44]. 本研究考虑外部溶剂压力${p/{p_{0} }}\geqslant1$的情况.

2 宏观与微观变形关系

凝胶发生自由溶胀时, 宏观网络与微观单链变形相同. 由于初始状态下微观单链蜷缩在凝胶网络内部, 凝胶在外力或位移约束情况下发生溶胀变形时, 网络与单链变形将会不一致. 为了改善仿射变形假设的模型对超弹性材料变形的预测能力, 放松在仿射变形中认为单链伸长率$\lambda $与网络伸长率$\bar{{\lambda }}$相等的假设, 引入定义在单位球上波动场$f$, 将单链伸长率和网络伸长率间的关系表示为^[19]

(10)$\begin{eqnarray} \label{eq10} \lambda =f\bar{{\lambda }} \end{eqnarray}$
式中, $\bar{{\lambda }}=\sqrt {{r}\cdot F^{\rm T}{Fr}} $, ${r}$是单位球上点的拉格朗日方向向量, $f$是定义在单位球上的波动场. 当$f=$1时, 即为仿射变形的全网络模型. $f$可通过最小平均自由能原理确定, 需满足的约束条件是^[19]

(11)$\begin{eqnarray} \label{eq11} \left\langle \lambda \right\rangle_{h} =\left\langle {\bar{{\lambda }}} \right\rangle_{h} \end{eqnarray}$
式中, $\left\langle\ \right\rangle_{h} $是$h$次方根平均值算子, 有

(12)$\begin{eqnarray} \left\langle v \right\rangle_{h} =\sqrt[h]{\left\langle {v^{h}} \right\rangle }\left[ {\frac{1}{4\pi }\int {\left(v\right)^{h}{\rm d}A} } \right]^{{1/h}} \end{eqnarray}$
最终得到非仿射变形单链的伸长率与宏观网络之间的关系^[19]

(13)$\begin{eqnarray} \label{eq13} \lambda =\left\langle {\bar{{\lambda }}} \right\rangle_{h} =\left[ {\frac{1}{4\pi }\int {\left( {\bar{{\lambda }}} \right)^{h}{\rm d}A} } \right]^{{1/h}} \end{eqnarray}$
式中, $\left\langle {\bar{{\lambda }}} \right\rangle_{h}$表示$\bar{{\lambda }}$的$h$次方根平均值, 积分值采用数值微球方法^[19]计算. $h(h>0$)是表征非仿射变形特征的参数, 用于描述单链伸长率与网络伸长率间的关系, $h$是材料参数, 也即不同的凝胶材料对应不同的$h$值. $h=2$时, $\lambda =\left\langle {\bar{{\lambda }}} \right\rangle_{2} =\sqrt {{{I_{1} }/3}} $, 式中$I_{1} =\lambda_{1}^{2} +\lambda_{2}^{2} +\lambda_{3}^{2} $, $\lambda_{1}$, $\lambda_{2}$和$\lambda_{3}$是3个主方向的伸长率, 此时自由能函数表达式与八链模型表达式一致. 当聚合物网络发生体积膨胀时, 宏观网络横截面面积的变化率为$\bar{{g}}$, 其中$\bar{{g}}=\sqrt {{r}\cdot F^{-1} F^{-T}{r}} $, 同时单链的伸长使圆管约束的直径减小, 约束圆管的截面面积也减小, 圆管截面面积变化率用无量纲形式表示为$g=\left( {{{d_{0} }/d}} \right)^{2}$. 建立网络变形和圆管变形间的联系$g=\left( {\bar{{g}}} \right)^{q}$^[19], $q$可视作材料参数, 用来描述微观圆管收缩与宏观网络面积变化之间的关系.

用于计算式(13)的数值微球方法介绍如下.

认为空间中所有的单链具有随机取向的特性且均匀分布在微球内, 单链在球面上每个位置处的概率密度为$1/4\pi$, 将式(13)的积分计算转化为在球面上$m$个离散点处函数值的代数和. 即

(14)$\begin{eqnarray} \left\langle a \right\rangle =\frac{1}{4\pi }\int {a{\rm d}A} \approx \sum\limits_{s=1}^m {a^{\left( s \right)}w^{\left( s \right)}} \end{eqnarray}$
式中, $a$是微球内状态变量, $w^{\left( s \right)}$是离散点处的权重, 满足$\left\langle {{r}} \right\rangle ={ 0}$, $\left\langle {{r}\otimes {r}} \right\rangle ={I}/3$, $\sum\limits_{s=1}^m {w^{\left( s \right)}} =1$.

研究表明, 通常采用42个离散点以及相应权重进行计算可以得到足够精确的结果^[31].

根据自由能函数(3)确定聚合物网络的名义应力为

(15)$\begin{eqnarray} \label{eq14} && {s}=\frac{\partial W}{\partial F}=NKT\left[ {\left\langle {\left( {\frac{\lambda }{\bar{{\lambda }}}} \right)^{2-h}\frac{3n-\lambda^{2}}{n-\lambda^{2}}{r}^{2}} \right\rangle F- F^{-1}} \right. -\\&&\qquad \left. {nqU\left\langle {\bar{{g}}^{q-2}{r}^{2}} \right\rangle \left( { F^{-1}} \right)^{3}} \right]-\left( {\varPi +p} \right)J F^{-1}\; \end{eqnarray}$
如果式(15)中, $h=2$, 且在不考虑单链圆管约束的情况下, 即$q=0$或$U=0$,

则该应力表达式等价于八链模型的应力表达式^[15].

如果假设单链与网络变形为仿射关系(即$\lambda =\bar{{\lambda }})$,

应力表达式等价于Cohen等^[30]采用模型的应力表达式.

3 数值结果

考虑3种不同情况的凝胶溶胀时的宏观和微观变形: (1)凝胶发生自由溶胀, 此时产生均匀各向同性变形; (2)凝胶被放置在容器中, 只能沿某一个方向发生溶胀, 此时凝胶产生均匀但在各个方向上不同的变形; (3)内表面固定的球形凝胶浸没在溶剂中的溶胀行为, 此时凝胶产生非均匀的且在各个方向上不同的变形.

将聚合物放入水溶液中使其溶胀, 在下面的计算中, 材料及环境参数取为^[30]: $KT=4.1\times 10^{-21}$ J, 每个水分子的体积$v_{\rm l} =3.0\times 10^{-29}$ m$^{3}$. 室温下, 水的饱和蒸气压$p_{0} =3$ kPa, 相互作用参数$\chi =0.5$. 除非特殊说明, 计算时取聚合物网络中单链密度$N=2.5\times 10^{25}$ chains/m$^{3}$, 每条单链含有链段数$n=100$.

3.1 自由溶胀

选择尺寸为$L$ $\times$ $L$ $\times$ $L$立方体凝胶, 内部含有随机取向且均匀分布的单链, 将其浸没在溶剂外部压力为$p$的溶剂中发生自由溶胀. 此时, 凝胶在3个相互垂直方向上的伸长率相同$\lambda_{1} =\lambda_{2} =\lambda_{3} =\lambda_{\rm free}$. 达到平衡状态时, 凝胶内外化学势相等, 同时满足力学边界条件${\sigma }=-p{I}$. 当单链完全伸展开, 其伸长率$\lambda_{\max } =\sqrt n $, 此时凝胶达到最大可能体积变形$J_{\max } =\lambda_{\max }^{3} =n^{{3/2}}$, 因此可以控制单链的链段数调控凝胶最大体积变形.

不考虑单链约束时, 发生自由溶胀时凝胶各个方向伸长率相等, 由式(13)积分结果

$\begin{eqnarray*} \lambda =\left( {\frac{1}{4\pi }\int {\left( {\bar{{\lambda }}} \right)^{h}{\rm d}A} } \right)^{{1/h}}=\left[ {\left( {\bar{{\lambda }}} \right)^{h}} \right]^{{1/h}}=\bar{{\lambda }}, \end{eqnarray*}$

发现单链与网络变形关系无论是非仿射还是仿射, 采用八链模型和全网络模型(仿射或非仿射变形)得到的真实应力均为

(16)$\begin{eqnarray} \label{eq16} \sigma =\frac{NKT}{J}\left( {\frac{\lambda^{2}}{3}\frac{3n-\lambda ^{2}}{n-\lambda^{2}}-1} \right)-\varPi -p \end{eqnarray}$
Cohen等^[30]采用仿射变形假设得到的自由溶胀情形的真实应力表达式为

(17)$\begin{eqnarray} \sigma =\frac{NKT}{J}\left( {\frac{\lambda^{2}}{3}\frac{3n-\lambda ^{2}}{n-\lambda^{2}}-\frac{3n-1}{3n-3}} \right)-\varPi -p \end{eqnarray}$
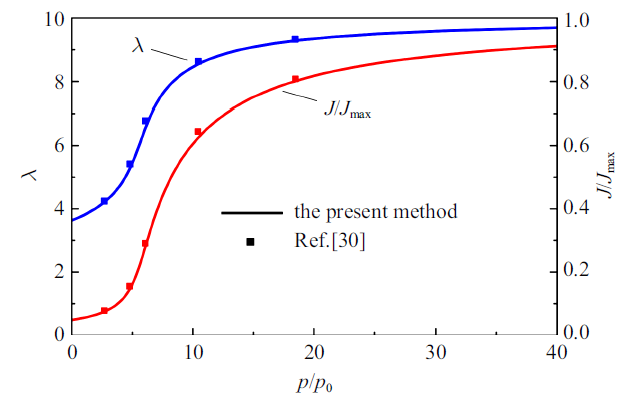
图2给出了凝胶在不同压力溶剂中达到平衡时的伸长率和体积变化的曲线, 本研究所采用的模型的结果与Cohen等^[30]采用仿射变形假设计算得到的结果相一致, 并且在自由溶胀情形可以覆盖采用仿射变形假设得到的结果. 从图2中可以发现, 随着外部溶剂压力增大, 进入网络中的溶剂分子越来越多, 导致凝胶体积逐渐增大并且呈非线性增大趋势. 当压力${p/{p_{0} }}\geqslant 40$时, 单链趋近于极限伸长即完全伸展状态, 此时凝胶网络容纳液体分子能力趋近于极限值, 即接近饱和状态.

图2

新窗口打开|下载原图ZIP|生成PPT
图2单链无约束凝胶自由溶胀伸长率和体积变化

Fig.2Stretch and the normalized volumetric ratio as a function of the normalized external solvent pressure in a freely swelling hydrogel with unconstrained polymer chain



在真实凝胶中, 单链会受到周围链的约束, 使其不能在凝胶内部任意移动. 考虑单链约束时, 有效圆管几何参数$U$会对自由溶胀产生影响. 采用圆管约束模型, 可得凝胶真实应力表达式

(18)$\begin{eqnarray} \label{eq17} \sigma =\frac{NKT}{J}\left( {\frac{\lambda^{2}}{3}\frac{3n-\lambda ^{2}}{n-\lambda^{2}}-\frac{nqU}{3}\lambda^{-q}-1} \right)-\varPi -p \end{eqnarray}$
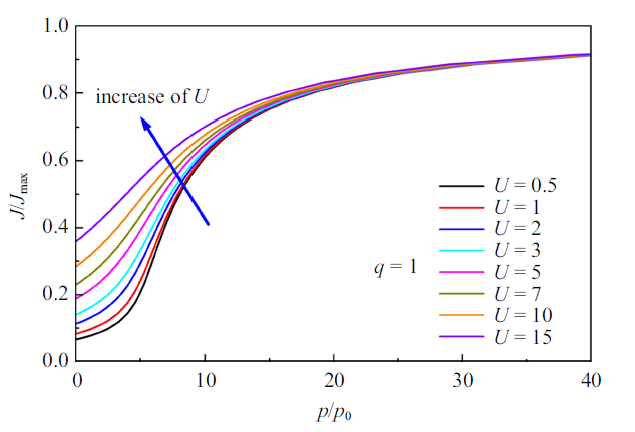
若凝胶具有不同有效圆管几何参数$U$, 发生自由溶胀时会产生不同的力学响应. 图3表示$q=1$条件下, 参数$U$对自由溶胀变形的影响, 参数$U$越大, 平衡时单链和网络的伸长率越大. 由式(18)发现表达式中不含有参数$h$, 因此参数$h$不会对自由溶胀产生影响. 在不考虑单链约束影响时, 浸没在溶剂中的所有材料达到平衡时具有相同溶胀率. 当溶剂压力${p/{p_{0} }}\geqslant 20$时, 参数$U$的影响基本消失, 主要原因是单链伸长已经接近完全伸展状态.

图3

新窗口打开|下载原图ZIP|生成PPT
图3具有不同有效圆管几何参数$U$的凝胶在溶胀至平衡状态时的体积随溶剂压力的演化规律

Fig.3Normalized volumetric ratio as a function of the normalized external solvent pressure for different values of the effective tube geometry parameter $U$



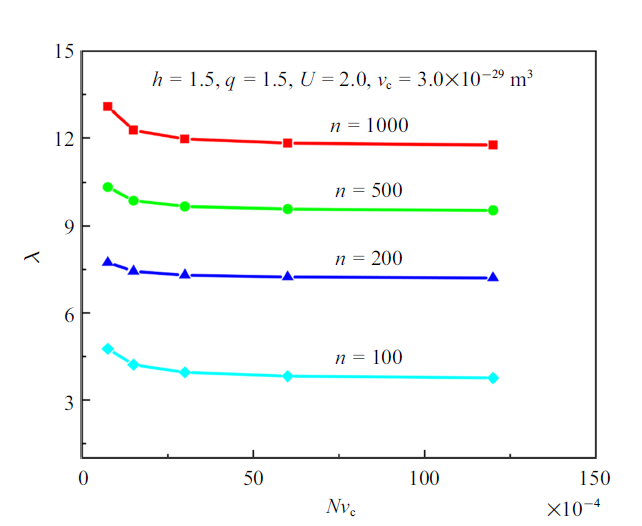
凝胶发生自由溶胀变形时, 单链的链段数和单链的密度对网络和单链的伸长率也有一定的影响. 从图4中可以看出, 当单链的密度$N$一定时, 随着单链的链段数$n$的增加, 凝胶网络和单链的伸长率也随之增大, 这是因为构成单链的链段数越多, 其长度越长, 导致单链的蜷缩程度越高. 单链的密度对凝胶溶胀影响也比较明显, 单链的链段数$n$一定时, 随单链密度的增大, 网络和单链的伸长率先快速下降, 然后趋于恒定值, 造成这一结果的原因是单链的密度越高(即凝胶网络交联点个数越多), 网络中可以容纳溶剂分子的空间越小使得能够进入网络的溶剂分子越少, 因此网络溶胀变形越小.

图4

新窗口打开|下载原图ZIP|生成PPT
图4溶胀至平衡状态时的伸长率随单链密度和单链链段数的变化

Fig.4Effects of chain density and the number of polymer segments on the swelling-induced stretch

3.2 单一方向溶胀

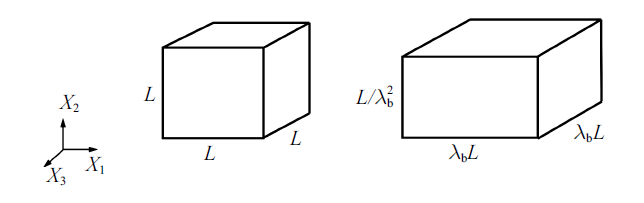
首先, 将尺寸为$L$ $\times$ $L$ $\times$ $L$的立方体聚合物先沿$X_{1} $和$X_{3} $方向等双轴拉伸至伸长率$\lambda_{\rm b} $, 使其具有新的尺寸$\lambda_{\rm b}L\times {L/{\lambda_{\rm b}^{2} }}\times \lambda_{\rm b} L$, 如图5所示. 然后, 将预拉伸后的聚合物放入尺寸为$\lambda_{\rm b} L\times H\times \lambda_{\rm b} L$容器中, 这里$H\gg {L/{\lambda_{\rm b}^{2} }}$. 最后, 将容器中放入压力为$p$的液体使聚合物发生溶胀变形, 不考虑容器内表面的摩擦, 凝胶只能沿$X_{2} $方向溶胀. 达到平衡时, 有$\lambda_{1} =\lambda_{3} =\lambda_{\rm b} $, $\sigma_{2} =-p$.

图5

新窗口打开|下载原图ZIP|生成PPT
图5凝胶预拉伸模型

Fig.5Hydrogel cube with biaxial pre-stretch



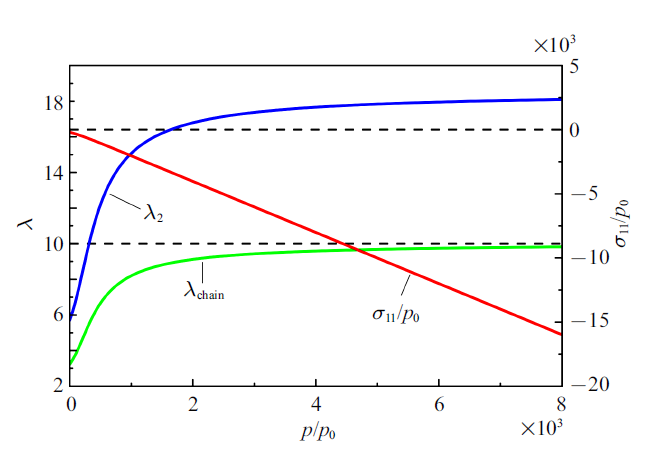
图6给出无预拉伸凝胶溶胀平衡时其网络和单链的伸长率和横向应力$\sigma_{11}$随标准化压力${p/{p_{0} }}$的变化. 这种情形可具体操作为, 例如将横截面尺寸为$L$ $\times$ $L$的凝胶置于内表面边长为$L$ $\times$ $L$的容器中进行溶胀. 当外部溶剂压力增加至${p/{p_{0} }}=4000$, 单链基本达到完全伸展状态. 注意到$X_{1} $和$X_{3} $方向应力一直都是压应力, 这是由于$X_{1} $和$X_{3} $方向的溶胀变形受到容器壁的限制而导致的.

图6

新窗口打开|下载原图ZIP|生成PPT
图6无预拉伸($\lambda _{\rm b}=1$)凝胶在受限溶胀至平衡时网络和单链的伸长率以及应力$\sigma_{11}$随压力的变化

Fig.6Stretches of network and chains and the normalized stress as a function of the normalized external solvent pressure in a constraint swelling hydrogel cube without pre-stretch ($\lambda_{\rm b}=1$)



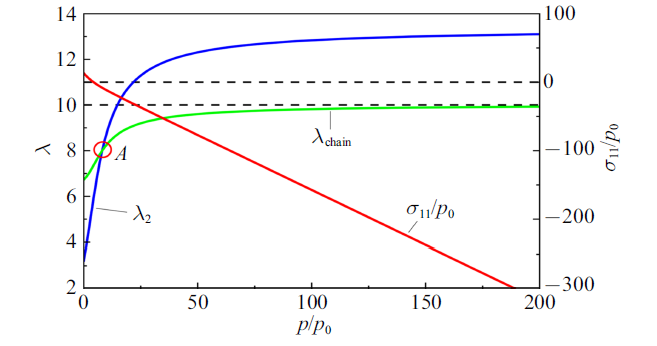
当对凝胶施加一定预拉伸时, 如图7所示, 凝胶出现单链变形和网络变形相等的溶胀平衡状态, 即$\lambda_{2} =\lambda _{\rm chain} =\lambda_{\rm b} $, 此时$X_{1} $方向的应力${{\left( {\sigma_{11} +p} \right)}/{p_{0} }}=0$. 这是因为对凝胶施加预拉伸时, 使网络中单链向三维空间伸展. 同时, 被拉伸的网络有收缩趋势, 对溶剂分子产生压力. 在外部溶剂压力较小时, 网络中预拉伸产生的应力大于吸收溶剂分子发生体积膨胀引起的应力, $X_{1} $方向为拉应力, 即${{\left( {\sigma_{11} +p} \right)}/{p_{0} }}>0$. 随着溶剂压力增大, 越来越多溶剂分子进入网络, 达到平衡时网络中预拉伸产生的应力小于体积膨胀产生的应力, $X_{1} $方向出现压应力, 即${{\left( {\sigma_{11} +p} \right)}/{p_{0} }}<0$. 因此, 在某一个溶剂压力作用下一定存在预拉伸产生的应力等于体积膨胀产生的应力, 即图7中$A$点, 对应的压力${p/{p_{0} }}\approx 7.9$, 伸长率为$\lambda_{2}=\lambda_{\rm b} =8$.

图7

新窗口打开|下载原图ZIP|生成PPT
图7预拉伸($\lambda _{\rm b}=8$)凝胶在溶胀至平衡时其伸长率和应力随压力的变化

Fig.7Stretch and the normalized stress as a function of the normalized external solvent pressure in a constraint swelling hydrogel cube with biaxial pre-stretch ($\lambda_{\rm b}=8$)



从图6和图7中可以看到, 单链极限伸长率不会超过10, 极限伸长率主要取决于构成单链的链段数. 根据图6单链变形曲线发现, 无预拉伸的凝胶中单链变形均小于网络变形, 其主要原因是模型中引入了圆管约束, 例如单链的相互缠结就是约束链运动的一种形式. 而从图7中看到, 具有预拉伸的凝胶在溶剂压力${p/{p_{0} }}\approx 7.9$时, 单链变形等于网络变形; 如果溶剂压力${p/{p_{0} }}\leqslant7.9$, 单链变形大于网络变形, 主要原因是预拉伸使得网络中绻缩的单链具有初始伸长率, 将凝胶放入溶剂中发生溶胀, 单链的伸长率继续增加.

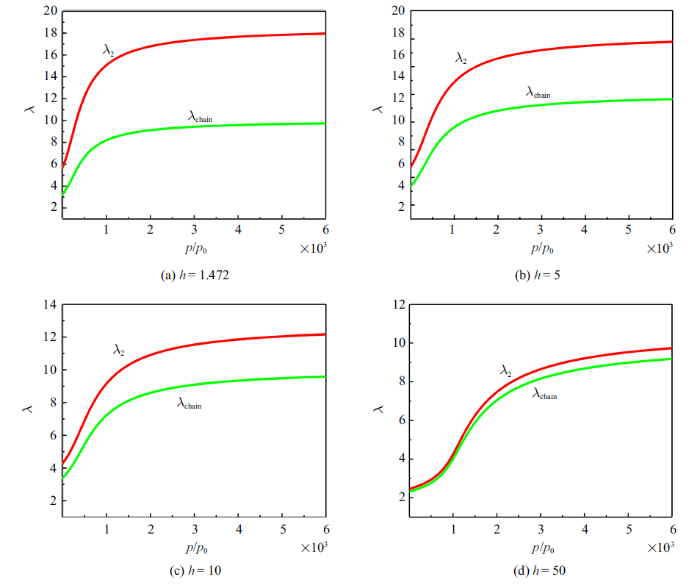
图8给出了参数$h$对无预拉伸凝胶平衡状态下伸长率与溶剂压力关系曲线的影响. 从图8中可以发现, 随着$h$的增大, 单链伸长率与网络伸长率$\lambda_{2} $间的差异逐渐减少. 当$h=50$时, 若溶剂压力${p/{p_{0} }}\leqslant 1500$, 溶胀平衡状态下单链伸长率接近于网络伸长率. 这也表明了材料参数$h$越大的凝胶发生溶胀变形时, 单链伸长率和网络伸长率差异越小. 表明$h$是调控单链伸长率和网络伸长率间关系的重要参数.

图8

新窗口打开|下载原图ZIP|生成PPT
图8参数$h$对无预拉伸凝胶平衡状态下伸长率与溶剂压力关系曲线的影响

Fig.8Effect of material parameter $h$ on the swelling-induced stretch in a constraint swelling hydrogel cube

3.3 球形凝胶溶胀

考虑含有刚性核的球形凝胶的溶胀, 这是非均匀溶胀情形. 在参考状态下, 球形凝胶的外半径和内半径之比${B/A}=2$, 其中$A$和$B$分别是球形凝胶的内半径和外半径. 在凝胶内部有一个半径为$\lambda_{0} A$的刚性核, 刚性核和凝胶在界面处完美结合, 即位移和应力均连续, 然后让其溶胀至平衡状态.

球形凝胶发生球对称受限溶胀时, 网络变形是非均匀的且径向和环向变形是不一致的, 各物理场均是位置坐标的函数. 当凝胶达到平衡时, 凝胶内外溶剂化学势相等$\mu_{\rm l} =\left( {p-p_{0} } \right)v_{\rm c} $, 平衡方程简化为

(19)$\begin{eqnarray} \label{eq19} \frac{{\rm d}s_{rr} }{{\rm d}R}+2\frac{s_{rr} -s_{\theta \theta } }{R}=0 \end{eqnarray}$
名义应力的表达式为

(20)$\begin{array}{l}\frac{s_{r r}}{N K T}=\lambda_{\mathrm{r}} \frac{3 n-\lambda^{2}}{n-\lambda^{2}} \lambda^{2-h}\left\langle\frac{r_{1}^{2}}{\bar{\lambda}^{2-h}}\right\rangle- \\\frac{n q U}{\lambda_{\mathrm{r}}^{3}}\left\langle\bar{g}^{q-2} r_{1}^{2}\right\rangle-\frac{1}{\lambda_{\mathrm{r}}}+\frac{\lambda_{\theta}^{2}}{N v_{\mathrm{c}}}\left[\ln \left(1-\frac{1}{J}\right)+\right. \\\left.\left(1-\frac{1}{n}\right) \frac{1}{J}+\frac{\chi}{J^{2}}-\frac{\left(2 p-p_{0}\right) v_{\mathrm{c}}}{K T}\right]\end{array}$
(21)$\begin{array}{c}\frac{s_{\theta \theta}}{N K T}=\lambda_{\theta} \frac{3 n-\lambda^{2}}{n-\lambda^{2}} \lambda^{2-h}\left\langle\frac{r_{2}^{2}}{\bar{\lambda}^{2-h}}\right\rangle- \\\frac{n q U}{\lambda_{\theta}^{3}}\left\langle\bar{g}^{q-2} r_{2}^{2}\right\rangle-\frac{1}{\lambda_{\theta}}+\frac{\lambda_{\mathrm{r}} \lambda_{\theta}}{N v_{\mathrm{c}}}\left[\ln \left(1-\frac{1}{J}\right)+\right. \\\left.\left(1-\frac{1}{n}\right) \frac{1}{J}+\frac{\chi}{J^{2}}-\frac{\left(2 p-p_{0}\right) v_{\mathrm{c}}}{K T}\right]\end{array}$
式中$\lambda_{\rm r} ={{{\rm d}r}/{{\rm d}R}}$和$\lambda_{\theta }={r/R}$分别为径向伸长率和环向伸长率. 溶剂分子体积分数为$c_{\rm l} =1-{1/{\left({\lambda_{\rm r} \lambda_{\theta }^{2} } \right)}}$. 边界条件为

(22)$\begin{eqnarray} \label{eq22} r\left( A \right)=\lambda_{0} A,\ \ \sigma_{rr} \left( B \right)=-p \end{eqnarray}$
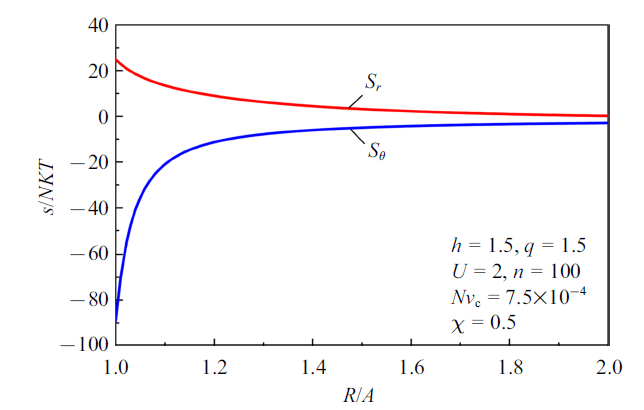
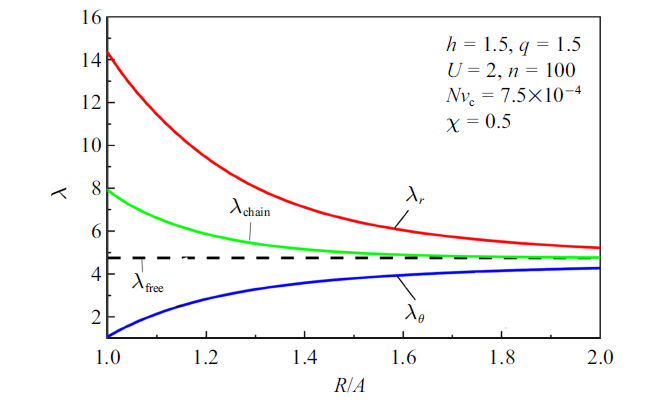
下文计算中设定${p/{p_{0} }}=1.5$, $n=100$, $h=1.5$, $q=1.5$, $U=2$, $Nv_{\rm c} =7.5\times 10^{-4}$, $\chi =0.5$. 图9给出了凝胶溶胀至平衡状态下网络的径向和环向名义应力沿径向的分布. 图中表明, 径向名义应力均为拉应力, 环向名义应力均为压应力. 由内向外, 网络的径向和环向名义应力的幅值逐渐减小. 图10给出了平衡时凝胶网络和单链伸长率的沿径向的分布. 从图10可以看出, 网络的径向和环向伸长率均大于1, 表明网络在径向和环向均是受到拉伸. 凝胶沿径向各点处的网络径向伸长率大于环向伸长率. 不同位置单链伸长率均有$\lambda_{\rm chain} <\sqrt n =10$, 即各单链均没有达到完全伸展. 在内表面附近, 单链伸长率高于自由溶胀时的伸长率, 但小于网络的径向伸长率, 这是由于内表面刚性核的固定约束使得出现径向拉应力的缘故. 随着坐标位置远离内表面, 内表面的位移约束影响逐渐减小, 单链伸长率接近网络伸长率, 且接近于自由溶胀时的网络伸长率.

图9

新窗口打开|下载原图ZIP|生成PPT
图9凝胶溶胀至平衡状态时的径向和环向应力沿径向分布

Fig.9Distributions of the stresses in a swollen spherical hydrogel with a rigid core

图10

新窗口打开|下载原图ZIP|生成PPT
图10凝胶溶胀平衡状态时的宏观和微观伸长率沿径向分布

Fig.10Distributions of the stretches of micro-chain and macro-network in a swollen spherical hydrogel with a rigid core



图11和图12分别给出了$U=2$, 6和12时凝胶中溶剂分子的体积分数和网络中的渗透压沿径向的分布. 由图11可以发现靠近刚性核位置, 溶剂分子体积分数减小, 这是因为内表面固定使得靠近内表面网络渗透压增大(如图12所示), 溶剂分子不易进入网络. 从图12中可以看出, 网络中的渗透压随参数$U$的增大而降低. 当${R/A}>1.2$时, 刚性核的影响逐渐消失, 溶剂分子体积分数的分布趋于均匀, 且趋于自由溶胀状态的数值. 溶剂分子的体积分数随参数$U$的增大而增大, 即单链的链段长度与圆管约束半径比值越大, 网络中的溶剂分子体积分数越大, 最终网络和单链的伸长率越大. 网络的渗透压会影响网络中溶剂分子的体积分数, 从图11和图12可以看出, 二者是一种负相关关系.

图11

新窗口打开|下载原图ZIP|生成PPT
图11凝胶溶胀平衡状态溶剂分子体积分数沿径向的分布

Fig.11Effect of parameter $U$ on the distributions of the volume fraction of solvent molecules in a swollen spherical hydrogel with a rigid core

图12

新窗口打开|下载原图ZIP|生成PPT
图12凝胶溶胀平衡状态渗透压沿径向的分布

Fig.12Effect of parameter $U$ on the distributions of the osmotic pressure in a swollen spherical hydrogel with a rigid core



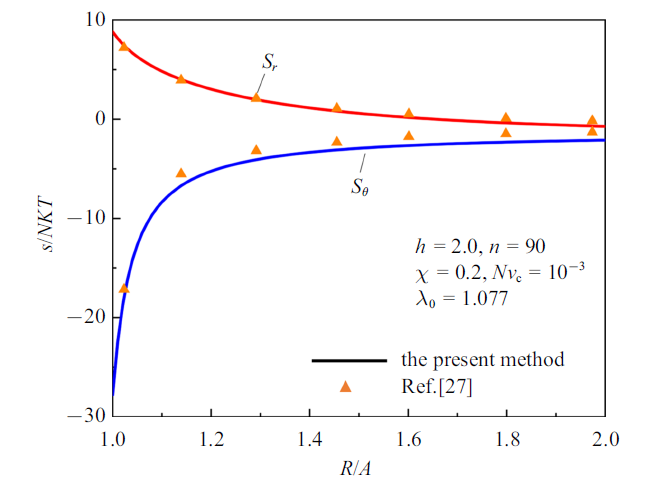
另取计算参数$n=90$, $h=2.0$, $q=0$, $U=0$,采用非仿射全网络模型计算得到的内含刚性核球壳凝胶溶胀至平衡状态时的径向和环向应力沿径向分布曲线如图13的实线所示. 图13中的离散点是Zhao等^[27]采用neo-Hookean模型的计算结果, 结果表明, 选取合适的参数时, 本研究的模型可以取得与采用neo-Hookean模型基本一致的结果.

图13

新窗口打开|下载原图ZIP|生成PPT
图13全网络模型与neo-Hookean模型计算结果的对比

Fig.13Comparison between the presented model and the neo-Hookean model

4 结论

基于全网络模型, 假设凝胶网络和单链变形为非仿射关系, 利用聚合物网络的单链受到由于周围链的作用而产生类似圆管状的约束的模型, 建立了可以预测溶胀引发的凝胶网络和单链变形的力学分析模型. 开展了三种不同情形的凝胶溶胀性能分析, 即立方体凝胶的自由溶胀和两个方向受限的单一方向溶胀以及具有刚性核的球形凝胶的非均匀溶胀.

自由溶胀时, 凝胶网络伸长率和单链伸长率一致. 伸长率随着参数$U$的增大而增大. 随着溶剂压力的增大, 网络伸长率和单链伸长率均趋近于渐近值$\sqrt n $. 两个方向受限的单一方向均匀溶胀情形, 此时凝胶网络伸长率和单链伸长率表现出不一致. 网络伸长率和单链伸长率可通过预拉伸进行调整. 特别是, 预拉伸增大到一定值时, 可出现单链变形和网络变形相等的溶胀平衡状态. 具有刚性核的球形凝胶发生溶胀时, 凝胶和单链均为非均匀变形, 在靠近刚性核的区域, 出现较大的径向拉应力和环向压应力, 这个区域对应的单链伸长率也较大. 靠近外表面区域的网络和单链伸长率接近自由溶胀伸长率. 网络的渗透压随参数$U$的增大而降低, 溶剂分子体积分数随参数$U$的增大而增大.

所提出的模型可用于分析和预测凝胶溶胀时微观单链的变形情况, 进而可通过调整单链微观结构来控制凝胶网络的溶胀变形, 为凝胶器件的设计和性能优化提供理论基础.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Bruggeman KF, Williams RJ, Nisbet DR. Dynamic and responsive growth factor delivery from electrospun and hydrogel tissue engineering materials
Advanced Healthcare Materials, 2018,7(1):1700836
[本文引用: 1]

[2] Rizwan M, Yahya R, Hassan A. et al. pH sensitive hydrogels in drug delivery: Brief history, properties, swelling, and release mechanism, material selection and applications
Polymers, 2017,9(4):137
[本文引用: 1]

[3] Wirthl D, Pichler R, Drack M. et al. Instant tough bonding of hydrogels for soft machines and electronics
Science Advances, 2017,3(6):e1700053
DOIURLPMID [本文引用: 1]
Introducing methods for instant tough bonding between hydrogels and antagonistic materials-from soft to hard-allows us to demonstrate elastic yet tough biomimetic devices and machines with a high level of complexity. Tough hydrogels strongly attach, within seconds, to plastics, elastomers, leather, bone, and metals, reaching unprecedented interfacial toughness exceeding 2000 J/m(2). Healing of severed ionic hydrogel conductors becomes feasible and restores function instantly. Soft, transparent multilayered hybrids of elastomers and ionic hydrogels endure biaxial strain with more than 2000% increase in area, facilitating soft transducers, generators, and adaptive lenses. We demonstrate soft electronic devices, from stretchable batteries, self-powered compliant circuits, and autonomous electronic skin for triggered drug delivery. Our approach is applicable in rapid prototyping and in delicate environments inaccessible for extended curing and cross-linking.

[4] Flory PJ. Statistical mechanics of swelling of network structures
The Journal of Chemical Physics, 1950,18(1):108-111
[本文引用: 2]

[5] Hong W, Zhao X, Zhou J. et al. A theory of coupled diffusion and large deformation in polymeric gels
Journal of the Mechanics and Physics of Solids, 2008,56(5):1779-1793
[本文引用: 2]

[6] 杨健鹏, 王惠明. 功能梯度球形水凝胶的化学力学耦合分析
力学学报, 2019,51(4):1054-1063
[本文引用: 1]

( Yang Jianpeng, Wang Huiming. Chemical-mechanical coupling analysis of functionally graded spherical hydrogels
Chinese Journal of Theoretical and Applied Mechanics. 2019,51(4):1779-1793 (in Chinese))
[本文引用: 1]

[7] 白渝平, 杨荣杰, 李建民 等. PVA-PAA IPN水凝胶的制备及其溶胀性质研究
高分子材料科学与工程, 2002,18(1):98-101
[本文引用: 1]

( Bai Yuping, Yang Rongjie, Li Jianmin et al. Preparation and swelling properties study of PVA-PAA IPN hydrogel
Chinese Polymer Materials Science and Engineering. 2002,18(1):98-101 (in Chinese))
[本文引用: 1]

[8] Treloar LRG. The elasticity of a network of long-chain molecules. I
Transactions of the Faraday Society, 1943,39:36-41
[本文引用: 1]

[9] Rivlin RS. Large elastic deformations of isotropic materials IV. Further developments of the general theory
Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1948,241(835):379-397
[本文引用: 1]

[10] Gent AN. A new constitutive relation for rubber
Rubber Chemistry and Technology, 1996,69(1):59-61
[本文引用: 1]

[11] Ogden RW. Non-linear Elastic Deformations
New York: Dover Publications, Inc., 1997
[本文引用: 1]

[12] Wang MC, Guth E. Statistical theory of networks of non-Gaussian flexible chains
The Journal of Chemical Physics, 1952,20(7):1144-1157
[本文引用: 1]

[13] Treloar LRG. The swelling of cross-linked amorphous polymers under strain
Transactions of the Faraday Society, 1950,46:783-789
[本文引用: 1]

[14] Flory PJ, Rehner Jr J. Statistical mechanics of cross-linked polymer networks I. Rubberlike elasticity
The Journal of Chemical Physics, 1943,11(11):512-520
[本文引用: 1]

[15] Arruda EM, Boyce MC. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials
Journal of the Mechanics and Physics of Solids, 1993,41:389-412
[本文引用: 2]

[16] Beatty MF. An average-stretch full-network model for rubber elasticity
Journal of Elasticity, 2003,70(1-3):65-86
[本文引用: 1]

[17] Marckmann G, Verron E. Comparison of hyperelastic models for rubber-like materials
Rubber Chemistry and Technology, 2006,79(5):835-858
[本文引用: 1]

[18] Boyce MC, Arruda EM. Constitutive models of rubber elasticity: A review
Rubber Chemistry and Technology, 2000,73(3):504-523
[本文引用: 2]

[19] Miehe C, G?ktepe S, Lulei F. A micro-macro approach to rubber-like materials——part I: The non-affine micro-sphere model of rubber elasticity
Journal of the Mechanics and Physics of Solids, 2004,52(11):2617-2660
[本文引用: 10]

[20] Huang R, Zheng S, Liu Z. et al. Recent advances of the constitutive models of smart materials-hydrogels and shape memory polymers
International Journal of Applied Mechanics, 2020,12(2):2050014
[本文引用: 1]

[21] Li Z, Liu Z. The elongation-criterion for fracture toughness of hydrogels based on percolation model
Journal of Applied Physics, 2020,127(21):215101
[本文引用: 1]

[22] Lei J, Xu S, Li Z. et al. Study on large deformation behavior of polyacrylamide hydrogel using dissipative particle dynamics
Frontiers in Chemistry, 2020,8:115
URLPMID [本文引用: 1]

[23] 彭向峰, 李录贤. 超弹性材料本构关系的最新研究进展
力学学报, 2020,52(5):1221-1234
[本文引用: 1]

( Peng Xiangfeng, Li Luxian. State of the art of constitutive relations of hyperelastic materials
Chinese Journal of Theoretical and Applied Mechanics. 2020,52(5):1221-1232 (in Chinese))
[本文引用: 1]

[24] 张希润, 蔡力勋, 陈辉. 基于能量密度等效的超弹性压入模型与双压试验方法
力学学报, 2020,52(3):787-796
[本文引用: 1]

( Zhang Xirun, Cai Lixun, Chen Hui. Hyperelastic indentation models and the dual-indentation method based on energy density equivalence
Chinese Journal of Theoretical and Applied Mechanics. 2020,52(3):787-796 (in Chinese))
[本文引用: 1]

[25] 史惠琦, 王惠明. 一种新型介电弹性体仿生可调焦透镜的变焦分析
力学学报, 2020,52(6):1719-1729
[本文引用: 1]

( Shi Huiqi, Wang Huiming. Theoretical nonlinear analysis of a biomimetic tunable lens driven by dielectric elastomer
Chinese Journal of Theoretical and Applied Mechanics. 2020,52(6):1719-1729 (in Chinese))
[本文引用: 1]

[26] Flory PJ. Thermodynamics of high polymer solutions
The Journal of Chemical Physics, 1942,10(1):51-61
[本文引用: 1]

[27] Zhao X, Hong W, Suo Z. Inhomogeneous and anisotropic equilibrium state of a swollen hydrogel containing a hard core
Applied Physics Letters, 2008,92(5):051904
[本文引用: 2]

[28] Hong W, Liu Z, Suo Z. Inhomogeneous swelling of a gel in equilibrium with a solvent and mechanical load
International Journal of Solids and Structures, 2009,46(17):3282-3289


[29] 苏恒迪, 颜慧贤, 金波. 基于Slip-Link 模型的凝胶大变形与扩散耦合瞬态问题分析
力学季刊, 2017,38(4):681-692
[本文引用: 1]

( Su Hengdi, Yan Huixian, Jin Bo. Analysis of coupled transient problem of gel large deformation and diffusion based on slip-link model
Chinese Quarterly of Mechanics. 2017,38(4):681-692 (in Chinese))
[本文引用: 1]

[30] Cohen N, McMeeking RM. On the swelling induced microstructural evolution of polymer networks in gels
Journal of the Mechanics and Physics of Solids, 2019,125:666-680
[本文引用: 6]

[31] Ba?ant P, Oh BH. Efficient numerical integration on the surface of a sphere
ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 1986,66(1):37-49
[本文引用: 2]

[32] Cohen N. A generalized electro-elastic theory of polymer networks
Journal of the Mechanics and Physics of Solids, 2018,110:173-191
[本文引用: 1]

[33] Cohen N, Dayal K, deBotton G. Electroelasticity of polymer networks
Journal of the Mechanics and Physics of Solids, 2016,92:105-126


[34] Cohen N, Menzel A, DeBotton G. Towards a physics-based multiscale modelling of the electro-mechanical coupling in electro-active polymers
Proceedings of the Royal Society A: Mathematical,Physical and Engineering Sciences, 2016,472(2186):20150462


[35] Cohen N, Saleh OA, McMeeking RM. Engineering the mechanical behavior of polymer networks with flexible self-assembled v-shaped monomers
Macromolecules, 2018,51(8):3149-3155


[36] Bleistein T, Jung A, Diebels S. A microsphere-based material model for open cell metal foams
Continuum Mechanics and Thermodynamics, 2020,32(1):255-267


[37] Cohen N. Programming the equilibrium swelling response of heterogeneous polymeric gels
International Journal of Solids and Structures, 2019,178:81-90
[本文引用: 1]

[38] Treloar LRG. The Physics of Rubber Elasticity
Oxford University Press, 1975: 101-124
[本文引用: 1]

[39] Heinrich G, Straube E. On the strength and deformation dependence of the tube-like topological constraints of polymer networks, melts and concentrated solutions. I. The polymer network case
Acta Polymerica, 1983,34(9):589-594
[本文引用: 1]

[40] Heinrich G, Kaliske M. Theoretical and numerical formulation of a molecular based constitutive tube-model of rubber elasticity
Computational and Theoretical Polymer Science, 1997,7(3-4):227-241
[本文引用: 1]

[41] Chester SA, Anand L. A thermo-mechanically coupled theory for fluid permeation in elastomeric materials: Application to thermally responsive gels
Journal of the Mechanics and Physics of Solids, 2011,59(10):1978-2006
[本文引用: 1]

[42] Doi M, Edwards SF. The Theory of Polymer Dynamics. New York: Oxford University Press, 1986: 205
[本文引用: 1]

[43] Cohen A. A Padéapproximant to the inverse Langevin function
Rheologica Acta, 1991,30(3):270-273
[本文引用: 1]

[44] Kang MK, Huang R. A variational approach and finite element implementation for swelling of polymeric hydrogels under geometric constraints
Journal of Applied Mechanics, 2010,77(6):061004
[本文引用: 1]