谢晨月, 袁泽龙, 王建春^,2), 万敏平, 陈十一南方科技大学 力学与航空航天工程系, 深圳 518055

ARTIFICIAL NEURAL NETWORK-BASED SUBGRID-SCALE MODELS FOR LARGE-EDDY SIMULATION OF TURBULENCE ¹⁾

Xie Chenyu, Yuan Zelong, Wang Jianchun^,2), Wan Minping, Chen ShiyiDepartment of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, China

通讯作者: 2)王建春, 副教授, 主要研究方向: 湍流和计算流体力学. E-mail:wangjc@sustech.edu.cn

收稿日期:2020-12-9接受日期:2020-12-24网络出版日期:2021-12-31

基金资助:

1)国家自然科学基金.91952104 国家自然科学基金.11702127 国家自然科学基金.91752201 国家数值风洞工程资助项目.NNW2019ZT1-A01 国家数值风洞工程资助项目.NNW2019ZT1-A04

Received:2020-12-9Accepted:2020-12-24Online:2021-12-31
作者简介 About authors


摘要
大涡模拟方法(LES)是研究复杂湍流问题的重要工具,在航空航天、湍流燃烧、气动声学、大气边界层等众多工程领域中具有广泛的应用前景.大涡模拟方法采用粗网格计算大尺度上的湍流结构,并用亚格子(SGS)模型近似表达滤波尺度以下的流动结构对大尺度流场的作用.传统的亚格子模型由于只利用了单点流场信息和简单的函数关系,在先验验证中相对误差较大, 在后验验证中耗散过强. 近几年来,机器学习方法在湍流建模问题中得到了越来越多的应用.本文介绍了基于人工神经网络(ANN)的湍流亚格子模型的最新进展.详细地讨论了人工神经网络混合模型、空间人工神经网络模型和反卷积人工神经网络模型的构造方法.借助于人工神经网络强大的数据插值能力,新的亚格子模型的先验精度和后验精度均有显著提升. 在先验验证中,新模型所预测的亚格子应力的相关系数超过了0.99,在预测精度上远高于传统的大涡模拟模型. 在后验验证中,新模型对各类湍流统计量和瞬态流动结构的预测都优于隐式大涡模拟方法、动态Smagorinsky模型、动态混合模型等传统模型.因此, 人工神经网络方法在发展复杂湍流的先进大涡模拟模型中具有很大的潜力.
关键词： 湍流;大涡模拟;亚格子模型;人工神经网络;机器学习

Abstract
Large eddy simulation (LES) is an important method to investigate different types of complex turbulent flows, which has been widely applied to the turbulent flows in aerospace, combustion, acoustics, atmospheric boundary layer, etc. Large eddy simulation effectively solves the large-scale motions of turbulence and models the effects of small-scale dynamics on the large-scale structures by using subgrid-scale (SGS) models. Traditional SGS models only use the single-point information based on some simple forms of analytical functions to approximate the SGS terms. Thus, traditional models exhibit quite large relative errors in the a priori study, and have excessive dissipations in the a posteriori study. Recently, machine learning approaches have been widely used to develop turbulence models, including the Reynolds-averaged Navier-Stokes (RANS) models and LES models. In this paper, we review the recent developments of artificial neural network (ANN) methods for SGS models in LES of turbulence. We discuss three different ANN-based SGS models, including artificial neural network mixed model (ANNMM), spatial artificial neural network (SANN) model and deconvolutional artificial neural network (DANN) model. Due to the strong data interpolation capability of artificial neural networks, the new SGS models exhibit improved accuracy in both a priori study and a posteriori study. In the a priori study, the new SGS models can predict the SGS stress much more accurately than the traditional SGS models: the correlation coefficients predicted by new SGS models can be made larger than 99%. In the a posteriori study, the new SGS models can give better predictions on turbulence statistics and instantaneous flow structures, as compared to a variety of traditional SGS models including the implicit LES (ILES), dynamic Smagorinsky model (DSM), and dynamic mixed model (DMM). It is shown that artificial neural network-based methods have strong potentials for the developments of advanced SGS models in the LES of complex turbulence.
Keywords：turbulence;large-eddy simulation;subgrid-scale model;artificial neural network;machine learning


PDF (15651KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
谢晨月, 袁泽龙, 王建春, 万敏平, 陈十一. 基于人工神经网络的湍流大涡模拟方法 ¹⁾. 力学学报[J], 2021, 53(1): 1-16 DOI:10.6052/0459-1879-20-420
Xie Chenyu, Yuan Zelong, Wang Jianchun, Wan Minping, Chen Shiyi. ARTIFICIAL NEURAL NETWORK-BASED SUBGRID-SCALE MODELS FOR LARGE-EDDY SIMULATION OF TURBULENCE ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(1): 1-16 DOI:10.6052/0459-1879-20-420


引言

湍流现象广泛存在于航空航天、天体物理、大气边界层等各类工程问题和自然现象中^[1]. 受限于巨大的计算量, 直接数值模拟(direct numerical simulation, DNS)方法无法求解高雷诺数湍流问题. 雷诺平均(Reynolds-averaged Navier-Stokes, RANS)方法基于雷诺平均方程, 主要求解湍流的平均场, 因此无法精确地模拟湍流在不同尺度上的流动结构. 大涡模拟(large eddy simulation, LES)方法采用粗网格计算大尺度上的湍流结构, 并用亚格子模型近似表达滤波尺度以下的流动结构对大尺度流场的作用, 从而能够有效地预测湍流在大尺度上的动量、能量和热量的传输^[1-9].

在大涡模拟方法中, 亚格子不封闭项表征亚网格尺度对大尺度运动的影响^[10-17]. 大涡模拟方法的一个核心问题是: 如何通过大尺度的流场信息构造亚格子模型? 传统亚格子模型包括Smagorinsky模型^[6,10,18-19]、相似模型^[20-21]、梯度模型^[21-23]、优化模型^[24-26]、一方程模型^[11,27-28]和二阶矩模型^[27,29-31]等.

最近几年来, 机器学习方法发展迅速, 并且在湍流建模问题中得到了越来越多的应用^[32-59], 包括: 用机器学习方法重构雷诺平均应力^[32-34]、基于全连接人工神经网络的亚格子模型^[35-36]、基于机器学习的反

卷积亚格子模型^[39-41]、基于循环神经网络和Mori-Zwanzig公式的时空亚格子模型^[48]等.

作者的研究团队从2019年开始, 发展了一系列基于人工神经网络的大涡模拟模型, 主要有以下3种情况. (1)人工神经网络显式代数模型,包括人工神经网络混合模型(artificial neural network mixed model, ANNMM)和非线性代数模型^[49-50]. 这类模型类似于传统代数模型, 具有显式表达式, 并通过人工神经网络方法对模型中的无量纲系数做优化. (2)人工神经网络隐式结构模型, 包括七点模型(ANN-7)和空间人工神经网络(spatial artificial neural network, SANN)模型^[51-55]. 这类模型的输入和输出的映射关系封装在人工神经网络中, 没有具体的显式表达式. 这类模型是亚格子模型的一种, 和传统的隐式大涡模拟方法有所区别: 隐式大涡模拟方法主要采用耗散型的数值格式去直接求解粗网格上的流体力学方程, 不加亚格子模型这一项, 而是用数值黏性去代替亚格子能流的耗散作用. (3)反卷积人工神经网络(deconvolutional artificial neural network, DANN)模型^[56].

本文详细地介绍了利用人工神经网络方法重构亚格子不封闭项的最新进展. 具体内容安排如下: 在第1节中, 讨论了可压缩湍流的人工神经网络模型, 包括人工神经网络混合模型和空间人工神经网络模型; 在第2节中, 介绍了不可压缩湍流的反卷积人工神经网络模型. 在第3节中, 对本文的内容进行了总结和展望.

1 可压缩湍流大涡模拟

可压缩湍流的速度场和热力学场存在强耦合, 同时涡量场、声波、激波和膨胀波之间存在非线性的耦合作用^[60-67]. 可压缩湍流的大涡模拟需要同时封闭动量方程和能量方程. 理想气体的可压缩湍流的无量纲化纳维-斯托克斯方程如下^[3,60-62]

(1)$\begin{eqnarray} &&\dfrac{\partial \rho }{\partial t}+\dfrac{\partial \left( {\rho u_{j} } \right)}{\partial x_{j} }=0 \end{eqnarray}$
(2)$\begin{eqnarray} \dfrac{\partial \left( {\rho u_{i} } \right)}{\partial t}+\dfrac{\partial \left( {\rho u_{i} u_{j} +p\delta_{ij} } \right)}{\partial x_{j} }=\dfrac{1}{Re}\dfrac{\partial \sigma_{ij} }{\partial x_{j} }+F_{i} \end{eqnarray}$
(3)$\begin{eqnarray} \dfrac{\partial E}{\partial t}+\dfrac{\partial \left[ {\left( {E+p} \right)u_{j} } \right]}{\partial x_{j} }=\dfrac{1}{\alpha }\dfrac{\partial }{\partial x_{j} }\left( {\kappa \dfrac{\partial T}{\partial x_{j} }} \right)+\dfrac{1}{Re}\dfrac{\partial \left( {\sigma_{ij} u_{i} } \right)}{\partial x_{j} }-\varLambda +F_{j} u_{j} \end{eqnarray}$
其中, $\sigma_{ij} =2\mu S_{ij} -2\mu S_{kk} \delta_{ij}/3$是黏性应力张量;

$\begin{eqnarray*} &&S_{ij} =\dfrac{1}{2}\left( {\dfrac{\partial u_{i} }{\partial x_{j} }+\dfrac{\partial u_{j} }{\partial x_{i} }} \right)\ \mbox{是应变率张量;} \\&&E=\dfrac{p}{\gamma -1}+\dfrac{1}{2}\rho \left( {u_{j} u_{j} } \right)\ \mbox{是单位体积的总能量;} \end{eqnarray*}$

$F_{i} $是单位体积的大尺度外力; $\varLambda$是单位体积的大尺度冷却函数^[61-62].

上述方程通过以下的特征物理量进行归一化: 特征长度$L_{r}$, 密度$\rho_{r} $, 速度$U_{r} $, 温度$T_{r} $, 单位体积的两倍动能$\rho_{r} U_{r}^{2} $, 动力学黏性系数$\mu_{r} $, 热扩散系数$\kappa_{r} $和压力$p_{r} =\rho_{r}U_{r}^{2} $. 雷诺数$Re=\rho_{r} U_{r} L_{r} /\mu_{r} $, 马赫数$M=U_{r}/c_{r} $, 普朗特数$Pr =\mu_{r} C_{p} /\kappa_{r} =0.7$是流场的三个无量纲控制参数, 其中声速$c_{r} =\sqrt {\gamma RT_{r} } $, 比热比$\gamma =C_{p} /C_{v} =1.4$, $R=C_{p} -C_{v} $是气体常数, 无量纲参数$\alpha =Pr Re\left( {\gamma -1} \right)M^{2}$.

可压缩湍流的泰勒雷诺数$Re_{\lambda } $和湍流马赫数$M_{t} $分别定义为^[61-62]

(4)$\begin{eqnarray} Re_{\lambda } =Re\dfrac{\left\langle \rho \right\rangle u^{rms}\lambda }{\sqrt 3 \left\langle \mu \right\rangle },\\ M_{t} =M\dfrac{u^{rms}}{\left\langle {\sqrt T } \right\rangle } \end{eqnarray}$
其中$\langle \rangle$是空间平均, $u^{rms}=\sqrt {\left\langle {u_{i} u_{i} } \right\rangle } $是速度均方根(rms), 泰勒微尺度定义为

(5)$\begin{eqnarray} \lambda =\sqrt {\dfrac{\left\langle {u_{i} u_{i} } \right\rangle }{\left\langle {\left( {\partial u_{1} /\partial x_{1} } \right)^{2}+\left( {\partial u_{2} /\partial x_{2} } \right)^{2}+\left( {\partial u_{3} /\partial x_{3} } \right)^{2}} \right\rangle }} \end{eqnarray}$
柯尔莫哥洛夫尺度$\eta $和积分尺度$L_{} $分别为^[61-62]

(6)$\begin{eqnarray} \left.\begin{array}{l} \eta =\left[ {\left\langle {\mu /\left( {Re\rho } \right)} \right\rangle ^{3}/\varepsilon } \right]^{1/4}\\ L_{I} =\dfrac{3\pi }{2\left( {u^{rms}} \right)^{2}}\int_0^\infty {\dfrac{E\left( k \right)}{k}{d}k} \end{array}\right\} \end{eqnarray}$
其中$\varepsilon =\left\langle {\sigma_{ij} S_{ij} /\left( {Re\rho } \right)} \right\rangle $是单位质量的动能耗散率.

单位质量的动能谱满足$\int_0^\infty {E\left( k \right){d}k} =\left( {u^{rms}} \right)^{2}/2$.

为高效地求解湍流场中的大尺度运动, 对纳维-斯托克斯方程做滤波,从而得到大涡模拟方程. 滤波器定义为$\bar{{f}}\left( {{x}} \right)=\int_D {f\left( {{{x}'}} \right)G\left( {{x},{{x}'};\varDelta } \right){d}{{x}'}} $, 其中$G$是滤波算子, $D$是滤波范围,$\varDelta $是滤波宽度, $\bar{{f}}$ 代表滤波后的物理量. 对于可压缩湍流,采用Favre滤波, 定义为$\tilde{{f}}=\overline {\rho f} /\bar{{\rho}}$^[68], 其中$\rho $是密度, $f$代表速度或温度. 无量纲的可压缩湍流大涡模拟控制方程如下^[3]

(7)$\begin{eqnarray}&& \dfrac{\partial \bar{{\rho }}}{\partial t}+\dfrac{\partial \left( {\bar{{\rho}}\tilde{{u}}_{j} } \right)}{\partial x_{j} }=0\end{eqnarray}$(7)
(8) $\begin{eqnarray}\dfrac{\partial \left( {\bar{{\rho }}\tilde{{u}}_{i} } \right)}{\partialt}+\dfrac{\partial \left( {\bar{{\rho }}\tilde{{u}}_{i} \tilde{{u}}_{j}+\bar{{p}}\delta_{ij} } \right)}{\partial x_{j}}-\dfrac{1}{Re}\dfrac{\partial \tilde{{\sigma }}_{ij} }{\partial x_{j}}- bar{{F}}_{i} =-\dfrac{\partial \bar{{\rho }}\tau_{ij} }{\partial x_{j} }\end{eqnarray}$
(9)$\begin{eqnarray}\dfrac{\partial \tilde{{E}}}{\partial t}+\dfrac{\partial \left[ {\left({\tilde{{E}}+\bar{{p}}} \right)\tilde{{u}}_{j} } \right]}{\partial x_{j}}-\dfrac{1}{\alpha }\dfrac{\partial }{\partial x_{j} }\left( {\tilde{{\kappa}}\dfrac{\partial \tilde{{T}}}{\partial x_{j} }}\right)-\dfrac{1}{Re}\dfrac{\partial \left( {\tilde{{\sigma }}_{ij}\tilde{{u}}_{i} } \right)}{\partial x_{j} }+\bar{{\varLambda }}-\bar{{F}}_{j}\tilde{{u}}_{j} =-\tilde{{u}}_{i} \dfrac{\partial \bar{{\rho }}\tau_{ij} }{\partial x_{j}}-\dfrac{1}{\left( {\gamma -1} \right)\gamma M^{2}}\dfrac{\partial\bar{{\rho}}Q_{j} }{\partial x_{j} } \end{eqnarray}$
(10)$\begin{eqnarray} \bar{{p}}=\dfrac{\bar{{\rho }}\tilde{{T}}}{\gamma M^{2}} \end{eqnarray}$
其中

$\begin{eqnarray*} \left\{ \begin{array}{l} \tilde{{\sigma }}_{ij} =2\tilde{{\mu }}\tilde{{S}}_{ij}-\dfrac{2}{3}\tilde{{\mu }}\tilde{{S}}_{kk} \delta_{ij}\\ \tilde{{S}}_{ij}=\dfrac{1}{2}\left( {\dfrac{\partial \tilde{{u}}_{i} }{\partial x_{j} }+\dfrac{\partial \tilde{{u}}_{j} }{\partial x_{i} }} \right)\\ \tilde{{E}}=\dfrac{\bar{{p}}}{\gamma -1}+\dfrac{1}{2}\bar{{\rho }}\left( {\tilde{{u}}_{j} \tilde{{u}}_{j} } \right) \end{array} \right. \end{eqnarray*}$

亚格子不封闭项包括

(11)$\begin{eqnarray} \tau_{ij} =\widetilde{u_{i} u_{j} }-\tilde{{u}}_{i} \tilde{{u}}_{j} ,Q_{j} =\widetilde{u_{j} T}-\tilde{{u}}_{j} \tilde{{T}} \end{eqnarray}$
其中$\tau_{ij} $是亚格子应力, $Q_{j} $是亚格子热通量. 假设运动学黏性系数在不同尺度上保持一致, 其他亚格子不封闭项可以忽略^[26]. 在本文中, 对亚格子应力$\tau_{ij}$和亚格子热通量$Q_{j} $发展高精度模型.

1.1 传统的亚格子模型

可压缩湍流的动态Smagorinsky模型(DSM)基于涡黏假设, 并考虑到了湍流能量从大尺度向小尺度的级串过程^[6,10,69-70], 表达式如下^[26,69]

(12)$\begin{eqnarray}&&\tau_{ij} -\dfrac{\delta_{ij} }{3}\tau_{kk} =-2C_{s}^{2} \varDelta^{2}\left|{\widetilde{S}} \right|\left( {\widetilde{S}_{ij} -\dfrac{\delta_{ij}}{3}\widetilde{S}_{kk} } \right)\end{eqnarray}$
(13)$\begin{eqnarray}\tau_{kk} =2C_{I} \varDelta^{2}\left| {\tilde{{S}}} \right|^{2}\end{eqnarray}$
(14)$\begin{eqnarray} Q_{j} =-\dfrac{\nu_{T} }{Pr _{T} }\dfrac{\partial \tilde{{T}}}{\partial x_{j} }=-C\dfrac{\varDelta^{2}\left| {\tilde{{S}}} \right|}{Pr _{T} }\dfrac{\partial \tilde{{T}}}{\partial x_{j} } \end{eqnarray}$
其中$C_{s}^{2} ,C_{I} ,C/Pr _{T} $是模型系数. 假设亚格子不封闭项在滤波宽度和测试滤波宽度保持尺度不变性, 则$C_{s}^{2}, C_{I} ,C/Pr _{T} $可以通过Germano公式动态求解^[71]

(15)$\begin{eqnarray} &&C_{s}^{2} =\dfrac{\left\langle {L_{ij} M_{ij} } \right\rangle }{\left\langle {M_{kl} M_{kl} } \right\rangle },C_{I} =\dfrac{\left\langle {L_{kk} \left( {\beta -\widehat{\alpha }} \right)} \right\rangle }{\left\langle {\left( {\beta -\widehat{\alpha }} \right)^{2}} \right\rangle } \end{eqnarray}$
(16)$\begin{eqnarray} \dfrac{C}{Pr _{T} }=\dfrac{\left\langle {K_{j} T_{j} } \right\rangle }{\left\langle {T_{j} T_{j} } \right\rangle } \end{eqnarray}$
其中

$\begin{eqnarray*}\left.\begin{array}{l}L_{ij} =\widehat{\left( {\overline {\rho u_{i} } \overline {\rho u_{j}} /\overline \rho } \right)}-\widehat{\overline {\rho u_{i} }}\widehat{\overline {\rho u_{j} } }/\widehat{\overline \rho }\\[2mm]M_{ij}=\beta_{ij} -\hat{{\alpha }}_{ij} , \alpha_{ij} =-2\varDelta^{2}\overline\rho \left| {\widetilde{S}} \right|\left( {\widetilde{S}_{ij} -\dfrac{\delta_{ij} }{3}\widetilde{S}_{kk} } \right)\\[2mm]\beta_{ij} =-2\widehat{\varDelta}^{2}\widehat{\overline \rho }\left| {\widehat{\widetilde{S}}} \right|\left({\widehat{\widetilde{S}}_{ij} -\dfrac{\delta_{ij}}{3}\widehat{\widetilde{S}}_{kk} } \right)\\[2mm]\alpha =2\varDelta^{2}\overline\rho \left| {\widetilde{S}} \right|^{2}, \beta =2\widehat{\varDelta}^{2}\widehat{\overline \rho }\left| {\widehat{\widetilde{S}}} \right|^{2}\\[2mm]T_{j} =-\widehat{\varDelta }^{2}\widehat{\overline \rho }\left|{\widehat{\widetilde{S}}} \right|\dfrac{\partial\widehat{\widetilde{T}}}{\partial x_{j} }+\varDelta^{2}\widehat{\overline \rho\left| {\widetilde{S}} \right|\dfrac{\partial \widetilde{T}}{\partial x_{j}}}\\[2mm]K_{j} =\widehat{\left( {\overline {\rho u_{j} } \overline {\rho T}/\overline \rho } \right)}-\widehat{\overline {\rho u_{j} }}\widehat{\overline {\rho T} }/\widehat{\overline \rho }.\end{array}\right.\end{eqnarray*}$

$\overline \bullet $ 表述滤波宽度为$\varDelta $,\ \ $\widehat{\bullet }$ 表示滤波宽度$2\varDelta$. 可压缩湍流的动态混合模型(DMM)由涡黏项和尺度相似项构成^{[21-22,26,72]}, 基本形式如下

(17)$\begin{eqnarray} &&\tau_{ij}^{\bmod } =C_{1} h_{1,ij} +C_{2} h_{2,ij} \end{eqnarray}$
(18)$\begin{eqnarray} T_{ij}^{\bmod } =C_{1} H_{1,ij} +C_{2} H_{2,ij} \end{eqnarray}$
其中

$\begin{eqnarray*} \left\{ \begin{array}{l} h_{1,ij} =-2\varDelta^{2}\left| {\widetilde{S}} \right|\left( {\widetilde{S}_{ij} -\dfrac{\delta_{ij} }{3}\widetilde{S}_{kk} } \right)\\[1mm]h_{2,ij} =\widehat{\tilde{{u}}_{i} \tilde{{u}}_{j} }-\widehat{\tilde{{u}}_{i} }\widehat{\tilde{{u}}_{j} }\\ H_{1,ij} =-2\widehat{\varDelta }^{2}\widehat{\overline \rho }\left| {\widehat{\widetilde{S}}} \right|\left( {\widehat{\widetilde{S}}_{ij} -\dfrac{\delta_{ij} }{3}\widehat{\widetilde{S}}_{kk} } \right)\\[3mm]H_{2,ij} =\widehat{\overline \rho }\left( {\overrightarrow {\widehat{\widetilde{u}}_{i} \widehat{\widetilde{u}}_{j} } -\overrightarrow {\widehat{\widetilde{u}}}_{i} \overrightarrow {\widehat{\widetilde{u}}} _{j} } \right) \end{array} \right. \end{eqnarray*}$

其中 $\overrightarrow \bullet $ 表示滤波宽度为$4\varDelta $.

定义均方误差$E_{\bmod } =\left\langle {\left( {L_{ij} -L_{ij}^{\bmod } } \right)^{2}} \right\rangle $, 其中$L_{ij} =T_{ij} -\widehat{\bar{{\rho }}\tau_{ij} }$, $L_{ij}^{\bmod } =T_{ij}^{\bmod } -\widehat{\bar{{\rho }}\tau_{ij}^{\bmod } }$, $T_{ij} =\hat{{\tilde{{\rho }}}}\left( {\widehat{\widetilde{u_{i} u_{j} }}-\widehat{\widetilde{u_{i} }}\widehat{\widetilde{u_{j} }}} \right)$, $L_{ij} =\hat{{\tilde{{\rho }}}}\left( {\widehat{\tilde{{u}}_{i} \tilde{{u}}_{j} }-\widehat{\widetilde{u_{i} }}\widehat{\widetilde{u_{j} }}} \right)$.

假设模型系数保持尺度不变, 同时最小化均方误差$E_{\bmod } $, 则模型系数$C_{1}

$和$C_{2} $为

(19)$\begin{eqnarray} &&C_{1} =\dfrac{\left\langle {M_{kl}^{2} } \right\rangle \left\langle {L_{ij} N_{ij} } \right\rangle -\left\langle {M_{kl} N_{kl} } \right\rangle \left\langle {L_{ij} M_{ij} } \right\rangle }{\left\langle {M_{kl}^{2} } \right\rangle \left\langle {N_{mn}^{2} } \right\rangle -\left\langle {M_{ij} N_{ij} } \right\rangle^{2}} \end{eqnarray}$
(20)$\begin{eqnarray} C_{2} =\dfrac{\left\langle {N_{kl}^{2} } \right\rangle \left\langle {L_{ij} M_{ij} } \right\rangle -\left\langle {M_{kl} N_{kl} } \right\rangle \left\langle {L_{ij} N_{ij} } \right\rangle }{\left\langle {M_{kl}^{2} } \right\rangle \left\langle {N_{mn}^{2} } \right\rangle -\left\langle {M_{ij} N_{ij} } \right\rangle^{2}} \end{eqnarray}$
其中$L_{ij} =\hat{{\tilde{{\rho }}}}\left( {\widehat{\tilde{{u}}_{i} \tilde{{u}}_{j} }-\widehat{\widetilde{u_{i} }}\widehat{\widetilde{u_{j} }}} \right)$, $M_{ij} =H_{1,ij} -\widehat{\bar{{\rho }}h_{1,ij} }$, $N_{ij} =H_{2,ij} -\widehat{\bar{{\rho }}h_{2,ij} }$.

同理, 亚格子热通量$Q_{j} $可以通过DMM模型写成如下形式

(21)$\begin{eqnarray} &&Q_{j}^{\bmod } =C_{q_{1} } h_{q_{1} ,j} +C_{q_{2} } h_{q_{2} ,j} \end{eqnarray}$
(22)$\begin{eqnarray} \Theta_{j}^{\bmod } =C_{q_{1} } H_{q_{1} ,j} +C_{q_{2} } H_{q_{2} ,j} \end{eqnarray}$
其中

$\begin{eqnarray*} \left\{ \begin{array}{l} h_{q_{1} ,j} =-\varDelta^{2}\left| {\tilde{{S}}} \right|\dfrac{\partial \tilde{{T}}}{\partial x_{j} }, \ \ h_{q_{2} ,j} =\widehat{\tilde{{u}}_{j} \tilde{{T}}}-\widehat{\widetilde{u_{j} }}\hat{{\tilde{{T}}}}\\ H_{q_{1} ,j} =-\hat{{\varDelta }}^{2}\hat{{\bar{{\rho }}}}\left| {\hat{{\tilde{{S}}}}} \right|\dfrac{\partial \hat{{\tilde{{T}}}}}{\partial x_{j} }, \ \ H_{q_{2} ,j} =\hat{{\bar{{\rho }}}}\left( {\overrightarrow {\widehat{\widetilde{u_{j} }}\widehat{\widetilde{T}}} -\overrightarrow {\widehat{\widetilde{u_{j} }}} \overrightarrow {\widehat{\widetilde{T}}} } \right) \end{array} \right. \end{eqnarray*}$

模型系数$C_{q_{1} } $和$C_{q_{2} } $为

(23)$\begin{eqnarray} &&C_{q_{1} } =\dfrac{\left\langle {T_{i}^{2} } \right\rangle \left\langle {L_{j} V_{j} } \right\rangle -\left\langle {T_{i} V_{i} } \right\rangle \left\langle {L_{j} T_{j} } \right\rangle }{\left\langle {V_{i}^{2} } \right\rangle \left\langle {T_{j}^{2} } \right\rangle -\left\langle {T_{i} V_{i} } \right\rangle^{2}} \end{eqnarray}$
(24)\begin{eqnarray} C_{q_{2} } =\dfrac{\left\langle {V_{i}^{2} } \right\rangle \left\langle {L_{j} T_{j} } \right\rangle -\left\langle {T_{i} V_{i} } \right\rangle \left\langle {L_{j} V_{j} } \right\rangle }{\left\langle {V_{i}^{2} } \right\rangle \left\langle {T_{j}^{2} } \right\rangle -\left\langle {T_{i} V_{i} } \right\rangle^{2}} \end{eqnarray}
其中$L_{j} =\hat{{\bar{{\rho }}}}\left( {\widehat{\tilde{{u}}_{j} \tilde{{T}}}-\widehat{\widetilde{u_{j} }}\hat{{\tilde{{T}}}}} \right)$, $T_{j} =H_{q_{1} ,j} -\widehat{\bar{{\rho }}h_{q_{1} ,j} }$, $V_{j} =H_{q_{2} ,j} -\widehat{\bar{{\rho }}h_{q_{2} ,j} }$.

1.2 人工神经网络混合模型(ANNMM)

人工神经网络混合模型(ANNMM)属于人工神经网络显式代数模型. 首先, 将亚格子应力分解为各向异性和各向同性部分^[49]: $\tau_{ij} =\tau _{ij}^{A} +\tau_{ij}^{I} $, 其中$\tau_{ij}^{A} =\tau_{ij} -\delta_{ij} \tau_{kk}/3 $, $\tau_{ij}^{I} =\delta_{ij} \tau_{kk}/3$. 然后, $\tau_{ij}^{A} $, $\tau_{ij}^{I} $, $Q_{j}

$可以通过梯度模型和Smagorinsky模型的线性组合来建模, 具体形式如下

(25)$\begin{eqnarray} &&\tau_{ij}^{A} =C_{1}^{A} \tau_{ij}^{A1} +C_{2}^{A} \tau_{ij}^{A2} \end{eqnarray}$
(25)$\begin{eqnarray} \tau_{kk} =C_{1}^{I} \tau_{kk}^{1} +C_{2}^{I} \tau_{kk}^{2} \end{eqnarray}$
(27)$\begin{eqnarray} Q_{j} =C_{1}^{Q} Q_{j}^{1} +C_{2}^{Q} Q_{j}^{2} \end{eqnarray}$
其中

$\begin{eqnarray*} \left\{ \begin{array}{l} \tau_{ij}^{A1} =\dfrac{\varDelta^{2}}{12}\dfrac{\partial \tilde{{u}}_{i} }{\partial x_{k} }\dfrac{\partial \tilde{{u}}_{j} }{\partial x_{k} }-\dfrac{\delta_{ij} }{3}\dfrac{\varDelta^{2}}{12}\dfrac{\partial \tilde{{u}}_{l} }{\partial x_{k} }\dfrac{\partial \tilde{{u}}_{l} }{\partial x_{k} }\\[4mm]\tau_{ij}^{A2} =2\varDelta^{2}\left| {\tilde{{S}}} \right|\left( {\tilde{{S}}_{ij} -\delta_{ij} \tilde{{S}}_{kk} }\big/3 \right) \\ \tau_{kk}^{1} =\dfrac{\varDelta^{2}}{12}\dfrac{\partial \tilde{{u}}_{l} }{\partial x_{k} }\dfrac{\partial \tilde{{u}}_{l} }{\partial x_{k} }\ \ \tau_{kk}^{2} =2\varDelta^{2}\left| {\tilde{{S}}} \right|\tilde{{S}}_{kk} \\[4mm] Q_{j}^{1} =\dfrac{\varDelta^{2}}{12}\dfrac{\partial \tilde{{u}}_{j} }{\partial x_{k} }\dfrac{\partial \tilde{{T}}}{\partial x_{k} }, \\ Q_{j}^{2} =\varDelta^{2}\left| {\tilde{{S}}} \right|\dfrac{\partial \tilde{{T}}}{\partial x_{j} } \end{array} \right. \end{eqnarray*}$

$C_{1}^{A}$, $C_{2}^{A}$, $C_{1}^{I}$, $C_{2}^{I}$, $C_{1}^{Q}$, $C_{2}^{Q}$是模型系数.

通过训练3个人工神经网络(ANN)分别预测$\tau_{ij}^{A} $, $\tau_{ij}^{I} $, $Q_{j} $, 不同ANN的输入与输出如表1所示, 其中, $\left| {\tilde{{\omega }}} \right|$是滤波后的涡量大小, $\tilde{{\theta }}$是滤波后的速度散度, $\sqrt {\tilde{{A}}_{ij} \tilde{{A}}_{ij} } $是滤波后的速度梯度张量大小, $\sqrt {\tilde{{S}}_{ij} \tilde{{S}}_{ij} } $是滤波后的应变率张量大小, $\left| {\partial \tilde{{T}}/\partial x_{i} } \right|$是滤波后的温度梯度大小,速度梯度张量定义为$\tilde{{A}}_{ij} =\partial \tilde{{u}}_{i} /\partial x_{j} $.


Table 1
Table 1Set of inputs and outputs for the ANNs

新窗口打开|下载CSV

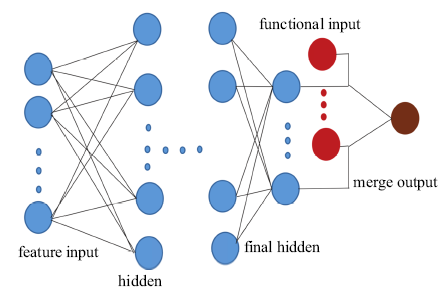
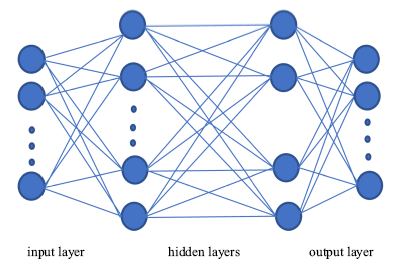
ANNMM模型的人工神经网络的具体结构如图1所示, 包括:输入层、隐藏层、输入基函数层、输出层^[49].ANNMM模型通过优化人工神经网络不同层的权重因子和偏置因子构建了滤波后物理量和目标函数(亚格子应力和亚格子热通量)之间的非线性关系.模型系数$C_{1}^{A} ,C_{2}^{A} ,C_{1}^{I} ,C_{2}^{I} ,C_{1}^{Q} ,C_{2}^{Q}$通过ANN1, ANN2和ANN3网络分别训练.人工神经网络在不同层上的神经元个数为M:20:20:2,其中M是输入层的神经元个数, 最后隐藏层输出模型系数$C_{1} $和$C_{2} $.隐藏层的激活函数取为tan-sigmoid函数

(28)$\begin{eqnarray} \sigma \left( a \right)=\dfrac{1-\mbox{e}^{-2a}}{1+\mbox{e}^{-2a}} \end{eqnarray}$
ANN1, ANN2和ANN3网络的损失函数分别为

$\left\langle {\sum_{i=1}^3 {\sum_{j=1}^i {\left( {\tau _{ij,ANN}^{A} -\tau_{ij,DNS}^{A} } \right)^{2}} } }\Big/6 \right\rangle $, $\left\langle {\left( {\tau_{kk,ANN} -\tau_{kk,DNS} } \right)^{2}} \right\rangle $, 以及$\left\langle {\sum_{j=1}^3 {\left( {Q_{j,ANN} -Q_{j,DNS} } \right)^{2}} }\Big/3 \right\rangle $.

损失函数通过反向传播算法进行最小化^[49].

图1

新窗口打开|下载原图ZIP|生成PPT
图1ANNMM模型的人工神经网络结构

Fig.1Schematic diagram of the ANNMM's network structure



考虑到tan-sigmoid激活函数的输出范围为[0,1],在ANN的训练过程中,将输入层${X}_{I} \Big( \left| {\tilde{{\omega }}} \right|$, $\tilde{{\theta }},\sqrt {\tilde{{A}}_{ij} \tilde{{A}}_{ij} } ,\sqrt {\tilde{{S}}_{ij} \tilde{{S}}_{ij} } ,\left| {\partial \tilde{{T}}/\partial x_{i} } \right| \Big)$通过最小 — 最大值(min-max scaling)归一化到[0,1]范围内

(29)$\begin{eqnarray} {Z}_{I} =\dfrac{{X}_{I} -\min \left\{ {{X}_{I}^{DNS} } \right\}}{\max \left\{ {{X}_{I}^{DNS} } \right\}-\min \left\{ {{X}_{I}^{DNS} } \right\}} \end{eqnarray}$
具体地, 将输出物理量$\tau_{ij}^A$, $\tau_{ij}^{A1}$, $\tau_{ij}^{A2}$归一化为

$\begin{eqnarray*} Z_{ij,O} =\frac{X_{ij,O} -X_{\min \max ,O} }{2X_{\min \max ,O}} \end{eqnarray*}$

其中

$\begin{eqnarray*} X_{\min \max ,O} = \dfrac{1}{6}\sum_{i=1}^3 {\sum_{j=1}^i {\left[ {\max \left( {X_{ij,O} } \right)-\min \left({X_{ij,O} } \right)} \right]\Big/2} } \end{eqnarray*}$

将$\tau_{kk} $, $\tau_{kk}^{1} $, $\tau_{kk}^{2} $归一化为

$\begin{eqnarray*} Z_{O} =\frac{X_{O} -X_{\min \max ,O}}{2X_{\min \max ,O} } \end{eqnarray*}$

其中

$\begin{eqnarray*} X_{\min \max ,O}=\left[ {\max \left({X_{O} } \right)-\min \left( {X_{O} } \right)} \right]\Big/2. \end{eqnarray*}$

将$Q_{j} $, $Q_{j}^{1} $, $Q_{j}^{2} $归一化为

$\begin{eqnarray*} Z_{j,O} =\frac{X_{j,O} -X_{\min \max ,O} }{2X_{\min \max ,O} } \end{eqnarray*}$

其中

$\begin{eqnarray*} X_{\min \max ,O} =\frac{1}{3}\sum_{j=1}^3 {\left[ {\max \left( {X_{j,O} } \right)-\min \left( {X_{j,O} } \right)} \right]/2} \end{eqnarray*}$

1.3 可压缩各向同性湍流的大涡模拟

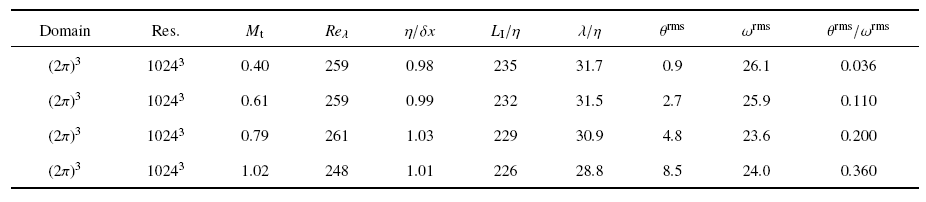
在可压缩各向同性湍流中验证各个亚格子模型.得到了可压缩各向同性湍流的直接数值模拟数据, 具体的参数和统计量如表2所示.湍流马赫数$M_{t} $在0.4~1.0的范围内, 泰勒雷诺数$Re_{\lambda }$约为250^[63-66]. 网格分辨率满足条件: $0.98\leqslant \eta /\delta x\leqslant 1.03$, 其中$\delta x$是直接数值模拟的网格宽度, 同时$2.61\leqslant k_{\max } \eta \leqslant 3.3$ (最大有效波数$k_{\max } $等于单个方向上的网格数的一半).

网格分辨率$k_{\max } \eta \geqslant 2.61$能够保证湍流小尺度物理量的统计收敛性^[61]. 速度散度和涡量的均方根分别定义为$\theta^{rms}=\sqrt {\left\langle {\theta ^{2}} \right\rangle } $, $\omega^{rms}=$ $\sqrt {\left\langle {\omega_{1}^{2} +\omega_{2}^{2} +\omega_{3}^{2} } \right\rangle } $. 采用紧致差分格式和加权基本无振荡(WENO)格式相结合的混合方法, 来开展可压缩均匀各向同性湍流的数值模拟^[73].该混合方法在光滑区域用八阶中心紧致差分格式^[74],在激波区域用七阶WENO格式^[75].


Table 2
Table 2Parameters and statistical quantities for DNS of compressible isotropic turbulence at 1024$^{3}$ grid resolution

新窗口打开|下载CSV

采用盒式滤波器对物理量进行滤波, 一维盒式滤波器定义如下^[66,69]

(30)$\begin{eqnarray} \bar{{f}}_{i} =\dfrac{1}{2n}\left( {f_{i-n/2} +2\sum_{j=i-n/2+1}^{i+n/2-1} {f_{j} } +f_{i+n/2} } \right) \end{eqnarray}$
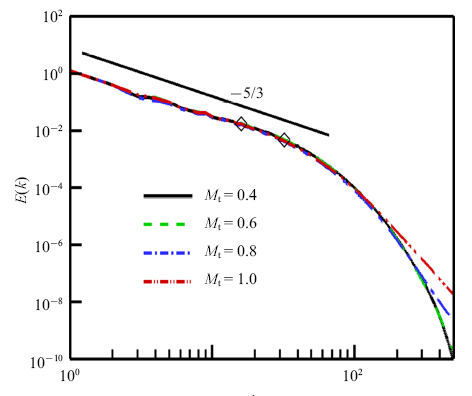
其中滤波宽度$\varDelta =n\delta x$, 主要考虑滤波宽度$\varDelta=16\delta x$. 如图2所示, 该滤波宽度位于惯性区, 同时约5%的湍动能被滤掉了^[26].

图2

新窗口打开|下载原图ZIP|生成PPT
图2可压缩湍流直接数值模拟数据的速度谱, 菱形表示滤波宽度为$\varDelta /\delta$ x=16, 32
Fig. 2Velocity spectrum from DNS. Diamonds represent filter widths $\varDelta /\delta$ x=16, 32


1.3.1 ANNMM模型的先验分析

使用可压缩湍流的直接数值模拟数据, 开展ANNMM模型的先验验证研究. 通过计算亚格子不封闭项的相关系数和相对误差, 研究神经网络超参数对ANNMM模型先验预测精度的影响^[49]. 模型预测的亚格子不封闭项$H^{{model}}$与真实亚格子不封闭项$H$的相关系数和相对误差分别为

(31)$\begin{eqnarray} &&C\left( H \right)=\dfrac{\left\langle {\left( {H-\left\langle H \right\rangle } \right)\left( {H^{{model}}-\left\langle {H^{{model}}} \right\rangle } \right)} \right\rangle }{\left( {\left\langle {\left( {H-\left\langle H \right\rangle } \right)^{2}} \right\rangle \left\langle {\left( {H^{{model}}-\left\langle {H^{{model}}} \right\rangle } \right)^{2}} \right\rangle } \right)^{1/2}} \end{eqnarray}$
(32)$\begin{eqnarray} E_{r} \left( H \right)=\dfrac{\left\langle {\left( {H-H^{{model}}} \right)^{2}} \right\rangle^{1/2}}{\left\langle {H^{2}} \right\rangle ^{1/2}} \end{eqnarray}$
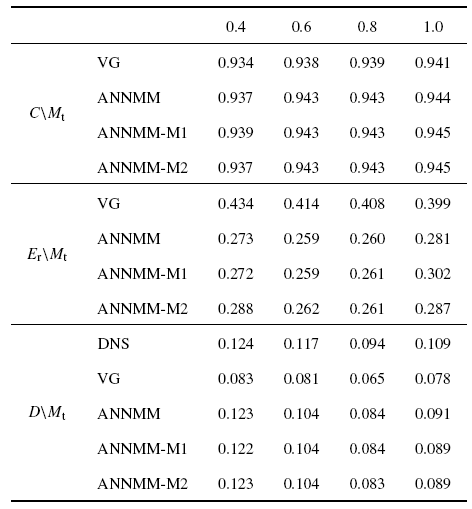
表3展示了不同的神经网络超参数对应的ANNMM模型的预测结果. 其中ANNMM-M1和ANNMM-M2模型的网络结构分别为M:40:40:2和M:20:20:20:2. 不同超参数的人工神经网络模型预测的$\tau_{11} $的相关系数和相对误差在$0.4\leqslant M_{t} \leqslant 1.0$的情况下保持一致,ANNMM模型的预测结果不随神经元个数和隐藏层深度的增大而显著变化. 速度梯度(VG)模型($\tau_{ij} =\varDelta^{2}\partial_{k} \tilde{{u}}_{i} \partial_{k} \tilde{{u}}_{j}/12 $, $Q_{j} =\varDelta ^{2}\partial_{k} \tilde{{u}}_{j} \partial_{k} \tilde{{T}}/12)$预测的相对误差约为40%. ANNMM模型预测的相对误差约为25%, 远低于VG模型. 同时ANNMM模型预测的$\tau_{11} $的均方根值更接近于滤波后的直接数值模拟(fDNS)的结果.

1.3.2 ANNMM模型的后验分析

在后验测试中, LES的网格分辨率为$128^{3}$ $(h_{LES} =\varDelta /2$, $FGR=\varDelta /h_{LES} =2)$^[76-78], 滤波宽度$\varDelta =16\delta x$. $FGR=2$使得LES的误差主要来自亚格子模型的误差, 而数值误差的影响非常小.

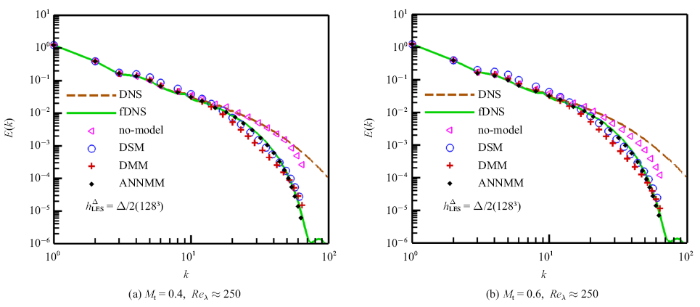
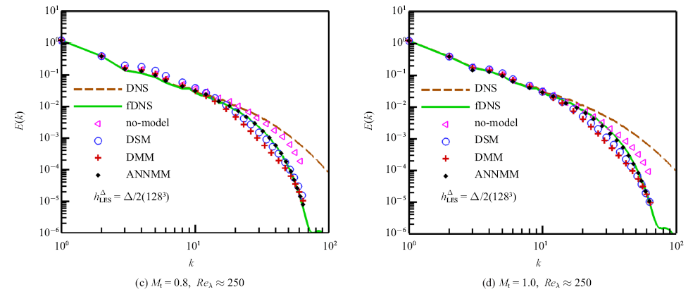
ANNMM模型和传统亚格子模型预测的速度谱如图3所示. 不加任何亚格子模型的情况(No-model)无法提供足够的耗散, 导致预测的速度谱高于fDNS结果; DSM和DMM模型在低波数出现能量聚集现象, 同时在高波数耗散过大. ANNMM模型预测的速度谱在全波数范围更接近fDNS结果.


Table 3
Table 3Correlation coefficient (C), relative error ($E_{r} )$ and root mean square value ($D$) of $\tau_{11} $ for different models at $M_{t}=0.4$, 0.6, 0.8, 1.0}

新窗口打开|下载CSV

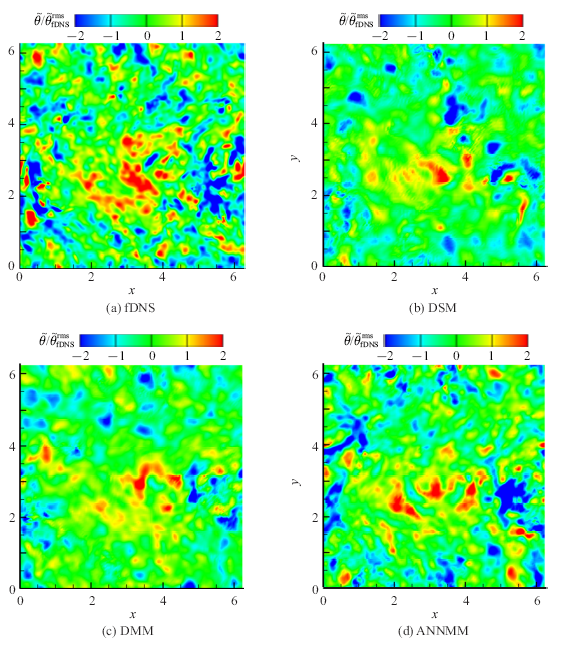
不同亚格子模型预测的瞬态速度散度云图如图4所示. 相比DSM和DMM模型, ANNMM模型可以重构出更多的小尺度结构, 同时预测的速度散度更接近滤波后的直接数值模拟(fDNS)的结果.

综上所述, ANNMM模型可以高精度地预测不同湍流马赫数情况下的可压缩湍流的统计特性和瞬态空间结构. 还发展了另外一种人工神经网络显式代数模型: 基于人工神经网络的非线性代数模型(ANN-NAM), 具体内容见参考文献[50].

1.4 空间人工神经网络(SANN)模型

空间人工神经网络(SANN)模型的神经网络结构如图5所示^[51-55]. SANN模型属于多点对单点的人工神经网络隐式结构模型.

该模型构建了不同空间点上的滤波后的物理量和当地点上的亚格子不封闭项之间的非线性映射关系.

人工神经网络(ANN)的输入层${X}_{I} $的神经元取为滤波后的速度和温度梯度. 亚格子应力和亚格子热通量的分量通过ANN分别训练. ANN的不同层神经元数量为: $M$:1024:512:1, 其中$M$是输入层神经元个数, 输出层为亚格子不封闭项的分量. 隐藏层的激活函数为Leaky-Relu函数

(33)$\begin{eqnarray}\label{eq33}\sigma \left( a \right)=\left\{ {\begin{array}{l@{\quad }l} a, & a>0 \\ 0.2a, & a\leqslant 0 \\ \end{array}} \right.\end{eqnarray}$
输出层的激活函数为线性函数$\sigma \left( a \right)=a$. ANN的损失函数$\left\langle {\left( {X_{O} -\tau_{ij} } \right)^{2}} \right\rangle $或$\left\langle {\left( {X_{O} -Q_{j} } \right)^{2}} \right\rangle $采用反向传播算法最小化^[51-55].

湍流的多尺度结构表明尺度接近滤波宽度$\varDelta $的湍流结构对重构亚格子模型至关重要^[79-82]. SANN模型采用两个控制参数主导神经网络输入层的结构:

图3

新窗口打开|下载原图ZIP|生成PPT
图3大涡模拟模型在128$^{3}(h_{LES} =\varDelta /2)$网格下的速度谱

Fig.3Spectrum of velocity for LES at grid resolution of 128$^{3}(h_{LES} =\varDelta /2)$}

图3

新窗口打开|下载原图ZIP|生成PPT
图3大涡模拟模型在128$^{3}(h_{LES} =\varDelta /2)$网格下的速度谱(续)

Fig.3Spectrum of velocity for LES at grid resolution of 128$^{3}(h_{LES} =\varDelta /2)$ (continued)}

图4

新窗口打开|下载原图ZIP|生成PPT
图4$M_{t} =0.4$和$t/\tau =3.37$ ($\tau =L_{I} /u^{rms}$是大涡翻转时间)情况下的归一化速度散度$\tilde{{\theta }}/\tilde{{\theta }}_{fDNS}^{rms}$云图, 同时LES网格为128$^{3}(h_{LES} =\varDelta /2)$, 滤波宽度为$\varDelta=16\delta x$

Fig.4Contours of the normalized velocity divergence $\tilde{{\theta}}/\tilde{{\theta }}_{fDNS}^{rms} $ on an arbitrarily selected $x$-$y$ slice, at $M_{t} =0.4$, and $t/\tau =3.37$ (here $\tau =L_{I} /u^{rms}$ is the large-eddy turnover time) for LES at grid resolution of 128$^{3}(h_{LES} =\varDelta /2)$ with the filter width $\varDelta =16\delta x$}

图5

新窗口打开|下载原图ZIP|生成PPT
图5SANN模型网络结构示意图

Fig.5Schematic diagram of the SANN's network structure



输入量的空间模板宽度$\varDelta_{s} $和滤波宽度$\varDelta $之比: $R_{s}=\varDelta _{s} /\varDelta $; 滤波宽度$\varDelta $和空间模板的网格尺度$\varDelta_{g} $之比: $R_{g} =\varDelta /\varDelta_{g} $. SANN($R_{s} ,R_{g} )$模型的输入参数空间为

(34)$\begin{eqnarray} &&\left\{ {\begin{array}{cccc} \dfrac{\partial \tilde{{u}}_{i}^{l,m,n} }{\partial x_{p} },&\dfrac{\partial \tilde{{u}}_{i}^{l\pm q_{1} ,m,n} }{\partial x_{p} },&\dfrac{\partial \tilde{{u}}_{i}^{l,m\pm q_{2} ,n} }{\partial x_{p} },&\dfrac{\partial \tilde{{u}}_{i}^{l,m,n\pm q_{3} } }{\partial x_{p} } \\ \dfrac{\partial \tilde{{T}}^{l,m,n}}{\partial x_{p} },&\dfrac{\partial \tilde{{T}}^{l\pm q_{1} ,m,n}}{\partial x_{p} },&\dfrac{\partial \tilde{{T}}^{l,m\pm q_{2} ,n}}{\partial x_{p} },&\dfrac{\partial \tilde{{T}}^{l,m,n\pm q_{3} }}{\partial x_{p} } \\ \end{array}} \right\} \end{eqnarray}$
(35)$\begin{eqnarray} \left\{ {q_{1} ,q_{2} ,q_{3} } \right\}\in \left\{ {1,2,...,R_{s} R_{g} } \right\} \end{eqnarray}$
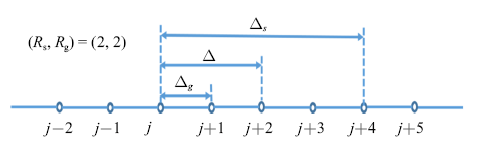
其中下标$p=1$, 2, 3是笛卡尔坐标, 下标$i=1$, 2, 3代表滤波后的速度分量, 上标$l,m,n$表示间距为$\varDelta_{g} $的离散空间位置. SANN ($R_{s} ,R_{g})$模型的输入层神经元总数是$M=12N=12(6R_{s} R_{g} +1)$. 一维情况下的输入层的空间点个数与($R_{s} ,R_{g} )$的关系如图6所示, $M$随着$R_{s} $和$R_{g} $增大而变大.

输入层${X}_{I} $和输出层$X_{O} $通过它们的均方根${X}_{I}^{rms}$和$X_{O}^{rms} $进行归一化

(36)$\begin{eqnarray} {Z}_{I} ={X}_{I} /{X}_{I}^{rms} ,Z_{O} =X_{O} /X_{O}^{rms} \end{eqnarray}$
特别的, $X_{O}^{rms} $由亚格子不封闭项的梯度模型得到.

图6

新窗口打开|下载原图ZIP|生成PPT
图6SANN模型的输入参数: ($R_{s} ,R_{g} )=(2, 2)$

Fig.6Input variables for the SANN model: ($R_{s} ,R_{g} )=(2, 2)$}



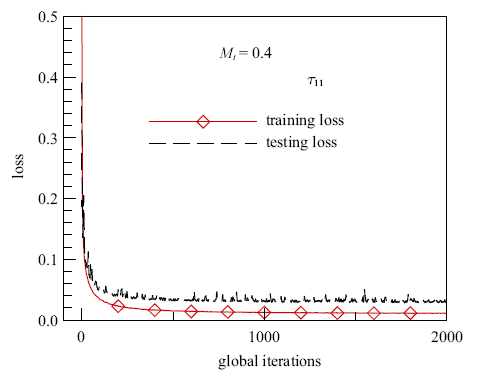
ANN的训练数据集是从直接数值模拟的数据中提取的包含$15\times64^{3}$个点的空间子集, 其中70%数据为训练集, 30%数据为测试集. SANN($R_{s} ,R_{g} )$模型通过Adam算法训练1000次(epoch)^[83],同时训练样本集大小(batch size)为1000. SANN($R_{s} ,R_{g} )$模型预测的损失函数随迭代步数的变化曲线如图7所示,训练集和测试集的损失函数随着迭代步数的增大而收敛.

图7

新窗口打开|下载原图ZIP|生成PPT
图7SANN(2, 1)模型在$M_{t} =0.4$时预测$\tau_{11} $的学习曲线

Fig.7Learning curves of the proposed SANN(2, 1) model of unclosed SGS terms $\tau_{11} $, at $M_{t} =0.4$

1.5 SANN模型的先验和后验分析

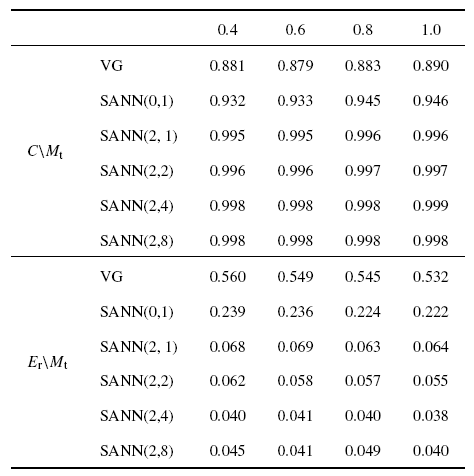
滤波宽度$\varDelta =32\delta x$的DNS数据被用于验证SANN模型精度. DNS数据参数如表2所示. 如图1所示, 滤波宽度$\varDelta =32\delta x$位于惯性区, 流场中约10%的湍动能被滤掉.

表4展示了在测试集上不同参数($R_{s} ,R_{g} )$对SANN($R_{s} ,R_{g} )$模型预测亚格子应力分量$\tau_{11} $的影响, 其中$R_{s} =2$. 在不同湍流马赫数情况下, SANN($R_{s} ,R_{g})$模型预测的相关系数和相对误差结果基本上是一致的. 速度梯度(VG)模型预测的相关系数约为0.88. SANN($R_{s} ,R_{g} )$模型预测的相关系数达到0.995, 相对误差小于10%, 远低于VG模型的50%. 当$R_{g} \geqslant 1$时, SANN模型预测的相关系数接近1. 随着$R_{g} $的增大, SANN模型预测的亚格子不封闭项与DNS数据提供的真实值趋于一致.

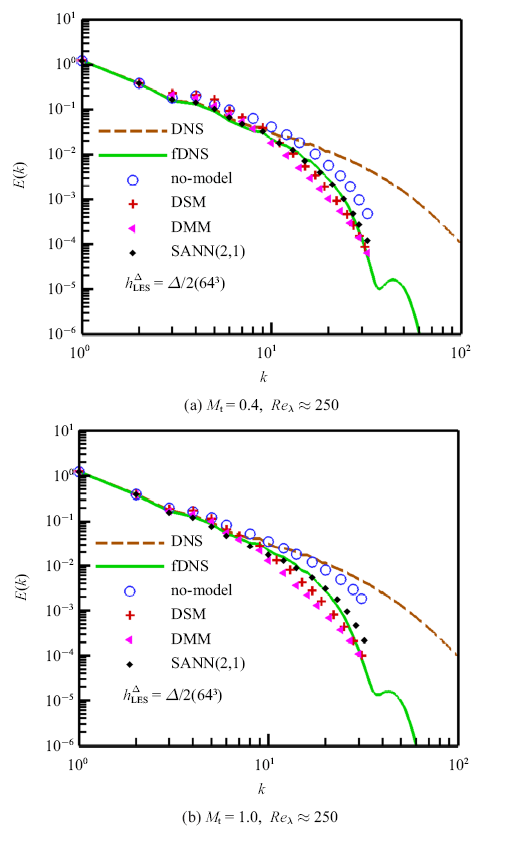
在后验测试中, LES的网格分辨率为64$^{3}(h_{LES} =\varDelta /2$, $FGR=2)$, 滤波宽度为$\varDelta =32\delta x$. SANN(2, 1)模型和传统亚格子模型预测的速度谱如图8所示. No-model模型(即隐式大涡模拟, ILES)预测速度谱的误差随着波数增大而明显变大. DSM和DMM模型在低波数$k\leqslant 10$的情况下出现能量聚集, 同时在高波数耗散过大. SANN(2, 1)模型预测的速度谱几乎与fDNS的结果重合.


Table 4
Table 4Correlation coefficient ($C$) and relative error ($E_{r} )$ of $\tau_{11} $ for different models at filter width $\varDelta /\delta x=32$ and $M_{t} =0.4$, 0.6, 0.8, 1.0 with $R_{s} =2$}

新窗口打开|下载CSV



不同亚格子模型预测的瞬态速度散度云图如图9所示. DSM, DMM和SANN(2, 1)模型均能预测出大尺度结构. SANN(2, 1)模型重构出更多的小尺度结构, 更接近滤波后的直接数值模拟结果, 在预测效果上优于DSM模型和DMM模型.

图8

新窗口打开|下载原图ZIP|生成PPT
图8SANN模型在64$^{3}(h_{LES} =\varDelta /2)$网格下预测的速度谱

Fig.8Spectrum of velocity with SANN models for LES at grid resolution of 64$^{3}(h_{LES} =\varDelta /2)$



综上所述, SANN模型在先验验证中的精度远高于传统模型, 在后验验证中预测的能谱和瞬态流动结构都和滤波后的直接数值模拟结果保持一致, 优于ILES方法、DSM和DMM模型的预测结果. SANN模型在不可压缩湍流大涡模拟中的研究见参考文献[55].

2 反卷积人工神经网络(DANN)模型

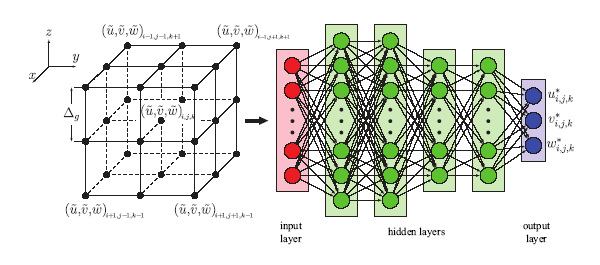
上述介绍的两种人工神经网络模型(ANNMM和SANN模型)是对亚格子不封闭项直接建模, 而反卷积人工神经网络(DANN)模型^[56]是一种间接建模的人工神经网络半隐式结构模型. 在这类模型的输入和输出的映射关系中, 出现了卷积算子和反卷积算子, 其中, 反卷积算子采用人工神经网络隐式结构模型. 首先通过人工神经网络建立不同空间点上的滤波后物理量和当地点上的原始未滤波物理量之间的非线性映射关系; 然后将人工神经网络重构的原始未滤波物理量代入亚格子不封闭项的计算公式, 得到建模的亚格子不封闭项.

本文将DANN模型应用于不可压缩均匀各向同性湍流, 亚格子不封闭项仅包含亚格子应力, 通过人工神经网络建立滤波后速度与原始未滤波速度的非线性映射关系, 其神经网络结构如图10所示.

图9

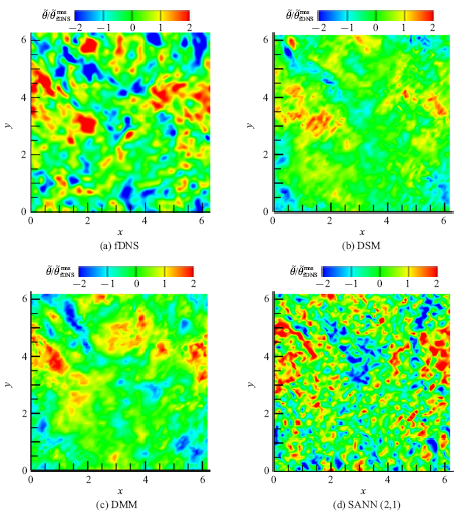
新窗口打开|下载原图ZIP|生成PPT
图9$M_{t} =0.4$和$t/\tau =3.37$ ($\tau =L_{I} /u^{rms}$是大涡翻转时间) 情况下的归一化速度散度$\tilde{{\theta }}/\tilde{{\theta }}_{fDNS}^{rms}$云图, 其中LES网格为64$^{3}(h_{LES} =\varDelta /2)$,滤波宽度为$\varDelta =32\delta x$类似于SANN模型, DANN模型采用两个控制参数主导神经网络输入层的结构: 输入量的空间模板在每个方向上的点数$D(D=2R_{s} +1)$; 滤波宽度$\varDelta $和空间模板的网格尺度$\varDelta_{g} $之比: $R_{g} =\varDelta /\varDelta_{g} $, 则输入层的神经元个数为$M=3\times D^{3}$. DANN($D,R_{g} )$模型共包含输入层${X}_{I} $、4个隐藏层${X}_{h} $和输出层${X}_{O} $, 其中输入和输出参数空间分别为

Fig.9Contours of the normalized velocity divergence $\tilde{{\theta }}/\tilde{{\theta }}_{fDNS}^{rms} $ on an arbitrarily selected x-y slice, at $M_{t} =0.4$, and $t/\tau =3.37$ (here $\tau =L_{I} /u^{rms}$ is the large-eddy turnover time) for LES at grid resolution of 64$^{3}(h_{LES} =\varDelta /2)$ with the filter width $\varDelta =32\delta x$} (37)$\begin{eqnarray} &&{X}_{I} :\left\{ {\tilde{{u}}_{l+i,m+j,n+k} ,\tilde{{v}}_{l+i,m+j,n+k} ,\tilde{{w}}_{l+i,m+j,n+k} } \right\} \end{eqnarray}



(38)$\begin{eqnarray} \left\{ {l,m,n} \right\}\in \left\{ {-\left\lfloor {D/2} \right\rfloor ,...,0,...,\left\lfloor {D/2} \right\rfloor } \right\} \end{eqnarray}$
(39)$\begin{eqnarray} {X}_{O} :\left\{ {u_{i,j,k}^{\ast } ,v_{i,j,k}^{\ast } ,w_{i,j,k}^{\ast } } \right\} \end{eqnarray}$
DANN模型的不同层神经元数量分别为$M$:128: 128:64:64:3, 其中输入层神经元个数$M=3\times D^{3}$, 输出层为原始未滤波速度分量. 隐藏层的激活函数为Leaky-Relu函数.

图10

新窗口打开|下载原图ZIP|生成PPT
图10DANN模型网络结构示意图

Fig.10Schematic diagram of the DANN's network structure



DANN模型的输入输出层分别选取滤波后速度的均值和标准差进行归一化

(40)$\begin{eqnarray} \tilde{{U}}_{i} =\dfrac{\tilde{{u}}_{i} -\left\langle {\tilde{{u}}_{i} } \right\rangle }{\sqrt {\left\langle {\left( {\tilde{{u}}_{i} -\left\langle {\tilde{{u}}_{i} } \right\rangle } \right)^{2}} \right\rangle } },\ \ \tilde{{U}}_{i}^{\ast } =\dfrac{u_{i}^{\ast } -\left\langle {\tilde{{u}}_{i} } \right\rangle }{\sqrt {\left\langle {\left( {u_{i}^{\ast } -\left\langle {\tilde{{u}}_{i} } \right\rangle } \right)^{2}} \right\rangle } } \end{eqnarray}$
将人工神经网络预测的原始未滤波物理量代入亚格子未封闭项的计算公式,即可得到DANN模型重构的亚格子应力

(41)$\begin{eqnarray} \tau_{ij}^{{DANN}} =\widetilde{u_{i}^{\ast } u_{j}^{\ast } }-\widetilde{u_{i}^{\ast } }\widetilde{u_{j}^{\ast } } \end{eqnarray}$
相比于人工神经网络全隐式结构的SANN模型, DANN模型具有良好的物理性质, 满足对称性和可实现性条件^[56].

类似于SANN模型, DANN($D,R_{g} )$模型的训练样本集是从DNS数据中随机选取包含$2\times 64^{3}$个点的空间子集,其中70%数据为训练集, 30%数据为测试集. 通过Adam算法训练2000次^[83], 学习率为0.01. 显式滤波选取高斯滤波器, 滤波宽度$\varDelta =32\delta x$.

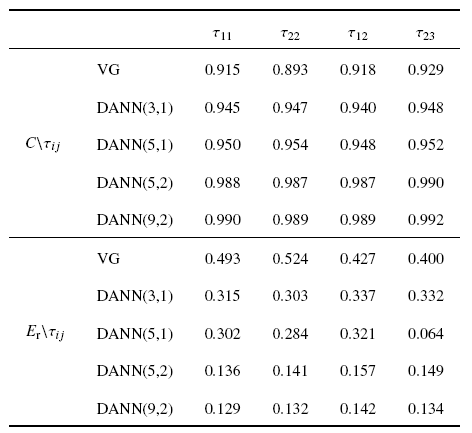
表5展示了在测试集上不同控制参数($D,R_{g} )$对DANN($D,R_{g} )$模型预测亚格子应力各个分量的影响, 其中滤波宽度$\varDelta =32\delta x$. 速度梯度(VG)模型预测的相关系数约为0.91. DANN($D,R_{g} )$模型预测的相关系数达到0.99, 相对误差小于15%, 远低于VG模型的49%. 随着$R_{g} $的增大, 空间模板的网格尺度越小, DANN模型预测的亚格子应力与DNS数据计算的真实值趋于一致.


Table 5
Table 5Correlation coefficient ($C$) and relative error ($E_{r} )$\\ of SGS stress components for different DANN models at filter width $\varDelta /\delta x=32$

新窗口打开|下载CSV

在后验测试中, LES的网格分辨率为64$^{3}(h_{LES} =\varDelta /2$, $FGR=2)$, 滤波宽度为$\varDelta =32\delta x$. DANN模型和传统亚格子模型预测的速度谱和局部放大图如图11所示. No-model模型(即隐式大涡模拟, ILES)预测的速度谱与fDNS偏差较大, 且预测误差随着波数的增大而显著增大. DSM和DMM模型在滤波尺度附近耗散过大, 导致能量不能从大尺度顺利地传递到小尺度, 在低波数$k\leqslant 10$的情况下出现能量聚集, 同时在高波数区域耗散过大. DANN(5,2)和DANN(9,2)模型预测的速度谱几乎与fDNS的结果完全重合, 很好地模拟了湍流的能量级串过程.

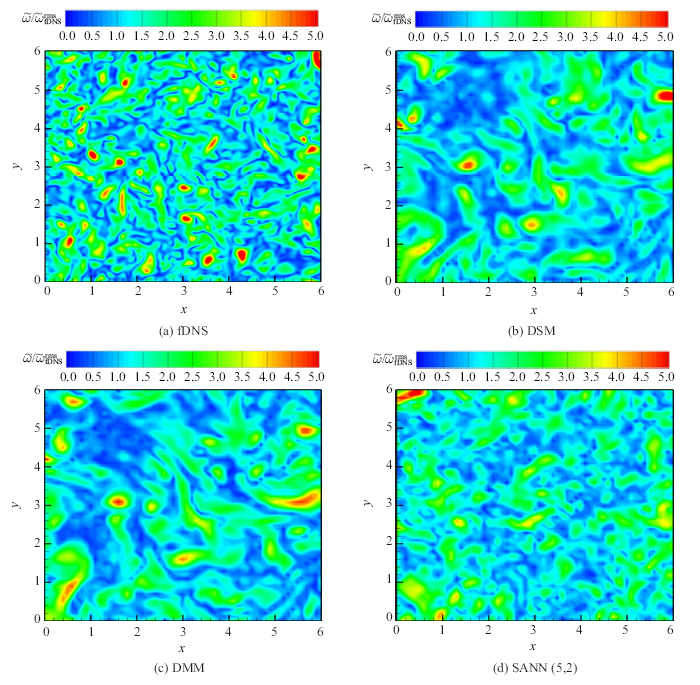
不同亚格子模型预测的瞬态涡量云图如图12所示. DSM和DMM模型耗散过强, 仅能预测出大尺度结构. DANN(5,2)模型可以重构出更多精细的小尺度结构, 更接近于滤波后的直接数值模拟结果, 在预测效果上明显优于DSM模型和DMM模型.

综上所述, DANN模型在先验验证中的精度远高于传统模型, 在后验验证中预测的能谱和瞬态流动结构都和滤波后的直接数值模拟结果保持一致, 优于ILES方法、DSM和DMM模型的预测结果. 此外, 相比于人工神经网络全隐式结构的SANN模型, 基于近似反卷积算子的DANN模型具有良好的物理性质, 满足对称性和可实现性条件^[56].

图11

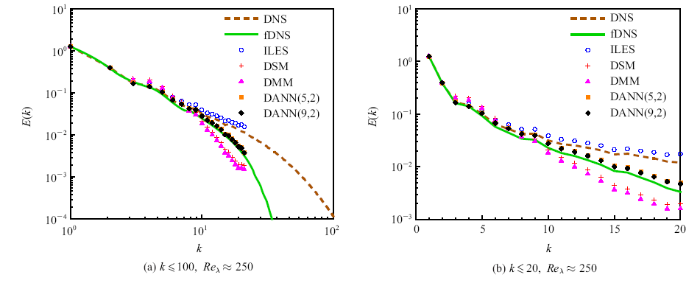新窗口打开|下载原图ZIP|生成PPT
图11DANN模型在64$^{3}(h_{LES} =\varDelta /2)$网格下预测的速度谱

Fig.11Spectrum of velocity with DANN models for LES at grid resolution of 64$^{3}(h_{LES} =\varDelta /2)$

图12

新窗口打开|下载原图ZIP|生成PPT
图12$t/\tau =5$情况下的瞬态归一化涡量$\tilde{{\omega }}/\tilde{{\omega }}^{rms}$云图, 其中LES网格为64$^{3}(h_{LES} =\varDelta /2)$, 滤波宽度为$\varDelta =32\delta x$

Fig.12Contours of the normalized vorticity magnitude $\tilde{{\omega }}/\tilde{{\omega }}^{rms}$ on an arbitrarily selected $x$--$y$ slice, at $t/\tau =5$ for LES at grid resolution\\[-1.3mm] of 64$^{3}(h_{LES} =\varDelta /2)$ with the filter width $\varDelta =32\delta x$}

3 结论

本文讨论了用机器学习方法重构湍流大涡模拟中的亚格子不封闭项的最新研究成果. 传统的亚格子模型具有计算量小、泛化能力强的优点. 但由于只利用了单点流场信息和简单的函数关系, 传统亚格子模型存在先验误差大、后验耗散过大的问题.

本文总结了几种不同的基于人工神经网络的高精度亚格子模型. 根据建模方法的不同, 分别介绍了人工神经网络显式代数模型中的ANNMM模型, 人工神经网络隐式结构模型中的SANN模型, 以及基于反卷积算子的DANN模型. 和传统的亚格子模型相比, SANN模型和DANN模型考虑了湍流的多尺度特征, 特别是尺度在$\varDelta /2$和$2\varDelta $之间的流动结构对亚格子不封闭项的作用. SANN和DANN模型的先验预测精度高, 相关系数达到0.99以上, 相对误差小于15%, 同时在后验验证中, 能够精确地预测湍流场的统计性质和空间结构.

上述这些研究结果, 展示了人工神经网络方法在发展高精度、高效率的亚格子模型方面的巨大潜力. 为了提高人工神经网络模型的可解释性和泛化能力, 需要将更多的湍流物理特性融入到人工神经网络模型中, 包括: 多样化的几何外形、复杂的湍流类型、涡结构与激波结构的相互作用, 以及湍流的时空特征等.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Pope S. Turbulent Flows
Cambridge University Press, 2000
[本文引用: 4]

[2] Sagaut P . Large Eddy Simulation for Incompressible Flows
Berlin: Springer, 2006


[3] Garnier E, Adams N, Sagaut P . Large Eddy Simulation for Compressible Flows
Verlag: Springer, 2009
[本文引用: 2]

[4] 张兆顺, 崔桂香, 许春晓 . 湍流大涡数值模拟的理论和应用. 北京: 清华大学出版社, 2008


( Zhang Zhaoshun, Cui Guixiang, Xu Chunxiao. Theory and Application of Large Eddy Simulation of Turbulent Flows. Beijing: Tsinghua University Press, 2008 (in Chinese))


[5] 傅德薰, 马延文, 李新亮 等. 可压缩湍流直接数值模拟. 北京: 科学出版社, 2010


( Fu Dexun, Ma Yanwen, Li Xinliang , et al. Direct Numerical Simulation of Compressible Turbulence. Beijing: Science Press, 2010 (in Chinese))


[6] Moin P, Squires K, Cabot W , et al. A dynamic subgrid-scale model for compressible turbulence and scalar transport
Phys. Fluids A, 1991,3(11):2746-2757
[本文引用: 2]

[7] Meneveau C, Katz J . Scale-invariance and turbulence models for large-eddy simulation
Annu. Rev. Fluid Mech., 2000,32(1):1-32


[8] Chen SY, Xia ZH, Pei SY , et al. Reynolds-stress-constrained large-eddy simulation of wall- bounded turbulent flows.
[J]. Fluid Mech., 2012,703:1-28


[9] Durbin PA . Some recent developments in turbulence closure modeling
Annu. Rev. Fluid Mech., 2018,50:77-103
[本文引用: 1]

[10] Smagorinsky J . General circulation experiments with the primitive equations. I. The basic experiment
Mon. Weather Rev., 1963,91:99-164
[本文引用: 3]

[11] Lilly DK . The representation of small-scale turbulence in numerical simulation experiments//Proceedings of the IBM Scientific Computing Symposium on Environmental Sciences (IBM, 1967):195-210
[本文引用: 1]

[12] Deardorff JW . A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers.
[J]. Fluid Mech., 1970,41(2):453-480


[13] 时北极, 何国威, 王士召 . 基于滑移速度壁模型的复杂边界湍流大涡模拟
力学学报, 2019, 51(3): 754-766


(Shi Beiji, He Guowei, Wang Shizhao. Large-eddy simulation of flows with complex geometries by using the slip-wall model
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(3):754-766 (in Chinese))


[14] 陈林烽 . 基于Navier-Stokes方程残差的隐式大涡模拟有限元模型
力学学报, 2020, 52(5):1314-1322


(Chen Linfeng. A residual-based unresolved-scale finite element modelling for implict large eddy simulation
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(5):1314-1322 (in Chinese))


[15] 吴霆, 时北极, 王士召 等. 大涡模拟的壁模型及其应用
力学学报, 2018,50(3):453-466 (in Chinese))


( Wu Ting, Shi Beiji, Wang Shizhao, et al. Wall-model for large-eddy simulation and its applications
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(3):453-466 (in Chinese))


[16] Han Q, Li XL, Yu CP . Subgrid-scale model based on the vorticity gradient tensor for rotating turbulent flows
Acta Mechanica Sinica, 2020,36(3):692-700


[17] Wang CH, Ge MW . Applying resolved-scale linearly forced isotropic turbulence in rational subgrid-scale modeling
Acta Mechanica Sinica, 2019,35(3):486-494
[本文引用: 1]

[18] Germano M, Piomelli U, Moin P , et al. A dynamic subgrid scale eddy-viscosity model
Phys. Fluids A, 1991,3:1760-1765
[本文引用: 1]

[19] Lilly D . A proposed modification of the Germano subgrid scale closure method
Phys. Fluids A, 4:633
[本文引用: 1]

[20] Bardina J, Ferziger JH, Reynolds WC. Improved subgrid scale models for large eddy simulation
AIAA Journal, 1980,80:1357
[本文引用: 1]

[21] Liu S, Meneveau C, Katz J . On the properties of similarity subgrid scale models as deduced from measurements in a turbulent jet.
[J]. Fluid Mech., 1994,275:83
[本文引用: 3]

[22] Clark RA . Evaluation of sub-grid scalar models using an accurately simulated turbulent flow.
[J]. Fluid Mech., 1979,91:1-16
[本文引用: 1]

[23] Vreman B, Geurts B, Kuerten H . Large eddy simulation of the temporal mixing layer using the Clark model
Theor. Comput. Fluid Dyn., 1996,8:309-324
[本文引用: 1]

[24] Langford JA, Moser RD . Optimal LES formulations for isotropic turbulence.
[J]. Fluid Mech., 1999,398:321-346
[本文引用: 1]

[25] Langford JA, Moser RD . Optimal large-eddy simulation results for isotropic turbulence.
[J]. Fluid Mech., 2004,521:273-294


[26] Xie CY, Wang JC, Li H , et al. A modified optimal LES model for highly compressible isotropic turbulence. Phys
Fluids, 2018,30:065108
[本文引用: 5]

[27] Deardorff JW . Three-dimensional numerical modeling of the planetary boundary layer//Workshop on Micrometeorology
edited by Haugen DA (American Meteorological Society, 1973)
[本文引用: 2]

[28] Chai XC, Mahesh K . Dynamic $k$-equation model for large-eddy simulation of compressible flows.
[J]. Fluid Mech., 2012,699:385
[本文引用: 1]

[29] Launder BE, Reece GJ, Rodi W . Progress in the development of a Reynolds stress turbulence closure.
[J]. Fluid Mech., 1975,68:537-566
[本文引用: 1]

[30] Speziale CG . Analytical methods for the development of Reynolds stress closures in turbulence
Annu. Rev. Fluid Mech., 1991,23:107-157


[31] Xie CY, Wang JC, Li H , et al. An approximate second-order closure model for large-eddy simulation of compressible isotropic turbulence
Commun. Comput. Phys., 2020,27:775-808
[本文引用: 1]

[32] Ling J, Kurzawski A, Templeton J . Reynolds averaged turbulence modelling using deep neural networks with embedded invariance.
[J]. Fluid Mech., 2016,807:155
[本文引用: 2]

[33] Xiao H, Wu JL, Wang JX , et al. Quantifying and reducing model-form uncertainties in Reynolds-averaged Navier-Stokes simulations: A data-driven, physics informed Bayesian approach.
[J]. Comput. Phys., 2016,324


[34] Duraisamy K, Iaccarino G, Xiao H . Turbulence modeling in the age of data
Annu. Rev. Fluid Mech., 2019,51:537
[本文引用: 1]

[35] Sarghini F, Defelice G, Santini S . Neural networks based subgrid scale modeling in large eddy simulations
Computers & Fluids, 2003,32:97-108
[本文引用: 1]

[36] Gamahara M, Hattori Y . Searching for turbulence models by artificial neural network. Phys. Rev
Fluids, 2017,2(5):054604
[本文引用: 1]

[37] Vollant A, Balarac G, Corre C . Subgrid-scale scalar flux modelling based on optimal estimation theory and machine-learning procedures.
[J]. Turbulence, 2017,18(9):854


[38] Kutz JNJ . Deep learning in fluid dynamics.
[J]. Fluid Mech., 2017,814:1


[39] Maulik R, San O . A neural network approach for the blind deconvolution of turbulent flows.
[J]. Fluid Mech., 2017,831:151
[本文引用: 1]

[40] Zhou ZD, Wang SZ, Jin GD . A structural subgrid-scale model for relative dispersion in large-eddy simulation of isotropic turbulent flows by coupling kinematic simulation with approximate deconvolution method. Phys
Fluids, 2018,30:105110


[41] Maulik R, San O, Rasheed A , et al. Data-driven deconvolution for large eddy simulations of Kraichnan turbulence. Phys
Fluids, 2018,30:125109
[本文引用: 1]

[42] Jofre L, Domino SP, Iaccarino G . A framework for characterizing structural uncertainty in large-eddy simulation closures. Flow, Turb. and
Combust., 2018,100:341


[43] Wang Z, Luo K, Li D , et al. Investigations of data-driven closure for subgrid-scale stress in large-eddy simulation. Phys
Fluids, 2018,30:125101


[44] Zhou ZD, He GW, Wang SZ , et al. Subgrid-scale model for large-eddy simulation of isotropic turbulent flows using an artificial neural network
Computers & Fluids, 2019,195:104319


[45] Zhu LY, Wang WW, Kou JQ , et al. Machine learning methods for turbulence modeling in subsonic flows around airfoils. Phys
Fluids, 2019,31:015105


[46] Maulik R, San O, Rasheed A , et al. Subgrid modelling for two dimensional turbulence using neural networks.
[J]. Fluid Mech., 2019,858:122


[47] Yu M, Huang WX, Xu CX . Data-driven construction of a reduced-order model for supersonic boundary layer transition.
[J]. Fluid Mech., 2019,874:1096-1114


[48] Ma C, Wang JC, E WN. Model reduction with memory and the machine learning of dynamical systems
Commun. Comput. Phys., 2019,25(4):947-962
[本文引用: 1]

[49] Xie CY, Wang JC, Li H , et al. Artificial neural network mixed model for large eddy simulation of compressible isotropic turbulence. Phys
Fluids, 2019,31:085112
[本文引用: 5]

[50] Xie CY, Yuan ZL, Wang JC . Artificial neural network-based nonlinear algebraic models for large eddy simulation of turbulence. Phys
Fluids, 2020,32:115101
[本文引用: 2]

[51] Xie CY, Wang JC, Li K , et al. Artificial neural network approach to large-eddy simulation of compressible isotropic turbulence
Phys. Rev. E, 2019,99:053113
[本文引用: 3]

[52] Xie CY, Li K, Ma C , et al. Modeling subgrid-scale force and divergence of heat flux of compressible isotropic turbulence by artificial neural network
Phys. Rev. Fluids, 2019,4:104605


[53] Xie CY, Wang JC, Li H , et al. Spatial artificial neural network model for subgrid-scale stress and heat flux of compressible turbulence
Theoretical and Applied Mechanics Letters, 2020,10:27-32


[54] Xie CY, Wang JC, Li H , et al. Spatially multi-scale artificial neural network model for large eddy simulation of compressible isotropic turbulence
AIP Advances, 2020,10:015044


[55] Xie CY, Wang JC, E WN. Modeling subgrid-scale forces by spatial artificial neural networks in large eddy simulation of turbulence
Phys. Rev. Fluids, 2020,5:054606
[本文引用: 4]

[56] Yuan ZL, Xie CY, Wang JC . Deconvolutional artificial neural network models for large eddy simulation of turbulence
Phys. Fluids, 2020,32:115106
[本文引用: 4]

[57] Rosofsky SG, Huerta EA . Artificial neural network subgrid models of 2-D compressible magnetohydrodynamic turbulence
Phys. Rev. D, 2020,101:084024


[58] Prat A, Sautory T, Navarro-Martinez S . A priori sub-grid modelling using artificial neural networks. Int.
[J]. Comut. Fluid. Dyn., 2020, 1-21


[59] Pawar S, San O . Data assimilation empowered neural network parameterizations for subgrid processes in geophysical flows
2020, arXiv: 2006. 08901
[本文引用: 1]

[60] Samtaney R, Pullin DI, Kosovic B . Direct numerical simulation of decaying compressible turbulence and shocklet statistics
Phys. Fluids, 2011,13:1415
[本文引用: 2]

[61] Wang JC, Shi YP, Wang LP , et al. Effect of shocklets on the velocity gradients in highly compressible isotropic turbulence
Phys. Fluids, 2011,23:125103
[本文引用: 4]

[62] Wang JC, Shi YP, Wang LP , et al. Effect of compressibility on the small scale structures in isotropic turbulence.
[J]. Fluid Mech., 2012,713:588
[本文引用: 4]

[63] Wang JC, Gotoh T, Watanable T . Spectra and statistics in compressible isotropic turbulence
Phys. Rev. Fluids, 2017,2:013403
[本文引用: 1]

[64] Wang JC, Gotoh T, Watanable T . Shocklet statistics in compressible isotropic turbulence
Phys. Rev. Fluids, 2017,2:023401


[65] Wang JC, Gotoh T, Watanable T . Scaling and intermittency in compressible isotropic turbulence
Phys. Rev. Fluids, 2017,2:053401


[66] Wang JC, Wan MP, Chen S , et al. Kinetic energy transfer in compressible isotropic turbulence.
[J]. Fluid Mech., 2018,841:581
[本文引用: 2]

[67] Wang JC, Wan MP, Chen S , et al. Cascades of temperature and entropy fluctuations in compressible turbulence.
[J]. Fluid Mech., 2019,867:195-215
[本文引用: 1]

[68] Favre A . Equations des gaz turbulents compressible. I. Formes generals.
[J]. Mec. 1965,4:361
[本文引用: 1]

[69] Martin MP, PiomelliI U, Candler G,. Subgrid-scale models for compressible large-eddy simulations
Theor. Comput. Fluid Dyn., 2000,13:361
[本文引用: 3]

[70] Lilly D . A proposed modification of the Germano subgrid scale closure method
Phys. Fluids A, 1992,4:633
[本文引用: 1]

[71] Germano M . Turbulence: The filtering approach.
[J]. Fluid Mech., 1992,238:325
[本文引用: 1]

[72] Shi YP, Xiao ZL, Chen SY . Constrained subgrid-scale stress model for large eddy simulation
Phys. Fluids, 2008,20:011701
[本文引用: 1]

[73] Wang JC, Wang LP, Xiao ZL , et al. A hybrid numerical simulation of isotropic compressible turbulence.
[J]. Comp. Phys., 2010,229:5257
[本文引用: 1]

[74] Lele SK . Compact finite difference schemes with spectral-like resolution.
[J]. Comput. Phys., 1992,103:16
[本文引用: 1]

[75] Balsara DS, Shu CW . Monotonicity preserving weighted essentially nonoscillatory schemes with increasingly high order of accuracy.
[J]. Comput. Phys., 2000 160:405
[本文引用: 1]

[76] Ghosal S . An analysis of numerical errors in large-eddy simulations of turbulence.
[J]. Comput. Phys., 1996,125:187
[本文引用: 1]

[77] Meyers J, Geurts BJ, Baelmans M . Database analysis of errors in large-eddy simulation
Phys. Fluids, 2003,15:2740


[78] Chow FK, Moin P . A further study of numerical errors in large-eddy simulations.
[J]. Comput. Phys., 2003,184:366
[本文引用: 1]

[79] Hughes TJR, Mazzei L, Jansen KE . Large eddy simulation and the variational multiscale method
Comput. Visualization Sci., 2000,3:47-59
[本文引用: 1]

[80] Eyink GL . Locality of turbulent cascades
Physica D, 2005,207:91-116


[81] Aluie H, Eyink GL . Localness of energy cascade in hydrodynamic turbulence. II. Sharp spectral filter
Phys. Fluids, 2009,21:115108


[82] Aluie H . Compressible turbulence: the cascade and its locality
Phys. Rev. Lett., 2011,106:174502
[本文引用: 1]

[83] Kingma DP, Adam JBA. A method for stochastic optimization
2014, arXiv: 1412. 6980
[本文引用: 2]