胡五龙^,*,?,2), 刘国峰^?, 晏石林^?, 范严伟^***武汉理工大学绿色智能江海直达船舶与邮轮游艇研究中心, 武汉 430070
^?武汉理工大学理学院, 武汉 430070
^**兰州理工大学能源与动力工程学院, 兰州 730050

PORE-SCALE LATTICE BOLTZMANN MODELING OF SOIL WATER DISTRIBUTION¹⁾

Hu Wulong^,*,?,2), Liu Guofeng^?, Yan Shilin^?, Fan Yanwei^***Green & Smart River-Sea-Going Ship, Cruise and Yacht Research Center, Wuhan University of Technology, Wuhan 430070, China
^?School of Science, Wuhan University of Technology, Wuhan 430070, China
^**College of Energy and Power Engineering, Lanzhou University of Technology, Lanzhou 730050, China

通讯作者: 2) 胡五龙, 副教授, 主要研究方向: 环境流体力学. E-mail:wulong.hu@whut.edu.cn

收稿日期:2020-06-13接受日期:2020-12-31网络出版日期:2021-02-07

基金资助:

1) 国家自然科学基金.11602180 武汉理工大学研究生优秀学位论文培育项目.2018-YS-079 中央高校基本科研业务费专项资金资助.2020IA-0-01

Received:2020-06-13Accepted:2020-12-31Online:2021-02-07
作者简介 About authors


摘要
土壤水控制着陆地生态系统几乎所有的物理和生物化学过程,准确描述土壤中水的分布与运动状态对人类发展和生态环境保护均有重要意义.土壤水分布不仅与孔隙结构有关, 而且受土壤固相表面润湿性的影响.一般对土壤水分布都是从宏观尺度进行描述,但土壤中的物理及生化过程都发生在孔隙中, 从孔隙尺度分析土壤水的分布规律,有助于更准确地理解土壤中的各种宏观现象.本文通过X射线扫描成像技术获取两个土样的三维孔隙结构,并采用改进的Shan-Chen格子玻尔兹曼模型,模拟了在不同润湿性条件下两个土样中孔隙水分布,分析了接触角对孔隙水分布的影响, 结果表明：接触角较大时,孔隙直径对液态水和水蒸气分布影响较小, 随着接触角减小,孔隙直径对液态水和水蒸气的分布影响增大;接触角对液、气、固之间的界面面积以及流体输运通道直径也有较大影响,液体输运通道直径随接触角减小而变小, 气体输运通道直径则随接触角的减小先增大,后减小; 土壤中液态水密度随接触角变化很小,但水蒸气密度随接触角减小而显著降低; 接触角较大时,饱和度对水蒸气密度无明显影响, 接触角较小时,饱和度的增大会显著提高水蒸气的密度.
关键词： 格子玻尔兹曼;润湿性;接触角;孔隙尺度模拟;孔隙介质

Abstract
Water in soil controls almost all physical and biogeochemical processes in terrestrial ecosystems and correctly describing its distribution and flow is critical in human development and ecological environment protection. Water distribution at pore scale is modulated by a multitude of abiotic and biotic factors such as the exudates secreted by plant roots and microbes, which could alter soil wettability and water surface tension. The combined impact of all these factors can be described by a single parameter, the contact angle. Practical studies on soil water distribution normally focus on large scale using continuum approaches by volumetrically averaging the microscopic processes out, but it is the physical and biochemical processes occurring in the pores that underpin the emerging phenomena at large scales. Studying the microscopic mechanisms underlying the microscopic water distribution is hence essential to improving the understanding of macroscopic phenomena. Since it is difficult to observe the water distribution at pore-scale due to the complexity of pores structure and the opaque nature of the soils, pore-scale modelling in combination with tomography has been increasingly used to bridge this gap. In this paper, we numerically investigated how a change in the contact angle reshaped water distribution using the Lattice Boltzmann model and X-ray computed tomography. Two soils with contrasting structures were acquired using X-ray computed tomography and they were then segmented to binary images consisting of pore and solid voxels. Water distribution in pore spaces of the soils was assumed to be controlled by capillary force and was simulated using a modified two-phase lattice Boltzmann model. The results show that with the contact angle increasing, the impact of the pore diameter on water distribution in both soils waned, and that a change in the contact angle also led to a change in the channel diameter for fluid flow and interfacial areas between liquid, solid and gas. It was found that as the contact angle decreased, the channel diameter for the liquid decreased while that for the gas increased first followed by a decline. The density of the liquid water was independent of the contact angle, but the density of the vapor decreased significantly as the contact angle increased. The effects of saturation on density of the vapor also increased as the contact angle decreased.
Keywords：lattice Boltzmann;wettability;contact angle;pore-scale modelling;porous media


PDF (9023KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
胡五龙, 刘国峰, 晏石林, 范严伟. 土壤水分布的孔隙尺度格子玻尔兹曼模拟研究¹⁾. 力学学报[J], 2021, 53(2): 568-579 DOI:10.6052/0459-1879-20-198
Hu Wulong, Liu Guofeng, Yan Shilin, Fan Yanwei. PORE-SCALE LATTICE BOLTZMANN MODELING OF SOIL WATER DISTRIBUTION¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(2): 568-579 DOI:10.6052/0459-1879-20-198

引言

土壤是人类、植物及微生物维持生命活动所需水分及营养物质的重要来源^[1]; 同时也是生态循环的主要组成部分^[2]. 水在土壤孔隙中的分布直接影响土壤中物质, 包括水、空气及其他有机或无机物质的存储及传输^[3], 并对土壤中微生物的活动范围及强度有着决定性的影响^[1].

土壤中水分分布一直广受农业、环境、生态等领域研究人员的关注, 并在不同角度不同尺度得到了大量的研究. 例如周启友和岛田纯^[4]通过野外观测及反演计算, 探讨了土壤水在空间分布的非均质性及各向异性. 张常亮等^[5]通过对天然降雨入渗后黄土中不同深度土层体积含水率为期一年的监测数据进行分析, 确定了黄土地区降雨入渗深度及浸润线以下水分迁移特点. 杜娟等^[6]采用野外观测手段研究了沙漠不同地形下土壤中水分时空变化特征, 发现土壤渗透性与孔隙结构、有机质及水分分布有密切关系. 这些研究加深了人们对土壤水分时空分布变异性及复杂性的理解, 但大部分研究都是对宏观现象的描述, 土壤中的所有物理过程及生化反应都发生在孔隙中, 从孔隙尺度模拟非饱和土壤中水及溶质的分布, 有助于对土壤中各过程和反应的理解.

土壤一般为非饱和状态, 土壤中水的运动实际是复杂的多相流, 在相当长时间内, 对于土壤水问题一直停留在定性描述或采用各种经验方法处理的层面上^[7]. 自1856年Darcy^[8]在大量实验的基础上提出达西定律, 1907年Buckingham^[9]提出毛管势理论, 到1931年Richard^[10]在达西定律的基础上推导出用于描述非饱和流的方程, 土壤水运动理论模型逐步建立起来. 此后土壤水运动研究的关注点转移到了基本方程的求解, 而其中的关键之一是土壤水分特征参数的确定, 1964年Brooks和Corey^[11]建立了饱和度、压力梯度及水力特性之间的关系, 并提出利用毛管压力-饱和度曲线来确定水力特性的方法; van Genuchten^[12]提出了估算非饱和土壤水力特征的半经验公式, 该公式后来成为了描述土壤水力特性的主要公式之一. 还有一些其他方法, 包括转换函数和神经网络等也被用于土壤水力特征及土壤水运动的研究中^[13-14]. 国内邵明安等^[15-16]也在土壤水运动、水力特征参数测量与计算方面做了大量的基础研究工作. 2019年Jin等^[17]在前人模型基础上, 将薄膜流模型和毛管流模型进行整合, 提出了一种可以描述全饱和度区间土水特征曲线的分形模型. 以上这些模型对于理解和模拟土壤中水的分布起到了非常关键的作用, 但此类模型及其参数都是土壤宏观特征的平均表征, 直接从孔隙尺度研究水在每个孔隙中的具体形态和分布, 有助于理解影响水分分布的因素及其作用机理, 并改进宏观模型. 早期的孔隙尺度模拟方法是将真实的土壤孔隙结构简化为由不同形状和尺寸的毛细管道组成的毛管束^[18], 或简化为由不同孔隙空间和喉道组成的孔隙网络^[19], 然后基于这些毛管束或孔隙网络模型模拟孔隙管道中的流体运动. 毛管束模型和孔隙网络模型为研究土壤中的物质输运和化学过程提供了很大帮助^[20-22], 但其无法反映土壤的真实孔隙结构和连通特征, 因此其在模拟土壤结构和水力特征方面往往存在较大误差^[23].

显微成像技术, 尤其是X射线断层扫描技术(X-CT)的发展, 使直接观测土壤中微纳米尺度物质及孔隙分布成为了可能^[24]. 但目前的X-CT和图像处理技术仍很难辨别土壤中的水和空气, 更难直接观测土壤中的动态过程^[25-26], 因此仍需要结合孔隙尺度模拟方法来研究土壤中的流体动力学问题. 利用X-CT获取土壤的真实三维孔隙结构, 结合计算流体力学(CFD)方法可直接模拟流体物质在孔隙中的运动. 直接孔隙尺度模拟中常用的CFD方法主要包括基于粒子的格子玻尔兹曼方法^[27-28](LBM)和光滑粒子动力学方法^[29](SPH), 以及基于网格的水平集方法^[30] (Level Set)、流体体积法^[31](VOF)以及有限体积法^[32](FVM)等. 这些CFD方法在模拟孔道中流动问题方面各有优劣势^[33], 其中LBM因其在处理复杂边界及多相流方面具有天然优势, 并且方便并行化计算, 近年来得到了迅速发展^[34-37]. 目前应用的LBM多相流基本模型主要有三种：颜色函数模型^[38-39]、自由能模型^[40-41]和 Shan-Chen伪势模型^[42-44], 本文选用伪势模型进行模拟研究. 伪势模型通过引入伪势来描述流体粒子之间的相互作用, 具有较好的物理意义, 并且易于程序实现, 因此得到了较广泛的应用. 但该模型缺少热力学一致性, 在模拟大密度比的多相流时容易造成数值不稳定, 虽然通过改进状态方程和力项, 使模型适用的密度比有了很大的提升^[43], 但是在模拟真实的复杂孔隙结构中多相流时仍非常困难, 尤其是对于孔隙直径分布广且微孔较多的孔隙结构.

土壤作为强非均匀性的多孔三相系统, 具有从纳米尺度至毫米尺度丰富的孔隙结构, 而土壤中的物理及生化反应都发生在孔隙壁面, 即液-固或气-固界面处. 接触角反映了土壤固相的润湿性, 控制着土壤孔隙中水的状态及分布. 最近研究表明植物根系分泌物^[45]、微生物活动产物^[46]及有机物^[47]会改变土壤颗粒表面的润湿性, 并进而影响土壤孔隙中的水分分布. 流体与固体壁面的接触角通常都采用实验方法测得, 但是对于结构复杂的多孔介质, 通过实验观测流体在孔隙内的流动非常困难. 利用LBM孔隙尺度模拟流体接触角是一种简便可行的办法, 自Briant^[48]于2004年提出利用LBM来模拟多相流体的接触线运动, 此后LBM被经常用于流体接触角研究, 尤其是模拟液滴在材料表面的行为. 张博^[49]将LBM应用于材料领域, 分析了液滴润湿行为与材料表面微纳结构的关系. 方可宁等^[50]利用LBM对加热基板上的液滴进行模拟, 研究了不同接触角液滴的铺展及蒸发过程. 胡梦丹等^[51]采用LBM对结构表面液滴的冷凝行为进行模拟研究, 分析了材料表面的几何尺寸和接触角的局部不均匀性对冷凝液滴形核位置及最终润湿状态的影响规律. 这些研究都是通过LBM方法模拟液滴在材料表面或简单管道中的运动状态, 鲜见针对真实三维孔隙结构中多相流的模拟, 更无对土壤中孔隙水受接触角影响的模拟研究.

本文采用改进的Shan-Chen格子玻尔兹曼模型, 直接模拟了不同接触角情况下水分在土壤孔隙中的分布, 探讨了接触角对孔隙水分分布状态的影响, 以期为进一步模拟土壤中流体运动及物质迁移提供基础, 并为土壤水资源研究及优化农业生产提供理论指导.

1 格子玻尔兹曼方法

在格子玻尔兹曼模型中, 流体的运动被描述成一系列离散的单密度分布函数. 标准的格子玻尔兹曼方程可表示为^[52]

(1)$\begin{eqnarray} \label{eq1} &&f_{i} ({ x}+c{ e}_{i} \Delta t,t+\Delta t)-f_{i} \left( {{ x},t} \right) = \\&&\qquad -\frac{\Delta t}{\tau }\left[ {f_{i} \left( {{ x},t} \right)-f_{i}^{\rm eq} \left( {{ x},t} \right)} \right]+{ F}_{i} ({ x},t) \end{eqnarray}$
其中$f_{i} ( x, t)$为流体粒子密度分布函数, $i$表示速度离散方向; $f_{i}^{\rm eq}$ ($ x, t)$为平衡态分布函数; $\tau $为无量纲松弛时间; $c=\Delta x$/$\Delta t$, 为流体粒子的格子速度; $\Delta x$ 和$\Delta t$分别为格子尺寸和格子时间步长, 一般取1. $ F ( x, t)$为流体粒子受到的作用力, 一般包括流流作用力$ F_{\rm int}$ ($ x, t)$、流固作用力$ F_{\rm s} ( x, t)$以及其他外体力$ F_{\rm b} ( x, t)$. 由于土壤中水受到的基质吸力远大于重力, 因此本文研究中忽略了重力影响.

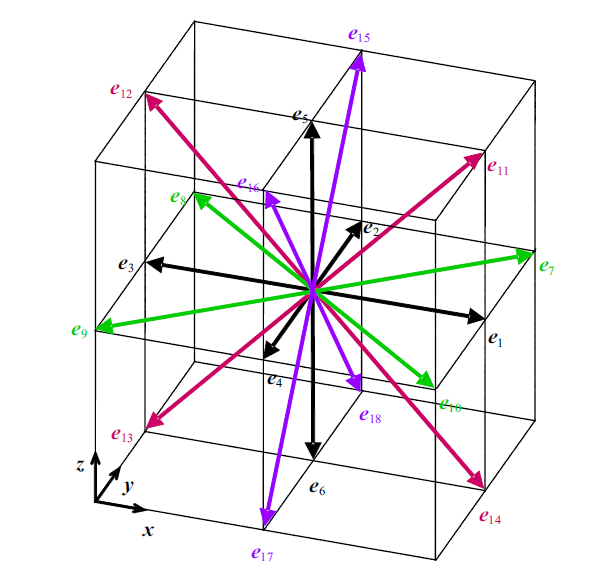
本文采用D3Q19格式, 即将粒子速度在空间上按照19个方向进行分解, 如图1所示. 离散后$i$方向的速度$ e_{i}$可表示为^[53]

(2)$\begin{eqnarray} \label{eq2} &&{ e}_{i}\! =\!\left\{ {\begin{array}{ll} (0,0,0),&i=0 \\ (\pm 1,0,0),(0,\pm 1,0),(0,0,\pm 1),&i=1,2,\cdots,6 \\ (\pm 1,\pm 1,0),(\pm 1,0,\pm 1),(0,\pm 1,\pm 1),& i=7,8,\cdots,18 \\ \end{array}} \right.\\&& \end{eqnarray}$
平衡态分布函数$f_{i}^{\rm eq}$ ($ x, t)$为麦克斯韦-玻尔兹曼分布的展开, 可表示为^[54]

(3)$\begin{eqnarray} \label{eq3} f_{i}^{\rm eq} ({ x},t)=w_{i} \rho \left[ {1+3({ e}_{i} \cdot { u})+\frac{9}{2}({ e}_{i} \cdot { u})^{2}-\frac{3}{2}{ u}^{2}} \right] \end{eqnarray}$
$\rho $和$ u$分别表示格点处的宏观密度和速度; $w_{i}$为权重系数, 在D3Q19格子系统中取^[53]

(4)$\begin{eqnarray} \label{eq4} w_{i} =\left\{ {\begin{array}{l@{\quad }l} 1/3,&i=0 \\ 1/18,& i=1,2,\cdots,6 \\ 1/36,& i=7,8,\cdots,18 \\ \end{array}} \right. \end{eqnarray}$
流体密度$\rho $和速度$ u$可通过流体粒子分布函数的一阶矩和二阶矩求得

(5)$\begin{eqnarray} \label{eq5} \rho =\sum\limits_{i=0}^{18} {f_{i} } \end{eqnarray}$
(6)$\begin{eqnarray} \label{eq6} \rho { u}=\sum\limits_{i=0}^{18} {{ e}_{i} f_{i} } \end{eqnarray}$
对应的流体运动黏度为$\upsilon = c_{\rm s}^{2}(\tau - 0.5)\Delta t$; $c_{\rm s}$为格子声速, 取$c_{\rm s}= 1/\sqrt{3}$.

图1

新窗口打开|下载原图ZIP|生成PPT
图1D3Q19 LBM速度离散模型示意图

Fig.1Schematic sketch of LBM discrete velocities in the D3Q19 scheme

1.1 流流作用力

在Shan-Chen模型中, 流体粒子之间的相互作用力可表示为^[55]

(7)$\begin{eqnarray} \label{eq7} { F}_{\rm int} ({ x},{ {x}'})=-G(\left| {{ x}-{ {x}'}} \right|)\psi ({ x})\psi ({ {x}'})({ {x}'}-{ x}) \end{eqnarray}$
其中$\psi $为伪势函数, 或称有效质量, 是流体密度的函数; $G$为格林函数, 表征流流粒子间相互作用力强度, 控制液、气相的分离及液气界面的表面张力, $G<0$表示流体粒子相互吸引. 对于D3Q19模型, 格林函数为^[56]

(8)$\begin{eqnarray} \label{eq8} G(| {{ x}-{ {x}'}} |)=\left\{ {\begin{array}{l@{\quad}l} g,& \left| {{ x}-{ {x}'}} \right|=1 \\ g/2,& \left| {{ x}-{ {x}'}} \right|=\sqrt 2 \\ 0,& \mbox{otherwise} \\ \end{array}} \right. \end{eqnarray}$
$g$为流流作用力强度系数. $ x$位置处的流体粒子受到周边流体粒子作用力的合力为^[55]

(9)$\begin{eqnarray} \label{eq9} { F}_{\rm int} ({ x})=-g\psi ({ x})c_{\rm s}^{2} \sum\limits_{i=0}^{18} {w\left( {\left| {{ e}_{i} } \right|^{2}} \right)} \psi ({ x}+{ e}_{i} ){ e}_{i} \end{eqnarray}$
其中$w$ ($|e_{i}|^{2}$)为权重系数, 对于D3Q19模型^[57]

(10)$\begin{eqnarray} \label{eq10} w\left( {\left| {{ e}_{i} } \right|^{2}} \right)=\left\{ {\begin{array}{l@{\quad }l} 1/6,& i=1,2,\cdots,6 \\ 1/12,&i=7,8,\cdots,18 \\ \end{array}} \right. \end{eqnarray}$

1.2 流固作用力

流体粒子与固相的流固作用力用下式表示^[55]

(11)$\begin{eqnarray} \label{eq11} { F}_{\rm s} ({ x})=-g_{\rm s} \psi ({ x})\sum\limits_{i=0}^{18} {w\left( {\left| {{ e}_{i} } \right|^{2}} \right)\psi (\rho_{\rm w} )s({ x}+{ e}_{i} )\cdot { e}_{i} } \end{eqnarray}$
式中$g_{\rm s}$为流固作用系数, 表征流体粒子与固相之间的作用力强度. 在有固相的LBM中, $g$与$g_{\rm s}$共同决定液固的本征接触角, 但在本文, 由于对模型进行了改进, 采用的Peng-Robinson(P-R)状态方程, 最终接触角仅依赖于$g_{\rm s}$. $s$ ($ x+ e_{i})$为标示函数, 当($ x+ e_{i})$为固相时, $s$ ($ x+ e_{i}) = 1$; 当($ x+ e_{i})$为流体时, $s$ ($ x+ e_{i}) = 0$; $\psi (\rho_{w})$取固定值1.

1.3 模型改进

在Shan-Chen模型中, $ F_{\rm int}( x) \cong -c_{0}\psi ( x)g\nabla \psi ( x)$对应的状态方程为$p = \rho c_{\rm s}^{2}+ 0.5c_{0}g\psi^{2}$, 伪势函数可表示为

(12)$\begin{eqnarray} \label{eq12} \psi =\sqrt {\frac{2(p-\rho c_{\rm s}^{2} )}{gc_{0} }} \end{eqnarray}$
其中$c_{0}$为常数, 对于D3Q19模型, $c_{0}=$6 ^[53].

很多研究已经表明, 原始的Shan-Chen模型不适用于密度比大的多相流体. 而实际上, 无论是水和水蒸气还是油与气, 其密度比都达到好几百甚至上千. 采用接近真实流体的状态方程可以大幅度提高LBM适用的密度比, 本文采用P-R状态方程, 改进后模型实现的最大密度比超过7000.

P-R状态方程为

(13)$\begin{eqnarray} \label{eq13} p=\frac{\rho RT}{1-b\rho }-\frac{a\alpha (T)\rho^{2}}{1+2b\rho -b^{2}\rho ^{2}} \end{eqnarray}$
$\alpha (T) = \{1 + (0.374 64 + 1.542 26\omega - 0.269 92\omega^{2})\times[1 - (T / T_{\rm c})^{0.5}]\}^{2}$, $\omega $为偏心因子, 对于水, $\omega = 0.344$; $T$为温度, $T_{\rm c}$为临界温度; $a =0.457 24R^{2}T_{\rm c}^{2}/p_{\rm c}$, $b = 0.077 8 RT_{\rm c}/p_{\rm c}$. 本文计算中取$a =1/49$, $b= 2/ 21$^[43].

为减小模型计算中产生的伪流, 提高稳定性, 将流体粒子间作用力改写为

(14)$\begin{eqnarray} \label{eq14} && { F}_{\rm int} ({ x})=-\lambda \frac{g}{2}c_{\rm s}^{2} \sum\limits_{i=1}^{18} {\omega (\left| {{ e}_{i} } \right|^{2})\psi ^{2}({ x}+{ e}_{i} ){ e}_{i} } -\\&&\qquad \frac{1-\lambda }{2}g\psi ({ x})c_{\rm s}^{2} \sum\limits_{i=1}^{18} {\omega (\left| {{ e}_{i} } \right|^{2})\psi ({ x}+{ e}_{i} ){ e}_{i} } \end{eqnarray}$
在引入作用力时采用精确差分法 (EDM), 此时, 外力项为

(15)$\begin{eqnarray} \label{eq15} { F}_{i} ({ x},t)=f_{i}^{\rm eq} \left( {\rho ,{ {u}'}} \right)-f_{i}^{\rm eq} \left( {\rho ,{ u}} \right) \end{eqnarray}$
其中$ u$通过式(6)求得, 而$ u' = u + F\Delta t / \rho $. EDM方法可以提高模型的热稳定性, 结合以上方法, 该LBM可模拟的最低温度达0.4$T_{\rm c}$.

2 材料及土样

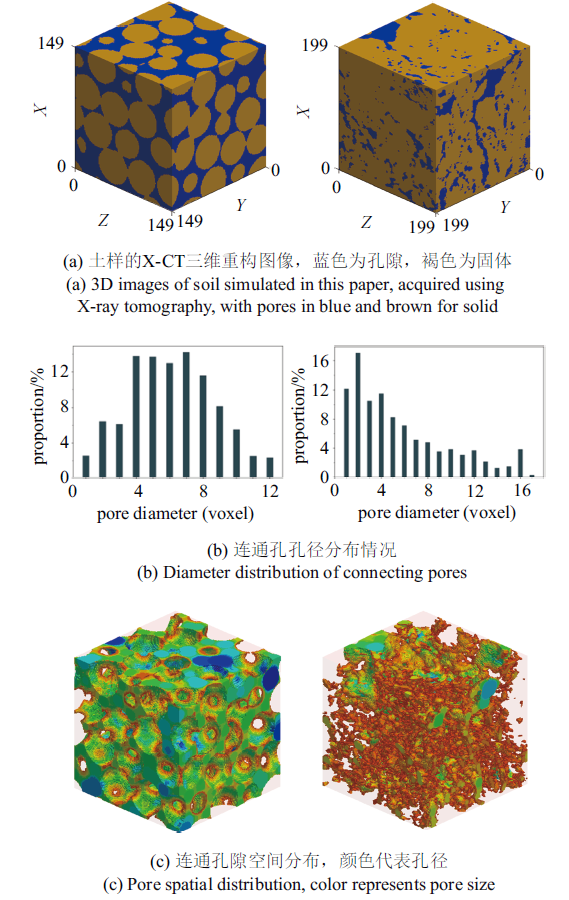
本文选取两个多孔材料的X-CT图像作为模拟对象, 如图2所示, 其中模拟土样是由微小玻璃珠粘结而成, 孔隙结构相对比较均匀, 尺寸为150$\times$150$\times$150像素 (voxel), 像素分辨率为40 $\mu $m, 孔隙率为0.368 1, 后文用土样1表示; 真实土样为2015年取自英国洛桑实验站的Highfield草地试验田 (51.810 3N, $-$0.374 8E), 该试验田为粉质黏壤土, 其基本理化性质见文献[58]表1中的Grassland, 后文用土样2表示. 土样2的提取过程如下：将田间提取的土壤样芯振碎, 然后分别过孔径为4 mm, 2 mm和0.71 mm的筛子, 随机挑选0.71$\sim$2 mm的团聚体, 再将挑选的团聚体通过Phoenix Nanotom扫描系统进行X-CT扫描, 扫描电压和电流分别为90 kV和65 $\mu $A, 分辨率为1.51 $\mu $m. 拍摄曝光时间为500 ms, 整个土样扫描时间为69 min, 共获取1440张投影图片. 利用扫描系统配套的软件Phoenix datos\textbar x2将投影图片重构为三维图像, 并导出三维图像的原始连续切片图, 然后利用开源软件ImageJ (https://imagej.nih.gov/ij/)将图片进行二值化处理, 土样2的详细获取及处理过程见文献[58]. 由于获得的土样初始图像较大, 为减少计算量, 截取200$\times$200$\times$200像素的立方体作为本文研究的土样2 (如图2), 其孔隙率为0.232 5. 为便于分析, 本文中所有物理量包括长度、密度等均直接采用格子单位, 其都可以转换成实际的物理单位, 1 lu = 1 voxel (lu为格子单位).

图2

新窗口打开|下载原图ZIP|生成PPT
图2两个土样的三维结构: 左边是模拟土样(土样1),右边是真实土样^[58] (土样2)

Fig.2Three dimensional structure of two soils used in the simulations, the artificial soil shows in left column and real soil shows in right



Table 1
表1
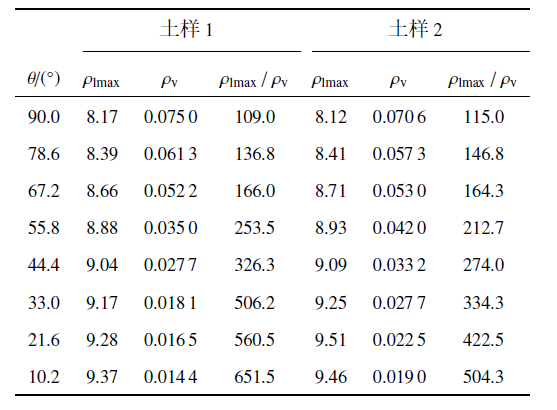
表1不同$\theta $两个土样中水分密度分布
Table 1Density of liquid and vapor water in two soils under different $\theta $

新窗口打开|下载CSV

假定水只在连通孔隙中流动, 为减少模拟中的计算量和所需内存, 计算前先提取连通孔隙, 并采用形态模型^[59]计算每个孔隙的直径. 两个土样的连通孔隙结构分别如图2所示, 土样1的平均孔径为6.12像素, 土样2的平均孔径为5.68像素. 由图可以看出两个土样的孔隙结构有明显差异, 其中土样1连通孔隙率为0.368, 孔径分布为正态分布, 而土样2连通孔隙率为0.221, 孔径分布近似泊松分布.

3 计算结果及讨论

3.1 接触角计算

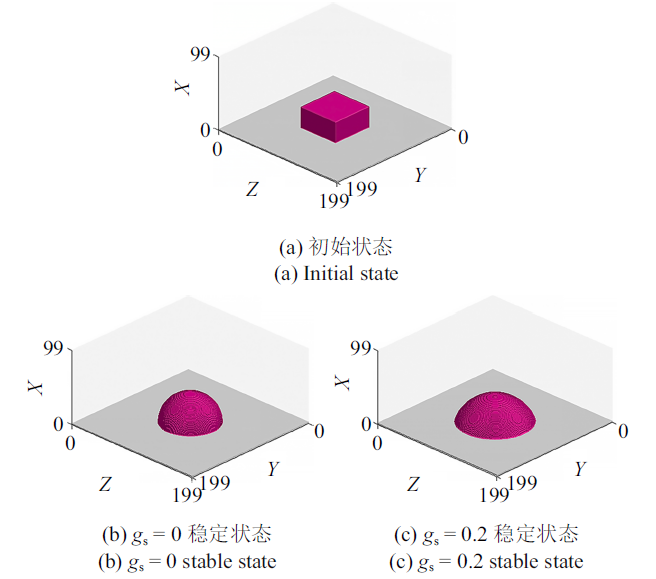
研究表明大部分土壤既不是完全亲水的, 也不是疏水的, 即接触角在0$^\circ$$\sim$90$^\circ$ 范围内变化^[47,60]. 在微生物或植物根系的作用下, 土壤与水的接触角会发生变化, 但仍属于亲水物质, 因此本文只研究接触角小于等于90$^\circ$的情况.

假定式 (10) 中$\psi (\rho ) = 1$, 改变$g_{\rm s}$的值, 即可获得不同的接触角. 为获取接触角与$g_{\rm s}$之间的关系, 先模拟一个水滴在固体平面上的稳定状态. 如图3(a)所示, 构建一长宽高($XYZ$)分别为200 lu $\times$ 200 lu$\times$100 lu的空间, 下边界设置2 lu厚的固体平面, 其他边界均设置为周期边界, 固体壁面采用反弹边界条件. 系统恒温, 温度设置为$T = 0.7T_{\rm c}$, $T_{\rm c}$为临界温度. 初始时刻在固体平面中央放置一长宽相等有一定高度的方体液滴, 密度为$\rho_{\rm l0}$; 其余空间为水蒸气, 密度为$\rho_{\rm v0}$, 如图3(a). 每1000次迭代计算输出一次结果, 当两次输出的液态水体积分数变化小于10$^{-7}$时, 则认为水的空间分布已经达到稳定状态. 设液态水与水蒸气的临界密度$\rho_{\rm c}= (\rho_{\rm l0} + \rho_{\rm v0})/2$, 图3(b)和图3(c)为稳定后的液态水在平面上的形态.

图3

新窗口打开|下载原图ZIP|生成PPT
图3水滴在固体平面上的状态变化

Fig.3The state of liquid water on a solid plane



液滴达到稳定状态后, 测量液滴的高度$h$、液滴与固体平面接触面直径$d$, 则接触角$\theta $可通过下式计算得出

(16)$\begin{eqnarray} \label{eq16} &&r=\frac{4h^{2}+d^{2}}{8h} \end{eqnarray}$
(17)$\begin{eqnarray} \label{eq17} \theta =\left\{ {\begin{array}{l@{\quad }l} \arcsin \lt(\dfrac{d}{2r}),&\theta \leqslant 90^{\circ} \\ \pi -\arcsin \lt(\dfrac{d}{2r}),&\theta >90^{\circ} \\ \end{array}} \right. \end{eqnarray}$
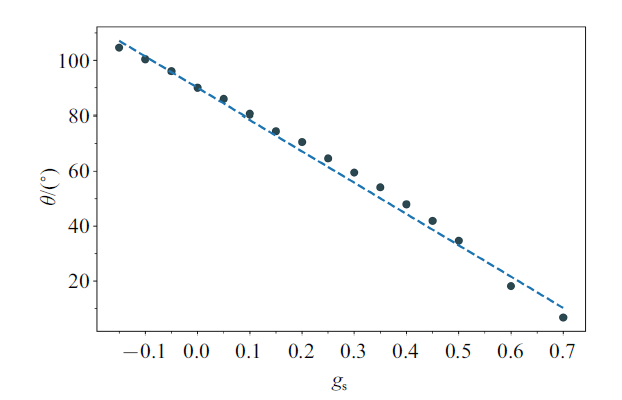
计算得到的接触角$\theta $与$g_{\rm s}$值如图4所示, 其关系可用直线$\theta =-114g_{\rm s}+ 90^\circ$近似表示, 假设土壤中水的接触角$\theta $与$g_{\rm s}$也服从此规律, 则后文中接触角$\theta $均可由$g_{\rm s}$依据此公式求得. 土壤孔隙中的流体接触角不仅与固液气相互作用及液体表面张力有关, 还受孔隙直径、壁面粗糙度的影响, 但对于同一土样, 其固体组分及内部孔隙结构不变, 流体接触角仅随$g_{\rm s}$而改变, 因此以上假设不会影响本文的研究.

图4

新窗口打开|下载原图ZIP|生成PPT
图4$T = 0.7T_{\rm c}$时液滴与光滑固体平面接触角$\theta $与$g_{\rm s}$的关系

Fig.4Relationship between contact angle $\theta $ of droplet on smooth solid plane and $g_{\rm s}$ under temperature $T = 0.7T_{\rm c}$

3.2 接触角对土壤水分布的影响

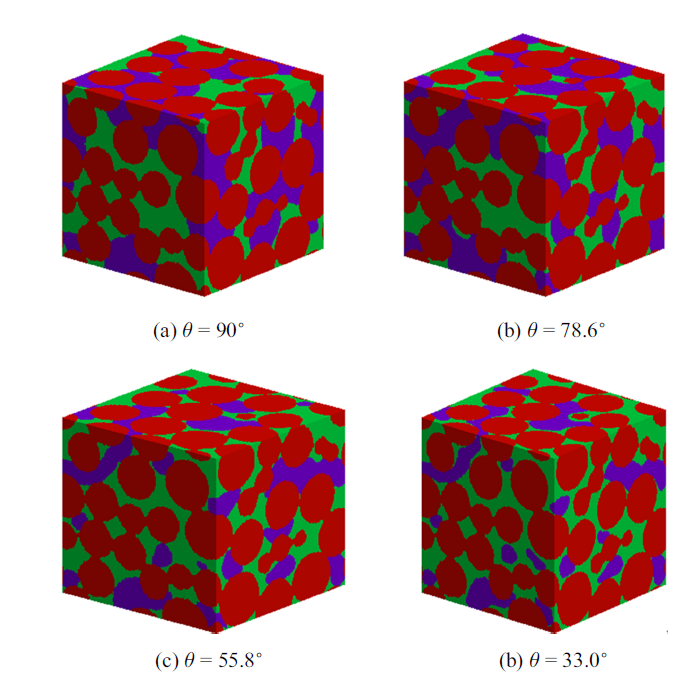
假定土壤孔隙中的水分布由毛管压力$p\propto \cos\theta\cdot\sigma/d$控制, 其中$\sigma$为气水表面张力, $\theta$为接触角, $d$为孔隙直径. 对于给定的接触角和表面张力, 每个孔都对应一毛管压力. 假定土样的底面与水液压相连, 并施加吸力$p$, 在毛管压力与吸力$p$的共同作用下, 水就会进入土样中毛管压力小于$p$且连通的孔隙^[59]. 依据上述方法对土样1设置初始水分分布, 然后模拟不同$\theta$情况下水分在土样中的运动及重分布, 土样1的初始饱和度约为0.35. 模拟中土样的所有边界均设置为周期边界, 固体壁面采用反弹边界条件. 温度$T=0.7T_{\rm c}$, 每迭代计算1000次输出一次结果, 当两次输出的液态水体积分数变化小于10$^{-7}$时, 则认为此时刻土样孔隙中的水分分布已经达到稳定状态. 土样1在不同$\theta $情况下的水分布如图5所示. 在不考虑重力的情况下, $\theta =90.0^\circ$ 时, 液态水和水蒸气分散分布于土壤的所有孔隙, 与孔隙直径无关. 随着$\theta $减小, 液态水的分布逐渐转移到固体土颗粒附近, 紧密围绕固体土颗粒, 形成水膜.

图5

新窗口打开|下载原图ZIP|生成PPT
图5不同$\theta$情况下土样1孔隙中液态水及水蒸气的分布: 红色为固体土颗粒, 绿色为液态水, 紫色为水蒸气

Fig.5Distribution of liquid and vapor water in soil 1 under different contact angles $\theta $, with solid in red, liquid in green and vapor in purple



图6展示了不同$\theta $, 水蒸气在土样1中的分布. 当$\theta =90.0^\circ$时, 水蒸气的分布图像棱角尖锐, 即水蒸气在大孔隙与小孔隙中均有分布, 说明接触角接近90.0$^\circ$ 时, 土壤固体壁面的表面自由能较低, 对液态水的吸引力较弱; 此时土壤中的毛管吸力几乎为零, 孔隙中水的基质势为零. 随着$\theta $减小, 水蒸气的分布图像棱角逐渐变得圆滑, 即水蒸气逐渐被挤出小孔隙, 说明随着接触角减小, 固体壁面对液态水会产生较大的吸引力, 导致液态水会迅速填充孔径较小的孔隙, 并排挤出气态水, 使水蒸气在大孔隙中汇集形成气泡; 土壤中的毛管吸力随接触角减小而增大, 此时孔隙水由于土壤固相的吸附产生负的基质势, 并且其值随接触角减小而减小.

图6

新窗口打开|下载原图ZIP|生成PPT
图6不同$\theta $时水蒸气在土样1中的分布

Fig.6Spatial distribution of vapor (red) in simulated soil under different contact angles $\theta$; the voxels of solid and liquid were made transparent



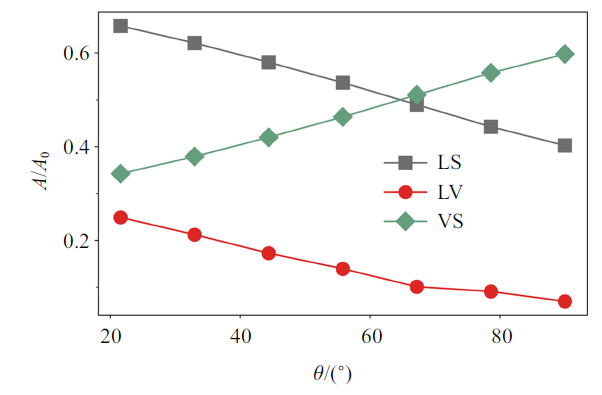
土壤中的物理及生化过程都发生在界面处, 因此在研究土壤中水分布时需要进一步分析流体与固体以及流体与流体之间的界面面积. 接触角会影响液态水与空气的分布, 也必然会影响液固、气固及液气界面面积. 为此对土样1中不同接触角情况下的液固 (LS)、气固 (VS) 及液气 (LV) 界面面积 ($A)$ 进行统计, 为研究方便, 对所有界面面积$A$均除以土样的固相总表面积$A_{0}$进行无量纲化. 结果如图7所示, LS和LV的面积均随$\theta $增大而减小, 而VS的面积随$\theta $增大而增大.

图7

新窗口打开|下载原图ZIP|生成PPT
图7土样1中液固(LS)、气固(VS)及液气(LV)界面面积($A/A_{0})$ 随$\theta$ 的变化

Fig.7Changes of interface area ($A/A_{0})$ in soil 1 with contact angle $\theta$



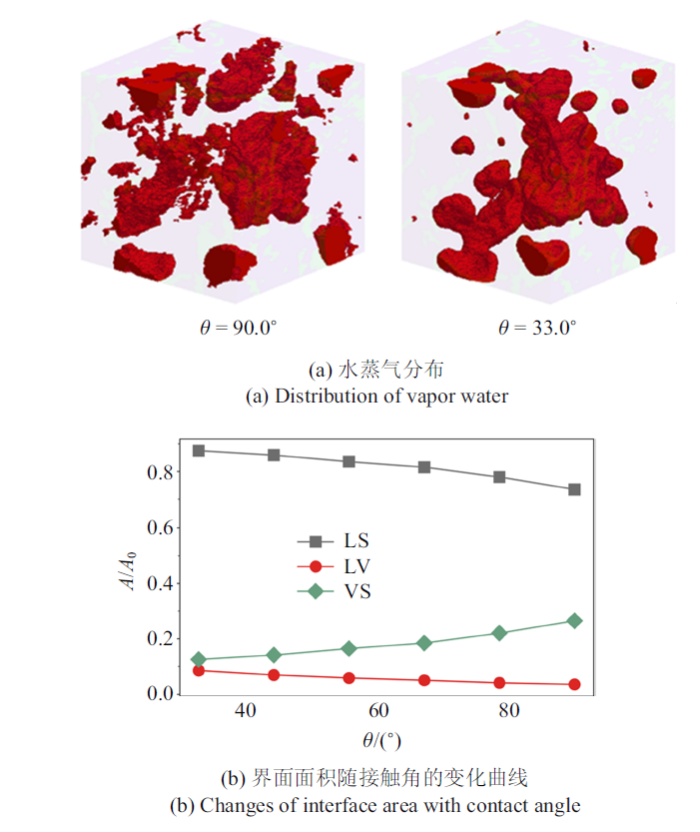
为验证以上规律对其他土样是否也成立, 选用一个孔隙结构与土样1相差较大且非均匀性强的土样2 (如图2), 按照前面的方法模拟饱和度约为0.60时, 不同$\theta $情况下土样中液态水及水蒸气的分布. 结果与土样1一致, 如图8所示, 在土样2中, 随着接触角减小, 液态水进入贴近土壤固相表面的小孔隙, 并沿着固相表面扩展形成水膜; 气态水逐渐被挤入大孔隙形成气泡; 液态水的表面面积随$\theta $减小而增大, 而水蒸气与固体的界面面积随$\theta $减小而减小. 由图7与图8(b)对比发现, 虽然两个土样中LS, LV及VS随$\theta $变化规律相同, 但土样1中的曲线变化明显比土样2的更显著, 这是由于土样1饱和度较低, 在$\theta $较大时, 大部分小孔隙仍未被液态水填充, LS界面面积小于VS界面面积; 随着$\theta $减小, 液态水进入小孔隙, 导致LS界面面积显著增大, 而VS界面面积减小. 土样2中孔隙结构非均匀性很强, 有非常多的小孔隙, 但由于土样2的饱和度较高, 大部分小孔隙在$\theta$较大时就已被液态水填充, 因此LS及VS界面面积随$\theta $变化较小.

图8

新窗口打开|下载原图ZIP|生成PPT
图8土样2的验证结果

Fig.8Verification results of soil 2

3.3 接触角对物质输运通道直径的影响

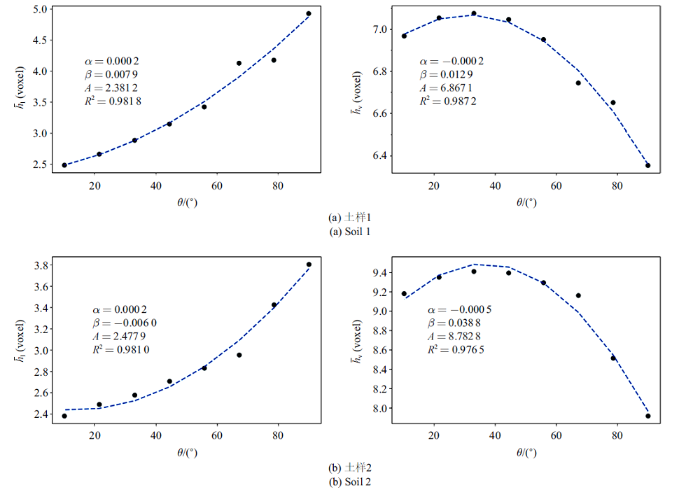
由式 (17) 可知接触角由液滴在固体表面的厚度($h)$和接触面直径($d)$决定, 其中$d$影响液固和气固界面面积; 而$h$决定液态水和水蒸气的厚度, 在三维孔隙结构中即为液态水和水蒸气占据的孔隙直径, 后文中直接简称液态水或水蒸气厚度, 用$h_{\rm l}$和$h_{\rm v}$表示. 若将土壤中液态水看作水及溶质运移的通道, 而将水蒸气看作气体输运的通道, 则$h_{\rm l}$和$h_{\rm v}$实际分别是土壤中液体和气体的输运通道直径. 采用前面提到的计算孔隙直径的方法, 分别计算$h_{\rm v}$和$h_{\rm l}$. 在不同$\theta $, 土样1中液态水的平均厚度$\bar{h}_{\rm l}$均随$\theta $减小而减小, 而$\bar{h}_{\rm v}$则均随$\theta $减小先增大后减小, 如图9(a)所示. 这是由于随着$\theta $减小, 水优先填充小孔隙, 积聚在大孔隙中的液态水沿着土壤固相表面扩展, 形成水膜, 液态水的厚度$h_{\rm l}$减小, $h_{\rm v}$则相应增大; 但是当$\theta $减小到一定程度后, 液态水充满所有小孔隙, 并且逐渐浸润了大孔隙的固相表面, 使原来在大孔隙中与土壤固相接触的水蒸气脱离固相表面, 形成游离在液态水中的气泡, $h_{\rm v}$减小. 对于土样1, $\bar{h}_{\rm l}$和$\bar{h}_{\rm v}$均可以用公式$\bar{h}=\alpha \theta^2+\beta \theta+A$进行拟合, 两个土样的拟合结果如图9(a)中曲线, 拟合参数值如图9所示, 参数$\alpha$, $\beta$值与土壤的孔隙结构及饱和度有关. 为验证以上规律与土壤孔隙结构无关, 又计算了土样2中不同$g_{\rm s}$的$h_{\rm l}$和$h_{\rm v}$, 结果如图9(b)所示. 在土样2中, $h_{\rm l}$和$h_{\rm v}$随$\theta $的变化规律与土样1相同, $\bar{h}_{\rm l}$和$\bar{h}_{\rm v}$也可以拟合为二次多项式.

图9

新窗口打开|下载原图ZIP|生成PPT
图9液态水及水蒸气通道平均直径随$\theta $的变化

Fig.9Changes of channel diameter for liquid water and vapor with $\theta $

3.4 水分密度分布

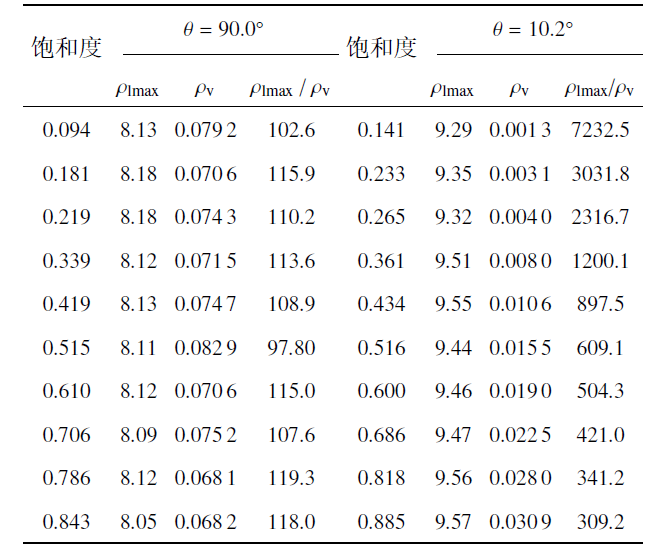
土壤中同时存在液态水和水蒸气, 在干旱半干旱地区, 土壤中水蒸气的作用尤为重要, 水蒸气的密度直接关系着土壤中水分含量. 为分析接触角对水蒸气密度的影响, 将不同$\theta $下土样1中水分密度分布进行统计, 结果如表1. 在土样1中, 紧贴土壤固相表面的液态水密度最大. 在饱和度一定的情况下, 随着接触角减小, 固体对流体的吸引力增强, 使得土粒表面的液态水由自由水向结合水转变, 流体势能降低. 最靠近土粒表面的为强结合水, 其密度$\rho_{\rm lmax}$随$\theta$减小而增大, 但增大幅度较小; 由于吸引力增强, 靠近土粒表面的一部分水蒸气会被土粒吸附变成液态水, 导致水蒸气密度$\rho_{\rm v}$随$\theta $减小显著减小, 因此两相流体的密度比$\rho_{\rm lmax}$/$\rho_{\rm v}$随$\theta $减小而迅速增大. 这说明接触角对土壤孔隙中水蒸气的密度有很大影响. 侧面反映土壤中微生物和植物根系可以通过分泌物提高附近土壤固相的润湿性, 减小水在土壤中的接触角, 吸附孔隙中的水蒸气, 增大液态水的含量, 导致土壤中水蒸气含量比周边土壤低, 从而达到吸取周边水分的目的. 为验证以上分析的正确性, 另外计算了不同$\theta$下土样2中液态水与气态水的密度, 结果如表1所示, 其规律与土样1一致.

为进一步分析土壤中水分密度分布随饱和度的变化, 对两个土样在不同饱和度的水分密度分布进行了统计, 表2列出了$\theta = 90.0^\circ$ 和$\theta =10.2^\circ$ 时土样2的水分密度分布情况. 由表2可以看出, 饱和度对土壤中液态水的最大密度并无影响. $\theta = 90.0^\circ$ 时,饱和度对水蒸气密度无明显影响, 但$\theta = 10.2^\circ$ 时, 饱和度的增大会显著提高水蒸气的密度, 降低土壤中液相与气相密度之比. 土样1中水分密度随饱和度的变化规律与土样2相同(文中未列出详细数据). 这一现象有重要的现实意义, 在干旱半干旱地区, 土壤的润湿性较弱, 表层土壤中的饱和度一般都非常低, 水主要以水蒸气的形态存在, 此时深层土中的水蒸气密度与表层土壤基本相同. 当表层土壤中的水蒸气进入大气或者被植物、微生物吸收时, 深层土壤的水蒸气又会补充上来, 这为表层植物和微生物的生存提供了水源, 但也造成大量水资源的蒸发浪费. 提高表层土壤的润湿性, 减小接触角, 一方面可以降低表层土壤的水蒸气含量, 减少地表水蒸发, 同时可为植物和微生物提供更多的液态水. 但目前尚缺乏这方面的研究, 将在后续研究中进一步论证.

Table 2
表2
表2不同饱和度下土样2中水分密度分布
Table 2Density of liquid and vapor water in soil 2 under different saturations

新窗口打开|下载CSV

4 结论

本文采用改进的Shan-Chen格子玻尔兹曼模型结合X-CT, 模拟了两个不同孔隙结构土样中不同润湿性条件下水分的分布, 分析了接触角对孔隙水分分布状态的影响, 初步得到了以下结论：

(1) 接触角较大时, 孔隙直径对液态水和水蒸气分布影响较小; 随着接触角减小, 液态水进入靠近土壤固相的小孔隙, 并沿着固相表面扩展形成水膜, 气态水逐渐被挤入大孔隙形成气泡; 接触角影响液态水与空气分布的同时, 也会影响液、气、固之间的界面面积.

(2) 随着接触角减小, 液体输运通道的平均直径减小; 而气体输运通道平均直径先增大, 后减小.

(3) 土壤中液态水的密度随接触角变化很小, 水蒸气密度随接触角减小显著降低. 接触角较大时, 饱和度对水蒸气密度无明显影响; 接触角较小时, 饱和度的增大会显著提高水蒸气密度.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Bacq-Labreuil A, Crawford J, Mooney SJ. et al. Cover crop species have contrasting influence upon soil structural genesis and microbial community phenotype
Scientific Reports, 2019,9(1):7473
[本文引用: 2]

[2] Kravchenko AN, Guber AK, Razavi BS. et al. Microbial spatial footprint as a driver of soil carbon stabilization
Nature Communications, 2019,10(1):3121
[本文引用: 1]

[3] Nam JH, Kaviany M. Effective diffusivity and water-saturation distribution in single-and two-layer PEMFC diffusion medium
International Journal of Heat and Mass Transfer, 2003,46(24):4595-4611
[本文引用: 1]

[4] 周启友, 岛田纯. 土壤水空间分布结构的时间稳定性
土壤学报, 2003,40(5):683-690
[本文引用: 1]

( Zhou Qiyou, Shimada J. Temporal stability of the spatial distribution pattern of soil water
Acta Pedologica Sinica, 2003,40(5):683-690 (in Chinese))
[本文引用: 1]

[5] 张常亮, 李萍, 李同录 等. 黄土中降雨入渗规律的现场监测研究
水利学报, 2014,45(6):728-734
[本文引用: 1]

( Zhang Changliang, Li Ping, Li Tonglu, et al. In-situ boservation on rainfall infiltration in loess
Journal of Hydraulic Engineering, 2014,45(6):728-734 (in Chinese))
[本文引用: 1]

[6] 杜娟, 刘淑娟, 徐先英 等. 内陆沙区丘间地土壤水分时空变化分析
中国农学通报, 2014,30(31):9-13
[本文引用: 1]

( Du Juan, Liu Shujuan, Xu Xianying, et al. The temporal and spatial variation analysis of soil moisture of interdune lowland in inland sandy areas
Chinese Agricultural Science Bulletin, 2014,30(31):9-13(in Chinese))
[本文引用: 1]

[7] 雷志栋, 胡和平, 杨诗秀. 土壤水研究进展与评述
水科学进展, 1999,10(3):311-318
[本文引用: 1]

( Lei Zhidong, Hu Heping, Yang Shixiu. A review of soil water research
Advances in Water Science. 1999,10(3):311-318(in Chinese))
[本文引用: 1]

[8] Darcy H. Les Fontaines Publiques de la Ville de Dijon: Exposition et Application
Victor Dalmont, 1856
[本文引用: 1]

[9] Buckingham E. Studies on the Movement of Soil Moisture
Bull. 38. USDA, Bureau of Soils, Washington, DC, 1907
[本文引用: 1]

[10] Richards LA. Capillary conduction of liquids through porous mediums
Physics, 1931,1(5):318-333
[本文引用: 1]

[11] Brooks R, Corey T. Hydraulic properties of porous media
Hydrology Papers (Colorado State University), 1964,24:37
[本文引用: 1]

[12] Van Genuchten MT. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils
Soil Science Society of America Journal, 1980,44(5):892-898
[本文引用: 1]

[13] Arya LM, Paris JF. A physicoempirical model to predict the soil moisture characteristic from particle-size distribution and bulk density data
Soil Science Society of America Journal, 1981,45(6):1023-1030
[本文引用: 1]

[14] Schaap MG, Leij FJ. Using neural networks to predict soil water retention and soil hydraulic conductivity
Soil and Tillage Research, 1998,47(1-2):37-42
[本文引用: 1]

[15] 邵明安, 王全九, Robert H. 推求土壤水分运动参数的简单入渗法I. 理论分析
土壤学报, 2000,37(1):1-8
[本文引用: 1]

( Shao Mingan, Wang Quanjiu, Robert H. A simple infiltration method for estimating soil hydraulic properties of unsaturated soils I. theoretical analysis
Acta Pedologica Sinica. 2000,37(01):1-8 (in Chinese))
[本文引用: 1]

[16] 邵明安, 王全九, Robert H. 推求土壤水分运动参数的简单入渗法II. 实验验证
土壤学报, 2000,37(2):217-224
[本文引用: 1]

( Shao Mingan, Wang Quanjiu, Robert H. A simple infiltration method for estimating soil hydraulic properties of unsaturated soils II. experimental results
Acta Pedologica Sinica. 2000,37(2):217-224 (in Chinese))
[本文引用: 1]

[17] Jin T, Cai X, Chen Y. et al. A fractal-based model for soil water characteristic curve over entire range of water content
Capillarity, 2019,2(4):66-75
[本文引用: 1]

[18] Kovscek A, Wong H, Radke C. A pore-level scenario for the development of mixed wettability in oil reservoirs
AIChE Journal, 1993,39(6):1072-1085
[本文引用: 1]

[19] Fatt I. The network model of porous media 1. Capillary pressure characteristics
Transactions of the American Institute of Mining and Metallurgical Engineers, 1956,207(7):144-159
[本文引用: 1]

[20] Bijeljic B, Blunt MJ. Pore-scale modeling and continuous time random walk analysis of dispersion in porous media
Water Resources Research, 2006,42(1):5
[本文引用: 1]

[21] Li L, Peters CA, Celia MA. Upscaling geochemical reaction rates using pore-scale network modeling
Advances in Water Resources, 2006,29(9):1351-1370


[22] Ebrahimi A, Or D. Microbial community dynamics in soil aggregates shape biogeochemical gas fluxes from soil profiles - upscaling an aggregate biophysical model
Global Change Biology, 2016,22(9):3141-3156
URLPMID [本文引用: 1]

[23] Hussain R, Mitchell J, Hammond PS. et al. Monitoring water transport in sandstone using flow propagators: A quantitative comparison of nuclear magnetic resonance measurement with lattice Boltzmann and pore network simulations
Advances in Water Resources, 2013,60:64-74
[本文引用: 1]

[24] Ostadi H, Rama P, Liu Y. et al. 3D reconstruction of a gas diffusion layer and a microporous layer
Journal of Membrane Science, 2010,351(1-2):69-74
[本文引用: 1]

[25] Borges JAR, Pires LF, Cássaro FAM. et al. X-ray microtomography analysis of representative elementary volume (REV) of soil morphological and geometrical properties
Soil and Tillage Research, 2018,182:112-122
[本文引用: 1]

[26] Cnudde V, Boone MN. High-resolution X-ray computed tomography in geosciences: A review of the current technology and applications
Earth-Science Reviews, 2013,123(4):1-17
[本文引用: 1]

[27] Ahrenholz B, T?lke J, Krafczyk M. Lattice-Boltzmann simulations in reconstructed parametrized porous media
International Journal of Computational Fluid Dynamics, 2006,20(6):369-377
[本文引用: 1]

[28] Zhang XX, Crawford JW, Young IM. A Lattice Boltzmann model for simulating water flow at pore scale in unsaturated soils
Journal of Hydrology, 2016,538:152-160
[本文引用: 1]

[29] Hu XY, Adams NA. A multi-phase SPH method for macroscopic and mesoscopic flows
Journal of Computational Physics, 2006,213(2):844-861
[本文引用: 1]

[30] Jettestuen E, Helland JO, Prodanovi? M. A level set method for simulating capillary-controlled displacements at the pore scale with nonzero contact angles
Water Resources Research, 2013,49(8):4645-4661
[本文引用: 1]

[31] Raeini AQ, Blunt MJ, Bijeljic B. Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method
Journal of Computational Physics, 2012,231(17):5653-5668
[本文引用: 1]

[32] Hu W, Liu G, Zhang X. A pore-scale model for simulating water flow in unsaturated soil
Microfluidics & Nanofluidics, 2018,22(7):71
[本文引用: 1]

[33] Golparvar A, Zhou Y, Wu K. et al. A comprehensive review of pore scale modeling methodologies for multiphase flow in porous media
Advances in Geo-Energy Research, 2018,2(4):418-440
[本文引用: 1]

[34] 李桥忠, 陈木凤, 李游 等. 浸没边界-简化热格子 Boltzmann 方法研究及其应用
力学学报, 2019,51(2):392-404
[本文引用: 1]

( Li Qiaozhong, Chen Mufeng, Li You, et al. Immersed boundary-simplified thermal lattice Boltzmann method for fluid-structure interaction problem with heat transfer and its application
Chinese Journal of Theoretical and Applied Mechanics. 2019,51(2):392-404 (in Chinese))
[本文引用: 1]

[35] 程志林, 宁正福, 曾彦 等. 格子Boltzmann方法模拟多孔介质惯性流的边界条件改进
力学学报, 2019,51(1):124-134


( Cheng Zhilin, Ning Zhengfu, Zeng Yan, et al. A lattice Boltzmann simulation of fluid flow in porous media using a modified boundary condition
Chinese Journal of Theoretical and Applied Mechanics. 2019,51(1):124-134 (in Chinese))


[36] 蔡文莱, 黄亚军, 刘伟阳 等. 柔性微粒介电泳分离过程的多尺度模拟
力学学报, 2019,51(2):405-414


( Cai Wenlai, Huang Yajun, Liu Weiyang, et al. Multiscal simulation of the dielectrophoresis separation process of flexible microparticle
Chinese Journal of Theoretical and Applied Mechanics. 2019,51(2):405-414 (in Chinese))


[37] 冯世亮, 周吕文, 吕守芹 等. 悬浮态上皮细胞粘附的力学-化学耦合模型及数值模拟
力学学报, 2020,52(3):854-863
[本文引用: 1]

( Feng Shiliang, Zhou Lü wen, Lü Shouqin, et al. Mechanochemical coupling model and numerical simulation for cell-cell adhesion in suspended epithelial cells
Chinese Journal of Theoretical and Applied Mechanics. 2019,51(3):854-863 (in Chinese))
[本文引用: 1]

[38] Leclaire S, Reggio M, Trépanier JY. Progress and investigation on lattice Boltzmann modeling of multiple immiscible fluids or components with variable density and viscosity ratios
Journal of Computational Physics, 2013,246:318-342
[本文引用: 1]

[39] Yu Y, Liu H, Liang D. et al. A versatile lattice Boltzmann model for immiscible ternary fluid flows
Physics of Fluids, 2019,31(1):012108
[本文引用: 1]

[40] W?hrwag M, Semprebon C, Moqaddam AM. et al. Ternary free-energy entropic lattice Boltzmann model with a high density ratio
Physical Review Letters, 2018,120(23):234501
DOIURLPMID [本文引用: 1]
A thermodynamically consistent free energy model for fluid flows comprised of one gas and two liquid components is presented and implemented using the entropic lattice Boltzmann scheme. The model allows a high density ratio, up to the order of O(10^{3}), between the liquid and gas phases, and a broad range of surface tension ratios, covering partial wetting states where Neumann triangles are formed, and full wetting states where complete encapsulation of one of the fluid components is observed. We further demonstrate that we can capture the bouncing, adhesive, and insertive regimes for the binary collisions between immiscible droplets suspended in air. Our approach opens up a vast range of multiphase flow applications involving one gas and several liquid components.

[41] Wang N, Semprebon C, Liu H. et al. Modelling double emulsion formation in planar flow-focusing microchannels
Journal of Fluid Mechanics, 2020,895:A22
[本文引用: 1]

[42] Qin F, Del Carro L, Moqaddam AM. et al. Study of non-isothermal liquid evaporation in synthetic micro-pore structures with hybrid lattice Boltzmann model
Journal of Fluid Mechanics, 2019,866:33-60
[本文引用: 1]

[43] Deng H, Jiao K, Hou Y. et al. A lattice Boltzmann model for multi-component two-phase gas-liquid flow with realistic fluid properties
International Journal of Heat and Mass Transfer, 2019,128:536-549
[本文引用: 2]

[44] Nekoeian S, Goharrizi AS, Jamialahmadi M. et al. A novel Shan and Chen type Lattice Boltzmann two phase method to study the capillary pressure curves of an oil water pair in a porous media
Petroleum, 2018,4(3):347-357
[本文引用: 1]

[45] Rabbi SMF, Tighe MK, Flavel RJ. et al. Plant roots redesign the rhizosphere to alter the three-dimensional physical architecture and water dynamics
New Phytologist, 2018,219(2):542-550
[本文引用: 1]

[46] Williams AJ, Pagliai M, Stoops G. Physical and biological surface crusts and seals//Interpretation of Micromorphological Features of Soils and Regoliths
Elsevier, 2018: 539-574
[本文引用: 1]

[47] Bachmann J, Goebel M-O, Woche SK. Small-scale contact angle mapping on undisturbed soil surfaces
Journal of Hydrology and Hydromechanics, 2013,61(1):3-8
[本文引用: 2]

[48] Briant A, Wagner A, Yeomans J. Lattice Boltzmann simulations of contact line motion. I. Liquid-gas systems
Physical Review E, 2004,69(3):031602
[本文引用: 1]

[49] 张博. 液滴润湿行为与表面微纳结构关系的模拟研究
[博士论文]. 北京: 北京化工大学, 2016
[本文引用: 1]

( Zhang Bo. Theoretical study on the relationship between wetting behaviors of microdroplets and substrate microstructures
[PhD Thesis]. Beijing: Beijing University of Chemical Technology, 2016 (in Chinese))
[本文引用: 1]

[50] 方可宁, 单彦广, 袁俊杰. 不同润湿性表面液滴铺展及蒸发过程的 LBM 数值模拟
新能源进展, 2019,7(4):346-353
[本文引用: 1]

( Fang Kening, Shan Yanguang, Yuan Junjie. LBM numerical simulation of droplet spreading and evaporation on surfaces with different wettability
Advances in New and Renewable Energy. 2019,7(4):346-353 (in Chinese))
[本文引用: 1]

[51] 胡梦丹, 张庆宇, 孙东科 等. 纳米结构超疏水表面冷凝现象的三维格子玻尔兹曼方法模拟
物理学报, 2019,68(3):120-129
[本文引用: 1]

( Hu Mengdan, Zhang Qingyu, Sun Dongke, et al. Three-dimensional lattice Boltzmann modeling of droplet condensation on superhydrophobic nanostructured surfaces
Acta Physica Sinica. 2019,68(3):120-129 (in Chinese))
[本文引用: 1]

[52] Chen S, Doolen GD. Lattice Boltzmann method for fluid flows
Annual Review of Fluid Mechanics, 1998,30:329-364
[本文引用: 1]

[53] Yuan P, Schaefer L. Equations of state in a lattice Boltzmann model
Physics of Fluids, 2006,18(4):042101
[本文引用: 3]

[54] Shan X, He X. Discretization of the velocity space in the solution of the Boltzmann equation
Physical Review Letters, 1998,80(1):65
[本文引用: 1]

[55] Chen L, Kang Q, Mu Y. et al. A critical review of the pseudopotential multiphase lattice Boltzmann model: Methods and applications
International Journal of Heat and Mass Transfer, 2014,76:210-236
[本文引用: 3]

[56] Martys NS, Chen H. Simulation of multicomponent fluids in complex three-dimensional geometries by the lattice Boltzmann method
Physical Review E, 1996,53(1):743
[本文引用: 1]

[57] Shan X. Analysis and reduction of the spurious current in a class of multiphase lattice Boltzmann models
Physical Review E, 2006,73(4):047701
[本文引用: 1]

[58] Bacq-Labreuil A, Crawford J, Mooney SJ. et al. Effects of cropping systems upon the three-dimensional architecture of soil systems are modulated by texture
Geoderma, 2018,332:73-83
DOIURLPMID [本文引用: 3]
Soil delivers fundamental ecosystem functions via interactions between physical and biological processes mediated by soil structure. The structure of soil is also dynamic and modified by natural factors and management intervention. The aim of this study was to investigate the effects of different cropping systems on soil structure at contrasting spatial scales. Three systems were studied in replicated plot field experiments involving varying degrees of plant-derived inputs to the soil, viz. perennial (grassland), annual (arable), and no-plant control (bare fallow), associated with two contrasting soil textures (clayey and sandy). We hypothesized the presence of plants results in a greater range (diversity) of pore sizes and that perennial cropping systems invoke greater structural heterogeneity. Accordingly, the nature of the pore systems was visualised and quantified in 3D by X-ray Computed Tomography at the mm and mum scale. Plants did not affect the porosity of clay soil at the mm scale, but at the mum scale, annual and perennial plant cover resulted in significantly increased porosity, a wider range of pore sizes and greater connectivity compared to bare fallow soil. However, the opposite occurred in the sandy soil, where plants decreased the porosity and pore connectivity at the mm scale but had no significant structural effect at the mum scale. These data reveal profound effects of different agricultural management systems upon soil structural modification, which are strongly modulated by the extent of plant presence and also contingent on the inherent texture of the soil.

[59] Hu WL, Huang N, Zhang XX. Impact of saturation on mass transfer rate between mobile and immobile waters in solute transport within aggregated soils
Journal of Hydrology, 2014,519:3557-3565
[本文引用: 2]

[60] Madsen M, Zvirzdin D, Petersen S. et al. Soil water repellency within a burned pi?on--juniper woodland: Spatial distribution, severity, and ecohydrologic implications
Soil Science Society of America Journal, 2011,75(4):1543-1553
[本文引用: 1]