高朋^,2), 侯磊^,3), 陈予恕哈尔滨工业大学航天学院, 哈尔滨 150001

NONLINEAR THERMAL ANALYSIS FOR THE INTER-SHAFT BEARING UNDER THE DYNAMIC LOAD ¹⁾

Gao Peng^,2), Hou Lei^,3), Chen YushuSchool of Astronautics, Harbin Institute of Technology, Harbin 150001, China

通讯作者: 2)高朋, 博士生, 主要研究方向: 航空发动机转子动力学、轴承热传递. E-mail:gaopeng_hit@126.com3)侯磊, 副教授, 主要研究方向: 航空发动机非线性转子动力学研究. E-mail:houlei@hit.edu.cn

收稿日期:2020-07-31接受日期:2020-11-13网络出版日期:2020-12-31

基金资助:

1) 国家科技重大专项.2017-IV-0008-0045 国家自然科学基金.11972129 辽宁省科技厅博士启动基金资助.2019BS182

Received:2020-07-31Accepted:2020-11-13Online:2020-12-31
作者简介 About authors


摘要
中介轴承作为双转子系统高低压转子重要的支承部件,其内圈和外圈均随着低压转子和高压转子高速旋转, 其传热问题更加突出.本文研究中介轴承在非线性动载荷作用下的非线性热行为.基于双转子系统动力学响应定义中介轴承动载荷,考虑中介轴承的径向游隙、分数指数非线性和参数激励等非线性因素,中介轴承动载荷会出现跳跃和双稳态等非线性行为. 考虑润滑剂的黏温关系,根据Palmgren经验公式建立动载荷作用下中介轴承的热传递模型,通过数值求解得到中介轴承稳态温度,发现动载荷的非线性行为导致中介轴承温度出现跳跃和双稳态等非线性热行为.分析转速比、偏心距、中介轴承径向游隙、Hertz接触刚度和滚子数目对中介轴承温度及非线性热行为的影响,表明偏心距、径向游隙和刚度只影响非线性热行为,而转速比和滚子数目对两者都有重要影响. 本文研究表明,动载荷相较于静载荷更适合描述中介轴承的实际载荷,由于双转子系统具有非线性振动特性, 中介轴承的热行为也表现出复杂的非线性行为.
关键词： 中介轴承;动载荷;双转子;跳跃现象;双稳态现象

Abstract
As an important supporting part between the higher pressure rotor and the lower pressure rotor in a dual-rotor system, inner and outer races are rotating with the lower and higher pressure rotors, the heat transfer of the inter-shaft bearing is more prominent. This paper studies the nonlinear thermal behaviors of the inter-shaft bearing under the nonlinear dynamic load. The dynamic load of the inter-shaft bearing is defined based on the dynamic responses of the dual-rotor system, where the nonlinear factors of the inter-shaft bearing such as the radial clearance, the fractional exponential nonlinearity and the parameter excitation are taken into consideration. Thus the nonlinear behaviors such as the jump and the bi-stable phenomena happen to the dynamic load. According to Palmgren's empirical formula, a heat transfer model of the inter-shaft bearing under the dynamic load is established with considering the viscosity-temperature relationship of the lubricant. Steady-state temperatures of the inter-shaft bearing are obtained by the numerical integration. It shows that the nonlinear thermal behaviors of the inter-shaft bearing such as the jump and the bi-stable phenomena are caused by the nonlinear behaviors of the dynamic load. Furthermore, effects of the rotation speed ratio, the unbalances, the inter-shaft bearing's radial clearance, Hertz contact stiffness and roller number on the temperatures and the nonlinear thermal behaviors of the inter-shaft bearing are analyzed. The results show that the unbalances, the radial clearance and the stiffness only affect the nonlinear thermal behaviors of the inter-shaft bearing; the rotation speed ratio and the roller number have a magnificent influence on both. This discovery implies that the dynamic load is more appropriate to describe the actual load of the inter-shaft bearing than the static load. The thermal behaviors of the inter-shaft bearing become nonlinear, which is much more complicated than before, due to nonlinear dynamic characteristics of the dual-rotor system.
Keywords：inter-shaft bearing;dynamic load;dual-rotor;jump phenomenon;bi-stable phenomenon


PDF (4921KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
高朋, 侯磊, 陈予恕. 动载荷作用下中介轴承的非线性热行为研究 ¹⁾. 力学学报[J], 2020, 53(1): 248-259 DOI:10.6052/0459-1879-20-261
Gao Peng, Hou Lei, Chen Yushu. NONLINEAR THERMAL ANALYSIS FOR THE INTER-SHAFT BEARING UNDER THE DYNAMIC LOAD ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 53(1): 248-259 DOI:10.6052/0459-1879-20-261

引言

随着转子系统向高速重载方向发展,对支承系统的动力学性能和热性能提出了更高的要求.中介轴承作为双转子系统中高、低压转子之间的重要支承和传动部件,其动力学特性^[1]和热特性^[2]相较于普通支承轴承更加复杂,甚至许多情况下是非线性的^[3]. 然而,目前关于中介轴承非线性热行为的研究几乎处于空白状态. 因此,对中介轴承非线性热行为机理进行深入地研究,阐明动力学参数以及热参数对其的影响是非常有必要的.

迄今为止,已经有许多****研究了轴承的Hertz接触分数指数非线性以及径向游隙等非线性因素对转子系统动力学特性的影响.Yamamoto^[4]研究了轴承径向游隙对轴承-转子系统共振特性的影响,发现共振峰的频率和振幅随径向游隙的增大而减小.Fukata等^[5]研究了球轴承在恒定径向载荷作用下的径向振动,发现轴承的Hertz接触分数指数非线性以及径向游隙等非线性因素会引起超谐共振和亚谐共振等非线性共振.Holmes等^[3]在试验台上复现了某中型喷气发动机中双转子结构的跳跃现象、亚谐共振和组合共振等非线性动力学行为.Mevel和Guyader^[6]基于Fukata的动力学模型研究了轻载球轴承通往混沌的两种不同路径,即次谐波路径和准周期路径. Tiwari等^[7-8]应用改进的谐波平衡法,从理论上模拟了轴承Hertz接触和径向游隙对水平转子非线性动力学行为的影响,并进行了实验验证.Ghafari等^[9]提出了考虑滚动体非线性刚度的集中质量-阻尼-弹簧模型,研究了径向游隙对轴承平衡点的影响. Bai等^[10]通过数值仿真和实验验证,建立了考虑轴承非线性因素六自由度动力学模型,研究了对称球轴承-转子系统的亚谐共振. Zhang等^[11-12]基于文献[7,8]中的分析方法HB-AFT,重点研究了轴承的Hertz接触分数指数非线性以及径向游隙等非线性因素对转子系统的共振滞后特性的影响.然而以上研究工作中, 都集中在轴承-转子系统的非线性动力学行为上,没有考虑轴承的热效应.

摩擦会阻碍物体运动并以摩擦热的形式造成能量损失.中介轴承运行中产生的摩擦热可使轴承温度升高, 可采用摩擦力矩来度量.摩擦力矩的大小很大程度上取决于润滑方式, 对于采用油润滑的圆柱滚子轴承,润滑油将占据轴承内部空间, 从而阻碍了滚子的运动^[13].摩擦力矩的大小与润滑剂的性能、填充量以及滚子运转速度都有关系, 然而,这些因素通常是紧密耦合在一起的, 很难区分开来^[14]. 1945年,Palmgren等^[15]通过对各种类型和尺寸的滚动轴承进行大量试验,得出了轴承摩擦力矩的经验公式,Palmgren经验公式作为一种预测滚动轴承摩擦力矩的精确方法已被广泛认可和使用.根据热传递的基础理论, Harris等^[13]建立了滚动轴承稳态热传递能量守恒方程,理论预测了滚动轴承主要零部件滚珠、内圈和外圈的稳态温度.Winer等^[16]则更进一步建立了圆锥滚子轴承和轴承座间的热传递模型,同时给出了转轴、轴承以及轴承座之间的热阻计算公式. DeMul等^[17-18]提出了一个五自由度轴承受力模型, 时采用矩阵法分析载荷与挠度之间的关系.Jorgensen和Shin^[19]提出了一个准三维传热模型来预测考虑热膨胀的主轴-轴承系统的稳态温度分布.基于Palmgren的经验公式, Stein和Tu^[14]提出了一个状态空间模型,用于预测由角接触球轴承的热膨胀而引起的预紧力,并分析了转速和初始预紧力的影响. Sun等^[20]开发了一种叶片损耗模拟方法,并建立了一个传热模型来估计叶片损耗以及轴承主要零部件的热膨胀数据.Takabi和Khonsari^[21]提出了油浴润滑的深沟球轴承非稳态热传递模型,从而用来研究轴承的瞬态温度.艾思源等^[22]聚焦于脂润滑的双列圆锥滚子轴承的热行为,并提出了一种准静态模型, 用以计算轴承载荷分布和运动参数.Than和Huang^[23]提出了一种将准静态模型与有限元相结合的方法,研究了高速主轴轴承在预载荷作用下的非线性热行为. 然而,上述文献均未考虑系统动力学特性对轴承热行为的影响.

本文提出一种将传热学与非线性动力学相结合的理论方法,研究双转子系统的非线性动力学特性对中介轴承热行为的影响机制,并详细分析动力学参数和热参数的影响规律.根据双转子系统的非线性动力响应定义出中介轴承的动载荷,借助Palmgren经验公式将其代入轴承热平衡方程,从而建立动载荷作用下的中介轴承非稳态热传递模型.通过数值模拟研究动载荷作用下的中介轴承热行为,发现轴承的运行温度不仅与转子系统的运行转速相关,也与转子系统的动力学特性息息相关, 这也为轴承的设计提供了一种新的思路.

1 中介轴承动载荷的非线性行为

简化双盘四支承的双转子系统如图1所示,每个转子有一个圆盘和一个转轴组成, 圆盘固结在转轴上.中介轴承位于高、低压转子之间, 其不同于通常用于支承的轴承,中介轴承外圈也会随着高压转子旋转. 其中$l_{i}$ ($i=1,2,3,4,5$)为轴的长度, $k_{i}$和$c_{i}$ ($i = 1, 2, 3$) 表示弹性支撑的刚度和阻尼系数,$\omega_{1}$和$\omega_{2}$ (rad/s) 是低压转子和高压转子转速.定义转速比为$\lambda ={\omega_{2}}/{\omega_{1} }$,由于高压转子转速大于低压转子, 故$\lambda >1$为双转子同向旋转,$\lambda <-1$为双转子反向旋转.

图1

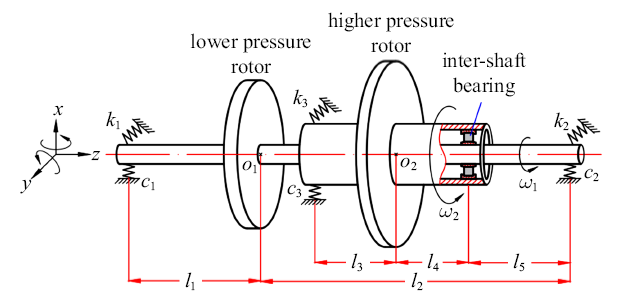新窗口打开|下载原图ZIP|生成PPT
图1简化双盘四支承的双转子系统

Fig.1Simple dual-rotor system with two disks and four supports



简化双盘四支承的双转子系统动力学方程可采用Lagrange第二方程推导, 具体推导过程见文献[24,25], 系统八自由度动力学方程如下

(1)$\begin{eqnarray} &&m_{1} \ddot{{x}}_{1}+c_{1} \left( {\dot{{x}}_{1} -\dot{{\theta }}_{y} l_{1} } \right)+c_{2} \left( {\dot{{x}}_{1} +\dot{{\theta }}_{y} l_{2} } \right)+k_{1} \left( {x_{1} -\theta_{y} l_{1} } \right)+ k_{2} \left( {x_{1} +\theta_{y} l_{2} } \right)=m_{1} \omega_{1}^{2}e_{1} \cos \left( {\omega_{1} t} \right)-F_{x} -m_{1} g \end{eqnarray}$
(2)$\begin{eqnarray} && m_{1} \ddot{{y}}_{1}+c_{1} \left( {\dot{{y}}_{1} +\dot{{\theta }}_{x} l_{1} } \right)+c_{2} \left( {\dot{{y}}_{1} -\dot{{\theta }}_{x} l_{2} } \right)+k_{1} \left( {y_{1} +\theta_{x} l_{1} } \right)+ k_{2} \left( {y_{1} -\theta_{x} l_{2} } \right)=m_{1} \omega_{1}^{2} e_{1} \sin \left( {\omega_{1} t} \right)-F_{y} \end{eqnarray}$
(3)$\begin{eqnarray} && J_{{d}_{1} } \ddot{{\theta }}_{x} +\omega_{1} J_{{p}_{1} } \dot{{\theta }}_{y} +c_{1} l_{1} \left( {\dot{{y}}_{1} +\dot{{\theta }}_{x} l_{1} } \right)-c_{2}l_{2} \left( {\dot{{y}}_{1} -\dot{{\theta }}_{x} l_{2} } \right)+ k_{1} l_{1} \left( {y_{1} +\theta_{x} l_{1} } \right)-k_{2} l_{2} \left( {y_{1} -\theta_{x} l_{2} } \right)=F_{y} \left( {l_{2} -l_{5} } \right) \end{eqnarray}$
(4)$\begin{eqnarray} &&J_{{d}_{1} } \ddot{{\theta }}_{y} -\omega_{1} J_{{p}_{1} } \dot{{\theta }}_{x} -c_{1} l_{1} \left( {\dot{{x}}_{1} -\dot{{\theta }}_{y} l_{1} } \right)+c_{2}l_{2} \left( {\dot{{x}}_{1} +\dot{{\theta }}_{y} l_{2} } \right)- k_{1} l_{1} \left( {x_{1} -\theta_{y} l_{1} } \right)+k_{2}l_{2} \left( {x_{1} +\theta_{y} l_{2} } \right)=-F_{x} \left( {l_{2} -l_{5} } \right) \end{eqnarray}$
(5)$\begin{eqnarray} && m_{2} \ddot{{x}}_{2}+c_{3} \left( {\dot{{x}}_{2} -\dot{{\varphi }}_{y} l_{3} } \right)+k_{3} \left( {x_{2} -\varphi_{y} l_{3} } \right)= m_{2} \omega_{2}^{2} e_{2} \cos \left( {\omega_{2} t} \right)+F_{x} -m_{2} g \end{eqnarray}$
(6)$\begin{eqnarray} && m_{2} \ddot{{y}}_{2}+c_{3} \left( {\dot{{y}}_{2} +\dot{{\varphi }}_{x} l_{3} } \right)+k_{3} \left( {y_{2} +\varphi_{x} l_{3} } \right)= m_{2} \omega_{2}^{2} e_{2} \sin \left( {\omega_{2} t} \right)+F_{y} \end{eqnarray}$
(7)$\begin{eqnarray} && J_{{d}_{2} } \ddot{{\varphi }}_{x} +\omega_{2} J_{{p}_{2} } \dot{{\varphi }}_{y} +c_{3} l_{3} \left( {\dot{{y}}_{2} +\dot{{\varphi }}_{x} l_{3} } \right)+ k_{3} l_{3} \left( {y_{2} +\varphi_{x} l_{3} } \right)=-F_{y} l_{4} \end{eqnarray}$
(8)$\begin{eqnarray} && J_{{d}_{2} } \ddot{{\varphi }}_{y} -\omega_{2} J_{{p}_{2} } \dot{{\varphi }}_{x} -c_{3} l_{3} \left( {\dot{{x}}_{2} -\dot{{\varphi }}_{y} l_{3} } \right)- k_{3} l_{3} \left( {x_{2} -\varphi_{y} l_{3} } \right)=F_{x} l_{4} \end{eqnarray}$
方程动力学参数物理意义及数值见文献[24,25].

对于航空发动机双转子系统, 中介轴承一般采用径向圆柱滚子轴承.中介轴承具有间隙、Hertz接触引起的分数指数以及变刚度^[26]等非线性因素,会对中介轴承的弹性恢复力产生不可忽视的影响.中介轴承运动示意图如图2所示.

第k个滚子的瞬时角位置可以表示为

$\begin{eqnarray*} \theta_{k} =\frac{2\pi }{N_{b}}\left( {k-1} \right)+\omega _{c} t \end{eqnarray*}$

其中保持架转速为$\omega_{c} =(\omega_{1} r_{i}+\omega_{2} r_{o})/(r_{i} +r_{o})$, 式中$r_{i}$, $r_{o}$分别表示中介轴承内、外圈半径.

根据几何关系, 第k个滚子与滚道间的相对变形为

$\begin{eqnarray*} &&\delta_{k} =\left\{ {\left[ {x_{1} +\theta_{y} \left( {l_{2} -l_{5} } \right)} \right]-\left( {x_{2} +\varphi_{y} l_{4} } \right)} \right\}{cos}\theta_{k} + \left\{ {\left[ {y_{1} -\theta_{x} \left( {l_{2} -l_{5} } \right)} \right]-\left( {y_{2} -\varphi_{x} l_{4} } \right)} \right\}\sin \theta_{k} -\delta_{0} \left( {k=1, 2, \cdots, N_{b}} \right) \end{eqnarray*}$

其中2$\delta_0$为中介轴承的径向游隙.

图2

新窗口打开|下载原图ZIP|生成PPT
图2中介轴承运动示意图

Fig.2Motion diagram of inter-shaft bearing



竖直方向和水平方向上的中介轴承恢复力为

(9)$\begin{eqnarray} \label{eq9} \left[ {{\begin{array}{*{20}c} {F_{x} } \\ {F_{y} } \\ \end{array} }} \right]=K_{b} \sum\limits_{k=1}^{N_{b} } {\delta_{k}^{10/9} H\left( {\delta_{k} } \right)} \left[ {{\begin{array}{*{20}c} {\cos \theta_{k} } \\ {\sin \theta_{k} } \\ \end{array} }} \right] \end{eqnarray}$
其中$H\left( \cdot \right)$为Heaviside函数, $K_{b}$和$N_{b}$表示中介轴承的Hertz接触刚度和滚子数目.

中介轴承采用德国FAG^?公司生产的型号为NU1020圆柱滚子轴承, 其参数列于表1.


Table 1
Table 1Parameters of the radial cylindrical roller bearing NU1020

新窗口打开|下载CSV

中介轴承动载荷定义为一个周期内竖直方向和水平方向上的中介轴承弹性恢复力的有效值^[27], 即方均根(root-mean-square, RMS), 定义式如下

(10)$\begin{eqnarray} \label{eq10} && F_{b} =\sqrt {\frac{\int_0^T {\left( {\left( {F_{x} \left( t \right)-\bar{{F}}_{x} } \right)^{2}+\left( {F_{y} \left( t \right)-\bar{{F}}_{y} } \right)^{2}} \right)} {d}t}{T}} = \sqrt {\frac{\sum\limits_{i=1}^N {\left( {\left( {F_{x} \left( i \right)-\bar{{F}}_{x} } \right)^{2}+\left( {F_{y} \left( i \right)-\bar{{F}}_{y} } \right)^{2}} \right)} }{N}} \end{eqnarray}$
其中, $T$是周期, $N$表示周期内的离散化点数, $\bar{{F}}_{x} $和$\bar{{F}}_{y}$为竖直方向和水平方向弹性恢复力周期内的平均值.

2 中介轴承非稳态热传递方程

2.1 中介轴承摩擦热

中介轴承一般采用圆柱滚子轴承, 总摩擦力矩$M$分为3个部分: 载荷摩擦力矩$M_{l}$、黏度摩擦力矩$M_{\nu}$和滚子端面-挡边摩擦力矩$M_{f}$. 中介轴承不承受轴向载荷, 因此可以忽略$M_{f}$, 则总摩擦力矩$M$为摩擦力矩单位统一采用N$\cdot$mm.

(11)\begin{eqnarray} \label{eq11} M=M_{l} +M_{\nu } \end{eqnarray}$
本文引用中介轴承动载荷$F_{b}$来计算, 而非以往文献采用的静载荷^[23], 则载荷摩擦力矩$M_{l}$为

(12)\begin{eqnarray} \label{eq12} M_{l} =f_{l} F_{b} D_{m} \end{eqnarray}$
式中, $f_{l}$是一个与轴承类型和载荷相关的系数, 对于带保持架的向心圆柱滚子轴承,$f_{l} =0.000 2\sim0.000 4$, 小值用于轻系列轴承, 大值用于重系列轴承^[13]; $D_{m}$是中介轴承节圆直径.

黏度摩擦力矩$M_{\nu}$显然与润滑剂黏度$\nu $有关, 采用运动黏度(cSt, 即mm$^{2}$/s)来表示. 中介轴承内、外圈均随低、高压转子同步运转, 因此采用内外圈转速差

$\begin{eqnarray*} \Delta n=\frac{60}{2\pi }\left| {\omega_{2} -\omega_{1} } \right|=\frac{60}{2\pi}\left| {\lambda -1} \right|\omega_{1} \end{eqnarray*}$

替代原公式中的转速, 单位为r/min. 则黏度摩擦力矩$M_{\nu}$为

(13)\begin{eqnarray} \label{eq13} M_{v} =\left\{\begin{array}{l@{\quad }l} 10^{-7}f_{v} \left( {\nu \cdot \Delta n} \right)^{2/3}D_{m}^{3}, & {\nu \cdot \Delta n\geqslant 2000}\\ {160\times 10^{-7}f_{v} D_{m}^{3} }, & {\nu \cdot \Delta n<2000} \\ \end{array}\right. \end{eqnarray}$
式中$f_{\nu}$是一个与轴承类型和润滑方式相关的系数, 带保持架的向心圆柱滚子轴承, 脂润滑$f_{\nu} =0.6\sim 1$,油雾润滑$f_{\nu} = 1.5\sim 2.8$, 油浴润滑$f_{\nu} =2.2\sim 4$, 小值用于轻系列轴承, 大值用于重系列轴承^[13].

中介轴承总摩擦热$Q$为

(14)$Q=Q_{l} +Q_{\nu } $
中介轴承载荷摩擦热$Q_{l}$为

(15)$Q_{l} =10^{-3}\left| {\omega_{2} -\omega_{1} } \right|M_{l} =10^{-3}\left| {\lambda -1} \right|\omega_{1} M_{l} $
中介轴承黏度摩擦热$Q_{\nu}$为

(16)$Q_{\nu } =10^{-3}\left| {\omega_{2} -\omega_{1} } \right|M_{\nu } =10^{-3}\left| {\lambda -1} \right|\omega_{1} M_{\nu }$
摩擦热单位统一采用W.

2.2 润滑剂黏温关系

润滑剂黏度通常是温度的函数, 由此可见, 温度对于黏度影响很大. 因此,在计算黏度摩擦热时, 需要考虑润滑剂的黏温关系曲线. 根据文献[23],润滑剂在30, 40, 50, 60, 70, 80 $^\circ$C下的运动黏度分别为15, 10, 7.8, 5.9, 5, 4 mm$^2$/s.

Reynolds黏温模型^[28]如下

(17)$\begin{eqnarray} \nu =\nu_{0} {e}^{-\gamma \left( {T-T_{0} } \right)} \end{eqnarray}$
式中, $\gamma $表示黏温系数, 矿物油有$\gamma =0.018\sim 0.036$ $^{\circ}$C$^{-1}$; $T_0$表示初始温度; $\nu_0$表示初始温度下的初始运动黏度.

利用Reynolds黏温模型拟合的实验数据^[23],拟合曲线如图3所示. 拟合曲线的黏温系数为$\gamma=0.026$ $^{\circ}$C$^{-1}$,这表明Reynolds黏温模型适用于该润滑剂. 根据拟合出的黏温关系曲线,可以得到任意温度下润滑剂的运动黏度. 此外, 润滑剂运动黏度随温度变化范围很大,这进一步证明了考虑润滑剂黏温关系的必要性.

2.3 中介轴承热传递模型

由于轴承钢GCr15的Biot数通常比较小($Bi<0.1$),可以采用集总参数法^[29]建立中介轴承热传递模型,忽略滚子、内圈和外圈的内部温差, 从而大大简化了建模难度.中介轴承的热结点及热传递网络如图4所示,图4(a)给出了中介轴承传热过程中的6个热结点,分别为中介轴承滚子、内圈、外圈、低压轴段、高压轴段和润滑剂.图4(b)给出了中介轴承热传递网络, $R_{ri}$,$R_{ro}$, $R_{i}$, $R_{o}$为热传导的接触热阻, $R_{Lr}$, $R_{Li}$, $R_{Lo}$,$R_{LP}$, $R_{HP}$为对流传热的热阻.

图3

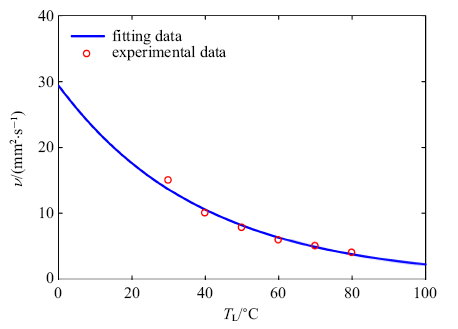新窗口打开|下载原图ZIP|生成PPT
图3润滑剂黏温关系曲线

Fig.3Lubricant viscosity-temperature curve

图4

新窗口打开|下载原图ZIP|生成PPT
图4中介轴承的热结点及热传递网络

Fig.4Thermal nodes and heat transfer network of the inter-shaft bearing



润滑剂温度假设为$T_{L} =({T_{r} +T_{i}+T_{o}})/{3}$, 即中介轴承滚子、内圈和外圈温度的平均值^[14]. 此外, 总摩擦热假设为平均分配^[14], 即分配给滚子的摩擦热$Q_{r}=0.5 Q_{t}$, 分配给内圈的摩擦热$Q_{i} =0.25 Q_{t} $, 分配给外圈的摩擦热$Q_{o} =0.25Q_{t}$. 对每个热结点列写热平衡方程, 即可得到中介轴承热传递控制方程

(18)$\frac{T_{i} -T_{r} }{R_{{ri}} }+\frac{T_{o} -T_{r} }{R_{{ro}} }+\frac{T_{L} -T_{r} }{R_{{Lr}} }+Q_{r} =m_{r} c_{{steel}} \frac{\partial T_{r} }{\partial t} $
(19)$\begin{eqnarray} \frac{T_{r} -T_{i} }{R_{{ri}} }+\frac{T_{{LP}} -T_{i} }{R_{i} }+\frac{T_{L} -T_{i} }{R_{{Li}} }+Q_{i} =m_{i} c_{{steel}} \frac{\partial T_{i} }{\partial t} \end{eqnarray}$
(20)$\begin{eqnarray} \frac{T_{r} -T_{o} }{R_{{ro}} }+\frac{T_{{HP}} -T_{o} }{R_{o} }+\frac{T_{L} -T_{o} }{R_{{Lo}} }+Q_{o} = m_{o} c_{{steel}} \frac{\partial T_{o} }{\partial t} \end{eqnarray}$
(21)$\begin{eqnarray} \frac{T_{i} -T_{{LP}} }{R_{i} }+\frac{T_{\infty } -T_{{LP}} }{R_{{LP}} }=m_{{LP}} c_{{steel}} \frac{\partial T_{{LP}} }{\partial t} \end{eqnarray}$
(22)$\begin{eqnarray} \frac{T_{o} -T_{{HP}} }{R_{o} }+\frac{T_{\infty } -T_{{HP}} }{R_{{HP}} }=m_{{HP}} c_{{steel}} \frac{\partial T_{{HP}} }{\partial t} \end{eqnarray}$
式中, $t$为时间, $c_{steel}$表示钢的比热容,$m_{r}$, $m_{i}$, $m_{o}$, $m_{LP}$, $m_{HP}$分别是滚子、内圈、外圈、低压轴段和高压轴段的质量;内圈-低压轴段热阻$R_{i} ={\ln \left( {{{d_{i} }/{d_{L} }}} \right)}/({2\pi k_{{steel}} {B}})$, 外圈-高压轴段热阻$R_{o} ={\ln \left( {{{d_{{H}} }/{d_{o} }}} \right)}/({2\pi k_{{steel}} {B}})$; 滚子-内圈热阻$R_{{ri}} ={R_{i}^{{one}} }/{n_{b}}$, 滚子-外圈热阻$R_{{ro}} ={R_{o}^{{one}}}/{n_{b} }$, 式中$n_{b}$为平均受力滚子数^[30], $R^{{one}}={1.13}/({k_{{steel}} \sqrt {A\cdot Pe^{\ast }} })$为单个滚子与内圈或外圈的热阻, 其中$A$表示滚子与内圈或外圈接触面面积, $Pe^{\ast }$表示修正的Peclet数^[31].

而对流传热热阻的计算通常简化为Nusselt数的计算, 通过下式

$\begin{eqnarray*} R_{\nu } =\frac{1}{Ah}=\frac{1}{A}\cdot \frac{L}{k\cdot Nu} \end{eqnarray*}$

式中, $h$为表面传热系数, $k$为流体热导率, $L$为特征长度, $A$为对流传热面积.

润滑剂-滚子的Nusselt数^[32]准则方程为

$\begin{eqnarray*} Nu=\left( {0.35+0.34{ }Re^{0.5}+0.15{ }Re^{0.58}} \right)Pr^{0.3} \end{eqnarray*}$

式中, $Re={VL}/{\nu }$为Reynolds数, $Pr={\nu}/{\alpha}$为Prandtl数, 该准则方程适用于$10^{-1}<Re<10^{5}$.

润滑剂-内圈或外圈的Nusselt数^[33]准则方程为

$\begin{eqnarray*} Nu=\left\{ \begin{array}{l@{\quad }l} 2, & {Ta < 41}\\ 0.167 Ta^{0.69}Pr^{0.4}, & 41 \leq Ta < 100,\\ 0.401 Ta^{0.5}Pr^{0.4}, & 100 < Ta,\\ \end{array} \right. \end{eqnarray*}$

式中$Ta=Re\sqrt{{\delta_{{io}} }/{r}} $为Taylor数, 其中$\delta _{{io}} =({d_{o} -d_{i}})/{2}$表示中介轴承内外圈的间距, $r$表示滚道半径.

高压轴段或低压轴段-环境Nusselt数^[34]准则方程为

$\begin{eqnarray} Nu=\left\{\begin{array}{l@{\quad }l} {0.003 08 Re+4.432}, & {Re < 7300}\\ {Re^{0.37}}, & 7300 \leq Re < 9600\\ {30.5 Re^{-0.004 2}}, & {9600 < Re} \hfill \\ \end{array} \right. \end{eqnarray}$

3 结果与讨论

3.1 中介轴承动载荷非线性行为

由于中介轴承弹性恢复力存在不可忽视的非线性因素,导致双转子系统动力学方程也是非线性的.本文采用四阶Runge-Kutta法求解系统动力学方程(1)~(8),得到了双转子系统的非线性动力学响应, 根据中介轴承弹性恢复力表达式(9),中介轴承弹性恢复力同时也就得到了. 图5表示当转速$\omega_{1} = 715$ rad/s时竖直方向水平方向上的弹性恢复力的时间历程曲线, 双转子系统参数: 转速比$\lambda = 1.2$, 低压转子偏心距$e_{1} =3$ $\mu$m以及高压转子偏心距$e_{2} =2$ $\mu$m.竖直方向和水平方向的中介轴承弹性恢复力都是时变的,其中水平方向弹性恢复力$F_{y}$在0附近周期性变化,而竖直方向弹性恢复力$F_{x}$在600 N附近周期性变化,这是因为系统在竖直方向存在重力.中介轴承弹性恢复力在竖直方向和水平方向均是时变的, 因此,当双转子系统以特定转速运行时,采用弹性恢复力的形式来描述中介轴承所承受的载荷显然是比较复杂的,这样并不利于中介轴承受力情况的描述和分析.

图5

新窗口打开|下载原图ZIP|生成PPT
图5中介轴承弹性恢复力

Fig.5Restoring forces of the inter-shaft bearing



图6表示动载荷以及振幅随转速变化曲线.升速曲线表示转速由低到高的过程, 而降速曲线表示转速由高到低的过程.与中介轴承弹性恢复力相比, 当双转子系统以特定转速运行时,中介轴承动载荷变成了一个恒定的常数,因此,利用动载荷来描述中介轴承的受力状况显然比时变的弹性恢复力更加简单方便.

图6

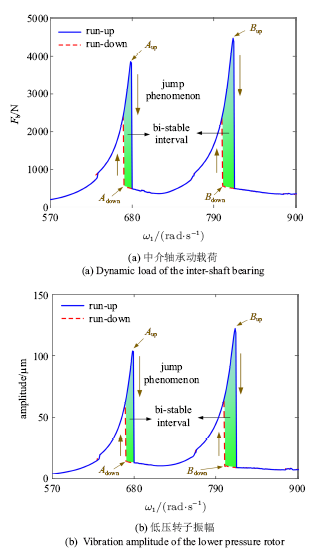新窗口打开|下载原图ZIP|生成PPT
图6动载荷以及振幅随转速变化曲线

Fig.6The dynamic load and the vibration amplitude against the rotation speed



由图6(b)中双转子系统幅频曲线可以看出, 在$\omega_{1} = 570$~900 rad/s转速区间内, 系统存在两个共振区,分别由高压转子高低压转子的不平衡激励引起. 升速过程中, 振幅急剧增大,直至转速达到$\omega_{A_{up} } $和$\omega_{B_{up} } $, 振幅骤降, 即发生了跳跃现象; 降速过程中,当转速达到$\omega_{A_{down} } $和$\omega_{B_{down} } $, 振幅骤增, 即发生了跳跃现象. 当转速处于$\omega_{1} \in \left[ {\omega_{A_{down} } , \omega _{A_{up} } } \right]$和$\omega_{1} \in \left[ {\omega_{B_{down} } , \omega_{B_{up} } } \right]$, 升速曲线和降速曲线没有重合在一起, 即出现双稳态现象. 从数学上,这意味着系统动力方程(1)~(8)在两个双稳态区间$\left[ {\omega_{A_{down} } , \omega_{A_{up} } }\right]$和$\left[ {\omega_{B_{down} } , \omega_{B_{up} } } \right]$内存在两个稳定解, 系统动力方程收敛到哪一个稳定解取决于系统运动的初始状态. 升速过程和降速过程中, 系统在4个跳跃点$A_{down}$, $A_{up}$, $B_{down}$和$B_{up}$的运动初始状态不同,因此升速曲线和降速曲线在双稳态区间不重合. 由图6(a)可以看出, 中介轴承动载荷变化规律与系统振幅变化规律一致. 动载荷在4个跳跃点$A_{down}$, $A_{up}$, $B_{down}$和$B_{up}$处也发生跳跃现象, 而在两个双稳态区间$\left[ {\omega _{A_{down} } , \omega_{A_{up} } } \right]$和$\left[ {\omega_{B_{down} } ,\omega_{B_{up} } } \right]$内也发生双稳态现象.

总而言之, 双转子系统动力学建模中,考虑了中介轴承径向游隙、Hertz接触的分数指数关系以及变刚度等非线性因素,同时根据系统的非线性动力学影响定义了中介轴承的动载荷, 因此,动载荷会发生跳跃和双稳态等非线性现象^[35],这也说明中介轴承动载荷能够在一定程度上反映系统的非线性动力学特性.

3.2 中介轴承非线性热行为

中介轴承热传递控制方程(18)~(22)本质上是一阶常微分方程组,本文采用四阶Runge-Kutta法进行数值求解, 计算精度默认为$<10^{-6}$,初始温度等于环境温度$T_{\infty } =20$$^{\circ}$C, 计算时间设置为10 000 s, 计算时间应足够大, 确保温度收敛于稳态温度.参数取值如下: 转速比$\lambda =1.2$、低压转子偏心距$e_{1} =3$ $\mu$m、高压转子偏心距$e_{2} =2$ $\mu$m.

当中介轴承处于稳态热传递状态时, 其滚子、内圈以及外圈温度随低压转子转速变化曲线如图7(a)所示, 图7(b)为中介轴承线性化时滚子、内圈以及外圈温度随低压转子转速变化曲线, 中介轴承线性化方法及过程参见文献[25]. 由图7(a)可以看到, 无论是升速曲线还是降速曲线, 都有滚子温度$T_{r}$高于内圈温度$T_{i}$高于外圈温度$T_{o}$, 即$T_{r} >T_{i} >T_{o} $. 同时发现,升速曲线和降速曲线的$T_{r}$, $T_{i}$和$T_{o}$随转速的变化规律基本相同, 因此,后文以$T_{r}$为例对中介轴承的非线性热行为进行详细分析. 在共振区$A$和$B$内,升\noindent 速曲线$T_{r}$急速升高, 直到转速增至$\omega_{A_{up} } $和$\omega_{B_{up} } $, 出现跳跃现象, 即$T_{r}$骤降;降速曲线$T_{r}$缓慢降低, 直到转速降至$\omega_{A_{down} }$和$\omega_{B_{down} } $, 出现跳跃现象, 即$T_{r}$骤增. 当转速处于$\omega_{1} \in \left[ {\omega_{A_{down} } , \omega_{A_{up} } } \right]$和$\omega_{1} \in \left[ {\omega _{B_{down} } , \omega_{B_{up} } }\right]$范围内时, 升速曲线和降速曲线的$T_{r}$不重合, 即出现了双稳态现象. 对比图7(a)和图7(b), 可以看出, 当中介轴承线性化之后, 其热行为的跳跃和双稳态现象均会消失不见!

图7

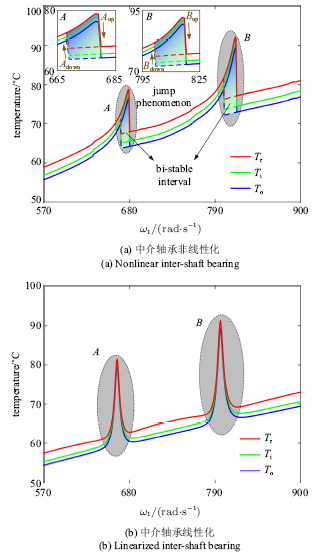新窗口打开|下载原图ZIP|生成PPT
图7滚子、内圈和外圈的稳态温度随转速变化曲线 (实线为升速曲线,虚线为降速曲线)

Fig.7Steady-state temperatures of rollers, inner race and outer race against rotation speed (solid lines represent run-up curves, dotted lines represent run-down curves)



为了便于后文进一步分析中介轴承的非线性热行为, 现定义相关符号和参数:$A_{down}$, $A_{up}$, $B_{down}$和$B_{up}$表示"跳跃点"; $\omega_{A_{down} } $, $\omega_{A_{up} } $, $\omega _{B_{down} } $和$\omega_{B_{up}}$表示"跳跃点频率"; $\Delta T_{A_{down} } $, $\Delta T_{A_{up} } $, $\Delta T_{B_{down} } $和$\Delta T_{B_{up} } $表示"跳跃幅值"; $\Delta \omega_{A}=\left[ {\omega_{A_{down} } , \omega_{A_{up}} } \right]$和$\Delta \omega_{B} =\left[ {\omega_{B_{down} } , \omega_{B_{up} } } \right]$表示"双稳态区间".

为了进一步揭示非线性热行为的内在机理, 非常有必要进行摩擦热分析,包括总摩擦热分析、载荷摩擦热分析和黏度摩擦热分析. 图8为中介轴承总摩擦热、载荷摩擦热和黏度摩擦热随转速的变化曲线,其中实线表示升速曲线, 虚线表示降速曲线. 可以看到, 升速过程中,总摩擦热$Q$、载荷摩擦热$Q_{l}$和黏度摩擦热$Q_{\nu}$在跳跃点$A_{up}$和$B_{up}$处均出现跳跃现象; 升速过程中,三者在跳跃点$A_{down}$和$B_{down}$处均出现跳跃现象. 此外,在$A_{up}$和$B_{up}$处, $Q_{l}$向下跳跃而$Q_{\nu}$向上跳跃,但$Q_{l}$跳跃幅值显著大于$Q_{\nu}$跳跃幅值, 因此$Q$与$Q_{l}$跳跃方向相同;在$A_{down}$和$B_{down}$处, $Q_{l}$向上跳跃而$Q_{\nu}$向下跳跃,但$Q_{l}$跳跃幅值显著大于$Q_{\nu}$跳跃幅值, 因此$Q$与$Q_{l}$跳跃方向相同. 同时,三者在双稳态区间$\Delta \omega_{A} $和$\Delta \omega_{B}$内均出现双稳态现象.

图8

新窗口打开|下载原图ZIP|生成PPT
图8中介轴承摩擦热随转速变化曲线

Fig.8Friction heat of the inter-shaft bearing against rotation speed



总而言之, 中介轴承温度出现非线性热行为, 即跳跃和双稳态现象,直接原因是总摩擦热出现非线性行为,而根本原因是双转子系统非线性动力学特性所导致的中介轴承动载荷出现的非线性行为.之所以产生这一独特的现象是因为本文引入中介轴承动载荷代入Palmgren经验公式来计算载荷摩擦热,如果仍旧采用静载荷则无法发现中介轴承的非线性热行为.

3.3 转速比的影响

图9为不同转速比下滚子温度随转速变化曲线对比,转速比分别取$\lambda =1.1$, $\lambda =1.15$, $\lambda =1.2$和$\lambda=1.25$. 可见, 转速比$\lambda$不仅影响滚子温度$T_{r}$而且影响共振区$A$和$B$内中介轴承非线性热行为.随着$\lambda $的增大, $T_{r}$显著增大; 跳跃点频率$\omega_{B_{down} } $和$\omega_{B_{up} } $基本不变,而$\omega_{A_{down} } $和$\omega_{A_{up} }$则显著降低; 跳跃幅值$\Delta T_{A_{down} } $, $\Delta T_{A_{up} } $, $\Delta T_{B_{down} } $和$\Delta T_{B_{up} } $均明显增大; 双稳态区间$\Delta \omega_{A} $和$\Delta \omega_{B} $长度也基本不变, 但$\Delta \omega_{B}$略宽于$\Delta \omega_{A} $.

图9

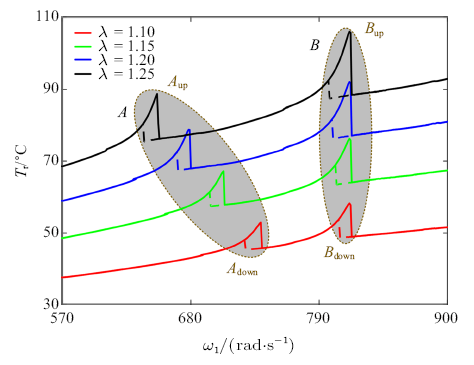新窗口打开|下载原图ZIP|生成PPT
图9不同转速比下滚子温度随转速变化曲线

Fig.9Variation for temperature of rollers with rotation speed under different rotation speed ratio



通过比较跳跃点频率$\omega_{A_{down} } $, $\omega_{A_{up} } $, $\omega_{B_{down} } $, $\omega_{B_{up} } $与转速比$\lambda $的大小关系, 可发现

(23)$\begin{eqnarray} \label{eq23} \frac{\omega_{B_{down} } }{\omega_{A_{down} } }\approx \lambda \approx \frac{\omega_{B_{up} } }{\omega _{A_{up} } } \end{eqnarray}$
由式(23)可看出, 转速比对跳跃点频率$\omega_{A_{down} }$和$\omega_{A_{up} } $有着至关重要的影响, 换言之,转速比决定了中介轴承出现非线性热行为的4个"跳跃点"和两个"双稳态区间"的相对位置.

3.4 偏心距的影响

首先分析低压转子偏心距的影响, 图10为不同低压转子偏心距下滚子温度随转速变化曲线对比, 低压转子偏心距分别取$e_{1}=2$ $\mu$m, $e_{1} =3$ $\mu$m, $e_{1} =4$ $\mu$m和$e_{1} =5$ $\mu$m. 可见, 滚子温度$T_{r}$除共振区$B$外几乎重合, 表明低压转子偏心距$e_{1}$只影响共振区$B$. 随着$e_{1}$的增大, 跳跃点频率$\omega_{A_{down} } $和$\omega_{A_{up} } $基本不变, 而$\omega_{B_{down} } $和$\omega_{B_{up} }$则显著增大; 跳跃幅值$\Delta T_{A_{down} } $和$\Delta T_{A_{up} } $基本不变, 而$\Delta T_{B_{down} } $和$\Delta T_{B_{up} } $则明显增大; 双稳态区间$\Delta \omega _{A} $长度基本不变, 而$\Delta \omega_{B} $则变窄.

最后分析高压转子偏心距的影响, 图11为不同高压转子偏心距下滚子温度随转速变化曲线对比, 高压转子偏心距分别取$e_{2}=2$ $\mu$m, $e_{2} =3$ $\mu$m, $e_{2} =4$ $\mu$m和$e_{2} =5$ $\mu$m. 可见, 滚子温度$T_{r}$除共振区$A$外几乎重合, 表明高压转子偏心距$e_{2}$只影响共振区$A$. 随着$e_{2}$的增大, 跳跃点频率$\omega_{B_{down} } $和$\omega_{B_{up} } $基本不变, 而$\omega_{A_{down} } $和$\omega_{A_{up} }$则显著增大; 跳跃幅值$\Delta T_{B_{down} } $和$\Delta T_{B_{up} } $基本不变, 而$\Delta T_{A_{down} }$和$\Delta T_{A_{up} } $则明显增大; 双稳态区间$\Delta \omega _{B} $长度基本不变, 而$\Delta \omega_{A} $则变窄.

图10

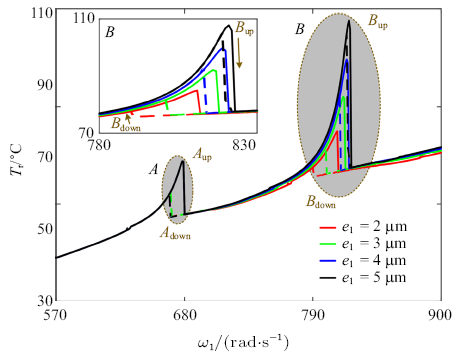新窗口打开|下载原图ZIP|生成PPT
图10不同低压转子偏心距下滚子温度随转速变化曲线

Fig.10Temperature and friction heat against rotation speed under different unbalances of lower pressure rotor

图11

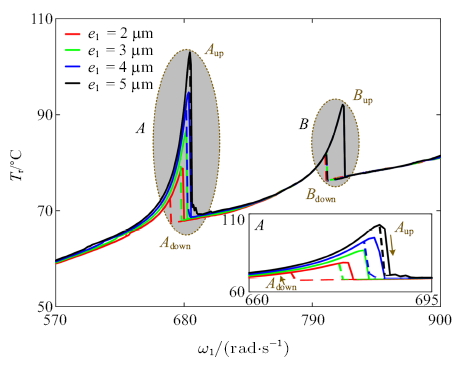新窗口打开|下载原图ZIP|生成PPT
图11不同高压转子偏心距下滚子温度随转速变化曲线

Fig.11Temperature and friction heat against rotation speed under different unbalances of higher pressure rotor



总而言之, 低压转子偏心距只影响共振区$B$, 而高压转子偏心距只影响共振区$A$,随着对应的偏心距的增大, 对应的跳跃点频率和跳跃幅度均增大,而对应的双稳态区间则变窄.

3.5 中介轴承径向游隙的影响

图12为不同径向游隙下滚子温度随转速变化曲线对比, 径向游隙分别取$\delta_{0} =3$ $\mu$m, $\delta_{0} =5$ $\mu$m, $\delta_{0} =8$ $\mu$m和$\delta_{0} =10$ $\mu$m. 可见, 径向游隙$\delta $主要影响共振区$A$和$B$内中介轴承非线性热行为,随着$\delta $的增大, 滚子温度$T_{r}$的最大值几乎不变; 跳跃点频率$\omega_{A_{down} } $, $\omega_{A_{up} } $, $\omega_{B_{down} } $和$\omega_{B_{up} } $均略微降低;跳跃幅值$\Delta T_{A_{down} } $, $\Delta T_{A_{up} } $, $\Delta T_{B_{down} } $和$\Delta T_{B_{up} } $均略微增大; 双稳态区间$\Delta \omega_{A}$和$\Delta \omega_{B} $均明显变宽. 值得注意的是, 当$\delta_{0} =3$ $\mu$m时, 中介轴承跳跃现象和双稳态现象等非线性热行为"消失了",这意味着径向游隙的存在是引起中介轴承温度出现非线性热行为的因素之一.

图12

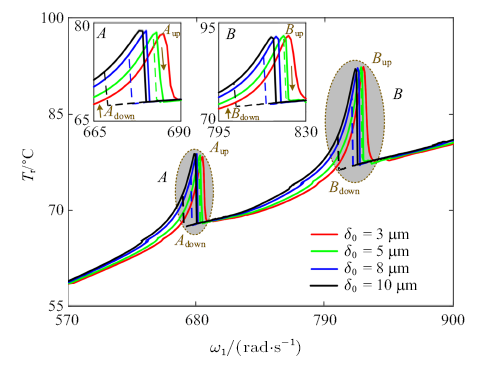新窗口打开|下载原图ZIP|生成PPT
图12不同径向游隙下滚子温度随转速变化曲线

Fig.12Temperature and friction heat against rotation speed under different radial clearance



中介轴承径向游隙延迟了滚子与内圈和外圈的接触时间,这相当于以另一种方式降低了中介轴承的刚度, 从而降低了跳跃点频率. 此外,径向游隙本质上是一种非线性因素,适当减小径向间隙将显著抑制中介轴承非线性热行为,即减小跳跃幅值和缩窄双稳态区间, 当径向间隙减小到一定值时,中介轴承非线性热行为甚至会消失.

3.6 中介轴承Hertz接触刚度的影响

图13为不同中介轴承Hertz接触刚度下滚子温度随转速变化曲线对比, 径向游隙分别取$K_{b} =8K_{{b0}}$, $K_{b}=10K_{{b0}} $, $K_{b} =15K_{{b0}} $和$K_{b} =20K_{{b0}} $ ($K_{{b0}} =10^{7}$ ${N}/{m}^{10/9})$. 可见, 中介轴承Hertz接触刚度$K_{b}$主要影响共振区$A$和$B$内中介轴承非线性热行为,随着$K_{b}$的增大, 滚子温度$T_{r}$的最大值几乎不变; 跳跃点频率$\omega_{A_{down} } $, $\omega_{A_{up} } $, $\omega_{B_{down} } $和$\omega_{B_{up} } $均显著增大;跳跃幅值$\Delta T_{A_{down} } $, $\Delta T_{A_{up} } $, $\Delta T_{B_{down} } $和$\Delta T_{B_{up} } $均略微减小; 双稳态区间$\Delta \omega_{A}$和$\Delta \omega_{B} $也略微变窄.

图13

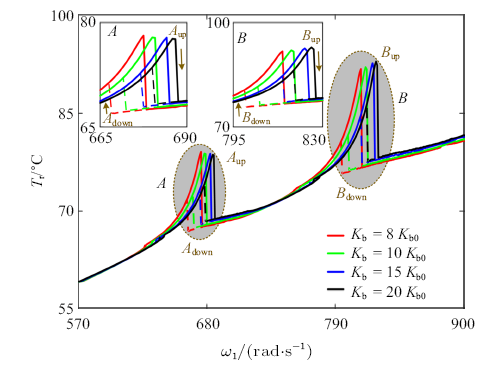新窗口打开|下载原图ZIP|生成PPT
图13不同中介轴承Hertz接触刚度下滚子温度随转速变化曲线

Fig.13Temperature and friction heat against rotation speed under different Hertz contact stiffness of the inter-shaft bearing

3.7 中介轴承滚子数目的影响

图14为不同滚子数目下滚子温度随转速变化曲线对比,径向游隙分别取$N_{b} =12$, $N_{b} =16$, $N_{b}=20$和$N_{b} =24$. 可见,滚子数目$N_{b}$不仅影响滚子温度$T_{r}$而且影响共振区$A$和$B$内中介轴承非线性热行为.随着$N_{b}$的增大, $T_{r}$显著减小; 跳跃点频率$\omega_{A_{down}} $, $\omega_{A_{up} } $, $\omega_{B_{down} }$和$\omega_{B_{up} } $均显著增大; 跳跃幅值$\Delta T_{A_{down} } $, $\Delta T_{A_{up} } $, $\Delta T_{B_{down} } $和$\Delta T_{B_{up} } $均略微减小; 双稳态区间$\Delta \omega_{A} $和$\Delta \omega_{B} $也略微变窄.

图14

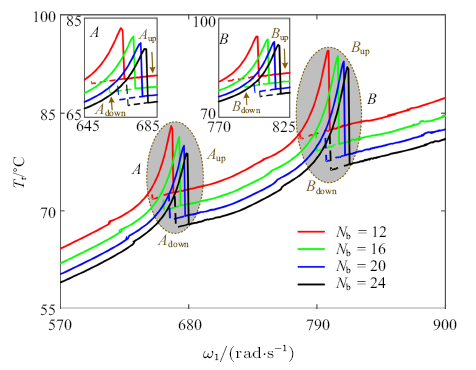新窗口打开|下载原图ZIP|生成PPT
图14不同滚子数目下滚子温度随转速变化曲线

Fig.14Temperature and friction heat against rotation speed under different roller numbers of the inter-shaft bearing

4 结论

本文考虑中介轴承的径向游隙、分数指数非线性和参数激励等多种非线性因素,基于双转子系统非线性动力响应定义了中介轴承动载荷,同时考虑了润滑剂的黏温关系,根据Palmgren经验公式建立了动载荷作用下的中介轴承热传递模型,研究了动载荷非线性行为对中介轴承温度的影响, 并进行了详细的参数分析.主要结论如下:

(1) 中介轴承的非线性动载荷将导致中介轴承温度出现非线性热行为, 即表现出跳跃和双稳态现象.

(2) 转速比和滚子数目对中介轴承温度和非线性热行为都有重要影响, 降低转速比或增加滚子数目不仅能够有效降低温度, 而且有利于抑制非线性热行为.

(3) 偏心距、中介轴承径向游隙和Hertz接触刚度均只影响中介轴承非线性热行为, 降低转子偏心距、适当缩小径向游隙或增大Hertz接触刚度均有利于抑制非线性热行为.

本文研究表明,双转子系统的非线性动力学特性会使中介轴承热行为表现出复杂非线性行为,未来的工作将集中在非线性热行为的实验验证上.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 侯磊, 陈予恕 . 非线性共振及其计算和应用
机械工程学报, 2019,55(13):1-12.
[本文引用: 1]

( Hou Lei, Chen Yushu . Nonlinear resonance and its calculations and applications
Journal of Mechanical Engineering, 2019,55(13):1-12 (in Chinese))
[本文引用: 1]

[2] 范纪华, 陈立威, 王明强 等. 旋转中心刚体- FGM 梁刚柔热耦合动力学特性研究
力学学报, 2019,51(6):1905-1917.
[本文引用: 1]

( Fan Jihua, Chen Liwei, Wang Mingqiang , et al. Research on dynamics of a rigid-flexible-thermal coupling rotating hub-FGM beam
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(6):1905-1917 (in Chinese))
[本文引用: 1]

[3] Holmes R, Dede MM . Non-linear phenomena in aero-engine rotor vibration
Journal of Power Engineering, 1989,203(11):25-34
[本文引用: 2]

[4] Yamamoto T . On critical speeds of a shaft supported by a ball bearing
Transactions of the JSME, 1955,21:182-192
[本文引用: 1]

[5] Fukata S, Gad EH, Kondou T , et al. On the radial vibrations of ball bearings (computer simulation)
Bulletin of The JSME, 1985,28(239):899-904
[本文引用: 1]

[6] Mevel B, Guyader JL . Routes to chaos in ball bearings
Journal of Sound & Vibration, 1993,162(3):471-487
[本文引用: 1]

[7] Tiwari M, Gupta K, Prakash O . Effect of radial internal clearance of a ball bearing on the dynamics of a balanced horizontal rotor
Journal of Sound & Vibration, 2000,238(5):723-756
[本文引用: 2]

[8] Tiwari M, Gupta K, Prakash O . Dynamic response of an unbalanced rotor supported on ball bearings
Journal of Sound & Vibration, 2000,238(5):757-779
[本文引用: 2]

[9] Ghafari S H, AbdelRahman EM, Golnaraghi F, et al. Vibrations of balanced faultfree ball bearings
Journal of Sound & Vibration, 2010,329(9):1332-1347
[本文引用: 1]

[10] Bai CQ, Zhang HY, Xu QY . Subharmonic resonance of a symmetric ball bearingrotor system. International Journal of
Non-Linear Mechanics, 2013,50:1-10
[本文引用: 1]

[11] Zhang ZY, Chen YS, Cao QJ . Bifurcations and hysteresis of varying compliance vibrations in the primary parametric resonance for a ball bearing
Journal of Sound & Vibration, 2015,350:171-184
[本文引用: 1]

[12] Zhang ZY, Chen YS, Li ZG . Influencing factors of the dynamic hysteresis in varying compliance vibrations of a ball bearing
Science China-Technological Sciences, 2015,58(5):775-782
[本文引用: 1]

[13] Harris TA, Kotzalas MN . Essential Concepts of Bearing Technology
Taylor & Francis, 2006: 133-135
[本文引用: 4]

[14] Stein JL, Tu JF . A statespace model for monitoring thermally induced preload in anti-friction spindle bearings of high-speed machine tools
Journal of Dynamic Systems, Measurement, and Control, 1994,116(3):372-386
[本文引用: 4]

[15] Palmgren A, Ruley B . Ball and Roller Bearing Engineering.
Philadelphia: SKF Industries, inc, 1945
[本文引用: 1]

[16] Winer WO, Bair S, Gecim B . Thermal resistance of a tapered roller bearing
ASLE Transactions, 1986,29(4):539-547
[本文引用: 1]

[17] Demul JM, Vree JM, Maas DA . Equilibrium and associated load distribution in ball and roller bearings loaded in five degrees of freedom while neglecting friction——Part I: General theory and application to ball bearings
Journal of Tribology, 1989,111(1):142-148
[本文引用: 1]

[18] Demul JM, Vree JM, Maas DA . Equilibrium and associated load distribution in ball and roller bearings loaded in five degrees of freedom while neglecting friction——Part II: Application to roller bearing and experimental verifacation
Journal of Tribology, 1989,111(1):149-155
[本文引用: 1]

[19] Jorgensen BR, Shin YC . Dynamics of machine tool spindle/bearing systems under thermal growth
Journal of Tribology, 1997,119(4):875-882
[本文引用: 1]

[20] Sun G, Palazzolo A, Provenza A , et al. Long duration blade loss simulations including thermal growths for dual-rotor gas turbine engine
Journal of Sound & Vibration, 2008,316:147-163
[本文引用: 1]

[21] Takabi J, Khonsari MM . Experimental testing and thermal analysis of ball bearings
Tribology International, 2013,60:93-103
[本文引用: 1]

[22] Ai SY, Wang W, Wang Y , et al. Temperature rise of double-row tapered roller bearings analyzed with the thermal network method
Tribology International, 2015,87:11-22
[本文引用: 1]

[23] Than VT, Huang JH . Nonlinear thermal effects on high-speed spindle bearings subjected to preload
Tribology International, 2016,96:361-372
[本文引用: 4]

[24] 高朋, 侯磊, 陈予恕 . 双转子中介轴承系统非线性振动特性
振动与冲击, 2019,38(15):1-10.
[本文引用: 2]

( Gao Peng, Hou Lei, Chen Yushu . Nonlinear vibration characteristics of a dual-rotor system with inter-shaft bearing
Journal of Vibration and Shock, 2019,38(15):1-10 (in Chinese))
[本文引用: 2]

[25] Gao P, Hou L, Yang R , et al. Local defect modelling and nonlinear dynamic analysis for the inter-shaft bearing in a dual-rotor system
Applied Mathematical Modelling, 2019,68:29-47
[本文引用: 3]

[26] 焦卫东, 蒋永华, 李刚 等. 任意斜裂纹转子的耦合振动研究
力学学报, 2020,52(2):533-543.
[本文引用: 1]

( Jiao Weidong, Jiang Yonghua, Li Gang , et al. Study on coupled vibrations of rotor with an arbitrary slant crack
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(2):533-543 (in Chinese))
[本文引用: 1]

[27] Tandon N, Choudhury A . A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings
Journal of Tribology, 1999,32(8):469-480
[本文引用: 1]

[28] Okoya SS . Flow, thermal criticality and transition of a reactive third-grade fluid in a pipe with reynolds' model viscosity
Journal of Hydrodynamics, 2016,28(1):84-94
[本文引用: 1]

[29] Holman JP. Heat Transfer , 10th Edition
New York: McGraw Hill, 2010: 51-52
[本文引用: 1]

[30] Gao P, Chen YS, Hou L . Nonlinear thermal behaviors of the inter-shaft bearing in a dual-rotor system subjected to the dynamic load
Nonlinear Dynamics, 2020,101(1):191-209
[本文引用: 1]

[31] Muzychka YS, Yovanovich MM . Thermal resistance models for non-circular moving heat sources on a half space
Journal of Heat Transfer, 2001,123(4):624-632
[本文引用: 1]

[32] Fand RM . Heat transfer by forced convection from a cylinder to water in crossflow
International Journal of Heat & Mass Transfer, 1965,8(7):995-1010
[本文引用: 1]

[33] Gazley C . Heat-transfer characteristics of the rotational and axial flow between concentric cylinders
Transactions ASME, 1958,108:79-90
[本文引用: 1]

[34] 杨泽亮, 卓献荣, 杨承 等. 水平高速旋转圆柱表面对流换热的实验研究
工业加热, 2002,31(5):17-20.
[本文引用: 1]

( Yang Zeliang, Zhuo Xianrong, Yang Cheng , et al. An experimental research on convective heat transfer on the surface of horizontal cylinder rotating with high speed
Industrial Heating, 2002,5:17-20 (in Chinese))
[本文引用: 1]

[35] 李航, 申永军, 李向红 等. Duffing 系统的主--亚谐联合共振
力学学报, 2020,52(2):514-521.
[本文引用: 1]

( Li Hang, Shen Yongjun, Li Xianghong , et al. Primary and subharmonic simultaneous resonance of Duffing oscillator
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(2):514-521 (in Chinese))
[本文引用: 1]