,2), 陈皓, 范晶晶, 温玉芬, 张正, 马友林中国运载火箭技术研究院,北京 100076GENERAL REYNOLDS ANALOGY RELATION ON BLUNT-NOSED BODIES$^{\bf 1)}$
Chen Xingxing,2), Chen Hao, Fan Jingjing, Wen Yufen, Zhang Zheng, Ma YoulinChina Academy of Launch Vehicle Technology,Beijing 100076,China通讯作者: 2) 陈星星,工程师,主要研究方向：高速空气动力学与气动加热. E-mail:chxx@mail.ustc.edu.cn
收稿日期:2019-12-20接受日期:2020-06-6网络出版日期:2020-07-18
| 基金资助: |
Received:2019-12-20Accepted:2020-06-6Online:2020-07-18
作者简介 About authors
摘要
钝头体壁面的摩阻和热流分布规律不同,平板流动中的雷诺比拟关系在钝头体壁面失效. 文章在前期高超声速广义雷诺比拟理论研究工作的基础上,利用数值仿真的方法对不同外形和来流参数条件下的钝头体广义雷诺比拟关系开展进一步研究. 通过建立钝头体绕流边界层的理论分析模型,得到了钝头体壁面雷诺比拟系数的线性分布预示公式. 采用数值求解 N-S 方程的方法,计算了圆柱和幂次体壁面的摩阻和热流以及二者之间的比拟系数. 通过与前期数值和理论结果对比,以及计算收敛性和网格无关性检验,对数值方法进行了验证. 通过在不同雷诺数 ($Re_\infty = 3.98\times 10^2 \sim 1.59\times 10^6$) 和马赫数 ($M_\infty = 3\sim 12$) 条件下的计算结果对比分析雷诺比拟系数的分布,总结了钝头体中广义雷诺比拟关系受外形和来流条件的影响,评估了广义雷诺比拟理论的适用性. 研究发现,在较高雷诺数条件下,离驻点较远的下游 ($\theta > 60^\circ$) 部位,雷诺比拟系数的分布不同程度地偏离理论预示的线性规律. 相比于圆柱外形,幂次体壁面的雷诺比拟系数分布的线性规律相对较好,其分布斜率略低于圆柱壁面的结果. 研究表明,如果针对实际外形和雷诺数进行适当修正,可以提高广义雷诺比拟关系的预示精度.
关键词：
Abstract
The classical Reynolds analogy relation fail on blunt-nosed bodies, as the distributions of skin frictions on curved wall surfaces differ from that on heat fluxes. With a theoretical research background on hypersonic Reynolds analogy relations, numerical simulations are presented in this paper to study the general Reynolds analogy relation on blunt-nosed bodies, as circular cylinder and power-law body, under different incoming flows. A linear relation of Reynolds analogy is obtained by theoretical analysis on the boundary layer along those surfaces. Also, numerical methods are applied to obtain solutions of N-S equations, from which skin frictions and heat fluxes and their analogy coefficients around cylinders and power-law bodies are calculated. The methods are validated by comparing the distribution of Reynolds analogy coefficients and the stagnation point heat transfer rate with former numerical and theoretical results. The convergence and grid independence are verified for the TVD method. The variation of Reynolds analogy relations are investigated in the range of $Re_\infty = 3.98\times 10^2 \sim 1.59\times 10^6$ and $M_\infty = 3\sim 12$. The present study shows that the general Reynolds analogy relation predicts the ratio between skin frictions and heat fluxes on regimes near the stagnations point for hypersonic flows. Downstream the stagnation point of circular cylinders (where $\theta > 60^\circ$), the Reynolds analogy relation deviates from the theoretical linear relationship in varying degrees with the growing of Reynolds number. Numerical results demonstrate that, comparing with the general Reynolds analogy relations on circular cylinders, Reynolds analogy coefficients are lower and fit linear distributions better for power-law bodies. Analyses indicate that modifications based on the shape of noses or the Reynolds number may improve the accuracy of theoretical predictions.
Keywords：
PDF (3639KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
陈星星, 陈皓, 范晶晶, 温玉芬, 张正, 马友林. 钝头体中的广义雷诺比拟关系$^{\bf 1)}$. 力学学报[J], 2020, 52(4): 1055-1062 DOI:10.6052/0459-1879-19-365
Chen Xingxing, Chen Hao, Fan Jingjing, Wen Yufen, Zhang Zheng, Ma Youlin.
引言
雷诺比拟描述了流体在壁面上的剪切和传热之间的关联关系,最早由雷诺在 1874 年提出[1],在各类流体传热传质问题中受到广泛关注和研究. 在边界层理论研究的早期,Blasius[2]在不可压缩的半无穷长平板绕流中找到了边界层方程的第一个理论解,从中可以计算得到平板壁面的雷诺比拟关系,结果表明摩阻系数和热流系数的比值,即雷诺比拟系数,为常数 $1/2$.不可压缩平板绕流中的雷诺比拟关系具有十分简单的形式,直观地揭示了边界层中动量和能量输运之间的关系. 更进一步的研究表明,即使考虑更加复杂的效应,如可压缩流动[3-4]、尖前缘的稀薄气体效应[5-6]、燃烧[7-8]等,平板绕流中的雷诺比拟系数仍然为常数.
对于工程实践中更常见的湍流边界层流动,雷诺比拟也受到广泛的关注和应用. 文献[9,10,11,12,13,14] 利用雷诺比拟关系构建解析理论预示平板和尖锥表面的热流分布,这些理论方法在工程中得到了广泛的应用. Chi 等[15]利用动量方程的湍流模型和雷诺比拟关系构造了能量方程的湍流模型. 作为目前湍流流动中少数的理论结果之一,雷诺比拟关系还被用来与各类数值计算、试验测量结果进行对比验证[16-18].
近年来,陈星星等[19]进一步对弯曲壁面上的雷诺比拟关系开展了研究,提出了广义雷诺比拟以描述雷诺比拟系数与壁面外形之间的关系. 传统的雷诺比拟关系适用于平板、尖锥绕流等边界层流向压力梯度为零的流动,而对于存在流向压力梯度的流动,则热流和摩阻的比拟关系一般不是常数[20]. 以二维的圆柱绕流和轴对称的圆球绕流为例,其热流峰值处于驻点位置,沿壁面向下游单调下降,而摩阻则在驻点处为零,沿壁面向下游先增加后减小,二者的比值随壁面位置变化.
陈星星等通过对钝头体壁面附近层流边界层方程的理论分析,推导出在高超声速条件下,壁面摩阻和热流的雷诺比拟系数随与壁面当地倾斜角 (壁面当地切线与来流方向夹角的余角) 呈正比关系,其比例系数与壁温相关而与马赫数、雷诺数无关. 理论分析结果与 DSMC 数值仿真计算结果吻合[19]. 进一步地,陈星星等[21]还将钝头体中的广义雷诺比拟关系推广到的包含化学反应流动的情形.
广义雷诺比拟关系理论与 DSMC 数值模拟计算结果吻合较好. 但是受 DSMC 方法的限制[22-24],主要适用于稀薄气体或近连续区流动的计算,雷诺数较低,而对于工程中常见的较高雷诺数流动,乃至湍流流动,在当前计算机硬件水平下,采用 DSMC 方法很难实现.
另一方面,高超声速钝头体绕流问题是高速气体动力学中的经典问题,在各类航天飞行器中广泛存在,长期以来受到深入研究. 文献[25,26] 分别研究了钝头体壁面和驻点热流问题,给出了理论预示方法. 国内王智慧等[27-29]提出了驻点热流受稀薄气体效应影响的理论判据. 在数值求解 N-S 方程方面,文献[30,31,32] 研究了不同离散格式、不同数值网格对钝头体热流计算结果的影响. Schwartzentruber 等[33]对比了采用 DSMC 方法和数值求解 N-S 方法计算得到的圆柱表面摩阻和热流大小.
为了对钝头体中的广义雷诺比拟关系开展进一步研究,本文采用数值求解 N-S 方程的方法计算了不同雷诺数、不同外形条件下的钝头体绕流问题,并将壁面上的雷诺比拟系数分布与理论预示结果进行对比,为广义雷诺比拟关系研究提供数据支撑.
1 圆柱壁面的广义雷诺比拟关系
1.1 理论预示
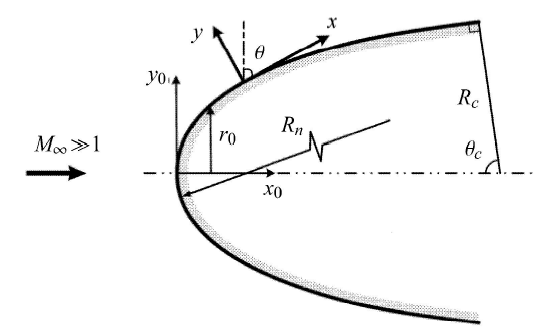
分别定义摩阻系数 $C_{\rm f} = {\tau _{\rm w} } /{(2\rho _\infty U_\infty ^2 )}$ 和热流系数 $C_{\rm h} = {\dot {q}_{\rm w} } / {(2\rho _\infty U_\infty ^3 )}$,其中 $\tau _{\rm w} $ 为壁面剪切力,$\dot {q}_{\rm w} $ 为壁面热流,$\rho _\infty $ 为来流密度,$U_\infty $ 为来流速度.对于如图 1 所示的高超声速绕钝头体流动,壁面摩阻和热流系数的比值为
$ \dfrac{C_{\rm f}}{C_{\rm h}} = 2Pr\dfrac{u_{\rm e} {f}"_{\rm w} }{U_\infty {g}'_{\rm w} } $
其中,$Pr$ 为气体普朗特常数,$u_{\rm e} $ 为沿流向的边界层外缘速度,${f}"_{\rm w} $ 和 ${g}'_{\rm w}$ 分别为壁面上气流无量纲速度和温度的法向梯度. 式中摩阻和热流系数的比值 ${C_{\rm f}}/ {C_{\rm h}}$ 即为雷诺比拟系数.
根据可压缩流动的 Bernoulli 方程得到的钝头体边界层外缘速度分布公式[34]
式中,$\gamma $ 为气体常数,$p_{\rm w}$ 为壁面压力,$p_0 $ 为驻点压力. 在来流马赫数 $M_\infty \gg 1$ 的条件下,上式可以近似为关于壁面当地倾斜角 $\theta $ 的线性分布[35]: $u_{\rm e} \propto \theta $,$\theta $ 的定义见图 1. 此时可以得到线性的广义雷诺比拟关系式[19]
其中,$C_{\rm r}$ 为一个与壁面温度相关的比例系数,根据前期研究结果, 对于二维圆柱外形
对于轴对称圆球外形
$ C_{\rm rsp} = Pr\sqrt {\dfrac{2\left( {\gamma - 1} \right)}{\gamma }} \dfrac{2.35 + 1.1{T_{\rm w} } /{T_0 }}{1 - {T_{\rm w} } / {T_0 }} $
式中,$T_{\rm w} $ 为壁面温度,$T_0 $ 为来流气体总温.
图1
新窗口打开|下载原图ZIP|生成PPT图1钝头体绕流示意图
Fig.1Hypersonic flow around a blunt-nosed body
1.2 N-S 方程数值计算
为了对更一般条件下的广义雷诺比拟问题开展研究,本文采用数值求解 N-S 方程的方法模拟圆柱绕流问题,计算壁面的摩阻分布和热流分布. 采用不同的数值方法进行计算,并与理论预示以及文献[32] 中公开发表的数值计算结果进行对比. 计算工具为 CFD++软件 (TVD 格式)[36]. 物理模型为以空气为介质的理想气体定常层流流动.为了方便对比,计算参数与文献[32] 保持一致：圆柱半径 8cm,来流条件等效为海拔 70km 高度处大气条件：来流静压 $p = 4.85$Pa, 来流密度 $\rho _\infty = 7.48\times 10^{ - 5}$kg/m$^3$,来流马赫数 $M_\infty $ 为 3, 6, 12,其中不同马赫数对应的壁面温度 $T_{\rm w}$ 依次分别为 300K, 500K, 1000K.
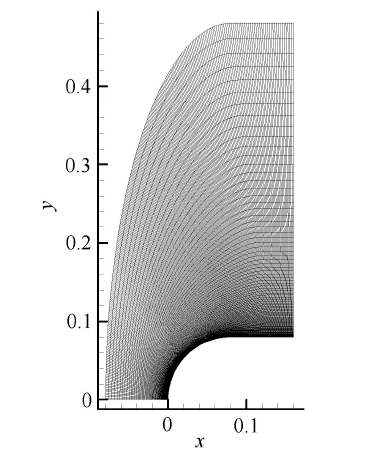
计算使用对称半模型结构化网格,如图 2 所示,在圆柱 $\theta \!=\! 90^\circ$ 的位置和计算出口边界之间使用一段平直壁面作为过渡. 网格数 量为 261 (沿壁面) $\times $125 (壁面法向). 沿壁面法向的第一层网格高度为$1.5\times 10^{- 5}$m.
图2
新窗口打开|下载原图ZIP|生成PPT图2计算域与网格示意图
Fig.2Computation regime and mesh
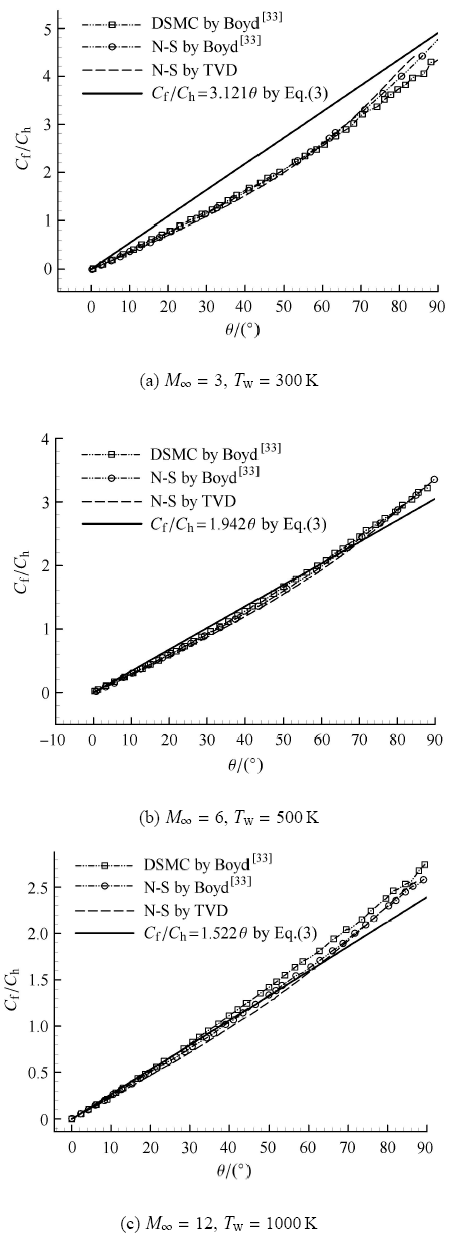
不同马赫数条件下圆柱壁面的雷诺比拟系数计算结果见图 3. 根据 Schwartzentruber 等[32]的计算结果,相比于 DSMC 方法,采用 N-S 方程计算得到的驻点热流偏大 3.5% $\sim$ 10.1%,表明在 70km 高度处,8cm 半径的圆柱绕流存在局部稀薄气体效应,处于近连续流动区. 对于摩阻和热流的雷诺比拟系数 $ C_{\rm f} / C_{\rm h}$,采用 DSMC 方法和 N-S 方程计算得到的结果基本一致.
图3
新窗口打开|下载原图ZIP|生成PPT图3不同马赫数条件下的雷诺比拟关系
Fig.3General Reynolds analogy relation in different Mach number
本文采用 TVD 格式数值求解 N-S 方程的结果也同时显示在图中. 可见 3 种数值方法计算得到的雷诺比拟关系较为一致. 在高超声速 ($M_\infty = 6$, 12) 条件下,不同数值方法,包括 DMSC 方法以及不同数值格式求解 N-S 方程计算得到的雷诺比拟关系均与理论预示的结果吻合较好.
在 $M_\infty = 3$ 的条件下,数值计算相对理论预示结果的偏差较大. 由于广义雷诺比拟关系成立的前提是来流满足高超声速 ($M_\infty \geqslant 5$) 条件,数值和理论方法预示结果的偏差符合预期. 从对比结果来看,数值计算得到的雷诺比拟系数明显小于高超声速理论的预示结果,且雷诺比拟系数关于 $\theta $ 的分布呈一定程度的非线性规律.
对不同来源、不同方法的计算数据对比分析发现,对于超声速圆柱绕流中的雷诺比拟关系,采用基于粒子碰撞和统计抽样的 DSMC 方法和基于连续介质假设求解 N-S 控制方程方法计算的结果基本一致.在高超声速条件下,数值计算结果与理论预示结果吻合较好,而在较低马赫数 ($M_\infty =3$) 条件下,数值计算结果与理论预示结果则存在一定区别,表明当前的高超声速广义雷诺比拟关系的理论结果还需要进一步改进才可以适应一般超声速流动的情形.
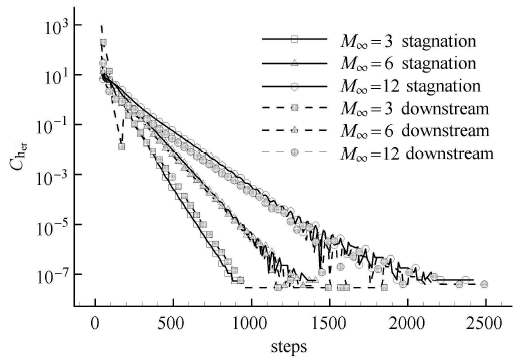
为了对计算结果进行确认,检查了本文采用的 TVD 格式计算结果的收敛性以及不同网格数目对计算结 果的影响. 不同马赫数条件下驻点热流以及下游 ($\theta = 90^\circ$) 位置的热流计算结果收敛历程见图 4. 图中纵坐标 $C_{\rm h_{\rm er}} $ 为各时间步计算得到的热流值 $C_{\rm h_{\rm i}} $ 与最后一步计算的热流值 $C_{\rm h_{\rm n}} $ 之间的相对误差：$C_{\rm h_{\rm er}} = {\left( {C_{\rm h_{\rm i}} - C_{\rm h_{\rm n}} } \right)}/ {C_{\rm h_{\rm n}} }$. 可见,计算过程中热流值稳步收敛,最终收敛结果的波动幅度小于 $10^{- 7}$. 使用不同密度网格计算得到的雷诺比拟系数结果见图 5. 三套网格对应的壁面附近第一层网格高度由疏到密各自为 $2.2\times 10^{-5}$m, $1.5\times 10^{-5}$m 和 $1.0\times 10^{- 5}$m.可见,在不同的马赫数条件下,网格数目对雷诺比拟系数的影响较小.
图4
新窗口打开|下载原图ZIP|生成PPT图4热流系数计算相对误差随迭代步数的变化
Fig.4Heat Fluxes vary with iteration steps
图5
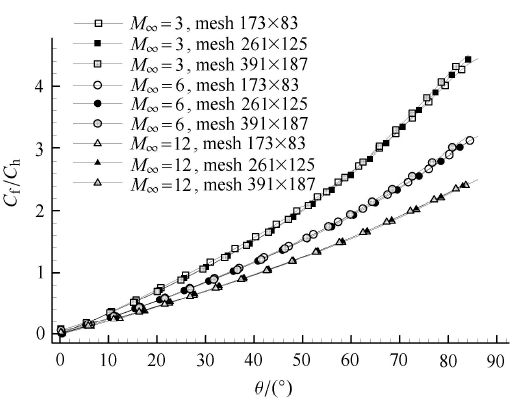
新窗口打开|下载原图ZIP|生成PPT图5不同网格数目下的雷诺比拟系数计算结果
Fig.5Reynolds analogy coefficients under different amount of mesh
1.3 雷诺数对广义雷诺比拟关系的影响
在文献[32] 提供的来流条件下,数值求解 N-S 方程以及 DSMC 方法的雷诺比拟计算结果与理论预示结果均吻合较好. 但是计算条件的来流密度和来流雷诺数较低. 参考王智慧等[27,29]提出的驻点稀薄气体流动判据 $Wr = {M_\infty ^{1.5} } /{Re_\infty }$,对于海拔高度 $H=70$km,参考长度 8cm 的计算条件,马赫数 $M_\infty = 3$,6,12 时,雷诺数 $Re_\infty $ 分别为 398,796,1592;$Wr$ 分别为 0.013,0.018,0.026. 对于计算的 3 种状态,$Wr$ 参数的大小表明流动处于近连续区. 而在常见的工程问题中,来流雷诺数往往大若干量级. 为了在更一般的流动问题中考察广义雷诺比拟关系的适应性,在上述计算条件的基础上,计算了更大雷诺数条件下的圆柱绕流问题,计算条件见表 1. 计算选择高超声速的 $M_\infty = 6$ 和 12 状态,在维持来流温度以及壁面温度条件下,通过提高来流压力条件增大雷诺数.Table 1
表1
表1计算条件
Table 1
 |
新窗口打开|下载CSV
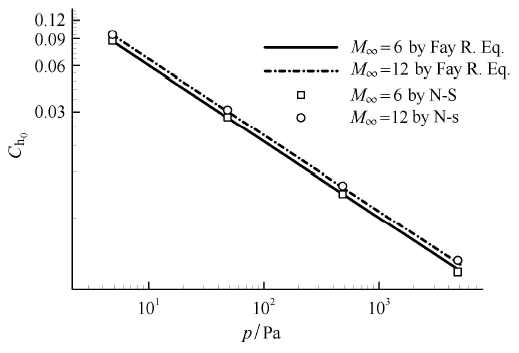
不同马赫数和来流压力条件下驻点处的热流系数 $C_{{\rm h}_0}$ 计算结果如图 6 所示. 将数值计算结 果与 Fay Riddell 公式[26]预示的结果进行了对比. 对比结果表明,采用数值求解 N-S 方程的方法计算得到的驻点热流与边界层理论公式的预示结果一致.
图6
新窗口打开|下载原图ZIP|生成PPT图6驻点热流系数计算结果
Fig.6Heat flux coefficients on stagnation point
图 7 中显示了不同雷诺数条件下,驻点下游热流和摩阻系数的分布曲线. 图中采用驻点热 流系数 $C_{{\rm h}_0} $ 和最大摩阻系数 $C_{{\rm f}_{\rm m}} $ 对热流系数和摩阻系数作归一化处理. 由图可见,不同来流压力条件下,沿圆柱壁面的热流和摩阻分布规律基本一致,而在驻点下游较远的位置 ($\theta > 60^\circ$),不同来流压力条件下,归一化的热流和摩阻曲线出现了一定程度的差别.
图7
新窗口打开|下载原图ZIP|生成PPT图7归一化的热流和摩阻分布
Fig.7Normalized heat fluxes and skin frictions
归一化的热流和摩阻分布曲线预示不同雷诺数条件下的雷诺比拟关系规律近似一致.由图 8 可见,不同来流压力 $p$,也就是不同雷诺数条件下,广义雷诺比拟关系具有如下规律：
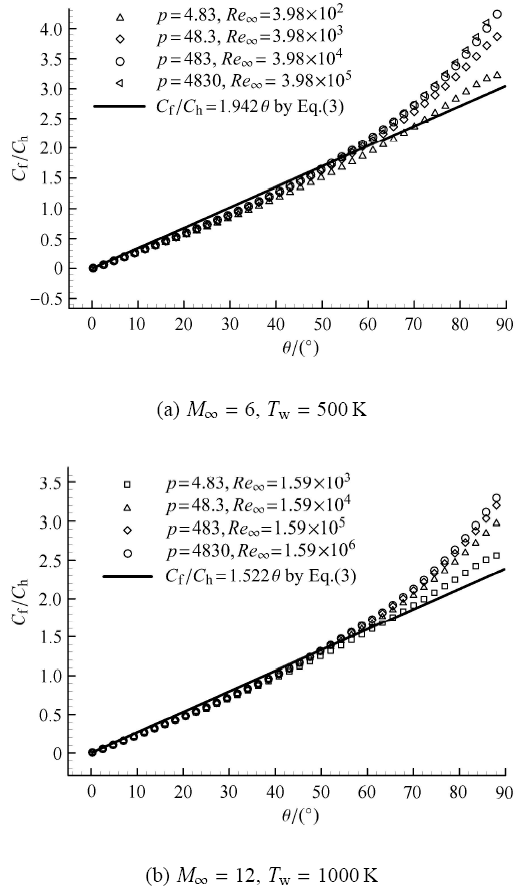
(1) 在 $\theta \leqslant 60^\circ $ 时,不同雷诺数条件下的 $ C_{\rm f} / C_{\rm h}$ 曲线分布一致,数值计算的雷诺比拟关系与理论吻合较好. 在 $\theta = 60^\circ $ 时,数值计算与理论预示结果的相对误差为 2.1%$\sim$6.5%;
(2) 在 $\theta > 60^\circ $ 时,$ C_{\rm f} / C_{\rm h}$ 随雷诺数增大而增大,且偏离理论预示的线性关系. 在 $\theta = 90^\circ $ 时,数值计算与理论预示结果的相对误差最大为 31.6%.
图8
新窗口打开|下载原图ZIP|生成PPT图8不同来流条件下的广义雷诺比拟关系
Fig. 8General Reynolds analogy relation with $p = 4.83\sim 4830$
针对不同雷诺数条件的计算结果表明,对于圆柱外形,即使是较大雷诺数条件,理论推导的线性广义雷诺比拟关系仍然可以较好地预示 $ C_{\rm f} / C_{\rm h}$ 分布. 但是在比较靠近下游的区域,数值计算得到的广义雷诺比拟关系则与理论预示存在差异,且二者之间的差异随雷诺数增大而加大.
对于圆柱下游区域数值计算的雷诺比拟关系与线性理论预示结果的区别,可能是由于在靠近下游的部位,边界层的自相似程度发生变化,导致线性的广义雷诺比拟关系理论基础与实际情况有所区别. 另外,圆柱壁面的热流分布随 $\theta $ 快速降低,在靠近下游的区域,数值计算得到的热流相对误差可能随之加大,导致雷诺比拟关系的计算结果与实际情况出现差别.
2 幂次体壁面的广义雷诺比拟关系
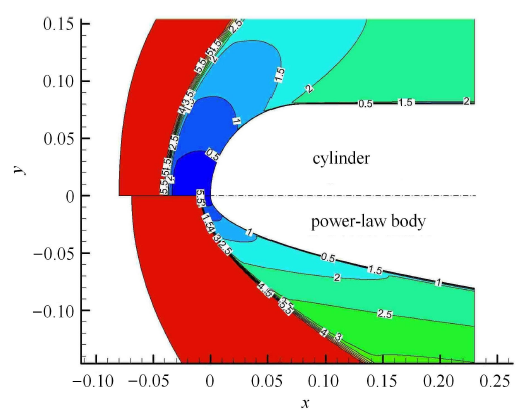
理论上,广义雷诺比拟关系适用于一般的钝头体外形. 除圆柱以外,本文另外选取一种幂次外形钝头体,采用数值求解 N-S 的方法计算了不同来流条件下的壁面雷诺比拟关系. 幂次体曲线方程为 $y = 0.16x^{0.5}$, $x = 0\sim 0.23$m. 计算的来流条件与表 1 一致.幂次体外形与圆柱外形计算得到的流场马赫数云图如图 9 所示. 幂次体壁面附近的流动图像仍然是由脱体弓形激波主导,但由于外形相对更加尖锐,激波脱体距离比圆柱外形明显减小.
图9
新窗口打开|下载原图ZIP|生成PPT图9圆柱和幂次体绕流马赫数云图
Fig.9Mach number counters on flows around a cylinder and power-law body
不同来流马赫数和压力条件下计算得到的壁面雷诺比拟系数见图 10. 结果表明,在不同的雷诺数条件下幂次体壁面的雷诺比拟系数基本一致,且相比于圆柱外形,比拟系数更接近线性分布. 另一方面,在幂次体壁面,雷诺比拟系数 $ C_{\rm f} / C_{\rm h}$ 沿 $\theta $ 分布的斜率小于圆柱外形上分布. 在 $M_\infty = 6$, $T_{\rm w} = 500$K 的条件下,式 (2) 预示的圆柱壁面的雷诺比拟关系为 $C_{\rm r_{\rm cy}} = 1.942$,而幂次体外形的计算结果则近似为 $C_{\rm r_{\rm power}} \approx 1.48$;$M_\infty = 12$, $T_{\rm w} = 1000$K 条件下,圆柱壁面的结果为 $C_{\rm r_{\rm cy}} = 1.522$,而幂次体外形的计算结果近似为 $C_{\rm r_{\rm power}} \approx 1.24$. 在 $\theta = 80^\circ$ 时,数值计算与理论预示结果的相对误差最大为 10.2%.
图10
新窗口打开|下载原图ZIP|生成PPT图10幂次体壁面的雷诺比拟关系
Fig.10Reynolds analogy relations on a power-law body
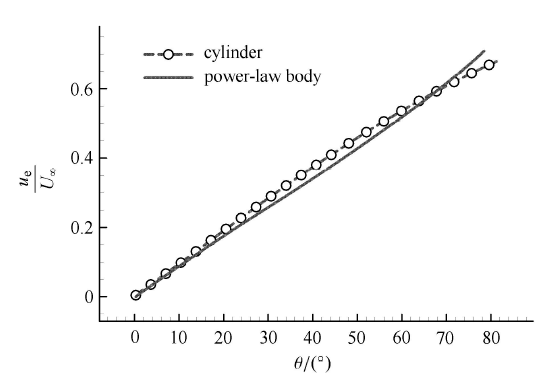
利用 CFD 方法计算钝体壁面压力分布,根据式 (1) 分别计算得到的圆柱体和幂次体 $u_{\rm e} $ 速度分布见图 11. 结果表明不同外形边界层外缘的速度分布存在一定差异,可能是导致不同钝头外形下雷诺比拟系数分布规律有所区别的原因. 具体的影响机理还有待后续进一步的理论研究.
图11
新窗口打开|下载原图ZIP|生成PPT图11边界层外缘速度分布
Fig.11Velocities along boundary layer edge
3 结论
本文采用数值求解 N-S 方程的方法研究了钝头体壁面的广义雷诺比拟关系. 采用不同的数值方法计算了不同来流条件和钝头外形下的壁面的热流、摩阻以及雷诺比拟系数的分布. 数值计算结果与理论预示以及文献中公布的数据吻合.通过改变来流压力条件,计算了不同雷诺数条件下圆柱壁面的热流和摩阻分布,数值计算得到的驻点热流与经典理论预示结果一致. 不同来流条件下的归一化热流分布和摩阻分布在距离驻点下游较远的位置随雷诺数增加存在一定差异. 受其影响,在不同的雷诺数条件下,壁面雷诺比拟关系在较下游的位置也存在一定区别,较高雷诺数下计算得到的 $ C_{\rm f}/C_{\rm h}$ 随 $\theta $ 分布曲线偏离理论预示的线性分布规律.
本文同时计算了抛物线形钝头体壁面的雷诺比拟关系. 在相同的来流条件下,相比于圆柱外形,幂次体壁面的雷诺比拟关系与线性规律吻合较好,且在不同雷诺数条件下的区别较小. 受到钝头体外形对边界层外缘以及边界层内速度和温度的影响,不同外形壁面的雷诺比拟系数存在一定区别.
本文的数值计算和对比研究结果表明,理论预示的广义雷诺比拟关系存在于较大范围的雷诺数区间以及不同类型的钝头体外形中. 在实际工程应用中,如果针对具体的流动条件和钝头外形进行修正,则可以进一步提高预示精度.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
//
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 3]
2nd ed.
[本文引用: 1]
//
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
//
URL [本文引用: 1]
URL [本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 2]
DOIURL [本文引用: 2]
[博士论文].
[PhD Thesis].
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 5]
[本文引用: 1]
DOIURL [本文引用: 1]
.,
[本文引用: 1]
[本文引用: 1]
