熊春宝²⁾, 胡倩倩³⁾, 郭颖^,4)天津大学建筑工程学院, 天津 300072

DYNAMIC RESPONSE OF SATURATED POROUS ELASTIC FOUNDATION UNDER POROSITY ANISOTROPY$^{\bf 1)}$

Xiong Chunbao²⁾, Hu Qianqian³⁾, Guo Ying^,4)School of Civil Engineering, Tianjin University, Tianjin 300072, China

通讯作者: 4)郭颖, 博士, 主要从事介质的多场耦合动力响应研究. E-mail:gytha_ying@tju.edu.cn

收稿日期:2020-03-23接受日期:2020-05-15网络出版日期:2020-07-18

基金资助:

1)国家重点研发计划.2016YFC0802008 天津市自然科学基金.19JCYBJC22200

Received:2020-03-23Accepted:2020-05-15Online:2020-07-18
作者简介 About authors
2)熊春宝,教授,主要从事结构健康监测方面研究.E-mail:luhai_tj@126.com

3)胡倩倩,硕士,主要从事介质的多场耦合动力响应研究.E-mail:15549078321@163.com



摘要
由于不同的沉积条件和应力状态, 天然土体通常表现出一定的各向异性特征. 文章研究地基上表面受温度载荷和机械载荷时, 孔隙率各向异性参数变化对饱和多孔弹性地基热-水-力耦合动力响应问题的影响. 基于Lord-Shulman广义热弹性理论, 结合孔隙率各向异性基本假设, 建立了孔隙率各向异性饱和多孔弹性地基热-水-力耦合动力响应模型, 利用正则模态法推导出无量纲竖向位移、超孔隙水压力、竖向应力和温度分布的解析表达式并加以图示. 正则模态法是一种利用加权残差求得解析解的方法, 相较于其他方法能快速求解偏微分方程. 当孔隙率各向异性参数为1时, 可将该各向异性耦合动力响应模型退化为热-水-力耦合动力响应模型验证该地基模型的合理性. 着重分析了孔隙率各向异性参数变化对不同物理量的影响. 结果表明: 孔隙率各向异性参数变化对物理量均有一定影响. 在地基上表面受温度载荷作用时, 对超孔隙水压力和竖向应力影响最为明显; 在地基上表面受机械载荷作用时, 对超孔隙水压力和温度影响明显. 整体而言, 无论地基上表面受何种载荷, 随着各向异性参数增大, 峰值逐渐减小, 在地基深度增加方向峰值所在位置向靠近地基上表面方向移动.
关键词： 热-水-力耦合模型;各向异性;孔隙率;正则模态法;动力响应

Abstract
Natural soils usually exhibit some anisotropic characteristics due to different deposition conditions and stress states. This study investigated the effects of coupled thermo-hydro-mechanical dynamics on an anisotropy of porosity, fully saturated, and poroelastic half-space subgrade whose surface is subjected to either thermal load or mechanical load in the direction of increasing the depth of the foundation and the direction of the wave propagation. Based on the Lord-Shulman generalized thermoelastic theory and the basic assumption of anisotropy of porosity, the coupled thermo-hydro-mechanical dynamic model for the porosity anisotropy saturated porous elastic foundation is established. The general relationships among non-dimensional vertical displacement, excess pore water pressure, vertical stress, and temperature distribution deduce by using normal mode analysis and depict them graphically. Normal mode analysis is a method using weighted residuals to derive analytical solutions and can thus solve partial differential equations more quickly compared to other methods. When the anisotropic parameter of porosity equals one the dynamic model of this anisotropic foundation can be reduced to a foundation model consistent with the coupled thermo-hydro-mechanical dynamic model, thus verifying the accuracy of the foundation model. The effects of anisotropic parameters of porosity on different physical variables are analyzed emphatically. The results show that the different anisotropic porosity coefficient parameters has a certain influence on all physical variables. The anisotropic porosity has a significant effect on the non-dimensional excess pore water pressure and the vertical stress when the upper surface of the foundation under thermal load, while has obviously effect on the excess pore water and temperature under mechanical load. As a whole, whatever the load is on the surface of the foundation, the peak of the curve decreases gradually and the location of the peak moves closer to the surface in the direction of increasing along the foundation depth as the increase of anisotropy parameters.
Keywords：coupled themo-hydro-mechanical model;anisotropy;porosity;normal mode analysis;dynamic response


PDF (512KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
熊春宝, 胡倩倩, 郭颖. 孔隙率各向异性下饱和多孔弹性地基动力响应$^{\bf 1)}$. 力学学报[J], 2020, 52(4): 1120-1130 DOI:10.6052/0459-1879-20-091
Xiong Chunbao, Hu Qianqian, Guo Ying. DYNAMIC RESPONSE OF SATURATED POROUS ELASTIC FOUNDATION UNDER POROSITY ANISOTROPY$^{\bf 1)}$. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(4): 1120-1130 DOI:10.6052/0459-1879-20-091

引言

温度、渗流及应力场等多场耦合问题在地热资源开发、核废料处理以及垃圾填埋等工程领域中十分常见, ****们针对多孔介质热-水-力耦合作用理论开展了一系列研究. Biot^[1]将多孔介质视为线弹性体, 提出了耦合热弹性理论以消除经典热弹理论中弹性变化对温度没有影响的悖论; Lord和Shulman^[2]发现Biot理论中因热传导方程扩散而使得热传播速度无限大的错误, 通过修正热传导模型建立了Lord-Shulman广义热弹性理论; Noorishad等^[3]首次推导了饱和土体的温度-应力-渗流耦合基本方程, 打开了饱和土体热-水-力三场耦合模型研究的新方向. 国内, 白冰^[4-5]建立了饱和多孔介质热-水-力完全耦合模型的基本控制方程, 分析了热源作用下多孔饱和介质的动力响应问题及循环温度载荷的影响; Liu等^[6-7]利用Laplace变换及反变换, 分析了一维多孔弹性圆柱以及空腔球壳的热流固耦合问题; 熊春宝等^[8-10]引入正则模态法对饱和多孔弹性地基热-水-力耦合模型进行求解并分析参数变化对相应物理量的影响; 刘干斌等^[11]推导了饱和多孔介质热流固耦合效应下的热弹性波动控制方程; 陈迪等^[12-13]通过建立考虑热渗效应和热流固耦合效应的饱和土体固结方程, 研究了圆柱热固结问题; 刘硕等^[14]提出一种新的近场动力学与有限元法的耦合方法求解材料的热传导问题; 朱强华等^[15]提出一种基于特征正交分解和有限元法的瞬态非线性热传导问题的模型分析方法等.

以上这些研究基本都是将土体视为各向同性介质, 忽略了其本身的各向异性特征. 实际上, 自然界中绝大多数土体是天然形成的, 在产生的过程中由于沉积作用会呈现出各向异性的特征^[16]. 国外, Rajapakse和Wang^[17-18]给出了二维均质半无限大地基在横观各向同性和正交各向异性基础上受简谐载荷作用的位移、应力响应; Abousleiman和Ekbote^[19]以及Kanj和Abousleiman^[20]给出了横观各向同性材料热力学问题的一般控制方程, 分析了中空圆柱的热力学特性; Ai等^[21-23]利用不同的积分变换方法研究了各向异性弹性体的热弹动力响应和平面应变问题; Beskou等^[24-25]采用傅里叶级数展开法分析了半无限大各向同性弹性地基上横观各向异性板受到移动载荷作用时的动力响应问题. 国内, 艾智勇等^[26-27]推导了层状横观各向同性地基平面变形问题的解; 韩泽军等^[28]提出了一种新的算法, 用于求解横观各向同性层状地基在时间简谐载荷作用下任意点的应力响应; 张春丽等^[29-30]基于薄板理论建立了直角坐标系正交各向异性弹性地基上覆无限大弹性板的路基路面三维空间力学模型, 推导了板和地基在移动载荷作用下稳态响应的微分方程; 郑保敬等^[31]提出一种模型降阶方法分析非均质材料结构在复杂载荷作用下的动态响应等. 还有一些****研究了特殊的各向异性参数对土体热-水-力耦合作用的影响, 比如Wang等^[32]研究了热传导系数各向异性参数以及渗透系数各向异性参数变化对介质的影响; 夏建中等^[33]考虑渗透系数各向异性提出了在热源作用下的二维热固结模型; Ai和Cang^[34]研究了渗透系数各向异性参数变化对二维多层地基非轴对称固结的影响等. 还有一些****将孔隙率看做各向同性物理量来考虑孔隙率的影响, 比如王立安等^[35]基于Biot波动理论, 建立了孔隙率、密度、剪切模量和渗透系数相互耦合的非均匀饱和半空间模型; 李腾风等^[36]考虑了孔隙率变化对热源作用下非饱和土体水热耦合作用影响等. 针对孔隙率各向异性的研究较为少见, 戴婷等^[37]基于功能梯度圆板中细观孔隙依赖于各自组分变化得到整体孔隙计算式, 在考虑温度影响下建立了材料湿热模型等.

本文在饱和多孔弹性地基基础上引入孔隙率各向异性参数, 并结合Lord-Shulman广义热弹性理论, 建立了考虑孔隙率各向异性的热-水-力耦合动力响应模型并推导其基本控制方程, 采用正则模态法对控制方程进行求解, 得到了各物理量的解析表达, 研究了孔隙率各向异性参数变化对饱和多孔弹性地基的影响. 此外, 还将控制方程进行退化验证模型的合理性.

1 控制方程

1.1 基本假设

本文将孔隙率各向异性参数引入饱和多孔弹性地基模型中, 研究孔隙率各向异性参数变化对饱和多孔弹性地基热-水-力耦合作用下的动力响应问题的影响, 基本假设如下:

(1)饱和多孔地基为流固耦合两相介质, 内部固体颗粒不可压缩, 同时不考虑溶质的影响;

(2)假设地基为二维半无限大弹性体, 介质变形为小变形;

(3)孔隙水渗流服从达西定律;

(4)满足Lord-Shulman广义热弹性理论;

(5)固液两相处于热平衡状态;

(6)假设地基孔隙率处于各向异性状态, 假定竖直方向孔隙率为固定参数, 水平方向孔隙率由各向异性参数控制.

1.2 问题模型

在地基上表面分别受到温度载荷和机械载荷作用, 孔隙率各向异性饱和多孔弹性地基热-水-力耦合问题的计算模型示意图如图1所示.

图1

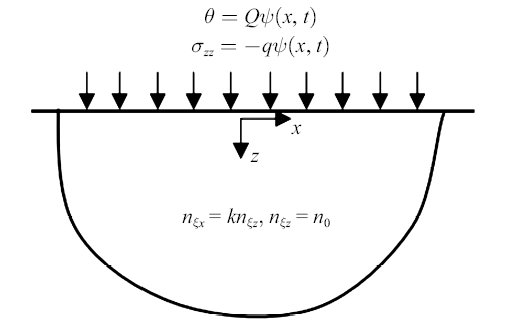新窗口打开|下载原图ZIP|生成PPT
图1计算模型示意图

Fig. 1Schematic diagram of calculation model

1.3 基本控制方程

几何方程

(1)\begin{eqnarray}{\varepsilon}_{{ij}} =\dfrac{1}{2}\left( {{u}_{{i},{j}} +{u}_{{j},{i}} } \right)\end{eqnarray}
式中, ${\varepsilon }_{{ij}} $表示应变张量, ${u}_{i} $表示位移张量, ","表示对于坐标求导.

本构方程

(2)\begin{eqnarray}{\sigma }_{{ij}} =2G{\varepsilon }_{{ij}} +\left( {\lambda e-\beta _1 \theta -P} \right)\delta _{ij}\end{eqnarray}
式中, ${\sigma }_{{ij}} $表示应力张量, $\lambda ,G$表示拉梅常数, $e$表示体积应变, $\theta $表示温度变化, $\theta =T-T_0 $, $T$表示绝对温度, $T_0 $表示初始温度, $\delta _{ij} $表示Kronecker符号, $\beta _1 $表示体积应变, $\beta _1 =\left( {3\lambda +2G} \right)\alpha _{\rm s} $, $\alpha _{\rm s} $表示土颗粒线性热膨胀系数, $P$表示超孔隙水压力.

运动方程

(3)\begin{eqnarray}{\sigma }_{{ij},{j}} +{F}_{i} =\rho _\xi {\ddot{{u}}}_{i}\end{eqnarray}
式中, ${F}_{i} $表示体力张量, $\rho _\xi $表示不同方向的密度, $\rho_\xi =n_\xi \rho _{\rm w} +\left( {1-n_\xi }\right)\rho _{\rm s} $, $\rho _{\rm w}$表示孔隙水密度, $\rho _{\rm s} $表示土颗粒密度, 字母上方"."表示对于时间$t$的求导.

热传导方程

(4)\begin{eqnarray}K{\theta }_{,{ii}} =\rho _\xi C_E \left( {{\dot{{\theta }}}+\tau {\ddot{{\theta }}}} \right)+\beta _1 T_0 \left( {{\dot{{e}}}+\tau {\ddot{{e}}}} \right)\end{eqnarray}
式中, $K$表示热传导系数, $C_E $表示单位质量介质的比热容, $\tau $表示弛豫时间.

不计体力的运动平衡方程

(5)\begin{eqnarray}G{u}_{{i},{jj}} +\left( {\lambda +G} \right){u}_{{j},{ij}} -\beta _1 {\theta }_{,{i}} -{P}_{,{i}} =\rho _\xi {\ddot{{u}}}_{i}\end{eqnarray}
能量方程

(6)\begin{eqnarray}m\left( {{\dot{{\theta }}}+\tau {\ddot{{\theta }}}} \right)+\beta _1 T_0 \left( {{\dot{{e}}}+\tau {\ddot{{e}}}} \right)=K{\theta }_{,{ii}}\end{eqnarray}
式中, $m$表示介质比热容, $c_{\rm w} $表示孔隙水比热容, $c_{\rm s} $表示土颗粒比热容, $m=n_\xi \rho _{\rm w} c_{\rm w} +\left( {1-n_\xi } \right)\rho _{\rm s} c_{\rm s} $.

结合达西定律的流体平衡方程

(7)\begin{eqnarray}b\left( {\alpha _u {\dot{{\theta }}}-{\dot{{e}}}} \right)+\rho _{\rm w} {\ddot{{e}}}+{P}_{,{ii}} =0\end{eqnarray}
式中, $\alpha _u $表示介质线膨胀系数, $\alpha _{\rm w} $表示孔隙水线性热膨胀系数, $\alpha _{\rm s} $表示土颗粒线性热膨胀系数, 其中, $\alpha _u =n_\xi \alpha _{\rm w} +\left( {1-n_\xi } \right)\alpha _{\rm s} $, $k_{\rm d} $表示介质的渗透系数, $g$表示重力加速度, $b={\rho _{\rm w} g}/{k_{\rm d} }$.

基于二维半无限大弹性地基假设, 同时为使后续公式推导过程更为简化, 引入笛卡尔坐标系$\left( {x,y,z} \right)$, 将位移分量表示为$u_i =\left({u,0,w} \right)$.

为使计算结果具有一定的普适性, 引入下列无量纲量, 该组无量纲量同参考文献^[38]

(8)$\begin{eqnarray} \left.\begin{array}{l} \left( {'x,'u} \right)=V_x \eta \left( {x,u} \right), \ \ '\theta =\dfrac{\beta _1 \theta }{\lambda +2G}\\ \left( {'z,'w} \right)=V_z \eta \left( {z,w} \right), \ \ V_x =\sqrt {\dfrac{\lambda +2G}{\rho _{\xi x} }} \left( {'t,'\tau } \right)=V_x V_z \eta \\ \left( {t,\tau } \right), \ \ V_z =\sqrt {\dfrac{\lambda +2G}{\rho _{\xi z} }}\\ 'P=\dfrac{P}{\lambda +2G}, \ \ '\sigma =\dfrac{\sigma }{G}, \ \ \eta =\dfrac{m}{K}\\ \end{array}\right\} \end{eqnarray}$
根据方程(8), 方程(1)$\sim$(7)可简化为(为书写简便, 省略点号)

(9)$\sigma _{xx} =\beta ^2\dfrac{\partial u}{\partial x}+\left( {\beta ^2-2} \right)\dfrac{\partial w}{\partial z}-\beta ^2\theta -\beta ^2P$
(10)$\sigma _{zz} =\left( {\beta ^2-2} \right)\dfrac{\partial u}{\partial x}+\beta ^2\dfrac{\partial w}{\partial z}-\beta ^2\theta -\beta ^2P$
(11)$\tau _{xz} =\dfrac{\partial u}{\partial z}+\dfrac{\partial w}{\partial x}$
(12)$\beta ^2\dfrac{\partial ^2u}{\partial x^2}-\beta ^2\dfrac{\partial \theta }{\partial x}+\varphi _0 \dfrac{\partial ^2u}{\partial z^2}-\beta ^2\dfrac{\partial P}{\partial x} + \left( {\beta ^2-1} \right)\dfrac{\partial ^2w}{\partial x\partial z}=\beta ^2\varphi _0 \dfrac{\partial ^2u}{\partial t^2}$
(13)$\beta ^2\dfrac{\partial ^2w}{\partial z^2}+\left( {\beta ^2-1} \right)\dfrac{\partial ^2u}{\partial x\partial z}-\beta ^2\dfrac{\partial \theta }{\partial z}-\beta ^2\dfrac{\partial P}{\partial z}+\dfrac{\partial ^2w}{\varphi _0 \partial x^2}=\beta ^2\dfrac{\partial ^2w}{\varphi _0 \partial t^2}$
(14)$\left( {1+\tau \dfrac{\partial }{\partial t}} \right)\left[ {\dfrac{\partial \theta }{\partial t}+\varphi _2 \left( {\dfrac{\partial ^2u}{\partial x\partial t}+\dfrac{\partial ^2w}{\partial z\partial t}} \right)} \right] =\varphi _1 \dfrac{\partial ^2\theta }{\partial x^2}+\dfrac{\partial ^2\theta }{\varphi _1 \partial z^2}$
(15)$\varphi _3 \dfrac{\partial \theta }{\partial t}+\varphi _6 \left( {\dfrac{\partial ^3u}{\partial x\partial t^2}+\dfrac{\partial ^3w}{\partial z\partial t^2}} \right)+\varphi _1 \dfrac{\partial ^2P}{\partial x^2} -\varphi _4 \dfrac{\partial ^2u}{\partial x\partial t}-\varphi _5 \dfrac{\partial ^2w}{\partial z\partial t}+\dfrac{\partial ^2P}{\varphi _1 \partial z^2}=0$
式中

$\begin{eqnarray*} &&\beta ^2=\dfrac{\lambda +2G}{G},\ \ \varphi _0 =\dfrac{\rho _{\xi x} }{\rho _{\xi z} },\ \ \varphi _1 =\sqrt {\dfrac{\rho _{\xi z} }{\rho _{\xi x} }} \end{eqnarray*}$

$\varphi _2 =\dfrac{\beta _1^2 T_0 }{m\left( {\lambda +2G}\right)},\ \ \varphi _3 =\dfrac{ba_u }{\eta \beta _1 },\ \ \varphi _4=\dfrac{n_{\xi x} b}{\eta \left( {\lambda +2G} \right)}$

$\varphi _5=\dfrac{n_{\xi z} b}{\eta \left( {\lambda +2G} \right)},\ \ \varphi _6 =\dfrac{\rho _{\rm w} }{\sqrt {\rho _{\xi x} \rho _{\xi z}}}$

1.4 边界条件

本文讨论地基上表面受到温度载荷、机械载荷作用时的热-水-力耦合动力响应问题, 其中边界条件如下.

(1)地基上表面受温度载荷作用

① 地基上表面应力自由

(16)\begin{eqnarray}\sigma _{xz} =0,\ \ \sigma _{zz} =0\end{eqnarray}
② 地基上表面受到温度载荷作用

(17)$\theta =Q\psi \left( {x,t} \right)$
(18)$\psi \left( {x,t} \right)=\psi ^* \left( {a,\omega } \right)\exp \left( {\omega t+{\rm i}ax} \right)$
式中, $Q$表示温度载荷, $\omega $表示频率(复时间常数), $a$表示$x$轴方向的波数, $\psi ^* \left( {a,\omega } \right)$表示载荷振幅, i为虚数单位, i $=\sqrt {-1} $.

③ 地基上表面可透水

(19)\begin{eqnarray}P=0\end{eqnarray}
(2)地基上表面受机械载荷作用

① 地基上表面受机械载荷作用

(20)\begin{eqnarray}\sigma _{xz} =0,\ \ \sigma _{zz} =-q\psi \left( {x,t} \right)\end{eqnarray}
式中, $q$表示机械载荷.

② 地基上表面不考虑温度载荷

(21)\begin{eqnarray}\theta =0\end{eqnarray}
③ 地基上表面可透水

(22)\begin{eqnarray}P=0\end{eqnarray}

2 二维热-水-力耦合问题的正则模态分析

所考虑的物理量的解均可以按照以下正则模态的形式进行分解

(23)\begin{eqnarray}&&\left[ {u,w,\sigma _{ij} ,\theta ,P} \right]\left( {x,z,t} \right) =\left[ {u^* \left( z \right),w^* \left( z \right),\sigma _{ij} ^* \left( z \right),\theta ^* \left( z \right),P^* \left( z \right)} \right]\cdot \exp \left( {\omega t+{\rm i}ax} \right)\end{eqnarray}
式中, $u^* \left( z \right)$, $w^* \left( z \right)$, $\sigma _{ij}^* \left( z \right)$, $\theta ^* \left( z \right)$, 和$P^* \left( z\right)$分别表示所考虑的物理场的振幅.

对方程(9)$\sim$(15)进行正则模态分解可得如下方程

(24)$\sigma _{xx}^* =\beta ^2u^* {\rm i}a+\left( {\beta ^2-2} \right)\dfrac{\partial w^* }{\partial z}-\beta ^2\theta ^* -\beta ^2P^*$
(25)$\sigma _{zz}^* =\left( {\beta ^2-2} \right)u^* {\rm i}a+\beta ^2\dfrac{\partial w^* }{\partial z}-\beta ^2\theta ^* -\beta ^2P^*$
(26)$\tau _{xz}^* =\dfrac{\partial u^* }{\partial z}+{\rm i}aw^*$
(27)$\left( {\dfrac{\partial ^2}{\partial z^2}-\varphi _0 } \right)u^* +\varphi _1 \dfrac{\partial w^* }{\partial z}-\varphi _2 \theta ^* -\varphi _2 P^* =0$
(28)$\left( {\dfrac{\partial ^2}{\partial z^2}-\varphi _3 } \right)w^* +\varphi _4 \dfrac{\partial u^* }{\partial z}-\dfrac{\partial \theta ^* }{\partial z}-\dfrac{\partial P^* }{\partial z}=0$
(29)$\left( {\dfrac{\partial ^2}{\partial z^2}-\varphi _5 } \right)\theta ^* =\varphi _6 u^* +\varphi _7 \dfrac{\partial w^* }{\partial z}$
(30)$\left( {\dfrac{\partial ^2}{\partial z^2}-\varphi _8 } \right)P^* -\varphi _9 u^* -\varphi _{10} \dfrac{\partial w^* }{\partial z}+\varphi _{11} \theta ^* =0$
式中

$\phi _0 =\beta ^2\left( {\omega ^2+\dfrac{a^2}{\varphi _0 }} \right),\ \ \phi _1 =\dfrac{\left( {\beta ^2-1} \right){\rm i}a}{\varphi _0 }$

$\phi _2 =\dfrac{\beta ^2{\rm i}a}{\varphi _0 },\ \ \phi _3 =\dfrac{a^2+\beta ^2w^2}{\varphi _0 \beta ^2},\ \ \phi _4 =\dfrac{\left( {\beta ^2-1} \right){\rm i}a}{\beta ^2}$

$\phi _5 =\varphi _1^2 a^2+\varphi _1 \omega +\varphi _1 \tau \omega ^2,\ \ \phi _6 =\varphi _1 \varphi _2 {\rm i}a\omega +\varphi _1 \varphi _2 \tau \omega ^2{\rm i}a$

$\phi _7 =\varphi _1 \varphi _2 \omega +\varphi _1 \varphi _2 \tau \omega ^2,\ \ \phi _9 =\varphi _1 \varphi _4 {\rm i}a\omega -\varphi _1 \varphi _6 {\rm i}a\omega ^2$

$\phi _8 =\varphi _1^2 a^2,\ \ \phi _{10} =\varphi _1 \varphi _5 \omega -\varphi _1 \varphi _6 \omega ^2,\ \ \phi _{11} =\varphi _1 \varphi _3 \omega$

令$\wp ={\partial }/{\partial z}$, 对分解后的方程进行简化整理

(31)$\left( {\wp ^2-\phi _0 } \right)u^* +\phi _1 \wp w^* -\phi _2 \theta ^* -\phi _2 P^* =0$
(32)$\left( {\wp ^2-\phi _3 } \right)w^* +\phi _4 \wp u^* -\theta ^* -P^* =0$
(33)$\left( {\wp ^2-\phi _5 } \right)\theta ^* =\phi _6 u^* +\phi _7 \wp w^*$
(34)$\left( {\wp ^2-\phi _8 } \right)P^* -\phi _9 u^* -\phi _{10} \wp w^* +\phi _{11} \theta ^* =0$
消去$w^* (z)$, $\theta ^* (z)$和$P^* \left( z \right)$, 可以得到一个关于$u^* \left( z \right)$的8阶偏微分方程

(35)$\begin{eqnarray}\left( {\wp ^{8}-B_1 \wp ^6+B_2 \wp ^4-B_3 \wp ^2+B_4 } \right)u^* \left( z \right)=0\end{eqnarray}$
将方程(35)因式分解后可得

(36)$\begin{eqnarray}\left( {\wp ^2-k_1^2 } \right)\left( {\wp ^2-k_2^2 } \right)\left( {\wp ^2-k_3^2 } \right)\left( {\wp ^2-k_4^2 } \right)u^* \left( z \right)=0\end{eqnarray}$
式中, $k_i^2 \left( {i=1,2,3,4} \right)$是如下八阶方程的特征根

(37)$\begin{eqnarray}k^{8}-B_1 k^6+B_2 k^4-B_3 k^2+B_4 =0\end{eqnarray}$
其中

$B_1 =k_1^2 +k_2^2 +k_3^2 +k_4^2 $

$B_2 =k_1^2 k_2^2 +k_1^2 k_3^2 +k_1^2 k_4^2 +k_2^2 k_3^2 +k_2^2 k_4^2 +k_3^2 k_4^2$

$B_3 =k_1^2 k_2^2 k_3^2 +k_1^2 k_2^2 k_4^2 +k_1^2 k_3^2 k_4^2 +k_2^2 k_3^2 k_4^2 $

$B_4 =k_1^2 k_2^2 k_3^2 k_4^2$

方程的解可表示为如下形式

(38)$u^* \left( z \right)=\sum\limits_{n=1}^4 {M_{1n} \left( {a,\omega } \right)} e^{-k_n z}$
(39)$w^* \left( z \right)=\sum\limits_{n=1}^4 {M_{1n} '\left( {a,\omega } \right)} e^{-k_n z}$
(40)$\theta ^* \left( z \right)=\sum\limits_{n=1}^4 {M_{1n} "\left( {a,\omega } \right)} e^{-k_n z}$
(41)$P^* \left( z \right)=\sum\limits_{n=1}^4 {M_{1n} "'\left( {a,\omega } \right)} e^{-k_n z}$
其中

$M_{1n} '\left( {a,\omega } \right)=H_{1n} M_{1n} \left( {a,\omega } \right),\ M_{1n} "\left( {a,\omega } \right)=H_{2n} M_{1n} \left( {a,\omega } \right)$

$M_{1n} "'\left( {a,\omega } \right)=H_{3n} M_{1n} \left( {a,\omega } \right),\ H_{1n} =\dfrac{m_4 \phi _2 -m_1 m_5 }{m_2 m_5 -m_3 \phi _2 }$

$H_{2n} =\dfrac{\phi _6 }{m_6 }+\dfrac{m_7 H_{1n} }{m_6 },\ H_{3n} =\dfrac{\phi _9 }{m_8 }+\dfrac{m_9 H_{1n} }{m_8 }-\dfrac{\phi _{11} H_{2n} }{m_8 }$

代入应力分量表达式中得

(42)$\sigma _{xx}^* =\sum\limits_{n=1}^4 {H_{4n} M_{1n} \left( {a,\omega } \right)} e^{-k_n z}$
(43)$\sigma _{zz}^* =\sum\limits_{n=1}^4 {H_{5n} M_{1n} \left( {a,\omega } \right)} e^{-k_n z}$
(44)$\tau _{xz}^* =\sum\limits_{n=1}^4 {H_{6n} M_{1n} \left( {a,\omega } \right)} e^{-k_n z}$
式中

$H_{4n} ={\rm i}a\beta ^2-k_n \left( {\beta ^2-2} \right)H_{1n} -\beta ^2H_{2n} -\beta ^2H_{3n}$

$H_{5n} ={\rm i}a\left( {\beta ^2-2} \right)-k_n \beta ^2H_{1n} -\beta ^2H_{2n} -\beta ^2H_{3n}$

$H_{6n} =-k_n +{\rm i}aH_{1n}$

3 算例分析及结果讨论

以饱和多孔半无限大弹性地基为例, 分别在地基的上表面施加温度载荷和机械载荷, 研究孔隙率各向异性参数变化对地基深度增加方向和波的传播方向上竖向位移、超孔隙水压力、竖向应力及温度的影响. 根据求得的解析解表达式, 利用Maple软件, 结合边界条件得到了各物理的分布规律图.

3.1 计算模型验证

本文是考虑孔隙率各向异性参数的影响而建立的控制方程, 当孔隙率各向异性参数$k=1.0$时方程可退化为各向同性耦合动力响应方程, 其结果可与参考文献^[38]进行对比, 从而验证模型的合理性.

研究中所需要的基本参数取值同参考文献^[38]一致, $\psi ^* =1$, $a=1.2$. 其他参数详见表1.

Table 1
表1
表1饱和多孔弹性地基热-水-力多物理场耦合基本参数
Table 1Basic parameters of themo-hydro-mechanical coupling of saturated porous elastic foundation

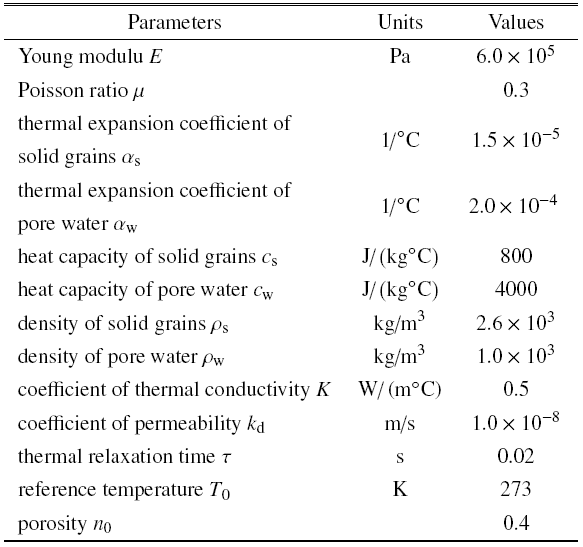新窗口打开|下载CSV

3.2 地基深度增加方向各物理量变化规律

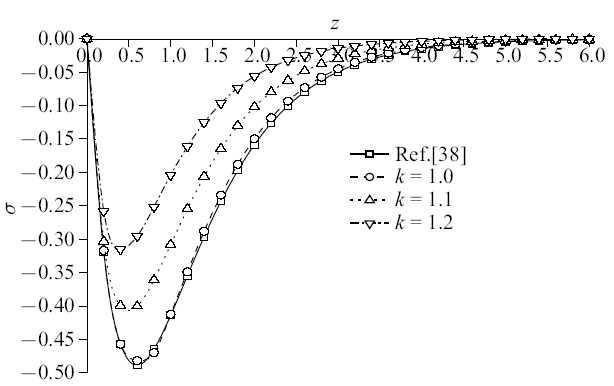
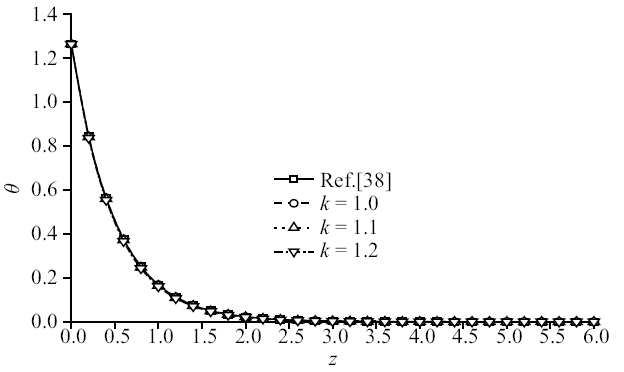
在地基上表面分别施加温度载荷和机械载荷作用, 研究地基深度增加方向上孔隙率各向异性参数变化对各物理量的影响. 以下8幅图为$x=1.0$平面上$t=0.5$时各物理量的变化规律图. 其中, 退化模型曲线与参考文献结果曲线吻合较好, 进而验证了模型的合理性.

图2$\sim\!$图5为温度载荷下竖向位移、超孔隙水压力、竖向应力和温度变化规律图, 整体来说, 孔隙率各向异性参数变化对竖向位移和温度影响较小, 对超孔隙水压力和竖向应力影响较大. 竖向位移变化趋势都是由压缩状态逐渐转为膨胀最后趋于平缓衰减至零; 温度则是逐渐衰减至零. 超孔隙水压力曲线和竖向应力曲线峰值均逐渐减小, 且峰值出现位置向地基深度减小方向移动, 超孔隙水压力减幅为52.72%和61.06%, 竖向应力减幅为16.92%和26.13%. 这主要是由于孔隙水对温度较为敏感, 随着孔隙率各向异性参数增大, 两个方向孔隙分布更不均匀影响地基排水速率, 进而使得超孔隙水压力变小, 而超孔隙水压力变化影响了竖向应力的变化.

图2

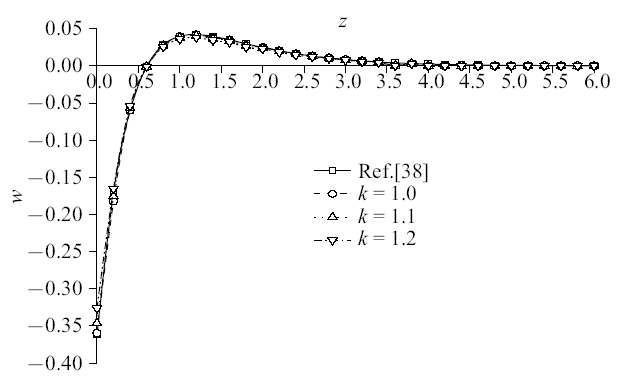新窗口打开|下载原图ZIP|生成PPT
图2温度载荷作用时无量纲竖向位移分布规律图

Fig. 2The distribution of non-dimension vertical displacement under thermal load

图3

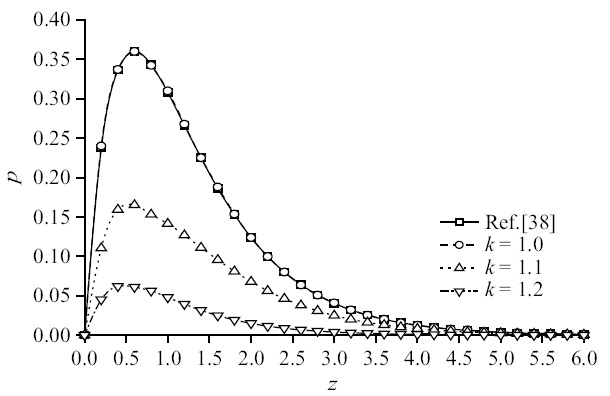新窗口打开|下载原图ZIP|生成PPT
图3温度载荷作用时无量纲超孔隙水压力分布规律图

Fig. 3The distribution of non-dimension excess pore water pressure under thermal load

图4

新窗口打开|下载原图ZIP|生成PPT
图4温度载荷作用时无量纲竖向应力分布规律图

Fig. 4The distribution of non-dimension vertical stress under thermal load

图5

新窗口打开|下载原图ZIP|生成PPT
图5温度载荷作用时无量纲温度分布规律图

Fig. 5The distribution of non-dimension temperature under thermal load



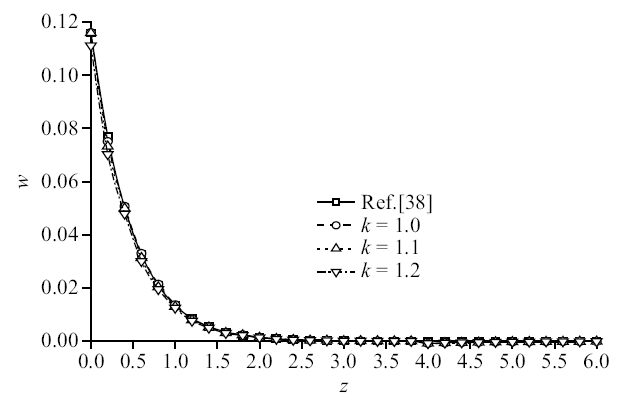
图6$\sim\!$图9为机械载荷下竖向位移、超孔隙水压力、竖向应力和温度变化规律图, 整体来说, 孔隙率各向异性对竖向位移和竖向应力影响较小, 对超孔隙水压力和温度影响较大. 图6和图8中, 竖向位移和竖向应力均逐渐衰减至零, 但应力衰减速率比位移衰减速率略快. 图7超孔隙水压力曲线随各向异性参数的增加逐渐减小, 尤其是峰值处, 有较为明显变化, 峰值减幅为8.89%和9.82%; 图9中随着各向异性参数的增大, 温度的峰值逐渐减小, 减幅依次为18.46%和19.74%.

图6

新窗口打开|下载原图ZIP|生成PPT
图6机械载荷作用时无量纲竖向位移分布规律图

Fig. 6The distribution of non-dimension vertical displacement under mechanical load

图7

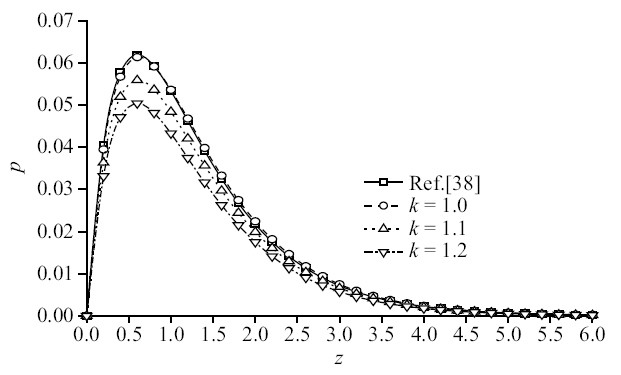新窗口打开|下载原图ZIP|生成PPT
图7机械载荷作用时无量纲超孔隙水压力分布规律图

Fig. 7The distribution of non-dimension excess pore water pressure under mechanical load

图8

新窗口打开|下载原图ZIP|生成PPT
图8机械载荷作用时无量纲竖向应力分布规律图

Fig. 8The distribution of non-dimension vertical stress under mechanical load

图9

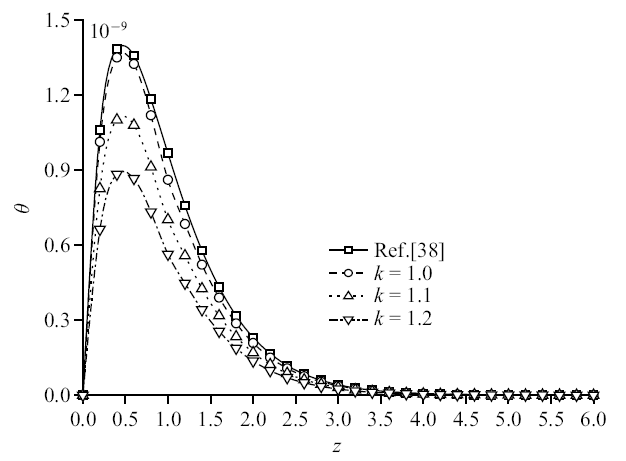新窗口打开|下载原图ZIP|生成PPT
图9机械载荷作用时无量纲温度分布规律图

Fig. 9The distribution of non-dimension temperature under mechanical load



从图6$\sim\!$图9可以看出, 温度曲线量级相对较小, 说明单纯的机械载荷作用产生的热量不多, 可忽略不计. 孔隙率各向异性参数变化对超孔隙水压力和温度的影响趋势相同, 但对温度的影响更明显, 这是由于随着各向异性参数增大, 使得地基热量耗散更为迅速, 引起明显的温度变化, 而孔隙率各向异性参数的变化影响了地基中孔隙的分布, 参数增大, 孔隙分布更为不均匀, 导致超孔隙水压力峰值减小.

3.3 波的传播方向上各物理量变化规律

本节从波的传播方向上研究了地基上表面分别施加温度载荷和机械载荷作用时孔隙率各向异性参数变化对所考虑物理量的影响. 图10$\sim\!$图17为$z=1.0$平面上$t=0.5$时各物理量的变化规律图.

图10

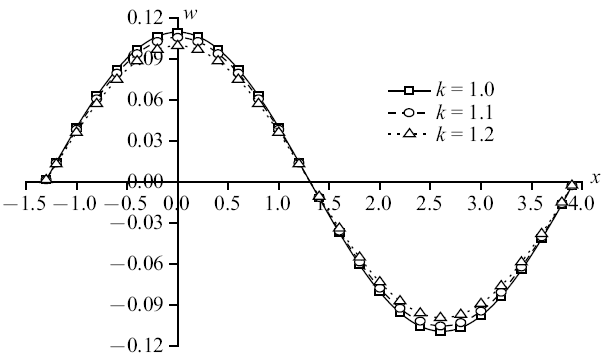新窗口打开|下载原图ZIP|生成PPT
图10温度载荷作用时无量纲竖向位移分布规律图

Fig. 10The distribution of non-dimension vertical displacement under thermal

图11

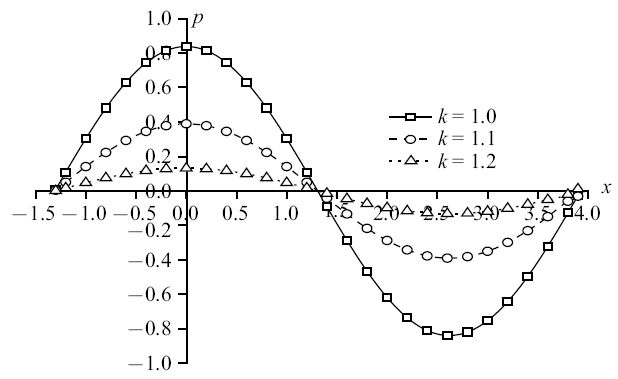新窗口打开|下载原图ZIP|生成PPT
图11温度载荷作用时无量纲超孔隙水压力分布规律图

Fig. 11The distribution of non-dimension excess pore water pressure under thermal load

图12

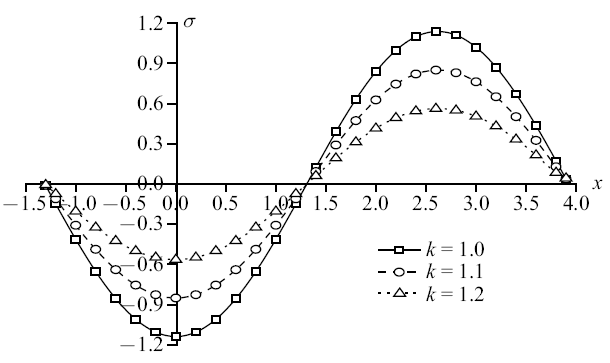新窗口打开|下载原图ZIP|生成PPT
图12温度载荷作用时无量纲竖向应力分布规律图

Fig. 12The distribution of non-dimension vertical stress under thermal load

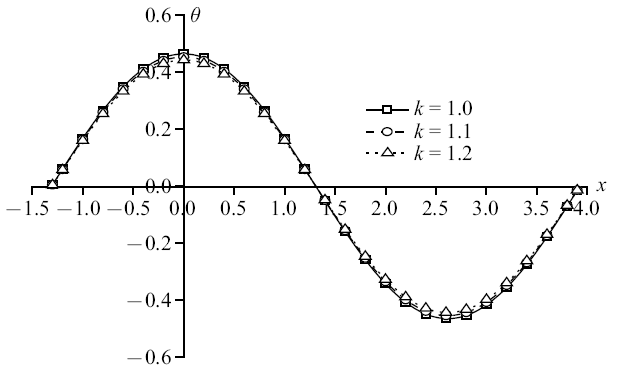
图13

新窗口打开|下载原图ZIP|生成PPT
图13温度载荷作用时无量纲温度分布规律图

Fig. 13The distribution of non-dimension temperature under thermal load

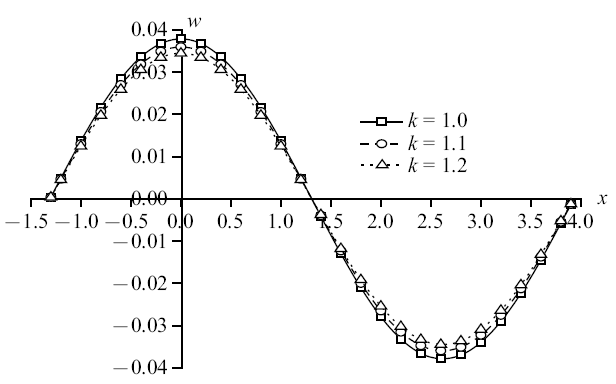
图14

新窗口打开|下载原图ZIP|生成PPT
图14机械载荷作用时无量纲竖向位移分布规律图

Fig. 14The distribution of non-dimension vertical displacement under mechanical load

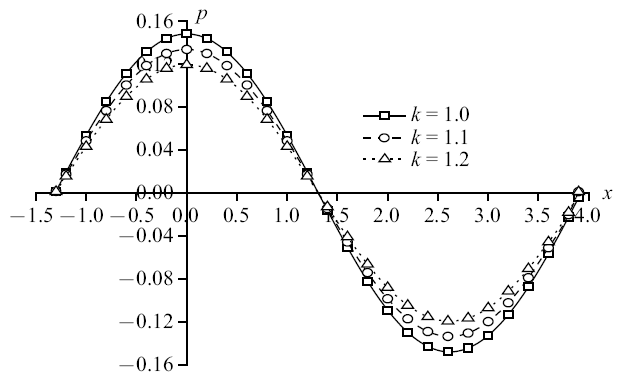
图15

新窗口打开|下载原图ZIP|生成PPT
图15机械载荷作用时无量纲超孔隙水压力分布规律图

Fig. 15The distribution of non-dimension excess pore water pressure under mechanical load

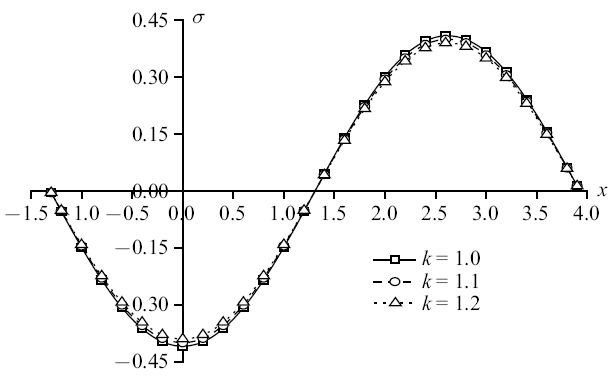
图16

新窗口打开|下载原图ZIP|生成PPT
图16机械载荷作用时无量纲竖向应力分布规律图

Fig. 16The distribution of non-dimension vertical stress under mechanical load

图17

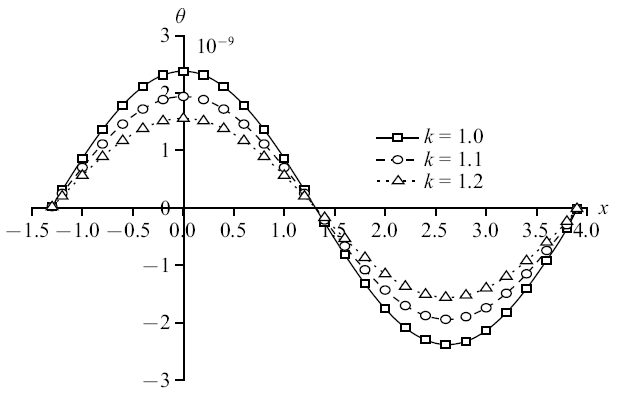新窗口打开|下载原图ZIP|生成PPT
图17机械载荷作用时无量纲温度分布规律图

Fig. 17The distribution of non-dimension temperature under mechanical load



图10$\sim\!$图13为温度载荷下竖向位移、超孔隙水压力、竖向应力和温度变化规律图. 整体来说, 随着孔隙率各向异性参数的增大, 物理量峰值逐渐减小. 可以明显看出, 孔隙率各向异性参数变化对超孔隙水压力和竖向应力的影响远超于竖向位移和温度. 其中, 超孔隙水压力减幅依次为53.50%和66.15%, 竖向应力减幅依次为25.26%和33.77%, 而竖向位移减幅在4%附近, 温度减幅稳定在2%左右. 这是因为孔隙率的变化影响到孔隙水, 随着各向异性参数增大, 孔隙分布更为不均匀, 孔隙水排出速率受到影响, 导致超孔隙水压力减幅明显, 而超孔隙水压力变化又会影响竖向应力, 使得竖向应力变化.

图14$\sim\!$图17为机械载荷下竖向位移、超孔隙水压力、竖向应力和温度的变化规律图. 孔隙率各向异性对竖向位移和竖向应力变化不太明显, 减幅相对较小; 对超孔隙水压力和温度变化明显, 其中温度减幅更大, 为18.46%和19.74%. 单纯的机械载荷作用产生于地基中的温度很小, 孔隙率的变化使得地基散热更为迅速, 所以对温度的影响更加明显.

4 结论

本文在饱和多孔弹性地基基础上引入孔隙率各向异性参数, 并结合Lord-Shulman广义热弹性理论, 建立了考虑孔隙率各向异性的热-水-力耦合动力响应模型并推导其基本控制方程, 采用正则模态法对简化方程进行求解, 得到了各物理量的解析表达, 分析了孔隙率各向异性参数变化对相关物理量的影响. 主要结论如下:

(1) 考虑孔隙率各向异性参数的饱和多孔弹性地基热-水-力耦合动力响应模型可退化为各向同性饱和多孔弹性地基热-水-力耦合动力响应模型, 退化后物理量变化规律与参考文献^[38]曲线分布规律一致, 验证了模型的合理性;

(2) 地基深度增加方向上, 地基上表面受温度载荷作用时, 孔隙率各向异性参数变化对超孔隙水压力和竖向应力影响明显, 随着各向异性参数增大, 峰值逐渐减小, 峰值所在位置向靠近地基上表面移动; 地基上表面受机械载荷作用时, 孔隙率各向异性参数变化对超孔隙水压力和温度影响明显, 随着各向异性参数增大, 峰值逐渐减小, 峰值所在位置向靠近地基上表面移动;

(3) 波的传播方向上, 孔隙率各向异性参数变化对各物理量均有影响, 使得峰值逐渐减小, 地基上表面受温度载荷作用时, 对超孔隙水压力和竖向应力影响明显; 地基上表面受机械载荷作用时, 对超孔隙水压力和温度影响明显.

附录

${\varepsilon }_{{ij}} $ 应变张量 ${u}_{i} $ 位移张量

${\sigma }_{{ij}} $ 应力张量 $\lambda ,G$ 拉梅常数

${e}$ 体积应变 $\theta $ 温度变化

$T$ 绝对温度 $T_0 $ 初始温度

$\delta _{ij} $ Kronecker符号 $\beta _1 $ 体积应变

$P$ 超孔隙水压力 ${F}_{i} $ 体力张量

$\rho _\xi $ 不同方向的密度 $\rho _{\xi x} $ 水平方向的密度

$\rho _{\xi z} $ 竖直方向的密度 $\rho _{\rm w} $ 孔隙水密度

$\rho _{\rm s} $ 土颗粒密度 $n_\xi $ 不同方向的孔隙率

$n_{\xi x} $ 水平方向的孔隙率 $n_{\xi z} $ 竖直方向的孔隙率

$K$ 热传导系数 $C_E $ 单位质量介质比热容

$\tau $ 热弛豫时间 $m$ 介质比热容

$c_{\rm w} $ 孔隙水比热容 $c_{\rm s} $ 土颗粒比热容

$\alpha _u $ 介质线膨胀系数 $k_{\rm d} $ 介质的渗透系数

$\alpha _{\rm w} $ 孔隙水线性热膨胀系数 $\alpha _{\rm s} $ 土颗粒线性热膨胀系数

$g$ 重力加速度 $Q$ 温度载荷

$\omega $ 频率(复时间常数) $a$ $x$轴方向的波数

$\psi ^* \left( {a,\omega } \right)$ 载荷振幅 $q$ 机械载荷

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Biot MA. Thermoelasticity and irreversible thermodynamics
Journal of Applied Physics, 1956,27(3):240-253
DOIURL [本文引用: 1]

[2] Lord HW, Shulman YA. A generalized dynamical theory of thermoelasticity
Journal of the Mechanics and Physics of Solids, 1967,15(5):299-309
DOIURL [本文引用: 1]

[3] Noorishan J, Tsang CF, Witherspoo PA. Coupled thermal-hydraulic-mechanical phenomena in saturated fractured porous
Journal of Geophysical Research, 1984,89(B12):365-373
[本文引用: 1]

[4] 白冰. 饱和多孔介质热-水-力控制方程耦合项的意义及耦合影响分析
岩土力学, 2006,27(4):519-536
[本文引用: 1]

( Bai Bing. Effects of coupling schemes of thermo-hydro-mechanica governing equations for saturated porous medium
Rock and Soil Mechanics, 2006,27(4):519-536 (in Chinese))
[本文引用: 1]

[5] 白冰. 循环温度载荷作用下饱和多孔介质热-水-力耦合响应
工程力学, 2007,24(5):87-92
[本文引用: 1]

( Bai Bing. Thermo-hydro-mechanical responses of saturated porous media under cyclic thermal loading
Engineering Mechanics, 2007,24(5):87-92 (in Chinese))
[本文引用: 1]

[6] Liu GB, Xie KH, Zheng RY. Thermo-elastodynamic response of a spherical cavity in saturated poroelastic medium
Applied Mathematical Modelling, 2010,34(8):2203-2222
DOIURL [本文引用: 1]

Abstract

In this paper, an attempt has been made to investigate the thermo-hydro-elastodynamic response of a spherical cavity in isotropic saturated poroelastic medium when subjected to a time dependent thermal/mechanical source. The fully coupling thermo-hydro-elastodynamic model is presented on the basis of equations of motion, fluid flow, feat flow and constitutive equation with effective stress and temperature change. Solutions of displacement, temperature and stresses are obtained by using a semi-analytical approach in the domain of Laplace transform. Numerical results are also performed for portraying the nature of variations of the field variables, i.e. the coefficient of thermo-osmosis, the permeability. In addition, comparisons are presented with the corresponding partially thermo-hydro-elastodynamic model and thermo-elastodynamic model to ascertain the validity and the difference between these models.

[7] Liu GB, Xie KH, Zheng RY. Mode of a spherical cavity's thermo-elastodynamic response in a saturated porous medium for non-torsional loads
Computers & Geotechnics, 2010,37(3):381-390
[本文引用: 1]

[8] Xiong CB, Guo Y, Diao Y. Normal mode analysis to a poroelastic half-space problem under generalized thermoelasticity
Latin American Journal of Solids and Stuctures, 2017,14:933-952
[本文引用: 1]

[9] 熊春宝, 郭颖, 刁钰 等. 载荷作用下多孔饱和地基的热-水-力耦合动力响应分析
计算力学学报, 2018,35(6):795-801


( Xiong Chunbao, Guo Ying, Diao Yu, et al. Coupled thermo-hydro-mechanical dynamic response of saturated porous foundation under normal load
Chinese Journal of Computational Mechanics, 2018,35(6):795-801 (in Chinese))


[10] 熊春宝, 郭颖, 刁钰. 考虑热-水-力耦合效应的饱和多孔地基动力响应分析
应用数学和力学, 2016,37(8):850-858
[本文引用: 1]

( Xiong Chunbao, Guo Ying, Diao Yu. Dynamic responses of saturated porous foundations under coupled thermo-hydro-mechanical effects
Applied Mathematics and Mechanics, 2016,37(8):850-858 (in Chinese))
[本文引用: 1]

[11] 刘干斌, 郑荣跃, 陶海冰. 饱和多孔介质中热弹性波传播特性研究
地下空间与工程学报, 2016,12(4):926-931
URL [本文引用: 1]
Based on the dynamic response model presented by the author for saturated medium with thermal, hydraulic and mechanical coupling, a thermo-hydro-mechanical coupled theory of thermo-elastic wave for the saturated porous mediumis established in this paper. By introducing a potential function and using the displacement vector, the dispersion equation for the thermo-elastic wave in saturated soil is derived, the characteristics of wave velocity, attenuation for p<sub>1, p2 ,T and S wave are discussed under different values of thermal expansion coefficient. The result indicated that the influence of thermal expansion coefficient on p1 and p2 was large, and the thermo-hydro-mechanical coupling effect could not be ignored. Other comparison results between thermo-elasticity theory (THM) and the theory of elasticity (HM) verify the validity of THM theory of wave presented in this paper.
( Liu Ganbin, Zheng Rongyue, Tao Haibing. Propagation of thermo-elastic wave in saturated porous media
Chinese Journal of Underground Space and Engineering, 2016,12(4):926-931 (in Chinese))
URL [本文引用: 1]
Based on the dynamic response model presented by the author for saturated medium with thermal, hydraulic and mechanical coupling, a thermo-hydro-mechanical coupled theory of thermo-elastic wave for the saturated porous mediumis established in this paper. By introducing a potential function and using the displacement vector, the dispersion equation for the thermo-elastic wave in saturated soil is derived, the characteristics of wave velocity, attenuation for p1, p2 ,T and S wave are discussed under different values of thermal expansion coefficient. The result indicated that the influence of thermal expansion coefficient on p1 and p2 was large, and the thermo-hydro-mechanical coupling effect could not be ignored. Other comparison results between thermo-elasticity theory (THM) and the theory of elasticity (HM) verify the validity of THM theory of wave presented in this paper.

[12] 陈迪, 郑荣跃, 刘干斌 等. 考虑热渗效应的有限热源固结近似解
力学与实践, 2016,38(3):294-298
DOIURL [本文引用: 1]
通过建立考虑热渗效应和热流固耦合效应的饱和土体固结方程,研究了无限长圆柱热固结问题. 利用Fourier 和Laplace 变换及其逆变换,给出了热固结问题的解析解;然后对空间内无限长圆柱形热源问题进行研究,得到非等温条件下柱体周围饱和土体温度、孔隙水压力的近似解,并总结其规律,分析了热渗系数、固结系数对温度作用下土体固结的影响.
( Chen Di, Zheng Rongyue, Liu Ganbin, et al. Approximate solution of finite heat source consolidation with consideration of the effect of thermo-osmosis
Mechanics in Engineering, 2016,38(3):294-298 (in Chinese))
DOIURL [本文引用: 1]
通过建立考虑热渗效应和热流固耦合效应的饱和土体固结方程,研究了无限长圆柱热固结问题. 利用Fourier 和Laplace 变换及其逆变换,给出了热固结问题的解析解;然后对空间内无限长圆柱形热源问题进行研究,得到非等温条件下柱体周围饱和土体温度、孔隙水压力的近似解,并总结其规律,分析了热渗系数、固结系数对温度作用下土体固结的影响.

[13] 郭华, 陶海冰, 刘干斌 等. 考虑热渗效应的有限长圆柱热固结解
力学季刊, 2018,39(1):171-181
[本文引用: 1]

( Guo Hua, Tao Haibing, Liu Ganbin, et al. Solution of finite length cylindrical thermosetting considering heat infiltration effect
Chinese Quarterly of Mechanics, 2018,39(1):171-181 (in Chinese))
[本文引用: 1]

[14] 刘硕, 方国东, 王兵 等. 近场动力学与有限元方法耦合求解热传导问题
力学学报, 2018,50(2):339-348
URL [本文引用: 1]

( Liu Shuo, Fang Guodong, Wang Bing, et al. Study of thermal conduction problem using coupled peridynamics and fifinite element method
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(2):339-348 (in Chinese))
URL [本文引用: 1]

[15] 朱强华, 杨恺, 梁钰 等. 基于特征正交分解的一类瞬态非线性热传导问题的新型快速分析方法
力学学报, 2020,52(1):124-138
[本文引用: 1]

( Zhu Qianghua, Yang Kai, Liang Yu, et al. A novel fast algorithm based on model order reduction for one class of transient nonlinear heat conduction problem
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(1):124-138 (in Chinese))
[本文引用: 1]

[16] 王炳军, 肖洪天, 党彦 等. 横观各向同性地基各向异性对应力场影响研究
四川大学学报(工程科学版), 2015,47(6):40-48
[本文引用: 1]

( Wang Bingjun, Xiao Hongtian, Dang Yan, et al. Influence of the anisotropy of a transversely isotropic foundation on additional stress fields
Journal of Sichuan University (Engineer Science Edition), 2015,47(6):40-48 (in Chinese))
[本文引用: 1]

[17] Rajapakse R, Wang Y. Elastodynamic Green's functions of orthotropic half plane
Journal of Engineering Mechanics, 1991,117(3):588-604
DOIURL [本文引用: 1]

[18] Wang Y, Rajapakse R. Transient fundamental solutions for a transversely isotropic elastic half space
Proceedings: Mathematical and Physical Science, 1993,442(1916):505-531
[本文引用: 1]

[19] Abousleiman Y, Ekbote S. Solutions for the inclined borehole in a porothermoelastic transversely isotropic medium
Journal of Applied Mechanics, 2005,72(2):102-114
DOIURL [本文引用: 1]

[20] Kanj M, Abousleiman Y. Porothermoelastic analyses of anisotropic hollow cylinders with applications
International Journal for Numerical and Analytical Methods in Geomechanics, 2005,29(1):103-126
DOIURL [本文引用: 1]

[21] Ai ZY, Ren GP. Dynamic analysis of a transversely isotropic multilayered half-plane subjected to a moving load
Soil Dynamics and Earthquake Engineering, 2016,83:162-166
DOIURL [本文引用: 1]

[22] Ai ZY, Xu CJ, Ren GP. Vibration of a pre-stressed plate on a transversely isotropic multilayered half-plane due to a moving load
Applied Mathematical Modelling, 2018,59(7):728-738
DOIURL

[23] Ai ZY, Liu CL, Wang LH. Transient response of a transversely isotropic multilayered half-space due to a vertical loading
Applied Mathematical Modelling, 2017,50(10):414-431
DOIURL [本文引用: 1]

[24] Beskou ND, Chen YY, Qian J. Dynamic response of an elastic plate on a cross-anisotropic poroelastic half-plane to a load moving on its surface
Transportation Geotechnics, 2018,14:98-106
DOIURL [本文引用: 1]

[25] Chen YY, Beskou ND, Qian J. Dynamic response of an elastic plate on a cross-anisotropic poroelastic half-plane to a load moving on its surface
Soil Dynamics and Earthquake Engineering, 2018,107:292-302
DOIURL [本文引用: 1]

[26] 艾智勇, 张逸帆, 王路君. 层状横观各向同性地基平面应变问题的扩展精细积分解
岩土力学, 2018,39(5):1885-1890, 1900
[本文引用: 1]

( Ai Zhiyong, Zhang Yifan, Wang Lujun. Extended precise integration solution for plane strain problem of transversely isotropic multilayered soils
Rock and Soil Mechanics, 2018,39(5):1885-1890, 1900 (in Chinese))
[本文引用: 1]

[27] 朱桂春, 史培新, 王占生. 层状横观各向同性地基变形问题的一个近似解
岩土工程学报, 2020,42(4):790-796
[本文引用: 1]

( Zhu Guichun, Shi Peixin, Wang Zhansheng. An approximate solution for deformation problems of transversely isotropic multi-layered soils
Chinese Journal of Geotechnical Engineering, 2020,42(4):790-796 (in Chinese))
[本文引用: 1]

[28] 韩泽军, 林皋, 周小文 等. 横观各向同性层状地基动应力响应的求解与分析
岩土力学, 2018,39(6):2287-2294
[本文引用: 1]

( Han Zejun, Lin Gao, Zhou Xiaowen. An approximate solution for deformation problems of transversely isotropic multi-layered soils
Rock and Soil Mechanics, 2018,39(6):2287-2294 (in Chinese))
[本文引用: 1]

[29] 张春丽, 王博, 祝彦知. 移动载荷下正交各向异性地基无限大板的动力响应
岩土工程学报, 2017,39(2):352-358
[本文引用: 1]

( Zhang Chunli, Wang Bo, Zhu Yanzhi. Dynamic response of infinite plate on orthotropic half-plane medium under moving loads
Chinese Journal of Geotechnical Engineering, 2017,39(2):352-358 (in Chinese))
[本文引用: 1]

[30] 王博, 张春丽, 祝彦知. 正交各向异性路基路面在移动载荷作用下的空间动力响应
郑州大学学报(工学版), 2019,40(1):50-54, 61
[本文引用: 1]

( Wang Bo, Zhang Chunli, Zhu Yanzhi. Efficiency analysis of structural extreme response estimation methods
Journal of Zhengzhou University (Engineering Science), 2019,40(1):50-54, 61 (in Chinese))
[本文引用: 1]

[31] 郑保敬, 梁钰, 高效伟 等. 功能梯度材料动力学问题的POD模型降阶分析
力学学报, 2018,50(4):787-797
URL [本文引用: 1]

( Zheng Baojing, Liang Yu, Gao Xiaowei, et al. Analysis for dynamic response of functionally graded materials using pod based reduced order model
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(4):787-797 (in Chinese))
URL [本文引用: 1]

[32] Wang LJ, Zhu B, Chen YM, et al. Precise model for predicting excess pore-water pressure of layered soils induced by thermal-mechanical loads
Journal of Engineering Mechanics, 2019,145(1):04018114
[本文引用: 1]

[33] 夏建中, 徐云飞, 尤玉云 等. 考虑热源下二维渗透各向异性饱和土热固结解析解
科技通报, 2019,35(1):101-107
[本文引用: 1]

( Xia Jianzhong, Xu Yunfei, You Yuyun, et al. Two-dimensional thermal consolidation study with anisotropic permeability under considering heat source
Bulletin of Science and Technology, 2019,35(1):101-107 (in Chinese))
[本文引用: 1]

[34] Ai ZY, Cang NR. Non-axisymmetric Biot consolidation analysis of multi-layered saturated poroelastic materials with anisotropic permeability
Soils & Foundations, 2013,53(3):408-416
[本文引用: 1]

[35] 王立安, 赵建昌, 侯小强 等. 非均匀饱和半空间的Lamb问题
岩土力学, 2020(5), DOI: 10.16285/j.rsm.2019.0591
URL [本文引用: 1]

( Wang Lian, Zhao Jianchang, Hou Xiaoqiang, et al. Lamb problem for non-homogeneous saturated half space
Rock and Soil Mechanics, 2020(5), DOI: 10.16285/j.rsm.2019.0591 (in Chinese))
URL [本文引用: 1]

[36] 李腾风, 王志良, 申林方 等. 基于格子Boltzmann方法非饱和土体水热耦合模型研究
工程力学, 2019,36(9):154-160, 196
[本文引用: 1]

( Wang Lian, Zhao Jianchang, Hou Xiaoqiang, et al. A coupled moisture-heat model for unsaturated soil based on lattice Boltzmann method
Engineering Mechanics, 2019,36(9):154-160, 196 (in Chinese))
[本文引用: 1]

[37] 戴婷, 戴宏亮, 李军剑 等. 含孔隙变厚度FG圆板的湿热力学响应
力学学报, 2019,51(2):212-223
[本文引用: 1]

( Dai Ting, Dai Hongliang, Li Junjian, et al. Hygeothermal mechanical behavior of a FG circular plate with variable thickness
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(2):212-223 (in Chinese))
[本文引用: 1]

[38] Guo Y, Zhu HB, Xiong CB, et al. A two-dimensional generalized thermo-hydro-mechanical-coupled problem for a poroelastic half-space
Waves in Random & Complex Media, 2018, doi: 10.1080/17455030.2018.1557758
URL [本文引用: 4]</sub>