 ,2)北京理工大学爆炸科学与技术国家重点实验室, 北京100081
,2)北京理工大学爆炸科学与技术国家重点实验室, 北京100081RESEARCH ON ELECTROMAGNETIC RADIATION DURING THE EXPLOSION PROGRESS OF COMPOSITION B EXPLOSIVES$^{\bf 1)}$
Ren Huilan, Chu Zhuxin, Li Jianqiao, Ma Tianbao ,2)State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China
,2)State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China通讯作者: 2)马天宝, 教授, 主要研究方向: 计算爆炸力学及弹药工程.madabal@bit.edu.cn
收稿日期:2020-01-9接受日期:2020-04-15网络出版日期:2020-07-18
| 基金资助: |
Received:2020-01-9Accepted:2020-04-15Online:2020-07-18
作者简介 About authors

摘要
炸药爆炸过程中产生明显的电磁辐射干扰在很多领域引起了重视, 爆炸产生电磁辐射的机理和理论模型都不成熟, 实验仍然是研究这一现象的重要手段. 本文设计了不同质量的B炸药爆炸电磁辐射实验, 测量了爆炸整个过程中不同时刻的电磁辐射信号. 通过小波分析方法对实测信号进行处理, 得到真实信号和信号的时频特点, 小波分析得到真实信号的频谱主要分布在0$\sim$50 kHz. 利用自主开发的EXPLOSION-3D软件对实验工况进行数值模拟, 得到爆炸过程不同时刻流场的特点. 对比实验结果和数值模拟结果得出: 第一个脉冲信号是由B炸药爆轰产生的高温高压等离子体直接产生的电磁脉冲; 第二个脉冲信号是由地面反射的冲击波追上前沿冲击波, 空气冲击波阵面处形成的等离子体产生的电磁脉冲; 第三个脉冲信号是冲击波撞击测量线圈引起的无效信号. 其中, 第一个电磁脉冲幅值与当量的1/3次方基本呈线性关系, 其到达时间对炸药药量不敏感; 第二个电磁脉冲出现的时间与炸药的当量成指数关系, 药量越大, 出现时间越晚. 通过对第二个脉冲信号的分析, 得出了冲击波反射形成电磁脉冲信号时的爆炸波流场特征, 为后续相关理论机理研究提供了验证数据.
关键词:
Abstract
The electromagnetic radiation interference, which can be obviously observed during the explosives process, has attracted attention in many fields. However, the corresponding generation mechanism and theoretical model are still immature, experiments are still the key approach to study this phenomenon. This paper designs experiments to collect the electromagnetic radiation signals, generated by different charges of composition B explosives (Comp B), and uses the wavelet transform method to obtain these signals time-frequency characteristics, namely the main spectrum distribution is in the range of 0$\sim$50 kHz. Furthermore, the self-developed EXPOSION-3D software is used to simulate the experimental conditions to obtain the characteristics of the flow field during the explosion. By comparing the experimental results with the numerical simulations, series of conclusions are given in the following. The first pulse signal is the electromagnetic pulse directly generated by the high-temperature and high-pressure plasma generated by the detonation of Comp B; the second pulse signal is an electromagnetic pulse generated by the plasma formed at the air shock wave front which is caught up by the reflected shock wave from the ground; the third pulse signal is an invalid signal caused by the shock wave hitting the measurement coils. The amplitude of the first electromagnetic pulse has a linear relationship with the 1/3 power of the charge, and its arrival time is not sensitive to the charge of explosive. The time of the second electromagnetic pulse is in an exponential relationship with the charge of explosive. Overall, this paper put forward the characteristics of the explosion wave flow field when the shock wave reflection forms the electromagnetic wave signal, which provides verification data for the subsequent theoretical research.
Keywords:
PDF (9621KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
任会兰, 储著鑫, 栗建桥, 马天宝. B炸药爆炸过程中电磁辐射研究$^{\bf 1)}$. 力学学报[J], 2020, 52(4): 1199-1210 DOI:10.6052/0459-1879-20-010
Ren Huilan, Chu Zhuxin, Li Jianqiao, Ma Tianbao.
引言
炸药爆炸是一个复杂的过程, 常伴随着光、热力学、电磁等效应, 其产生的电磁脉冲对不同电子设备都有不同程度的干扰, 甚至引起失效. 尤其在火箭分离过程中, 因为爆炸螺栓和聚能切割索等广泛应用的火工品爆炸而瞬态的电磁脉冲有可能会对分离面附近的电子设备造成干扰, 影响其正常工作, 甚至对火箭的飞行安全构成威胁[1]. 了解炸药爆炸过程的电磁辐射特性和规律, 可以加深对炸药爆轰以及冲击波传播过程的认识, 对提高爆炸力学测试系统的抗干扰能力具有很大帮助.在炸药爆炸电磁辐射理论方面, 由于化学爆炸的复杂性, 目前对其产生电磁脉冲的机制还只是提出了一些原理性解释. 主要的机制有电荷运动[2]、爆炸的热效应[3-4]、等离子体辐射[5]、约束等离子体中的横向等离子体共振[6]、爆轰产物中的带电粒子运动[7]、铝添加物对电磁辐射的影响[8]和磁场扩散与导电流体高速运动中引起的磁场运动[9]. 虽然都各自提出了机理推测, 但没有否定其他机理的可能性, 炸药爆炸电磁辐射现象还未形成普遍适用的机理和数学原理模型, 理论方面仍需要进一步研究.
在实验研究方面Kolsky[10]首次用探针发现炸药爆炸伴随着电磁辐射现象, 随后许多文章[11-14]用天线对该现象进行了验证研究, 主要初步分析炸药爆炸产生电磁辐射的原因及电磁辐射的影响因素. Soloviev等[15]不仅测量了电场信号也测量了磁场信号, 实验结果表明在爆轰初始阶段场强是以距离的4次幂减小的. Harlin等[16]分析了毫秒以内低频信号最大值的时间和冲击波传播时间的关系.Nemzek等[17]用10 kg的B炸药做了10次重复实验来验证炸药产生电磁脉冲的可重复性. 国内炸药电磁辐射研究较少, 曹景阳等[1]用天线对航天火工品的电磁辐射进行了地面实验, 王长利等分别对带壳装药热爆炸[18]、典型炸药爆炸[19]过程产生的电磁辐射特性进行研究. 综上所述, 在实验中大多用宽带天线收集电磁信号, 测量电场, 对于磁场的关注较少. 信号的测量时段也比较短, 大都在毫秒以内, 毫秒后的电磁信号很少有关注, 背景信号的影响也很少关注. 对爆炸所产生辐射的过程和特点并未形成系统的认识, 研究仍然处于发展的过程中.
由于炸药爆炸产生电磁辐射的机理和理论模型都不成熟, 实验仍然是研究这一现象的重要手段. 实验针对测量磁场信号少、毫秒后的辐射信号关注少和对背景信号分析少的情况, 本文设计了实验, 测量了B炸药从爆炸开始到结束整个过程中的磁场信号, 并通过小波分析方法处理实测信号[20-21], 得到真实信号, 从时域上分析得到的不同时刻的脉冲信号, 定量给出信号幅值、到达时间与药量关系. 针对不同时刻的脉冲信号产生的机理, 进行爆炸流场的数值模拟[22-25], 结合爆炸过程的数值模拟分析结果和实测结果, 分析了不同时刻出现电磁脉冲信号的原因.
1 炸药爆炸过程中的电磁辐射测量实验
1.1 实验设置
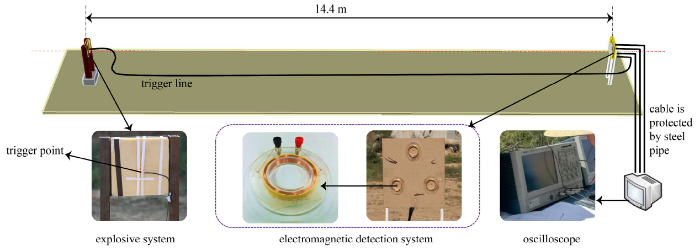
实验装置和布局如图1所示. 实验在空旷的室外场地进行, 实验分成两个系统, 一个是炸药系统, 另一个是磁场测量系统. 炸药系统是由炸药、传爆药柱、钢板和支架构成. 炸药选用B炸药, 起爆点为炸药中心, 采用传爆药柱起爆. 磁场测量系统是由磁场测量线圈[26]、支架、示波器和50 $\Omega $同轴电缆组成. 磁场测量线圈骨架是由亚克力材料制成, 线圈轴的外径是6 cm, 内径5 cm, 线圈高度是0.9 cm, 铜线直径是0.27 mm, 线圈的匝数为300匝. 为获得更多信号, 每次用3个测量线圈. 支架是由木板和PVC杆组成(非金属材料, 防止干扰到测量线圈). 采集到的信号经同轴电缆传输并由示波器记录波形, 实验中示波器的采样率为10 MS/s. 为防止爆炸飞石等击中缆线, 将其用钢管套住埋于地下.图1
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图1实验布局示意图
Fig. 1Diagram showing the experimental set up
炸药系统和磁场测量系统的中心在同一水平线上, 两者中心相距14.4 m, 两者之间靠爆炸产生的磁场产生联系. 为了统一时间, 将一根触发线放在传爆药柱旁边, 当传爆药柱爆炸时, 触发线通电被触发, 示波器开始记录信号, 此时作为信号记录的零时刻.
1.2 实验结果
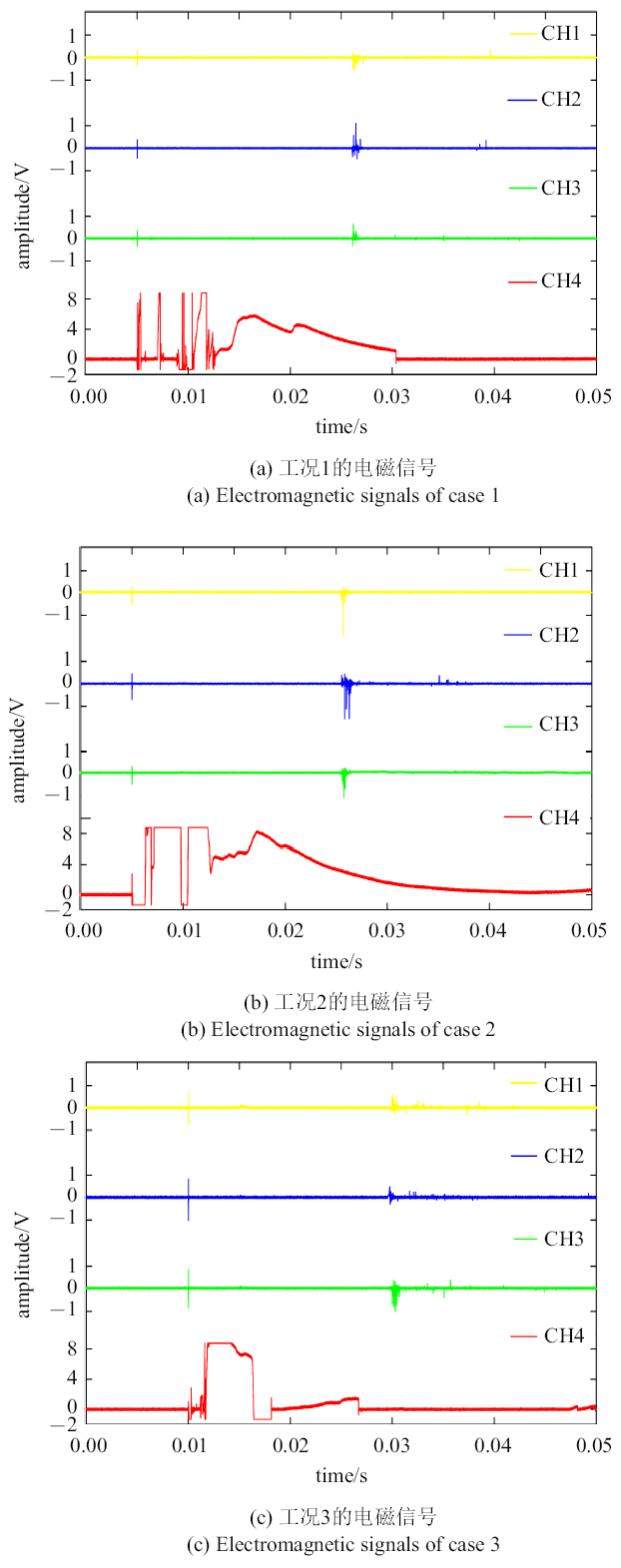
本文根据炸药质量不同设计了3组实验, 炸药质量分别为4.5 kg, 6.0 kg和7.5 kg, 分别记为工况1、工况2和工况3. 采集到的数据如图2所示. 每组实验包含4个通道的信号, 通道CH4是触发通道, 由于触发线直接处于爆炸产生的高温高压电离爆炸场中, 所以CH4通道的信号特别杂乱. 通道CH1, CH2, CH3是实测信号, 触发通道触发后有明显的电磁脉冲信号, 这些脉冲的重复性好, 原始信号图只能粗略看到一些信息, 需要对信号进一步处理, 进行更为细致的观察. 在实验之前, 我们也进行空白测量, 记录测试环境的背景信号.图2
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图2电磁信号实验结果
Fig. 2Electromagnetic signals in experiments
1.3 信号分析
由于爆炸实验环境十分复杂, 理想的实验背景环境难以达到, 实际测量数据不可避免地包含有复杂的背景信号和其他噪声信号, 实测数据受到的干扰. 因此, 进一步研究爆炸电磁辐射特性的前提和基础是对爆炸电磁脉冲实测数据进行适当的分析和处理[27]. 爆炸产生的电磁脉冲属于瞬变信号, 需要对时域和频域进行联合分析, 传统的傅里叶变换已不太适合, 小波变换是时间和频率的局部变换, 因而能有效地从信号中提取信息, 通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析, 解决了傅里叶变换不能解决的许多困难问题, 被誉为"数学显微镜"[28-30], 小波变换在时域和频域都具有表征信号局部特征的能力, 具有多分辨率分析的特点, 因此, 本文选择应用小波变换对炸药爆炸电磁脉冲进行分析和处理.1.3.1 信号小波分析
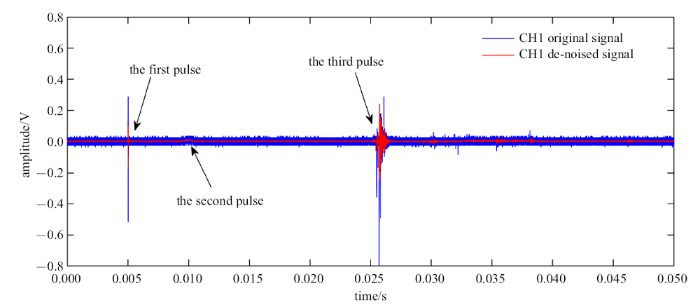
实验中的信号较多, 选取工况2的通道CH1的信号进行分析, 选用db7小波基进行5层分解[27], 用matlab编程对实测信号进行降噪处理. 整体信号的原始波形图和降噪波形图如图3所示. 对比原始信号和降噪信号发现, 原始信号的许多毛刺被有效地滤除, 降噪信号变得光滑, 而且小波降噪还能将噪声淹没的信号给提取出来, 得到了真实的爆炸电磁脉冲信号. 从图3中可以看出3个典型的脉冲, 根据时间先后分别记为第一个脉冲信号、第二个脉冲信号和第三个脉冲信号. 其出现的时间分别记为$t_{1}$, $t_{2}$, $t_{3}$.
图3
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图3工况2下CH1的原始波形和降噪波形对比图
Fig. 3Comparison between the original and de-noised waveforms of CH1 in case 2
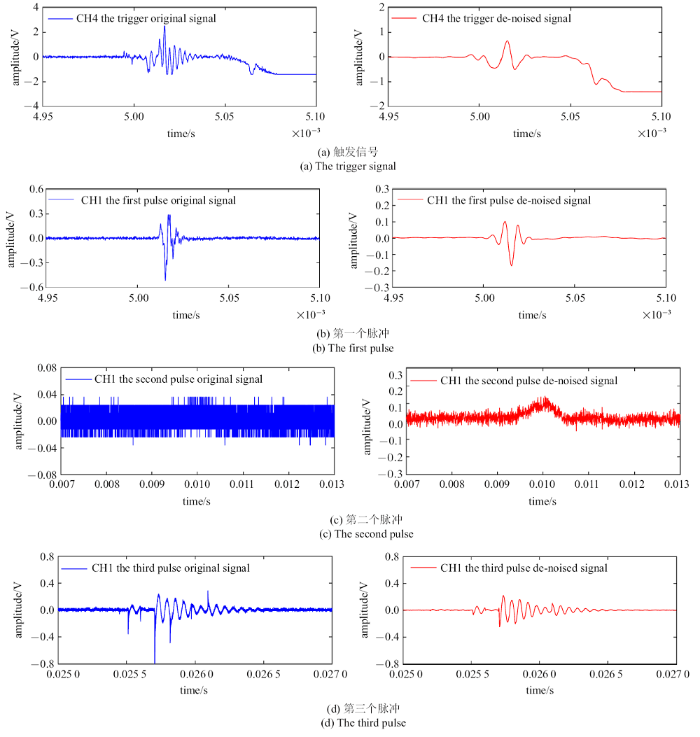
由于整体图不能够精确地读出时域信息, 故分别将3个脉冲进行局部放大, 如图4(b), 图4(c), 图4(d)所示. 另外将工况2的触发通道CH4的触发点处的信号局部放大, 如图4(a)所示.
图4
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图4工况2下的CH1通道典型脉冲原始信号和降噪信号的局部放大
Fig. 4Comparison between the original and de-noised waveforms of CH1 in case 2
从图4(a)中可以看出, 触发信号时间为4.991 ms, 从图4(b)中可以看出第一个脉冲信号出现的时间为5.010 ms, 第一个电磁脉冲信号的时间$t_{1}$和触发点的时间差为0.019 ms. 图4(c)中从原始信号的整体图中很难发现这一个信号, 经过滤波后才发现这一个微弱的信号. 第二个脉冲信号出现的时间为9.415 ms, 第二个电磁脉冲信号的时间$t_{2}$和触发点的时间差4.424 ms. 图4(d)可以看出, 小波降噪很好的去掉了背景信号和毛刺, 保留了原始信号的波形. 第三个脉冲信号出现的时间为25.505 ms, 第三个电磁脉冲信号的时间$t_{3}$和触发点的时间差为20.514 ms. 这样我们就得到了3个典型脉冲信号出现的时间.
1.3.2 信号频域分析
从频域上对工况2的CH1信号进行分析, 对背景信号、实测的原始信号和降噪信号分别进行快速傅里叶变换得到频域分布图, 如图5所示.
图5
 新窗口打开|下载原图ZIP|生成PPT
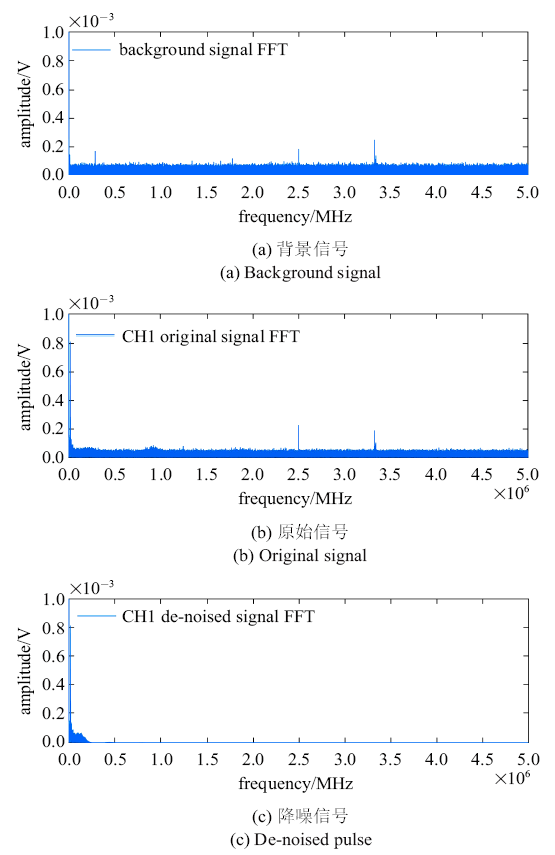
新窗口打开|下载原图ZIP|生成PPT图5工况2下的CH1信号的频谱图
Fig. 5Frequency spectrum of CH1 in case 2
图5(a)$\sim\!$图5(c)分别是背景信号、实测信号和降噪信号的FFT的结果图. 由于示波器采样率是10 MS/s, 根据奈奎斯特(Nyquist)采样定律, 最高频率为5 MHz. 对比图5(a)和图5(b)发现, 两者的频谱分布几乎相同, 这是因为低频信号被淹没在背景噪声中. 在2.5 MHz和3.3 MHz出现了较强的噪声信号. 观察图5(c)可以发现高频的频谱分量没有了, 只在300 kHz以下有频谱分量. 这说明背景信号被有效地滤除了. 我们将横轴拉伸放大, 观察0$\sim$300 kHz的频谱分布, 结果如图6所示.
图6
 新窗口打开|下载原图ZIP|生成PPT
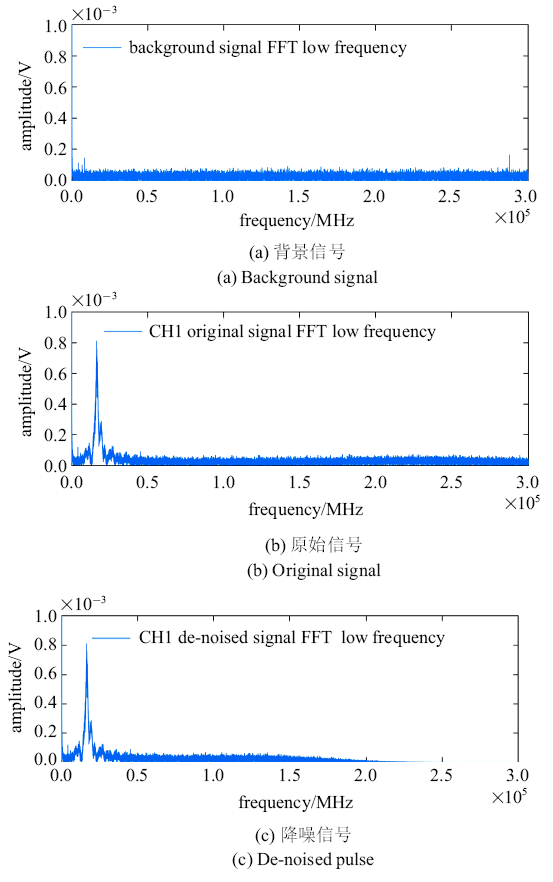
新窗口打开|下载原图ZIP|生成PPT图6工况2下的CH1信号的低频频谱图
Fig. 6Low frequency spectrum of CH1 in case 2
图6(a)$\sim\!$图6(c)分别是背景信号、实测信号、降噪信号的0$\sim$300 kHz的频谱分布图, 对比图6(a)和图6(b)可以看出, 背景信号在0$\sim$50 kHz没有频谱分量, 而实测信号在0$\sim$50 kHz有频谱分布. 这说明真实信号的频谱主要分布在0$\sim$50 kHz. 这与文献[8]得出的炸药爆炸产生的电磁辐射频率主要集中在1 MHz以内结论符合. 对比图6(b)和图6(c)发现, 0$\sim$50 kHz的频谱分量保存完好, 200 kHz以上的背景噪声被有效的滤除了. 综上, 小波降噪是将背景噪声进行滤除, 而保留了真实的信号. 从频域上看, 小波降噪方法处理信号是合适的.
1.3.3 信号时域分析
上面只分析了工况2的信号, 现将3个工况的每个通道的信号都进行同样的降噪处理, 分别计算出3个脉冲的时间, 如图7所示.
图7
 新窗口打开|下载原图ZIP|生成PPT
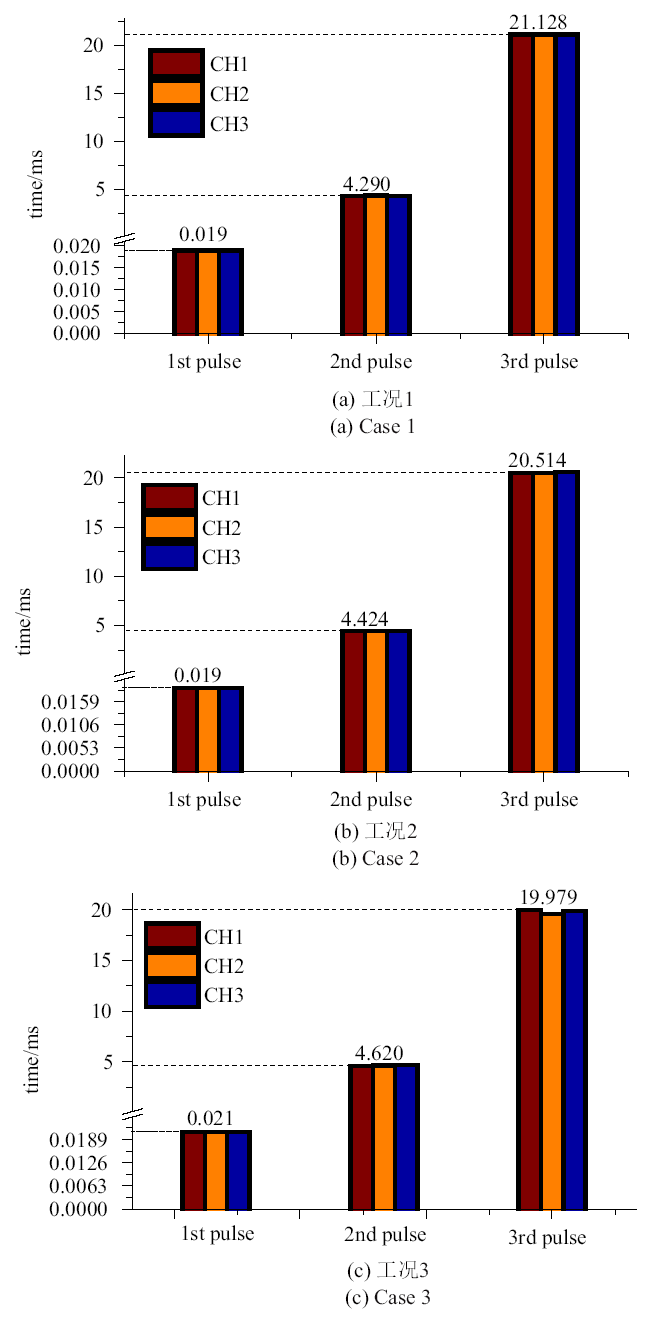
新窗口打开|下载原图ZIP|生成PPT图7三个工况典型脉冲信号的时间
Fig. 7The arriving time of each typical pulse in all three cases
图7中分别给出了工况1$\sim$3的每个通道的3个典型脉冲信号的时间统计图. 第一个脉冲信号, 每个柱状的高度都一致, 时间上一致性好. 出现的时间量级是微秒级别. 这个时间内, 没有其他信号源, 只有炸药爆炸能产生电磁脉冲信号. 时间尺度上与Harlin等[16]测得时间相符合. 这个脉冲信号是由炸药爆炸直接产生的, 炸药爆炸瞬间产生的巨大能量, 使气体温度迅速升高, 温度约3500 K, 导致气体电离形成等离子体, 电磁辐射的根源可能就是等离子体的辐射[31]. 第二个电磁脉冲信号出现的时间比较长, 大约在4 ms以后. 这个信号Cook[12]的文章中有所提及, 其产生的机理尚不明确. 第三个电磁脉冲信号出现的时间更久, 约为20 ms, 这个时间比较长, 爆轰过程已经结束. 这个阶段本来应该没有信号, 第三个脉冲信号反而比较强. 这个时间与冲击波前沿到达磁场测量线圈的时间接近, 第三个电磁脉冲信号可能是由于冲击波前沿冲击磁场测量线圈而引起的.
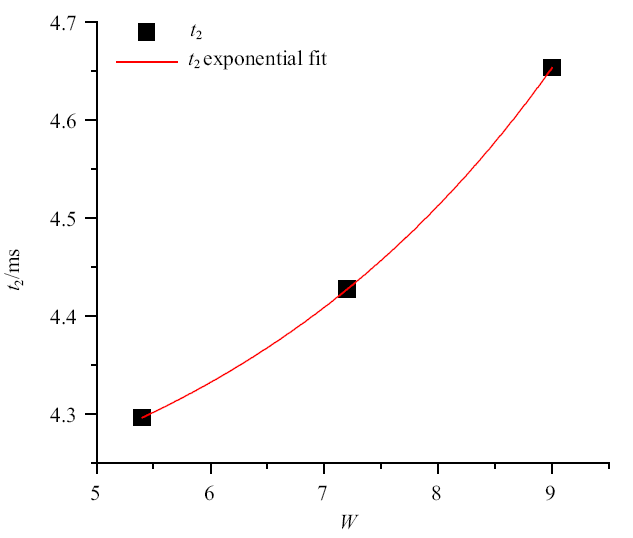
从3个信号出现的时间看, 第一个脉冲信号出现的时间$t_{1}$一致, 对药量不敏感; 第二个脉冲信号出现的时间$t_{2}$和炸药量成正相关; 第三个脉冲信号出现的时间$t_{3}$与炸药量成负相关. 根据杨亚东等[32]对冲击波的到达时间的研究, 第三个脉冲信号出现的时间规律符合文献结果相同, 从侧面证明了第三个电磁脉冲信号是冲击波前沿撞击线圈推测的正确性. 如果认为第二个脉冲信号是由于冲击波到达某处产生, 那么信号出现的时间特性应该符合杨亚东给出的拟合规律, 然而第二个脉冲出现的时间规律与文献结果相反, 因此其产生机理可能不仅是冲击波运动产生的, 我们仅考虑第二个电磁脉冲出现的时间与炸药的当量关系. 根据实验数据, 给出其出现时间与炸药当量的拟合公式(1), 拟合曲线如图8所示.
图8
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图8第二个电磁脉冲出现时间与炸药当量之间的关系
Fig. 8Relationship between the arriving time of the second pulse and the explosion equivalent
由于实验难度大, 实验的样本点较少, 因此该拟合公式仅适合于药量在4.5 kg到7.5 kg之间, 我们在后续研究中会进一步开展药量与电磁脉冲出现的时间研究.
提取不同药量炸药爆炸产生的3个脉冲信号的峰值如表1所示.
Table 1
表1
表1典型脉冲信号的幅值
Table 1
 |
新窗口打开|下载CSV
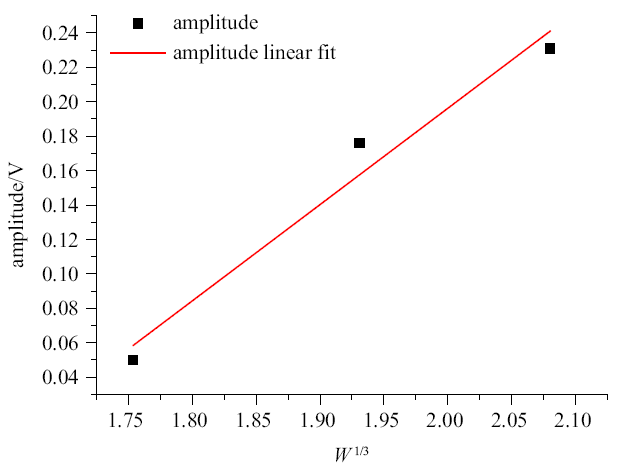
从表1可以看出, 第一个脉冲信号的幅值随着炸药的质量的增大而增大; 第二个脉冲信号的幅值很小; 第三个脉冲信号幅值较大. 考虑第二个信号出现时间, 这时随着冲击波衰减和爆轰产物膨胀, 爆轰产生的等离子体电离度相比于爆炸的初始阶段有很大的降低, 导致第二个脉冲信号的幅值很微弱, 由于实验采集信号过程中需要考虑第一个脉冲信号测量, 量程相对于第二个信号较大, 因此不同药量下第二个脉冲信号幅值分辨率较低, 不同药量下测得信号幅值差异很小, 没能给出第二个脉冲信号幅值与药量关系. 根据前面分析推测第三个脉冲信号是冲击波到达测量系统时刻引起的干扰, 不被认为是有效的电磁脉冲信号, 因此我们仅讨论第一个脉冲信号的幅值与炸药当量的关系, 将第一个电磁脉冲的幅值与炸药当量的1/3次方整理拟合关系如图9所示.
图9
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图9第一个电磁脉冲幅值与炸药当量之间的关系
Fig. 9Relationship between the amplitude of the first pulse and the explosion equivalent
从图9中可以看出信号幅值与炸药的当量的1/3次方基本呈线性关系, 这与文献[24]的实验结果得到的结论一致. 这也从侧面应证了第一个脉冲信号是由爆炸产生高温高压等离子体区域的电磁辐射产生的. 针对3个不同电磁脉冲信号产生的机理, 我们对实验工况进行数值模拟, 分析爆炸流场的特征, 来分析各个信号产生的原因.
2 实验工况爆炸过程的数值模拟
通过数值计算, 不仅可以了解物质运动的结果, 而且还可以了解物质运动的整体和局部细致过程, 尤其对于瞬态性强的流体弹塑性问题, 它更是一种重要的科学研究方法. 因此我们通过课题组自主开发的三维爆炸与冲击问题仿真软件EXPLOSION-3D[33-35], 对本次实验工况进行数值模拟分析, 通过对比实验信号出现时刻的爆轰流场特征, 分析三个电磁脉冲信号产生的原因.2.1 实验工况的数值模拟
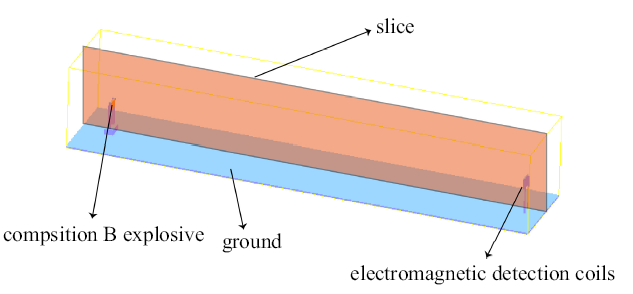
根据实验数据, 建立模型, 如图10所示. 将线圈、炸药支架和地面等效为刚体, 炸药中心离地面高1.05 m, 计算域为3 m$\times$3 m$\times $16 m, 采用等步长离散计算域, 网格步长为0.01 m, 离散30$\times $300$\times$1600个网格, 共1.44亿个网格. 为了观察中心截面的爆炸流场状态, 在模型的中心设置了一个切片, 通过后处理软件, 能清晰的看到切片上的压力分布.图10
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图10实验工况的数值计算模型
Fig. 10Numerical model of the experimental case
软件中采用理想气体状态方程对空气进行描述, 形式如下[36]
式中, $\rho$为密度, $e$比内能, $k$为空气的等熵指数, 数值计算中取$k=1.4$.
炸药爆轰产物的状态方程在程序里选用可变指数多方气体状态方程
式中, $P$为压力, $k_{0}$是爆轰产物的多方指数, $k_{1}$是爆轰产物充分膨胀下的多方指数, $b$为调节系数, $\rho$为当地密度, $\rho_{0}$为初始密度, $e$为比内能. $P_{\rm CJ}$为CJ爆轰时产生的压力, $D_{\rm CJ}$为CJ爆轰时的冲击波速度. B炸药的参数为 $\rho_{0}=1.717$ g/cm$^{3}$, $e_{0}=7.98$ kJ/g, $k_{0}=3.0$, $k_{1}=3.16$, $b=1.0$, $P_{\rm CJ}= 29.5$ GP, $D_{\rm CJ} = 7980$ m/s.
2.2 数值模拟结果及分析
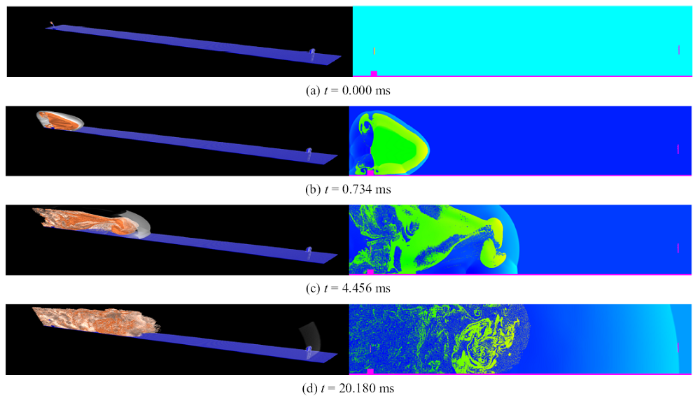
通过EXPLOSION-3D软件的后处理系统VISC2D和VISC3D将数值结算结果的压力云图处理如图11所示, 图11的左边是三维模型的一半的三维图, 右边是对应切片的二维切片图. 从二维切片图中我们可以看到各个时刻的压力分布图, 也可以看到冲击波传到的各个位置的时间. $t = 0.000$ ms时刻, 为初始时刻, 如图11(a)所示. $t= 0.734$ ms时刻, 这时候爆轰产物刚到达地面. 当空气冲击波遇到刚性壁面时, 质点速度骤然变为零, 壁面处质点不断聚集, 使压力和密度增加, 于是形成反射冲击波, 如图11(b)所示. $t= 4.456$ ms时刻, 反射波阵面在被压缩加热的空气中运动, 速度大于入射波阵面, 反射波最终赶上入射波当入射角大于临界角时, 入射波和反射波的交点逐渐开始离开地面, 两波交点之下的波阵面为马赫反射波, 如图11(c)所示. $t = 20.180$ ms时刻, 冲击波波阵面到达磁场测量线圈, 如图11(d)所示.图11
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图116 kg B炸药爆轰后不同时刻的数值模拟结果图
Fig. 11Numerical simulation results of 6 kg composition B explosives at different time after detonation
从压力的二维切片云图可以清晰地看出, 冲击波前沿波阵面到达各个位置的时间, 其中冲击波阵面到达测量线圈的数值计算时间是$t=20.180$ ms. 试验中工况2的3个通道的第三个脉冲信号出现的平均时间$t = 20.233$ ms, 这两者相吻合, 可以推测出第三个脉冲信号是冲击波阵面冲击磁场测量线圈引起的, 这也与前面的实验结果的分析一致.
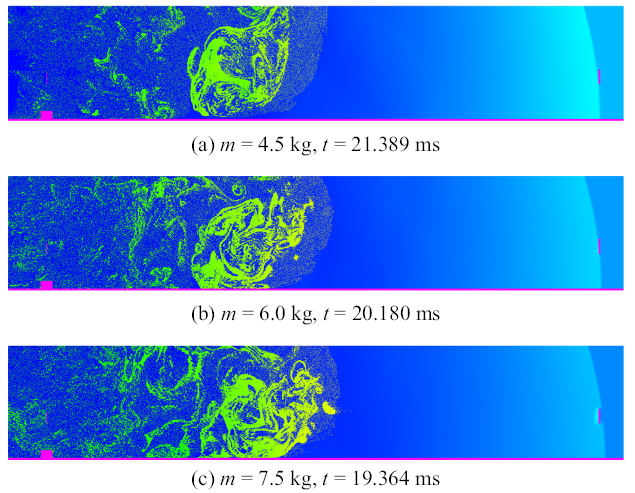
改变药量, 将3种药量的工况分别进行数值模拟, 将3个实验工况冲击波前沿到达线圈位置时刻的二维切片图整理如图12所示. 图12中可以清晰的看出冲击波前沿到达线圈位置的时刻, 将每个工况中第三个脉冲信号的平均时间与冲击波阵面到达测量线圈的时间对比, 总结如图13所示.
图12
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图12不同工况下第三个脉冲时刻的二维切片压力图
Fig. 12Two-dimensional slices of the pressure distribution in each case when the third pulse arrived
图13
 新窗口打开|下载原图ZIP|生成PPT
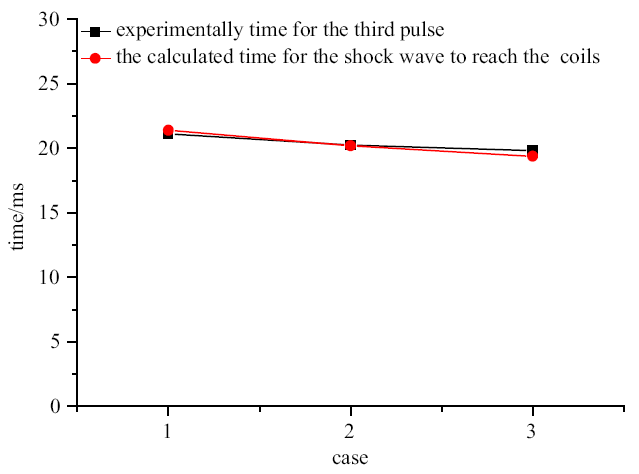
新窗口打开|下载原图ZIP|生成PPT图13实验测得第三个脉冲时间和数值计算冲击波到达测量线圈时间的对比
Fig. 13Comparison between the arriving time of the third pulse in experiments and the calculated time when the shock wave reaches the measurement coils
图13中给出了3种不同药量的工况下数值计算得到的冲击波阵面到达测量线圈的时间和第三个脉冲信号的实测平均时间, 通过对比可以发现, 第三个脉冲信号出现的时间和冲击波阵面到达测量线圈的时间吻合, 这证实了第三个信号是由冲击波冲击磁场测量线圈引起的, 是无效信号. 所以整个爆炸过程中, 只有前两个电磁辐射信号是有效信号.
在第三个脉冲信号之前, 在4.4 ms时出现一个明显脉冲, 即第二个脉冲信号, 此时冲击波还没到达线圈, 也没有其他的干扰, 只能是爆炸过程中产生的电磁信号. 从第二个脉冲信号出现时刻对应的压力云图, 可以看出入射波和反射波的交点逐渐开始离开地面, 两波交点之下的波阵面为马赫反射波. 将三种工况的第二个脉冲对应时刻的冲击波阵面的数值计算结果的二维压力切片云图总结如图14所示.
图14
 新窗口打开|下载原图ZIP|生成PPT
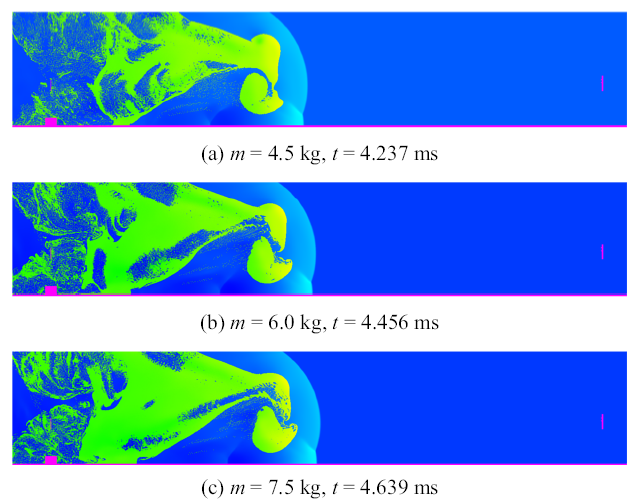
新窗口打开|下载原图ZIP|生成PPT图14不同工况下第二个脉冲时刻的二维切片压力图
Fig. 14Two-dimensional slices of the pressure distribution in each case when the second pulse arrived
观察压力切片云图发现, 在第二个电磁脉冲出现的时刻都有一个相同的特征即地面反射冲击波恰好追上前沿冲击波, 这样会导致空气冲击波阵面处形成非平衡、不完全电离的等离子体, 生成的等离子体电磁辐射产生了电磁脉冲.
关于常规爆炸产生电磁效应的机理, 当前尚无统一认识, 最近有研究表明[37-38], 冲击波后物质存在电离, 则冲击激波附近会诱导电荷分离, 产生分离电场并伴随激波运动, 因此很可能电磁辐射和冲击波运动有关. 除了上述研究外, 还有文献[9]认为炸药爆炸过程中产生的磁场扰动是由导电气体在自然磁场中运动产生的磁场压缩和扩散造成的, 因此可以采用磁流体力学理论来解释爆炸产生导电气体的运动和磁场产生的机理. 其中爆炸产生等离子体的电导率是重要参数之一, 与等离子体电子数密度息息相关, 如果导电区域电导率足够高, 则地磁场的磁力线会被冻结在高速运动的导电气体中一起运动, 从而引起空间电磁场的改变, 如果电离气体的电导率较弱, 即类似于常规炸药爆炸产生的电离气体, 则导电气体的高速运动不能完全冻结磁力线, 磁场会发生扩散, 相应的产生的电磁辐射较弱. 这一等离子体参数可以由热力学方法给出. 文献[39]中通过热力学方法计算出了电导率, 根据作者的分析, 冲击波在地面上反射的时候, 冲击波前沿的电离度会是自由区域的2到3倍, 这与实验中出现第二次电磁脉冲时, 地面反射冲击波追上前沿冲击波产生的现象相符合. 所以, 冲击波前沿产生电离物质电离度的升高, 在背景磁场下运动会产生电磁辐射很可能就是第二个电磁脉冲信号产生的原因.
3 结论
本文针对炸药爆炸过程中产生电磁辐射现象, 设计不同药量的B炸药爆炸实验, 测量了整个爆炸过程中产生的电磁脉冲信号, 应用小波分析对实测信号进行处理, 并用EXPLOSION-3D软件对整个爆炸过程进行数值模拟. 根据本文研究内容, 得到如下主要结论.(1)信号实测结果和爆炸场数值模拟结果对比, 可以得出整个过程中先后出现的3个信号, 前两个是有效信号. 定量的分析了两个有效信号与炸药当量的关系得出, 第一个电磁脉冲幅值与炸药当量的1/3次方基本呈线性关系, 其到达时间对炸药药量不敏感; 第二个电磁脉冲出现的时间与炸药的当量成指数关系, 药量越大, 出现时间越晚.
(2)应用小波变换对实测信号进行分析和处理, 频域分析可以得出, 真实信号的频谱主要分布在0$\sim$50 kHz. 这与文献[8]得出的炸药爆炸产生的电磁辐射频率主要集中在1 MHz以内结论符合.
(3)采用磁流体力学理论解释了第二个电磁脉冲信号的产生时刻爆炸场出现的地面反射冲击波追上前沿冲击波的现象, 分析了其产生电磁辐射的原因.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
URL [本文引用: 2]

Simulative experiments on the ground were carried out to measure the radiation by chemical explosion of aerospace explosives in stage separation and evaluate the impaction on the electronics in the rocket. Electromagnetic pulses by different explosives were captured by a rod antenna and measured by a real time analyzer. The results show that radiation increases as the energy of the explosion. When using a mild linear shaped charge,considerable pulses were recorded in dozens of milliseconds after the separation, with the frequencies around megahertz and magnitude about several V/m on single frequency. Electromagnetic environment inside and outside the rocket were recorded and compared by simple dipoles, and current pulses induced on the circuits inside the rocket were also measured. The conclusion could direct the anti-interference design on the inner electronics of launch vehicle.
URL [本文引用: 2]

Simulative experiments on the ground were carried out to measure the radiation by chemical explosion of aerospace explosives in stage separation and evaluate the impaction on the electronics in the rocket. Electromagnetic pulses by different explosives were captured by a rod antenna and measured by a real time analyzer. The results show that radiation increases as the energy of the explosion. When using a mild linear shaped charge,considerable pulses were recorded in dozens of milliseconds after the separation, with the frequencies around megahertz and magnitude about several V/m on single frequency. Electromagnetic environment inside and outside the rocket were recorded and compared by simple dipoles, and current pulses induced on the circuits inside the rocket were also measured. The conclusion could direct the anti-interference design on the inner electronics of launch vehicle.
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 3]
[本文引用: 3]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
URL [本文引用: 1]

The explosive shock wave pressure is an important parameter which is used for the evaluation of explosion effect, and the characteristic of shock wave pressure is closely related to charge and detonation mode. A measurement method and the results of overpressure of charge with shell measured in the case of thermal explosion were described, and the results were analyzed according to the structure of explosive cave. The results show that the electromagnetic radiation is emitted due to the electrokinetic effect and the friction between explosion product and shell when the charge explodes, and the signal duration and complexity of electromagnetic radiation generated by the charge with shell are different from those generated by the bare charge.
URL [本文引用: 1]

The explosive shock wave pressure is an important parameter which is used for the evaluation of explosion effect, and the characteristic of shock wave pressure is closely related to charge and detonation mode. A measurement method and the results of overpressure of charge with shell measured in the case of thermal explosion were described, and the results were analyzed according to the structure of explosive cave. The results show that the electromagnetic radiation is emitted due to the electrokinetic effect and the friction between explosion product and shell when the charge explodes, and the signal duration and complexity of electromagnetic radiation generated by the charge with shell are different from those generated by the bare charge.
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]

Numerical simulations of explosion and impact problems have important engineering application value in the fields of national defense and civil security. Numerical simulations for these problems have a lot of di culties because the explosion and impact problems are strongly nonlinear transient dynamic problems in which multi-material mechanical behaviors are involved under the condition of high strain rate, high temperature and high pressure. Therefore, in this paper , the pseudo arc-length method for 3D nonlinear hyperbolic conservation system is proposed and the process of the algorithm realization is analyzed. The numerical results show that the algorithm improves the resolution of the shock wave strong discontinuity e ectively. The additive Runge-Kutta method for gaseous detonation numerical simulation is developed. In this method, the nonlinear convection part is solved implicitly while the chemical reaction source part is handled explicitly. The results show that the additive Runge-Kutta method can well capture and accurately describe the complex structure and typical characteristics. The parallel Eulerian numerical method of 3D multi-material hydrodynamics is investigated for the requirement of large-scale computation in engineering practical physical problems. The 3D explosion and impact problem parallel computation hydrocode is developed and the test method for this parallel hydrocode is proposed. According to the above works, some problems of large-scale and high-precision calculations for explosion and impact problems are solved. Finally, the experimental and numerical investigations on heavy-caliber shaped-charge penetration in thick concrete target are carried out, and the e ectiveness of the proposed numerical method is demonstrated by typical explosion and impact engineering problems.
DOIURL [本文引用: 1]

Numerical simulations of explosion and impact problems have important engineering application value in the fields of national defense and civil security. Numerical simulations for these problems have a lot of di culties because the explosion and impact problems are strongly nonlinear transient dynamic problems in which multi-material mechanical behaviors are involved under the condition of high strain rate, high temperature and high pressure. Therefore, in this paper , the pseudo arc-length method for 3D nonlinear hyperbolic conservation system is proposed and the process of the algorithm realization is analyzed. The numerical results show that the algorithm improves the resolution of the shock wave strong discontinuity e ectively. The additive Runge-Kutta method for gaseous detonation numerical simulation is developed. In this method, the nonlinear convection part is solved implicitly while the chemical reaction source part is handled explicitly. The results show that the additive Runge-Kutta method can well capture and accurately describe the complex structure and typical characteristics. The parallel Eulerian numerical method of 3D multi-material hydrodynamics is investigated for the requirement of large-scale computation in engineering practical physical problems. The 3D explosion and impact problem parallel computation hydrocode is developed and the test method for this parallel hydrocode is proposed. According to the above works, some problems of large-scale and high-precision calculations for explosion and impact problems are solved. Finally, the experimental and numerical investigations on heavy-caliber shaped-charge penetration in thick concrete target are carried out, and the e ectiveness of the proposed numerical method is demonstrated by typical explosion and impact engineering problems.
[本文引用: 1]
[本文引用: 1]
URL [本文引用: 1]
URL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]

The basic principle and the parallel design strategy of the PMMIC-3D parallel program which using Euler method based on the message passing interface (MPI) mode were stated. After numerically stimulating the fortification mode, it can be seen that the results of numerical stimulation basically match with the reality and the physical laws. The shock waves of explosive detonation in fortifications not only had a higher peak overpressure, but also had a longer duration of action. When the shock wave met the wall, it would reflect and produce the reflected high pressure. Because of the diffraction convergence, the local high pressure would be brought about in a certain region behind the wall, in which the destructive effect was much larger compared with the shock waves of air explosion. The propagation process and the interaction of shock waves can be seen clearly by the numerical stimulation, which can determine the arrival time of the shock waves at various positions. The optimal explosive charge can be ensured by comparing the overpressure value of shock waves at different places.
DOIURL [本文引用: 1]

The basic principle and the parallel design strategy of the PMMIC-3D parallel program which using Euler method based on the message passing interface (MPI) mode were stated. After numerically stimulating the fortification mode, it can be seen that the results of numerical stimulation basically match with the reality and the physical laws. The shock waves of explosive detonation in fortifications not only had a higher peak overpressure, but also had a longer duration of action. When the shock wave met the wall, it would reflect and produce the reflected high pressure. Because of the diffraction convergence, the local high pressure would be brought about in a certain region behind the wall, in which the destructive effect was much larger compared with the shock waves of air explosion. The propagation process and the interaction of shock waves can be seen clearly by the numerical stimulation, which can determine the arrival time of the shock waves at various positions. The optimal explosive charge can be ensured by comparing the overpressure value of shock waves at different places.
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
