THE EFFECT OF PERIODIC PERTURBATION ON MULTI SCALES IN A TURBULENT BOUNDARY LAYER FLOW UNDER DRAG REDUCTION1)
WangShuaijie中图分类号:O357.5
文献标识码:A
通讯作者:
收稿日期:2018-12-4
网络出版日期:2019-05-18
版权声明:2019力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (6838KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
drag reduction
引 言
相干结构[1-3]在壁湍流的产生、维持和演化发展中起着重要作用,它与壁湍流中高壁面摩擦事件有密切的相关.最近的研究表明,随着雷诺数的升高,在管道湍流、槽道湍流和平板湍流边界层中,对数律区存在着大尺度结构,并引起了广泛的关注[4-7].Kim和Adrian[4]对管道湍流进行研究,发现流向脉动速度的预乘能谱在对数律区存在双峰,从能谱的角度证明了超大尺度结构的存在;Hutchins和Marusic[8]用热线阵列对平板湍流边界层中的大尺度运动进行研究,发现了对数律区存在大尺度条带结构的证据.他们发现,这些结构在流向方向上的尺度达到20倍的边界层厚度,并推测外区的大尺度结构能延伸至壁面,并对内区流动具有调制作用.Mathis等[9]将这种调制作用进行了定量化,通过低通滤波将湍流脉动信号分解为大尺度分量和小尺度分量,用大尺度脉动分量与小尺度脉动包络线的相关系数作为调制系数来描述大尺度运动对小尺度的调制关系,发现随着雷诺数的增大,其调制作用逐渐增强.Marusic等[10]进一步给出了利用对数律区大尺度信号来预测近壁区流向速度的数学模型.随后,Ganapathisubramani等[11]用条件平均的方法研究了大尺度结构对小尺度结构的调幅和调频作用,发现在近壁区,小尺度脉动强度随着大尺度脉动的增加而增加;而在尾流区,则呈现出相反的趋势.随着大尺度脉动的增加,小尺度强度的变化既不是线性的,也不是对称的,并认为调幅调制的影响仅出现在近壁区.Guala等[12]对大气边界层进行研究,发现大尺度运动与从近壁区含能涡到耗散尺度之间的所有尺度都存在相互作用.Hutchins等[13]用壁面摩擦感受器阵列和移动的热线探针对湍流边界层大尺度超级结构进行实验测量并进行三维条件平均,其结果表明,在低壁面摩擦和高壁面摩擦事件上面,分别存在向前倾的低速和高速结构.由于湍流控制的重要性和许多工程领域的直接现实意义,对湍流控制的方法和减阻机理的研究一直是湍流研究的前沿课题.随着人们对湍流相干结构的理解以及湍流预测方法的发展,使得主动控制成为湍流控制技术的研究热点[14-17].在众多的主动控制方案中,壁面变形是较为可靠、高效的一种.Quadrio和Ricco[18]和Skote[19]分别采用DNS方法,通过壁面展向振荡获得44.7%和50.0%的减阻效果.Jacobson和Reynolds[20]使用压电陶瓷振子实现壁面变形来对湍流边界层进行控制,由于压电陶瓷振子频率稳定性好,精度高,适用频率范围宽等特点,可以作为很好的控制材料.Bai等[21]用压电陶瓷振子列实现局部壁面展向震荡,得到50%的局部最大减阻率.张浩等[22]、Zheng等[23]对单个压电振子在不同工况下的控制效果进行研究,得到最大26.83%的减阻率.Qiao等[24]比较了压电振子主动控制下开环和闭环时的减阻率,在占空比为50%时,能实现23%的减阻率.Bai等[25]对双振子进行研究实现了18.54%的减阻率.
本文通过使用压电陶瓷振子对壁湍流施加周期扰动,实现了湍流边界层的主动减阻控制.本文第一部分介绍了实验所用的仪器与设备,及实验工况和采样参数.第二部分通过滤波,把原始脉动信号分成大尺度脉动和小尺度脉动,并通过对比大、小尺度脉动的均方根值及条件平均结果,来分析扰动对边界层内不同尺度的影响.
1 实验设备与装置
实验在天津大学流体实验室三元回流式风洞中进行. 风洞实验段长1.5m,宽0.8 m,高0.6 m. 用于产生湍流边界层的为长1.7 m,宽0.6m,厚0.015 m的有机玻璃平板,竖直放置在风洞实验段中.平板前缘有椭圆修型. 为了得到充分发展的湍流边界层,在距平板前缘8cm处沿展向放置直径为2 mm,长度为600 mm的拌线和宽度为450mm,长度为600 mm的240号砂纸,以加速流场转捩. 用TSI-IFA300型恒温热线风速仪和TSI-1621A-T1.5型单丝热线边界层探针进行流场测速[22-23,25-29]. 热敏元件为直径4 $\mu $m,长1.25mm的钨丝,并在TSI-1128型空气探针校准器上进行了标定.实验过程中,通过CCTS-1193E型三维自动控制坐标架固定探针支杆和移动探针位置.实验中采用壁面镶嵌的单晶悬臂梁式压电陶瓷振子对壁湍流产生周期激励.压电陶瓷振子的有效振动区域长度为30 mm,宽3.6 mm,厚0.44mm,上表面为铜,下表面为压电陶瓷,各厚0.22 mm.压电陶瓷振子位于距平板前缘下游1090mm处,两个压电振子沿展向镶嵌在壁面上的凹槽内,上表面与平板平齐.通过远方GK10005交流变频稳压电源为振子提供电源,并通过改变提供电源的频率与电压来控制振子的频率与振幅[23].
实验在$U_\infty = 9.2$ m/s的来流风速下进行,在振子自由端下游2mm处,分别在施加控制和不施加控制的工况,测量湍流边界层不同法向位置的流向脉动速度分量的时间序列.施加控制时,用稳压电源提供80 V,80 Hz及80 V,160Hz的正弦波交流电压$^{[22\mbox{-}23,25]}$.实验中,采样频率为100 kHz,每个空间点样本量为4 194304,采样时间为41.9 s. 实验测得基本流场中边界层厚度名义$\delta =46.19$ mm,动量损失雷诺数$Re_\theta = 2885$.
2 实验结果与分析
2.1 平均速度剖面
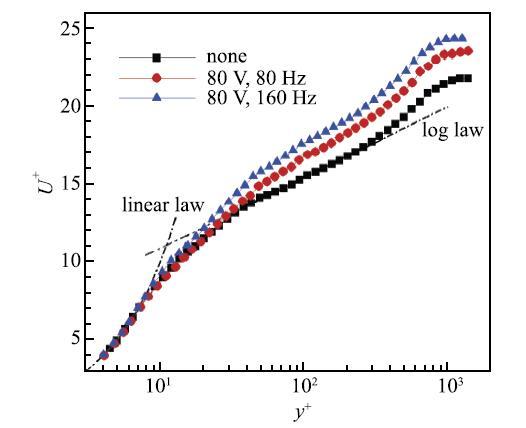
图3为施加控制和未控时的无量纲平均速度剖面,无量纲速度$U^ + = U / {u_\tau}$随无量纲壁面距离$y^ + = {yu_\tau } / \nu $的变化情况,其中$y$为壁面法向高度,$U$为平均速度,$\nu $为运动黏性系数. 根据湍流边界层的分层理论,由黏性底层流向平均速度与法向高度的线性关系,拟合出壁面摩擦速度$u_\tau$[20-24],计算可得未控时的壁面摩擦速度为$u_{\tau \rm n} = 0.383~7$ m/s. 在80 V,80 Hz和80 V,160 Hz工况下的壁面摩擦速度分别为0.362 3 m/s和0.365 4 m/s. 根据$\tau _{ w} = \rho u_\tau ^2 $,$\eta = {(\tau _{ wn} - \tau _{\rm wc} )} / {\tau _{wn} } 100$%计算减阻率. 其中空气密度$\rho = 1.025$ kg/m$^{3}$,$\tau _{\rm wn} $为不施加控制时的壁面剪切力,$\tau _{\rm wc} $为施加控制时的壁面剪切力. 计算可得80 V,80 Hz工况下的减阻率$\eta = 9.33$%,80 V,160 Hz工况下减阻率为$\eta = 10.82$%. 从图3中可以看出,施加控制的工况与不施加控制的工况相比, 边界层速度剖面的缓冲层增厚,对数律区上移,与其他减阻结果相一致[30-33].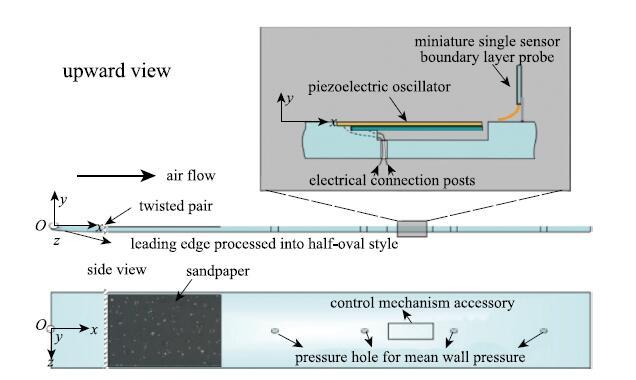
显示原图|下载原图ZIP|生成PPT图1平板示意图[
-->Fig. 1Schematic diagram of the experimental flat plate[
-->
显示原图|下载原图ZIP|生成PPT图2压电陶瓷及双压电陶瓷振子
-->Fig. 2Piezoelectric ceramics and double piezoelectric vibrators
-->
显示原图|下载原图ZIP|生成PPT图3平板湍流边界层平均速度剖面
-->Fig. 3Mean velocity profile of turbulent boundary layer over a smooth flat plate
-->
2.2 尺度分解
为了对边界层中的脉动信号进行分尺度分析,需要一个合适的方法来分离出大尺度脉动和小尺度脉动. 常见的分解方法有本征正交分解[34-35],小波分析[26,36],低通滤波[9,11]等. 本文采用低通滤波的方法. 低通滤波是通过特定的截断频率(波长)对流场信号进行分解. 湍流边界层的研究表明,随着雷诺数的升高,外区会出现含有高能量的大尺度信号,在尺度上有别于近壁的小尺度结构[4,6-8]. 由于大尺度和小尺度结构在空间波长有明显的差异,因此,本文选取${\lambda _x } / \delta = 2$作为截断波长,直接将原始脉动信号分解为了大尺度和小尺度成分,并对其在压电振子扰动下的特性进行了实验研究. 由于本实验中雷诺数相对较小,在外区并没有明显的代表大尺度运动的高能量部分[9]. 尽管如此,Tang等[28-29]的研究表明,当$Re_\tau \mbox{ = }980$时,在${\lambda _x } / \delta > 2$的部分存在具有高能量的大尺度区域,这在先前的研究中报道过[2, 37]. 因此,为了分离大尺度和小尺度结构,本文采用${\lambda _x } / \delta = 2$为截断波长把原始信号分成大尺度和小尺度. 此外,先前的研究结果表明截断波长${\lambda _x } / \delta = 1.5,2,3,4$时对最终结果的影响很小[11,28-29]. 图4为不施加控制时, $y^ + = 10$处一段原始信号及信号分解后相对应的大尺度脉动和小尺度脉动信号.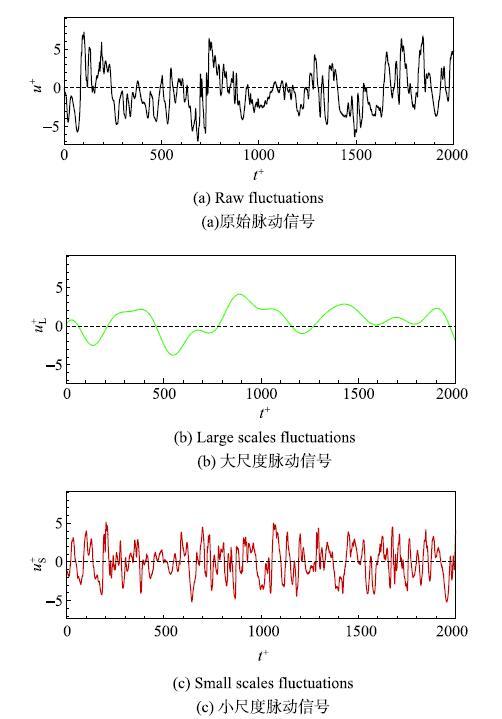
显示原图|下载原图ZIP|生成PPT图4不同尺度的脉动速度
-->Fig. 4Fluctuation velocity of different scales
-->
2.3 大小尺度脉动强度
对80 V,160Hz控制条件下的脉动速度信号和不施加控制条件下脉动速度信号进行尺度分解,得到的不同尺度脉动速度的均方根值随法向位置的变化情况如图5所示.图5(a)为大尺度脉动的均方根值$u_{\rm Lrms}^ + $随法向高度$y^ +$的变化情况.从图中可以看出,在不施加控制的条件下,大尺度脉动的均方根$u_{Lrms}^ + $随着$y^ + $的增大而变大,在$y^ + =17.5$时达到最大,之后随着$y^ + $的增大而逐渐减小.在施加控制的条件下,$u_{\rm Lrms}^ + $随$y^ +$的变化情况与不施加控制时的变化趋势类似,在$y^ + < 26$时,$u_{Lrms}^ + $随着$y^ + $的增大而增大,在$y^ + > 26$时,$u_{\rm Lrms}^+ $随着$y^ + $的增大而减小;相比于不施加控制时,在$y^ + <30$的近壁区,大尺度脉动的均方根值$u_{\rm Lrms}^ +$降低,说明压电振子引起的扰动抑制了近壁区的大尺度活动;在$y^ + >30$时,$u_{Lrms}^ +$与不施加控制时基本一致,这表明压电振子引起的扰动影响了近壁区的大尺度脉动,对$y^ + > 30$之外的大尺度脉动基本没有影响.图5(b)为小尺度脉动速度的均方根值$u_{\rm Srms}^ + $的变化情况.从图中可以看出,在不施加控制的工况下,$u_{\rm Srms}^ +$随着法向位置$y^ + $的增大而增大,在$y^ + =9.2$达到最大值,之后,随着法向位置$y^ + $的增大而减小.这是由于湍流最活跃的地方集中在缓冲层中,使得小尺度脉动强度的峰值出现在$y^+ = 10$左右. 在施加控制的工况下, $u_{\rm Srms}^ +$随着法向位置$y^ + $的变化情况与不施加控制时类似.相比于不施加控制时,在$y^ + < 40$时,施加控制条件下的$u_{Srms}^ + $明显高于未控条件下的$u_{\rm Srms}^ +$,这说明扰动增强了近壁区小尺度结构的脉动;在$y^ + >40$时,施加控制条件下的$u_{\rm Srms}^ +$与未控条件下基本一致,这表明压电振子引起的扰动影响了近壁区的小尺度脉动,对$y^+ > 40$之外的小尺度脉动基本没有影响.
显示原图|下载原图ZIP|生成PPT图5不同尺度脉动速度的均方根值
-->Fig. 5RMS values of fluctuation velocities at different scales
-->
从图5中施加控制和不施加控制工况下大、小尺度的脉动均方根值的对比可以看出压电振子的扰动调整了近壁区大小尺度的活动情况,抑制了近壁区大尺度脉动的强度,增强了小尺度的湍流活动.这与Bai等[21]在$Re_\theta = 1000$和$Re_\theta =1540$时频谱分析的结果及Bai等[25]在$Re_\theta =2766$时的小波分析结果相一致.从能量的角度来看,可以推测出,扰动改变了近壁区的能量分布,把大尺度的部分能量转输到了小尺度中,从而加强了小尺度的脉动,减弱了大尺度的脉动强度.由此也表明,相比于小尺度脉动,大尺度脉动与壁面摩擦阻力的产生有着更密切的关系[13].
2.4 大尺度脉动条件平均
为了进一步了解施加控制工况下,大尺度脉动随时间的变化情况,分别对大尺度信号为正和为负时的脉动进行条件平均,其方法如下$$ u_{\rm SP}^ + (\Delta t) = \langle {u_{\rm L}^ + (t + \Delta t)} |u_{\rm L}^ + (t) =0, u_{\rm L}^ + (t + \Delta t) > 0 \rangle (1) $$
$$ u_{\rm SN}^ + (\Delta t) = \langle {u_{\rm L}^ + (t + \Delta t)} |u_{\rm L}^ + (t) = 0, u_{\rm L}^ + (t + \Delta t) < 0 \rangle \tag{2} $$
其中$u_{\rm SP}^ + $为大尺度脉动信号为正时的条件平均,$u_{\rm SN}^ + $为大尺度脉动为负时的条件平均.
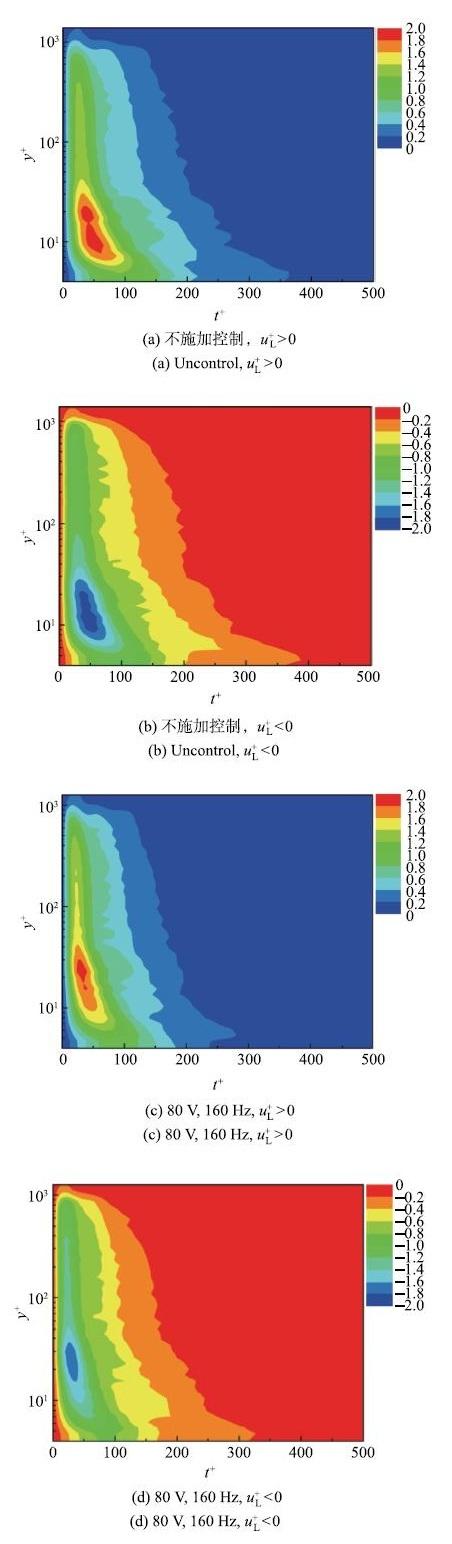
平均结果如图6所示. 从图中可以看出,在平板边界层中,大尺度脉动为正时和为负时的变化趋势类似,高强度的脉动集中在$7 < y^ + < 30$中间;在时间相位上,则在$t^ + = 50$附近的脉动最强. 在施加控制时,近壁区的大尺度脉动强度都减弱,尤其是$y^ + = 10$附近的减弱情况尤为明显. 由图可知,扰动使得近壁区的大尺度脉动减弱,同时,持续时间也稍有减少.
显示原图|下载原图ZIP|生成PPT图6大尺度脉动的条件平均
-->Fig. 6Conditional averaging of large scale fluctuations
-->
2.5 小尺度脉动条件平均
为了进一步了解扰动对小尺度脉动的影响,对流向脉动速度中的小尺度脉动信号进行了条件平均.本文主要关心压电振子产生的扰动对小尺度脉动幅值产生的影响.因此本文采用对小尺度脉动信号进行Hilbert变换后,并以${\lambda _x } / \delta >2$为截止频率进行低通滤波,得到小尺度脉动的包络线$E_{\rm L} \left({u_{\rm S}^ + } \right)$,用来表征小尺度脉动的振幅[9,38].为了观察大尺度脉动变化的同时小尺度脉动振幅的同步变化情况,对大尺度脉动$u_{L}^ + = 0$时刻附近小尺度脉动的变化情况进行了条件平均. 以$u_{L}^ + = 0$时刻的$u_{\rm L}^ +$两种不同变化情况为检测条件进行条件平均,所用方法如下所示\begin{equation} \label{eq1} u_{\rm SEa}^ + (\Delta t) = \langle { {E_{\rm L} ( {u_{\rm S}^ + } )(t + \Delta t)} |u_{\rm L}^ + (t) = 0, u_{\rm L}^ {+\prime } (t) > 0} \rangle \tag{3} \end{equation} \begin{equation} \label{eq2} u_{\rm SEb}^ + (\Delta t) = \langle { {E_{\rm L} ( {u_{\rm S}^ + } )(t + \Delta t)} |u_{\rm L}^ + (t) = 0,u_{\rm L}^ {+ \prime} (t) < 0} \rangle \tag{4} \end{equation}
其中,$u_{\rm SEa}^ + $为大尺度脉动$u_{\rm L}^ + =0$时刻附近,$u_{\rm L}^ +$为从负值变化到正值时的小尺度脉动的振幅条件平均;$u_{\rm SEb}^ +$为大尺度脉动$u_{\rm L}^ + = 0$时刻附近,$u_{\rm L}^ +$从正值变化到负值时的小尺度脉动的振幅条件平均.条件平均结果如图7所示.
显示原图|下载原图ZIP|生成PPT图7小尺度振幅的条件平均
-->Fig. 7Conditional averaging of small scale fluctuations amplitude
-->
从图7(a)和图7(b)可以看出,近壁区小尺度脉动振幅较大,随着法相位置的逐渐增大,小尺度脉动的振幅逐渐减小. 且小尺度脉动在近壁区的分布比较均匀.图7(c)和图7(d)是施加控制时的条件平均结果,对比图7(a)和图7(b)可以看出,压电振子的扰动增强了近壁区小尺度脉动的幅值;而边界层外区的小尺度脉动基本上没有变化.在近壁区,与大尺度脉动$u_{\rm L}^ +$为负时的小尺度脉动振幅增大相比,大尺度脉动$u_{\rm L}^ +$为正时小尺度脉动幅度相比于不施加控制时增长的更多.并且大尺度脉动$u_{\rm L}^ +$为正时,小尺度脉动振幅增加的区域主要集中在$4 < y^ + <16$,而在大尺度脉动$u_{\rm L}^ +$为负时,小尺度脉动振幅增加的区域主要集中在$8 < y^ + < 30$.由此可见,在近壁区施加控制工况下,小尺度脉动的幅值的增加量在时间相位上并不是均匀的.
结合图6和图7可以发现,压电振子产生的扰动使得近壁区大尺度脉动降低,同时也使得小尺度的脉动增强了.这与Zheng等[23],Bai等[25]的结论相一致.而小尺度脉动的增强则主要集中在大尺度为正的时间中.此外,从图6可以看出,在施加控制的工况下,大尺度脉动为正的持续时间略小于大尺度脉动为负的持续时间.这是由于壁面上的压电振子施加的扰动破坏了引起大尺度脉动为正的高速流体扫掠事件相关的湍流结构,使其破碎成小尺度结构,从而增加了小尺度的强度[3,21].近壁区的高速流体扫掠事件通常与壁面高摩擦阻力相关,通过破坏或抑制这种与壁面高摩擦阻力相关的大尺度湍流结构,从而达到减阻的效果.
3 结 论
本文从平均速度剖面、湍流度和对大,小尺度脉动的条件平均等方面对压电振子引起的湍流边界层减阻机理进行了研究,得出以下结论：(1)压电陶瓷振子引起的扰动作用范围仅限于平板湍流边界层近壁区,对于外区并没用明显的作用效果.
(2)通过滤波,把湍流脉动信号分成大、小尺度信号,并分别进行分析,发现压电振子引起的扰动对边界层中的大、小尺度都有影响.扰动减弱了大尺度的脉动强度,增强了小尺度的湍流强度.从能量的角度来看,扰动调整了近壁区的能量分布,使部分大尺度的能量转移到了小尺度中.
(3)通过对大尺度和小尺度脉动进行条件平均发现,小尺度脉动在$u_{\rm L}^ + > 0$时的增加比在$u_{\rm L}^ + < 0$更明显.说明压电振子的扰动主要是通过使大尺度高速流体破碎为小尺度结构,来影响相应的高摩擦事件,从而达到减阻效果.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . The role of coherent structures in the production and dissipation of turbulence in a boundary layer is characterized, summarizing the results of recent investigations. Coherent motion is defined as a three-dimensional region of flow where at least one fundamental variable exhibits significant correlation with itself or with another variable over a space or time range significantly larger than the smallest local scales of the flow. Sections are then devoted to flow-visualization experiments, statistical analyses, numerical simulation techniques, the history of coherent-structure studies, vortices and vortical structures, conceptual models, and predictive models. Diagrams and graphs are provided. |
| [2] | . Coherent structures in wall turbulence transport momentum and provide a means of producing turbulent kinetic energy. Above the viscous wall layer, the hairpin vortex paradigm of Theodorsen coupled with the quasistreamwise vortex paradigm have gained considerable support from multidimensional visualization using particle image velocimetry and direct numerical simulation experiments. Hairpins can autogenerate to form packets that populate a significant fraction of the boundary layer, even at very high Reynolds numbers. The dynamics of packet formation and the ramifications of organization of coherent structures (hairpins or packets) into larger-scale structures are discussed. Evidence for a large-scale mechanism in the outer layer suggests that further organization of packets may occur on scales equal to and larger than the boundary layer thickness. |
| [3] | . 正剪切湍流中相干结构的发现是 上世纪湍流研究的重大进展之一,这些大尺度的相干运动在湍流的动力学过程中起重要作用,也为湍流的控制指出了新的方向.壁湍流高摩擦阻力的产生与近壁区流 动结构密切相关,基于近壁区湍流动力学过程的减阻控制方案可以有效降低湍流的摩擦阻力,但是随着雷诺数的升高,这些控制方案的有效性逐渐降 . 正剪切湍流中相干结构的发现是 上世纪湍流研究的重大进展之一,这些大尺度的相干运动在湍流的动力学过程中起重要作用,也为湍流的控制指出了新的方向.壁湍流高摩擦阻力的产生与近壁区流 动结构密切相关,基于近壁区湍流动力学过程的减阻控制方案可以有效降低湍流的摩擦阻力,但是随着雷诺数的升高,这些控制方案的有效性逐渐降 |
| [4] | . Very large-scale motions in the form of long regions of streamwise velocity fluctuation are observed in the outer layer of fully developed turbulent pipe flow over a range of Reynolds numbers. The premultiplied, one-dimensional spectrum of the streamwise velocity measured by hot-film anemometry has a bimodal distribution whose components are associated with large-scale motion and a range of smaller scales corresponding to the main turbulent motion. The characteristic wavelength of the large-scale mode increases through the logarithmic layer, and reaches a maximum value that is approximately 12-14 times the pipe radius, one order of magnitude longer than the largest reported integral length scale, and more than four to five times longer than the length of a turbulent bulge. The wavelength decreases to approximately two pipe radii at the pipe centerline. It is conjectured that the very large-scale motions result from the coherent alignment of large-scale motions in the form of turbulent bulges or packets of hairpin vortices. |
| [5] | . Spanwise structure and growth mechanisms in a turbulent boundary layer are investigated experimentally. PIV measurements are obtained in the streamwise鈥搒panwise (x鈥搝) plane from the buffer layer to the top of the logarithmic region at Re(傻) = 1015 and 7705. The dominant motions of the flow are shown to be large-scale regions of momentum deficit elongated in the streamwise direction. Throughout the logarithmic layer, the regions are consistently bordered by vortices organized in the streamwise direction, offering strong support for a vortex packet model. Additionally, evidence is presented for the existence and organization of hairpin vortices in the region y^+ < 60. Statistical evidence is also presented for two important aspects of the vortex packet paradigm: vortex organization in the streamwise direction, and the clear association of the hairpin signature with local minima in streamwise velocity. Several spanwise length scales are shown to vary linearly with distance from the wall, revealing self-similar growth of spanwise structure in an average sense. Inspection of the data, however, suggests that individual structures do not grow strictly self-similarly in time. It is proposed that additional scale growth occurs by the merging of vortex packets on an eddy-by-eddy basis via a vortex re-connection mechanism similar to that suggested by Wark & agib (1989). The proposed mechanism provides a link between vortex-pairing concepts and the observed coalescence of streaky low-speed regions in the inner layer. |
| [6] | . A regime of very long meandering positive and negative streamwise velocity fluctuations, that we term ‘superstructures’, are found to exist in the log and lower wake regions of turbulent boundary layers. Measurements are made with a spanwise rake of 10 hot-wires in two separate facilities (spanning more than a decade ofReτ) and are compared with existing PIV and DNS results. In all cases, we note evidence of a large-scale stripiness in the streamwise velocity fluctuations. The length of these regions can commonly exceed 20δ. Similar length scales have been previously reported for pipes and DNS channel flows. It is suggested that the true length of these features is masked from single-point statistics (such as autocorrelations and spectra) by a spanwise meandering tendency. Support for this conjecture is offered through the study of a synthetic flow composed only of sinusoidally meandering elongated low- and high-speed regions. From detailed maps of one-dimensional spectra, it is found that the contribution to the streamwise turbulence intensities associated with the superstructures appears to be increasingly significant with Reynolds number, and scales with outer length variables (δ). Importantly, the superstructure maintains a presence or footprint in the near-wall region, seeming to modulate or influence the near-wall cycle. This input of low-wavenumber outer-scaled energy into the near-wall region is consistent with the rise in near-wall streamwise intensities, when scaled with inner variables, that has been noted to occur with increasing Reynolds number. In an attempt to investigate these structures at very high Reynolds numbers, we also report on recent large-scale sonic anemometer rake measurements, made in the neutrally stable atmospheric surface layer. Preliminary results indicate that the superstructure is present in the log region of this atmospheric flow atReτ= 6.6×105, and has a size consistent with outer scaling. |
| [7] | . Abstract = 2 460. The instantaneous velocity fields give evidence of hairpin vortices aligned in the streamwise direction forming very long zones of low speed fluid, which is flanked on either side by high-speed ones. Statistical support for the existence of hairpins is given by conditional averaged eddy within an increasing spanwise width as the distance from the wall increases, and the main vortex characteristic in different wall-normal regions can be reflected by comparing the proportion of ejection and its contribution to Reynolds stress with that of sweep event. The pre-multiplied power spectra and two-point correlations indicate the presence of large-scale motions in the boundary layer, which are consistent with what have been termed very large scale motions (VLSMs). The three dimensional spatial correlations of three components of velocity further indicate that the elongated low-speed and high-speed regions will be accompanied by a counter-rotating roll modes, as the statistical imprint of hairpin packet structures, all of which together make up the characteristic of coherent structures in the logarithmic region of the turbulent boundary layer (TBL). |
| [8] | . Hot-wire data acquired in a high Reynolds number facility are used to illustrate the need for adequate scale separation when considering the coherent structure in wall-bounded turbulence. It is found that a large-scale motion in the log region becomes increasingly comparable in energy to the near-wall cycle as the Reynolds number increases. Through decomposition of fluctuating velocity signals, it is shown that this large-scale motion has a distinct modulating influence on the small-scale energy (akin to amplitude modulation). Reassessment of DNS data, in light of these results, shows similar trends, with the rate and intensity of production due to the near-wall cycle subject to a modulating influence from the largest-scale motions. |
| [9] | . In this paper we investigate the relationship between the large- and small-scale energy-containing motions in wall turbulence. Recent studies in a high-Reynolds-number turbulent boundary layer (Hutchins & Marusic,Phil. Trans. R. Soc. Lond. A, vol. 365, 2007a, pp. 647–664) have revealed a possible influence of the large-scale boundary-layer motions on the small-scale near-wall cycle, akin to a pure amplitude modulation. In the present study we build upon these observations, using the Hilbert transformation applied to the spectrally filtered small-scale component of fluctuating velocity signals, in order to quantify the interaction. In addition to the large-scale log-region structures superimposing a footprint (or mean shift) on the near-wall fluctuations (Townsend,The Structure of Turbulent Shear Flow, 2nd edn., 1976, Cambridge University Press; Metzger & Klewicki,Phys. Fluids, vol. 13, 2001, pp. 692–701.), we find strong supporting evidence that the small-scale structures are subject to a high degree of amplitude modulation seemingly originating from the much larger scales that inhabit the log region. An analysis of the Reynolds number dependence reveals that the amplitude modulation effect becomes progressively stronger as the Reynolds number increases. This is demonstrated through three orders of magnitude in Reynolds number, from laboratory experiments atReτ~ 103–104to atmospheric surface layer measurements atReτ~ 106. |
| [10] | . The behavior of turbulent fluid motion, particularly in the thin chaotic fluid layers immediately adjacent to solid boundaries, can be difficult to understand or predict. These layers account for up to 50% of the aerodynamic drag on modern airliners and occupy the first 100 meters or so of the atmosphere, thus governing wider meteorological phenomena. The physics of these layers is such that the most important processes occur very close to the solid boundary鈥攖he region where accurate measurements and simulations are most challenging. We propose a mathematical model to predict the near-wall turbulence given only large-scale information from the outer boundary layer region. This predictive capability may enable new strategies for the control of turbulence and may provide a basis for improved engineering and weather prediction simulations. |
| [11] | . In this study we examine the impact of the strength of the large-scale motions on the amplitude and frequency of the small scales in high-Reynolds-number turbulent boundary layers. Time series of hot-wire data are decomposed into large- and small-scale components, and the impact of the large scale on the amplitude and frequency of the small scales is considered. The amplitude modulation effect is examined by conditionally averaging the small-scale intensity ( ${ u}_{S}^{2} $ ) for various values of the large-scale fluctuation ( ${u}_{L} $ ). It is shown that ${ u}_{S}^{2} $ increases with increasing value of ${u}_{L} $ in the near-wall region, whereas, farther away from the wall, ${ u}_{S}^{2} $ decreases with increasing ${u}_{L} $ . The rate of increase in small-scale intensity with the strength of the large-scale signal is neither symmetric (about ${u}_{L} = 0$ ) nor linear. The extent of the frequency modulation is examined by counting the number of occurrences of local maxima or minima in the small-scale signal. It is shown that the frequency modulation effect is confined to the near-wall region and its extent diminishes rapidly beyond ${y}^{+ } = 100$ . A phase lag between the large- and small-scale fluctuations, in terms of amplitude modulation, has also been identified, which is in agreement with previous studies. The phase lag between large- and small-scale fluctuations for frequency modulation is comparable to that of amplitude modulation in the near-wall region. The combined effect of both amplitude and frequency modulation is also examined by computing conditional spectra of the small-scale signal conditioned on the large scales. In the near-wall region, the results indicate that the peak value of pre-multiplied spectra increases with increasing value of ${u}_{L} $ , indicating amplitude modulation, while the frequency at which this peak occurs also increases with increasing value of ${u}_{L} $ , revealing frequency modulation. The overall trends observed from the conditional spectra are consistent with the results obtained through statistical analyses. Finally, a physical mechanism that can capture most of the above observations is also presented. |
| [12] | . Simultaneous streamwise velocity measurements across the vertical direction obtained in the atmospheric surface layer (Re0304 090903 5 0103 105) under near thermally neutral conditions are used to outline and quantify interactions between the scales of turbulence, from the very-large-scale motions to the dissipative scales. Results from conditioned spectra, joint probability density functions and conditional averages show that the signature of very-large-scale oscillations can be found across the whole wall region and that these scales interact with the near-wall turbulence from the energy-containing eddies to the dissipative scales, most strongly in a layer close to the wall, z+ 090905 103. The scale separation achievable in the atmospheric surface layer appears to be a key difference from the low-Reynolds-number picture, in which structures attached to the wall are known to extend through the full wall-normal extent of the boundary layer. A phenomenological picture of very-large-scale motions coexisting and interacting with structures from the hairpin paradigm is provided here for the high-Reynolds-number case. In particular, it is inferred that the hairpin-packet conceptual model may not be exhaustively representative of the whole wall region, but only of a near-wall layer of z+ = O(103), where scale interactions are mostly confined. |
| [13] | . An array of surface hot-film shear-stress sensors together with a traversing hot-wire probe is used to identify the conditional structure associated with a large-scale skin-friction event in a high-Reynolds-number turbulent boundary layer. It is found that the large-scale skin-friction events convect at a velocity that is much faster than the local mean in the near-wall region (the convection velocity for large-scale skin-friction fluctuations is found to be close to the local mean at the midpoint of the logarithmic region). Instantaneous shear-stress data indicate the presence of large-scale structures at the wall that are comparable in scale and arrangement to the superstructure events that have been previously observed to populate the logarithmic regions of turbulent boundary layers. Conditional averages of streamwise velocity computed based on a low skin-friction footprint at the wall offer a wider three-dimensional view of the average superstructure event. These events consist of highly elongated forward-leaning low-speed structures, flanked on either side by high-speed events of similar general form. An analysis of small-scale energy associated with these large-scale events reveals that the small-scale velocity fluctuations are attenuated near the wall and upstream of a low skin-friction event, while downstream and above the low skin-friction event, the fluctuations are significantly amplified. In general, it is observed that the attenuation and amplification of the small-scale energy seems to approximately align with large-scale regions of streamwise acceleration and deceleration, respectively. Further conditional averaging based on streamwise skin-friction gradients confirms this observation. A conditioning scheme to detect the presence of meandering large-scale structures is also proposed. The large-scale meandering events are shown to be a possible source of the strong streamwise velocity gradients, and as such play a significant role in modulating the small-scale motions. |
| [14] | . |
| [15] | . This article focuses on the feedback control of turbulence for skin friction reduction and reviews the state of the art of control algorithms and distributed microsensors and microactuators. From a viewpoint of possible practical applications, we discuss only the control schemes based on the wall-surface sensing of shear stress and pressure fluctuations with their assessment in direct numerical simulation. The rapid development of microelectromechanical systems (MEMS) flow sensors/actuators is sketched, and a prototype feedback control system assembled for a turbulent channel flow is introduced. Finally, several major remaining issues in control algorithms and massive fabrication of microdevices are discussed. |
| [16] | . Turbulence physics responsible for high skin-friction drag in turbulent boundary layers is first reviewed. A self-sustaining process of near-wall turbulence structures is then discussed from the perspective of controlling this process for the purpose of skin-friction drag reduction. After recognizing that key parts of this self-sustaining process are linear, a linear systems approach to boundary-layer control is discussed. It is shown that singular-value decomposition analysis of the linear system allows us to examine different approaches to boundary-layer control without carrying out the expensive nonlinear simulations. Results from the linear analysis are consistent with those observed in full nonlinear simulations, thus demonstrating the validity of the linear analysis. Finally, fundamental performance limit expected of optimal control input is discussed. |
| [17] | |
| [18] | . <div class="abstract" data-abstract-type="normal">Direct numerical simulations of the incompressible Navier鈥揝tokes equations are employed to study the turbulent wall-shear stress in a turbulent channel flow forced by lateral sinusoidal oscillations of the walls. The objective is to produce a documented database of numerically computed friction reductions. To this aim, the particular numerical requirements for such simulations, owing for example to the time-varying direction of the skin-friction vector, are considered and appropriately accounted for.A detailed analysis of the dependence of drag reduction on the oscillatory parameters allows us to address conflicting results hitherto reported in the literature. At the Reynolds number of the present simulations, we compute a maximum drag reduction of 44.7%, and we assess the possibility for the power saved to be higher than the power spent for the movement of the walls (when mechanical losses are neglected). A maximum net energy saving of 7.3% is computed.Furthermore, the scaling of the amount of drag reduction is addressed. A parameter, which depends on both the maximum wall velocity and the period of the oscillation, is found to be linearly related to drag reduction, as long as the half-period of the oscillation is shorter than a typical lifetime of the turbulent near-wall structures. For longer periods of oscillation, the scaling parameter predicts that drag reduction will decrease to zero more slowly than the numerical data. The same parameter also describes well the optimum period of oscillation for fixed maximum wall displacement, which is smaller than the optimum period for fixed maximum wall velocity, and depends on the maximum displacement itself. |
| [19] | . We study collisions of recently discovered ageostrophic modons in rotating shallow water model at different values of impact parameter and find that two new types of coherent vortex structures may be formed during this process: “nonlinear” modons, i.e., coherent dipoles with essentially nonlinear scatter plot and coherent tripoles. Both are known for incompressible 2D Euler equations, but were not reported in the “compressible” shallow water model. Inelastic scattering with strong filamentation and shearing is also possible. Surprisingly, the strongly nonlinear process of coherent structure formation leads to almost no emission of inertia-gravity waves. |
| [20] | . Coherent structures play an important role in the dynamics of turbulent shear flows. The ability to control coherent structures could have significant technological benefits with respect to flow phenomena such as skin friction drag, transition, mixing, and separation. This paper describes the development of an actuator concept that could be used in large arrays for actively controlling transitional and turbulent boundary layers. The actuator consists of a piezoelectrically driven cantilever mounted flush with the flow wall. When driven, the resulting flow disturbance over the actuator is a quasi-steady pair of counter-rotating streamwise vortices with common-flow away from the wall. The vortices decay rapidly downstream of the actuator; however, they produce a set of high- and low-speed streaks that persist far downstream (well over 40 displacement thicknesses). The amplitude of the actuator drive signal controls the strength of the generated vortices. The actuator is fast, compact, and generates a substantial disturbance in the flow. Its performance has been demonstrated using a small array of sensors and actuators in low-speed water laminar boundary layers with imposed steady and unsteady disturbances. Experiments are reported in which transition from a large disturbance was delayed by 40 displacement thicknesses, and in which the mean and spanwise variation of wall shear under an array of high- and low-speed streaks was substantially reduced downstream of a single transverse array of actuators. |
| [21] | . Active control of a turbulent boundary layer has been experimentally investigated with a view to reducing the skin-friction drag and gaining some insight into the mechanism that leads to drag reduction. A spanwise-aligned array of piezo-ceramic actuators was employed to generate a transverse travelling wave along the wall surface, with a specified phase shift between adjacent actuators. Local skin-friction drag exhibits a strong dependence on control parameters, including the wavelength, amplitude and frequency of the oscillation. A maximum drag reduction of 50聽% has been achieved at 17聽wall units downstream of the actuators. The near-wall flow structure under control, measured using smoke鈥搘ire flow visualization, hot-wire and particle image velocimetry techniques, is compared with that without control. The data have been carefully analysed using techniques such as streak detection, power spectra and conditional averaging based on the variable-interval time-average detection. All the results point to a pronounced change in the organization of the perturbed boundary layer. It is proposed that the actuation-induced wave generates a layer of highly regularized streamwise vortices, which acts as a barrier between the large-scale coherent structures and the wall, thus interfering with the turbulence production cycle and contributing partially to the drag reduction. Associated with the generation of regularized vortices is a significant increase, in the near-wall region, of the mean energy dissipation rate, as inferred from a substantial decrease in the Taylor microscale. This increase also contributes to the drag reduction. The scaling of the drag reduction is also examined empirically, providing valuable insight into the active control of drag reduction. |
| [22] | . <p>利用安装在壁面上的单个压电振子周期振荡,采用开环主动控制方案,实现了对平板湍流边界层相干结构猝发的主动控制和壁湍流减阻.根据不同的输入电压幅值和频率,完成了10种工况的实验.在压电振子下游2mm处,用热线风速仪和迷你热线单丝探针,精细测量湍流边界层不同法向位置瞬时流向速度信号的时间序列,分析了在<em>Re<sub>ø</sub></em>=2183压电振子振动对湍流边界层平均速度剖面、减阻率和相干结构猝发过程的影响.实验结果表明,施加控制的工况使平均速度剖面对数律层上移,产生减阻效果;压电振子振幅越大,减阻率越高,减阻效果越明显;通过对施加控制前后流向瞬时速度的多尺度湍涡结构脉动动能的尺度分析,当压电振子振动频率与壁湍流能量最大尺度的猝发频率相近时,减阻率达到最大,为25%,说明控制壁湍流能量最大尺度相干结构的猝发是实现壁湍流减阻的关键;通过对比相干结构猝发的流向速度分量条件相位平均波形,发现施加控制的工况中相干结构猝发流向速度分量的波形幅值明显降低,且流向速度在扫掠后期高速阶段迅速衰减,缩短了高速流体的下扫过程,说明压电振子的振动能抑制相干结构的高速流体下扫过程,减弱高速流体与壁面的强烈剪切过程,并使近壁区域相干结构的振幅显著减弱,迁移速度加快,从而减小壁面摩擦阻力.</p> . <p>利用安装在壁面上的单个压电振子周期振荡,采用开环主动控制方案,实现了对平板湍流边界层相干结构猝发的主动控制和壁湍流减阻.根据不同的输入电压幅值和频率,完成了10种工况的实验.在压电振子下游2mm处,用热线风速仪和迷你热线单丝探针,精细测量湍流边界层不同法向位置瞬时流向速度信号的时间序列,分析了在<em>Re<sub>ø</sub></em>=2183压电振子振动对湍流边界层平均速度剖面、减阻率和相干结构猝发过程的影响.实验结果表明,施加控制的工况使平均速度剖面对数律层上移,产生减阻效果;压电振子振幅越大,减阻率越高,减阻效果越明显;通过对施加控制前后流向瞬时速度的多尺度湍涡结构脉动动能的尺度分析,当压电振子振动频率与壁湍流能量最大尺度的猝发频率相近时,减阻率达到最大,为25%,说明控制壁湍流能量最大尺度相干结构的猝发是实现壁湍流减阻的关键;通过对比相干结构猝发的流向速度分量条件相位平均波形,发现施加控制的工况中相干结构猝发流向速度分量的波形幅值明显降低,且流向速度在扫掠后期高速阶段迅速衰减,缩短了高速流体的下扫过程,说明压电振子的振动能抑制相干结构的高速流体下扫过程,减弱高速流体与壁面的强烈剪切过程,并使近壁区域相干结构的振幅显著减弱,迁移速度加快,从而减小壁面摩擦阻力.</p> |
| [23] | . Hot-wire measurements on a turbulent boundary layer flow perturbed by a wall-mounted cylinder roughness element (CRE) are carried out in this study. The cylindrical element protrudes into the logarithmic layer, which is similar to those employed in turbulent boundary layers by Ryan et al. (AIAA J 49:2210–2220, 2011. doi:10.2514/1.j051012) and Zheng and Longmire (J Fluid Mech 748:368–398, 2014.... [Show full abstract] |
| [24] | . This work explores experimentally the control of a turbulent boundary layer over a flat plate based on wall perturbation generated by piezo-ceramic actuators. Different schemes are investigated, including the feed-forward, the feedback, and the combined feed-forward and feedback strategies, with a view to suppressing the near-wall high-speed events and hence reducing skin friction drag. While the strategies may achieve a local maximum drag reduction slightly less than their counterpart of the open-loop control, the corresponding duty cycles are substantially reduced when compared with that of the open-loop control. The results suggest a good potential to cut down the input energy under these control strategies. The fluctuating velocity, spectra, Taylor microscale and mean energy dissipation are measured across the boundary layer with and without control and, based on the measurements, the flow mechanism behind the control is proposed. |
| [25] | . An experimental investigation was performed for active control of coherent structure bursting in the near-wall region of the turbulent boundary layer. By means of synchronous and asynchronous vibrations with double piezoelectric vibrators,the influence of periodic vibration of the double piezoelectric vibrators on the mean velocity profile, drag reduction rate, and coherent structure bursting is analyzed at Re_胃= 2766. The case with 100 V/160 Hz-ASYN is superior to other conditions in the experiment and a relative drag reduction rate of 18.54% is exciting. Asynchronous vibration is more effective than synchronous vibration in drag reduction at the same voltage and frequency. In all controlled cases, coherent structures at large scales are regulated while the small-scale structures are stimulated. The fluctuating velocity increases significantly. A periodic regulating effect on the coherent structure can be seen in the ASYN control conditions at the frequency of 160 Hz. |
| [26] | . When using a miniature single sensor boundary layer probe,the time sequences of the stream-wise velocity in the turbulent boundary layer(TBL) are measured by using a hot wire anemometer.Beneath the fully developed TBL,the wall pressure fluctuations are attained by a microphone mechanism with high spatial resolution.Analysis on the statistic and spectrum properties of velocity and wall pressure reveals the relationship between the wall pressure fluctuation and the energy-containing structure in the buffer layer of the TBL.Wavelet transform shows the multi-scale natures of coherent structures contained in both signals of velocity and pressure.The most intermittent wall pressure scale is associated with the coherent structure in the buffer layer.Meanwhile the most energetic scale of velocity fluctuation at y+= 14 provides a specific frequency f9鈮 147 Hz for wall actuating control with Re蟿= 996. |
| [27] | . 在湍流相干结构动力学方程中，非相干结构成分对相干结构贡献的雷诺应力的模型为涡黏性模型,即涡黏性系数乘以相干结构平均速度变形率的形式. 基于非相干结构成分对相干结构贡献的雷诺应力与相干结构速度变形率之间存在相位差的事实，在理论上提出了非相干结构成分对相干结构贡献的雷诺应力复涡黏性模型的假设. 应用热线测速技术，在低速风洞中对湍流边界层非相干结构成分对相干结构贡献的雷诺应力与相干结构法向速度变形率之间的相位关系进行了实验测量. 通过分析湍流相干结构猝发过程中非相干结构成分对相干结构贡献的雷诺应力与相干结构速度变形率之间的相位关系，研究了相干结构雷诺应力分量与流向速度法向梯度之间的相位差沿湍流边界层法向的变化规律，肯定了湍流相干结构复涡黏性系数模型的合理性. . 在湍流相干结构动力学方程中，非相干结构成分对相干结构贡献的雷诺应力的模型为涡黏性模型,即涡黏性系数乘以相干结构平均速度变形率的形式. 基于非相干结构成分对相干结构贡献的雷诺应力与相干结构速度变形率之间存在相位差的事实，在理论上提出了非相干结构成分对相干结构贡献的雷诺应力复涡黏性模型的假设. 应用热线测速技术，在低速风洞中对湍流边界层非相干结构成分对相干结构贡献的雷诺应力与相干结构法向速度变形率之间的相位关系进行了实验测量. 通过分析湍流相干结构猝发过程中非相干结构成分对相干结构贡献的雷诺应力与相干结构速度变形率之间的相位关系，研究了相干结构雷诺应力分量与流向速度法向梯度之间的相位差沿湍流边界层法向的变化规律，肯定了湍流相干结构复涡黏性系数模型的合理性. |
| [28] | . Hot-wire measurements on a turbulent boundary layer flow perturbed by a wall-mounted cylinder roughness element (CRE) are carried out in this study. The cylindrical element protrudes into the logarithmic layer, which is similar to those employed in turbulent boundary layers by Ryan et al. (AIAA J 49:2210-2220, 2011. doi: 10.2514/1.j051012) and Zheng and Longmire (J Fluid Mech 748:368-398, 2014. doi: 10.1017/jfm.2014.185) and in turbulent channel flow by Pathikonda and Christensen (AIAA J 53:1-10, 2014. doi: 10.2514/1.j053407). The similar effects on both the mean velocity and Reynolds stress are observed downstream of the CRE perturbation. The series of hot-wire data are decomposed into large- and small-scale fluctuations, and the characteristics of large- and small-scale bursting process are observed, by comparing the bursting duration, period and frequency between CRE-perturbed case and unperturbed case. It is indicated that the CRE perturbation performs the significant impact on the large- and small-scale structures, but within the different impact scenario. Moreover, the large-scale bursting process imposes a modulation on the bursting events of small-scale fluctuations and the overall trend of modulation is not essentially sensitive to the present CRE perturbation, even the modulation extent is modified. The conditionally averaging fluctuations are also plotted, which further confirms the robustness of the bursting modulation in the present experiments. |
| [29] | . |
| [30] | . In this study, the coherent structures, which were effected by superhydrophobic (SH) surfaces in turbulent channel flow, were investigated by time-resolved particle image velocimetry (TRPIV). Hierarchical structured SH surfaces which have micro-nano secondary structures were applied in the experiment. Drag reduction rate is approximately 11% at Re胃鈮1300, which is based on momentum thickness. Coherent structures (low-speed streak, hairpin vortex and hairpin vortex packets) with scale information were obtained by conditional sampling and averaging method. Compared to the hydrophilic (PH) surfaces, the conditional averaged hairpin vortex structures of SH surfaces have a lager spacing of vortex legs, a smaller angle of inclination along streamwise and spanwise directions. Accordingly, a smaller-scale hairpin vortex packet with three swirling motions was emerged. Through the comparative research on angle of inclination, the lifting movement of vortex in wall-normal direction was also weaker than PH case. These shows that the existence of SH surfaces restricts the development of coherent structures and induces drag reduction effects. |
| [31] | . 基于相同雷诺数下清水和高分子聚合物溶液壁湍流的高时间分辨率粒子图像测速技术(time-resolved particle image velocimetry, TRPIV)的对比实验,从高聚物溶液对湍流边界层动量能量输运影响的角度分析其减阻的机理。对比两者的雷诺应力发现高聚物的存在抑制了湍流输运过程。这一影响与高聚物对壁湍流中占主导地位的涡旋运动和低速条带等相干结构的作用密切相关。运用条件相位平均、相关函数和线性随机估计(linear stochastic estimation, LSE)等方法,分析提取了高聚物溶液流场中的发卡涡和发卡涡包等典型相干结构的空间拓扑形态。相比于清水,高聚物溶液中相干结构的流向尺度增大,涡旋运动的发展及低速流体喷射的强度受到削弱,表明了添加的高聚物阻碍了湍流原有的能量传递和自维持的机理。正是通过影响相干结构,高聚物抑制了湍流边界层中近壁区与外区之间的动量和能量输运,使得湍流的无序性降低,从而减小了湍流流动的阻力。 . 基于相同雷诺数下清水和高分子聚合物溶液壁湍流的高时间分辨率粒子图像测速技术(time-resolved particle image velocimetry, TRPIV)的对比实验,从高聚物溶液对湍流边界层动量能量输运影响的角度分析其减阻的机理。对比两者的雷诺应力发现高聚物的存在抑制了湍流输运过程。这一影响与高聚物对壁湍流中占主导地位的涡旋运动和低速条带等相干结构的作用密切相关。运用条件相位平均、相关函数和线性随机估计(linear stochastic estimation, LSE)等方法,分析提取了高聚物溶液流场中的发卡涡和发卡涡包等典型相干结构的空间拓扑形态。相比于清水,高聚物溶液中相干结构的流向尺度增大,涡旋运动的发展及低速流体喷射的强度受到削弱,表明了添加的高聚物阻碍了湍流原有的能量传递和自维持的机理。正是通过影响相干结构,高聚物抑制了湍流边界层中近壁区与外区之间的动量和能量输运,使得湍流的无序性降低,从而减小了湍流流动的阻力。 |
| [32] | . <p>超疏水壁面由于具有减阻和自清洁功能而成为国内外减阻和海洋防污等研究领域的热点之一，而20世纪湍流中相干结构的发现为湍流的控制指出新的方向，尤其近壁区涡结构对摩擦阻力贡献很大.利用高时间分辨率粒子图像测速技术，研究了超疏水壁面（SH）以及亲水壁面（PH）湍流边界层中正负展向涡的空间分布特征，研究逆向涡对超疏水壁面近壁区流动结构的影响和超疏水壁面的减阻机理.首先利用空间多尺度局部平均涡量的概念提取壁湍流发卡涡展向涡头（顺向涡）和逆向涡，实现了准确识别涡心并排除小尺度涡的干扰；然后根据检测到的顺向涡和逆向涡流线分布图，发现逆向涡始终处于正向涡的上游和下方，并且对正向涡的进一步发展起抑制作用；最后对两种壁面边界层中逆向涡数量以及出现概率进行对比，发现具有减阻效果的超疏水壁面边界层中出现更多逆向涡.说明逆向涡可抑制上方顺向涡与壁面的强烈剪切，并使靠近壁面的流体加速，从而产生减阻效果；超疏水壁面中涡结构具有更大的角，使其更好地阻碍了发卡涡头附近强烈的喷射和扫略；超疏水壁面逆向涡出现概率明显大于亲水壁面.这些结果表明：超疏水壁面表现出的减阻特性（<em>Re</em><sub><em>δ</em></sub>≈13 500，减阻5.8%）与两板产生逆向涡的差异有关.</p> . <p>超疏水壁面由于具有减阻和自清洁功能而成为国内外减阻和海洋防污等研究领域的热点之一，而20世纪湍流中相干结构的发现为湍流的控制指出新的方向，尤其近壁区涡结构对摩擦阻力贡献很大.利用高时间分辨率粒子图像测速技术，研究了超疏水壁面（SH）以及亲水壁面（PH）湍流边界层中正负展向涡的空间分布特征，研究逆向涡对超疏水壁面近壁区流动结构的影响和超疏水壁面的减阻机理.首先利用空间多尺度局部平均涡量的概念提取壁湍流发卡涡展向涡头（顺向涡）和逆向涡，实现了准确识别涡心并排除小尺度涡的干扰；然后根据检测到的顺向涡和逆向涡流线分布图，发现逆向涡始终处于正向涡的上游和下方，并且对正向涡的进一步发展起抑制作用；最后对两种壁面边界层中逆向涡数量以及出现概率进行对比，发现具有减阻效果的超疏水壁面边界层中出现更多逆向涡.说明逆向涡可抑制上方顺向涡与壁面的强烈剪切，并使靠近壁面的流体加速，从而产生减阻效果；超疏水壁面中涡结构具有更大的角，使其更好地阻碍了发卡涡头附近强烈的喷射和扫略；超疏水壁面逆向涡出现概率明显大于亲水壁面.这些结果表明：超疏水壁面表现出的减阻特性（<em>Re</em><sub><em>δ</em></sub>≈13 500，减阻5.8%）与两板产生逆向涡的差异有关.</p> |
| [33] | . 壁湍流中的相干结构与壁面的高摩擦阻力密切相关,研究壁面纵向微小沟槽对展向涡的影响规律,有助于深入认识沟槽壁面的减阻机理。在自由来流速度控制在0.18m/s的水槽中(Reτ=190),采用高时间分辨率粒子图像测速技术,测量光滑平板和沟槽板(s+=2h+=16.3)湍流边界层,分别获得了15998个瞬时速度矢量场。使用λci识别展向涡,比较了2种壁面流动中不同法向位置处展向涡的数量、平均强度、平均尺度及各尺度展向涡所占的数量比例。结果表明:沟槽使近壁区顺向涡的数量减小,逆向涡的数量增大,并削弱了展向涡的强度;沟槽使近壁区小尺度顺向涡和中尺度逆向涡的比例增加,中尺度顺向涡和大尺度逆向涡的比例减小,使得近壁区顺向涡的尺度差异变小,对近壁区逆向涡的尺度差异几乎无影响;沟槽减小了对数律区小尺度顺向涡的数量比例,并增大了大尺度顺向涡的数量比例,对数律区逆向涡数量比例的变化规律和顺向涡正好相反。 . 壁湍流中的相干结构与壁面的高摩擦阻力密切相关,研究壁面纵向微小沟槽对展向涡的影响规律,有助于深入认识沟槽壁面的减阻机理。在自由来流速度控制在0.18m/s的水槽中(Reτ=190),采用高时间分辨率粒子图像测速技术,测量光滑平板和沟槽板(s+=2h+=16.3)湍流边界层,分别获得了15998个瞬时速度矢量场。使用λci识别展向涡,比较了2种壁面流动中不同法向位置处展向涡的数量、平均强度、平均尺度及各尺度展向涡所占的数量比例。结果表明:沟槽使近壁区顺向涡的数量减小,逆向涡的数量增大,并削弱了展向涡的强度;沟槽使近壁区小尺度顺向涡和中尺度逆向涡的比例增加,中尺度顺向涡和大尺度逆向涡的比例减小,使得近壁区顺向涡的尺度差异变小,对近壁区逆向涡的尺度差异几乎无影响;沟槽减小了对数律区小尺度顺向涡的数量比例,并增大了大尺度顺向涡的数量比例,对数律区逆向涡数量比例的变化规律和顺向涡正好相反。 |
| [34] | . http://link.springer.com/article/10.1007%2Fs11426-011-4446-0 |
| [35] | . Vortex dynamics of a circular cylinder controlled by a synthetic jet positioned at the back stagnation point is experimentally investigated using particle image velocimetry (PIV) technique. The proper orthogonal decomposition (POD) method is adopted to present the variations of the POD energy, mode, coefficient, corresponding dominant frequency, and the reconstructed spanwise vorticity. It is found that the dominant dimensionless control parameters should be the synthetic jet stroke lengthL0/D, whereDis the diameter of the experimental circular cylinder, and the equivalent momentum coefficientCμ. For the same stroke lengthL0/D=3.3, the states of the wake vortex shedding are determined by the momentum coefficient. They can be categorized into three groups summarizing all the parameters tested: antisymmetric Karman vortex shedding mode(Cμ≤0.027), vortex synchronization with shedding modes varying between the symmetric and antisymmetric ones(0.061≤Cμ≤0.109), and vortex synchronization with symmetric shedding mode(0.213≤Cμ≤0.378). When the symmetric shedding mode occurs, the corresponding spanwise vorticity modes show two parallel rows of half-arrowhead structures with alternate signs that are antisymmetric about the centerline. The POD modes based on the streamwise and vertical velocities also exhibit regular variations with different wake vortex shedding states. |
| [36] | Scitation is the online home of leading journals and conference proceedings from AIP Publishing and AIP Member Societies |
| [37] | . Large-scale motions (LSMs; having wavelengths up to 2-3 pipe radii) and very-LSMs (having wavelengths more than 3 pipe radii) have been shown to carry more than half of the kinetic energy and Reynolds shear stress in a fully developed pipe flow. Studies using essentially the same methods of measurement and analysis have been extended to channel and zero-pressure-gradient boundary-layer flows to determine whether large structures appear in these canonical wall flows and how their properties compare with that of the pipe flow. The very large scales, especially those of the boundary layer, are shorter than the corresponding scales in the pipe flow, but otherwise share a common behaviour, suggesting that they arise from similar mechanism(s) aside from the modifying influences of the outer geometries. Spectra of the net force due to the Reynolds shear stress in the channel and boundary layer flows are similar to those in the pipe flow. They show that the very-large-scale and main turbulent motions act to decelerate the flow in the region above the maximum of the Reynolds shear stress. |
| [38] | . Wavelet analysis is employed to examine amplitude and frequency modulations in broadband signals. Of particular interest are the streamwise velocity fluctuations encountered in wall-bounded turbulent... |
