INFLUENCE OF WATER LEVEL ON ICE LOAD ON UPWARD-DOWNWARD CONICAL STRUCTURE BASED ON DEM ANALYSIS1)
LongXue中图分类号:P751,P731.15
文献标识码:A
版权声明:2019力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (24275KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
在高纬度寒区海域,锥体平台结构因具有良好的抗冰性能而被广泛应用,如渤海的导管架平台、加拿大Confederation桥墩、芬兰Kemi-hspace{-1mm}Ⅰ灯塔等[1- 3].海冰与锥体结构作用时的主要破坏模式为弯曲破坏,且作用在锥体结构上的冰载荷具有明显的周期性[4- 5].由于海冰的弯曲强度较小,且载荷作用周期较长,锥体结构在减小冰载荷和降低冰激振动方面具有显著优势[6- 7].为保障寒区海域平台结构的安全运行,海冰的力学性质、锥体结构参数以及锥体结构冰载荷特性等相关研究受到较多关注[8- 10].理论分析、现场测量、室内模型试验及数值模拟是海洋结构冰载荷研究的主要方法[11-13],其中数值模拟具有成本低、周期短以及可重复性高等优点,成为工程海冰领域的重要研究途径.
我国对锥体海洋平台结构的现场测量主要是在渤海JZ20-2和JZ9-3海域的导管架海洋平台上展开的,并基于大量实测数据建立了锥体结构的动冰力函数和冰力谱[14- 15].Qu等[16]对实测冰载荷进行谱分析,研究锥体冰载荷的频率及冰激振动情况,为锥体冰载荷的研究提供了重要的现场数据.但由于现场实测结果受到复杂环境和测试误差等因素的影响,深入探究单一变量对冰载荷的影响具有较大难度.为研究锥体尺寸参数对其抗冰性能的影响,Xu等[17]建立了渤海JZ20-2MUQ平台的等比例缩放模型,并在德国汉堡冰池(HSVA)进行了相关室内模型试验.该试验结果表明冰排与窄锥结构作用后呈楔型断裂,而与宽锥作用后呈板形断裂且冰载荷较大.Tian等[18]在冰池内的模型试验中发现,当锥径与冰厚比值小于30时冰载荷随锥径的增大而增大.以上研究均表明锥径大小是影响冰载荷和海冰破坏模式的重要因素.
对于渤海锥体导管架海洋平台结构,潮汐变化会引起海冰作用位置处锥径的差异,并导致锥体冰载荷的显著变化.海冰与正锥作用将发生向上弯曲破坏,而与倒锥作用将发生向下弯曲破坏[19].当水线处的锥体直径相同时,正锥冰载荷要明显大于倒锥冰载荷[17].史庆增等[20]在试验中发现海冰与正倒锥交界处作用时发生挤压破碎的情况.但对于该挤压破碎发生机理的研究还不够完善,且海冰与锥体不同位置作用的冰载荷及破坏模式问题还需更深入研究.
在冰载荷的现场测量和模型试验中,均较难测得海冰内部裂纹的发生和演化过程,而数值方法则可深入分析影响冰载荷变化的海冰断裂特征[21- 22].采用有限元方法可对海冰与锥体作用过程中海冰的应力分布进行研究,但缺少对海冰断裂过程的分析[23].采用光滑粒子流体动力学方法可模拟海冰与船舶结构作用,但难以模拟海冰破碎后的动力学过程[24].另外,近场动力学等粒子方法也可对海冰的断裂过程进行模拟[25].但以上方法受到边界参数等影响较大,对海冰破碎过程的模拟具有一定的局限性.近年来,离散元方法(discrete element method,DEM)不仅可计算离散颗粒材料的力学性质[26 -28],在模拟海冰、岩石、石英玻璃等脆性材料中也有广泛应用,可更准确高效地用于描述脆性材料由连续体向散体转化的破碎特性[29- 30]. Hopkins[31]最早采用二维离散元模拟平整冰在斜面结构前的破碎堆积并形成冰脊的过程.Paavilainen等[32]采用二维有限元和离散元耦合方法(FEM-DEM)模拟了海冰在斜坡上的断裂堆积过程.为进一步提高离散元方法的准确性,Lau[33]采用三维块体离散元模型计算海冰的破碎过程,但计算规模难以满足工程应用需求.狄少丞等[34]将GPU高性能运算引入离散元方法中,并用于海冰与多桩腿结构作用的数值模拟,有效解决了工程尺度下离散元的计算效率问题.目前,离散元方法在海洋结构、船舶结构、核电站取水口等的结构设计及冰载荷计算中应用广泛,为具体的工程实践提供了有力的参考依据[35- 36].
本文采用具有粘结破碎功能的离散元方法模拟平整冰与正倒锥体结构的相互作用过程,研究海冰与锥体不同位置作用时海冰的破坏模式和冰载荷的变化规律,分析正倒锥交界处海冰破坏模式的变化情况,并揭示海冰与锥体结构不同位置作用时的破碎机理和冰载荷特性.
1 海冰与锥体结构作用的离散元方法
1.1 海冰颗粒单元的平行粘结模型
采用离散元模拟海冰与锥体作用时,将海冰视为具有一定质量和大小的球形颗粒集合.按照六方最密堆积的方式将球形颗粒规则排列成平整冰.该排列方式具有对称性好,密集度高等特点[34].通过平行粘结模型将排列后的颗粒互相粘结,粘结颗粒间通过平行圆盘传递力和力矩,如图1所示[37].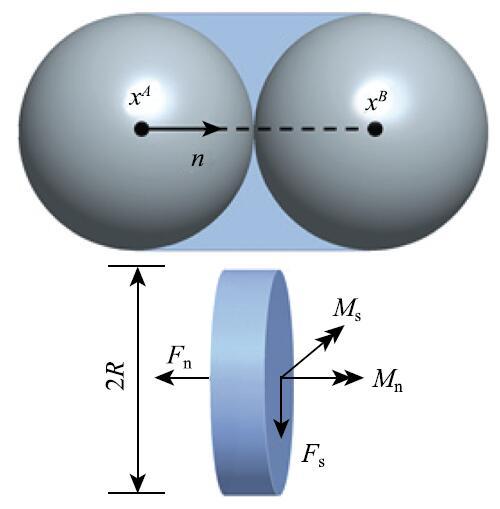
显示原图|下载原图ZIP|生成PPT图1球体颗粒的平行粘结模型...
-->Fig. 1Parallel bond method of spherical particles
-->
在平行粘结模型中,分别为颗粒间的法向力和切向力,$M_{n}$和$M_{s}$分别为颗粒间的法向力矩和切向力矩.根据梁在横力作用下的弯曲理论,作用在粘结圆盘上的最大正应力和最大剪应力可分别表示为[37]
\begin{equation}\label{eq1} \sigma _{\max } = \frac{ F_{n} }{A} + {sign}(F_{n}) \frac{\left| {M_{s} } \right|}{I}R, \quad\tau _{\max } = \frac{\left| {F_{s} } \right|}{A} +\frac{\left| {M_{n} } \right|}{J}R \tag{1}\end{equation}
式中,$A$为粘结圆盘的横截面积,$J$为粘结圆盘的极惯性矩,$I$为粘结圆盘的惯性矩,可分别表示为
\begin{equation}\label{eq2} A = \pi R^2, \quad I = \frac{1}{4}\pi R^4, \quad J= \frac{1}{2}\pi R^4 \tag{2}\end{equation}
式中,$R$为粘结圆盘的半径,即球体颗粒的半径.
1.2 海冰粘结颗粒单元的失效准则
为模拟海冰的断裂过程,这里考虑粘结颗粒单元间的粘结失效功能,其失效模式主要分为拉伸失效和剪切失效.图2中当粘结圆盘的最大正应力$\sigma_{\max}>0$时,则表示两个粘结颗粒处于压缩状态,其可发生剪切破坏;相反,当$\sigma_{\max}<0$时,则表示两个粘结颗粒处于拉伸状态,其可发生剪切或拉伸破坏.当粘结圆盘的最大正应力$\sigma$}$_{\max}$超过颗粒间的拉伸强度$\sigma $}$^{t}$,即$\sigma $}$_{\max}>\sigma ^{t}$,粘结圆盘发生拉伸失效;当最大剪应力$\tau$}$_{\max}$超过颗粒间的剪切强度$\tau ^{s}$,即$\tau$}$_{\max}>\tau ^{s}$时,粘结圆盘发生剪切失效.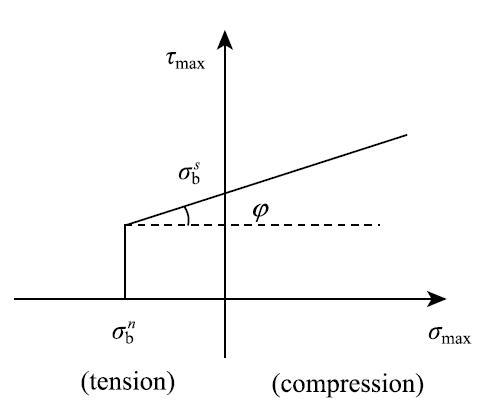
显示原图|下载原图ZIP|生成PPT图2粘结颗粒的破坏失效准则...
-->Fig.2Failure criterion of bonded particles
-->
颗粒单元的拉伸破坏强度$\tau ^{t}$和剪切破坏强度$\tau$}$^{s}$与颗粒间法向粘结强度$\sigma _{b}^{n}$和切向粘结强度$\sigma _{b}^{s} $密切相关.本文采用摩尔-库伦摩擦准则对剪切破坏强度进行确定[38],即
$$\sigma ^{t} = \sigma _{b}^{n} \tag{3}$$
$$\tau ^{s} = \sigma _{b}^{s} + \mu _{b} \sigma_{\max } \tag{4}$$
式中,$\mu_{b}$是海冰粘结颗粒之间的内摩擦系数,$\mu$}$_{b }$ = tan$\varphi $},$\varphi$}为粘结颗粒单元间的内摩擦角.
粘结颗粒间法向和切向粘结强度的选取是影响离散元计算准确性的关键.它决定了海冰材料的压缩强度和弯曲强度等物理力学性质,也影响海冰与海洋结构作用时的破坏模式.此外,颗粒之间粘结失效可视为冰内裂纹的产生,粘结破坏的颗粒数量增加意味着冰内裂纹的扩展,宏观表现为海冰的断裂过程.当海冰与海洋结构相互作用发生破碎后,离散的海冰颗粒单元间的接触力采用赫兹接触模型进行计算,以确定碎冰的运动规律.
1.3 海冰强度与温盐分布的对应关系
海冰强度与其温度、盐度均有密切关系.由于海水和空气温度不同,同时受海冰生消过程中冰内盐度的变化,海冰内部竖直剖面上的温度和盐度分布不是均匀的,由此导致海冰的强度分布也随之变化.渤海海冰的强度与温盐之间的关系可写作[4]$$v_{b} = S_{i} \left(0.532 + \frac{49.185}{\left|{T_{i} } \right|}\right) \tag{5}$$
$$\sigma _{f} = 2.98{e}^{-5.06\sqrt {v_{b} } } \tag{6}$$
式中,$T_{i}$为海冰温度(\textcelsius),$-$0.5\textcelsius~$\ge T_{i} \ge $ $-$22.9\textcelsius;$S_{i}$为海冰盐度(‰);$v_{b}$为海冰的卤水体积(‰);$\sigma $}$_{f}$为海冰的弯曲强度(MPa).
当海冰与正锥体作用时,其下表面发生拉伸破坏,而与倒锥体作用时,则其上表面发生拉伸破坏.由于海冰上下表面及其内部的温度、盐度均有一定的差异,导致海冰内部强度的不同.本文在海冰的离散元计算中,将考虑其竖直剖面内强度的差异.为简化计算,这里忽略海冰剖面内盐度的变化,并假设海冰温度在竖直剖面内呈线性分布,从而将海冰强度设为海冰温度的线性函数.
海冰的弯曲强度($\sigma $}$_{f})$与颗粒单元的粘结强度($\sigma $}$_{b})$紧密相关,可通过对海冰的三点弯曲试验确定海冰宏观强度与离散元微观参数之间的关系[39]
\begin{equation}\label{eq7} \sigma _{b} = \sigma _{f} / (1.77-1.81{e}^{-\frac{h_{i} / D_{p} }{4.78}})\tag{7}\end{equation}
式中,$D_{p}$为颗粒单元直径;$h_{i}$为海冰厚度.
该关系式与渤海现场试验中测得的海冰弯曲强度对比验证结果良好[37],可用于渤海海冰力学性质的模拟分析,是海冰离散元参数选取的重要依据.
2 海冰与正倒锥结构作用的离散元分析}
2.1 海冰离散元参数的设定
以渤海JZ20-2平台的锥体结构与海冰的相互作用为研究对象(如图3),并参考渤海海冰的物理力学性质,建立海冰和锥体结构作用的离散元模型.为对比分析正锥和倒锥的冰载荷,在本文离散元模拟中设定正倒锥的倾斜角$\alpha$}均为60$^\circ$,锥体最大直径为4.0 m,最小直径为1.5m,如图4(a)所示.当水位线高度($H)$发生变化时,水线处的锥径($D)$也随之变化.图4(b)为海冰的离散元模型,海冰不与结构碰撞的三个边界均采用弹簧边界进行弹性约束.该弹簧边界的刚度与颗粒间的接触刚度相同且在$x$方向具有与海冰相同的运动速度.这样可采用有限尺寸的海冰区域近似模拟无限大平整冰与锥体结构的相互作用.同时,考虑海水对海冰单元的浮力和拖曳作用,并将海水流速设为常值[13].
显示原图|下载原图ZIP|生成PPT图3渤海JZ20-2正倒锥体导管架海洋平台...
-->Fig.3The JZ20-2 jacket platform with upward-downward\ cone in the Bohai Sea
-->
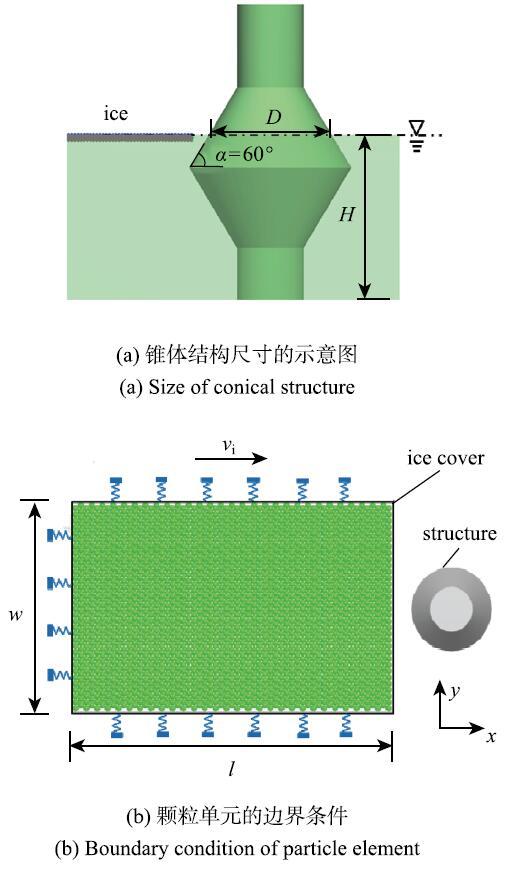显示原图|下载原图ZIP|生成PPT图4海冰与锥体结构相互作用的离散元模型...
-->Fig.4DEM of the interaction between ice and conical structure
-->
这里的离散元计算参数由渤海海冰物理力学性质的现场和室内实测数据确定[4,16],并列于表1中.首先根据式(5)和式(6)可推算海冰上下表面的弯曲强度,冰层上表面弯曲强度为1.91MPa,下表面的弯曲强度为1.26 MPa.再由式(7)对颗粒单元的粘结强度进行推算,上表面颗粒间的粘结强度为1.86 MPa,下表面颗粒间的粘结强度最小为1.22MPa,并对中间颗粒的粘结强度进行线性插值.
Table 1
表1
表1离散元计算的主要参数
Table 1Main parameters of DEM calculation
| Definition | Symbol | Value |
|---|---|---|
| density of sea water | Pw | 1035.0 kg/m3 |
| density of sea ice | Pi | 920.0 kg/m3 |
| velocity of sea ice | Vi | 0.4 m/s |
| thickness of sea ice | h | 0.23 m |
| calculation area size of sea ice | l x w | 13.0 mx13.0 m |
| elastic modulus of sea ice | E | 1.0 GPa |
| diamete of particle cell | dp | 0.054 m |
| total number of particle elements | N | 2.9x105 |
| friction coefficient of particle element | 0.2 | |
| coefficient of friction between sea ice and structure | 0.2 | |
| salinity of sea ice | S i | 1.0 %〇 |
| upper and lower surface temperatures of sea ice | T | -7.0°C,-1.73°C |
新窗口打开
2.2 正锥与倒锥上冰载荷的对比分析
在渤海现场监测中,在正锥体上安装了压力传感器以测量结构冰载荷[1,16-17].这里采用该现场实测数据与离散元模拟结果进行对比验证.在对比分析海冰作用在正、倒锥体上的破坏模式时,均取结构水线处锥径为3.2m,其他计算参数相同.(1) 正锥体上的冰载荷
图5为不同时刻海冰作用在正锥体上的破碎过程,用不同颜色区分海冰弯曲破碎后的碎冰分布情况.冰排与正锥作用时,冰排内部产生径向裂纹及环向裂纹使冰排发生向上的弯曲破坏.破碎后的海冰多呈楔形块状分布在锥体周围,并在后续冰排的推动下沿锥面继续向上爬升并不断堆积.爬升的碎冰块在重力作用下将滑入水中,然后在海水的拖曳作用下向前继续漂移并从锥体两侧清除,由此形成一个完整的冰载荷周期.从冰块的破坏特性看,模拟结果与图6中渤海JZ20-2海洋平台的实测结果在规律上基本一致.
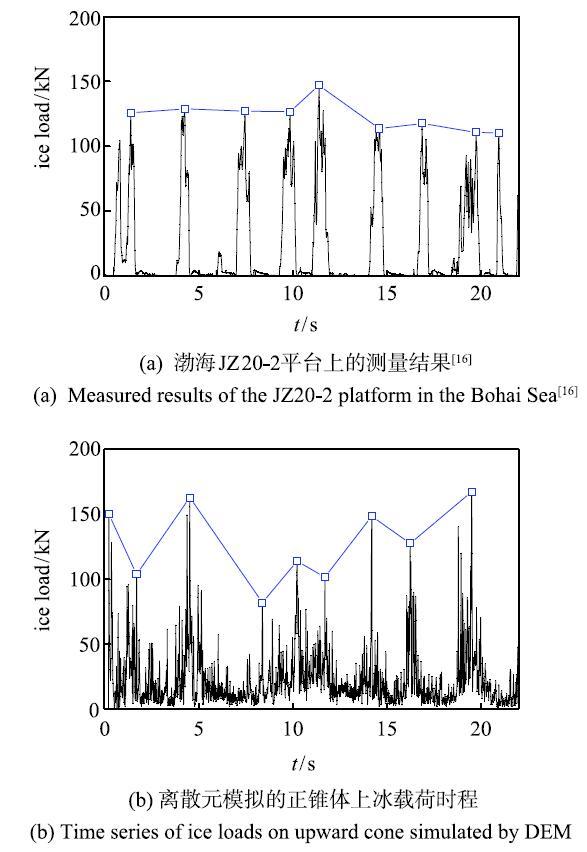
图7(a)为渤海JZ20-2锥体平台上的冰载荷实测数据,图7(b)为本文离散元计算结果.该图表明离散元模拟的锥体冰载荷与实测结果在形式上均有明显的周期性特点.这是由于海冰与锥体作用时均发生弯曲破坏.在冰排和结构作用的加载和卸载过程中,冰排发生弯曲破碎时会形成较大的作用力.冰排破碎后,该作用力迅速减小直到后续冰排再次作用到锥体上.除考虑冰载荷的最大值外,还采用冰载荷时程中冰载荷峰值的均值作为对比分析的主要指标,以降低冰载荷时程的随机性影响.这里,渤海实测冰载荷峰值的最大值和均值分别为145.9 kN和116.9kN,而本文离散元方法计算得的结果分别为166.5 kN和128.5 kN.可以看出,离散元的计算结果比实测结果略大.但考虑到离散元计算中的海冰参数与现场实测结果存在一定差异,该结果误差在可接受范围内.
从图7(a)和图7(b)还可发现,在22s内的实测值和计算值均有9个明显的冰载荷峰值.这说明计算所得的冰载荷周期与实测结果较为接近.由此可见,从冰排的破坏模式、冰载荷的大小和周期上来看,离散元计算结果与渤海实测数据均比较一致,从而验证了该离散元方法及计算参数在锥体结构冰载荷模拟中的准确性.
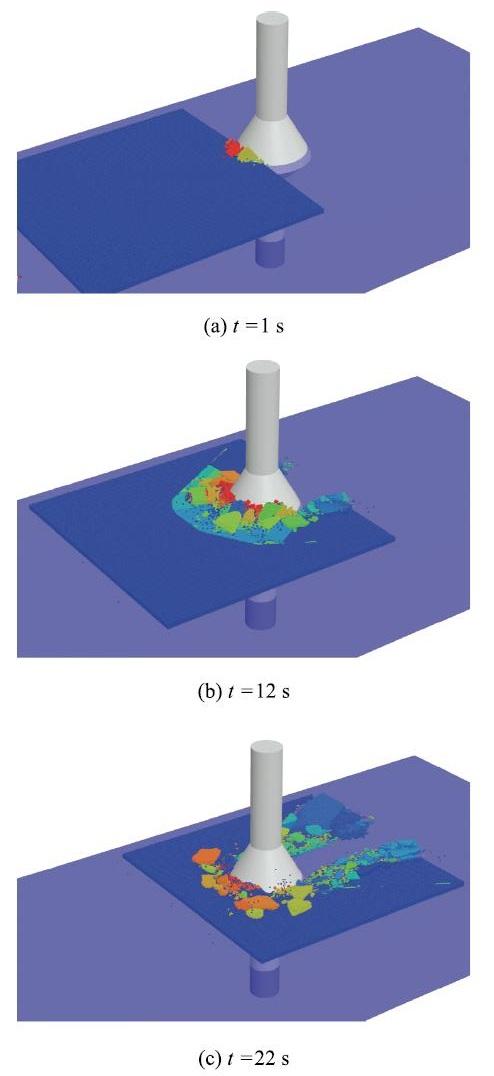显示原图|下载原图ZIP|生成PPT图5离散元模拟海冰与正锥体作用的破坏过程...
-->Fig.5Failure process of sea ice acting on upward cone simulated by DEM
-->
显示原图|下载原图ZIP|生成PPT图6渤海JZ20-2平台海冰与正锥体作用...
-->Fig.6Interaction of sea ice and upward cone observed on the JZ20-2 platform in the Bohai Sea
-->
显示原图|下载原图ZIP|生成PPT图7渤海实测冰载荷与离散元模拟结果对比...
-->Fig.7Comparison of ice loads on upward cone measured in the Bohai Sea and simulated with DEM
-->
(2) 倒锥体上的冰载荷
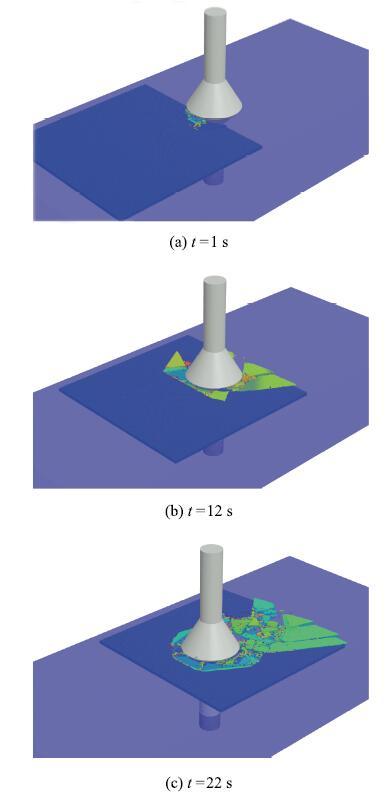
潮汐会对海洋平台结构的水线高度造成影响,进而决定了海冰对锥体结构的作用位置.在较低水位时,海冰将作用于倒锥体上.图8为海冰与倒锥作用的离散元模拟结果.对于倒锥结构,海冰会发生向下的弯曲破坏,产生的碎块在海水的浮力和拖曳力作用下直接被清除.与正锥海冰的破坏过程相比,缺少碎冰沿结构表面堆积攀爬的过程.对比图5和图8中不同颜色的海冰碎块尺度,海冰与正锥作用后的海冰破碎尺寸明显小于倒锥的海冰碎块.海冰在倒锥体上破碎的实测现象如图9所示,其在冰块破碎规律上与本文离散元计算结果相一致.
显示原图|下载原图ZIP|生成PPT图8离散元模拟海冰与倒锥体作用的破坏过程...
-->Fig.8Breaking process of sea ice acting on downward cone simulated with DEM
-->
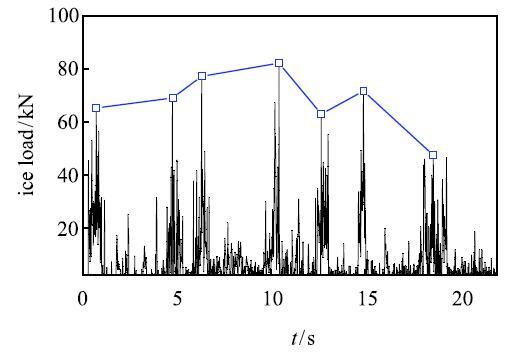
图10为离散元模拟的倒锥体上冰载荷变化情况,其最大值为81.9kN,峰值的均值为67.9 kN.在以上正锥体和倒锥体的冰载荷计算中,海冰的计算参数包括锥径和流速等均相同.但正锥体上的冰载荷要明显大于倒锥体上的冰载荷,正锥体上的冰载荷周期也相应地小于倒锥体上的冰载荷周期.这主要是由于海冰在正锥体上会有破碎、爬升和清除过程,而在倒锥体上只有破碎和清除过程.碎冰块在正锥体的爬升过程中,上爬的碎冰块会对锥前冰盖在破碎前产生约束,从而提高了海冰发生弯曲破碎的作用力,即对锥体结构的作用力.然而,仅在冰排与倒锥体作用时,海冰在水面下受到的浮力稍大于重力,其不会在锥体前发生堆积,从而使海冰发生弯曲破坏的作用力也相对较小.
显示原图|下载原图ZIP|生成PPT图9渤海JZ20-2平台监测海冰与倒锥作用情况...
-->Fig.9Interaction of sea ice and downward cone observed the JZ20-2 platform in the Bohai Sea
-->
显示原图|下载原图ZIP|生成PPT图10离散元模拟的倒锥体上冰载荷时程...
-->Fig.10Time series of ice loads on downward cone simulated by DEM
-->
2.3 正锥与倒锥上海冰断裂长度的对比
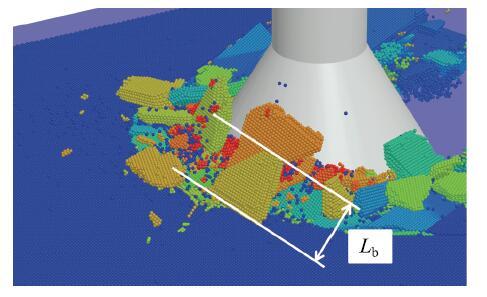
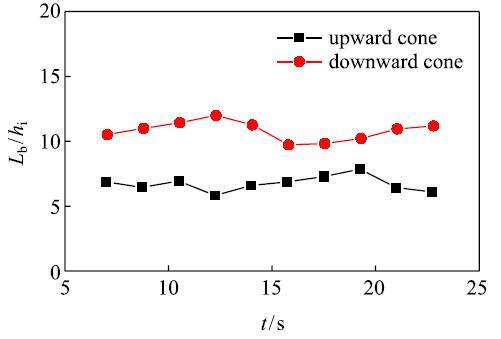
在海冰与锥体结构作用的弯曲破坏过程中,海冰的断裂长度决定了冰载荷的周期,同时也对冰载荷的大小有显著影响.这里定义无量纲海冰断裂长度$\lambda $}=$L_{b}$/$h_{i}$,式中$L_{b}$为断裂长度;$h_{i}$为海冰厚度.渤海JZ20-2锥体海洋平台上的场测量结果表明,$\lambda$}均值在7.0左右[15].海冰的断裂长度不仅与其强度、密度、摩擦系数等因素有关,同时还受锥角、锥径及冰速等诸多因素的影响.下面采用离散元方法对海冰与正、倒锥作用的断裂长度进行对比分析.在计算海冰的断裂长度时,仅选取冰排在锥体结构前初次发生断裂时的径向长度,如图11所示.图12将以上DEM计算得到的海冰与正锥、倒锥作用时的断裂长度进行对比,图中断裂长度值为对应时下刻锥体前所有断裂冰块尺寸的平均值.海冰作用在正、倒锥体上的无量纲断裂长度$\lambda$}分别为6.9\和10.8,即倒锥体上的断裂长度要明显大于正锥体.
显示原图|下载原图ZIP|生成PPT图11离散元模拟海冰的断裂长度...
-->Fig.11Breaking length of ice cover simulated with DEM
-->
显示原图|下载原图ZIP|生成PPT图12正倒锥的海冰断裂长度...
-->Fig.12Breaking length of ice cover acting on upward and\ downward cones
-->
3 海冰与正倒锥作用位置对冰载荷的影响
3.1 锥径影响下正锥和倒锥体上的冰载荷
随着潮汐水位的升降,海冰将分别作用于正锥体或倒锥体上,同时水线处锥径也会产生变化.下面通过离散元方法对正锥和倒锥上不同锥径下的冰载荷进行计算并对比分析.由于冰载荷时程具有显著的随机性,这里选取冰载荷时程曲线中所有载荷峰值点的平均值进行对比.图13(a)为正锥和倒锥上冰载荷随锥径的变化情况.从中可以看出,正锥与倒锥上冰载荷都随锥径的增大而增大,且倒锥体上的冰载荷明显低于倒锥体.图13(b)为正锥和倒锥上无量纲海冰断裂长度$\lambda$}随锥径的变化情况.结果表明,锥径对海冰断裂长度的影响并不明显,但正锥体作用下的海冰断裂长度要明显小于倒锥体.下面分别从海冰的破碎过程、受力情况及海冰温度分布等三个方面分析正倒锥上冰载荷和断裂长度的差异.当海冰与正锥作用时,正锥水平方向的冰载荷可分为破碎力和攀爬力两部分.破碎力是在海冰发生弯曲破坏时产生的冰载荷;攀爬力则是碎冰块在锥体表面攀爬和堆积产生的.当海冰与倒锥作用时,海冰弯曲破坏时同样会产生破碎力,但碎冰块在重力和浮力共同作用下,很难在倒锥体表面爬升,其爬升力可以忽略不计.此外,当锥径越大时,海冰与锥\体的等效接触面积也就越大,正锥体上的海冰堆积和攀爬作用也会增大,从而导致了冰载荷显著增大.
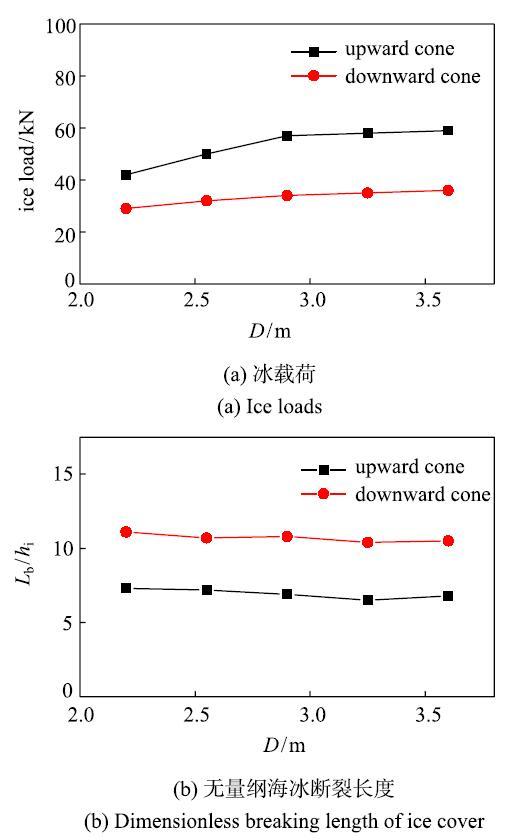显示原图|下载原图ZIP|生成PPT图13锥径对冰载荷及断裂长度的影响...
-->Fig.13Effect of cone diameter on ice load and breaking length
-->
当海冰作用于正锥体结构而向上发生弯曲破碎时,海冰向上翘起并沿结构表面攀爬.当海冰脱离水面后浮力消失,向下的重力作用会阻止海冰继续向上弯曲.然而,当海冰作用于倒锥体结构而向下发生弯曲破坏时,海冰始终处于水面下方,同时受重力和浮力的作用.该向上的合力同样会阻碍海冰向下弯曲,但该合力明显小于重力.因此,海冰向上弯曲时受到的结构阻力要大于向下弯曲时的阻力,从而使正锥体产生较大的冰载荷.
此外,由于海冰的上、下表面分别与空气和海水接触,其上表面的温度一般要明显低于下表面,使海冰的上表面弯曲强度要大于下表面.为此,在本文离散元计算时也考虑了海冰温度的分布情况,并依此设定了相应的海冰单元间的粘结强度.当海冰作用于正锥体上而发生向上弯曲时,海冰的下表面发生拉伸破坏;而当作用于倒锥体上时,海冰则发生上表面的拉伸破坏.由于海冰上表面的强度要高于下表面强度,导致海冰向下弯曲时不易发生破碎,从而使海冰作用于倒锥体上时的断裂长度较大,且冰载荷周期也较大.以上情况同样影响到冰荷载的差异,即正锥体上的冰载荷降低,倒锥体上的冰载荷增大.但受以上海冰爬升模式、浮力作用等因素的影响,正锥体上的冰载荷依然相对较大.
3.2 正倒锥交界处的冰载荷
随着潮汐水位高度的变化,海冰与正倒锥交界处相互作用时可能会发生由弯曲破坏向挤压破坏的转化.将海冰和正倒锥体交界处的作用按照作用位置分为三种类别,即：偏上接触、中心接触和偏下接触,如图14所示.其中冰层中线高度为$H_{ic$ (虚线),正倒锥交界处高度为$H_{st}$ (实线).在对海冰与正倒锥体交界面接触的离散元模拟时,也按以上3种情况进行计算,结果如图15所示.当$H_{ic}>H_{st}$时,海冰与锥体交界处碰撞后产生局部脱落后向上弯曲破碎.破碎后海冰沿锥体表面向上攀爬,类似于海冰和正锥体作用的现象.由于海冰上弯,在冰排远离接触面位置出现由下而上延伸的弯曲裂纹.当$H_{ic}=H_{st}$时,海冰被锥体交界线从中间劈裂,破碎海冰分别由上下挤出,冰层中线处始终与结构有接触而产生持续挤压破碎.当$H_{ic}<H_{st}$时,海冰与锥体交界处碰撞后也会呈现局部破坏现象,然后向下发生弯曲破坏.破坏后的冰块完全浸没于水中,类似于海冰和倒锥体作用的现象.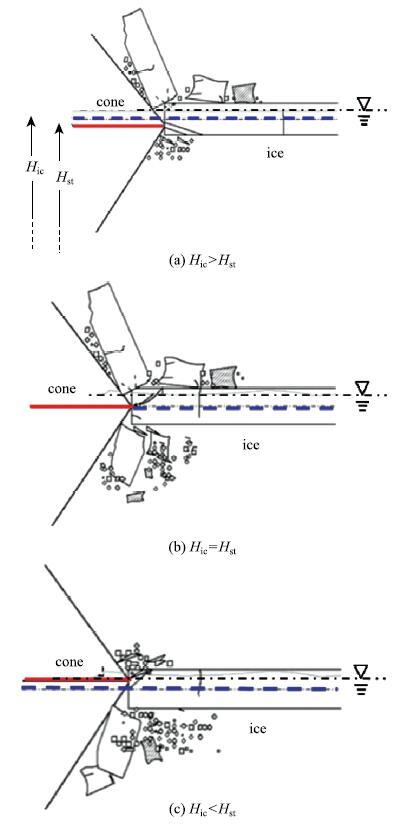
显示原图|下载原图ZIP|生成PPT图14海冰与正倒锥交界处作用的三种模式...
-->Fig.14Three different contact modes between sea ice and the interface of upward-downward cone
-->
显示原图|下载原图ZIP|生成PPT图15三种模式下海冰破坏过程的对比...
-->Fig.15Comparison of sea ice damage process in three modes
-->
采用离散元方法对以上3种作用模式下的冰荷载进行模拟分析,如图16所示.可以发现,当海冰与正倒锥交界面发生偏上或偏下接触时,冰载荷均呈现明显的周期性变化规律,海冰破坏模式为弯曲破坏,如图16(a)和图16(c)所示.这两种破坏模式下的冰载荷峰值比较接近,但在偏下接触模式中的冰载荷周期要明显大于偏下接触模式,说明海冰发生向下弯曲断裂时的断裂长度较大.图16(b)为中心接触模式下的冰载荷. 可以发现,当作用时间$t>10$s\ 后,冰载荷不再有连续性周期变化,海冰呈现为挤压破碎.由此可见,只有当海冰中间层与正倒锥体交界处高度极为接近时,海冰中间层部分才会发生局部挤压破碎.
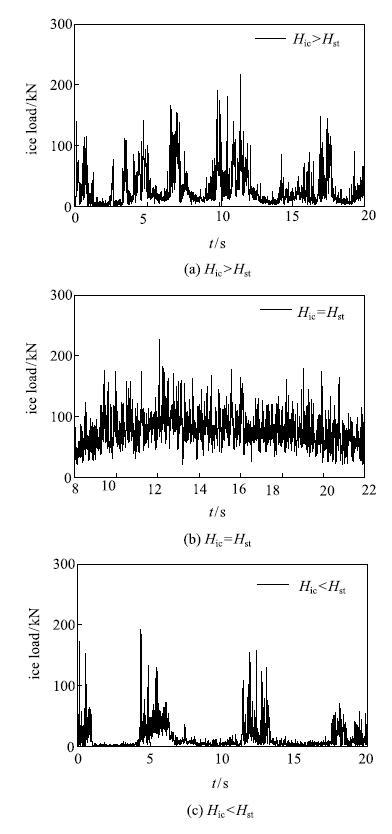显示原图|下载原图ZIP|生成PPT图16三种不同作用模式下冰载荷时程曲线...
-->Fig.16Time series of ice loads under three different acting modes
-->
从以上3种接触模式下的冰载荷幅值上看,海冰发生挤压破碎时并未造成冰载荷的明显增大,冰载荷峰值与弯曲破坏的冰载荷峰值较为接近.这是由于海冰在正倒锥体交界面上发生的挤压破碎只作用于结构接触的较小区域内,海冰也多呈现为上下劈开型破坏.破碎后的冰块也相对较大,并在锥体上很快清除.这与海冰作用于直立结构时的挤压破坏现象有较大区别.海冰与直立结构作用后呈粉末状破坏,并在海冰与结构的接触面上不断堆积[40].此时,冰排中间层同时受到结构物和破碎冰堆积作用的挤压,使得冰层与结构物保持连续作用并形成高压区,并产生持续较高的冰载荷作用[41- 42].从冰载荷时程曲线上看,虽然两者均为挤压破碎形式,但是两者的发生机理存在较大差异,使得冰载荷峰值的差别也较大.由此可见,海冰与正倒锥交界处作用时会存在挤压破碎的可能,但由于该挤压破碎仅发生在冰层局部位置,不会导致冰载荷的明显升高.
4 结论
本文采用具有粘结-破碎作用的球体离散元方法构造了平整冰计算模型,对潮汐水位变化下海冰与锥体结构的作用过程进行了模拟,确定了海冰与锥体作用位置对冰载荷及海冰破坏模式的影响.计算结果表明,海冰与正锥体作用时,冰载荷主要由海冰破坏时的破碎力和破碎后冰块的攀爬力两部分决定.而海冰与倒锥体作用时,碎冰块在浮力和重力作用下没有明显的堆积现象,且弯曲破坏时受到的锥体摩擦力也相对较小,最终导致冰载荷明显小于正锥体.在水位变化影响下,正锥体和倒锥体上的冰载荷均随锥径的增大而增大,但正锥体上的冰载荷增加趋势更为显著.正锥体上的海冰断裂长度要明显小于倒锥体上的海冰断裂长度.此外,本文计算表明海冰在正倒锥交界处也会呈现局部挤压破碎现象,但不会形成平台结构的持续较高的冰载荷作用.以上研究结果验证了离散元方法对分析海冰破碎特性及确定海洋工程结构冰载荷的可行性,可为锥体结构的抗冰设计提供参考依据.The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . . |
| [7] | . . |
| [8] | . . |
| [9] | . |
| [10] | . . |
| [11] | . |
| [12] | . . |
| [13] | . . |
| [14] | . . |
| [15] | . . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . . |
| [20] | . . |
| [21] | . . |
| [22] | . |
| [23] | . . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . . |
| [28] | . . |
| [29] | . . |
| [30] | . . |
| [31] | . |
| [32] | . |
| [33] | . |
| [34] | . . |
| [35] | . . |
| [36] | . . |
| [37] | . |
| [38] | . |
| [39] | . |
| [40] | . |
| [41] | . |
| [42] | . |
