HEAD-ON COLLISION BETWEEN TWO HYDROELASTIC SOLITARY WAVES WITH PLOTNIKOV--TOLAND'S PLATE MODEL1)
BhattiM. M., LuDongqiang中图分类号:TV131.2
文献标识码:A
收稿日期:2018-07-27
接受日期:2018-07-27
网络出版日期:2018-11-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (2476KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
波浪碰撞的研究是海洋工程和海洋学中的重要课题之一. 早在1834年, Scott Russell就观测到孤立波, 而Korteweg和 de Vries在1895 年用KdV方程描述孤立波.Gardner 等 [1]通过逆散射变换(IST)方法研究了孤立波之间碰撞这一引人注目的 现象,发现在碰撞过程中, 孤立波相互交换它们的位置和能量,并在分离后重新获得它们原 本的形态. IST方法[1]适用于所有KdV 孤立波沿着相似的方向传播. 然而,对于一对孤立波之间的迎面碰撞,可以使用有效的渐近展开来解析求解方程. Poincaré--Lighthill--Kuo(PLK) 方法 [2-5], 实质上包含了变形坐标法, 已成功应用于孤立波之间的迎面碰撞问题.针对两个孤立波之间的迎面碰撞的问题, Maxworthy [6]通过实验发现, 波动达到的最大振幅是初始波振幅 的两倍,在相互作用过程中它们会造成时间延迟. 戴世强 [7] 描述了在表面张力作用下两层流体中孤立波之间的相互作用,研究了在考虑原始近似的情况下非线性和色散的影响不能相互平衡的两个临界情况. Mirie 和 Su [8]分析了两种 修正KdV孤立波之间的迎面碰撞,其中考虑立方非线性与二次非线性平衡了色散性. Dai 等 [9]给出了不可压缩 Mooney--Rivlin 弹性杆中孤立波迎面碰撞的四阶 级数解.Cohen 和 Dai [10] 研究了可压缩超弹性杆中的非线性轴对称长振幅波. 最近, Ozden 和 Demiray [11]应用扩展的PLK方法分析一对重 力孤立波的迎面碰撞,并将PLK方法与扩展的PLK方法进行了比较, 发现两种方法所得的数学结果是相同的.孤立波在非可积系统中的相互作用是非弹性的, 并且在碰撞之后孤立波交换能量. 孤立波存在于各种领域, 如流体、等离子体和液晶等. 例如在浅水域,具有有限振幅、非正弦型 的内孤立波, 沿着分层流体的密度界面传播.在不同情况下, 孤立波的振幅与水深具有可 比性,即海床边界在孤立波的演化行为中起重要作用. Hsieh 等 [12] 在数值上研究了内部孤立波越过水下海脊的传播行为. Agafontsev 等 [13] 借助非线性 Schr$\ddot{o}$dinger 方程,分析了密度比接近临界时的深水内孤立波, 研究了超临界分岔和亚临界分岔的情况.
在过去几年, 非线性水弹性问题因其在工程、生物和物理科学中的众多应用而受到极大关注, 这些应用涉及可变形体和运动流体. 极地区域海水冻结而成的冰盖,可作为运输道路和 飞机跑道,其表面上的滑行载荷将诱发挠曲重力波(水弹性波).主要基于Kirchoff--Love 板 理论,冰盖下二维非线性水弹性数值和解析模型得以广泛研究.不同的线性和非线性模型非常有助于分析大型和小型浮式结构(如机场和大型船舶)与波浪的相互作用 [14-18]. Korobkin 和 Khabakhpasheva [19]研究了非定常非线性水弹性波对弹 性板的影响. Davys 等 [20]分析了由集中点源产生的波, 并利用不同 的渐近 Fourier变换方法发现了波峰的不同模式. Sahoo 等 [21] 研究了具有不同几何特征和边缘条件下表面波的散射,他们发现水动力学特性主要取决于波浪 条件、几何构型和边缘条件.
许多****在实验和理论方面研究了冰盖的水弹性行为. P$\check{a}$r$\check{a}$u 和Vanden-Broeck [22]利用边界积分法研究了冰盖下定常运动压力源产生 的非线性波. 近来,Plotnikov 和 Toland [23] 在流体无旋流动和 结构满足Kirchoff定律的假设下, 基于特殊 Cossert 超弹性壳理论,提出了漂浮在海洋上的 弹性薄片的理论和数学模型,以此研究非线性水弹性波. Milewski 等 [24]采用数值求解和渐近分析两种方法研究了以弹性板为边界深水中的非线性水弹性波. Wang 和 Lu [25]探讨了薄弹性板覆盖下流体中 行进的非线性水弹性波的解析结果. 今年,本文作者 [26] 使用PLK方法 讨论了水弹性孤立波之间的迎面碰撞,考虑有侧向压缩力的情况下时薄弹性板的线性数学 模型,并获得了水弹性孤立波的三阶KdV方程.
基于上述进展情况, 本文主要目的是研究在薄冰覆盖流体中行进的非线性水弹性孤立波之间的迎面碰撞. 将 Plotnikov 和 Toland [23]发展的新模型应用到 冰层的模拟. 更一般地, 考虑了流体的表面张力.据作者所知, 这是研究流体与冰层相互作 用的全新模型.我们考虑这对孤立波遵循小振幅 $ \left( a_0/H_0 \ll 1 \right) $ 长波$ \left( \lambda / H_0 \gg 1 \right) $ 假设, 式中 $a_0$, $H_0$ 和$\lambda$ 分别是波幅、水深 和波长. 进一步, 我们假设 Ursell 数约为1, 即 $a_0 \lambda^2/ H_0^3 \approx 1 $. 在第2 节中, 我们使用 PLK方法得到了非线性控制方程的三阶近似解. PLK 方法对于研究孤立波之间的碰撞非常有效 [27]. 在第4节和第5 节中, 讨论并用图形展示了相关物理参数的响应特性.
1 数学描述
考虑在有限深渠道中传播的水弹性波. 选取直角坐标系, 使得 $x$ 轴、$z$ 轴分别沿着水平、垂直方向. 水平底部位于 $z=0$. 冰层的挠度 (即水弹性波的波形)表示为 $z=H(x,t)$, 其中 $t$ 是时间. 势流假设下流动速度场用势函数$\phi(x,z,t)$表述, 满足$\nabla^2\phi=0$, 其中 0<z<H.底部边界条件为法向速度为零, 即无渗透条件 $\partial \phi/ \partial z=0$ (当 $z=0)$.流体与冰层界面处$(z=H(x,t))$的运动学边界条件为
$$ \frac{\partial H}{\partial t} + \nabla \phi \cdot \nabla H = \frac{\partial \phi}{\partial z} (1)$$
动力学边界条件为
$$ \frac{\partial \phi}{\partial t} + \frac{1}{2}|\nabla \phi|^2 + gH +\frac{P_{{\rm e}}}{\rho} = B_{{\rm c}}(t) (2)$$
式中, $g$ 是重力加速度, $\rho$ 是流体密度, $P_{{\rm e}}$ 是流体与冰层界面处的压力, $B_{{\rm c}}(t)$ 是 Bernoulli 常数, 不失一般性以下设定$B_{{\rm c}}(t)=0$. 对于 Plotnikov 和 Toland 的模\linebreak 型[23], $P_{{\rm e}}$ 采用以下 形式
$$ P_{{\rm e}} = - T \kappa + D \left( \frac{\partial ^2 \kappa}{\partial s^2} +\frac{1}{2}\kappa^3 \right) (3)$$
式中, $T$ 流体表面张力系数; $D=Ed^3/[12(1-\nu^2)]$, 其中 $E$ 是杨氏模量, $d$和 $\nu$ 分别为板的厚度以及泊松比; $\kappa$是流体与冰层界面的曲率, 而 $s$ 是 这一界面的弧长. 曲率 $\kappa$ 在$H(x,t)$ 上写作
$$ \kappa=\frac{\partial ^2 H}{\partial x^2} \left[ 1+ \left(\frac{\partial H}{\partial x}\right)^2\right]^{-3/2} (4)$$
根据 Guyenne 和 P{\u{a}}r{\u{a}}u [28], 我们有
$$ \frac{\partial \kappa}{\partial s } =\left[1+\left(\frac{\partial H}{\partial x}\right)^2\right]^{-1/2} \frac{\partial \kappa}{\partial x} (5)$$
式 (3) 结合了流体的表面张力和冰层的结构弹性两种效应. 式(3)中第二项表示 Plotnikov 和 Toland 的模型, 其中线性部分是众所周知的线性Euler--Bernoulli 梁 或 Kirchoff--Love 板模型.
对于浅水长波, 我们可简单地将势函数 $\phi(x,z,t)$ 在 $z=0$ 处 表示成 Taylor 级数. 结合 $\nabla^2\phi=0$ $(0<z<H)$ 和 $\partial \phi/\partial z=0$
$(z=0)$, 可得
$$ \phi(x,z,t)=\sum_{n=0}^{\infty} (-1)^n \frac{z^{2n}}{(2n)!} \nabla^{2n}\varPhi (6)$$
式中
$$ \varPhi (x,t)=\phi(x,0,t) (7)$$
用以上得到的 $\varPhi $ 将式(1) 和式(2) 改写为
$$ \frac{\partial H}{\partial t } + \frac{\partial }{\partial x}\bigg[ H U +\sum_{n=1}^{\infty} (-1)^n \frac{H^{2n+1}}{(2n+1)!} \frac{\partial ^ {2n} U}{\partial x^{2n}}\bigg]=0 (8)$$
$$ \frac{\partial U}{\partial t} + \frac{\partial }{\partial x} \Bigg[ gH + \frac{U^2}{2} + \frac{P_{{\rm e}}}{\rho} + \sum_{n=1}^{\infty} (-1)^n \frac{H^{2n}}{(2n)!} \Bigg( \frac{\partial ^ {2n} U}{\partial t \partial x^{2n-1}} + $$
$$\qquad \frac{1}{2}\sum_{m=0}^{2n} (-1)^m \mathbb{C}_m^{2n} \frac{\partial ^m U}{\partial x^m} \frac{\partial ^{2n-m} U}{\partial x^{2n-m}} \Bigg)\Bigg]=0 (9)$$
式中 $U=\varPhi _x$ 是底部的切向速度, 而 $\mathbb{C}_m^{2n}$ 是二项式系数.
2 求解方法
式(8) 和式(9) 的解可借助奇异摄动法找到. 为此, 我们引入了以下坐标变换$$ \xi{_0} = \varepsilon^{\frac{1}{2}}k(x-Ct),\qquad \eta_0 = \varepsilon^{\frac{1}{2}}\bar{k}(x+\bar{\!C} t) (10)$$
式中, $k$ 和 $\bar{k}$ 分别是右行波和左行波的波数; 无量纲参数$\varepsilon$ $(0< \varepsilon \ll 1)$表示波幅的量级. 根据 Ursell 关系,水平波长的尺度选取 $\varepsilon^{\frac{1}{2}}$. $C$ 和 $\bar{\!C}$分别是右行孤立波和左行孤立波的波速. 使用变形 坐标法,我们引入以下变换
$$ \xi = \xi_0+\varepsilon k \theta (\xi,\eta),\qquad \eta = \eta_0+\varepsilon \bar{k} \varphi (\xi,\eta) (11)$$
式中, $\xi$ 和 $\eta$ 表示右行和左行的相位; $\theta(\xi,\eta)$ 和 $\varphi(\xi,\eta)$ 是对式 (8) 和式 (9) 摄动分析过程中推导出的相位偏移函数.
令
$$ H=H_0 (1+\zeta) (12)$$
式中 $\zeta (x,t)$ 是流体与冰层界面的无量纲高度, 而 $H_0$ 是未扰静水深度. 记$c(k)$为水弹性波中对应的相速度, 并近似设定
$$ c(k)=c_0\sqrt{1+\varGamma (kH_0)^4+\tau (kH_0)^2} (13)$$
式中
$$ c_0=\sqrt{gH_0}, \qquad \varGamma = \dfrac{D}{\rho g H_0^4 }, \qquad \tau =\dfrac{T}{\rho g H_0^2} (14)$$
当 $ D \rightarrow 0$ 和 $T \rightarrow 0$, 式 (13) 中的相速度退化为$c_0$, 即有限深浅水中纯重力波的相速度.
为了使推导更简化, 我们引入一个列向量 $\pmb T $
$$ T = ( ^{\zeta}_{U}) (15)$$
根据PLK方法,我们以下列幂级数的形式展开变量
$$\left.\begin{array}{l} \theta(\xi , \eta)=\theta_0(\eta) + \varepsilon \theta_1(\xi , \eta) +\varepsilon ^2\theta_2 (\xi , \eta) +\cdots \\ \varphi(\xi , \eta)=\varphi_0 (\xi )+ \varepsilon \varphi_1 (\xi , \eta) +\varepsilon ^2 \varphi_2 (\xi , \eta)+\cdots \\ C = c\left( 1+\varepsilon a c_1 +\varepsilon ^2 a^2 c_2+\cdots \right) \\ \bar{\!C} = \bar{ c}\left( 1+\varepsilon b \bar{c}_1 +\varepsilon ^2 b^2\bar{c}_2+\cdots \right) \\ \pmb T = \varepsilon \pmb T _1(\xi , \eta) +\varepsilon^2 \pmb T _2 (\xi , \eta)+\varepsilon^3 \pmb T _3 (\xi , \eta)+\cdots \end{array}\right\} (16)$$
式中, $\bar{c}=c(\bar{k})$; $c_1$, $c_2$, $c_3$, $\cdots $ 和 $\bar{c}_1$, $\bar{c}_2$,
$\bar{c}_3$, $\cdots$ 是摄动分析中通过消除长期项而确定的展开系数;$a$ 和 $b$ 是振幅 因子.
3 摄动分析
依式 (16)展开, 可得 $\varepsilon^{3/2}$, $\varepsilon ^{5/2}$, $\varepsilon^{7/2}$,$\cdots$系数的方程组, 它们按阶数显示如下.3.1 $\varepsilon^{3/2}$的系数
一阶方程组简化为$$\pmb M k \dfrac {\partial \pmb T _1 }{\partial \xi}+\bar {\pmb M} \bar{k} \dfrac {\partial \pmb T _1}{\partial \eta}=\textbf{0} (17)$$
式中
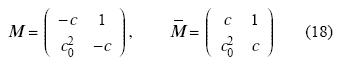
所得方程式高度耦合, 难以进行求解. 我们引入耦合方程的矩阵系统, 以获得每个阶的解.Su 和 Mirie [27] 使用一个因变量变换来获得解.然而这个变换不适用于水 弹性波速 (见式 (13)). 之后, 不同的**** $^{[9, 29]}$ 使用矩阵系统来获得单层和双层流体系统中的纯重力波解。
$\pmb M $ 和 $\bar {\pmb M }$ 的右、左特征向量分别是
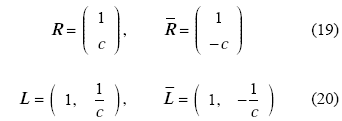
式 (19) 和式 (20) 中右、左特征向量用于分析每一阶的解. 左特征向量有助于使该耦合方程成为单一方程, 右特征向量用于求得每一阶的近似解.
考虑式 (17) 的以下形式解
$$\pmb T _1 = a A(\xi) \pmb R +b B(\eta) \bar {\pmb R } (21)$$
其中 $A(\xi)$ 和 $B(\eta)$ 是在下一阶中确定的任意函数.
一阶解可以写作
$$\left.\begin{array}{l} \zeta_1 = a A (\xi)+bB(\eta) \\ U_1 =c\left( a A (\xi)-b B(\eta) \right)\end{array}\right\} (22)$$
3.2 $\varepsilon^{5/2}$的系数
二阶方程简化为以下形式$$\hskip -8mm \pmb M k \dfrac {\partial \pmb T _2 }{\partial \xi} + akc \left( \pmb G_1 A'+ \pmb G_2 A A' + \pmb G_3 A"' + \pmb G_4 A' \right)+$$
$$\quad \bar {\pmb M } \bar{k} \dfrac {\partial \pmb T _2}{\partial \eta} +b \bar{k}c \left( \bar{ \pmb G}_1 B' +\bar{ \pmb G}_2 B B'+\bar{ \pmb G}_3 B"' +\bar{ \pmb G}_4 B' \right) =\textbf{0} (23)$$
其中, $ \pmb G_n$ 和 $\bar{ \pmb G}_n$ $(n=1,2,3,4)$ 在附录 A 中给出.
假设以下形式的一般解
$$\pmb T _2 = X(\xi,\eta)\pmb R + Y(\xi, \eta) \bar {\pmb R } (24)$$
在式 (23) 中使用式 (24), 并将其乘以 $ \pmb L$, 得到
$$ \pmb L \bar {\pmb M }\pmb R \bar{k} \dfrac {\partial X }{\partial \eta} + akc \big( \pmb L \pmb G_1 A' + \pmb L \pmb G_2 A A' + \pmb L \pmb G_3 A"' + \pmb L \pmb G_4 A' \big) +$$
$$ \quad b \bar{k} c \big( \pmb L \bar{ \pmb G}_1 B' + \pmb L\bar{ \pmb G}_2 B B' + \pmb L \bar{ \pmb G}_3 B"' + \pmb L \bar{ \pmb G}_4 B' \big) =0 (25)$$
式中, $ \pmb L \bar {\pmb M }\pmb R $, $ \pmb L \pmb G_n $ 和 $ \pmb L\bar{ \pmb G}_n $ $(n=1,2,3,4)$ 分别表示内积 $ \pmb L \cdot \bar{\pmb M } \cdot\pmb R $, $ \pmb L\cdot \pmb G_n $ 和 $ \pmb L\cdot \bar{ \pmb G}_n $. 上式进一步分为3个部分, 即(i)长期项, (ii)局部项和(iii)非局部项.
3.2.1 长期项
式 (25) 有3个不依赖于 $\eta$ 的项被称为长期项, 而其他项不是长期项. 因为如果我们将这些长期项关于 $\eta$ 做积分,所得值在空间和时间上都是无限的, 即表现出长 期项的奇异性质.为消除长期项, 设
$$ \pmb L \pmb G_1 A'+ \pmb L \pmb G_2 A A'+ \pmb L \pmb G_3 A"' =0 (26)$$
令
$$c_1 = \dfrac {1}{2}, \qquad k^2 H_0^2 =3 a (27)$$
则式 (26) 缩减为以下形式
$$\gamma A"'+ 3 AA'-A'=0 (28)$$
式中
$$ \gamma =1-3 \chi \tau, \qquad \chi = \dfrac{c_0^2}{c^2} (29)$$
上述 KdV 方程的解可以写成
$$ A = {\rm sech}^2 \dfrac {\xi}{2 \sqrt{\gamma}} (30)$$
同理
$$ B ={\rm sech}^2 \dfrac {\eta}{2 \sqrt{\gamma}} (31)$$
$$ \bar{c}_1 = \dfrac {1}{2 }, \qquad {\bar{k}}^2 H_0^2 =3 b (32)$$
3.2.2 非局部项
非局部项中有助于确定相位偏移. 因此, 我们将保留这些项. 在式 (25) 中非局部项是
$$ \pmb L \pmb G_4 =0 (33)$$
由此可得
$$\theta_0 = \dfrac{ b }{\mathop{k}\limits^{-\!\!-} \varUpsilon}\int_{-\infty}^{\eta} B {\rm d}\eta_1 (34)$$
式中
$$ \varUpsilon = 3+\chi (35)$$
同理, 我们得到
$$\varphi_0 = \dfrac{a}{k \varUpsilon} \int_{+\infty}^{\xi} A {\rm d}\xi_1 (36)$$
随着$\chi$ 趋向于1, 一阶相位偏移退化为纯重力波的解.
3.2.3 局部项
局部项是那些有助于研究左行和右行孤立波波速的项. 在式 (25) 中局部项可以写
成
$$ \pmb L \bar { M } \pmb R \bar{k} \dfrac {\partial X}{\partial \eta}+ L \bar{ G}_2 B B'+ \pmb L \bar{ \pmb G}_3 B"'+ \pmb L\bar{ \pmb G}_4 B'=0 (37)$$
将上式关于 $\eta$ 求积分, 可得简化后的方程
$$X (\xi,\eta) = C_{1} b^2 B^2 +C_{2} b^2 B -\dfrac{2ab}{\varUpsilon^2} A B +a^2 A_1(\xi) (38)$$
式中 $C_{1}$ 和 $C_{2}$ 见附录 B. 同理
$$ Y (\xi,\eta) = C_{1} a^2 A^2+ C_{2} a^2 A -\dfrac{2a b}{\varUpsilon^2} A B +b^2B_1(\eta) (39)$$
式中 $A_1(\xi)$ 和 $B_1(\eta)$ 是两个未知的任意函数, 将在下一阶中确定.
3.3 $\varepsilon^{7/2}$的系数
三阶方程组如下$$ \quad \pmb M k \dfrac {\partial \pmb T _3 }{\partial \xi} + akc \Big[ \pmb H _1 A'+\pmb H _2 A A' +\pmb H _3 A' A^2+$$$$ \pmb H _4 \left( A'A_1 +A A_1' \right) + \pmb H _5 A_1'+\pmb H _6 A_1"'+ \pmb H _7 A' +\bar{\pmb H }_8 A' \Big] +$$$$ \qquad \bar {\pmb M } \bar{k} \dfrac {\partial \pmb T _3}{\partial \eta} + b \bar{k} c \Big[ \bar{\pmb H }_1 B' +\bar{\pmb H }_2 B B' +\bar{\pmb H }_3 B' B^2 +$$$$ \qquad \bar{\pmb H}_4 \left(B'B_1 +B_1' B \right) +\bar{\pmb H }_5 B_1'+\bar{\pmb H}_6B_1"' + $$ $$ \qquad \bar{\pmb H }_7 B' +\pmb H_8 B' \Big]=\textbf{0} (40)$$
式中 $\pmb H _n$ 和 $\bar{\pmb H }_n$ $(n=1,2,\cdots, 8)$见附录 A.
我们假设以下形式的一般解
$$ \pmb T _3 = X_1(\xi,\eta)\pmb R + Y_1(\xi, \eta) \bar {\pmb R } (41)$$
在式 (40) 中使用式 (41), 并将其乘以 $ \pmb L$,我们得到
$$ \quad \pmb L \bar {\pmb M }\pmb R \bar{k} \dfrac {\partial X_1}{\partial \eta} + akc \big[ ( \pmb L \pmb H _1+ \pmb L \pmb H _2 A +$$
$$ \qquad \pmb L\pmb H _3 A^2+ \pmb L\pmb H _7 +\pmb L\bar{\pmb H }_8)A' + \pmb L\pmb {F}_5A_1' +$$$$ \qquad \pmb L\pmb H _6 A_1"' + \pmb L\pmb H _4 ( A' A_1 +A A_1') \big] +$$$$ \qquad b \bar{k}c \big[ ( \pmb L\pmb H _8 + \pmb L\bar{\pmb H }_1 + \pmb L\bar{\pmb H }_7 + \pmb L\bar{\pmb H }_2 B +$$$$ L\bar{\pmb H }_3 B^2)B' + \pmb L\bar{\pmb H }_4 (B'B_1 +B_1' B ) + $$$$ \qquad \pmb L \bar{\pmb H }_5B_1'+ \pmb L \bar{\pmb H }_6 B_1"' \big] =\textbf{0} (42)$$
式中, $ \pmb L \bar {\pmb M }\pmb R $, $ \pmb L\pmb H _n $ 和 $ \pmb L\bar{\pmb H }_n $ $(n=1,2,3,4)$ 分别表示内积 $ \pmb L \cdot \bar{\pmb M } \cdot\pmb R $, $ \pmb L\cdot\pmb H _n $ 和 $ \pmb L\cdot \bar{\pmb H }_n $. 上式进一步分为3个部分,即(i)长期项, (ii)局部项和(iii)非局部项.
3.3.1 长期项
在这一阶的长期项是
$$\quad ( \pmb L \pmb H _1 + \pmb L \pmb H _2 A + \pmb L\pmb H_3 A^2)A'+ \pmb L\pmb H _4 \left( A' A_1 +A A_1' \right) + $$$$ L\pmb H _5 A_1' + \pmb L\pmb H _6 A_1''' (43)$$
上式简化为
$$\quad A_1''' - A_1'+3\left(A_1 A'+A_1' A \right) +\left( -2 c_2 +C_{3} \right) A' +$$$$ \qquad C_{4} A A'+C_{5} A^2 A' (44)$$
对上式进行积分得到
$$ A_1" - A_1+ C_2 A_1 A +(-2 c_2 +C_{3} ) A + \dfrac{C_{4}}{2 } A^2 +\dfrac {C_{5}}{3}A^3 (45)$$
式中 $C_{3},C_{4}$ 和 $C_{5}$ 见附录 B.
令
$$ c_2 = \dfrac {C_{3}}{2} (46)$$
式 (44) 的解可以写作
$$ A_1 = C_{6} A + C_{7} A^2 (47)$$
式中 $C_{6}$ 和 $C_{7}$ 见附录 B. 同理可得
$$B_1 = C_{6} B + C_{7} B^2 (48)$$$$ \hskip 2cm \bar{c}_2 = \dfrac {C_{3}}{2} (49)$$
这就导出了式 (38) 和式 (39) 的求解.
3.3.2 非局部项
在这一阶解中, 非局部项是
$$ \pmb L\pmb H _7 A' =0 (50)$$
上式可以写作
$$\theta_1 = \bar{\theta}_{1,0} \int_{-\infty}^{\eta} B {\rm d}\eta_1 +\bar{\theta}_{1,1}\int_{-\infty}^{\eta} B^2 {\rm d}\eta_1 (51)$$
式中
$$ \bar{\theta}_{1,0} = \dfrac{b}{2 \mathop{k}\limits^{-\!\!-} \varUpsilon} [C_{8} A+C_{10}+a A (C_{9} +C_{11})] (52)$$
$$ \bar{\theta}_{1,1}= \dfrac{b^2 }{2 \mathop{k}\limits^{-\!\!-} \varUpsilon} (C_{12}+C_{13}) (53)$$
其中的 $C_{n}$ $(n=8,9, \cdots, 13)$ 见附录 B. 同理
$$\varphi_1 = \bar{\varphi}_{1,0} \int_{+\infty}^{\xi} A {\rm d}\xi_1 +\bar{\varphi}_{1,1}\int_{+\infty}^{\xi} A^2 {\rm d}\xi_1 (54)$$
式中
$$ \bar{\varphi}_{1,0} = \dfrac{a }{2 \mathop{k}\limits^{-\!\!-} \varUpsilon} \left[C_{8}+C_{10}+b B (C_{9} + C_{11}) \right] (55)$$
$$\bar{\varphi}_{1,1} = \dfrac{a^2 }{2 \mathop{k}\limits^{-\!\!-} \varUpsilon} ( C_{12}+C_{13} ) (56)$$
在式 (51) 中除了 $\bar{\theta}_{1,0}$ 中的第三项外, 所有项都类似于一阶解中的相位偏移, 并显示简单的相位偏移行为. 当 $\eta \rightarrow+\infty$, $\bar{\theta}_{1,0}$ 中的第三项取决于 $\xi$. 因此,波形在碰撞前后是不同的 (见图9), 因为 $\theta_1$ 进入到函数$A(\xi)$ 的自变量. 对于左行波,亦可观察到类似的行为.
3.3.3 局部项
局部项是
$$\quad \pmb L \bar {\pmb M }\pmb R \bar{k} \dfrac {\partial X_1 }{\partial \eta}+( \pmb L\pmb H _8 + \pmb L\bar{\pmb H }_1 + \pmb L \bar{\pmb H}_7 +\pmb L\bar{\pmb H }_2 B + \pmb L\bar{\pmb H }_3 B^2 ) B' +
$$$$\qquad \pmb L\bar{\pmb H }_4 \left(B'B_1 +B_1' B\right) + \pmb L \bar{\pmb H }_5 B_1'+$$
$$\qquad \pmb L \bar{\pmb H }_6B_1"' + \pmb L\bar{\pmb H }_8 A'=0 (57)$$
对上式求积分,我们得到
$$ X_1 = \dfrac{1}{\bar{k} } (C_{14} B+C_{15}B^2+C_{16}B^3)+a^3 A_2 (\xi) (58)$$
式中 $C_{14}$, $C_{15} $ 和 $ C_{16}$ 见附录 B. 同理
$$Y_1 = \dfrac{1}{k}(C_{14} A+C_{15}A^2+C_{16}A^3)+b^3 B_2 (\eta) (59)$$
式中 $A_2(\xi)$ 和 $B_2(\eta)$ 是两个未确定函数. 我们将在这里停止推导并省略$A_2(\xi)$ 和 $B_2(\eta)$ 的解.
4 结果分析
本小节综合上述的各阶级数解如下.流体和板界面的波形可以从式 (21) 和式 (24) 中获得
$$ \zeta=\varepsilon (aA+bB)+ \varepsilon^2 \left[ X (\xi, \eta)+ Y(\xi,\eta) \right] (60)$$
而 $X (\xi, \eta)$ 和 $ Y(\xi,\eta)$ 在式 (38) 和式 (39) 中定义.
通过式 (60) 可得变形轮廓. 为此, 必须消除式 (60) 中 $A(\xi)$ 和$B(\eta)$ 的乘积项. 从而得到流体和板界面上的变形轮廓. 取$B(\eta)=0$, 则
$$ \zeta =\varepsilon aA+\varepsilon^2 a^2 \left[ C_{1} a^2 A^2 +C_{2} a^2 A +a^2 A_1(\xi)\right] (61)$$
在流体和板界面上的碰撞过程中的最大波浪爬高 $\zeta_{{\rm max}}$ 可以通过在式(60) 中取 $A=B=1$ 而得
$$ \zeta_{{\rm max}} = \zeta\Big|_{A=B=1} (62)$$
从式 (21) 和式 (24) 中可以得到底部速度 $U$, 得
$$ U = \varepsilon c(aA-bB)+ \varepsilon^2 c\left[ X (\xi, \eta)- Y(\xi,\eta) \right] (63)$$
根据式 (27) 和式 (45), 波速的渐近解是
$$ C=c\left( 1+\dfrac {1}{2}\varepsilon a+\dfrac {C_{3}}{2}\varepsilon^2 a^2 +O(\varepsilon^3) \right) (64)$$
$$ \bar{\!C} =\bar{c} \left( 1+\dfrac {1}{2}\varepsilon b+ \dfrac {C_{3}}{2}\varepsilon^2 b^2+O(\varepsilon^3) \right) (65)$$
在碰撞过程中相位偏移是
$$ \theta = \theta_0 + \varepsilon \theta_1 +O(\varepsilon^2) (66)$$
$$ \varphi =\varphi_0 + \varepsilon \varphi_1 +O(\varepsilon^2) (67)$$
式中, $\theta_0$, $\theta_1$, $\varphi_0$和 $\varphi_1$ 分别在式 (34), 式(36), 式(51) 和 式(54) 中给出.
5 结果与讨论
本节给出所考虑水弹性波问题中涉及的相关参数的图形结果, 如图1 至图11 所示. 特别地,我们讨论了流体和板界面高度、变形曲线、碰撞期间的最大波浪爬高、相位偏移和波速的行为. 图中的各参数取为 $E=10^7 $ N/m$^{2}$, $d=0.05$ m,$g=9.8$ m/s$^{2}$, $\rho =1024$ kg/m$^{3}$, $H_0=1$ m 和$T=0.075$ N/m.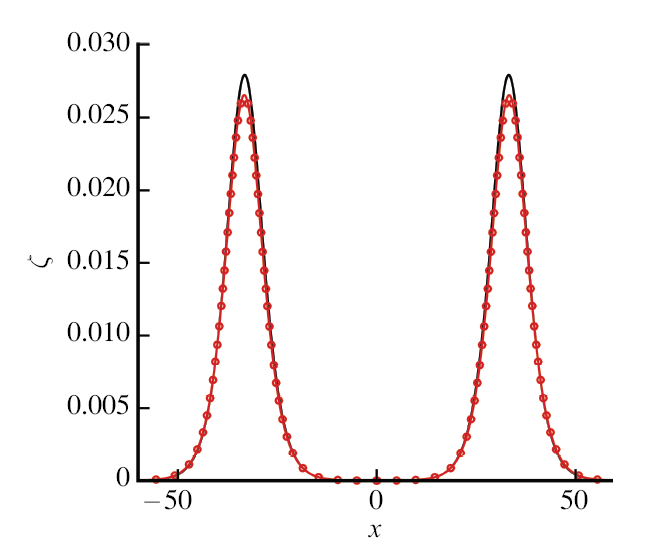
显示原图|下载原图ZIP|生成PPT图1线性(Kirchhoff--Love板)和非线性(Plotnikov--Toland薄板)模型的比较.实线: 非线性; 圆圈线: 线性
-->Fig.1Graphical comparison between linear (Kirchhoff--Love plate) model and nonlinear (Plotnikov and Toland's) model. Solid line: nonlinear model; Circle: linear model
-->
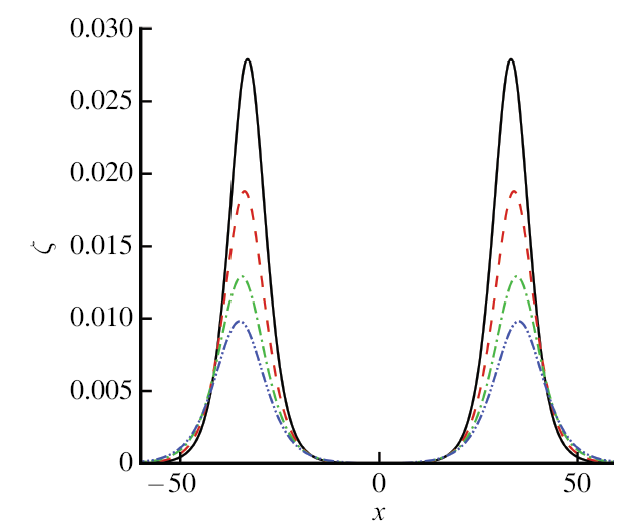
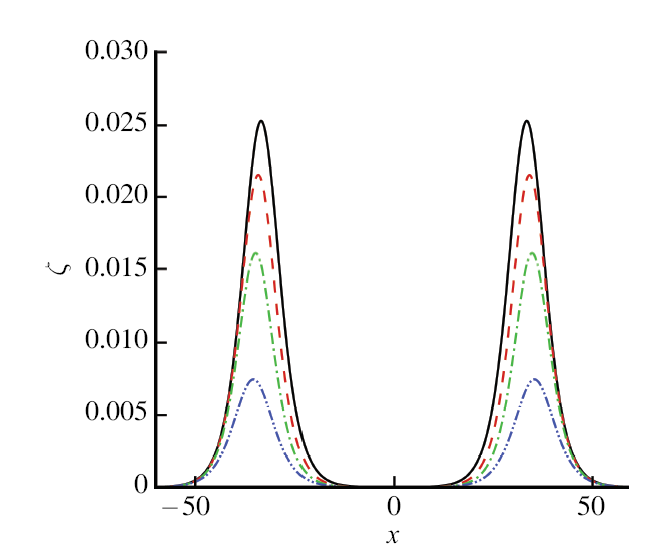
图1显示了薄弹性板线性和非线性模型之间的波形比较. 从图中可以看出, 两种模型在小振幅下的行为是相同的, 并且区别几乎可以忽略不计. 然而,非线性波形与大振幅下的线 性波形明显不同. 图2 显示式 (14)中不同的$\varGamma$ 所对应的 界面波形. 我们观察到弯曲刚度$\varGamma$ 的增大形成明显的抑制作用, 使得界面波 形高度倾向于减小.在物理上, 当杨氏模量 $E$ 上升时, 板的偏转变得更顽固, 并且发生非常高的反作用力以抵抗弹性板的变形. 在图 3 中描绘了表面张力系数$\tau$ 的增量 (见式 (14)) 显著降低了波形的振幅. 图 4 显示当取$\varGamma = 0$ 以及 $\tau=0$ 时与过去发表的纯重力波 [27]的结果进 行比较. 从该图中可看出的结果一致性.
显示原图|下载原图ZIP|生成PPT图2$\varGamma$不同$\varGamma$值时两孤立波的迎撞. 实线: $\varGamma=0$;虚线: $\varGamma=0.5$; 点虚线: $\varGamma=1.1$;双点虚线: $\varGamma=1.4$
-->Fig.2Head-on collision between two solitary waves for different values of $\varGamma$. solid line: $\varGamma=0$, dashed line: $\varGamma=0.5$, dot-dashed line: $\varGamma=1.1$, dot-dot-dashed line: $\varGamma=1.4$
-->
显示原图|下载原图ZIP|生成PPT图3$\varGamma$不同$\tau$值时两孤立波的迎撞. 实线: $\tau=1$;虚线: $\tau=1.5$; 点虚线: $\tau=2$; 双点虚线: $\tau=2.5$
-->Fig.3Head-on collision between two solitary waves for different values of $\tau$. Solid line: $\tau=1$, dashed line: $\tau=1.5$,dot-dashed line: $\tau=2$, dot-dot-dashed line: $
-->
显示原图|下载原图ZIP|生成PPT图4与已有结果的比较. 实线: Su and Mirie [
-->Fig.4Comparison of head-on collision process with previous results. Solid line: Su and Mirie [
-->
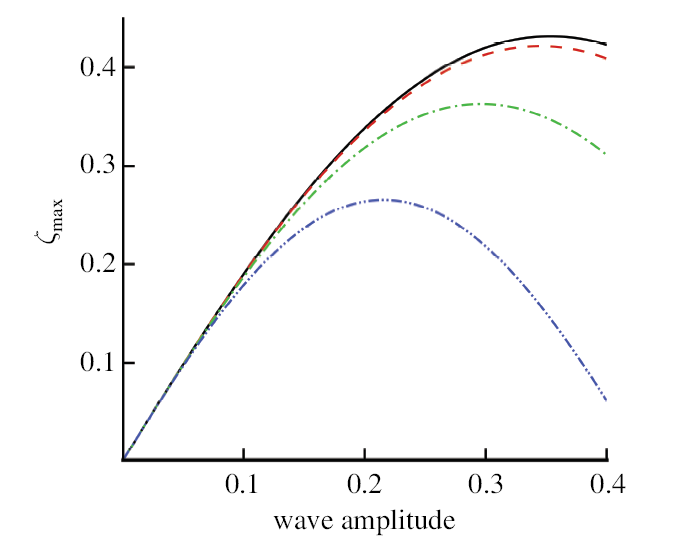
图 5和图 6 显示碰撞过程中的最大波浪爬高与波幅. 碰撞过程中的最大波浪爬高是通过式 (60) 中取 $A=B=1$ 而得到的,并且最大波浪爬高出现在 $\xi$ 和 $\eta$ 点上. 在图 5中显示随着波幅的增加, $\varGamma$趋向于抑制最大爬高. 如图 6 所示,由表面张力效应引起的行为现象相似.
显示原图|下载原图ZIP|生成PPT图5最大爬高与波幅关系. 实线:$\varGamma=0$; 虚线: $\varGamma=0.008$; 点虚线: $\varGamma=0.07$;双点虚线:$\varGamma=0.24$
-->Fig.5Maximum run-up vs. wave amplitude. Solid line:$\varGamma=0$, dashed line: $\varGamma=0.008$, dot-dashed line:$\varGamma=0.07$,dot-dot-dashed line: $\varGamma=0.24$
-->
显示原图|下载原图ZIP|生成PPT图6最大爬高与波幅关系. 实线:$\tau=0.5$; 虚线: $\tau=1$;点虚线: $\tau=1.2$, 双点虚线: $\tau=1.5$
-->Fig.6Maximum run-up vs. wave amplitude. Solid line:$\tau=0.5$, dashed line: $\tau=1$, dot-dashed line: $\tau=1.2$,dot-dot-dashed line:$\tau=1.5$
-->
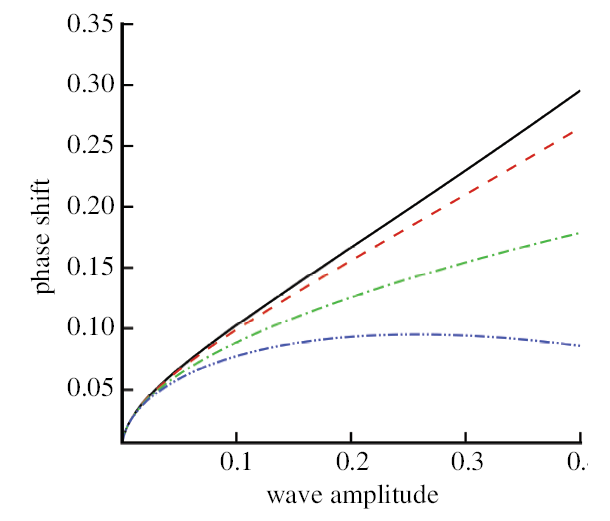
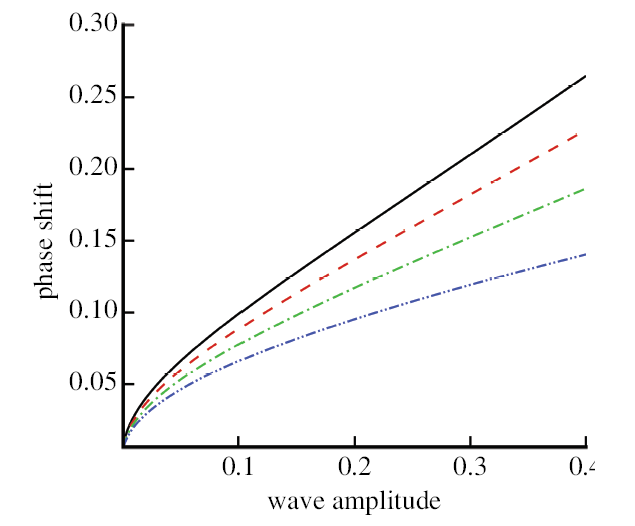
图 7和图 8 显示不同的$\varGamma$ 和 $\tau$ 时绘制的相位偏移.在更大的弯曲刚度 $\varGamma$ 和表面张力 $\tau$ 下显著降低相位偏移.
显示原图|下载原图ZIP|生成PPT图7相位偏移与波幅关系. 实线:$\varGamma=0$; 虚线: $\varGamma=0.1$; 点虚线: $\varGamma=0.5$;双点虚线:$\varGamma=1.1$
-->Fig.7Phase shift vs. wave amplitude. Solid line:$\varGamma=0$, dashed line: $\varGamma=0.1$, dot-dashed line:$\varGamma=0.5$,dot-dot-dashed line: $\varGamma=1.1$
-->
显示原图|下载原图ZIP|生成PPT图8相位偏移与波幅关系. 实线: $\tau=1$;虚线: $\tau=1.5$;点虚线: $\tau=2$; 双点虚线: $\tau=2.5$
-->Fig.8Phase shift vs. wave amplitude. Solid line: $\tau=1$,dashed line: $\tau=1.5$, dot-dashed line:$\tau=2$, dot-dot-dashed line: $\tau=2.5$
-->
图 9是依式 (61) 绘制的波形. 在碰撞之前 $\theta=0$, 波形是对称的.然而, 在碰撞之后 $\theta\neq 0$, 波形是不对称的,而在传播方向上向后倾斜.
显示原图|下载原图ZIP|生成PPT图9波形变化. 实线: 碰撞前; 虚线: 碰撞后
-->Fig.9Wave change. Solid line: before collision, dashed line: after collision
-->
图 10和图 11显示的波速与波幅的之间的关联. 我们可以看到波速随着波幅的增加而递增, 但当波幅从 $0.3$ 开始增大时, 波速就会下降.此外, 所有这些参数 递增时, 例如 $\varGamma$ 和 $\tau$,都会导致波速的增大.
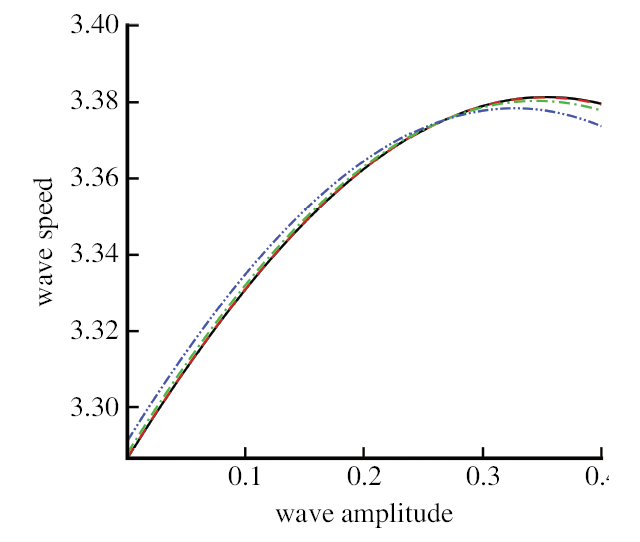显示原图|下载原图ZIP|生成PPT图10相位偏移与波幅关系. 实线:$\varGamma=0$; 虚线: $\varGamma=0.001$; 点虚线: $\varGamma=0.007$;双点虚线:$\varGamma=0.03$
-->Fig.10Wave speed vs. wave amplitude. Solid line:$\varGamma=0$, dashed line: $\varGamma=0.001$, dot-dashed line:$\varGamma=0.007$,dot-dot-dashed line: $\varGamma=0.03$
-->
显示原图|下载原图ZIP|生成PPT图11相位偏移与波幅关系. 实线: $\tau=0.5$; 虚线: $\tau=0.6$; 点虚线:$\tau=0.8$; 双点虚线: $\tau=1$
-->Fig.11Wave speed vs. wave amplitude. Solid line: $\tau=0.5$,dashed line: $\tau=0.6$, dot-dashed line: $\tau=0.8$,dot-dot-dashed line: $\tau=1$
-->
本文揭示了许多有趣的行为, 并为进一步研究水弹性孤立波之间的迎面碰撞提供了丰富的舞台. 值得一提的是, 在等式(3)中取 $T=0$ 和 $D=0$,当前结果会退化到由 Su 和 Mirie [27] 得到的纯重力波的结果.
6 结 论
我们描述了冰层覆盖的流体中两个非线性水弹性孤立波迎面碰撞, 并考虑了流体表面张力效应. 冰层假设为一个满足特殊 Cossert超弹性壳理论的Plotnikov--Toland薄弹性板模型. 首先,以含小参数的相位函数为随波坐标系变换控制方程, 以得到一组微分方程.使用含变 形坐标的 Poincaré--Lighthill--Kuo方法求解非线性微分方程, 求到三阶的 级数解.在图形和数学上对所有参数的影响进行讨论. 特别地, 阐明了弯曲刚度和表面张力对流体与板界面高度、底部速度、相位偏移、波速、变形曲线和碰撞过程中最大波浪爬高 幅度的影响.我们比较了线性和非线性模型, 并且观察到在较小振幅的孤立波上两种模型之间的影响可以忽略不计. 此外, 由于板的弹性和流体表面张力效应,孤立波的波幅趋于减小. 在碰撞 过程之后, 波形向后倾斜. 然而,表面张力效应对波形变化不会引起显著影响. 借助图形演 示,还推导并解释了最大波浪爬高幅度. 由于表面张力, 波浪爬高幅度减小,这与板厚度和杨氏模量的影响类似. 此外,由于板的弹性和流体表面张力效应, 相位偏移趋于显着减 小.我们发现由于表面张力的显着增加, 波速趋于增加.在没有薄弹性板和表面张力的情 况下, 本文结果退化到 Su 和Mirie [27] 获得的结果, 这证实了当前的方法 和所获得的结果是正确的.
致谢 本文原稿为英文,由第一和通信作者共同完成.中文部分由硕士生浦俊翻译、通信作者修改定稿.
附录 A
$$ G_3 =3a\left(^\dfrac {-1 }{6}_c \bigg( \dfrac {1}{2 } -\chi \tau \bigg) \right) {\rm (A3)}$$$$ G_4 = \left(\begin{array}{c}-2 \bar{k} \dfrac {\partial \theta_0}{\partial \eta} \\ c\bigg[ -b B+ \bar{k} \chi\dfrac {\partial \theta_0}{\partial \eta}\bigg( 1+\dfrac{1 }{\chi} \bigg)\bigg]\end{array}\right) {\rm (A4)}$$
$$ \bar{ \pmb G}_1= \dfrac{b }{2} \left(^1 _-c \right) {\rm (A5)}$$
$$ \bar{ G}_2=-b \left(^2 _-c\right) {\rm (A6)}$$
$$ \bar{ G}_3=3b \left(^\dfrac {1 }{6} _ c ( \dfrac {1 }{2 }-\chi \tau ) \right) {\rm (A7)}$$
$$ \bar{ G}_4 = \left(^{c}-2 k \dfrac {\partial \varphi_0}{\partial \xi} _c \bigg[ k \dfrac {\partial \varphi_0}{\partial \xi} \left(\chi+1\right)-a A \bigg] \right) {\rm (A8)}$$
$$\quad \pmb H _4=a\pmb E _2, \qquad \pmb H _5 =a\pmb E _1, \qquad \pmb H _6 =a E _3 {\rm (A12)}$$
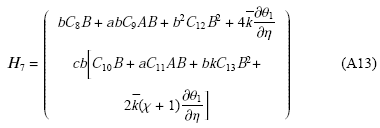
$$ H _8 = -k \dfrac{\partial \theta_1}{\partial \xi} \left(^0 _c (-1+ \chi) \right) {\rm (A14)}$$
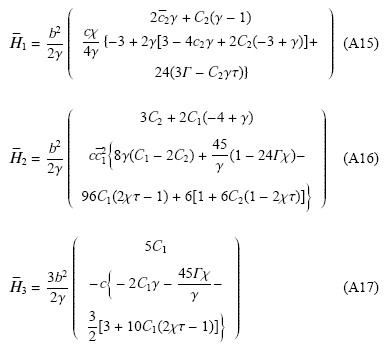
$$\quad \bar{\pmb H }_4=b \bar{\pmb E }_2,\qquad \bar{\pmb H }_5 = b\bar{\pmb E}_1,\qquad \bar{\pmb H }_6 =b \bar{\pmb E }_3 {\rm (A18)}$$
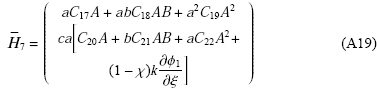
$$\bar{H}_8= \bar{k} \dfrac{\partial \varphi_1}{\partial \eta} \left(^2 _c(1-\chi) \right) {\rm (A20)}$$
附录 B
$$\quad C_1 = \dfrac{1}{2\varUpsilon}\bigg(1+\dfrac{3(2-3\chi \tau)}{ \gamma } \bigg) {\rm (B1)}$$$$\quad C_2 =-\dfrac{2-3\chi \tau}{\varUpsilon \gamma } {\rm (B2)}$$
$$\quad C_{3} = \dfrac{c_1}{\gamma} \bigg\{C_2(\gamma-1)-\dfrac{1}{4 }\{ -3+2\gamma [3+2 C_2 (-3+\gamma)] +$$
$$\qquad 24(3 \varGamma - C_2 \gamma \tau) \}\bigg\} {\rm (B3)}$$
$$C_{4}=\dfrac{c_1}{ \gamma} \{ 3 C_2 +2 C_1 (-4+\gamma)-c_1^2 \{8\gamma^2 (C_1 -2C_2)+$$
$$\qquad 45 (1 -24\varGamma \chi )+96\gamma C_1 (2\chi \tau-1) -$$
$$\qquad 6\gamma [-1+6C_2(-1 +2\chi\tau)]\}\} {\rm (B4)}$$
$$ C_{5}= \dfrac{c_1}{\gamma} \bigg\{ -15C_1+\dfrac{3 }{8 \gamma} [- 16C_1 \gamma^2 -45( 1-24\varGamma \chi)+$$
$$12 \gamma (-3 +10C_1+20C_1 \tau\chi) ] \bigg\}{\rm (B5)}$$
$$\quad C_{6} = -\dfrac{3C_{5}+2C_{4}}{6} {\rm (B6)}$$
$$\quad C_{7} = \dfrac{C_{5}}{4} {\rm (B7)}$$
$$C_{8} = c_1\bigg[(4bC_2 -3 a )+a \bigg(\dfrac{1}{\varUpsilon}-4C_2 +\dfrac{4}{\varUpsilon^2} \bigg) \bigg] {\rm (B8)}$$
$$\quad C_{9} = \dfrac{c_1}{\gamma}\bigg[9 +4\gamma \bigg(\dfrac{1}{\varUpsilon}-2C_1-\dfrac{8}{\varUpsilon^2}\bigg) \bigg] {\rm (B9)}$$
$$\quad C_{10} = \dfrac{c_1 }{\gamma} \bigg\{b\bigg[2 C_2 \gamma -3\bigg(1+\dfrac{2}{\varUpsilon}\bigg)\bigg] -$$
$$\qquad \dfrac{2\tau \chi}{\varUpsilon} \bigg(\dfrac{32}{\varUpsilon}+7\bigg) + a \bigg[ 9 +2C_2 +\dfrac{1}{\varUpsilon}(\gamma-3-2C_2\gamma) +$$
$$\qquad \dfrac{2 \chi C_2 \gamma}{\varUpsilon}\bigg]-C_{6}b\bigg\} {\rm (B10)}$$
$$\quad C_{11} =\dfrac{c_1}{\gamma}\bigg\{- \bigg[27-\dfrac{1}{\varUpsilon} (9+4\gamma)-\dfrac{18\tau\chi}{\varUpsilon}\bigg(\dfrac{8}{\varUpsilon}+3\bigg) \bigg]+$$
$$\qquad 4C_1 \gamma\bigg[1+\dfrac{1}{\varUpsilon}(1+\chi)\bigg] \bigg\} {\rm (B11)}$$
$$\quad C_{12} = 2 \bigg[C_1+\dfrac{4}{\varUpsilon^2}\bigg(\dfrac{1}{\varUpsilon}-1\bigg)\bigg] {\rm (B12)}$$
$$\quad C_{13} = \dfrac{1}{4 \gamma} \bigg\{4C_1\gamma-\bigg[ 9+\dfrac{1}{\varUpsilon}(18-8\gamma +72\tau \chi)\bigg] +$$
$$d\dfrac{16\chi}{\varUpsilon^2} \bigg( 27\tau + \dfrac{2\gamma}{\varUpsilon} \bigg) -C_{7}\bigg\} {\rm (B13)}$$
$$\quad C_{14} =- \dfrac{1}{ \pmb L \!\mathop{\pmb M }\limits^{ \ -\!\!- }\!\pmb R } \bigg( \pmb L\pmb H _8 + \pmb L\bar{\pmb H }_1 + \pmb L \bar{\pmb H }_7 +$$
$$\qquad \dfrac{ \pmb L \bar{\pmb H }_6 C_{6} }{\gamma} +\pmb L\bar{\pmb H }_8 A' \bigg) {\rm (B14)}$$
$$\quad C_{15} =- \dfrac{1}{ \pmb L\!\mathop{\pmb M}\limits^{ \ -\!\!- }\!\pmb R }\bigg[c_1 \pmb L\bar{\pmb H }_2 + \pmb L\bar{\pmb H }_4 C_{6}+\pmb L \bar{\pmb H }_5 C_{6}+$$
$$\qquad\dfrac{ \pmb L \bar{\pmb H}_6}{\gamma} \left( 4 C_{7} -3c_1 \right) \bigg] {\rm (B15)}$$
$$\quad C_{16} =- \dfrac{1}{ \pmb L \!\mathop{\pmb M }\limits^{ \ -\!\!- }\!\pmb R }\bigg( \dfrac{ \pmb L\bar{\pmb H}_3}{3}+ \pmb L\bar{\pmb H }_4 C_{7} + \pmb L \bar{\pmb H }_5C_{7} -$$
$$\qquad \dfrac{5 \pmb L \bar{\pmb H }_6 C_{7}}{\gamma} \bigg) {\rm (B16)}$$
$$\quad C_{17} = \dfrac{1}{2 \gamma} \bigg\{-2a\bigg(2C_2 \gamma+\dfrac{1}{\varUpsilon}\bigg)+b \bigg[ 4 \gamma\bigg( C_2-\dfrac{2}{\varUpsilon^2}\bigg)+$$
$$d\dfrac{1}{\varUpsilon}(1-\gamma)\bigg]\bigg\} {\rm (B17)}$$
$$\quad C_{18} = -\dfrac{1}{2 \varUpsilon \gamma}\bigg(\dfrac{16\gamma C_1}{\varUpsilon}+3+4\gamma \bigg) {\rm (B18)}$$
$$\quad C_{19} =\dfrac{ -c_1}{ \gamma} \bigg\{4\gamma \bigg[ C_1-\dfrac{2}{\varUpsilon^2}\bigg(\dfrac{1}{\varUpsilon}-1\bigg)\bigg]-\dfrac{3}{\varUpsilon}\bigg\} {\rm (B19)}$$
$$\quad C_{20} =-\dfrac{c_1}{ \gamma}\bigg\{-b\bigg[ 9 -2C_2 \gamma\bigg(-1+\dfrac{1}{\varUpsilon}\bigg)+$$
$$\qquad \bigg(9+\dfrac{1}{\varUpsilon}\bigg)\dfrac{1}{\varUpsilon}\bigg] +\dfrac{2b \chi }{\varUpsilon} \bigg( 3\tau -C_2 \gamma\bigg) +$$
$$\qquad a\bigg[ 3 -2\sqrt{\chi}\bigg (C_2\gamma+\dfrac{3}{\varUpsilon}\bigg) -$$
$$\qquad \dfrac{96 \tau \chi}{\varUpsilon^3} \bigg] -aC_{6} \bigg\} {\rm (B20)}$$
$$\quad C_{21} = \dfrac{1}{2 \gamma} \bigg\{\dfrac{-72 \chi \tau}{\varUpsilon^2} +4 C_1 \gamma\bigg(1-\dfrac{1}{\varUpsilon}+\dfrac{\chi}{\varUpsilon} \bigg) +$$
$$\qquad \bigg[ 27+\dfrac{1}{\varUpsilon}(27-4\gamma -18\tau \chi)\bigg]\bigg \} {\rm (B21)}$$
$$\quad C_{22}= \dfrac{-c_1^2}{\gamma}\bigg\{\dfrac{8\chi}{\varUpsilon} \bigg[\dfrac{1}{\varUpsilon} \bigg( 27\tau - \dfrac{2\gamma}{\varUpsilon}\bigg)-9\tau \bigg]+ 9\bigg(1-\dfrac{1}{\varUpsilon}\bigg)+$$
$$\qquad \gamma \bigg( \dfrac{8}{\varUpsilon}-16C_1\gamma C_{7}+27\bigg) \bigg\} {\rm (B22)}$$
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | |
| [23] | |
| [24] | . |
| [25] | |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
