APPLICATION OF SINGULAR PERTURBATION IN THE ANALYSIS OF LAMINAR PREMIXED FLAMES1)
ChenZheng中图分类号:O354.7
文献标识码:A
收稿日期:2018-07-23
接受日期:2018-07-23
网络出版日期:2018-11-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (2589KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
奇异摄动被广泛应用于求解力学问题的近似解.郭永怀对于奇异摄动理论的发展做出了杰出的贡献,他在 1953 年把~Poincare-Lighthill 方法推广应用于平板黏性流动的边界层问题 [1].该方法被钱学森称为~PLK 方法 (Poincare-Lighthill-Kuo method) [2].奇异摄动理论是在研究物理问题时产生的,一个典型的问题就是流体力学中大雷诺数下的黏性绕流 [3].Prandtl 首先在研究这类流动的过程中提出了边界层的概念.边界层是黏性流动中固体壁面附近黏性起主导作用的薄流体层.为了获得大雷诺数情况下 Navier-Stokes 方程的近似解,在边界层外可以求解欧拉方程,而在边界层内则需要求解简化 Navier-Stokes 方程而得到的 Prandtl 边界层方程.在对该问题进行奇异摄动理论分析时,需要采用大雷诺数假设.该假设导致边界层厚度远小于流向尺度,这两个长度的比值是一个小量,基于该小量可以对相关物理量做渐近展开.
燃烧中的层流预混火焰与流体力学中的边界层问题有着一定的相似之处,也可以采用奇异摄动理论进行分析.在层流预混火焰中,化学反应的活化能很大.由于化学反应对温度非常敏感,只有在温度很接近于绝热燃烧温度时才会有显著化学反应发生.这导致反应区的厚度远小于预热区的厚度.在大活化能假设下,由于反应区厚度与预热区厚度的比值跟活化能成反比,这两个厚度的比值是一个小量,基于该小量则可以做渐近展开.在层流预混火焰中,活化能的无量纲数为 Zel'dovich 数,这与流体中的雷诺数相对应.层流预混火焰中,反应区厚度和预热区厚度的比值跟 Zel'dovich 数成反比.这对应于层流边界层问题中,边界层厚度与流向尺度的比值反比于雷诺数的平方根.因此,对层流预混火焰,在大活化能假设下 (即 Zel'dovich 数很大) 可以采用奇异摄动方法进行求解.在燃烧研究中,该方法被称为大活化能渐近分析 (large activation energyasymptotics).
大活化能渐近分析在 20 世纪 30 年代首先被前苏联科学家 Zel'dovich 和 Frank-Kammenetskii[4-5] 应用于预混火焰的理论分析.但直到70 年代,西方****才了解他们的工作.在70 年代初,Bush 与其他**** [6-9] 开始将大活化能渐近理论分析应用于简单火焰的理论研究.随后,该方法在燃烧理论研究中获得了广泛的应用[10-13],使得燃烧理论在 20 世纪八九十年代得到了迅速发展.
本文将介绍大活化能渐近分析在一维平面预混火焰和球形传播火焰中的应用及相关研究进展.
1 一维平面预混火焰
1.1 预混火焰结构及特征尺度
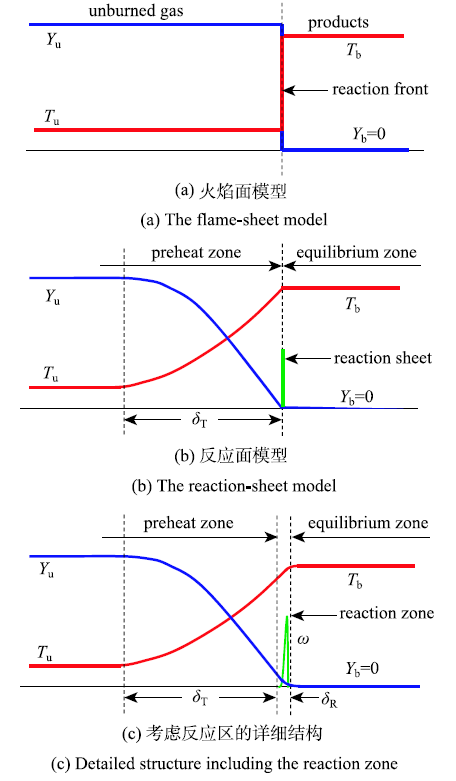
首先考虑一维平面绝热预混火焰.火焰在预混气体中传播时,反应区释放出的热量不断向未燃预混气体传递从而加热预混气体,同时未燃预混气体不断扩散进入化学反应区,从而维持化学反应持续进行.为了简化分析,通常将坐标系建立在火焰面上.在该坐标系中,火焰面是静止的,未燃预混气体以一定的流速流向火焰面.该流速被称为层流火焰速度,通常用 $S_{\rm u}$ 来表示.层流火焰速度的严格定义为平面、未拉伸、绝热、预混火焰相对于未燃烧混合物传播的速度 [12].层流火焰速度是预混燃气的基本性质,它是预混燃气扩散特性、化学反应特性及放热特性的综合体现.层流火焰速度可以被用来表征多种预混燃烧现象,如火焰驻定、熄火、回火、吹熄等 [12].对平面预混火焰开展理论分析的主要目标就是获得层流火焰速度的解析表达式.图1为包含不同层次信息的预混火焰结构示意图 [12],其中 $T$ 和 $Y$ 分别表示温度和不足组分 (贫燃料时为燃料,富燃料时为氧气) 的质量百分数.下标 u 和 b 分别代表未燃预混气体和燃烧产物.在火焰面模型中 (图1(a)),火焰被看作是一个分隔未燃预混气体和燃烧产物的分界面,在火焰面处 $T$ 和 $Y$ 均不连续.该模型不考虑火焰面附近的扩散和化学反应,其控制方程为欧拉型方程,即只有非稳态项和对流项.在反应面模型中 (图1(b)),火焰被看作是厚度为 $\delta _{ T}$ 的预热区和厚度为零的反应面的组合.在预热区中存在温度梯度和组分浓度梯度,因此需要考虑扩散过程：由于热传导,预混气体温度逐渐上升;由于质量扩散,燃料和氧化剂的质量百分数逐渐下降.
显示原图|下载原图ZIP|生成PPT图1包含不同层次信息的预混火焰结构示意图 [
-->Fig.1Schematic premixed flame structure at successive levels of detail [
-->
反应区厚度为零,被看作是一个热源 (燃料燃烧释放热量) 和质汇 (燃烧消耗燃料).在反应面前后,$T$ 和 $Y$ 是连续的,但其一阶导数不连续.该模型不考虑化学反应,其控制方程包括非稳态项、对流项及扩散项.在考虑反应区详细结构时 (图1(c)), 火焰被看作是厚度为 $\delta _{\rm T}$ 的预热区和厚度为 $\delta _{ R}$ 的反应区的组合.由于化学反应的活化能很高,反应区的厚度远远低于预热区的厚度,即 $\delta_{\rm R}\ll\delta _{\rm T}$.在反应区中,$T$ 和 $Y$ 及其导数都是连续的.该模型的控制方程包括非稳态项、对流项、扩散项和化学反应源项,需要通过大活化能渐近分析方法进行求解 [12].
考虑稳态预混火焰传播过程,在固定在火焰面上的坐标系中,火焰面是静止不动的.因此,关于温度和不足组分质量百分数的控制方程不含非稳态项.在预混火焰理论分析中,通常使用单步总包化学反应模型.关于温度和不足组分质量百分数的控制方程为带化学反应源项的常微分方程 [14]
$$mC_P \frac{{\rm d}T}{{\rm d}x} = \frac{{\rm d}}{{\rm d}x}\left(\lambda \frac{{\rm d}T}{{\rm d}x}\right) +q\omega (1)$$
$$m\frac{{\rm d}Y}{{\rm d}x} = \frac{{\rm d}}{{\rm d}x}\left( {\rho D\frac{{\rm d}Y}{{\rm d}x}} \right) - \omega (2)$$
其中,$x$ 为空间坐标,$C_{P}$ 为混合物的定压比热容,$\lambda$ 为混合物的热传递系数,$\rho$ 为混合物的密度,$D$ 为不足组分的质量扩散系数,$q$ 为燃烧单位质量不足组分的放热量,$\omega$ 为化学反应速率. $m$ 为穿过单位面积的质量流率,即 $m=\rho u$,其中 $u$ 为流速. 根据质量守恒,$m$ 为常数,即有 $m=\rho u=\rho_{\rm u}u_{\rm u}=\rho _{\rm b}u_{\rm b}$.根据层流火焰速度的定义,则有 $S_{\rm u}=u_{\rm u}$.在预混火焰理论分析中,求出 $m$ 后即可根据 $S_{\rm u}=m/\rho _{\rm u}$ 获得层流火焰速度.
对于单步总包化学反应模型,其化学反应速率为
$$\omega = \rho YA\cdot \exp ( - E_A / R^0T) (3)$$
其中,$A$ 为指前因子,$E_{A}$ 为总包反应的活化能,$R^{0}$ 为气体常数.
方程 (1) 和 (2) 的边界条件为
$$x \to - \infty : ~T = T_{\rm u}, \quad Y = Y_{\rm u} (4)$$$$\to + \infty :~ {\rm d}T / {\rm d}x = {\rm d}Y / {\rm d}x =0 (5)$$
其中,$T_{\rm u}$ 和 $Y_{\rm u}$ 分别为未燃预混气体的温度和不足组分质量百分数.如图1(c) 所示,在燃烧产物中不足组分质量百分数为零.对于绝热 (即不考虑辐射热损失) 平面预混火焰,燃烧产物的温度为绝热燃烧温度 $T_{\rm b}$.
联立方程 (1) 和 (2) 消去化学反应源项后进行积分,并利用边界条件 (4) 和 (5) 则可得到绝热燃烧温度为
$$T_{\rm b} = T_{\rm u} + qY_{\rm u} / C_P (6)$$
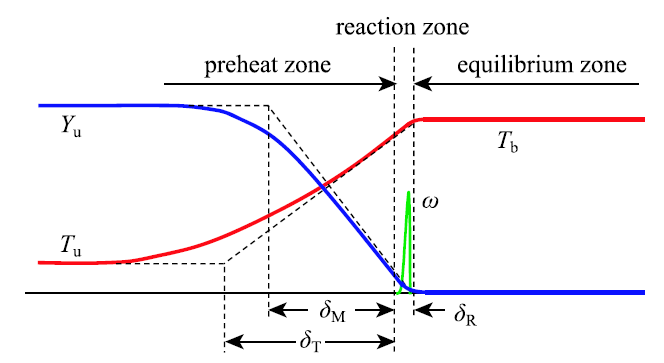
通常预热区的厚度 $\delta _{\rm T}$ 是基于温度分布而定义的.图2 中给出了分别基于温度分布和不足组分质量百分数分布的特征厚度 $\delta_{\rm T}$ 和 $\delta _{\rm M}$.在预热区中可以忽略化学反应源项,根据方程 (1) 和 (2) 可以推导出预热区温度特征厚度和组分特征厚度的比值为 [12]
$$\delta _{\rm T} / \delta _{\rm M} = Le (7)$$
其中,$Le=\lambda /(\rho C_{P}D)$ 为~Lewis 数,它是热扩散率和不足组分质量扩散率的比值.对大多数碳氢燃料的预混火焰,Lewis 数接近于 1.因此通常可以假设~Le$ \approx $1.
显示原图|下载原图ZIP|生成PPT图2层流预混火焰中不同特征尺度 [
-->Fig.2Different characteristic lengths in a laminar premixed flame[
-->
在 $Le=1$ 时,$\delta _{\rm T}=\delta _{\rm M}$ 且归一化的温度分布和不足组分质量百分数分布相互对称.联立方程 (1) 和 (2) 消去化学反应源项后进行积分,并利用边界条件 (4) 和 (5) 则可得
$$Y / Y_{\rm u} = 1 - (T - T_{\rm u} ) / (T_{\rm b} - T_{\rm u}) (8) $$
定义 Zel'dovich 数为
$$\beta = \frac{E_A }{R^{0}T_{\rm b}}\left(1 - \frac{T_{\rm u} }{T_{\rm b} }\right) (9)$$
则化学反应速率可写为
$$\omega = \rho Y_{\rm u} A(1 - \theta ) \cdot \exp\left\{ - \frac{\beta }{(1 - \sigma )[\sigma + (1 - \sigma )\theta]}\right\} (10) $$
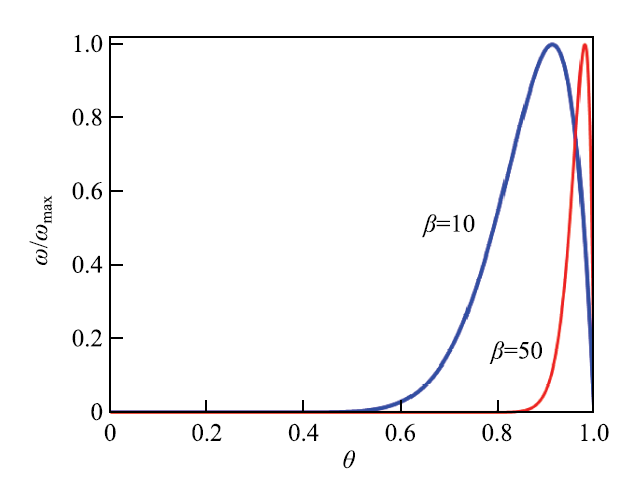
其中,$\theta =(T-T_{\rm u})/(T_{\rm b}-T_{\rm u})$ 和 $\sigma =T_{\rm u }/T_{\rm b}$ 分别为归一化无量纲温度和温度比. 图3 给出了在 $\sigma =0.15$,$\beta $ 分别为 10 和 50 时,化学反应速率随着温度的变化曲线.利用式 (10) 可以得出反应速率取极大值时的归一化温度为 $\theta _{\rm m}=1-1/(1-\sigma +\beta ) \approx 1-1/\beta $ [14].图3 表明,化学反应主要发生在温度接近于 $\theta _{\rm m}$ 的反应区内;而在预热区,由于温度低于 $\theta _{\rm m}$,化学反应速率几乎为零. 在活化能很大时 ($E_{A}\gg1$),对应有 $\beta \gg1$,从而导致化学反应被局限于一个很薄的区域中.可以证明,图1(c) 和图2 中反应区和预热区的厚度比为 $\delta _{\rm R}/\delta _{\rm T}=1/\beta $. 大活化能渐近分析正是利用 $\delta _{\rm R}/\delta _{\rm T}=1/\beta \ll 1$ 这一条件开展渐近理论分析.
显示原图|下载原图ZIP|生成PPT图3归一化化学反应速率随着归一化温度的变化 ($\sigma =0.15$)
-->Fig.3Change of normalized reaction rate with the normalized temperature for $\sigma =0.15$
-->
1.2 Zel'dovich 和 Frank-Kamenetskii 理论
Zel'dovich 和 Frank-Kammenetskii [4-5] 首先对大活化能假设下的一维层流预混火焰进行了严格的理论分析.他们考虑图4 所示的火焰结构,位于预热区与反应区分界面处 ($x=0$) 的点火温度为 $T_{\rm i}$. 只有温度高于 $T_{\rm i}$ 时,才会有化学反应发生.根据图3 中的结果,活化能越大,则点火温度为 $T_{\rm i}$ 越接近于绝热燃烧温度 $T_{\rm b}$,反应区的厚度也越薄.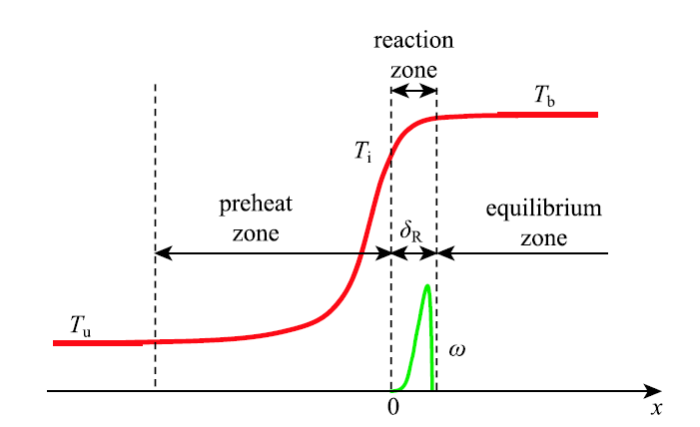
显示原图|下载原图ZIP|生成PPT图4根据温度分布划分的预混火焰三区结构
-->Fig.4The three-zone premixed flame structure based on temperature distribution
-->
假设 $Le=1$,则温度 $T$ 和不足组分质量百分数 $Y$ 满足关系式 (8).因此只需要求解温度方程 (1).在预热区,化学反应可以忽略,因此温度方程 (1) 简化为
$$mC_P\frac{{\rm d}T}{{\rm d}x} = \lambda \frac{{\rm d}^2T}{{\rm d}x^2} (11)$$
对上式在预热区进行积分,并利用边界条件得
$$\left.{\frac{{\rm d}T}{{\rm d}x}} \right|_{x = 0^ - } = \frac{mC_P}{\lambda }(T_{\rm i} - T_{\rm u} ) (12)$$
在化学反应区,由于其厚度很小,因此可以忽略对流项.
则温度方程 (1) 简化为 (假设 $\lambda$ 为常数)
$$\lambda\frac{{\rm d}^2T}{{\rm d}x^2} + q\omega = 0 (13)$$
上式可以变形为
$$\frac{{\rm d}}{{\rm d}x}\left(\frac{{\rm d}T}{{\rm d}x}\right)^2 = - \frac{2q\omega }{\lambda}\frac{{\rm d}T}{{\rm d}x} (14)$$
对上式在反应区进行积分得
$$\left. {\frac{{\rm d}T}{{\rm d}x}} \right|_{x = 0^ + } = \sqrt{\frac{2q}{\lambda }\int_{T_{\rm i} }^{T_{\rm b} } {\omega {\rm d}T} } (15)$$
在预热区和反应区的分界面上,左右两侧的温度梯度是连续的.则由式 (12) 和式 (15) 得
$$\frac{mC_P }{\lambda }(T_{\rm i} - T_{\rm u} ) = \sqrt{\frac{2q_F }{\lambda }\int_{T_{\rm i} }^{T_{\rm b} } {\omega {\rm d}T} } (16)$$
在大活化能条件下,化学反应区很薄且有 $T_{\rm i}\approx T_{\rm b}$. 因此上式左边项中的 $T_{\rm i}$ 可以用 $T_{\rm b}$ 近似取代. 而上式右边项中的积分下限 $T_{\rm i}$ 可以用 $T_{\rm u}$ 近似取代.这是因为在预热区的化学反应速率近似为零,改变积分下限并不影响积分结果.利用绝热燃烧温度的表达式 (6),上式可写为
$$m = \left({\frac{2\lambda }{C_P } \cdot \frac{1}{T_{\rm b} - T_{\rm u} }\cdot \frac{1}{Y_{\rm u} } \cdot \int_{T_{\rm u} }^{T_{\rm b} }{\omega {\rm d}T} } \right)^{1 / 2} (17)$$
在活化能很大时 ($E_{A}\gg 1)$,化学反应源项中的指数项可以近似为
$$\exp \left( - \frac{E_A }{R^0T}\right) \approx \exp \left( - \frac{E_A }{R^0T_{\rm b} }\right)\exp \left( - \frac{E_A (T_{\rm b} - T)}{R^0T_{\rm b}^2}\right) (18)$$
该近似由 Frank-Kamenetskii[5] 首次提出,在燃烧理论分析中被广泛应用.将式 (18) 和式 (8) 代入式 (3) 和式 (17) 中,并利用大活化能假设 ($E_{A}\gg1$),则可以得到层流火焰速度的解析表达式
$$S_{\rm u} = \left[{\frac{2\alpha }{\beta ^2}A \cdot \exp \left( - \frac{E_{\rm a}}{R^0T_{\rm ad} }\right)} \right]^{1 / 2} (19)$$
其中 $\alpha=\lambda /(\rho _{u}C_{P})$ 为未燃预混气体的热传导率. 上式与 Mallard和 Le Chatelier[15] 的热理论给出的结果一致,即层流火焰速度正比于化学反应速率和热传导率的二分之一次方.上述结果针对反应级数为 1 的总包反应,对于任意反应级数的总包反应也可开展类似的分析 [12,14,16].
1.3 平面预混火焰大活化能渐近分析
在预混火焰理论分析中,将火焰结构分为如图2所示的预热区、化学反应区以及平衡区 [12]. 在大活化能 ($E_{A}\gg1)$ 条件下,化学反应对温度非常敏感,只有在反应区才需要考虑化学反应.大活化能 ($E_{A}\gg 1$) 是开展渐近理论分析的前提 $^{[10 - 12]}$.在大活化能 ($E_{A}\gg1$) 条件下,化学反应区和预热区的厚度比为一个小量,记为 $\varepsilon$,渐近解可以被写成这个小量的级数形式.后面的分析表明该小量等于 Zel'dovich 数的倒数,即 $\varepsilon=1/\beta$ [12].分别对 3 个区域求出渐近解,接着根据相邻区域分界面处的连续性进行匹配,最终可以得到层流火焰速度的解析表达式 [12].在预热区 ($x<0$),化学反应项可以被忽略,所以控制方程可以简化为如下的对流扩散方程
$$mC_P \frac{{\rm d}T}{{\rm d}x} = \lambda \frac{{\rm d}^2T}{{\rm d}x^2} (20) $$
$$m\frac{{\rm d}Y}{{\rm d}x} = \rho D\frac{{\rm d}^2Y}{{\rm d}x^2} (21)$$
这两个常微分方程的渐近解可以写成关于小量 $\varepsilon$ 的级数形式 (只考虑零阶项和一阶项)
$$T^ - (x) = T_0^ - (x) +\varepsilon T_1^ - (x) (22)$$
$$Y^ - (x) = Y_0^ - (x) +\varepsilon Y_1^ - (x) (23)$$
其中,上标中的“$-$”表示预热区 ($x<0$).
结合式 (4) 中的边界条件,可以解得
$$T^ - (x) = T_{\rm u} + C_1 {\rm e}^{mC_P x/ \lambda } + \varepsilon C_2 {\rm e}^{mC_P x / \lambda } (24)$$
$$Y^ - (x) = Y_{\rm u} + C_3 {\rm e}^{mx / (\rho D)} + \varepsilon C_4 {\rm e}^{mx / (\rho D)} (25)$$
其中 $C_{i}$($i=1,2,3,4$) 是待定积分常数.
在下游平衡区 ($x>0$),不足组分在化学反应区被完全消耗掉.在绝热条件 (即不考虑辐射热损失) 下,燃烧产物达到绝热燃烧温度. 因此有
$$T^ + (x) = T_{\rm b}, \quad Y^ + (x) = 0 (26)$$
其中上标中的“+”表示下游平衡区 ($x>0$).
如前文所述,化学反应区和预热区的厚度比为 $\varepsilon $.为了有效地分辨化学反应区,需要引入坐标变换 $\xi =x/\varepsilon$ 将反应区拉长 [12].这也是奇异摄动法中处理奇异点处边界层的常用处理方法 [17].在内部反应区,可以将渐近解写成如下形式
$$T_{\rm in} (\xi ) = \theta _0- \varepsilon \theta _1 (\xi ) (27)$$
$$Y_{\rm in} (\xi ) = \phi_0 + \varepsilon \phi _1 (\xi ) (28) $$
其中,$\theta _0$ 和 $\phi_0$ 是零阶项,而 $\theta _1(\xi )$ 和 $\phi_1(\xi )$ 是一阶项的大小.化学反应区不同于预热区和平衡区,它跟上游与下游的边界都不直接接触.因此不能用边界条件 (4) 和 (5) 去求解化学反应区的温度分布和不足组分的质量百分数分布,而是需要用到反应区内部解和外部解的连续性匹配条件.
内部解与外部解在反应区下游的匹配条件为
$$\mathop {\lim}\limits_{\xi \to + \infty } T_{\rm in} (\xi ) = \mathop {\lim}\limits_{\xi \to + \infty } T^ + (X) (29)$$$$\mathop {\lim }\limits_{\xi \to + \infty } Y_{\rm in} (\xi ) =\mathop {\lim }\limits_{\xi \to + \infty } Y^ + (X) (30)$$$$\mathop {\lim }\limits_{\xi \to + \infty } {\rm d}T_{\rm in} /d\xi = \mathop {\lim }\limits_{\xi \to + \infty } {\rm d}T^ + /{\rm d}\xi (31)$$$$ \mathop {\lim }\limits_{\xi \to + \infty } {\rm d}Y_{\rm in} /{\rm d}\xi = \mathop {\lim }\limits_{\xi \to + \infty } {\rm d}Y^+ / {\rm d}\xi(32)$$
将内部解与外部解代入上述匹配条件可得
$$\theta _0 - T_b = \phi _0 = \theta _1 ( + \infty ) = \phi _1 ( +\infty ) = 0 (33)$$$${\rm d}\theta _1 ( + \infty ) / {\rm d}\xi = {\rm d}\phi _1 ( +\infty ) / {\rm d}\xi = 0 (34)$$
内部解与外部解在反应区上游进行匹配时,需要将外部解进行坐标变换 $\xi=x/\varepsilon $,并对式 (24) 和式 (25) 在反应区进行渐近展开
$$T^ -(\xi ) \approx T_{\rm u} + C_1 + \varepsilon \cdot (\xi C_1 mC_P /\lambda + C_2 ) (35)$$
$$Y^ - (\xi ) = Y_{\rm u} + C_3 +\varepsilon \cdot [\xi C_3 m / (\rho D) + C_4 ] (36)$$
利用类似于式 (29) 至式 (32) 的匹配条件可得
$$C_1 = T_{\rm b} - T_{\rm u}, \quad C_3 = - Y_{\rm u} (37)$$$$\theta _1 ( - \infty ) \to + \infty , \quad \phi _1 ( - \infty )\to + \infty (38)$$$$\frac{{\rm d}\theta _1 ( - \infty )}{{\rm d}\xi } = -\frac{(T_{\rm b} - T_{\rm u} )mC_P }{\lambda }, \quad \frac{{\rm d}\phi _1 ( - \infty )}{{\rm d}\xi } = - \frac{Y_{\rm u} m}{\rho D}\qquad (39)$$
接下来对化学反应区进行求解. 上面已经解出零阶项解为 $\theta_{0}=T_{\rm b}$ 和 $\phi _{0}=0$. 接下来求解一阶项 $\theta _1(\xi)$ 和 $\phi _1(\xi )$. 将式 (27) 与式 (28) 以及坐标转换 $\xi=x/\varepsilon$ 代入方程 (1) 和 (2) 中,可以发现对流项比扩散项小一个量级,从而可以被忽略.因此内部反应区的控制方程被化简为如下的扩散反应方程
$$\frac{{\rm d}^2\theta _1 }{{\rm d}\xi ^2} = \varepsilon \omega q,\quad (\rho D)\frac{{\rm d}^2\phi _1 }{{\rm d}\xi ^2} =\varepsilon \omega (40)$$
其中反应区的反应速率项为
$$\omega = \rho\varepsilon \phi _1 A \cdot \exp [ - E_{\rm a} / R^0(T_{\rm b} -\varepsilon \theta _1 )] (41)$$
联合式 (40) 中的两个方程消去反应项,并结合 $\xi \to +\infty$ 处的边界条件进行积分可得到
$$(\lambda / q)\theta _1 = (\rho D)\phi _1 (42)$$
将式 (41) 和式 (42) 代入式 (40),并利用式 (18) 中的~Frank-Kamenetskii 近似可得
$$\frac{{\rm d}^2\theta _1 }{{\rm d}\xi ^2} = D_{\rm a} \theta _1 \exp \left( -\frac{\varepsilon E_{\rm a} }{R^0T_{\rm b}^2 }\theta _1\right) (43)$$
其中 $D_{\rm a} = \varepsilon ^2(A / D)\exp ( -E_{\rm a} / R^0T_{\rm b} )$ 为 Damkohler 数. 将小量 $\varepsilon$ 取值为~Zel'dovich 数的倒数,即 $\varepsilon =1/\beta$,同时引入变换 $\tilde {\theta }_1 = \theta _1 / (T_{\rm b} -T_{\rm u} )$,式 (43) 可变形为
$$\frac{{\rm d}}{{\rm d}\tilde {\theta }_1}\left(\frac{{\rm d}\tilde {\theta }_1 }{{\rm d}\xi }\right)^2 =2D_{\rm a} \tilde {\theta }_1 \exp ( - \tilde {\theta }_1) (44)$$
对上式进行积分,并使用 $\xi \to +\infty $ 和 $\xi \to-\infty $ 处的边界条件可得
$$mC_P / \lambda = \sqrt {2D_{\rm a}} (45) $$
该式可以变形为
$$S_{\rm u} = \left[ {\frac{2\alpha Le}{\beta ^2}A \cdot\exp \left( - \frac{E_{\rm a} }{R^0T_{\rm ad} }\right)} \right]^{1/ 2} (46)$$
上述结果在 $Le=1$ 时与式 (19) 一致.因此大活化能渐近分析可以得到任意~Lewis 数下的层流火焰速度的解析表达式.式 (46) 只适用于总反应级数为 1 的总包反应模型,通过渐近理论分析也可以获得考虑任意反应级数总包反应模型的层流火焰速度解析表达式 [16].值得注意的是,通过大活化能渐近理论分析获得的层流火焰速度的解析表达式,可以定性描述化学反应活化能、热传导率、活化能、火焰温度以及压力对层流火焰速度的影响规律,
但不能定量地预测不同工况下的层流火焰速度.
在上述理论分析中,平衡区燃烧产物的温度保持为绝热燃烧温度 $T_{\rm b}$.而在实际燃烧过程中,由于辐射热损失,燃烧产物随着离开反应区的距离增大,其温度会逐渐下降直至达到环境温度.此时,平衡区燃烧产物温度变化的特征厚度为预热区厚度的 $\beta $ 倍.预热区反应物和平衡区燃烧产物的辐射热损失均会影响平面火焰燃烧强度,即降低火焰温度和层流火焰速度.这是因为辐射热损失会增大化学反应区两侧的温度梯度,对应消耗化学反应产生的热量,占用了用于加热未燃预混气体的热量.
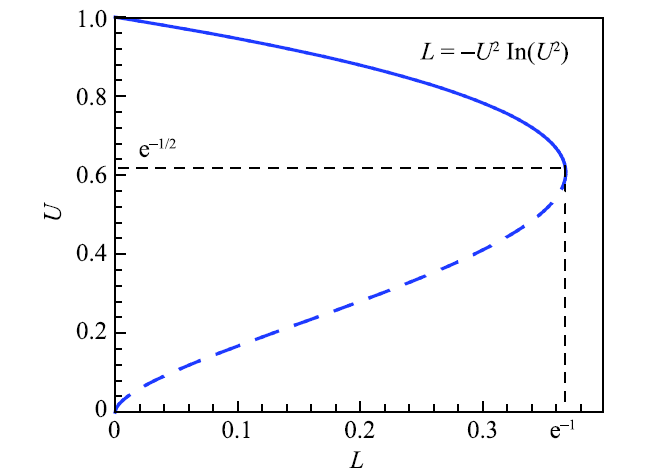
通过大活化能渐近分析 [12,18],可以得到归一化的层流火焰速度 $U$ 与无量纲热损失系数 $L$ 之间的关系为
$$L = - U^2\ln (U^2) (47)$$
其中 $U$ 是有热损失时的层流火焰速度与绝热条件下的层流火焰速度的比值.图5 给出了上式描述的 $U$ 随着 $L$ 变化的曲线.对于给定热损失系数,存在两个解：快速火焰解 (图中实线部分) 和慢速火焰解 (图中虚线部分).稳定性分析结果 [12,18] 表明快速火焰解是稳定的、在实际燃烧过程中可以实现;而慢速火焰解是不稳定的、不会出现在实际燃烧过程中.图5 表明,当无量纲热损失系数达到临界值 $L={\rm e}^{ -1}$ 时,快速火焰解和慢速火焰解相交到一点,对应 $U={\rm e}^{ - 1 /2}$. 该点对应预混气体的可燃极限 [12,18-19].可以看出,预混气体在趋向于可燃极限时,其层流火焰速度并不会降为零.
显示原图|下载原图ZIP|生成PPT图5归一化层流火焰速度随着无量纲热损失系数的变化
-->Fig.5Change of the normalized laminar flame speed with the non-dimensional heat loss coefficient
-->
值得注意的是,辐射热损失在理论分析中通常被简化处理.例如,不同组分的热辐射特性对辐射波长具有不同的依赖性,甚至有的组分 (如二氧化碳) 则需要考虑辐射重吸收 (radiation re-absorption).这些在已有的理论分析中均没有被考虑到,需要通过数值模拟来实现.
上述理论分析研究的是一维平面火焰的稳态结构和传播速度.在实际燃烧过程中,平面火焰不一定是稳定的.图6 显示贫燃料甲烷/氢气/空气的平面火焰具有胞状结构.这是由于预混气体的 Lewis 数小于 1,火焰受到热{--}扩散不稳定性 (thermal-diffusive instability) 的作用.除了热{--}扩散不稳定性,平面火焰还受到流体动力学不稳定性 (hydrodynamic instability) 和振荡不稳定性 (pulsating instability) 的影响.流体动力学不稳定性 [20] 是由于火焰面前后急剧的密度变化所致.随着膨胀比 (反应物与燃烧产物的密度比) 的增大,则流体动力学不稳定性越强.另外,有限火焰厚度会抑制流体动力学不稳定性,火焰面越薄则流体动力学不稳定性越强.因此高压下的预混火焰会受到强烈的流体动力学不稳定性影响. 文献 [18,21-25] 采用大活化能渐近分析研究了平面预混火焰的热{--}扩散不稳定性.以往的研究结果表明,在~Lewis 数小于 1 时,预混火焰会受到热{--}扩散不稳定性而出现如图6 所示的胞状结构.Sivashinsky[26] 的研究表明热{--}扩散不稳定性会导致层流火焰出现湍流化.与热{--}扩散不稳定性相反,振荡不稳定性通常发生在~Lewis 数较大的预混火焰中.Sivashinsky[21] 通过渐近理论分析发现,振荡不稳定性产生的条件是 $\beta(Le-1)>10.9$. Law 与 Sung[25] 通过一维数值模拟研究了层流预混火焰的振荡不稳定性,数值模拟获得的振荡不稳定临界条件与理论分析结果相吻合.关于预混火焰稳定性的研究,读者可参考相关综述文章 [24-25,27 -30] 和专著 [12-13].
显示原图|下载原图ZIP|生成PPT图6贫燃料甲烷/氢气/空气平面火焰实验图像 [
-->Fig.6Experimental images of fuel lean CH$_{4}$/H$_{2}$/air flames [
-->
理论研究通常采用无限大空间中自由传播的一维平面火焰模型.但在实际燃烧过程中,平面火焰是通过平面火焰器来实现的.预混气体垂直于平面火焰器表面流出,在平面火焰器上方一定距离处形成驻定平面火焰.该平面火焰驻定机制是：火焰与平面火焰器表面之间的间距越小,则火焰热损失越大,从而导致火焰越弱、层流火焰速度下降、火焰向远离平面火焰器表面的方向移动.Eng 等 [32] 对平面火焰器驻定的平面火焰进行了理论和实验研究,他们揭示了热损失稳定平面火焰的机制,并解释了平面火焰被吹熄与可燃极限之间的差别.Matthews 等 [33] 采用大活化能渐近分析方法,研究了平面火焰器驻定的平面火焰的火焰结构和稳定性.他们发现火焰下游 (即燃烧产物区) 的辐射热损失会比上游 (即预热区) 的辐射热损失更有效地促发火焰面不稳定.Chao[34] 和~Kurdyumov 等 [35-36] 采用大活化能渐近分析方法,研究了辐射热损失如何影响平面火焰器驻定的平面火焰的稳定性.他们发现辐射热损失会减小火焰稳定区域.
2 球形传播火焰
2.1 球形传播火焰及其应用
上一节讨论的平面火焰是不受拉伸率 (stretch rate) 作用的.但在实际燃烧过程中,由于流场不均匀或者火焰面弯曲,预混火焰会受到拉伸率的作用.拉伸率定义为在拉格朗日描述下火焰面面积的相对变化率 [11-12,37-38].球形传播火焰和对冲火焰是研究拉伸率影响的最典型的两类预混火焰.这两类火焰都是一维的,因此也得到了广泛的理论研究. Sivashinsky[39] 首次采用大活化能渐近分析方法研究了一维球形传播火焰,揭示了~Lewis 数对球形火焰传播速度的影响规律.Sivashinsky [40] 还对受限空间中的球形传播火焰进行了理论分析.采用大活化能渐近分析方法,Clavin 及其合作者 [24,41] 推导出了用于量化拉伸率影响球形传播火焰速度的~Markstein 长度的解析表达式,Frankel和 ~Sivashinsky[42-43] 研究了热膨胀和~Lewis 数对球形火焰传播和熄火的影响,Matalon 及其合作者 [44-45] 揭示了辐射热损失对球形传播火焰的影响,Clavin 等 [46] 推导出了量化曲率和非均匀流场影响球形传播火焰速度的~Markstein 长度,Kelley 等 [47] 研究了受限空间内压力升高对球形传播火焰的影响.球形传播火焰在实验中易于实现.在密闭空间中,通过分压法可以制备不同当量比下燃料和空气的预混气体.在中心处采用电火花点火后,则可以得到球形传播火焰.球形传播火焰在燃烧基础研究中得到了广泛的应用,主要体现在两方面：点火过程研究和层流火焰速度测量.
点火是燃烧研究中最为基础的问题,也是燃烧研究的热点问题.点火分为强迫点火 (例如通过电火花进行点火) 与自发着火 (例如,在测量着火延迟时间的激波管实验中,反射激波后发生自着火)[12]. 球形传播火焰被应用于研究强迫点火过程.在实际发动机中,电火花点火得到了广泛的应用.然而,由于其复杂性,点火理论一直是燃烧领域中的一个难点. Lewis 和 VonElbe[48] 以及 Zel'dovich 等 [5] 较早提出了描述电火花点火的燃烧理论,他们认为：(1) 临界点火尺寸跟熄火距离或者火焰厚度成正比;(2) 最小点火能正比于熄火距离或者火焰厚度的立方.然而,上述理论只考虑了热量扩散而忽略了燃料和氧化剂的质量扩散.后续火焰球的研究则同时考虑了热量扩散和质量扩散 [5,49-51].火焰球半径被认为是控制点火的特征长度,而最小点火能则被认为正比于火焰球半径的立方 [50].但是,以往的点火理论均没有将点火核形成与后续火焰传播很好地结合起.He 等 [52-53] 以及~Chen 等 [54-55] 发展了能够同时描述点火与球形火焰传播的燃烧理论,从而能够更准确地预测临界点火条件.研究结果表明,对于具有较高~Lewis 数 (热量和质量扩散系数之比) 的预混气体,即使小于火焰球半径的球形火焰仍能够向外传播 [55].这就推翻了火焰球半径是控制点火的特征长度这一观点 [55].Law 及其合作者 [56] 通过实验验证了上述理论的正确性.本文下一节将详细介绍该理论及其相关结论.
层流火焰速度是反映预混燃气燃烧特性的重要参数.球形传播火焰由于火焰结构简单、拉伸率定义明确且能够获得高压下的结果,被广泛用来测量不同燃料的层流火焰速度 [57-64].目前,球形传播火焰法是测量宽压力和温度范围内层流火焰速度的唯一方法.球形传播火焰法通过记录火焰半径或者容器内压力随时间的变化来确定层流火焰速度.在球形火焰传播初期,火焰的拉伸效应很大,而压力上升可以忽略不计.随着火焰半径增大,压力逐步上升,拉伸效应变得可以忽略不计.根据燃烧室设计和压力上升大小,有两种基于球形传播火焰的层流火焰速度测量方法：定压法和定容法.定压法使用具有较小半径的火焰,使得压力上升是可忽略的.而在定容法中,则是采用具有较大半径的火焰,对应有明显的压力上升 [65].定压球形传播火焰法具有两个优点：(1) 火焰传播过程被记录下来,可以得到火焰不稳定的信息;(2) 火焰传播速度是拉伸率的函数,通过外推到零拉伸率可以得到无拉伸层流火焰速度.然而,由于需要开设视窗,定压法的上限压力通常低于定容法.定容球形传播火焰法的优点是,在同一次实验中可以测得很宽的压力和温度范围内的层流火焰速度.然而,定容法的缺点是不确定球形火焰传播不稳定性的出现,从而导致层流火焰速度测量精度降低.虽然这两种球形传播火焰方法被广泛用来测量层流火焰速度,但如何提高测量精度和如何准确测量高温高压下的层流火焰速度仍然是基础燃烧研究的热点问题 [64-66].
关于点火与球形传播火焰的渐近理论分析有助于发展点火理论与准确测量层流火焰速度,下面将介绍理论研究的相关进展.
2.2 考虑单步总包反应的点火与球形传播火焰理论
以往的点火理论 [5,48-51]将点火核形成与后续球形火焰传播分离开来进行研究,没有考虑点火核的非稳态传播过程,因此不能准确地预测临界点火条件.通过渐近理论分析发展了能够同时描述点火与球形火焰传播的理论,能够更准确地预测临界点火条件 [54].考虑如图7 所示的理论模型：在静止预混燃气中,位于球心处的点火能量 $Q$ (类似于电火花点火) 引发球形火焰向外传播.由于点火能及拉伸率的作用,球形火焰传播速度 $U$ 和火焰温度 $T_{\rm f}$ 均会随着火焰半径 $R$ 而变化.理论研究的目标就是获得不同点火能、不同热损失以及不同Lewis 数下,$U$ 随着 $R$ 变化的解析表达式,并在此基础上确定临界点火条件 [54].
显示原图|下载原图ZIP|生成PPT图7球形传播火焰示意图
-->Fig.7Schematic flame structure of spherically propagating flames
-->
将坐标系固定在火焰面上,则火焰以准稳态方式向外传播.同时引入常密度和常热力学参数假设,则无量纲化的温度方程和组分方程为 (具体推导见文献[54])
$$- U\frac{{\rm d}T}{{\rm d}r} = \frac{1}{r^2}\frac{{\rm d}}{{\rm d}r}\left(r^2\frac{{\rm d}T}{{\rm d}r}\right) - h \cdot T+ \omega (48)$$$$- U\frac{{\rm d}Y}{{\rm d}r} = \frac{Le^{ - 1}}{r^2}\frac{{\rm d}}{{\rm d}r}\left(r^2\frac{{\rm d}Y}{{\rm d}r}\right) -\omega (49)$$
其中,$T$ 为归一化无量纲温度,即对于未燃预混气体有 $T=0$,而绝热燃烧温度则对应 $T=1$.球形传播火焰速度 $U$ 则是通过绝热平面火焰速度进行无量纲化.长度和坐标 $r$ 则通过绝热平面火焰厚度进行无量纲化. $\omega$ 为无量纲化学反应速率,$h$ 为无量纲热损失强度 $^{[54]})$.相应的边界条件为
$$r = 0: r^2{\rm d}T / {\rm d}r = - Q,\quad Y = 0 (50)$$$$r = \infty :\quad T = 0, \quad Y = 1 (51)$$
其中 $Q$ 为无量纲化点火能 [54].在单步总包化学反应的活化能很大时,化学反应主要集中在火焰面附近的反应区,且反应区的厚度远小于预热区厚度及火焰半径.类似于平面预混火焰,对方程 (48) 和 (49) 描述的准稳态球形传播火焰也可以采用大活化能渐近分析.
首先对一维绝热球形传播预混火焰进行大活化能渐近分析. 在理论分析中,采用常用的常密度 (即忽略热膨胀) 假设 [10-12,43,53-54] 以及常热物性参数与输运系数假设.在球坐标系中,关于温度 $T$ 和燃料质量百分数 $Y$ 的控制方程为
$$\rho C_P \frac{{\rm d}T}{{\rm d}t} = \frac{\lambda }{r^2}\frac{{\rm d}}{{\rm d}r}\left(r^2\frac{{\rm d}T}{{\rm d}r}\right) +q\omega (52)$$
$$\rho \frac{{\rm d}Y}{{\rm d}t} = \frac{\rho D}{r^2}\frac{{\rm d}}{{\rm d}r}\left(r^2\frac{{\rm d}Y}{{\rm d}r}\right) - \omega (53)$$
其中,$r$ 为空间坐标,$\rho$ 为密度,$C_{P}$ 为混合物的等压比热容,$\lambda$ 为热传导系数,$q$ 为燃烧单位质量燃料的放热量,$D$ 为燃料的质量扩散系数.由于常密度模型忽略了热膨胀,所以在控制方程里面没有对流项. 化学反应速率由式 (3) 给出.
为了简化分析过程,采用固定在火焰面 $r=R(t)$ 上的坐标系 ($\tau $, $\xi$). 在这个新坐标系 ($\tau =t$, $\xi=r-R(t))$ 中,火焰可以被看成准稳定状态,即 $\partial /\partial \tau=0$. 准稳态假设的合理性已经被数值模拟所验证 [12].在准稳态假设下,位于新坐标系中的控制方程被简化为
$$ - \rho C_PU\frac{\mbox{d}T}{\mbox{d}\xi } = \frac{\lambda }{(\xi +R)^2}\frac{\mbox{d}}{\mbox{d}\xi }\left[(\xi +R)^2\frac{\mbox{d}T}{\mbox{d}\xi }\right] + q\omega (54)$$
$$ -\rho U\frac{\mbox{d}Y}{\mbox{d}\xi } = \frac{\rho D}{(\xi +R)^2}\frac{\mbox{d}}{\mbox{d}\xi }\left[(\xi +R)^2\frac{\mbox{d}Y}{\mbox{d}\xi }\right] - \omega (55) $$
其中 $U={\rm d}R(t)/{\rm d}t$ 是火焰传播速度. 对应边界条件为
$$\xi = -R, \quad \mbox{d}T / \mbox{d}\xi = 0, \quad \mbox{d}Y /\mbox{d}\xi = 0 (56)$$$$\xi \to + \infty , \quad T = T_u , \quad Y = Y_u (57)$$
类似于平面火焰的理论分析,将球形火焰结构分为预热区、化学反应区和平衡区. 在活化能较大时,化学反应对温度非常敏感,可以认为反应只在化学反应区内进行.化学反应区和预热区的厚度比是个小量 $\varepsilon$,即 Zel'dovich 数的倒数. 与平面火焰的渐近理论分析过程类似,分别对 3 个区域求出渐近解,接着由连续性匹配得到最终的结果.以下简要给出渐进理论分析结果,详细推导可参阅文献[67].
在预热区可忽略化学反应,温度和燃料质量百分数在预热区的解为
$$T^ +(\xi ) = T_{\rm u} + C_1 \int_{R + \xi }^\infty {s^{ - 2}{\rm e}^{- Us / \alpha }{\rm d}s} + \varepsilon \cdot C_2 \int_{R + \xi}^\infty {s^{ - 2}{\rm e}^{ - Us / \alpha }{\rm d}s} (58)$$
$$Y^+ (\xi ) = Y_{\rm u} + C_3 \int_{R + \xi }^\infty {s^{ - 2}{\rm e}^{ - Us / D}{\rm d}s} + \varepsilon \cdot C_4 \int_{R + \xi}^\infty {s^{ - 2}{\rm e}^{ - Us / D}{\rm d}s} (59)$$
其中,$C_{1}$,$C_{2}$,$C_{3}$,$C_{4}$ 是待定积分常数,可以通过和反应区解的连续性匹配得到.
燃料在反应区被完全消耗掉. 因此在平衡区 $(-R<\xi <0)$ 的解为
$$T^ -(\xi ) = T_{\rm b}, \quad Y^ - (\xi ) = 0 (60)$$
其中 $T_{\rm b}$ 是已燃气体的温度,将通过匹配条件确定.
对于化学反应区,引入坐标变换 $X=\xi /\varepsilon$ 将空间坐标进行拉伸. 化学反应区的渐近解可以表示为
$$T_{\rm in} (X) =\theta _0 - \varepsilon \theta _1 (X) + O(\varepsilon ^2) (61)$$
$$Y_{\rm in} (X) = \phi _0 + \varepsilon \phi _1 (X) + O(\varepsilon^2) (62)$$
其中,$\theta_{0}$ 和 $\phi _{0}$ 是零阶项,而 $\theta_{1}(X)$ 和 $\phi _{1}(X)$ 是一阶扰动项的大小.类似于平面火焰的渐近理论分析,通过内部解和外部解在交界面处的匹配条件可得
$$\theta _0 - T_{\rm b} = \phi _0 = 0, \quad \theta _1 ( - \infty ) =\phi _1 ( - \infty ) = 0 (63)$$$${\rm d}\theta _1 ( - \infty ) / {\rm d}X = {\rm d}\phi _1 ( -\infty ) / {\rm d}X = 0 (64)$$$$\left.{\begin{array}{l}C_1 = (T_{\rm b} - T_{\rm u}) /\int_R^\infty {s^{ - 2}{\rm e}^{ - Us / \alpha }{\rm d}s},\\[3mm]C_3 = - Y_{\rm u} / \int_R^\infty {s^{ - 2}{\rm e}^{ - Us /D}{\rm d}s}\end{array}}\right\} (65)$$
$$\theta _1 ( + \infty ) \to + \infty ,\quad \phi _1 ( + \infty ) \to + \infty (66)$$$$\left.{\begin{array}{l}\dfrac{{\rm d}\theta _1 ( + \infty)}{{\rm d}X} = \dfrac{(T_{\rm b} - T_{\rm u} )R^{ - 2}{\rm e}^{ -UR /\alpha }}{\int_R^\infty {s^{ - 2}{\rm e}^{ -Us/\alpha}{\rm d}s}}\\[7mm]\dfrac{{\rm d}\phi _1 ( + \infty )}{{\rm d}X} = \dfrac{Y_u R^{ -2}{\rm e}^{ - UR / D}}{\int_R^\infty {s^{ - 2}{\rm e}^{ - Us /D}{\rm d}s} }\end{array}}\right\} (67)$$
球形火焰与平面火焰在化学反应区中渐近求解过程相同,可以推导出以下关系式 [67]
$$\frac{\lambda}{q}\frac{{\rm d}^2\theta_1}{{\rm d}X^2}=\rho D\frac{{\rm d}^2\phi_1}{{\rm d}X^2} (68)$$$$\frac{{\rm d}^2\theta _1 }{{\rm d}X^2} = D_{\rm a} \theta _1 \exp\left( - \frac{\varepsilon E_{\rm a} }{R^0T_{\rm b}^2 }\theta _1\right) (69)$$dl
将匹配关系 (63)$\sim$(67) 代入上述方程可以得到关于火焰温度 $T_{\rm b}$、火焰传播速度 $U$ 及火焰半径 $R$ 的方程\linebreak 组 [67]
$$T_{\rm b}=T_{\rm u}+\frac{qY_{\rm u}}{C_P}\frac{1}{Le}{\rm e}^{\frac{UR}{\alpha}(1-Le)}\frac{\int_R^\infty s^{-2}{\rm e}^{-Us/\alpha}{\rm d}s}{ \int^\infty_Rs^{-2}{\rm e}^{-Us/D}{\rm d}s} (70)$$
$$\frac{R^{ - 2}{\rm e}^{ - UR / \alpha }}{\int_R^\infty {s^{ - 2}{\rm e}^{ -Us / \alpha }{\rm d}s} } = \sqrt {\dfrac{2}{\beta^2}\dfrac{A}{D}\exp \left( - \dfrac{E_{\rm a} }{R^0T_{\rm b}}\right)} (71) $$
通过数值求解方程组 (70) 和 (71),可以得到球形火焰传播过程中火焰传播速度 $U$ 和火焰温度 $T_{\rm b}$ 随着火焰半径 $R$ 的变化 [67].
上述分析可以进而推广到考虑热损失和点火能对球形传播火焰的影响. 通过渐近理论分析可以得到在不同点火能 $Q$、不同热损失 $h$ 以及不同~Lewis 数 $Le$ 下,球形火焰传播速度 $U$ 随着火焰半径 $R$ 变化的解析表达式 [54,67].以下关系为热损失强度为零时 ($h=0$,即绝热火焰) 的特殊形式 [54,67]
$$T_b \frac{R^{ - 2}{\rm e}^{ - UR}}{\int_R^\infty {s^{ -2}{\rm e}^{ - Us}{\rm d}s} } - Q \cdot R^{ - 2}{\rm e}^{ - UR} =\frac{1}{Le}\frac{R^{ - 2}{\rm e}^{ -ULeR}}{\int_R^\infty {s^{ - 2}{\rm e}^{ - ULes}{\rm d}s} } = \\ \qquad [\sigma + (1 - \sigma )T_{\rm b} ]^2\exp \left(\frac{\beta}{2}\frac{T_{\rm f} - 1}{\sigma + (1 - \sigma )T_{\rm b}}\right) (72)$$
当温度比 $\sigma $、Zel'dovich 数 $\beta$、Lewis 数 $Le$、点火能 $Q$ 以及热损失强度 $h$ 给定时,通过数值求解上式就可以得到球形火焰传播过程中火焰传播速度 $U$ 和火焰温度 $T_{\rm b}$ 随着火焰半径 $R$ 的变化.图8 给出了在无点火能 ($Q=0$) 时,不同热损失下球形火焰传播速度随着火焰半径的变化曲线.$h=0$ 对应于绝热情况,在火焰半径很大时趋于平面火焰,因此其无量纲传播速度趋于 1.在热损失强度为 $h=0.01$ 时,存在两支 $U-R$ 曲线,其中上支 $U-R$ 曲线为快速火焰,在实验中可以被观察到的;而下支 $U-R$ 曲线是慢速火焰,是不稳定的,不可能出现在实验中.这与图5 中关于平面火焰的结论一致.但继续增大热损失强度到 $h=0.025$ 和 0.05,球形传播火焰在达到一定半径后会熄火,这对应于微重力实验中观察到的自熄火火焰 (self-extinguishingflame) [68-69].其原因是拉伸率强化火焰而辐射热损失弱化火焰,在火焰半径较大时辐射热损失的影响占主导,从而导致火焰在半径达到一定数值时出现熄火.图8 中 $U=0$ 对应于静止火焰球 [5,49 -51] 的解,而 $R=1000$ 则对应于曲率趋于零的球形火焰 (接近于平面火焰).因此,该理论能够完整地描述从火焰球到球形传播火焰转变的整个过程,从而能够被用来准确地预测临界点火条件.
显示原图|下载原图ZIP|生成PPT图8不同热损失下球形火焰传播速度随着火焰半径的变化 ($Le=0.8$) [
-->Fig.8Change of spherical flame propagation speed with flame radius for $Le=0.8$ and different values of heat loss intensities [
-->
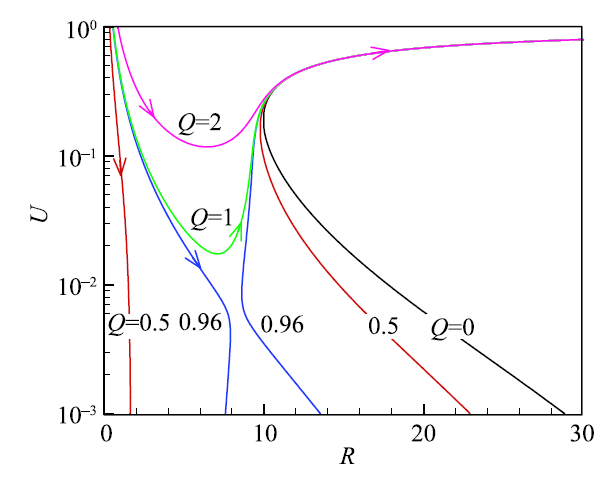
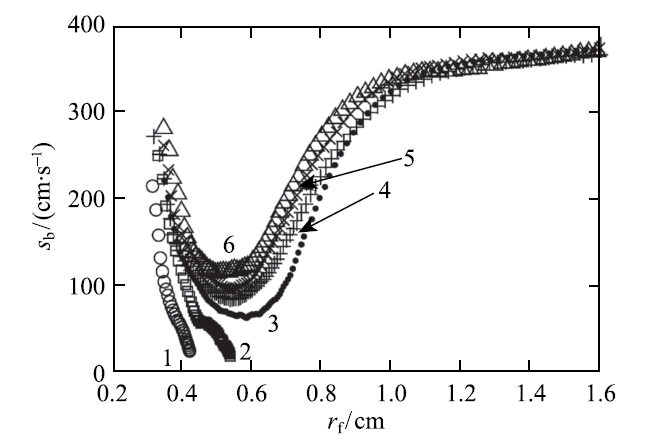
图9为基于上述理论得出的不同点火能下球形火焰传播速度随着火焰半径的变化曲线.当点火能为零时 ($Q=0$),最小的无量纲火焰半径为 $R=9$,当 $R<9$ 时则不存在球形传播火焰解.当 $Q=0.5$ 时,则出现左右两支 $U-R$ 解,左边的 $U-R$ 解对应点火核从中心传播出来后会逐渐减速,在 $R=2$ 附近出现熄火,因此点火失败.增大点火能到 $Q=0.96$ 时,点火核传播到 $R=8$ 附近仍会熄灭,同样是点火熄灭.继续增大点火能到 $Q=1$ 时,左右两支 $U-R$ 解合并到一起,点火核可以沿着合并后的 $U-R$ 解持续不断地向外传播,因此点火成功.左右两支 $U-R$ 解合并到一起时对应的点火能被称为最小点火能,此时火焰传播速度最小值对应的半径被称为临近点火半径 [54-55].对于图9 所示的结果,无量纲最小点火能和临界点火半径分别为 1 和 8.图10 展示了~Kelley 等 [56] 在氢气/空气中开展电火花点火实验的结果.图10 中的曲线 1 和 2 对应点火能量较小的工况,点火核在向外传播时其速度逐渐下降直至发生熄火,这与图9 中 $Q=0.5$ 和 0.96 的理论结果一致.但点火能较大时,图10 中的曲线 3 至 6 表明点火核先减速后加速,能够顺利传播出去,点火成功.这也与图9 中 $Q=1$ 和 2 的理论结果一致.因此,实验结果说明该理论可以用来描述点火过程.
显示原图|下载原图ZIP|生成PPT图9不同点火能下球形火焰传播速度随着火焰半径的变化($Le=2$) [
-->Fig.9Change of spherical flame propagation speed with flame radius for Le=0.8 and different ignition powers [
-->
显示原图|下载原图ZIP|生成PPT图10不同点火能下,当量比为 5.1 的氢气/空气中的球形火焰传播速度随着火焰半径的变化情况 [
-->Fig.10Change of spherical flame propagation speed with flame radius for different ignition energies deposited into hydrogen/air mixture with the equivalence ratio of 5.1 [
-->
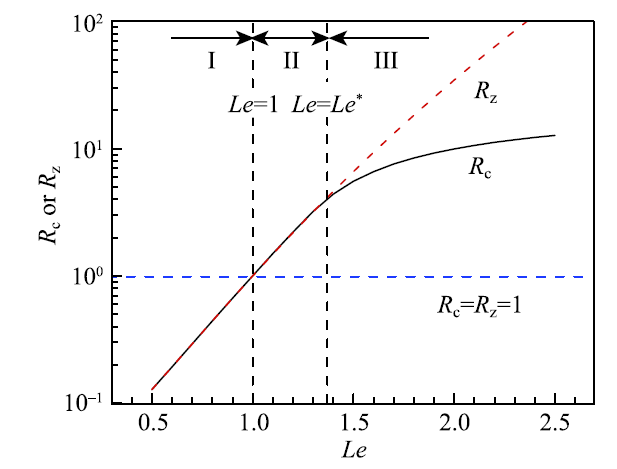
传统点火理论 [5,48-51] 认为火焰厚度、熄火距离或者静止火焰球半径是控制点火的特征长度.图11 给出了不同 Lewis 数下的临界点火半径与火焰球半径.这两个半径都是基于火焰厚度来无量纲化的.可以看出,只有在 Lewis 数等于 1 时,临界点火半径才等于火焰厚度.在图示的 I 区和 II 区,临界点火半径等于火焰球半径,因此火焰球是控制点火的特征尺度.但在 Lewis 数较大的 III 区,临界点火半径小于火焰球半径,而且随着~Lewis 数增大,两者的差别会急剧增加.由于 Lewis 数是热传导率与质量扩散率的比值,燃料的输运特性 (热传导和质量扩散) 在很大程度上决定了初始火焰的传播,是控制点火的关键因素.对于不同的燃料,其输运特性差别很大,所以初始火焰传播状况完全不同.另外,理论表明,最小点火能正比于临界点火半径的立方,这与数值模拟和实验结果一致 [55].
显示原图|下载原图ZIP|生成PPT图11临界点火半径 $R_{C}$ 与火焰球半径 $R_{Z}$ 随着~Lewis 数的变化 [
-->Fig.11Change of the critical ignition radius and the flame ball radius with the Lewis number [
-->
上述点火与球形火焰传播理论除了被用于解释临界点火条件外,还被应用于测量层流火焰速度的球形传播方法中.
在等压球形传播火焰法测量层流火焰速度时,需要采用线性或者非线性模型来外推得到零拉伸率下的层流火焰速度.
根据式 (52) 可以推导出以下线性和非线性模型关系式
$$S_{\rm b} = S_{\rm b}^0 - L_{\rm b}(2S_{\rm b} / R_{\rm f} ) (73)$$$$S_{\rm b} / S_{\rm b}^0 = 1 - 2L_{\rm b} R_{\rm f} (74)$$$$(S_{\rm b} / S_{\rm b}^0 )\ln (S_{\rm b} / S_{\rm b}^0 ) = -L_{\rm b} (2S_{\rm b} / R_{\rm f} ) (75)$$
其中 $R_{\rm f}$ 为火焰半径,$S_{\rm b}$ 和 $S_{\rm b}^{0}$ 为相对于已燃气体的层流火焰速度,$L_{\rm b}$ 为相对于已燃气体的~Markstein 长度. 相关文献[70,71,72,73,74]研究了采用不同线性和非线性模型对层流火焰速度测量精度的影响.式 (73)$\sim$ 式 (75) 对应的模型都具有一阶精度,但这些模型在不同~Lewis 数下的误差互不相同 [70].为了降低采用这些模型拟合带来的误差,需要尽可能使得预混气体的 Lewis 数接近于 1[72].
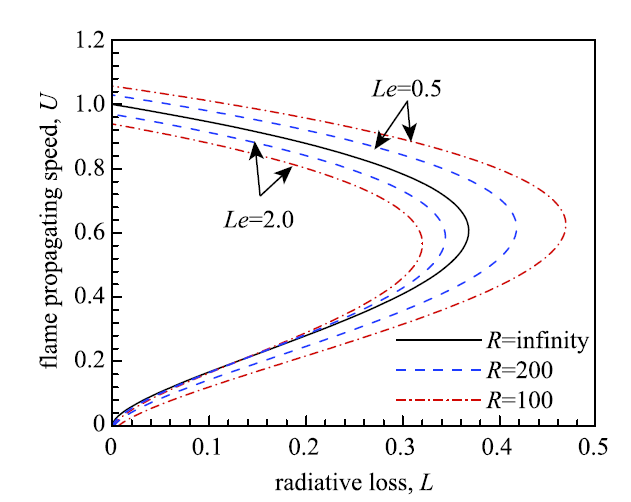
另外,通过渐近理论分析和数值模拟,系统地研究了热辐射对近可燃极限预混气体球形火焰传播过程的影响 [75].首先,建立了考虑热辐射的球形火焰传播理论,揭示了热辐射强度对火焰传播速度的影响.通过理论分析,获得了火焰传播速度与火焰温度随火焰半径变化的解析表达式,进而研究了不同强度的辐射热损失对不同燃料球形火焰的传播速度的影响.研究结果表明,热辐射对火焰传播速度的影响程度与燃料的 Lewis 数以及火焰曲率有关 [75].图12 表明热辐射对平面火焰传播速度的影响跟~Lewis 数无关,但对于具有一定曲率/拉伸率的球形传播火焰,热辐射的影响跟 Lewis 数相关.相同曲率下,Lewis 数越大,则热辐射导致的可燃极限越低.对于同一 Lewis 数,$Le=2$ 时曲率越大则可燃极限越低,而在 $Le=0.5$ 时曲率越大则可燃极限越高.这是由于曲率/拉伸率与 Lewis 数的耦合作用导致的.
显示原图|下载原图ZIP|生成PPT图12不同火焰半径及~Lewis 数下,火焰传播速度随着辐射热损失的变化[
-->Fig.12Change of flame propagating speed with radiative loss for different flame radii and Lewis number [
-->
结合理论分析和数值模拟,研究了辐射热损失和辐射重吸收对球形火焰传播过程的影响,量化了热辐射导致的热效应及流动效应对层流火焰速度测量的影响 [63],提出了适用于不同碳氢燃料的定量表征热辐射影响的经验公式 [76],使用该经验公式可以直接修正球形传播火焰法测量层流火焰速度过程中热辐射导致的误差.另外,发现了辐射重吸收会很大程度地减弱辐射冷却导致的流动效应,从而使得球形传播火焰速度几乎不受热辐射的影响 [77-78].
2.3 考虑链式反应的点火与球形传播火焰理论
经典的点火理论分析均基于单步化学反应,因此只能反映燃料Lewis 数对预混气体点火的影响.然而,实际碳氢燃料的点火过程中会涉及燃料和基元组分的多步化学反应.因此,点火与火焰传播情况不仅受到燃料质量扩散的影响,还与其他基元组分 (特别是与链支化反应有关的自由基) 的质量扩散情况有关.图13 为单步总包反应与两步反应模型对应的火焰结构示意图.对于单步总包反应,燃料直接转化为产物并同时释放出热量.对于两步反应模型,首先通过链起始反应和链支化反应生成自由基,然后自由基被链终止反应消耗掉并同时释放出热量.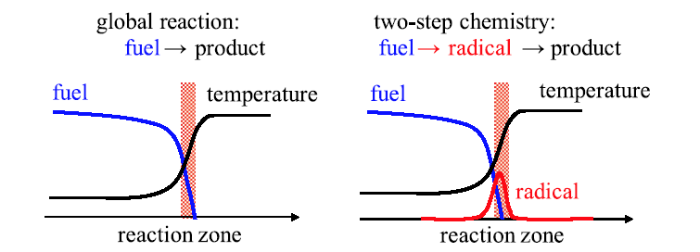
显示原图|下载原图ZIP|生成PPT图13单步总包反应与两步反应模型对应的火焰结构示意图
-->Fig.13Schematic flame structures based on one-step global chemistry and two-step chemistry
-->
为了能够揭示自由基的输运特性对点火与火焰传播过程的影响,在理论分析中采用改进后的~Zel'dovich-Li {n}án 两步反应模型 [79-80]
$$\mbox{F} + \mbox{Z} \to \mbox{2Z} (76)$$$$\mbox{Z} + \mbox{M} \to \mbox{P} + \mbox{M} (77)$$
其中,F 代表燃料,P 为产物,Z 为自由基,M 为任何类型的第三体组分.第一步反应为关于自由基的链支化反应,假定该反应不吸收和释放热量,反应速率满足~Arrhenius 公式.第二步反应为链终止反应,该反应将自由基中的化学能全部转化为热量,假设该反应的反应速率不随温度变化 (即其活化能为零).上述两步反应模型被广泛应用于预混火焰的理论分析中 $^{[79 - 89]}$.
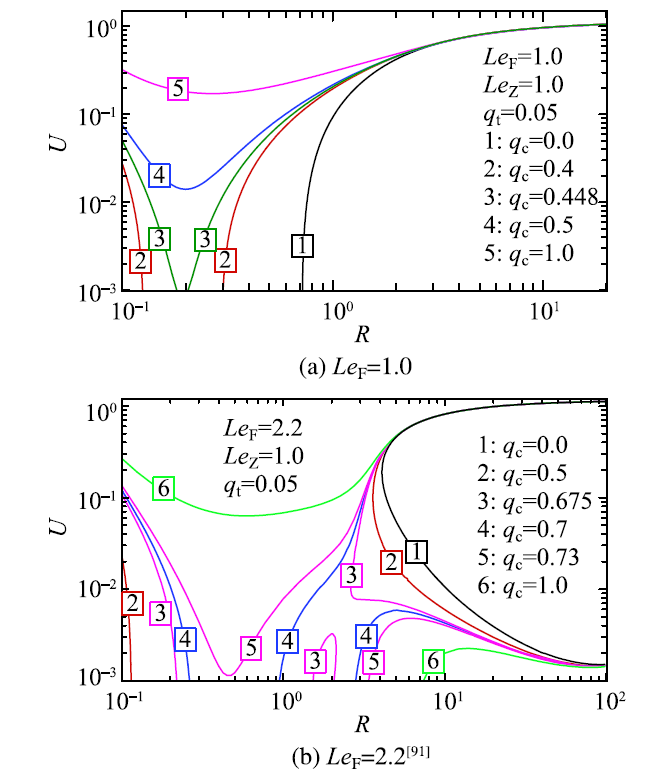
同样考虑类似于图7 的点火与球形传播火焰模型,假设链支化反应的活化能很大,通过渐近理论分析可以建立基于两步反应模型的点火与火焰传播理论 [90].大活化能渐近理论分析的具体过程在此不再重复,详细推导见文献[90].在此基础上,研究了热点火过程、化学点火过程以及两者间的差异 [91].图14 为基于两步反应的点火与火焰传播理论预测结果.通过与图9 中基于单步反应的理论结果进行对比,可以发现在 Lewis 等于 1 时,两者的结果是相似的.但在 Lewis 数较大时,图14(b) 中曲线 4 表明会出现三支 $U-R$ 解.因此基于单步反应的热点火与基于两步反应的化学点火在特定条件下存在着差异 [91].
显示原图|下载原图ZIP|生成PPT图14不同点火能下球形火焰传播速度随着火焰半径的变化
-->Fig.14Change of spherical flame propagation speed with flame radius
-->
对于热点火,研究结果表明最小点火能和临界点火半径随着燃料 Lewis 数的增大而增大,而随着自由基~Lewis 数的增大而减小.这是因为大 Lewis 数自由基具有低质量扩散特性,对点火具有促进作用.对于化学点火,基于火焰球半径随相关参数的变化特性和临界点火条件,可以将化学点火机理分为 3 种情况 [91]：(1) 火焰球解随着化学点火能的增加而逐渐减小,临界点火条件为火焰传播曲线过 ($U$,$R)$ 平面的原点;(2) 当化学点火能逐渐增大时,火焰球解的个数分别为零、二个和一个,临界点火条件为 $U-R$ 图中的 C 形曲线和钟形曲线相交;(3) 当化学点火能较小时无火焰球解,而当化学点火能超过某一值时则有一个火焰球解,临界点火状态为 C 形曲线和火焰核分支曲线相交.研究还发现：化学点火和热点火在火焰核分支的产生、临界点火条件与火焰半径较小时的火焰传播曲线均存在显著差异.同时,我们开展了基于详细化学反应机理的直接数值模拟,其结果验证了理论分析结论的正确性 [91].
2.4 关于球形传播火焰的其他理论研究
以往的点火与球形传播火焰理论只考虑气相燃烧,而航空发动机高空再点火则发生在气液两相燃气中.建立了考虑有限速率液滴蒸发的点火与火焰传播理论模型,并通过渐近理论分析获得了描述火焰核传播与临界点火条件的解析表达式 [92].在此基础上,分析了液滴蒸发速率对临界点火半径、最小点火能量、火焰传播速度以及 Markstein 长度的影响规律及机制,解释了高空条件下航空煤油在贫燃料工况下难以点火的现象 [92].另外,还揭示了有限速率液滴蒸发对熄火过程的影响 [93].但本文理论分析对液滴蒸发进行了简化处理,没有考虑单个液滴表面由于蒸发引起的 Stefan 流.上述理论分析表明,在点火与球形火焰传播过程中,各个组分的质量扩散具有十分重要的作用.通常由浓度梯度引起的 Fick 扩散是占主导地位的,而由温度梯度引起的 Soret 扩散则相对较小 [12].因此,在理论分析和数值模拟中,通常只考虑 Fick 扩散而忽略 Soret 扩散.但对于氢气或大分子碳氢燃料的层流燃烧过程,当存在较大温度梯度时,Soret扩散的影响不可忽略 [94].建立了考虑~Soret 扩散的点火与球形传播火焰模型,通过大活化能渐近分析获得了相应的解析解 [95].在此基础上,研究了 Soret 扩散对点火与球形火焰传播的影响 [95],发现~Soret 扩散会降低轻质燃料的最小点火能而增加大分子燃料的最小点火能.对于具有拉伸率的球形传播火焰,Soret 扩散会与 Lewis 数以及当量比相结合来改变火焰燃烧强度.对于轻质燃料,Soret 扩散会增加贫燃火焰的强度和降低富燃火焰的强度;而对于大分子燃料,Soret 扩散的作用正好相反 [95].
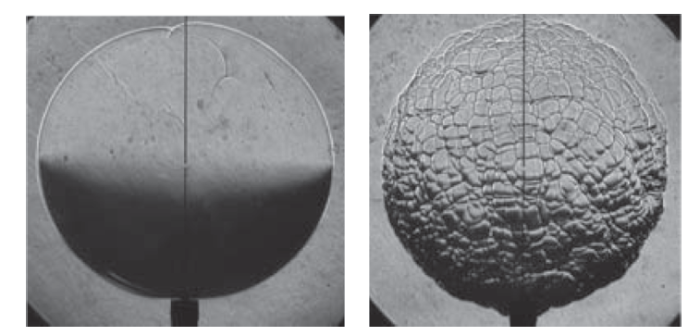
类似于平面火焰,球形传播火焰也会受到热{--}扩散不稳定性、流体动力学不稳定性以及振荡不稳定性的影响.Bechtold 和 Matalon [96]对球形传播火焰开展了线性稳定性分析,获得了扰动增长率随着扰动波长变化的解析表达式.他们 [97-98] 还基于大活化能渐近分析获得表征热{--}扩散不稳定性的 Markstein 数的解析表达式.球形火焰的正拉伸率会使得火焰趋于稳定 [12,25],因此在火焰半径较小时 (对应拉伸率较大),球形火焰面是光滑的.而在火焰半径较大时,火焰可能同时受到热{--}扩散不稳定性和流体动力学不稳定性的作用.热{--}扩散不稳定性在 Lewis 数小于 1 时起作用.而流体动力学不稳定性则跟火焰面前后的密度差别和火焰厚度有关.环境压强越高,火焰越薄,则流体动力学不稳定性越强.图15 为丙烷/空气球形传播火焰的纹影图像 [99].在当量比为 0.8 时,预混气体的~Lewis 数大于 1,因此球形传播火焰是稳定的,火焰面为光滑的球形.而在当量比为 1.4 时,预混气体的 Lewis 数小于 1,球形火焰由于受到热{--}扩散不稳定性的作用而呈现胞状结构.
显示原图|下载原图ZIP|生成PPT图15丙烷/空气球形传播火焰的纹影图像,火焰半径为 2.5 cm,环境压强为 5 atm (左图当量比为 0.8,右图当量比为 1.4) [
-->Fig.15Schlieren images of spherical propagating flames in C$_{3}$H$_{8}$/air mixtures at 5 atm. The flame radius is 2.5 cm (The equivalence ratio is 0.8 and 1.4 respectively for the left and right images) [
-->
热{--}扩散不稳定性和流体动力学不稳定性均会导致火焰加速传播,近年来关于球形火焰加速传播及其向爆轰转变是球形传播火焰的研究热点 [100-106]. Bradley 等 [100] 开展了半径达到 4m 的大尺度球形传播火焰实验,发现火焰加速传播过程可以用以下关系式描述
$$S = 773.9 \times \frac{3}{2} \left( {\frac{R_{\rm f} -0.91}{773.9}} \right)^{1 / 3} (78)$$
其中火焰半径 $R_{\rm f}$ 的单位为~cm,火焰传播速度 $S$ 的单位为 cm/s.上式积分之后则得到火焰半径 $R_{\rm f}$ 随着时间 $t$ 呈幂指数增长的形式
$$R_{\rm f} = 0.91 + 773.9t^{3 / 2} (79)$$
通常,球形火焰的加速传播过程可用 Gostintsev等 [107] 首次提出的幂律模型来描述
$$R_{\rm f} = R_{\rm f0} + At^\alpha (80)$$
其中 $A$ 是常系数,$\alpha$ 是加速指数.这两个参数均依赖于预混气体的种类 [108].火焰加速出现在火焰半径为 $R_{\rm f0}$,并从火焰加速出现时开始计时 (即 $t=0$ 时 $R_{\rm f}=R_{\rm f0})$.通常假设加速指数为常数,因而有
$$S = \frac{{\rm d}R_{\rm f} }{{\rm d}t} = \alpha A^{\frac{1}{\alpha }}(R_{\rm f} - R_{\rm f0} )^{1 -\frac{1}{\alpha }} (81)$$
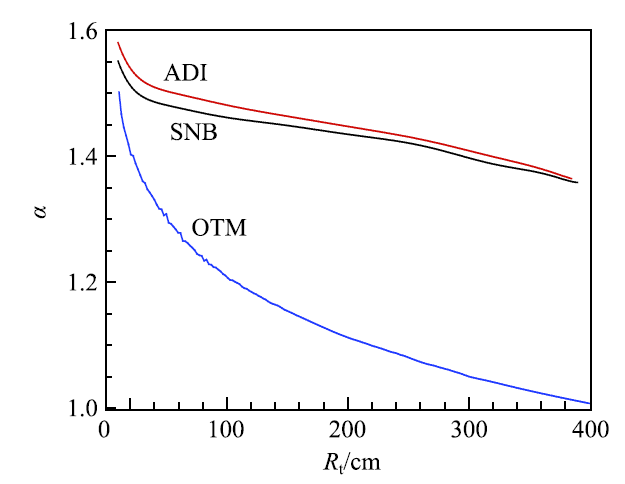
图16给出了通过数值模拟 [78] 得到的火焰加速指数随着火焰半径的变化情况.其中 ADI、OTM 及 SNB 分别代表绝热情况、只考虑辐射热损失、以及同时考虑辐射热损失与辐射重吸收.图示结果表明,在只考虑辐射热损失时,加速指数会随着火焰半径的增大而迅速衰减,这与实验结果 [100] 不吻合.因此在研究火焰加速传播时,需要考虑辐射重吸收对火焰传播的影响.
显示原图|下载原图ZIP|生成PPT图16火焰加速指数随着火焰半径的变化情况 [
-->Fig.16Change of the acceleration exponent with flame radius for unstable spherical flame [
-->
上述内容主要介绍了大活化能渐近分析在一维平面预混火焰和球形传播火焰中的应用及相关研究进展.大活化能渐近分析在扩散火焰、部分预混火焰、自着火及缓燃转爆轰、以及其他形式的预混火焰 (如对冲预混火焰、管道中预混火焰传播、本森灯火焰等) 也有着广泛应用,相关研究进展可参考相关综述文章 [24-25,27-30, 109-111]和专著 [10-13].
3 总结与展望
大活化能渐近分析在燃烧理论中有着广泛的应用.囿于篇幅和作者的学识,本文只介绍了大活化能渐近分析在一维平面预混火焰和球形传播火焰中的应用.对于一维平面预混火焰,通过大活化能渐近分析可以获得层流火焰速度及可燃极限的解析表达式,进而可以解释影响层流火焰速度及可燃极限的各种因素.对于球形传播火焰,通过大活化能渐近分析可以发展点火与球形传播火焰理论,该理论可以完整地描述从火焰球到球形传播火焰转变的整个过程.基于该理论,可以揭示 Lewis 数和自由基输运特性对临界点火条件与球形火焰传播的影响规律.另外,对于平面火焰和球形传播火焰,可以采用大活化能渐近分析获得预混气体的临界失稳条件.虽然大活化能渐近分析在平面预混火焰和球形传播火焰的研究中得到了广泛的应用,但作者认为还有以下几个方面的亟待进一步研究:
(1) 虽然部分研究中考虑了关于自由基的链支化与链终止反应,但实际燃烧过程中的化学反应过程极为复杂.为了揭示化学反应影响点火、火焰传播及熄火过程的规律和机制,需要在大活化能渐近分析考虑更复杂的化学反应机理.目前可行的方法为反应速率比值渐近分析方法 (rate-ratio asymptotic analysis) [112-113].但由于其远比大活化能渐近分析更为复杂,反应速率比值渐近分析方法很少被应用在球形传播火焰的理论研究中.
(2) 近年来,低温化学反应及其引发的冷火焰受到了广泛的关注 [114-116].目前关于预混冷火焰的研究还只能通过数值模拟和实验,尚缺乏关于预混冷火焰形成、传播和熄灭的大活化能渐近分析.其中的难点在于,需要发展能够准确地描述低温化学反应,并适用于渐近理论分析的简化反应模型.
(3) 本文讨论的点火与球形火焰传播均发生在原先静止的气体中,而在实际燃烧过程中,环境气体是流动.流动会导致自由基不易累积起来,从而会增大最小点火能.因此需要采用大活化能渐近分析,研究流动对点火与球形传播火焰的影响.
(4) 在关于有辐射热损失的预混火焰的大活化能渐近分析中,通常只考虑热辐射导致的热损失,而忽略辐射重吸收的影响.在富含二氧化碳稀释的预混气体中,二氧化碳辐射重吸收对火焰的强化作用通常是不可忽略的 [77,117].因此对该类预混燃气的平面火焰及球形传播火焰,在采用大活化能渐近分析时,需要同时考虑热辐射导致的热损失和辐射重吸收导致的加热效应.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | . |
| [34] | . |
| [35] | . |
| [36] | . |
| [37] | . |
| [38] | . |
| [39] | . |
| [40] | . |
| [41] | . |
| [42] | . |
| [43] | . |
| [44] | . |
| [45] | . |
| [46] | . |
| [47] | . |
| [48] | |
| [49] | . |
| [50] | . |
| [51] | . |
| [52] | . |
| [53] | . |
| [54] | . |
| [55] | . |
| [56] | . |
| [57] | . |
| [58] | . |
| [59] | . |
| [60] | . |
| [61] | . |
| [62] | . |
| [63] | . |
| [64] | . |
| [65] | . |
| [66] | . |
| [67] | . |
| [68] | . |
| [69] | . |
| [70] | . |
| [71] | . |
| [72] | . |
| [73] | . |
| [74] | . |
| [75] | . |
| [76] | . |
| [77] | . |
| [78] | . |
| [79] | . |
| [80] | . |
| [81] | . |
| [82] | . |
| [83] | . |
| [84] | . |
| [85] | . |
| [86] | . |
| [87] | . |
| [88] | . |
| [89] | . |
| [90] | . |
| [91] | . |
| [92] | . |
| [93] | . |
| [94] | . |
| [95] | . |
| [96] | . |
| [97] | . |
| [98] | . |
| [99] | . |
| [100] | . |
| [101] | . |
| [102] | . |
| [103] | . |
| [104] | . |
| [105] | . |
| [106] | . |
| [107] | . |
| [108] | |
| [109] | . |
| [110] | . |
| [111] | . |
| [112] | . |
| [113] | . |
| [114] | . |
| [115] | . |
| [116] | . |
| [117] | . |
