, 陈立EXPERIMENTAL STUDY OF DYNAMIC AERODYNAMIC SWEPT EFFECT ON YAW OSCILLATING AIRFOIL1)
LiGuoqiang, ChenLi中图分类号:O355
文献标识码:A
通讯作者:
收稿日期:2018-06-4
网络出版日期:2018-09-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (23563KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
风电机组近年来从兆瓦级别发展到多兆瓦级, 超大型化叶片的重量随着叶轮直径增加而成立方关系地急剧上升[1]. 大型风力机实际运动过程很复杂, 叶片或翼型常常工作在动态失速状态下, 动态失速是一个严重的非线性、非定常气动现象[2], 目前还缺乏对非定常失速气动特性的深刻理解, 无法全面准确描述动态失速现象和规律[3]. 动态振荡过程往往伴随着俯仰(迎角$\alpha$周期性变化)和横摆(后掠角/横摆角$\beta$周期性变化)同时进行[4], 如图1所示, 俯仰振荡会造成风力机实际极限载荷高于设计和计算值, 而横摆运动多数时候可能会减小极限载荷. 以前对许多动态问题不清楚的阶段, 工程上不惜以增加叶片结构重量为代价而采用偏安全的设计, 所以通常忽略横摆振荡的影响, 国内外关于翼型动态特性的研究主要集中在俯仰振荡方面. 为了提高叶片性能、降低结构冗余设计量, 气动载荷评估应该更加精确, 以降低叶片重量和成本.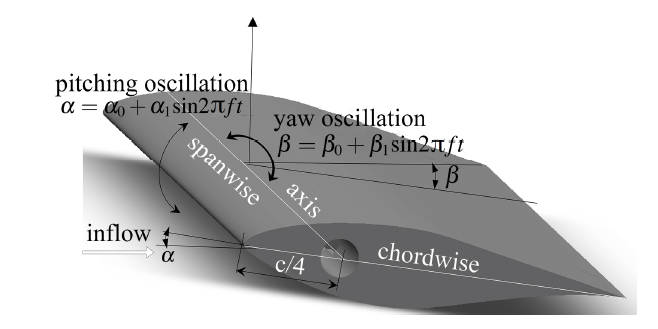
显示原图|下载原图ZIP|生成PPT图1翼型振荡运动规律示意图
-->Fig.1Schematic of airfoil oscillation motion law
-->
水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Butterfield[5]通过测量一个直径10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, Parker等[6], Bjorck[7], Walker 等[8], Favier等[9]和Babbitt等[10]等采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU)[11], 20 世纪90年代, 其在AARL$3\times5$亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA)呼吁世界各地研究机构开展翼型动态试验研究, 以获取"更精准、更全面"的气动数据[3], 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12-13]、西北工业大学[14-15]等建立和发展了翼型动态试验技术, 通过动态测力[12]、测压[15]和PIV[16]等多种手段来研究翼型动态气动特性, 由俯仰振荡单自由度向俯仰/沉浮两自由度振荡[17]发展, 由定常来流向非定常来流[18-19]发展.
目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[20-21]或翼型径向流动[22-25]的研究, 可认为是关于后掠角不变的静态"掠效应(sweep effect)"的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[26-28]. 然而, 风力机摆振[29]过程往往伴随着后掠角不断变化的动态"掠效应"的影响, 摆振和其他非定常运动耦合会导致失速更加复杂[4]. 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态"掠效应". 迄今为止, 公开的文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获取风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要探索横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型横摆振荡动态风洞试验技术, 揭示了翼型横摆动态失速形成机理. 基于"电子凸轮"技术实现了振荡运动参数的无级变化, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态"掠效应"研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用.
1 研究方法
1.1 试验方法
试验在中国空气动力研究与发展中心FL-11风洞中完成, 该风洞风速低于70 m/s 时湍流度达到0.000 8, 轴向静压梯度优于规范指标0.005.驱动装置由工控机、运动控制柜、伺服电机、行星减速机、电机支座和传动轴组件构成. 工控机运行人机界面软件, 实现系统参数设置、控制指令输入和运行状态监视等功能, 通过以太网与伺服运动控制器通讯, 运动控制器是该控制系统的核心, 实现系统组态、位置闭环控制、"电子凸轮"轨迹规划等功能. 控制系统采用位置伺服控制技术, 主要由全数字运动控制器(位控板)、全数字交流伺服系统、驱动模块和角位移传感器等组成.
试验模型为S809翼型, 如图2所示, 其弦长为300 mm, 展长为1400 mm, 展弦比为4.67, 横摆振荡传动轴位于1/4弦长、1/2展长处. 模型设计为由中间等直段和两端整流翼尖组成的三段式结构. 采用玻璃钢蒙皮和铝合金骨架结构, 中间加铺PMI泡沫芯材, 模型重量为35 kg, 惯量为0.2 $\text{kg}\cdot \text{m}^2$. 模型中间剖面为动态压力测量剖面, 共布置27个内径1.6 mm 的测压孔; 距离中间剖面300 mm的截面共布置51个内径0.6 mm的静压测压孔. 模型试验阻塞度为8.3%.
显示原图|下载原图ZIP|生成PPT图2横摆振荡S809翼型模型
-->Fig.2S809 airfoil model for yaw oscillation
-->
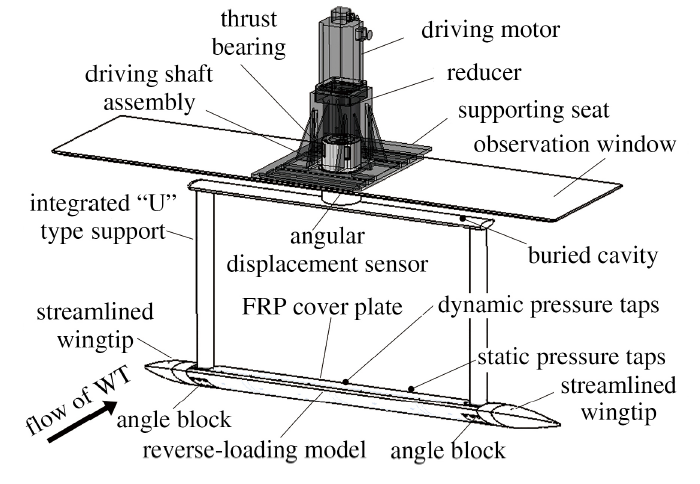
模型被水平横跨在风洞中央, 由安装在洞顶上端的电机通过传动轴组件连接"U"形支杆驱动模型作横摆振荡, 如图3所示. 采用"模型对称中截面为动态测压剖面, 支杆连接模型两端"的试验构型, 其设计依据是: (a) 支杆放置两端、测压孔居中可以最大程度地减小支杆和模型端部三维效应对动态压力测量的气动干扰; (b) 模型横摆运动时, 正中的测压截面在旋转方向的线速度分量最小甚至可以忽略, 便于只针对横摆角周期性正弦变化, 即"掠效应"问题直接开展研究. 模型采用反装构型, 在不同固定迎角($\alpha_0=-4^{\circ}\sim20^{\circ}$, 间隔$3^{\circ}$) 下开展横摆振荡, 迎角的变化通过更换支杆和模型之间的角度块来实现.
显示原图|下载原图ZIP|生成PPT图3装置驱动模型作正弦横摆振荡示意图
-->Fig.3Schematic diagram for the sinusoidal yaw oscillation of model driven by the driving device
-->
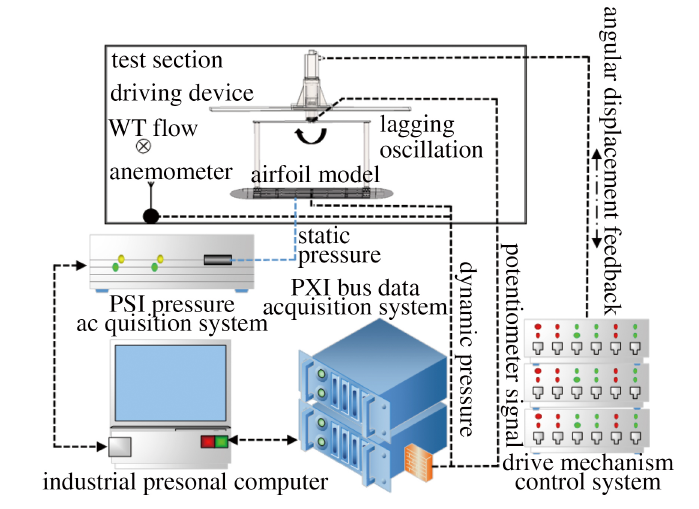
安装于试验模型端的电位计式角位移传感器的输出信号与交流伺服电机端的光电编码器输出信号同时作用于运动控制器, 构成位置反馈双闭环伺服控制系统, 实现振荡运动规律的精确控制; 角位移传感器输出的绝对值模拟信号与动态压力传感器信号一起接入动态数据采集系统, 实现角位移信号与对应动态压力信号的同步采集. 角位移传感器采用CONTELEC GL300型电位计. 测压元件采用ENDVECO 8510B 系列差压式动态压力传感器, 单个传感器连接4根电缆, 并引入参考压及测量端压力两根测压软管. 参考速压用T4-800型风速管测量得到, 风速管的静压管和总压管接入压力采集系统进行实时采集. 采用PXI总线数据采集系统保证多通道同步采集能力, PXI 总线主要由前置放大器、数据采集器、通讯卡、控制计算机和数据处理计算机等部分组成, 并配套编写相应的数据采集和处理程序. 同步采集参数主要包括风洞来流总压/静压、模型实时角位移、模型压力数据等, 如图4所示. 将翼型角位移作为一个参数实时采集, 确保和27个压力数据采集同步. 试验时压力采样采用电位计任意位置信号触发, 不同模型振荡频率, 每周期采样数量皆为256个点, 采样周期固定为16个周期. 对采集后的压力传感器数据进行六阶傅里叶滤波和低通滤波处理, 再平均成1个周期数据, 将1周期数据进行六阶最小二乘多项式拟合, 按等相位角间隔输出固定数量角位移(256个点)和对应的压力数据.
显示原图|下载原图ZIP|生成PPT图4翼型动态测压试验同步测量采集示意图
-->Fig.4Scheme of synchronous measurement and acquisition for airfoil dynamic pressure test
-->
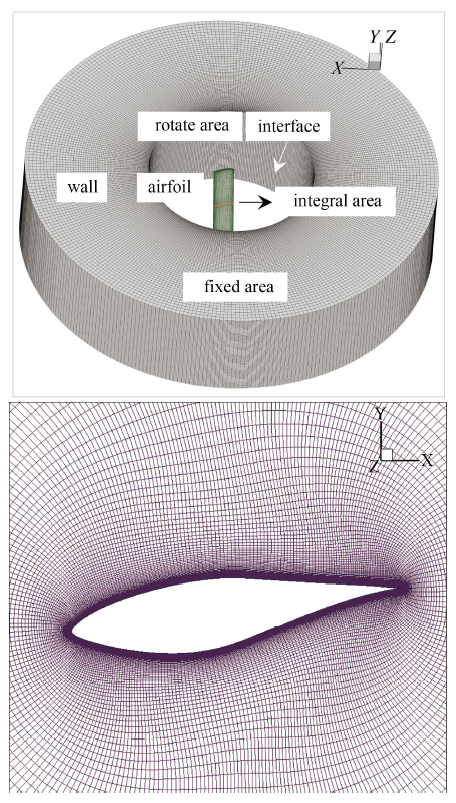
显示原图|下载原图ZIP|生成PPT图5翼型横摆振荡动态计算网格
-->Fig.5Dynamic calculation grid for airfoil yaw oscillation
-->
横摆振荡动态风洞试验模型横摆角变化规律
试验在不同的初始横摆角$\beta_0$、振荡幅度$\beta_1$、振荡频率$f$和初始迎角$\alpha_0$下开展.
1.2 数值方法
采用基于SST $k-\omega$模式的IDDES方法, 求解三维N-S方程组, 空间离散均选用二阶迎风格式, 求解方法为密度基非稳态求解, 压力远场为边界条件, 来流马赫数为0.088, 表压为标准大气压、温度为288 K, 壁面采用固壁无滑移边界条件. 采用刚性动网格和滑移网格技术, 网格运动采用弹簧光顺法和局部网格重构法, 横摆振荡中心位于翼型1/4弦长、1/2展长处, 内迭代步数为200步.计算网格区域整体分为旋转区域和固定区域, 旋转区域为直径2.4 m的圆柱计算域, 固定区域为直径6 m的圆柱计算域, 计算区域$Y$方向高1.4 m, 交界面采用滑移边界; 翼型第一层法向无量纲网格尺寸$y<1$, 计算域共920万结构性网格, 靠近翼型和壁面附近的网格进行加密(图 5). 翼型正中0.028 m宽的片段作为积分平面, 以获得翼型气动力系数, 便于和翼型动态压力测量试验数据进行对比.
2 结果分析
2.1 数据处理方法
翼型模型气动系数按照风轴系给出. 风轴系定义为: 原点为模型对称剖面弦线1/4位置, $x$ 轴指向来流为正, $y$轴逆来流方向垂直向左为正, $z$轴按照右手法则确定. 数据处理按照: 数据采集$\rightarrow$周期平均$\rightarrow$系数计算$\rightarrow$压力积分的步骤进行, 从而获取升力系数、压差阻力系数和俯仰力矩系数.压力系数按如下公式计算
其中, $C_{pi}$为测压点压力系数, $p_i$为测压点静压, $p_{\infty}$为来流静压, $p_0$ 为来流总压, $q_{\infty}$为来流动压.
作用在翼型上的法向力系数$C_\text N$和轴向力系数$C_\text A$通过积分翼型表面压力分布获得, 通过内插值获得整个函数区间的函数值后, 根据函数值进行数值积分, 其积分公式如下
\begin{align}&C_\text N=\int^1_0C_{p\text l}\text d\bar{x}-\int^1_0C_{p\text u}\text d\bar{x}\tag*{(3)}\\&C_\text A=\int^{\bar{y}_{u\,\text{max}}}_{\bar{y}_{l\,\text{max}}}C_{p\text{be}}\text d\bar{y}-\int^{\bar{y}_{u\,\text{max}}}_{\bar{y}_{l\,\text{max}}}C_{p\text{af}}\text d\bar{y}\tag*{(4)}\end{align}
式中, $C_{p\text u}$和$C_{p\text l}$分别为翼型上、下表面压力系数; $C_{p\text{be}}$ 和$C_{p\text{af}}$ 分别为翼型最大厚度之前和最大厚度之后的压力系数; $\bar{x}=x/c$ 为$x$坐标相对于弦长$c$无量纲量; $\bar{y}=y/c$为$y$ 坐标相对于弦长$c$的无量纲量; $\bar{y}_{u\,\text{max}}$, $\bar{y}_{l\,\text{max}}$分别为翼型上、下表面最大纵坐标相对于弦长$c$的无量纲量.
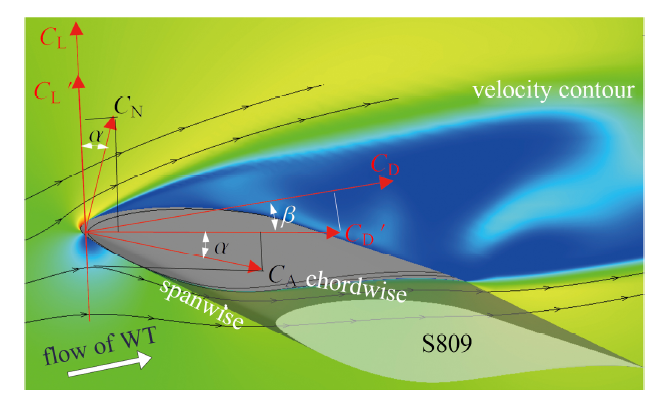
分别求出翼型体轴系下的升力系数$C'_{\text L}$和压差阻力系数$C'_{\text D}$, 风轴系下的升力系数$C_{\text L}$ 和压差阻力系数$C_{\text D}$, 如图6所示
显示原图|下载原图ZIP|生成PPT图6坐标系示意图
-->Fig.6Diagram of coordinate system
-->
\begin{align}&C'_\text L=C_\text N\text{cos}\alpha-C_\text A\text{sin}\alpha\tag*{(5)}\\&C_\text L=C'_\text L\tag*{(6)}\\&C'_\text D=C_\text N\text{sin}\alpha+C_\text A\text{cos}\alpha\tag*{(7)}\\&C_\text D=C'_\text D\text{cos}\beta\tag*{(8)}\end{align}
体轴系和风轴系下翼型绕1/4弦点的俯仰力矩系数$C'_\text m$和$C_\text m$用下式计算获得
2.2 数据结果验证
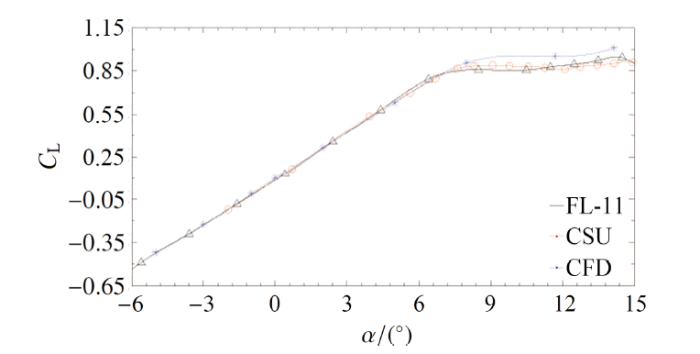
最终得到的试验结果主要是$C_\text L\sim\beta$, $C_\text D\sim\beta$, $C_\text m\sim\beta$ 的迟滞回线.雷诺数为$6.2\times10^5$下, S809翼型FL-11风洞试验结果、CFD(computational fluid dynamics) 计算结果与CSU(科罗拉多州立大学)[30]的风洞数据分别进行对比验证. 由升力系数曲线(图7)可知, FL-11 结果、CFD结果和CSU 数据在线性段均吻合良好, 总体评价, 翼型横摆振荡动态试验测量和数值计算的结果具有较高的精准度. FL-11 和CSU风洞试验结果受洞壁干扰、模型粗糙度等因素的影响, 造成了其失速迎角相对于计算结果略有提前, 且最大升力系数有所减小.
显示原图|下载原图ZIP|生成PPT图 7风洞试验和数值计算所得翼型升力系数曲线与国外风洞公开数据对比
-->Fig.7Comparison of lift coefficient curves obtained from wind tunnel test and numerical calculation with foreign wind tunnel data
-->
2.3 非定常迟滞特性分析
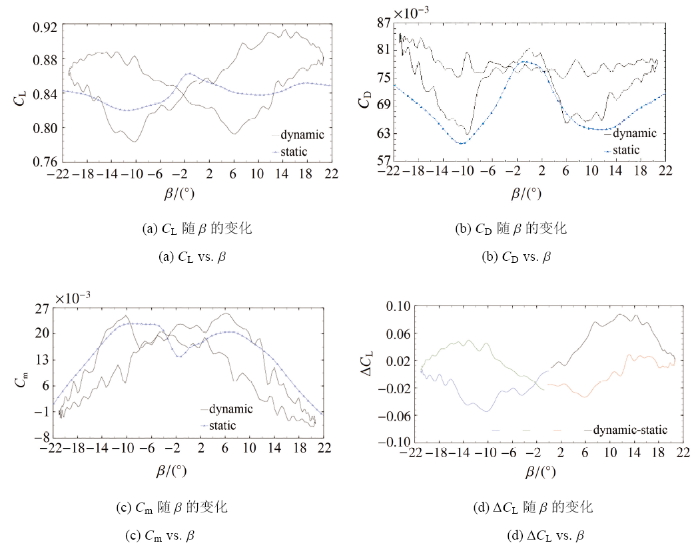
2.3.1 动态"掠效应"下翼型气动特性如图8所示, 横摆振荡动态"掠效应"影响下, 翼型气动力/力矩系数随横摆角变化的曲线存在明显的迟滞效应; 横摆振荡翼型力/力矩曲线和静态气动力/力矩曲线差异明显, 定义二者差量为$\Delta C_\text L$; 由图可知, $C_\text L-\beta$、$C_\text D-\beta$曲线整体均呈明显的"W"形, $C_\text m-\beta$ 曲线整体呈明显的"M"形, $\Delta C_\text L-\beta$曲线呈明显的"$\infty$"形; 总体来看, 静态"掠效应"下$C_\text L-\beta$曲线分布在横摆振荡动态$C_\text L-\beta$迟滞曲线的中间部位, $C_\text D-\beta$迟滞曲线较静态曲线有所抬升, $C_\text m-\beta$迟滞曲线较静态曲线有所下降.
显示原图|下载原图ZIP|生成PPT图8横摆振荡动态"掠效应"与静态"掠效应"下, 翼型气动力/力矩系数对比($Re=6.2\times10^5$, $\alpha_0=14^{\circ}$, $\beta_1=20^{\circ}$, $f=0.75~\text{Hz}$)
-->Fig.8Comparison of aerodynamic/moment coefficients of airfoils under yaw oscillation dynamic "sweep effect" and static "sweep effect"($Re=6.2\times10^5$, $\alpha_0=14^{\circ}$, $\beta_1=20^{\circ}$ and $f=0.75~\text{Hz}$)
-->
2.3.2 振荡频率影响
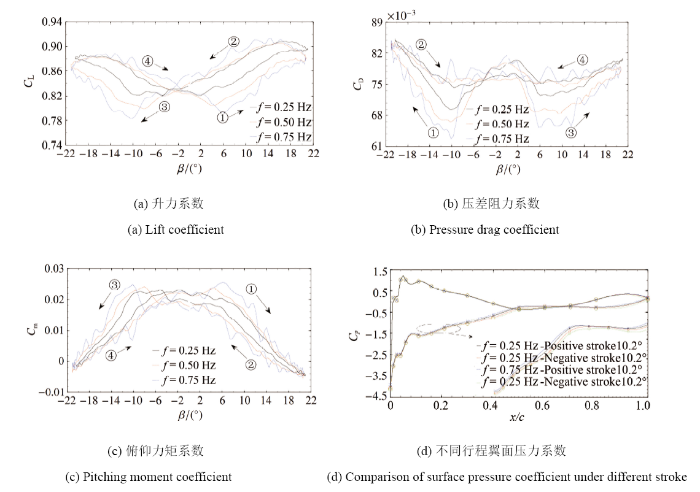
图9给出了$Re=6.2\times10^5$下, 不同振荡频率对翼型动态气动特性的影响规律曲线. 曲线中的编号”①”~”④”及箭头所示为振荡运动的顺序和走向, 其中”①”和”③”为正行程(positive stroke, 横摆角绝对值 增大的方向), ”②”和”④”为负行程(negative stroke, 横摆角绝对值 减小的方向). 由图可知, 负行程下翼型的气动力系数相对于正行程的更高; 负行程下翼型气动力系数整体上随着振荡频率增大而略有增大; 正行程下则随着振荡频率的增大而明显减小, 且减小的幅度相对负行程增大的幅度明显更高; 随着翼型振荡频率的增大, 横摆振荡翼型的升力系数、压差阻力系数和俯仰力矩系数的迟滞环面积均增大, $C_\text L$迟滞环面积: 0.826 5$\rightarrow$1.610 5$\rightarrow$\mbox{2.174 4}, $C_\text D$ 迟滞环面积: 0.649 8$\rightarrow$0.799 2$\rightarrow$1.906 8, $C_\text m$迟滞环面积: 0.069 4$\rightarrow$0.2684$\rightarrow$0.399 1, 显示出翼型三维流动的非定常性增强, 即翼型动态掠效应的变化使得气动参数随迎角变化的迟滞特性增强. 图9(d) 所示的负行程下翼型吸力面吸力相对正行程增大, 解释了不同行程下气动力系数出现迟滞回环的根源; 且随着横摆振荡频率的增大, 负行程相对于正行程下翼型吸力面的吸力值增大的幅度也随之增大.
显示原图|下载原图ZIP|生成PPT图9不同振荡频率下翼型气动力/力矩系数曲线($\alpha_0=14^{\circ}$, $\beta_1=20^{\circ}$)
-->Fig.9Lift, pressure drag and pitching moment coefficient under different oscillating frequencies ($\alpha_0=14^{\circ}$ and $\beta_1=20^{\circ}$)
-->
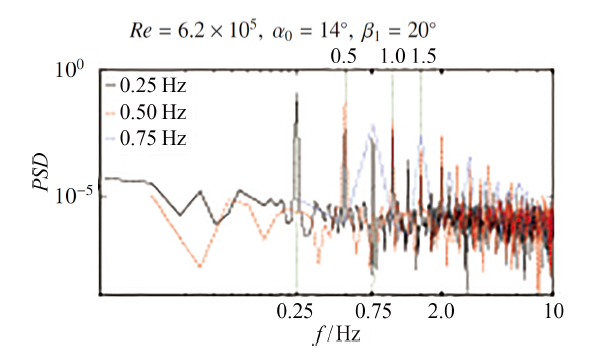
对动态压力积分获取的16个周期的瞬态$C_\text L$进行周期图法功率谱密度(power spectral density, PSD)分析, PSD分布如图10所示, 不同阶次的能量集中反映了翼型振荡过程中流场结构的多尺度性和多频率性[31]. 可以看出: (1) 翼型升力系数$PSD$分布在翼型振荡频率的倍频处存在明显的能量集中; (2) 随着振荡频率的增大, 翼型倍频处能量集中的幅值有明显增大的趋势, 这是由于振荡频率的增大导致了翼型各频次的动态涡结构的强度和迟滞效应均增大, 反映了横摆运动翼型的流动的非定常性增强, 这与俯仰振荡翼型的流动特性规律相一致.
显示原图|下载原图ZIP|生成PPT图 10不同振荡频率翼型升力系数功率谱
-->Fig.10Power spectral density (PSD) of $C_\text L$ under different oscillation frequency
-->
2.3.3 初始迎角影响
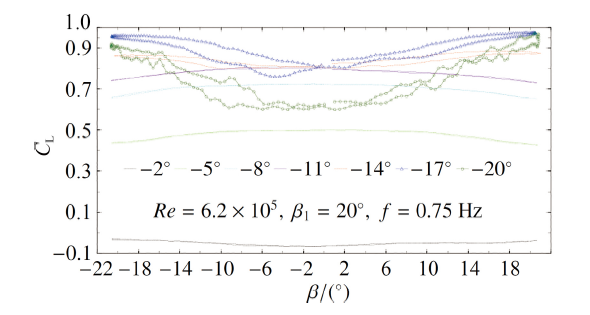
图11给出了不同初始迎角下翼型$C_\text L-\beta$曲线, 可以看出, 随着初始迎角在$-2^{\circ}\sim 17^{\circ}$ 范围内增大, 翼型升力系数整体上有增加的趋势, 当初始迎角为$20^{\circ}$时, 翼型的升力系数突然下降, 分析认为是由于翼型大迎角下动态深失速导致的; 初始迎角为$-2^{\circ}\sim11^{\circ}$范围内, 横摆振荡翼型的$C_\text L-\beta$迟滞回线面积均较小, 所反映出的升力系数迟滞效应并不明显, 初始迎角增大至$14^{\circ}$ 时, 翼型表面产生了动态分类涡, 可以观察出升力系数明显的迟滞效应的发生, 随着初始迎角继续增大至$17^{\circ}$和$20^{\circ}$, $C_\text L-\beta$迟滞效应继续增强. 究其原因, 认为初始迎角在$14^{\circ}$以上和以下, 翼型对应的流动形态明显不同, 将在3.4.3节进行详细论述.
显示原图|下载原图ZIP|生成PPT图11不同初始迎角下翼型$C_\text L-\beta$曲线
-->Fig.11$C_\text L-\beta$ curves of airfoil at different initial AOA
-->
2.3.4 振幅影响
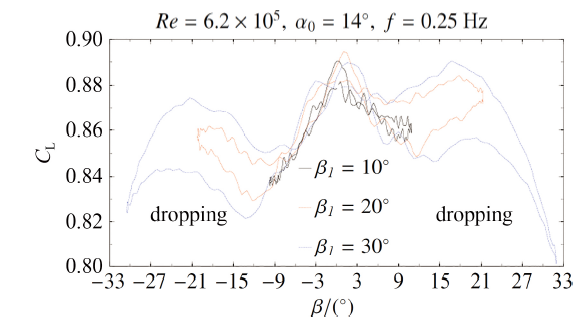
图12给出了不同振幅下翼型$C_\text L-\beta$曲线, 可知振幅越大, 升力系数迟滞环面积越大, 这与俯仰振荡的规律一致; 振幅$\beta_1=10^{\circ}$时, 翼型的$C_\text L-\beta$ 曲线形状呈"$^{\wedge}$"形; 振幅$\beta_1=20^{\circ}$ 时, 翼型的$C_\text L-\beta$ 曲线形状呈"W" 形; 当振幅$\beta_1$达到$30^{\circ}$ 时, 翼型的$C_\text L$-$\beta$曲线形状呈"$^{\wedge\wedge\wedge}$"形, 即在$\beta>20^{\circ}$ 或$\beta<-20^{\circ}$ 时, 翼型升力系数迟滞环形状出现"下垂"现象.
显示原图|下载原图ZIP|生成PPT图 12不同振幅下$C_\text L-\beta$ 曲线
-->Fig.12$C_\text L-\beta$ curves under different amplitudes
-->
2.4 气动迟滞形成机理
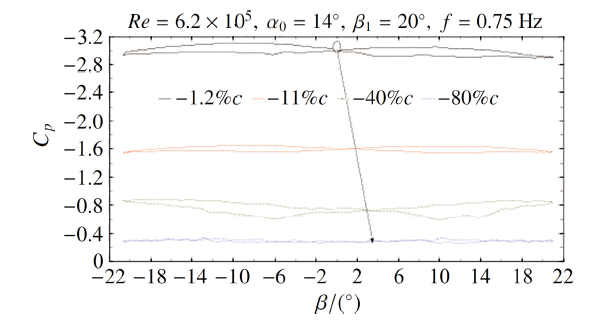
2.4.1 翼面非定常压力分析图13给出了翼型吸力面不同位置的压力系数随横摆角的变化曲线, 可以看出, 不同位置的压力系数随着横摆角变化均存在迟滞效应; 0.012 $c$处和0.4 $c$处的压力系数迟滞回线面积较大, 分析认为是前缘附近0.012 $c$处的剪切层涡和0.4 $c$处的动态分离涡随着翼型横摆运动而在吸力面周期性移动的结果, 剪切层涡和动态分离涡的在横摆振荡过程中的产生、发展、运动、破裂和重建过程存在明显的迟滞效应, 从而引起压力系数随横摆角的变化形成迟滞回线; 0.11 $c$处的压力系数迟滞效应次之; 后缘附近0.8 $c$ 处的压力系数迟滞特性最弱, 这是由于该位置的后缘分离涡一直相对较为集中和稳定地存在.
显示原图|下载原图ZIP|生成PPT图 13吸力面不同位置压力系数随横摆角变化
-->Fig.13Variation of pressure coefficient at different positions of suction surface with the change of yawing angle
-->
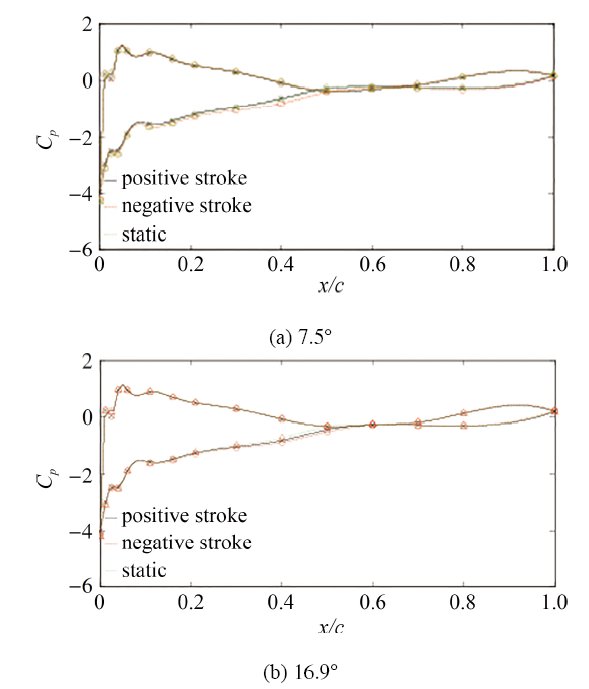
图14给出了横摆角分别为$7.5^{\circ}$和$16.9^{\circ}$时, 正行程、负行程和静态条件下翼型表面压力分布曲线对比图, 不难看出: (1) 翼型压力面的压力分布基本保持一致; (2) 翼型吸力面的压力分布呈现出明显的不同; 横摆角为$7.5^{\circ}$ 时, 按照吸力值由大到小分别为负行程、静态和正行程; 横摆角为$16.9^{\circ}$ 时, 按照吸力值由大到小分别为负行程、正行程和静态;较大的吸力值会促进翼型升力系数的增大, 3种不同运动形式下上翼面吸力值的变化规律也印证并解释了图8(a)所示$C_\text L-\beta$ 曲线的规律.
显示原图|下载原图ZIP|生成PPT图14横摆振荡和静态下翼型表面压力分布对比($Re=6.2\times10^5$, $\alpha_0=14^{\circ}$, $\beta_1=20^{\circ}$, $f=0.75~\text{Hz}$)
-->Fig.14Comparison of airfoil pressure distribution under yaw oscillation and static condition($Re=6.2\times10^5$, $\alpha_0=14^{\circ}$, $\beta_1=20^{\circ}$ and $f=0.75~\text{Hz}$)
-->
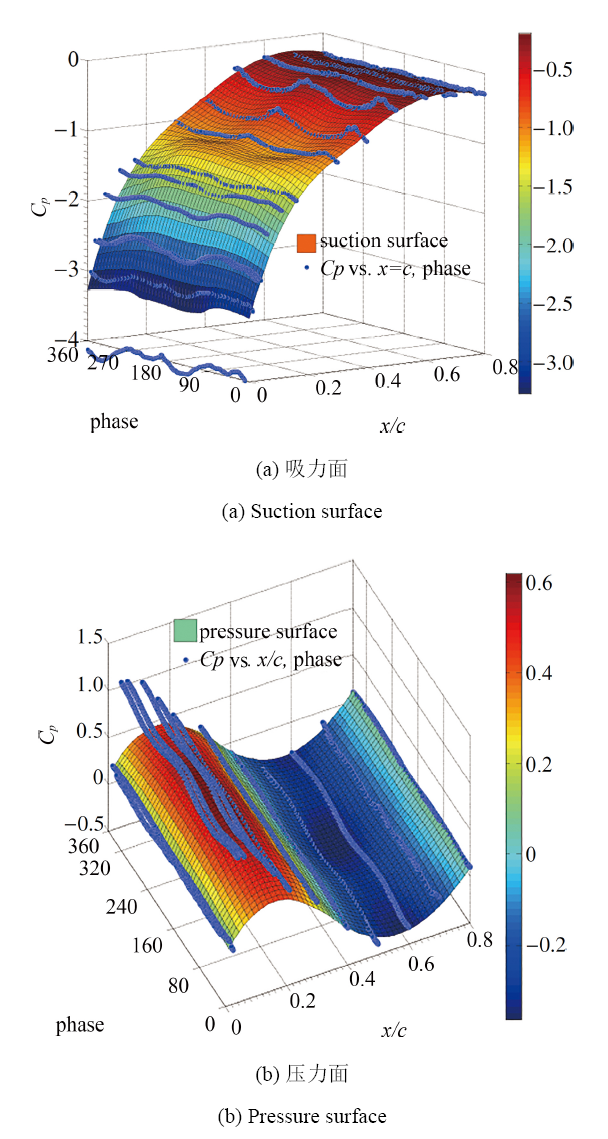
图15给出了一个完整振荡周期内, 翼型吸力面和压力面的压力系数分布三维拟合图, $x/c$坐标为翼型弦长方向的相对位置, Phase 坐标为翼型在一个完整振荡周期内所处的相位角, $C_p$为翼型表面压力系数. 可知吸力面$x/c=0.2\sim0.6$范围的压力系数在一个横摆振荡周期内的变化波动较为明显, 随着相位角的增加, 吸力面的吸力值变化经历了"增大? 减小?平缓?增大? 减小?恢复"的周期性发展过程; 压力面的压力系数在一个振荡周期内的变化波动相对较小, 压力分布曲面相对平整; 不难推断, 吸力面的压力系数周期性变化是翼型力/力矩系数迟滞回环形成的主要诱因, 压力面的压力系数变化的贡献则相对较小.
显示原图|下载原图ZIP|生成PPT图15一个振荡周期内翼型表面压力分布三维拟合图($Re=6.2\times10^5$, $\alpha_0=14^{\circ}$, $\beta_1=20^{\circ}$, $f=0.75~\text{Hz}$)
-->Fig.15Fitting three-dimensional diagram of airfoil pressure distribution in one oscillatory cycle($Re=6.2\times10^5$, $\alpha_0=14^{\circ}$, $\beta_1=20^{\circ}$ and $f=0.75~\text{Hz}$)
-->
2.4.2 惯性力效应
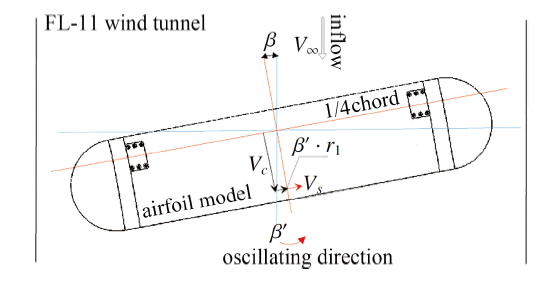
在翼型横摆振荡过程中, 翼型与流场之间的相对速度发生周期性改变, 这相当于在原来翼型与气流之间的相对运动基础上增加了一个横摆运动诱导速度, 由此引起翼型的气动力相应地变化. 由于横摆运动导致合成速度的改变, 进而引起气动力的周期性变化, 本文称之为"惯性力效应". 翼型弦向相对坐标$r_1$位置处的名义气流速度推导如下:
对式(1)进行求导, 计算出翼型横摆振荡运动角速度为
如图16所示, 弦向相对气流速度为
展向相对气流速度为
合成相对气流速度为
其中, 前半部分为"掠效应"中的静态分量, 后半部分为"掠效应"中的动态分量. 根据3.3.3 节所述: 横摆振荡运动参数一致, 即运动的合成速度$V_r$基本一致, 然而不同初始迎角下翼型的气动迟滞特性差异较大, 不难推断出" 惯性力效应"对翼型的非定常气动特性的影响量较小.
显示原图|下载原图ZIP|生成PPT图16横摆振荡翼型表面气流速度示意图
-->Fig.16Schematic diagram of airflow velocity on the surface of yaw oscillating airfoil
-->
2.4.3 黏性力效应
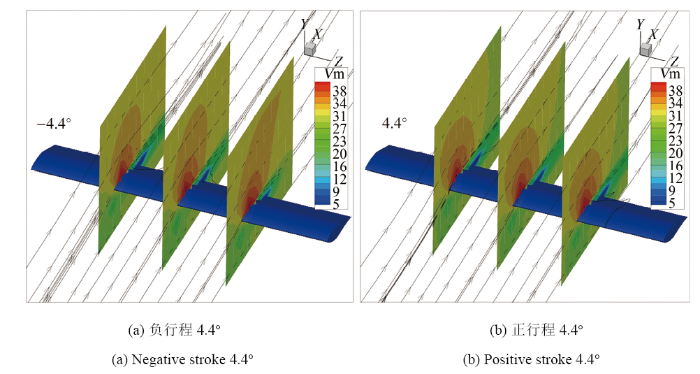
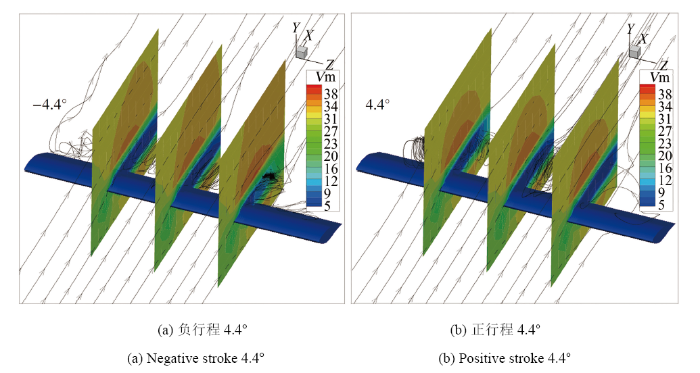
图17为横摆振荡翼型动态流场的数值计算结果, 初始迎角$\alpha_0=14^{\circ}$时, 负行程和正行程$4.4^{\circ}$ 横摆角下, 靠近前缘和中部区域的流动均较好地附着在翼型表面, 但翼型后缘位置附近产生了较轻度的动态分离, 并诱发出较微弱的展向三维流动, 翼型绕流的三维效应使得图中沿翼展方向的三个不同截面的速度云分布也存在一定差别, 这也是后掠翼型流动的重要特征之一.
显示原图|下载原图ZIP|生成PPT图17不同横摆角下翼型绕流($Re=6.2\times10^5$, $\alpha_0=14^{\circ}$, $\beta_1=20^{\circ}$, $f=0.50~\text{Hz}$)
-->Fig.17Airfoil flow around different yaw angles($Re=6.2\times10^5$, $\alpha_0=14^{\circ}$, $\beta_1=20^{\circ}$ and $f=0.50~\text{Hz}$)
-->
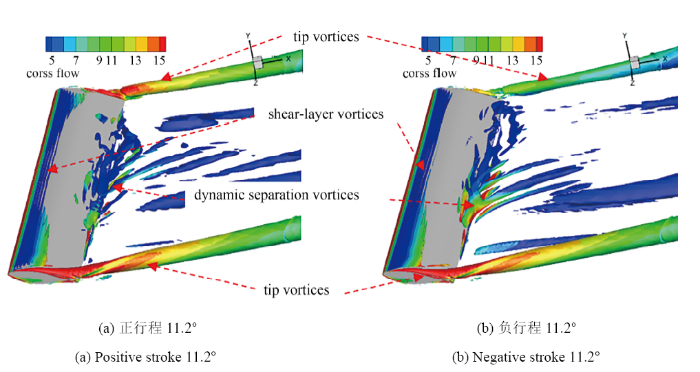
如图18所示, "cross flow"为展向和法向速度的均方根, 表征翼型表面涡的三维流动. 可知在初始迎角$\alpha_0=14^{\circ}$下, 翼型端部诱导出明显的翼尖涡结构, 表征为端部三维效应[32], 且沿着流向较为集中地发展和扩张, 负行程时上方翼尖涡较正行程时的明显减弱; 由图还可以观察出后缘中部区域轻度的动态分离涡和前缘附近区域的剪切层涡两种相干涡结构, 它们之间相互作用相互影响的过程非常复杂.
显示原图|下载原图ZIP|生成PPT图18$Q=0.3$等值面发展图($Re=6.2\times10^5$, $\alpha_0=14^{\circ}$, $\beta_1=20^{\circ}$, $f=0.50~\text{Hz}$)
-->Fig.18$Q=0.3$, development chart isosurface ($Re=6.2\times10^5$, $\alpha_0=14^{\circ}$, $\beta_1=20^{\circ}$ and $f=0.50~\text{Hz}$)
-->
如图19所示, 在较大初始迎角$\alpha_0=20^{\circ}$下, 相比于$\alpha_0=14^{\circ}$(图 17), 翼型动态分离由后缘扩散至前缘, 且三维动态分离涡[33-34] 随着横摆角的周期性变化沿展向周期性移动, 这种非定常分离流中存在多个时间相关的相干结构, 其相互作用和演化是非常复杂和非线性的, 且动态分离涡具有明显的离心不稳定性[35], 这也是吸力面压力波动和非定常迟滞的根源.
显示原图|下载原图ZIP|生成PPT图19不同横摆角下翼型绕流($Re=6.2\times10^5$, $\alpha_0=20^{\circ}$, $\beta_1=20^{\circ}$, $f=0.50~\text{Hz}$)
-->Fig.19Airfoil flow around different yaw angles($Re=6.2\times10^5$, $\alpha_0=20^{\circ}$, $\beta_1=20^{\circ}$ and $f=0.50~\text{Hz}$)
-->
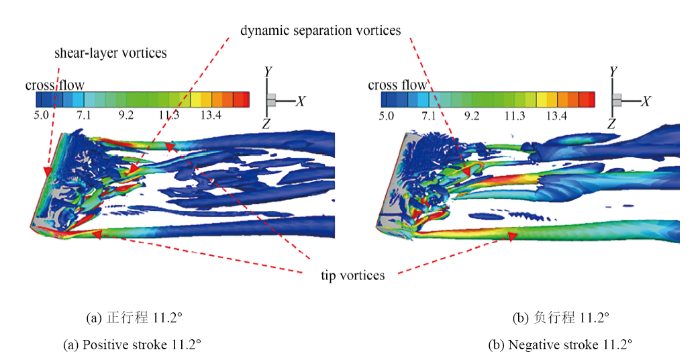
由图20可以看出, $\alpha_0=20^{\circ}$时, 除了翼尖端部S的强三维效应, 在翼型的中部区域, 也有较强三维效应, 相比于$\alpha_0=14^{\circ}$(图 18), 动态分离涡的强度和影响区域均明显增大; 且随着横摆角周期性振荡, 翼面剪切层涡和动态分离涡周期性地移动变化, 表现为三维流动特性也周期性地随之演化, 这种三维效应是翼型横摆运动动态"掠效应"引起的, 和端部的三维效应有明显的不同, 动态"掠效应"所致的强三维流动区域沿翼展方向相对较为分散地排列. 由三维动态流场的运动迟滞和变速剪切所致的流动非定常特征, 本文称之为"黏性力效应".
显示原图|下载原图ZIP|生成PPT图20$Q=0.3$等值面发展图($Re=6.2\times10^5$, $\alpha_0=20^{\circ}$, $\beta_1=20^{\circ}$, $f=0.50~\text{Hz}$)
-->Fig.20$Q=0.3$ development chart isosurface ($Re=6.2\times10^5$, $\alpha_0=20^{\circ}$, $\beta_1=20^{\circ}$ and $f=0.50~\text{Hz}$)
-->
3 结 论
本文针对翼型动态 "掠效应" 首次开展了横摆振荡风洞试验研究, 探索了横摆翼型的气动迟滞形成机理, 建立的横摆振荡试验技术可为风力机动态 "掠效应" 的研究提供技术支撑, 得出以下结论.(1) 横摆振荡翼型的气动曲线也存在明显的迟滞效应, 且随着振荡频率、初始迎角和振幅的增加, 翼型的动态气动迟滞特性均增强; (2) $C_\text L-\beta$和 $C_\text D-\beta$迟滞回线整体呈"W"形, $C_\text m-\beta$ 迟滞回线整体呈"M" 形, $\Delta C_\text L-\beta$ 迟滞回线呈"$\infty$"形; (3) 吸力面的压力系数周期性波动是翼型力/力矩系数迟滞回环形成的主要诱因, 压力面的压力系数变化的贡献则相对较小; 翼型不同吸力面位置的压力系数随横摆角的变化均存在迟滞效应, 其中1.2% $c$处和40% $c$处的压力系数迟滞回线面积较大, 迟滞的形成受"惯性力效应"影响较小, 受"黏性力效应"影响较大, 即是由于翼型表面剪切层涡和动态分离涡周期性的产生、发展、运动、破裂和重建的结果; (4) 负行程下振荡翼型的气动力系数相对于正行程下的更高, 且负行程下翼型的气动力系数随着振荡频率的增大而整体上略有增大, 正行程下则随着振荡频率的增加而明显减小; (5) 翼型升力系数PSD分布在振荡频率的倍频处存在明显的能量集中, 且随着振荡频率增大, 倍频处能量集中的幅值有明显增大趋势, 反映了横摆运动翼型的流动非定常性在增强; (6) 振幅$\beta_1=10^{\circ}$ 时, $C_\text L-\beta$曲线形状呈"$^{\wedge}$"形; 振幅$\beta_1=30^{\circ}$ 时, $C_\text L-\beta$曲线形状呈"$^{\wedge\wedge\wedge}$"形, 即在横摆角$\beta>20^{\circ}$或$\beta<-20^{\circ}$ 时, 翼型升力系数迟滞环形状出现"下垂"现象.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . . |
| [2] | . . |
| [3] | . . |
| [4] | . . |
| [5] | . |
| [6] | . |
| [7] | |
| [8] | . |
| [9] | // |
| [10] | . |
| [11] | |
| [12] | . . |
| [13] | . |
| [14] | . . |
| [15] | . . |
| [16] | . . |
| [17] | . . |
| [18] | . . |
| [19] | . . |
| [20] | , |
| [21] | // |
| [22] | . [硕士论文]. . [Master Thesis]. |
| [23] | . . |
| [24] | . . |
| [25] | // |
| [26] | // |
| [27] | // |
| [28] | // |
| [29] | . . |
| [30] | . |
| [31] | . . |
| [32] | . |
| [33] | . . |
| [34] | . |
| [35] | . |
