, 吴加峰COMPLEX MODE SUPERPOSITION METHOD BASED ON FREQUENCY DEPENDENT VISCOUS DAMPING MODEL1)
SunPanxu, WuJiafeng中图分类号:TU311.3
文献标识码:A
通讯作者:
收稿日期:2018-04-4
接受日期:2018-04-4
网络出版日期:2018-09-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (6894KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
物理模型采用数学动力方程求解时, 选择合理的阻尼模型是关乎计算分析结果可靠性的关键因素之一[1]. 迄今为止已有多种阻尼理论被提出, 包括黏性阻尼模型、复阻尼模型、分数导数理论等[2]. 黏性阻尼模型具有数学处理上的简易性, 而复阻尼模型易于描述材料的阻尼特性, 故这两种阻尼理论应用最为广泛[3-4].另一方面, 黏性阻尼模型在结构稳态反应中每周期耗散能量与外激励频率相关, 这与大部分工程材料在较宽频率范围内每周期耗散能量与外频率无关的现象不符[5-8], 复阻尼模型的时程计算结果存在发散现象[9], 为克服黏性阻尼模型和复阻尼模型的缺陷, 有必要寻求一种新阻尼模型以改善结构动力时程响应计算的合理性和适用性.Lee等[10]将黏性阻尼模型与复阻尼模型相结合; 尚守平等[11]提出阻尼力与加速度成正比, 但上述得到的新运动方程通解中仍含有发散项. 朱镜清等[7]直接舍弃通解中发散项的计算方法, 保证了计算结果的稳定性, 但这种处理在数学上是不正确的[12]. Wang[13]采用Rayleigh阻尼矩阵等效复阻尼矩阵, 但上述方法得到的计算结果与复阻尼模型存在一定的误差, 且计算结果不具有唯一性. Clough [14]、Chen[15] 等对复阻尼模型进行了修正, 假定阻尼力的大小与结构体系的位移大小成正比, 且与速度的方向相反, 进而提出了迟滞阻尼理论, 但无法保证系统的线性特点. Pan 等[16] 在Biot 阻尼模型基础上研究了卷积型阻尼运动方程的构建和求解; Reggio[17] 将Maxwell-Wiechert本构模型等效于复阻尼本构模型, 亦可得到在时域内稳定收敛的运动方程. 上述方法的实质是采用黏弹性材料的本构模型作为结构体系的阻尼力模型, 计算过程复杂, 是否符合材料的阻尼特性亦有待进一步验证. 朱镜清[18]利用复化对偶原则, 在复阻尼模型基础上提出了频率相关黏性阻尼模型, 可直接在实数域中进行计算.
由具有不同阻尼特性的材料组成的混合结构, 其阻尼矩阵不再与刚度矩阵保持比例关系, 结构无阻尼自由振动模态向量矩阵无法使阻尼矩阵对角化, 传统的实模态叠加法将不再适用[19]. 为此, 潘旦光[20]、黄维等[21-22]基于位移误差最小原则得到了最佳等效阻尼比, 并采用Rayleigh阻尼模型计算竖向混合结构的动力响应; Luco等[23]基于拉格朗日插值函数将Caughey阻尼矩阵等效于非比例阻尼矩阵; 汪梦甫[24]、Neugebauer等[25,26] 在黏性阻尼模型基础上, 利用基于状态空间法的复模态叠加法计算非比例线性阻尼体系的动力反应; Qin[27]、 楼梦麟等[28]研究了非比例阻尼体系复模态的实模态摄动法; 国巍等[29]将直接积分法和强迫解耦法联系起来求解非比例结构的地震响应; 段绍伟等[30]、Mohamed等[31]采用模态应变能法计算非比例线性阻尼体系的响应; Zoghaib等[32]提出利用共振模态和拉普拉斯变换相结合计算非比例线性阻尼体系的时域响应和频域响应. 上述方法均建立在黏性阻尼模型基础上, 但存在计算结果不唯一、合理性不易被判定的缺点. 复阻尼模型可直接采用复模态叠加法计算混合结构的动力响应[33-34], 但需剔除发散项, 遵循复化对偶原则.
本文在上述研究的基础上, 利用傅里叶变换过滤复阻尼模型的发散项, 得到了在频域上与复阻尼模型等效的频率相关黏性阻尼模型. 频率相关黏性阻尼模型可克服黏性阻尼中每周期耗散能量与外激励频率相关的缺陷, 还避免了复阻尼模型的发散. 在单自由体系响应的计算基础上, 本工作采用频率相关黏性阻尼模型与复阻尼模型的转换关系, 研究了基于频率相关黏性阻尼模型的复模态叠加法, 以期为混合结构的振型分解反应谱法提供理论依据. 相比非比例阻尼体系的基于黏性阻尼模型的复模态叠加法, 基于频率相关黏性阻尼模型的复模态叠加法中阻尼矩阵仅依赖于结构的损耗因子, 计算结果具有唯一性, 合理性易判定; 矩阵维度不增加, 计算量相对较小.
1 基于复阻尼模型的频率相关黏性阻尼模型
复阻尼模型假定简谐激励作用下, 结构内部的阻尼应力与弹性应力成正比, 而与速度同相. 在简谐荷载作用下, 复阻尼模型中阻尼力每个周期消耗的能量与外荷载激励的频率无关, 该特点与实际相符, 因此在结构动力响应计算中得到了较广泛使用. 单自由度体系的复阻尼运动方程为\begin{align*}m\ddot{x}(t)+\text{i}\eta kx(t)+kx(t)=-mg(t)-\text{i}mg'(t)\tag*{(1)}\end{align*}
其中, $m$为结构质量, $k$为结构刚度, $g(t)$为地震加速度, $g(t)$通过复化对偶原则[9]可计算得到$g'(t)$, $\text{i}$为虚数单位, $\text{i}=\sqrt{-1}$.
$\eta$为复阻尼系数, 即为结构的损耗因子, 其与阻尼比的关系为[35-36]
\begin{align*}\eta=2\xi\tag*{(2)}\end{align*}
其中, $\xi$为阻尼比.
令$g(t)=0$, 得到方程(1)的自由振动方程为
\begin{align*}m\ddot{x}(t)+\text{i}\eta kx(t)+kx(t)=0\tag*{(3)}\end{align*}
采用待定系数法, 求解方程(3), 得到方程的通解为
\begin{align*}x(t)=a_1\text{e}^{\text{i}\lambda_1t}+a_2\text{e}^{\text{i}\lambda_2t}\tag*{(4)}\end{align*}
其中, $a_1$和$a_2$为任意复常数, $\lambda_1$和$\lambda_2$为
\begin{equation*}\left.\begin{split}&\lambda_1=\sqrt[4]{1+\eta^2}\sqrt{\dfrac{k}{m}}\text{e}^{\text i\tfrac{\text{arctg} \eta}{2}}\\&\lambda_2=-\sqrt[4]{1+\eta^2}\sqrt{\dfrac{k}{m}}\text{e}^{\text i\tfrac{\text{arctg} \eta}{2}}\end{split}\right\}\tag*{(5)}\end{equation*}
令$a_2=a_{21}+\text{i}a_{22}$, 则
\begin{align*}&a_2\text{e}^{\text{i}\lambda_2t}=\text{exp}\Bigg\lbrack\sqrt[4]{1+\eta^2}\sqrt{\dfrac{k}{m}}t~\text{sin}\left(\dfrac{\text{arctg}\eta}{2}\right)\Bigg\rbrack\cdot(a_{21}+\\&\qquad \text{i}a_{22})\text{exp}\Bigg\lbrack-\text{i}\sqrt[4]{1+\eta^2}\sqrt{\dfrac{k}{m}}t~\text{cos}\left(\dfrac{\text{arctg}\eta}{2}\right)\Bigg\rbrack\tag*{(6)}\end{align*}
取式(6)的实部$x_1(t)$, 可得
\begin{align*}x_1(t)&=\text{exp}\left(\sqrt[4]{1+\eta^2}\sqrt{\dfrac{k}{m}}t~\text{sin}\left(\dfrac{\text{arctg}\eta}{2}\right)\right)\cdot\\&\Bigg\lbrace a_{21}\text{cos}\Bigg[\sqrt[4]{1+\eta^2}\sqrt{\dfrac{k}{m}}t~\text{cos}\left(\dfrac{\text{arctg}\eta}{2}\right)\Bigg]+\\&a_{22}\text{sin}\Bigg[\sqrt[4]{1+\eta^2}\sqrt{\dfrac{k}{m}}t~\text{cos}\left(\dfrac{\text{arctg}\eta}{2}\right)\Bigg]\Bigg\rbrace\tag*{(7)}\end{align*}
由式(7)可知, 随着时间$t$的增大, $x_1(t)$逐渐增大, 即方程的通解$x(t)$存在发散项, 复阻尼运动方程无法计算结构自由振动的位移响应, 为病态方程. 方程(3)中含有指数增长项$\text{e}^{\tau t}(\tau >0)$, 时间$t$的范围为$[0,+\infty)$, 则指数增长项的傅里叶变换为
\begin{align*}x(\text{i}\varpi )=\int^{+\infty}_{0}\text{e}^{\tau t}\text{e}^{-\text{i}\varpi t}\text{d}t\tag*{(8)}\end{align*}
指数增长函数在$[0,+\infty)$不可积分, 因此式(8)是不成立的, 傅里叶变换过程相当于滤波器, 可筛选掉方程(3)通解中的指数增长项.
复阻尼模型本构关系在频域范围内成立, 对方程(1)进行傅里叶变换, 得到频域运动方程为
\begin{align*}-\varpi^2mx(\text{i}\varpi)+k(1+\text{i}\eta)x(\text{i}\varpi)=-mg(\text{i}\varpi)-\text{i}mg'(\text{i}\varpi)\tag*{(9)}\end{align*}
其中, $\varpi$为结构位移响应的振动频率, $x(\text{i}\varpi)$为$x(t)$的傅里叶变换, $g(\text{i}\varpi)$为$g(t)$的傅里叶变换.
当结构位移响应的振动频率不为零时, 方程(9)可转化为
\begin{align*}-\varpi^2& mx(\text{i}\varpi)+kx(\text{i}\varpi)+\dfrac{\text{i}\eta k}{\varpi}\varpi x(\text{i}\varpi)=\\&-mg(\text{i}\varpi)-\text{i}mg'(\text{i}\varpi)\tag*{(10)}\end{align*}
经傅里叶逆变换之后, 得频率相关黏性阻尼时域运动方程为
\begin{align*}m\ddot{x}(t)+kx(t)+\dfrac{\eta k}{\varpi}\dot{x}(t)=-mg(t)-\text{i}mg'(t)\tag*{(11)}\end{align*}
结构位移响应的振动频率不为零时, 经过时频域转化的方程(11)与方程(1)是等价的. 实数域计算时可不考虑方程(11)右端虚部分量.
基于频率相关黏性阻尼模型的阻尼力为
\begin{align*}F_{P}=-\dfrac{ck}{\varpi}\dot{x}(t)\tag*{(12)}\end{align*}
式(12)表明基于频率相关黏性阻尼模型的结构阻尼力大小与速度大小成正比, 同时与结构的振动频率成反比, 方向与速度的方向相反.
1.1 稳定性分析
基于频率相关黏性阻尼的单自由度体系时域自由振动方程为\begin{align*}m\ddot{x}(t)+kx(t)+\dfrac{\eta k}{\varpi}\dot{x}(t)=0\tag*{(13)}\end{align*}
采用复平面法求解, 假定通解为
\begin{align*}x(t)=A\text{e}^{\text{i}(pt+\gamma )}\tag*{(14)}\end{align*}
将式(14)代入方程(13), 得到
\begin{align*}-p^2+\text{i}\dfrac{\eta\omega^2}{\varpi}p+\omega^2=0\tag*{(15)}\end{align*}
其中, $\omega$为结构无阻尼自振频率, $\omega=\sqrt{\dfrac{k}{m}}$.令$p=\alpha+\text{i}\beta$, 则
\begin{equation*}\left.\begin{split}&\alpha^2=\omega^2-\dfrac{\eta^2\omega^4}{4\varpi^2}\\&\beta=\dfrac{\eta\omega^2}{2\varpi}\end{split}\right\}\tag*{(16)}\end{equation*}
取式(14)的实部, 得到
\begin{align*}x(t)=A\text{e}^{-\beta t}\text{cos}(\alpha t+\gamma )\tag*{(17)}\end{align*}
由式(17)知, 位移响应的振动频率为$|\alpha|$, 则
\begin{align*}|\alpha|=\varpi\tag*{(18)}\end{align*}
进一步得
\begin{align*}\varpi^4-\omega^2\varpi^2+\dfrac{1}{4}\eta^2\omega^4=0\tag*{(19)}\end{align*}
由方程(19), 可解得
\begin{align*}\varpi=\sqrt{\dfrac{\omega^2+\sqrt{\omega^4-\eta^2\omega^4}}{2}}\tag*{(20)}\end{align*}
将式(16)和式(20)代入式(17), 可得到位移为
\begin{align*}x(t)=[C_1\text{cos}(\varpi t)+C_2\text{sin}(\varpi t)]\text{e}^{-\tfrac{\eta\omega^2}{2\varpi}t}\tag*{(21)}\end{align*}
其中
\begin{equation*}\left.\begin{split}&C_1=x(t_0) &C_2=\dfrac{\dot{x}(t_0)+x(t_0)\dfrac{\eta\omega^2}{2\varpi}}{\varpi}\\&\varpi=\sqrt{\dfrac{\omega^2+\sqrt{\omega^4-\eta^2\omega^4}}{2}}\end{split}\right\}\tag*{(22)}\end{equation*}
式(22)表明, 频率相关黏性阻尼模型下单自由度体系的自由振动方程通解中不含指数增长项, 其位移响应理论上是稳定收敛的.
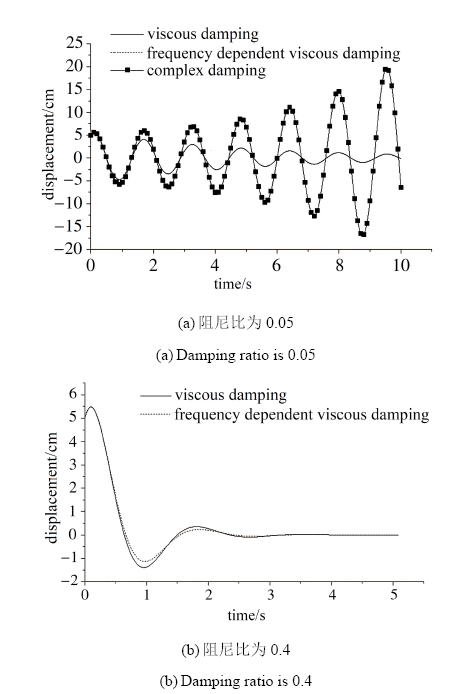
以无阻尼自振频率为4~rad/s的单自由度结构体系为例, 结构的初始位移为5 cm, 初始速度10 cm/s, 分别采用黏性阻尼模型、频率相关黏性阻尼模型、复阻尼模型计算体系的自由振动响应, 得到的位移时程如图1 所示. 如图1(a)所示, 当材料的阻尼比取为0.05, 复阻尼模型计算的结构自由振动位移存在发散现象; 频率相关黏性阻尼模型与黏性阻尼模型计算的结构自由振动收敛稳定, 且位移响应近似相等, 这是由于在小阻尼情况下, 频率相关黏性阻尼模型下结构的有阻尼振动频率近似等于结构的无阻尼自振频率(由式(20)可知). 需说明的是, 由于复阻尼运动方程的通解中直接剔除发散项的做法在数学上是不合理的[12], 故在图1的计算结果中, 复阻尼模型计算时未采用剔除发散项的处理方法(下同).
显示原图|下载原图ZIP|生成PPT图1不同阻尼模型计算的结构自由振动位移时程
-->Fig.1Structural free vibration time history displacements with different damping models
-->
当结构的阻尼比较大时, 频率相关黏性阻尼模型下结构的有阻尼振动频率小于结构的无阻尼自振频率(由式(20)可知), 使得频率相关黏性阻尼模型下阻尼力大于黏性阻尼模型下阻尼力. 因此, 如图1(b)所示, 当材料的阻尼比取0.4时, 频率相关黏性阻尼模型下结构的自由振动位移小于黏性阻尼模型下结构的自由振动位移.
1.2 能量耗散分析
设单自由度结构体系在激励频率为$\theta $的谐波作用下, 结构的稳态位移响应为\begin{align*}x(t)=X_1\text{sin}(\theta t)+X_2\text{cos}(\theta t)\tag*{(23)}\end{align*}
简谐载荷作用下结构的稳态响应如式(23)所示, 结构的振动频率$\varpi$为$\theta$, 则阻尼力为
\begin{align*}F_{P}=-\eta k\left\lbrack X_1\text{cos}(\theta t)-X_2\text{sin}(\theta t)\right\rbrack\tag*{(24)}\end{align*}
在频率相关黏性阻尼模型中, 阻尼力与位移的关系与复阻尼模型相同. 阻尼力在一个周期内消耗的能量为
\begin{align*}\Delta W_{P}=-\int^{\tfrac{2\pi}{\theta}}_{0}F_{p}\text{d}x(t)=\textrm{π}\eta k(X^{~2}_1+X^{~2}_2)\tag*{(25)}\end{align*}
由式(25)可知, 每周期阻尼力耗散的能量与外激励频率无关.
综上, 频率相关黏性阻尼模型在保留了每周期耗散能量与外激励频率无关的优点基础上, 保证了结构自由振动位移时程稳定收敛.
2 基于频率相关黏性阻尼模型的单自由度体系振动响应
2.1 谐波作用下单自由度体系的振动响应
谐波作用下结构的时域运动方程为\begin{align*}\ddot{x}(t)+\omega^2x(t)+\dfrac{\eta\omega^2}{\varpi}\dot{x}(t)=\dfrac{p_0}{m}\text{sin}(\theta t)\tag*{(26)}\end{align*}
其中, $\omega$为结构的自振频率, 即$\omega=\sqrt{k/m}$.
方程(26)的补解与结构自由振动时的解形式相同. 由于线弹性系统具有频率保持不变特性, 其特解的频率与激励频率相同, 假定特解形式为
\begin{align*}x_p(t)=G_1\text{cos}(\theta t)+G_2\text{sin}(\theta t)\tag*{(27)}\end{align*}
此时, $\varpi=\theta$, 将式(27)代入方程(26)可得
\begin{equation*}\left.\begin{split}&G_1=\dfrac{-p_0\eta\omega^2/m}{(\omega^2-\theta^2)^2+(\eta\omega^2)^2}\\&G_2=\dfrac{p_0(\omega^2-\theta^2)/m}{(\omega^2-\theta^2)^2+(\eta\omega^2)^2}\end{split}\right\}\tag*{(28)}\end{equation*}
则方程(23)的解为
\begin{align*}x(t)=&[D_1\text{cos}(\varpi t)+D_2\text{sin}(\varpi t)]\text{e}^{-\tfrac{\eta w^2}{2\varpi}t}+\\&G_1\text{cos}(\theta t)G_2\text{sin}(\theta t)\tag*{(29)}\end{align*}
其中
\begin{equation*}\left.\begin{split}&D_1=x(t_0)-G_1\\&D_2=\dfrac{\dot{x}(t_0)+\eta\omega^2[x(t_0)-G_1]/2\varpi-\theta G_2}{\varpi}\\&\varpi=\sqrt{\dfrac{\omega^2+\sqrt{\omega^4-\eta^2\omega^4}}{2}}\end{split}\right\}\tag*{(30)}\end{equation*}
由式(28)可知, 频率相关黏性阻尼模型的动力放大系数
\begin{align*}D_p=\dfrac{1}{\sqrt{\left(1-\dfrac{\theta^2}{\omega^2}\right)^2+\eta^2}}\tag*{(31)}\end{align*}
黏性阻尼模型的动力放大系数
\begin{align*}D_n=\dfrac{1}{\sqrt{\left(1-\dfrac{\theta^2}{\omega^2}\right)^2+\left(\eta\dfrac{\theta}{\omega}\right)^2}}\tag*{(32)}\end{align*}
由式(31)和式(32)可知, 只有当外激励频率和结构无阻尼自振频率相等时, 两种阻尼理论下结构的稳态响应相同.
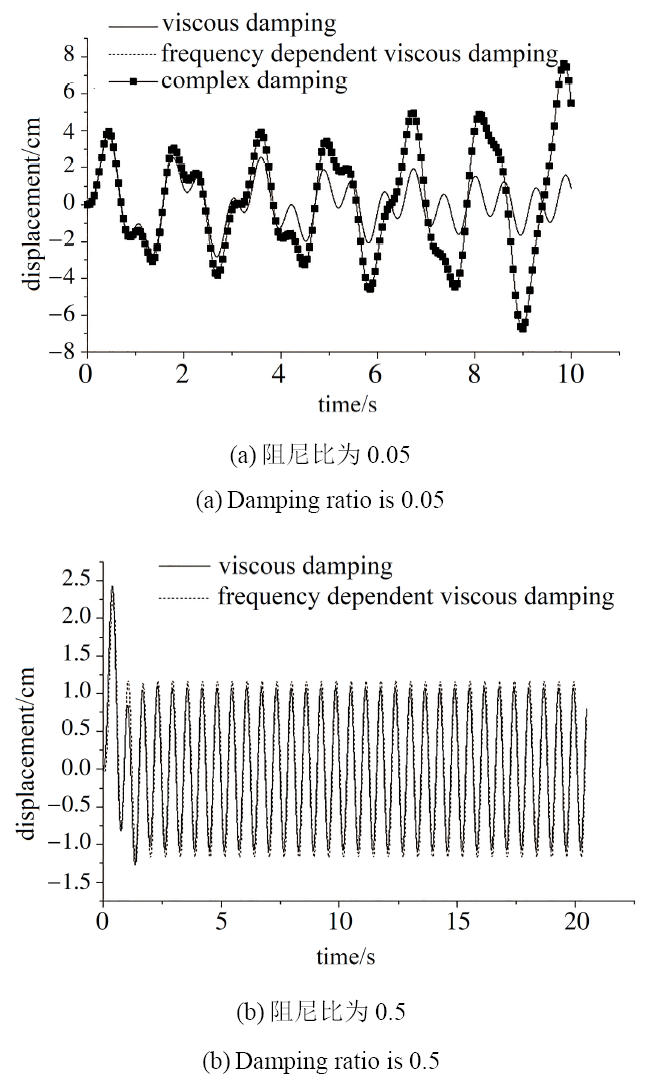
以无阻尼自振频率为4~rad/s的单自由度结构为例, 结构的初始位移为0, 初始速度0, 选择频率为10~rad/s的正弦波作用在结构上, 仍然分别采用黏性阻尼模型、频率相关黏性阻尼模型、复阻尼模型计算体系的强迫振动响应(见图2). 小阻尼情况下, 式(31)和式(32)近似相等. 当材料的阻尼比取0.05时, 结构的位移时程如图2(a)所示, 频率相关黏性阻尼模型与黏性阻尼模型计算的结构位移近似相等, 且明显收敛稳定, 而复阻尼模型计算的结构位移存在发散现象. 当材料的阻尼比选为0.5 时, 结构的位移时程如图2(b)所示, 外激励频率大于结构无阻尼自振频率, 使得频率相关黏性阻尼模型下结构动力放大系数较大, 因此频率相关黏性阻尼模型下结构稳态位移大于黏性阻尼模型下结构的稳态位移.
显示原图|下载原图ZIP|生成PPT图2不同阻尼理论计算的谐波作用下结构位移时程
-->Fig.2Structural time history displacements under the function of harmonic with different damping models
-->
2.2 地震作用下单自由度体系的振动响应
地震作用下单自由度体系的时域运动方程为\begin{align*}\ddot{x}(t)+\omega^2x(t)+\dfrac{\eta\omega^2}{\varpi}\dot{x}(t)=-g(t)\tag*{(32)}\end{align*}
采用时域逐步积分法求解地震作用下的结构动力响应, 具有计算量小、快速直观等优点, 但逐步积分法依赖于积分的时间步长, 时间步长不仅影响计算精度, 还可能影响算法的稳定性. 为保证地震作用下结构的时域计算结果不受算法稳定性的影响, 本文采用基于三角级数的近似解析算法, 其误差仅来源于三角级数计算得到的地震波数据与实际地震波数据之间的误差, 计算精度较高, 不受时间步长的影响, 是无条件稳定的.
目前, 地震加速度时程采用三角多项式逼近已经是一种常用的数值方法, 借助于快速傅里叶变换方法, 可快速确定三角多项式中的参数, 计算量较小, 且利用三角多项式计算得到的地震加速度值与实际记录的地震加速度值近似相等. 地震作用加速度可采用三角多项式展开[37-39]
\begin{equation*}g(t)=A_0+\sum^{N/2}_{i=1}A_i{\rm sin}(\theta_it)+\sum^{N/2}_{i=1}B_i{\rm cos}(\theta_it)\tag*{(34)}\end{equation*}
其中, $A_0$为常数, $A_i$和$B_i$为三角插值公式系数, $\theta_i$为谐波频率.
地震作用下的时域运动方程可表示为
\begin{equation*}\begin{split}\ddot{x}(t)+&\omega^2x(t)+\dfrac{\eta\omega^2}{\varpi}\dot{x}(t)=-\Bigg[A_0+\\&\sum^{N/2}_{i=1}A_i{\rm sin}(\theta_it)+\sum^{N/2}_{i=1}B_i{\rm cos}\left(\theta_it\right)\Bigg]\end{split}\tag*{(35)}\end{equation*}
由叠加原理得
\begin{align*}&\ddot{x}(t)+\omega^2x(t)+\dfrac{\eta\omega^2}{\varpi}\dot{x}(t)=-\Bigg[\sum^{N/2}_{i=1}A_i{\rm sin}(\theta_it)+\\&\qquad \sum^{N/2}_{i=1}B_i{\rm cos}(\theta_it)\Bigg]\tag*{(36)}\\&\omega^2x(t)=-A_0\tag*{(37)}\end{align*}
方程(36)的特解为
\begin{equation*}x_p(t)=\sum^{N/2}_{i=1}J_i{\rm sin}(\theta_it)+\sum^{N/2}_{i=1}K_i{\rm cos}(\theta_it)\tag*{(38)}\end{equation*}
将式(38)代入方程(36)可得
\begin{equation*}\left.\begin{split}&J_i=\dfrac{-(\omega^2-\theta^2_i)A_i-\eta\omega^2B_i}{(\omega^2-\theta^2_i)^2+\eta^2\omega^4}\\&\quad\qquad\qquad\quad\qquad\qquad\quad(i=1,2,\cdots,N/2)\\&K_i=\dfrac{\eta\omega^2A_i-(\omega^2-\theta^2_i)B_i}{(\omega^2-\theta^2_i)^2+\eta^2\omega^4}\end{split}\tag*{(39)}\right\}\end{equation*}
方程(36)的补解与自由振动解形式相同, 则其解为
\begin{equation*}\begin{split}x(t)&=[E_1{\rm cos}(\varpi t)+E_2{\rm sin}(\varpi t)]{\rm e}^{-\frac{\eta\omega^2}{2\varpi}t}+\\&\sum^{N/2}_{i=1}J_i{\rm sin}(\theta_it)+\sum^{N/2}_{i=1}K_i{\rm cos}(\theta_it)\end{split}\tag*{(40)}\end{equation*}
方程(37)的解为
\begin{equation*}x(t)=-\dfrac{A_0}{\omega^2}\tag*{(41)}\end{equation*}
方程(35)的解为
\begin{equation*}\begin{split}x(t)&=-\dfrac{A_0}{\omega^2}+[E_1{\rm cos}(\varpi t)+E_2{\rm sin}(\varpi t)]{\rm e}^{-\frac{\eta\omega^2}{2\varpi}t}+\\&\sum^{N/2}_{i=1}J_i{\rm sin}(\theta_it)+\sum^{N/2}_{i=1}K_i{\rm cos}(\theta_it)\end{split}\tag*{(42)}\end{equation*}
其中
\begin{equation*}\left.\begin{split}&E_1=x(t_0)+\dfrac{A_0}{\omega^2}- \sum^{N/2}_{i=1}K_i\\&E_2=\dfrac{\dot{x}(t_0)+\dfrac{\eta\omega^2}{2\varpi}\Bigg[x(t_0)+\dfrac{A_0}{\omega^2}- \sum\limits^{N/2}_{i=1}K_i\Bigg]- \sum\limits^{N/2}_{i=1}\theta_iJ_i}{\varpi}\\&\varpi=\sqrt{\dfrac{\omega^2+\sqrt{\omega^4-\eta^2\omega^4}}{2}}\end{split}\tag*{(43)}\right\}\end{equation*}
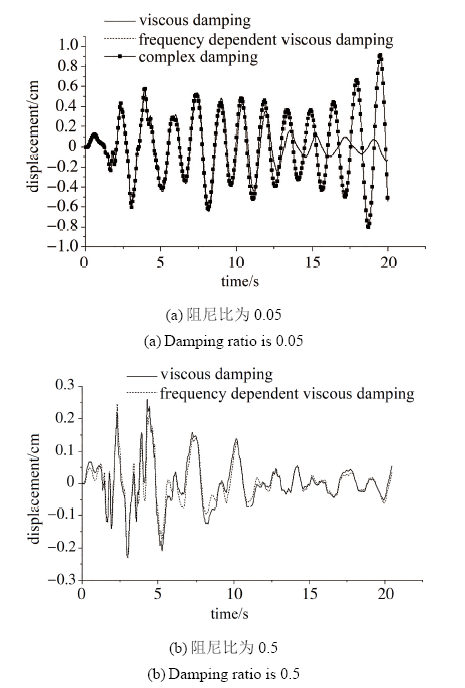
以无阻尼自振频率为4~rad/s的单自由度结构为例, 结构的初始位移为0, 初始速度0, 分别采用黏性阻尼模型、频率相关黏性阻尼模型、复阻尼模型计算体系的地震响应(见图3). 当材料的阻尼比选为0.05时, 迁安波作用下结构的位移时程如图3(a)所示, 频率相关黏性阻尼模型与黏性阻尼模型计算的结构位移近似相等, 且明显收敛稳定, 而复阻尼模型计算的结构位移存在发散现象. 当材料的阻尼比选为0.5时, 迁安波作用下结构的位移时程如图3(b)所示, 由于阻尼比较大, 频率相关黏性阻尼模型与黏性阻尼模型计算的结构位移时程局部存在较大差异, 且不可忽略.
显示原图|下载原图ZIP|生成PPT图3不同阻尼理论计算的迁安波作用下结构位移时程
-->Fig.3Structural time history displacements under the function of Qian'an wave with different damping models
-->
3 基于频率相关黏性阻尼模型的复模态叠加法
不同材料的阻尼比一般不同, 故由不同阻尼特性的材料组成的混合结构, 其阻尼矩阵为非比例矩阵, 不再满足经典阻尼条件. 因此, 混合结构的动力计算无法直接采用实模态叠加法. 本文依据频率相关黏性阻尼模型与复阻尼模型之间的转换关系, 提出了基于频率相关黏性阻尼的复模态叠加法, 可直接用于混合结构.地震作用下多自由度混合结构体系的时域运动方程为
\begin{equation*} {M} {\ddot{x}}(t)+ {Kx}(t)+ {K}_\eta {\dot{x}}(t)=- {ME}[g(t)+\text{i}g'(t)]\tag*{(44)}\end{equation*}
其中, $ {M}$为质量矩阵, $ {K}$为刚度矩阵, $ {E}$为与地震动输入有关的向量($N\times1$), 与$g(t)$方向相同的位移自由度元素为1.
$ {K}_\eta$为阻尼矩阵, 可表示为
\begin{equation*} {K}_\eta=\dfrac{1}{\varpi}\sum^s_{j=1}\eta_j {K}_j\tag*{(45)}\end{equation*}
其中, $s$为混合结构中不同阻尼特性材料的种类总数, $\eta_j$为第$j$种材料对应的损耗因子, $ {K}_j$为第$j$种材料对应的刚度矩阵.
对方程(44)进行傅里叶变换, 可得
\begin{equation*}\begin{split}-\varpi^2& {M\varOmega}({\rm i}\varpi)+ {K\varOmega}({\rm i}\varpi)+{\rm i}\varpi {K}_\eta\varOmega({\rm i}\varpi)=\\&- {ME}[\varGamma({\rm i}\varpi)+{\rm i}\varGamma({\rm i}\varpi)]\end{split}\tag*{(46)}\end{equation*}
对方程(45)进行傅里叶逆变换, 可得
\begin{equation*} {K\dot{x}}(t)+ {Kx}(t)+i\sum^s_{j=1}\eta_j {K}_j {x}(t)=- {ME}[g(t)+\text{i}g'(t)]\tag*{(47)}\end{equation*}
求解方程(47)的特征方程可得$N$个复特征向量, 按排列组成复特征向量矩阵
\begin{equation*} {\varPhi}=[ {\phi}_1\quad {\phi}_2\quad\cdots\quad {\phi}_N]\tag*{(48)}\end{equation*}
任意两个复特征向量满足
\begin{equation*}\dfrac{ {\phi}^{\rm T}_m {M} {\phi}_n}{ {\phi}^{\rm T}_n {M} {\phi}_n}=\begin{cases}0, \,&m\neq n\\m_n, \,& m=n\end{cases}\tag*{(49)}\end{equation*}
\begin{align*}&\dfrac{ {\phi}^{\rm T}_m(K+{\rm i}\sum\limits_e {\eta}_eK_e) {\phi}_n}{ {\phi}^{\rm T}_n {M} {\phi}_n}=\begin{cases}0, \qquad \ \,\, m\neq n\\k_n+{\rm i}c_n,m=n\end{cases}\tag*{(50)}\\&\dfrac{- {\phi}^{\rm T}_n {M} E}{ {\phi}^{\rm T}_n {M} \phi_n}[g(t)+{\rm i}g'(t)]=g_n\tag*{(51)}\end{align*}
其中, $m_n$, $k_n$和$c_n$为实数, $g_n$为复数.
$ x(t)$可由复特征向量线性组合表示, 即
\begin{equation*} {x}(t)=\sum^N_{n=1} {\phi}_ny_n(t)\tag*{(52)}\end{equation*}
将式(52)代入方程(47), 利用复特征向量的正交性可实现复运动方程的解耦, 故第$n$个运动方程为
\begin{equation*}m_n\ddot{y}(t)+k_ny(t)+{\rm i}c_ny(t)=g_n\tag*{(53)}\end{equation*}
利用前文所时频域转换, 方程(53)可转换为
\begin{equation*}m_n\ddot{y}(t)+k_ny(t)+\dfrac{c_n}{\varpi_n}\dot{y}(t)=g_n\tag*{(54)}\end{equation*}
令
\begin{equation*}\left.\begin{split}&y(t)=y_1(t)+{\rm i}y_2(t)\\&g_n=g_{n1}+{\rm i}g_{n2}\end{split}\tag*{(55)}\right\}\end{equation*}
方程(54)可转化为
\begin{equation*}m_n\ddot{y}_1(t)+k_ny_1(t)+\dfrac{c_n}{\varpi_n}\dot{y}_1(t)=g_{n1}\tag*{(56)}\end{equation*}
\begin{equation*}m_n\ddot{y}_2(t)+k_ny_2(t)+\dfrac{c_n}{\varpi_n}\dot{y}_2(t)=g_{n2}\tag*{(57)}\end{equation*}
对应的齐次方程为
\begin{equation*}m_n\ddot{y}_1(t)+k_ny_1(t)+\dfrac{c_n}{\varpi_n}\dot{y}_1(t)=0\tag*{(58)}\end{equation*}\begin{equation*}m_n\ddot{y}_2(t)+k_ny_2(t)+\dfrac{c_n}{\varpi_n}\dot{y}_2(t)=0\tag*{(59)}\end{equation*}
方程(58)和(59)对应的特征方程为
\begin{equation*}m_n\lambda^2_n+k_n+\dfrac{c_n}{\varpi_n}\lambda_n=0\tag*{(60)}\end{equation*}
求解方程(60), 可得
\begin{equation*}\left.\begin{split}\lambda_{n1}=-\dfrac{c_n}{2m_n\varpi_n}+{\rm i}\sqrt{\dfrac{k_n}{m_n}-\dfrac{c_n^{~2}}{4m_n^{~2}\varpi_n^{~2}}}\\\lambda_{n2}=-\dfrac{c_n}{2m_n\varpi_n}-{\rm i}\sqrt{\dfrac{k_n}{m_n}-\dfrac{c_n^{~2}}{4m_n^{~2}\varpi_n^{~2}}}\end{split}\tag*{(61)}\right\}\end{equation*}
进而得到特征根的虚部与对应的频率相等, 即
\begin{equation*}\varpi_n=\sqrt{\dfrac{k_n}{m_n}-\dfrac{c^{~2}_n}{4m_n^{~2}\varpi_n^{~2}}}\tag*{(62)}\end{equation*}
进一步求解方程(62), 得
\begin{equation*}\varpi_n=\sqrt{\dfrac{k_n+\sqrt{k^{~2}_n-c^{~2}_n}}{2m_n}}\tag*{(63)}\end{equation*}
可得方程(58)和(59)的补解为
\begin{equation*}\begin{split}y_{1c}(t)&=\Bigg[F_1{\rm cos}\left(\sqrt{\dfrac{k_n+\sqrt{k^{~2}_n-c^{~2}_n}}{2m_n}}t\right)+\\&L_1{\rm sin}\left(\sqrt{\dfrac{k_n+\sqrt{k^{~2}_n-c^{~2}_n}}{2m_n}}t\right)\Bigg]\cdot\\&{\rm exp}\left(-\dfrac{c_n}{2m_n}\sqrt{\dfrac{2m_n}{k_n+\sqrt{k^{~2}_n-c^{~2}_n}}}\right)\end{split}\tag*{(64)}\end{equation*}
\begin{equation*}\begin{split}y_{2c}(t)&=\Bigg[F_2{\rm cos}\left(\sqrt{\dfrac{k_n+\sqrt{k^{~2}_n-c^{~2}_n}}{2m_n}}t\right)+\\&L_2{\rm sin}\left(\sqrt{\dfrac{k_n+\sqrt{k^{~2}_n-c^{~2}_n}}{2m_n}}t\right)\Bigg]\cdot\\&{\rm exp}\left(-\dfrac{c_n}{2m_n}\sqrt{\dfrac{2m_n}{k_n+\sqrt{k^{~2}_n-c^{~2}_n}}}t\right)\end{split}\tag*{(65)}\end{equation*}
地震加速度可采用三角多项式进行表示, 进而得到
\begin{equation*}g_{n1}=P_{10}+\sum^{N/2}_{i=1}P_{1i}{\rm sin}(\gamma_it)+\sum^{N/2}_{i=1}Q_{1i}{\rm cos}(\gamma_it)\tag*{(66)}\end{equation*}\begin{equation*}g_{n2}=P_{20}+\sum^{N/2}_{i=1}P_{2i}{\rm sin}(\kappa_it)+\sum^{N/2}_{i=1}Q_{2i}{\rm cos}(\kappa_it)\tag*{(67)}\end{equation*}
将式(66)代入方程(56), 式(67)代入方程(57), 可得
\begin{equation*}\begin{split}m_n\ddot{y}_1(t)&+k_ny_1(t)+\dfrac{c_n}{\varpi}\dot{y}_1(t)=P_{10}+\\&\sum^{N/2}_{i=1}P_{1i}{\rm sin}(\gamma_it)+\sum^{N/2}_{i=1}Q_{1i}{\rm cos}(\gamma_it)\end{split}\tag*{(68)}\end{equation*}
\begin{equation*}\begin{split}m_n\ddot{y}_2(t)&+k_ny_2(t)+\dfrac{c_n}{\varpi}\dot{y}_2(t)=P_{20}+\\&\sum^{N/2}_{i=1}P_{2i}{\rm sin}(\kappa_it)+\sum^{N/2}_{i=1}Q_{2i}{\rm cos}(\kappa_it)\end{split}\tag*{(69)}\end{equation*}
方程(68)可进一步转化为
\begin{align*}&m_n\ddot{y}_1(t)+k_ny_1(t)+\dfrac{c_n}{\gamma_i}\dot{y}_1(t)=\sum^{N/2}_{i=1}P_{1i}{\rm sin}(\gamma_it)+\\&\qquad \qquad \sum^{N/2}_{i=1}Q_{1i}{\rm cos}(\gamma_it)\tag*{(70)}\\&k_ny_1(t)=P_{10}\tag*{(71)}\end{align*}
令方程(70)的特解为
\begin{equation*}y_{1p}(t)=\sum^{N/2}_{i=1}R_{1i}{\rm sin}(\gamma_it)+\sum^{N/2}_{i=1}S_{1i}{\rm cos}(\gamma_it)\tag*{(72)}\end{equation*}
将式(72)代入方程(70)可得
\begin{equation*}\left.\begin{split}&R_{1i}=\dfrac{(-m_n\gamma^2_i+k_n)P_{1i}+c_nQ_{1i}}{(-m_n\gamma^2_i+k_n)^2+c^2_n}\\&\qquad\qquad\qquad\qquad\qquad\qquad(i=1,2,\cdots,N/2)\\&S_{1i}=\dfrac{-c_nP_{1i}+(-m_n\gamma^2_i+k_n)Q_{1i}}{(-m_n\gamma^2_i+k_n)^2+c^2_n}\end{split}\tag*{(73)}\right\}\end{equation*}
方程(71)的解为
\begin{equation*}y_1(t)=\dfrac{P_{10}}{k_n}\tag*{(74)}\end{equation*}
方程(68)的特解为
\begin{equation*}y_{1p}(t)=\dfrac{P_{10}}{k_n}+\sum^{N/2}_{i=1}R_{1i}{\rm sin}(\gamma_it)+\sum^{N/2}_{i=1}S_{1i}{\rm cos}(\gamma_it)\tag*{(75)}\end{equation*}
进而得到方程(56)的解为
\begin{equation*}\begin{split}y_1(t)=&\dfrac{P_{10}}{k_n}+[F_1{\rm cos}(\varpi_nt)+L_1{\rm sin}(\varpi_nt)]\cdot\\&{\rm exp}\Bigg(-\dfrac{c_n}{2m_n\varpi_n}t\Bigg)+\sum^{N/2}_{i=1}R_{1i}{\rm sin}(\gamma_it)+\\&\sum^{N/2}_{i=1}S_{1i}{\rm cos}(\gamma_it)\end{split}\tag*{(76)}\end{equation*}
其中
\begin{equation*}\left.\begin{split}&F_1=y_1(t_0)-\dfrac{P_{10}}{k_n}-\sum^{N/2}_{i=1}S_{1i}\\&L_1=\Bigg[\dot{y}_1(t_0)+\dfrac{c_n}{2m_n\varpi_n}\Bigg(y_1(t_0)-\dfrac{P_{10}}{k_n}-\\&\quad\quad\sum^{N/2}_{i=1}S_{1i}\Bigg)-\sum^{N/2}_{i=1}\gamma_iR_{1i}\Bigg]\Bigg/\varpi_n\\&\varpi_n=\sqrt{\dfrac{k_n+\sqrt{k^{~2}_n-c^{~2}_n}}{2m_n}}\end{split}\tag*{(77)}\right\}\end{equation*}
同理得到方程(57)的解为
\begin{equation*}\begin{split}y_2(t)=&\dfrac{P_{20}}{k_n}+[F_2{\rm cos}(\varpi_nt)+L_2{\rm sin}(\varpi_nt)]\cdot\\&\ {\rm exp}\Bigg(-\dfrac{c_n}{2m_n\varpi_n}t\Bigg)+\sum^{N/2}_{i=1}R_{2i}{\rm sin}(\kappa_it)+\\&\sum^{N/2}_{i=1}S_{2i}{\rm cos}(\kappa_it)\end{split}\tag*{(78)}\end{equation*}
其中
\begin{equation*}\left.\begin{split}&F_2=y_2(t_0)-\dfrac{P_{20}}{k_n}-\sum^{N/2}_{i=1}S_{2i}\\&L_2=\Bigg[\dot{y}_2(t_0)+\dfrac{c_n}{2m_n\varpi_n}\Bigg(y_2(t_0)-\dfrac{P_{20}}{k_n}-\sum^{N/2}_{i=1}S_{2i}\Bigg)-\\&\qquad \sum^{N/2}_{i=1}\gamma_iR_{2i}\Bigg]\Bigg/\varpi_n\\&R_{2i}=\dfrac{(-m_n\kappa^2_i+k_n)P_{2i}+c_nQ_{2i}}{(-m_n\kappa^2_i+k_n)^2+c^2_n}\\&S_{2i}=\dfrac{-c_nP_{2i}+(-m_n\kappa^2_i+k_n)Q_{2i}}{(-m_n\kappa^2_i+k_n)^2+c^2_n}\\&\varpi_n=\sqrt{\dfrac{k_n+\sqrt{k^{~2}_n-c^{~2}_n}}{2m_n}}\\&\quad(i=1,2,\cdots,N/2)\end{split}\tag*{(79)}\right\}\end{equation*}
利用式(55)计算出$y(t)$, 进一步由式(52)得到$x(t)$, 从而实现了基于频率相关黏性阻尼模型的混合结构复模态叠加法.
由式(48)可知, 当结构为单一材料结构时, 阻尼矩阵为比例矩阵, 复振型向量的虚部为零, 复振型向量退化为实振型向量, 基于频率相关黏性阻尼模型的复模态叠加法退化为传统的实模态叠加法, 因此基于频率相关黏性阻尼模型的复模态叠加法不仅适用于混合材料结构, 还适用于单一材料结构.
4 算例分析
以阻尼特性不同的两种材料组成的一维四自由度体系为例, 建立竖向混合结构, 模型A和模型B仅阻尼比不同, 具体参数取值如图4所示.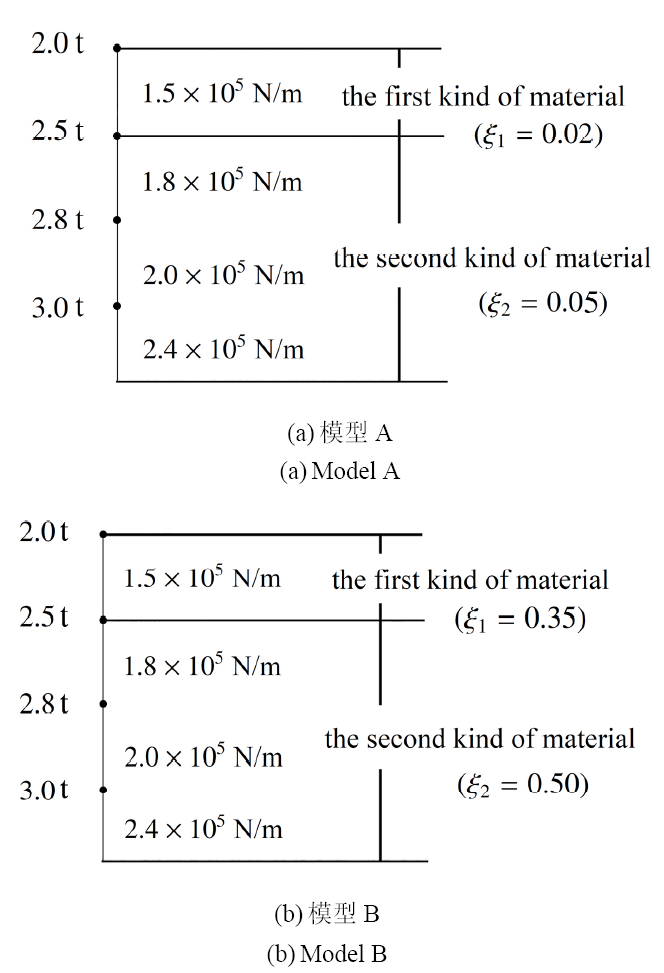
显示原图|下载原图ZIP|生成PPT图4模型参数
-->Fig.4Parameters of models
-->
质量矩阵为
\begin{equation*} {M}=\begin{bmatrix}2.0&0&0&0\\0&2.5&0&0\\0&0&2.8&0\\0&0&0&3.0\end{bmatrix}\text{t}\tag*{(80)}\end{equation*}
刚度矩阵为
\begin{equation*} {K}=\begin{bmatrix}1.5&-1.5&0&0\\-1.5&3.3&-1.8&0\\0&-1.8&3.8&-2.0\\0&0&-2.0&4.4\end{bmatrix}\times10^5\text{~N/m}\tag*{(81)}\end{equation*}
黏性阻尼模型在状态空间法的基础上, 将矩阵的维度增加一倍, 然后采用复模态叠加法计算混合结构的位移时程[24]. 对于简单混合结构, 黏性阻尼模型下可仅考虑第一阶振型的自振频率[40], 则阻尼矩阵为
\begin{align*} {K}_{ {z}}=\dfrac{1}{\omega_1}\sum\limits^s_{j=1}\eta_j {K}_j\tag*{(82)}\end{align*}
其中, $\omega_1$为第一阶振型对应的无阻尼自振频率.
频率相关黏性阻尼模型下模型A的阻尼矩阵为
\begin{equation*} {K}_{a\eta}=\dfrac{1}{\varpi}\begin{bmatrix}0.06&-0.06&0&0\\-0.06&0.24&-0.18&0\\0&-0.18&0.38&-0.20\\0&0&-0.20&0.44\end{bmatrix}\times10^5\text{~N/m}\tag*{(83)}\end{equation*}
由式(82)可计算出在黏性阻尼模型下模型A的阻尼矩阵为
\begin{equation*} {K}_{az}=\begin{bmatrix}0.18&-0.18&0&0\\-0.18&0.74&-0.55&0\\0&-0.55&1.16&-0.61\\0&0&-0.61&1.35\end{bmatrix}\times10^4\text{~N/m}\tag*{(84)}\end{equation*}
频率相关黏性阻尼模型下模型B的阻尼矩阵为
\begin{equation*} {K}_{b\eta}=\dfrac{1}{\varpi}\begin{bmatrix}1.05&-1.05&0&0\\-1.05&2.85&-1.85&0\\0&-1.80&3.80&-2.00\\0&0&-2.00&4.40\end{bmatrix}\times10^5\text{~N/m}\tag*{(85)}\end{equation*}
由式(82)可计算黏性阻尼模型下模型B的阻尼矩阵为
\begin{equation*} {K}_{bz}=\begin{bmatrix}0.32&-0.32&0&0\\-0.32&0.87&-0.55&0\\0&-0.55&1.16&-0.61\\0&0&-0.61&1.35\end{bmatrix}\times10^5\text{~N/m}\tag*{(86)}\end{equation*}
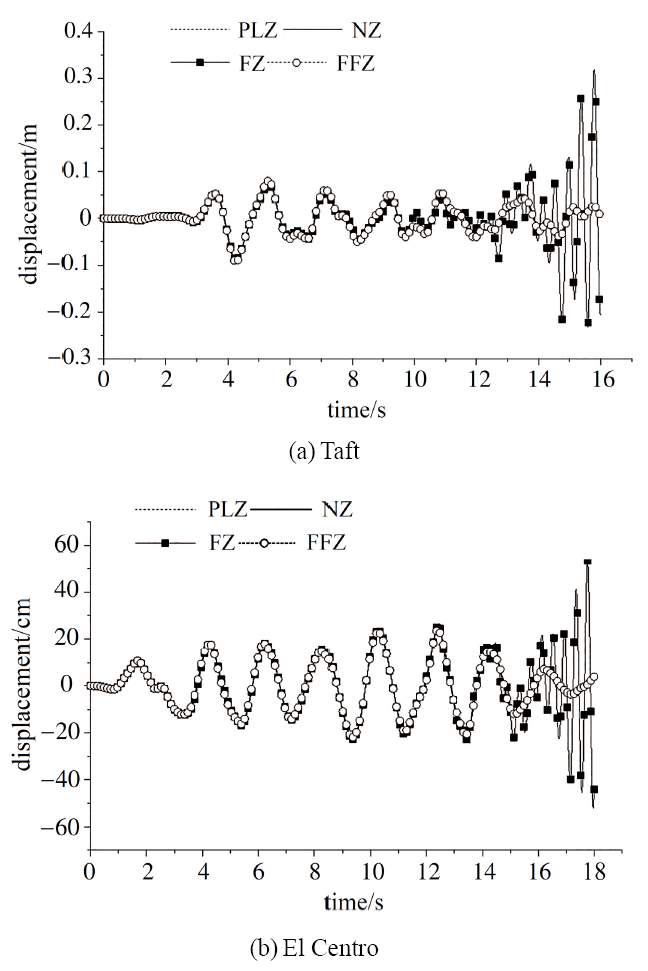
分别采用基于频率相关黏性阻尼模型的复模态叠加法(PLZ)、基于黏性阻尼模型的复模态叠加法(NZ)和基于复阻尼模型的复模态叠加法(FZ)计算模型A、模型B在地震波作用下的位移时程, 所得结果如图5和图6所示, 并将其与基于复阻尼模型的频域法(FFZ)计算结果对比. 其中, FFZ避免了复阻尼模型时域发散现象, 其计算结果可视为精确解[41].
显示原图|下载原图ZIP|生成PPT图5模型A的顶层位移时程
-->Fig.5Top time history displacements of Model A
-->
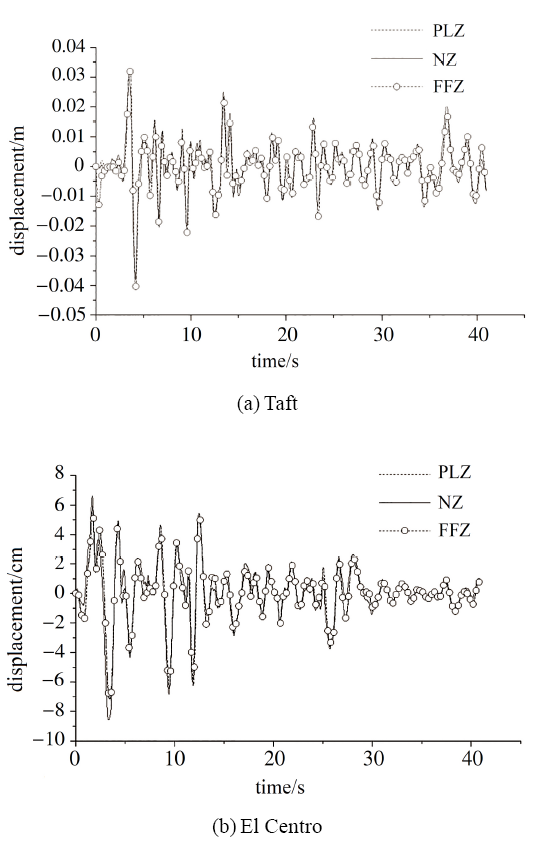显示原图|下载原图ZIP|生成PPT图6模型B的顶层位移时程
-->Fig.6Top time history displacements of Model B
-->
在图5中, 随着地震作用时间增加, FZ计算的位移时程呈现发散现象; PLZ、NZ和FFZ近似相等, 且一直保持稳定收敛的特点. 在图5(a)、图5(b)
中, 当地震持时分别小于11~s和14~s时, PLZ与NZ、FZ、FFZ近似相等, 更进一步证明了PLZ的正确性.
相对于模型A, 模型B的材料阻尼比明显增大. 如图6所示, PLZ与FFZ近似相等, 而NZ与FFZ存在较大差异. 如图6所示, Taft波作用下, PLZ和FFZ的位移均在4.18~s处达到最大值$I$, NZ的位移在4.16~s处达到最大值$I$, PLZ和NZ发生位移最大值的时间近似相等(见图6(a)), 但PLZ与FFZ的最大位移值相对误差$\delta $为0.61%, NZ与FFZ的最大位移值相对误差$\delta $为6.79%(见表1); El Centro波作用下, PLZ和FFZ的位移均在3.42 s处达到最大值$I$, NZ的位移在3.32~s处达到最大值$I$~(见图6b), PLZ 和NZ发生位移最大值的时间近似相等, 但PLZ与FFZ的相对误差$\delta $为0.30%, NZ与FFZ 的最大位移值相对误差$\delta $为20.05%~(见表1).
Table 1
表1
表1模型B的位移响应
Table 1Displacement responses of Model B
| FFZ | Taft PLZ | NZ | FFZ | El Centro PLZ | NZ | |
|---|---|---|---|---|---|---|
| I/cm | 4.080 | 4.105 | 3.803 | 7.086 | 7.107 | 8.507 |
| δ/% | — | 0.61 | 6.79 | — | 0.30 | 20.05 |
新窗口打开
采用基于黏性阻尼模型的复模态叠加法时, 模型A和模型B的复特征向量矩阵维数是8; 采用基于频率相关黏性阻尼模型的复模态叠加法时, 模型A和模型B的复特征向量矩阵维数是4, 维度没有增加. 因此, 相比基于黏性阻尼模型的复模态叠加法, 基于频率相关黏性阻尼模型的复模态叠加法计算量较小.
此外, 本文算例为简单混合结构, 黏性阻尼模型下可选择第一阶振型的自振频率确定阻尼矩阵. 对于实际工程结构, 通常不能仅考虑第一阶振型, 还需要考虑其他高阶振型, 而不同的振型组合, 将得到不同的阻尼矩阵, 因此基于黏性阻尼模型的复模态叠加法计算结果不具有唯一性. 本文提出的基于频率相关黏性阻尼模型阻尼矩阵仅依赖于结构的损耗因子, 复模态叠加法计算结果具有唯一性, 合理性易被判定.
5 结 论
经理论推导和算例分析, 得到以下结论:(1)依据频率相关黏性阻尼模型的特点, 得到了频率相关黏性阻尼运动方程的精确解. 算例分析表明, 基于复阻尼理论的频率相关黏性阻尼模型不仅克服了黏性阻尼中每周期耗散能量与外激励频率相关的缺陷, 还避免了复阻尼模型的发散问题.
(2)利用频率相关黏性阻尼模型与复阻尼模型的转换关系, 提出了基于频率相关黏性阻尼模型的复模态叠加法, 不仅可适用于由阻尼特性不同材料组成的混合结构, 还可适用于单一材料结构.
(3)与基于黏性阻尼模型的复模态叠加法相比, 基于频率相关黏性阻尼模型的复模态叠加法不仅计算结果唯一, 且不增加矩阵维度, 具有较高的计算效率.
(4)在小阻尼情况下, 基于频率相关黏性阻尼模型的复模态叠加法与基于黏性阻尼模型的复模态叠加法计算结果近似相等, 且与基于复阻尼模型的频域法计算结果一致. 随着材料阻尼比增大, 基于频率相关黏性阻尼模型的复模态叠加法与基于黏性阻尼模型的复模态叠加法计算结果的差异逐渐增大, 且不可忽略, 但基于频率相关黏性阻尼模型的复模态叠加法与复阻尼模型的频域计算结果仍保持一致.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . . |
| [2] | . |
| [3] | . . |
| [4] | . . |
| [5] | . |
| [6] | . |
| [7] | . . |
| [8] | . |
| [9] | . . |
| [10] | . |
| [11] | . . |
| [12] | . . |
| [13] | . |
| [14] | |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . . |
| [19] | . . |
| [20] | . . |
| [21] | . . |
| [22] | . |
| [23] | . |
| [24] | . . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . . |
| [29] | . . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | . . |
| [34] | . . |
| [35] | . |
| [36] | . |
| [37] | |
| [38] | |
| [39] | . . |
| [40] | |
| [41] | . . |
